Radar Emitter Signal Intra-Pulse Modulation Open Set Recognition Based on Deep Neural Network
Abstract
:1. Introduction
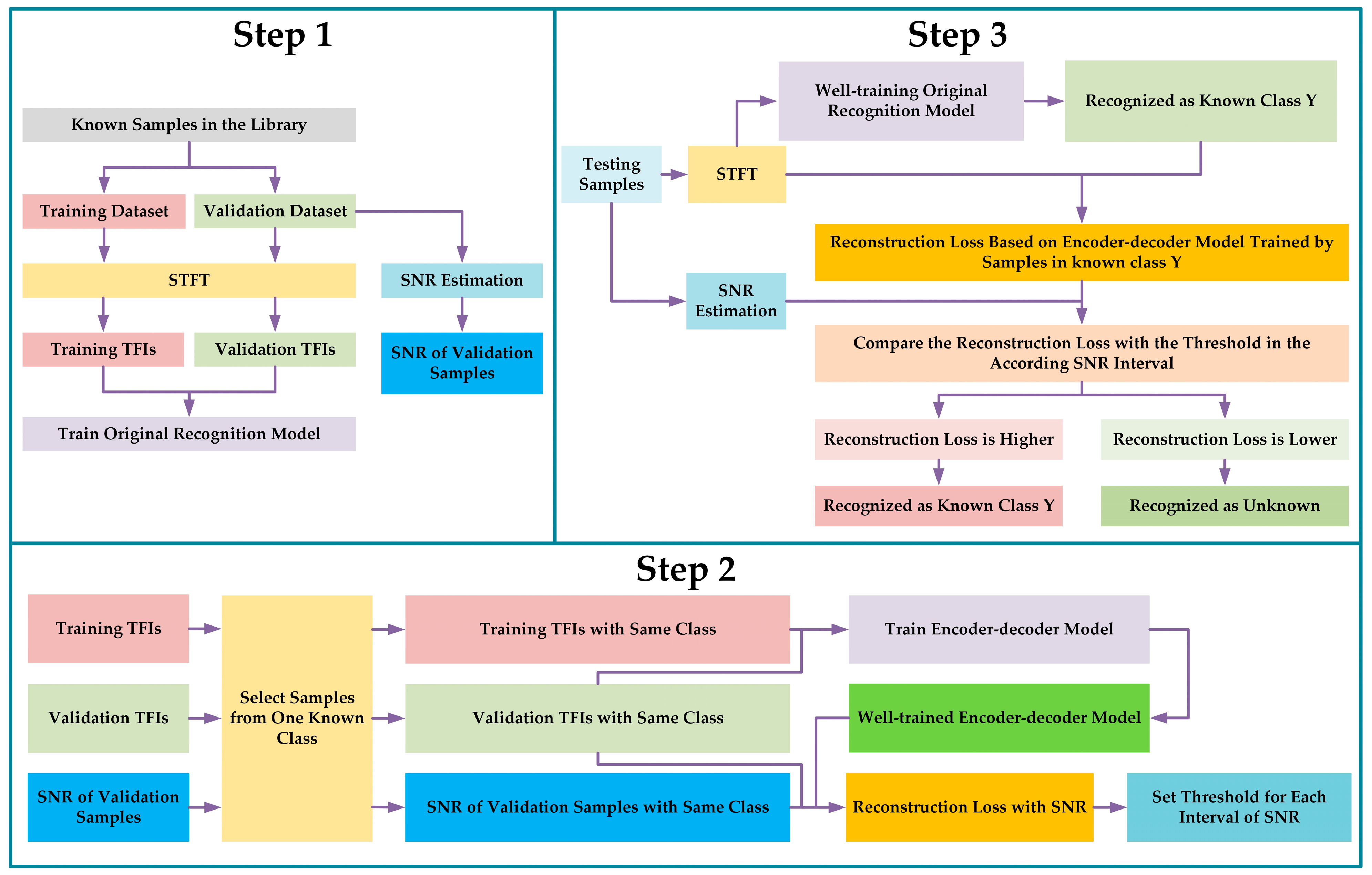
2. Materials and Methods
- (1)
- Split the known samples dataset into a training dataset and validation dataset. Note that both the training dataset and validation dataset do not contain unknown samples.
- (2)
- Estimate the SNR for each sample in the validation dataset.
- (3)
- Convert the training samples and validation samples into TFIs by using STFT.
- (4)
- Train an original recognition model in the CSR way with TFIs.
- (1)
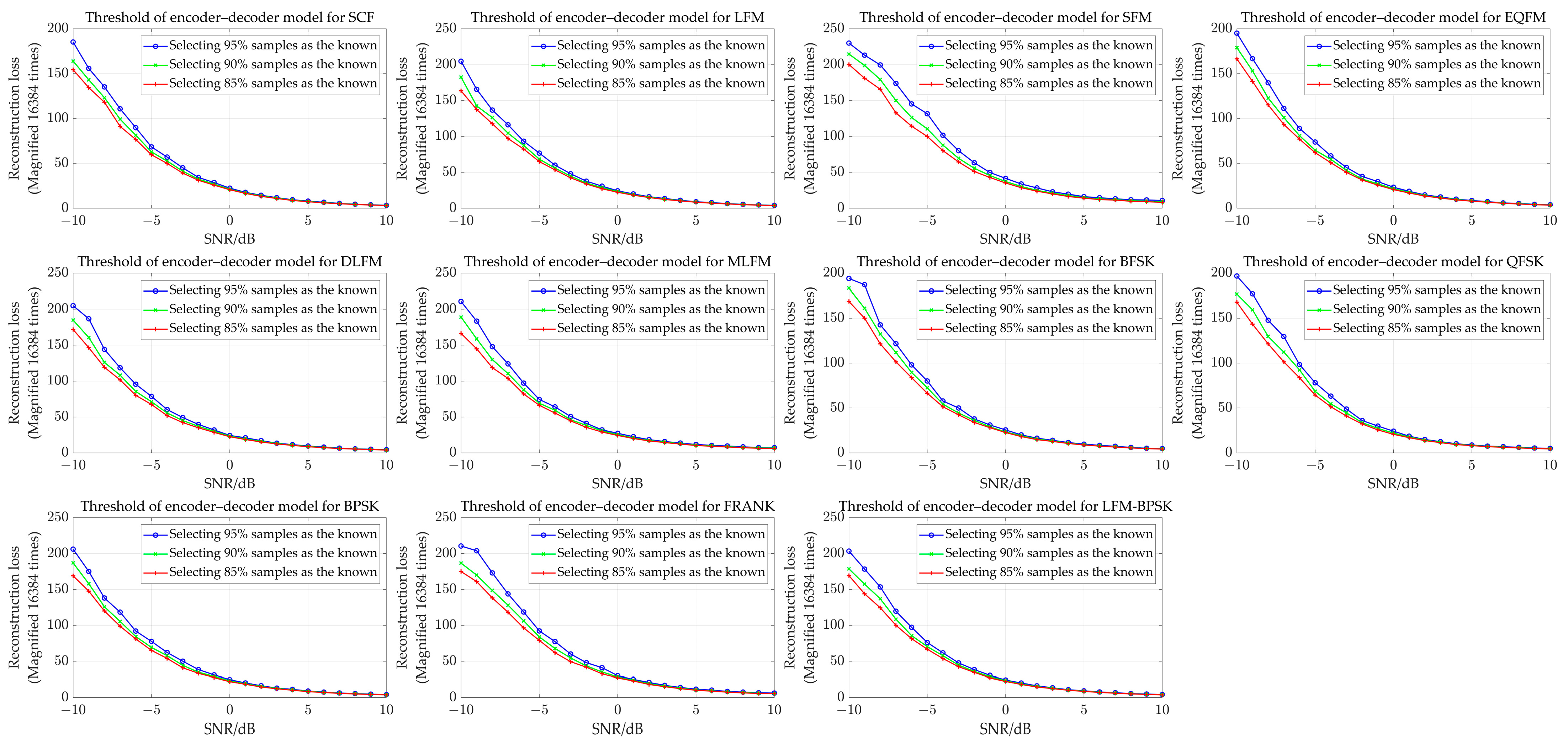
- Select the samples from one known class and only use these TFIs to train the encoder–decoder model. Then, use the corresponding encoder–decoder model to calculate the reconstruction loss of the corresponding validation TFIs. As the SNR of the validation samples has been obtained, by setting the interval of SNR, the corresponding reconstruction loss in each interval of SNR could be counted. In this paper, the reconstruction loss is mean square error (MSE). Note that the number of encoder–decoder models is the same as the number of known classes. For example, if there are 11 known classes, then there will be 11 corresponding encoder–decoder models, where each model is only responsible for reconstructing one class.
- (2)
- Set the threshold for reconstruction loss in each interval of SNR. The details of the threshold setting are introduced as follows: For a known class, we could calculate the reconstruction loss of its validation samples from each SNR interval. Assuming that each SNR interval contains 400 samples, for example, then, we sort these 400 samples’ reconstruction losses from a low value to a high value for each interval. Then we set, for example, the top highest 1%, 2%, …, 25%, etc. reconstruction losses of these 400 samples as the threshold. Similarly, we could get the thresholds for the other known classes based on the above operation. Note that the ratio (1%, 2%, …, 25%, etc.) is the same for each SNR interval in each known class. After obtaining all of the thresholds for each SNR interval of all of the known classes, we could evaluate the recognition accuracy in the validation dataset through the corresponding thresholds controlled by the same ratio (like 5%). For example, if we set the ratio as 5%, that means the corresponding threshold will be related to the top 5% highest reconstruction losses in each SNR interval for each known class in the validation dataset. Based on the ratio, the recognition results will be revised (some samples will be labeled as unknown), leading to different mean recognition accuracies in the known class validation dataset. Therefore, by setting a suitable ratio, it could be ensured that the methods have 80%, 85%, 90%, and 95%, respectively, mean recognition accuracy (also the mean recognition accuracy for known classes) on the corresponding validation dataset. For example, when we set the ratios as 4% and 20%, the mean recognition accuracies on the validation dataset are 95% and 80%, respectively. Based on this threshold setting with 80%, 85%, 90%, and 95% mean recognition accuracy on the validation dataset, we test the methods with the corresponding testing dataset.
- (3)
- Perform (1) and (2) in Step 2 until all of the known classes are covered.
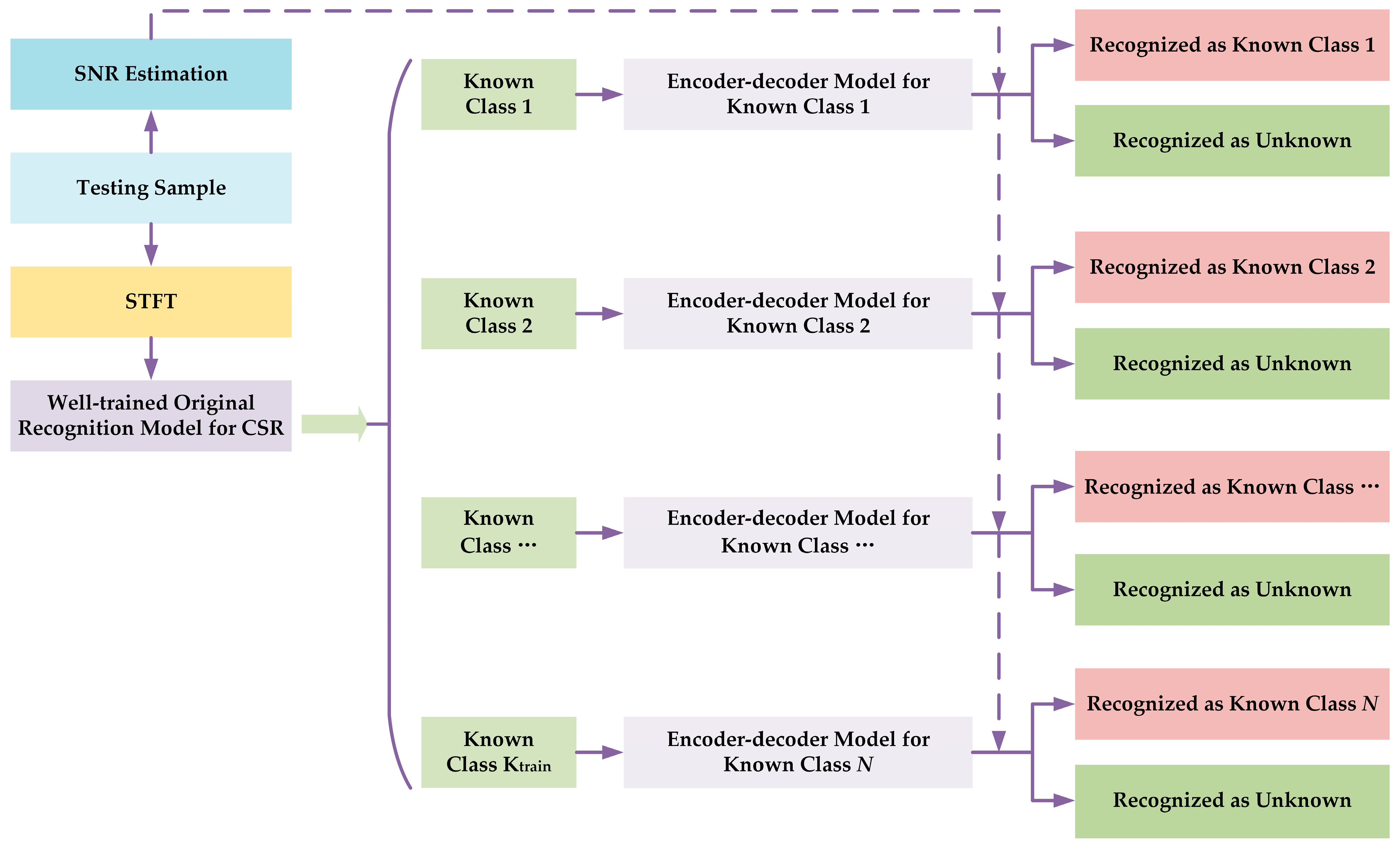
- (1)
- Estimate the SNR for the testing samples and convert the testing samples to TFIs by using STFT. Now the testing samples contain the unknown class.
- (2)
- Use the well-trained recognition model in Step 1 to predict the class of the testing sample.
- (3)
- Based on the prediction result, use the corresponding encoder–decoder model to calculate the reconstruction loss of this testing sample. For example, if a testing sample is recognized as category , then only the encoder–decoder model for category will be used to calculate its reconstruction loss.
- (4)
- Based on the SNR and reconstruction loss of the testing sample and the threshold for reconstruction loss in each interval of the SNR for the used encoder–decoder model, the final recognition result for this sample will be obtained. Note that if the reconstruction loss is higher than the threshold, then the corresponding sample is seen as the unknown class. If it is not, the corresponding sample is seen as the known class, and its label is the predicted result from the original recognition model.
2.1. Data Preprocessing
2.2. SNR Estimation
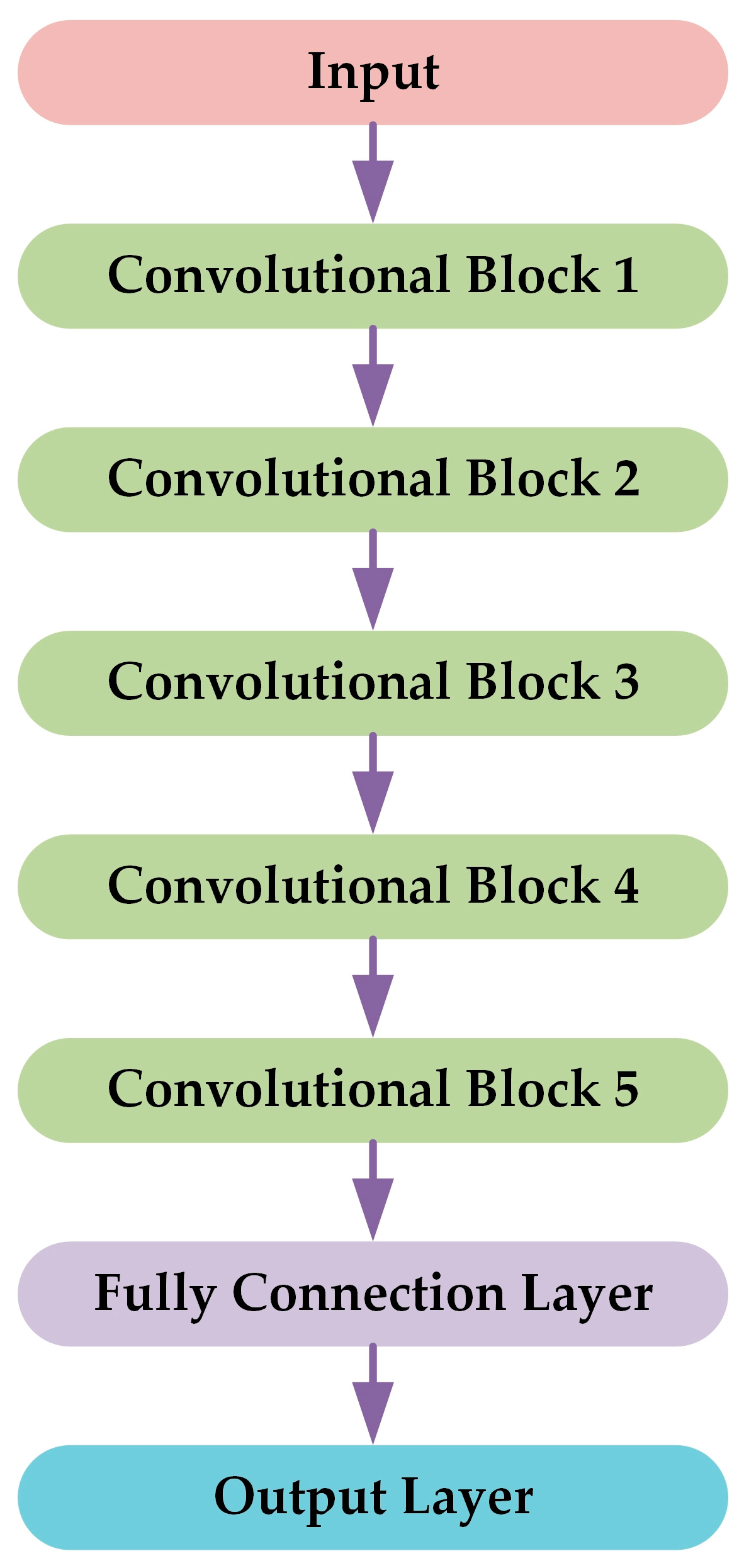
2.3. Original Recognition Model for CSR
2.4. Encoder–Decoder Model
3. Dataset and Experimental Settings
3.1. Intra-Pulse Modulation Radar Emitter Signal Datasets
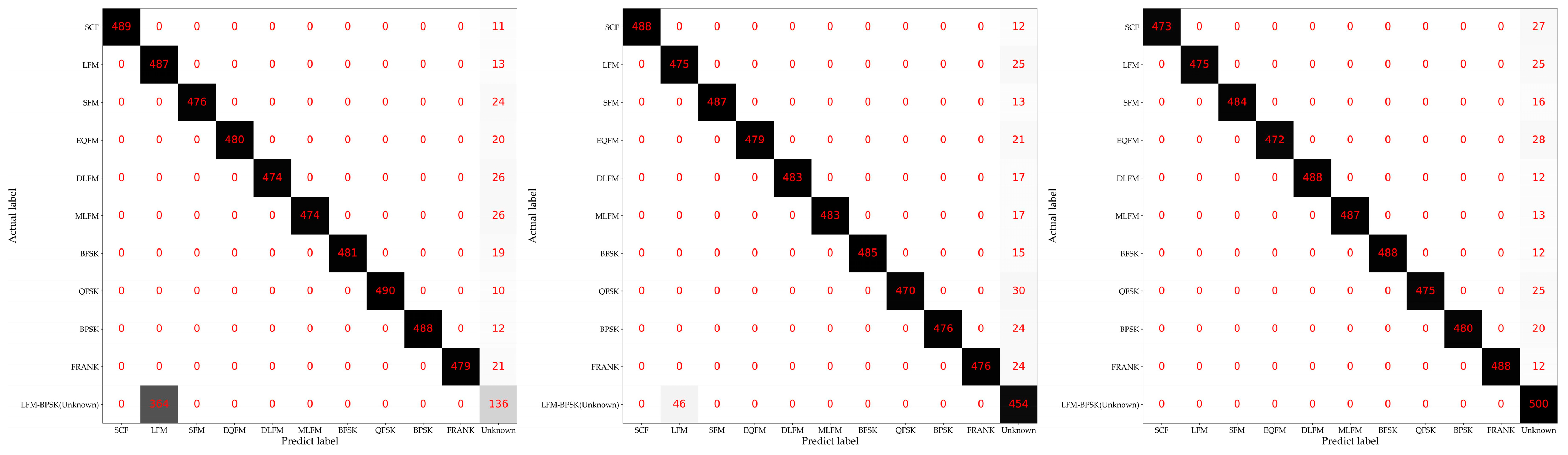
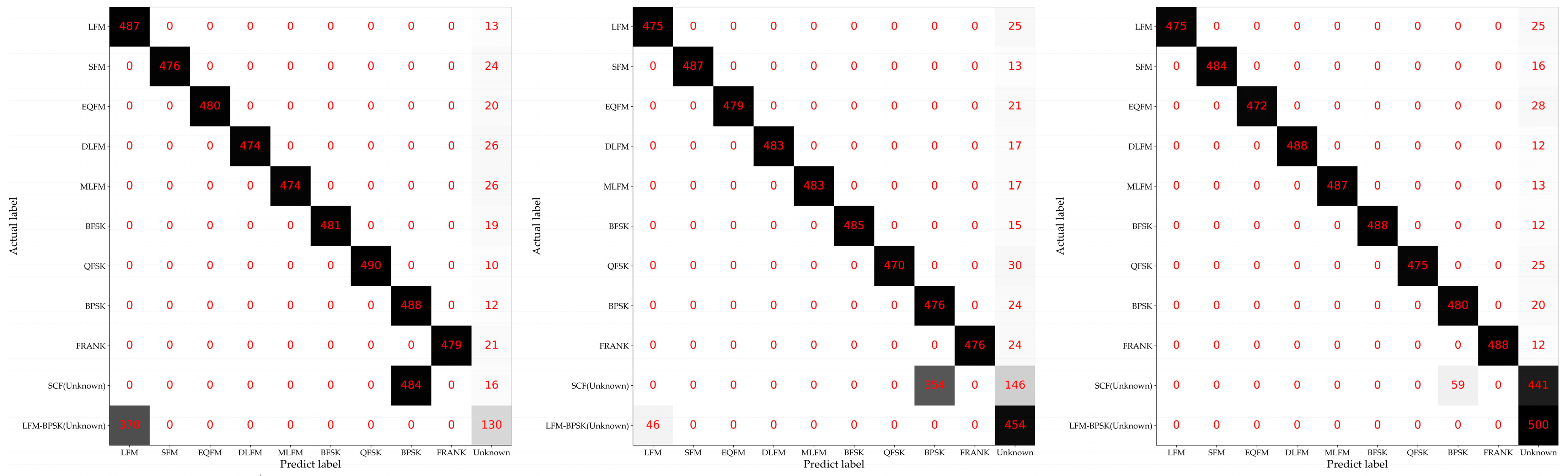
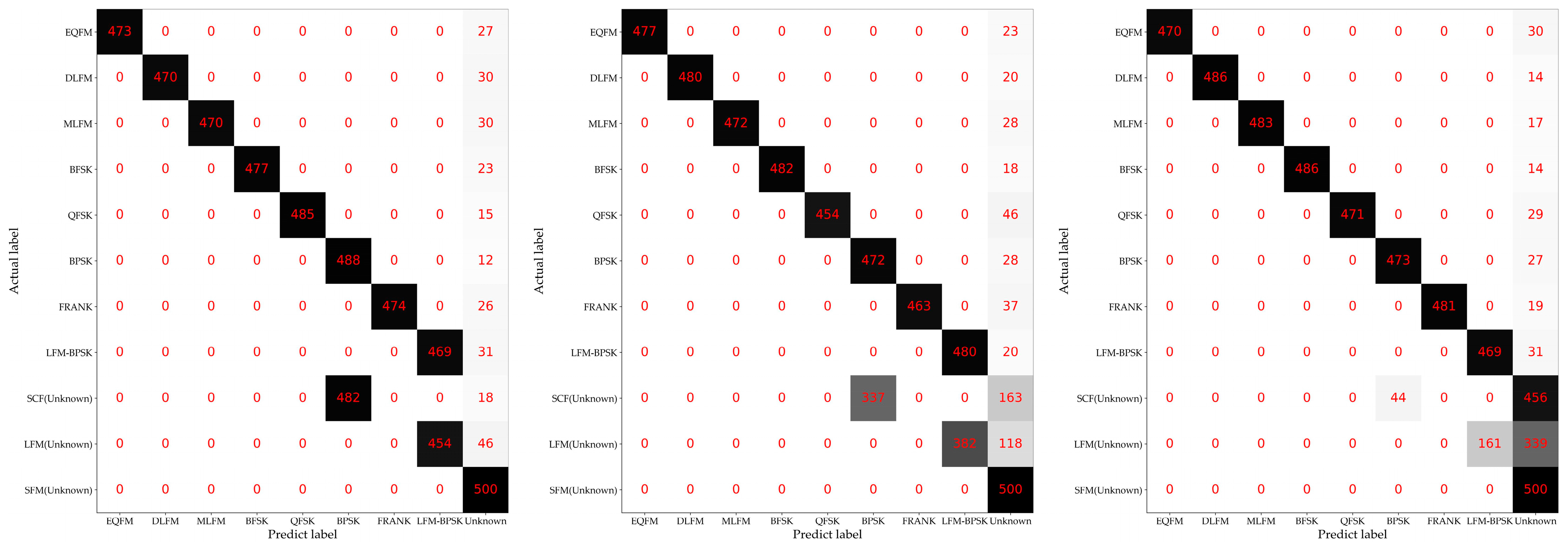
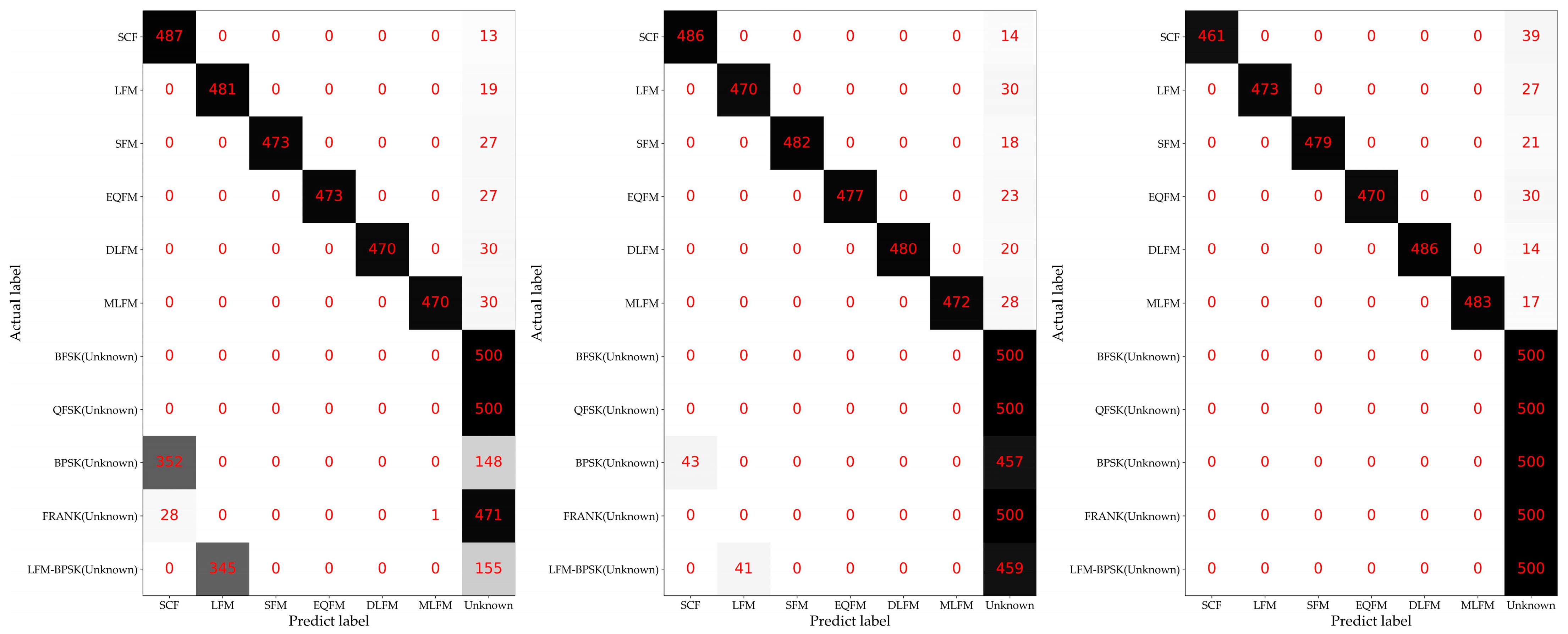
3.2. Description of the Experiments with Different Openness
3.3. Baseline Methods
4. Experiments
4.1. Training Details and Computational Cost
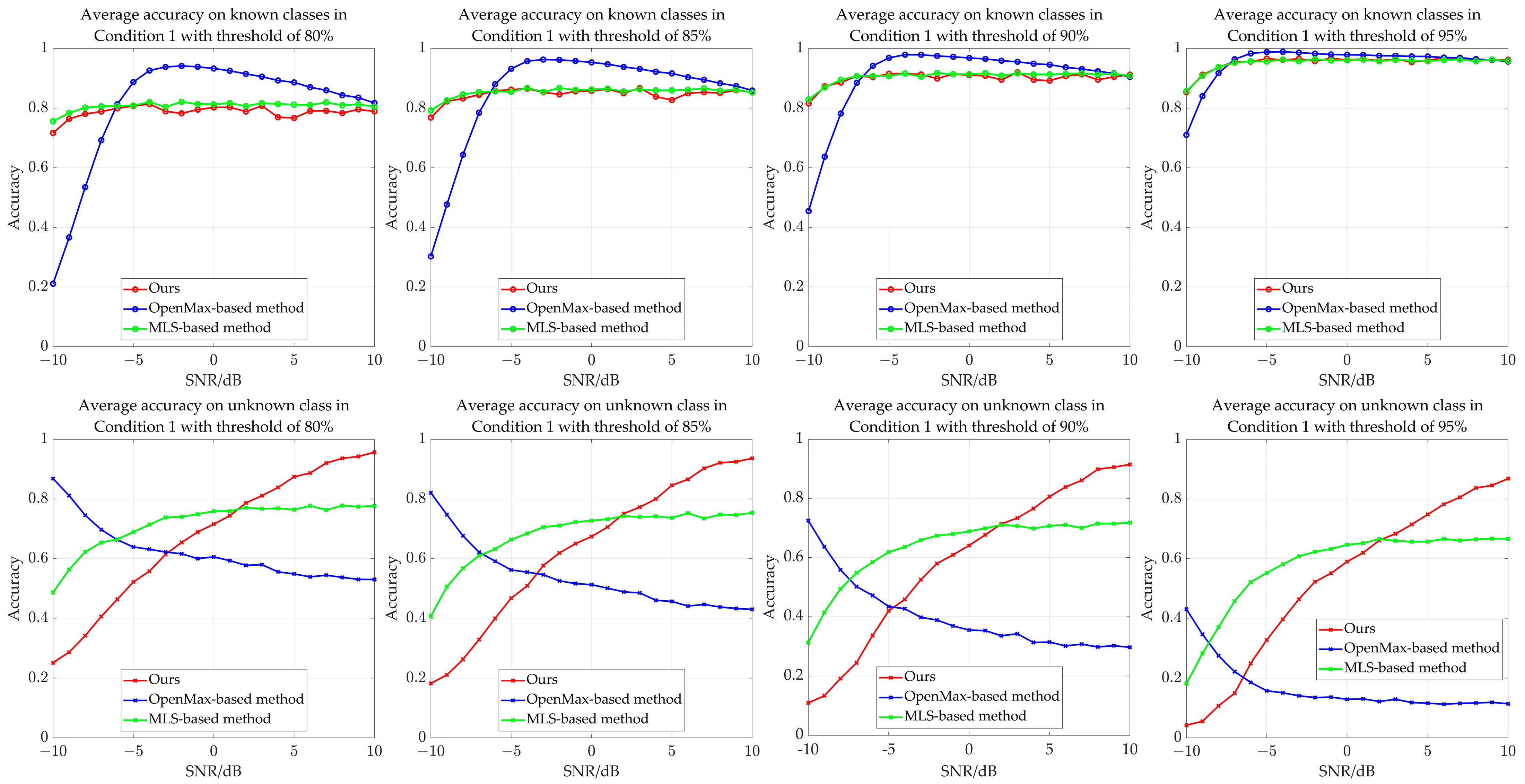
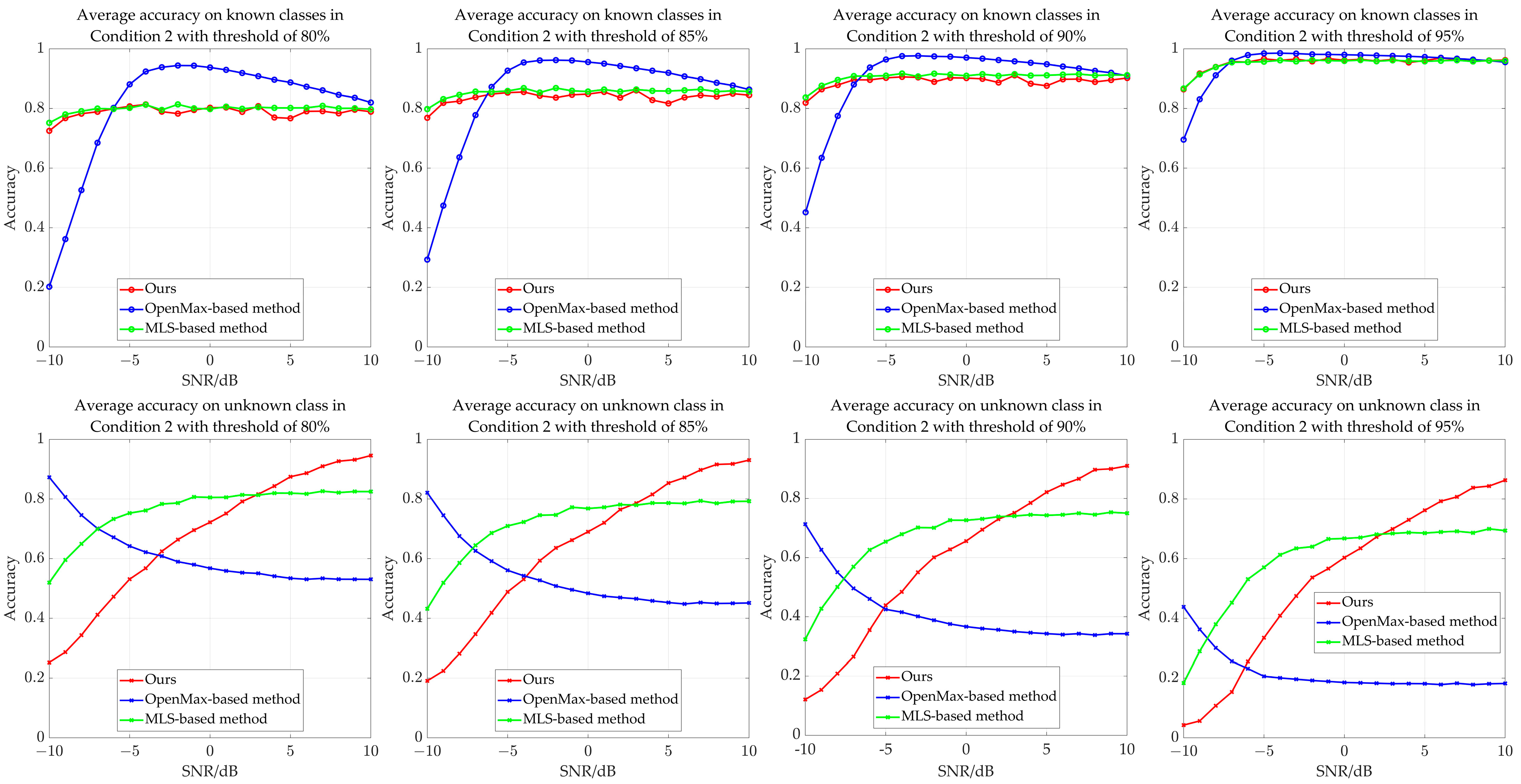
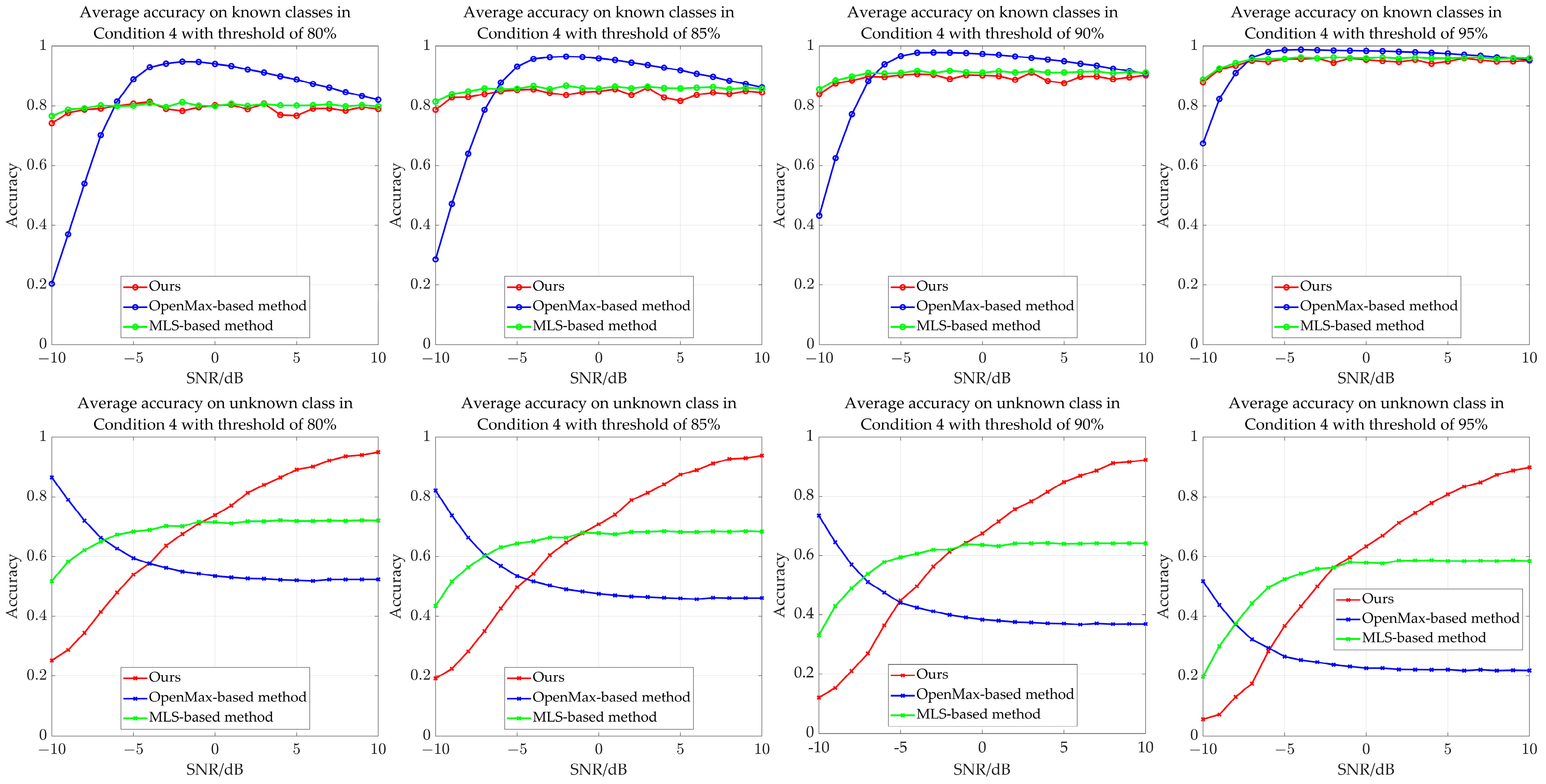
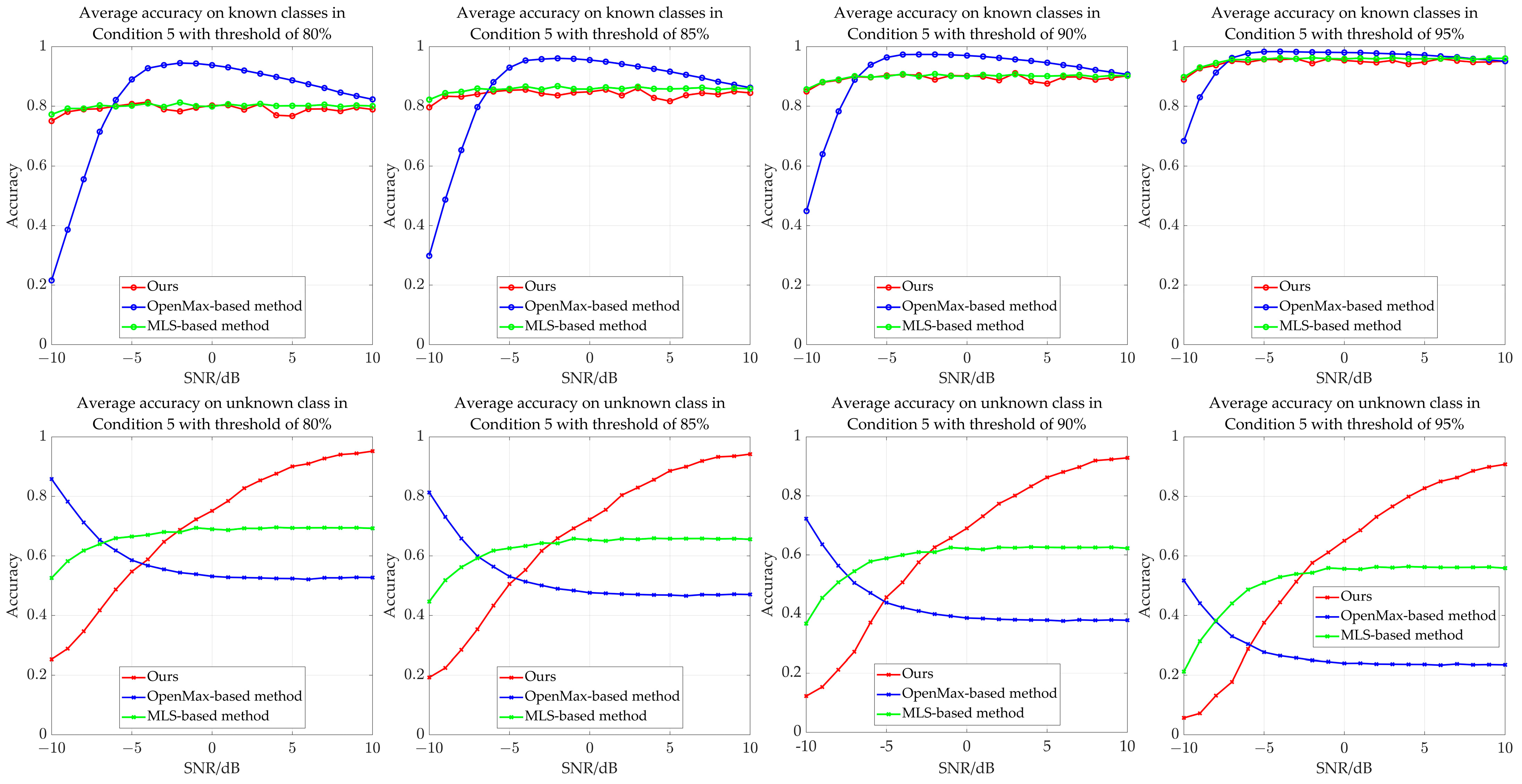
4.2. Experimental Results of the Proposed Method and Baseline Methods
5. Discussion
5.1. Ablation Study on the Structure of the Reconstruction Model on Recognition Accuracy
5.2. Application Scenarios
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, G. Principle of Radar Countermeasure, 2nd ed.; Xidian University Press: Xi’an, China, 2012. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Barton, D.K. Radar System Analysis and Modeling; Artech: London, UK, 2004. [Google Scholar]
- Wiley, R.G.; Ebrary, I. ELINT: The Interception and Analysis of Radar Signals; Artech: London, UK, 2006. [Google Scholar]
- Qu, Z.; Mao, X.; Deng, Z. Radar Signal Intra-Pulse Modulation Recognition Based on Convolutional Neural Network. IEEE Access 2018, 6, 43874–43884. [Google Scholar] [CrossRef]
- Yu, Z.; Tang, J.; Wang, Z. GCPS: A CNN Performance Evaluation Criterion for Radar Signal Intrapulse Modulation Recognition. IEEE Commun. Lett. 2021, 25, 2290–2294. [Google Scholar] [CrossRef]
- Yuan, S.; Wu, B.; Li, P. Intra-Pulse Modulation Classification of Radar Emitter Signals Based on a 1-D Selective Kernel Convolutional Neural Network. Remote Sens. 2021, 13, 2799. [Google Scholar] [CrossRef]
- Wu, B.; Yuan, S.; Li, P.; Jing, Z.; Huang, S.; Zhao, Y. Radar Emitter Signal Recognition Based on One-Dimensional Convolutional Neural Network with Attention Mechanism. Sensors 2020, 20, 6350. [Google Scholar] [CrossRef]
- Si, W.; Wan, C.; Deng, Z. Intra-Pulse Modulation Recognition of Dual-Component Radar Signals Based on Deep Convolutional Neural Network. IEEE Commun. Lett. 2021, 25, 3305–3309. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Wan, C.; Si, W.; Deng, Z. Research on modulation recognition method of multi-component radar signals based on deep convolution neural network. IET Radar Sonar Navig. 2023, 17, 1313–1326. [Google Scholar] [CrossRef]
- Cai, J.; He, M.; Cao, X.; Gan, F. Semi-Supervised Radar Intra-Pulse Signal Modulation Classification With Virtual Adversarial Training. IEEE Internet Things J. 2023. [Google Scholar] [CrossRef]
- Yuan, S.; Li, P.; Wu, B.; Li, X.; Wang, J. Semi-Supervised Classification for Intra-Pulse Modulation of Radar Emitter Signals Using Convolutional Neural Network. Remote Sens. 2022, 14, 2059. [Google Scholar] [CrossRef]
- Hendrycks, D.; Gimpel, K. A baseline for detecting misclassified and out-of-distribution examples in neural networks. arXiv 2016, arXiv:1610.02136. [Google Scholar]
- Bendale, A.; Boult, T.E. Towards Open Set Deep Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1563–1572. [Google Scholar] [CrossRef]
- Sun, C.; Du, Y.; Qiao, X.; Wu, H.; Zhang, T. Research on the Enhancement Method of Specific Emitter Open Set Recognition. Electronics 2023, 12, 4399. [Google Scholar] [CrossRef]
- Zhou, Y.; Shang, S.; Song, X.; Zhang, S.; You, T.; Zhang, L. Intelligent Radar Jamming Recognition in Open Set Environment Based on Deep Learning Networks. Remote Sens. 2022, 14, 6220. [Google Scholar] [CrossRef]
- Auger, F.; Flandrin, P. Improving the readability of time-frequency and time-scale representations by the reassignment method. IEEE Trans. Signal Process. 1995, 43, 1068–1089. [Google Scholar] [CrossRef]
- Wang, X.; Huang, G.; Zhou, Z.; Tian, W.; Yao, J.; Gao, J. Radar Emitter Recognition Based on the Energy Cumulant of Short Time Fourier Transform and Reinforced Deep Belief Network. Sensors 2018, 18, 3103. [Google Scholar] [CrossRef] [PubMed]
- Hoang, L.M.; Kim, M.; Kong, S.-H. Automatic Recognition of General LPI Radar Waveform Using SSD and Supplementary Classifier. IEEE Trans. Signal Process. 2019, 67, 3516–3530. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Vaze, S.; Han, K.; Vedaldi, A.; Zisserman, A. Open-set recognition: A good closed-set classifier is all you need. arXiv 2021, arXiv:2110.06207. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Huang, H.; Lin, L.; Tong, R.; Hu, H.; Zhang, Q.; Iwamoto, Y.; Han, X.; Chen, Y.-W.; Wu, J. UNet 3+: A Full-Scale Connected UNet for Medical Image Segmentation. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1055–1059. [Google Scholar] [CrossRef]
- Lv, Q.; Quan, Y.; Feng, W.; Sha, M.; Dong, S.; Xing, M. Radar Deception Jamming Recognition Based on Weighted Ensemble CNN With Transfer Learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5107511. [Google Scholar] [CrossRef]
- Zhou, X.; Bai, X.; Xue, R. ISAR Target Recognition Based on Capsule Net. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021; pp. 39–42. [Google Scholar] [CrossRef]
- Guo, D.; Chen, B.; Chen, W.; Wang, C.; Liu, H.; Zhou, M. Variational Temporal Deep Generative Model for Radar HRRP Target Recognition. IEEE Trans. Signal Process. 2020, 68, 5795–5809. [Google Scholar] [CrossRef]




| Type | Frequency | Parameters | Details |
|---|---|---|---|
| SCF | 10 MHz–90 MHz | None | None |
| LFM | 10 MHz–90 MHz | Bandwidth: 10 MHz–70 MHz | 1. Both up LFM and down LFM are included 2. Both max value and min value of the instantaneous frequency for LFM range from 10 MHz to 70 MHz |
| SFM | 10 MHz–90MHz | Bandwidth: 10 MHz–70 MHz | Both max value and min value of the instantaneous frequency for SFM range from 10 MHz to 70 MHz |
| EQFM | 10 MHz–90 MHz | Bandwidth: 10 MHz–70 MHz | 1. The instantaneous frequency increases first and then decreases, or decreases first and then increases 2. Both max value and min value of the instantaneous frequency for EQFM range from 10 MHz to 70 MHz |
| DLFM | 10 MHz–90 MHz | Bandwidth: 10 MHz–70 MHz | 1. The instantaneous frequency increases first and then decreases, or decreases first and then increases 2. Both max value and min value of the instantaneous frequency for DLFM range from 10 MHz to 70 MHz |
| MLFM | 10 MHz–90 MHz 10 MHz–90 MHz | Bandwidth: 10 MHz–70 MHz Bandwidth: 10 MHz–70 MHz Segment ratio: 20–80% | 1. Up LFM and down LFM are included in each of the two parts 2. Both max value and min value of the instantaneous frequency for each part of the MLFM range from 10 MHz to 70 MHz 3. The distance of the instantaneous frequency in the end of the first part and the instantaneous frequency in the start of the last part is more than 10 MHz |
| BFSK | 10 MHz–90 MHz 10 MHz–90 MHz | 5, 7, 11, 13-bit Barker code | The distance of two sub-carrier frequency is more than 10 MHz |
| QFSK | 10 MHz–90 MHz 10 MHz–90 MHz 10 MHz–90 MHz 10 MHz–90 MHz | 16-bit Frank code | The distance of each two sub-carrier frequency is more than 10 MHz |
| BPSK | 10 MHz–90 MHz | 5, 7, 11, 13-bit Barker code | None |
| FRANK | 10 MHz–90 MHz | Phase number: 6, 7, 8 | None |
| LFM-BPSK | 10 MHz–90 MHz | Bandwidth: 10 MHz–70 MHz 5, 7, 11, 13-bit Barker code | 1. Both up LFM and down LFM are included 2. Both max value and min value of the instantaneous frequency for LFM-BPSK range from 10 MHz to 70 MHz |
| FLOPs | 4.5 M |
| Parameters | 2.2 M |
| Training Time/Iteration (Batch Size: 64) | 13.7 ms |
| Forward Time (Single Sample) | 2.3 ms |
| FLOPs | 3.8 M |
| Parameters | 1.9 M |
| Training Time/Iteration (Batch Size: 40) | 23 ms |
| Forward Time (Single Sample) | 4.9 ms |
| SNR/dB | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 |
|---|---|---|---|---|---|
| −10 | 0.8745 | 0.8853 | 0.8971 | 0.9081 | 0.9196 |
| −9 | 0.9356 | 0.9409 | 0.9469 | 0.9529 | 0.9594 |
| −8 | 0.9672 | 0.9698 | 0.9730 | 0.9761 | 0.9794 |
| −7 | 0.9881 | 0.9889 | 0.9899 | 0.9911 | 0.9925 |
| −6 | 0.9956 | 0.9955 | 0.9959 | 0.9964 | 0.9969 |
| −5 | 0.9980 | 0.9981 | 0.9984 | 0.9984 | 0.9988 |
| −4 | 0.9993 | 0.9995 | 0.9996 | 0.9995 | 0.9997 |
| −3 | 0.9999 | 0.9998 | 0.9998 | 0.9999 | 0.9999 |
| −2 | 0.9999 | 0.9999 | 0.9999 | 1.0000 | 1.0000 |
| −1 | 1.0000 | 0.9999 | 0.9999 | 1.0000 | 1.0000 |
| 0 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 1 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2 | 0.9998 | 0.9998 | 0.9999 | 0.9999 | 0.9999 |
| 3 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 4 | 0.9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 5 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 6 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 7 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 8 | 1.0000 | 0.9999 | 1.0000 | 1.0000 | 1.0000 |
| 9 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 10 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Average Accuracy | 0.9885 | 0.9894 | 0.9905 | 0.9915 | 0.9927 |
| Method (Average Accuracy Threshold of 80%) | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | |
| Ours | 0.7869 | 0.6762 | 0.7876 | 0.6784 | 0.7884 | 0.6854 | 0.7891 | 0.6896 | 0.7900 | 0.6977 |
| OpenMax | 0.8063 | 0.6207 | 0.8058 | 0.6095 | 0.8079 | 0.5960 | 0.8100 | 0.5838 | 0.8124 | 0.5811 |
| MLS | 0.8077 | 0.7183 | 0.7983 | 0.7657 | 0.7992 | 0.7208 | 0.7996 | 0.6879 | 0.8003 | 0.6684 |
| Method (Average Accuracy Threshold of 85%) | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | |
| Ours | 0.8468 | 0.6337 | 0.8377 | 0.6444 | 0.8386 | 0.6524 | 0.8394 | 0.6575 | 0.8403 | 0.6665 |
| OpenMax | 0.8517 | 0.5357 | 0.8515 | 0.5308 | 0.8519 | 0.5279 | 0.8527 | 0.5248 | 0.8532 | 0.5265 |
| MLS | 0.8547 | 0.6842 | 0.8548 | 0.7231 | 0.8557 | 0.6797 | 0.8562 | 0.6455 | 0.8569 | 0.6267 |
| Method (Average Accuracy Threshold of 90%) | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | |
| Ours | 0.9000 | 0.5891 | 0.8905 | 0.6031 | 0.8915 | 0.6121 | 0.8924 | 0.6182 | 0.8934 | 0.6283 |
| OpenMax | 0.9014 | 0.4014 | 0.9017 | 0.4132 | 0.9018 | 0.4258 | 0.9014 | 0.4333 | 0.9012 | 0.4353 |
| MLS | 0.9059 | 0.6380 | 0.9060 | 0.6704 | 0.9071 | 0.6304 | 0.9077 | 0.5944 | 0.8987 | 0.5880 |
| Method (Average Accuracy Threshold of 95%) | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | |
| Ours | 0.9530 | 0.5248 | 0.9539 | 0.5324 | 0.9449 | 0.5576 | 0.9459 | 0.5652 | 0.9470 | 0.5767 |
| OpenMax | 0.9533 | 0.1667 | 0.9511 | 0.2177 | 0.9522 | 0.2407 | 0.9513 | 0.2669 | 0.9494 | 0.2793 |
| MLS | 0.9515 | 0.5750 | 0.9519 | 0.5951 | 0.9530 | 0.5600 | 0.9539 | 0.5242 | 0.9548 | 0.5086 |
| Method (Average Accuracy Threshold of 80%) | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | |
| Ours | 0.7869 | 0.6762 | 0.7876 | 0.6784 | 0.7884 | 0.6854 | 0.7891 | 0.6896 | 0.7900 | 0.6977 |
| AM1 | 0.8099 | 0.3696 | 0.8006 | 0.3817 | 0.8015 | 0.3818 | 0.8023 | 0.3815 | 0.8033 | 0.3790 |
| AM2 | 0.8006 | 0.4427 | 0.8014 | 0.4504 | 0.8022 | 0.4515 | 0.8031 | 0.4520 | 0.8040 | 0.4516 |
| AM3 | 0.7996 | 0.5993 | 0.8003 | 0.6027 | 0.8011 | 0.6091 | 0.8019 | 0.6108 | 0.8028 | 0.6134 |
| U-Net | 0.8024 | 0.3333 | 0.8031 | 0.3273 | 0.8039 | 0.3320 | 0.8047 | 0.3345 | 0.8057 | 0.3371 |
| UNet3+ | 0.7998 | 0.3605 | 0.8005 | 0.3645 | 0.8014 | 0.3696 | 0.8022 | 0.3717 | 0.8032 | 0.3742 |
| Method (Average Accuracy Threshold of 85%) | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | |
| Ours | 0.8468 | 0.6337 | 0.8377 | 0.6444 | 0.8386 | 0.6524 | 0.8394 | 0.6575 | 0.8403 | 0.6665 |
| AM1 | 0.8490 | 0.3421 | 0.8498 | 0.3468 | 0.8508 | 0.3473 | 0.8517 | 0.3472 | 0.8526 | 0.3446 |
| AM2 | 0.8496 | 0.4065 | 0.8504 | 0.4141 | 0.8513 | 0.4158 | 0.8522 | 0.4168 | 0.8532 | 0.4168 |
| AM3 | 0.8489 | 0.5620 | 0.8496 | 0.5664 | 0.8505 | 0.5736 | 0.8514 | 0.5760 | 0.8523 | 0.5793 |
| U-Net | 0.8500 | 0.2768 | 0.8508 | 0.2720 | 0.8517 | 0.2762 | 0.8526 | 0.2791 | 0.8536 | 0.2816 |
| UNet3+ | 0.8494 | 0.3042 | 0.8501 | 0.3082 | 0.8511 | 0.3135 | 0.8519 | 0.3162 | 0.8529 | 0.3189 |
| Method (Average Accuracy Threshold of 90%) | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | |
| Ours | 0.9000 | 0.5891 | 0.8905 | 0.6031 | 0.8915 | 0.6121 | 0.8924 | 0.6182 | 0.8934 | 0.6283 |
| AM1 | 0.9076 | 0.2937 | 0.8992 | 0.3066 | 0.9001 | 0.3074 | 0.9011 | 0.3077 | 0.9021 | 0.3053 |
| AM2 | 0.9077 | 0.3616 | 0.8991 | 0.3765 | 0.9001 | 0.3788 | 0.9010 | 0.3801 | 0.9021 | 0.3803 |
| AM3 | 0.8989 | 0.5161 | 0.8998 | 0.5216 | 0.9007 | 0.5299 | 0.9017 | 0.5332 | 0.9027 | 0.5374 |
| U-Net | 0.8989 | 0.2133 | 0.8997 | 0.2086 | 0.9007 | 0.2124 | 0.9016 | 0.2154 | 0.9026 | 0.2176 |
| UNet3+ | 0.8987 | 0.2437 | 0.8995 | 0.2479 | 0.9005 | 0.2535 | 0.9014 | 0.2567 | 0.9025 | 0.2601 |
| Method (Average Accuracy Threshold of 95%) | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | |
| Ours | 0.9530 | 0.5248 | 0.9539 | 0.5324 | 0.9449 | 0.5576 | 0.9459 | 0.5652 | 0.9470 | 0.5767 |
| AM1 | 0.9560 | 0.2457 | 0.9473 | 0.2615 | 0.9484 | 0.2628 | 0.9494 | 0.2633 | 0.9505 | 0.2612 |
| AM2 | 0.9563 | 0.3089 | 0.9473 | 0.3276 | 0.9484 | 0.3304 | 0.9494 | 0.3322 | 0.9505 | 0.3326 |
| AM3 | 0.9576 | 0.4428 | 0.9492 | 0.4650 | 0.9502 | 0.4744 | 0.9512 | 0.4787 | 0.9523 | 0.4837 |
| U-Net | 0.9563 | 0.1223 | 0.9472 | 0.1371 | 0.9483 | 0.1400 | 0.9492 | 0.1427 | 0.9503 | 0.1442 |
| UNet3+ | 0.9565 | 0.1547 | 0.9574 | 0.1582 | 0.9487 | 0.1809 | 0.9497 | 0.1848 | 0.9508 | 0.1890 |
| Reconstruction Model | Ours | AM1 | AM2 | AM3 | U-Net | UNet3+ |
| Average Reconstruction Loss (The original value based on MSE is magnified 16,384 times (equals to 128 × 128)) | 36.7777 | 4.5015 | 10.3470 | 24.0721 | 0.0294 | 0.0333 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, S.; Li, P.; Wu, B. Radar Emitter Signal Intra-Pulse Modulation Open Set Recognition Based on Deep Neural Network. Remote Sens. 2024, 16, 108. https://doi.org/10.3390/rs16010108
Yuan S, Li P, Wu B. Radar Emitter Signal Intra-Pulse Modulation Open Set Recognition Based on Deep Neural Network. Remote Sensing. 2024; 16(1):108. https://doi.org/10.3390/rs16010108
Chicago/Turabian StyleYuan, Shibo, Peng Li, and Bin Wu. 2024. "Radar Emitter Signal Intra-Pulse Modulation Open Set Recognition Based on Deep Neural Network" Remote Sensing 16, no. 1: 108. https://doi.org/10.3390/rs16010108
APA StyleYuan, S., Li, P., & Wu, B. (2024). Radar Emitter Signal Intra-Pulse Modulation Open Set Recognition Based on Deep Neural Network. Remote Sensing, 16(1), 108. https://doi.org/10.3390/rs16010108






