Genetic Programming Guided Mapping of Forest Canopy Height by Combining LiDAR Satellites with Sentinel-1/2, Terrain, and Climate Data
Abstract
:1. Introduction
2. Study Sites and Data
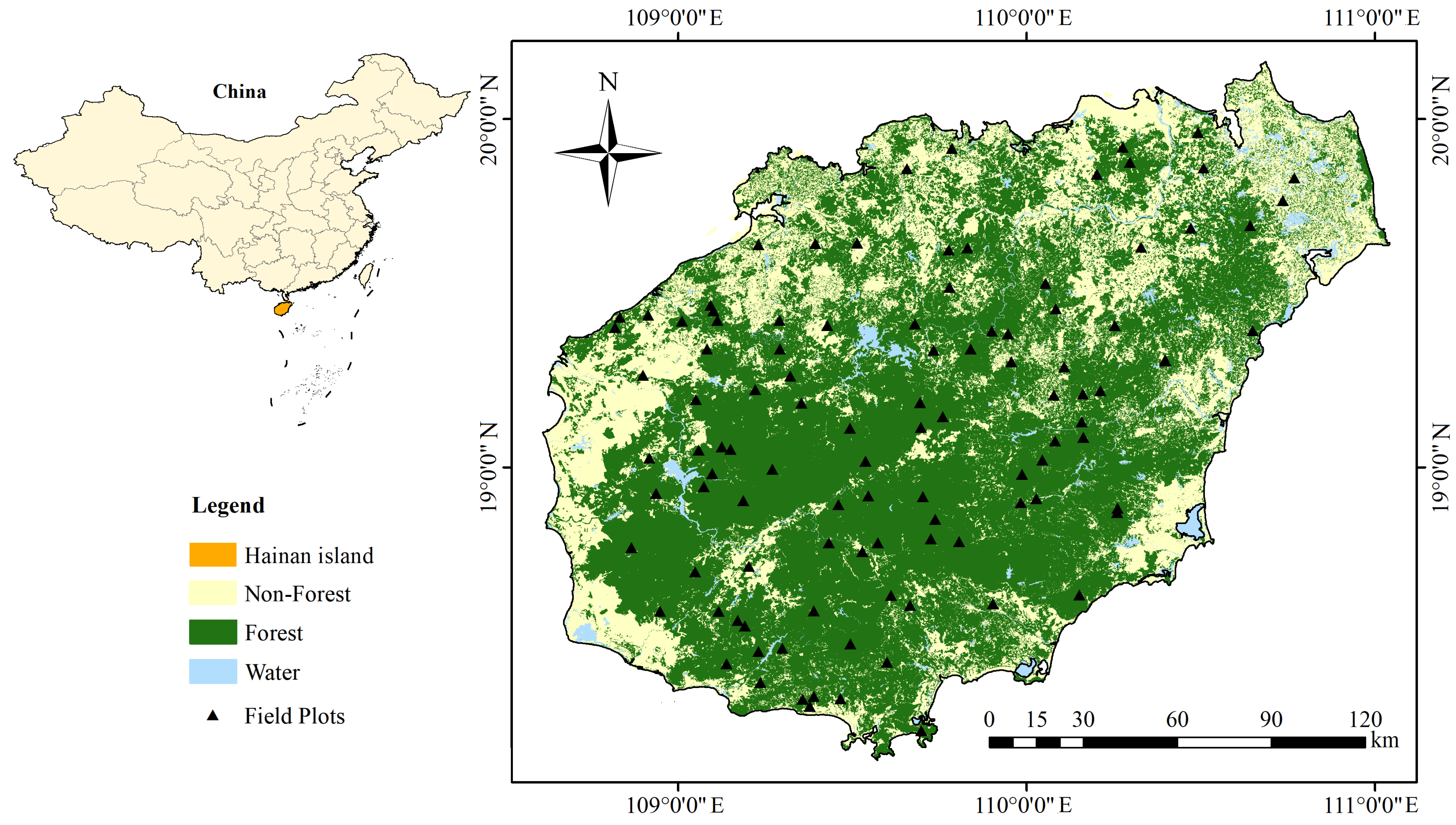
2.1. Study Area
2.2. Data Collection and Preprocessing
2.2.1. GEDI L2A Data
2.2.2. ICESat-2 ATL08 Data
2.2.3. Sentinel Data
2.2.4. Climate, Terrain, and Land Cover Data
2.2.5. Field Plot Data
3. Methods
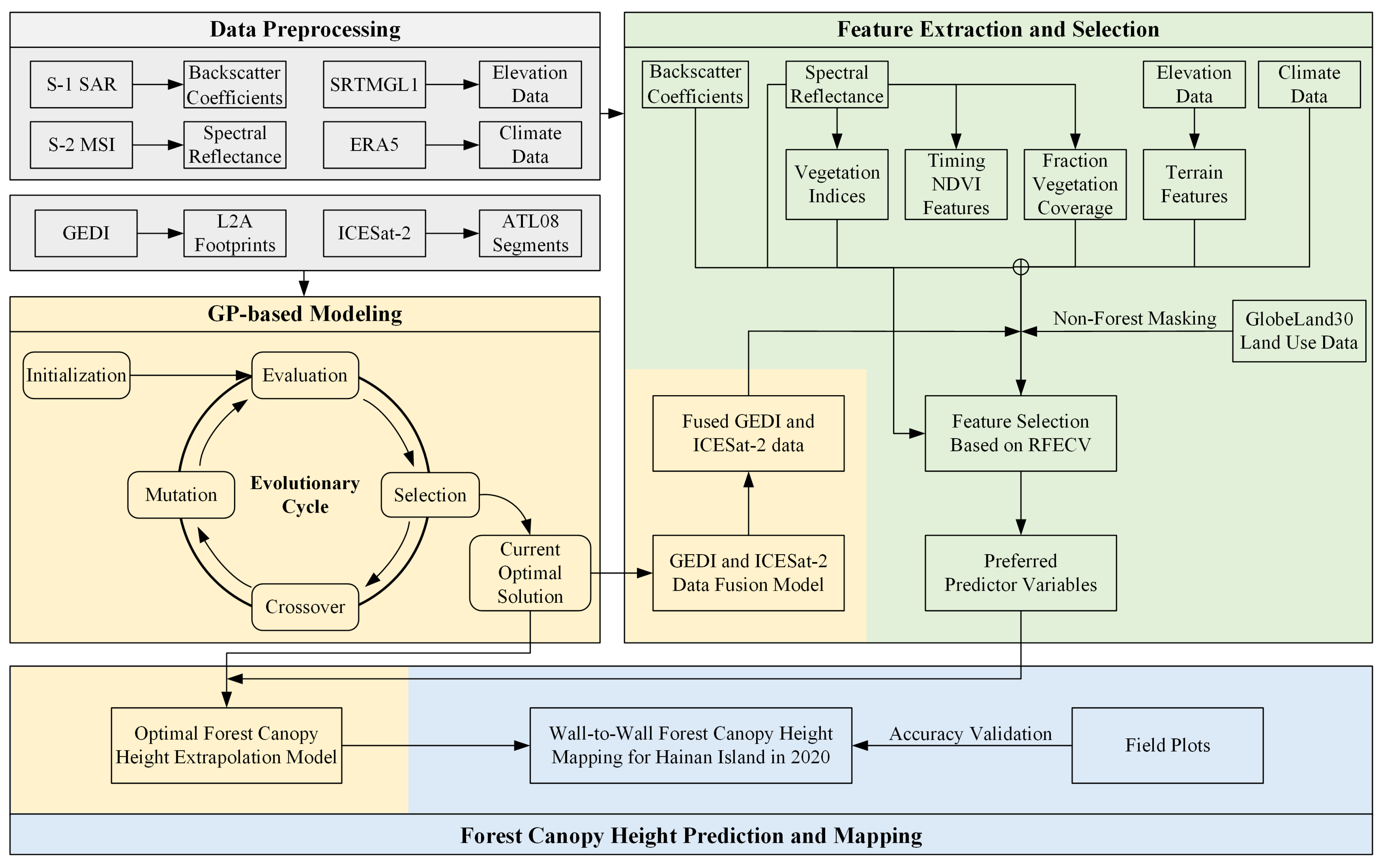
3.1. Feature Extraction and Selection
3.2. Modeling Based on the GP Algorithm
3.2.1. The GP Algorithm
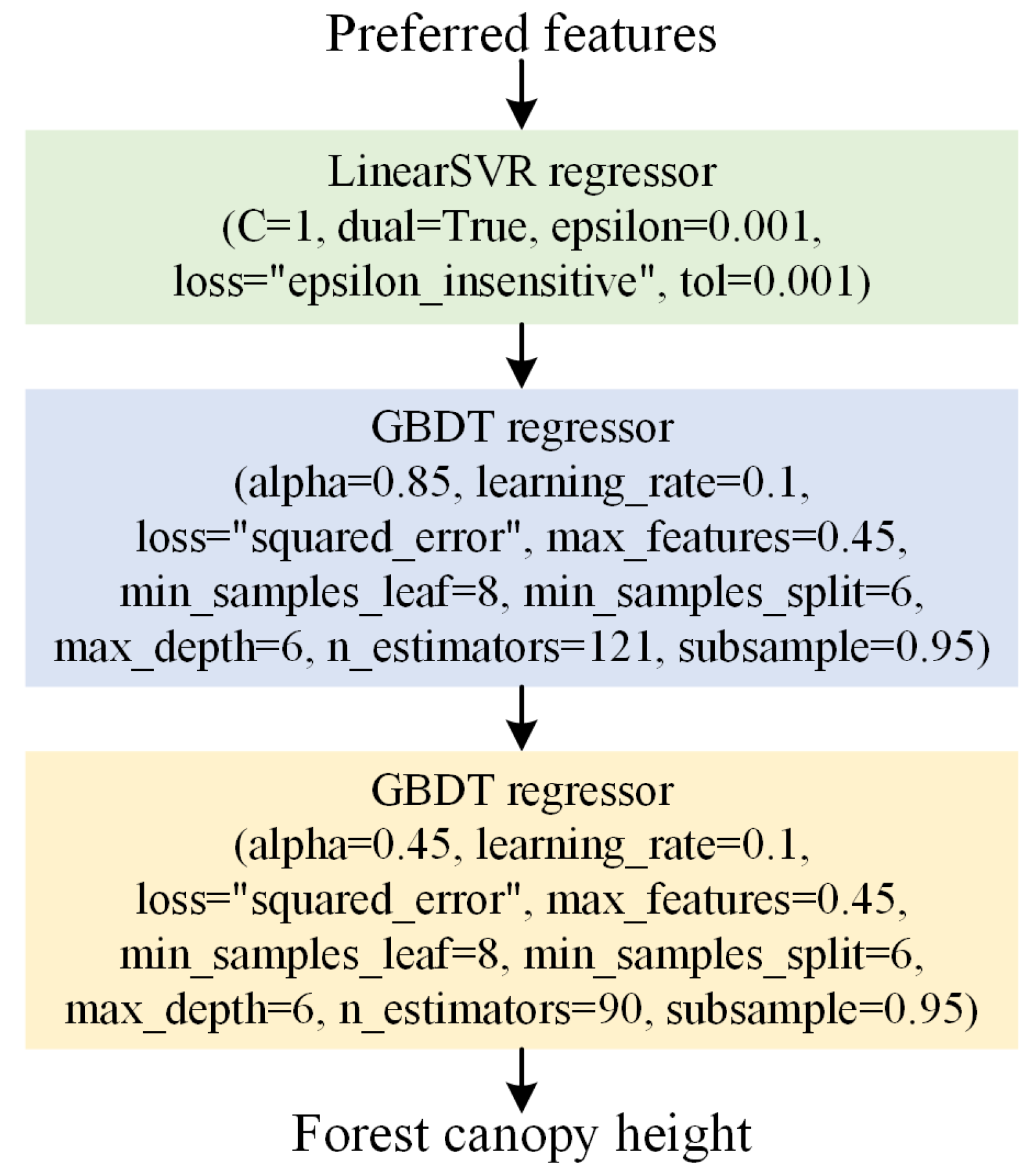
3.2.2. Constructing the GIF Model Based on GP
3.2.3. Constructing the FCHE Model Based on GP
3.3. Accuracy Evaluation
4. Results
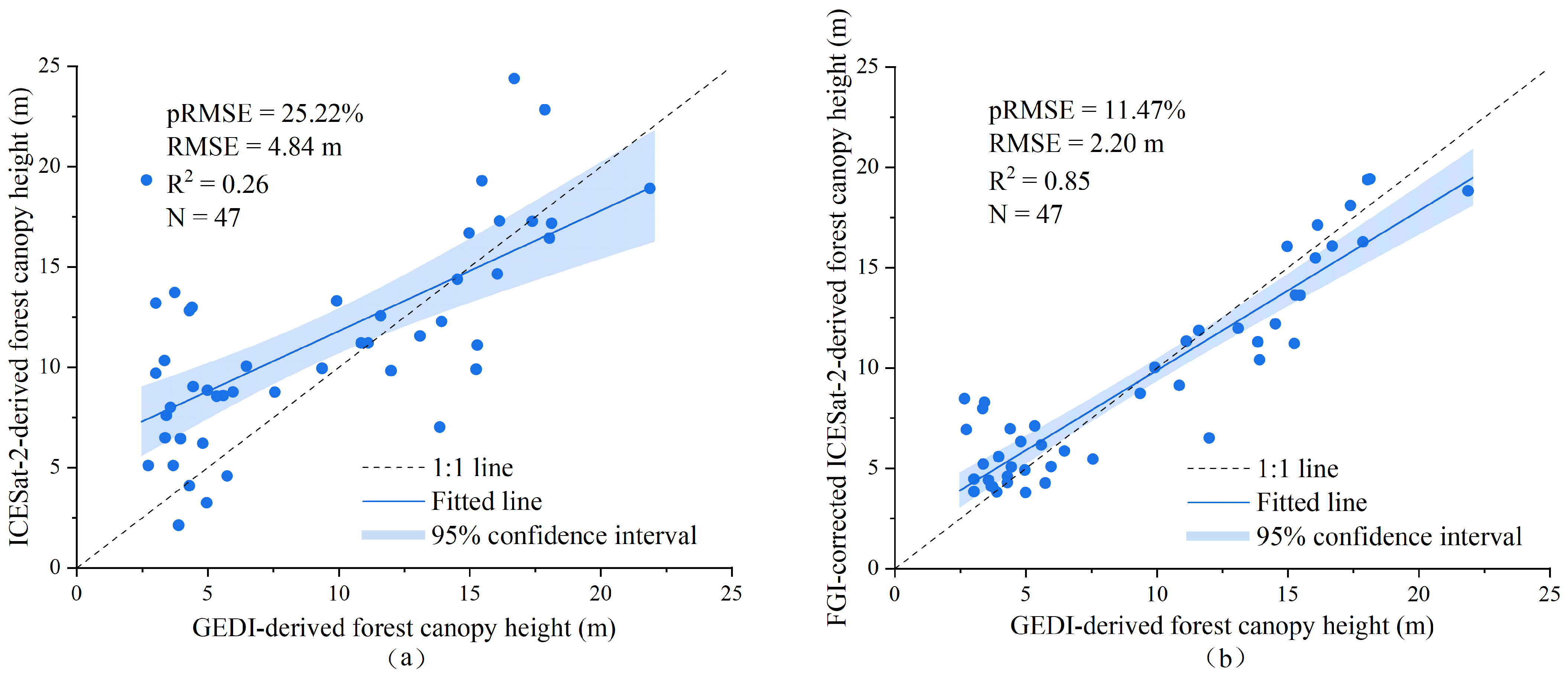
4.1. GIF Model Construction
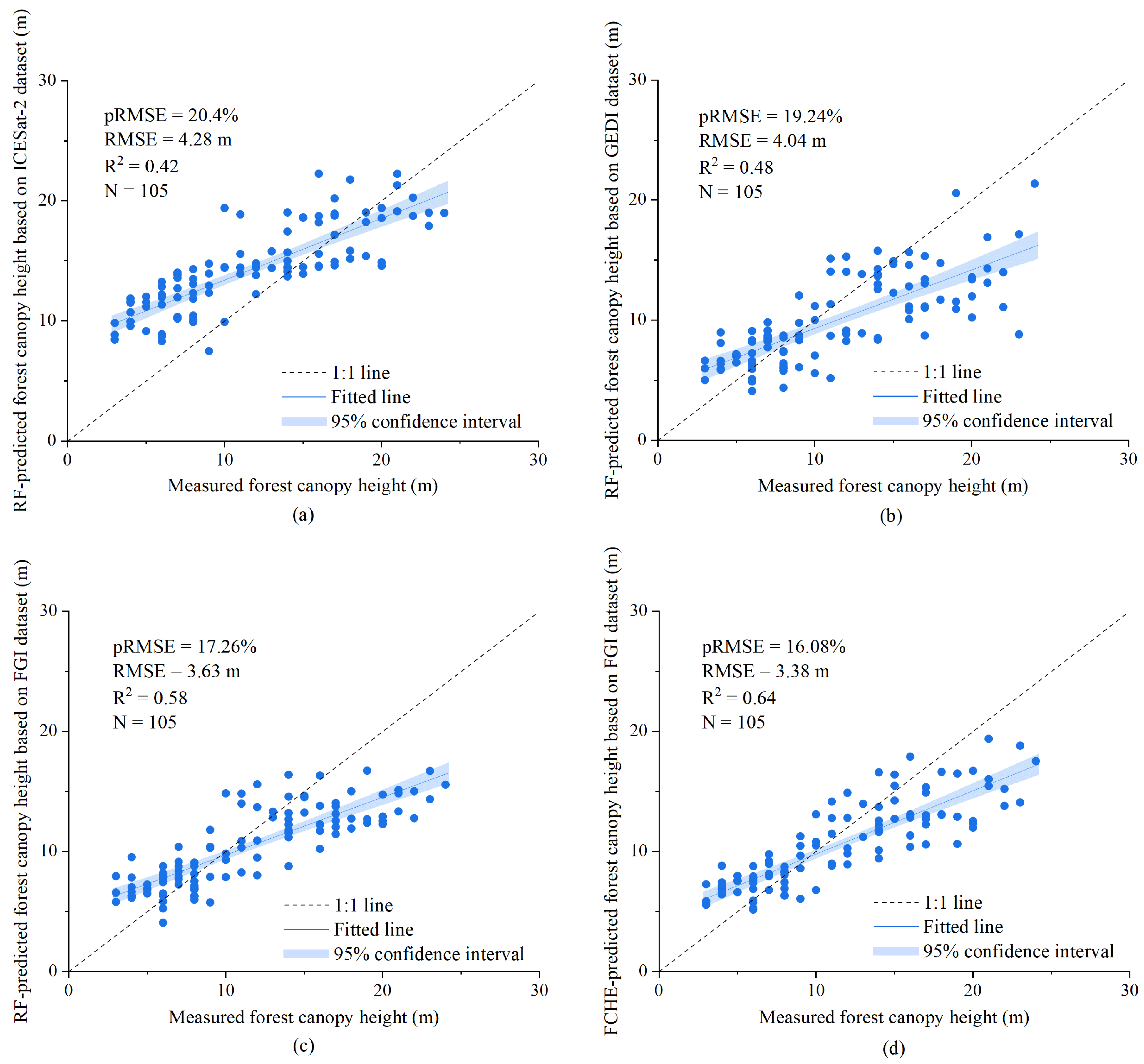
4.2. Forest Canopy Height Prediction, Validation, and Mapping
5. Discussion
5.1. Advantages of the Proposed Forest Canopy Height Prediction Method
5.2. Limitations and Potential Refinements
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Hyperparameter | (1) | (2) | (3)/(4) | |
|---|---|---|---|---|
| Experiment | ||||
| n_estimators | 146 | 168 | 167 | |
| max_features | 19 | 14 | 18 | |
| min_samples_split | 3 | 2 | 6 | |
| min_samples_leaf | 3 | 5 | 9 | |
| bootstrap | 0 | 0 | 0 | |
| max_depth | 19 | 18 | 19 | |
References
- Lang, N.; Kalischek, N.; Armston, J.; Schindler, K.; Dubayah, R.; Wegner, J.D. Global canopy height regression and uncertainty estimation from GEDI LIDAR waveforms with deep ensembles. Remote Sens. Environ. 2022, 268, 112760. [Google Scholar] [CrossRef]
- Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Queinnec, M.; Luther, J.E.; Bolton, D.K.; White, J.C.; Wulder, M.A.; van Lier, O.R.; Hermosilla, T. Modelling lidar-derived estimates of forest attributes over space and time: A review of approaches and future trends. Remote Sens. Environ. 2021, 260, 112477. [Google Scholar] [CrossRef]
- Huang, X.; Cheng, F.; Wang, J.; Duan, P.; Wang, J. Forest Canopy Height Extraction Method Based on ICESat-2/ATLAS Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5700814. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, C.; Nie, S.; Pan, F.; Xi, X.; Hu, Z. Mapping forest height using photon-counting LiDAR data and Landsat 8 OLI data: A case study in Virginia and North Carolina, USA. Ecol. Ind. 2020, 114, 106287. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-resolution mapping of forest canopy height using machine learning by coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping global forest canopy height through integration of GEDI and Landsat data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Liu, X.; Su, Y.; Hu, T.; Yang, Q.; Liu, B.; Deng, Y.; Tang, H.; Tang, Z.; Fang, J.; Guo, Q. Neural network guided interpolation for mapping canopy height of China’s forests by integrating GEDI and ICESat-2 data. Remote Sens. Environ. 2022, 269, 112844. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Matsumoto, K. The effect of forest certification on conservation and sustainable forest management. J. Clean. Prod. 2022, 363, 132374. [Google Scholar] [CrossRef]
- Huang, W.; Min, W.; Ding, J.; Liu, Y.; Hu, Y.; Ni, W.; Shen, H. Forest height mapping using inventory and multi-source satellite data over Hunan Province in southern China. For. Ecosyst. 2022, 9, 100006. [Google Scholar] [CrossRef]
- Zhu, X. Forest Height Retrieval of China with a Resolution of 30 m Using ICESat-2 and GEDI Data. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2021. [Google Scholar]
- Wallner, A.; Friedrich, S.; Geier, E.; Meder-Hokamp, C.; Wei, Z.; Kindu, M.; Tian, J.; Döllerer, M.; Schneider, T.; Knoke, T. A remote sensing-guided forest inventory concept using multispectral 3D and height information from ZiYuan-3 satellite data. Forestry 2022, 95, 331–346. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Guo, Z. Estimation of tree height and aboveground biomass of coniferous forests in North China using stereo ZY-3, multispectral Sentinel-2, and DEM data. Ecol. Ind. 2021, 126, 107645. [Google Scholar] [CrossRef]
- Guo, Q.; Su, Y.; Hu, T.; Guan, H.; Jin, S.; Zhang, J.; Zhao, X.; Xu, K.; Wei, D.; Kelly, M.; et al. Lidar boosts 3D ecological observations and modelings: A review and perspective. IEEE Geosci. Remote Sens. Mag. 2020, 9, 232–257. [Google Scholar] [CrossRef]
- Zhu, X.; Nie, S.; Wang, C.; Xi, X.; Lao, J.; Li, D. Consistency analysis of forest height retrievals between GEDI and ICESat-2. Remote Sens. Environ. 2022, 281, 113244. [Google Scholar] [CrossRef]
- Zhou, X.; Li, C. Mapping the vertical forest structure in a large subtropical region using airborne LiDAR data. Ecol. Ind. 2023, 154, 110731. [Google Scholar] [CrossRef]
- Jiang, F.; Zhao, F.; Ma, K.; Li, D.; Sun, H. Mapping the forest canopy height in Northern China by synergizing ICESat-2 with Sentinel-2 using a stacking algorithm. Remote Sens. 2021, 13, 1535. [Google Scholar] [CrossRef]
- Kacic, P.; Hirner, A.; Da Ponte, E. Fusing Sentinel-1 and-2 to Model GEDI-Derived Vegetation Structure Characteristics in GEE for the Paraguayan Chaco. Remote Sens. 2021, 13, 5105. [Google Scholar] [CrossRef]
- Liao, Z.; Van Dijk, A.I.; He, B.; Larraondo, P.R.; Scarth, P.F. Woody vegetation cover, height and biomass at 25-m resolution across Australia derived from multiple site, airborne and satellite observations. Int. J. Appl. Earth Obs. Geoinf. 2020, 93, 102209. [Google Scholar] [CrossRef]
- Xi, Z.; Xu, H.; Xing, Y.; Gong, W.; Chen, G.; Yang, S. Forest canopy height mapping by synergizing icesat-2, sentinel-1, sentinel-2 and topographic information based on machine learning methods. Remote Sens. 2022, 14, 364. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, X.; Gong, P.; Huang, H.; Li, Z.; Li, X. Earth science applications of ICESat/GLAS: A review. Int. J. Remote Sens. 2011, 32, 8837–8864. [Google Scholar] [CrossRef]
- Chen, L.; Ren, C.; Zhang, B.; Wang, Z.; Liu, M.; Man, W.; Liu, J. Improved estimation of forest stand volume by the integration of GEDI LiDAR data and multi-sensor imagery in the Changbai Mountains Mixed forests Ecoregion (CMMFE), northeast China. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102326. [Google Scholar] [CrossRef]
- Nandy, S.; Srinet, R.; Padalia, H. Mapping forest height and aboveground biomass by integrating ICESat-2, Sentinel-1 and Sentinel-2 data using Random Forest algorithm in northwest Himalayan foothills of India. Geophys. Res. Lett. 2021, 48, e2021GL093799. [Google Scholar] [CrossRef]
- Pourshamsi, M.; Xia, J.; Yokoya, N.; Garcia, M.; Lavalle, M.; Pottier, E.; Balzter, H. Tropical forest canopy height estimation from combined polarimetric SAR and LiDAR using machine-learning. ISPRS J. Photogramm. Remote Sens. 2021, 172, 79–94. [Google Scholar] [CrossRef]
- Liu, C.; Lyu, W.; Zhao, W.; Zheng, F.; Lu, J. Exploratory research on influential factors of China’s sulfur dioxide emission based on symbolic regression. Environ. Monit. Assess. 2023, 195, 41. [Google Scholar] [CrossRef] [PubMed]
- Niu, G.; Yi, X.; Chen, C.; Li, X.; Han, D.; Yan, B.; Huang, M.; Ying, G. A novel effluent quality predicting model based on genetic-deep belief network algorithm for cleaner production in a full-scale paper-making wastewater treatment. J. Clean. Prod. 2020, 265, 121787. [Google Scholar] [CrossRef]
- Asadzadeh, M.Z.; Gänser, H.P.; Mücke, M. Symbolic regression based hybrid semiparametric modelling of processes: An example case of a bending process. Appl. Eng. Sci. 2021, 6, 100049. [Google Scholar] [CrossRef]
- Kommenda, M.; Burlacu, B.; Kronberger, G.; Affenzeller, M. Parameter identification for symbolic regression using nonlinear least squares. Genet. Program. Evolvable Mach. 2020, 21, 471–501. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Zhu, M.; Wang, W.; Liang, Q.; Zou, Y.; Li, C.; Tang, P.; Ren, H. Carbon storage and economic assessment of the main forest types vegetation in Hainan. J. Cent. South Univ. Forest. Technol. 2017, 37, 92–98. [Google Scholar]
- Chen, Y. Risk Assessment of Typhoon Disaster in Hainan Island Based on GIS. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2021. [Google Scholar]
- Han, G.; Chen, J.; He, C.; Li, S.; Wu, H.; Liao, A.; Peng, S. A web-based system for supporting global land cover data production. ISPRS J. Photogramm. Remote Sens. 2015, 103, 66–80. [Google Scholar] [CrossRef]
- Gu, X.; Chen, B.; Ting, Y.; Guangyang, L.; Zhixiang, W.; Weili, K. Spatio-temporal Changes of Forest in Hainan Island from 2007 to 2018 Based on Multi-source Remote Sensing Data. Chin. J. Trop. Crops 2022, 43, 418–429. [Google Scholar]
- Beck, J.; Wirt, B.; Armston, J.; Hofton, M.; Luthcke, S.; Tang, H. Global Ecosystem Dynamics Investigation (GEDI) Level 02 User Guide. Doc. Version 2021, 2, 14–15. [Google Scholar]
- Dubayah, R.; Hofton, M.; Blair, J.B.; Armston, J.; Tang, H.; Luthcke, S. GEDI L2A Elevation and Height Metrics Data Global Footprint Level V002. 2021. Available online: https://lpdaac.usgs.gov/products/gedi02_av002/ (accessed on 14 August 2022).
- Neuenschwander, A.L.; Pitts, K.L.; Jelley, B.P.; Robbins, J.; Klotz, B.; Popescu, S.C.; Nelson, R.F.; Harding, D.; Pederson, D.; Sheridan, R. ATLAS/ICESat-2 L3A Land and Vegetation Height, Version 5. 2021. Available online: https://nsidc.org/data/atl08/versions/5 (accessed on 19 July 2022).
- Zhang, J.; Tian, J.; Li, X.; Wang, L.; Chen, B.; Gong, H.; Ni, R.; Zhou, B.; Yang, C. Leaf area index retrieval with ICESat-2 photon counting LiDAR. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102488. [Google Scholar] [CrossRef]
- Liu, A.; Cheng, X.; Chen, Z. Performance evaluation of GEDI and ICESat-2 laser altimeter data for terrain and canopy height retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Quart. J. Roy. Meteor. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, 1–23. [Google Scholar] [CrossRef]
- Jun, C.; Ban, Y.; Li, S. Open access to Earth land-cover map. Nature 2014, 514, 434. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Chen, L.; Chen, F.; Ban, Y.; Li, S.; Han, G.; Tong, X.; Liu, C.; Stamenova, V.; Stamenov, S. Collaborative validation of GlobeLand30: Methodology and practices. Geo-Spat. Inf. Sci. 2021, 24, 134–144. [Google Scholar] [CrossRef]
- Miao, J.; Niu, L. A survey on feature selection. Procedia Comput. Sci. 2016, 91, 919–926. [Google Scholar] [CrossRef]
- Xing, H.; Niu, J.; Feng, Y.; Hou, D.; Wang, Y.; Wang, Z. A coastal wetlands mapping approach of Yellow River Delta with a hierarchical classification and optimal feature selection framework. CATENA 2023, 223, 106897. [Google Scholar] [CrossRef]
- Huang, H.; Liu, C.; Wang, X.; Biging, G.S.; Chen, Y.; Yang, J.; Gong, P. Mapping vegetation heights in China using slope correction ICESat data, SRTM, MODIS-derived and climate data. ISPRS J. Photogramm. Remote Sens. 2017, 129, 189–199. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Fortin, F.A.; De Rainville, F.M.; Gardner, M.A.G.; Parizeau, M.; Gagné, C. DEAP: Evolutionary algorithms made easy. J. Mach. Learn Res. 2012, 13, 2171–2175. [Google Scholar]
- Olson, R.S.; Moore, J.H. TPOT: A tree-based pipeline optimization tool for automating machine learning. In Proceedings of the Workshop on Automatic Machine Learning; PMLR: New York, NY, USA, 2016; pp. 66–74. [Google Scholar]
- Rahman, M.F.; Onoda, Y.; Kitajima, K. Forest canopy height variation in relation to topography and forest types in central Japan with LiDAR. For. Ecol. Manag. 2022, 503, 119792. [Google Scholar] [CrossRef]
- Le, T.T.; Fu, W.; Moore, J.H. Scaling tree-based automated machine learning to biomedical big data with a feature set selector. Bioinformatics 2020, 36, 250–256. [Google Scholar] [CrossRef]
- Long, M.; Zhu, H.; Wang, J.; Jordan, M.I. Deep transfer learning with joint adaptation networks. In Proceedings of the International Conference on Machine Learning; PMLR: New York, NY, USA, 2017; pp. 2208–2217. [Google Scholar]
- Tan, C.; Sun, F.; Kong, T.; Zhang, W.; Yang, C.; Liu, C. A survey on deep transfer learning. In Proceedings of the Artificial Neural Networks and Machine Learning–ICANN 2018: 27th International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; Proceedings, Part III 27. Springer: Cham, Switzerland, 2018; pp. 270–279. [Google Scholar]
- Ni, W.; Zhang, Z.; Sun, G. Assessment of slope-adaptive metrics of GEDI waveforms for estimations of forest aboveground biomass over mountainous areas. J. Remote Sens. 2021, 2021, 9805364. [Google Scholar] [CrossRef]
- Li, B.; Zhao, T.; Su, X.; Fan, G.; Zhang, W.; Deng, Z.; Yu, Y. Correction of Terrain Effects on Forest Canopy Height Estimation Using ICESat-2 and High Spatial Resolution Images. Remote Sens. 2022, 14, 4453. [Google Scholar] [CrossRef]


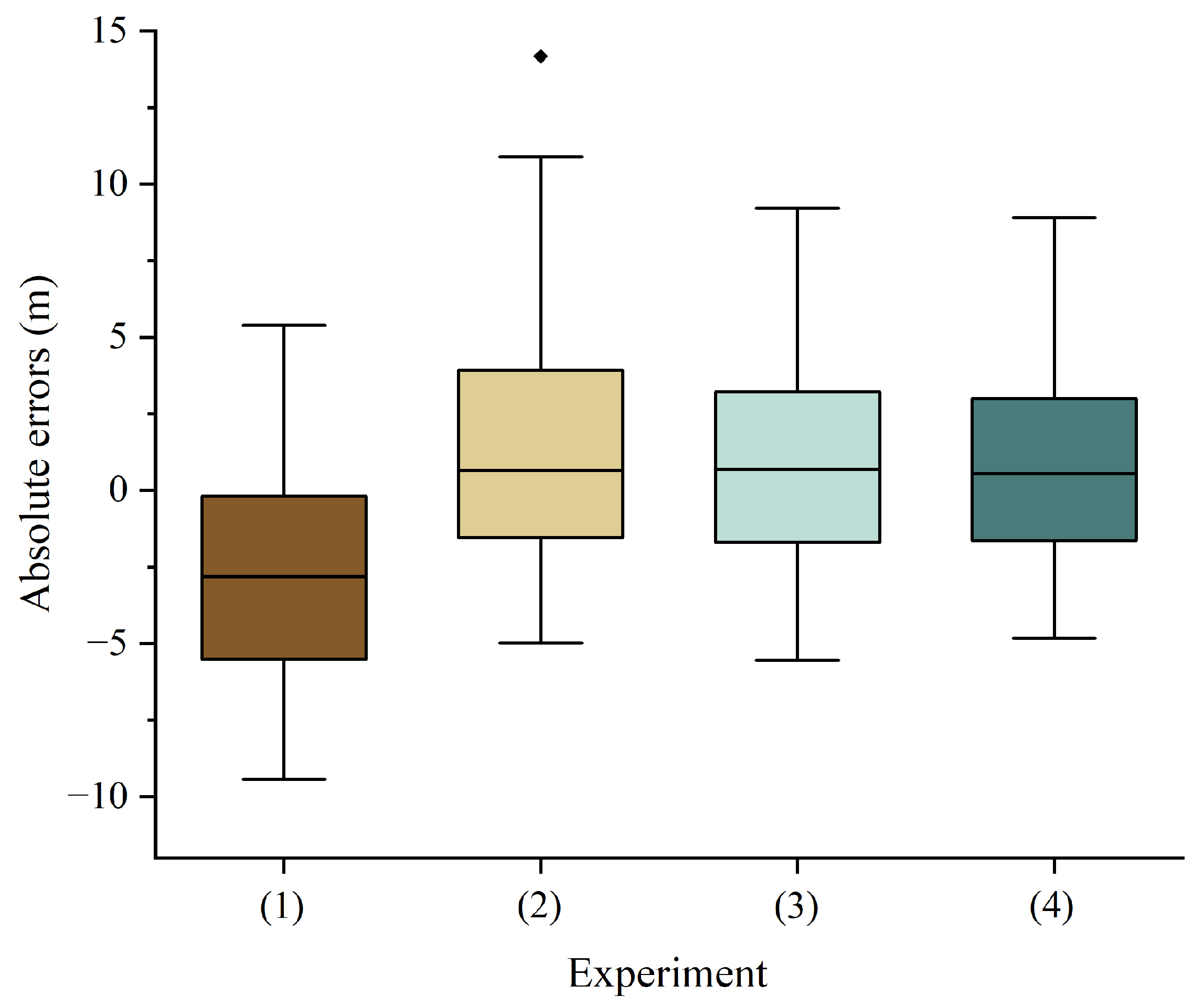
| Dataset | Label and Threshold | Rationale |
|---|---|---|
| GEDI | degrade_flag = 0 | Retaining data that indicates the good status of pointing and positioning information [33]. |
| quality_flag = 1 | Retaining data with valid waveforms [33]. | |
| solar_elevation < 0 | Retaining data acquired at night, as the observation precision of daytime data is significantly lower than that of nighttime data [6]. | |
| sensitivity > 0.9 | Retaining data with high sensitivity [33]. | |
| 2.5 < RH95 < 40 | Retaining data within this range is contingent upon field measurement results. | |
| ICESat-2 | cloud_flag_atm < 2 | Retaining footprints that are less influenced by cloud [34]. |
| h_canopy_uncertainty = 3.4028235 × 1038 | Eliminating data with high measurement uncertainty [34]. | |
| night_flag = 0 | Retaining data acquired at night, as the observation precision of daytime data is significantly lower than that of nighttime data [6]. | |
| SNR > 10 | Retaining data with high signal-to-noise ratio [10]. | |
| 2.5 < h_canopy < 40 | Retaining data within this range is contingent upon field measurement results. |
| Metric | Description |
|---|---|
| latitude | Latitude of each segment center |
| longitude | Longitude of each segment center |
| h_canopy | Forest canopy height (98th percentile height) |
| SNR | Signal-to-noise ratio |
| canopy_h_metrics | 10th, 15th, 20th, 25th, 30th, 35th, 40th, 45th, 50th, 55th, 60th, 65th, 70th, 75th, 80th, 85th, 90th, and 95th percentile height |
| h_max_canopy | Maximum canopy height |
| h_mean_canopy | Mean canopy height |
| h_median_canopy | Median canopy height |
| h_min_canopy | Minimum canopy height |
| terrain_slope | Slope of ground |
| beam_azimuth | Beam azimuth |
| dem_h | Ground elevation |
| fvc | Fraction of vegetation coverage |
| Type | Variable | Description |
|---|---|---|
| Spectral reflectance | B, G, R, RE1, RE2, RE3, NIR, NNIR, SWIR1, SWIR2 | S-2 2-8, 8A, 11, 12 bands |
| Vegetation indices | NDVI | (NIR − R)/(NIR + R) |
| Enhanced Vegetation Index (EVI) | 2.5 × ((NIR − R)/(NIR + 6 × R − 7.5 × B + 1)) | |
| Leaf Area Index (LAI) | 3.618 × EVI − 0.118 | |
| Atmospherically Resistant Vegetation Index (ARVI) | ((NIR − (2 × R) + B)/(NIR + (2 × R) + B)) | |
| Structure Insensitive Pigment Index (SIPI) | (NIR − B)/(NIR − R) | |
| Red Edge Chlorophyll Index (RECI) | (RE3/RE1) − 1 | |
| Green Chlorophyll Index (GCI) | (NIR/G) − 1 | |
| Red Green Ratio Index (RGRI) | R/G | |
| MERIS Terrestrial Chlorophyll Index (MTCI) | (RE2 − RE1)/(RE1 − R) | |
| Soil Adjust Vegetation Index (SAVI) | (NIR − R) × (1 + 0.5)/(NIR + R + 0.5) | |
| Difference Vegetation Index (DVI) | NIR-R | |
| Timing NDVI features | Maximum NDVI, minimum NDVI, mean NDVI, stdDev NDVI | Maximum, minimum, mean, and standard deviation of temporal NDVI |
| Climate data | Precipitation, temperature | Average precipitation and temperature from 2000 to 2020 |
| Terrain features | Elevation, slope, aspect | Elevation, slope and aspect of ground |
| Backscatter coefficients | VV, VH | Backscattering coefficients values of VV and VH polarization |
| Biophysical features | Fraction of vegetation coverage (FVC) | Proportion of ground cover by vegetation |
| Dataset | Feature |
|---|---|
| GEDI | B, G, R, RE1, RE2, NIR, SWIR1, SWIR2, SIPI, RECI, GCI, RGR, MTCI, maximum NDVI, minimum NDVI, mean NDVI, stdDev NDVI, DEM, slope, aspect, temperature, VV, VH, FVC; |
| ICESat-2 | G, R, NIR, SWIR1, SWIR2, MTCI, maximum NDVI, minimum NDVI, mean NDVI, DEM, slope, temperature, VV, VH; |
| GIF | B, G, R, RE1, NIR, SWIR1, SWIR2, MTCI, maximum NDVI, minimum NDVI, mean NDVI, stdDevNDVI, DEM, slope, aspect, VV, VH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Yao, F.; Zhang, J.; Ma, E.; Yao, L.; Dong, Z. Genetic Programming Guided Mapping of Forest Canopy Height by Combining LiDAR Satellites with Sentinel-1/2, Terrain, and Climate Data. Remote Sens. 2024, 16, 110. https://doi.org/10.3390/rs16010110
Wu Z, Yao F, Zhang J, Ma E, Yao L, Dong Z. Genetic Programming Guided Mapping of Forest Canopy Height by Combining LiDAR Satellites with Sentinel-1/2, Terrain, and Climate Data. Remote Sensing. 2024; 16(1):110. https://doi.org/10.3390/rs16010110
Chicago/Turabian StyleWu, Zhenjiang, Fengmei Yao, Jiahua Zhang, Enhua Ma, Liping Yao, and Zhaowei Dong. 2024. "Genetic Programming Guided Mapping of Forest Canopy Height by Combining LiDAR Satellites with Sentinel-1/2, Terrain, and Climate Data" Remote Sensing 16, no. 1: 110. https://doi.org/10.3390/rs16010110
APA StyleWu, Z., Yao, F., Zhang, J., Ma, E., Yao, L., & Dong, Z. (2024). Genetic Programming Guided Mapping of Forest Canopy Height by Combining LiDAR Satellites with Sentinel-1/2, Terrain, and Climate Data. Remote Sensing, 16(1), 110. https://doi.org/10.3390/rs16010110








