Abstract
Forages are the most important kind of crops at high latitudes and are the main feeding source for ruminant-based dairy industries. Maximizing the economic and ecological performances of farms and, to some extent, of the meat and dairy sectors require adequate and timely supportive field-specific information such as available biomass. Sentinel-2 satellites provide open access imagery that can monitor vegetation frequently. These spectral data were used to estimate the dry matter yield (DMY) of harvested forage fields in northern Sweden. Field measurements were conducted over two years at four sites with contrasting soil and climate conditions. Univariate regression and multivariate regression, including partial least square, support vector machine and random forest, were tested for their capability to accurately and robustly estimate in-season DMY using reflectance values and vegetation indices obtained from Sentinel-2 spectral bands. Models were built using an iterative (300 times) calibration and validation approach (75% and 25% for calibration and validation, respectively), and their performances were formally evaluated using an independent dataset. Among these algorithms, random forest regression (RFR) produced the most stable and robust results, with Nash–Sutcliffe model efficiency (NSE) values (average ± standard deviation) for the calibration, validation and evaluation of 0.92 ± 0.01, 0.55 ± 0.22 and 0.86 ± 0.04, respectively. Although relatively promising, these results call for larger and more comprehensive datasets as performances vary largely between calibration, validation and evaluation datasets. Moreover, RFR, as any machine learning algorithm regression, requires a very large dataset to become stable in terms of performance.
1. Introduction
Leys are temporary forages (either harvested or grazed) which are part of a crop rotation. In Nordic countries, forages are the main feeding source for livestock in dairy and meat production systems. In Sweden, ley dominates the agricultural land use, and comprised 44% of the total arable lands in 2022 [1]. Leys are typically harvested 2–4 times per year in southern Sweden, and 2–3 times in northern Sweden. Determining the harvest window, especially for first harvest, is important for farmers, since it directly affects the forage yield and quality and, ultimately, the profitability [2]. Accurate estimations of forage biomass is one of the factors for determining the harvest time and is also important for fertilization strategies and herbicide spraying [3].
Traditional approaches involving field sampling and laboratory measuring are destructive and time- and resource-consuming. As an alternative, several studies explored the utilization of hand-held rising plate meters and field spectrometers (e.g., FieldSpec, Yara N-sensor) to make rapid and accurate biomass in situ estimations of forages [4,5,6,7]. Rising plate meters are easy-to-use and inexpensive tools that measure the height and density of swards from which biomass can be derived based on species-dependent calibration curves. However, these tools have limited spatialization capabilities. Field spectrometers provide high-resolution spectral information, but their use for practical applications is limited by their costs and, more importantly, limited spatialization capabilities compared to imaging sensors. Alternatively, open-access satellites (e.g., Landsat, MODIS and Sentinel-2) supply multispectral images with a spatial resolution ranging between 10 and 250 m for large-scale vegetation monitoring [8,9,10]. Satellite imaging systems offer several advantages, such as technical maturity and stability, open access to data and a large field of view [11].
The Sentinel-2 satellites constellation provides open access images with a relatively high spatial resolution (10–60 m) and high frequency of revisit [12] of about 2 days in northern Sweden. These time series of satellite images can be useful indicators to monitor the biomass and growth of crops [13,14,15].
Traditional satellite-based biomass estimation models are usually developed by linking spectral-derived vegetation index (hereafter referred to as VI, such as the normalized difference vegetation index, NDVI) and field measurements using basic univariate regression (UR) models, such as linear, polynomial, exponential, power, etc. [10,16]. However, with increasingly larger datasets, multivariate regressions (MR), e.g., partial least square regression (PLSR) and machine learning-based support vector machine (SVM) regression (SVR) and random forest (RF) regression (RFR), have become increasingly used for the estimation of crop traits, such as leaf area index (LAI [17,18]), plant nitrogen nutrition [19,20] and biomass [3,5,21,22]. PLSR aims to extract latent factors that represent most of the variation between predictor and response variables to reduce overfit [23,24]. Therefore, PLSR is able to encompass more explanatory variables (e.g., individual bands and VIs) to build regression models with greater robustness compared to traditional regression approaches. SVM is a nonparametric statistical technique without data distribution assumptions. It was originally proposed by Vapnik [25] for classification purposes by setting labels for datasets and searching separation hyperplanes; it was later developed further for regressions [26]. Similar to SVM, RF requires no specific data distribution assumption, but the difference is that it uses an ensemble-learning method, which utilizes multiple algorithms (trees) over one model to make a more accurate prediction [27], and it was also developed for regressions. RFR can deal with small size datasets [28] as well as high dimensional and collinear data [29] at a high running speed.
Currently, to the authors’ best knowledge, few studies are reported to have tested the use of Sentinel-2 to estimate forage biomass production (e.g., [9,16,30,31]) and there are no relevant studies in Nordic countries where the revisit frequency of Sentinel-2 satellite constellations is higher due to the higher latitude, but on the other hand, the availability of the data is affected by the high occurrence of clouds [32,33]. Thus, the aim of this study was to build and compare several regression models for forage biomass estimation using Sentinel-2 multispectral data in northern Sweden. The objective was to build regression models for dry matter yield (DMY) estimation using different approaches and compare their performance.
2. Materials and Methods
2.1. Field Measurements
The overall workflow of this study is shown in Figure 1. The field samplings were conducted from 2019 to 2020 in northern Sweden (63.0–65.5°N, Figure 2) at four locations: Ås, Lännäs, Öjebyn and Röbäcksdalen. The fields in different locations were mixes of different species, including timothy (Phleum pratense), red clover (Trifolium pratense) and weeds (e.g., Elymus repens).
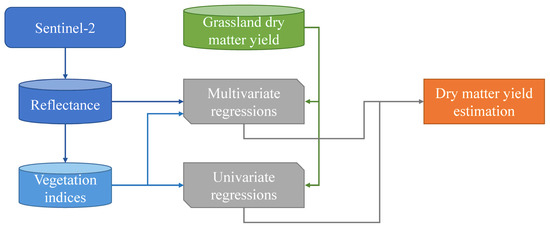
Figure 1.
Overall workflow of this study.
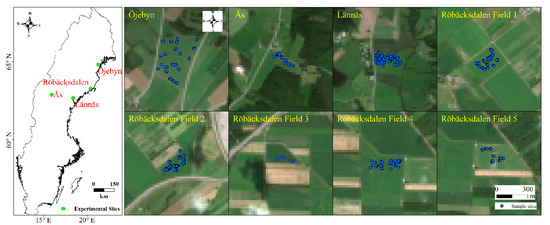
Figure 2.
Locations of the study sites across northern Sweden. The green dots in the left figure show the experimental sites and the blue dots in the right figures denote the field sampling sites. The scale in the left figure is for whole Sweden, and the scale at the corner in the right figures is for the right 8 figures showing different fields.
One-way ANOVA tests based on daily climate parameters were conducted to check the seasonal and spatial meteorological difference. The residual normality and variance homogeneity were checked, and if the conditions were not fulfilled, non-parametric Kruskal–Wallis rank sum test was used alternatively. Based on the analyses, there were no significant seasonal differences (p > 0.05) among the four locations in terms of the climate conditions for the field season (approximately from 1 May to 30 September). For example, mean temperature ranged from 11–13 °C in two years and four places (Table 1). The exception was Öjebyn, where the precipitation in 2019 was significantly higher than 2020.

Table 1.
Meteorological conditions of the four study sites during the growing season (May–September) in 2019 and 2020. The temperature shown is daily averaged for the whole growing season, whereas precipitation and radiation are accumulated values. Data were obtained from Lantmet [34].
The spatial variations in each season depended on climate parameters. In each season, the spatial variations of temperature among different locations were not significant (p > 0.05); however, the spatial differences of precipitation and radiation among different locations were significant (p < 0.05). For example, the average precipitation in Öjebyn was 355.1 in 2019, which was more than for other sites (Table 1). The exception occurred in 2020 for precipitation, in which there was a significant difference in precipitation among different locations.
In each sampling site and year, a quadrat with 50 cm sides was used to take samples from May to September. Each sample consisted of three subsamples with a spacing of 1–2 m between quadrats. GPS coordinates were recorded and samples were taken 8 cm above the ground to follow the typical farming practice (Table 2). Subsamples were hand-separated into three groups (grass, clover and weeds) for botanical composition (BC) measurement. Subsamples were stored at 4 °C before fresh weight was measured. Subsamples were then oven-dried at 60 °C for 48 h and weighed again for DMY determination for different species [3]. Total DMY was calculated as the sum of DMY from each group. BC was expressed as the proportion of DMY from each species relative to the total DMY. Sample (i.e., related to one Sentinel-2 pixel) DMY was obtained by averaging the three subsample values.

Table 2.
Locations, coordinates, working years, management and number of sample points (n, 3 subsamples were averaged as 1 observation, i.e., sample point) of the study sites. Organic means no chemical fertilizer or herbicide was applied. Conventional indicates that the field was managed using chemical fertilizers and possibly herbicides.
2.2. Remote Sensing Data
Sentinel-2 A and B level 2A images with 20 m spatial resolution obtained over the sites of interest in 2019 and 2020 were downloaded during the growing season from the European Space Agency (ESA) Copernicus website. The characteristics of the spectral bands (wavelength and bandwidth) are described on the Copernicus web portal [35].
The scene classification map (SCL) produced using the Sen2Cor algorithm from the European Space Agency classifies Sentinel-2 images to twelve classes, including cloud, shadow, vegetation, soil, water and snow [36], with Level 2A images at 20 m spatial resolution. This was used to mask all of the pixels, which were recognized as non-vegetation, before further processing and analysis.
2.3. Extraction of Reflectance Data
To avoid discrepancies between field measurements and radiometric information, a threshold of 3 days of difference between imaging date and sampling date was applied, which means that if the time difference between the available cloud-free satellite imagery and field sampling was more than 3 days, then the observation would be discarded. Reflectance information for each subsample from each band was extracted using the “extract” function from package “raster” in R environment [37].
The extracted reflectance values and total DMY values of the three subsamples were averaged for regression analysis. The spatial and temporal distribution of collected datasets are listed in Table 3. There are less observations (n) compared to those listed in Table 2 due to the exclusion of samples based on the difference between dates of available Sentinel-2 data and field sampling data. Since the datasets were from different locations, years and sampling days, there was no autocorrelation issue for all of the datasets, which was determined by using the “acf” function from the package “forecast” in R environment [37].

Table 3.
The number of samples available after data preprocessing for each site and year.
2.4. Regression Models
Several regression methods were tested to estimate DMY in this study: VI-based univariate regressions and multivariate regressions, including machine learning algorithms.
Plant biomass-related VIs were identified through a literature search using the following keywords: “dry matter”, “nitrogen”, “chlorophyll”, “biomass”, “index”, “Sentinel-2”, “satellite” and “remote sensing”. The descriptions and calculation formulae are in Table 4. All analyses were conducted using R environment [37].
2.4.1. Univariate Regression Models
The VIs were correlated with DMY by several UR models: linear, exponential, power, polynomial and logarithmic. Models were built using the ‘lm’ function in R environment [37].
2.4.2. Multivariate Regression Models
PLSR, SVR and RFR were used as multivariate regression models, with pixelwise individual spectral bands and calculated VIs (Table 4) as the input variables. This approach enables all of the spectral information to be utilized [38,39,40].
PLSR links the predictor and response variables by decomposing data matrices so that only the most important linear combinations are utilized in the regression, optimizing the covariance between predictor and response variables. The “pls” package [41] was used to run PLSR. The proper number of components was determined by minimizing the root mean square error (RMSE) for the K-fold cross-validated predictions, with K = 10.
In the basic form, SVM is a binary classifier (linear or nonlinear) which identifies the boundary between two different classes, assuming that the multidimensional data are distinguishable. In practice, SVMs define an optimal separation hyperplane to divide the datasets into several discrete predefined classes within the training data [42]. SVM regression analysis is expected to produce a continuous prediction output [26]. The package “e1071” was used to conduct SVR. A grid search was implemented with a radial kernel to determine the hyperparameters ε, C and γ to an optimal manner as they measure and define the model prediction errors so that they affect the accuracy and generality capabilities of the SVR. The details of ε, C and γ were presented in Cristianini and Shawe-Taylor’s paper [43].
RFR utilized two-thirds of the samples (in-bag samples) to train several regression trees, and the remaining one-third (out-of-bag (OOB) samples) was used for internal cross-validation [27]. Each tree split was defined using a random subsection of the predictor variables at each node. The average of the results from all the trees is the final result [44]. The “RandomForest” package was used to build the models, which were tuned using the “tuneRF” function, and a default ntree was set to 500. The detailed procedures of RFR algorithms running can be found in Peng et al.’s work [19]. Two measures (%IncMSE and IncNodePurity) were calculated to show the importance of predictor variables [45]. The mean square error, %IncMSE, is measured as the mean decrease in accuracy of predictions of the OOB samples when a given variable is not included in the model. The training residual sum of squares, IncNodePurity, describes the total decrease in node impurity derived from splits over that variable.

Table 4.
Vegetation indices (VIs) used in the study and heat map of Nash–Sutcliffe efficiency (NSE) for univariate regressions. B3, B4 and B8A are green, red and near infrared; B11 and B12 are shortwave infrared bands 11 and 12, respectively; B5, B6 and B7 are vegetation red-edge bands 1, 2 and 3, respectively. The sequence of VIs is sorted by the calibration NSE values with the order from largest to lowest values.
Table 4.
Vegetation indices (VIs) used in the study and heat map of Nash–Sutcliffe efficiency (NSE) for univariate regressions. B3, B4 and B8A are green, red and near infrared; B11 and B12 are shortwave infrared bands 11 and 12, respectively; B5, B6 and B7 are vegetation red-edge bands 1, 2 and 3, respectively. The sequence of VIs is sorted by the calibration NSE values with the order from largest to lowest values.
| Vegetation Index | Name of Vegetation Index | Formula | Reference | Calibration (n = 49) | Validation (n = 16) | Evaluation (n = 9) | ||
|---|---|---|---|---|---|---|---|---|
| REDVI2 | Red Edge Difference Vegetation Index | B8A − B6 | [46] | |||||
| REDVI1 | Red Edge Difference Vegetation Index | B8A − B5 | [46] | |||||
| MCARI11 | Modified chlorophyll absorption in reflectance aindex | [(B8A − B5) − 0.2 × (B8A − B3)] × (B8A/B5) | [46] | |||||
| GDVI | Green Difference Vegetation Index | B8A − B3 | [47] | |||||
| GOSAVI | Green optimized soil adjusted vegetation index | (1 + 0.16) × (B8A − B3)/(B8A + B3 + 0.16) | [47] | |||||
| TCI | Terrestrial chlorophyll index | (B6 − B5)/(B5 − B4) | [48] | |||||
| NDRE1 | Normalized Difference Red-edge Index | (B8A − B5)/(B8A + B5) | [49] | |||||
| SWIR11-TCARI3 | SWIR11 related transformed Chlorophyll Absorption Reflectance Index | 3 × [(B7 − B11) − 0.2 × (B7 − B3) × (B7/B11)] | [50] | |||||
| CIre1 | Red-edge Chlorophyll Index | (B8A/B5) − 1 | [51] | |||||
| NDI1 | Normalized difference index | (B8A − B5)/(B8A + B4) | [52] | |||||
| MCARI13 | Modified chlorophyll absorption in reflectance index | [(B8A − B7) − 0.2 × (B8A − B3)] × (B8A/B7) | [46] | |||||
| DVI | Difference vegetation index | B8A − B4 | [53] | |||||
| SWIR11-MCARI3 | SWIR11 related modified chlorophyll absorption in reflectance index | [(B7 − B11) − 0.2 × (B7 − B3)] × (B7/B11) | [50] | |||||
| SWIR11-OSAVI | SWIR11 related optimized soil adjusted vegetation index | (1 + 0.16) × (B8A − B11)/(B8A + B11 + 0.16) | [50] | |||||
| GNDVI | Green Normalized Difference Vegetation Index | (B8A − B3)/(B8A + B3) | [54] | |||||
| SWIR12-MCARI3 | SWIR12 related modified chlorophyll absorption in reflectance index | [(B7 − B12) − 0.2 × (B7 − B3)] × (B7/B12) | [50] | |||||
| SWIR12-OSAVI | SWIR12 related optimized soil adjusted vegetation index | (1 + 0.16) × (B8A − B12)/(B8A + B12 + 0.16) | [50] | |||||
| CIgreen | Green Chlorophyll Index | (B8A/B3) − 1 | [55] | |||||
| GRVI | Green ratio Vegetation index | B8A/B3 | [56] | |||||
| MTVI | Modified Triangular Vegetation Index | 1.5 × (1.2 × (B8A − B3) − 2.5 × (B4 − B3))/sqrt((2 × B8A + 1)2 − (6 × B8A − 5 × sqrt(B4)) − 0.5) | [57] | |||||
| S2REP2 | Sentinel-2 red-edge position | 705 + 35 × [0.5 × (B7 + B4) − B5]/(B6 − B5) | [50] | |||||
| OSAVI | Optimized soil adjusted vegetation index | (1 + 0.16) × (B8A − B4)/(B8A + B4 + 0.16) | [58] | |||||
| MCARI23 | Modified chlorophyll absorption reflectance index | [(B7 − B4) − 0.2 × (B7 − B3)] × (B7/B4) | [59] | |||||
| TCARI3 | Transformed Chlorophyll Absorption Reflectance Index | 3 × [(B7 − B4) − 0.2 × (B7 − B3) × (B7/B4)] | [60] | |||||
| SWIR11-MCARI2 | SWIR11 related modified chlorophyll absorption in reflectance index | [(B6 − B11) − 0.2 × (B6 − B3)] × (B6/B11) | [50] | |||||
| SWIR11-TCARI2 | SWIR11 related transformed Chlorophyll Absorption Reflectance Index | 3 × [(B6 − B11) − 0.2 × (B6 − B3) × (B6/B11)] | [50] | |||||
| SWIR12-MCARI2 | SWIR12 related modified chlorophyll absorption in reflectance index | [(B6 − B12) − 0.2 × (B6 − B3)] × (B6/B12) | [50] | |||||
| NNIR | Normalized NIR Index | B8A/(B8A + B4 + B3) | [47] | |||||
| SWIR12-TCARI3 | SWIR12 related transformed Chlorophyll Absorption Reflectance Index | 3 × [(B7 − B12) − 0.2 × (B7 − B3) × (B7/B12)] | [50] | |||||
| IRECI1 | Inverted Red-Edge Chlorophyll Index | (B8A − B4)/(B6 − B5) | [61] | |||||
| MCARI22 | Modified chlorophyll absorption reflectance index | [(B6 − B4) − 0.2 × (B6 − B3)] × (B6/B4) | [59] | |||||
| TCARI2 | Transformed Chlorophyll Absorption Reflectance Index | 3 × [(B6 − B4) − 0.2 × (B6 − B3) × (B6/B4)] | [60] | |||||
| IRECI2 | Inverted Red-Edge Chlorophyll Index | (B7 − B4)/(B6 − B5) | [62] | |||||
| RVI | Ratio Vegetation index | B8A/B4 | [56] | |||||
| CIre3 | Red-edge Chlorophyll Index | (B8A/B7) − 1 | [51] | |||||
| NDRE3 | Normalized Difference Red-edge Index | (B8A − B7)/(B8A + B7) | [49] | |||||
| NDI3 | Normalized difference index | (B8A − B7)/(B8A + B4) | [52] | |||||
| NDVI | Normalized Difference Vegetation Index | (B8A − B4)/(B8A + B4) | [63] | |||||
| NDI2 | Normalized difference index | (B8A − B6)/(B8A + B4) | [52] | |||||
| SWIR11-MCARI1 | SWIR11 related modified chlorophyll absorption in reflectance index | [(B5 − B11) − 0.2 × (B5 − B3)] × (B5/B11) | [50] | |||||
| S2REP1 | Sentinel-2 red-edge position | 705 + 35 × [0.5 × (B8A + B4) − B5]/(B6 − B5) | [61] | |||||
| SWIR12-TCARI2 | SWIR12 related transformed Chlorophyll Absorption Reflectance Index | 3 × [(B6 − B12) − 0.2 × (B6 − B3) × (B6/B12)] | [50] | |||||
| GDR | Green reflectance divide red reflectance | B3/B4 | [64] | |||||
| SWIR11-NRI | SWIR11 related Normalized ratio index | (B11 − B4)/(B11 + B4) | [50] | |||||
| MCARI12 | Modified chlorophyll absorption in reflectance index | [(B8A − B6) − 0.2 × (B8A − B3)] × (B8A/B6) | [46] | |||||
| SWIR12-NRI | SWIR12 related Normalized ratio index | (B12 − B4)/(B12 + B4) | [50] | |||||
| CIre2 | Red-edge Chlorophyll Index | (B8A/B6) − 1 | [51] | |||||
| NDRE2 | Normalized Difference Red-edge Index | (B8A − B6)/(B8A + B6) | [49] | NSE | ||||
| REDVI3 | Red Edge Difference Vegetation Index | B8A − B7 | [46] | 1 | ||||
| GMR | Green reflectance minus red reflectance | B3 − B4 | [64] | 0.8 | ||||
| MCARI21 | Modified chlorophyll absorption reflectance index | [(B5 − B4) − 0.2 × (B5 − B3)] × (B5/B4) | [59] | 0.6 | ||||
| CVI | Chlorophyll vegetation index | (B8A/B3) × (B4/B3) | [65] | 0.4 | ||||
| SWIR12-TCARI1 | SWIR12 related transformed Chlorophyll Absorption Reflectance Index | 3 × [(B5 − B12) − 0.2 × (B5 − B3) × (B5/B12)] | [50] | 0.2 | ||||
| SWIR12-MCARI1 | SWIR12 related modified chlorophyll absorption in reflectance index | [(B5 − B12) − 0.2 × (B5 − B3)] × (B5/B12) | [50] | 0 | ||||
| SWIR11-TCARI1 | SWIR11 related transformed Chlorophyll Absorption Reflectance Index | 3 × [(B5 − B11) − 0.2 × (B5 − B3) × (B5/B11)] | [50] | −0.2 | ||||
| TCARI1 | Transformed Chlorophyll Absorption Reflectance Index | 3 × [(B5 − B4) − 0.2 × (B5 − B3) × (B5/B4)] | [60] | −0.4 | ||||
2.5. Model Evaluation
We used a calibration/validation/evaluation strategy to test the robustness of the models. Data from Röbäcksdalen 2019 were used as the evaluation dataset. The remaining dataset was randomly sampled for calibration (75%) and validation (25%).
Since the size of the analysis dataset was limited (Table 3), all of the univariate and multivariate models were independently tested 300 times to evaluate the effect of the data splitting on the performance of the models.
Performances of the models were assessed using Nash–Sutcliffe model efficiency (NSE) and root mean square error (RMSE):
where and are observed and modeled values, respectively, and are mean observed and modeled values, and n is the total number of observations.
3. Results
3.1. Dry Matter Yield Distribution
The average sampled DMY across the whole growing season in 2019 and 2020 were, respectively, 1.16 and 0.56 t ha−1 at Ås, 0.78 and 0.95 t ha−1 at Lännäs, and 1.38 and 1.32 t ha−1 at Röbäcksdalen. At Öjebyn, the samples were only taken in 2019 and the average DMY was 2.76 t ha−1. The variation in sampled DMY between different sites and years had a wide range (Figure 3), which was beneficial for model calibration. At Öjebyn, the DMY was significantly higher than other stations in 2019, and the main reason might be that there was a more intense solar radiation (2852 MJ m−2 during the growing season in 2019, see Table 1).
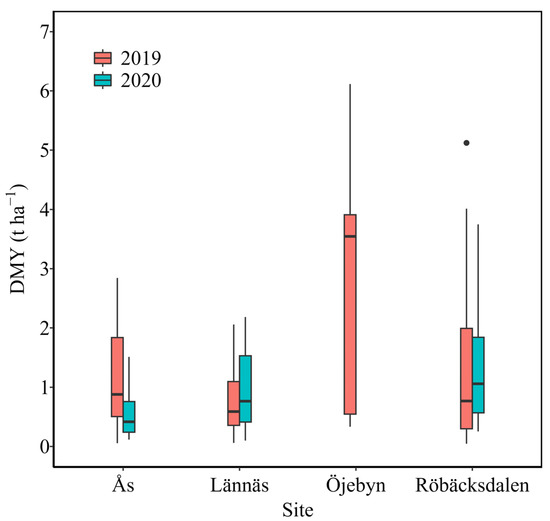
Figure 3.
Variation in forage dry matter yield (DMY) of the dataset (180 samples, Table 2) at four sites in 2019 and 2020. The horizontal lines in the boxplot show the first quartile (Q1), median and third quartile (Q3) of the datasets. The upper end of the black line is the upper bound for detecting outliers (Q3 + 1.5 × (Q3–Q1)) and the bottom end of the black line is the lower bound for detecting outliers (Q3 + 1.5 × (Q3–Q1)). The black dot shows outlier, which was removed for the regression analyses.
The measured BC varied among different locations. At Ås, the clover was the dominant species (more than 50%). At Lännäs and Röbäcksdalen, timothy was the main species (on average more than 70%). At Öjebyn, the proportion of weeds was higher compared to other places due to the organic management approaches (no herbicides were used).
3.2. Univariate Regressions
The results of UR are shown in Table 4 as a heat map. Generally, the fits between VIs and DMY differed from moderate to poor depending on the VI. None of the calibration and validation NSE values exceeded 0.55. Among these VIs, red-edge-related VIs had stronger correlations with DMY compared to others. Short-wave infrared (SWIR)-related VIs did not show a strong ability to correlate with DMY. Surprisingly, accuracies for evaluation were higher than for calibration and validation (e.g., average NSE of 0.51 among 56 VIs for evaluation against 0.33 and 0.22 for calibration and validation). However, the evaluation dataset only had nine samples; therefore, the results must be interpreted cautiously.
3.3. Multivariate Regressions
Table 5 shows the results from the PLSR, SVR and RFR models. Overall, calibration accuracies were high, with mean NSE and RMSE ranging from 0.81 to 0.95 and 0.19 to 0.39 t ha−1, respectively. However, for the validation, the accuracies decreased. Mean NSE ranged from 0.34 to 0.61, and mean RMSE increased to 0.58 to 0.75 t ha−1. Evaluation underlined obvious model differences, as RFR performed better than PLSR and SVR (mean NSE and RMSE value of 0.86 and 0.26 t ha−1).

Table 5.
Statistical analysis results for the multivariate regressions, using methods from partial least square regression (PLSR), random forest regression (RFR) and support vector regression (SVR). The values show the statistical distribution (mean ± standard deviation) of NSE and RMSE from running the model 300 times.
For both calibration and validation, the SVR and RFR performed better than PLSR. The accuracy of SVR was slightly higher than RFR due to the relatively higher mean NSE, but RFR performed more stably for calibration since standard deviation (SD) values were lower. When considering the evaluation dataset, RFR showed a better performance than PLSR and SVR, with higher NSE and less spread of values.
Based on the calculations of the variable importance measures (%IncMSE and IncNodePurity) shown in Figure 4, the bands of near infrared (NIR) and red-edge and the related VIs (e.g., REDVI1, REDVI 2, NDRE1, TCI, CIre1) are the most important for the RFR analysis.
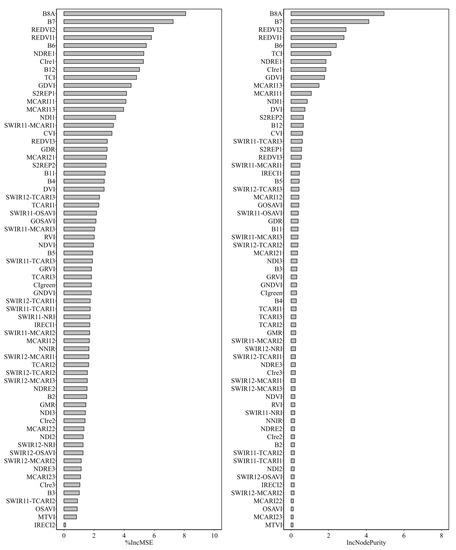
Figure 4.
Importance of predictor variables (individual bands and vegetation indices) according to the random forest regression analysis in explaining the dry matter yield (DMY). Descriptions of the individual bands and indices are given in Table 4.
Figure 5 shows the effect of running the model 300 times on the NSE of calibration, validation and evaluation. SVR and RFR show similar median values of validation NSE but the values were lower comparing to calibration, yet the majority of NSE values distributed from 0.4 to 0.8 suggest relatively comparable accuracies for SVR and RFR. In addition, the variation in NSE values intuitively indicates that RFR was more stable, especially for model calibration and evaluation, which is confirmed by the results shown in Table 5 (lower SD values for RF calibration).
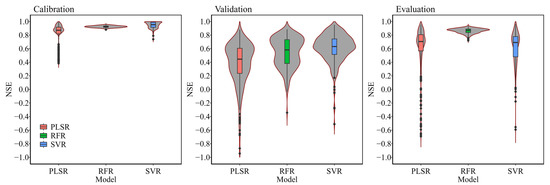
Figure 5.
Variation in Nash–Sutcliffe efficiency (NSE) of running the models 300 times using partial least square regression (PLSR), random forest regression (RFR) and support vector machine-based regression (SVR). The horizontal lines in the boxplot show the first quartile, median and third quartile of NSE values.
Figure 6 shows scatterplots of observed versus RFR-estimated DMY, using a model with a calibration NSE value of 0.92 (Table 5), which was the average value of randomizing the samples and running the model 300 times (Table 5). The corresponding NSE values for validation and evaluation of the selected RFR model were 0.62 and 0.84, respectively. The distributions of scatterplot points showed that the effect from the BC on the selected RFR model was mild.
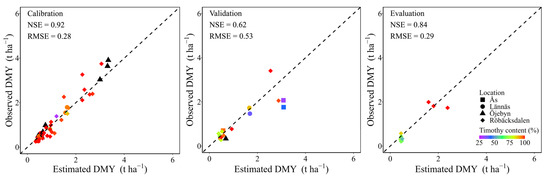
Figure 6.
Observed versus estimated dry matter yield (DMY, t ha−1) for selected random forest regression (RFR) model with a calibration NSE value of 0.92 (average value of 300 runs, Table 5). The timothy contents (%) are marked with different colors and the black color indicates that the botanical compositions of the samples were not measured, hence there was no data.
4. Discussion
Even though several VIs (e.g., red-edge band-related, Table 4) fitted moderately with DMY (NSE values for model calibration were higher than 0.5), the overall VI-based UR performed inadequately (Table 4). The evaluation accuracies were much higher than expected, which was likely derived from the small size of the evaluation dataset (n = 9); however, the accuracies of calibration and validation were low, which further indicates that the overall accuracy of UR models was not convincing. Adar et al. [38] reported similar results where the VIs calculated from satellite images were proven to have been insufficient to capture the submeter variability of rangelands due to the relatively coarse spatial resolution. Several VIs, such as NDVI, also have saturation issues when the LAI reaches three [40,66], which could contribute to the poor correlation as well. Indeed, in northern Sweden, crops in general and grasslands in particular grow exceedingly fast once temperature is not limiting due to long daylight hours, and canopy closure is rapidly reached. Another reason could be that the datasets used in this study included several sites and years, resulting in different conditions (Table 1 and Table 2), which made it challenging to build a robust model to accommodate this heterogeneity based on simple VIs.
In contrast to the relatively poor performance of UR, MR performed notably better with higher calibration NSE values, thus emphasizing the advantages of PLSR and especially nonparametric machine learning-based regression approaches (SVR and RFR), which do not have distributional assumptions and variance requirements [26,67]. The most notable enhancement of MR over UR is that it can manage multiple variables in a single model and take advantage of more explanatory variables, and thus, information.
PLSR and RFR can identify the importance of predictor variables based on either principal components analysis and consequent components selection [68] or the OOB indices calculation [19,67]. Thus, less important and collinear variables can be discarded, which could significantly improve the model performance. In this study, RFR outperformed PLSR to a certain extent in model calibration, validation and evaluation (Table 5) and the possible reason would be that RFR has a stronger ability to produce relatively robust models [69]. For SVR, unlike PLSR and RFR, it cannot distinguish the importance of variables and select the variables by statistical analysis, but the model accuracy would be advanced to a large extent once the parameters of the kernel are correctly set [3,38]. However, it is also the main drawback for SVR as it needs computation and time to find the right kernel and there is a risk that the found kernel is not optimal [26]. RFR has apparent merits, such as easy operation, high efficiency and reliable robustness [29]. Several remote sensing-based studies in other areas have found similar results, i.e., simple VIs were not able to produce sufficiently robust models for prediction, but RFR could improve performance, such as potato N status estimation [19] and lake transparency monitoring [70].
It was observed in this study that the BC had little effect on the selected RFR model. RF has a strong ability to integrate different datasets from different sources into a single model for classification or regression analyses [19,71]. A previous study reported that the effect from BC on the Sentinel-2 satellite data-based regression modeling for pasture biomass estimation was unclear [9]. This study answered this question to a certain extent and it should be continued to be explored and quantified in future studies.
By applying the selected RFR model shown in Figure 6, it is possible to map the instantaneous DMY of ley fields before harvest (Figure 7). From the map, farmers could potentially identify the variation within and among fields, which could help to determine the optimal harvest time and plan the harvesting sequence.
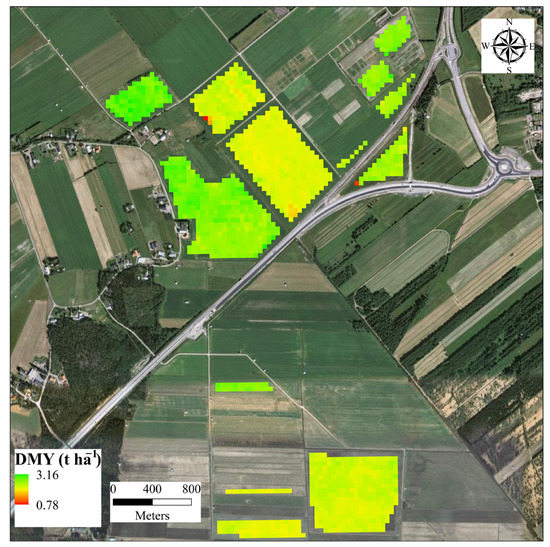
Figure 7.
Layout of the estimated dry matter yield (DMY) for the first harvest from Sentinel-2 imagery obtained on 09 June 2019, one week before the first harvest using a selected RFR model, at Röbäcksdalen field research station. The background imagery is obtained from Google Earth.
However, it should be mentioned that due to the coverage of clouds and shadows, there was some important missing information. As the example in Figure 8 shows, the time-series DMY estimation from Sentinel-2 images using the RFR model reflected the growth pattern of leys, including the reduction in biomass following harvests; however, as key information was missing due to the presence of clouds or shadows (the interval between available cloud-free Sentinel-2 images before the second harvest was 15 days), the time-series DMY estimation could not precisely track the growth conditions between the first and second harvests.
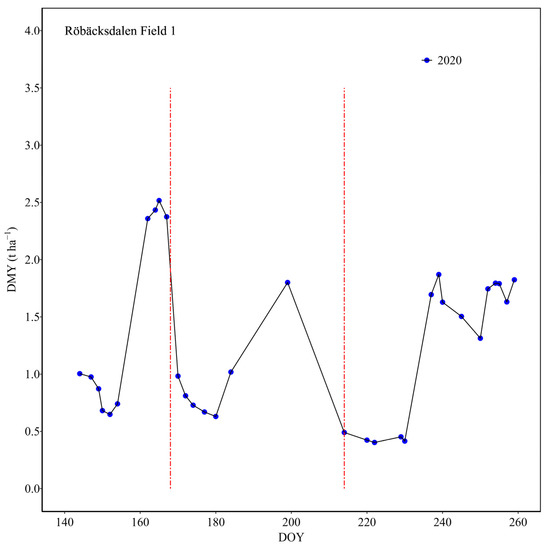
Figure 8.
Example of forage dry matter yield (DMY) during the growing season, estimated from Sentinel-2 imagery in 2020 at Röbäcksdalen field research station using a selected random forest regression (RFR) model. The red-dashed vertical lines indicate the timing of the first and second harvests.
Table 6 further illustrates the mean intervals between cloud-free Sentinel-2 images and the corresponding standard deviations for each experimental field and year. Mean intervals between available cloud-free Sentinel-2 images ranged from 4–9 days and 3–7 days, depending on the location in 2019 and 2020, respectively. Furthermore, there were larger gaps (e.g., 20 days) between Sentinel-2 images in June and July (Figure 9), which makes it hard to track the information at the most needed time. Therefore, including more datasets, such as Sentinel-1 imagery, which is insensitive to clouds, would be helpful in the future [72,73]. Statistical methods such as the weighted ensemble of radial basis function (RBF) convolution filters [74] can be used to detect time-series imagery outliers (e.g., clouds and shadows) and approximate missing data to create more frequent time-series data, and should be tried in future research. Including multispectral data from Landsat-8 could be another good solution to fill in the missing data. However, because of the coarser spatial resolution (30 m) and the lack of red-edge bands from Landsat-8 data [75], more caution should be taken and the effect from these differences on the modeling should be explored.

Table 6.
The mean and standard deviation values of the intervals between available cloud-free Sentinel-2 images from May to September in 2019 and 2020.
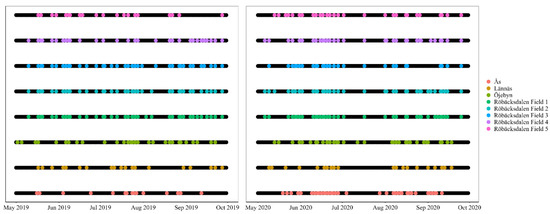
Figure 9.
Distribution of all of the available Sentinel-2 images (black dots) and available cloud-free Sentinel-2 images (colored dots) during the growing season (May–September) in 2019 and 2020 for different study locations.
In this study, even though MR algorithms created relatively robust models, especially for model calibration and evaluation, there were obvious overfitting problems when the validation was taken into consideration. The relatively small dataset size (Table 3) is a potential reason, and the reason why SVR and RFR produced better results than PLSR was most likely because both SVR [76] and RFR [29] could function with small-sized model training datasets.
The signal from soil could be another reason, especially at earlier growing stages. Adar et al. [38] found that the forage DMY prediction models derived from machine learning algorithms can be much improved by using satellite pixels with over 50% canopy cover. This study attempted to use individual bands as predictor variables, but the results were poorer (data not shown), and the possible reason as to why involving VIs as predictor variables improved the model accuracy could be that several soil-sensitive VIs (e.g., OSAVI and GOSAVI) contributed to overcome the soil effects.
Physical inversion [77,78] and hybrid inversion models combining physical modeling and machine learning algorithms [79] are also relevant approaches to account for multiple factors, such as soil optical properties, and compensate for limited training data. The integration of Sentinel-1 and Sentinel-2 data would be another solution, since incorporating Sentinel-1 and Sentinel-2 data would increase the predictor variable diversity, and thus, more likelihood can be included in the modeling, and the model could yield more accurate results [39,73].
5. Conclusions
- (i)
- DMY estimation of harvested forages in northern Sweden from Sentinel-2 data using univariate and multivariate regression models was tested in this study. The results demonstrate precise in-season DMY estimation by the random forest algorithm. Multivariate models performed better than the univariate models in terms of accuracy. Using both individual band reflectances and VIs as predictor variables improved the accuracy of multivariate regression models compared to only utilizing individual bands.
- (ii)
- It was challenging to develop a sufficiently robust model to estimate forage DMY by using Sentinel-2 data. The overfitting problem demonstrated by low model validation accuracy was the main indicator of this. The reasons may be the coarse spatial resolution and the small model training datasets. Data fusion by combining Sentinel-2 and Sentinel-1 data would be a potential way to overcome this. Furthermore, more datasets are needed for robust model building, and we therefore require continued resources and possibly international collaboration for further data collection. Nevertheless, even though model validation was slightly less accurate, the high accuracy of model calibration and evaluation showed that the selected model was promising.
- (iii)
- The estimated time-series of DMY fitted well with the recorded harvesting dates. The methods established in this study could be used to develop a decision support system to assist farmers in making decisions on fertilization and harvest timing.
Author Contributions
Conceptualization, J.P., D.P. and J.M.; Methodology, J.P., D.P., J.-B.F., M.S. and J.M.; Software, J.P.; Formal analysis, J.P.; Investigation, J.P.; Data curation, N.Z. and J.M.; Writing—original draft, J.P.; Writing—review & editing, N.Z., D.P., J.-B.F., M.S. and J.M.; Visualization, J.P.; Supervision, D.P. and J.M.; Project administration, J.M.; Funding acquisition, J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was co-funded by Regional Agricultural Research for Northern Sweden and Swedish Farmers’ Foundation for Agricultural Research, grant number #10/2018; Kempe Foundation, grant number JCK-2126.
Data Availability Statement
Data will be available on request.
Acknowledgments
Authors acknowledge the Regional Agricultural Research for northern Sweden (RJN) and the Swedish Farmers’ Foundation for Agricultural Research (SLF), which funded the project: Monitoring forage fields in northern Sweden with satellite imagery (Vallsat, project ID: #10/2018) for financial support. Special appreciation is given to Kempe foundation for financial support. The authors also thank staff from the research stations at Ås, Lännäs, Öjebyn and Röbäcksdalen for the help of field work. The study was supported by SITES (Swedish Infrastructure for Ecosystem Sciences), a national coordinated infrastructure, supported by the Swedish Research Council.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jordbruksverket. Agricultural Statistics. Available online: https://statistik.sjv.se/PXWeb/pxweb/sv/Jordbruksverkets%20statistikdatabas/?rxid=5adf4929-f548-4f27-9bc9-78e127837625 (accessed on 2 December 2022).
- Gunnarsson, C.; Spörndly, R.; Rosenqvist, H.; De Toro, A.; Hansson, P.A. A method of estimating timeliness costs in forage harvesting illustrated using harvesting systems in Sweden. Grass Forage Sci. 2009, 64, 276–291. [Google Scholar] [CrossRef]
- Zhou, Z.; Morel, J.; Parsons, D.; Kucheryavskiy, S.V.; Gustavsson, A.-M. Estimation of yield and quality of legume and grass mixtures using partial least squares and support vector machine analysis of spectral data. Comput. Electron. Agric. 2019, 162, 246–253. [Google Scholar] [CrossRef]
- Biewer, S.; Erasmi, S.; Fricke, T.; Wachendorf, M. Prediction of yield and the contribution of legumes in legume-grass mixtures using field spectrometry. Precis. Agric. 2009, 10, 128–144. [Google Scholar] [CrossRef]
- Sun, S.; Zuo, Z.; Yue, W.; Morel, J.; Parsons, D.; Liu, J.; Peng, J.; Cen, H.; He, Y.; Shi, J.; et al. Estimation of biomass and nutritive value of grass and clover mixtures by analyzing spectral and crop height data using chemometric methods. Comput. Electron. Agric. 2022, 192, 106571. [Google Scholar] [CrossRef]
- Hakl, J.; Hrevušová, Z.; Hejcman, M.; Fuksa, P. The use of a rising plate meter to evaluate lucerne (Medicago sativa L.) height as an important agronomic trait enabling yield estimation. Grass Forage Sci. 2012, 67, 589–596. [Google Scholar] [CrossRef]
- Hall, A.; Turner, L.; Irvine, L.; Kilpatrick, S. Pasture management and extension on Tasmanian dairy farms-who measures up? Rural. Ext. Innov. Syst. J. 2017, 13, 32–40. [Google Scholar]
- Battude, M.; Al Bitar, A.; Morin, D.; Cros, J.; Huc, M.; Marais Sicre, C.; Le Dantec, V.; Demarez, V. Estimating maize biomass and yield over large areas using high spatial and temporal resolution Sentinel-2 like remote sensing data. Remote Sens. Environ. 2016, 184, 668–681. [Google Scholar] [CrossRef]
- Chen, Y.; Guerschman, J.; Shendryk, Y.; Henry, D.; Harrison, M.T. Estimating Pasture Biomass Using Sentinel-2 Imagery and Machine Learning. Remote Sens. 2021, 13, 603. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, L.; Xie, D.; Yin, X.; Liu, C.; Liu, G. Application of Synthetic NDVI Time Series Blended from Landsat and MODIS Data for Grassland Biomass Estimation. Remote Sens. 2016, 8, 10. [Google Scholar] [CrossRef]
- Khanal, S.; KC, K.; Fulton, J.P.; Shearer, S.; Ozkan, E. Remote Sensing in Agriculture—Accomplishments, Limitations, and Opportunities. Remote Sens. 2020, 12, 3783. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Misra, G.; Cawkwell, F.; Wingler, A. Status of Phenological Research Using Sentinel-2 Data: A Review. Remote Sens. 2020, 12, 2760. [Google Scholar] [CrossRef]
- Segarra, J.; Buchaillot, M.L.; Araus, J.L.; Kefauver, S.C. Remote Sensing for Precision Agriculture: Sentinel-2 Improved Features and Applications. Agronomy 2020, 10, 641. [Google Scholar] [CrossRef]
- Veloso, A.; Mermoz, S.; Bouvet, A.; Le Toan, T.; Planells, M.; Dejoux, J.-F.; Ceschia, E. Understanding the temporal behavior of crops using Sentinel-1 and Sentinel-2-like data for agricultural applications. Remote Sens. Environ. 2017, 199, 415–426. [Google Scholar] [CrossRef]
- Punalekar, S.M.; Verhoef, A.; Quaife, T.; Humphries, D.; Bermingham, L.; Reynolds, C. Application of Sentinel-2A data for pasture biomass monitoring using a physically based radiative transfer model. Remote Sens. Environ. 2018, 218, 207–220. [Google Scholar] [CrossRef]
- Chen, Z.; Jia, K.; Xiao, C.; Wei, D.; Zhao, X.; Lan, J.; Wei, X.; Yao, Y.; Wang, B.; Sun, Y. Leaf area index estimation algorithm for GF-5 hyperspectral data based on different feature selection and machine learning methods. Remote Sens. 2020, 12, 2110. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F. A hybrid training approach for leaf area index estimation via Cubist and random forests machine-learning. ISPRS J. Photogramm. Remote Sens. 2018, 135, 173–188. [Google Scholar] [CrossRef]
- Peng, J.; Manevski, K.; Kørup, K.; Larsen, R.; Andersen, M.N. Random forest regression results in accurate assessment of potato nitrogen status based on multispectral data from different platforms and the critical concentration approach. Field Crops Res. 2021, 268, 108158. [Google Scholar] [CrossRef]
- Zha, H.; Miao, Y.; Wang, T.; Li, Y.; Zhang, J.; Sun, W.; Feng, Z.; Kusnierek, K. Improving Unmanned Aerial Vehicle Remote Sensing-Based Rice Nitrogen Nutrition Index Prediction with Machine Learning. Remote Sens. 2020, 12, 215. [Google Scholar] [CrossRef]
- Ali, I.; Cawkwell, F.; Dwyer, E.; Green, S. Modeling managed grassland biomass estimation by using multitemporal remote sensing data—A machine learning approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 3254–3264. [Google Scholar] [CrossRef]
- Bispo, P.d.C.; Rodríguez-Veiga, P.; Zimbres, B.; do Couto de Miranda, S.; Henrique Giusti Cezare, C.; Fleming, S.; Baldacchino, F.; Louis, V.; Rains, D.; Garcia, M.; et al. Woody Aboveground Biomass Mapping of the Brazilian Savanna with a Multi-Sensor and Machine Learning Approach. Remote Sens. 2020, 12, 2685. [Google Scholar] [CrossRef]
- Bhadra, S.; Sagan, V.; Maimaitijiang, M.; Maimaitiyiming, M.; Newcomb, M.; Shakoor, N.; Mockler, T.C. Quantifying Leaf Chlorophyll Concentration of Sorghum from Hyperspectral Data Using Derivative Calculus and Machine Learning. Remote Sens. 2020, 12, 2082. [Google Scholar] [CrossRef]
- Thorp, K.R.; Dierig, D.A.; French, A.N.; Hunsaker, D.J. Analysis of hyperspectral reflectance data for monitoring growth and development of lesquerella. Ind. Crops Prod. 2011, 33, 524–531. [Google Scholar] [CrossRef]
- Vapnik, V. Estimation of Dependences Based on Empirical Data; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chemura, A.; Mutanga, O.; Dube, T. Separability of coffee leaf rust infection levels with machine learning methods at Sentinel-2 MSI spectral resolutions. Precis. Agric. 2017, 18, 859–881. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Dusseux, P.; Guyet, T.; Pattier, P.; Barbier, V.; Nicolas, H. Monitoring of grassland productivity using Sentinel-2 remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2022, 111, 102843. [Google Scholar] [CrossRef]
- Guerini Filho, M.; Kuplich, T.M.; Quadros, F.L.F.D. Estimating natural grassland biomass by vegetation indices using Sentinel 2 remote sensing data. Int. J. Remote Sens. 2020, 41, 2861–2876. [Google Scholar] [CrossRef]
- Cai, Z.; Junttila, S.; Holst, J.; Jin, H.; Ardö, J.; Ibrom, A.; Peichl, M.; Mölder, M.; Jönsson, P.; Rinne, J. Modelling daily gross primary productivity with sentinel-2 data in the nordic region–comparison with data from modis. Remote Sens. 2021, 13, 469. [Google Scholar] [CrossRef]
- Karlsen, S.R.; Stendardi, L.; Tømmervik, H.; Nilsen, L.; Arntzen, I.; Cooper, E.J. Time-series of cloud-free sentinel-2 ndvi data used in mapping the onset of growth of central spitsbergen, svalbard. Remote Sens. 2021, 13, 3031. [Google Scholar] [CrossRef]
- Lantmet. Available online: https://www.slu.se/fakulteter/nj/om-fakulteten/centrumbildningar-och-storre-forskningsplattformar/faltforsk/vader/lantmet/ (accessed on 8 October 2022).
- ESA. Available online: https://sentinels.copernicus.eu/web/sentinel/user-guides/sentinel-2-msi/resolutions/spatial (accessed on 10 October 2022).
- ESA. Sentinel-2 MSI—Level 2A Products Algorithm Theoretical Basis Document. Available online: https://step.esa.int/thirdparties/sen2cor/2.10.0/docs/S2-PDGS-MPC-L2A-SRN-V2.10.0.pdf (accessed on 8 April 2023).
- R Core Team. R: A Language and Environment for Statistical Computing, Version 3.0.2; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Adar, S.; Sternberg, M.; Paz-Kagan, T.; Henkin, Z.; Dovrat, G.; Zaady, E.; Argaman, E. Estimation of aboveground biomass production using an unmanned aerial vehicle (UAV) and VENμS satellite imagery in Mediterranean and semiarid rangelands. Remote Sens. Appl. Soc. Environ. 2022, 26, 100753. [Google Scholar] [CrossRef]
- Naidoo, L.; van Deventer, H.; Ramoelo, A.; Mathieu, R.; Nondlazi, B.; Gangat, R. Estimating above ground biomass as an indicator of carbon storage in vegetated wetlands of the grassland biome of South Africa. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 118–129. [Google Scholar] [CrossRef]
- Reddersen, B.; Fricke, T.; Wachendorf, M. A multi-sensor approach for predicting biomass of extensively managed grassland. Comput. Electron. Agric. 2014, 109, 247–260. [Google Scholar] [CrossRef]
- Wehrens, R.; Mevik, B.-H. The pls package: Principal component and partial least squares regression in R. J. Stat. Softw. 2007, 18, 1–23. [Google Scholar]
- Sheykhmousa, M.; Mahdianpari, M.; Ghanbari, H.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support vector machine versus random forest for remote sensing image classification: A meta-analysis and systematic review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6308–6325. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Oliveira, S.; Oehler, F.; San-Miguel-Ayanz, J.; Camia, A.; Pereira, J.M.C. Modeling spatial patterns of fire occurrence in Mediterranean Europe using Multiple Regression and Random Forest. For. Ecol. Manag. 2012, 275, 117–129. [Google Scholar] [CrossRef]
- Gareth, J.; Daniela, W.; Trevor, H.; Robert, T. An Introduction to Statistical Learning: With Applications in R; Spinger: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Cao, Q.; Miao, Y.; Wang, H.; Huang, S.; Cheng, S.; Khosla, R.; Jiang, R. Non-destructive estimation of rice plant nitrogen status with Crop Circle multispectral active canopy sensor. Field Crops Res. 2013, 154, 133–144. [Google Scholar] [CrossRef]
- Sripada, R.P.; Heiniger, R.W.; White, J.G.; Weisz, R. Aerial color infrared photography for determining late-season nitrogen requirements in corn. Agron. J. 2005, 97, 1443–1451. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Magney, T.S.; Eitel, J.U.; Vierling, L.A. Mapping wheat nitrogen uptake from RapidEye vegetation indices. Precis. Agric. 2017, 18, 429–451. [Google Scholar] [CrossRef]
- Herrmann, I.; Pimstein, A.; Karnieli, A.; Cohen, Y.; Alchanatis, V.; Bonfil, D.J. LAI assessment of wheat and potato crops by VENμS and Sentinel-2 bands. Remote Sens. Environ. 2011, 115, 2141–2151. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Gitelson, A.A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and -3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Morier, T.; Cambouris, A.N.; Chokmani, K. In-Season Nitrogen Status Assessment and Yield Estimation Using Hyperspectral Vegetation Indices in a Potato Crop. Agron. J. 2015, 107, 1295–1309. [Google Scholar] [CrossRef]
- Lepine, L.C.; Ollinger, S.V.; Ouimette, A.P.; Martin, M.E. Examining spectral reflectance features related to foliar nitrogen in forests: Implications for broad-scale nitrogen mapping. Remote Sens. Environ. 2016, 173, 174–186. [Google Scholar] [CrossRef]
- Dimitrov, P.; Kamenova, I.; Roumenina, E.; Filchev, L.; Ilieva, I.; Jelev, G.; Gikov, A.; Banov, M.; Krasteva, V.; Kolchakov, V.; et al. Estimation of biophysical and biochemical variables of winter wheat through Sentinel-2 vegetation indices. Bulg. J. Agric. Sci. 2019, 25, 819–832. [Google Scholar]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Huang, S.; Miao, Y.; Zhao, G.; Yuan, F.; Ma, X.; Tan, C.; Yu, W.; Gnyp, M.L.; Lenz-Wiedemann, V.I.; Rascher, U. Satellite remote sensing-based in-season diagnosis of rice nitrogen status in Northeast China. Remote Sens. 2015, 7, 10646–10667. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Daughtry, C.; Walthall, C.; Kim, M.; De Colstoun, E.B.; McMurtrey Iii, J. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Chemura, A.; Mutanga, O.; Odindi, J.; Kutywayo, D. Mapping spatial variability of foliar nitrogen in coffee (Coffea arabica L.) plantations with multispectral Sentinel-2 MSI data. ISPRS J. Photogramm. Remote Sens. 2018, 138, 1–11. [Google Scholar] [CrossRef]
- Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogramm. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef]
- Bowen, T.R.; Hopkins, B.G.; Ellsworth, J.W.; Cook, A.G.; Funk, S.A. In-season variable rate N in potato and barley production using optical sensing instrumentation. In Proceedings of the Western Nutrient Management Conference, Salt Lake City, UT, USA; 2005; pp. 141–148. [Google Scholar]
- Wang, Y.; Wang, D.; Zhang, G.; Wang, J. Estimating nitrogen status of rice using the image segmentation of GR thresholding method. Field Crops Res. 2013, 149, 33–39. [Google Scholar] [CrossRef]
- Vincini, M.; Frazzi, E.; D’Alessio, P. A broad-band leaf chlorophyll vegetation index at the canopy scale. Precis. Agric. 2008, 9, 303–319. [Google Scholar] [CrossRef]
- Xie, Q.; Dash, J.; Huang, W.; Peng, D.; Qin, Q.; Mortimer, H.; Casa, R.; Pignatti, S.; Laneve, G.; Pascucci, S.; et al. Vegetation Indices Combining the Red and Red-Edge Spectral Information for Leaf Area Index Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1482–1493. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Bao, Y.; Luo, J.; Jin, X.; Xu, X.; Song, X.; Yang, G. Exploring the Best Hyperspectral Features for LAI Estimation Using Partial Least Squares Regression. Remote Sens. 2014, 6, 6221–6241. [Google Scholar] [CrossRef]
- Otgonbayar, M.; Atzberger, C.; Chambers, J.; Damdinsuren, A. Mapping pasture biomass in Mongolia using partial least squares, random forest regression and Landsat 8 imagery. Int. J. Remote Sens. 2019, 40, 3204–3226. [Google Scholar] [CrossRef]
- Shen, M.; Duan, H.; Cao, Z.; Xue, K.; Qi, T.; Ma, J.; Liu, D.; Song, K.; Huang, C.; Song, X. Sentinel-3 OLCI observations of water clarity in large lakes in eastern China: Implications for SDG 6.3.2 evaluation. Remote Sens. Environ. 2020, 247, 111950. [Google Scholar] [CrossRef]
- Lebourgeois, V.; Dupuy, S.; Vintrou, É.; Ameline, M.; Butler, S.; Bégué, A. A combined random forest and OBIA classification scheme for mapping smallholder agriculture at different nomenclature levels using multisource data (simulated Sentinel-2 time series, VHRS and DEM). Remote Sens. 2017, 9, 259. [Google Scholar] [CrossRef]
- Crabbe, R.A.; Lamb, D.W.; Edwards, C.; Andersson, K.; Schneider, D. A preliminary investigation of the potential of sentinel-1 radar to estimate pasture biomass in a grazed pasture landscape. Remote Sens. 2019, 11, 872. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, X.; Bajgain, R.; Starks, P.; Steiner, J.; Doughty, R.B.; Chang, Q. Estimating leaf area index and aboveground biomass of grazing pastures using Sentinel-1, Sentinel-2 and Landsat images. ISPRS J. Photogramm. Remote Sens. 2019, 154, 189–201. [Google Scholar] [CrossRef]
- Schwieder, M.; Leitão, P.J.; da Cunha Bustamante, M.M.; Ferreira, L.G.; Rabe, A.; Hostert, P. Mapping Brazilian savanna vegetation gradients with Landsat time series. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 361–370. [Google Scholar] [CrossRef]
- Loveland, T.R.; Irons, J.R. Landsat 8: The plans, the reality, and the legacy. Remote Sens. Environ. 2016, 185, 1–6. [Google Scholar] [CrossRef]
- Mantero, P.; Moser, G.; Serpico, S.B. Partially supervised classification of remote sensing images through SVM-based probability density estimation. IEEE Trans. Geosci. Remote Sens. 2005, 43, 559–570. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Berger, K.; Verrelst, J.; Féret, J.-B.; Wang, Z.; Wocher, M.; Strathmann, M.; Danner, M.; Mauser, W.; Hank, T. Crop nitrogen monitoring: Recent progress and principal developments in the context of imaging spectroscopy missions. Remote Sens. Environ. 2020, 242, 111758. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).