Abstract
With the rapid development of marine business, the intelligent detection of ship targets has become the key to marine safety. However, it is difficult to accurately detect maritime infrared targets due to severe sea clutter interference in strong wind waves or dim sea scenes. To adapt to diverse marine environments, a dual-mode sea background model is proposed for target detection. According to the global contrast of the image, the scene is divided into the sea surface with violent changes and the sea surface with stable changes. In the first stage, the preliminary background model suitable for steadily changing scenes is proposed. The pixel-level foreground mask is generated through the background block filter and the posterior probability criterion. Moreover, the learning rate parameter is adjusted using the detection results of two adjacent frames. In the second stage, the background model suitable for highly fluctuating scenes is proposed. Moreover, the local correlation feature is used to enhance the local contrast of the frame. The experimental results for the different scenes show that the proposed method has a better detection performance than the other comparison algorithms.
1. Introduction
Infrared maritime target detection is the basis for maritime target search and tracking systems. It is used for emergency rescue, marine environmental protection, territorial sea protection and other fields [1,2,3,4,5,6]. However, the infrared imaging quality is affected by the resolution of the infrared sensor, environment temperature, imaging distance, etc. In many cases, the gray distribution of the target is uneven and the outline is not clear [7,8,9]. Moreover, due to the low ambient temperature difference, the contrast between the target and the wave clutter is low. In addition, interference caused by illumination, large and random sea waves, weather and imaging noise results in a complex and diverse sea surface with low signal-to-clutter ratios. All these factors lead to difficulties for infrared maritime target detection. Consequently, for various complex maritime sea backgrounds, robust and accurate infrared target detection is a challenging task.
Up to now, a variety of methods have been proposed, including single-frame methods and background modeling methods for infrared maritime target detection. Compared with the background modeling methods, single-frame methods often require less computation and run faster. The key to solving this problem is to separate the targets from interference by background filtering and using feature differences. The global background subtraction filter and the adaptive row mean subtraction filter [10] are iteratively applied for background suppression and target enhancement, respectively. In addition to using background filtering, Yang et al. [11] proposed an integrated target saliency measure method using the local heterogeneity property of the targets and the non-local self-correlation property of the background to segment the targets. Zhang et al. [12] formulated the foreground segmentation problem with the feature difference in the similarity of directional edge components between the targets and interference. However, because this kind of method uses less information, its detection effect in a challenging sea scene still requires improvement. Zhang et al. [13] characterized the local intensity and gradient properties to detect small infrared targets. However, the intensity value of the target is not always greater than that of its locally neighboring pixels.
1.1. Related Work
Background modeling is a typical sequential detection method, in which the moving boats are considered as the foreground and the dynamic wave clutter is considered as the background. At present, background modeling methods are broadly categorized into statistical models, non-parametric models, neural network models, etc. Due to significant illumination changes and dynamic movement of the seawater over time, it is challenging to model variations in the sea background using these methods.
The statistical modeling approaches represent distributions of background changes using parametric models. The most popular statistical modeling approaches are the single Gaussian background model [14], Gaussian mixture model (GMM) [15] and improved GMM-based approaches [16,17,18]. The single Gaussian background models every pixel as a Gaussian probability density function, and the Gaussian mixture model uses the mixture of several weighed Gaussians to model every pixel. However, these approaches have a poor performance when the foreground objects move slowly, as exemplified by the shareable Gaussian mixture models in [19]. In [20], T. S. F. Haines et al. modeled every pixel with the mixture of several weighed Dirichlet processes for background subtraction. In [21], Kratika Garg et al. employed Bayesian probabilistic modeling for the block-based feature and proposed a rapid and robust background modeling technique for foreground detection (RRBM). The background modeling approach, by eliminating gray-level co-occurrence matrix features with an improved local Zernike moment and color components of intensity, effectively categorized the foreground and background pixels [22].
In our previous work, two background statistical modeling methods for maritime infrared target detection in the Fourier domain were proposed, including the adaptive single Gaussian background modeling algorithm (FASGM) [23] and the background modeling algorithm of multi-feature fusion (BMMFF) [24]. The FASGM method designs a comprehensive discrimination flag based on the variance in the test frames’ amplitude spectrum within a short temporal window and the initial Gaussian decision. The adaptive Gaussian discrimination coefficients are set based on each category, and an entropy filter in the Fourier domain is designed to enhance the contrast. The FASGM method has an excellent detection performance for dim targets; however, a small amount of seawater is still mistakenly detected for the highly fluctuating sea surface. The BMMFF method uses multiple features that can effectively distinguish the target and seawater, i.e., the background subtraction feature, global correlation feature and oscillation speed feature of the test frames’ amplitude spectrum. The background subtraction feature extracts the foreground by comparing the local statistical characteristics of the test frame and the background. Two strategies are used to update the background in cases with or without sudden waves in two adjacent test frames. The BMMFF method has a good performance under the influence of interference from sudden and continuous bright waves, but for a small number of dim scenes, its performance needs to be improved.
The non-parametric method establishes a non-parametric background model for each pixel through density estimation or historical information. The advantage is that it can adapt to any unknown data distribution without specifying the potential model and explicit estimation parameters. The coarse-to-fine detection algorithm extracts foreground objects on the basis of non-parametric background and foreground models represented by binary descriptors [25]. The visual background extraction (VIBE) method is a universal and non-parametric background subtraction method for video sequences, which categorizes the pixel by comparing its intensity with a set of historical background values [26]. The background subtraction algorithm [27] based on a modified ViBe model uses an improved local binary similarity pattern descriptor instead of simply relying on pixel intensities as its core component (LOBSTER). The algorithm described in [28] is also a variant of ViBe, which uses the dynamic adaptive learning rate and pixel-based adaptive threshold (PBAS). The universal pixel-level segmentation method, which uses spatiotemporal binary features and color information (SuBSENSE), is characterized as a non-parametric method [29]. The locally statistical dual-mode background subtraction approach (LSDS) [30] adopts a local intensity pattern comparison for foreground detection based on the assumption that the background pattern is generally more homogeneous than the foreground pattern. The dual-target non-parametric background model (DTNBM) [31] fuses the gray value and gradient as the feature to signify each pixel.
Moreover, in recent years, the background subtraction algorithm, based on spatial features learned by convolutional neural networks, was proposed. In [32], the algorithm uses a background model reduced to a single background image and a scene-specific training dataset to feed the convolutional neural network, which proves itself able to learn how to subtract the background from an input image patch. L. Yang et al. [33] presented a deep background modeling approach utilizing a fully convolutional network. In the network block constructing the deep background model, the coarse information of the high-layer information and the fine information of the low layer are combined using skip architecture, which can improve feature representation. In [34], a multi-view receptive field encoder–decoder convolutional neural network was introduced for video foreground extraction. Moreover, in [35], the multiscale 3D fully convolutional network was proposed for the mapping of image sequences to pixel-wise classification results and to learn deep and hierarchical multiscale spatial-temporal features of the input image sequence.
1.2. Motivation and Highlights of This Paper
Many methods employ different background modeling strategies for infrared maritime target detection and achieve relatively good detection results. However, there still remain some difficulties in infrared target detection in ocean background conditions. Due to strong, dynamic wave clutter, it is difficult for the background model to adapt to changes in the actual sea scene. Moreover, the low contrast between the target and background makes it difficult for each pixel to be correctly classified by the background model. In addition, factors such as illumination changes, weather changes and image noise may increase the complexity of the model. Due to the need to suppress sea clutter with serious interference and to obtain accurate detection results, a method that can detect targets in various sea scenes will have wide a scope for application.
In this paper, we present a dual-mode background modeling technique that can be used to effectively detect foreground masks in various sea scenes. The proposed method divides the seawater into sea surfaces with stable changes or violent fluctuations using global contrast. For the steadily changing sea surface, a relatively simple background-updating method is adopted. For the violently fluctuating sea surface, a background-updating method with a variable learning rate is adopted. The preliminary background model used in the first stage is suitable for the steadily changing scene, which generates accurate pixel-level foreground masks through the background sub-block filter and the posterior probability criterion. The precise background model used in the second stage is suitable for highly fluctuating scenes, and the model is maintained using the modified learning rate. In addition, the background subtraction result is filtered using the local linear correlation feature, which is helpful for detecting the foreground in various scenes.
The model has better applicability to different sea surfaces based on the concept of sea surface classification. Moreover, based on the concept of combining background subtraction with posterior probability judgment, the background model can effectively suppress various types of sea clutter without the need for excessive subsequent morphological processing. The work conducted in this study has certain reference value for the theoretical development of maritime infrared sequence image target detection. The main highlights of this paper are three-fold:
- A dual-mode background modeling approach which can accurately detect foregrounds in various sea scenes is proposed. For the steadily changing scene, background sub-block filtering based on the pixel property combined with a posterior criterion is adopted. For the violently fluctuating scene, background sub-block filtering based on the regional property combined with a posterior criterion is adopted.
- The global contrast of the image is adopted to judge whether it belongs to a steadily changing scene or a highly fluctuating scene.
- The local correlation feature between the test frame and the updated background is proposed to suppress the local sea clutter.
2. Method
The method proposed basically includes three major steps: the modeling of the background, filtering in the frequency domain and the detection of the foreground. A flowchart of the proposed method is shown in Figure 1. Details are provided in the following sections.
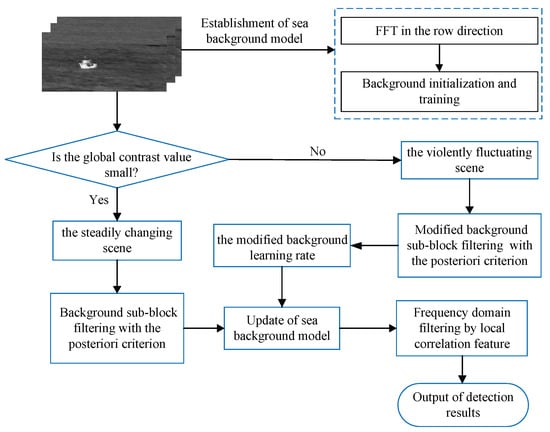
Figure 1.
Flowchart of the proposed method.
2.1. Initialization of the Sea Background Model
Considering that the amplitude spectrum sequence of a maritime infrared image sequence is more stable than the gray value sequence, background construction is carried out in the Fourier domain [23]. First, one transforms each frame of the infrared maritime sequence image to the Fourier domain in the row direction. Then, the amplitude spectrum of the kth frame is obtained. Let be the kth frame with a size of and be the amplitude spectrum of the kth frame, where and .
Suppose that there are n frames of continuous pure seawater images for background model training and the value of n is related to the length of the captured video. To initialize the background model, the first frame of the sequence image is used. The mean parameter is initialized as the amplitude spectrum of the first frame, and the variance parameter is initialized as a zero matrix. That is, and .
When the kth pure seawater image is read in, the model is updated as follows:
Here, and are the mean and variance parameter of the kth updated background model, respectively.
2.2. The Preliminary Background Model
The learning rate parameter is important for the background model, which determines the accuracy of the updated background. Since the sea surface changes randomly, the learning rate parameter of the background model should not be constant. Assuming that the change in the sea surface is relatively stable, the learning rate value is first set as a constant. The learning rate value is then adjusted according to the area difference in the detected target between two adjacent test frames.
For the steadily changing sea surface, when the target appears, there will be a clear difference in the amplitude spectrum between the target area and the sea background area. Thus, we use the change in the amplitude spectrum of each frequency point relative to the background, i.e., the amplitude spectrum difference, as the key feature for the classification process.
For each frequency point in a local sub-block with a size of , the amplitude spectrum difference between the test frame and the background model is calculated as follows:
Each sub-block consisting of is marked as a region of interest (RoI). The template value of the background block filter is set as times the standard deviation of the sequence, namely,
A subtraction operation is performed on each RoI and the background filter value , and the response value of the filter is 1 if the difference is positive, namely
For the steadily changing sea surface, the amplitude spectrum at location deviates greatly from that of the sea background if is equal to 1. Otherwise, it is considered that the amplitude spectrum at location is close to that of the sea background. However, for scenes with large waves, some points meeting Equation (5) belong to the sea background.
To eliminate the interference of these sea clutter points, a posterior probability criterion is used. For each frequency point with an amplitude spectrum difference in the local sub-block, the posterior probability of it being the foreground can be described as follows:
Here, m is an adjustable parameter, and its value is generally set as for different scenes. The posterior probability constitutes the preliminary binary detection image in the Fourier domain.
For the background update procedure, we follow a selective update strategy, as follows:
Here, the learning rate a is assumed to be an adjustable constant.
2.3. Adjustment of the Learning Rate of the Background Model
Due to the continuity of the sea scene over a short time, if the detection results of two adjacent frames differ greatly, this indicates that there are clear errors in the detection results of the two frames, and the learning rate value of the background model needs to be modified. That is, the learning rate is set to a larger value to incorporate the latest information on the sea scene. Otherwise, if the detection results of two adjacent frames are close, this indicates that the sea scene changes stably, and the learning rate value need not be changed.
Let be the connected area of each frequency point in the binary image of the k-th test frame. Thus, the modification strategy for the learning rate value is as follows:
Here, denotes the learning rate value of the background model at location for the k-th test frame, and T is an adjustable threshold.
2.4. The Precise Background Model
The preliminary background model is useful for classifying sea waves and targets for the steadily changing sea surface. However, for the violently fluctuating sea surface, the preliminary background model needs to be modified to obtain better detection effects. Thus, global contrast is used to determine whether the sea surface belongs to a steadily changing scene or a highly fluctuating scene. The global contrast is defined as follows:
Here, denotes the average gray value of the k-th test frame. If C is greater than the threshold ( is a user-settable threshold for global contrast), it is considered that the seawater fluctuates violently, and the preliminary background model is modified.
Within the local sub-block centered at point , the feature difference between the test frame and the background model is calculated as follows:
Here, is the mean of the k-th test frame’s amplitude spectrum in the sub-block, and is the mean of the updated background’s mean parameter in the sub-block.
Each sub-block consisting of is marked as a region of interest (RoI). The template value of the background block filter is set as times the standard deviation of the updated background’s mean parameter in the sub-block, namely,
A subtraction operation is performed on each RoI and the background filter value , and the response value of the filter is 1 if the difference is positive in Equation (5). Similarly, for each frequency point with an amplitude spectrum difference in the local sub-block, the posterior probability of each point being foreground is described in Equation (6).
Background maintenance must meet the requirement that the model can absorb the random variations in the sea scene. To accurately update the background model, the modified learning rate is used.
If , the sea scenes at location of the two consecutive frames are clearly different, and the model is updated as follows:
If , the sea scenes at location of the two consecutive frames are relatively close, and the model is updated as follows:
Here, denotes the learning rate of the background model at location for the k-th test frame, is the binary detection result, and and are the mean and variance at location of the k-th updated background, respectively.
2.5. Local Correlation Feature between the Test Frame and the Background
Due to the local similarity between seawater regions, the similarity between the local seawater area of the test frame and the corresponding updated background area is strong, while the similarity between the local target area of the test frame and the corresponding updated background area is weak. Therefore, the local correlation feature between the test frame and the updated background can enhance the local target area and suppress the local sea clutter.
and are divided into small sub-blocks with sizes of each, and each sub-block is transformed into the 2D Fourier domain, namely,
Here, denotes the 2D Fourier transformation, and and denote the ith sub-block of and , respectively. and denote the 2D Fourier frequency spectra of and , respectively.
The local linear correlation of and is calculated as follows:
Here, denotes the 2D inverse Fourier transformation, and denotes the conjugate of .
Then, the local correlation feature between and is obtained by a reverse transformation:
Here, is the number of sub-blocks of the test frame. Clearly, the local correlation feature between the seawater sub-block of the test frame and the sub-block of the updated background is small. Similarly, the local correlation feature between the target sub-block of the test frame and the sub-block of the updated background is large. Therefore, feature is regarded as a filter in the Fourier domain.
where is the number of sub-blocks of the test frame. Obviously, the local correlation feature between the seawater sub-block of the test frame and the sub-block of the updated background is small. Similarly, the local correlation feature between the target sub-block of the test frame and the sub-block of the updated background is large. Therefore, feature is regarded as a filter in the Fourier domain.
The filtering process of the background subtraction result by filter is shown in Figure 2. Figure 2a shows the original test frames. Figure 2b shows the amplitude spectrum of the original test frames. Feature between the test frame and the updated background is shown in Figure 2c. Figure 2d shows the filtering results of the background subtraction result in the Fourier domain. The filtered images in the spatial domain are shown in Figure 2e. It can be seen from Figure 2e that the hull in the filtered images using filter is relatively complete, and the image contrast is much higher than that of the original test frames. Thus, feature is conducive to improving the local contrast of the test frame.
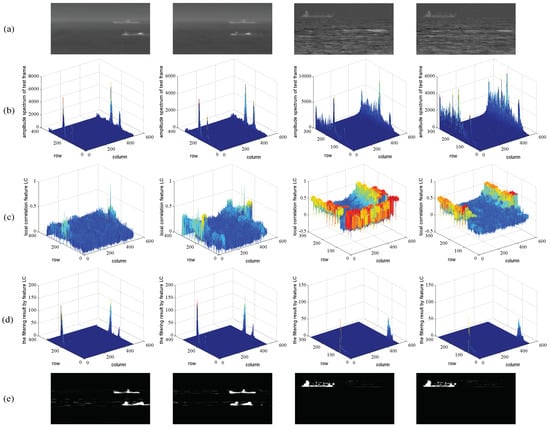
Figure 2.
Filtering process using the local correlation feature. (a) Original test frames; (b) amplitude spectrum of test frames; (c) local correlation feature between the test frame and the updated background; (d) filtering results in the Fourier domain by local correlation feature; (e) filtered images by local correlation feature.
2.6. Foreground Detection
The local correlation feature can enhance the local contrast of the test frame; thus, it is used to filter the background subtraction result in the Fourier domain. Then, one applies inverse Fourier transformation to the filtering result to obtain the detection result in the spatial domain, namely,
Here, denotes the inverse Fourier transformation in the row direction, and and denote the amplitude spectrum and phase spectrum of the kth test frame, respectively.
However, a small amount of sea clutter still remains in the preliminary detection result . Therefore, the salient target area is extracted, and the significance map of the preliminary detection result is obtained [23]. One builds a new image using the significance maps of both the preliminary detection result and the original test frame, as follows:
Here, and are the significance maps of the preliminary detection result and the original test frame, respectively. Additionally, and have the same significant target area, and and are two adjustable parameters.
Then, threshold segmentation is carried out for to obtain the final detection result. The threshold is set as follows:
Here, is the mean value of . is a control parameter, and its range is . The foreground region is obtained as follows:
3. Experimental Results
3.1. Results and Analysis
Figure 3 and Figure 4 show the detection results of maritime infrared sequence images obtained using the proposed method. Figure 3a and Figure 4a show the original test frames from different maritime infrared scenes. It can be seen that the sea scenes have different contrasts and various types of sea clutter; hence, it is challenging to accurately detect the targets. Figure 3b and Figure 4b show the preliminary detection results before segmentation. As seen from Figure 3b and Figure 4b, most of the complex and diverse backgrounds have been effectively suppressed, and the targets have been accurately located in the scene. Figure 3c and Figure 4c show the fusion results of the significance maps of both the preliminary results and the original images. It can be seen that the target area is enhanced and that the sea clutter is further suppressed using the fusion strategy. The detection results in Figure 3d and Figure 4d demonstrate that most of the sea clutter is removed and that the ship targets are accurately detected in various scenes.
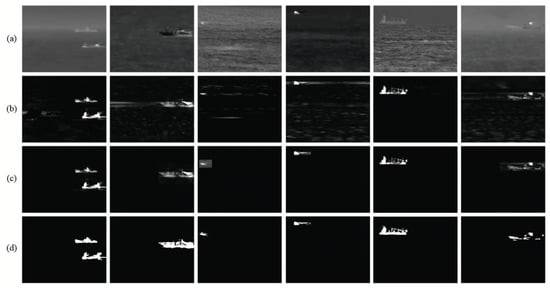
Figure 3.
Detection results of the proposed method. (a) Original images; (b) preliminary results before segmentation; (c) fusion results of the significant map of the preliminary result and the original image; (d) final detection results.
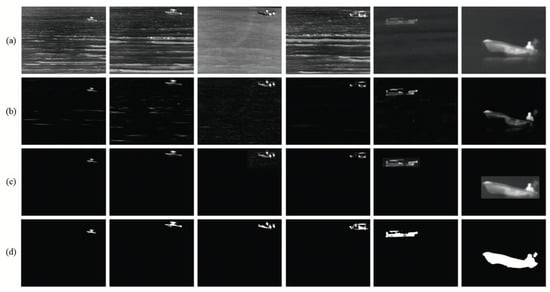
Figure 4.
Detection results of the proposed method. (a) Original images; (b) preliminary results before segmentation; (c) fusion results of the significant map of the preliminary result and the original image; (d) final detection results.
3.2. Comparison of the Results
We compared the proposed approach with the state-of-the-art techniques using maritime videos that were captured by our research group using an infrared thermographer. The visual comparison results are shown in Figure 5 and Figure 6, demonstrating that the proposed method outperforms the comparative methods, including SuBSense [29], LSDS [30], RRBM [21], LOBSTER [27], PBAS [28], FASGM [23] and BMMFF [24] in terms of visual effects. Figure 5a and Figure 6a show different maritime infrared scenes with different targets and seawater fluctuations. The results of SuBSense, LSDS, RRBM, LOBSTER, PBAS, FASGM, BMMFF and the proposed method are shown in Figure 5b and Figure 6b, Figure 5c and Figure 6c, Figure 5d and Figure 6d, Figure 5e and Figure 6e, Figure 5f and Figure 6f, Figure 5g and Figure 6g, Figure 5h and Figure 6h, and Figure 5i and Figure 6i, respectively.

Figure 5.
Comparison results. (a) Source frames; (b) detection results of SuBSense; (c) detection results of LSDS; (d) detection results of RRBM; (e) detection results of LOBSTER; (f) detection results of PBAS; (g) detection results of FASGM; (h) detection results of BMMFF; (i) detection results of the proposed method.
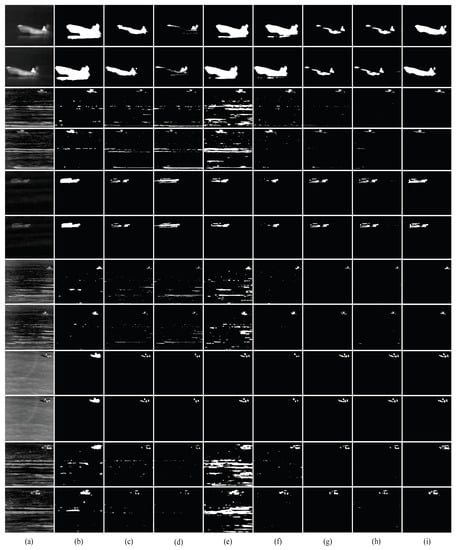
Figure 6.
Comparison results. (a) Source frames; (b) detection results of SuBSense; (c) detection results of LSDS; (d) detection results of RRBM; (e) detection results of LOBSTER; (f) detection results of PBAS; (g) detection results of FASGM; (h) detection results of BMMFF; (i) detection results of the proposed method.
4. Experimental Analysis
4.1. Qualitative Comparison and Discussion
The SuBSense method performs well for images with smaller waves and higher contrast, such as those in the fifth and sixth rows in Figure 6b. However, partial sea clutter is incorrectly classified as the target in the high sea clutter scene, as in the third, seventh and eleventh rows in Figure 6b. In addition, this method fails if the target is dark and weak, as in the third, fifth, seventh and ninth rows in Figure 5b.
For dark scenes with positive local contrast, LSDS can basically extract the weak target, as in the first, third and fifth rows in Figure 5c. However, for the dark scenes with weaker local contrast, some of the targets are misclassified as the background components, as shown in the sixth and seventh rows in Figure 5c. In addition, the representative image is defined as the median of the images in the buffer, which is not accurate for highly dynamic scenes. Thus, the detection effect is poor for the scene with brighter and larger sea waves, as shown in the third, seventh and eleventh rows in Figure 6c.
The RRBM method utilizes the robust block-level feature for modeling the background. However, the block intensity variance feature still cannot represent an accurate sea background for varying sea clutter. For example, in the fourth and seventh rows of Figure 6d, much sea clutter is incorrectly classified as the target. The detected targets are incomplete for the dim scenes with uneven targets, as in the second, ninth and twelfth rows in Figure 5d and the ninth row in Figure 6d. In addition, the partial dim hull is missed in the scenes with weak targets, such as the sixth row in Figure 5d.
The LOBSTER method is based on a modified ViBe model and improved local binary similarity feature, which is sometimes unsuitable for noisy or blurred regions. Such a case is illustrated in the third, seventh and eleventh rows of Figure 6e. It can be noted that many pixels are falsely labeled as foreground, since the improved local binary similarity vectors of the background model and the high dynamic sea clutter are still quite different. Moreover, the detected hull of dim targets in low-contrast scenes is incomplete compared with the real ship, as in the third, fifth and seventh rows in Figure 5e. This is due to the non-representative feature used for the local comparisons.
The PBAS method is effective for scenes with high contrast, such as those in the first and eighth rows in Figure 6f. However, the ever-changing sea waves seriously affect the detection performance. While the targets are detected, some waves are not removed, as can be seen from the third and eleventh rows in Figure 6f. Moreover, the targets in the dark and weak sea scenes are not completely detected, as in the seventh, ninth and eleventh rows in Figure 5f and the ninth row in Figure 6f. The targets are missed in the second, third and sixth rows in Figure 5f.
The FASGM method is effective for most different sea clutter scenes, as shown in Figure 5g and Figure 6g. However, its detection performance is still slightly inferior to that of the proposed method. The FASGM method has lower detection integrity for targets than the proposed method, as shown in the first to fourth, seventh and eleventh rows in Figure 5g. In addition, a small portion of the sea clutter is enhanced along with the target, as in the ninth and twelfth rows in Figure 5g and the third and fourth rows in Figure 6g.
The BMMFF method can successfully segment targets in most sea scenes and filter out most of the sea clutter. However, a significant number of detected targets are missing, and some sea clutter remains in the results, as shown in the seventh and eighth rows of Figure 5h. In some scenes with large sea waves, a small amount of sea clutter still remains in the detected results, as in the fourth and tenth rows in Figure 5h and the fourth, eighth and twelfth rows in Figure 6h.
The proposed method can accurately detect different targets in different sea scenes, as shown in Figure 5i and Figure 6i. As can be seen from the third, seventh and eleventh rows in Figure 6i, the method can detect targets in sea scenes with violent fluctuations better than the other comparative methods. From the second, third, seventh and eleventh rows in Figure 5i and the ninth row in Figure 6i, it can be seen that the detection results of the uneven dim targets show more details and are much closer to the actual targets. The sixth row in Figure 5i shows that the method can accurately detect the weak targets in the challenging sea scene. The reason for the good performance is that the proposed method uses different and effective modeling strategies for seawaters with different fluctuations, rendering it applicable to various sea scenes. By using the background sub-block filter and the posterior probability criterion, the sea clutter is effectively suppressed. In addition, the adjustment of the learning rate is introduced, and the local linear correlation feature is used to enhance the local contrast of the test frame. Thus, the proposed method achieves a good detection result.
4.2. Quantitative Comparison
For the quantitative evaluation of test results, three measures are used: the misclassification error () [36], relative foreground area error () [36] and f-measure values () [20]. denotes the percentage of background pixels incorrectly classified as the foreground and foreground pixels incorrectly classified as the background. denotes the area accuracy of the detected result compared with the true image. The is defined as the harmonic mean of the precision () and recall (). The three measures are defined as follows:
Here, and denote the background and foreground pixels of the original image, respectively. and denote the background and foreground pixels of the detected result, respectively. denotes the cardinality of a set. and denote the areas of the true target and detected target, respectively. is the proportion of the correct classification of ship pixels to all actual detected pixels. The is the proportion of correct classifications of ship pixels relative to the total true ship pixels.
Figure 7 shows detailed comparisons of twelve representative scenes in , and . We find that our background model approach has a superior performance compared with the other classical background modeling approaches for most of complex scenes. The , and performances of the other comparison algorithms are poor for some scenes with serious interference. On the whole, the proposed method offers the most stable performance for different scenes.
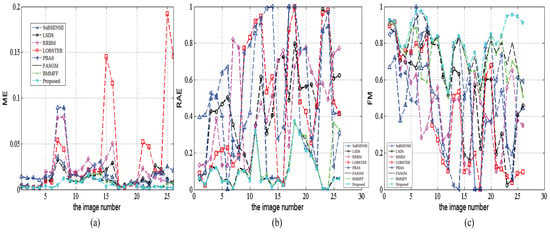
Figure 7.
Comparisons of three metrics. (a) The ME curve; (b) the RAE curve; (c) the FM curve.
Table 1 lists the average values of three metrics for twelve scenes, and , and represent the average values of , and , respectively. It can be seen that the proposed method has the lowest average and , and highest average value compared with the other methods. The average value of for the proposed method is reduced by approximately compared with SuBSENSE. The average value of for the proposed method is reduced by approximately compared with LSDS, while the average value of the proposed method is increased by approximately compared with LSDS. The average values of and for the proposed method are reduced by approximately and compared with FASGM, respectively, while the average value of for the proposed method is increased by approximately compared with FASGM, which demonstrates that the proposed method performs better overall.

Table 1.
The average values of three metrics of comparison methods.
The variance values of three metrics for twelve scenes are reported in Table 2, and , and represent the variance values of , and , respectively. It can be seen that the proposed method has the lowest variance values of , and compared with the other methods. The variance values of and for the proposed method are reduced by approximately and compared with LSDS, respectively, while the variance value of for the proposed method is reduced by approximately compared with RRBM. The variance values of and for the proposed method are reduced by approximately and compared with FASGM, respectively, which demonstrates that the proposed method is the most stable and robust for various scenes in terms of and . The variance value of for the proposed method is reduced by approximately compared with FASGM, which demonstrates that the two methods perform similarly on stability in term of .

Table 2.
The variance values of three metrics of comparison methods.
5. Conclusions and Future Work
In this paper, we introduced a novel dual-mode background modeling technique for the foreground detection of maritime infrared scenes. First, a rule based on global contrast is adopted to judge whether the scene is a steadily changing scene or a highly fluctuating scene. For the steadily changing scene, background sub-block filtering, based on the pixel property combined with a posterior probability criterion, is adopted for foreground detection. For the violently fluctuating scene, background sub-block filtering, based on the regional property combined with a posterior probability criterion, is adopted for foreground detection. Moreover, the learning rate of the background model is modified using the area difference of two adjacent frames’ connected regions. Moreover, the local correlation feature between the test frame and the updated background is proposed to suppress the local sea clutter. It achieves robustness for scenes with large waves and dark seawater. This can be attributed to our robust background model and our classification framework that effectively detects the foreground in different scenes. The experimental results of different sea scenes confirm that the proposed method achieves a higher accuracy than the state-of-the-art techniques. Thus, the proposed algorithm has good application value in the field of maritime intelligent object detection and is convenient for coastal defense. Moreover, this research has important reference value for the development of and improvement in target detection theory using maritime infrared images.
In the future, we will aim to explore the deep background subtraction approach with a deep neural network so as to improve the detection performance and applicability of the approach for different types of scenes, such as sea scenes with complex cloud interference and sea surfaces with extremely uneven brightness.
Author Contributions
Conceptualization, J.P.; Formal analysis, A.Z. and J.P.; Funding acquisition, J.P.; Methodology, A.Z.; investigation, A.Z., W.X. and J.P.; Resources, J.P.; Software, A.Z. and J.P.; Supervision, W.X.; Validation, W.X.; Writing—original draft, A.Z.; Writing—review and editing, A.Z., W.X. and J.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Open Foundation of Guangdong Key Laboratory of Intelligent Information Processing and Shenzhen Key Laboratory of Media Security, the National Natural Science Foundation of China under Grant (62071303, 62201355), China Postdoctoral Science Foundation (2021M702275), and Shenzhen Science and Technology Projection (JCYJ20190808151615540).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, B.; Benli, E.; Motai, Y.; Dong, L.; Xu, W. Robust Detection of Infrared Maritime Targets for Autonomous Navigation. IEEE Trans. Intell. Veh. 2020, 5, 635–648. [Google Scholar] [CrossRef]
- Lu, Y.; Dong, L.; Zhang, T.; Xu, W. A Robust Detection Algorithm for Infrared Maritime Small and Dim Targets. Sensors 2020, 20, 1237. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Xiong, W.; Chen, X.; Lu, Y. Experimental Study of Maritime Moving Target Detection Using Hitchhiking Bistatic Radar. Remote Sens. 2022, 14, 3611. [Google Scholar] [CrossRef]
- Ren, L.; Ran, X.; Peng, J.; Shi, C. Saliency Detection for Small Maritime Target Using Singular Value Decomposition of Amplitude Spectrum. IETE Tech. Rev. 2017, 34, 631–641. [Google Scholar] [CrossRef]
- Wu, J.; Li, J.; Li, R.; Xi, X.; Gui, D.; Yin, J. A Fast Maritime Target Identification Algorithm for Offshore Ship Detection. Appl. Sci. 2022, 12, 4938. [Google Scholar] [CrossRef]
- Wu, H.; Xian, J.; Mei, X.; Zhang, Y.; Wang, J.; Cao, J.; Mohapatra, P. Efficient target detection in maritime search and rescue wireless sensor network using data fusion. Comput. Commun. 2019, 136, 53–62. [Google Scholar] [CrossRef]
- Wang, B.; Dong, L.; Zhao, M.; Wu, H.; Ji, Y.; Xu, W. An infrared maritime target detection algorithm applicable to heavy sea fog. Infrared Phys. Technol. 2015, 71, 56–62. [Google Scholar] [CrossRef]
- Zhao, E.; Dong, L.; Dai, H. Infrared Maritime Small Target Detection Based on Multidirectional Uniformity and Sparse-Weight Similarity. Remote Sens. 2022, 14, 5492. [Google Scholar] [CrossRef]
- Yang, P.; Dong, L.; Xu, H.; Dai, H.; Xu, W. Robust Infrared Maritime Target Detection via Anti-Jitter Spatial–Temporal Trajectory Consistency. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, F.; Chen, X.; Bai, X.; Sun, C. Iterative infrared ship target segmentation based on multiple features. Pattern Recogn. 2014, 47, 2839–2852. [Google Scholar] [CrossRef]
- Yang, P.; Dong, L.; Xu, W. Infrared Small Maritime Target Detection Based on Integrated Target Saliency Measure. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2369–2386. [Google Scholar] [CrossRef]
- Zhang, M.; Dong, L.; Zheng, H.; Xu, W. Infrared maritime small target detection based on edge and local intensity features. Infrared Phys. Technol. 2021, 119, 103940. [Google Scholar] [CrossRef]
- Hong, Z.; Lei, Z.; Ding, Y.; Hao, C. Infrared small target detection based on local intensity and gradient properties. Infrared Phys. Technol. 2018, 89, 88–96. [Google Scholar]
- Benezeth, Y.; Jodoin, P.; Emile, B.; Laurent, H.; Rosenberger, C. Comparative study of background subtraction algorithms. J. Electron. Imaging 2010, 19, 033003. [Google Scholar]
- Stauffer, C.; Grimson, W. Learning patterns of activity using real-time tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 747–757. [Google Scholar] [CrossRef]
- Chen, Z.; Ellis, T. A self-adaptive Gaussian mixture model. Comput.Vis. Image Understand. 2014, 122, 35–46. [Google Scholar] [CrossRef]
- Li, D.; Xu, L.; Goodman, E. Illumination-robust foreground detection in a video surveillance system. IEEE Trans. Circ. Syst. Video Technol. 2013, 23, 1637–1650. [Google Scholar] [CrossRef]
- Mukherjee, D.; Wu, Q.; Nguyen, T. Multiresolution based Gaussian mixture model for background suppression. IEEE Trans.Image Process. 2013, 22, 5022–5035. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Lu, H. Learning sharable models for robust background subtraction. In Proceedings of the IEEE International Conference on Multi-Media and Expo (ICME), Turin, Italy, 29 June–3 July 2015; pp. 1–6. [Google Scholar]
- Haines, T.; Xiang, T. Background subtraction with Dirichlet process mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 670–683. [Google Scholar] [CrossRef]
- Garg, K.; Ramakrishnan, N.; Prakash, A.; Srikanthan, T. Rapid and Robust Background Modeling Technique for Low-Cost Road Traffic Surveillance Systems. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2204–2215. [Google Scholar] [CrossRef]
- Moudgollya, R.; Sunaniya, A.; Midya, A.; Chakraborty, J. A multi features based background modeling approach for moving object detection. Optik 2022, 260, 168980. [Google Scholar] [CrossRef] [PubMed]
- Zhou, A.; Xie, W.; Pei, J. Background Modeling in the Fourier Domain for Maritime Infrared Target Detection. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 2634–2649. [Google Scholar] [CrossRef]
- Zhou, A.; Xie, W.; Pei, J. Background Modeling Combined With Multiple Features in the Fourier Domain for Maritime Infrared Target Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Yang, M.; Huang, C.; Liu, W.; Lin, S.; Chuang, K. Binary Descriptor Based Nonparametric Background Modeling for Foreground Extraction by Using Detection Theory. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 595–608. [Google Scholar] [CrossRef]
- Barnich, O.; Droogenbroeck, M. ViBe: A universal background subtraction algorithm for video sequences. IEEE Trans. Image Process. 2011, 20, 1709–1724. [Google Scholar] [CrossRef] [PubMed]
- St-Charles, P.; Bilodeau, G. Improving background subtraction using local binary similarity patterns. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Steamboat Springs, CO, USA, 24–26 March 2014; pp. 509–515. [Google Scholar]
- Martin, H.; Philipp, T.; Gerhard, R. Background segmentation with feedback: The pixel-based adaptive segmenter. In Proceedings of the IEEE Computer Software and Applications Conference on Computer Vision and Pattern Recognition Workshops (COMPSAC), Providence, RI, USA, 16–21 June 2012; pp. 38–43. [Google Scholar]
- St-Charles, P.; Bilodeau, G.; Bergevin, R. SuBSENSE: A universal change detection method with local adaptive sensitivity. IEEE Trans. Image Process. 2015, 24, 359–373. [Google Scholar] [CrossRef]
- Huynh-The, T.; Hua, C.; Tu, N.; Kim, D. Locally statistical dual-mode background subtraction approach. IEEE Access. 2019, 7, 9769–9782. [Google Scholar] [CrossRef]
- Zhong, Z.; Wen, J.; Zhang, B.; Xu, Y. A general moving detection method using dual-target nonparametric background model. Knowl.-Based Syst. 2019, 164, 85–95. [Google Scholar] [CrossRef]
- Braham, M.; Droogenbroeck, M. Deep background subtraction with scene-specific convolutional neural networks. In Proceedings of the International Conference on Systems Signals and Image Processing (IWSSIP), Bratislava, Slovakia, 23–25 May 2016; pp. 113–116. [Google Scholar]
- Yang, L.; Li, J.; Luo, Y.; Zhao, Y.; Cheng, H.; Li, J. Deep Background Modeling Using Fully Convolutional Network. IEEE Trans. Intell. Transp. Syst. 2018, 19, 254–262. [Google Scholar] [CrossRef]
- Thangarajah, A.; Jonathan, Q.; Zhang, W. Video Foreground Extraction Using Multi-View Receptive Field and Encoder-Decoder DCNN for Traffic and Surveillance Applications. IEEE Trans. Veh. Technol. 2019, 68, 9478–9493. [Google Scholar]
- Wang, Y.; Zhu, L.; Yu, Z. Foreground Detection for Infrared Videos with Multiscale 3-D Fully Convolutional Network. IEEE Geosci. Remote Sens. Lett. 2019, 16, 712–716. [Google Scholar] [CrossRef]
- Liu, Z.; Bai, X.; Sun, C.; Zhou, F.; Li, Y. Infrared ship target segmentation through integration of multiple feature maps. Image Vis. Comput. 2016, 48, 14–25. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).