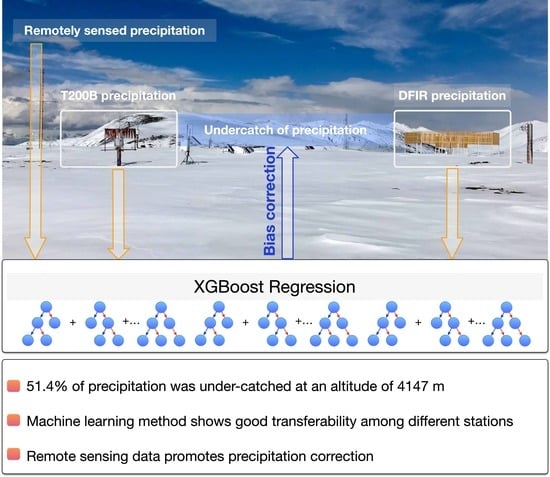
Machine Learning-Based Bias Correction of Precipitation Measurements at High Altitude
Abstract
1. Introduction
2. Data and Methods
2.1. Study Site and Data
Remote Sensing Precipitation
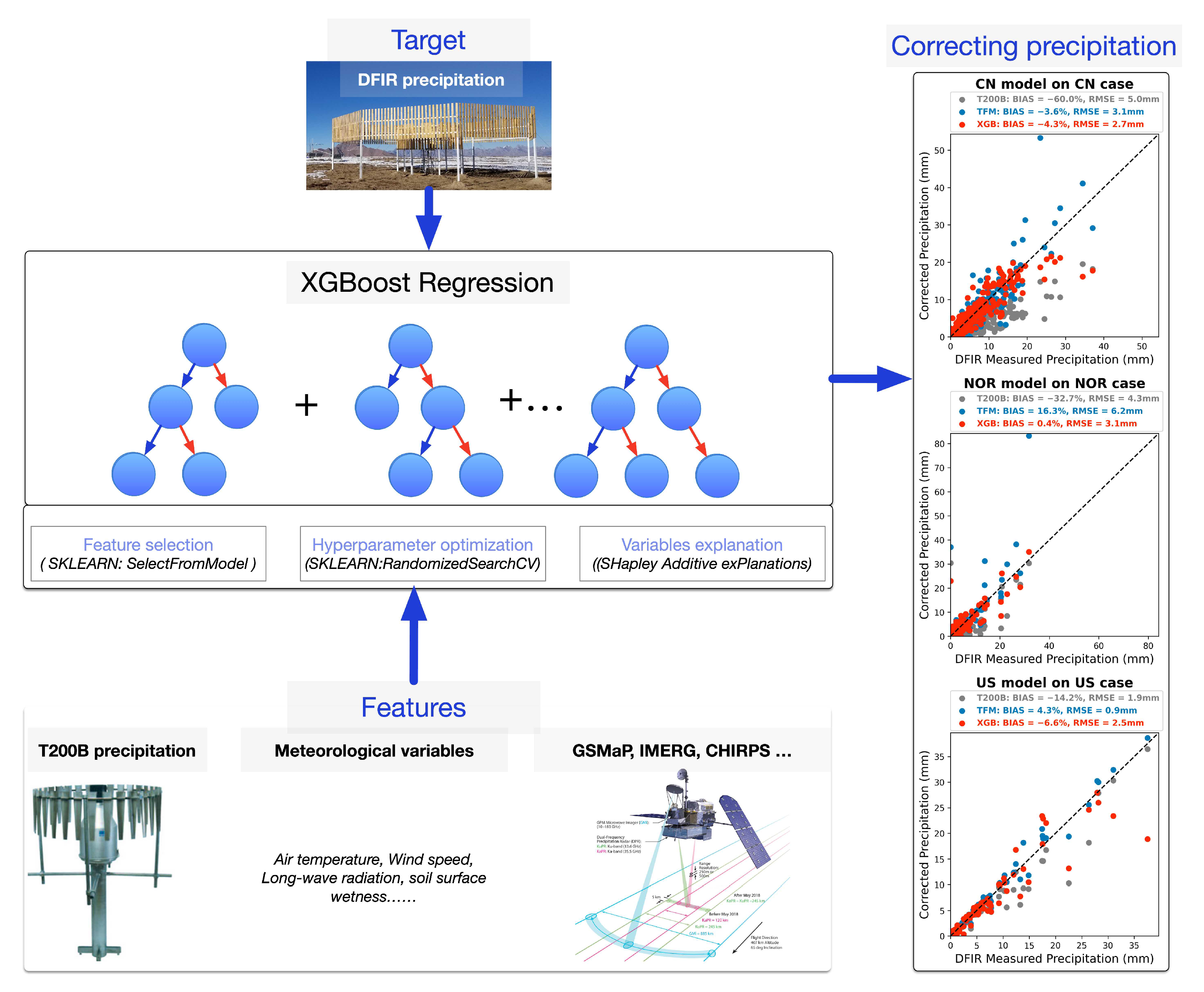
2.2. Method
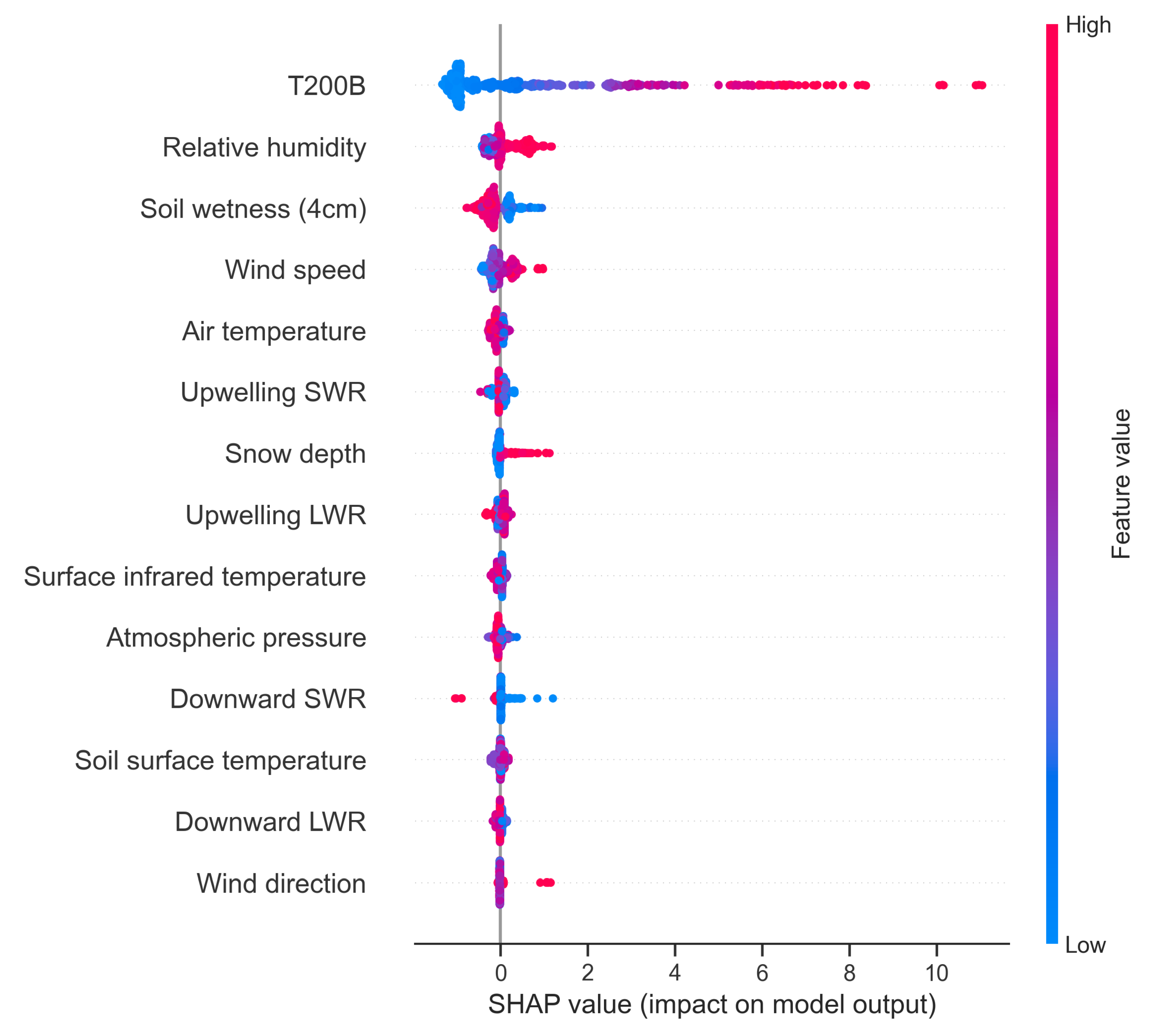
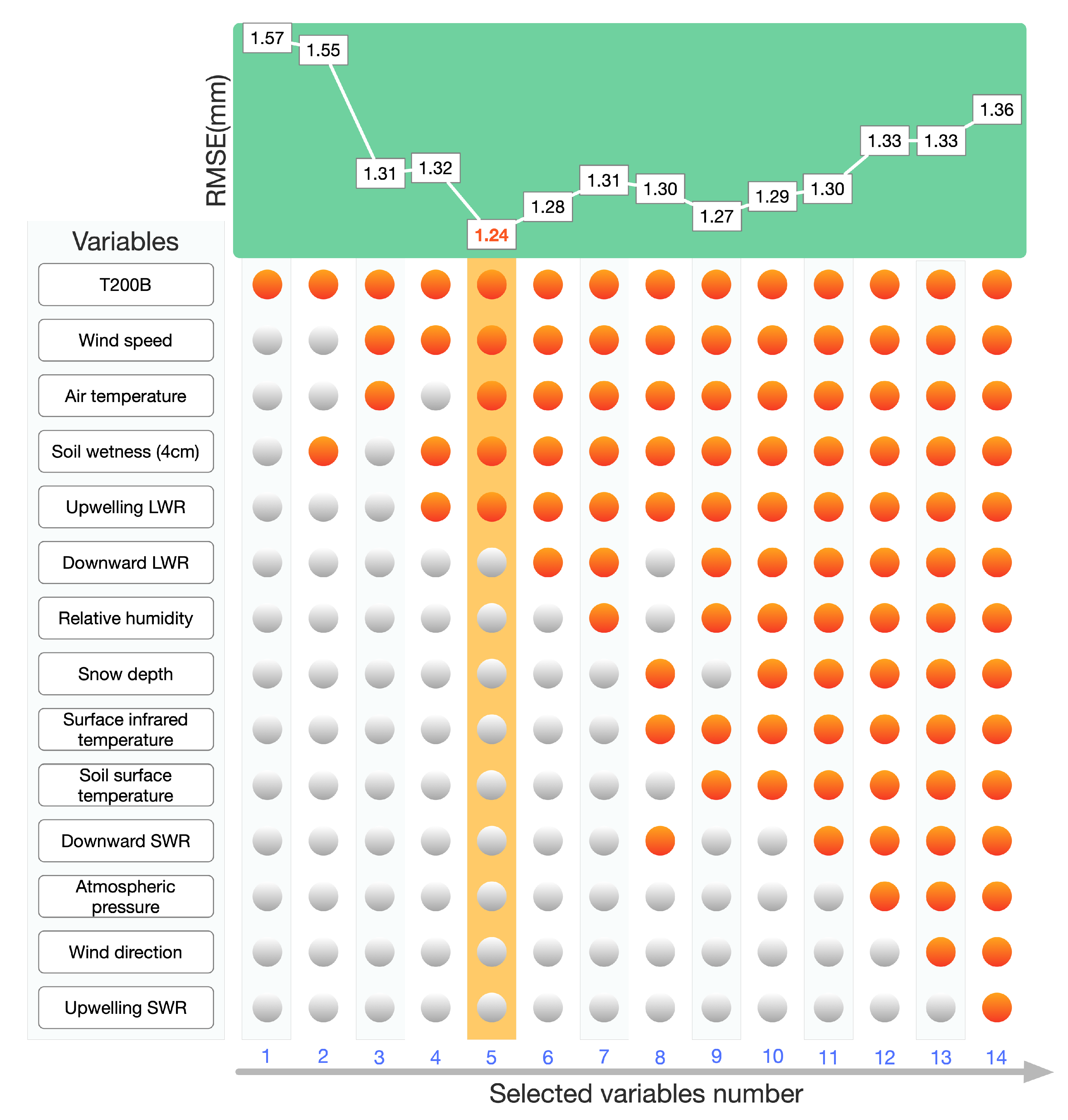
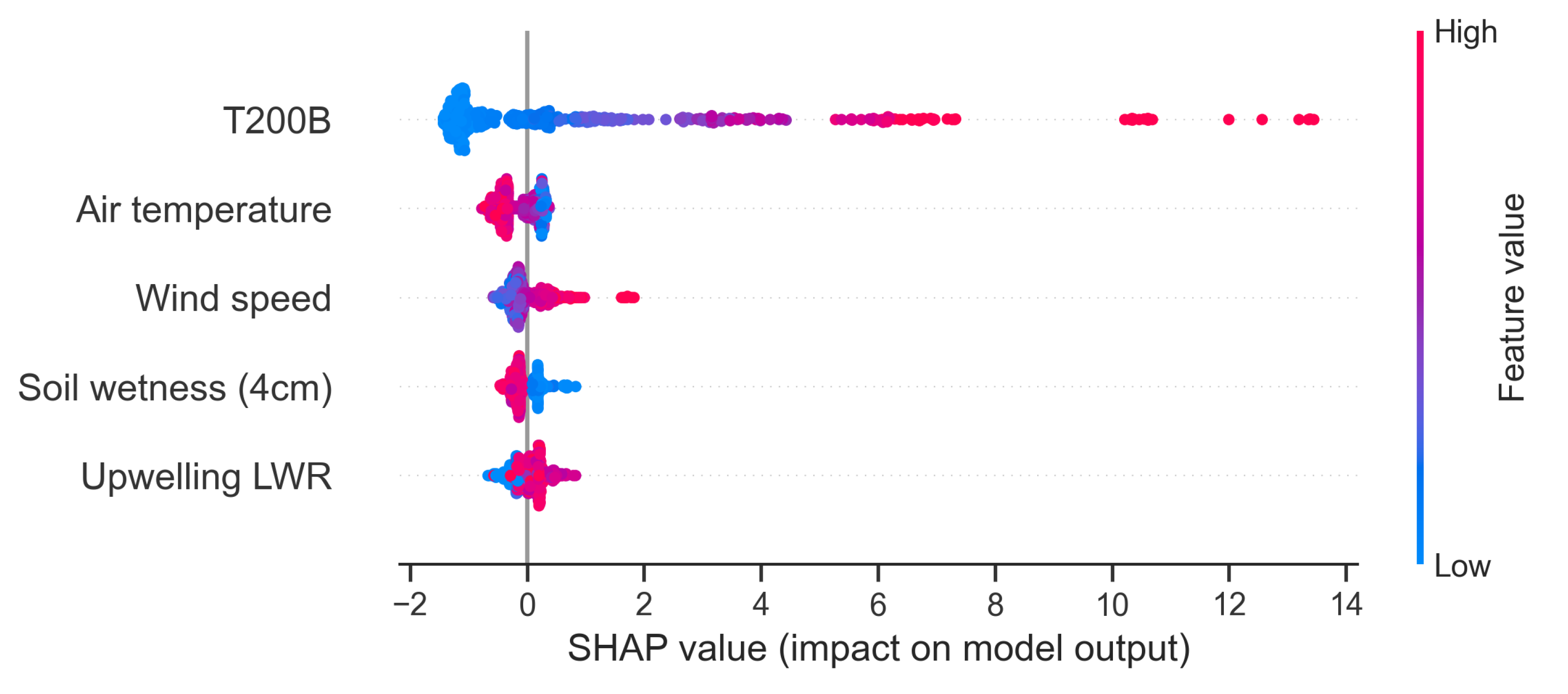
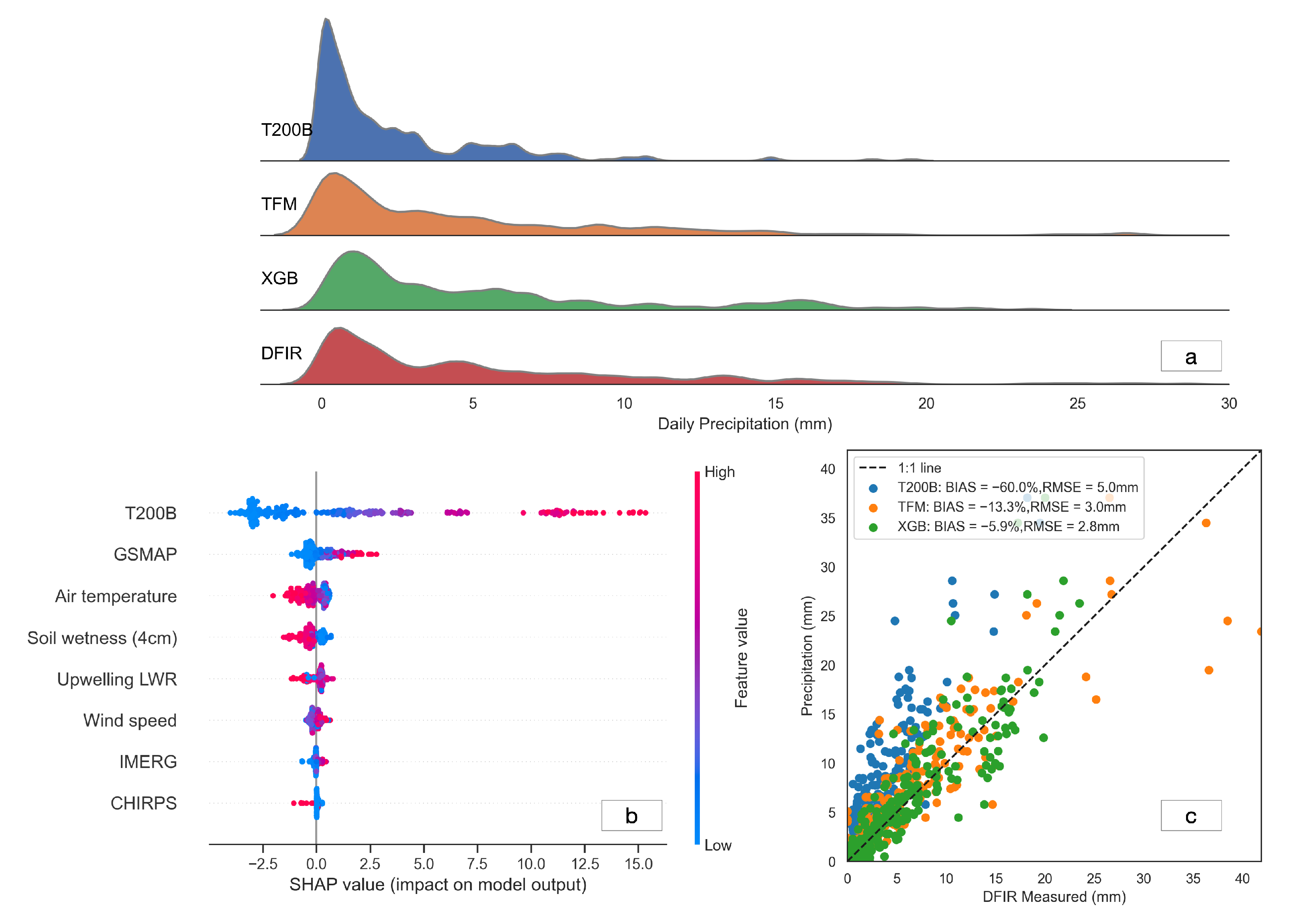
Selecting Features and Explaining the Contribution of the Features
2.3. The Transfer Function Method
2.4. Accuracy Metrics
3. Results
3.1. How Much Precipitation Was Under-Estimated?
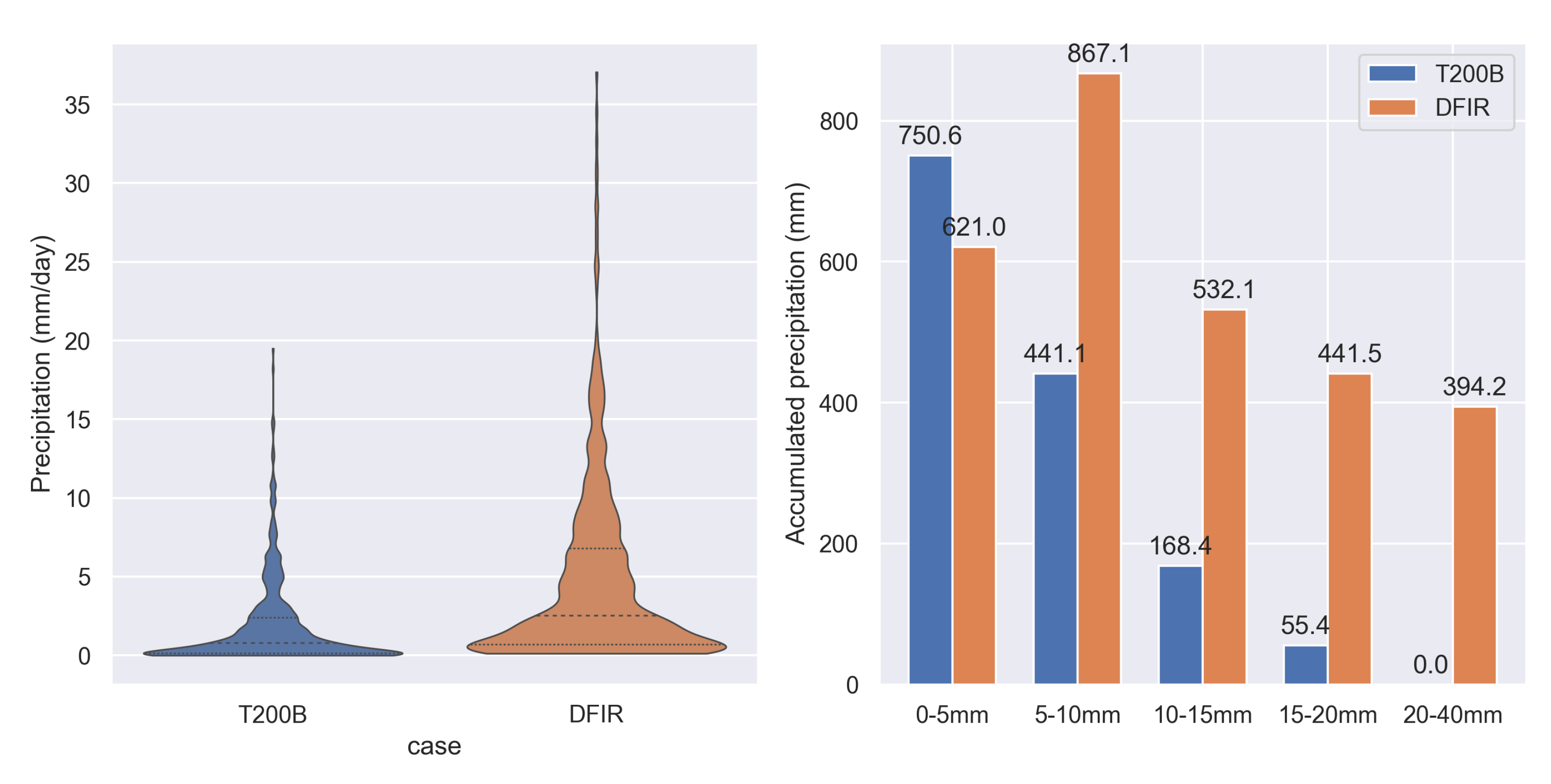
3.1.1. In Situ Underestimation
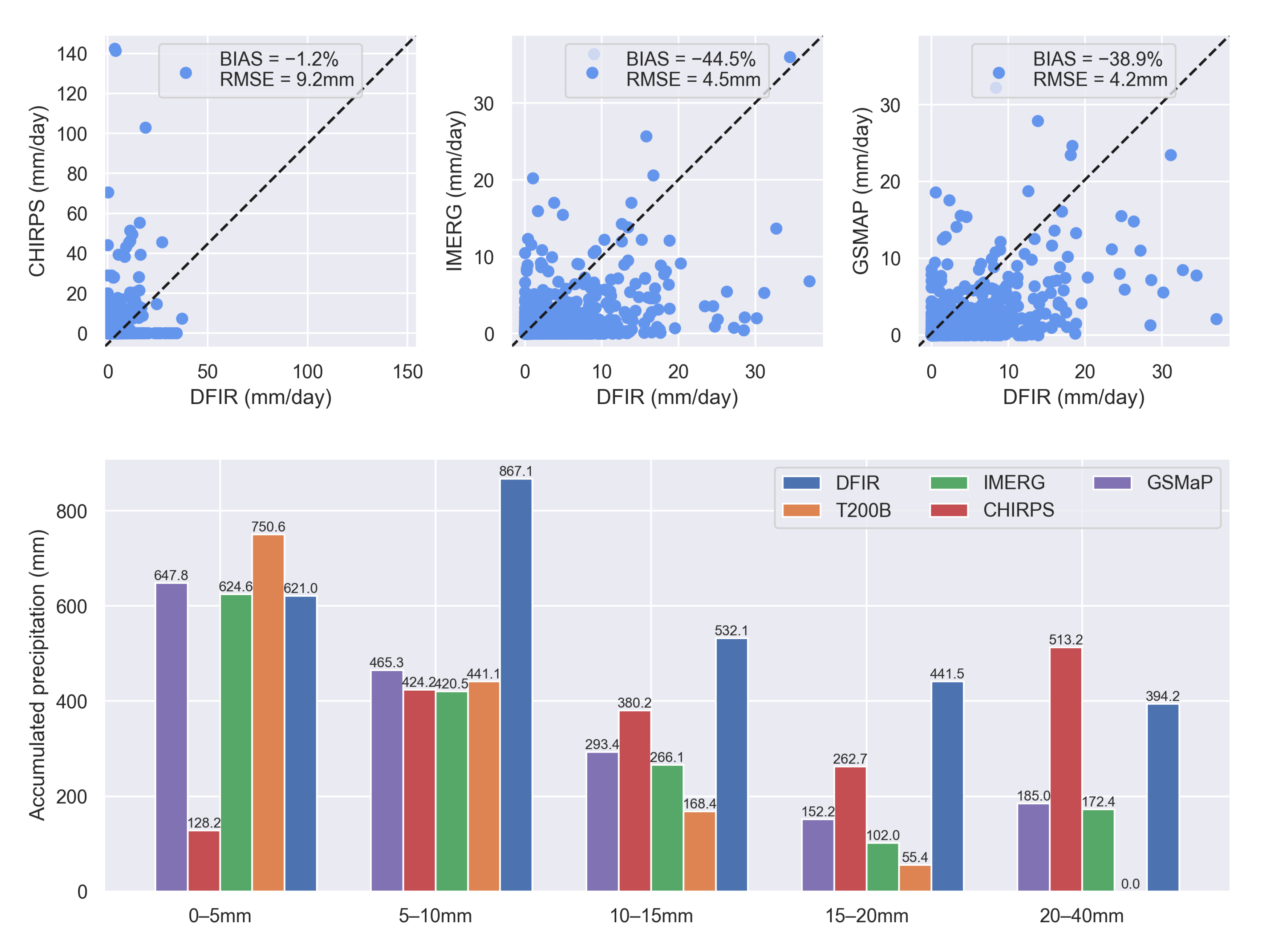
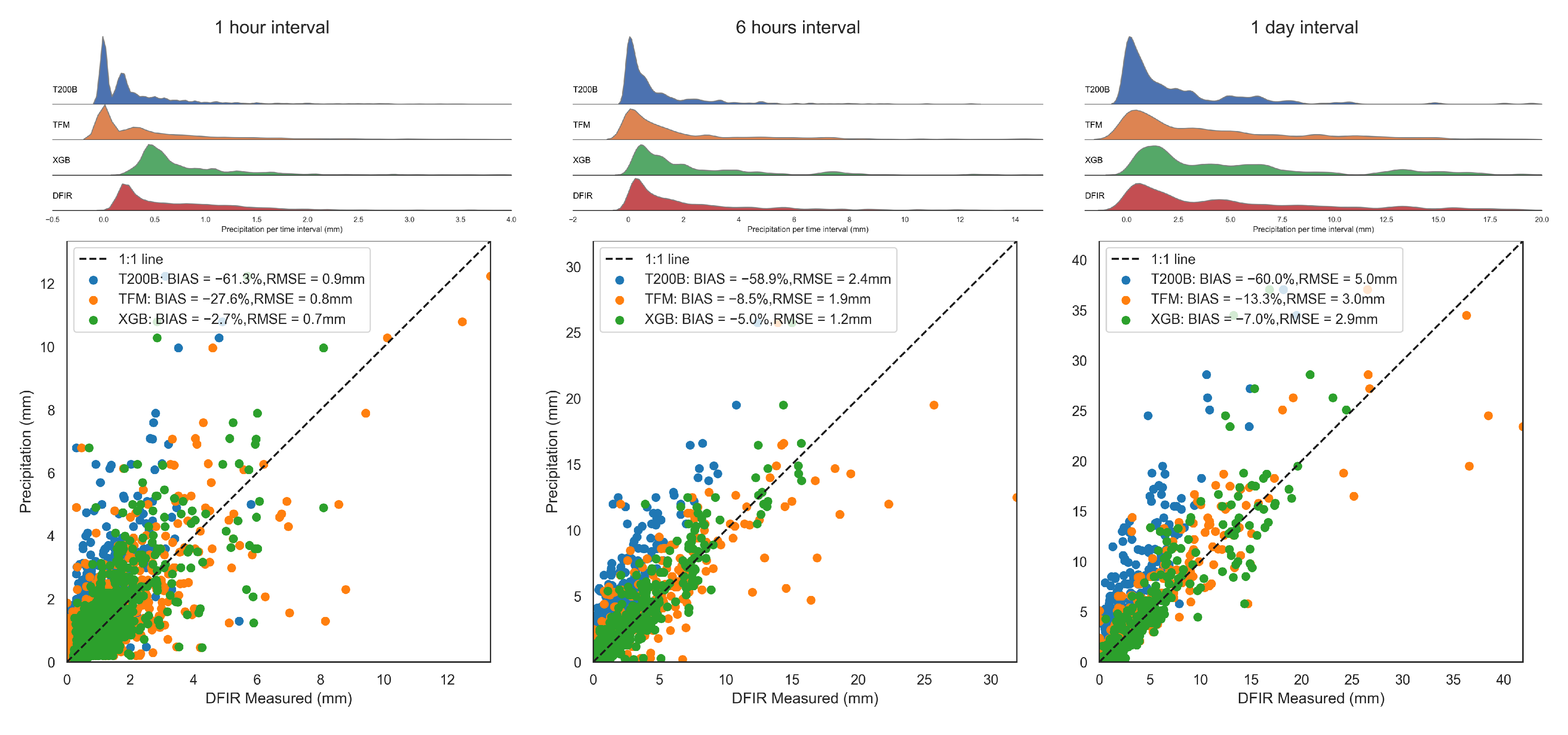
3.1.2. Misestimation of Precipitation by Remotely Sensed Precipitation
3.2. How Can the Machine Learning Method Promote the Bias Correction of Single Fenced Precipitation Measurements?
3.2.1. Feature Selection
3.2.2. Corrected Precipitation Results Using In Situ Meteorological Variables
3.3. How Could Remotely Sensed Precipitation Be Used in Machine Learning to Promote Precipitation Correction?
4. Discussion
4.1. Can the Machine Learning Method Be Transferred to Other Regions?
4.2. Advantages and Notices of Applying Machine Learning Method in Correcting Precipitation Measurement
4.3. Implications of Machine-Learning Method on Obtaining More Accurate Precipitation in the High Altitude Region in the Future
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BIAS | total mass BIAS |
| CCCASON | Climate Change Canada Automated Surface Observation Network |
| CHIRPS | Climate Hazards Group InfraRed Precipitation with Station data |
| CMORPH | CPC MORPHing technique |
| CN station | Yakou station in ChiNa |
| DFIR | Double Fence Intercomparison Reference |
| GSMaP | Global Satellite Mapping of Precipitation |
| IMERG | Integrated Multi-satellitE Retrievals for GPM |
| NOR station | the used station in NORway |
| RMSE | Root-Mean-Square Error |
| SHAP | SHapley Additive exPlanations |
| TFM | Transfer Function Method |
| TRMM | Tropical Rainfall Measuring Mission |
| US station | the used station in United States |
| WMO | World Meteorological Organization |
| WMO-SPICE | WMO - Solid Precipitation Intercomparison Experiment |
| XGBoost | Extreme Gradient Boosting |
| XGB | XGBoost regression method |
References
- Ma, J.; Li, H.; Wang, J.; Hao, X.; Shao, D.; Lei, H. Reducing the Statistical Distribution Error in Gridded Precipitation Data for the Tibetan Plateau. J. Hydrometeorol. 2020, 21, 2641–2654. [Google Scholar] [CrossRef]
- Yang, D.; Goodison, B.E.; Metcalfe, J.R.; Louie, P.; Leavesley, G.; Emerson, D.; Hanson, C.L.; Golubev, V.S.; Elomaa, E.; Gunther, T.; et al. Quantification of Precipitation Measurement Discontinuity Induced by Wind Shields on National Gauges. Water Resour. Res. 1999, 35, 491–508. [Google Scholar] [CrossRef]
- Chen, R.; Liu, J.; Kang, E.; Yang, Y.; Han, C.; Liu, Z.; Song, Y.; Qing, W.; Zhu, P. Precipitation Measurement Intercomparison in the Qilian Mountains, North-Eastern Tibetan Plateau. Cryosphere 2015, 9, 1995–2008. [Google Scholar] [CrossRef]
- Sugiura, K.; Ohata, T.; Yang, D. Catch Characteristics of Precipitation Gauges in High-Latitude Regions with High Winds. J. Hydrometeorol. 2006, 7, 984–994. [Google Scholar] [CrossRef]
- Jia, Y.; Li, Z.; Wang, F.; Chen, P. Correction of Precipitation Measurement for Weighing Precipitation Gauges in a Glacierized Basin in the Tianshan Mountains. Front. Earth Sci. 2023, 11, 1115299. [Google Scholar] [CrossRef]
- Yang, D. Double Fence Intercomparison Reference (DFIR) vs. Bush Gauge for “True” Snowfall Measurement. J. Hydrol. 2014, 509, 94–100. [Google Scholar] [CrossRef]
- Goodison, B.E.; Louie, P.Y.T.; Yang, D. WMO Solid Precipitation Measurement Intercomparison–Final Report; Technical Report WMO/TD—No. 872; World Meteorological Organization: Geneva, Switzerland, 1998. [Google Scholar]
- Yang, D.; Ohata, T. A Bias-Corrected Siberian Regional Precipitation Climatology. J. Hydrometeorol. 2001, 2, 122–139. [Google Scholar] [CrossRef]
- Yang, D. An Improved Precipitation Climatology for the Arctic Ocean. Geophys. Res. Lett. 1999, 26, 1625–1628. [Google Scholar] [CrossRef]
- Yang, D.; Kane, D.; Zhang, Z.; Legates, D.; Goodison, B. Bias Corrections of Long-Term (1973–2004) Daily Precipitation Data over the Northern Regions. Geophys. Res. Lett. 2005, 32, L19501. [Google Scholar] [CrossRef]
- Pan, X.; Yang, D.; Li, Y.; Barr, A.; Helgason, W.; Hayashi, M.; Marsh, P.; Pomeroy, J.; Janowicz, R.J. Bias Corrections of Precipitation Measurements across Experimental Sites in Different Ecoclimatic Regions of Western Canada. Cryosphere 2016, 10, 2347–2360. [Google Scholar] [CrossRef]
- WMO. IOM Report, 131. WMO Solid Precipitation Intercomparison Experiment (SPICE) (2012–2015); WMO: Geneva, Switzerland, 2018. [Google Scholar]
- Wolff, M.A.; Isaksen, K.; Petersen-Øverleir, A.; Ødemark, K.; Reitan, T.; Brækkan, R. Derivation of a New Continuous Adjustment Function for Correcting Wind-Induced Loss of Solid Precipitation: Results of a Norwegian Field Study. Hydrol. Earth Syst. Sci. 2015, 19, 951–967. [Google Scholar] [CrossRef]
- Kochendorfer, J.; Rasmussen, R.; Wolff, M.; Baker, B.; Hall, M.E.; Meyers, T.; Landolt, S.; Jachcik, A.; Isaksen, K.; Brækkan, R.; et al. The Quantification and Correction of Wind-Induced Precipitation Measurement Errors. Hydrol. Earth Syst. Sci. 2017, 21, 1973–1989. [Google Scholar] [CrossRef]
- Kochendorfer, J.; Nitu, R.; Wolff, M.; Mekis, E.; Rasmussen, R.; Baker, B.; Earle, M.E.; Reverdin, A.; Wong, K.; Smith, C.D.; et al. Testing and Development of Transfer Functions for Weighing Precipitation Gauges in WMO-SPICE. Hydrol. Earth Syst. Sci. 2018, 22, 1437–1452. [Google Scholar] [CrossRef]
- Smith, C.D.; Mekis, E.; Hartwell, M.; Ross, A. The Hourly Wind-Bias-Adjusted Precipitation Data Set from the Environment and Climate Change Canada Automated Surface Observation Network (2001–2019). Earth Syst. Sci. Data 2022, 14, 5253–5265. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, R.; Han, C.; Wang, L.; Guo, S.; Liu, J. Correcting Precipitation Measurements Made with Geonor T-200B Weighing Gauges near the August-One Ice Cap in the Qilian Mountains, Northwest China. J. Hydrometeorol. 2021, 22, 1973–1985. [Google Scholar] [CrossRef]
- Smith, C.D.; Ross, A.; Kochendorfer, J.; Earle, M.E.; Wolff, M.; Buisán, S.; Roulet, Y.A.; Laine, T. Evaluation of the WMO Solid Precipitation Intercomparison Experiment (SPICE) Transfer Functions for Adjusting the Wind Bias in Solid Precipitation Measurements. Hydrol. Earth Syst. Sci. 2020, 24, 4025–4043. [Google Scholar] [CrossRef]
- Liu, Z.; Ostrenga, D.; Teng, W.; Kempler, S. Tropical Rainfall Measuring Mission (TRMM) Precipitation Data and Services for Research and Applications. Bull. Am. Meteorol. Soc. 2012, 93, 1317–1325. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method That Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Kubota, T.; Aonashi, K.; Ushio, T.; Shige, S.; Takayabu, Y.N.; Kachi, M.; Arai, Y.; Tashima, T.; Masaki, T.; Kawamoto, N.; et al. Global Satellite Mapping of Precipitation (GSMaP) Products in the GPM Era. In Satellite Precipitation Measurement: Volume 1; Levizzani, V., Kidd, C., Kirschbaum, D.B., Kummerow, C.D., Nakamura, K., Turk, F.J., Eds.; Advances in Global Change Research; Springer International Publishing: Cham, Switzerland, 2020; pp. 355–373. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Integrated Multi-satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In Satellite Precipitation Measurement: Volume 1; Levizzani, V., Kidd, C., Kirschbaum, D.B., Kummerow, C.D., Nakamura, K., Turk, F.J., Eds.; Advances in Global Change Research; Springer International Publishing: Cham, Switzerland, 2020; pp. 343–353. [Google Scholar] [CrossRef]
- Gagne, D.J.; McGovern, A.; Xue, M. Machine Learning Enhancement of Storm-Scale Ensemble Probabilistic Quantitative Precipitation Forecasts. Weather Forecast. 2014, 29, 1024–1043. [Google Scholar] [CrossRef]
- Wang, F.; Tian, D.; Carroll, M. Customized Deep Learning for Precipitation Bias Correction and Downscaling. Geosci. Model Dev. 2023, 16, 535–556. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Yang, D.; Wang, J.; Gao, B.; Pan, X.; Zhang, Y.; Hao, X. Tracing Snowmelt Paths in an Integrated Hydrological Model for Understanding Seasonal Snowmelt Contribution at Basin Scale. J. Geophys. Res. Atmos. 2019, 124, 8874–8895. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Liu, S.; Li, H.; Xu, Z.; Tan, J.; Zhang, Y.; Ren, Z.; Xiao, L.; Deng, J.; et al. Integrated Hydrometeorological, Snow and Frozen-Ground Observations in the Alpine Region of the Heihe River Basin, China. Earth Syst. Sci. Data 2019, 11, 1483–1499. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In KDD ’16: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Masuda, M.; Yatagai, A.; Kamiguchi, K.; Tanaka, K. Daily Adjustment for Wind-Induced Precipitation Undercatch of Daily Gridded Precipitation in Japan. Earth Space Sci. 2019, 6, 1469–1479. [Google Scholar] [CrossRef]
- Yang, Y.; Palm, S.P.; Marshak, A.; Wu, D.L.; Yu, H.; Fu, Q. First Satellite-Detected Perturbations of Outgoing Longwave Radiation Associated with Blowing Snow Events over Antarctica. Geophys. Res. Lett. 2014, 41, 730–735. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Chen, H. A Machine Learning Approach to Derive Precipitation Estimates at Global Scale Using Space Radar and Ground-Based Observations. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 5376–5379. [Google Scholar] [CrossRef]
- Lei, H.; Zhao, H.; Ao, T. Ground Validation and Error Decomposition for Six State-of-the-Art Satellite Precipitation Products over Mainland China. Atmos. Res. 2022, 269, 106017. [Google Scholar] [CrossRef]
- Ren, J.; Xu, G.; Zhang, W.; Leng, L.; Xiao, Y.; Wan, R.; Wang, J. Evaluation and Improvement of FY-4A AGRI Quantitative Precipitation Estimation for Summer Precipitation over Complex Topography of Western China. Remote Sens. 2021, 13, 4366. [Google Scholar] [CrossRef]
- Lei, H.; Zhao, H.; Ao, T. A Two-Step Merging Strategy for Incorporating Multi-Source Precipitation Products and Gauge Observations Using Machine Learning Classification and Regression over China. Hydrol. Earth Syst. Sci. 2022, 26, 2969–2995. [Google Scholar] [CrossRef]
- Yang, X.; Yang, S.; Tan, M.L.; Pan, H.; Zhang, H.; Wang, G.; He, R.; Wang, Z. Correcting the Bias of Daily Satellite Precipitation Estimates in Tropical Regions Using Deep Neural Network. J. Hydrol. 2022, 608, 127656. [Google Scholar] [CrossRef]
- Karozis, S.; Klampanos, I.A.; Sfetsos, A.; Vlachogiannis, D. A Deep Learning Approach for Spatial Error Correction of Numerical Seasonal Weather Prediction Simulation Data. Big Earth Data 2023, 1–20. [Google Scholar] [CrossRef]
- Lei, H.; Zhao, H.; Ao, T.; Hu, W. Quantifying the Reliability and Uncertainty of Satellite, Reanalysis, and Merged Precipitation Products in Hydrological Simulations over the Topographically Diverse Basin in Southwest China. Remote Sens. 2023, 15, 213. [Google Scholar] [CrossRef]
- Sevruk, B.; Ondrás, M.; Chvíla, B. The WMO Precipitation Measurement Intercomparisons. Atmos. Res. 2009, 92, 376–380. [Google Scholar] [CrossRef]
- Lei, H.; Li, H.; Zhao, H.; Ao, T.; Li, X. Comprehensive Evaluation of Satellite and Reanalysis Precipitation Products over the Eastern Tibetan Plateau Characterized by a High Diversity of Topographies. Atmos. Res. 2021, 259, 105661. [Google Scholar] [CrossRef]


| Type | Variables | Sensors/Sources | Resolution |
|---|---|---|---|
| Meteorological variables | Precipitation (DFIR) (mm) | T200B-M3 with Double fences | 1 H; 6 H; Daily |
| Precipitation (mm) | Geonor: T200B-M3 | 1 H; 6 H; Daily | |
| Wind speed (m/s) | Campbell: WXT520 | 1 H; 6 H; Daily | |
| Wind direction (°) | Campbell: WXT520 | 1 H; 6 H; Daily | |
| Air temperature (°C) | Vaisala: HMP45C | 1 H; 6 H; Daily | |
| Relative humidity (%) | Vaisala: HMP45C | 1 H; 6 H; Daily | |
| Soil surface wetness (%) | CSI: CS616 | 1 H; 6 H; Daily | |
| Soil surface temperature (°C) | CSI: 109 | 1 H; 6 H; Daily | |
| Upwelling Longwave radiation (W/m2) | Kipp-Zonen: CNR4 | 1 H; 6 H; Daily | |
| Downward Longwave radiation (W/m2) | Kipp-Zonen: CNR4 | 1 H; 6 H; Daily | |
| Upwelling shortwave radiation (W/m2) | Kipp-Zonen: CNR4 | 1 H; 6 H; Daily | |
| Downward shortwave radiation (W/m2) | Kipp-Zonen: CNR4 | 1 H; 6 H; Daily | |
| Surface infrared temperature (°C) | Avalon: IRTC3 | 1 H; 6 H; Daily | |
| Snow depth (m) | CSI:SR50A | 1 H; 6 H; Daily | |
| Atmospheric pressure (hpa) | Setra: CS100 | 1 H; 6 H; Daily | |
| Remote sensing precipitation | GSMaP | Microwave, Infrared, gauge | 1 H; 0.1° |
| IMERG | Microwave, Infrared, gauge | 0.5 H; 0.1° | |
| CHIRPS | Reanalysis data, Infrared, gauge | Daily; 0.05° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, Y.; Lei, H.; Hao, X. Machine Learning-Based Bias Correction of Precipitation Measurements at High Altitude. Remote Sens. 2023, 15, 2180. https://doi.org/10.3390/rs15082180
Li H, Zhang Y, Lei H, Hao X. Machine Learning-Based Bias Correction of Precipitation Measurements at High Altitude. Remote Sensing. 2023; 15(8):2180. https://doi.org/10.3390/rs15082180
Chicago/Turabian StyleLi, Hongyi, Yang Zhang, Huajin Lei, and Xiaohua Hao. 2023. "Machine Learning-Based Bias Correction of Precipitation Measurements at High Altitude" Remote Sensing 15, no. 8: 2180. https://doi.org/10.3390/rs15082180
APA StyleLi, H., Zhang, Y., Lei, H., & Hao, X. (2023). Machine Learning-Based Bias Correction of Precipitation Measurements at High Altitude. Remote Sensing, 15(8), 2180. https://doi.org/10.3390/rs15082180