Abstract
As an essential data-driven model, machine learning can simulate runoff based on meteorological data at the watershed level. It has been widely used in the simulation of hydrological runoff. Considering the impact of snow cover on runoff in high-altitude mountainous areas, based on remote sensing data and atmospheric reanalysis data, in this paper we established a runoff simulation model with a random forest model and ANN (artificial neural network) model for the Xiying River Basin in the western Qilian region The verification of the measured data showed that the NSE (Nash–Sutcliffe efficiency), RMSE (root mean square error), and PBIAS (percent bias) values of the random forest model and ANN model were 0.701 and 0.748, 6.228 m3/s and 4.554 m3/s, and 4.903% and 8.329%, respectively. Considering the influence of ice and snow on runoff, the simulation accuracy of both the random forest model and ANN model was improved during the period of significant decreases in the annual snow and ice water equivalent in the Xiying River Basin from April to May, after the snow remote sensing data were introduced into the model. Specifically, for the random forest model, the NSE increased by 0.099, the RMSE decreased by 0.369 m3/s, and the PBIAS decreased by 1.689%. For the ANN model, the NSE increased by 0.207, the RMSE decreased by 0.700 m3/s, and the PBIAS decreased by 1.103%. In this study, based on remote sensing data and atmospheric reanalysis data, the random forest model and ANN model were used to effectively simulate hydrological runoff processes in high-altitude mountainous areas without observational data. In particular, the accuracy of the machine learning simulations of snowmelt runoff (especially during the snowmelt period) was effectively improved by introducing the snow remote sensing data, which can provide a methodological reference for the simulation and prediction of snowmelt runoff in alpine mountains.
1. Introduction
As an essential component of the cryosphere, snow cover has a significant impact on climate change, water cycle processes, and ecosystem structures and functions [1,2]. In addition, seasonal snow cover is very sensitive to changes in temperature and climate, and is an important sensitivity indicator of climate [3,4,5]. Seasonal snowmelt water is one of the most important freshwater resources in China, which not only provides a large amount of water recharge for inland rivers in arid regions but also is essential for human production and existence in the middle and lower reaches of the basin [6]. Along with climate warming, the water cycle elements in the arid zone of northwest China are constantly changing, exacerbating the uncertainty of local water resources, especially during the snowmelt period, which is prone to snowmelt flood events [7]. The arid zone of northwest China is a high-risk area for snowmelt flood events, which can cause damage to local facilities such as transportation structures, downstream rivers, reservoirs, and farmland [8,9]. With rising global temperatures, the melting speed of glaciers and snow cover is accelerated, the melting period of snow cover is advanced, and the flood peak of snowmelt floods is increased [10,11], leading to increases in the frequency and severity of snowmelt flood events [12,13].
Snowmelt floods are serious natural disasters that often occur in high-latitude and high-altitude mountainous areas all over the world, and the snowmelt flooding can damage local roads, bridges, and other infrastructure, which can cause severe losses of life and property [9,14]. In recent decades, severe snowmelt floods have occurred in Wushu, Manas, and Hutubi in Xinjiang, China. In order to effectively prevent snowmelt floods in advance, scholars worldwide have used various hydrological models to simulate runoff [15,16]. Unfortunately, along with the accumulation of the global greenhouse effect and the intensification of global warming, the robustness of traditional physical hydrological models established by numerous experts and scholars based on previous climatic conditions of different calibration cycles has gradually declined [17,18,19,20,21]. On the other hand, as data-driven models that have received widespread attention, machine learning models are widely used in various complex engineering problems because of their strong generalization ability, strong learning ability, and ability to handle high-dimensional data. Many researchers have started to focus on the application of machine learning in hydrological processes, especially basin-scale runoff simulations [22,23]. Compared with traditional hydrological models, machine learning models do not need to consider the complex and variable physical processes within a watershed. By using past meteorological datasets to explore the complex non-linear relationships between input factors and runoff volumes, more accurate runoff simulation results can be obtained. In recent years, many scholars have carried out basin-scale runoff simulation and prediction studies based on machine learning algorithms, including various machine learning models such as the SVM (support vector machine) [24], random forests [25], LSTM (long short-term memory) [26], and ANN [27] methods. Machine learning has been applied as a novel technique to improve runoff simulations and flood prediction accuracy. It plays a crucial role in flood risk management strategies [28].
Machine learning methods have been used in recent years to construct runoff models for high-altitude mountainous areas. They primarily rely on meteorological factors such as precipitation or temperature, and snow characteristics within the watershed have been less considered in the studies conducted due to the lack of snow data with high spatial and temporal resolution. In studies simulating runoff in high-altitude mountain areas, the models usually simulate runoff in the snowmelt period more accurately, but the effect is poor because the annual precipitation in high-altitude mountain areas is low, and it is usually covered by large areas of seasonal snow. When the temperatures rise in spring, the snowmelts, thereby entering the runoff and replenishing the rivers. Snow and ice melt rapidly under increasingly extreme climatic conditions, and with the increase in extreme warming events, snowmelt floods are prone to occur in high-altitude mountain basins. In this study, the daily cloudless high-resolution snow area and snow water equivalent products are used to simulate and verify snowmelt runoff data on a daily scale through machine learning and atmospheric reanalysis data, in order to better simulate the hydrological in high-altitude mountainous areas.
Therefore, this study uses atmospheric reanalysis data and high-temporal snow remote sensing data, combined with a machine learning method to simulate runoff in areas lacking observation data. The Xiying River Basin is selected as the typical snowmelt runoff study area in this study. Based on the use of the random forest model and ANN model, the characteristics of the snow cover and environment in the snowmelt runoff basin are analyzed, and the runoff in the study area is simulated and verified. This study provides a methodological reference for the simulation of the snowmelt runoff in arid regions of northwest China, and even in the northern hemisphere, where there is a lack of observational data. At the same time, the results of the study can help improve the planning and management of water resources by local governments, and could have positive implications for the prevention and mitigation of spring snowmelt flood disasters.
2. Research Area
The Xiying River, located in Wuwei, Gansu Province, China, originates from the northern foot of the LengBei Ridge of the Qilian Mountains, and is one of the eight tributaries in the upper reaches of the Shiyang River Basin and the first major tributary in the basin. The Xiying River Basin is located between 37°28′N–37°57′N and 101°4′E–102°15′E (Figure 1), with a high southwest and low northeast topography, a basin area of 1444.67 km2, and an average elevation range of 1874~4905 m. The floods in the Xiying River Basin are mainly caused by climate warming or extreme rainfall. The average annual runoff in the basin is 3.88 × 108 m3 [29]. The Xiying River Basin is a semiarid alpine region with a temperate continental climate, with an average annual temperature of −1.67 °C and a total yearly precipitation of 412.7 mm. From 1990 to 2021, the average daily runoff of the basin showed an increasing trend, with an average annual increase of about 0.939 m3/s·(10a)−1, and the runoff rate was about 10%, which was related to the decreases in glacier, snow cover, and snow water equivalent in the basin. The annual average snow cover area of the Xiying River Basin is 796.75 km2, accounting for 55.15% of the total area of the basin. In the high-altitude areas in the southern part of the basin, the snow days generally exceed 180 days. The study area of this paper mainly covers the catchment area of the Xiying River Outlet Control Station, Jiutiaoling Hydrological Station, and above.
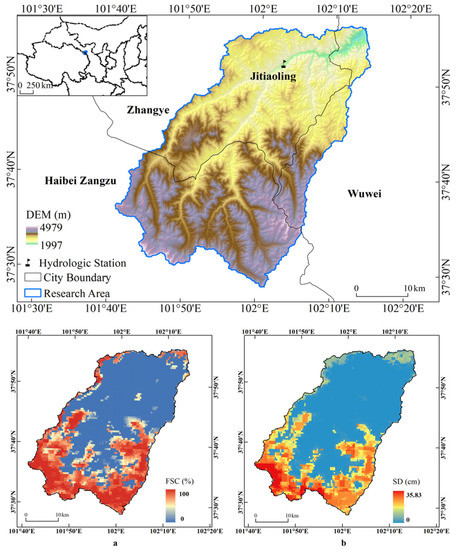
Figure 1.
Research area overview, with a product diagram of SSE-mod FSC snow cover (a) and SDD-mod SD snow depth (b) data in the research area (1 January 2013).
3. Data and Preprocessing
3.1. Meteorological Data
The meteorological data used in this study were derived from the ERA5 product provided by the European Center for Medium-Range Weather Forecasts (ECMWF). ERA 5 is the fifth-generation atmospheric reanalysis data for the global climate, which combines the reanalysis model data with observations data from all over the world to form a global meteorological data set. Its temporal resolution is three hours, with a spatial resolution of 0.1°. The ERA5 data used in this study include the soil temperature, temperature, potential evaporation, precipitation, soil water content, solar radiation, and wind speed.
3.2. Remote Sensing Data
3.2.1. Snow Cover Data
The snow cover data used in this study were obtained from the Chinese regional daily cloud-free snow accumulation ratio product SSE-mod FSC (Spatial–Spectral–Environmental MODIS Fractional Snow Cover) produced by Zhao et al. [30]. The SSE-mod FSC data are based on MOD09GA and MYD09GA MODIS surface reflectance data, incorporating Aqua and Terra data to fill in the vacant values, combined with a linear spectral mixture analysis unmixing algorithm to construct the accumulation area-scale data for the MODIS product FSC snow. A multiple model fusion de-clouding algorithm was used to prepare the final long time series daily cloud-free SSE-mod FSC data [31,32,33,34]. The temporal resolution is 1 day, and the spatial resolution is 0.005°. This study uses SSE-mod FSC data from 2013 to 2021.
3.2.2. Snow Depth Data
The snow depth data used in this study were derived from the SDD-mod SD (Spatial Dynamic Downscaling MODIS Snow Depth) data prepared by Hu et al. [35] based on the downscaling algorithm for the snow depth fusion of AMSR-2 and FSC data. The SDD-mod SD snow depth data are derived based on the Grody decision tree discrimination algorithm, which discriminates snow from non-snow elements (rainfall, frozen soil, and cold desert) by brightness temperature values, combined with a static empirical. The snow depth is calculated based on the relationship between observed brightness temperature difference and measured snow depth; the FSC snow ratio data are used to discriminate between snow and non-snow elements and to invert the snow depth based on snow recession curves. The final product is a daily cloud-free snow depth product generated by fusing multi-source remote sensing data. The temporal resolution is 1 day, and the spatial resolution is 0.005°. This study uses SDD-mod SD data from 2013 to 2021.
Snow cover is a key and essential component of the hydrological cycle in high-altitude mountains. There is usually considerable seasonal snow in the basin, which melts into runoff and rivers in the next spring due to warming. Figure 1 illustrates the SSE-mod FSC snow cover area proportion product (a) and the SDD-mod SD snow depth product (b) for the Xiying River Basin. The snow cover area and snow water equivalent in the research area were acquired indirectly from the above two datasets as inputs to the machine learning model, and were accepted as in Equations (1) and (2). The snow density used in this study was the average snow density (0.16 g/cm3) in the Qilian Mountains [36]:
where SFSC is the snow cover area (km2), FSC is the proportion of pixel snow cover area, Si is the pixel area, SW is the pixel snow water equivalent, SDi is the pixel snow depth, and snow is the ρsnow density.
3.3. Runoff Data
The daily runoff data from 2013 to 2021 used in this study were measured from Jiutiaoling Hydrological Station in the Xiying River Basin, the national hydrological station for Xiying River, Gansu (Figure 1). The Jiutiaoling Hydrological Station was established in 1988 and is a national hydrological station. The hydrological station measured the average annual runoff of the outlet of the Xiying River Basin to be 11.8 m3/s, and the average annual runoff for many years was 372 million m3. According to the historical data of the hydrological station, the Xiying River Basin experienced severe floods in 1895 and 1945, and the peak runoff values were 807 m3/s and 453 m3/s, respectively. Among them, the runoff data unit for the Jiutiaoling Hydrological Station was m3/s. The runoff data were used for model training and validation.
4. Research Methodology
4.1. Random Forest
The random forests model is a supervised machine learning model with a short training time, high accuracy, and robustness in the training bagging process compared to other machine learning algorithms [37]. In the training process, the model will randomly and independently draw sub-sample sets to construct decision trees for training, and will randomly select a subset of features from which the optimal features are selected for splitting. The random forest model is built with the integration of several random decision trees, which are not related to each other. The results of each of decision tree are averaged to acquire the final regression (or classification) results.
In the random forest model constructed in this study, the data are divided into a training set (2013~2019) and verification set (2020~2021). The training set is input into the random forest model, the number of decision trees is adjusted, along with the depth and number of branches of the model, and multiple cross-validations are performed so that the validation results of the model test set are optimal to obtain the final random forest model:
where h(x) is the random forest output, which is also the average result of multiple decision trees; T is the number of decision trees; h(x, θt) is the decision tree output based on x and θt; x is the independent variable; θt is a random variable obeying an identical independent distribution.
4.2. Artificial Neural Networks
The ANN model is a purely empirical model applied to runoff simulations, without considering the physical characteristics of the basin and only exploring the linear (or non-linear) relationships between the input and output variables [38]. The ANN model is widely used in various disciplines because of its high non-linear processing capability, self-learning capability, and adaptability [39,40,41].
In the ANN model built in this study, the gradient descent (GD) algorithm and backpropagation (BP) algorithm were used to construct a feed-forward neural network (15 hidden layers with 1024 nodes per layer). During the construction of the model, the loss function (accuracy metric) was set as the RMSE, and the model was optimized through multiple cross-validations. The activation function of the hidden layer of the model is set to the hyperbolic tangent function, and the model is trained using Adam’s algorithm.
4.3. Feature Selection
The input features of a machine learning model are very important for the accuracy of the model training results. When simulating runoff at the watershed level, in addition to the input variables used in previous runoff simulation studies (various meteorological characteristics such as the precipitation, temperature, soil moisture content, etc.), other essential elements within the watershed should also be considered. In this study, the daily runoff of Xiying River Basin is simulated based on a machine learning algorithm, which takes into account not only the conventional meteorological elements, but also the characteristics of ice and snow in the basin. The input features include the total precipitation, temperature at 2 m, evapotranspiration, solar radiation, soil water content, soil temperature, snow cover area, snow water equivalent, and wind speed. Among the input features, the total precipitation is the daily accumulation, and other variables are the daily average.
In watershed-scale hydrological modeling studies, the temperature and precipitation are usually the most critical factors influencing runoff variability [39]. Precipitation in the basin is the direct cause of runoff variability in most rivers around the world, while changes in temperature cause glaciers and snow cover in the basin to melt, and for snow and ice meltwater to sink into the river and cause runoff variability [42]. The Xiying River Basin has intense evapotranspiration, the basin is perennially under permafrost, and snow and ice meltwater flows through the ground and sinks into the river, resulting in a high soil water content in the basin, while the wind speed accelerates the snowmelt. Hence, the model introduces various meteorological factors such as the evapotranspiration, solar radiation, soil water content, and soil temperature to simulate runoff.
Snow cover or glacial meltwater is one of the most significant sources of runoff recharge in high-altitude watersheds. The Xiying River Basin has a multi-year average snow cover area of 796.75 km2, accounting for 55.15% of the total basin area. According to the snow remote sensing data (SSE-mod FSC snow cover data and SSD-mod SD snow depth data) and runoff change trend, it can be concluded that there is a strong negative correlation between the snow cover, snow water equivalent, and runoff in the Xiying River Basin, and it is proven that changes in snow and ice characteristics in the study area affect the runoff to some extent. In addition, the wind speed is also an essential factor affecting the glacier and snowmelt rate; therefore, the wind speed was introduced to simulate runoff. According to the atmospheric reanalysis data from 1990 to 2021, under the climate background, the daily runoff in the Xiying River Basin showed a warming trend (0.0422 °C·(10a)−1) and the annual average total precipitation did not change much. This was presumed to be attributed to the seasonal snow accumulation in the Xiying River Basin and the rapid melting of the upper glaciers. The change in runoff in the Xiying River Basin coincides with the yearly decrease in the average annual snow cover area and snow water equivalent in the study area. This corresponds to the fact that the snow line rises and many glaciers retreat or even disappear in the mountainous regions of the upper Shiyang River Basin [43].
4.4. Evaluation Parameter
The regression evaluation metrics are some of the most critical components in assessing model performance. Three evaluation metrics are used to evaluate the accuracy of the results—the Nash–Sutcliffe efficiency (NSE), percent bias (PBIAS), and root mean square error (RMSE).
The NSE is an evaluation parameter generally used to evaluate the quality of hydrological models, and the NSE values range from negative infinity to 1. A value closer to 1 indicates that the model has better quality and is more credible; the closer it is to 0, the closer the model is to the average of the observed values, i.e., the overall result is credible, but the simulation process has a significant error; an NSE much less than 0 indicates that the model is unreasonable. The specific mathematical formula for the NSE is as follows:
where Xo is the observed actual runoff and Xm is the model-simulated runoff.
Although the NSE verifies the accuracy of the model results, it cannot provide information on the degree of deviation from the model simulation. Therefore, the PBIAS is used as an evaluation parameter for the statistical model deviation criterion. The closer the PBIAS is to 0, the less deviation of the model results; a PBIAS less than 0 means that the model prediction is over-predicted, while a PBIAS greater than 0 means that the model results are underpredicted. The specific mathematical equation for the PBIAS is as follows:
By combining the NSE and PBIAS, one can only obtain the overall accuracy and degree of deviation of the model, but the actual deviation value cannot be obtained. The RMSE measures the deviation of the predicted value from the true value. The smaller the RMSE value, the more accurate the model simulation, and the mathematical formula for the RMSE is as follows:
5. Results and Analysis
5.1. Results of the Random Forest Model
Machine learning can be used to acquire simulation results with high accuracy through complex internal structures and a large amount of training data. Based on the random forest model, the atmospheric reanalysis data, snow accumulation remote sensing data, and runoff data from 2013 to 2019 in the Xiying River Basin were used as training samples to simulate the runoff data from 2020 to 2021 in the Xiying River Basin, and the simulation results were verified with the measured runoff data from 2020 to 2021 in the Xiying River Basin. The results are shown in Figure 2, where the NSE, RMSE, and PAIBS of the random forest model simulation results are 0.701, 4.954 m3/s, and 4.903%, respectively. The evaluation of random forest model based on the simulation results in 2020 and 2021 is shown in Table 1, where the NSE values are 0.701 and 0.696, respectively; the RMSE values are 5.037 m3/s and 4.869 m3/s, respectively; and the PAIBS values are 12.254% and 1.393%, respectively. The overall model results were good, but the random forest model simulation accuracy was poor from June to August, when extreme precipitation events are likely to occur [44], mainly due to the flawed nature of the EAR5 atmospheric reanalysis data. When the EAR5 atmospheric reanalysis data were inverted for extreme precipitation weather, the error with the observed data was significant, and the larger the threshold (i.e., the stronger the storm), the larger the error [44,45], which led to the results of the runoff simulation under extreme weather deviating significantly from the observed values.
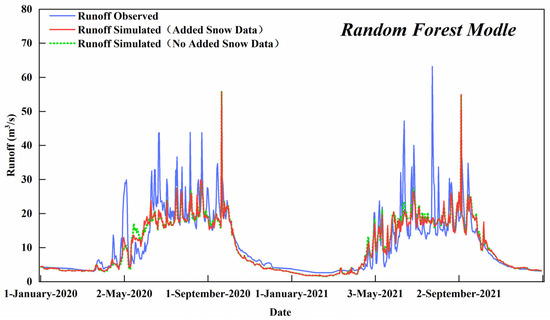
Figure 2.
Simulation results for the random forest model of the Xiying River Basin from 2020 to 2021.

Table 1.
Evaluation parameters for the random forest model of the Xiying River Basin from 2020 to 2021.
According to the location and time, snowmelt floods in the arid areas of northwest China can be divided. One type covers warm snowmelt floods from March to April, mainly in northern and western Xinjiang, while mixed rain and snow floods after May mainly occur in the Qilian Mountain, Kunlun Mountain, and Tianshan Mountain [8]. The simulation results from March to July in the high-incidence period of snowmelt floods in 2020 and 2021 were selected for a comparative analysis (Figure 3 and Table 2). The results show that after introducing the snow remote sensing data into the random forest model, the NSE increased to 0.600, the RMSE decreased to 6.256 m3/s, and the PBIAS increased to 9.301%. Although the PBIAS rose slightly, its impact can be ignored, and the overall accuracy of the model was improved. The snow remote sensing data were introduced into the random forest model, making the internal tree branches of the random forest model more complicated and optimizing the simulation results of the model.
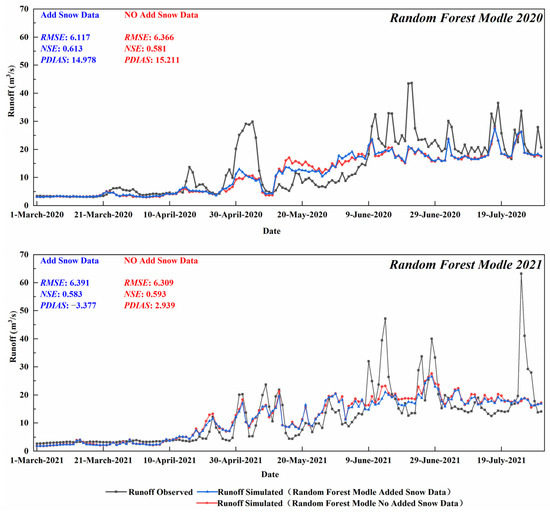
Figure 3.
Simulation results for the random forest model of the Xiying River Basin from March to July, 2020 to 2021.

Table 2.
Evaluation parameters for the random forest model of the Xiying River Basin from March to July, 2020 to 2021.
5.2. ANN Model Result
The results of machine learning models are subject to change. The results from a single machine learning model are not enough to prove that snow data can improve machine learning simulations of runoff from unknown mountain areas at high altitudes. Therefore, this study also validates the runoff simulation based on the ANN model for the Xiying River Basin. In the process of constructing the ANN model, the study area’s atmospheric reanalysis data from 2013 to 2019, snow cover remote sensing data, and runoff data were also used as training samples for the model. We simulated the runoff data from 2020 to 2021 with the ANN model with or without snow cover remote sensing data, and compared the simulation results with the actual measured runoff data (Figure 4 and Table 3). The NSE, RMSE, and PBIAS of the model without snow remote sensing data were 0.723, 4.776 m3/s, and 7.3%, respectively, while the NSE, RMSE, and PBIAS of the model with snow remote sensing data were 0.748, 4.554 m3/s, and 8.329%, respectively. With the introduction of snow remote sensing data, the model gave NSE, RMSE, and PBIAS values for 2020 and 2021 at 0.754, 4.570 m3/s, and 19.378%, and 0.736, 4.539 m3/s, and 4.553%, respectively. The ANN model, with the introduction of snow remote sensing data, improved the NSE by 0.025, while the RMSE decreased by 0.222 m3/s and the PBIAS increased slightly. Overall, the accuracy of the ANN model runoff simulation improved in general.
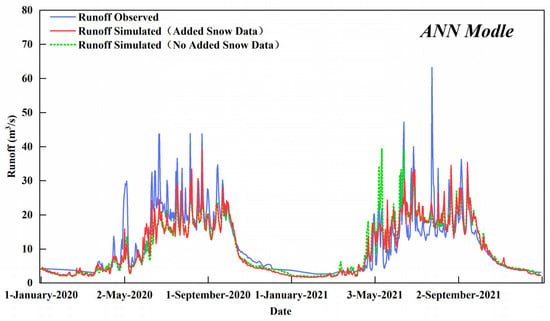
Figure 4.
Simulation results of the ANN model of the Xiying River Basin from 2020 to 2021.

Table 3.
Evaluation parameters for the ANN model of the Xiying River Basin from 2020 to 2021.
With the introduction of snow remote sensing data, the accuracy of the ANN model runoff simulation improved, and the optimization was more obvious in the flood period with high snow melting rates (March to July), but the effect was poor in January to February and August to December. In this study, by comparing the ANN model runoff simulation results for March to July (Figure 5 and Table 4), the ANN NSE increased from 0.554 to 0.602, the RMSE decreased from 6.607 m3/s to 6.237 m3/s, and the PBIAS increased from 7.399% to 9.380% in 2020 and 2021 after the introduction of snow cover remote sensing data. The overall impact of the model simulations on the PBIAS, although also increasing, is small. The improvement in the ANN model simulations during periods of high snowmelt flooding is mainly since the precipitation data inverted from the ERA5 atmospheric reanalysis data is the sum of the liquid and solid precipitation. Liquid precipitation can directly affect runoff by sinking into rivers; solid precipitation lags in its effect on the runoff due to altitude and climatic factors. Solid precipitation at low altitudes melts and flows into the runoff on the same day or the next day due to the high surface temperatures, solar radiation, and evapotranspiration. Solid precipitation at high altitudes does not affect the runoff immediately due to the lower temperatures, and is stored in the surface layer of the basin as seasonal snow, which melts and contributes to the river in the following spring when the temperature rises and recharges the runoff. In this study, considering the impact of the snow on runoff in the basin, the snow cover area and snow water equivalent were introduced into the model to reflect the seasonal changes in snow water equivalent in the basin, improve the lag of the solid precipitation on the runoff, and enhance the model’s simulation results for the snowmelt runoff.
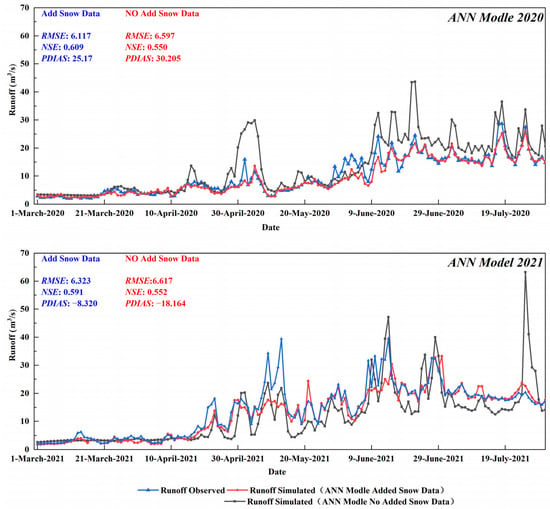
Figure 5.
Simulation results for the ANN model of the Xiying River Basin from March to July, 2020 to 2021.

Table 4.
Evaluation parameters for the ANN model of the Xiying River Basin from March to July, 2020 to 2021.
5.3. Accuracy Evaluation of Snowmelt Period
Snowmelt floods in the arid regions of northwest China generally occur from March to July each year. Xiying River Basin is located in the Qilian Mountains. According to the monthly average snow area (SSE mod FSC) data and snow water equivalent data (SDD-mod SD), it was found that at the beginning of April every year, the melting rate of the ice and snow in the basin gradually accelerates, with large amounts of seasonal snowmelt. By the end of May, the seasonal snow has almost completely melted. Therefore, in this study, the snowmelt period for Xiying River Basin is defined as the first ten days of April to the last ten days of May. The runoff simulation results of the random forest model and ANN model for April and May were compared and analyzed (Figure 6 and Table 5), and both the random forest model and ANN model were significantly enhanced by the introduction of snow cover remote sensing data into the model. The NSE, RMSE, and PBIAS of the random forest model with the introduction of snow remote sensing data were 0.333, 5.125 m3/s, and −0.346%, respectively. Compared to the model without snow remote sensing data, the NSE of the model improved by 0.099, the RMSE decreased by 0.369 m3/s, and the PBIAS decreased by 1.689%. The ANN model improved more significantly compared to the random forest model. The NSE, RMSE, and PBIAS of the ANN model with the introduction of snow remote sensing data were 0.239, 5.476 m3/s, and 3.672%, respectively; compared to the model without snow remote sensing data, the NSE improved by 0.207, the RMSE decreased by 0.7 m3/s, and the PBIAS de-creased by 1.103%. From April to May each year, the snow cover area and snow water equivalent in the Xiying River Basin decline rapidly. A large amount of the seasonal snow melts and sinks into the runoff, making it vulnerable to snowmelt flooding downstream. The introduction of snow cover remote sensing data can effectively improve the simulation accuracy of snowmelt runoff data while verifying the importance of snow cover remote sensing data on the runoff in the Xiying River Basin.
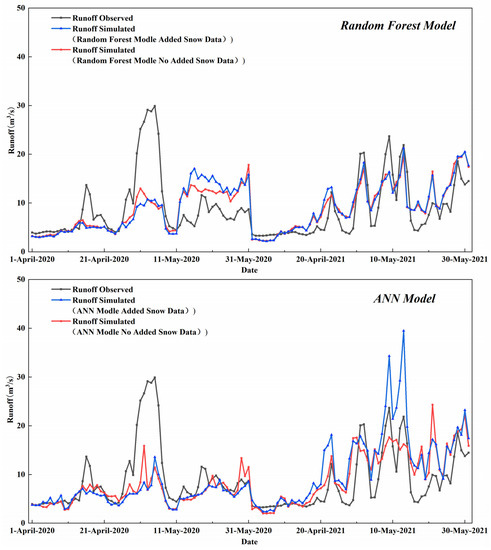
Figure 6.
Simulation results for the random forest model and ANN model of the Xiying River Basin from April to May, 2020 to 2021.

Table 5.
Verification results for the random forest model and ANN model of the Xiying River Basin from April to May, 2020 to 2021.
5.4. Analysis of Model Validation Results
In this study, runoff simulations were carried out for a watershed with no observational data. Based on an atmospheric reanalysis and remote sensing data, a machine learning model was used to simulate runoff in the Xiying River watershed. The model was constructed by taking into account the snow cover characteristics of the basin, which improved the simulation results of both the random forest and ANN models. Here, we compare the Pearson correlation coefficients between different input features and runoff (Figure 7). In order to make a more intuitive comparison, the Pearson correlation coefficients in the figure are all absolute values. It can be seen that soil temperature and temperature are strongly correlated with runoff. At the same time, precipitation is moderately correlated, which proves to a certain extent that temperature has a more significant influence on runoff than precipitation in alpine mountain hydrological systems. The Pearson correlation coefficients for the snow cover area and snow water equivalent are more vital than those for precipitation. Due to the small amount of precipitation in high-altitude mountain areas, there is a large area of seasonal snow all year round. Spring climate warming causes seasonal snowmelt in the basin, which has a great influence on the changes in snowmelt runoff. In recent years, rising temperatures have accelerated the rates of glacial melting and snowmelt, providing a more excellent water supply for runoff, while leading to a greater susceptibility to snowmelt flooding [46]. In previous hydrological studies based on machine learning models, many scholars have considered simulating runoff based on basin-scale precipitation, temperature, and other meteorological factors, and the overall accuracy of the models is high. However, the simulation of runoff during the spring snowmelt period is relatively poor. Based on the previous runoff simulation studies, this study improves the simulation of snowmelt runoff in alpine mountains by machine learning models using remote sensing data for snow accumulation, making the model results more consistent with the hydrological process in cold regions.
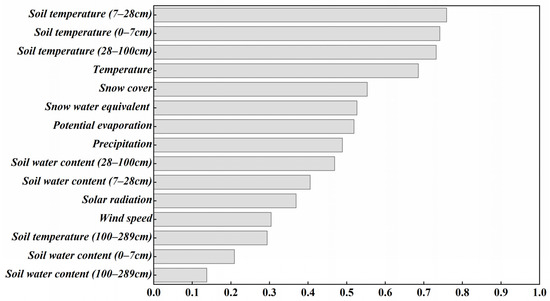
Figure 7.
Pearson correlation coefficients of the input features.
6. Discussion
Many studies show that machine learning is widely used in the field of hydrological modeling. Compared with traditional hydrological models, machine learning focuses more on improving the accuracy of the simulation and prediction processes. Our machine learning model is a data-driven model. Through the complex relationship between input and output, it still has high simulation accuracy without considering the physical characteristics of the river basin, which is the biggest advantage of machine learning. In the past decades, hydrology has been the subject of many machine learning models, such as multiple linear regression [47], SVM [48], MLP (multilayer perceptron) [49], RBF (radial basis function) [50], and ANN [51] models. These machine learning models are helpful for runoff simulation in different basins. However, as a black box model, our hydrological model constructed using machine learning gives a vague description of the modeling process, shows a lack of theoretical support, has poor applicability, and provides a poor explanation, which makes it difficult to compare different models meaningfully. Moreover, the problems related feature selection, the over-fitting of results, and the multi-model selection of hydrological simulations in time series have not been completely solved, and there are still a lot of research directions and spaces to be covered.
Snowmelt runoff basins are usually located in high-altitude mountain areas. In the research process, the primary problem is obtaining various monitoring data, and the use of satellite remote sensing data has solved this problem. In recent years, there have been few studies on snowmelt runoff simulations at the daily scale, which is mainly due to the lack of meteorological data and snow data of high temporal and spatial resolution. Although the ERA5 atmospheric reanalysis data used in this research have a high time resolution and the ERA5 products cover the whole world, they have made a great contribution to the research of global hydrology. However, the EAR5 atmospheric reanalysis data still have some shortcomings, such as their low spatial resolution, slow updating times, and obvious deviation in the inversion of extreme weather events. The SSE-mod FSC and SDD-mod SD data prepared based on remote sensing satellite data update the speed block and have a high spatial and temporal resolution. However, there is still some deviation in the inversion of snow area and snow depth data in mountainous areas, which makes the simulation effect of this study not very significant. Nowadays, spatial downscaling, data fusion, and deep learning algorithms are the main directions for us to obtain high temporal and spatial resolution data. In the future, based on the high temporal resolution, high spatial resolution, more accurate remote sensing data, and atmospheric reanalysis data, more research can be done on the simulation of snowmelt runoff.
With the rapid warming and wetting of the world, the accuracy of traditional physical and hydrological models is gradually decreasing. Although the “process-oriented” hydrological model has a solid theoretical foundation, the accuracy of the runoff simulation process decreases gradually in different calibration periods due to the rapid changes in climate. However, there is no conflict between the traditional hydrophysical “process-oriented“ model and the “data-oriented” machine learning model, and the combination of them may make the runoff simulations more accurate. For example, Khandelwal et al. [52] proposed an in-depth framework based on LSTM, combined with the SWAT (Soil and Water Assessment Tool). The key to their framework is to link the weather driving factors with runoff, to assist in simulating the intermediate process and to construct hydrological models, instead of simply simulating the runoff directly according to meteorological characteristics. They integrate hydrophysical processes into machine learning models in order to better simulate runoff. Okkan et al. [53] carried out research based on ANN and SVR models, and integrated a machine learning model into a CRR model. The dynamic water balance model is recommended as the CRR model. Then, all free parameters in these nested hybrid models are calibrated simultaneously. The machine learning part of the nested scheme deals with various output variables, which are derived from three conceptual parameters of monthly runoff simulation. In order to better simulate runoff, in our research we combined a machine learning model with a hydrophysical model. As the global weather is constantly changing, many physical factors such as wind and snow, soil freezing and thawing, and rain and snow mixing patterns need to be considered when constructing snowmelt runoff models. Therefore, in the upcoming research, we could combine the machine learning model with the traditional hydrological model and improve the robustness of the traditional hydrological model under the background of global warming and rapid humidity changes, so as to improve the runoff simulation ability.
7. Conclusions
In this study, the random forest model and ANN model were constructed based on big data (atmospheric reanalysis data and snow cover remote sensing data), and runoff simulations were carried out for areas lacking actual measurement data. Taking the Qilian Mountains and Xiying River Basin as an example, the runoff data from the Xiying River Jiutiaoling National Basic Hydrological Station were used for validation. At the same time, the machine learning model was introduced into the runoff simulation results of the snow remote sensing data, and the following main conclusions were acquired.
The random forest and ANN models based on snow cover big data can better simulate the runoff data in areas lacking observation data. The NSE, RMSE, and PBIAS of the random forest and ANN models were 0.701 and 0.748, 6.228 m3/s and 4.554 m3/s, and 4.903% and 8.329%, respectively. The results show that the machine learning model has high accuracy in simulating runoff and is an effective method for simulating watershed-scale runoff. At the same time, machine learning is also an effective method for simulating watershed scale runoff. With the introduction of snow remote sensing data, the runoffs simulated by the random forest model and ANN model were compared. It was found that the snow remote sensing data can improve the accuracy of the machine learning model to simulate the runoff to a certain extent, especially in the snowmelt period. For the snowmelt period in the Xiying River Basin, the NSE of the random forest model increased by 0.099, the RMSE decreased by 0.369 m3/s, and the PBIAS decreased by 1.689%. Similarly, the NSE of the ANN model increased by 0.207, the RMSE decreased by 0.700 m3/s, and the PBIAS decreased by 1.103%. The introduction of snow remote sensing data into the random forest and ANN models effectively improved the simulation accuracy of the snowmelt runoff data. The simulation results of the random forest and ANN models were compared, showing that the non-linear structure of the ANN model was slightly more accurate than the tree structure of the random forest model, both in the overall and snowmelt periods. With the introduction of high spatial and temporal snow remote sensing data into the model, the accuracy of the ANN model was also significantly improved compared to the random forest model. From this study, we conclude that the ANN model has more potential than the random forest model in the field of hydrological modeling.
In this study, we used machine learning methods to simulate runoff in the Xiying River Basin based on atmospheric reanalysis data and for the remote sensing of high temporal and spatial snow cover data. The results showed that machine learning can be used to better simulate hydrological processes in alpine mountains, while the introduction of snow cover remote sensing data can improve the accuracy of machine learning models for snowmelt runoff in alpine mountains, while also providing a methodological reference for the simulation of snowmelt runoff in high-altitude mountainous areas.
Author Contributions
Conceptualization, G.W. and X.H.; data curation, G.W. and X.H.; writing—original draft preparation, G.W.; writing—review and editing, X.H., X.Y., J.W., H.L., R.C. and Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant no. U22A20564), the National Key Research Program of China (grant no. 2019YFC1510503), and the National Natural Science Foundation of China (grant no. 41971325).
Data Availability Statement
Thanks to National Cryosphere Desert Data Center (http://www.ncdc.ac.cn), accessed on 1 April 2022.
Acknowledgments
Thanks for the server resources provided by Google Earth Engine.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fontrodona-Bach, A.; Schaefli, B.; Woods, R.; Teuling, A.J.; Larsen, J.R. NH-SWE: Northern Hemisphere Snow Water Equivalent dataset based on in-situ snow depth time series. Earth Syst. Sci. Data Discuss. 2023, 1–33. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, R.; Long, Y.; Zhang, W. Spatial Trend and Impact of Snowmelt Rate in Spring across China’s Three Main Stable Snow Cover Regions over the Past 40 Years Based on Remote Sensing. Remote Sens. 2022, 14, 4176. [Google Scholar] [CrossRef]
- Choi, G.; Robinson, D.A.; Kang, S. Changing northern hemisphere snow seasons. J. Clim. 2010, 23, 5305–5310. [Google Scholar] [CrossRef]
- Zhu, L.; Ives, A.R.; Zhang, C.; Guo, Y.; Radeloff, V.C. Climate change causes functionally colder winters for snow cover-dependent organisms. Nat. Clim. Chang. 2019, 9, 886–893. [Google Scholar] [CrossRef]
- Martin, E.; Etchevers, P. Impact of climatic changes on snow cover and snow hydrology in the French Alps. In Global Change and Mountain Regions; Springer: Dordrecht, The Netherlands, 2005; pp. 235–242. [Google Scholar]
- Yang, Y.; Chen, R.; Liu, G.; Liu, Z.; Wang, X. Trends and variability in snowmelt in China under climate change. Hydrol. Earth Syst. Sci. 2022, 26, 305–329. [Google Scholar] [CrossRef]
- Wu, X.; Shen, Y.; Wang, N.; Pan, X.; Zhang, W.; He, J.; Wang, G. Coupling the WRF model with a temperature index model based on remote sensing for snowmelt simulations in a river basin in the Altay Mountains, northwest China. Hydrol. Process. 2016, 30, 3967–3977. [Google Scholar] [CrossRef]
- Chen, R.S.; Shen, Y.P.; Mao, W.F.; Zhang, S.Q.; Lv, H.s.; Liu, Y.Q.; Liu, Z.W.; Fang, S.F.; Zhang, W.; Chen, C.Y.; et al. Progress and Issues on Key Technologies in Forecasting of Snowmelt Flood Disaster in Arid Areas, Northwest China. Adv. Earth Sci. 2021, 36, 233–244. [Google Scholar]
- Shen, Y.P.; Su, H.C.; Wang, G.Y.; Mao, W.F.; Wang, S.D.; Han, P.; Wang, N.L.; Li, Z.Q. The Respomses of Glaciers and Snow Cover to Climate Change in Xinjiang (II): Hazards Effects. J. Glaciol. Geocryol. 2013, 35, 1355–1370. [Google Scholar]
- Chen, Y.; Li, Z.; Fan, Y.; Wang, H.; Fang, G. Progress and prospects of climate change impacts on hydrology in the arid region of northwest China. Environ. Res. Lett. 2015, 139, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Vafakhah, M.; Nouri, A.; Alavipanah, S.K. Snowmelt-runoff estimation using radiation SRM model in Taleghan watershed. Environ. Earth Sci. 2015, 73, 993–1003. [Google Scholar] [CrossRef]
- Fang, S.; Xu, L.; Pei, H.; Liu, Y.; Liu, Z.; Zhu, Y.; Yan, J.; Zhang, H. An integrated approach to snowmelt flood forecasting in water resource management. IEEE Trans. Ind. Inform. 2013, 10, 548–558. [Google Scholar] [CrossRef]
- Şengül, S.; İspirli, M.N. Predicting Snowmelt Runoff at the Source of the Mountainous Euphrates River Basin in Turkey for Water Supply and Flood Control Issues Using HEC-HMS Modeling. Water 2022, 14, 284. [Google Scholar] [CrossRef]
- Cirella, G.; Iyalomhe, F. Flooding Conceptual Review: Sustainability-Focalized Best Practices in Nigeria. Appl. Sci. 2018, 8, 1558. [Google Scholar] [CrossRef]
- Hagen, J.S.; Cutler, A.; Trambauer, P.; Weerts, A.; Suarez, P.; Solomatine, D. Development and evaluation of flood forecasting models for forecast-based financing using a novel model suitability matrix. Prog. Disaster Sci. 2020, 6, 100076. [Google Scholar] [CrossRef]
- Pham, B.T.; Luu, C.; Phong, T.V.; Nguyen, H.D.; Le, H.V.; Tran, T.Q.; Ta, H.T.; Prakash, I. Flood risk assessment using hybrid artificial intelligence models integrated with multi-criteria decision analysis in Quang Nam Province, Vietnam. J. Hydrol. 2021, 592, 125815. [Google Scholar] [CrossRef]
- Pomeroy, J.; Brown, T.; Fang, X.; Shook, K.; Pradhananga, D.; Armstrong, R.; Harder, P.; Marsh, C.; Costa, D.; Krogh, S. The Cold Regions Hydrological Modelling Platform for hydrological diagnosis and prediction based on process understanding. J. Hydrol. 2022, 615, 128711. [Google Scholar] [CrossRef]
- Shibuo, Y.; Ikoma, E.; Valeriano, O.S.; Wang, L.; Lawford, P.; Kitsuregawa, M.; Koike, T. Implementation of Real-Time Flood Prediction and its Application to Dam Operations by Data Integration Analysis System. J. Disaster Res. 2016, 11, 1052–1061. [Google Scholar] [CrossRef]
- Shortridge, J.E.; Guikema, S.D.; Zaitchik, B.F. Machine learning methods for empirical streamflow simulation: A comparison of model accuracy, interpretability, and uncertainty in seasonal watersheds. Hydrol. Earth Syst. Sci. 2016, 20, 2611–2628. [Google Scholar] [CrossRef]
- Thirel, G.; Andréassian, V.; Perrin, C. On the need to test hydrological models under changing conditions. Hydrol. Sci. J. 2015, 60, 1165–1173. [Google Scholar] [CrossRef]
- Fowler, K.J.A.; Peel, M.C.; Western, A.W.; Zhang, L.; Peterson, T.J. Simulating runoff under changing climatic conditions: Revisiting an apparent deficiency of conceptual rainfall-runoff models. Water Resour. Res. 2016, 52, 1820–1846. [Google Scholar] [CrossRef]
- Huntingford, C.; Jeffers, E.S.; Bonsall, M.B.; Christensen, H.M.; Lees, T.; Yang, H. Machine learning and artificial intelligence to aid climate change research and preparedness. Environ. Res. Lett. 2019, 14, 124007. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Wang, J.; Bao, W.; Gao, Q.; Si, W.; Sun, Y. Coupling the Xinanjiang model and wavelet-based random forests method for improved daily streamflow simulation. J. Hydroinform. 2021, 23, 589–604. [Google Scholar] [CrossRef]
- Behrouz, M.S.; Yazdi, M.N.; Sample, D.J. Using Random Forest, a machine learning approach to predict nitrogen, phosphorus, and sediment event mean concentrations in urban runoff. J. Environ. Manag. 2022, 317, 115412. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, C.; Wu, Q.; Jian, S.; Li, Z.; Chen, Y.; Zhang, G.; Zhang, Z.; Wang, S. Research on particle swarm optimization in LSTM neural networks for rainfall-runoff simulation. J. Hydrol. 2022, 608, 127553. [Google Scholar] [CrossRef]
- Rajurkar, M.; Kothyari, U.; Chaube, U. Modeling of the daily rainfall-runoff relationship with artificial neural network. J. Hydrol. 2004, 285, 96–113. [Google Scholar] [CrossRef]
- Sarchani, S.; Seiradakis, K.; Coulibaly, P.; Tsanis, I. Flood Inundation Mapping in an Ungauged Basin. Water 2020, 12, 1532. [Google Scholar] [CrossRef]
- Chen, T.X.; Lv, H.S.; Zhu, Y.H. Analysis of flood characteristics in Xiying River Basin based on GEV distribution. Arid. Zone Res. 2021, 38, 1563–1569. [Google Scholar] [CrossRef]
- Zhao, H.; Hao, X.; Wang, J.; Li, H.; Huang, G.; Shao, D.; Su, B.; Lei, H.; Hu, X. The Spatial–Spectral–Environmental Extraction Endmember Algorithm and Application in the MODIS Fractional Snow Cover Retrieval. Remote Sens. 2020, 12, 3693. [Google Scholar] [CrossRef]
- Criminisi, A.; Pérez, P.; Toyama, K. Region filling and object removal by exemplar-based image inpainting. IEEE Trans. Image Process. 2004, 13, 1200–1212. [Google Scholar] [CrossRef]
- Tuptewar, D.; Pinjarkar, A. Robust exemplar based image and video inpainting for object removal and region filling. In Proceedings of the 2017 International Conference on Intelligent Computing and Control (I2C2), Coimbatore, India, 23–24 June 2017; pp. 1–4. [Google Scholar]
- Chen, B.; Huang, B.; Chen, L.; Xu, B. Spatially and temporally weighted regression: A novel method to produce continuous cloud-free Landsat imagery. IEEE Trans. Geosci. 2016, 55, 27–37. [Google Scholar] [CrossRef]
- Jing, Y.; Shen, H.; Li, X.; Guan, X. A two-stage fusion framework to generate a spatio–temporally continuous MODIS NDSI product over the Tibetan Plateau. Remote Sens. 2019, 11, 2261. [Google Scholar] [CrossRef]
- Hu, X.J.; Hao, X.H.; Wang, J.; Dai, L.Y.; Zhao, H.Y.; Li, H.Y. Snow Depth Downscaling Algorithm based on the Fusion of AMSR2 and MODIS Data: A Case Study in Northern Xinjiang, China. Remote Sens. Technol. Appl. 2021, 36, 1236–1246. [Google Scholar]
- Hao, X.H.; Wang, J.; Chen, T.; Zhang, P.; Laing, J.; Li, H.Y.; Li, Z.; Bai, Y.J.; Bai, Y.F. The Spatial Distribution and Properties of Snow Cover in Binggou Watershed, Qilian Mountains: Measurement and Analysis. J. Glaciol. Geocryol. 2009, 31, 284–292. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Daliakopoulos, I.N.; Tsanis, I.K. Comparison of an artificial neural network and a conceptual rainfall–runoff model in the simulation of ephemeral streamflow. Hydrol. Sci. J. 2016, 61, 2763–2774. [Google Scholar] [CrossRef]
- Mas, J.F.; Flores, J.J. The application of artificial neural networks to the analysis of remotely sensed data. Int. J. Remote Sens. 2007, 29, 617–663. [Google Scholar] [CrossRef]
- Lippmann, R.P. An introduction to computing with neural nets. ACM SIGARCH Comput. Archit. News 1988, 16, 7–25. [Google Scholar] [CrossRef]
- Tetko, I.V.; Livingstone, D.J.; Luik, A.I. Neural network studies. 1. Comparison of overfitting and overtraining. J. Chem. Inf. 1995, 35, 826–833. [Google Scholar] [CrossRef]
- Nourani, V.; Komasi, M.; Mano, A. A multivariate ANN-wavelet approach for rainfall–runoff modeling. Water Resour. Manag. 2009, 23, 2877–2894. [Google Scholar] [CrossRef]
- Liu, M.C.; Li, L.P.; Shi, Z.C.; Qin, S.J. Distribution characteristics of runoff in Shiyang River basin and its responses to climate change—The case study of Xiying River. Agric. Res. Arid. Areas 2013, 31, 193–198. [Google Scholar]
- Jiang, Q.; Li, W.; Fan, Z.; He, X.; Sun, W.; Chen, S.; Wen, J.; Gao, J.; Wang, J. Evaluation of the ERA5 reanalysis precipitation dataset over Chinese Mainland. J. Hydrol. 2021, 595, 125660. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, F.Q. Daily Extreme Precipitation and Trend in China. Sci. Sin. (Terrae) 2017, 47, 1469–1482. [Google Scholar]
- Xu, J.; Chen, Y.; Bai, L.; Xu, Y. A hybrid model to simulate the annual runoff of the Kaidu River in northwest China. Hydrol. Earth Syst. Sci. 2016, 20, 1447–1457. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso: A retrospective. B-Stat. Methodol. 2011, 73, 273–282. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. In Proceedings of the 9th International Conference on Neural Information Processing Systems, Denver, CO, USA, 3–5 December 1996; Volume 9. [Google Scholar]
- Zhou, G.; Cui, M.; Wan, J.; Zhang, S.J.S. A Review on Snowmelt Models: Progress and Prospect. Sustainability 2021, 13, 11485. [Google Scholar] [CrossRef]
- Moradkhani, H.; Hsu, K.-l.; Gupta, H.V.; Sorooshian, S. Improved streamflow forecasting using self-organizing radial basis function artificial neural networks. J. Hydrol. 2004, 295, 246–262. [Google Scholar] [CrossRef]
- Nourani, V. An emotional ANN (EANN) approach to modeling rainfall-runoff process. J. Hydrol. 2017, 544, 267–277. [Google Scholar] [CrossRef]
- Khandelwal, A.; Xu, S.; Li, X.; Jia, X.; Stienbach, M.; Duffy, C.; Nieber, J.; Kumar, V. Physics guided machine learning methods for hydrology. arXiv 2020, arXiv:2012.02854. [Google Scholar]
- Okkan, U.; Ersoy, Z.B.; Kumanlioglu, A.A.; Fistikoglu, O. Embedding machine learning techniques into a conceptual model to improve monthly runoff simulation: A nested hybrid rainfall-runoff modeling. J. Hydrol. 2021, 598, 126433. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).