Abstract
Two significant uncertainties that are crucial for landslide susceptibility prediction modeling are attribute interval numbers (AIN) division of continuous landslide impact factors in frequency ratio analysis and various susceptibility prediction models. Five continuous landslide impact factor interval attribute classifications (4, 8, 12, 16, 20) and three data-driven models (deep belief networks (DBN), random forest (RF), and neural network (back propagation (BP)) were used for a total of fifteen different scenarios of landslide susceptibility prediction studies in order to investigate the effects of these two factors on modeling and perform a landslide susceptibility index uncertainty analysis (including precision evaluation and statistical law). The findings indicate that: (1) The results demonstrate that for the same model, as the interval attribute value rises from 4 to 8 and finally to 20, the forecast accuracy of landslide susceptibility initially increases gradually, then progressively grows until stable. (2) The DBN model, followed by the RF and BP models, provides the highest prediction accuracy for the same interval attribute value. (3) AIN = 20 and DBN models have the highest prediction accuracy under 15 combined conditions, while AIN = 4 and BP models have the lowest. The accuracy and efficiency of landslide susceptibility modeling are higher when the AIN = 8 and DBN models are combined. (4) The landslide susceptibility index uncertainty predicted by the deeper learning model and the bigger interval attribute value is comparatively low, which is more in line with the real landslide probability distribution features. The conditions that the environmental component attribute interval is divided into eight parts and DBN models are used allow for the efficient and accurate construction of the landslide susceptibility prediction model.
1. Introduction
For precisely anticipating the spatial distribution law of possible landslides or high landslide prone areas, which is beneficial to the development of landslide disaster prevention and management, reliable landslide susceptibility prediction modeling is of paramount importance [1,2,3]. Many geotechnical engineering uncertainties, such as load uncertainty, uncertainty in geotechnical parameters, and uncertainty in computational and analytical models, have an impact on landslide susceptibility and inevitably increase landslide risks [4,5]. Although the risk of landslides cannot be totally removed, engineering methods such as monitoring, early warning, strengthening, and treatment can be used to lower the risk to a level that is deemed acceptable by society, also known as the acceptable risk level [6,7,8]. The first stage in determining a landslide’s susceptibility is to determine its risk, and a precise susceptibility assessment forms the cornerstone of the risk assessment that follows [9,10,11]. Landslide susceptibility assessment is crucial, and it is one of the main areas of interest in landslide risk studies [12,13,14].
In order to correctly estimate landslide susceptibility, deterministic models and data-driven models are crucial [15,16]. The deterministic model has the drawback of it being difficult to gather geomechanical parameters, as well as some restrictions in the large-scale study region [17,18,19]. The following modeling steps are included in data-driven models, which are better suited for large-scale study areas: (1) nonlinear correlation analysis between environmental impact factors and the landslide catalog database; (2) determination of input and output variables; (3) determination of training and test sets; (4) selection of appropriate data-driven models; and (5) prediction result uncertainty analysis. The landslide susceptibility index and environmental parameters are linked in step (1), which also serves as the foundation for data-driven models. The right to evidence, information entropy, frequency ratio (FR), and other techniques are frequently used in step (1) [20,21,22,23]. The correlation characteristics between landslides and their environmental elements are quantitatively studied using FR factor [24], which has a simple FR factor structure and can effectively express the impact of environmental factors on the probability of landslides.
Studies already conducted have demonstrated that there are numerous uncertainties in the prediction of landslide susceptibility by data-driven models, including when using FR factors [25,26,27]: there is no universally accepted definition for the AIN of continuous environmental factors; and the majority of them are determined arbitrarily by researchers [28,29,30]. As a result of these subjectivities, data-driven models’ prediction susceptibility is more unclear because the FR values of continuous environmental components calculated under various AIN situations vary greatly [31,32,33]. The environmental factor division will be excessively coarse if the AIN value is too low, which will lower the model’s prediction accuracy. However, a high AIN number makes modeling more difficult to calculate and complex [34,35,36]. This research employs the AIN values of 4, 8, 12, 16, and 20 to calculate the FR value of environmental elements in order to investigate the modeling impact of data-driven models under various AIN situations. The findings of several models predicting landslide susceptibility are highly variable, making it challenging to ascertain which model has the best effect on the uncertainty problem of the data-driven model predicting landslide susceptibility in step (4) above [37]. Deep learning and shallow machine learning are now the two categories that the most often employed data-driven models fall under. Convolutional neural network models (CNNs), recurrent neural networks (RNNs), and deep belief networks are a few examples of deep learning models. The BP neural network, decision tree, and RF model [38,39,40,41,42] are examples of shallow machine learning models. In order to examine the impact of various data-driven models on the prediction of landslide susceptibility, the BP model and RF model of shallow machine learning are chosen, while the DBN model is chosen as the deep learning model. The estimation of the FR factor AIN value in step (1) and the comparative study of several data-driven models in step (4) are the two uncertainties that this research focuses on most. Taking Ruijin City, Jiangxi Province, as the research area, 5 AIN values and 3 data-driven models were determined to form 15 different combinations. The accuracy of the susceptibility prediction findings for each combination is then assessed, along with the importance of the susceptibility index and its distribution law.
The main achievements, including contributions to the field can be summarized as follows:
- (1)
- The FR value of the landslide interval, which can clearly depict the relative impact of each attribute interval of environmental factors on the occurrence of landslides, is calculated by conducting interval analysis of the 11 primary landslide impact factors in Ruijin City;
- (2)
- More sophisticated machine learning models can significantly increase the prediction accuracy of landslide susceptibility, as demonstrated by the use of various data-driven algorithms to simulate landslide susceptibility based on landslide locations;
- (3)
- The experimental findings from the real-world landslide dataset indicate that the modeling uncertainty will increase with the attribute division of various landslide impact factor intervals, whereas the accurate landslide impact factor interval can clearly better ensure the modeling accuracy and reliability.
The remainder of this essay is structured as follows: Predictive modeling techniques are briefly reviewed in Section 2. The study area is briefly summarized in Section 3. The proposed methodological theory and the specific implementation procedure are described in Section 4. In Section 5, a real-world case is used to demonstrate the usefulness of our methodology, and some of the outcomes are discussed below. In Section 6, we have a discussion of landslide sensitivity analysis. Finally, Section 7 draws conclusions.
2. Preliminaries
2.1. Research Ideas
- (1)
- The research area’s landslide catalog and associated environmental components were gathered (Figure 1). A FR analysis was then conducted using different AIN values for continuous environmental parameters (4, 8, 12, 16, 20);
 Figure 1. Modeling flow chart.
Figure 1. Modeling flow chart. - (2)
- The model training and test datasets are partitioned according to the most widely used 7:3 ratio, with the FR values of all the collected environmental parameters used as model input variables and the landslide catalog and randomly selected non-landslides used as output variables;
- (3)
- From the data-driven model, three models were chosen to forecast landslide susceptibility: DBN, RF, and BP;
- (4)
- In order to create 15 different situations, the FR values generated by 4 AIN were coupled with 3 different types of models. Susceptibility modeling was then completed;
- (5)
- The research area’s grid units’ landslide susceptibility indices were predicted and mapped using the established model;
- (6)
- Three perspectives were used to analyze the uncertainty of the prediction results: the receiver operation characteristic (ROC) curve accuracy evaluation, the susceptibility index difference, and its distribution law;
- (7)
- The value law of AIN in FR analysis was studied, and the effects of different kinds of data-driven models on predictability were examined.
2.2. Overview of Data-Driven Models
2.2.1. FR
The FR method [43,44,45,46] is based on the assumption that areas with similar geological conditions have similar probabilities of landslides. The FR value can quantitatively indicate the relative influence of each attribute interval of environmental factors on the occurrence of landslide, as shown in (1), where is the landslide area in the th attribute interval of an environmental factor, is the total area of landslides in the study area, and is the area of the th attribute interval of environmental factors. is the total area of the study area. greater than 1 indicates that the attribute interval of the environmental factor is conducive to the development of landslide, and the higher the value, the greater the contribution to the development of landslide. Conversely, less than 1 indicates that the environmental factor attribute interval is not conducive to landslide development, and the formula is as follows:
2.2.2. RF
The main idea behind random forest is that the results of multiple classifier combinations judgments are better than the judgment results of a single classifier [47,48,49]. Random forest is an ensemble learning method that combines bagging methods to generate multiple independent training sets and multiple classification and regression trees to make predictions [50]. The unsampled 1/3 of the data in each random sampling is called out of bag (OOB). This part of the data is used to estimate the internal error. The OOB error of each tree is obtained, and the OOB error of the random forest is obtained by averaging the OOB error of all trees.
The OOB error is an unbiased estimate, approximated by cross-validation, and the generalization error bounded by the random forest is [51]:
where is the generalization error of the random forest, is the average correlation between classification and regression trees, and is the average strength of the decision tree.
2.2.3. DBN
The study of artificial neural networks is where the idea of deep learning originated. To determine the distributed nature of data, it combines low-level elements to create a more abstract high-level representation (property class or attribute). An effective unsupervised learning algorithm is DBN. It has currently found widespread use in a variety of domains, including speech recognition and image categorization [52]. DBN (Figure 2) learns features from aspects that may be crucial to the incidence of landslides, which is a substantial advantage in creating landslide sensitivity zoning maps. Researchers often employ the 11 danger factors discussed in this study; however, it is challenging to understand and quantify these elements’ intricate linkages and intrinsic relationships. The original features of the elements are heavily relied upon in traditional network training techniques such as backpropagation BPNN and radial basis function (RBF), which are unable to disclose the combined impact of the components. DBN is thought to be a more effective solution in this situation. In light of this, this study tries to apply DBN to the Ruijin City landslide sensitivity zoning map.
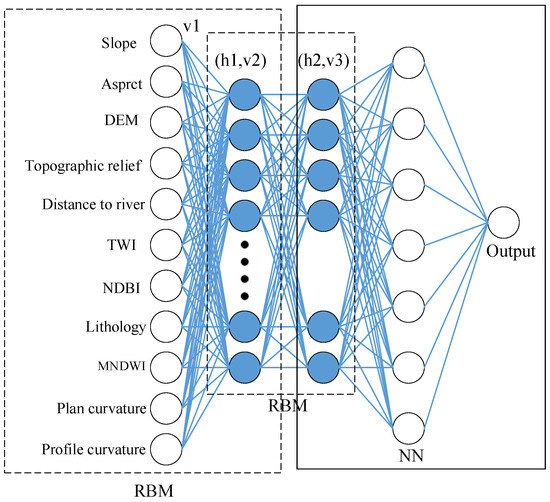
Figure 2.
DBN network.
2.2.4. BP
A multi-layer feedforward neural network based on error backpropagation learning is the BP neural network [53]. Currently, the three-layer BP neural network—which has just one intermediary layer—is the most frequently utilized for processing engineering problems. Its basic operating concept is as follows. The three layers in the BP model include input layer , hidden layer , and output layer , assuming that the expected output layer is , the th neuron in the hidden layer, and the th neuron in the output layer satisfies:
where and are weights and thresholds between input-hidden layers, respectively, and are the weights and thresholds between the implied-output layers, respectively, and and are activation functions. The main idea of the BP model is to formulate a suitable activation function to minimize the root mean square error (MSE) between the expected output layer and the actual output layer by adjusting the weights and thresholds [54].
The BP neural network model is built in this study to determine the landslide susceptibility index of all units in the study area. In this paper, the output value of the unit where the landslide occurs is assumed to be 1 and the output value of the non-landslide unit is 0.
2.3. Uncertainty Analysis Method
The impact of these two uncertainty aspects can be better mitigated by examining the manifestation and influence degree of various AIN values and data-driven models in susceptibility index prediction. Initially, utilizing AIN and data-driven models in combination, 15 working circumstances were subjected to landslide susceptibility prediction. The accuracy of the results was assessed using the area under the ROC curve. The Friedman two-factor rank ANOVA analysis test method was then used to assess the variations in the distribution of susceptibility indices under varied operating circumstances at the 0.05 significant level. Then, the mean and standard deviation are used to examine the numerical distribution features of the landslide susceptibility index as predicted by typical AIN and data-driven models. Eventually, through comparative analysis, the optimal AIN partitioning and data-driven model combination is discovered.
3. Application and Results
3.1. Geographical Environment Characteristics of Ruijin City
This article adds to and improves upon the issues already present in landslide susceptibility prediction models by concentrating primarily on the prevention and treatment of landslide disasters. The traditional evaluation approach completely takes into account the prediction modeling’s uncertainty issues, which are primarily separated into various attribute interval impact factors and various data-driven models. To completely validate the viability of the landslide susceptibility prediction modeling process, the inadequacies and deficiencies in the process are analyzed and appropriate improvement strategies are offered. Ruijin City, which is vulnerable to landslide disasters, is chosen as the research region for the aforementioned reasons.
With a total size of 2241.4 km2, Ruijin City is situated southeast of Ganzhou City in Jiangxi Province (see Figure 3). The area has a subtropical monsoon climate and receives 780 mm of precipitation annually. The lithology of the strata is mostly made up of metamorphic rock, carbonate rock, and clastic rock, with an elevation range of 139–1117 m. The northeastern, northwestern, and southwestern portions of the county border are mountainous, and the southeast is hilly with a river valley basin. Ruijin City has seen an increase in accumulation layer landslides due to the city’s complex natural environment, geological characteristics, seasonal heavy rainfall, and slope excavation. According to the Ruijin Land Bureau’s list of land disasters, 370 landslides—mostly small and medium-sized shallow landslides—had occurred in Ruijin City by the end of 2014. The average area of the landslide and its impact zone is approximately 13,000 m2, and the precise shape of the landslide boundary is a polygon surface. Quaternary silty clay and crushed stones make up the majority of the landslide body, and the slope body’s overall downward movement is the primary movement mechanism. The majority of these landslides occur near highways, in residential neighborhoods, or in ravine surroundings.
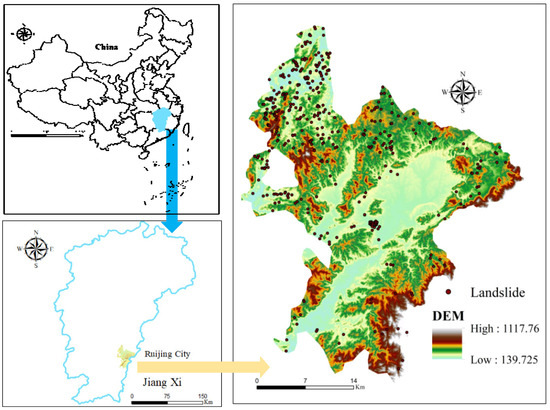
Figure 3.
Location of the study area and landslide inventory map.
3.2. Landslide Catalogue and Its Environmental Factors
A regional landslide disaster catalog database was built to examine the features of landslide disasters in the research area. It was based on the geological hazard survey data in Ruian City and integrated with remote sensing photos (Table 1). (1) The region’s 1:100,000 topographic maps are used to extract basic information such as elevation, slope, and aspect; (2) the region’s 1:100,000 geological map and 1:200,000 structural outline map are used to extract information such as structure, lithology, stratigraphic inclination, etc.; (3) the distribution map of geological hazard points in the entire region is combined with remote sensing image data obtained from satellites; (4) data from landslide field investigations and key detailed surveys are used to update each landslide’s specific information (occurrence date, scale, material composition, soft sandwich thickness, etc.); (5) data from the local disaster management department are used to forecast reservoir water levels and determine the local rainfall pattern over many years. Relevant studies demonstrate that the 25 m resolution raster cells are compliant with the national basic spatial database’s database construction standards, effectively expressing the spatial characteristics of landslide susceptibility without increasing the amount of model calculation required [55]. As a result, this article assesses landslide susceptibility using a DEM with a 25 m resolution. The size and type of the landslide are not taken into consideration in this article because the study’s main objective is to evaluate large-scale regional susceptibility. To map the actual distribution of landslides, we import the centroid coordinates of the landslide locations as points into the GIS environment (Figure 3). The landslide is primarily a small-to-medium-sized shallow landslide, with an average area of roughly 6000 m2, according to the landslide catalog. The movement mechanism is primarily the overall downward movement of the slope, and the nature of the accumulation layer is primarily Quaternary silty clay mixed with broken stone.

Table 1.
Data sources used in this study.
This paper identifies the landslide environmental factors using remote sensing images and GIS platforms based on the pertinent research literature on predicting landslide susceptibility in Jiangxi Province, the relationship between landslides and their environmental factors, and the difficulty of obtaining environmental factors. From the data source, 11 environmental characteristics were chosen in all: (1) topographic and geomorphological variables such as elevation, slope, aspect, section curvature, plane curvature, and terrain undulation; (2) stratigraphic lithology; (3) hydro environmental variables such as the topographic wetness index (TWI) and the modified normalized difference water index (MNDWI); and (4) land cover variables such as the normalized difference vegetation index (NDVI) and the normalized difference built-up index (NDBI).
3.3. Landslide Susceptibility Prediction Unit
The landslide susceptibility test is based on the prediction unit. In the smallest amount of data required for the prediction modeling process, each prediction cell represents landslide-related data, including numerous geographic details and other research area characteristics. Data can be gridded for comparison, quantitative evaluation of the prediction outcomes for each area, and fine management of the modeling scenario and prediction probability inside each cell thanks to the division of the cells [56]. In GIS, the common methods of dividing cells are raster cells, slope cells, geographical cells, and administrative units, among which raster cells and slope cells are the most common and widely used in landslide susceptibility prediction, field exploration, and research division [57]. The slope unit is a research unit which, while taking into consideration topographic parameters, water distribution, etc., divides the actual geomorphological condition of the mountain according to contours, valleys, and ridges. The benefit of the slope unit is that through data analysis, it is able to specifically observe how each component affects the slope. Its drawbacks include the fact that the division method is limited by the topographic and geomorphological conditions, that it is more difficult to divide in regions with complex topography and frequently requires two to three additional subdivisions of a slope unit, that it is too inefficient in practice and necessitates a lot of human and material resources for manual research, and that it is subjective and overly dependent on expert knowledge [58]. Raster cells are chosen as the primary study object in this paper after taking into account the study area’s general situation and the accuracy of the susceptibility prediction. Raster cells have the advantages of easy division, consistent shape, and high computing efficiency, even though they are unable to reflect the defined terrain of the studied area [59]. Additionally, the use of regular-shaped raster cells will differ from the actual situation of a landslide and geological environment; however, by choosing raster cells with greater accuracy, this error range can be minimized. For example, in this paper, 25 m resolution raster cells are used as input objects, which can meet the accuracy of the data and also ensure the effectiveness of conducting landslide susceptibility in a large area.
3.4. Environmental Factor Frequency Ratio Analysis
There are certain variations in the FR values estimated under various AIN settings for continuous environmental factors, which would cause a variety of uncertainties in the precision of susceptibility prediction and the distribution characteristics of susceptibility index. The AIN values are set to 4, 8, 12, 16, 20 in order to investigate this uncertainty law, and after that, the appropriate FR values for each environmental element are computed. Table 2 displays the FR outcomes for the topographic geomorphological components (Figure 4) under various AIN values. The hydrological environment’s impact on landslide formation [60] was characterized in this study using distance to river and MNDWI (Figure 4g,k), and Table 3 displays the FR values of the MNDWI factors. The results of the FR value calculations are provided in Table 4, and at the same time, NDBI and NDVI were chosen as land cover variables (Figure 4j,i), illustrating the influence of human activities and natural vegetation on landslide formation [61].

Table 2.
Frequency ratio of topographical factors.
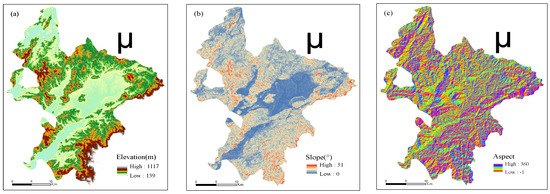
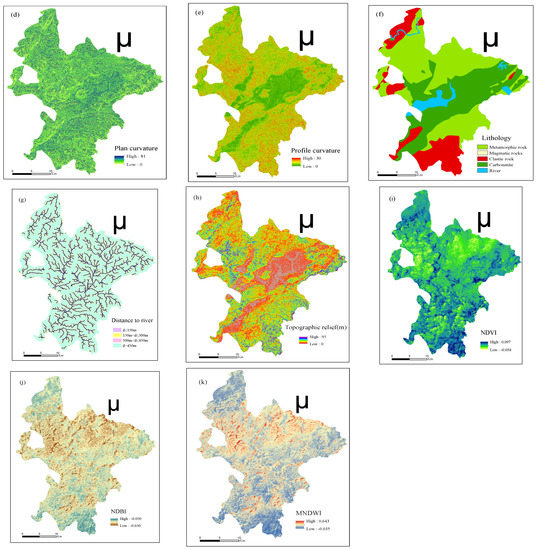
Figure 4.
The topographical factors, land cover, hydrology, and geological factors: (a) Elevation, (b) Slope, (c) Aspect, (d) Plan curvature, (e) Profile curvature, (f) Lithology, (g) Distance to river, (h) Topographic relief, (i) NDVI, (j) NDBI and (k)MDWI.

Table 3.
Frequency ratio of hydrologic factors.

Table 4.
FR of land cover and geological factors.
4. Landslide Susceptibility Prediction
4.1. Spatial Dataset Preparation
As input variables for the model, the FR values determined by 11 environmental factors under 5 AIN working conditions were reallocated to each environmental factor. At 25 m resolution, Ruijin City is divided into 8,633,837 rasters. The 370 landslides that have occurred are divided into 507,852 raster cells with 25m resolution (assigned 1), and the same number of non-landslide rasters as the landslide raster (assigned 0) are randomly selected as the model output variable [62]. In the landslide and non-landslide grids, the model training set and test set [63] are randomly divided by 7∶3. Finally, the trained model is updated with the FR value from the raster cells across the entire study region, and the landslide susceptibility index for each grid cell is determined.
4.2. Susceptibility Prediction under Different AIN and Data-Driven Model Working Conditions
4.2.1. DBN Model Predicts Landslide Susceptibility
The DBN network that makes up the landslide prediction model developed in this research is made up of two layers of RBM and one BP network; the model structure is depicted in Figure 2. The two RBMs are fully coupled, while the BP network has a one-way connection. The impact factor is input into the first layer of the RBM, which has 50 neurons. The second hidden layer, , is the input layer for the BP network, and it is through the BP network output layer that the outcome of the landslide prediction is determined. The network training process is as follows: the training sample composition impact factor matrix is input to the first layer of RBM display layer in accordance with the characteristics of RBM; the feature expression of the factor is obtained in the hidden layer ; and the hidden layer can be used again as the input of the first layer RBM to obtain , in accordance with the reconstruction error to describe the training effect of the first layer of RBM and after meeting the accuracy requirements; at this point, h1 is used as the display layer of the second layer of RBM as input, and the training of the second RBM is repeated until it meets the requirements; the training result of is then used as the input factor of the BP network, and after a hidden layer, the network weight is adjusted in accordance with the BP error backward propagation algorithm to obtain the landslide prediction value, which completes the training and prediction process of the entire DBN.
4.2.2. RF Models Forecast the Susceptibility to Landslides
For the RF model, R language is used to iteratively calculate different random forest out-of-bag errors, and the smaller the out-of-bag error, the higher the accuracy of the corresponding model prediction. After analysis, the optimal number of random features is 3, and the number of random forest decision trees is 500.
4.2.3. BP Model Predicts Landslide Susceptibility
A three-layer BP model was created using 3000 datapoints (containing 1500 landslide rasters and 1500 non-landslide rasters), of which 2400 samples were utilized for model training and the remaining 600 samples were used for model validation. The remaining model parameters are shown in Table 5 after normalizing the 11 kernel factor sets chosen by the rough set method. The training sample set is used as the input layer, and the output layer is the landslide state corresponding to each sample (where 1 denotes a landslide raster and 0 denotes a non-landslide raster).

Table 5.
Parameter settings in BP model.
The model has 15 hidden layer nodes, which is the best number when compared to 5, 10, 12, and 15. The Levenberg—Marquardt optimization algorithm was used for training, and it has been shown to have high generalization properties and to be capable of producing accurate prediction results [64].
4.3. Landslide Susceptibility Mapping
In this paper, the predicted landslide susceptibility indices under 15 different combinations of working conditions are first imported into ArcGIS 10.3 software, and then classified according to the distribution law of susceptibility index and the natural break point method: very high, high, medium, low, and very low prone zones. Among the 15 combined working conditions, the susceptibility prediction results under the AIN value of 8 and the combination of other models are shown in Figure 5. The prediction results of the AIN value of 4, 8, 12, 16, 20 and the combined working conditions of the DBN model are shown in Figure 6, while the prediction results of susceptibility under the remaining combined conditions are not shown. The majority of Ruijin City is located in the very low-landslide-prone zone, as shown in Figure 5; however, the proportion of high- and very high-prone areas in RF and DBN models is higher than that in low- and very low-prone areas. The results of the field survey are consistent with the weights determined by the RF and BP models, which demonstrate that slope and elevation are the two most significant environmental factors. The majority of the landslides are found in regions with medium slopes and elevations, such as mountainous hills.
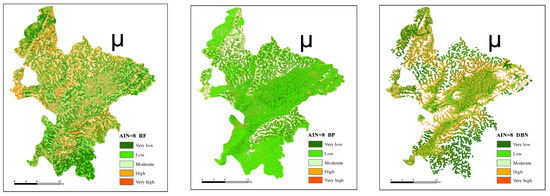
Figure 5.
Landslide susceptibility maps of AIN = 8, three different models.
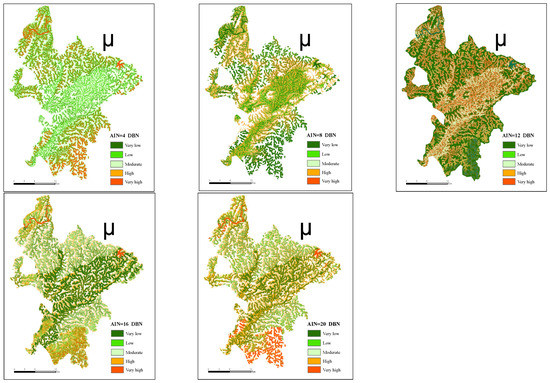
Figure 6.
Landslide susceptibility maps of different AINs and DBN models.
5. Uncertainty Analysis of Susceptibility Prediction
5.1. Evaluation of Proximate Prediction Accuracy
The ROC curve (Figure 7) and its AUC value (Table 6) were used to examine the prediction accuracy after calculating the landslide susceptibility index under 15 various working conditions, and a three-dimensional graph was utilized to visually depict the change law of the AUC value. The stronger the data-driven model’s prediction ability, the more clearly the ROC curve is convex to the upper left corner. The prediction performance is closer the closer the curves are, and the prediction performance is more different the more obvious the interval between the curves. In the same model and under different AIN working conditions, taking the DBN model as an example, it can be seen from Figure 7 and Table 6 that the accuracy of the DBN model is the highest when the AIN is 20 (AUC = 0.854), followed by the models when AIN is 16, 12, 8 and 4. It can be seen from the ROC curve (Figure 7) that the interval between the ROC curve when AIN is 4 and the curve when AIN is 8, 12, 16 or 20 is obvious, showing that the predictability prediction performance of vulnerability when AIN is 4 is poor. The ROC curve gradually convexes to the upper left corner but is very close when AIN rises from 8 to 20, showing that the DBN model’s prediction accuracy in these four scenarios gradually improves but remains consistent overall. The process of raising the AIN value from 4 to 8, 12, 16, and 20 demonstrates that AIN = 8 is the crucial value for correct susceptibility prediction, and that AIN = 8 has a significant impact on the DBN model’s prediction ability. The remaining four models displayed similarities to DBN in their regularities, showing that greater AIN values can provide more specific information about the impact of environmental factors on landslide development, which is helpful in enhancing susceptibility prediction accuracy. Additionally, Table 6 demonstrates how the AUC value of each model is arranged from the largest to the smallest DBN > RF > BP under the same AIN value and various data-driven model working conditions. As can be observed, the DBN model has the best prediction performance, followed by the RF and BP models, and the DBN model outperforms shallow machine learning, indicating that deep learning models are more accurate at making predictions than shallow machine learning models. Additionally, when the AIN is 4, the DBN model outperforms other models in terms of prediction accuracy when the AIN is 4. Additionally, Table 6 demonstrates how the AUC value of each model is arranged from the largest to the smallest DBN > RF > BP under the same AIN value and various data-driven model working conditions. As can be observed, the DBN model has the best prediction performance, followed by the RF and BP models, and the DBN model outperforms shallow machine learning, indicating that deep learning models are more accurate at making predictions than shallow machine learning models. Additionally, when the AIN is 4, the DBN model outperforms other models in terms of prediction. It demonstrates that the deep learning model can, to some extent, make up for the drawbacks of incomplete input variable information, and that the more sophisticated deep learning, the more advantageous it is for mapping landslide susceptibility.
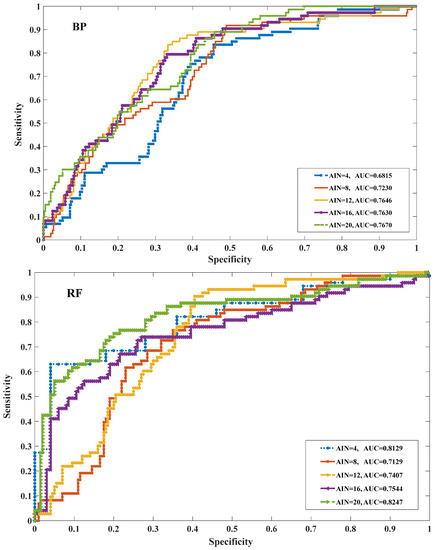
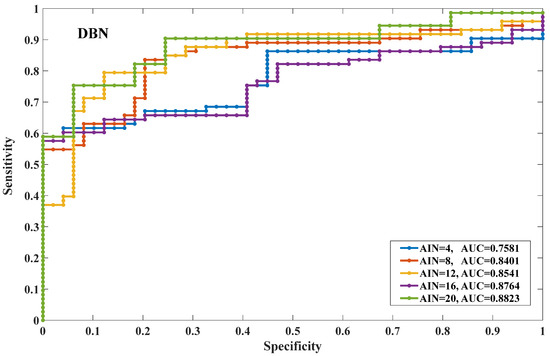
Figure 7.
ROC curves of each model and different AINs.

Table 6.
AUC values of different data-based models and different AIN values.
Finally, Table 6 and Figure 7 compare the change in the accuracy of easy prediction for various combinations of AIN values and data-driven model. The findings demonstrate that the AIN = 20 and DBN model’s combined operating conditions yield the maximum AUC accuracy for predicting landslide susceptibility. The accuracy of susceptibility prediction is lowest when using the AIN = 4 and BP models, and it gradually improves as the AIN value rises and data-driven models are upgraded from machine learning to deep learning.
5.2. Analysis of the Significance of Differences in Susceptibility Results
The significance of the difference in susceptibility index under the operating conditions of any two groups of various AIN and data-driven models was tested using the Friedman two-factor rank-by-rank ANOVA analysis method. The difference in susceptibility index between the two groups of working conditions is significant if the test result is smaller than 0.05. (Table 7). Using the DBN model in Table 7 as an illustration, the difference in susceptibility predicted by AIN = 4 and AIN = 12, 16, and 20 is less than 0.05, and the prediction accuracy of DBN is higher when AIN = 20. The difference in susceptibility between AIN = 4 and AIN = 20 is large, which also indirectly suggests that the effect of AIN = 4 is subpar. Additionally, the significance of the susceptibility index difference between AIN = 8, 12, 16, and 20 was greater than 0.05, showing that there was little variation between AIN 8 and 20. DBNs’ regular patterns are comparable to those of other models.

Table 7.
Friedman two⁃way ANOVA tests by rank for different AIN values and different models.
The significance of the DBN, BP, and RF models in predicting susceptibility in Table 6 is less than 0.05 when the AIN value is 8, demonstrating a significant difference between shallow machine learning models and deep learning models. The significance of the BP and RF models is greater than 0.05, which shows that there is little difference in the projected susceptibility index between the different shallow machine learning models. Additionally, Table 7 shows that the deep learning model’s prediction performance is superior to that of the shallow machine learning model. A similar rule is also displayed when AIN have different values.
5.3. Distribution of Susceptibility Index under Typical Working Conditions
In this study, the average level and dispersion of the landslide susceptibility index distribution are represented by the mean value and standard deviation, respectively.
5.3.1. AIN Is 8 and Susceptibility Index Features under Different Models
The distribution of prediction susceptibility index of different data-driven models can be explored using the example of AIN = 8. The five models’ susceptibility indicators were sorted according to mean size: Mean (DBN) > Mean (BP) > Mean (RF). Most of the susceptibility indices of the BP and RF models are concentrated near their mean values (medium susceptibility interval) and are distributed in a quasi-normal distribution among them, indicating that the probability of landslides predicted by the BP and RF models is typically high. When combined with their AUC accuracy values, it is clear that these two models are not very good at identifying landslides. Similar to other distribution laws, the DBN model’s susceptibility index distribution is concentrated in the very low and low susceptibility intervals and gradually diminishes in the remaining susceptibility intervals. As a result of the research area’s low percentage of known landslide areas, the landslide susceptibility index is focused in the low and very low categories, which is more in line with the study area’s real landslide development conditions. Additionally, the dispersion degree of the three models is ranked as Standard (RF) > Standard (BP) > Standard (DBN), indicating that the RF, BP, and DBN models can accurately reflect the differences in susceptibility indices between different raster cells and can reflect as many known landslide catalogs as possible with fewer high susceptibility indices. This indirectly suggests that deep learning models can predict landslide susceptibility more effectively.
5.3.2. Distribution Characteristics of Susceptibility Index of DBN Model and AIN Working Conditions
Taking the DBN model as an example, the mean size ranking of the susceptibility index under different AIN values is: Mean (4) > Mean (8) > Mean (12) > Mean (16) > Mean (20). The standard deviation size rankings are: Standard (20) > Standard (16) > Standard (12) > Standard (8) > Standard (4). From the above comparison, it can be seen that the mean value of the susceptibility index with an AIN value of 4 is the largest and shows a normal distribution, and the minimum standard deviation value indicates that the susceptibility index is mostly concentrated around the mean. With the gradual increase of AIN value, its mean gradually decreases, and the standard deviation value gradually increases. It can be seen that when the AIN value gradually increases, the landslide susceptibility index gradually approaches the distribution law of medium, low, and very low susceptibility intervals, and the distribution law of the susceptibility index is more scientific and reasonable. Combined with the prediction accuracy of susceptibility, DBN predicts more landslides with fewer high- and extremely high-prone areas in the process of increasing AIN value, which has higher prediction performance. However, acquiring accurate landslide environmental variables is a requirement for carrying out landslide susceptibility prep work, merging landslide susceptibility prediction results and susceptibility index comprehensive analysis, and is a prerequisite for valid susceptibility results.
6. Discussion
The variable values of the original environment components fluctuate within a specific range to replicate the errors of the data itself by dividing different attribute intervals of the original environment and various data-driven models. The outcomes of the modeling of landslide susceptibility under various data-driven models are then compared to examine any potential uncertainties in the forecast process. According to the results of the uncertainty analysis in the preceding subsection, it is evident that the original data based on the DBN, BP, and RF models can yield reasonably accurate and reasonable susceptibility prediction results. This finding further suggests that the uncertainty of landslide susceptibility indices predicted by larger interval attribute values and deep learning models is relatively low. The accuracy of the acquired data is verified using a variety of uncertainty analysis techniques in this paper, which also demonstrates the research findings by suggesting sensitivity analysis, relative importance analysis of environmental factors, and the interpretability of machine learning. Finally, by interpreting DBN, it is further explained that changes in frequency ratio values can indicate the likelihood of landslides.
Although acquiring extremely accurate environmental parameters for landslides is a difficult undertaking, doing so can significantly increase forecast accuracy and reduce uncertainty in landslide susceptibility predictions. These characteristics are now primarily derived through field research and picture interpretation from remote sensing. The following factors are crucial to the quality of landslide environmental factors: (1) the accuracy of basic topographic maps and remote sensing images; (2) the complexity of topography and geological and tectonic conditions in the study area; (3) the method of remote sensing image interpretation, the professional quality of interpreters, and the depth of research. In general, the compatibility of the base picture chosen, the technique used to interpret the remote sensing images, and the practitioner’s expertise with the specific geographic conditions all have a major role in the quality of environmental aspects. The study also has a flaw in that there are still not enough simulations, which means that chance and randomness still exist. Hence, the reliability of the work can be effectively improved by increasing the number of simulations. Moreover, the actual landslides may be located in a different place from where they were mapped in the research area by tens or even hundreds of meters. This could result in changes in the geographic circumstances of the landslides. In addition, this study’s selection of non-landslides has a fault. Although the conventional method of choosing non-landslides is to randomly choose them from the study area, this will result in randomly chosen non-landslides being areas where landslides have already occurred or where there may be potential landslide hazard. These errors will make it more difficult to predict whether an area will be susceptible to landslides.
In conclusion, the errors of landslide samples and associated environmental factors need to be properly evaluated before performing landslide susceptibility prediction modeling in order to determine whether their data errors are within a reasonable interval and can be used for subsequent research work, and how to reduce these errors should be the focus of landslide research.
7. Conclusions
- (1)
- When the frequency ratio analysis of the continuous environmental factor for landslides was conducted, the set AIN value increased from 4 to 8, and the accuracy of the susceptibility prediction increased quickly; when the AIN value increases from 8 to 20, the growth rate of susceptibility prediction accuracy slows down until it stabilizes. An important threshold for accurate prediction is an AIN value of 8, which can be used to avoid overly complex frequency ratio calculations.
- (2)
- The DBN model, followed by the RF and BP models, has the highest accuracy in predicting landslide susceptibility under all AIN working conditions, demonstrating that deep learning models can significantly increase the susceptibility prediction accuracy, and that the depth model typically outperforms shallow machine learning models in this regard.
- (3)
- When AIN value and data-driven models are combined, an AIN value of 20 and the DBN model have the highest prediction accuracy of landslide susceptibility, an AIN value of 4 and the BP model have the lowest accuracy, and an AIN value of 8 and the DBN model have the highest efficiency of landslide susceptibility prediction modeling.
- (4)
- This research also examines the uncertainty of vulnerability prediction modeling from the perspectives of the distinction significance of the landslide susceptibility index predicted by various working conditions and the distribution law of the susceptibility index, in addition to the AUC accuracy evaluation. The findings demonstrate that the projected landslide susceptibility index has reduced uncertainty and is more in accordance with the actual landslide probability distribution characteristics with larger AIN values and more sophisticated deep learning models such as DBN.
Author Contributions
Y.X. (Yin Xing): Writing—original draft, Funding acquisition. S.H.: Supervision. Y.C.: Software, Investigation, Writing—review and editing. W.X.: Methodology, Supervision. P.W.: Project administration, Investigation, Data curation. Y.X. (Yunfei Xiang): Software, Validation, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Postgraduate Research and Practice Innovation Program of Jiangsu Province (KYCX20_0484) and the Fundamental Research Funds for the Central Universi-ties (B200203105).
Data Availability Statement
Not applicable.
Acknowledgments
We would highly thank the Department of Surveying and Mapping of Jiangxi Province for providing relevant data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, F.; Zhang, J.; Zhou, C.; Wang, Y.; Huang, J.; Zhu, L. A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 2020, 17, 217–229. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.; Han, Z.; Pham, B.T. Improved landslide assessment using support vector machine with bagging, boosting, and stacking ensemble machine learning framework in a mountainous watershed, Japan. Landslides 2020, 17, 641–658. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Jiang, S.H.; Zhou, C.; Huang, J.; Guo, Z. Landslide susceptibility prediction based on a semi-supervised multiple-layer perceptron model. Landslides 2020, 17, 2919–2930. [Google Scholar] [CrossRef]
- Khalaj, S.; BahooToroody, F.; Abaei, M.M.; BahooToroody, A.; De Carlo, F.; Abbassi, R. A methodology for uncertainty analysis of landslides triggered by an earthquake. Comput. Geotech. 2020, 117, 103262. [Google Scholar] [CrossRef]
- Ji, J.; Cui, H.; Zhang, T.; Song, J.; Gao, Y. A GIS-based tool for probabilistic physical modelling and prediction of landslides: GIS-FORM landslide susceptibility analysis in seismic areas. Landslides 2022, 19, 2213–2231. [Google Scholar] [CrossRef]
- Skrzypczak, I.; Kokoszka, W.; Zientek, D.; Tang, Y.; Kogut, J. Landslide hazard assessment map as an element supporting spatial planning: The flysch Carpathians region study. Remote Sens. 2021, 13, 317. [Google Scholar] [CrossRef]
- Shahri, A.A.; Spross, J.; Johansson, F.; Larsson, S. Landslide susceptibility hazard map in southwest Sweden using artificial neural network. Catena 2019, 183, 104225. [Google Scholar] [CrossRef]
- Saleem, N.; Huq, M.E.; Twumasi, N.Y.D.; Javed, A.; Sajjad, A. Parameters derived from and/or used with digital elevation models (DEMs) for landslide susceptibility mapping and landslide risk assessment: A review. ISPRS Int. J. Geo-Inf. 2019, 8, 545. [Google Scholar] [CrossRef]
- Myronidis, D.; Papageorgiou, C.; Theophanous, S. Landslide susceptibility mapping based on landslide history and analytic hierarchy process (AHP). Nat. Hazard. 2016, 81, 245–263. [Google Scholar] [CrossRef]
- Rahmati, O.; Kornejady, A.; Samadi, M.; Deo, R.C.; Conoscenti, C.; Lombardo, L.; Dayal, K.; Mehrjardi, R.T.; Bui, D.T. PMT: New analytical framework for automated evaluation of geo-environmental modelling approaches. Sci. Total Environ. 2019, 664, 296–311. [Google Scholar] [CrossRef]
- Alqadhi, S.; Mallick, J.; Talukdar, S.; Bindajam, A.A.; Van Hong, N.; Saha, T.K. Selecting optimal conditioning parameters for landslide susceptibility: An experimental research on Aqabat Al-Sulbat, Saudi Arabia. Environ. Sci. Pollut. Res. 2022, 29, 3743–3762. [Google Scholar] [CrossRef] [PubMed]
- Kornejady, A.; Ownegh, M.; Bahremand, A. Landslide susceptibility assessment using maximum entropy model with two different data sampling methods. Catena 2017, 152, 144–162. [Google Scholar] [CrossRef]
- Chowdhuri, I.; Pal, S.C.; Chakrabortty, R.; Malik, S.; Das, B.; Roy, P. Torrential rainfall-induced landslide susceptibility assessment using machine learning and statistical methods of eastern Himalaya. Nat. Hazard. 2021, 107, 697–722. [Google Scholar] [CrossRef]
- Dai, X.; Zhu, Y.; Sun, K.; Zou, Q.; Zhao, S.; Li, W.; Hu, L.; Wang, S. Examining the Spatially Varying Relationships between Landslide Susceptibility and Conditioning Factors Using a Geographical Random Forest Approach: A Case Study in Liangshan, China. Remote Sens. 2023, 15, 1513. [Google Scholar] [CrossRef]
- Xing, Y.; Yue, J.; Chen, C.; Cai, D.; Hu, J.; Xiang, Y. Prediction interval estimation of landslide displacement using adaptive chicken swarm optimization-tuned support vector machines. Appl. Intell. 2021, 51, 8466–8483. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Guo, J.; Jiang, S.H.; Li, S.; Guo, Z. Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. Catena 2020, 191, 104580. [Google Scholar] [CrossRef]
- Xing, Y.; Yue, J.; Chen, C.; Qin, Y.; Hu, J. A hybrid prediction model of landslide displacement with risk-averse adaptation. Comput. Geosci. 2020, 141, 104527. [Google Scholar] [CrossRef]
- Huang, F.; Chen, J.; Liu, W.; Huang, J.; Hong, H.; Chen, W. Regional rainfall-induced landslide hazard warning based on landslide susceptibility mapping and a critical rainfall threshold. Geomorphology 2022, 408, 108236. [Google Scholar] [CrossRef]
- Ada, M.; San, B.T. Comparison of machine-learning techniques for landslide susceptibility mapping using two-level random sampling (2LRS) in Alakir catchment area, Antalya, Turkey. Nat. Hazards 2018, 90, 237–263. [Google Scholar] [CrossRef]
- Jiang, S.H.; Huang, J.; Huang, F.; Yang, J.; Yao, C.; Zhou, C.B. Modelling of spatial variability of soil undrained shear strength by conditional random fields for slope reliability analysis. Appl. Math. Modell. 2018, 63, 374–389. [Google Scholar] [CrossRef]
- Chang, Z.; Catani, F.; Huang, F.; Yang, J.; Yao, C.; Zhou, C.B. Landslide susceptibility prediction using slope unit-based machine learning models considering the heterogeneity of conditioning factors. J. Rock Mech. Geotech. Eng. 2022, in press. [Google Scholar] [CrossRef]
- Xing, Y.; Yue, J.; Guo, Z.; Chen, Y.; Hu, J.; Travé, A. Large-scale landslide susceptibility mapping using an integrated machine learning model: A case study in the Lvliang mountains of China. Front. Earth Sci. 2021, 9, 622. [Google Scholar] [CrossRef]
- Xing, Y.; Yue, J.; Chen, C. Interval estimation of landslide displacement prediction based on time series decomposition and long short-term memory network. IEEE Access. 2019, 8, 3187–3196. [Google Scholar] [CrossRef]
- Chen, X.; Chen, W. GIS-based landslide susceptibility assessment using optimized hybrid machine learning methods. Catena 2021, 196, 104833. [Google Scholar] [CrossRef]
- Zhu, A.X.; Miao, Y.; Liu, J.; Bai, S.; Zeng, C.; Ma, T.; Hong, H. A similarity-based approach to sampling absence data for landslide susceptibility mapping using data-driven methods. Catena 2019, 183, 104188. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Xu, Y.; Zhu, Z.; Chen, C.W.; Sahana, M.; Khosravi, K.; Yang, Y.; Pham, B.T. Torrential rainfall-triggered shallow landslide characteristics and susceptibility assessment using ensemble data-driven models in the Dongjiang Reservoir Watershed, China. Nat. Hazard. 2019, 97, 579–609. [Google Scholar] [CrossRef]
- Lin, Q.; Lima, P.; Steger, S.; Glade, T.; Jiang, T.; Zhang, J.; Liu, T.; Wang, Y. National-scale data-driven rainfall induced landslide susceptibility mapping for China by accounting for incomplete landslide data. Geosci. Front. 2021, 12, 101248. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Zhu, A.X. Modeling landslide susceptibility using LogitBoost alternating decision trees and forest by penalizing attributes with the bagging ensemble. Sci. Total Environ. 2020, 718, 137231. [Google Scholar] [CrossRef]
- Tehrani, F.S.; Calvello, M.; Liu, Z.; Zhang, L.; Lacasse, S. Machine learning and landslide studies: Recent advances and applications. Nat. Hazard. 2022, 114, 1197–1245. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Panahi, M.; Kornejady, A.; Wang, J.; Xie, X.; Cao, S. Spatial prediction of landslide susceptibility using an adaptive neuro-fuzzy inference system combined with frequency ratio, generalized additive model, and support vector machine techniques. Geomorphology 2017, 297, 69–85. [Google Scholar] [CrossRef]
- Wankhade, M.; Rao, A.C.S.; Kulkarni, C. A survey on sentiment analysis methods, applications, and challenges. Artif. Intell. Rev. 2022, 55, 5731–5780. [Google Scholar]
- Mrówczyńska, M.; Skiba, M.; Leśniak, A.; Bazan-Krzywoszańska, A.; Janowiec, F.; Sztubecka, M.; Grech, R.; Kazak, J.K. A new fuzzy model of multi-criteria decision support based on Bayesian networks for the urban areas’ decarbonization planning. Energy Convers. Manag. 2022, 268, 116035. [Google Scholar] [CrossRef]
- Aidinidou, M.T.; Kaparis, K.; Georgiou, A.C. Analysis, prioritization and strategic planning of flood mitigation projects based on sustainability dimensions and a spatial/value AHP-GIS system. Expert Syst. Appl. 2023, 211, 118566. [Google Scholar] [CrossRef]
- El-Haddad, B.A.; Youssef, A.M.; Pourghasemi, H.R.; Pradhan, B.; El-Shater, A.H.; El-Khashab, M.H. Flood susceptibility prediction using four machine learning techniques and comparison of their performance at Wadi Qena Basin, Egypt. Nat. Hazard. 2021, 105, 83–114. [Google Scholar] [CrossRef]
- Kmoch, A.; Kanal, A.; Astover, A.; Kull, A.; Virro, H.; Helm, A.; Pärtel, M.; Ostonen, L.; Uuemaa, E. EstSoil-EH: A high-resolution eco-hydrological modelling parameters dataset for Estonia. Earth Syst. Sci. Data 2021, 13, 83–97. [Google Scholar] [CrossRef]
- Tahan, M.; Tsoutsanis, E.; Muhammad, M.; Karim, Z.A.A. Performance-based health monitoring, diagnostics and prognostics for condition-based maintenance of gas turbines: A review. Appl. Energy 2017, 198, 122–144. [Google Scholar] [CrossRef]
- Huang, F.; Yan, J.; Fan, X.; Yao, C.; Huang, J.; Chen, W.; Hong, H. Uncertainty pattern in landslide susceptibility prediction modelling: Effects of different landslide boundaries and spatial shape expressions. Geosci. Front. 2022, 13, 101317. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Parbha, P. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Xia, M.; Zheng, X.; Imran, M.; Shoaib, M. Data-driven prognosis method using hybrid deep recurrent neural network. Appl. Soft Comput. 2020, 93, 106351. [Google Scholar] [CrossRef]
- Rajabi, A.M.; Khodaparast, M.; Mohammadi, M. Earthquake-induced landslide prediction using back-propagation type artificial neural network: Case study in northern Iran. Nat. Hazard. 2022, 110, 679–694. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, H.; Park, H.J.; Heo, J.H. Temporal prediction modeling for rainfall-induced shallow landslide hazards using extreme value distribution. Landslides 2021, 18, 321–338. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, Y.; Huang, F.; Fan, X.; Huang, J. Landslide susceptibility zonation method based on C5. 0 decision tree and K-means cluster algorithms to improve the efficiency of risk management. Geosci. Front. 2021, 12, 101249. [Google Scholar] [CrossRef]
- Samia, J.; Temme, A.; Bregt, A.; Wallinga, J.; Guzzetti, F.; Ardizzone, F.; Rossi, M. Do landslides follow landslides? Insights in path dependency from a multi-temporal landslide inventory. Landslides 2017, 14, 547–558. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Lee, C.W. Assessment of landslide susceptibility using statistical-and artificial intelligence-based FR—RF integrated model and multiresolution DEMs. Remote Sens. 2019, 11, 999. [Google Scholar] [CrossRef]
- Hu, X.; Wu, S.; Zhang, G.; Zheng, W.; Liu, C.; He, C.; Liu, Z.; Guo, X.; Zhang, H. Landslide displacement prediction using kinematics-based random forests method: A case study in Jinping Reservoir Area, China. Eng. Geol. 2021, 283, 105975. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Z.Y.; Xu, C. Slope unit-based landslide susceptibility mapping using certainty factor, support vector machine, random forest, CF-SVM and CF-RF models. Front. Earth Sci. 2021, 9, 589630. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Niu, R.; Peng, L. Landslide susceptibility prediction based on positive unlabeled learning coupled with adaptive sampling. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11581–11592. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? Catena 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Li, H.; Xu, Q.; He, Y.; Fan, X.; Li, S. Modeling and predicting reservoir landslide displacement with deep belief network and EWMA control charts: A case study in Three Gorges Reservoir. Landslides 2020, 17, 693–707. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, L.; Gui, L.; Du, J.; Yin, K.; Do, H.M. Landslide displacement prediction based on variational mode decomposition and WA-GWO-BP model. Landslides 2020, 17, 567–583. [Google Scholar] [CrossRef]
- Xu, S.; Niu, R. Displacement prediction of Baijiabao landslide based on empirical mode decomposition and long short-term memory neural network in Three Gorges area, China. Comput. Geosci. 2018, 111, 87–96. [Google Scholar] [CrossRef]
- Medina, V.; Hürlimann, M.; Guo, Z.; Lloret, A.; Vaunat, J. Fast physically-based model for rainfall-induced landslide susceptibility assessment at regional scale. Catena 2021, 201, 105213. [Google Scholar] [CrossRef]
- Van Dao, D.; Jaafari, A.; Bayat, M.; Mafi-Gholami, D.; Qi, C.; Moayedi, H.; Van Phong, T.; Ly, H.B.; Le, T.T.; Trong Trinh, P. A spatially explicit deep learning neural network model for the prediction of landslide susceptibility. Catena 2020, 188, 104451. [Google Scholar]
- Chang, Z.; Du, Z.; Zhang, F.; Huang, F.; Chen, J.; Li, W.; Guo, Z. Landslide susceptibility prediction based on remote sensing images and GIS: Comparisons of supervised and unsupervised machine learning models. Remote Sens. 2020, 12, 502. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, W. Optimization of computational intelligence models for landslide susceptibility evaluation. Remote Sens. 2020, 12, 2180. [Google Scholar] [CrossRef]
- Conoscenti, C.; Ciaccio, M.; Caraballo-Arias, N.A.; Gómez-Gutiérrez, Á.; Rotigliano, E.; Agnesi, V. Assessment of susceptibility to earth-flow landslide using logistic regression and multivariate adaptive regression splines: A case of the Belice River basin (western Sicily, Italy). Geomorphology 2015, 242, 49–64. [Google Scholar] [CrossRef]
- Zou, Q.; Jiang, H.; Cui, P.; Zhou, B.; Jiang, Y.; Qin, M.; Liu, Y.; Li, C. A new approach to assess landslide susceptibility based on slope failure mechanisms. Catena 2021, 204, 105388. [Google Scholar] [CrossRef]
- Geertsema, M.; Highland, L.; Vaugeouis, L. Environmental impact of landslides. In Landslides—Disaster Risk Reduction; Springer: Cham, Switzerland, 2009; pp. 589–607. [Google Scholar]
- Lucchese, L.V.; de Oliveira, G.G.; Pedrollo, O.C. Mamdani fuzzy inference systems and artificial neural networks for landslide susceptibility mapping. Nat. Hazard. 2021, 106, 2381–2405. [Google Scholar] [CrossRef]
- Lima, P.; Steger, S.; Glade, T. Counteracting flawed landslide data in statistically based landslide susceptibility modelling for very large areas: A national-scale assessment for Austria. Landslides 2021, 18, 3531–3546. [Google Scholar] [CrossRef]
- Ly, H.B.; Nguyen, M.H.; Pham, B.T. Metaheuristic optimization of Levenberg—Marquardt-based artificial neural network using particle swarm optimization for prediction of foamed concrete compressive strength. Neural Comput. Appl. 2021, 33, 17331–17351. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).