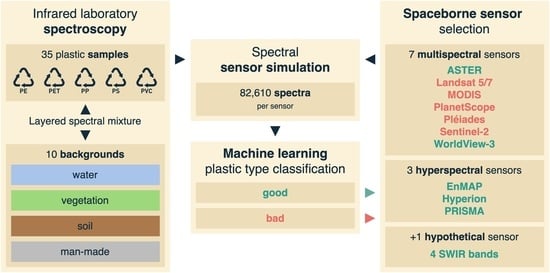
Potential of Optical Spaceborne Sensors for the Differentiation of Plastics in the Environment
Abstract
1. Introduction
2. Data and Methods
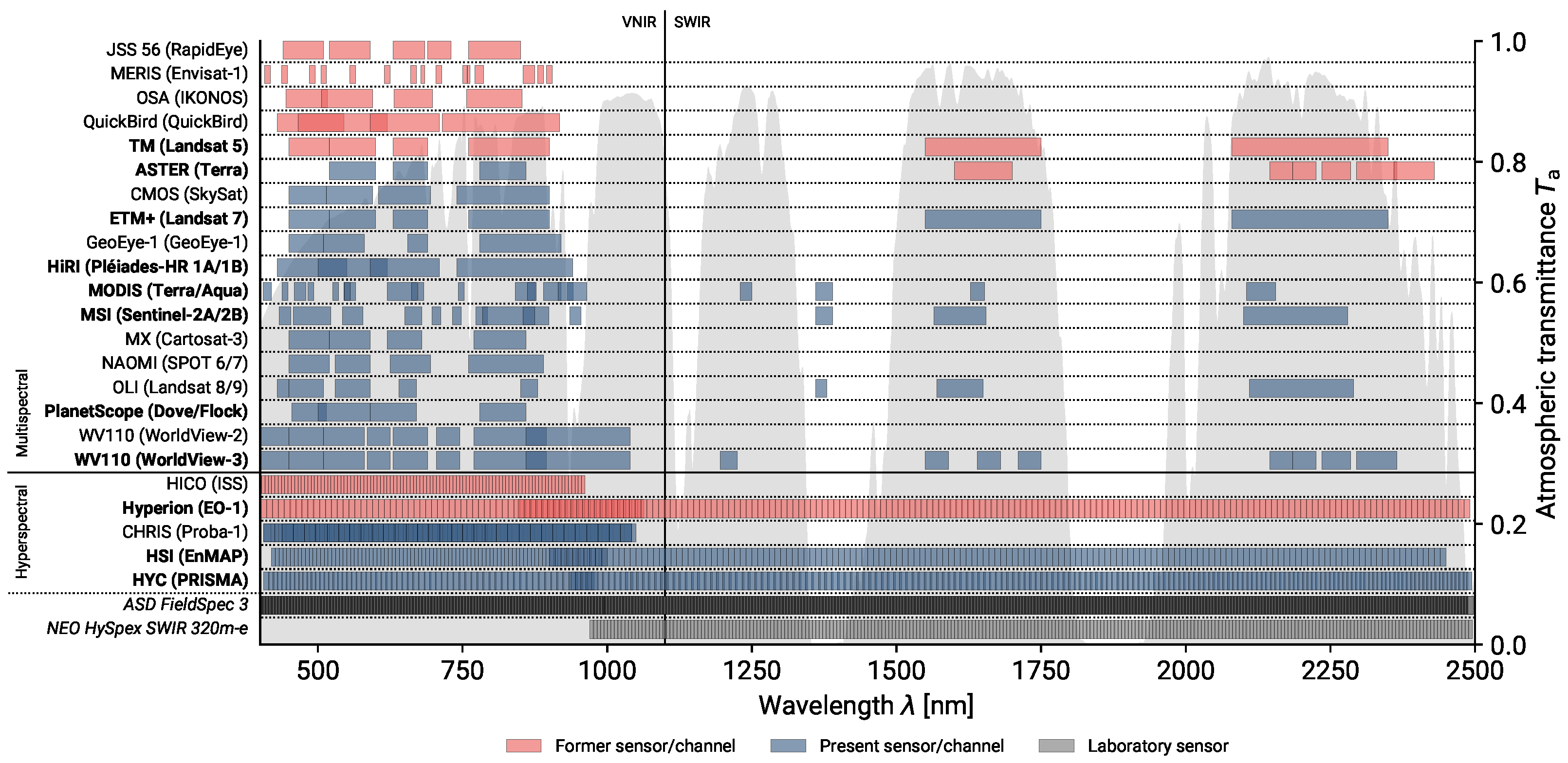
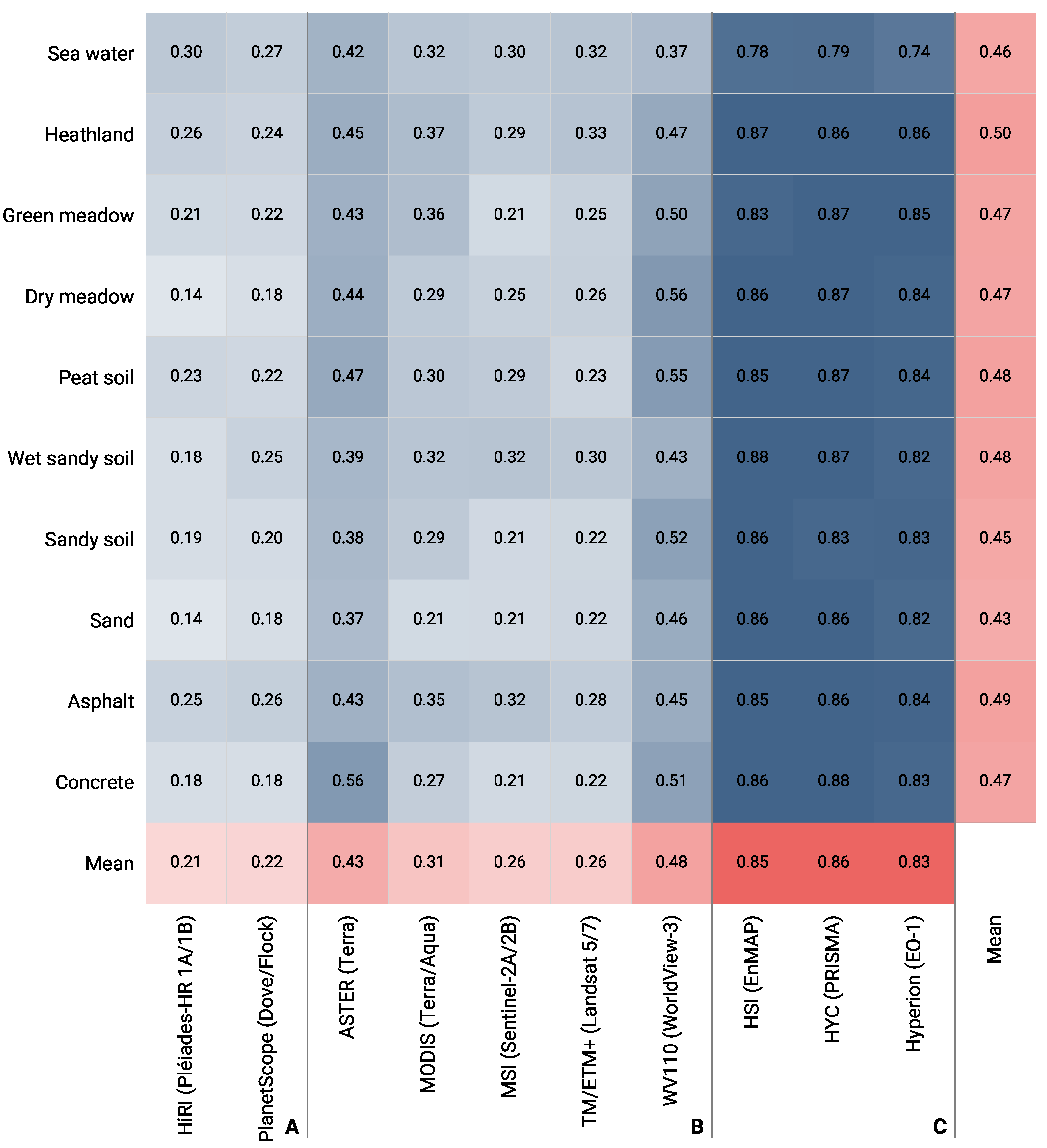
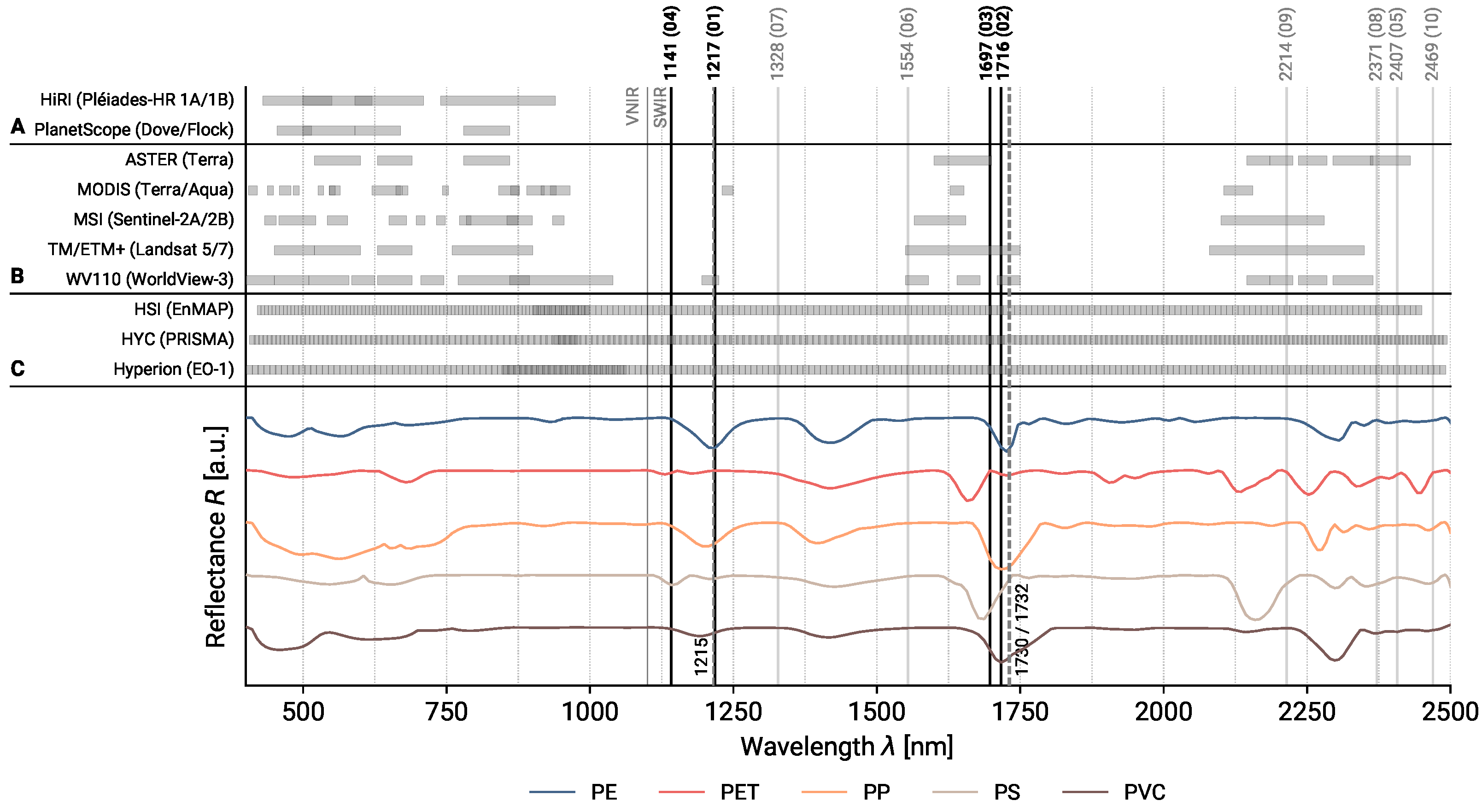
2.1. Spaceborne Sensor Selection
2.2. Spectral Database
2.2.1. Plastic Samples
2.2.2. ASD Data Collection
2.2.3. HySpex Data Collection and Processing
2.3. Spectral Database Processing
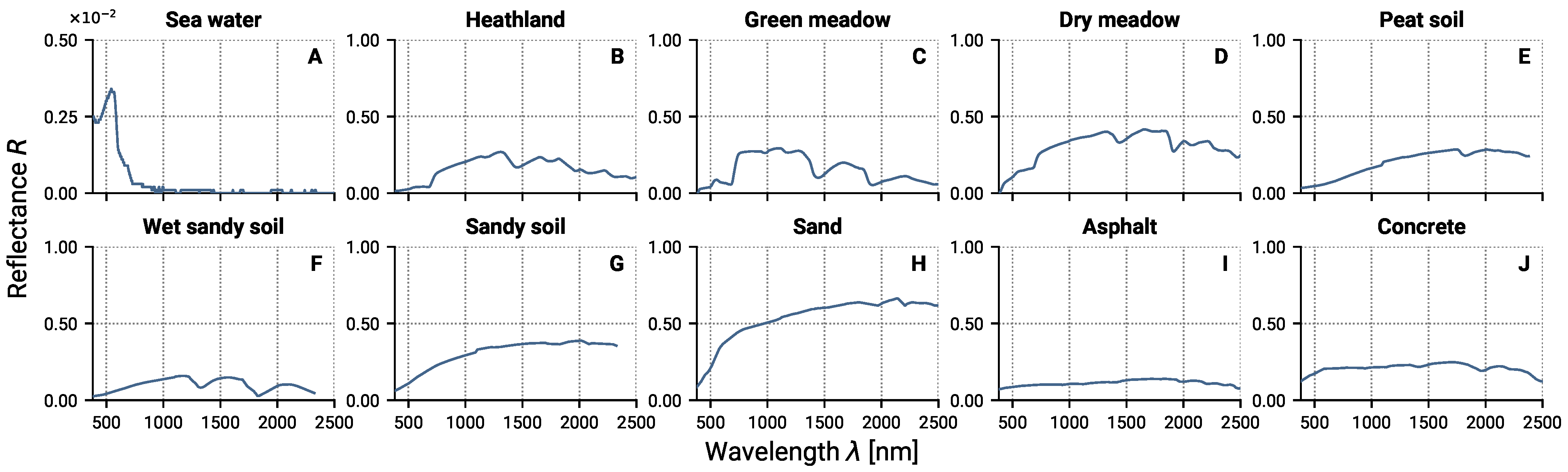
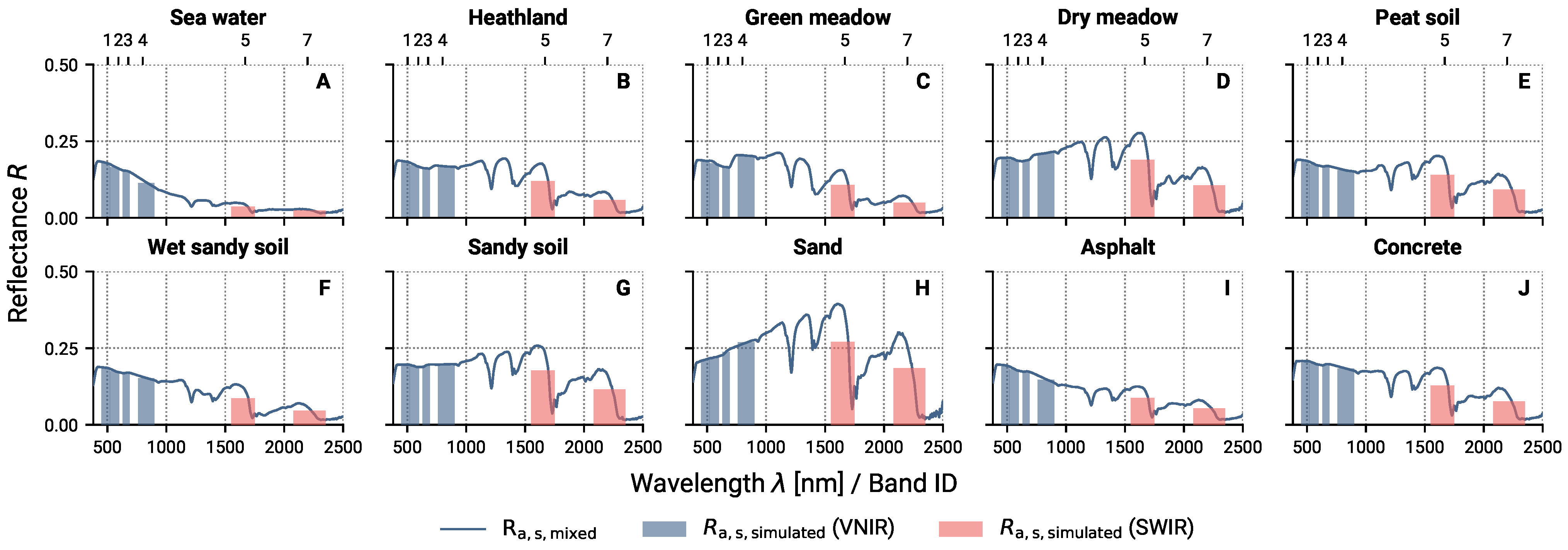
2.3.1. Layered Spectral Mixture with Background Surfaces
2.3.2. Spectral Sensor Simulation
2.3.3. Continuum Removal
2.4. Classification
2.4.1. Classifiers
2.4.2. Performance Metrics
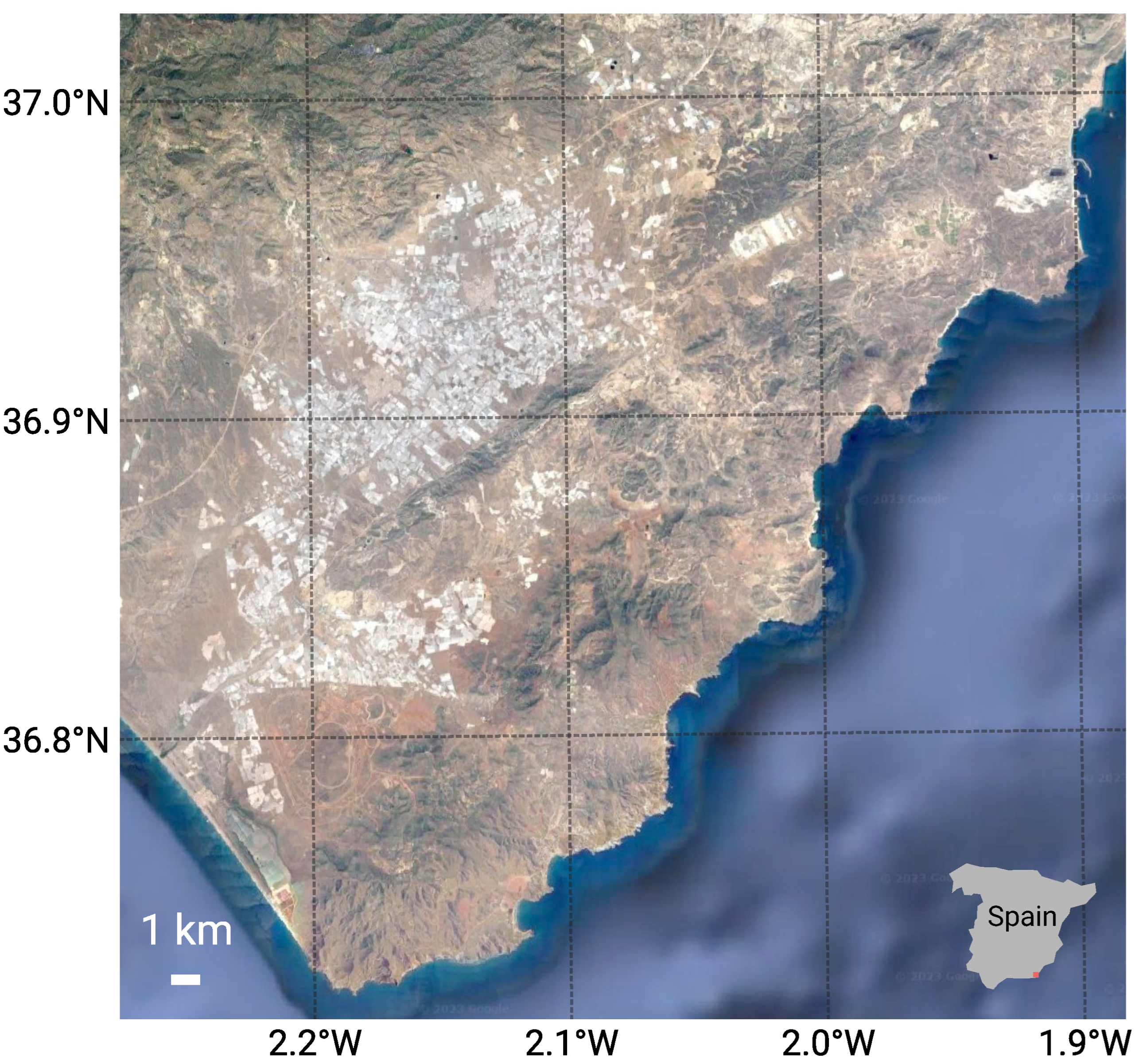
2.4.3. Case Study Almería
2.5. Hypothetical Sensor Definition
3. Results
3.1. Classification
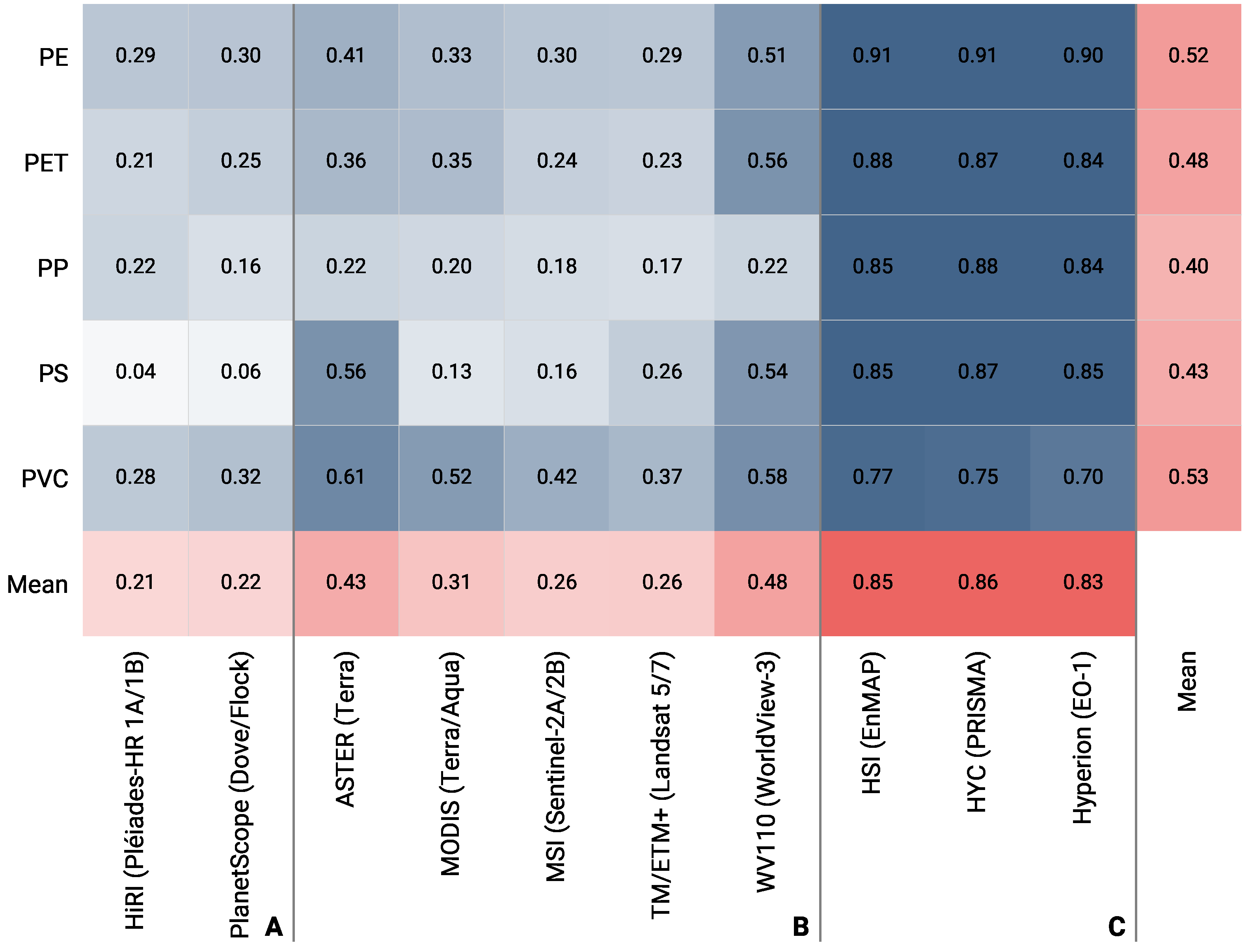
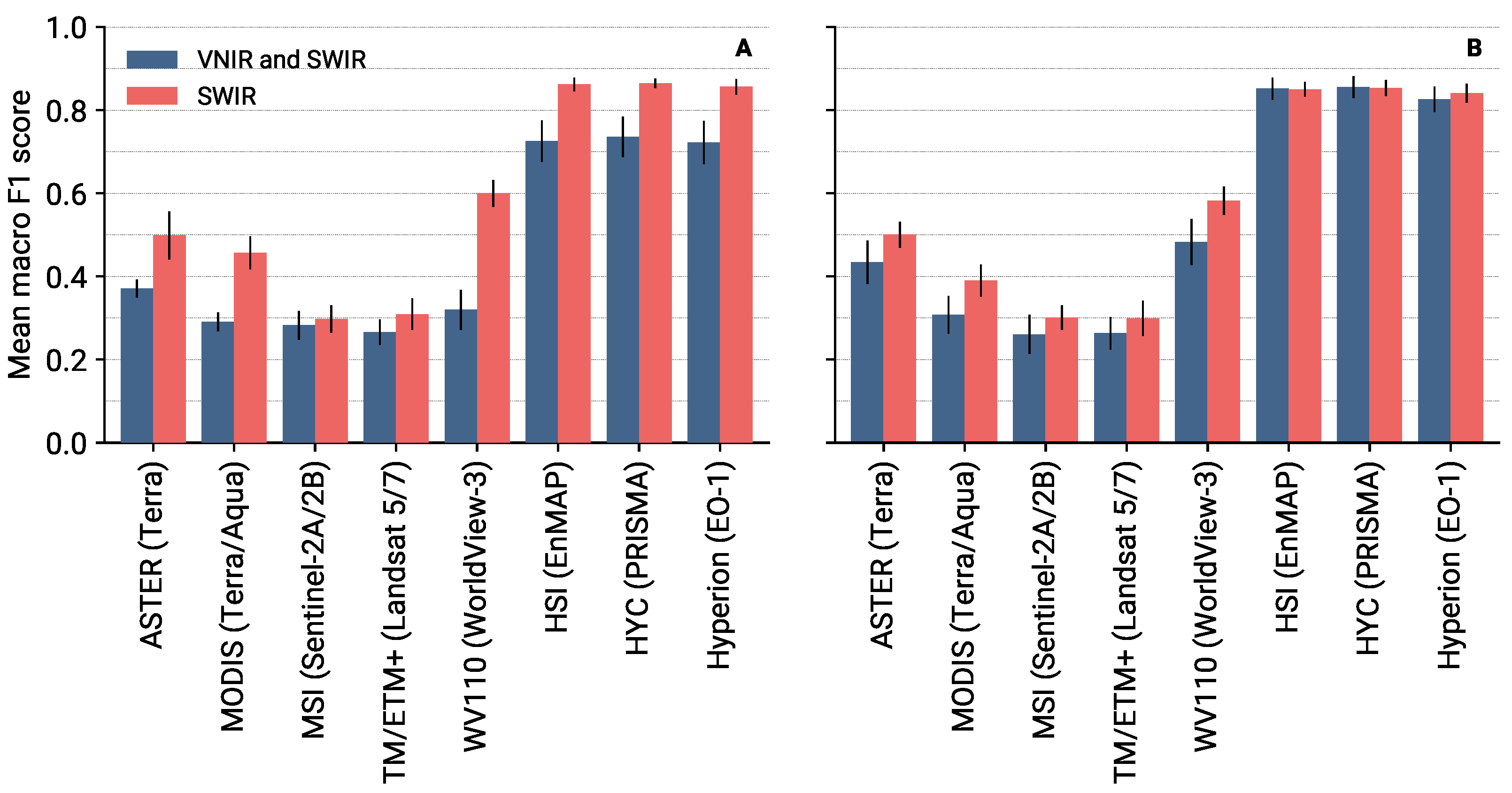
3.1.1. Macro F1 Scores: Influence of Sensor, Background, and Noise
3.1.2. F1 Scores: Influence of Plastic Type
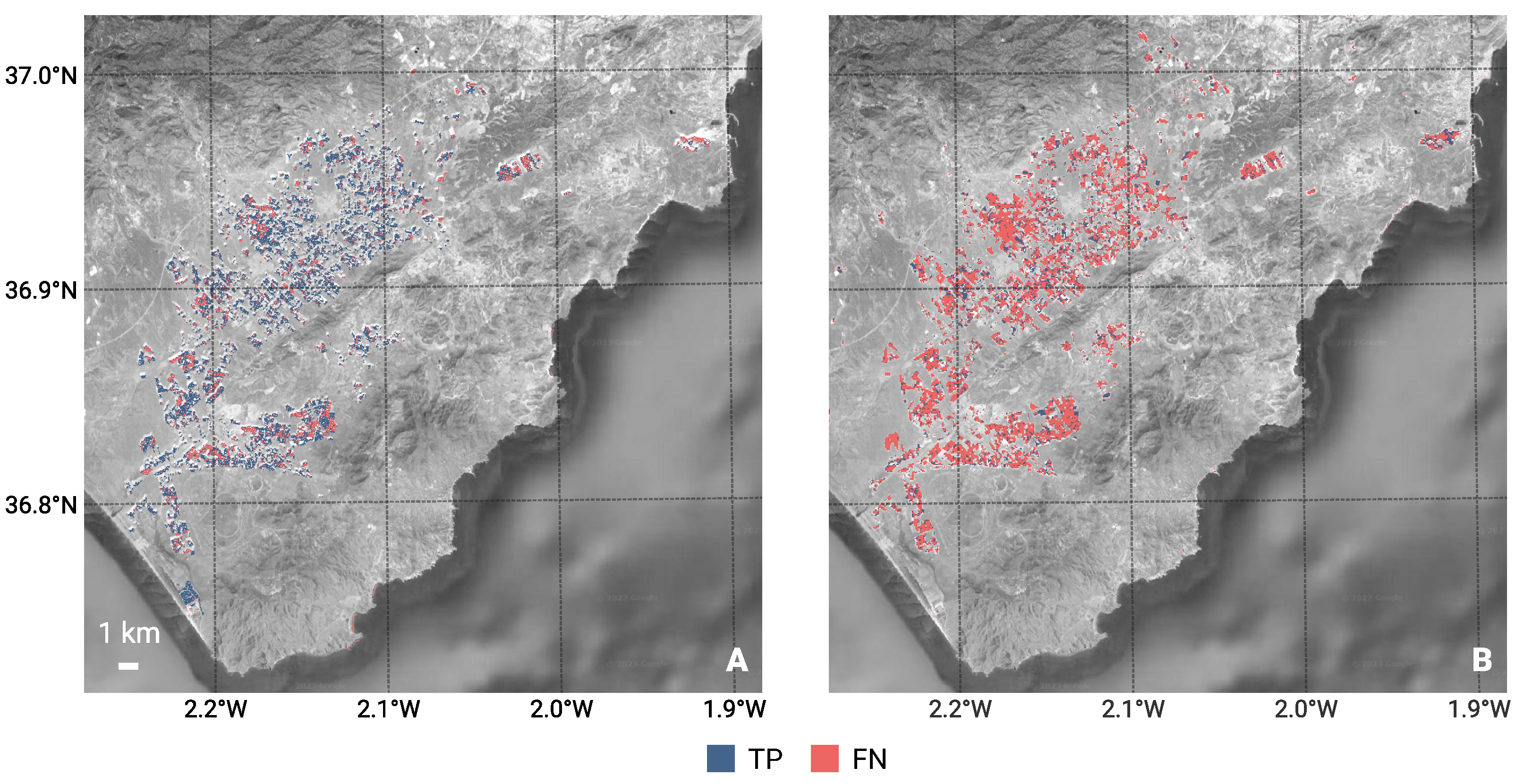
3.1.3. Case Study Almería
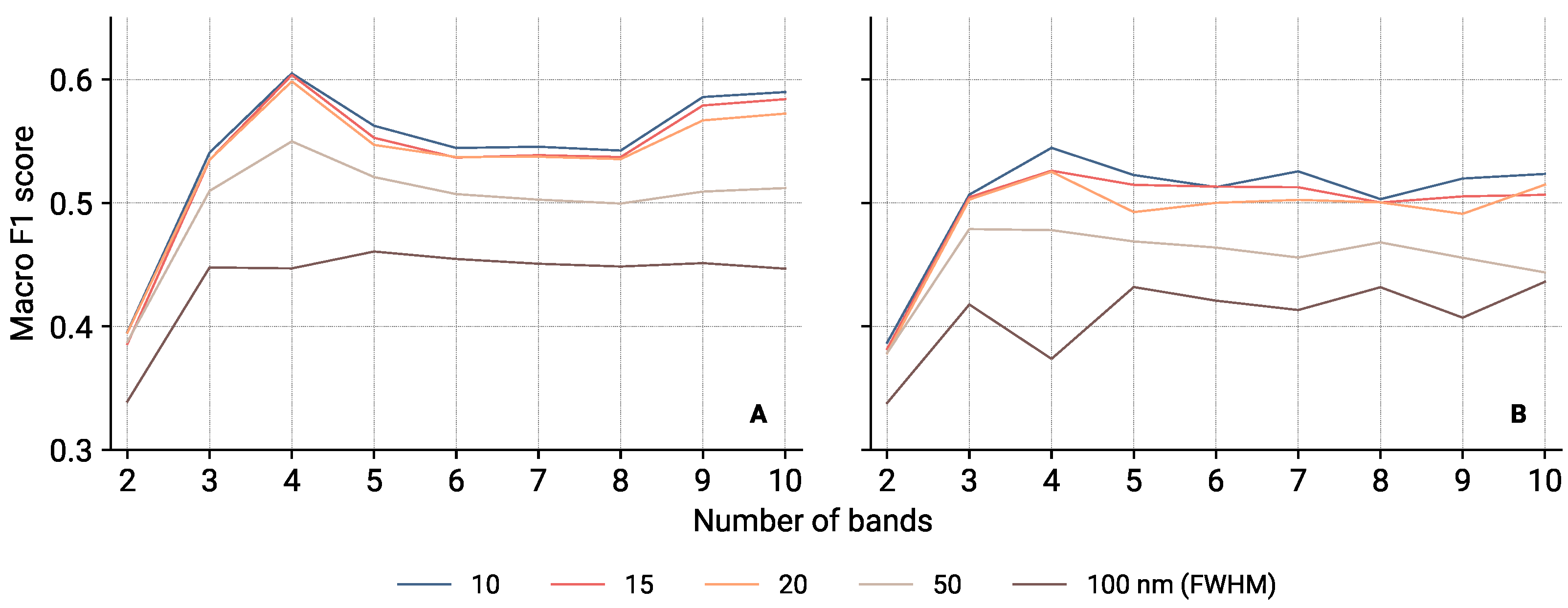
3.2. Hypothetical Sensor Definition
4. Discussion
4.1. Channel Characteristics
4.1.1. Continuum Removal
4.1.2. Background Surfaces
4.2. Classification
4.3. Applicability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASI | Agenzia Spaziale Italiana |
| ASTER | Advanced Spaceborne Thermal Emission and Reflection Radiometer |
| CHIME | Copernicus Hyperspectral Imaging Mission for the Environment |
| EO-1 | Earth Observing-1 |
| ESA | European Space Agency |
| ETM+ | Enhanced Thematic Mapper Plus |
| FN | False negatives |
| FWHM | Full width at half maximum |
| GSD | Ground sampling distance |
| HiRI | High-Resolution Imager |
| IR | Infrared |
| ISA | Israeli Space Agency |
| k-NN | k-nearest neighbors |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| MODTRAN | Moderate resolution atmospheric transmission |
| MSI | MultiSpectral Instrument |
| NASA | National Aeronautics and Space Administration |
| NIR | Near infrared |
| NEO | Norsk Elektro Optikk |
| OLI | Operational Land Imager |
| PE | Polyethylene |
| PE-HD | High-density polyethylene |
| PE-LD | Low-density polyethylene |
| PET | Polyethylene terephthalate |
| PP | Polypropylene |
| PRISMA | Precursore Iperspettrale della Missione Applicativa |
| PS | Polystyrene |
| PTFE | Polytetrafluoroethylene |
| PU | Polyurethane |
| PVC | Polyvinyl chloride |
| RF | Random forest |
| RIC | International Resin Identification Code |
| ROI | Region of interest |
| SBG | Surface Biology and Geology |
| SHALOM | Spaceborne Hyperspectral Applicative Land and Ocean Mission |
| SNR | Signal-to-noise ratio |
| SRF | Spectral response function |
| SSI | Spectral sampling interval |
| SWIR | Short wave infrared |
| TM | Thematic Mapper |
| TN | True negatives |
| TP | True positives |
| UAV | Uncrewed aerial vehicle |
| VIS | Visible part of the electromagnetic spectrum |
| VNIR | Visible and near infrared |
| WV110 | WorldView-110 |
Appendix A. Details on the Spectral Database Processings
Appendix A.1. Data Cleaning of HySpex Data
| Flag | Meaning | Number of Spectra |
|---|---|---|
| 1 | Interference | 297 (2.9%) |
| 2 | 3 (<0.1%) | |
| 3 | Slumps | 1606 (15.8%) |
| 4 | Outliers () | 1204 (11.8%) |
| 5 | Solitaries | 297 (2.9%) |
| 1921 (18.8%) |
Appendix A.2. Extracting Real Reflectance and Transmittance from HySpex Data

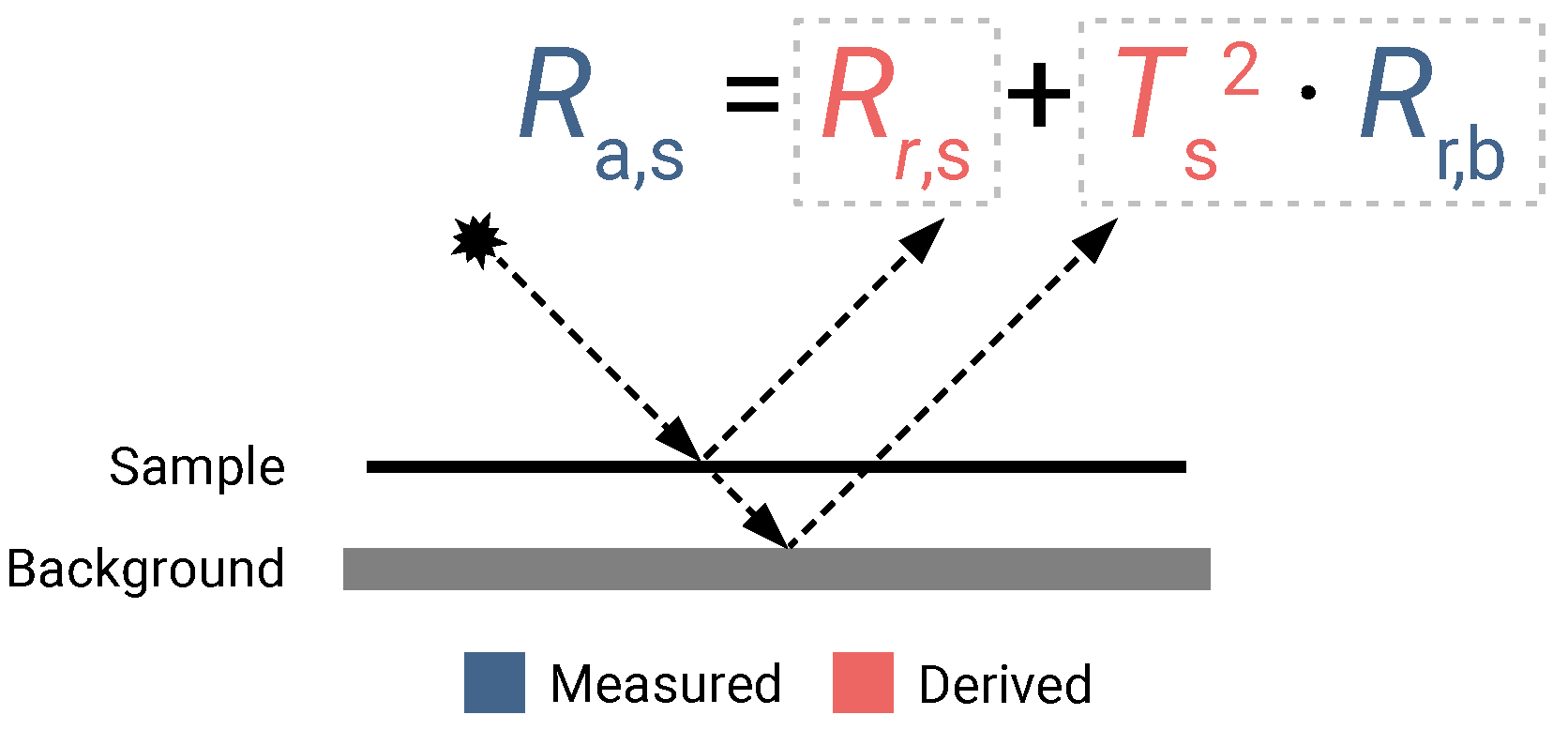
Appendix A.3. Merging of ASD and HySpex Data
Appendix B. Details on the Sensors Selected for Spectral Sensor Simulations
Appendix B.1. SRFs of the Multispectral Sensors

Appendix C. Details on the Machine Learning Classifiers
Appendix C.1. Parameter Tuning for the Machine Learning Classifiers
| Sensor | k-NN | RF | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | Metric | k | Weights | Bootstrap | Criterion | MSS | MSL | NE | |
| Pléiades | ball_tree | chebyshev | 8 | distance | True | entropy | 3 | 3 | 20 |
| PlanetScope | ball_tree | chebyshev | 9 | uniform | True | entropy | 4 | 4 | 10 |
| ASTER | ball_tree | manhattan | 4 | distance | True | entropy | 3 | 3 | 15 |
| MODIS | ball_tree | chebyshev | 4 | uniform | True | gini | 4 | 2 | 15 |
| Sentinel-2 | ball_tree | euclidean | 4 | distance | True | entropy | 4 | 4 | 10 |
| Landsat 5/7 | ball_tree | manhattan | 5 | distance | False | gini | 3 | 3 | 10 |
| WorldView-3 | ball_tree | chebyshev | 4 | distance | False | entropy | 3 | 2 | 20 |
| EnMAP | ball_tree | manhattan | 6 | distance | True | entropy | 4 | 4 | 50 |
| Hyperion | ball_tree | manhattan | 6 | uniform | True | entropy | 4 | 4 | 25 |
| PRISMA | ball_tree | manhattan | 6 | distance | True | entropy | 4 | 4 | 50 |
Appendix C.2. Cross Validation Setup
References
- Geyer, R.; Jambeck, J.R.; Law, K.L. Production, use, and fate of all plastics ever made. Sci. Adv. 2017, 3, e1700782. [Google Scholar] [CrossRef] [PubMed]
- Hopewell, J.; Dvorak, R.; Kosior, E. Plastics recycling: Challenges and opportunities. Philos. Trans. R. Soc. B Biol. Sci. 2009, 364, 2115–2126. [Google Scholar] [CrossRef] [PubMed]
- Avio, C.G.; Gorbi, S.; Regoli, F. Plastics and microplastics in the oceans: From emerging pollutants to emerged threat. Mar. Environ. Res. 2017, 128, 2–11. [Google Scholar] [CrossRef]
- Rillig, M.C. Microplastic in Terrestrial Ecosystems and the Soil? Environ. Sci. Technol. 2012, 46, 6453–6454. [Google Scholar] [CrossRef]
- Derraik, J.G. The pollution of the marine environment by plastic debris: A review. Mar. Pollut. Bull. 2002, 44, 842–852. [Google Scholar] [CrossRef] [PubMed]
- Barnes, D.K.A.; Galgani, F.; Thompson, R.C.; Barlaz, M. Accumulation and fragmentation of plastic debris in global environments. Philos. Trans. R. Soc. B Biol. Sci. 2009, 364, 1985–1998. [Google Scholar] [CrossRef] [PubMed]
- Kukulka, T.; Proskurowski, G.; Morét-Ferguson, S.; Meyer, D.W.; Law, K.L. The effect of wind mixing on the vertical distribution of buoyant plastic debris. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Forsberg, P.L.; Sous, D.; Stocchino, A.; Chemin, R. Behaviour of plastic litter in nearshore waters: First insights from wind and wave laboratory experiments. Mar. Pollut. Bull. 2020, 153, 111023. [Google Scholar] [CrossRef]
- Andrady, A.L. Persistence of plastic litter in the oceans. In Marine Anthropogenic Litter; Springer: Berlin/Heidelberg, Germany, 2015; pp. 57–72. [Google Scholar]
- Laskar, N.; Kumar, U. Plastics and microplastics: A threat to environment. Environ. Technol. Innov. 2019, 14, 100352. [Google Scholar] [CrossRef]
- Wright, S.L.; Kelly, F.J. Plastic and Human Health: A Micro Issue? Environ. Sci. Technol. 2017, 51, 6634–6647. [Google Scholar] [CrossRef]
- Revel, M.; Châtel, A.; Mouneyrac, C. Micro(nano)plastics: A threat to human health? Curr. Opin. Environ. Sci. Health 2018, 1, 17–23. [Google Scholar] [CrossRef]
- Swain, S.K.; Mohammad, J. Nanostructured Polymer Composites for Biomedical Applications; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Workman, J.; Workman, J. Handbook of Organic Compounds: Methods and Interpretations; Academic Press: Cambridge, MA, USA, 2001; Volume 1. [Google Scholar]
- Eisenreich, N.; Rohe, T. Infrared spectroscopy in analysis of plastics recycling. In Encyclopedia of Analytical Chemistry: Applications, Theory and Instrumentation; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Osswald, T.A. (Ed.) International Plastics Handbook: The Resource for Plastics Engineers, 1st ed.; Hanser: Munich, Germany; Cincinnati, OH, USA, 2006. [Google Scholar]
- Hausdorff, H.H. Short Cuts to the Analysis of Plastics by Infrared Spectroscopy. Appl. Spectrosc. 1950, 5, 8–13. [Google Scholar] [CrossRef]
- Kraft, E. Analysis of Plastics by ATR Spectroscopy; Modern Plastics; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Davies, A.M.C.; Grant, A.; Gavrel, G.M.; Steeper, R.V. Rapid analysis of packaging laminates by near-infrared spectroscopy. Analyst 1985, 110, 643. [Google Scholar] [CrossRef]
- Cloutis, E.A. Spectral Reflectance Properties of Hydrocarbons: Remote-Sensing Implications. Science 1989, 245, 165–168. [Google Scholar] [CrossRef] [PubMed]
- Kühn, F.; Oppermann, K.; Hörig, B. Hydrocarbon Index—An algorithm for hyperspectral detection of hydrocarbons. Int. J. Remote Sens. 2004, 25, 2467–2473. [Google Scholar] [CrossRef]
- Lu, L.; Di, L.; Ye, Y. A Decision-Tree Classifier for Extracting Transparent Plastic-Mulched Landcover from Landsat-5 TM Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4548–4558. [Google Scholar] [CrossRef]
- Maximenko, N.; Chao, Y.; Moller, D. Developing a Remote Sensing System to Track Marine Debris. Eos 2016, 97. [Google Scholar] [CrossRef]
- Lanorte, A.; De Santis, F.; Nolè, G.; Blanco, I.; Loisi, R.V.; Schettini, E.; Vox, G. Agricultural plastic waste spatial estimation by Landsat 8 satellite images. Comput. Electron. Agric. 2017, 141, 35–45. [Google Scholar] [CrossRef]
- Yang, D.; Chen, J.; Zhou, Y.; Chen, X.; Chen, X.; Cao, X. Mapping plastic greenhouse with medium spatial resolution satellite data: Development of a new spectral index. ISPRS J. Photogramm. Remote Sens. 2017, 128, 47–60. [Google Scholar] [CrossRef]
- Goddijn-Murphy, L.; Peters, S.; van Sebille, E.; James, N.A.; Gibb, S. Concept for a hyperspectral remote sensing algorithm for floating marine macro plastics. Mar. Pollut. Bull. 2018, 126, 255–262. [Google Scholar] [CrossRef]
- Biermann, L.; Vincente, V.M.; Sailley, S.; Mata, A.; Steele, C. Towards a method for detecting macroplastics by satellite: Examining Sentinel-2 earth observation data for floating debris in the coastal zone. In Proceedings of the 21st EGU General Assembly, EGU2019, Vienna, Austria, 7–12 April 2019; p. 1. [Google Scholar]
- Hafeez, S.; Wong, M.S.; Abbas, S.; Kwok, C.Y.T.; Nichol, J.; Lee, K.H.; Tang, D.; Pun, L. Detection and Monitoring of Marine Pollution Using Remote Sensing Technologies. In Monitoring of Marine Pollution; Fouzia, H.B., Ed.; IntechOpen: Rijeka, Croatia, 2018; Chapter 2. [Google Scholar] [CrossRef]
- Martínez-Vicente, V.; Clark, J.R.; Corradi, P.; Aliani, S.; Arias, M.; Bochow, M.; Bonnery, G.; Cole, M.; Cózar, A.; Donnelly, R.; et al. Measuring Marine Plastic Debris from Space: Initial Assessment of Observation Requirements. Remote Sens. 2019, 11, 2443. [Google Scholar] [CrossRef]
- Kuester, T.; Bochow, M. Spectral Modeling of Plastic Litter in Terrestrial Environments-Use of 3D Hyperspectral Ray Tracing Models to Analyze the Spectral Influence of Different Natural Ground Surfaces on Remote Sensing Based Plastic Mapping. In Proceedings of the 2019 10th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 September 2019; IEEE: Amsterdam, The Netherlands, 2019; pp. 1–7. [Google Scholar]
- Biermann, L.; Clewley, D.; Martinez-Vicente, V.; Topouzelis, K. Finding Plastic Patches in Coastal Waters using Optical Satellite Data. Sci. Rep. 2020, 10, 5364. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Kuester, T.; Bochow, M.; Bohn, N.; Brell, M.; Kaufmann, H. A knowledge-based, validated classifier for the identification of aliphatic and aromatic plastics by WorldView-3 satellite data. Remote Sens. Environ. 2021, 264, 112598. [Google Scholar] [CrossRef]
- Zhou, S.; Kaufmann, H.; Bohn, N.; Bochow, M.; Kuester, T.; Segl, K. Identifying distinct plastics in hyperspectral experimental lab-, aircraft-, and satellite data using machine/deep learning methods trained with synthetically mixed spectral data. Remote Sens. Environ. 2022, 281, 113263. [Google Scholar] [CrossRef]
- Berk, A.; Conforti, P.; Kennett, R.; Perkins, T.; Hawes, F.; van den Bosch, J. MODTRAN6: A Major Upgrade of the MODTRAN Radiative Transfer Code; SPIE: Baltimore, MD, USA, 2014; p. 90880H. [Google Scholar] [CrossRef]
- Vázquez-Guardado, A.; Money, M.; McKinney, N.; Chanda, D. Multi-spectral infrared spectroscopy for robust plastic identification. Appl. Opt. 2015, 54, 7396. [Google Scholar] [CrossRef]
- ASD Inc. FieldSpec 3 User Manual; Technical Report ASD Document 600540 Rev. I; ASD Inc.: Falls Church, VA, USA, 2010. [Google Scholar]
- Lenhard, K.; Baumgartner, A.; Schwarzmaier, T. Independent Laboratory Characterization of NEO HySpex Imaging Spectrometers VNIR-1600 and SWIR-320m-e. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1828–1841. [Google Scholar] [CrossRef]
- Rogass, C.; Koerting, F.M.; Mielke, C.; Brell, M.; Boesche, N.K.; Bade, M.; Hohmann, C. Translational imaging spectroscopy for proximal sensing. Sensors 2017, 17, 1857. [Google Scholar] [CrossRef]
- Siegert, F.; Atwood, E.C.; Piehl, S.; Bochow, M.; Laforsch, C.; Franke, J. Belastung Aquatischer Ökosysteme Mit Kunststoffmüll: Globales und Lokales Monitoring Mittels Satellitengestützter Methoden: Schlussbericht; Berichtszeitraum: 1 July 2013–31 July 2017; Technical Report; Universität Bayreuth: Bayreuth, Germany, 2018. [Google Scholar] [CrossRef]
- Neumann, C.; Itzerott, S.; Weiss, G.; Kleinschmit, B.; Schmidtlein, S. Mapping multiple plant species abundance patterns—A multiobjective optimization procedure for combining reflectance spectroscopy and species ordination. Ecol. Inform. 2016, 36, 61–76. [Google Scholar] [CrossRef]
- Roessner, S.; Segl, K.; Heiden, U.; Kaufmann, H. Automated differentiation of urban surfaces based on airborne hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1525–1532. [Google Scholar] [CrossRef]
- Blasch, G.; Spengler, D.; Itzerott, S.; Wessolek, G. Organic Matter Modeling at the Landscape Scale Based on Multitemporal Soil Pattern Analysis Using RapidEye Data. Remote Sens. 2015, 7, 11125–11150. [Google Scholar] [CrossRef]
- Spengler, D. Anwendung Vierdimensionaler Bestandsmodelle für die Charakterisierung von Getreidearten aus Hyperspektralen Fernerkundungsdaten. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2013. [Google Scholar]
- Bochow, M. Automatisierungspotenzial von Stadtbiotopkartierungen durch Methoden der Fernerkundung; Logos-Verlag: Berlin, Germany, 2010. [Google Scholar]
- Küster, T. Modellierung von Getreidebestandsspektren zur Korrektur BRDF-Bedingter Einflüsse auf Vegetationsindizes im Rahmen der EnMAP-Mission. Ph.D. Thesis, Humboldt-Universität Zu Berlin, Berlin, Germay, 2011. [Google Scholar] [CrossRef]
- Segl, K.; Richter, R.; Küster, T.; Kaufmann, H. End-to-end sensor simulation for spectral band selection and optimization with application to the Sentinel-2 mission. Appl. Opt. 2012, 51, 439. [Google Scholar] [CrossRef] [PubMed]
- She, X.; Zhang, L.; Cen, Y.; Wu, T.; Huang, C.; Baig, M. Comparison of the Continuity of Vegetation Indices Derived from Landsat 8 OLI and Landsat 7 ETM+ Data among Different Vegetation Types. Remote Sens. 2015, 7, 13485–13506. [Google Scholar] [CrossRef]
- Mielke, C.; Boesche, N.K.; Rogass, C.; Kaufmann, H.; Gauert, C. New geometric hull continuum removal algorithm for automatic absorption band detection from spectroscopic data. Remote Sens. Lett. 2015, 6, 97–105. [Google Scholar] [CrossRef]
- Clark, R.N. Spectral properties of mixtures of montmorillonite and dark carbon grains: Implications for remote sensing minerals containing chemically and physically adsorbed water. J. Geophys. Res. Solid Earth 1983, 88, 10635–10644. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning; Cambridge University Press: Cambridge, UK, 2014; p. 416. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Valera, D.; Belmonte, L.; Molina-Aiz, F.; López, A. Greenhouse Agriculture in Almeria. A Comprehensive Techno-Economic Analysis; Cajamar Caja Rural: Almeria, Spain, 2016. [Google Scholar]
- Karaca, A.C.; Ertürk, A.; Güllü, M.K.; Elmas, M.; Ertürk, S. Plastic Waste Sorting Using Infrared Hyperspectral Imaging System. In Proceedings of the 2013 21st Signal Processing and Communications Applications Conference (SIU), Haspolat, Turkey, 24–26 April 2013; p. 4. [Google Scholar]
- Garaba, S.P.; Dierssen, H.M. An airborne remote sensing case study of synthetic hydrocarbon detection using short wave infrared absorption features identified from marine-harvested macro- and microplastics. Remote Sens. Environ. 2018, 205, 224–235. [Google Scholar] [CrossRef]
- Moroni, M.; Mei, A.; Leonardi, A.; Lupo, E.; Marca, F. PET and PVC Separation with Hyperspectral Imagery. Sensors 2015, 15, 2205–2227. [Google Scholar] [CrossRef] [PubMed]
- Garnaud, J.C. Plasticulture magazine: Amilestone for a history of progress in plasticulture. Plasticulture 2000, 1, 30–43. [Google Scholar]
- Yang, Z.; Yu, X.; Dedman, S.; Rosso, M.; Zhu, J.; Yang, J.; Xia, Y.; Tian, Y.; Zhang, G.; Wang, J. UAV remote sensing applications in marine monitoring: Knowledge visualization and review. Sci. Total Environ. 2022, 838, 155939. [Google Scholar] [CrossRef]
- Tian, Y.; Yang, Z.; Yu, X.; Jia, Z.; Rosso, M.; Dedman, S.; Zhu, J.; Xia, Y.; Zhang, G.; Yang, J.; et al. Can we quantify the aquatic environmental plastic load from aquaculture? Water Res. 2022, 219, 118551. [Google Scholar] [CrossRef]
- Pukelsheim, F. The Three Sigma Rule. Am. Stat. 1994, 48, 88–91. [Google Scholar] [CrossRef]
- Lillesaeter, O. Spectral reflectance of partly transmitting leaves: Laboratory measurements and mathematical modeling. Remote Sens. Environ. 1982, 12, 247–254. [Google Scholar] [CrossRef]
- Miller, J.R.; Steven, M.D.; Demetriades-Shah, T.H. Reflection of layered bean leaves over different soil backgrounds: Measured and simulated spectra. Int. J. Remote Sens. 1992, 13, 3273–3286. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Ustin, S.L. Leaf Optical Properties: A State of the Art; Cambridge University Press: Cambridge, UK, 2001; p. 10. [Google Scholar]
- Chen, C.; Breiman, L. Using Random Forest to Learn Imbalanced Data; University of California: Berkeley, CA, USA, 2004. [Google Scholar]
- Wah, Y.B.; Rahman, H.A.A.; He, H.; Bulgiba, A. Handling imbalanced dataset using SVM and k-NN approach. AIP Conf. Proc. 2016, 1750, 020023. [Google Scholar] [CrossRef]
- Ramezan, C.A.; Warner, T.A.; Maxwell, A.E. Evaluation of Sampling and Cross-Validation Tuning Strategies for Regional-Scale Machine Learning Classification. Remote Sens. 2019, 11, 185. [Google Scholar] [CrossRef]



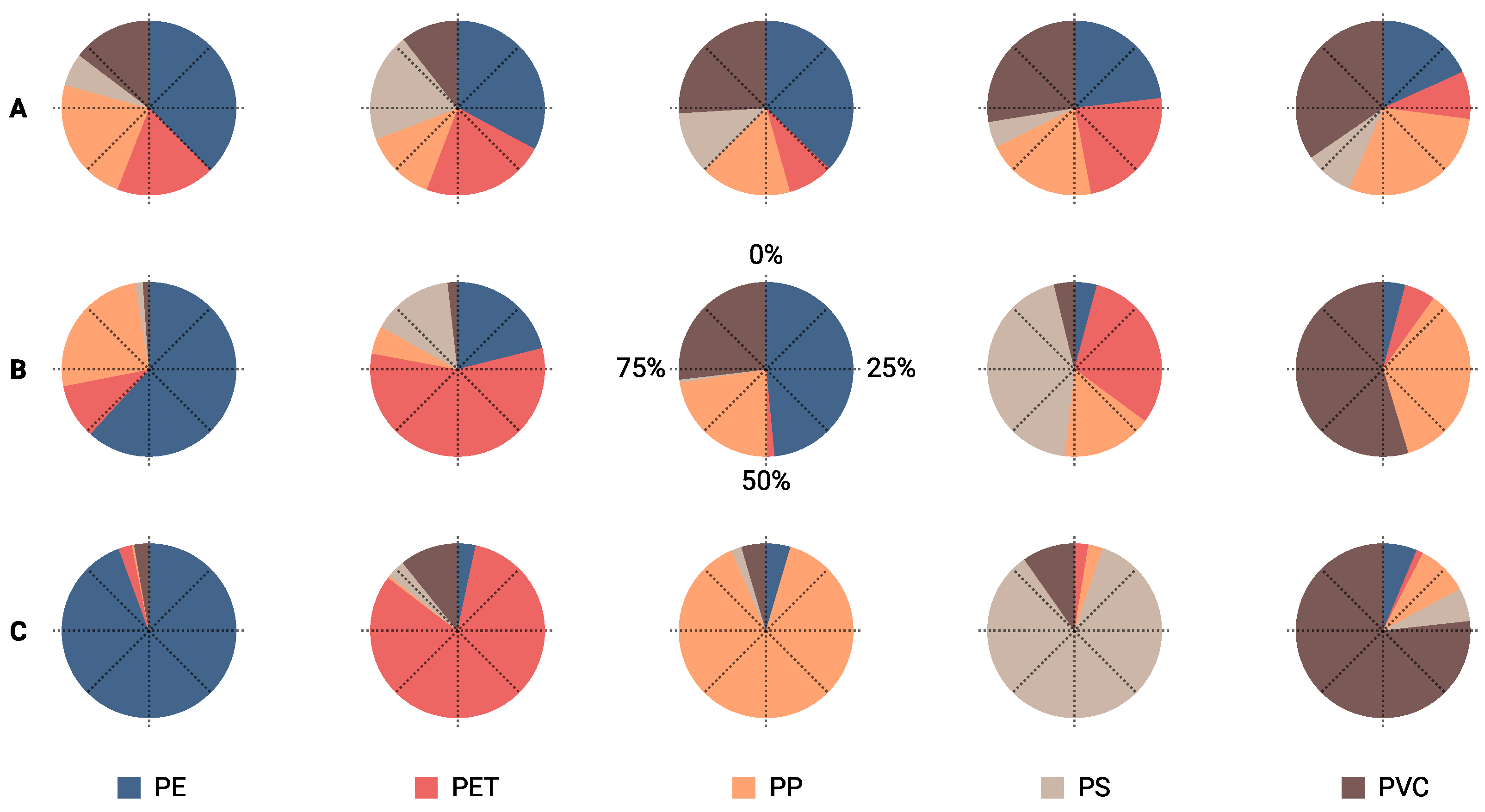
| Acronym | Chemical Notation | Number of Samples |
|---|---|---|
| PE-HD | High-density polyethylene | 8 |
| PE-LD | Low-density polyethylene | 9 |
| PET | Polyethylene terephthalate | 8 |
| PP | Polypropylene | 12 |
| PS | Polystyrene | 8 |
| PVC | Polyvinyl chloride | 8 |
| Sensor | Open Data | High Spatial Resolution | Archive Data Only |
|---|---|---|---|
| ASTER | yes | no | yes |
| WorldView-3 | no | yes | no |
| Hyperion | yes | no | yes |
| EnMAP | yes | no | no |
| PRISMA | yes | no | no |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmidt, T.; Kuester, T.; Smith, T.; Bochow, M. Potential of Optical Spaceborne Sensors for the Differentiation of Plastics in the Environment. Remote Sens. 2023, 15, 2020. https://doi.org/10.3390/rs15082020
Schmidt T, Kuester T, Smith T, Bochow M. Potential of Optical Spaceborne Sensors for the Differentiation of Plastics in the Environment. Remote Sensing. 2023; 15(8):2020. https://doi.org/10.3390/rs15082020
Chicago/Turabian StyleSchmidt, Toni, Theres Kuester, Taylor Smith, and Mathias Bochow. 2023. "Potential of Optical Spaceborne Sensors for the Differentiation of Plastics in the Environment" Remote Sensing 15, no. 8: 2020. https://doi.org/10.3390/rs15082020
APA StyleSchmidt, T., Kuester, T., Smith, T., & Bochow, M. (2023). Potential of Optical Spaceborne Sensors for the Differentiation of Plastics in the Environment. Remote Sensing, 15(8), 2020. https://doi.org/10.3390/rs15082020