On Evaluating the Predictability of Sea Surface Temperature Using Entropy
Abstract
1. Introduction
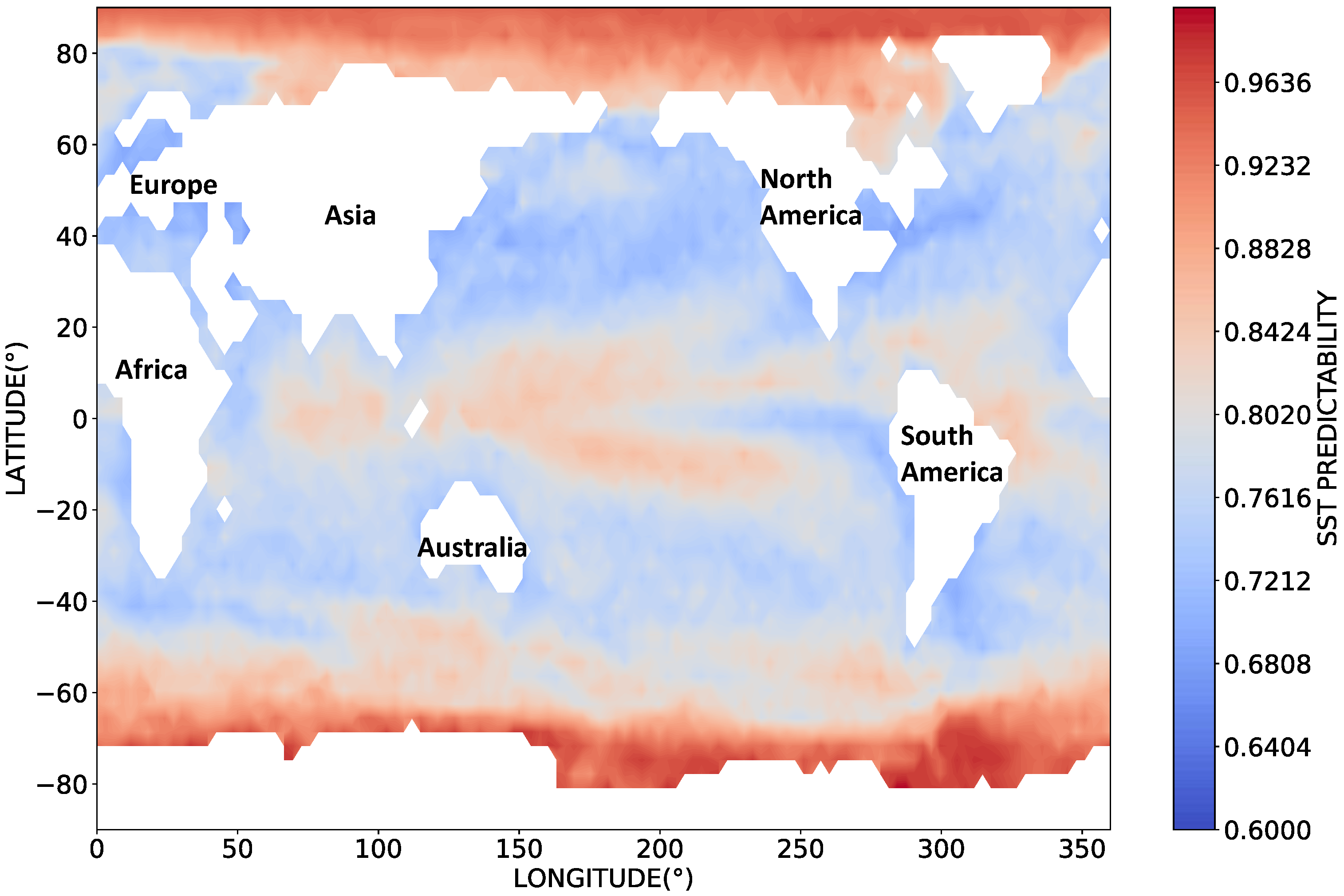
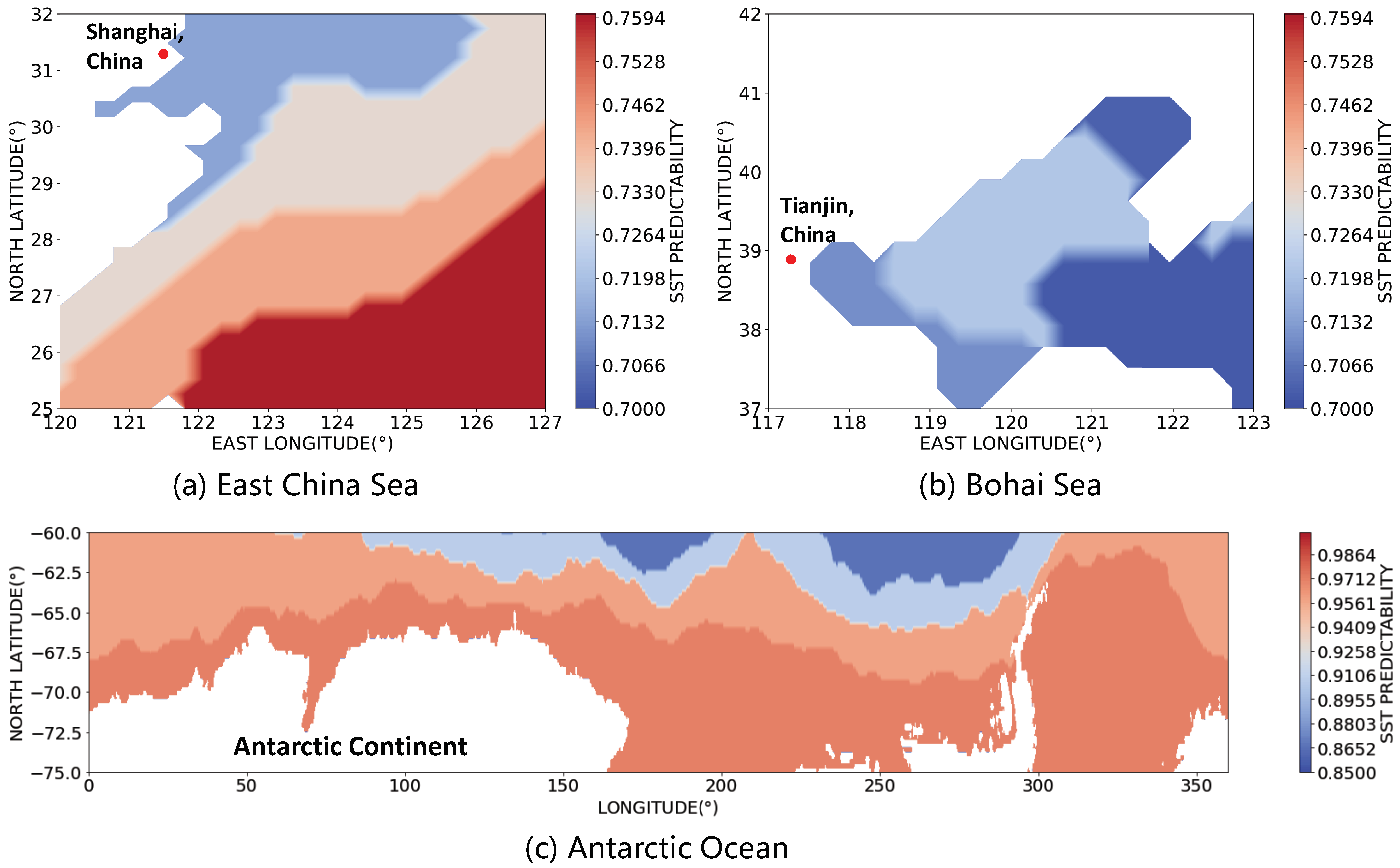
- We introduce entropy to quantify the predictability of the coarse-grained SST in all grid sea regions of size around the world, as well as the predictability of the fine-grained SST in grid regions of size in three typical local sea areas (i.e., the East China Sea, the Bohai Sea, and the Antarctic Ocean), and discover the differences of SST predictability in different oceanic areas.
- We develop multiple SST prediction models, including a physical model, i.e., Copernicus Marine global analysis and forecast product, AutoRegressive Integrated Moving Average(ARIMA) model, Long Short-Term Memory(LSTM) model, Multi-layer Perceptron (MLP) model, and Spatio-Temporal Graph Convolutional Network (STGCN) model, to make SST prediction. The results of these models demonstrate the effectiveness of the predictability evaluation method.
- We analyze the dynamics of the predictability of SST over a long time period from both global and local aspects, and identify the important causes that lead to the changes in SST predictability.
2. Material and Methods
2.1. Datasets
2.2. Problem Statement
2.3. Methods
2.3.1. Entropy-Based Predictability Evaluation for SST
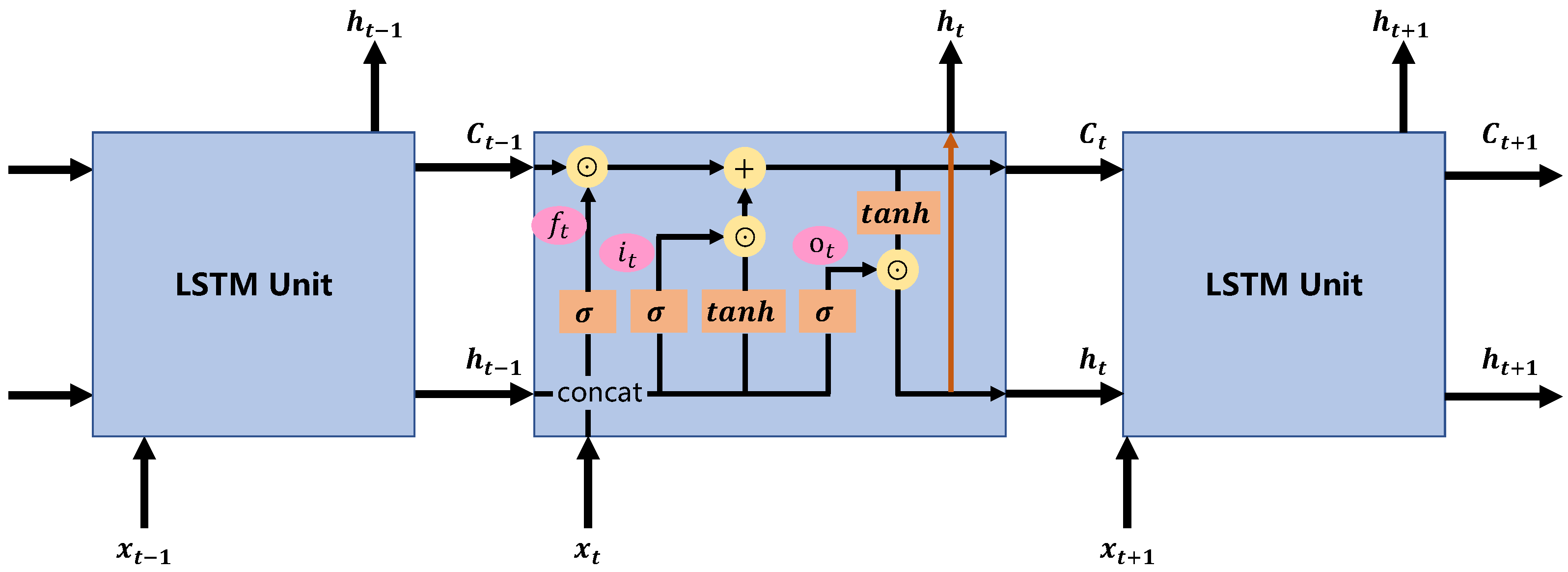
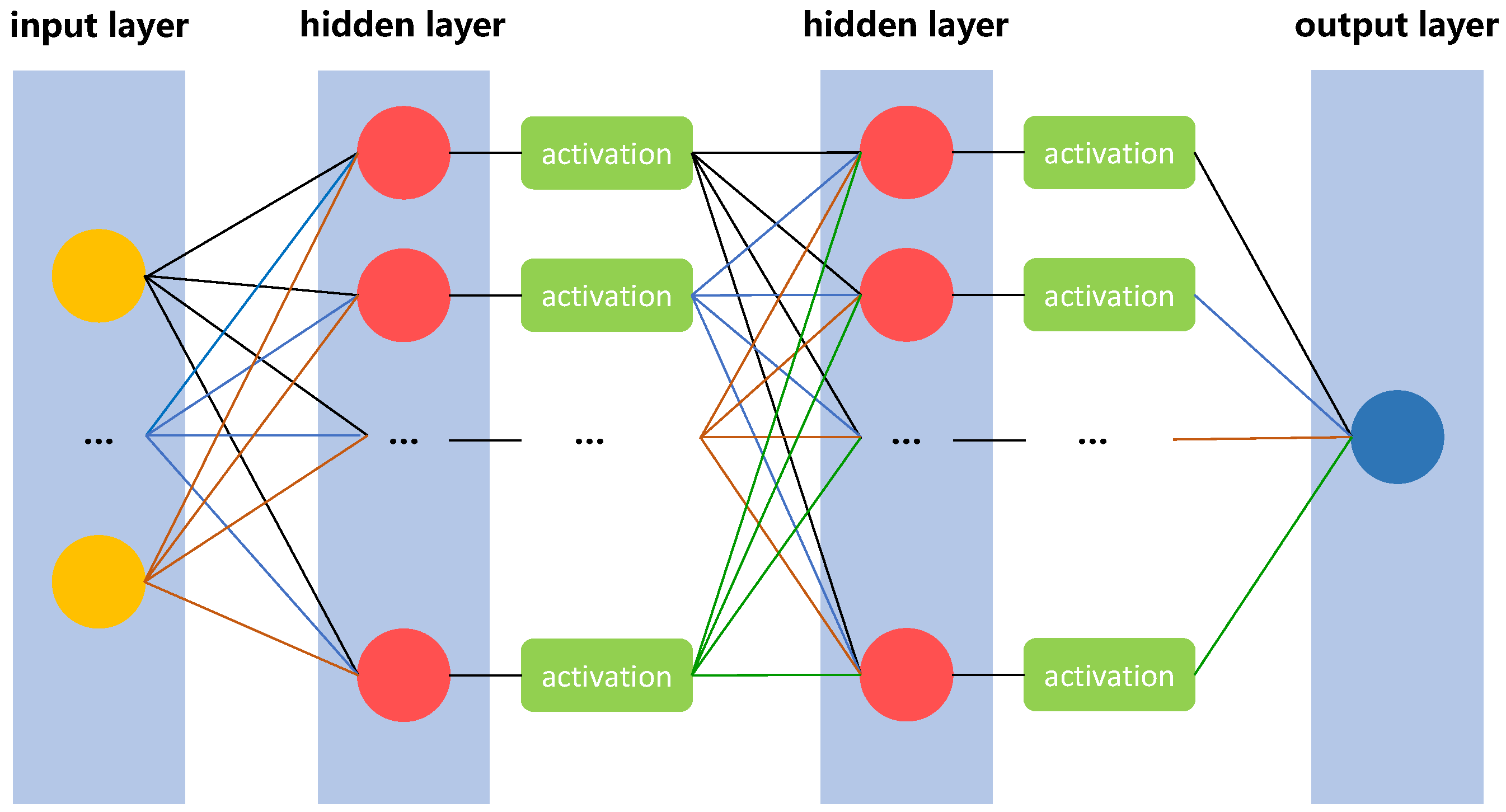
2.3.2. SST Prediction Models
2.3.3. Analyzing the Dynamics of SST Predictability
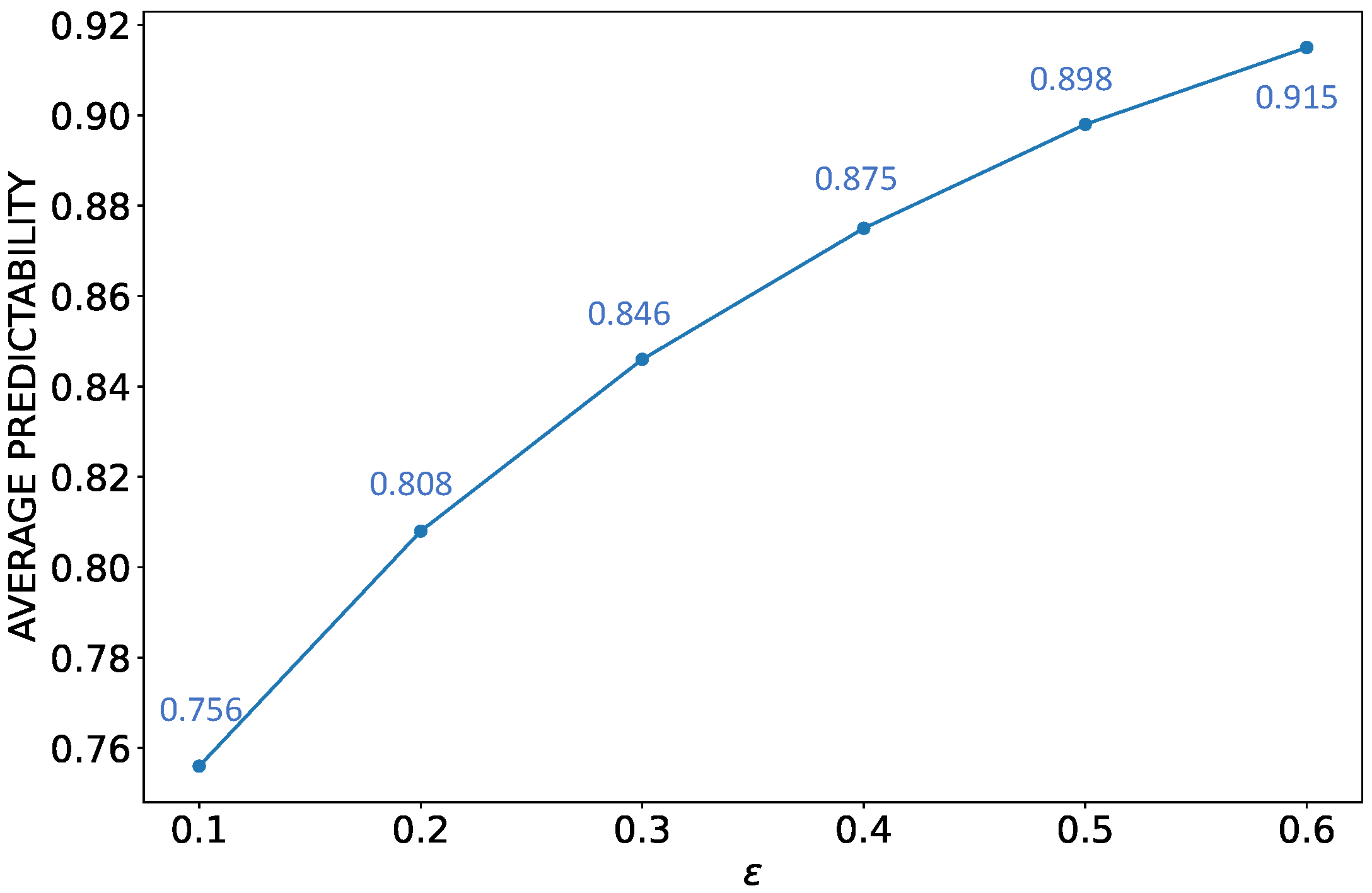
2.4. Evaluation Settings
3. Results and Discussion
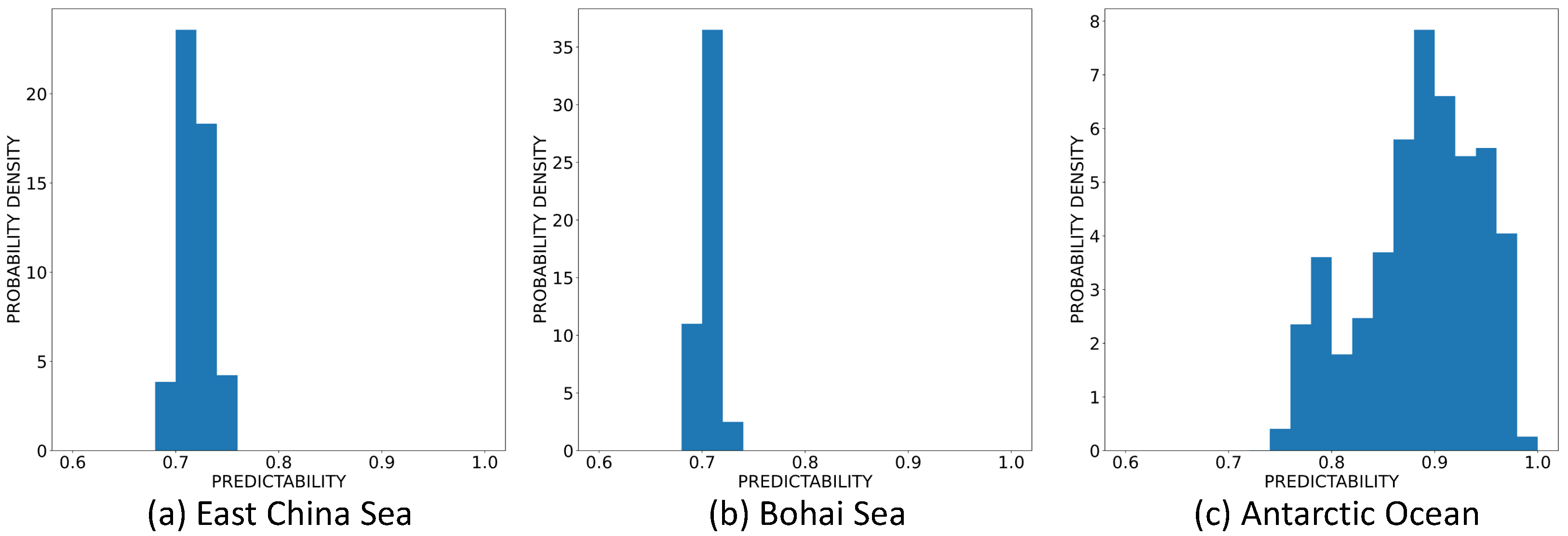
3.1. Predictability of SST
3.2. SST Predictability vs. Prediction Performance
3.3. Dynamics of SST Predictability
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SST | Sea Surface Temperature |
| ECS | East China Sea |
| ARIMA | Autoregressive integrated moving average |
| LSTM | Long Short-Term Memory |
| RNN | Recurrent Neural Network |
| MLP | Multi-layer Perceptron |
| STGCN | Spatio-Temporal Graph Convolutional Network |
| EOF | Empirical Orthogonal Function |
| AIC | Akaike Information Criterion |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| OISST | Optimum Interpolation SST |
| NOAA | National Oceanic and Atmospheric Administration |
| AVHRR | Advanced Very High-Resolution Radiometer |
| VIIRS | Visible Infrared Imaging Radiometer Suite |
| NCEI | National Centers for Environmental Information |
References
- Moros, M.; Emeis, K.; Risebrobakken, B.; Snowball, I.; Kuijpers, A.; McManus, J.; Jansen, E. Sea surface temperatures and ice rafting in the Holocene North Atlantic: Climate influences on northern Europe and Greenland. Quat. Sci. Rev. 2004, 23, 2113–2126. [Google Scholar] [CrossRef]
- Hurwitz, M.M.; Newman, P.; Garfinkel, C. On the influence of North Pacific sea surface temperature on the Arctic winter climate. J. Geophys. Res. Atmos. 2012, 117, 1–13. [Google Scholar] [CrossRef]
- Hittawe, M.M.; Langodan, S.; Beya, O.; Hoteit, I.; Knio, O.M. Efficient SST prediction in the Red Sea using hybrid deep learning-based approach. In Proceedings of the 20th IEEE International Conference on Industrial Informatics, INDIN 2022, Perth, Australia, 25–28 July 2022; pp. 107–117. [Google Scholar] [CrossRef]
- Feng, Y.; Sun, T.; Li, C. Study On Long Term Sea Surface Temperature (SST) Prediction Based On Temporal Convolutional Network (TCN) Method. In Proceedings of the ACM TURC 2021: ACM Turing Award Celebration Conference, Hefei, China, 30 July 2021–1 August 2021; pp. 28–32. [Google Scholar] [CrossRef]
- Zhao, K.; Khryashchev, D.; Freire, J.; Silva, C.; Vo, H. Predicting taxi demand at high spatial resolution: Approaching the limit of predictability. In Proceedings of the 2016 IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 5–8 December 2016; pp. 833–842. [Google Scholar]
- Hoegh-Guldberg, O.; Jacob, D.; Bindi, M.; Brown, S.; Camilloni, I.; Diedhiou, A.; Djalante, R.; Ebi, K.; Engelbrecht, F.; Guiot, J.; et al. Impacts of 1.5 C global warming on natural and human systems. In Global Warming of 1.5 °C; IPCC Secretariat: Geneva, Switzerland, 2018. [Google Scholar]
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global surface temperature change. Rev. Geophys. 2010, 48, 1–29. [Google Scholar] [CrossRef]
- Bulgin, C.E.; Merchant, C.J.; Ferreira, D. Tendencies, variability and persistence of sea surface temperature anomalies. Sci. Rep. 2020, 10, 7986. [Google Scholar] [CrossRef] [PubMed]
- Robles-Tamayo, C.M.; Valdez-Holguín, J.E.; García-Morales, R.; Figueroa-Preciado, G.; Herrera-Cervantes, H.; López-Martínez, J.; Enríquez-Ocaña, L.F. Sea surface temperature (SST) variability of the eastern coastal zone of the gulf of California. Remote Sens. 2018, 10, 1434. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.; Wang, B. Multidecade Trends of Sea Surface Temperature, Chlorophyll-a Concentration, and Ocean Eddies in the Gulf of Mexico. Remote Sens. 2022, 14, 3754. [Google Scholar] [CrossRef]
- Mohamed, B.; Ibrahim, O.; Nagy, H. Sea Surface Temperature Variability and Marine Heatwaves in the Black Sea. Remote Sens. 2022, 14, 2383. [Google Scholar] [CrossRef]
- Mohamed, B.; Nilsen, F.; Skogseth, R. Interannual and Decadal Variability of Sea Surface Temperature and Sea Ice Concentration in the Barents Sea. Remote Sens. 2022, 14, 4413. [Google Scholar] [CrossRef]
- Hussein, K.A.; Al Abdouli, K.; Ghebreyesus, D.T.; Petchprayoon, P.; Al Hosani, N.; Sharif, O.H. Spatiotemporal Variability of Chlorophyll-a and Sea Surface Temperature, and Their Relationship with Bathymetry over the Coasts of UAE. Remote Sens. 2021, 13, 2447. [Google Scholar] [CrossRef]
- Yujia, Z.; Weifu, S.; Jie, Z. Analysis of SST Spatial and Temporal Characteristics in the North Pacific Using Remote Sensing Data. In Proceedings of the IGARSS 2022 - 2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 6891–6894. [Google Scholar] [CrossRef]
- Ba, S.O.; Fablet, R.; Pastor, D.; Chapron, B. Descriptors for sea surface temperature front regularity characterization. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 669–672. [Google Scholar]
- Sutton, R.; Allen, M.R. Decadal predictability of North Atlantic sea surface temperature and climate. Nature 1997, 388, 563–567. [Google Scholar] [CrossRef]
- Davis, R.E. Predictability of sea surface temperature and sea level pressure anomalies over the North Pacific Ocean. J. Phys. Oceanogr. 1976, 6, 249–266. [Google Scholar] [CrossRef]
- Song, C.; Qu, Z.; Blumm, N.; Barabási, A.L. Limits of predictability in human mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Wetter, E.; Bharti, N.; Tatem, A.J.; Bengtsson, L. Approaching the limit of predictability in human mobility. Sci. Rep. 2013, 3, 2923. [Google Scholar] [CrossRef] [PubMed]
- Smith, G.; Wieser, R.; Goulding, J.; Barrack, D. A refined limit on the predictability of human mobility. In Proceedings of the 2014 IEEE International Conference on Pervasive Computing and Communications (PerCom), Budapest, Hungary, 24–28 March 2014; pp. 88–94. [Google Scholar] [CrossRef]
- Wang, J.; Mao, Y.; Li, J.; Xiong, Z.; Wang, W.X. Predictability of road traffic and congestion in urban areas. PLoS ONE 2015, 10, e0121825. [Google Scholar] [CrossRef]
- Chen, G.; Hoteit, S.; Viana, A.C.; Fiore, M.; Sarraute, C. Spatio-Temporal Predictability of Cellular Data Traffic. Ph.D. Thesis, INRIA Saclay-Ile-de-France, Palaiseau, France, 2017. [Google Scholar]
- Zhou, X.; Zhao, Z.; Li, R.; Zhou, Y.; Zhang, H. The predictability of cellular networks traffic. In Proceedings of the 2012 International Symposium on Communications and Information Technologies (ISCIT), Gold Coast, Australia, 2–5 October 2012; pp. 973–978. [Google Scholar] [CrossRef]
- Chand, S. Modeling predictability of traffic counts at signalised intersections using Hurst exponent. Entropy 2021, 23, 188. [Google Scholar] [CrossRef]
- Tao, Y.; Cui, H.; Nian, Y.; Hong, Y.; Wang, J.; Zhang, H. Behavior predictability and consistency of mobile users’ traffic usage between different years based on entropy theory. Int. J. Commun. Syst. 2019, 32, e4052. [Google Scholar] [CrossRef]
- Oh, M.; Kim, S.; Lim, K.; Kim, S.Y. Time series analysis of the Antarctic Circumpolar Wave via symbolic transfer entropy. Phys. A Stat. Mech. Its Appl. 2018, 499, 233–240. [Google Scholar] [CrossRef]
- Kleeman, R. Measuring dynamical prediction utility using relative entropy. J. Atmos. Sci. 2002, 59, 2057–2072. [Google Scholar] [CrossRef]
- Ikuyajolu, O.J.; Falasca, F.; Bracco, A. Information entropy as quantifier of potential predictability in the tropical Indo-Pacific basin. Front. Clim. 2021, 3, 675840. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Banzon, V.; Freeman, E.; Graham, G.; Hankins, B.; Smith, T.; Zhang, H.M. Improvements of the daily optimum interpolation sea surface temperature (DOISST) version 2.1. J. Clim. 2021, 34, 2923–2939. [Google Scholar] [CrossRef]
- Thomas, M.; Joy, A.T. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Wei, L.; Guan, L.; Qu, L.; Guo, D. Prediction of sea surface temperature in the China seas based on long short-term memory neural networks. Remote Sens. 2020, 12, 2697. [Google Scholar] [CrossRef]
- Wei, L.; Guan, L.; Qu, L. Prediction of sea surface temperature in the South China Sea by artificial neural networks. IEEE Geosci. Remote. Sens. Lett. 2019, 17, 558–562. [Google Scholar] [CrossRef]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI-18. International Joint Conferences on Artificial Intelligence Organization, Stockholm, Sweden, 13–19 July 2018; pp. 3634–3640. [Google Scholar] [CrossRef]
- Dauphin, Y.N.; Fan, A.; Auli, M.; Grangier, D. Language modeling with gated convolutional networks. In Proceedings of the International Conference on Machine Learning. PMLR, Sydney, NSW, Australia, 6–11 August 2017; pp. 933–941. [Google Scholar]
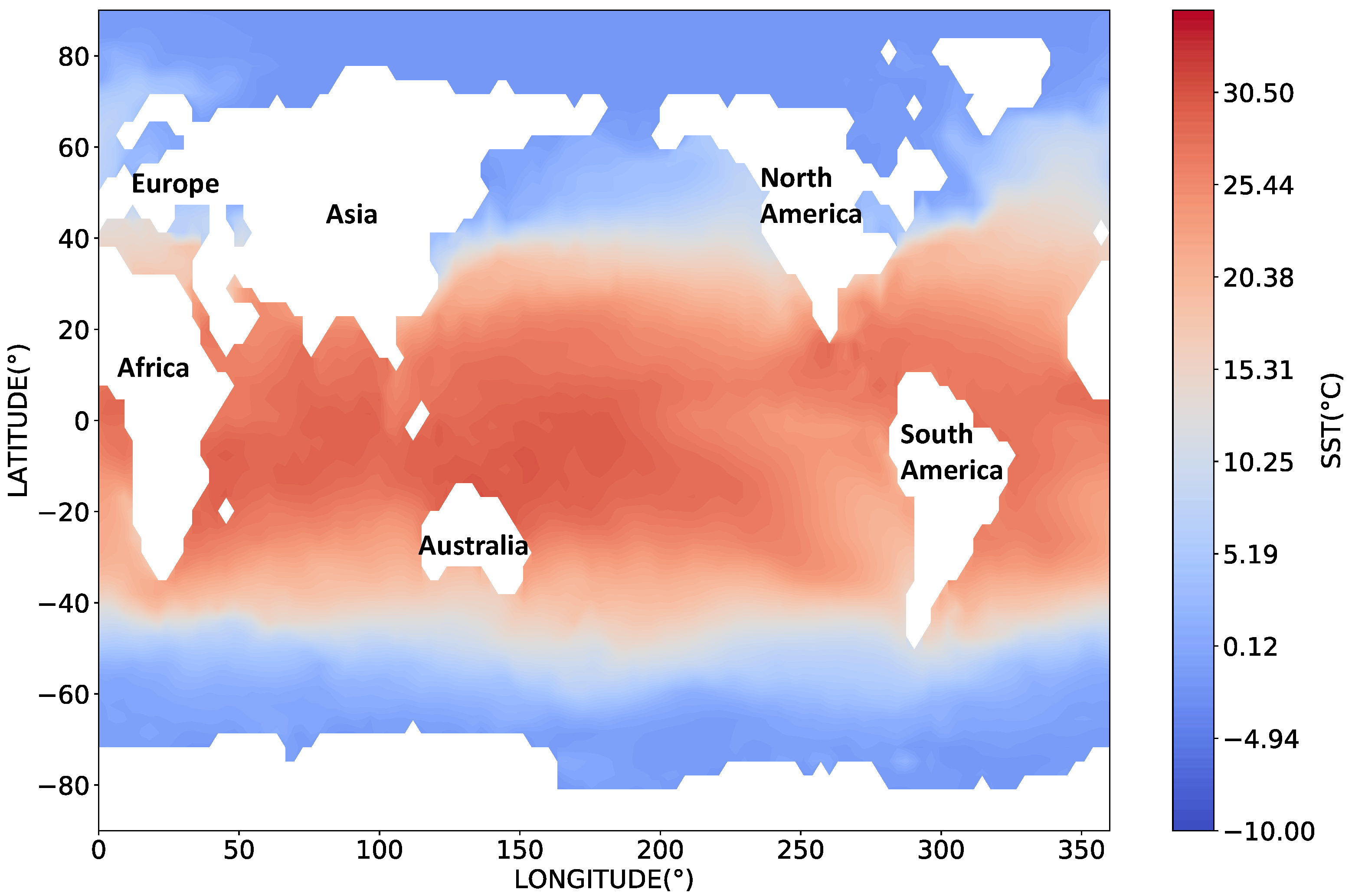
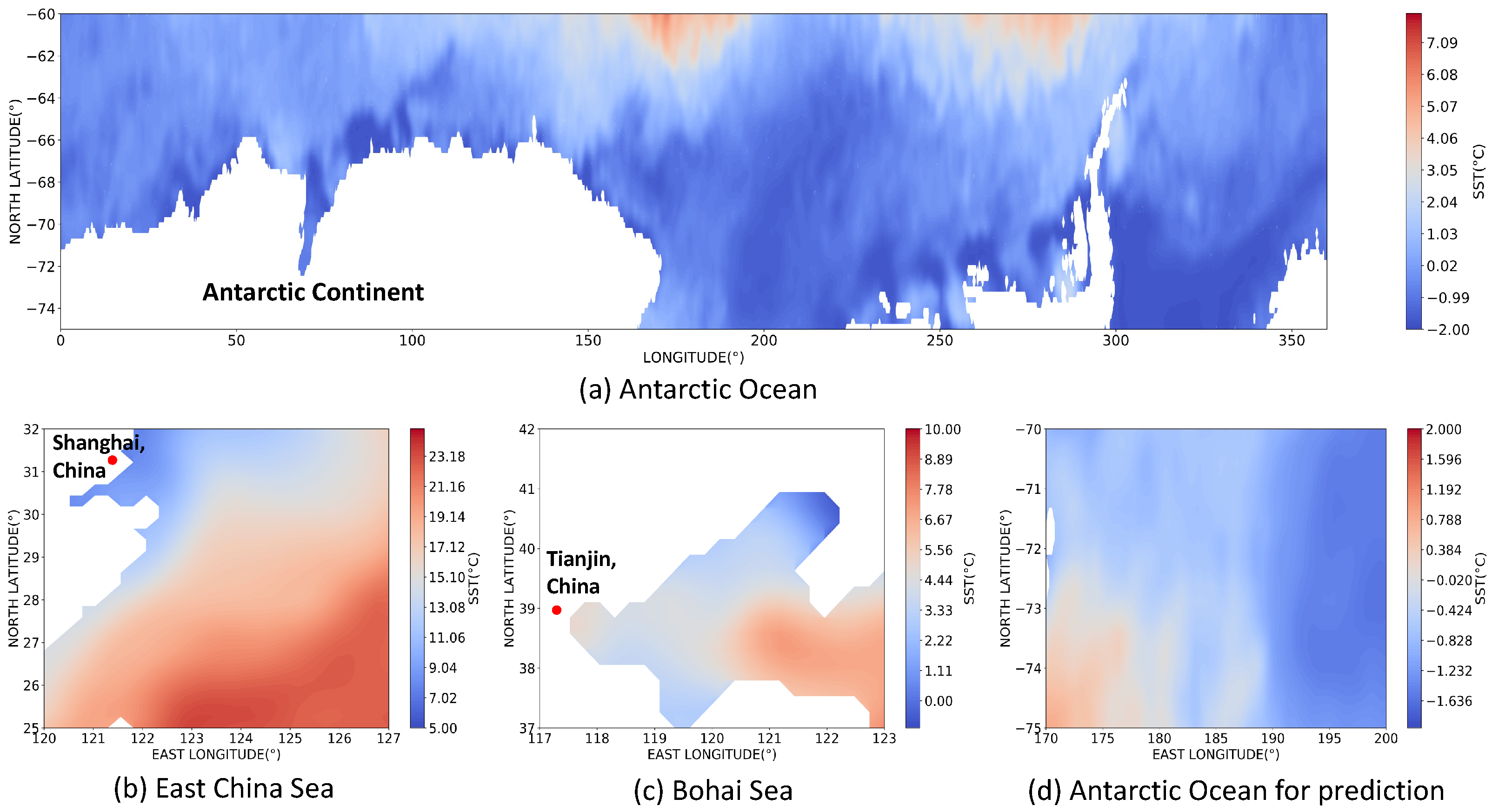


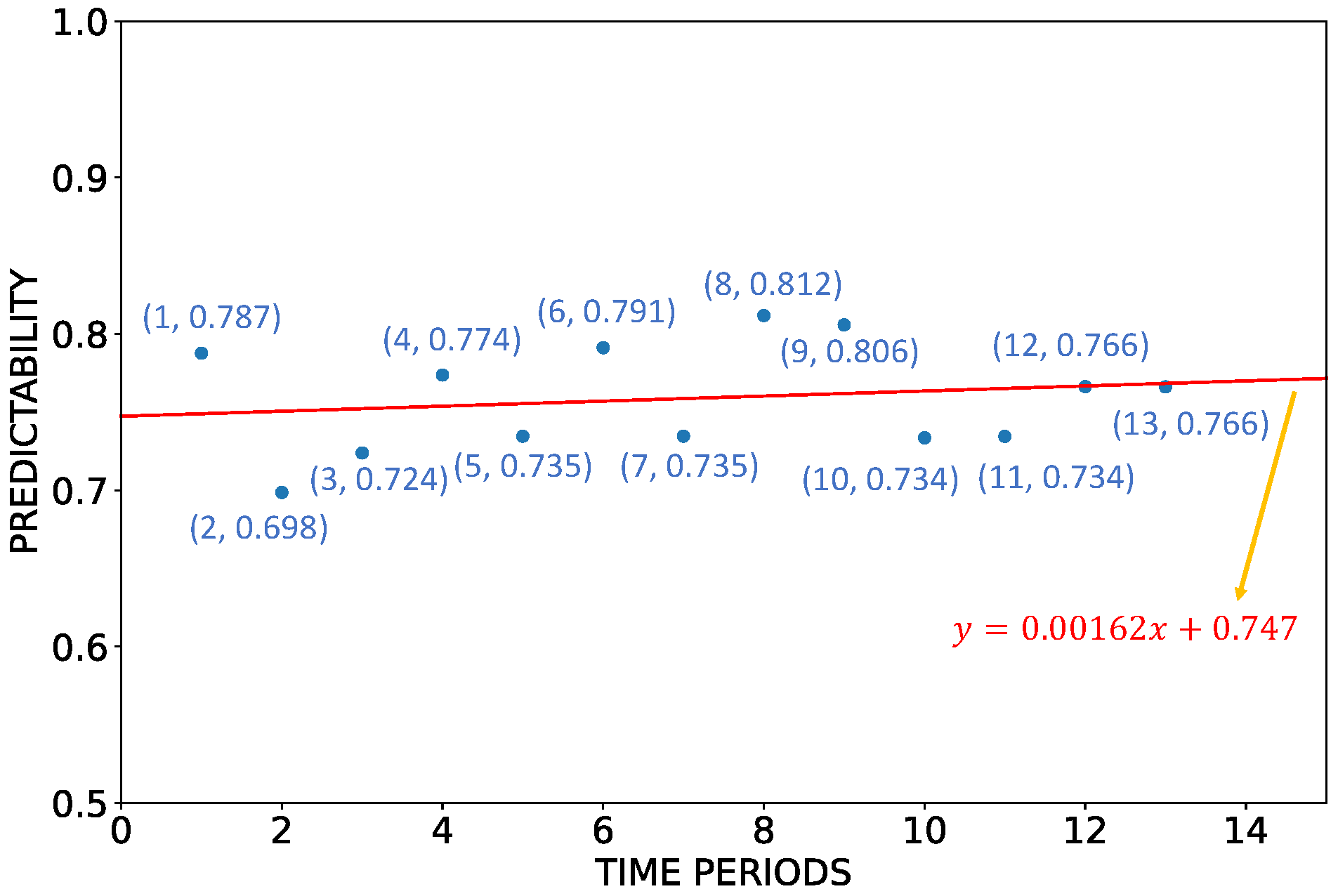


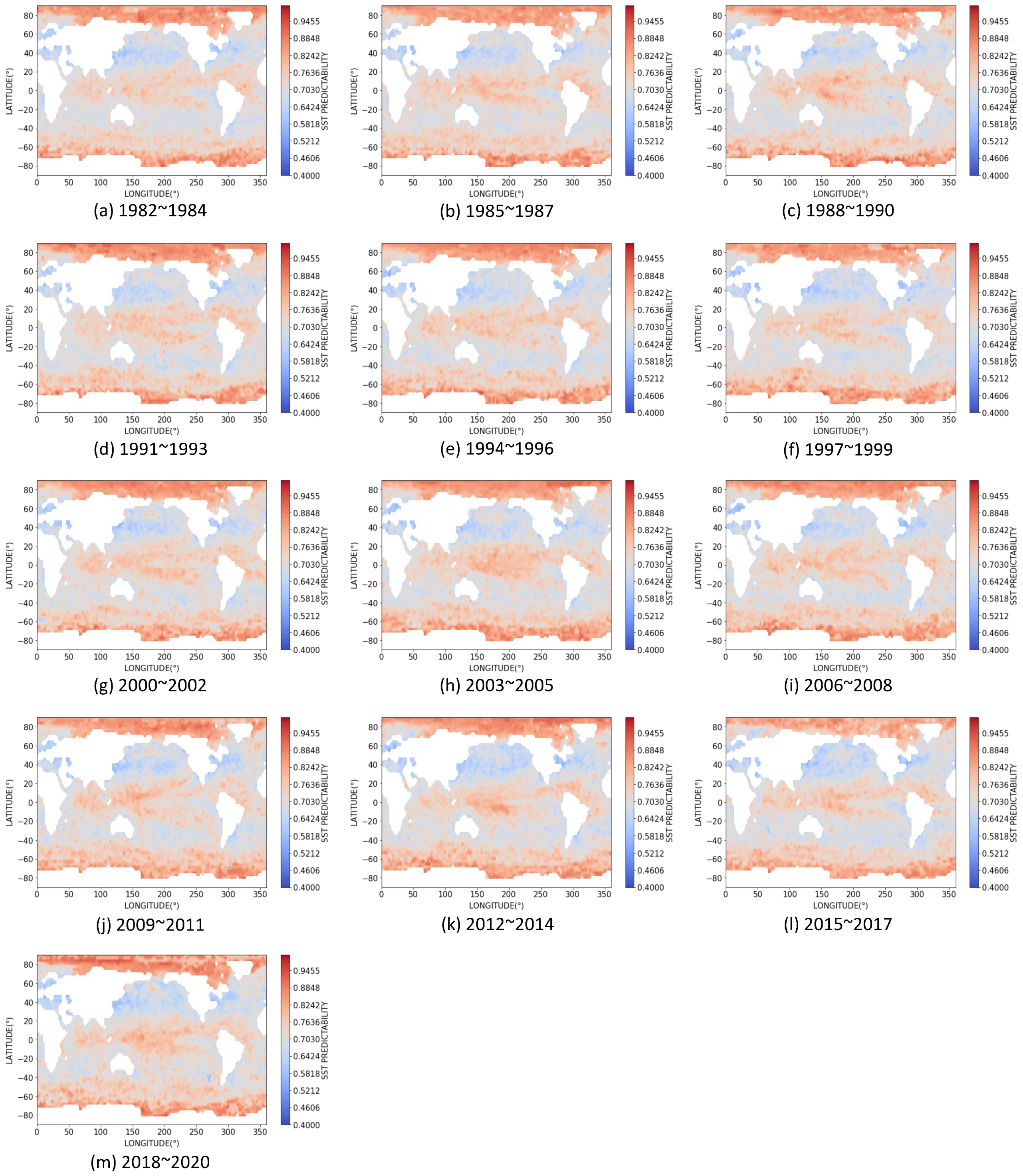
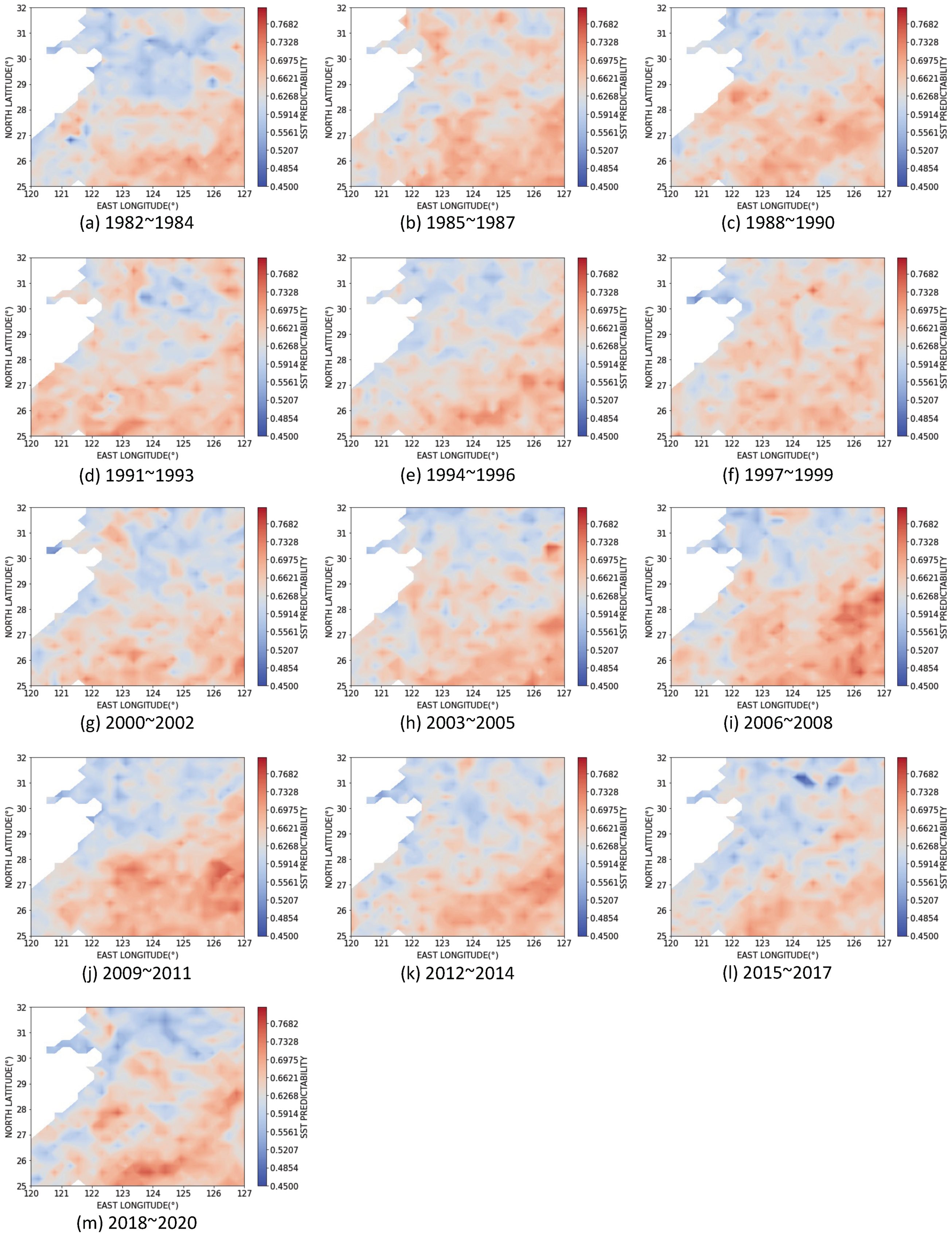

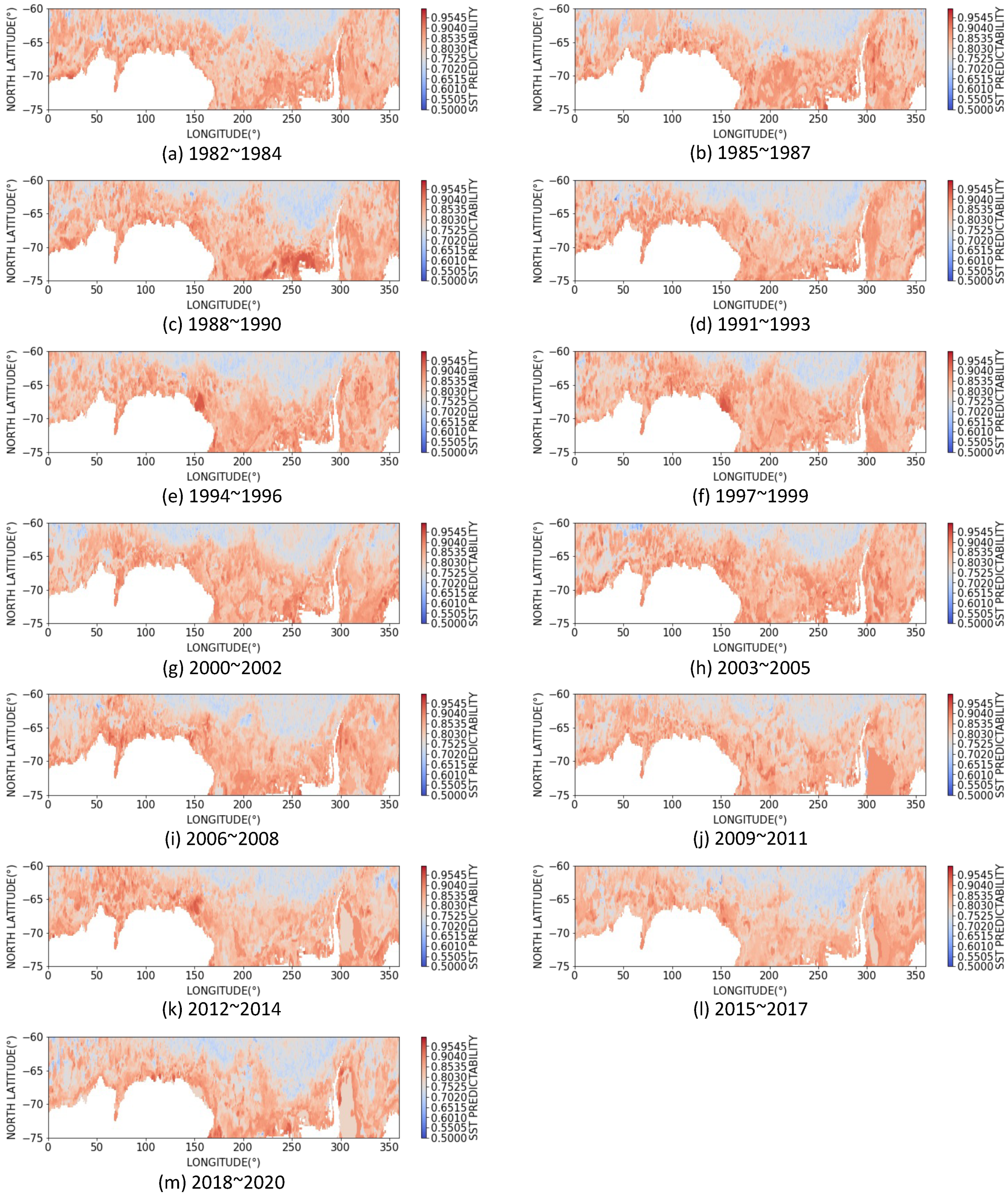
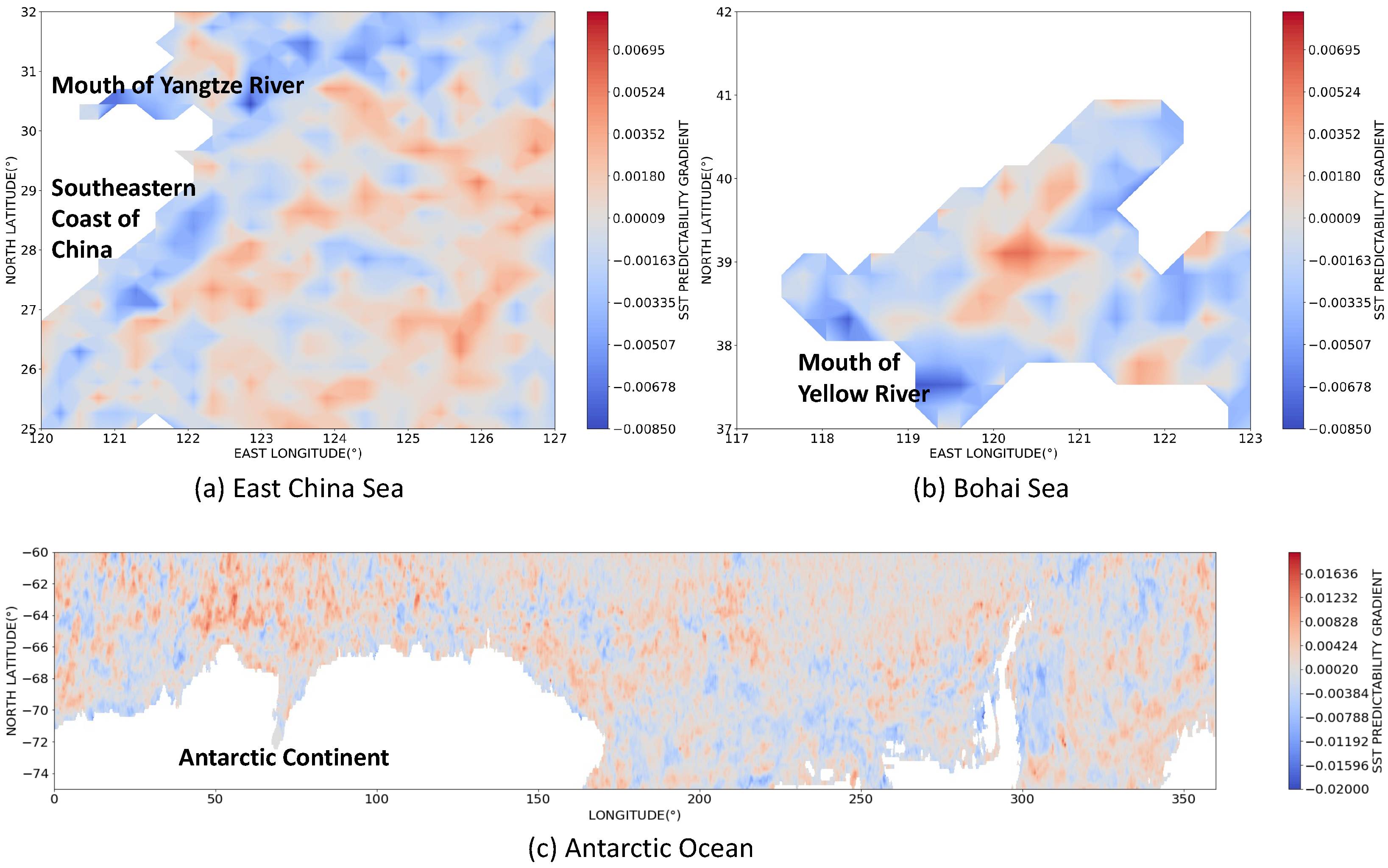
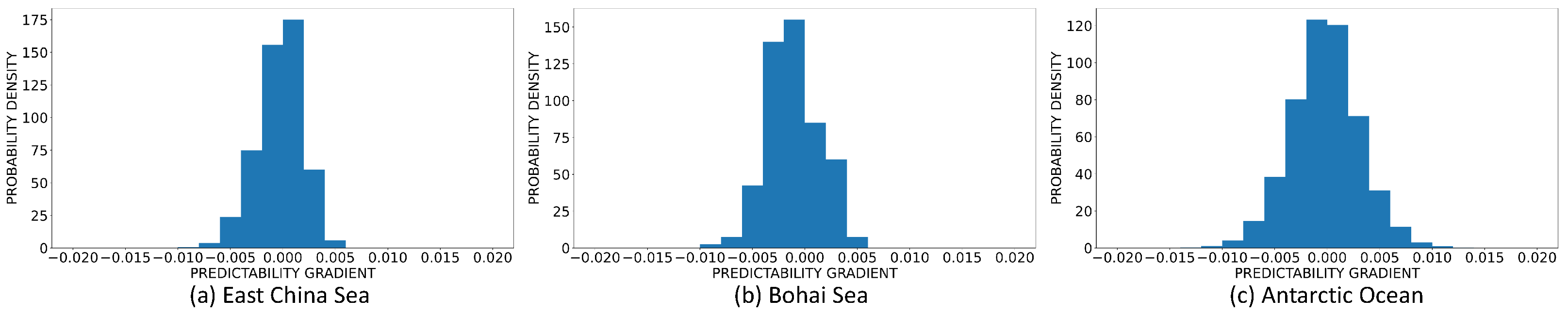
| Sea Area | Maximum Gradient | Minimum Gradient |
|---|---|---|
| East China Sea | 0.00519 | −0.00849 |
| Bohai Sea | 0.00592 | −0.00801 |
| Antarctic Ocean | 0.0162 | −0.0172 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, C.; Peng, H.; Yang, H.; Li, W.; Guan, J. On Evaluating the Predictability of Sea Surface Temperature Using Entropy. Remote Sens. 2023, 15, 1956. https://doi.org/10.3390/rs15081956
Jin C, Peng H, Yang H, Li W, Guan J. On Evaluating the Predictability of Sea Surface Temperature Using Entropy. Remote Sensing. 2023; 15(8):1956. https://doi.org/10.3390/rs15081956
Chicago/Turabian StyleJin, Chang, Han Peng, Hanchen Yang, Wengen Li, and Jihong Guan. 2023. "On Evaluating the Predictability of Sea Surface Temperature Using Entropy" Remote Sensing 15, no. 8: 1956. https://doi.org/10.3390/rs15081956
APA StyleJin, C., Peng, H., Yang, H., Li, W., & Guan, J. (2023). On Evaluating the Predictability of Sea Surface Temperature Using Entropy. Remote Sensing, 15(8), 1956. https://doi.org/10.3390/rs15081956








