Abstract
Recent advances in satellite observations of methane provide increased opportunities for inverse modeling. However, challenges exist in the satellite observation optimization and retrievals for high latitudes. In this study, we examine possibilities and challenges in the use of the total column averaged dry-air mole fractions of methane () data over land from the TROPOspheric Monitoring Instrument (TROPOMI) on board the Sentinel 5 Precursor satellite in the estimation of fluxes using the CarbonTracker Europe- (CTE-) atmospheric inverse model. We carry out simulations assimilating two retrieval products: Netherlands Institute for Space Research’s (SRON) operational and University of Bremen’s Weighting Function Modified Differential Optical Absorption Spectroscopy (WFM-DOAS). For comparison, we also carry out a simulation assimilating the ground-based surface data. Our results show smaller regional emissions in the TROPOMI inversions compared to the prior and surface inversion, although they are roughly within the range of the previous studies. The wetland emissions in summer and anthropogenic emissions in spring are lesser. The inversion results based on the two satellite datasets show many similarities in terms of spatial distribution and time series but also clear differences, especially in Canada, where emission maximum is later, when the SRON’s operational data are assimilated. The TROPOMI inversions show higher emissions from oil and gas production and coal mining from Russia and Kazakhstan. The location of hotspots in the TROPOMI inversions did not change compared to the prior, but all inversions indicated spatially more homogeneous high wetland emissions in northern Fennoscandia. In addition, we find that the regional monthly wetland emissions in the TROPOMI inversions do not correlate with the anthropogenic emissions as strongly as those in the surface inversion. The uncertainty estimates in the TROPOMI inversions are more homogeneous in space, and the regional uncertainties are comparable to the surface inversion. This indicates the potential of the TROPOMI data to better separately estimate wetland and anthropogenic emissions, as well as constrain spatial distributions. This study emphasizes the importance of quantifying and taking into account the model and retrieval uncertainties in regional levels in order to improve and derive more robust emission estimates.
1. Introduction
Methane () is the second most powerful anthropogenic greenhouse gas after carbon dioxide, contributing to ∼23% of the Earth’s atmospheric radiative forcing since 1750 [1]. Its atmospheric burden has increased by approximately 2.6 times since the pre-industrial times, reaching 1895 ppb in 2021 [2]. The atmospheric growth rate has been accelerating in recent years [3], and in 2021, the measured growth rate reached a record high since 1984 (18.3 ppb year) [2]. In the northern high latitudes (NHLs), the most recent two- to-three-year atmospheric growth is higher than the global mean [4]. The exact cause is unclear, but Arctic amplification [5,6] could potentially increase emissions from wetlands [7,8,9] and permafrost [10,11]. In addition, Russia is one of the largest oil and natural gas producers in the world, and emissions, due to their production and consumption, are expected to increase [12].
The latest report from the Global Carbon Project Methane [13] estimated that 24 Tg year (∼4% of global total) is emitted from 60°N–90°N, and 117 Tg year (∼20% of global total) is emitted from Canada, Europe and Russia together, based on the top-down estimates for 2017 [14]. The proportion of anthropogenic to total emissions varies between the regions in the NHLs. In Eurasia, the anthropogenic sources, such as those from oil and gas production and which use coal mining, agriculture and waste, are estimated to contribute over 60% of the total emissions while in Canada, the contribution is estimated to be ∼20–30% [15,16]. Although their contribution to the global total is not as significant as, e.g., mid-latitude and tropical regions, large discrepancies are found in their estimates between different inventories, models and their setups [15,16,17,18,19].
The seasonality of NHL emission is strongly driven by natural ecosystems, such as wetlands. Due to their response to temperature and water availability, emissions are high during summer and low in winter. However, even the timing of the maximum emissions varies between models by two to three months (June–August) based on land–ecosystem process-based models [20,21]. Atmospheric inverse models have been more successful in finding robust estimates [22,23,24], with the estimated maximum month being slightly later than the process-based models in general. The estimated timing of the start of the emission season is also later in the atmospheric inversions, especially in the North American continent [16,22,24].
The anthropogenic biogenic sources, such as rice cultivation, manure management, landfills and waste water treatments, can produce seasonality in emissions [25,26], as well as fossil fuel sources [22,27]. The seasonality of anthropogenic emissions is not included in the national reports, but some global inventories such as the Emissions Database for Global Atmospheric Research (EDGAR) include such seasonality [28,29]. However, as Tsuruta et al. [23] showed, the seasonality of the anthropogenic emissions derived from the atmospheric inversion could be a result of strong correlation with wetland emissions when the spatial representativeness of the observations is not sufficient. In the NHL, only a few ground-based observations are located close to the anthropogenic sources [30,31,32,33,34]. Therefore, the ground-based observations would have difficulties in constraining anthropogenic emissions well. On the other hand, recent studies showed the ability of using high-resolution satellites to detect additional sources of emissions, such as leakage from pipe lines as well as oil and gas plants [35,36,37].
Previously, satellite retrievals of total column averaged dry-air mole fractions () from SCanning Imaging Absorption spectroMeter for Atmospheric CartograpHY (SCIAMACHY) on board ENVIronmental SATellite (ENVISAT), and Thermal And Near infrared Sensor for carbon Observations–Fourier Transform Spectrometer (TANSO–FTS) on board the Greenhouse Gases Observing Satellite (GOSAT), have been used to estimate NHL emissions, e.g., [17,24,38,39,40,41,42,43,44]. However, nearly all of the studies pointed out the latitudinal and seasonal differences in between the retrievals and model estimates using prior or posterior emissions derived by assimilating the surface data. Although the magnitude varies with the underlying transport models and retrievals they used, it is often the case that model estimates show higher values in the NHLs [24,39,45]. In addition, Houweling et al. [41] pointed out that seasonal differences are also important to consider. Without correcting the regional and seasonal differences, inversions assimilating satellite data become difficult to interpret, such that the flux distribution differs unrealistically from the surface inversion [46]. Therefore, it has been a common practice to correct those differences based on surface inversion, measured from ground (e.g., TCCON data), or data before carrying out the satellite inversion, e.g., [17,40,46,47], or simply discard the high latitude data, e.g., [16,38,42,43,48]. More recently, Qu et al. [49] studied the use of the Netherlands Institute for Space Research’s (SRON) v1.0 operational TROPOspheric Monitoring Instrument (TROPOMI) data [50] in the global inversion, but they found high positive bias (i.e., model estimates are higher) in in NHLs after inversions, indicating the problem remains. However, it is challenging to quantify before carrying out the inversions exactly how many corrections should be applied as some of the signals from the satellites may indicate the fluxes that were not perfectly captured by the surface inversion.
In this study, we examine the use of the TROPOMI retrievals in estimation of NHL fluxes using an atmospheric inverse model, CarbonTracker Europe- (CTE- [51]). We use the two TROPOMI retrievals, the SRON’s operational and the University of Bremen’s Weighting Function Modified Differential Optical Absorption Spectroscopy (WFM-DOAS) [52], to examine how regional fluxes and their seasonality would be affected when those data are assimilated in the atmospheric inversion. In addition, we carry out an inversion using the surface data, and compare results with those driven by the TROPOMI data. By optimizing fluxes on grid-base at a 1° × 1° resolution, we examine whether the TROPOMI data can bring additional understanding of emission hotspots. The focus of this study is on seasonal cycles and spatial distributions for NHLs (above 45°N) in 2018.
2. Materials and Methods
2.1. CTE- Atmospheric Inverse Model
CTE- [51] is an atmospheric inverse model based on ensemble Kalman filter (EnKF) [53,54]. The flux-scaling factors are optimized by minimizing the cost function
where is a vector of prior states, is a state covariance matrix, is a vector of atmospheric observations, is an observation operator and is an observational covariance matrix.
In this study, we use the TM5 atmospheric transport model [55] as the observation operator. TM5 is run at 6° × 4° resolution globally with a 1° × 1° zoom region over Europe, which is surrounded by the intermediate 3° × 2° region [56]. The vertical resolution is 25 hybrid levels. The model is constrained by the European Centre for Medium-Range Weather Forecasts (ECMWFs) ERA5 meteorological fields [57], which are interpolated to TM5 model resolution and at 3-hourly temporal resolution. For the initial condition, 3-dimensional concentration fields are taken from the previous study assimilating surface observations [58].
The anthropogenic and biospheric fluxes (see Section 2.2) are optimized simultaneously at 1° × 1° resolution over Canada, USA, Europe and Russia, and region-wise elsewhere globally (Supplementary Figure S1). The temporal resolution is three days for the inversions using the TROPOMI data and seven days for the inversion using the surface data (see Section 2.3 and Section 2.4 for datasets). The EnKF lag-window of five is employed for both, i.e., the lag-window is 15 days for the TROPOMI inversions and five weeks for the surface inversion. Different temporal resolutions were applied as the number of data points are significantly different between the surface and TROPOMI data. Sufficient number of data points is needed to be assimilated for each time step, but the number should be limited to some extent to make the simulations computationally feasible [59]. In the current CTE-, temporal correlation is not taken into account for the ensemble members, but only to the mean states [51,53,54]. The length of lag-windows defines information content in the observation on temporal dimension, and therefore, the differences could be significant, especially when comparing short temporal changes. However, in this study, we focus on the annual-to-monthly scale seasonal changes, and leave the analysis on short-term changes in future studies. The prior uncertainties for the anthropogenic and biospheric fluxes are set as 80% and 20% of the fluxes over land and ocean regions, respectively, and assumed to be uncorrelated. The spatial correlation is defined by an exponential decay [54], with correlation length of 100 km between the 1° × 1° grid-based optimization regions, 500 km over other land regions and 900 km over ocean regions.
2.2. Prior Fluxes
Biospheric fluxes, i.e., those from wetlands, peatlands, permafrost and mineral soils, are taken from Land surface Processes and eXchanges DYPTOP (LPX-Bern) model version 1.4 [60]. The seasonal cycle of the biospheric fluxes is mainly driven by meteorological conditions, such as temperature and precipitation, and flux responses to them in each soil type. The data are provided on monthly temporal resolution. The spatial distribution depends much on soil types, where wetland and peatlands mainly emit during summer, while mineral soils can be sources or sinks. The net fluxes are often positive (i.e., emission) during summer over wet areas, and negative (i.e., sink) on dry soils. The fluxes during winter can be small, especially when the soil is frozen. The total fluxes from LPX-Bern v1.4 are 119 Tg year for 2018, accounting for 22% of the total global fluxes. For the NHLs (above 45°N), the fluxes are 22 Tg year, corresponding to 26% of the NHL regional total fluxes.
Anthropogenic fluxes, such as those from agriculture, landfills and production and use of oil, gas and coal, are taken from the EDGAR v6.0 inventory [29,61,62,63]. The data are originally at 0.1° × 0.1° × monthly resolution, and are aggregated to 1° × 1° × monthly resolution for the simulations. The emissions are high in cities, oil and gas plants, and livestock farms. The seasonality from the anthropogenic sources is often assumed to be small, although biogenic fluxes (livestock, manure and landfills) could be dependent on temperature [25,26]. The global fluxes from those sources are 374 Tg year for 2018, accounting for 70% of the global total fluxes. For NHL, the fluxes are 49 Tg year, corresponding to 58% of the NHL regional total fluxes.
Other natural sources from biomass burning, termites, geological and ocean sources are taken into account to close the global budget. We did not include fluxes from lakes and rivers specifically, although it is one of the largest uncertainties in budgets [13]. The biomass-burning emissions are taken from the Global Fire Emissions Database (GFED) v4.2 [64], emissions from termites are taken from [13], geological sources from [65] and ocean fluxes from [66]. Among those, biomass-burning emissions have seasonal cycles, i.e., monthly and annually varying data are used. For those from geological sources and ocean, the data do not have seasonality and year-to-year variations. The geological emission is scaled down from the original data to 23 Tg year based on Intergovernmental Panel on Climate Change (IPCC) AR6 WG1 report [67]. The other natural sources together contribute 8% and 16% of the global and NHL regional total fluxes for 2018, respectively.
2.3. TROPOMI
We use two retrieval products: the SRON operational product v01.02.02 and v01.03.01 (OPER) [50] and the University of Bremen’s WFM-DOAS research data v1.2 (WFMD) [52]. The OPER data are taken from the Sentinel-5P Pre-Operations Data Hub (https://s5phub.copernicus.eu/dhus/#/home, accessed on 15 December 2019), and the WFMD data from the University of Bremen’s website (https://www.iup.uni-bremen.de/carbon_ghg/products/tropomi_wfmd/index_v12.php, accessed on 15 December 2019). TROPOMI methane products include retrieved dry-air mole fraction of methane () together with its error estimate and averaging kernel.
Both data are preprocessed to exclude potentially bad-quality observations based on the product specifications from the data producers. For the WFMD data, only soundings with quality flag = 0 are considered, and for the OPER data, only soundings with QA value >= 0.5 are considered. Both data are preprocessed to 1° × 1° × daily resolution by taking the median of the grid as the observation. After preproceessing, the number of data above 45°N for 2018 is 571147 and 436547 for WFMD and OPER, respectively (see also Supplementary Figure S2). For the calculation of averaging kernel (AK), the prior and profile information are taken from the retrieval, which has the closest value to the daily median. The observational uncertainties, which are the square root of the diagonals of the matrix in Equation (1), are calculated as aggregation errors + transport model errors. The aggregating errors are calculated as the standard deviation of values in 1° × 1° × daily grid. In order to avoid using too small errors, the minimum aggregation error is set as 5 ppb. The transport model error is set as a globally uniform value of 15 ppb, i.e., the minimum observational uncertainty is theoretically 20 ppb. The WFMD data originally provide retrievals over ocean, but we use only the data over land because the validation over ocean is limited to few remote island sites globally, and to be consistent with the OPER data that provide only land observations from nadir observations. We do not apply any seasonal or latitudinal bias correction before carrying out the inversions.
To compare the retrieved data to the model estimates, modeled values are calculated using the following equation:
where N is the number of vertical layers in the retrieval, is a prior value from the retrieval at layer i, and are averaging kernel and pressure weight at retrieved layer i, respectively, and is the differences of model and prior values at layer i, i.e., . is linearly interpolated from the model layers to the retrieval layers based on the logarithmic of the pressure profiles. We did not take into account the differences in the surface pressure between TM5 and the TROPOMI retrievals specifically.
We acknowledge that the differences between the TM5 horizontal resolution and observations could affect the discrepancies between the modeled and observed values. The effect outside the zoom region could be a concern, as model resolution is coarser than the observations. Although we did not find statistically significant differences in the discrepancies within and outside of the zoom region, further examination on the effect of transport model resolution would be needed to clarify the effect.
2.4. Ground-Based Observations
2.4.1. Surface Atmospheric Data
The ground-based surface atmospheric data are taken from the global and regional observational networks, mainly those in the NOAA GLOBALVIEWplus ObsPack v3.0 dataset [68]. In addition, the observations from the NHL stations provided by the Finnish Meteorological Institute [23] and the National Institute for Environmental Studies (Monitoring of Greenhouse Gases over Siberia by Tower, Ver1.2 [32]) are used. For the assimilation and evaluation, the data are filtered according to the institution’s flags, and only those of high quality and those representing well-mixed conditions are used. For the hourly continuous observations, the data are preprocessed to daily means by taking average of 12–16 local time, except for the high altitude mountain sites from which average of 0–4 local time is taken. The observational uncertainty varies between the sites from 4.5 to 75 ppb. Globally, there are 153 stations, where the data for 2018 are available, and we used 69 stations located above 45°N in the inversion (see Figure 1 and Supplementary Figure S3 for location of the sites). The list of sites is found in Supplementary Table S1.
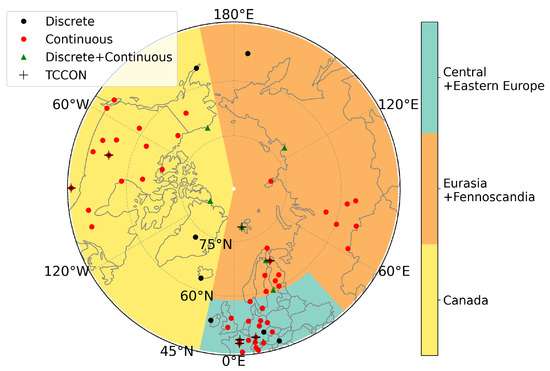
Figure 1.
Location of ground-based stations where the atmospheric data are available for 2018. The background colors illustrate the regional definition used to calculate regional emissions.
2.4.2. TCCON Data
The Total Carbon Column Observing Network (TCCON) consists of 28 operational sites globally, where the spectrum of near-infrared radiation of direct sunlight is measured with ground-based Fourier Transform Spectrometers (FTSs) [69]. TCCON is currently the main validation network for satellite observations of methane and other trace gases; the benefit of TCCON measurements is that solar-viewing FTSs measure direct sunlight and therefore the measurements are not affected by surface properties, such as albedo, or atmospheric scattering from aerosols. In this work, the TCCON data are used only for evaluations.
We use the TCCON GGG2020 data [70] from seven sites (Table 1); Ny-Ålesund (Norway) [71], Sodankylä (Finland) [72], East Trout Lake (Canada) [73], Karlsruhe (Germany) [74], Paris (France) [75], Orléans (France) [76] and Park Falls (USA) [77]. The criteria for choosing the sites are (1) the site is located at latitude above 45°N and (2) the retrieval data are available for at least six months during which there are observations from at least seven days.

Table 1.
Bias, RMSE and correlation against observations at TCCON sites, calculated from daily averages. RMSE* is calculated from anomalies of the daily averages, i.e., mean over time is subtracted from the datasets. Positive biases indicate model overestimation. For each site, the simulation with the smallest bias and RMSE and the strongest correlation are marked in bold. * The sites which have ground-based observations assimilated in InvSURF.
To temporally co-locate the from the TCCON and model, we consider the TCCON observations that are made the closest in time to the time steps of the model (hourly) and set the time limit to half an hour; if there is a TCCON observation made within ± half an hour of the model time step, the TCCON and modeled values are taken into account. The TCCON averaging kernels are applied to the model estimates [78]:
where is the averaging kernel corrected value from the model, is the TCCON prior , is the TCCON pressure weighting function, is the TCCON averaging kernel, is the model profile and is the TCCON prior profile. After applying the averaging kernel, daily means and monthly quantiles are calculated for evaluation.
2.4.3. AirCore Profile Data
AirCore is a sampling system for atmospheric gas profiling, first introduced by Karion et al. [79]. The sampler is built in a form of 100-meter-long coiled thin metal tube. It is lifted up to 35 km by a meteorological balloon from where it descends using a parachute. When ascending, the valve on the other end of the tube is open and the pressure in the tube pushes the fill gas out. During the descent, the growing ambient pressure re-fills the tube with air from all altitudes. When the sampling system reaches the ground, the valve is closed and the system is returned to laboratory for analysis within a few hours. In the narrow tube, mixing is slow and thus the air sample holds information on the vertical profile of the atmospheric gases. The air samples are analyzed using a cavity ring-down spectrometer (Picarro Inc. model G2401). We use the data from the balloon soundings launched from the Arctic Space Centre in Sodankylä, Finland [80,81,82], also hosting the Sodankylä TCCON site.
For the comparison, the model estimates are horizontally interpolated at Sodankylä TCCON coordinates (67.37°N, 26.63°E). For the time collocation, the average over the AirCore sampling time is compared to the closest hourly values in the model estimates. The statistics (bias, root-mean-square error (RMSE)) are calculated by vertically interpolating the AirCore data to model grids. In this work, the AirCore data are used only for evaluations.
2.5. Simulation Setups and Regional Definitions
In this study, we carry out three inversions for 2018 using three sets of atmospheric data: (1) TROPOMI WFMD data (InvWFMD), (2) TROPOMI OPER data (InvOPER) and (3) ground-based surface data (InvSURF). In InvWFMD and InvOPER, only the satellite data are assimilated, and are together defined as the TROPOMI inversions. We carry out global inversions, but the analyses focus on NHLs (above 45°N). The NHL is further divided into three regions as defined in Figure 1. The regional definition is chosen based on continents, emission magnitudes and seasonal cycle amplitudes, so that the regional emissions may be comparable to some extent.
3. Results
In the following sections, the term prior and posterior mole fractions are used to indicate the model estimates derived from prior and posterior fluxes, respectively. The correlation presented in the following sections are the Pearson’s correlation coefficient. We acknowledge some of the limitations using the method, and other metrics, e.g., the index of agreement [83] could represent the agreement better in some cases.
3.1. Mixing Ratios at Ground-Based Stations
This section focuses on differences between the modelled and observed mixing ratios in order to assess the inversion results. The comparison of the modeled atmospheric against surface observations generally shows ±30 ppb biases and moderate-to-high correlation (Figure 2). The agreement is generally better in InvSURF, as those data are assimilated in the inversion. In the TROPOMI inversions, although biases are not significantly larger than those in InvSURF at most of the sites ( ppb), the seasonality at the NHL sites shows overestimation of surface during March, May and June as well as in winter, and underestimation during August and September (Figure 3a). This is a general feature for all NHL sites. In all inversions, biases of greater than −40 ppb are found in Noyabrsk (NOY), Russia (63.43°E, 75.78°N). Although the number of data is limited, all models underestimate throughout the year (Supplementary Figure S4). The observation uncertainty used in InvSURF at Noyabrsk is 30 ppb, i.e., if the differences between prior and observed atmospheric are within 30 ppb × 3 = 90 ppb, the data are assimilated. The largest positive bias is found in Baranova (BAR), Russia (101.62°E, 79.28°N), in the TROPOMI inversions, where the biases in the TROPOMI inversions and the prior are more than 20 ppb, but the agreement in InvSURF is good ( ppb). At Baranova, the overestimation is prominent, except in August–October when wetland emissions are high in Siberia (Supplementary Figure S4).
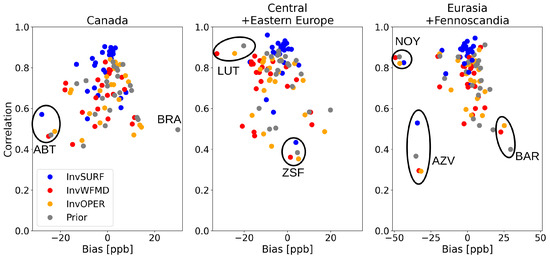
Figure 2.
Bias and correlation between modeled and observed atmospheric assimilated in InvSURF above 45°N. For InvWFMD and InvOPER, the modeled values are calculated using the posterior fluxes. Positive bias indicates model overestimation of . The regional definitions are as in Figure 1. The sites with high bias or relatively weak correlation are specified.
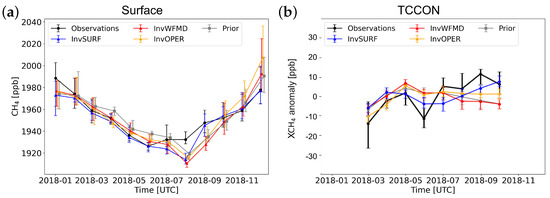
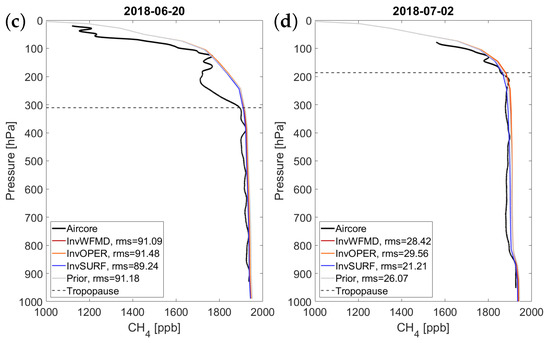
Figure 3.
Observed and modeled atmospheric at Sodankylä, which has all the ground-based datasets. Monthly median and first and third quantiles at surface station against the assimilated data in InvSURF (a), quantiles of anomaly against TCCON retrievals where annual means are subtracted (b) and profile against AirCore measurements (c,d).
Comparison to TCCON retrievals shows overestimation of the modeled mole fractions throughout the year in all inversions and at all NHL sites (Table 1, Supplementary Figure S5). The positive biases are especially high at the sites located above 50°N with more than ∼40 ppb, while other sites have a mean bias of 27 ppb. In addition, seasonality does not perfectly match the observations, especially in the TROPOMI inversions (Figure 3b, Supplementary Figure S6). In InvOPER, the correlation between the modeled and TCCON is strongest or second-strongest (Table 1), but the annual minima are approximately two months later than TCCON, except for Ny-Ålesund and East Trout Lake (Supplementary Figure S6). Unlike the other sites, the annual minima are found in early spring at those sites, which are the months affected by polar vortex. The correlation is weaker in InvWFMD, but the general feature of the seasonal cycle is similar to InvOPER. Low in spring is best captured in InvOPER, where InvWFMD and InvSURF estimates are often higher (Supplementary Figure S6). This feature is not clearly seen in the comparison to the surface observations, indicating possible effects of the upper atmosphere, e.g., polar vortex. For example, at Ny-Ålesund, the low TCCON in April is affected by polar vortex (Supplementary Figure S5), but the observed surface is not low. The model is able to capture the surface well, but not . For autumn to winter, we find similar biases to those compared to the surface observations: the anomaly exhibits lower values during autumn and higher values during winter compared to TCCON (Figure 3, Supplementary Figure S6). At Sodankylä, the seasonality in InvSURF is captured slightly better, although the summer minimum is overestimated, and underestimation during autumn is strong (Figure 3b).
In most cases, the shapes of the vertical profiles in Sodankylä from the inversions do not differ by the types of the assimilated data (surface vs. TROPOMI). The model estimates generally agree well with the observations in troposphere, where the posterior mean bias above 400 hPa is 10–12 ppb, but show higher mole fractions in the stratosphere with a mean bias of 98–103 ppb below 400 hPa. The AirCore measurements show a depleted mole fraction in the lower stratosphere, which is especially prominent during 18–20 June, but such depletion is not captured in the model estimates (Figure 3c, Supplementary Figures S7 and S8). The shape of the profile is slightly better captured in, e.g., 2 July (Figure 3d). However, the tropopause height is significantly higher then, and the overestimation of the model estimates at the lower stratosphere still exists. Based on the analysis of the air mass, those days were not in the polar vortex.
3.2. Seasonal Cycle of Emissions
The monthly fluxes in the NHL regions (Figure 1) show that the seasonal cycle amplitude is the largest in wetlands over Canada and Eurasia+Fennoscandia, with the highest emissions during summer (Figure 4). The seasonal cycle amplitude is the largest in InvSURF among the inversions in both regions (Figure 4). The TROPOMI inversions show smaller amplitudes, where summer emissions are reduced from the prior. This is expected, as prior values are higher than the retrievals during summer (Supplementary Figure S9). The wetland emissions reach their annual maximum in August in Canada and Eurasia+Fennoscandia in InvSURF, while the estimates in the TROPOMI inversion are one to two months later. In Central+Eastern Europe, the wetland emissions are small, and the seasonal cycle is distinctive from the other regions, such that it is at its minimum in summer and maximum in winter. This is because the region has little wetlands and the fluxes are dominated by mineral soils, which are mostly net sink of .
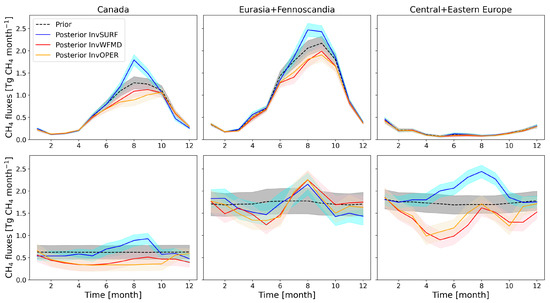
Figure 4.
Monthly biospheric (top) and anthropogenic (bottom) fluxes over the NHL regions for 2018. The shaded areas show standard deviation of the ensemble members. For priors, the uncertainty is that used in the inversion.
The anthropogenic emissions in InvSURF show clear seasonality, with maximum in summer–autumn in all regions. This indicates a strong correlation between the wetland and anthropogenic flux-scaling factors optimized in InvSURF. On the contrary, the TROPOMI inversions generally show lower emissions during spring and autumn compared to winter. The regional monthly scaling factors (posterior/prior) display the strongest correlation between biospheric and anthropogenic fluxes in InvSURF, especially in Canada (Corr = 0.73) and Eurasia+Fennoscandia (Corr = 0.54). The correlation is much weaker in the TROPOMI inversions (Corr = −0.15 and −0.38, Corr = 0.47 and −0.35). In Central+Eastern Europe, the correlation is moderate in all inversions (0.44–0.58), and the weakest in InvSURF.
In both TROPOMI inversions, high anthropogenic fluxes are found in August in Eurasia+Fennoscandia and Central+Eastern Europe. This is in line with previous studies by Berchet et al. [27], who suggested the emission peak is driven by gas production or biomass burning. For Eurasia+Fennoscandia countries, there is little seasonality in anthropogenic emissions in InvSURF, except for Russia, while the TROPOMI inversions show high August emissions also in Kazakhstan (Supplementary Figure S10). The winter posterior fluxes in the TROPOMI inversions stayed close to the prior, and this is due to the limitation of the data availability [84].
The differences between InvWFMD and InvOPER are small in Eurasia+Fennoscandia, but higher fluxes are found in InvWFMD in Canada, especially during summer–autumn (Figure 4). The differences in the regional annual totals are only ∼0.4 Tg year (Table 2), i.e., the lower summer emissions in InvOPER are partly compensated by the higher anthropogenic emissions in winter (Figure 4). In Central+Eastern Europe, the anthropogenic fluxes are higher in InvOPER nearly throughout the year, ending up with ∼1.2 Tg year differences in the regional annual total emissions (Table 2). Nevertheless, our estimates are roughly in line with the previous studies using atmospheric inverse models [15,16,22].

Table 2.
Annual emissions and their uncertainty for 2018 (Tg year). The uncertainties are calculated as standard deviation of the ensembles.
3.3. Spatial Distribution of Emissions
The spatial distribution of the posterior fluxes shows high wetland emissions in southern Alaska, Hudson Bay Lowlands (HBL) in Canada, northern Fennoscandia and West Siberian Lowlands (WSL) in Russia, as expected (Figure 5a). The differences between the TROPOMI inversions and InvSURF generally show that emissions in the TROPOMI inversions are lower in the NHLs. The regional emissions are lower in the TROPOMI inversions compared to InvSURF, especially during summer when fluxes are high (Figure 4), which results in smaller annual fluxes. However, in east Canada, the differences are small, and the estimates in the TROPOMI inversions are higher than those in InvSURF in some grid cells. The differences near the coasts and the UK are minor despite some emission hotspots. In addition, the TROPOMI inversions do not show strong emissions or higher emissions than InvSURF over northern Europe as they do over, e.g., the eastern side of Canada. This thus supports the result that the hot and dry summer of 2018 in Europe did not result in a positive anomaly in emissions [58].
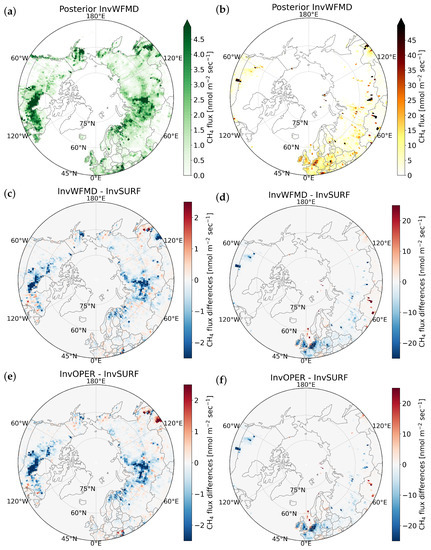
Figure 5.
Annual mean posterior fluxes for 2018 above 45°N, estimated in InvWFMD (a,b), and the differences of posterior fluxes between the TROPOMI inversions and InvSURF (c–f). The positive differences indicate higher fluxes in the TROPOMI inversions. The left column illustrates those for biospheric fluxes and right column for anthropogenic emissions. Note the differences in color scales.
The spatial anomaly (regional mean is subtracted from the estimates) over Fennoscandia shows high wetland emissions over northern Sweden, Finland and the northwest of Russia (Figure 6). The choice of the region is again somewhat arbitrary: the region is large enough to see details of spatial anomaly, but small enough to discriminate the effect of large regional (e.g., latitudinal) biases. The fluxes in Russia are higher than those in Sweden and Finland in the prior, while the regional differences are decreased in the posterior; the fluxes over Sweden and Finland are increased in InvSURF and those in Russia are decreased in the TROPOMI inversions from the prior. In other words, all inversions suggest that wetland emissions are equally high in Fennoscandia and in the northwest of Russia.
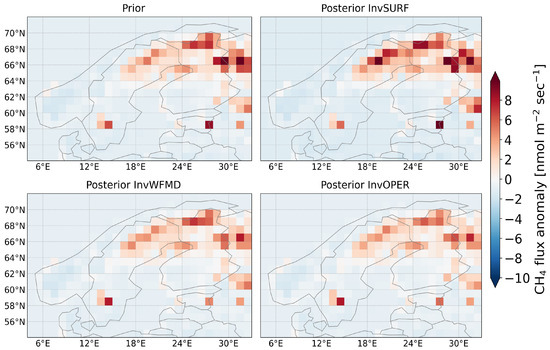
Figure 6.
Spatial anomaly of wetland fluxes in Fennoscandia, averaged over June–August 2018. The regional mean over [4°E–33°E, 54°N–72°N] is subtracted from the flux estimates.
For anthropogenic emissions, hotspots are more pronounced and limited to small regions, such that high emissions are found in cities and locations where active oil and gas production, as well as livestock farming take place. The locations of the hotspots after inversion do not change significantly from the prior (Supplementary Figure S11). InvWFMD generally shows lower emissions than InvSURF. However, the emissions in the islands of the North Sea and Kara Sea are higher in InvWFMD. In the islands of the Kara Sea, emission hotspots are found already in the prior, where EDGAR v6.0 indicates the emissions from the agricultural sector (enteric fermentation and manure management) are present. Nevertheless, in all inversions, the in situ and the TROPOMI data over islands and ice regions could have affected emissions in the Arctic ocean, but they could also be the effect of spatial correlation between the Arctic and lower-latitude ocean regions. The prior fluxes are assumed to be uncorrelated over land, ocean and ice.
The higher emissions in these regions in the TROPOMI inversions are likely to be a reason for the overestimation of mole fraction against in situ observations in Baranova, Russia (Supplementary Figure S4). We also find positive bias in winter, spring and early summer, at Storhofdi, Vestmannaeyjar, Iceland (20.29°W, 63.4°N) and Ny-Ålesund, Svalbard (11.89°E, 78.91°N) (Supplementary Figure S4). Although this is a general feature of other NHL sites (see Section 3.1), it could be an evidence for the overestimation of the anthropogenic emissions, especially during winter, considering that wetland emissions are much smaller in winter compared to the anthropogenic emissions (Figure 4).
In Kazakhstan, both TROPOMI inversions show higher anthropogenic emissions compared to InvSURF (Figure 5). This could be (1) due to the effect of spatial correlation, such that the emissions over Russia are decreased, and the surrounding lower-latitude regions are correspondingly increased, (2) latitudinal bias in the TROPOMI retrievals or the transport model or (3) actual signal in the TROPOMI inversions. In Kazakhstan, only two in situ sites are available in the southeast (lower than 45°N), and therefore, the TROPOMI data probably have stronger constraints on the emissions. Note that Kazakhstan is not optimized on grid bases (Supplementary Figure S1).
3.4. Uncertainty Estimates
The uncertainty reductions in the TROPOMI inversion are spatially more homogeneous, while the reductions are highest near the observational stations in InvSURF (Figure 7). This indicates that the good spatial coverage of the satellite data reduces the flux uncertainty on locations where the surface data are not available. Uncertainty reductions are often high in the regions where prior fluxes (and their uncertainties) are high and observations with small observational uncertainties are located. Such regions are found near anthropogenic sources in Europe, mid southern Canada and near biospheric sources in the HBL area in Canada and northern Europe (Figure 7). However, despite high biospheric emissions in Eurasian wetland regions, uncertainty reduction rates are not exceptionally high in all inversions. The uncertainty reductions in the Arctic ocean and some southern regions are high as those regions are optimized region-wise, i.e., there are more observations per optimization region as constraints.
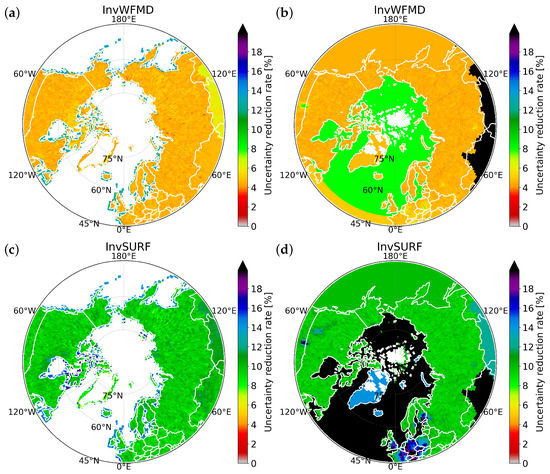
Figure 7.
Annual mean uncertainty reduction rates above 45°N for 2018 estimated in InvWFMD (a,b) and InvSURF (c,d). The left columns (a,c) are for the biospheric fluxes and right columns (b,d) for the anthropogenic emissions.
The grid-wise uncertainty reduction rate is smaller in the TROPOMI inversions in general (Figure 7), although the regional posterior uncertainties are comparable to InvSURF in the NHL regions, and lower than InvSURF on a global level (Table 2). There could be a few explanations for this. First, temporal optimization resolution is different in InvSURF (seven days) and the TROPOMI inversions (three days). Since our assimilated data in the TROPOMI inversions are aggregated to 1° × 1° × daily resolution (see Section 2.3), the number of observations may be twice larger in the surface inversion at the location where surface data are available (in situ data are also aggregated to daily values). In addition, the observational uncertainty for the satellite data is generally higher than those for the surface data. In general, when observational uncertainty is greater, there will be less influence on the optimization, leading to a smaller uncertainty reduction rate.
Secondly, we did not use so-called localization [54]. Localization gives limits on how far in distance the observations can influence the fluxes. The grid-wise uncertainty reduction close to the observation location would be higher if the localization was used. When it is switched off, the uncertainty reduction is likely to be spread more equally in space, especially when observation uncertainties are correlated. This also indicates potentially high spatial correlation in the observation uncertainties, which is not properly taken into account in the inversions.
4. Discussion
4.1. Effect of Assimilated Data in Seasonal Cycle of Fluxes
Annual maximum emissions from wetlands are found to be between August and September in this study. However, the in situ flux measurements in NHLs based on, e.g., the Eddy covariance technique often show earlier summer maximum, most commonly from June to July in North America [85,86], and from July to August in Eurasia [34,87,88]. Several reasons can be considered for the late summer maximums, especially in the TROPOMI inversions. One is the uncertainty in the transport model, e.g., long-range and vertical transport, and seasonality of prescribed atmospheric sinks. The posterior surface-mixing ratios agree well with the observations in InvSURF, which may infer that the tropospheric seasonality is fairly well captured over the NHL regions. The shape of the vertical profiles do not differ much between the inversions, and the comparisons to AirCore measurements also suggest that there may be significant transport model errors in the upper atmosphere. Based on the comparison to the TCCON data, the underestimation of during late summer and autumn, is found in InvSURF. It indicates that the upper atmospheric biases in the model could in fact cause later summer maximum emissions. Several studies indicate that the polar vortex needs to be properly modeled and taken into account for a good estimation of in spring [24,46,89,90,91,92], but the reasons for the summer biases in the NHLs need to be studied further.
Lindqvist et al. [84] showed that the OPER data have significant seasonal differences compared to TCCON at NHL sites. At East Trout Lake, the range of maximum to minimum differences for OPER is almost 100 ppb (from about +50 ppb in early spring to -50 ppb in summer and autumn) [84]. This could potentially be one of the reasons for the late seasonal maximum in wetland emissions in Canada in InvOPER. In the other regions, emission seasonality in InvWFMD and InvOPER are similar, possibly indicating that not only seasonal differences, but also systematic differences between the retrievals and model estimates affect the seasonality of the fluxes.
We did not correct spatial (latitudinal) differences against InvSURF or TCCON data before carrying out the TROPOMI inversion, as suggested by, e.g., Houweling et al. [41,47]. We find that the estimated from InvSURF and the TROPOMI inversions have seasonal and latitudinal differences, where from InvSURF is, e.g., ∼20 ppb higher than the WFMD data in August 2018 (Supplementary Figure S12). This is probably one of the reasons why the TROPOMI inversions show lower flux estimates at the NHLs; the inversion tried to reduce emissions to match the values. The NHL flux seasonality is dominated by wetland emissions, and therefore this also caused the lower summer fluxes and thus smaller seasonal cycle amplitude. As can be seen from Table 2, global emissions are higher in the TROPOMI inversions compared to InvSURF, indicating higher emissions in the Southern latitudes.
4.2. Seasonal Cycle of Anthropogenic Fluxes
The seasonality in the anthropogenic emissions cannot be validated as reliable independent data are not available for the whole region. However, the seasonality in InvSURF can be the result of a correlation with the wetland emissions. Although we assumed no correlation in the prior fluxes between the anthropogenic and wetland fluxes, the inversion increases emissions from both sources during summer with strong correlation between the anthropogenic and wetland flux-scaling factors, especially for Canada and Eurasia+Fennoscandia (see Section 3.2). As many in situ sites are located at remote locations to anthropogenic sources in these regions, the ability of the data to constrain anthropogenic fluxes is questionable.
The satellite data are more equally spread within the region, and can have a stronger influence on the anthropogenic fluxes, except in winter. Both the TROPOMI inversions show high emissions in August in Eurasia. Anthropogenic emissions in this study include those from fossil fuels, agriculture and waste management. A similar peak was found in Berchet et al. [59], where they speculated the cause to be either oil and gas extraction or wildfires. We did not optimize biomass-burning emissions, i.e., not categorized as anthropogenic emissions, but according to GFED, the biomass-burning emissions peaked in August in Russia in 2018 with about 0.4 Tg month. This corresponds to ∼30% of the regional anthropogenic emissions. The August peak is found also in Kazakhstan, where the anthropogenic emissions are dominated by the energy sector, especially from coal [93]. Although further investigation is needed by, e.g., carrying out inversion for other years, the higher emissions in the TROPOMI inversions may have indicated additional emissions not detected by surface networks.
Our Eurasian+Fennoscandia anthropogenic emissions show an increase from February to March in InvWFMD. This is in line with previous studies by Thompson et al. [22], Berchet et al. [27], suggesting that the emission in spring could increase due to gas production. Although we do not see such a peak in the Russian anthropogenic emissions, but rather in Kazakhstan’s (Supplementary Figure S10), our results show increases in Russia where oil and gas, as well as coal emissions in the prior are high (Supplementary Figures S13 and S14). Those locations nicely correlate with oil fields in Sakha Republic and coal basins in the Siberian regions, such as Irkutsk and Kansk-Achinsk. We do not find such peak in InvOPER and InvSURF. In InvSURF, this is probably due to the lack of observations near the hotspots (see Figure 1). The observations at Yakutsk would have helped better quantify the emissions [27], but the observations were not available for 2018. In InvOPER, there are observational gaps during spring close to those emission locations. However, further analysis is needed to conclude whether the gap has been spatially extensive enough, and whether some other causes, such as spatial and temporal biases in the retrievals, caused the differences in InvWFMD.
4.3. Confidence in TCCON Comparison
Our posterior mean estimates show systematic differences of ∼20–50 ppb against the TCCON data. In the previous studies, e.g., Tsuruta et al. [51], we did not find as strong a bias as in this study. The larger biases found in this study may be due to underlying fluxes, stratospheric chemistry and using different versions of the TCCON data. The systematic differences are greater than the monthly mean differences between simulations at most of the sites. This questions our analysis on the seasonality of , whether the differences between the simulations are significant. Nevertheless, the differences in the seasonality are driven by the assimilated data and inversion setups related to the assimilation, such as observational uncertainty.
We also found that agreement between the model estimates and TCCON data could differ significantly by using different versions of the TCCON data. Out results show that the correlation at Park Falls are very weak and weakest among the NHL sites (Table 1) when the GGG2020 data are used. However, when the model estimates are compared to the earlier version, GGG2014, the correlation is much stronger (0.6–0.7).
While TCCON provides useful information for the evaluation of the satellite data and the model results, the TCCON data also have uncertainties [69,70]. Therefore, the evaluation with the TCCON data may not tell the whole story, and analysis should be continued using other inversion-independent data for a more comprehensive examination of whether an estimated posterior seasonal cycle is realistic.
4.4. Observational Uncertainty Used in Inversions
We find that the grid-wise uncertainty reduction rate is smaller in the TROPOMI inversions in general, although regional uncertainty reduction is comparable to InvSURF. We assume observations to be uncorrelated in space and time in order to apply the ensemble square root filter [54,94]. However, since the uncertainties in the satellite data could be highly correlated, the assumption may have not been valid. The TROPOMI retrievals errors may be dependent region-wise over, e.g., snow surface, but uncorrelated with snow-free surface [84]. They also showed the differences in the biases between snow and snow-free surface, i.e., the errors are probably dependent region-wise over, e.g., snow surface, but uncorrelated with snow-free surface. In addition, the observational uncertainty includes transport model uncertainty, which can be correlated based on, e.g., parameterization and input meteorological data.
The assumption of uncorrelated errors has been commonly used in atmospheric inverse models, e.g., [13,46,59,95]. As discussed by Houweling et al. [47] and references therein, accounting for the satellite data uncertainty is challenging. In this study, we assumed total observation uncertainty (transport model error + retrieval error) to be at a minimum of 20 ppb, and did not correct the spatiotemporal patterns of the errors before inversion. The uncertainty is within the range of those used in other satellite inversions using SCIAMACHY and GOSAT, e.g., [13,17,24,42,46,96,97]. However, considering that the errors may be correlated, non-diagonal terms should have been compensated by higher-standard deviations in the diagonal approximation. The TROPOMI data are assumed to have better precision than previous generation satellites, e.g., [90,98,99], but further examination is needed to quantify the appropriate uncertainty range to be used in the inversions.
5. Conclusions
This study examined the impacts of using the TROPOMI data in the estimation of the NHL emissions using the CTE- atmospheric inverse model for the first time. Our analysis showed that the assimilation of the TROPOMI data can be useful in the estimation of NHL regional budgets and seasonality. However, some differences to the inversion using surface ground-based data are found, indicating that more detailed analysis of the cause is needed on regional levels and in time to better quantify the regional budgets from various data sources.
The transport model biases need to be improved to better estimate the profiles. We found large differences in the profiles compared to AirCore measurementsm especially in the stratosphere. However, further study is needed to identify the exact causes; potential causes are transport (e.g., stratosphere–troposphere exchange), stratospheric chemistry and model resolutions. We also found limited improvements in the agreement with the observations from prior to posterior at surface stations. Although it was within the range of expected values (i.e., within pre-defined observational uncertainty), the exact cause and way to be improved are to be explored. Additional ground-based measurements, especially those providing information about vertical profiles and anthropogenic sources would be required. In addition, the differences between model and retrievals in the NHLs are not specific only to the retrievals or models used in this study, and therefore, a community effort is needed.
While the biases in the retrieved and modeled total column are not fully quantified, the partial column retrievals [100,101,102,103] could be potential alternatives to be used in the atmospheric inverse models. Tropospheric agrees generally well between the model and ground-based observations, and is more directly affected by the emission magnitude compared to the stratosphere. Although it would introduce additional source of uncertainty by introducing additional parameters in the retrievals, the tropospheric partial column data may have smaller biases and differences to the models. This would not only serve as constraints to the atmospheric inversions, but also for the evaluation of the transport model biases and emission estimates from the inversions and bottom-up estimates.
In addition, we carried out the inversion only for one year, but the features found in this paper may not be consistent for other years. The year 2018 may have not been optimal as the TROPOMI’s nominal operational mode only started in the end of April 2018, and therefore, the beginning of 2018 has reduced data density and potentially also reduced quality. There are also continuous updates on the retrieval products [104,105]. We will continue investigating by carrying out simulations for extended periods of time and using the new retrieval products.
For future work, we recommend using various versions of the TROPOMI data in the atmospheric inversion, but either WFMD or updated versions of OPER data could perhaps be better-suited than OPER v1.0 data for estimation of seasonality in the northern North America. The observational uncertainty could be increased, or the observational error correlation could be taken into account. In addition, the comparison to inversion using surface data should be continued as well as the evaluation of the model estimates using various assimilation-independent datasets.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/rs15061620/s1, Table S1: List of surface observation sites used in InvSURF, and located above 45 °N. The altitudes are the sampling heights from which atmospheric is sampled in TM5. Observation Uncertainty (Obs. Unc.) is used to define diagonal values in the observation covariance matrix. Data type is categorized into two: discrete (D) and continuous (C). Table S2: Statistics of agreements between the modelled and observed values at surface stations located above 45 °N. The statistics are calculated for the assimilated data. Positive values in bias means overestimation of model estimates. For sites with same sitecode, additional information (contributor and/or data type) is given. For details for the site information, please see Table S1. Figure S1: Optimization regions used in CTE- simulations. Region in black is optimized on 1° × 1° grid bases, and elsewhere region-wise. (top) global, and (bottom) zoom over NHL and Europe. Figure S2: Number of the preprocessed TROPOMI observations and monthly average assimilation rates for InvWFMD and InvOPER. Figure S3: Location of the surface atmospheric observational sites at the TM5 non-zoom region (top) and TM5 zoom regions (bottom). The underlying colour maps illustrate the horizontal resolution of TM5. Figure S4: Monthly median of observed and modelled atmospheric at Baranova, Noyabrsk, Storhofdi and Ny-Ålesund. The error bars illustrate the first and third quantiles. The quantiles are calculated from assimilated data in InvSURF. Note the differences in y-axis. Figure S5: Daily averaged at the NHL TCCON sites. Figure S6: Monthly median anomalies of observed and modelled atmospheric at the NHL TCCON sites. The error bars illustrate the first and third quantiles. The quantiles are calculated from daily averaged data. Figure S7: Observed (AirCore) and modelled profiles at Sodankylä. Figure S8: Differences between modelled and AirCore profiles up to tropopause at Sodankylä. Figure S9: Monthly mean differences between prior and TROPOMI retrievals in August 2018. Positive values indicate the higher prior values compared to the retrievals. Figure S10: Monthly anthropogenic fluxes per country and above 45°N. Figure S11: Annual mean posterior fluxes above 45°N for 2018. estimated in prior (a,b), and the differences between InvWFMD and prior (c,d) and those between InvWFMD and InvOPER (e,f). The left columns are for biospheric fluxes and right columns for anthropogenic emissions. The positive differences indicates higher fluxes from InvWFMD. Note the differences in color scales. Figure S12: Monthly mean (solid line) and standard deviation (dashed lines) of the differences between the posterior and the WFMD retrieval data for August 2018. Figure S13: Monthly mean differences in estimated anthropogenic emissions between March 2018 and February 2018 from InvWFMD. Figure S14: Annual average emissions from coal (left) and oil and gas industry (right) from the prior (EDGAR v6.0).
Author Contributions
The research is designed by A.T. and T.A.; model code is developed by A.T. with help from L.B. and J.H.; analysis and evaluation is conducted by A.T. together with T.A., H.L., E.K., T.K. and L.B.; TROPOMI data are processed for CTE- by H.L. and E.K.; TROPOMI WFMD data are provided by O.S. and M.B. (Michael Buchwitz); X.L. provided surface atmospheric data by NOAA; Sodankylä AirCore data are provided by R.K. and H.C.; TCCON data are provided by R.K. (Sodankylä), D.W. (East Trout Lake), M.B. (Matthias Buschmann) (Ny Ålesund), B.H. (Karlsruhe), J.N. (Orléans), C.R. (Park Falls) and Y.T. (Paris); A.T. prepared the original draft; E.K., H.L., T.K., L.B., J.H., O.S., M.B. (Michael Buchwitz), X.L., R.K., M.B. (Matthias Buschmann), B.H., J.N., Y.T., D.W., J.T. and T.A. contributed to manuscript preperation; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Academy of Finland (307331 UPFORMET, 351311 GHGSUPER, 281255 ICOS Finland, 345531 FIRI 2022-2025, 331829 CitySpot), European Space Agency (ESRIN Contract No: 4000125046/18/I-NB ESA-MethEO, ESRIN Contract No: 4000126450/19/I-NB GHG-CCI+), and European Union (776810 EU-H2020 VERIFY, 958927 EU-H2020 CoCO2).
Data Availability Statement
All the model results, inputs and code will be provided on request from the corresponding author (Aki Tsuruta, aki.tsuruta@fmi.fi).
Acknowledgments
We thank Sebastian Lienert, Jurek Müller and Fortunat Joos, Climate and Environmental Physics, Physics Institute, University of Bern, for providing the prior wetland fluxes from LPX-Bern v1.4 model. We are grateful for Agencia Estatal de Meteorología (AEMET), CSIRO Oceans and Atmosphere, Dirección Meteorológica de Chile (DMC), Environment and Climate Change Canada (ECCC), the Environmental and Chemical Processes Laboratory, University of Crete (ECPL/UOC), the Hungarian Meteorological Service (HMS), the Institute for Atmospheric Sciences and Climate (ISAC), Laboratoire des Sciences du Climat et de l’Environnement (LSCE), the National Institute of Water and Atmospheric Research Ltd. (NIWA), the Environment Division Global Environment and Marine Department Japan Meteorological Agency (JMA), the Main Geophysical Observatory (MGO), Meteorology, Climatology and Geophysics Agency Indonesia (BMKG), the Max Planck Institute for Biogeochemistry, National Institute for Environmental Studies (NIES), Netherlands Organisation for Applied Scientific Research (TNO), Norwegian Institute for Air Research (NILU), Ricerca sul Sistema Energetico (RSE), the Swiss Federal Laboratories for Materials Science and Technology (EMPA), Umweltbundesamt Germany/Federal Environmental Agency (UBA), Umweltbundesamt Austria/Environment Agency Austria (EAA) as the data provider for Sonnblick, the Southern African Weather Service (SAWS), University of Bristol (UNIVBRIS), University of Exeter, University of Urbino (UNIURB) and University of Wisconsin-Madison (UofWI) for performing high-quality CH4 measurements at global sites and making them available through the Obspack, GAW-WDCGG and personal communications. The TCCON data were obtained from the TCCON Data Archive hosted by CaltechDATA at https://tccondata.org (accessed on 2 May 2022). The Paris TCCON site has received funding from Sorbonne Université, the French research center CNRS, the French space agency CNES and Région Île-de-France.
Conflicts of Interest
The authors declare no conflict of interest. Furthermore, the funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Etminan, M.; Myhre, G.; Highwood, E.J.; Shine, K.P. Radiative Forcing of Carbon Dioxide, Methane, and Nitrous Oxide: A Significant Revision of the Methane Radiative Forcing. Geophys. Res. Lett. 2016, 43, 12614–12623. [Google Scholar] [CrossRef]
- Lan, X.; Thoning, K.; Dlugokencky, E. Trends in Globally-Averaged CH4, N2O, and SF6 Determined from NOAA Global Monitoring Laboratory Measurements; Version 2022-10; Global Monitoring Laboratory: Boulder, CO, USA, 2022. [CrossRef]
- Tollefson, J. Scientists raise alarm over ‘dangerously fast’ growth in atmospheric methane. Nature 2022. [Google Scholar] [CrossRef]
- Lan, X.; Nisbet, E.G.; Dlugokencky, E.J.; Michel, S.E. What do we know about the global methane budget? Results from four decades of atmospheric CH4 observations and the way forward. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2021, 379, 20200440. [Google Scholar] [CrossRef] [PubMed]
- Meredith, M.; Sommerkorn, M.; Cassotta, S.; Derksen, C.; Ekaykin, A.; Hollowed, A.; Kofinas, G.; Mackintosh, A.; Melbourne-Thomas, J.; Muelbert, M.; et al. Polar Regions. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.O., Roberts, D., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2019. [Google Scholar]
- Rantanen, M.; Karpechko, A.Y.; Lipponen, A.; Nordling, K.; Hyvärinen, O.; Ruosteenoja, K.; Vihma, T.; Laaksonen, A. The Arctic has warmed nearly four times faster than the globe since 1979. Commun. Earth Environ. 2022, 3, 1–10. [Google Scholar] [CrossRef]
- Helbig, M.; Quinton, W.L.; Sonnentag, O. Warmer spring conditions increase annual methane emissions from a boreal peat landscape with sporadic permafrost. Environ. Res. Lett. 2017, 12, 115009. [Google Scholar] [CrossRef]
- Tarnocai, C. The effect of climate change on carbon in Canadian peatlands. Glob. Planet. Chang. 2006, 53, 222–232. [Google Scholar] [CrossRef]
- Zhang, Z.; Zimmermann, N.E.; Stenke, A.; Li, X.; Hodson, E.L.; Zhu, G.; Huang, C.; Poulter, B. Emerging role of wetland methane emissions in driving 21st century climate change. Proc. Natl. Acad. Sci. USA 2017, 114, 9647–9652. [Google Scholar] [CrossRef]
- Schuur, E.a.G.; McGuire, A.D.; Schädel, C.; Grosse, G.; Harden, J.W.; Hayes, D.J.; Hugelius, G.; Koven, C.D.; Kuhry, P.; Lawrence, D.M.; et al. Climate change and the permafrost carbon feedback. Nature 2015, 520, 171–179. [Google Scholar] [CrossRef]
- Miner, K.R.; Turetsky, M.R.; Malina, E.; Bartsch, A.; Tamminen, J.; McGuire, A.D.; Fix, A.; Sweeney, C.; Elder, C.D.; Miller, C.E. Permafrost carbon emissions in a changing Arctic. Nat. Rev. Earth Environ. 2022, 3, 55–67. [Google Scholar] [CrossRef]
- Ahmed, M.; Shuai, C.; Ahmed, M. Analysis of energy consumption and greenhouse gas emissions trend in China, India, the USA, and Russia. Int. J. Environ. Sci. Technol. 2022. [Google Scholar] [CrossRef]
- Saunois, M.; Stavert, A.R.; Poulter, B.; Bousquet, P.; Canadell, J.G.; Jackson, R.B.; Raymond, P.A.; Dlugokencky, E.J.; Houweling, S.; Patra, P.K.; et al. The Global Methane Budget 2000–2017. Earth Syst. Sci. Data 2020, 12, 1561–1623. [Google Scholar] [CrossRef]
- Jackson, R.B.; Saunois, M.; Bousquet, P.; Canadell, J.G.; Poulter, B.; Stavert, A.R.; Bergamaschi, P.; Niwa, Y.; Segers, A.; Tsuruta, A. Increasing anthropogenic methane emissions arise equally from agricultural and fossil fuel sources. Environ. Res. Lett. 2020, 15, 071002. [Google Scholar] [CrossRef]
- Stavert, A.R.; Saunois, M.; Canadell, J.G.; Poulter, B.; Jackson, R.B.; Regnier, P.; Lauerwald, R.; Raymond, P.A.; Allen, G.H.; Patra, P.K.; et al. Regional trends and drivers of the global methane budget. Glob. Chang. Biol. 2022, 28, 182–200. [Google Scholar] [CrossRef]
- Baray, S.; Jacob, D.J.; Maasakkers, J.D.; Sheng, J.X.; Sulprizio, M.P.; Jones, D.B.A.; Bloom, A.A.; McLaren, R. Estimating 2010–2015 anthropogenic and natural methane emissions in Canada using ECCC surface and GOSAT satellite observations. Atmos. Chem. Phys. 2021, 21, 18101–18121. [Google Scholar] [CrossRef]
- Wang, F.; Maksyutov, S.; Tsuruta, A.; Janardanan, R.; Ito, A.; Sasakawa, M.; Machida, T.; Morino, I.; Yoshida, Y.; Kaiser, J.W.; et al. Methane Emission Estimates by the Global High-Resolution Inverse Model Using National Inventories. Remote Sens. 2019, 11, 2489. [Google Scholar] [CrossRef]
- Chan, E.; Worthy, D.E.J.; Chan, D.; Ishizawa, M.; Moran, M.D.; Delcloo, A.; Vogel, F. Eight-Year Estimates of Methane Emissions from Oil and Gas Operations in Western Canada Are Nearly Twice Those Reported in Inventories. Environ. Sci. Technol. 2020, 54, 14899–14909. [Google Scholar] [CrossRef]
- Sheng, J.X.; Jacob, D.J.; Maasakkers, J.D.; Sulprizio, M.P.; Zavala-Araiza, D.; Hamburg, S.P. A high-resolution (0.1° × 0.1°) inventory of methane emissions from Canadian and Mexican oil and gas systems. Atmos. Environ. 2017, 158, 211–215. [Google Scholar] [CrossRef]
- Bohn, T.J.; Melton, J.R.; Ito, A.; Kleinen, T.; Spahni, R.; Stocker, B.D.; Zhang, B.; Zhu, X.; Schroeder, R.; Glagolev, M.V.; et al. WETCHIMP-WSL: Intercomparison of wetland methane emissions models over West Siberia. Biogeosciences 2015, 12, 3321–3349. [Google Scholar] [CrossRef]
- Bloom, A.A.; Bowman, K.W.; Lee, M.; Turner, A.J.; Schroeder, R.; Worden, J.R.; Weidner, R.; McDonald, K.C.; Jacob, D.J. A global wetland methane emissions and uncertainty dataset for atmospheric chemical transport models (WetCHARTs version 1.0). Geosci. Model Dev. 2017, 10, 2141–2156. [Google Scholar] [CrossRef]
- Thompson, R.L.; Sasakawa, M.; Machida, T.; Aalto, T.; Worthy, D.; Lavric, J.V.; Lund Myhre, C.; Stohl, A. Methane fluxes in the high northern latitudes for 2005–2013 estimated using a Bayesian atmospheric inversion. Atmos. Chem. Phys. 2017, 17, 3553–3572. [Google Scholar] [CrossRef]
- Tsuruta, A.; Aalto, T.; Backman, L.; Krol, M.C.; Peters, W.; Lienert, S.; Joos, F.; Miller, P.A.; Zhang, W.; Laurila, T.; et al. Methane budget estimates in Finland from the CarbonTracker Europe-CH4 data assimilation system. Tellus B Chem. Phys. Meteorol. 2019, 71, 1565030. [Google Scholar] [CrossRef]
- Zhang, Y.; Jacob, D.J.; Lu, X.; Maasakkers, J.D.; Scarpelli, T.R.; Sheng, J.X.; Shen, L.; Qu, Z.; Sulprizio, M.P.; Chang, J.; et al. Attribution of the accelerating increase in atmospheric methane during 2010–2018 by inverse analysis of GOSAT observations. Atmos. Chem. Phys. 2021, 21, 3643–3666. [Google Scholar] [CrossRef]
- Arndt, C.; Leytem, A.B.; Hristov, A.N.; Zavala-Araiza, D.; Cativiela, J.P.; Conley, S.; Daube, C.; Faloona, I.; Herndon, S.C. Short-term methane emissions from 2 dairy farms in California estimated by different measurement techniques and US Environmental Protection Agency inventory methodology: A case study. J. Dairy Sci. 2018, 101, 11461–11479. [Google Scholar] [CrossRef]
- Cárdenas, A.; Ammon, C.; Schumacher, B.; Stinner, W.; Herrmann, C.; Schneider, M.; Weinrich, S.; Fischer, P.; Amon, T.; Amon, B. Methane emissions from the storage of liquid dairy manure: Influences of season, temperature and storage duration. Waste Manag. 2021, 121, 393–402. [Google Scholar] [CrossRef]
- Berchet, A.; Pison, I.; Chevallier, F.; Paris, J.D.; Bousquet, P.; Bonne, J.L.; Arshinov, M.Y.; Belan, B.D.; Cressot, C.; Davydov, D.K.; et al. Natural and anthropogenic methane fluxes in Eurasia: A mesoscale quantification by generalized atmospheric inversion. Biogeosciences 2015, 12, 5393–5414. [Google Scholar] [CrossRef]
- Janssens-Maenhout, G.; Crippa, M.; Guizzardi, D.; Muntean, M.; Schaaf, E.; Dentener, F.; Bergamaschi, P.; Pagliari, V.; Olivier, J.G.J.; Peters, J.A.H.W.; et al. EDGAR v4.3.2 Global Atlas of the three major greenhouse gas emissions for the period 1970–2012. Earth Syst. Sci. Data 2019, 11, 959–1002. [Google Scholar] [CrossRef]
- Crippa, M.; Solazzo, E.; Huang, G.; Guizzardi, D.; Koffi, E.; Muntean, M.; Schieberle, C.; Friedrich, R.; Janssens-Maenhout, G. High resolution temporal profiles in the Emissions Database for Global Atmospheric Research. Sci. Data 2020, 7, 121. [Google Scholar] [CrossRef] [PubMed]
- Canadian Environmental Sustainability Indicators: Greenhouse Gas Concentrations. 2021. Available online: www.canada.ca/en/environment-climate-change/services/environmental-indicators/greenhouse-gasconcentrations.html (accessed on 5 August 2022).
- ICOS-EU Atmosphere Stations. Available online: https://www.icos-cp.eu/observations/atmosphere/stations (accessed on 29 August 2022).
- Sasakawa, M.; Shimoyama, K.; Machida, T.; Tsuda, N.; Suto, H.; Arshinov, M.; Davydov, D.; Fofonov, A.; Krasnov, O.; Saeki, T.; et al. Continuous measurements of methane from a tower network over Siberia. Tellus B 2010, 62, 403–416. [Google Scholar] [CrossRef]
- Winderlich, J.; Chen, H.; Gerbig, C.; Seifert, T.; Kolle, O.; Lavrič, J.V.; Kaiser, C.; Höfer, A.; Heimann, M. Continuous low-maintenance CO2/CH4/H2O measurements at the Zotino Tall Tower Observatory (ZOTTO) in Central Siberia. Atmos. Meas. Tech. 2010, 3, 1113–1128. [Google Scholar] [CrossRef]
- Tuovinen, J.P.; Aurela, M.; Hatakka, J.; Räsänen, A.; Virtanen, T.; Mikola, J.; Ivakhov, V.; Kondratyev, V.; Laurila, T. Interpreting eddy covariance data from heterogeneous Siberian tundra: Land-cover-specific methane fluxes and spatial representativeness. Biogeosciences 2019, 16, 255–274. [Google Scholar] [CrossRef]
- Zhang, Y.; Gautam, R.; Pandey, S.; Omara, M.; Maasakkers, J.D.; Sadavarte, P.; Lyon, D.; Nesser, H.; Sulprizio, M.P.; Varon, D.J.; et al. Quantifying methane emissions from the largest oil-producing basin in the United States from space. Sci. Adv. 2020, 6, eaaz5120. [Google Scholar] [CrossRef]
- Ialongo, I.; Stepanova, N.; Hakkarainen, J.; Virta, H.; Gritsenko, D. Satellite-based estimates of nitrogen oxide and methane emissions from gas flaring and oil production activities in Sakha Republic, Russia. Atmos. Environ. X 2021, 11, 100114. [Google Scholar] [CrossRef]
- Schneising, O.; Buchwitz, M.; Reuter, M.; Vanselow, S.; Bovensmann, H.; Burrows, J.P. Remote sensing of methane leakage from natural gas and petroleum systems revisited. Atmos. Chem. Phys. 2020, 20, 9169–9182. [Google Scholar] [CrossRef]
- Alexe, M.; Bergamaschi, P.; Segers, A.; Detmers, R.; Butz, A.; Hasekamp, O.; Guerlet, S.; Parker, R.; Boesch, H.; Frankenberg, C.; et al. Inverse modelling of CH4 emissions for 2010–2011 using different satellite retrieval products from GOSAT and SCIAMACHY. Atmos. Chem. Phys. 2015, 15, 113–133. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Frankenberg, C.; Meirink, J.F.; Krol, M.; Dentener, F.; Wagner, T.; Platt, U.; Kaplan, J.O.; Körner, S.; Heimann, M.; et al. Satellite chartography of atmospheric methane from SCIAMACHY on board ENVISAT: 2. Evaluation based on inverse model simulations. J. Geophys. Res. 2007, 112, D02304. [Google Scholar] [CrossRef]
- Pandey, S.; Houweling, S.; Krol, M.; Aben, I.; Chevallier, F.; Dlugokencky, E.J.; Gatti, L.V.; Gloor, E.; Miller, J.B.; Detmers, R.; et al. Inverse modeling of GOSAT-retrieved ratios of total column CH4 and CO2 for 2009 and 2010. Atmos. Chem. Phys. 2016, 16, 5043–5062. [Google Scholar] [CrossRef]
- Houweling, S.; Krol, M.; Bergamaschi, P.; Frankenberg, C.; Dlugokencky, E.J.; Morino, I.; Notholt, J.; Sherlock, V.; Wunch, D.; Beck, V.; et al. A multi-year methane inversion using SCIAMACHY, accounting for systematic errors using TCCON measurements. Atmos. Chem. Phys. 2014, 14, 3991–4012. [Google Scholar] [CrossRef]
- Maasakkers, J.D.; Jacob, D.J.; Sulprizio, M.P.; Scarpelli, T.R.; Nesser, H.; Sheng, J.X.; Zhang, Y.; Hersher, M.; Bloom, A.A.; Bowman, K.W.; et al. Global distribution of methane emissions, emission trends, and OH concentrations and trends inferred from an inversion of GOSAT satellite data for 2010–2015. Atmos. Chem. Phys. 2019, 19, 7859–7881. [Google Scholar] [CrossRef]
- Lu, X.; Jacob, D.J.; Wang, H.; Maasakkers, J.D.; Zhang, Y.; Scarpelli, T.R.; Shen, L.; Qu, Z.; Sulprizio, M.P.; Nesser, H.; et al. Methane emissions in the United States, Canada, and Mexico: Evaluation of national methane emission inventories and 2010–2017 sectoral trends by inverse analysis of in situ (GLOBALVIEWplus CH4 ObsPack) and satellite (GOSAT) atmospheric observations. Atmos. Chem. Phys. 2022, 22, 395–418. [Google Scholar] [CrossRef]
- Wecht, K.J.; Jacob, D.J.; Frankenberg, C.; Jiang, Z.; Blake, D.R. Mapping of North American methane emissions with high spatial resolution by inversion of SCIAMACHY satellite data. J. Geophys. Res. Atmos. 2014, 119, 7741–7756. [Google Scholar] [CrossRef]
- Turner, A.J.; Jacob, D.J.; Wecht, K.J.; Maasakkers, J.D.; Lundgren, E.; Andrews, A.E.; Biraud, S.C.; Boesch, H.; Bowman, K.W.; Deutscher, N.M.; et al. Estimating global and North American methane emissions with high spatial resolution using GOSAT satellite data. Atmos. Chem. Phys. 2015, 15, 7049–7069. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Frankenberg, C.; Meirink, J.F.; Krol, M.; Villani, M.G.; Houweling, S.; Dentener, F.; Dlugokencky, E.J.; Miller, J.B.; Gatti, L.V.; et al. Inverse modeling of global and regional CH4 emissions using SCIAMACHY satellite retrievals. J. Geophys. Res. 2009, 114, D22301. [Google Scholar] [CrossRef]
- Houweling, S.; Bergamaschi, P.; Chevallier, F.; Heimann, M.; Kaminski, T.; Krol, M.; Michalak, A.M.; Patra, P. Global inverse modeling of CH4 sources and sinks: An overview of methods. Atmos. Chem. Phys. 2017, 17, 235–256. [Google Scholar] [CrossRef]
- Maasakkers, J.D.; Jacob, D.J.; Sulprizio, M.P.; Scarpelli, T.R.; Nesser, H.; Sheng, J.; Zhang, Y.; Lu, X.; Bloom, A.A.; Bowman, K.W.; et al. 2010–2015 North American methane emissions, sectoral contributions, and trends: A high-resolution inversion of GOSAT observations of atmospheric methane. Atmos. Chem. Phys. 2021, 21, 4339–4356. [Google Scholar] [CrossRef]
- Qu, Z.; Jacob, D.J.; Shen, L.; Lu, X.; Zhang, Y.; Scarpelli, T.R.; Nesser, H.; Sulprizio, M.P.; Maasakkers, J.D.; Bloom, A.A.; et al. Global distribution of methane emissions: A comparative inverse analysis of observations from the TROPOMI and GOSAT satellite instruments. Atmos. Chem. Phys. 2021, 21, 14159–14175. [Google Scholar] [CrossRef]
- Hu, H.; Hasekamp, O.; Butz, A.; Galli, A.; Landgraf, J.; de Brugh, J.A.; Borsdorff, T.; Scheepmaker, R.; Aben, I. The operational methane retrieval algorithm for TROPOMI. Atmos. Meas. Tech. 2016, 9, 5423–5440. [Google Scholar] [CrossRef]
- Tsuruta, A.; Aalto, T.; Backman, L.; Hakkarainen, J.; Laan-Luijkx, I.T.v.d.; Krol, M.C.; Spahni, R.; Houweling, S.; Laine, M.; Dlugokencky, E.; et al. Global methane emission estimates for 2000–2012 from CarbonTracker Europe-CH4 v1.0. Geosci. Model Dev. 2017, 10, 1261–1289. [Google Scholar] [CrossRef]
- Schneising, O.; Buchwitz, M.; Reuter, M.; Bovensmann, H.; Burrows, J.P.; Borsdorff, T.; Deutscher, N.M.; Feist, D.G.; Griffith, D.W.T.; Hase, F.; et al. A scientific algorithm to simultaneously retrieve carbon monoxide and methane from TROPOMI onboard Sentinel-5 Precursor. Atmos. Meas. Tech. 2019, 12, 6771–6802. [Google Scholar] [CrossRef]
- van der Laan-Luijkx, I.T.; van der Velde, I.R.; van der Veen, E.; Tsuruta, A.; Stanislawska, K.; Babenhauserheide, A.; Zhang, H.F.; Liu, Y.; He, W.; Chen, H.; et al. The CarbonTracker Data Assimilation Shell (CTDAS) v1.0: Implementation and global carbon balance 2001–2015. Geosci. Model Dev. 2017, 10, 2785–2800. [Google Scholar] [CrossRef]
- Peters, W.; Miller, J.B.; Whitaker, J.; Denning, A.S.; Hirsch, A.; Krol, M.C.; Zupanski, D.; Bruhwiler, L.; Tans, P.P. An ensemble data assimilation system to estimate CO2 surface fluxes from atmospheric trace gas observations. J. Geophys. Res. 2005, 110, D24304. [Google Scholar] [CrossRef]
- Krol, M.; Houweling, S.; Bregman, B.; Broek, M.v.d.; Segers, A.; Velthoven, P.v.; Peters, W.; Dentener, F.; Bergamaschi, P. The two-way nested global chemistry-transport zoom model TM5: Algorithm and applications. Atmos. Chem. Phys. 2005, 5, 417–432. [Google Scholar] [CrossRef]
- Tsuruta, A.; Aalto, T.; Backman, L.; Peters, W.; Krol, M.; van der Laan-Luijkx, I.T.; Hatakka, J.; Heikkinen, P.; Dlugokencky, E.J.; Spahni, R. Evaluating atmospheric methane inversion model results for Pallas, northern Finland. Boreal Environ. Res. 2015, 20, 506–525. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Thompson, R.L.; Groot Zwaaftink, C.D.; Brunner, D.; Tsuruta, A.; Aalto, T.; Raivonen, M.; Crippa, M.; Solazzo, E.; Guizzardi, D.; Regnier, P.; et al. Effects of extreme meteorological conditions in 2018 on European methane emissions estimated using atmospheric inversions. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2022, 380, 20200443. [Google Scholar] [CrossRef]
- Berchet, A.; Sollum, E.; Thompson, R.L.; Pison, I.; Thanwerdas, J.; Broquet, G.; Chevallier, F.; Aalto, T.; Berchet, A.; Bergamaschi, P.; et al. The Community Inversion Framework v1.0: A unified system for atmospheric inversion studies. Geosci. Model Dev. 2021, 14, 5331–5354. [Google Scholar] [CrossRef]
- Lienert, S.; Joos, F. A Bayesian ensemble data assimilation to constrain model parameters and land-use carbon emissions. Biogeosciences 2018, 15, 2909–2930. [Google Scholar] [CrossRef]
- Crippa, M.; Guizzardi, D.; Schaaf, E.; Solazzo, E.; Muntean, M.; Monforti-Ferrario, F.; Olivier, J.; Vignati, E. Fossil CO2 and GHG emissions of all world countries—2021 Report. In Technical Report, EDGAR—Emissions Database for Global Atmospheric Research; United Nations Environment Programme: Nairobi, Kenya, 2022; in prep. [Google Scholar]
- Crippa, M.; Guizzardi, D.; Muntean, M.; Schaaf, E.; Lo Vullo, E.; Solazzo, E.; Monforti-Ferrario, F.; Olivier, J.; Vignati, E. EDGAR v6.0 Greenhouse Gas Emissions. European Commission, Joint Research Centre (JRC) [Dataset] PID. Available online: http://data.europa.eu/89h/97a67d67-c62e-4826-b873-9d972c4f670b (accessed on 1 July 2021).
- EDGARv6.0. Available online: https://edgar.jrc.ec.europa.eu/index.php/dataset_ghg60 (accessed on 24 September 2022).
- Giglio, L.; Randerson, J.T.; van der Werf, G.R. Analysis of daily, monthly, and annual burned area using the fourth-generation global fire emissions database (GFED4). J. Geophys. Res. Biogeosci. 2013, 118, 317–328. [Google Scholar] [CrossRef]
- Etiope, G.; Ciotoli, G.; Schwietzke, S.; Schoell, M. Gridded maps of geological methane emissions and their isotopic signature. Earth Syst. Sci. Data 2019, 11, 1–22. [Google Scholar] [CrossRef]
- Weber, T.; Wiseman, N.A.; Kock, A. Global ocean methane emissions dominated by shallow coastal waters. Nat. Commun. 2019, 10, 4584. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.; et al. (Eds.) Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2021: The Physical Science Basis; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Schuldt, K.N.; Aalto, T.; Andrews, A.; Aoki, S.; Arduini, J.; Baier, B.; Bergamaschi, P.; Biermann, T.; Biraud, S.C.; Boenisch, H.; et al. Multi-Laboratory Compilation of Atmospheric Methane Data for the Period 1983–2020; obspack_ch4_1_GLOBALVIEWplus_v3.0_2021-05-07; NOAA Earth System Research Laboratory, Global Monitoring Laboratory: Boulder, CO, USA, 2021. [CrossRef]
- Wunch, D.; Toon, G.C.; Blavier, J.F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.T.; Sherlock, V.; Wennberg, P.O. The Total Carbon Column Observing Network. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 2087–2112. [Google Scholar] [CrossRef]
- Laughner, J.L.; Roche, S.; Kiel, M.; Toon, G.C.; Wunch, D.; Baier, B.C.; Biraud, S.; Chen, H.; Kivi, R.; Laemmel, T.; et al. A new algorithm to generate a priori trace gas profiles for the GGG2020 retrieval algorithm. Atmos. Meas. Tech. Discuss. 2022; 1–41, in preprint. [Google Scholar] [CrossRef]
- Buschmann, M.; Petri, C.; Palm, M.; Warneke, T.; Notholt, J.; Engineers, A.S. TCCON Data from Ny-Alesund, Svalbard, Norway, Release GGG2020R0; TCCON Data archive; CaltechDATA, California Institute of Technology: Pasadena, CA, USA, 2022. [Google Scholar] [CrossRef]
- Kivi, R.; Heikkinen, P.; Kyro, E. TCCON Data from Sodankyla, Finland, Release GGG2020R0; TCCON data archive; CaltechDATA, California Institute of Technology: Pasadena, CA, USA, 2017. [Google Scholar] [CrossRef]
- Wunch, D.; Mendonca, J.; Colebatch, O.; Allen, N.; Blavier, J.F.L.; Kunz, K.; Roche, S.; Hedelius, J.; Neufeld, G.; Springett, S.; et al. TCCON Data from East Trout Lake, Canada, Release GGG2020R0; TCCON data archive; CaltechDATA, California Institute of Technology: Pasadena, CA, USA, 2020. [Google Scholar] [CrossRef]
- Hase, F.; Blumenstock, T.; Dohe, S.; Groß, J.; Kiel, M. TCCON data from Karlsruhe, Germany, Release GGG2020R0; TCCON data archive; CaltechDATA, California Institute of Technology: Pasadena, CA, USA, 2017. [Google Scholar] [CrossRef]
- Te, Y.; Jeseck, P.; Janssen, C. TCCON Data from Paris, France, Release GGG2020R0; TCCON data archive; CaltechDATA, California Institute of Technology: Pasadena, CA, USA, 2017. [Google Scholar] [CrossRef]
- Warneke, T.; Messerschmidt, J.; Notholt, J.; Weinzierl, C.; Deutscher, N.; Petri, C.; Grupe, P.; Vuillemin, C.; Truong, F.; Schmidt, M.; et al. TCCON Data from Orleans, France, Release GGG2020R0; TCCON data archive; CaltechDATA, California Institute of Technology: Pasadena, CA, USA, 2017. [Google Scholar] [CrossRef]
- Wennberg, P.O.; Roehl, C.; Wunch, D.; Toon, G.C.; Blavier, J.F.; Washenfelder, R.; Keppel-Aleks, G.; Allen, N.; Ayers, J. TCCON Data from Park Falls, Wisconsin, USA; TCCON data archive; CaltechDATA, California Institute of Technology: Pasadena, CA, USA, 2017. [Google Scholar] [CrossRef]
- Rodgers, C.D.; Connor, B.J. Intercomparison of remote sounding instruments. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Karion, A.; Sweeney, C.; Tans, P.; Newberger, T. AirCore: An Innovative Atmospheric Sampling System. J. Atmos. Ocean. Technol. 2010, 27, 1839–1853. [Google Scholar] [CrossRef]
- Paul, D.; Chen, H.; Been, H.A.; Kivi, R.; Meijer, H.A.J. Radiocarbon analysis of stratospheric CO2 retrieved from AirCore sampling. Atmos. Meas. Tech. 2016, 9, 4997–5006. [Google Scholar] [CrossRef]
- Sha, M.K.; De Mazière, M.; Notholt, J.; Blumenstock, T.; Chen, H.; Dehn, A.; Griffith, D.W.T.; Hase, F.; Heikkinen, P.; Hermans, C.; et al. Intercomparison of low- and high-resolution infrared spectrometers for ground-based solar remote sensing measurements of total column concentrations of CO2, CH4, and CO. Atmos. Meas. Tech. 2020, 13, 4791–4839. [Google Scholar] [CrossRef]
- Tu, Q.; Hase, F.; Blumenstock, T.; Kivi, R.; Heikkinen, P.; Sha, M.K.; Raffalski, U.; Landgraf, J.; Lorente, A.; Borsdorff, T.; et al. Intercomparison of atmospheric CO2 and CH4 abundances on regional scales in boreal areas using Copernicus Atmosphere Monitoring Service (CAMS) analysis, COllaborative Carbon Column Observing Network (COCCON) spectrometers, and Sentinel-5 Precursor satellite observations. Atmos. Meas. Tech. 2020, 13, 4751–4771. [Google Scholar] [CrossRef]
- Willmott, C.J. On the Validation of Models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Lindqvist, H.; Kivimäki, E.; Tsuruta, A.; Karppinen, T.; Backman, L.; Schneising, O.; Buchwitz, M.; Lorente Delgado, A.; Kivi, R.; Chen, H.; et al. Evaluation of Sentinel 5P TROPOMI methane observations at high latitudes. Remote Sensing, 2023; in preperation. [Google Scholar]
- Hanis, K.L.; Tenuta, M.; Amiro, B.D.; Papakyriakou, T.N. Seasonal dynamics of methane emissions from a subarctic fen in the Hudson Bay Lowlands. Biogeosciences 2013, 10, 4465–4479. [Google Scholar] [CrossRef]
- Long, K.D.; Flanagan, L.B.; Cai, T. Diurnal and seasonal variation in methane emissions in a northern Canadian peatland measured by eddy covariance. Glob. Chang. Biol. 2010, 16, 2420–2435. [Google Scholar] [CrossRef]
- Rinne, J.; Tuittila, E.S.; Peltola, O.; Li, X.; Raivonen, M.; Alekseychik, P.; Haapanala, S.; Pihlatie, M.; Aurela, M.; Mammarella, I.; et al. Temporal Variation of Ecosystem Scale Methane Emission From a Boreal Fen in Relation to Temperature, Water Table Position, and Carbon Dioxide Fluxes. Glob. Biogeochem. Cycles 2018, 32, 1087–1106. [Google Scholar] [CrossRef]
- Rinne, J.; Tuovinen, J.P.; Klemedtsson, L.; Aurela, M.; Holst, J.; Lohila, A.; Weslien, P.; Vestin, P.; Łakomiec, P.; Peichl, M.; et al. Effect of the 2018 European drought on methane and carbon dioxide exchange of northern mire ecosystems. Philos. Trans. R. Soc. B Biol. Sci. 2020, 375, 20190517. [Google Scholar] [CrossRef]
- Kivimäki, E.; Lindqvist, H.; Hakkarainen, J.; Laine, M.; Sussmann, R.; Tsuruta, A.; Detmers, R.; Deutscher, N.M.; Dlugokencky, E.J.; Hase, F.; et al. Evaluation and Analysis of the Seasonal Cycle and Variability of the Trend from GOSAT Methane Retrievals. Remote Sens. 2019, 11, 882. [Google Scholar] [CrossRef]
- Lorente, A.; Borsdorff, T.; Butz, A.; Hasekamp, O.; aan de Brugh, J.; Schneider, A.; Wu, L.; Hase, F.; Kivi, R.; Wunch, D.; et al. Methane retrieved from TROPOMI: Improvement of the data product and validation of the first 2 years of measurements. Atmos. Meas. Tech. 2021, 14, 665–684. [Google Scholar] [CrossRef]
- Stanevich, I.; Jones, D.B.A.; Strong, K.; Parker, R.J.; Boesch, H.; Wunch, D.; Notholt, J.; Petri, C.; Warneke, T.; Sussmann, R.; et al. Characterizing model errors in chemical transport modeling of methane: Impact of model resolution in versions v9-02 of GEOS-Chem and v35j of its adjoint model. Geosci. Model Dev. 2020, 13, 3839–3862. [Google Scholar] [CrossRef]
- Ostler, A.; Sussmann, R.; Patra, P.K.; Houweling, S.; Bruine, M.D.; Stiller, G.P.; Haenel, F.J.; Plieninger, J.; Bousquet, P.; Yin, Y.; et al. Evaluation of column-averaged methane in models and TCCON with a focus on the stratosphere. Atmos. Meas. Tech. 2016, 9, 4843–4859. [Google Scholar] [CrossRef]
- Zhumabayev, D.; Bakdolotov, A.; De Miglio, R.; Litvak, V.; Baibakisheva, A.; Sarbassov, Y.; Baigarin, K. Kazakhstan’s Road to Net Zero GHG Emissions; NUR: Nur-Sultan, Kazakhstan, 2022. [Google Scholar]
- Whitaker, J.S.; Hamill, T.M. Ensemble Data Assimilation without Perturbed Observations. Mon. Wea. Rev. 2002, 130, 1913–1924. [Google Scholar] [CrossRef]
- Thompson, R.L.; Stohl, A. FLEXINVERT: An atmospheric Bayesian inversion framework for determining surface fluxes of trace species using an optimized grid. Geosci. Model Dev. 2014, 7, 2223–2242. [Google Scholar] [CrossRef]
- Meirink, J.F.; Eskes, H.J.; Goede, A.P.H. Sensitivity analysis of methane emissions derived from SCIAMACHY observations through inverse modelling. Atmos. Chem. Phys. 2006, 6, 1275–1292. [Google Scholar] [CrossRef]
- Monteil, G.; Houweling, S.; Butz, A.; Guerlet, S.; Schepers, D.; Hasekamp, O.; Frankenberg, C.; Scheepmaker, R.; Aben, I.; Röckmann, T. Comparison of CH4 inversions based on 15 months of GOSAT and SCIAMACHY observations. J. Geophys. Res. Atmos. 2013, 118, 11–807. [Google Scholar] [CrossRef]
- Buchwitz, M.; Reuter, M.; Schneising, O.; Boesch, H.; Guerlet, S.; Dils, B.; Aben, I.; Armante, R.; Bergamaschi, P.; Blumenstock, T.; et al. The Greenhouse Gas Climate Change Initiative (GHG-CCI): Comparison and quality assessment of near-surface-sensitive satellite-derived CO2 and CH4 global data sets. Remote Sens. Environ. 2015, 162, 344–362. [Google Scholar] [CrossRef]
- Dils, B.; Buchwitz, M.; Reuter, M.; Schneising, O.; Boesch, H.; Parker, R.; Guerlet, S.; Aben, I.; Blumenstock, T.; Burrows, J.P.; et al. The Greenhouse Gas Climate Change Initiative (GHG-CCI): Comparative validation of GHG-CCI SCIAMACHY/ENVISAT and TANSO-FTS/GOSAT CO2 and CH4 retrieval algorithm products with measurements from the TCCON. Atmos. Meas. Tech. 2014, 7, 1723–1744. [Google Scholar] [CrossRef]
- Saad, K.M.; Wunch, D.; Toon, G.C.; Bernath, P.; Boone, C.; Connor, B.; Deutscher, N.M.; Griffith, D.W.T.; Kivi, R.; Notholt, J.; et al. Derivation of tropospheric methane from TCCON CH4 and HF total column observations. Atmos. Meas. Tech. 2014, 7, 2907–2918. [Google Scholar] [CrossRef]
- Wang, Z.; Deutscher, N.M.; Warneke, T.; Notholt, J.; Dils, B.; Griffith, D.W.T.; Schmidt, M.; Ramonet, M.; Gerbig, C. Retrieval of tropospheric column-averaged CH4 mole fraction by solar absorption FTIR-spectrometry using N2O as a proxy. Atmos. Meas. Tech. 2014, 7, 3295–3305. [Google Scholar] [CrossRef]
- Holl, G.; Walker, K.A.; Conway, S.; Saitoh, N.; Boone, C.D.; Strong, K.; Drummond, J.R. Methane cross-validation between three Fourier transform spectrometers: SCISAT ACE-FTS, GOSAT TANSO-FTS, and ground-based FTS measurements in the Canadian high Arctic. Atmos. Meas. Tech. 2016, 9, 1961–1980. [Google Scholar] [CrossRef]
- Kuze, A.; Kikuchi, N.; Kataoka, F.; Suto, H.; Shiomi, K.; Kondo, Y. Detection of Methane Emission from a Local Source Using GOSAT Target Observations. Remote Sens. 2020, 12, 267. [Google Scholar] [CrossRef]
- Hachmeister, J.; Schneising, O.; Buchwitz, M.; Lorente, A.; Borsdorff, T.; Burrows, J.P.; Notholt, J.; Buschmann, M. On the influence of underlying elevation data on Sentinel-5 Precursor TROPOMI satellite methane retrievals over Greenland. Atmos. Meas. Tech. 2022, 15, 4063–4074. [Google Scholar] [CrossRef]
- Schneising, O.; Buchwitz, M.; Hachmeister, J.; Vanselow, S.; Reuter, M.; Buschmann, M.; Bovensmann, H.; Burrows, J.P. Advances in retrieving methane and carbon monoxide from TROPOMI onboard Sentinel-5 Precursor. Atmos. Meas. Tech. Discuss. 2022, 16, 669–694. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).