Quantifying Forest Litter Fuel Moisture Content with Terrestrial Laser Scanning
Abstract
1. Introduction
1.1. Remote Sensing of Moisture
1.2. Passive vs. Active Sensors
1.3. Terrestrial Laser Scanning (TLS)
1.4. Study Objectives
2. Materials and Methods
2.1. Materials
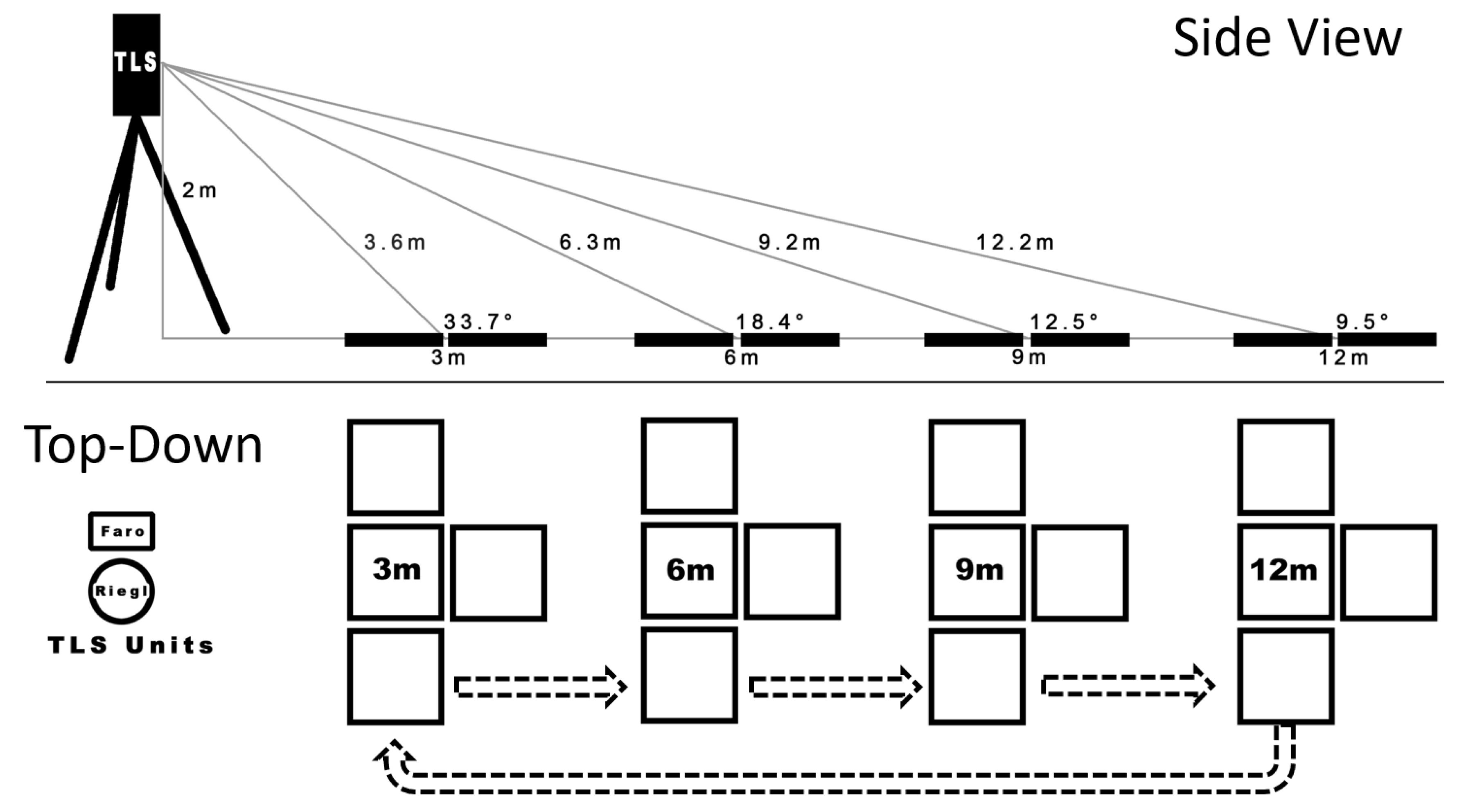
2.2. Experimental Design
2.2.1. TLS Data Collection
2.2.2. Spectrometer Data Collection
2.3. Terrestrial Laser Scanners
2.4. Data Processing
2.5. Analysis
2.5.1. Spectrometer
2.5.2. TLS Intensity
3. Results
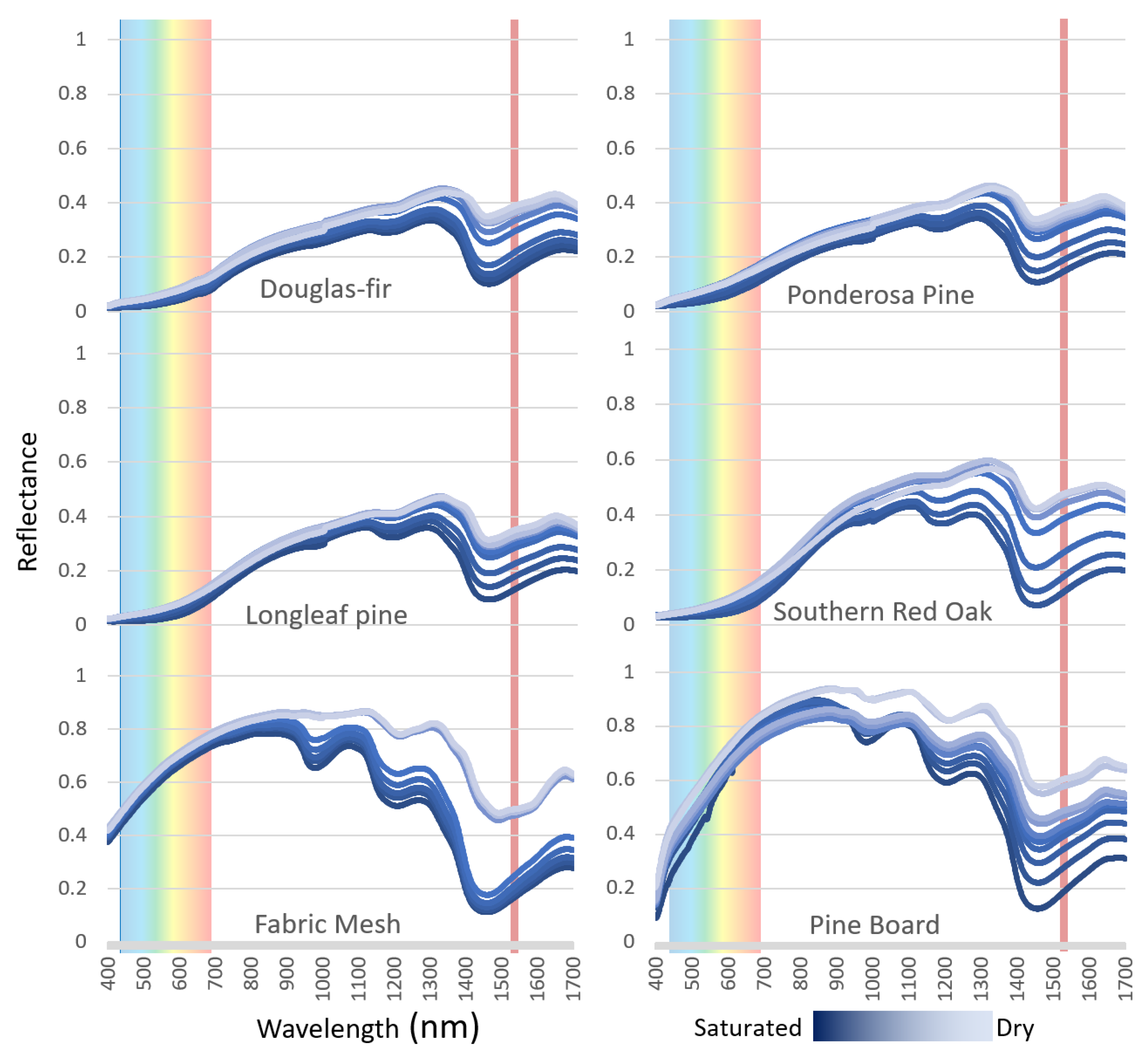
3.1. Moisture & Spectral Signature
3.2. Spectrometer & TLS Intensity
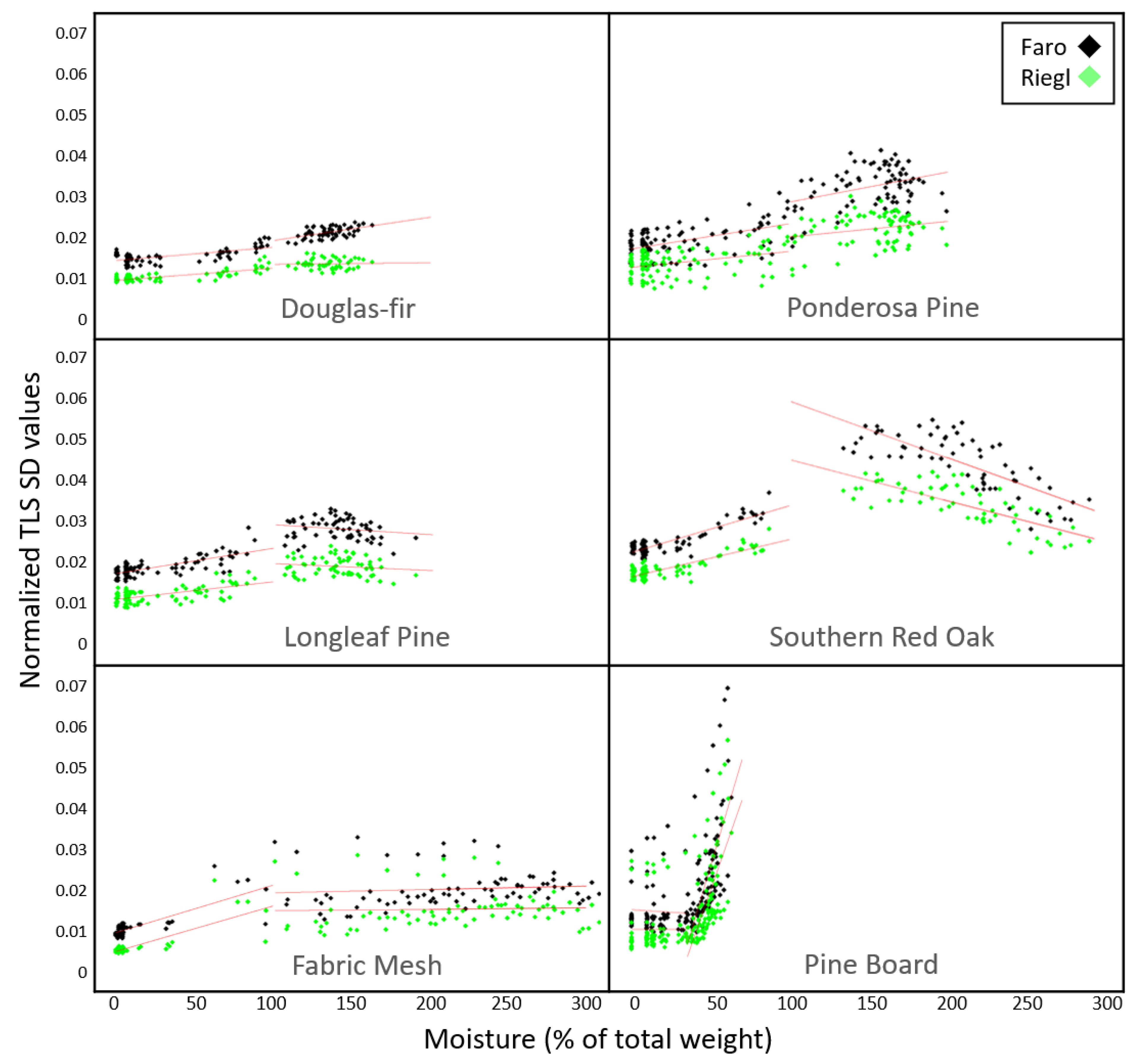
3.3. TLS Metrics & Moisture
3.4. Angle and Distance & TLS Metrics
3.5. Model Coefficients
4. Discussion
4.1. Moisture & Spectral Signature
4.2. Spectrometer & TLS Intensity
4.3. TLS Metrics & Moisture
4.4. Angle and Distance & TLS Metrics
Intensity Calibration
4.5. Model Coefficients
4.6. Future Research
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Intermountain Forest & Range Experiment Station, Forest Service, US Department of Agriculture: Ogden, UT, USA, 1972; Volume 115. [Google Scholar]
- Rothermel, R.C. How to Predict the Spread and Intensity of Forest and Range Fires; US Department of Agriculture, Forest Service, Intermountain Forest and Range: Ogden, UT, USA, 1983; Volume 143. [Google Scholar]
- Countryman, C.M. Moisture in Living Fuels Affects Fire Behavior. Fire Manag. 1974, 35, 10–14. [Google Scholar]
- Jolly, W.M. Sensitivity of a Surface Fire Spread Model and Associated Fire Behaviour Fuel Models to Changes in Live Fuel Moisture. Int. J. Wildland Fire 2007, 16, 503–509. [Google Scholar] [CrossRef]
- Matthews, S. Dead Fuel Moisture Research: 1991–2012. Int. J. Wildland Fire 2014, 23, 78–92. [Google Scholar] [CrossRef]
- Flannigan, M.D.; Wotton, B.M.; Marshall, G.A.; De Groot, W.J.; Johnston, J.; Jurko, N.; Cantin, A.S. Fuel Moisture Sensitivity to Temperature and Precipitation: Climate Change Implications. Clim. Chang. 2016, 134, 59–71. [Google Scholar] [CrossRef]
- Viney, N.R. A Review of Fine Fuel Moisture Modelling. Int. J. Wildland Fire 1991, 1, 215–234. [Google Scholar] [CrossRef]
- Keane, R.E.; Gray, K. Comparing Three Sampling Techniques for Estimating Fine Woody down Dead Biomass. Int. J. Wildland Fire 2013, 22, 1093–1107. [Google Scholar] [CrossRef]
- Rowell, E.; Prichard, S.; Varner, J.M.; Shearman, T.M. Re-Envisioning Fire and Vegetation Feedbacks. In Wildland Fire Dynamics; Speer, K., Goodrick, S., Eds.; Cambridge University Press: Cambridge, UK, 2022; pp. 156–182. ISBN 978-1-108-58024-3. [Google Scholar]
- Yebra, M.; Dennison, P.E.; Chuvieco, E.; Riaño, D.; Zylstra, P.; Hunt, E.R.; Danson, F.M.; Qi, Y.; Jurdao, S. A Global Review of Remote Sensing of Live Fuel Moisture Content for Fire Danger Assessment: Moving towards Operational Products. Remote Sens. Environ. 2013, 136, 455–468. [Google Scholar] [CrossRef]
- Pimont, F.; Parsons, R.; Rigolot, E.; de Coligny, F.; Dupuy, J.-L.; Dreyfus, P.; Linn, R.R. Modeling Fuels and Fire Effects in 3D: Model Description and Applications. Environ. Model. Softw. 2016, 80, 225–244. [Google Scholar] [CrossRef]
- Gergel, D.R.; Nijssen, B.; Abatzoglou, J.T.; Lettenmaier, D.P.; Stumbaugh, M.R. Effects of Climate Change on Snowpack and Fire Potential in the Western USA. Clim. Chang. 2017, 141, 287–299. [Google Scholar] [CrossRef]
- Ma, W.; Zhai, L.; Pivovaroff, A.; Shuman, J.; Buotte, P.; Ding, J.; Christoffersen, B.; Knox, R.; Moritz, M.; Fisher, R. Assessing Climate Change Impacts on Live Fuel Moisture and Wildfire Risk Using a Hydrodynamic Vegetation Model. Biogeosciences 2021, 18, 4005–4020. [Google Scholar] [CrossRef]
- Rossa, C.G.; Fernandes, P.M. Live Fuel Moisture Content: The ‘Pea under the Mattress’ of Fire Spread Rate Modeling? Fire 2018, 1, 43. [Google Scholar] [CrossRef]
- Pollet, J.; Brown, A. Fuel Moisture Sampling Guide; Utah State Office, Bureau of Land Management: Salt Lake City, UT, USA, 2007. [Google Scholar]
- Haines, D.A.; Frost, J.S. Weathering Effects on Fuel Moisture Sticks: Corrections and Recommendations; Department of Agriculture, Forest Service, North Central Forest Experiment: St. Paul, MN, USA, 1978; Volume 154. [Google Scholar]
- Ceccato, P.; Gobron, N.; Flasse, S.; Pinty, B.; Tarantola, S. Designing a Spectral Index to Estimate Vegetation Water Content from Remote Sensing Data: Part 1: Theoretical Approach. Remote Sens. Environ. 2002, 82, 188–197. [Google Scholar] [CrossRef]
- Datt, B. Remote Sensing of Water Content in Eucalyptus Leaves. Aust. J. Bot. 1999, 47, 909–923. [Google Scholar] [CrossRef]
- Tian, Q.; Tong, Q.; Pu, R.; Guo, X.; Zhao, C. Spectroscopic Determination of Wheat Water Status Using 1650–1850 Nm Spectral Absorption Features. Int. J. Remote Sens. 2001, 22, 2329–2338. [Google Scholar] [CrossRef]
- Tucker, C.J. Remote Sensing of Leaf Water Content in the near Infrared. Remote Sens. Environ. 1980, 10, 23–32. [Google Scholar] [CrossRef]
- Wang, J.; Xu, R.; Yang, S. Estimation of Plant Water Content by Spectral Absorption Features Centered at 1450 Nm and 1940 Nm Regions. Environ. Monit. Assess. 2008, 157, 459. [Google Scholar] [CrossRef]
- Makowiecki, A.S.; Steinbrenner, J.E.; Wimer, N.T.; Glusman, J.F.; Lapointe, C.B.; Daily, J.W.; Hamlington, P.E.; Rieker, G.B. Dual Frequency Comb Spectroscopy of Solid Fuel Pyrolysis and Combustion: Quantifying the Influence of Moisture Content in Douglas Fir. Fire Saf. J. 2020, 116, 103185. [Google Scholar] [CrossRef]
- Qi, Y.; Dennison, P.E.; Jolly, W.M.; Kropp, R.C.; Brewer, S.C. Spectroscopic Analysis of Seasonal Changes in Live Fuel Moisture Content and Leaf Dry Mass. Remote Sens. Environ. 2014, 150, 198–206. [Google Scholar] [CrossRef]
- Watanabe, K.; Mansfield, S.D.; Avramidis, S. Application of Near-Infrared Spectroscopy for Moisture-Based Sorting of Green Hem-Fir Timber. J. Wood Sci. 2011, 57, 288–294. [Google Scholar] [CrossRef]
- Barber, N.; Alvarado, E.; Kane, V.R.; Mell, W.E.; Moskal, L.M. Estimating Fuel Moisture in Grasslands Using UAV-Mounted Infrared and Visible Light Sensors. Sensors 2021, 21, 6350. [Google Scholar] [CrossRef] [PubMed]
- Vinnikov, K.Y.; Robock, A.; Qiu, S.; Entin, J.K.; Owe, M.; Choudhury, B.J.; Hollinger, S.E.; Njoku, E.G. Satellite Remote Sensing of Soil Moisture in Illinois, United States. J. Geophys. Res. Atmos. 1999, 104, 4145–4168. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. Satellite Remote Sensing Applications for Surface Soil Moisture Monitoring: A Review. Front. Earth Sci. China 2009, 3, 237–247. [Google Scholar] [CrossRef]
- Dragozi, E.; Giannaros, T.M.; Kotroni, V.; Lagouvardos, K.; Koletsis, I. Dead Fuel Moisture Content (DFMC) Estimation Using MODIS and Meteorological Data: The Case of Greece. Remote Sens. 2021, 13, 4224. [Google Scholar] [CrossRef]
- Hao, X.; Qu, J.J. Retrieval of Real-Time Live Fuel Moisture Content Using MODIS Measurements. Remote Sens. Environ. 2007, 108, 130–137. [Google Scholar] [CrossRef]
- Gillon, D.; Dauriac, F.; Deshayes, M.; Valette, J.C.; Moro, C. Estimation of Foliage Moisture Content Using near Infrared Reflectance Spectroscopy. Agric. For. Meteorol. 2004, 124, 51–62. [Google Scholar] [CrossRef]
- Kemppinen, J.; Niittynen, P.; Riihimäki, H.; Luoto, M. Modelling Soil Moisture in a High-Latitude Landscape Using LiDAR and Soil Data. Earth Surf. Process. Landf. 2018, 43, 1019–1031. [Google Scholar] [CrossRef]
- Carson, W.W.; Andersen, H.-E.; Reutebuch, S.E.; McGaughey, R.J. LIDAR Applications in Forestry—An Overview. In Proceedings of the ASPRS Annual Conference, Denver, CO, USA, 23–28 May 2004; pp. 1–9. [Google Scholar]
- Dubayah, R.O.; Drake, J.B. Lidar Remote Sensing for Forestry. J. For. 2000, 98, 44–46. [Google Scholar]
- Hudak, A.T.; Evans, J.S.; Stuart Smith, A.M. LiDAR Utility for Natural Resource Managers. Remote Sens. 2009, 1, 934–951. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar Sampling for Large-Area Forest Characterization: A Review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Stavros, E.N.; Coen, J.; Peterson, B.; Singh, H.; Kennedy, K.; Ramirez, C.; Schimel, D. Use of Imaging Spectroscopy and LIDAR to Characterize Fuels for Fire Behavior Prediction. Remote Sens. Appl. Soc. Environ. 2018, 11, 41–50. [Google Scholar] [CrossRef]
- Bright, B.C.; Hudak, A.T.; McGaughey, R.; Andersen, H.-E.; Negrón, J. Predicting Live and Dead Tree Basal Area of Bark Beetle Affected Forests from Discrete-Return Lidar. Can. J. Remote Sens. 2013, 39, S99–S111. [Google Scholar] [CrossRef]
- Korpela, I.; Ørka, H.O.; Hyyppä, J.; Heikkinen, V.; Tokola, T. Range and AGC Normalization in Airborne Discrete-Return LiDAR Intensity Data for Forest Canopies. ISPRS J. Photogramm. Remote Sens. 2010, 65, 369–379. [Google Scholar] [CrossRef]
- Lang, M.W.; Kim, V.; McCarty, G.W.; Li, X.; Yeo, I.-Y.; Huang, C.; Du, L. Improved Detection of Inundation below the Forest Canopy Using Normalized LiDAR Intensity Data. Remote Sens. 2020, 12, 707. [Google Scholar] [CrossRef]
- Garroway, K.; Hopkinson, C.; Jamieson, R. Surface Moisture and Vegetation Influences on Lidar Intensity Data in an Agricultural Watershed. Can. J. Remote Sens. 2011, 37, 275–284. [Google Scholar] [CrossRef]
- Krooks, A.; Kaasalainen, S.; Hakala, T.; Nevalainen, O. Correction of Intensity Incidence Angle Effect in Terrestrial Laser Scanning. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 2, 145–150. [Google Scholar] [CrossRef]
- Hasegawa, H. Evaluations of LIDAR Reflectance Amplitude Sensitivity towards Land Cover Conditions. Bull. Geogr. Surv. Inst. 2006, 53, 43–50. [Google Scholar]
- Kashani, A.G.; Olsen, M.J.; Parrish, C.E.; Wilson, N. A Review of LiDAR Radiometric Processing: From Ad Hoc Intensity Correction to Rigorous Radiometric Calibration. Sensors 2015, 15, 28099–28128. [Google Scholar] [CrossRef]
- Loudermilk, E.L.; Hiers, J.K.; O’Brien, J.J.; Mitchell, R.J.; Singhania, A.; Fernandez, J.C.; Cropper, W.P.; Slatton, K.C. Ground-Based LIDAR: A Novel Approach to Quantify Fine-Scale Fuelbed Characteristics. Int. J. Wildland Fire 2009, 18, 676–685. [Google Scholar] [CrossRef]
- Rowell, E.; Seielstad, C. Characterizing Grass, Litter, and Shrub Fuels in Longleaf Pine Forest Pre-and Post-Fire Using Terrestrial LiDAR. In Proceedings of the SilviLaser, Vancouver, BC, Canada, 16–19 September 2012; pp. 16–19. [Google Scholar]
- Rowell, E.M.; Seielstad, C.A.; Ottmar, R.D. Development and Validation of Fuel Height Models for Terrestrial Lidar–RxCADRE 2012. Int. J. Wildland Fire 2015, 25, 38–47. [Google Scholar] [CrossRef]
- Plyler, E.K.; Sleator, W.W. Further Study of the Absorption of Infrared Radiation by Water Vapor. Phys. Rev. 1931, 37, 1493. [Google Scholar] [CrossRef]
- Ponomarev, O.A.; Zakir’ianov, F.K.; Terpugov, E.L.; Fesenko, E.E. Absorption of Infrared Radiation by a Thin Water Layer. Biofizika 2001, 46, 402–407. [Google Scholar]
- Suchocki, C.; Katzer, J.; Rapiński, J. Terrestrial Laser Scanner as a Tool for Assessment of Saturation and Moisture Movement in Building Materials. Period. Polytech. Civ. Eng. 2018, 62, 694–699. [Google Scholar] [CrossRef]
- Suchocki, C.; Katzer, J. Terrestrial Laser Scanning Harnessed for Moisture Detection in Building Materials—Problems and Limitations. Autom. Constr. 2018, 94, 127–134. [Google Scholar] [CrossRef]
- Jin, J.; De Sloover, L.; Verbeurgt, J.; Stal, C.; Deruyter, G.; Montreuil, A.-L.; De Maeyer, P.; De Wulf, A. Measuring Surface Moisture on a Sandy Beach Based on Corrected Intensity Data of a Mobile Terrestrial LiDAR. Remote Sens. 2020, 12, 209. [Google Scholar] [CrossRef]
- Danson, F.M.; Gaulton, R.; Armitage, R.P.; Disney, M.; Gunawan, O.; Lewis, P.; Pearson, G.; Ramirez, A.F. Developing a Dual-Wavelength Full-Waveform Terrestrial Laser Scanner to Characterize Forest Canopy Structure. Agric. For. Meteorol. 2014, 198, 7–14. [Google Scholar] [CrossRef]
- Gaulton, R.; Danson, F.M.; Pearson, G.; Lewis, P.E.; Disney, M. The Salford Advanced Laser Canopy Analyser (SALCA): A Multispectral Full Waveform LiDAR for Improved Vegetation Characterisation. In Proceedings of the Remote Sensing and Photogrammetry Society Conference, Remote Sensing and the Carbon Cycle, London, UK, 5 May 2010; Volume 5. [Google Scholar]
- Hancock, S.; Gaulton, R.; Danson, F.M. Angular Reflectance of Leaves with a Dual-Wavelength Terrestrial Lidar and Its Implications for Leaf-Bark Separation and Leaf Moisture Estimation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3084–3090. [Google Scholar] [CrossRef]
- Elsherif, A.; Gaulton, R.; Mills, J. Estimation of Vegetation Water Content at Leaf and Canopy Level Using Dual-Wavelength Commercial Terrestrial Laser Scanners. Interface Focus 2018, 8, 20170041. [Google Scholar] [CrossRef] [PubMed]
- Gaulton, R.; Danson, F.M.; Ramirez, F.A.; Gunawan, O. The Potential of Dual-Wavelength Laser Scanning for Estimating Vegetation Moisture Content. Remote Sens. Environ. 2013, 132, 32–39. [Google Scholar] [CrossRef]
- Junttila, S.; Sugano, J.; Vastaranta, M.; Linnakoski, R.; Kaartinen, H.; Kukko, A.; Holopainen, M.; Hyyppä, H.; Hyyppä, J. Can Leaf Water Content Be Estimated Using Multispectral Terrestrial Laser Scanning? A Case Study with Norway Spruce Seedlings. Front. Plant Sci. 2018, 9, 299. [Google Scholar] [CrossRef] [PubMed]
- Junttila, S.; Vastaranta, M.; Liang, X.; Kaartinen, H.; Kukko, A.; Kaasalainen, S.; Holopainen, M.; Hyyppä, H.; Hyyppä, J. Measuring Leaf Water Content with Dual-Wavelength Intensity Data from Terrestrial Laser Scanners. Remote Sens. 2017, 9, 8. [Google Scholar] [CrossRef]
- Junttila, S.; Hölttä, T.; Puttonen, E.; Katoh, M.; Vastaranta, M.; Kaartinen, H.; Holopainen, M.; Hyyppä, H. Terrestrial Laser Scanning Intensity Captures Diurnal Variation in Leaf Water Potential. Remote Sens. Environ. 2021, 255, 112274. [Google Scholar] [CrossRef]
- Elsherif, A.; Gaulton, R.; Shenkin, A.; Malhi, Y.; Mills, J. Three Dimensional Mapping of Forest Canopy Equivalent Water Thickness Using Dual-Wavelength Terrestrial Laser Scanning. Agric. For. Meteorol. 2019, 276, 107627. [Google Scholar] [CrossRef]
- Elsherif, A.; Gaulton, R.; Mills, J.P. The Potential of Dual-Wavelength Terrestrial Laser Scanning in 3d Canopy Fuel Moisture Content Mapping. ISPRS Geospat. Week 2019, XLII-2/W13, 975–979. [Google Scholar] [CrossRef]
- Calders, K.; Disney, M.I.; Armston, J.; Burt, A.; Brede, B.; Origo, N.; Muir, J.; Nightingale, J. Evaluation of the Range Accuracy and the Radiometric Calibration of Multiple Terrestrial Laser Scanning Instruments for Data Interoperability. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2716–2724. [Google Scholar] [CrossRef]
- Tan, K.; Chen, J.; Qian, W.; Zhang, W.; Shen, F.; Cheng, X. Intensity Data Correction for Long-Range Terrestrial Laser Scanners: A Case Study of Target Differentiation in an Intertidal Zone. Remote Sens. 2019, 11, 331. [Google Scholar] [CrossRef]
- Raj, T.; Hashim, F.H.; Huddin, A.B.; Ibrahim, M.F.; Hussain, A. A Survey on LiDAR Scanning Mechanisms. Electronics 2020, 9, 741. [Google Scholar] [CrossRef]
- Suchocki, C. Comparison of Time-of-Flight and Phase-Shift TLS Intensity Data for the Diagnostics Measurements of Buildings. Materials 2020, 13, 353. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial Laser Scanning in Forest Ecology: Expanding the Horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- San José Alonso, J.I.; Martínez Rubio, J.; Fernández Martín, J.J.; García Fernández, J. Comparing Time-Of and Phase-Shift the Survey of the Royal Pantheon in the Basilica of San Isidoro (LEÓN). ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 3816, 377–385. [Google Scholar] [CrossRef]
- ASD ASD FieldSpec 4 Wide-Res Field Spectroradiometer. Available online: https://Www.Malvernpanalytical.Com/2017 (accessed on 11 December 2021).
- FARO Scene [Computer Software]; Version 2019.2. Available online: http://www.faro.com (accessed on 1 March 2021).
- Riegl RiScan Pro [Computer Software]; Version 2.6.1; 2021. Available online: https://www.riegl.com/ (accessed on 1 March 2021).
- CloudCompare [Computer Software]; Version 2.11; 2019. Available online: http://www.cloudcompare.org (accessed on 1 March 2021).
- Di Biase, V.; Hanssen, R.F.; Vos, S.E. Sensitivity of Near-Infrared Permanent Laser Scanning Intensity for Retrieving Soil Moisture on a Coastal Beach: Calibration Procedure Using In Situ Data. Remote Sens. 2021, 13, 1645. [Google Scholar] [CrossRef]
- Zahiri, Z.; Laefer, D.F.; Gowen, A. Characterizing Building Materials Using Multispectral Imagery and LiDAR Intensity Data. J. Build. Eng. 2021, 44, 102603. [Google Scholar] [CrossRef]
- Bowyer, P.; Danson, F.M. Sensitivity of Spectral Reflectance to Variation in Live Fuel Moisture Content at Leaf and Canopy Level. Remote Sens. Environ. 2004, 92, 297–308. [Google Scholar] [CrossRef]
- Paltridge, G.W.; Mitchell, R.M. Atmospheric and Viewing Angle Correction of Vegetation Indices and Grassland Fuel Moisture Content Derived from NOAA/AVHRR. Remote Sens. Environ. 1990, 31, 121–135. [Google Scholar] [CrossRef]
- Wade, D. Fuel Moisture and Prescribed Burning. South. Fire Exch. Fact Sheet 2013, 5, 5–8. [Google Scholar]
- Zhu, X.; Wang, T.; Darvishzadeh, R.; Skidmore, A.K.; Niemann, K.O. 3D Leaf Water Content Mapping Using Terrestrial Laser Scanner Backscatter Intensity with Radiometric Correction. ISPRS J. Photogramm. Remote Sens. 2015, 110, 14–23. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Krooks, A.; Kukko, A.; Kaartinen, H. Radiometric Calibration of Terrestrial Laser Scanners with External Reference Targets. Remote Sens. 2009, 1, 144–158. [Google Scholar] [CrossRef]
- Li, Y.; Duthon, P.; Colomb, M.; Ibanez-Guzman, J. What Happens for a ToF LiDAR in Fog? IEEE Trans. Intell. Transp. Syst. 2021, 22, 6670–6681. [Google Scholar] [CrossRef]
- Strand, M.P.; Witherspoon, N.H.; Holloway Jr, J.H.; Tinsley, K.R.; Petee, D.A.; Taylor, J.S., Jr.; Branham, E.A.; Thomas, J.P. Environmental Factors Impacting the Performance of Airborne Lidar Sensors in the Surf Zone. In Proceedings of the Detection and Remediation Technologies for Mines and Minelike Targets VIII, Orlando, FL, USA, 21–25 April 2003; SPIE: Bellingham, WA, USA, 2003; Volume 5089, pp. 274–283. [Google Scholar]
- Levy, J.S.; Johnson, J.T.E. Remote Soil Moisture Measurement from Drone-Borne Reflectance Spectroscopy: Applications to Hydroperiod Measurement in Desert Playas. Remote Sens. 2021, 13, 1035. [Google Scholar] [CrossRef]





| Sample Type | Weight Range (Grams) | Weight Mean (Grams) | Depth of Sample |
|---|---|---|---|
| Douglas-fir (DF) | 119–156 | 135 | ~3 cm |
| Ponderosa pine (PP) | 104–158 | 129 | Uncompacted |
| Longleaf pine (LLP) | 70–123 | 101 | Uncompacted |
| Southern red oak (SRO) | 27–35 | 31 | Uncompacted |
| Fabric mesh (FM) | 66–74 | 67 | ~0.5 cm |
| Pine board (PB) | 514–596 | 569 | ~1.5 cm |
| Sample Type | Scan Intervals (Hours from First Scan) | Angle | N * |
|---|---|---|---|
| Pine board (PB) | 0, 2, 4, 8, 12, 24, 48, 72, 120, OD | 0, 45, 90 | 3840–lidar 1280–weight |
| Fabric mesh (FM) | 0, 2, 4, 8, 12, 24, 36, 48, OD | 0, 45, 90 | 3456–lidar 1152–weight |
| Douglas-fir (DF) | 0, 1, 2, 4, 8, 12, 24, 36, 48, OD | 0 | 1280 |
| Ponderosa pine (PP) | 0, 1, 2, 4, 8, 12, 24, 36, 48,120, OD | 0 | 1408 |
| Longleaf pine (LLP) | 0, 1, 2, 4, 8, 12, 24, 36, 48, OD | 0 | 1280 |
| Southern red oak (SRO) | 0, 1, 2, 4, 8, 12, 24, 36, OD | 0 | 1152 |
| Unit Specs | Approximate number of pulses per sample | |||||
| TLS | Min Range | Max Range | Scan Angle Increment | 3 m | 6 m | 9 m |
| FARO | 0.6 m | ~350 m | 0.018° | ~34,000 | ~6000 | ~2000 |
| RIEGL | 2.5 m | ~2000 m | 0.010° | ~103,000 | ~18,500 | ~6000 |
| Footprint Size | ||||||
| TLS | Beam Divergence | Diameter at Exit | Ellipsoid at 3 m (mm) | Ellipsoid at 6 m (mm) | Ellipsoid at 9 m (mm) | Ellipsoid at 12 m (mm) |
| FARO | 0.3 mrad * | 2.2 mm | 3.3 × 5.9 | 4.1 × 13 | 5 × 23.1 | 5.9 × 35.7 |
| RIEGL | 0.3 mrad | 18 mm | 19.1 × 34.4 | 19.9 × 63 | 20.8 × 96.1 | 21.7 × 131.5 |
| Mean & SD | DF R2 | PP R2 | LLP R2 | SRO R2 | FM 0 R2 | FM 45 R2 | FM 90 R2 | PB 0 R2 | PB 45 R2 | PB 90 R2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FARO | ALL | 0.65 | 0.40 | 0.28 | 0.83 | 0.66 | 0.84 | 0.88 | 0.25 | 0.44 | 0.49 |
| RIEGL | ALL | 0.86 | 0.56 | 0.69 | 0.95 | 0.92 | 0.94 | 0.92 | 0.32 | 0.54 | 0.50 |
| FARO | 3 M | 0.94 | 0.78 | 0.86 | 0.95 | 0.91 | 0.96 | 0.96 | 0.43 | 0.59 | 0.52 |
| RIEGL | 3 M | 0.95 | 0.76 | 0.90 | 0.98 | 0.96 | 0.98 | 0.98 | 0.46 | 0.65 | 0.61 |
| FARO | 6 M | 0.81 | 0.55 | 0.68 | 0.94 | 0.87 | 0.94 | 0.95 | 0.34 | 0.58 | 0.60 |
| RIEGL | 6 M | 0.92 | 0.60 | 0.79 | 0.97 | 0.94 | 0.97 | 0.98 | 0.38 | 0.58 | 0.63 |
| FARO | 9 M | 0.62 | 0.45 | 0.19 | 0.91 | 0.66 | 0.86 | 0.84 | 0.25 | 0.47 | 0.45 |
| RIEGL | 9 M | 0.83 | 0.51 | 0.72 | 0.96 | 0.93 | 0.97 | 0.97 | 0.30 | 0.55 | 0.67 |
| FARO | 12 M | 0.54 | 0.37 | 0.07 | 0.85 | 0.66 | 0.89 | 0.86 | 0.17 | 0.44 | 0.44 |
| RIEGL | 12 M | 0.88 | 0.49 | 0.68 | 0.93 | 0.92 | 0.97 | 0.97 | 0.26 | 0.50 | 0.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batchelor, J.L.; Rowell, E.; Prichard, S.; Nemens, D.; Cronan, J.; Kennedy, M.C.; Moskal, L.M. Quantifying Forest Litter Fuel Moisture Content with Terrestrial Laser Scanning. Remote Sens. 2023, 15, 1482. https://doi.org/10.3390/rs15061482
Batchelor JL, Rowell E, Prichard S, Nemens D, Cronan J, Kennedy MC, Moskal LM. Quantifying Forest Litter Fuel Moisture Content with Terrestrial Laser Scanning. Remote Sensing. 2023; 15(6):1482. https://doi.org/10.3390/rs15061482
Chicago/Turabian StyleBatchelor, Jonathan L., Eric Rowell, Susan Prichard, Deborah Nemens, James Cronan, Maureen C. Kennedy, and L. Monika Moskal. 2023. "Quantifying Forest Litter Fuel Moisture Content with Terrestrial Laser Scanning" Remote Sensing 15, no. 6: 1482. https://doi.org/10.3390/rs15061482
APA StyleBatchelor, J. L., Rowell, E., Prichard, S., Nemens, D., Cronan, J., Kennedy, M. C., & Moskal, L. M. (2023). Quantifying Forest Litter Fuel Moisture Content with Terrestrial Laser Scanning. Remote Sensing, 15(6), 1482. https://doi.org/10.3390/rs15061482









