Long-Term Performance Evaluation of BeiDou PPP-B2b Products and Its Application in Time Service
Abstract
1. Introduction
2. Methods
2.1. Recovery and Evaluation of PPP-B2b Products
2.2. PPP Time Service
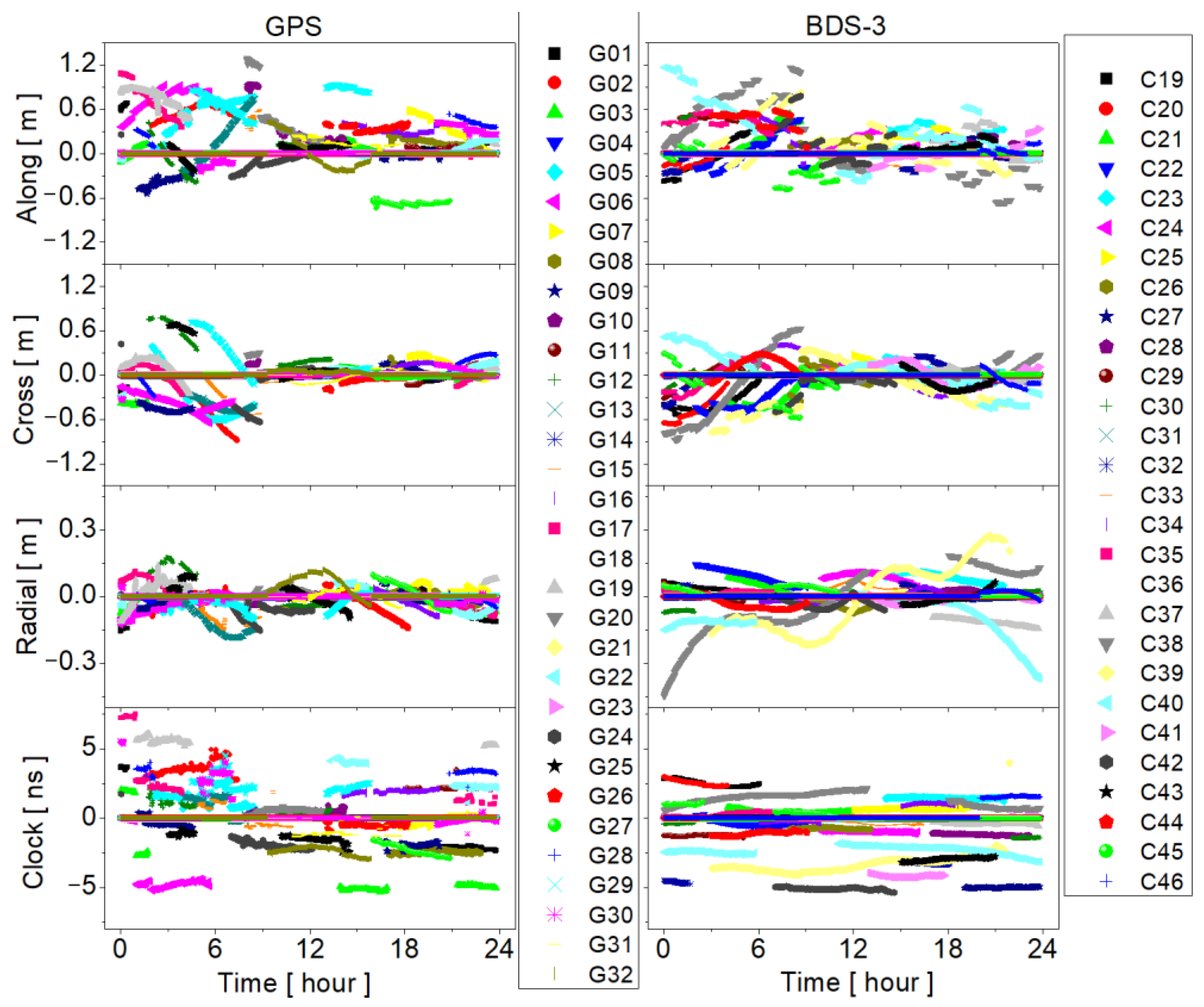
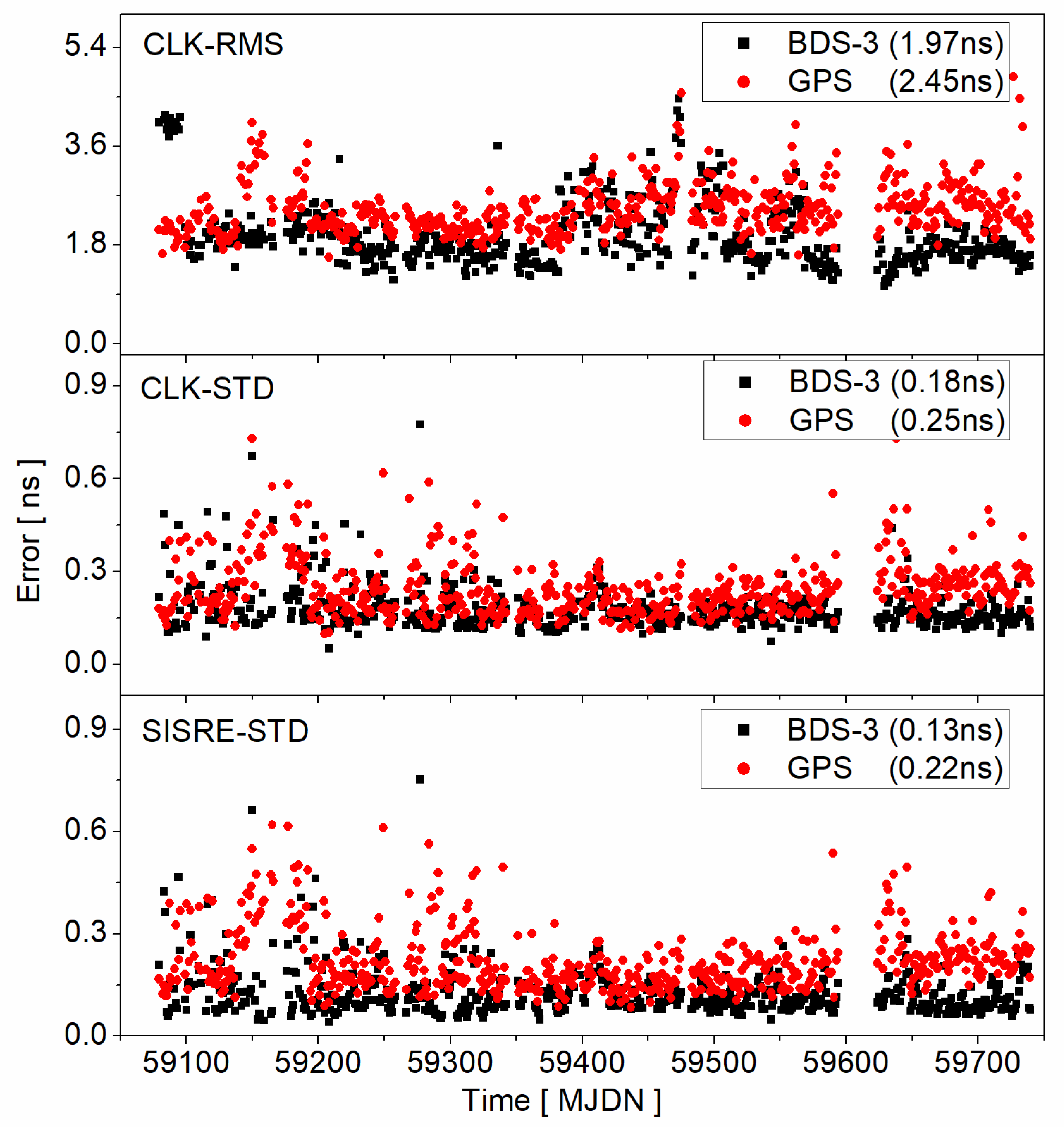
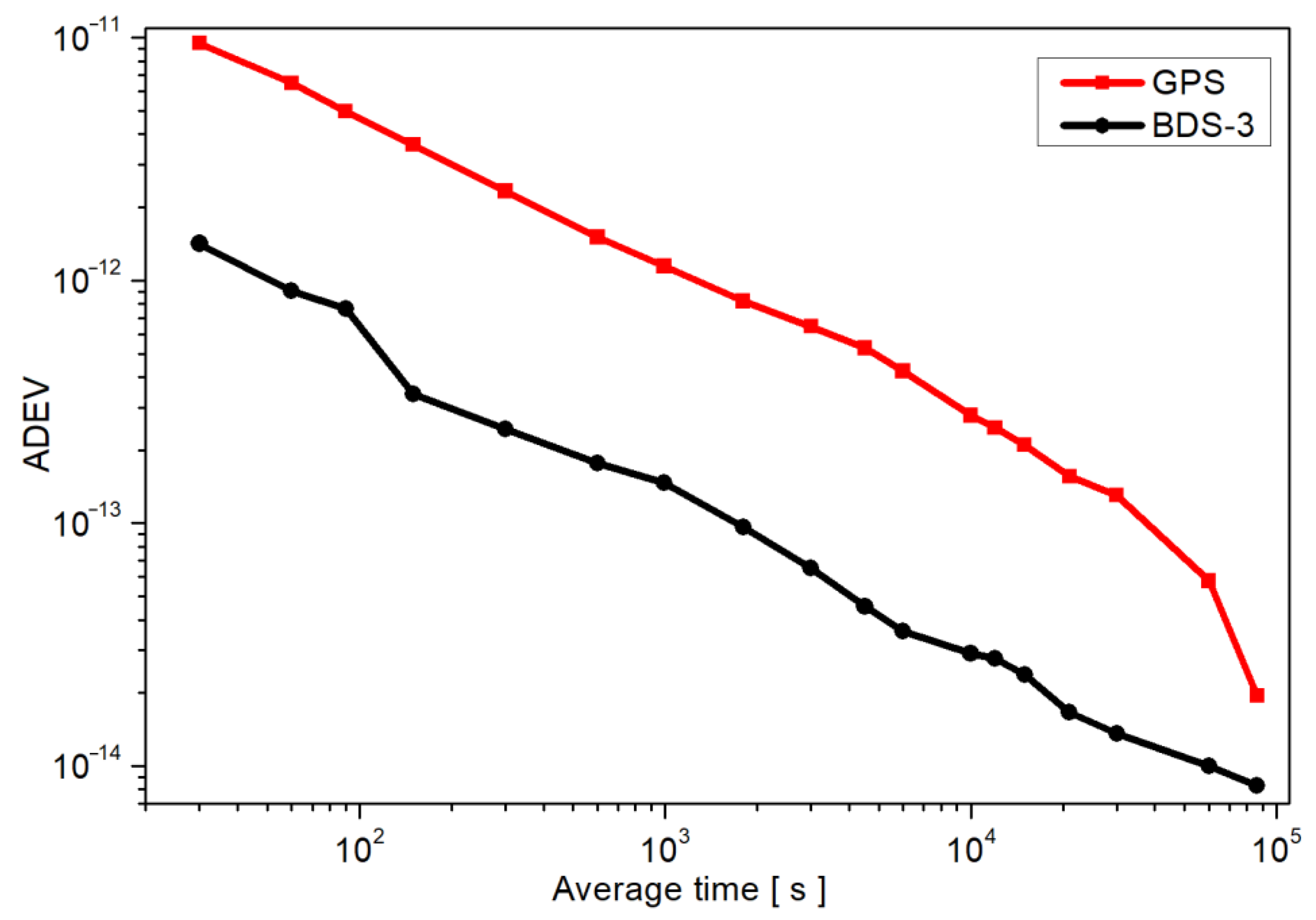
3. Evaluation of PPP-B2b Products
4. Experiment
4.1. Data and Strategy
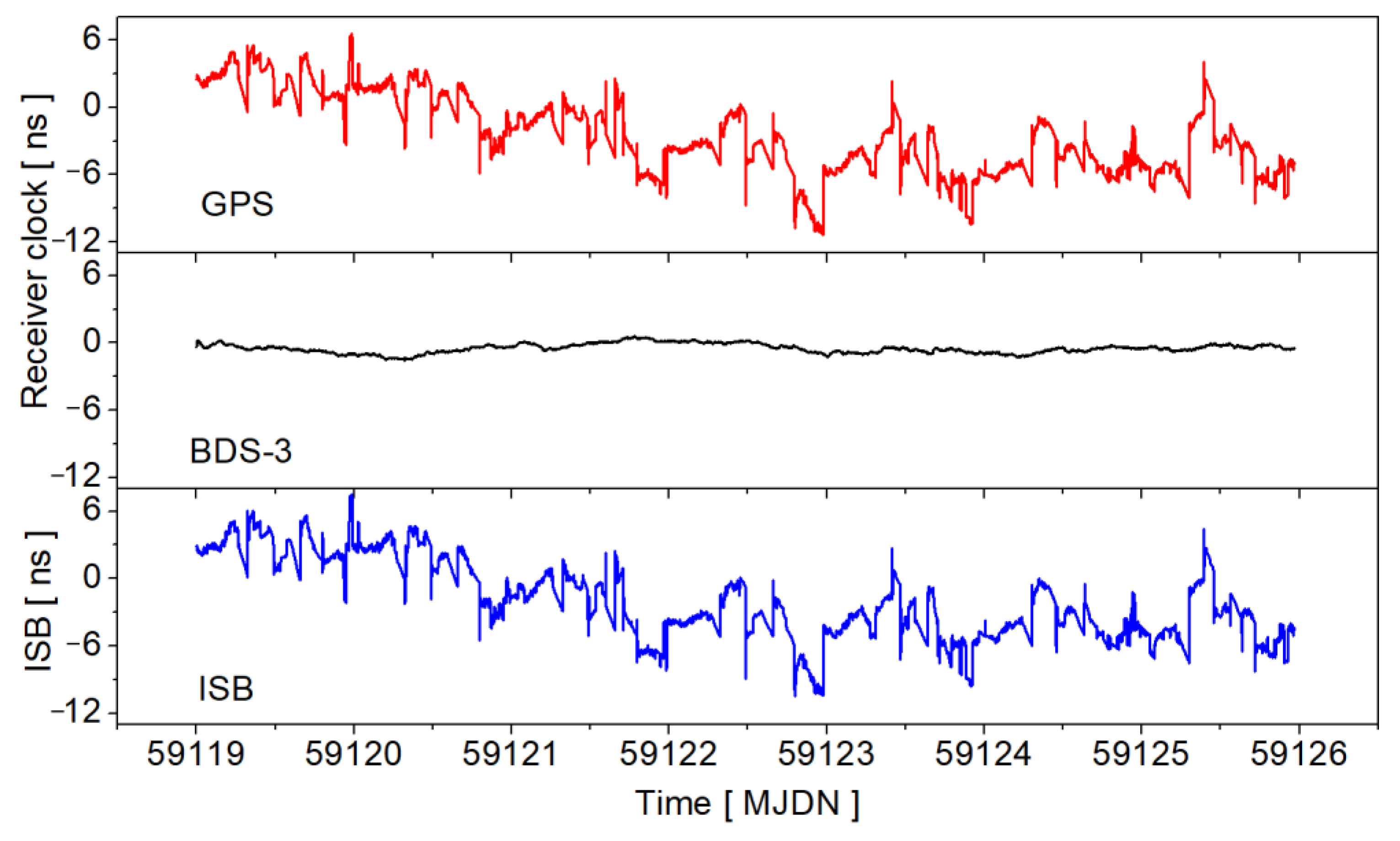
4.2. PPP One-Way Timing
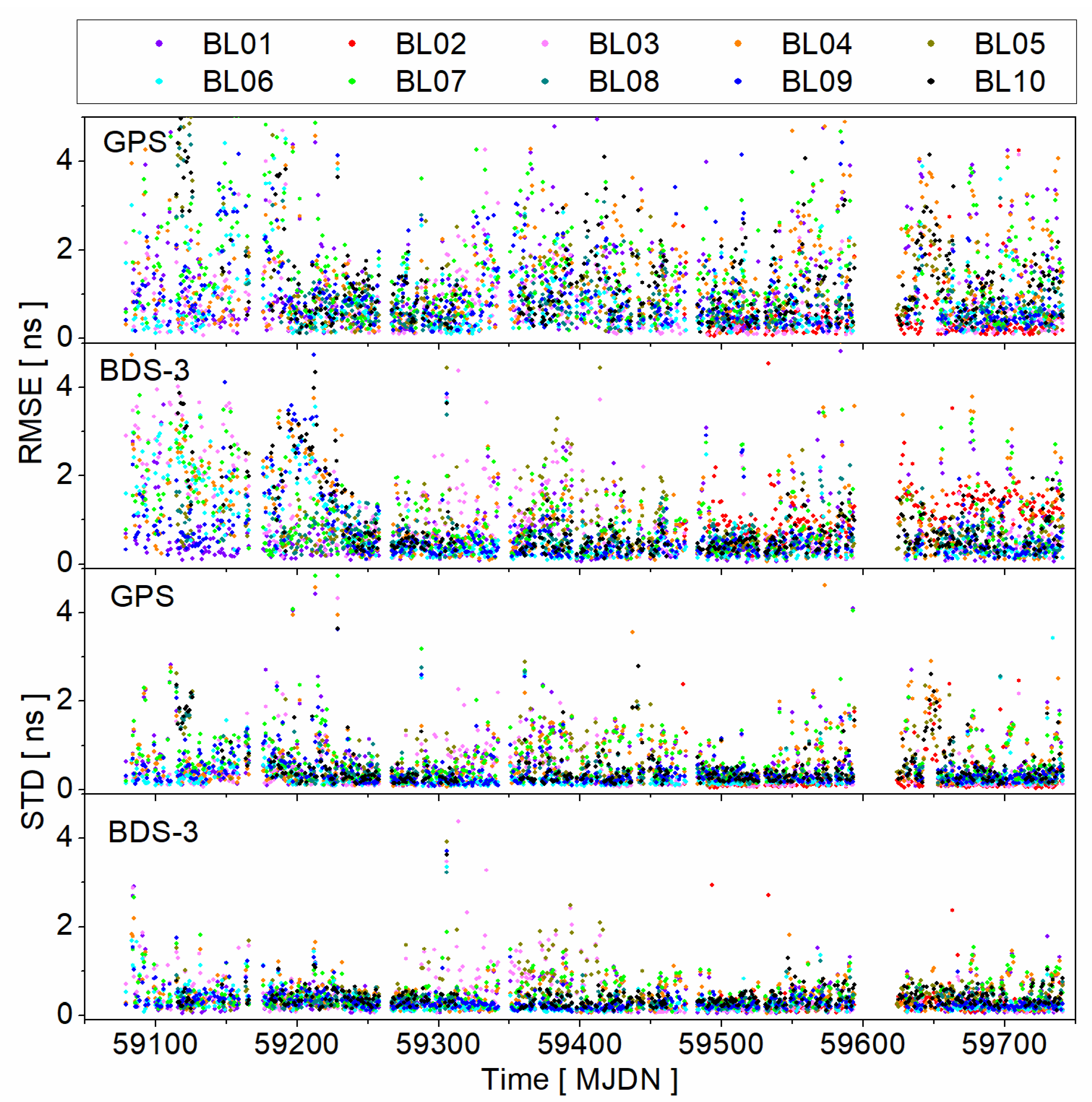
4.3. PPP Time Synchronization
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Schaer, S. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)–achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Li, X.; Huang, J.; Li, X.; Shen, Z.; Han, J.; Li, L.; Wang, B. Review of PPP–RTK: Achievements, challenges, and opportunities. Satell. Navig. 2022, 3, 28. [Google Scholar] [CrossRef]
- Geng, J.; Guo, J.; Meng, X.; Gao, K. Speeding up PPP ambiguity resolution using triple-frequency GPS/BeiDou/Galileo/QZSS data. J. Geodesy 2020, 94, 6. [Google Scholar] [CrossRef]
- Zhang, P.; Tu, R.; Han, J.; Gao, Y.; Zhang, R.; Lu, X. Characterization of biases between BDS-3 and BDS-2, GPS, Galileo and GLONASS observations and their effect on precise time and frequency transfer. Meas. Sci. Technol. 2021, 32, 035006. [Google Scholar] [CrossRef]
- Cai, H.; Meng, Y.; Geng, C.; Gao, W.; Zhang, T.; Li, G.; Shao, B.; Xin, J.; Lu, J.; Mao, Y.; et al. BDS-3 performance assessment: PNT, SBAS, PPP, SMC and SAR. Acta Geod. Cartogr. Sin. 2021, 50, 427–435. [Google Scholar]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef]
- Liu, C.; Gao, W.; Liu, T.; Wang, D.; Yao, Z.; Gao, Y.; Nie, X.; Wang, W.; Li, D.; Zhang, W.; et al. Design and implementation of a BDS precise point positioning service. Navigation 2020, 67, 875–891. [Google Scholar] [CrossRef]
- Tang, C.; Hu, X.; Chen, J.; Liu, L.; Zhou, S.; Guo, R.; Li, X.; He, F.; Liu, J.; Yang, J. Orbit determination, clock estimation and performance evaluation of BDS-3 PPP-B2b service. J. Geodesy 2022, 96, 60. [Google Scholar] [CrossRef]
- Yang, Y.; Ding, Q.; Gao, W.; Li, J.; Xu, Y.; Sun, B. Principle and performance of BDSBAS and PPP-B2b of BDS-3. Satell. Navig. 2022, 3, 5. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, Y.; Li, J. Performance evaluation of BDS-3 PPP-B2b precise point positioning service. GPS Solutions 2021, 25, 142. [Google Scholar] [CrossRef]
- Gong, X.; Lou, Y.; Zheng, F.; Gu, S.; Shi, C.; Liu, J.; Jing, G. Evaluation and calibration of BeiDou receiver-related pseudorange biases. GPS Solutions 2018, 22, 98. [Google Scholar] [CrossRef]
- Gong, X.; Gu, S.; Zheng, F.; Wu, Q.; Liu, S.; Lou, Y. Improving GPS and Galileo precise data processing based on calibration of signal distortion biases. Measurement 2021, 174, 108981. [Google Scholar] [CrossRef]
- Gong, X.; Zheng, F.; Gu, S.; Zhang, Z.; Lou, Y. The long-term characteristics of GNSS signal distortion biases and their empirical corrections. GPS Solutions 2022, 26, 52. [Google Scholar] [CrossRef]
- Tao, J.; Liu, J.; Hu, Z.; Zhao, Q.; Chen, G.; Ju, B. Initial Assessment of the BDS-3 PPP-B2b RTS compared with the CNES RTS. GPS Solutions 2021, 25, 131. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Zhang, M. Comprehensive Analyses of PPP-B2b Performance in China and Surrounding Areas. Remote Sens. 2022, 14, 643. [Google Scholar] [CrossRef]
- Ren, Z.; Gong, H.; Peng, J.; Tang, C.; Huang, X.; Sun, G. Performance assessment of real-time precise point positioning using BDS PPP-B2b service signal. Adv. Space Res. 2021, 68, 3242–3254. [Google Scholar] [CrossRef]
- Zhang, W.; Lou, Y.; Song, W.; Sun, W.; Zou, X.; Gong, X. Initial assessment of BDS-3 precise point positioning service on GEO B2b signal. Adv. Space Res. 2021, 69, 690–700. [Google Scholar] [CrossRef]
- Song, W.; Zhao, X.; Lou, Y.; Sun, W.; Zhao, Z. Performance Evaluation of BDS-3 PPP-B2b Service. Geomat. Inf. Sci. Wuhan Univ. 2021. [Google Scholar] [CrossRef]
- Zhu, E.; Guo, H.; Li, J.; Xiao, H.; Duan, R. Performance Analysis of Real-Time PPP Based on BDS-3 PPP-B2b Service. J. Geod. Geodyn. 2022, 42, 616–621. [Google Scholar]
- He, C.; Gu, S.; Liu, C.; Gao, W.; Zheng, F.; Gong, X.; Li, W. Simulation research on PPP-RTK performance based on BDS GEO satellite. Meas. Sci. Technol. 2022, 33, 065025. [Google Scholar] [CrossRef]
- Yang, H.; Ji, S.; Weng, D.; Wang, Z.; He, K.; Chen, W. Assessment of the Feasibility of PPP-B2b Service for Real-Time Coseismic Displacement Retrieval. Remote Sens. 2022, 13, 5011. [Google Scholar] [CrossRef]
- Xu, X.; Nie, Z.; Wang, Z.; Wang, B.; Du, Q. Performance Assessment of BDS-3 PPP-B2b/INS Loosely Coupled Integration. Remote Sens. 2022, 14, 2957. [Google Scholar] [CrossRef]
- Geng, T.; Li, Z.; Xie, X.; Liu, W.; Li, Y.; Zhao, Q. Real-time ocean precise point positioning with BDS-3 service signal PPP-B2b. Measurement 2022, 203, 111911. [Google Scholar] [CrossRef]
- Lu, X.; Chen, L.; Shen, N.; Wang, L.; Jiao, Z.; Chen, R. Decoding PPP Corrections From BDS B2b Signals Using a Software-Defined Receiver: An Initial Performance Evaluation. IEEE Sensors J. 2021, 21, 7871–7883. [Google Scholar] [CrossRef]
- Zhang, R.; He, Z.; Ma, L.; Xiao, G.; Guang, W.; Ge, Y.; Zhang, X.; Zhang, J.; Tang, J.; Li, X. Analysis of BDS-3 PPP-B2b Positioning and Time Transfer Service. Remote Sens. 2022, 14, 2769. [Google Scholar] [CrossRef]
- Guo, W.; Zuo, H.; Mao, F.; Chen, J.; Gong, X.; Gu, S.; Liu, J. On the satellite clock datum stability of RT-PPP product and its application in one-way timing and time synchronization. J. Geodesy 2022, 96, 52. [Google Scholar] [CrossRef]
- Li, B.; Ge, H.; Bu, Y.; Zheng, Y.; Yuan, L. Comprehensive assessment of real-time precise products from IGS analysis centers. Satell. Navig. 2022, 3, 12. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, 199–208. [Google Scholar] [CrossRef]
- Wu, J.; Wu, S.; Hajj, G.; Bertiger, W.; Lichten, S. Effects of antenna orientation on GPS carrier phase. Manuscr. Geod. 1993, 18, 91–98. [Google Scholar]
- Peng, Y.; Dai, X.; Lou, Y.; Gong, X.; Zheng, F. BDS-2 and BDS-3 combined precise orbit determination with hybrid ambiguity resolution. Measurement 2022, 188, 110593. [Google Scholar] [CrossRef]




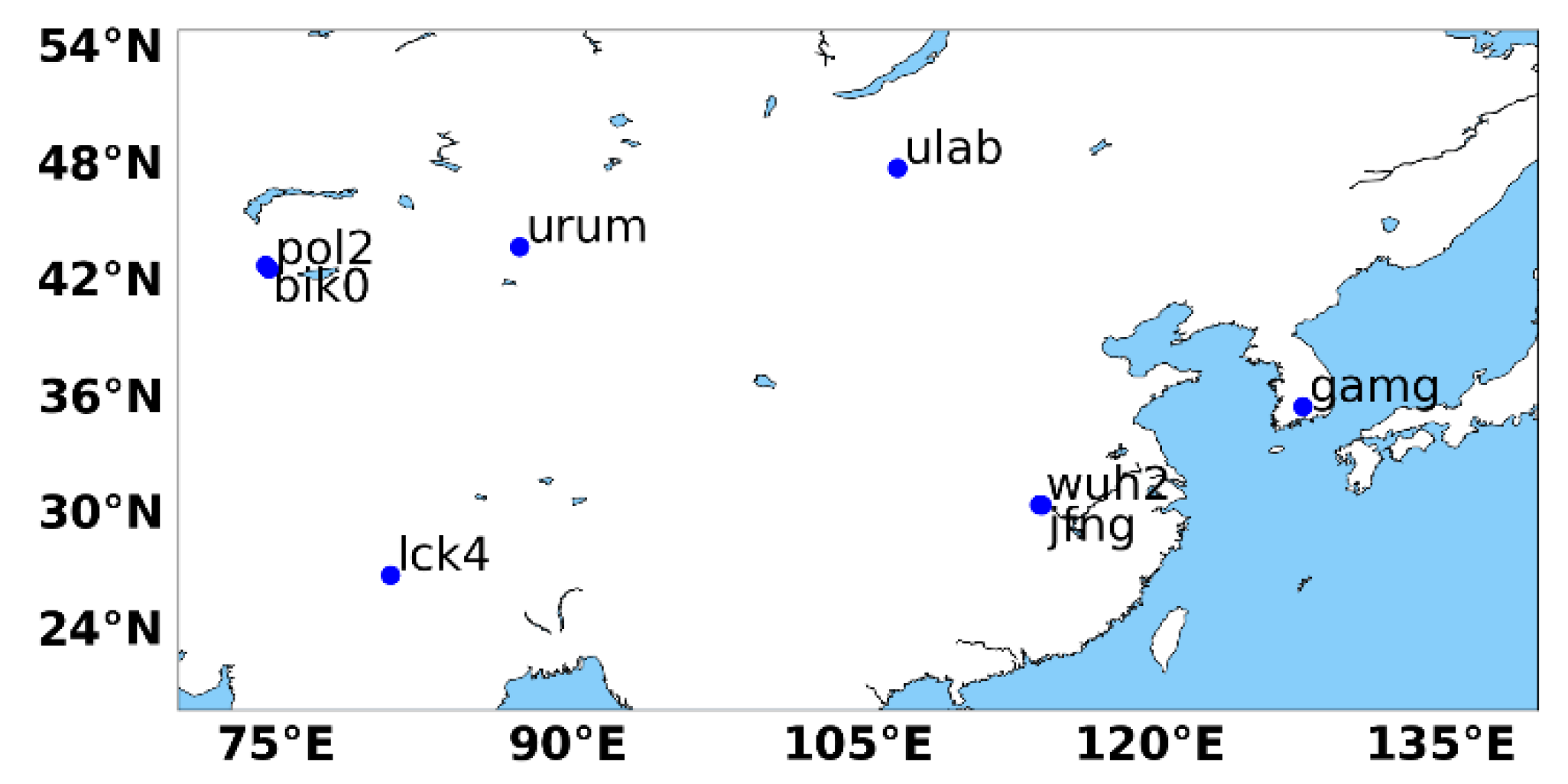

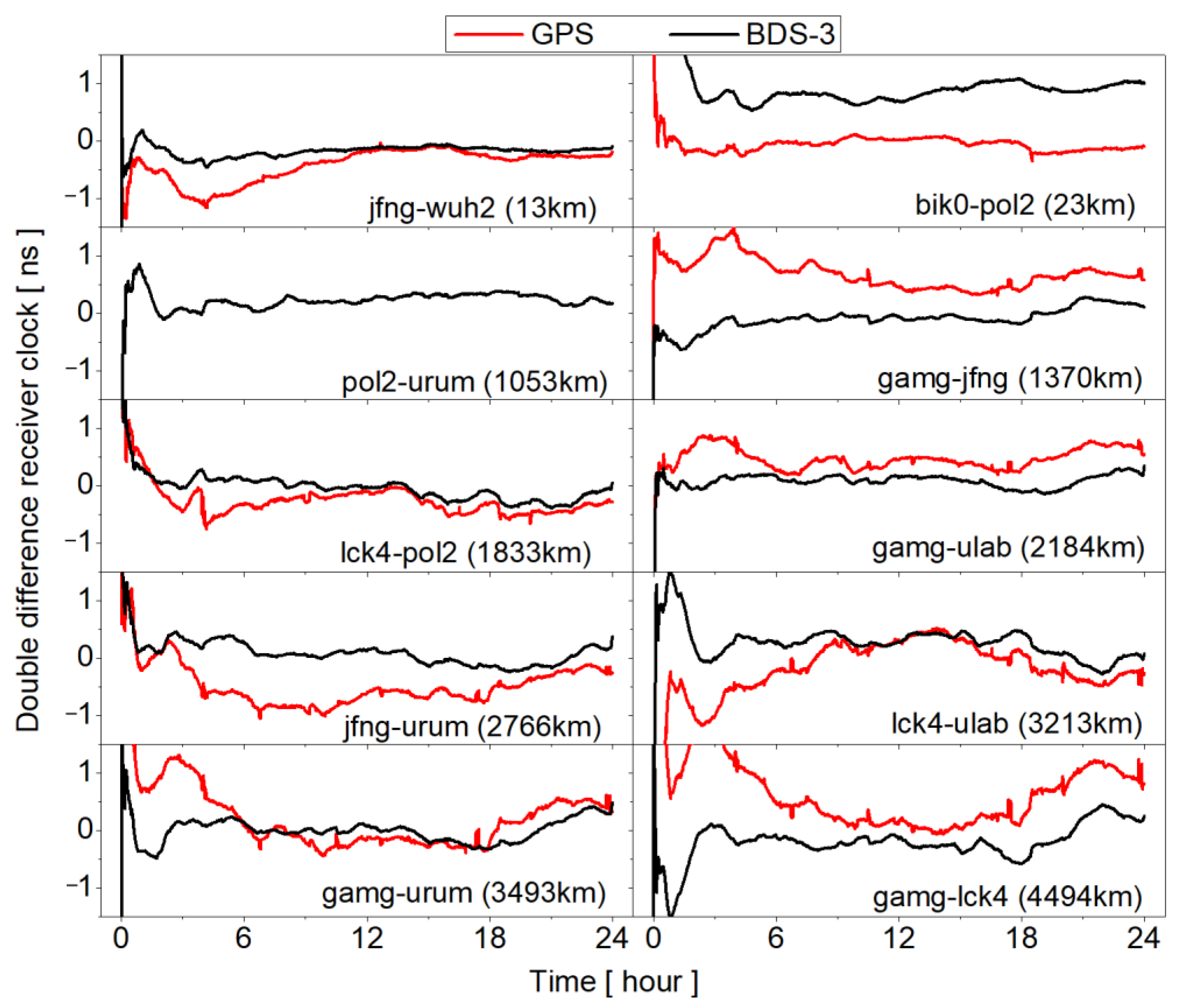
| Number | Station Name | Length (km) |
|---|---|---|
| BL01 | jfng—wuh2 | 13 |
| BL02 | bik0—pol2 | 23 |
| BL03 | pol2—urum | 1053 |
| BL04 | gamg—jfng | 1370 |
| BL05 | lck4—pol2 | 1833 |
| BL06 | gamg—ulab | 2184 |
| BL07 | jfng—urum | 2766 |
| BL08 | lck4—ulab | 3213 |
| BL09 | gamg—urum | 3493 |
| BL10 | gamg—lck4 | 4494 |
| Items | Strategy |
|---|---|
| Satellite orbit and clock | Fixed by broadcast ephemeris and PPP-B2b |
| Troposphere delay | Corrected by GPT2 model and estimated zenith troposphere with GMF mapping function [29] |
| Ionosphere delay | Eliminate 1st order ionosphere delay by IF combination |
| Receiver clock | Estimated as white noise for each satellite system |
| Ambiguity | Float solution and estimated as a constant value for each arc |
| Receiver coordinate | Estimated as static parameters |
| Observations | GPS: L1/L2 BDS-3: B1I/B3I |
| Cutoff elevation | 7° |
| Weighting () | , applied for code/phase |
| Satellite antenna phase center | BDS-3 PCO from official website; GPS PCOs and PCVs from IGS MGEX |
| Phase wind-up | Corrected with [30] |
| Processing interval | 30 s |
| Number | Length (km) | RMSE (ns) | STD (ns) | ||
|---|---|---|---|---|---|
| GPS | BDS-3 | GPS | BDS-3 | ||
| BL01 | 13 | 1.24 | 0.73 | 0.64 | 0.40 |
| BL02 | 23 | 0.46 | 1.19 | 0.27 | 0.27 |
| BL03 | 1053 | 0.80 | 1.01 | 0.40 | 0.44 |
| BL04 | 1370 | 1.42 | 1.04 | 0.68 | 0.46 |
| BL05 | 1833 | 1.03 | 0.77 | 0.52 | 0.47 |
| BL06 | 2184 | 0.90 | 0.74 | 0.30 | 0.28 |
| BL07 | 2766 | 1.58 | 1.02 | 0.74 | 0.47 |
| BL08 | 3213 | 0.94 | 0.66 | 0.44 | 0.35 |
| BL09 | 3493 | 1.00 | 0.72 | 0.41 | 0.32 |
| BL10 | 4494 | 1.24 | 0.87 | 0.50 | 0.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Q.; Chen, L.; Liu, L.; Zhao, D.; Gong, X.; Lou, Y.; Guan, Q. Long-Term Performance Evaluation of BeiDou PPP-B2b Products and Its Application in Time Service. Remote Sens. 2023, 15, 1358. https://doi.org/10.3390/rs15051358
He Q, Chen L, Liu L, Zhao D, Gong X, Lou Y, Guan Q. Long-Term Performance Evaluation of BeiDou PPP-B2b Products and Its Application in Time Service. Remote Sensing. 2023; 15(5):1358. https://doi.org/10.3390/rs15051358
Chicago/Turabian StyleHe, Qianqian, Liang Chen, Lei Liu, Daiyan Zhao, Xiaopeng Gong, Yidong Lou, and Qi Guan. 2023. "Long-Term Performance Evaluation of BeiDou PPP-B2b Products and Its Application in Time Service" Remote Sensing 15, no. 5: 1358. https://doi.org/10.3390/rs15051358
APA StyleHe, Q., Chen, L., Liu, L., Zhao, D., Gong, X., Lou, Y., & Guan, Q. (2023). Long-Term Performance Evaluation of BeiDou PPP-B2b Products and Its Application in Time Service. Remote Sensing, 15(5), 1358. https://doi.org/10.3390/rs15051358






