Estimation of Cotton Nitrogen Content Based on Multi-Angle Hyperspectral Data and Machine Learning Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Data Acquisition
2.2.1. Measurement of Canopy Multi-Angular Hyperspectral Reflectance
2.2.2. Determination of Aboveground N Concentrations
2.3. Evaluation of the Spectral Index of Nitrogen Nutrition in Cotton
2.3.1. Construction of the Spectral Index
2.3.2. Classical Vegetation Index Screening
2.4. Model Construction and Verification
3. Results
3.1. Change in the Law of Spectral Reflectance of the Cotton Canopy under Different VZAs
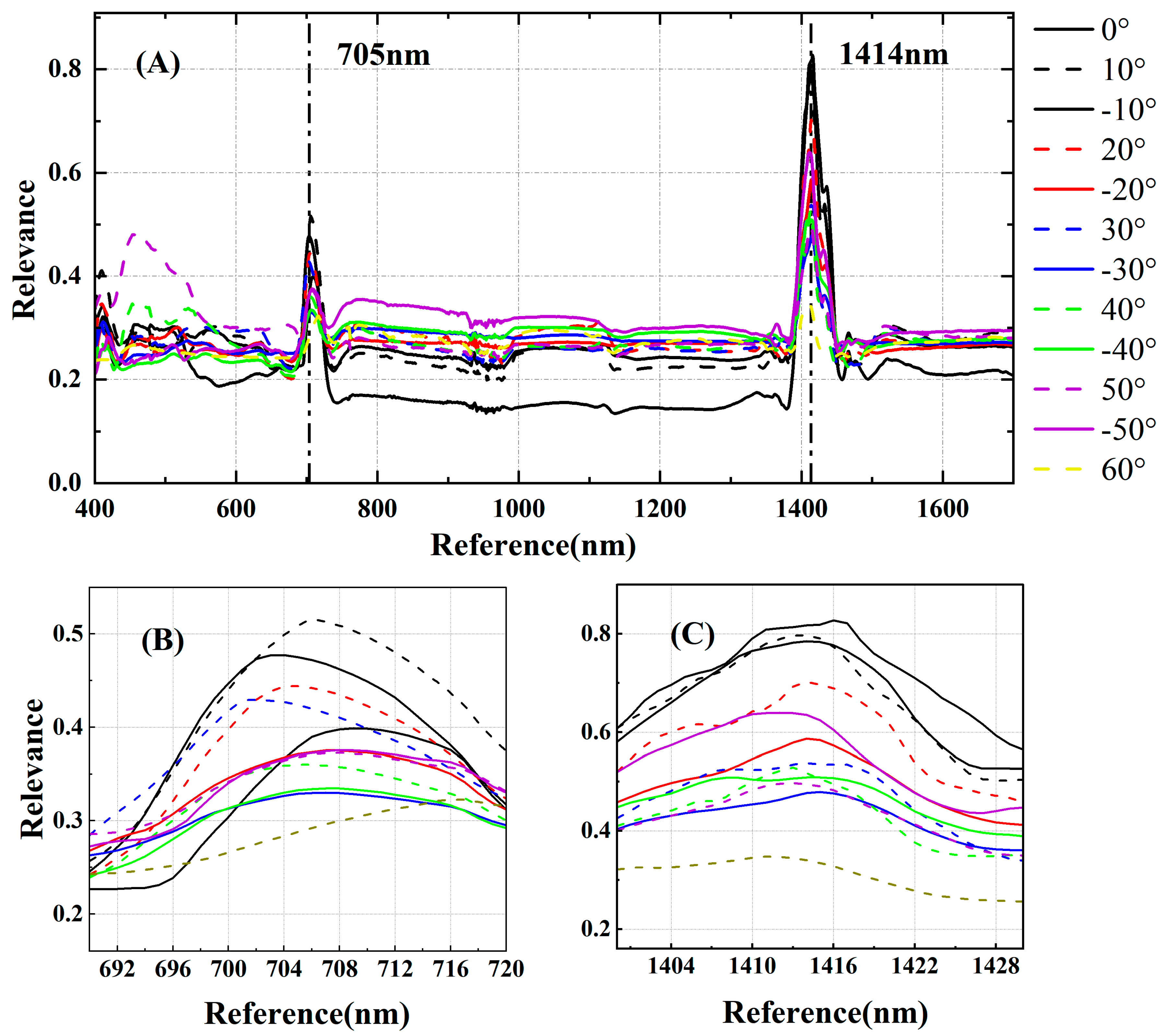
3.2. Nitrogen-Sensitive Spectral Band Screening of Different VZAs
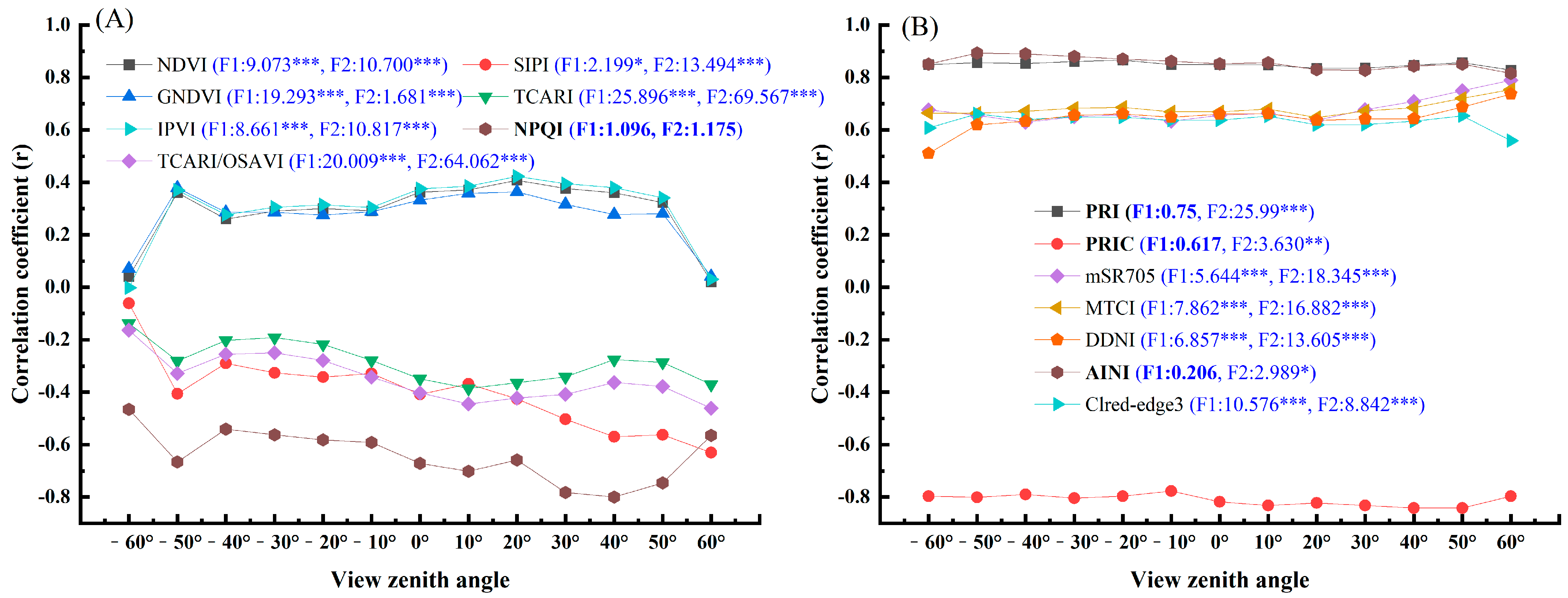
3.3. Nitrogen-Sensitive Spectral Index Screening of Different VZAs
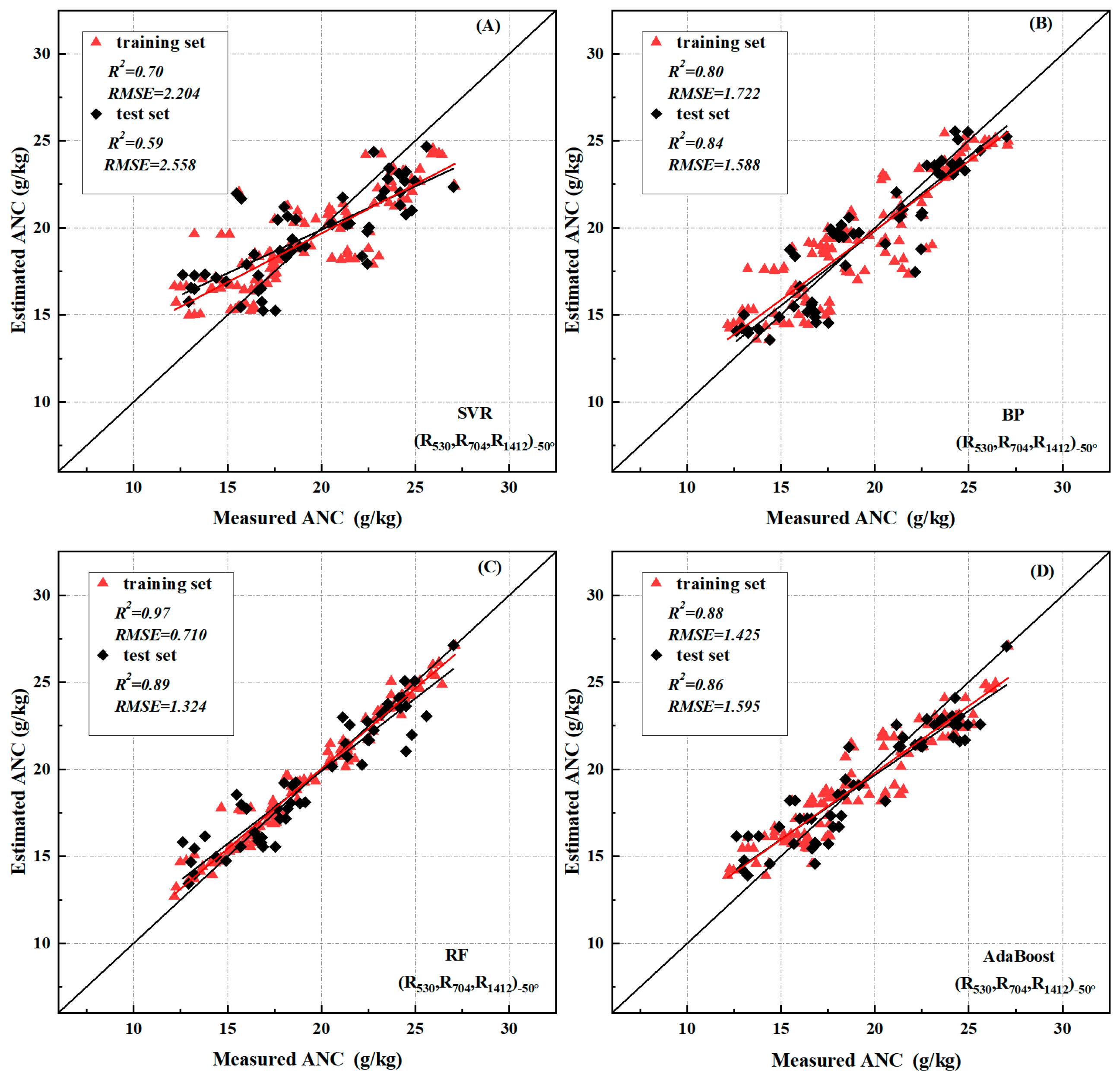
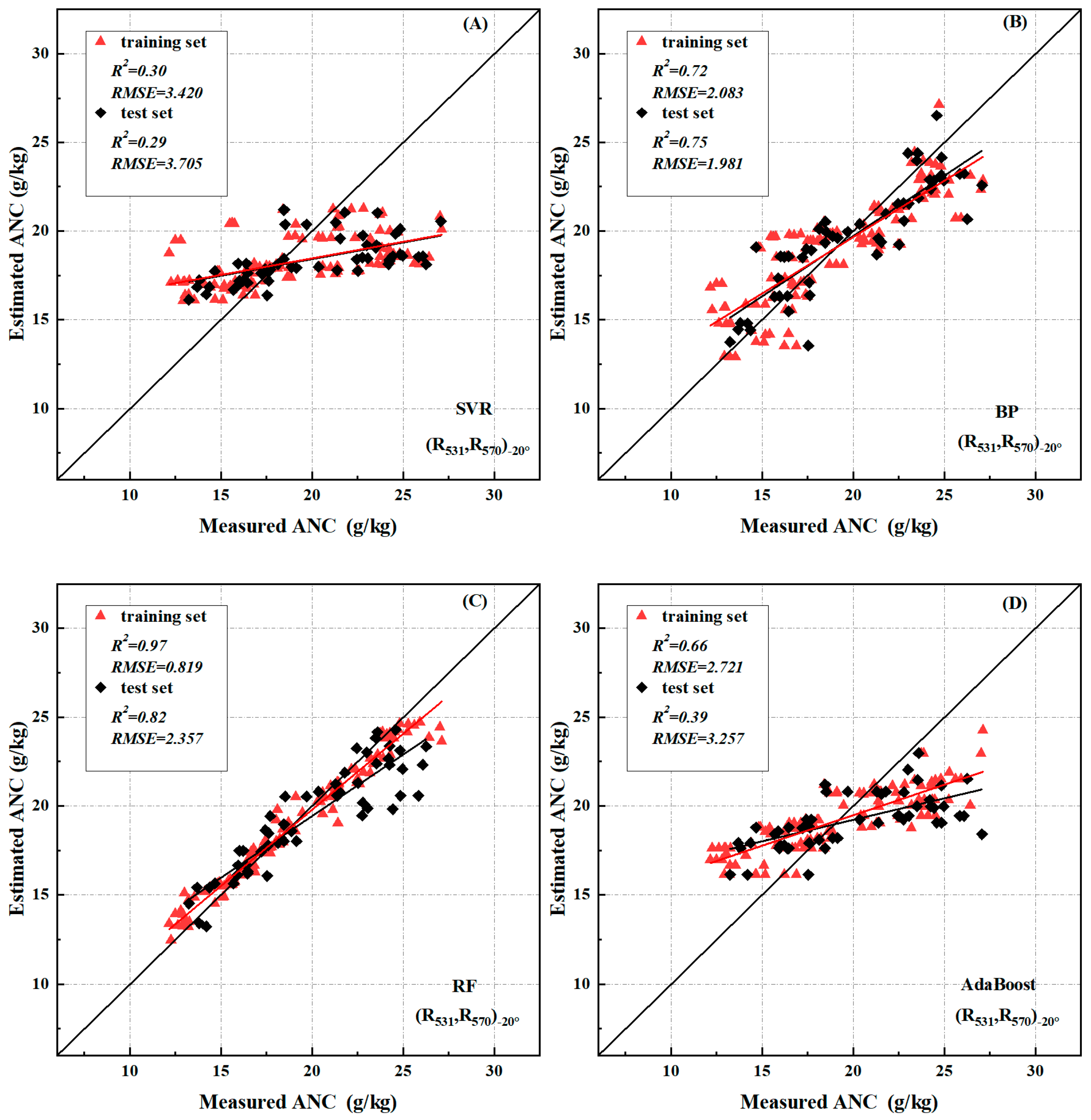
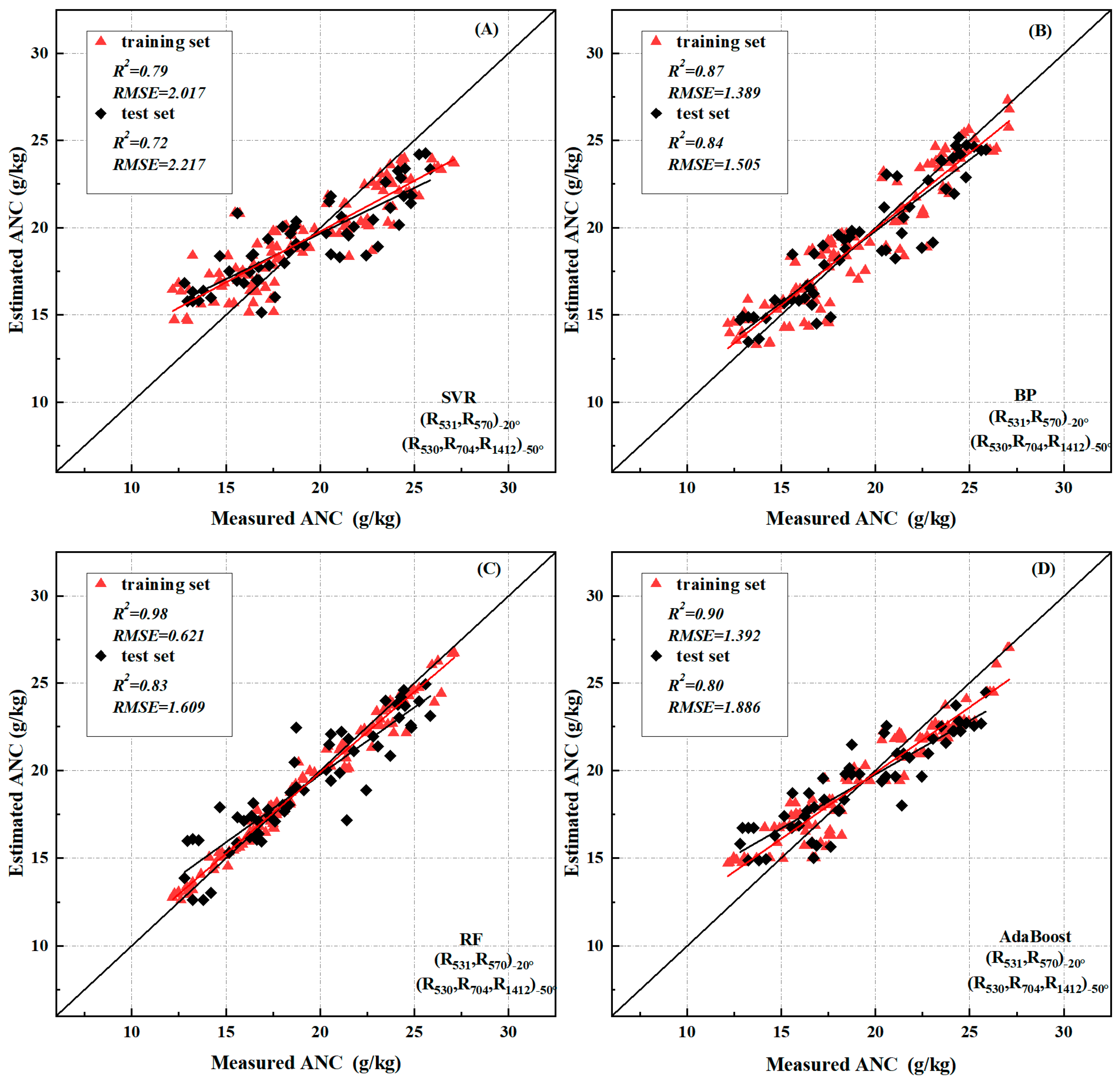
3.4. Cotton Nitrogen Content Estimation Model Based on Multi-Angle Spectral Data
4. Discussion
4.1. Effect of VZA on Canopy Reflectivity
4.2. The Spectral Index Estimates the Difference in ANC
4.3. Future Applications and Limitations of Research
5. Conclusions
- (1)
- (2)
- The existing spectral indices selected in this study have obvious angular sensitivity to changes in the correlation between ANC, and the correlation coefficients in the zenith direction are smaller than those of off-nadir observations (Table 3).
- (3)
- RF models combining the −50° AINI index and the −20° PRI index can better predict the change of ANC in cotton (test set R2 = 0.98, RMSE = 0.590, validation set R2 = 0.85, RMSE = 1.532) (Figure 9).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, J.; Song, X.; Yang, G.; Du, X.; Mei, X.; Yang, X. Remote sensing monitoring of rice and wheat canopy nitrogen: A review. Remote Sens. 2022, 14, 5712. [Google Scholar]
- Song, L.; Wang, L.; Yang, Z.; He, L.; Feng, Z.; Duan, J.; Feng, W.; Guo, T. Comparison of algorithms for monitoring wheat powdery mildew using multi-angular remote sensing data. Crop J. 2022, 10, 1312–1322. [Google Scholar]
- Bian, Z.; Roujean, J.L.; Fan, T.; Dong, Y.; Hu, T.; Cao, B.; Li, H.; Du, Y.; Xiao, Q.; Liu, Q. An angular normalization method for temperature vegetation dryness index (TVDI) in monitoring agricultural drought. Remote Sens. Environ. 2023, 284, 113330. [Google Scholar]
- He, L.; Song, X.; Feng, W.; Guo, B.; Zhang, Y.; Wang, Y.; Wang, C.; Guo, T. Improved remote sensing of leaf nitrogen concentration in winter wheat using multi-angular hyperspectral data. Remote Sens. Environ. 2016, 174, 122–133. [Google Scholar]
- Gao, F.; Jin, Y.; Schaaf, C.B.; Strahler, A.H. Bidirectional NDVI and atmospherically resistant BRDF inversion for vegetation canopy. IEEE Trans. Geosci. Remote Sensing. 2002, 40, 1269–1278. [Google Scholar]
- Chen, J.M.; Liu, J.; Leblanc, S.G.; Lacaze, R.; Roujean, J. Multi-angular optical remote sensing for assessing vegetation structure and carbon absorption. Remote Sens. Environ. 2003, 84, 516–525. [Google Scholar]
- Strahler, A.H.; Jupp, D.L. Modeling bidirectional reflectance of forests and woodlands using Boolean models and geometric optics. Remote Sens. Environ. 1990, 34, 153–166. [Google Scholar] [CrossRef]
- Kennedy, B.E.; King, D.J.; Duffe, J. Retrieval of Arctic Vegetation Biophysical and Biochemical Properties from CHRIS/PROBA Multi-Angle Imagery Using Empirical and Physical Modelling. Remote Sens. 2021, 13, 1830. [Google Scholar] [CrossRef]
- Chen, H.; Huang, W.; Li, W.; Niu, Z.; Zhang, L.; Xing, S. Estimation of LAI in winter wheat from multi-angular hyperspectral VNIR data: Effects of view angles and plant architecture. Remote Sens. 2018, 10, 1630. [Google Scholar] [CrossRef]
- Stagakis, S.; Markos, N.; Sykioti, O.; Kyparissis, A. Monitoring canopy biophysical and biochemical parameters in ecosystem scale using satellite hyperspectral imagery: An application on a Phlomis fruticosa Mediterranean ecosystem using multiangular CHRIS/PROBA observations. Remote Sens. Environ. 2010, 114, 977–994. [Google Scholar]
- Kong, W.; Huang, W.; Liu, J.; Chen, P.; Qin, Q.; Ye, H.; Peng, D.; Dong, Y.; Mortimer, A.H. Estimation of canopy carotenoid content of winter wheat using multi-angle hyperspectral data. Adv. Space Res. 2017, 60, 1988–2000. [Google Scholar]
- Roosjen, P.P.; Brede, B.; Suomalainen, J.M.; Bartholomeus, H.M.; Kooistra, L.; Clevers, J.G. Improved estimation of leaf area index and leaf chlorophyll content of a potato crop using multi-angle spectral data-potential of unmanned aerial vehicle imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 14–26. [Google Scholar] [CrossRef]
- Li, W.; Sun, Z.; Lu, S.; Omasa, K. Estimation of the leaf chlorophyll content using multiangular spectral reflectance factor. Plant Cell Environ. 2019, 42, 3152–3165. [Google Scholar] [CrossRef]
- Yang, Q.; Huang, W.; Zhao, J.; Dong, L.; Huang, L.; Zhang, D.; Liu, L.; Yang, G.; Song, X. Effect of Canopy Geometry on Estimation of Leaf Area Index in Winter Wheat Using Multi-angle Spectrum. Int. J. Agric. Biol. 2013, 15, 1187–1192. [Google Scholar]
- Guo, B.; Zhu, Y.; Feng, W.; He, L.; Wu, Y.; Zhou, Y.; Ren, X.; Ma, Y. Remotely estimating aerial N uptake in winter wheat using red-edge area index from multi-angular hyperspectral data. Front. Plant Sci. 2018, 9, 675. [Google Scholar] [CrossRef]
- Wang, L.; Liao, Q.; Xu, X.; Li, Z.; Zhu, H. Estimating the vertical distribution of chlorophyll in winter wheat based on multi-angle hyperspectral data. Remote Sens. Lett. 2020, 11, 1032–1041. [Google Scholar]
- Jackson, R.D.; Teillet, P.M.; Slater, P.N.; Fedosejevs, G.; Jasinski, M.F.; Aase, J.K.; Moran, M.S. Bidirectional measurements of surface reflectance for view angle corrections of oblique imagery. Remote Sens. Environ. 1990, 32, 189–202. [Google Scholar]
- Kimes, D.S.; Newcomb, W.W.; Tucker, C.J.; Zonneveld, I.S.; Van Wijngaarden, W.; De Leeuw, J.; Epema, G.F. Directional reflectance factor distributions for cover types of Northern Africa. Remote Sens. Environ. 1985, 18, 1–19. [Google Scholar] [CrossRef]
- Ranjan, R.; Chopra, U.K.; Sahoo, R.N.; Singh, A.K.; Pradhan, S. Assessment of plant nitrogen stress in wheat (Triticum aestivum L.) through hyperspectral indices. Int. J. Remote Sens. 2012, 33, 6342–6360. [Google Scholar] [CrossRef]
- Yao, H.; Zhang, Y.; Yi, X.; Zhang, X.; Fan, D.; Chow, W.S.; Zhang, W. Diaheliotropic leaf movement enhances leaf photosynthetic capacity and photosynthetic light and nitrogen use efficiency via optimising nitrogen partitioning among photosynthetic components in cotton (Gossypium hirsutum L.). Plant Biol. 2018, 20, 213–222. [Google Scholar]
- Dumas, J. Procédés de l’analyse organique. Ann. Chim. Phys. 1831, 47, 198–205. [Google Scholar]
- Yang, M.; Huang, C.; Kang, X.; Qin, S.; Ma, L.; Wang, J.; Zhou, X.; Lv, X.; Zhang, Z. Early Monitoring of Cotton Verticillium Wilt by Leaf Multiple “Symptom” Characteristics. Remote Sens. 2022, 14, 5241. [Google Scholar]
- Li, F.; Miao, Y.; Feng, G.; Yuan, F.; Yue, S.; Gao, X.; Liu, Y.; Liu, B.; Ustin, S.L.; Chen, X. Improving estimation of summer maize nitrogen status with red edge-based spectral vegetation indices. Field Crop. Res. 2014, 157, 111–123. [Google Scholar]
- Evain, S.; Flexas, J.; Moya, I. A new instrument for passive remote sensing: 2. Measurement of leaf and canopy reflectance changes at 531 nm and their relationship with photosynthesis and chlorophyll fluorescence. Remote Sens. Environ. 2004, 91, 175–185. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf-area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with Erts. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I.; Gamon, J.A. Assessment of photosynthetic radiation—Use efficiency with spectral reflectance. New Phytol. 1995, 131, 291–296. [Google Scholar]
- Penuelas, J.; Baret, F.; Filella, I. Semi-empirical indices to assess carotenoids/chlorophyll a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Daughtry, C.S.; Walthall, C.L.; Kim, M.S.; De Colstoun, E.B.; McMurtrey Iii, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar]
- Schleicher, T.D.; Bausch, W.C.; Delgado, J.A.; Ayers, P.D. Evaluation and refinement of the nitrogen reflectance index (NRI) for site-specific fertilizer management. In Proceedings of the 2001 ASAE Annual Meeting: American Society of Agricultural and Biological Engineers, New Orleans, LA, USA, 23–27 June 1998; p. 1. [Google Scholar]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Marshak, A.; Knyazikhin, Y.; Davis, A.B.; Wiscombe, W.J.; Pilewskie, P. Cloud-vegetation interaction: Use of normalized difference cloud index for estimation of cloud optical thickness. Geophys. Res. Lett. 2000, 27, 1695–1698. [Google Scholar] [CrossRef]
- Peñuelas, J.; Gamon, J.A.; Fredeen, A.L.; Merino, J.; Field, C.B. Reflectance indices associated with physiological changes in nitrogen-and water-limited sunflower leaves. Remote Sens. Environ. 1994, 48, 135–146. [Google Scholar] [CrossRef]
- Gamon, J.A.; Penuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar]
- Feng, W.; Guo, B.; Wang, Z.; He, L.; Song, X.; Wang, Y.; Guo, T. Measuring leaf nitrogen concentration in winter wheat using double-peak spectral reflection remote sensing data. Field Crop. Res. 2014, 159, 43–52. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar]
- Crippen, R.E. Calculating the vegetation index faster. Remote Sens. Environ. 1990, 34, 71–73. [Google Scholar]
- Dash, J.; Curran, P.J. Evaluation of the MERIS terrestrial chlorophyll index (MTCI). Adv. Space Res. 2007, 39, 100–104. [Google Scholar] [CrossRef]
- Barnes, J.D.; Balaguer, L.; Manrique, E.; Elvira, S.; Davison, A.W. A reappraisal of the use of DMSO for the extraction and determination of chlorophylls a and b in lichens and higher plants. Environ. Exp. Bot. 1992, 32, 85–100. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Kimes, D.S. Dynamics of directional reflectance factor distributions for vegetation canopies. Appl. Optics. 1983, 22, 1364–1372. [Google Scholar]
- He, L.; Zhang, H.; Zhang, Y.; Song, X.; Feng, W.; Kang, G.; Wang, C.; Guo, T. Estimating canopy leaf nitrogen concentration in winter wheat based on multi-angular hyperspectral remote sensing. Eur. J. Agron. 2016, 73, 170–185. [Google Scholar] [CrossRef]
- Colwell, J.E. Vegetation canopy reflectance. Remote Sens. Environ. 1974, 3, 175–183. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Schull, M.A.; Stenberg, P.; Moettus, M.; Rautiainen, M.; Yang, Y.; Marshak, A.; Carmona, P.L.; Kaufmann, R.K.; Lewis, P. Hyperspectral remote sensing of foliar nitrogen content. Proc. Natl. Acad. Sci. USA 2012, 110, E185–E192. [Google Scholar] [CrossRef]
- Lu, N.; Wang, W.; Zhang, Q.; Li, D.; Yao, X.; Tian, Y.; Zhu, Y.; Cao, W.; Baret, F.; Liu, S. Estimation of nitrogen nutrition status in winter wheat from unmanned aerial vehicle based multi-angular multispectral imagery. Front. Plant Sci. 2019, 10, 1601. [Google Scholar]
- Asner, G.P. Biophysical and biochemical sources of variability in canopy reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Raper, T.B.; Varco, J.J. Canopy-scale wavelength and vegetative index sensitivities to cotton growth parameters and nitrogen status. Precis. Agric. 2015, 16, 62–76. [Google Scholar]
- Schutt, J.B.; Kimes, D.S.; Newcomb, W.W. Effect of heliotropism on the bidirectional reflectance of irrigated cotton. Remote Sens. Environ. 1985, 17, 13–25. [Google Scholar] [CrossRef]
- Verrelst, J.; Schaepman, M.E.; Koetz, B.; Kneubühler, M. Angular sensitivity analysis of vegetation indices derived from CHRIS/PROBA data. Remote Sens. Environ. 2008, 112, 2341–2353. [Google Scholar] [CrossRef]
- Yang, P. Exploring the interrelated effects of soil background, canopy structure and sun-observer geometry on canopy photochemical reflectance index. Remote Sens. Environ. 2022, 279, 113133. [Google Scholar] [CrossRef]
- Song, X.; Xu, D.; He, L.; Feng, W.; Wang, Y.; Wang, Z.; Coburn, C.A.; Guo, T. Using multi-angle hyperspectral data to monitor canopy leaf nitrogen content of wheat. Precis. Agric. 2016, 17, 721–736. [Google Scholar] [CrossRef]
- Burkart, A.; Aasen, H.; Alonso, L.; Menz, G.; Bareth, G.; Rascher, U. Angular dependency of hyperspectral measurements over wheat characterized by a novel UAV based goniometer. Remote Sens. 2015, 7, 725–746. [Google Scholar]
- Roosjen, P.P.; Suomalainen, J.M.; Bartholomeus, H.M.; Kooistra, L.; Clevers, J.G. Mapping reflectance anisotropy of a potato canopy using aerial images acquired with an unmanned aerial vehicle. Remote Sens. 2017, 9, 417. [Google Scholar]
- Roosjen, P.P.; Suomalainen, J.M.; Bartholomeus, H.M.; Clevers, J.G. Hyperspectral reflectance anisotropy measurements using a pushbroom spectrometer on an unmanned aerial vehicle—Results for barley, winter wheat, and potato. Remote Sens. 2016, 8, 909. [Google Scholar] [CrossRef]
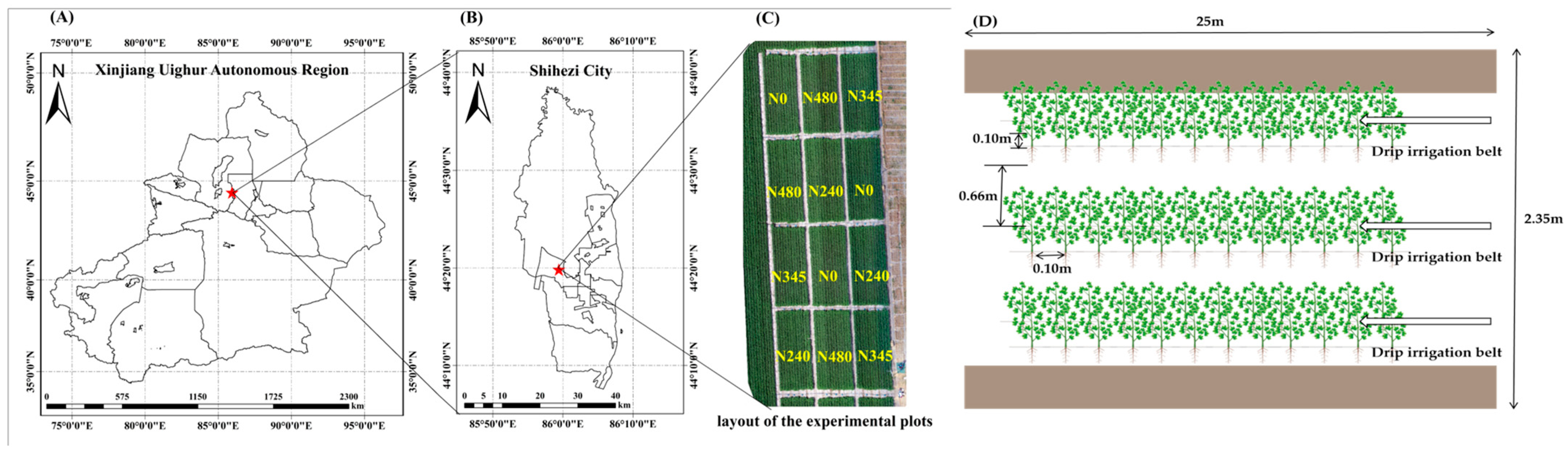
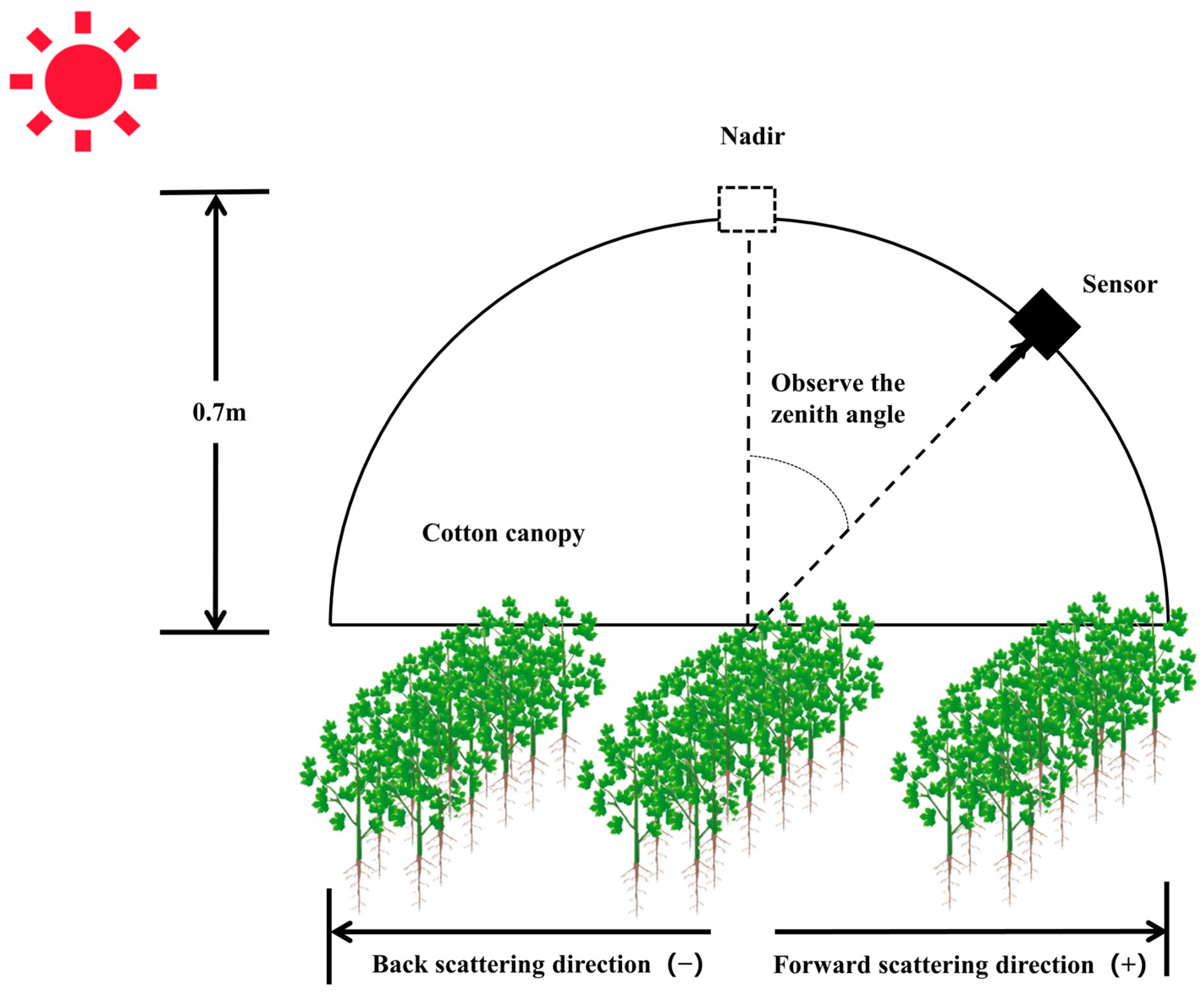





| Date/Dosage | Treatment/Proportion | N0 (0 kg/ha) | N240 (240 kg/ha) | N480 (480 kg/ha) | N345 (345 kg/ha) |
|---|---|---|---|---|---|
| 13 June | 5% | 0 | 75.16 | 150.32 | 108.04 |
| 21 June | 5% | 0 | 75.16 | 150.32 | 108.04 |
| 30 June | 10% | 0 | 150.32 | 300.64 | 216.09 |
| 6 July | 15% | 0 | 225.48 | 450.96 | 324.13 |
| 14 July | 18% | 0 | 270.58 | 541.16 | 388.96 |
| 21 July | 18% | 0 | 270.58 | 541.16 | 388.96 |
| 27 July | 17% | 0 | 255.55 | 511.09 | 367.35 |
| 5 August | 8% | 0 | 120.26 | 240.51 | 172.87 |
| 11 August | 4% | 0 | 60.13 | 120.26 | 86.43 |
| Spectral Index | Name | Definition or Equation | Reference | |
|---|---|---|---|---|
| 1 | DVI | Difference vegetation index | DVI = R890 − R670 | Jorden (1969) [25] |
| 2 | NDVI | Normalized difference vegetation index | NDVI = (R890 − R670)/(R890 + R670) | Rouse et al. (1974) [26] |
| 3 | SAVI | Soil-adjusted vegetation index | SAVI = [(1 + L) (R890 − R670)]/(R890 + R670 + L), L = 0.5 | Huete (1988) [27] |
| 4 | PRI | Photochemical reflectance index | PRI = (R531 − R570)/(R531 + R570) | Penuelas (1995) [28] |
| 5 | SIPI | Structure Insensitive Pigment Index | SIPI = (R800 − R445)/(R800 − R680) | Penuelas (1995) [29] |
| 6 | GNDVI | Green Normalized difference vegetation index | GNDVI = (R750 − R550)/(R750 + R550) | Gitelson et al. (1996) [30] |
| 7 | OSAVI | Optimized Soil Adjusted Vegetation Index | OSAVI = (1 + 0.16)(R800 − R670)/(R800 − R670 + 0.16) | Rondeaux et al. (1996) [31] |
| 8 | TCARI | Transformed chlorophyll absorption reflectance index | TCARI = 3[(R700 − R670) − 0.2(R700 − R550) (R700/R670)] | Daughtry et al. (2000) [32] |
| 9 | NRI | Nitrogen reflectance index | NRI = (R570 − R670)/(R570 + R670) | Schleicher et al. (1998) [33] |
| 10 | TCARI/OSAVI | TCARI/OSAVI | TCARI/OSAVI = TCARI/OSAVI | Haboudane et al. (2002) [34] |
| 11 | NDCI | Double-peak canopy nitrogen index | NDCI = (R762 − R527)/(R762 + R527) | Marshak et al. (2000) [35] |
| 12 | NPCI | Normalized pigment chlorophyll ratio index | NPCI = (R430 − R680)/(R430 + R680) | Peuelas et al. (1994) [36] |
| 13 | PRIC | Photochemical reflectance index correction | PRIC = (R570 − R539)/(R570 + R539) | Gamon et al. (1992) [37] |
| 14 | DDNI | Novel double-peak area index | DDNI = (R755 + R680 − 2 × R705)/(R755 − R680) | Feng et al. (2014) [38] |
| 15 | mSR705 | Modified Red-edge Ratio | mSR705 = (R750 − R445)/(R705 + R445) | Sims et al. (2002) [39] |
| 16 | IPVI | Infrared Percentage Vegetation Index | IPVI = R800/(R800 + R670) | Crippen et al. (1990) [40] |
| 17 | MTCI | Modified triangular vegetation index | MTCI = (R754 − R709)/(R709 − R681) | Dash et al. (2007) [41] |
| 18 | NPQI | Normalized Phaeophytinization Index | NPQI = (R415 − R435)/(R415 + R435) | Barnes et al. (1992) [42] |
| 19 | CIred-edge3 | Red edge model | CIred-edge3 = (R790/R720) − 1 | Gitelson et al. (2005) [43] |
| Spectral Indices | −60° | −50° | −40° | −30° | −20° | −10° | 0° | 10° | 20° | 30° | 40° | 50° | 60° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| visible band | |||||||||||||
| PRI | 0.849 ** | 0.857 ** | 0.853 ** | 0.861 ** | 0.866 ** | 0.849 ** | 0.849 ** | 0.848 ** | 0.835 ** | 0.836 ** | 0.847 ** | 0.857 ** | 0.829 ** |
| PRIC | −0.796 ** | −0.801 ** | −0.790 ** | −0.804 ** | −0.796 ** | −0.777 ** | −0.818 ** | −0.832 ** | −0.822 ** | −0.832 ** | −0.842 ** | −0.842 ** | −0.796 ** |
| NPQI | −0.465 ** | −0.666 ** | −0.541 ** | −0.563 ** | −0.582 ** | −0.592 ** | −0.671 ** | −0.702 ** | −0.658 ** | −0.782 ** | −0.800 ** | −0.746 ** | −0.565 ** |
| visible band, Red edge | |||||||||||||
| GNDVI | 0.071 | 0.379 ** | 0.286 ** | 0.286 ** | 0.275 ** | 0.288 ** | 0.333 ** | 0.358 ** | 0.364 ** | 0.316 ** | 0.278 ** | 0.281 ** | 0.041 |
| TCARI | −0.138 | −0.281 ** | −0.202 ** | −0.192 ** | −0.217 ** | −0.279 ** | −0.349 ** | −0.386 ** | −0.364 ** | −0.341 ** | −0.276 ** | −0.286 ** | −0.371 ** |
| NRI | 0.065 | 0.173 * | 0.092 | 0.08 | 0.137 | 0.095 | 0.098 | 0.113 | 0.201 ** | 0.229 ** | 0.229 ** | 0.206 ** | 0.116 |
| NDCI | −0.034 | 0.229 ** | 0.142 | 0.144 | 0.152 * | 0.162 * | 0.213 ** | 0.234 ** | 0.269 ** | 0.215 ** | 0.170 * | 0.173 * | −0.036 |
| NPCI | 0.166 * | 0.231 ** | 0.08 | 0.034 | 0.115 | 0.05 | 0.105 | 0.077 | 0.152 * | 0.186 * | 0.129 | 0.078 | 0.147 * |
| mSR705 | 0.676 ** | 0.656 ** | 0.629 ** | 0.651 ** | 0.658 ** | 0.633 ** | 0.656 ** | 0.664 ** | 0.637 ** | 0.678 ** | 0.709 ** | 0.750 ** | 0.790 ** |
| AINI | 0.851 ** | 0.893 ** | 0.890 ** | 0.880 ** | 0.871 ** | 0.862 ** | 0.852 ** | 0.857 ** | 0.830 ** | 0.827 ** | 0.844 ** | 0.851 ** | 0.816 ** |
| visible band, Red edge, NIR | |||||||||||||
| SIPI | −0.061 | −0.406 ** | −0.290 ** | −0.326 ** | −0.342 ** | −0.328 ** | −0.408 ** | −0.368 ** | −0.425 ** | −0.503 ** | −0.570 ** | −0.562 ** | −0.630 ** |
| TCARI/OSAVI | −0.164 * | −0.328 ** | −0.255 ** | −0.250 ** | −0.279 ** | −0.342 ** | −0.403 ** | −0.445 ** | −0.422 ** | −0.408 ** | −0.363 ** | −0.378 ** | −0.461 ** |
| Red edge, NIR | |||||||||||||
| DVI | 0.052 | 0.041 | 0.077 | 0.106 | 0.095 | 0.099 | 0.055 | 0.049 | 0.097 | 0.076 | 0.161 * | 0.168 * | 0.097 |
| NDVI | 0.04 | 0.361 ** | 0.260 ** | 0.291 ** | 0.300 ** | 0.292 ** | 0.363 ** | 0.371 ** | 0.408 ** | 0.377 ** | 0.361 ** | 0.323 ** | 0.021 |
| SAVI | 0.02 | 0.068 | 0.084 | 0.113 | 0.117 | 0.157 * | 0.127 | 0.122 | 0.181 * | 0.146 | 0.208 ** | 0.227 ** | 0.071 |
| OSAVI | −0.007 | −0.042 | 0.021 | 0.056 | 0.059 | 0.121 | 0.08 | 0.07 | 0.107 | 0.103 | 0.183 * | 0.198 ** | 0.122 |
| DDNI | 0.510 ** | 0.619 ** | 0.633 ** | 0.656 ** | 0.661 ** | 0.649 ** | 0.660 ** | 0.663 ** | 0.637 ** | 0.642 ** | 0.643 ** | 0.687 ** | 0.737 ** |
| IPVI | −0.002 | 0.370 ** | 0.276 ** | 0.306 ** | 0.314 ** | 0.305 ** | 0.376 ** | 0.385 ** | 0.423 ** | 0.395 ** | 0.380 ** | 0.341 ** | 0.031 |
| MTCI | 0.665 ** | 0.664 ** | 0.671 ** | 0.683 ** | 0.686 ** | 0.669 ** | 0.669 ** | 0.680 ** | 0.647 ** | 0.672 ** | 0.685 ** | 0.721 ** | 0.754 ** |
| CIred-edge3 | 0.607 ** | 0.661 ** | 0.640 ** | 0.650 ** | 0.648 ** | 0.637 ** | 0.638 ** | 0.653 ** | 0.619 ** | 0.620 ** | 0.633 ** | 0.654 ** | 0.559 ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Yang, M.; Chen, X.; Ma, L.; Yin, C.; Qin, S.; Wang, L.; Lv, X.; Zhang, Z. Estimation of Cotton Nitrogen Content Based on Multi-Angle Hyperspectral Data and Machine Learning Models. Remote Sens. 2023, 15, 955. https://doi.org/10.3390/rs15040955
Zhou X, Yang M, Chen X, Ma L, Yin C, Qin S, Wang L, Lv X, Zhang Z. Estimation of Cotton Nitrogen Content Based on Multi-Angle Hyperspectral Data and Machine Learning Models. Remote Sensing. 2023; 15(4):955. https://doi.org/10.3390/rs15040955
Chicago/Turabian StyleZhou, Xiaoting, Mi Yang, Xiangyu Chen, Lulu Ma, Caixia Yin, Shizhe Qin, Lu Wang, Xin Lv, and Ze Zhang. 2023. "Estimation of Cotton Nitrogen Content Based on Multi-Angle Hyperspectral Data and Machine Learning Models" Remote Sensing 15, no. 4: 955. https://doi.org/10.3390/rs15040955
APA StyleZhou, X., Yang, M., Chen, X., Ma, L., Yin, C., Qin, S., Wang, L., Lv, X., & Zhang, Z. (2023). Estimation of Cotton Nitrogen Content Based on Multi-Angle Hyperspectral Data and Machine Learning Models. Remote Sensing, 15(4), 955. https://doi.org/10.3390/rs15040955







