Structural Nonlinear Damage Identification Method Based on the Kullback–Leibler Distance of Time Domain Model Residuals
Abstract
1. Introduction
2. Basic theory of AR model
2.1. AR Model
2.2. Order Determination of AR Model
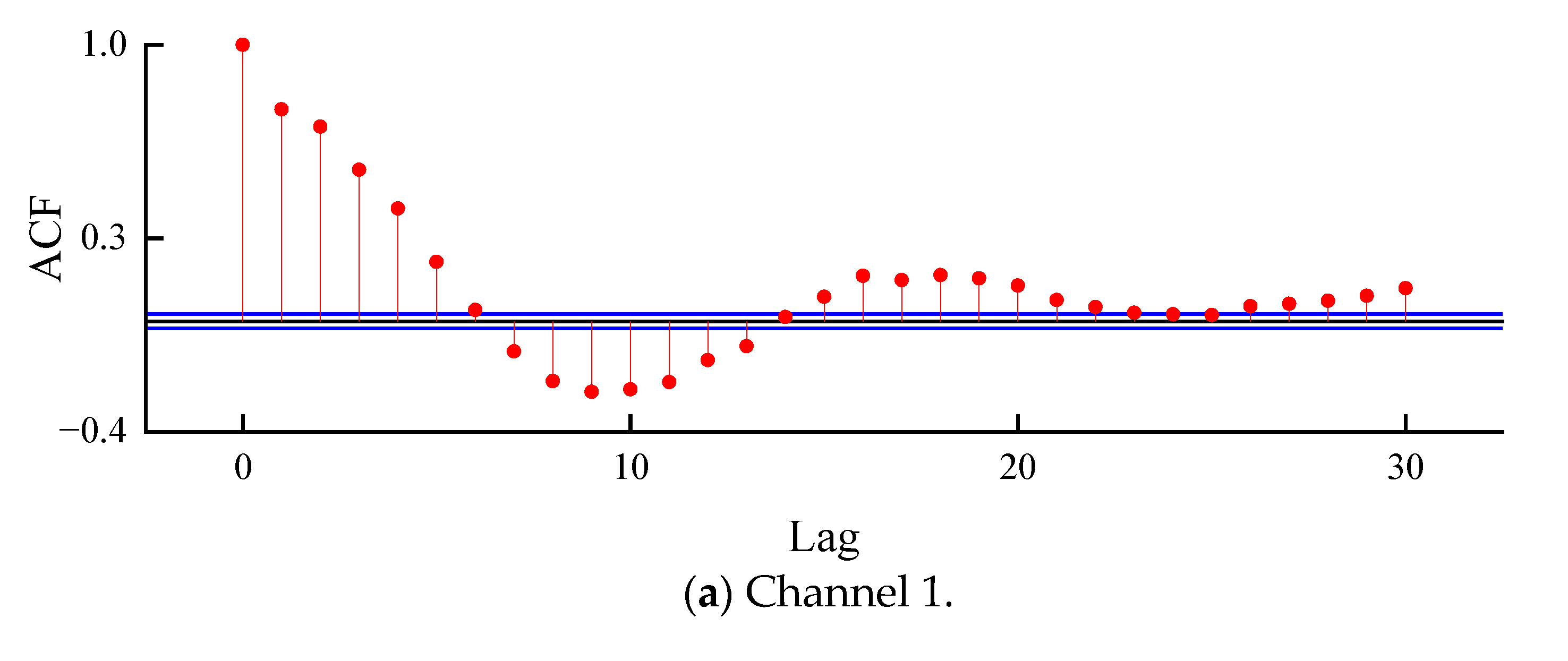
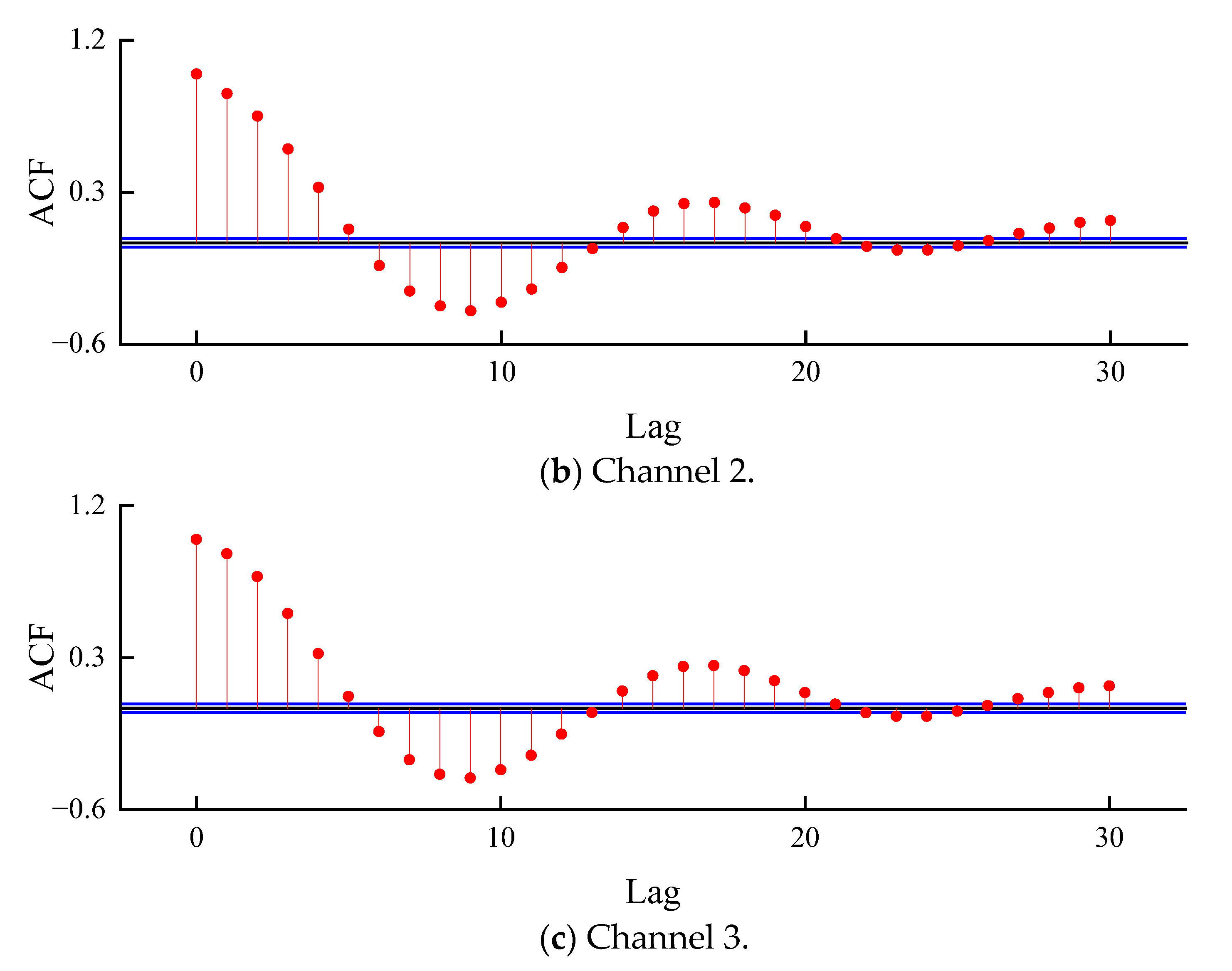
2.3. Parameter Estimation of AR Model
3. Damage Identification Based on the KL Distance of Time Series Model Residual
3.1. Nonlinear Damage in Time Domain
3.2. Nonlinear Damage Identification Based on the SOVI
3.3. Nonlinear Damage Identification Method Based on the KL Distance of the AR Model Residual
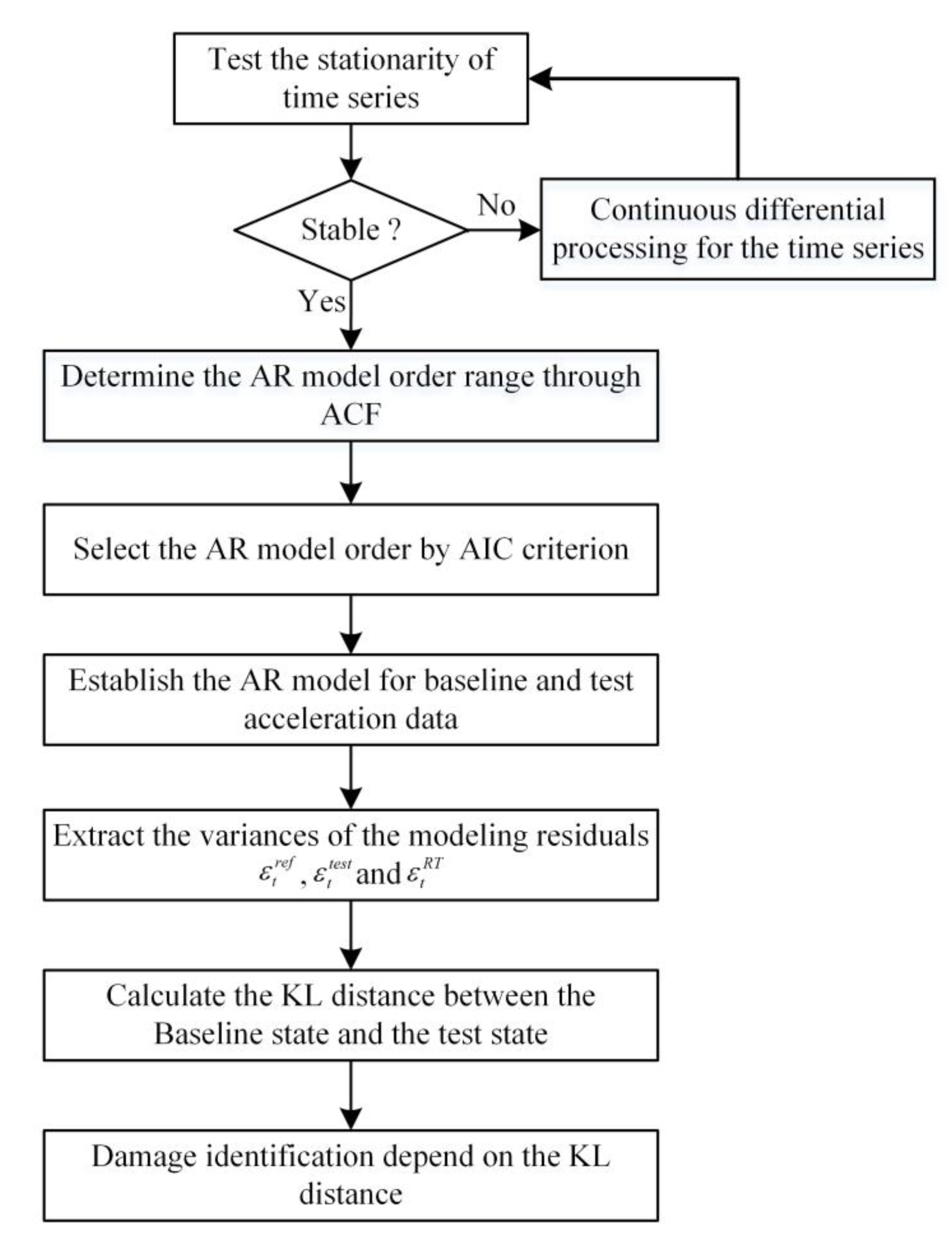
3.4. Process of Damage Identification Using the KL Distance of the AR Model Residual
4. Numerical Example
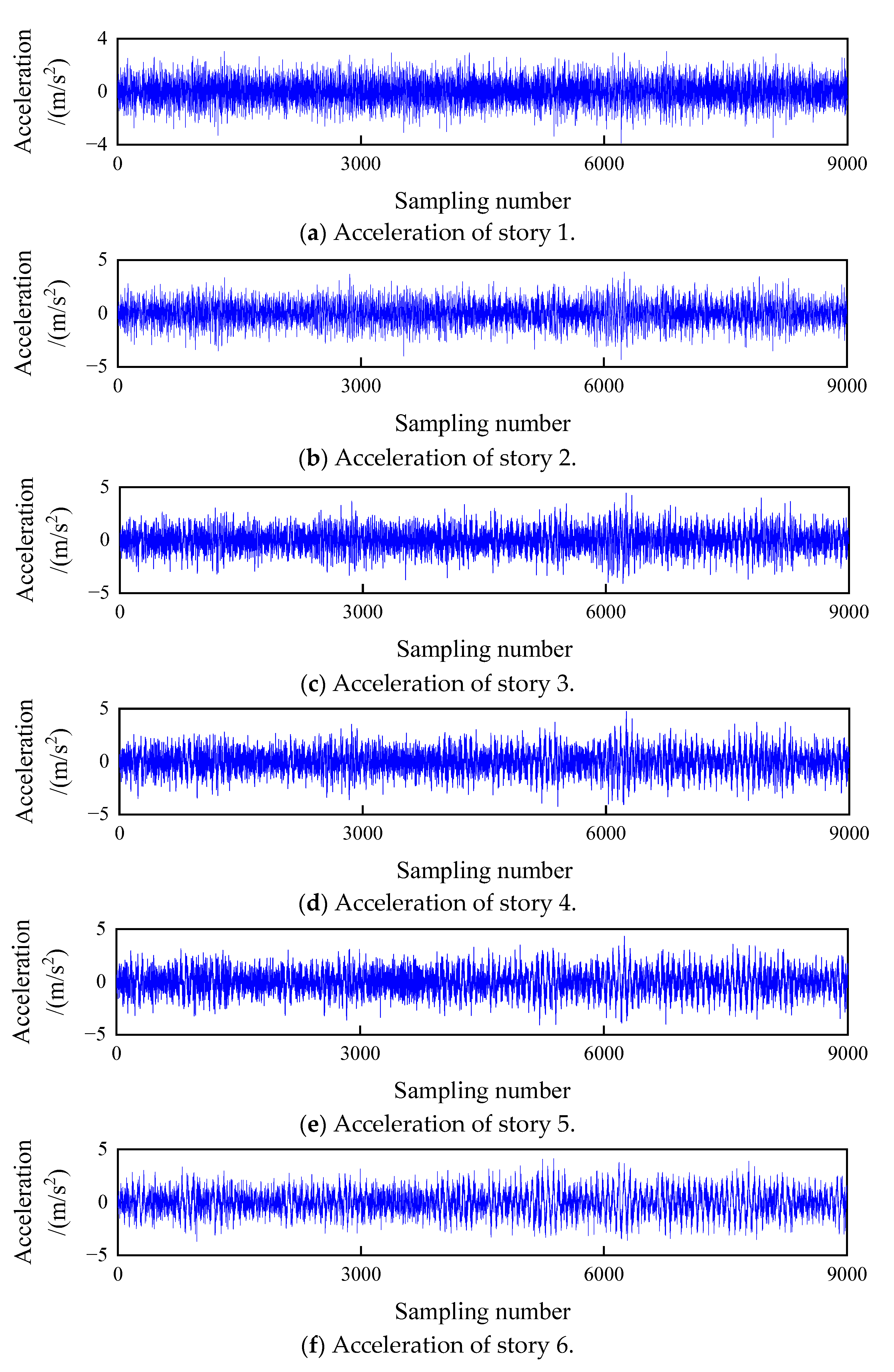
4.1. Simulation of Eight-Story Shear Building Model
4.2. Establishment of AR Model
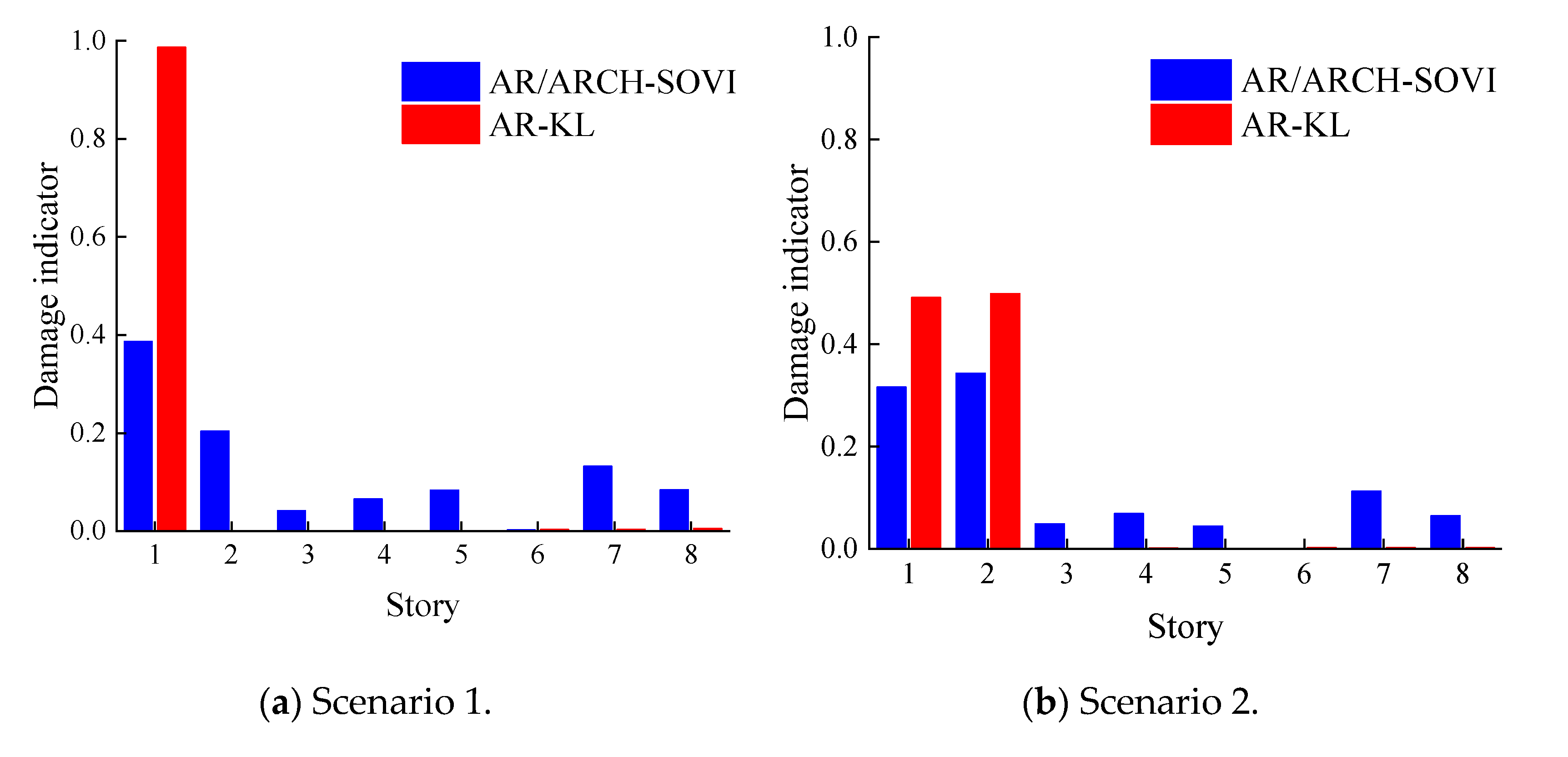
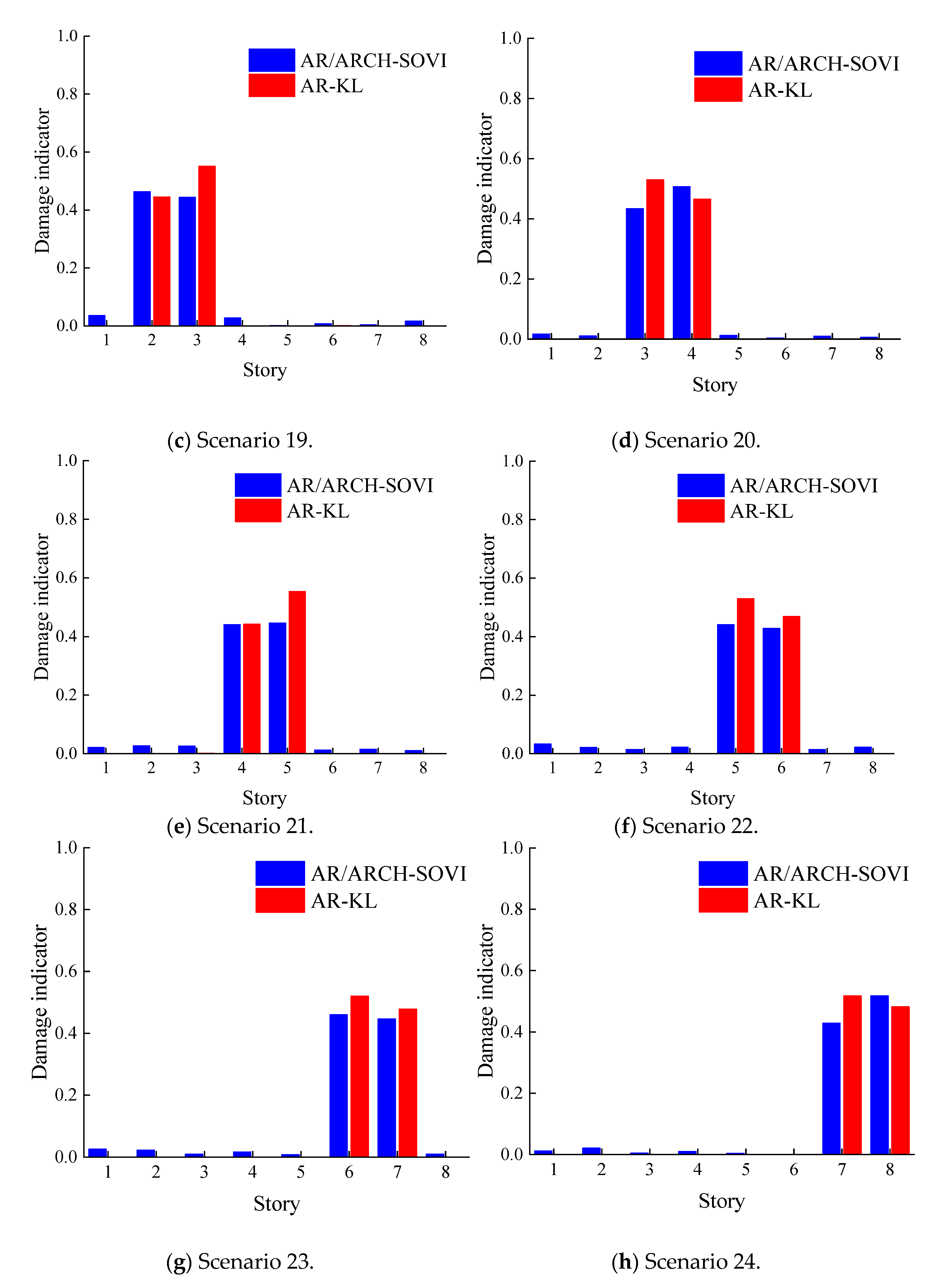
4.3. Nonlinear Damage Identification Results
5. Experimental Study on the Stand Structure Model
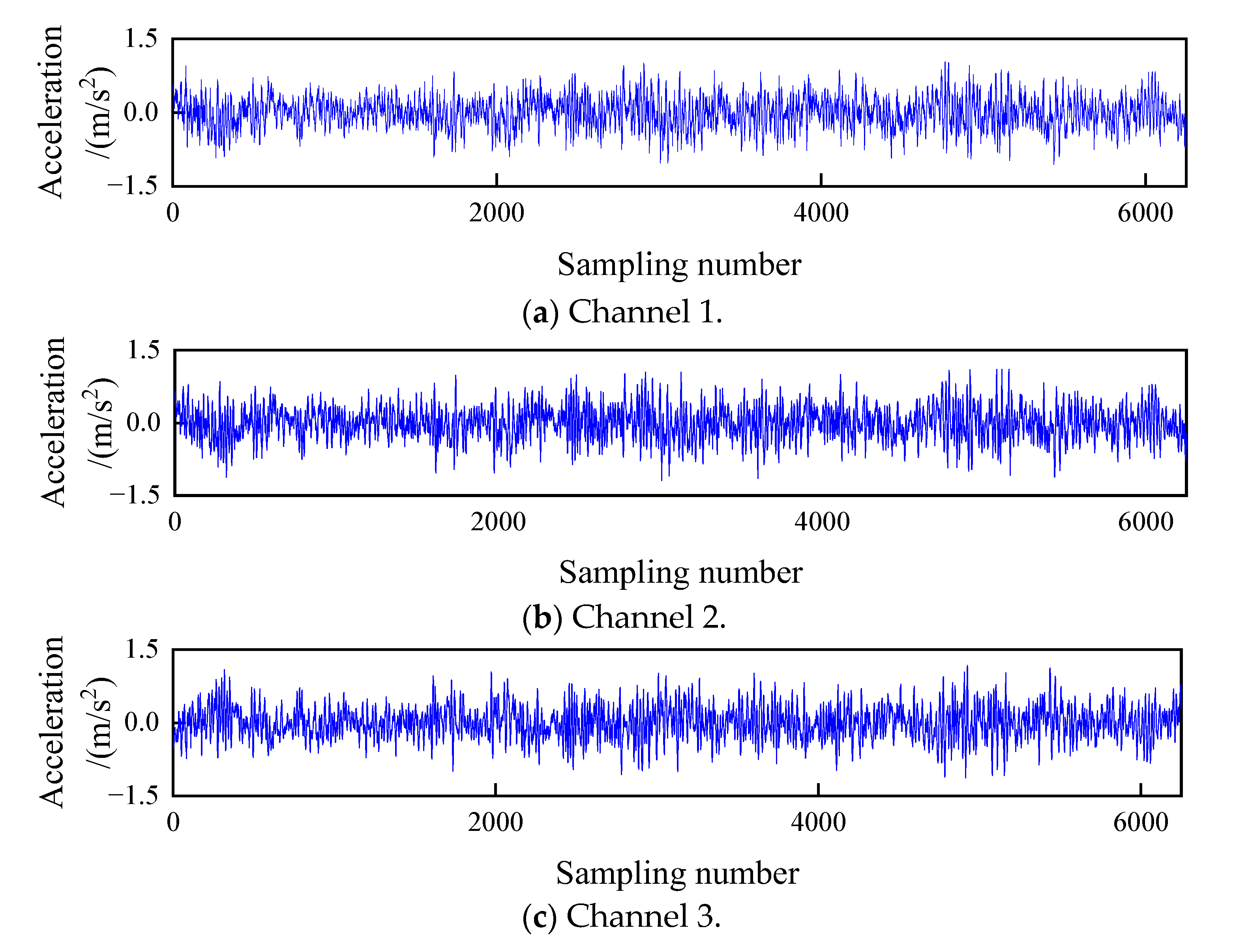
5.1. Introduction of the Stand Structure Model Experiment
5.2. Modeling Analysis of AR Model
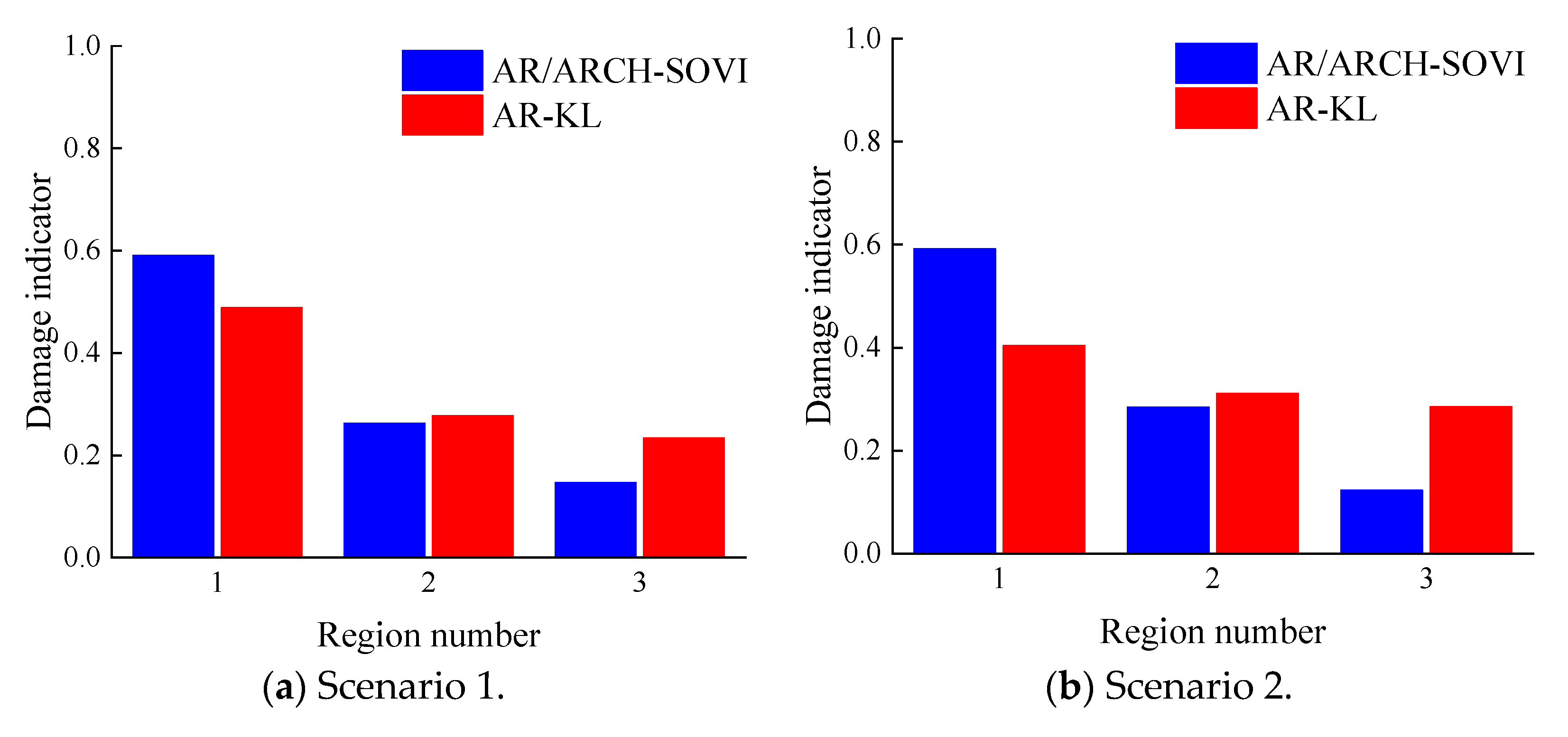
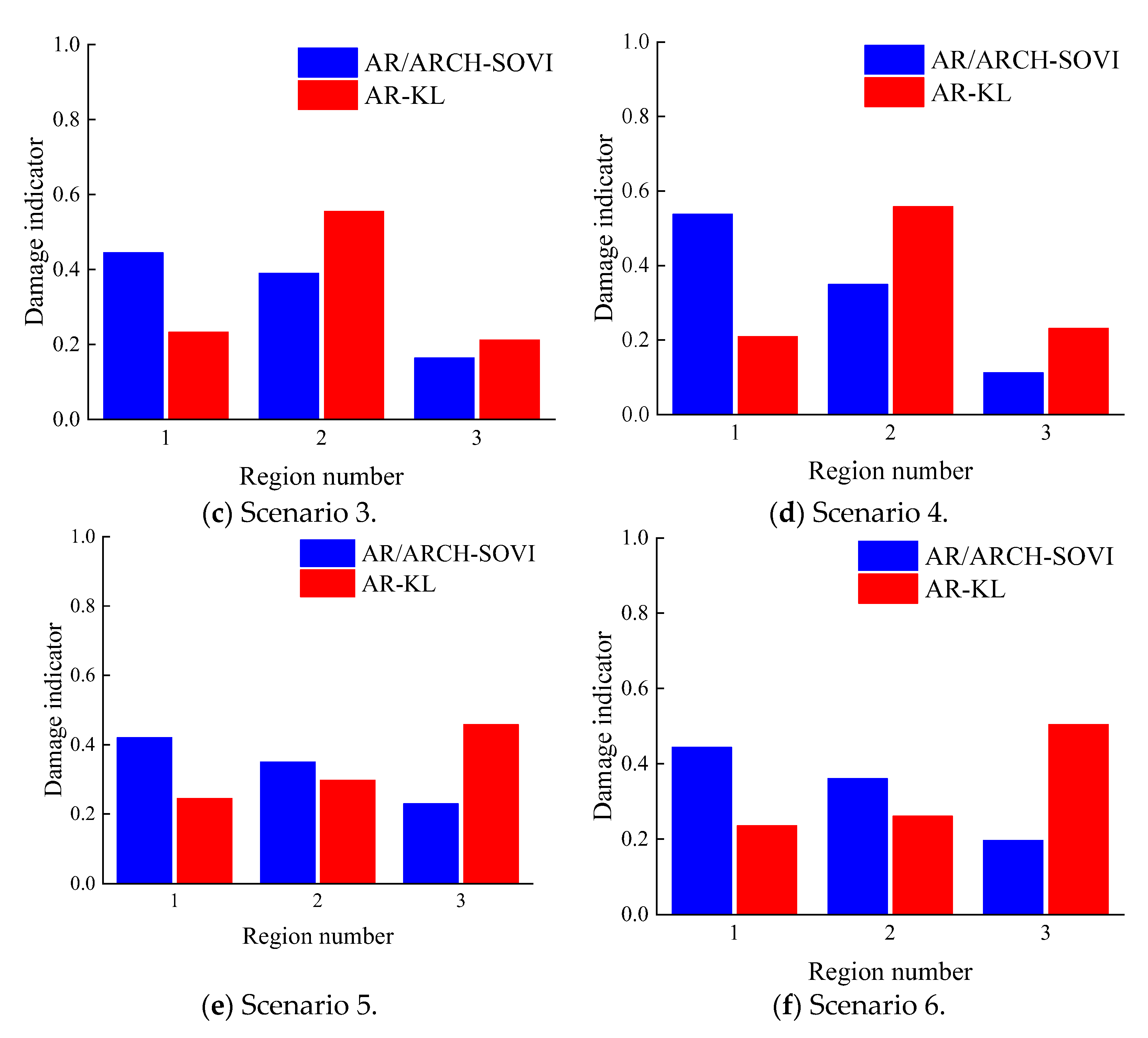
5.3. Damage Identification Results of the Stand Structure Model Experiment
6. Discussion
7. Conclusions
- (1)
- The proposed method is a damage identification method based on the substructure. The damage indicator of the damaged story is larger than the other stories, which can determine the structural damage location accurately.
- (2)
- The proposed method can accurately distinguish nonlinear damage of a multi-degree-of-freedom shear structure caused by bilinear stiffness changes. This method is robust enough to analyze environmental noise and small damage.
- (3)
- The proposed method can effectively find nonlinear damage in a multi-story and multi-span complex structure caused by bolt looseness, which is beneficial in practical applications.
- (4)
- In this paper, only a multi-degrees-of-freedom shear structure and a stand structure were used to verify the proposed method, and the nonlinear damage identification problem of more structural types should be considered in subsequent research.
- (5)
- This paper only considers the damage identification results of white noise conducted from the ground to the structure, and the damage identification results of excitation at different locations should be considered in subsequent research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Worden, K.; Farrar, C.R.; Haywood, J.; Todd, M. A review of nonlinear dynamics applications to structural health monitoring. Struct. Control. Health Monit. 2008, 15, 540–567. [Google Scholar] [CrossRef]
- Adams, D.E.; Farrar, C.R. Classifying Linear and Nonlinear Structural Damage Using Frequency Domain ARX Models. Struct. Health Monit.-Int. J. 2002, 1, 185–201. [Google Scholar] [CrossRef]
- Lakshmi, K.; Keerthivas, M. Damage diagnosis of high-rise buildings under variable ambient conditions using subdomain approach. Inverse Probl. Sci. Eng. 2021, 29, 2579–2610. [Google Scholar] [CrossRef]
- Li, Y.; Sun, W.; Jiang, R.; Han, Y. Signal-segments cross-coherence method for nonlinear structural damage detection using free-vibration signals. Adv. Struct. Eng. 2020, 23, 1041–1054. [Google Scholar] [CrossRef]
- Prawin, J.; Rao, A.R.M. Damage detection in nonlinear systems using an improved describing function approach with limited instrumentation. Nonlinear Dyn. 2019, 96, 1447–1470. [Google Scholar] [CrossRef]
- Chen, L.; Yu, L.; Fu, J.; Ng, C.T. Nonlinear damage detection using linear ARMA models with classification algorithms. Smart Struct. Syst. 2020, 26, 23–33. [Google Scholar]
- Prawin, J.; Rama Mohan Rao, A. Vibration-based breathing crack identification using non-linear intermodulation components under noisy environment. Struct. Health Monit. 2019, 19, 86–104. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, R.; Tapia, J.; Wang, S.; Sun, W. Structural damage identification based on short-time temporal coherence using free-vibration response signals. Measurement 2020, 151, 107209. [Google Scholar] [CrossRef]
- Xin, Y.; Li, J.; Hao, H. Damage Detection in Initially Nonlinear Structures Based on Variational Mode Decomposition. Int. J. Struct. Stab. Dyn. 2020, 20, 2042009. [Google Scholar] [CrossRef]
- Chomette, B. Nonlinear multiple breathing cracks detection using direct zeros estimation of higher-order frequency response function. Commun. Nonlinear Sci. Numer. Simul. 2020, 89, 105330. [Google Scholar] [CrossRef]
- Zheng, Z.D.; Lu, Z.R.; Chen, W.H.; Liu, J.K. Structural damage identification based on power spectral density sensitivity analysis of dynamic responses. Comput. Struct. 2015, 146, 176–184. [Google Scholar] [CrossRef]
- Esfandiari, A. An innovative sensitivity-based method for structural model updating using incomplete modal data. Struct. Control. Health Monit. 2017, 24, 1896–1905. [Google Scholar] [CrossRef]
- Mirzaee, A.; Shayanfar, M.; Abbasnia, R. Damage Detection of Bridges Using Vibration Data by Adjoint Variable Method. Shock. Vib. 2014, 2014, 698658. [Google Scholar] [CrossRef]
- Zhu, H.; Yu, H.; Gao, F.; Weng, S.; Sun, Y.; Hu, Q. Damage identification using time series analysis and sparse regularization. Struct. Control. Health Monit. 2020, 27, e2554. [Google Scholar] [CrossRef]
- Mei, L.; Li, H.; Zhou, Y.; Li, D.; Long, W.; Xing, F. Output-Only Damage Detection of Shear Building Structures Using an Autoregressive Model-Enhanced Optimal Subpattern Assignment Metric. Sensors 2020, 20, 2050. [Google Scholar] [CrossRef]
- Do, N.T.; Gül, M. A time series based damage detection method for obtaining separate mass and stiffness damage features of shear-type structures. Eng. Struct. 2020, 208, 109914. [Google Scholar] [CrossRef]
- Prawin, J.; Rama Mohan Rao, A. Reference-Free Breathing Crack Identification of Beam-Like Structures Using an Enhanced Spatial Fourier Power Spectrum with Exponential Weighting Functions. Int. J. Struct. Stab. Dyn. 2019, 19, 1950017. [Google Scholar] [CrossRef]
- Voggu, S.; Sasmal, S. Dynamic nonlinearities for identification of the breathing crack type damage in reinforced concrete bridges. Struct. Health Monit.-Int. J. 2021, 20, 339–359. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, H.; Tan, X.; Chai, H.K.; Wang, R.; Zhang, Y. Fundamental mode shape estimation and element stiffness evaluation of girder bridges by using passing tractor-trailers. Mech. Syst. Signal Process. 2022, 169, 108746. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, H.; Tan, X.; Wang, R.; Zhang, Y. Mode Shape Identification and Damage Detection of Bridge by Movable Sensory System. IEEE Trans. Intell. Transp. Syst. 2022, 24, 1299–1313. [Google Scholar] [CrossRef]
- Cao, M.; Lu, Q.; Su, Z.; Radzieński, M.; Xu, W.; Ostachowicz, W. A nonlinearity-sensitive approach for detection of “breathing” cracks relying on energy modulation effect. J. Sound Vib. 2022, 524, 116754. [Google Scholar] [CrossRef]
- Yang, Y.; Ling, Y.; Tan, X.; Wang, S.; Wang, R. Damage identification of frame structure based on approximate Metropolis–Hastings algorithm and probability density evolution method. Int. J. Struct. Stab. Dyn. 2022, 22, 2240014. [Google Scholar] [CrossRef]
- Akaike, H. Maximum Likelihood Identification of Gaussian Autoregressive Moving Average Models. Biometrika 1973, 60, 255–265. [Google Scholar] [CrossRef]
- Amerini, F.; Meo, M. Structural health monitoring of bolted joints using linear and nonlinear acoustic/ultrasound methods. Struct. Health Monit.-Int. J. 2011, 10, 659–672. [Google Scholar] [CrossRef]
- Prawin, J.; Rao, A.R.M. A method for detecting damage-induced nonlinearity in structures using weighting function augmented curvature approach. Struct. Health Monit.-Int. J. 2019, 18, 1154–1167. [Google Scholar] [CrossRef]
- Niu, Z.R. Two-step structural damage detection method for shear frame structures using FRF and Neumann series expansion. Mech. Syst. Signal Process. 2021, 149, 18. [Google Scholar] [CrossRef]
- Rébillat, M.; Hajrya, R.; Mechbal, N. Nonlinear structural damage detection based on cascade of Hammerstein models. Mech. Syst. Signal Process. 2014, 48, 247–259. [Google Scholar] [CrossRef]
- Cheng, J.J.; Guo, H.Y.; Wang, Y.S. Structural Nonlinear Damage Detection Method Using AR/ARCH Model. Int. J. Struct. Stab. Dyn. 2017, 17, 1750083. [Google Scholar] [CrossRef]
- Prawin, J.; Lakshmi, K.; Rao, A.R.M. A novel vibration based breathing crack localization technique using a single sensor measurement. Mech. Syst. Signal Process. 2019, 122, 117–138. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Xu, W.; Su, Z.; Radzieński, M.; Cao, M.; Ostachowicz, W. Nonlinear pseudo-force in a breathing crack to generate harmonics. J. Sound Vib. 2021, 492, 115734. [Google Scholar] [CrossRef]




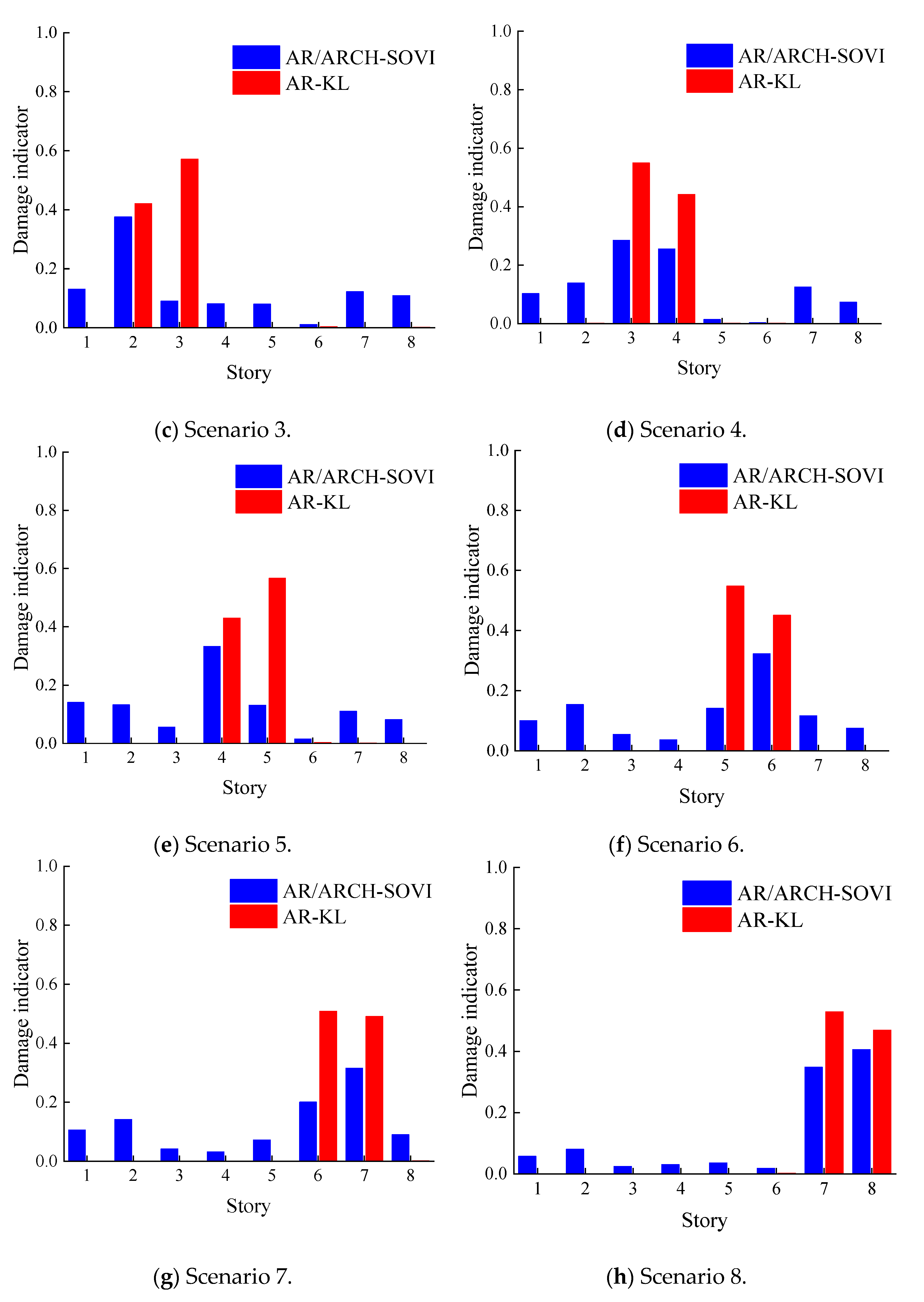
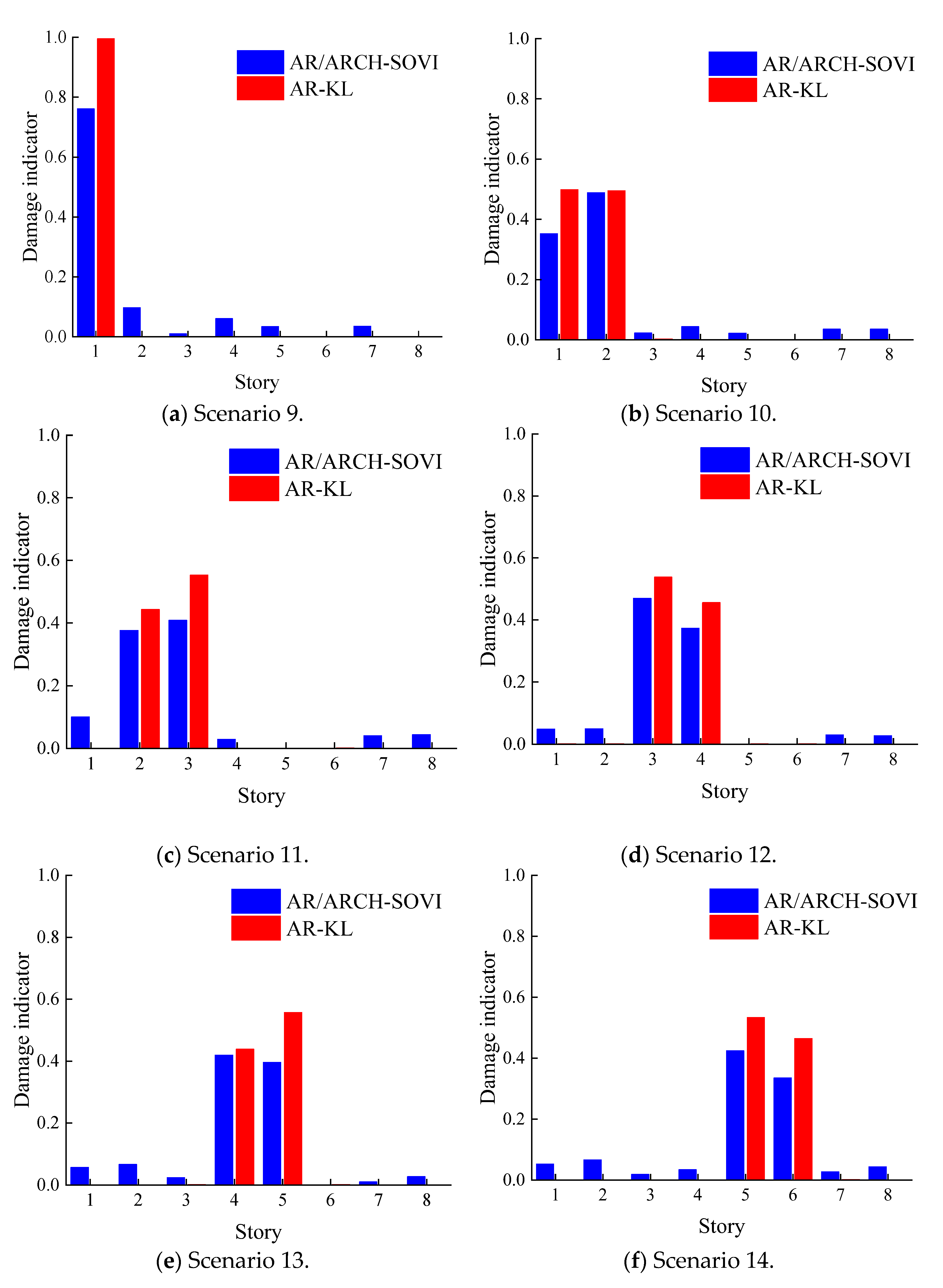
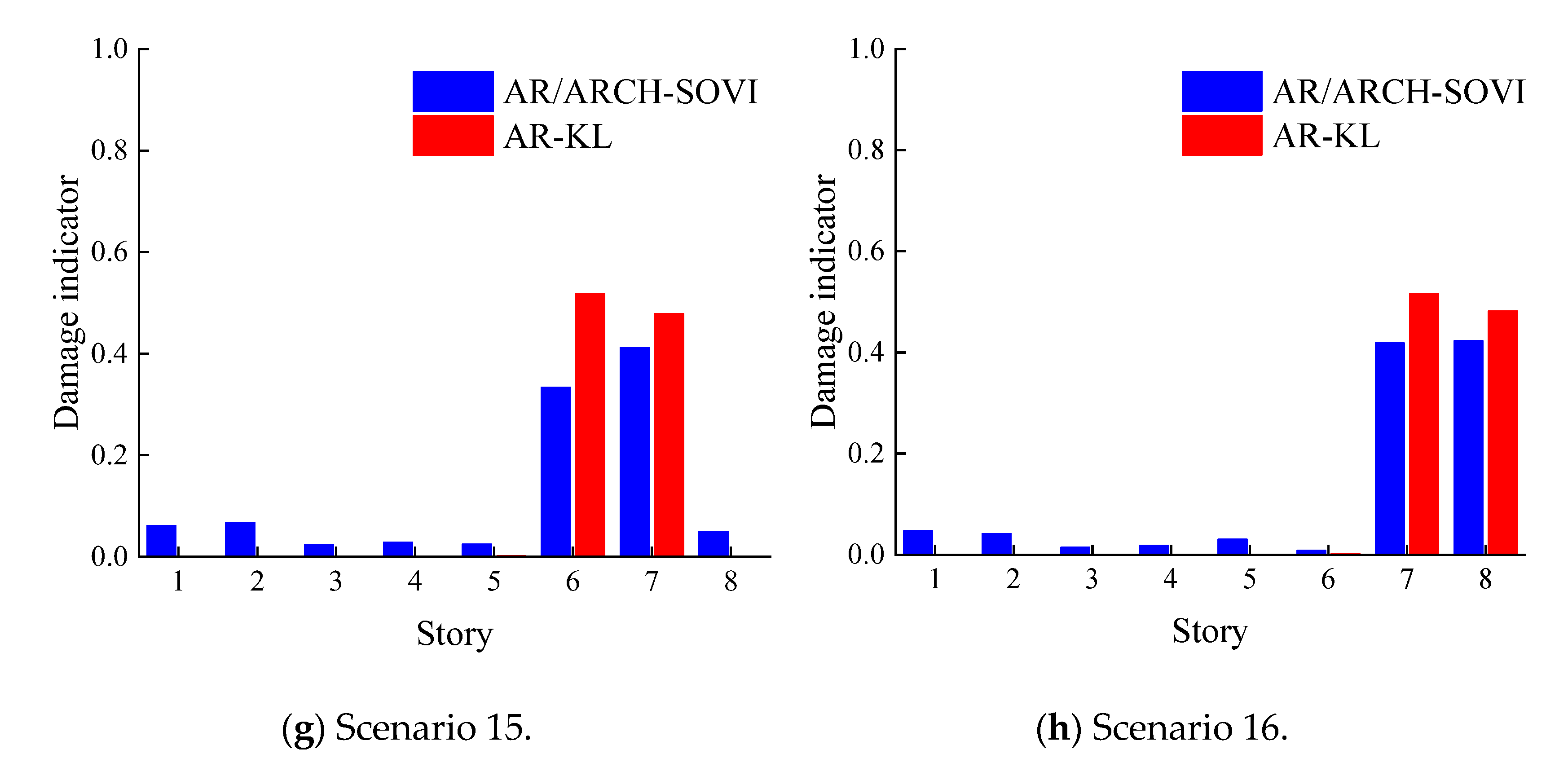
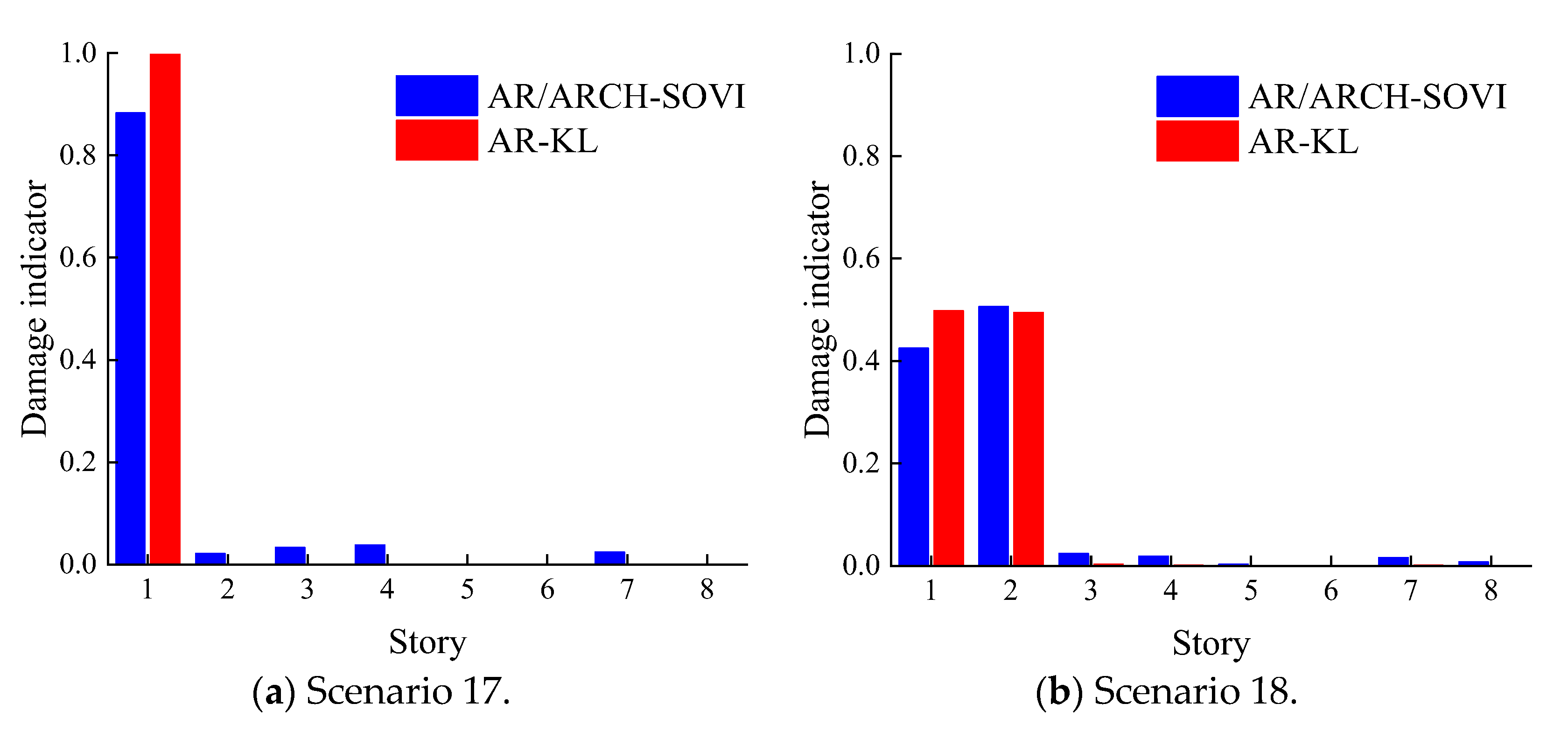


| Damage Scenarios | Damage Story | Damage Level | Excitation Amplitude/(kn) |
|---|---|---|---|
| 1 | 1 | 10% | 250 |
| 2 | 2 | 10% | 250 |
| 3 | 3 | 10% | 250 |
| 4 | 4 | 10% | 250 |
| 5 | 5 | 10% | 250 |
| 6 | 6 | 10% | 250 |
| 7 | 7 | 10% | 250 |
| 8 | 8 | 10% | 250 |
| 9 | 1 | 30% | 250 |
| 10 | 2 | 30% | 250 |
| 11 | 3 | 30% | 250 |
| 12 | 4 | 30% | 250 |
| 13 | 5 | 30% | 250 |
| 14 | 6 | 30% | 250 |
| 15 | 7 | 30% | 250 |
| 16 | 8 | 30% | 250 |
| 17 | 1 | 30% | 100 |
| 18 | 2 | 30% | 100 |
| 19 | 3 | 30% | 100 |
| 20 | 4 | 30% | 100 |
| 21 | 5 | 30% | 100 |
| 22 | 6 | 30% | 100 |
| 23 | 7 | 30% | 100 |
| 24 | 8 | 30% | 100 |
| Damage Scenario | Damaged Region | Bolt-Loosened Braces Number |
|---|---|---|
| 1 | 1 | B2 |
| 2 | 1 | B1, B2, B3 |
| 3 | 2 | B5 |
| 4 | 2 | B4, B5, B6 |
| 5 | 3 | B8 |
| 6 | 3 | B7, B8, B9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, H.; Guo, H. Structural Nonlinear Damage Identification Method Based on the Kullback–Leibler Distance of Time Domain Model Residuals. Remote Sens. 2023, 15, 1135. https://doi.org/10.3390/rs15041135
Zuo H, Guo H. Structural Nonlinear Damage Identification Method Based on the Kullback–Leibler Distance of Time Domain Model Residuals. Remote Sensing. 2023; 15(4):1135. https://doi.org/10.3390/rs15041135
Chicago/Turabian StyleZuo, Heng, and Huiyong Guo. 2023. "Structural Nonlinear Damage Identification Method Based on the Kullback–Leibler Distance of Time Domain Model Residuals" Remote Sensing 15, no. 4: 1135. https://doi.org/10.3390/rs15041135
APA StyleZuo, H., & Guo, H. (2023). Structural Nonlinear Damage Identification Method Based on the Kullback–Leibler Distance of Time Domain Model Residuals. Remote Sensing, 15(4), 1135. https://doi.org/10.3390/rs15041135





