Physical Mechanism and Parameterization for Correcting Radar Wave Velocity in Yellow River Ice with Air Temperature and Ice Thickness
Abstract
1. Introduction
- Ice thicknesses via radar detection and measured by drilling holes were collected. Ice temperature profiles under the radar were measured. Meteorological data of the entire ice season from nearby Toudaoguai Hydrological Station were gathered. Ice density, sediment content, and crystal structure of the ice sample were tested in the Toudaoguai Hydrological Station;
- The measured ice physical data were combined to analyze the tread of the radar wave velocity or dielectric permittivity in granular and columnar ice within the ice sample;
- Based on the sequence of 13 measured ice thicknesses, we sought to determine the physical logical relationship. It shows that the radar wave velocity or dielectric permittivity was controlled by the unfrozen water content in the ice. The unfrozen water content was dominated by the ice temperature, and the ice temperature was influenced by air temperature, radiation, and ice thickness;
- One parameterization scheme for dynamically correcting the radar wave velocity with air temperature and ice thickness was set up and improved the radar detection accuracy of ice thickness. The theoretical mechanism and statistical analyses results are also provided based on the previous literature;
- A method for developing a parameterization scheme for more complicated ice conditions, for example, frazil ice on the bottom of the ice cover and accumulated broken ice blocks in ice jams, was proposed as a correction to the method. A complete theoretical basis for high-precision GPR detection of the thickness of different types of ice in the Yellow River will be developed in the future.
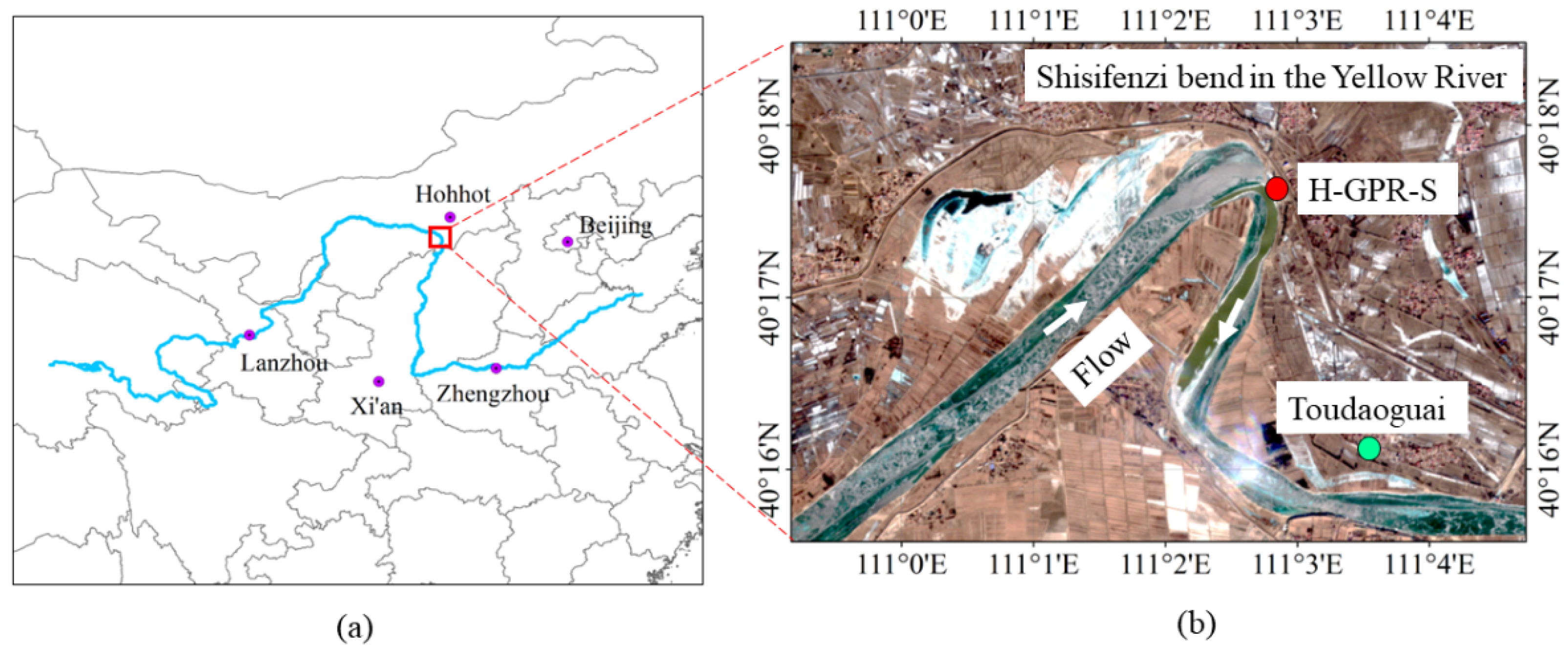
2. Hanging Ground-Penetrating Radar Set and the Characteristics of Air Temperature and Ice Thickness in Winter
3. Theoretical Basis for Correcting Radar Wave Velocity
4. Results
4.1. Ice Sample
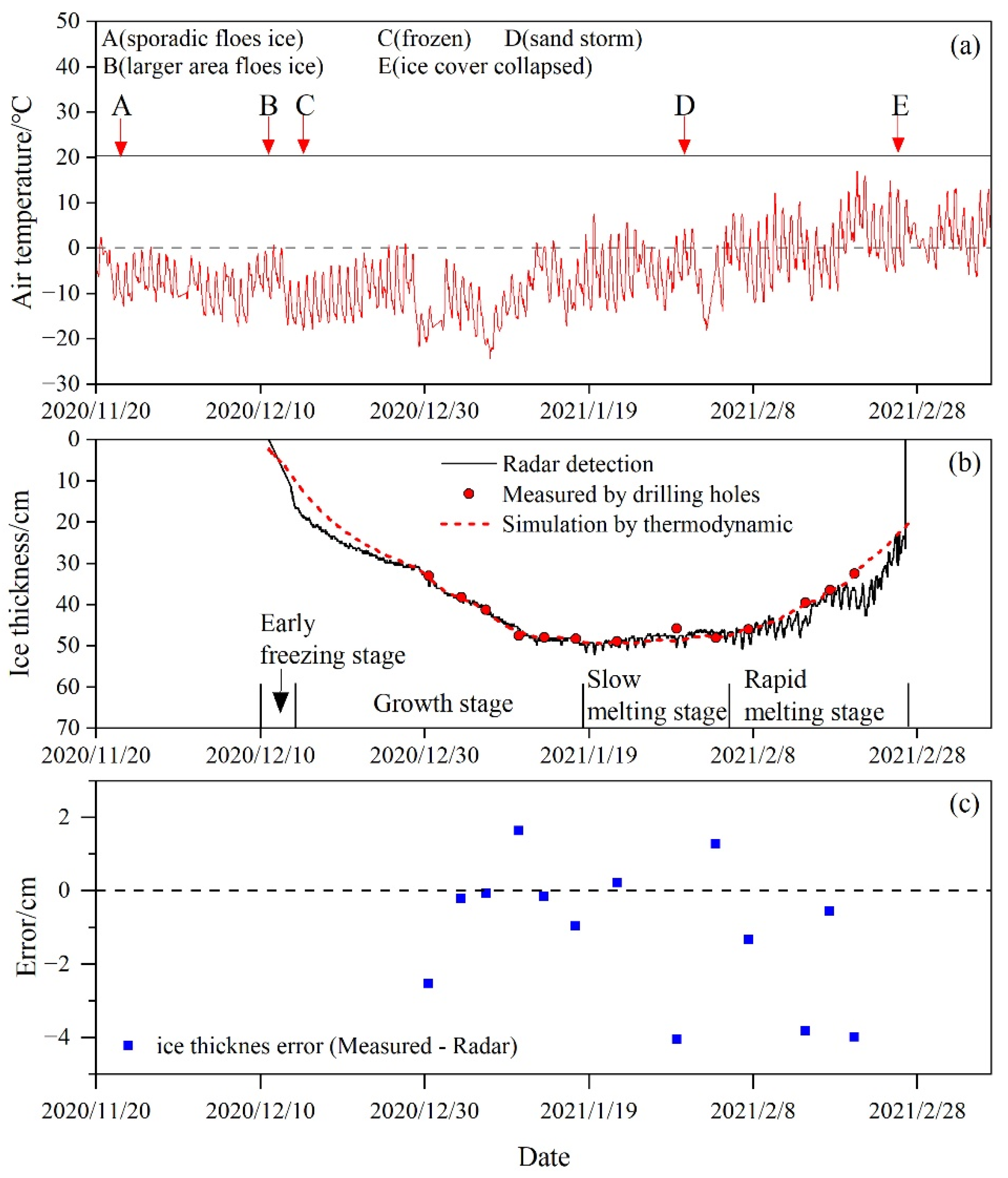
4.2. Natural Ice
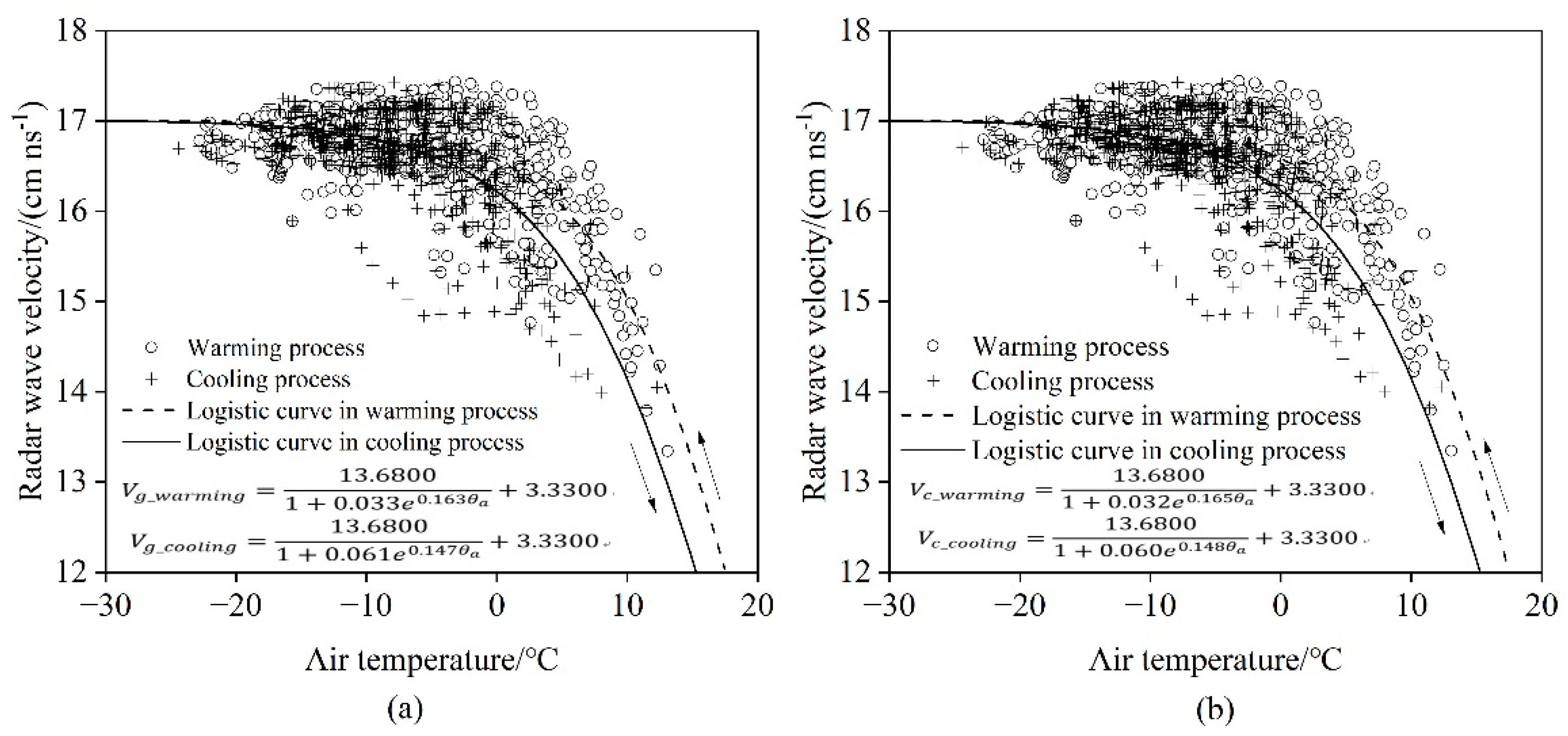
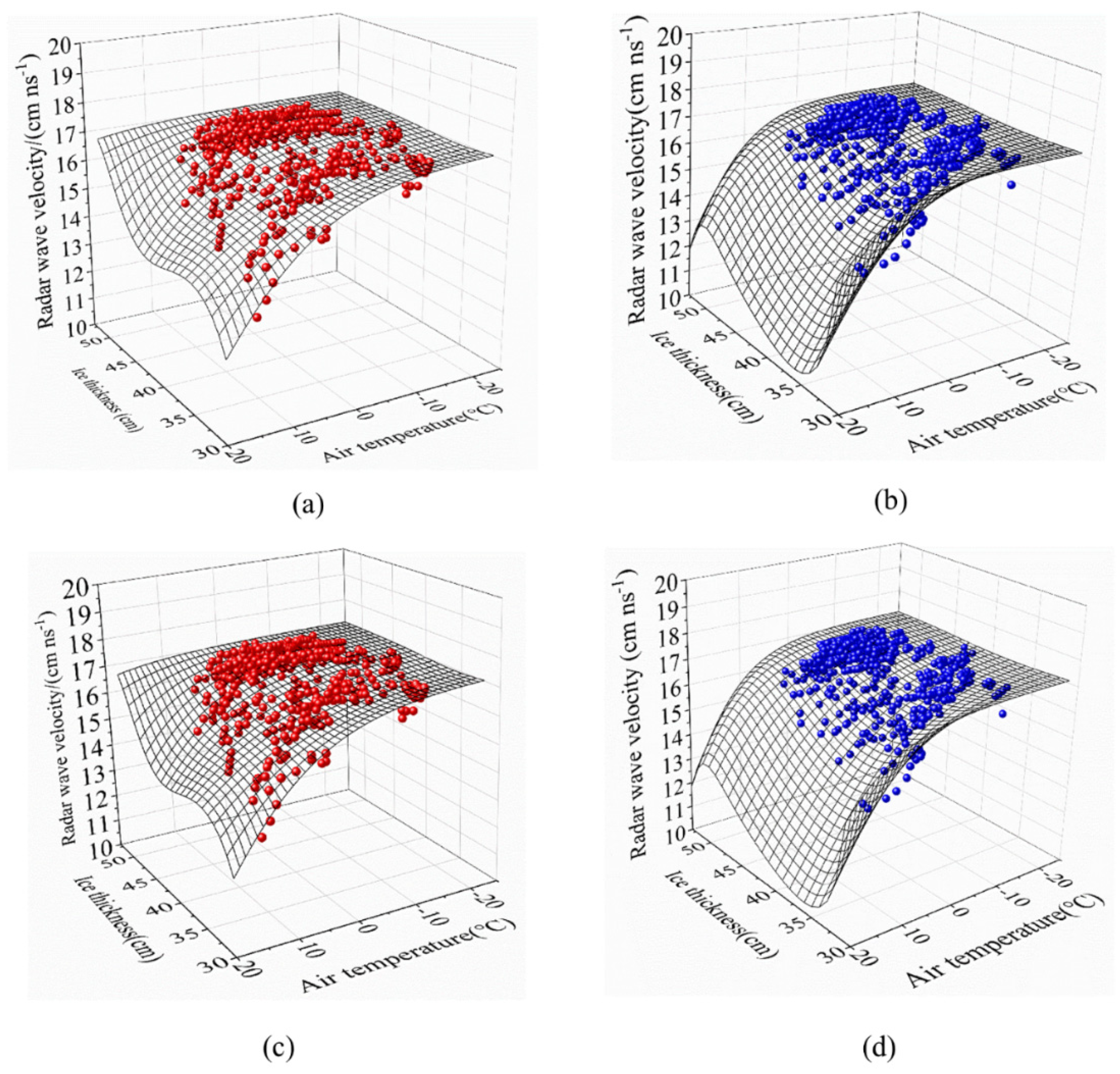
4.3. The Statistical Correction Expression for Radar Wave Velocity in Ice
5. Discussion
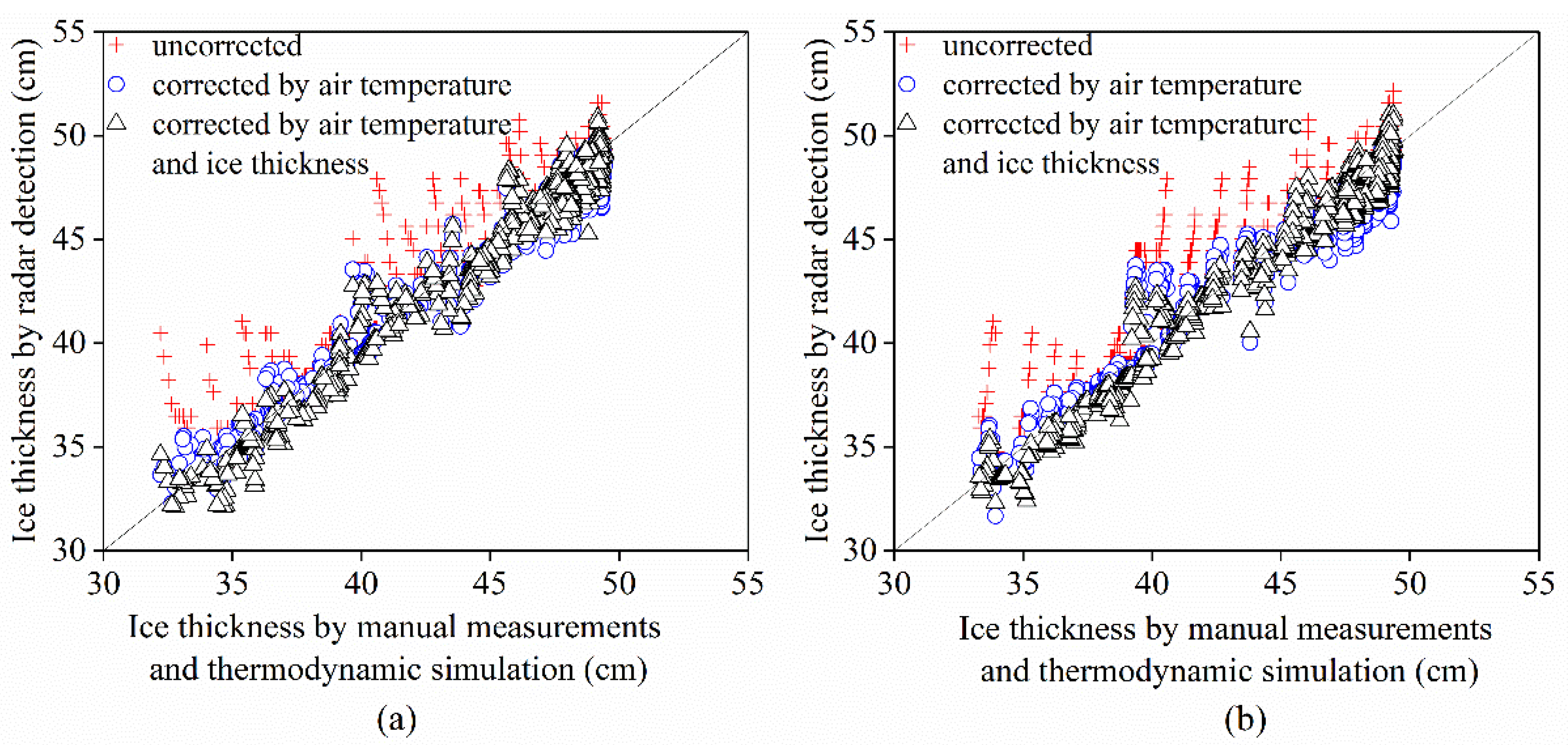
- To correct the radar wave velocity by air temperature and ice thickness in future practice, the following steps should be followed. (a) Previous ice thicknesses and air temperatures should be recorded. (b) Air temperature during calibration should be measured. (c) The difference between these previous and measured air temperatures should be calculated. (d) When a positive result is obtained from step (c), the correction coefficient of the warming process in Table 3 should be selected, while when a negative result is obtained, the correction coefficient of the cooling process should be selected, as shown in Table 3. Finally, (e) according to the correction coefficient of step (d), the current radar wave velocity should automatically be calculated using Equation (7), and the ice thickness should also be automatically calculated. If the test is taken for the first time, the researcher is advised to use the ideal radar wave velocity in ice for the first time, repeat the test five times following steps (a)–(b), and take the ice thicknesses measured for the last time;
- The unfrozen water content in ice is the core factor controlling radar wave velocity. Theoretically, air temperature is the main influence factor of radar wave velocity through ice temperature (Equation (6)), and ice thickness is the secondary influence factor of ice temperature. The combined effect of air temperature and ice thickness on radar wave velocity (Equation (7)) does not perform significantly better than Equation (6). If the accuracy requirement is not very high, the simple Equation (6) is enough. Using the unfrozen water content to evaluate the radar wave velocity is basic research, except for the GPR results of inversed unfrozen water fractions in ice [20,21], which can be inversed under controlled temperature in laboratory using X-ray computed tomography (CT) [44,45] and magnetic resonance imaging (MRI) [46,47]. Both technologies can obtain the volume fractions of different phases but cannot give the fixed index because there are different chemical materials in air and water. These chemical materials also make the index vary in a certain range [48]. We have used CT scan technology to measure ice samples from Bohai, the Arctic, and Wuliangsu Lake near the Yellow River since 1994 [49,50,51]. However, the objectives of obtaining the phase volume from fraction were not achieved. We will continue this study after we have new types of CT scanner later;
- In addition, the grain boundary also affects unfrozen water content; the more grain boundaries, the more unfrozen water content for a given ice temperature. The effect of grain size on the unfrozen water content is the new direction of future efforts. Lastly, solar radiation, cloud cover and wind speed also affect the vertical ice temperature profile. It is necessary to use ice thermodynamic models to calculate the ice temperature. In fact, these thermodynamic models have been continuously modified through the effort to cover the middle and high latitudes, such as the contributions from Cheng (2021) [52], and the parameterizations for the daily ice surface albedos for clear days and cloudy days also were explored [53]. At present, for the cases of polar and high-latitude ice with local cloud, solar radiation, and wind features, it is not necessary to correct radar wave velocity in real time, but radar wave velocity can instead be corrected in periods, such as the early freezing period, growth period, and thaw period. In the future, the new modification method will be developed based on ice thermodynamic models;
- Thirteen manually measured ice thicknesses were inadequate for statistical analysis using the measured ice thicknesses directly. A thermodynamic model was employed to simulate ice thickness; however, the thermodynamic model failed to produce satisfactory results for the dynamic ice thickness variations. In particular, the heat flux of the ice–water interface might vary in different areas of the Yellow River. Thus, it is necessary to consider that both thermodynamics and dynamics contributed to the practical ice thickness of the Yellow River, especially for the unfrozen frazil ice and accumulated broken ice in ice jams in the Yellow River, which possess a high content of unfrozen water. This shows that current statistical parameters do not include measured data of these areas with high water content, and corrections to such areas may thus fall short of high precision. To address this issue, ongoing research and opportunities are required. In future research, the following should be considered: (a) When experimenting with a fixed H–GPR–S, attention should be paid to granular, columnar, and frazil ice in the ice layers and the occurrence of flowing frazil ice and stacked broken ice beneath the ice cover. Additionally, a high-precision sensor for measuring ice thickness and temperature should be installed beneath and inside of the ice, respectively. Sensors for testing frazil and stacked broken ice should be developed under the ice layers. (b) When experimenting with a mobile towing radar, notes should be made on the difference in ice crystal structure in vertical sections of ice layers at every measuring point, particularly the difference in the distribution location and sediment content, and the water content characteristics of frazil ice and stacked broken ice. If sediment content in ice changes with time and position, the dielectric permittivity of ice needs to be reevaluated. However, for floating ice, the sediment content in ice is difficult to measure quickly. When floating ice freezes into ice cover, the sediment content of the floating ice in different places can be measured [22]. We plan to first try to normalize the sediment content for different ice types at different locations in Yellow River, and then the influence of sediment content in ice on the dielectric permittivity will be considered in future efforts. (c) In the future, both radar-detected data and physically measured ice layer data [4,33] will be available and sufficiently accumulated. Such data and the theoretical basis presented in this paper should be applied to build statistical correction coefficients for multiple types of radar wave velocities in ice, which encompasses the thermodynamic and dynamic effects in winter for the Yellow River;
- When thermal growth of ice thickness is detected via a mobile towing radar, a sensor for air temperature should be used. Because manual measurements are often performed during the day when the air temperature is warm, the correction coefficient of air temperature and ice thickness in the warming process should be adopted. For hummock and frazil ice frozen in the Yellow River, the statistics for granular ice should be used. For lake ice, columnar ice statistics should be used, while for flat ice after the ice floes stop moving, the weighted result of granular ice on the 0.15 m of the surface layer and the other columnar ice should be used; in the future, fixed H–GPR–S experiments in other rivers should not be conducted by detecting flat ice and avoiding hummock ice. Instead, both should be selected in the same terrain and meteorological environment so that scientific data can be accumulated to determine the influences of the structure and component differences of flat ice and hummock ice on the high-precision radar detection of ice thickness.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, L.; Yu, D.; Wang, Z.Y.; Wang, X. Soil water content estimation using high-frequency ground penetrating radar. Water 2019, 11, 1036. [Google Scholar] [CrossRef]
- Abdelmawla, A.; Kim, S.S. Application of ground penetrating radar to estimate subgrade soil density. Infrastructures 2020, 5, 12. [Google Scholar] [CrossRef]
- Ruffell, A.; Parker, R. Water penetrating radar. J. Hydrol. 2021, 597, 126300. [Google Scholar] [CrossRef]
- Liu, J.; Wang, S.; He, Y.; Li, Y.; Wang, Y.; Wei, Y.; Che, Y. Estimation of ice thickness and the features of subglacial media detected by ground penetrating radar at the Baishui river glacier No. 1 in Mt. Yulong, China. Remote Sens. 2020, 12, 4105. [Google Scholar] [CrossRef]
- Shah, M.Y.; Ayemi, K.K.; Shrivastava, P.K. GPR survey and physical measurements of sea ice in Quilty Bay, Larsemann hills, East Antarctica and its correlation with local atmospheric parameters. J. Geol. Soc. India 2017, 90, 371–377. [Google Scholar] [CrossRef]
- O’Sadnick, M.; Ingham, M.; Eicken, H.; Pettit, E. In situ field measurements of the temporal evolution of low-frequency sea-ice dielectric properties in relation to temperature, salinity, and microstructure. Cryosphere 2016, 10, 2923–2940. [Google Scholar] [CrossRef]
- Mitterer, C.; Heilig, A.; Schweizer, J.; Eisen, O. Upward-looking ground-penetrating radar for measuring wet-snow properties. Cold Reg. Sci. Technol. 2011, 69, 129–138. [Google Scholar] [CrossRef]
- Sudakova, M.; Sadurtdinov, M.; Skvortsov, A.; Tsarev, A.; Malkova, G.; Molokitina, N.; Romanovsky, V. Using ground penetrating radar for permafrost monitoring from 2015–2017 at CALM Sites in the Pechora River Delta. Remote Sens. 2021, 13, 3271. [Google Scholar] [CrossRef]
- Arcone, S.A.; Delaney, A.J. Airborne river-ice thickness profiling with helicopter-borne UHF short-pulse radar. J. Glaciol. 1987, 33, 330–340. [Google Scholar] [CrossRef]
- Arcone, S.A. Dielectric permittivity and layer-thickness interpretation of helicopter-borne short-pulse radar waveforms reflected from wet and dry river-ice sheets. IEEE Geosci. Remote 1991, 29, 768–777. [Google Scholar] [CrossRef]
- Li, Z.; Jia, Q.; Zhang, B.; Leppäranta, M.; Lu, P.; Huang, W. Influences of gas bubble and ice density on ice thickness measurement by GPR. Appl. Geophys. 2010, 7, 105–113. [Google Scholar] [CrossRef]
- Liu, H.; Sato, M. New GPR system for accurate velocity and thickness estimation of snow and ice on a frozen lake. In Proceedings of the 10th SEGJ International Symposium, Kyoto, Japan, 20–22 November 2011. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; Sato, M. New ground penetrating radar system for quantitative characterization of snow and sea ice. In Proceedings of the IET International Radar Conference 2013, Xi’an, China, 14–16 April 2013. [Google Scholar] [CrossRef]
- Liu, H.; Takahashi, K.; Sato, M. Measurement of Dielectric Permittivity and Thickness of Snow and Ice on a Brackish Lagoon Using GPR. IEEE J-STARS 2014, 7, 820–827. [Google Scholar] [CrossRef]
- Gusmeroli, A.; Grosse, G. Ground penetrating radar detection of subsnow slush on ice-covered lakes in interior Alaska. Cryosphere 2012, 6, 1435–1443. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, F.; Liu, Z.; Han, H.; Li, Z. Field experimental study of the characteristics of GPR images of Yellow River ice. South-To-North Water Transfers Water Sci. Technol. 2017, 15, 121–125. (In Chinese) [Google Scholar] [CrossRef]
- Kämäri, M.; Alho, P.; Colpasert, A.; Lotsari, E. Spatial vaiation of river ice thickness in meandering river. Cold Reg. Sci. Technol. 2017, 137, 17–29. [Google Scholar] [CrossRef]
- Fu, H.; Liu, Z.; Guo, X.; Cui, H. Double-frequency ground penetrating radar for measurement of ice thickness and water depth in rivers and canals: Development, verification and application. Cold Reg. Sci. Technol. 2018, 154, 85–94. [Google Scholar] [CrossRef]
- Bai, X.; Wang, L.; Luo, X.; Mi, H.; Chen, H.; Liu, L.; Ji, M.; Gao, Y. A layer tracking method for ice thickness detection based on GPR mounted on the UAV. In Proceedings of the 4th International Conference on Imaging, Signal Processing and Communications (ICISPC), Kumamoto, Japan, 23–25 October 2020. [Google Scholar] [CrossRef]
- Murray, T.; Stuart, G.W.; Fry, M.; Gamble, N.H.; Crabtree, M.D. Englacial water distribution in a temperate glacier from surface and borehole radar velocity analysis. J. Glaciol. 2000, 46, 389–398. [Google Scholar] [CrossRef]
- Murray, T.; Booth, A.D.; Rippin, D. Water-content of glacier-ice: Limitations on estimates from velocity analysis of surface ground penetrating radar surveys. J. Environ. Eng. Geoph. 2007, 12, 87–99. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Xiu, Y.; Li, C.; Zhang, B.; Deng, Y. Microstructural characteristics of frazil particles and the physical properties of frazil ice in the Yellow River, China. Crystals 2021, 11, 617. [Google Scholar] [CrossRef]
- Launiainen, J.; Cheng, B. Modelling of ice thermodynamics in natural water bodies. Cold Reg. Sci. Technol. 1998, 27, 153–178. [Google Scholar] [CrossRef]
- Li, C.; Li, Z.; Yang, Y.; Wang, Q.; Zhang, B.; Deng, Y. Theory and application of ice thermodynamics and mechanics for sinking naturally gabions mattress on ice. J. Hydraul. Eng. 2022, 53, 445–455. (In Chinese) [Google Scholar] [CrossRef]
- Ji, H.; Shi, H.; Mou, X.; Tuo, Y. Study on the pool ice growth-decay and numerical modeling. J. Hydraul. Eng. 2016, 47, 1352–1362. (In Chinese) [Google Scholar] [CrossRef]
- Lu, P.; Cao, X.; Li, G.; Huang, W.; Leppäranta, M.; Arvola, L.; Huotari, J.; Li, Z. Mass and heat balance of a lake ice cover in the Central Asian Arid Climate Zone. Water 2020, 12, 2888. [Google Scholar] [CrossRef]
- Evans, S. Dielectric properties of ice and snow: A review. J. Glaciol. 1965, 5, 773–792. [Google Scholar] [CrossRef]
- Koh, G. Complex dielectric permittivity of ice at 1.8 GHz. Cold Reg. Sci. Technol. 1997, 25, 119–121. [Google Scholar] [CrossRef]
- Lunt, I.A.; Hubbard, S.S.; Rubin, Y. Soil moisture content estimation using ground-penetrating radar reflection data. J. Hydrol. 2005, 307, 254–269. [Google Scholar] [CrossRef]
- Xu, Q.; Yan, X.; Grantz, D.; Wang, Z.; Cheng, X.; Yu, S.; Fan, L.; Ma, Y.; Cheng, Q. An ice correction model for dielectric sensor to improve accuracy of soil water potential measurement in frozen soils. Soil Till. Res. 2021, 211, 105003. [Google Scholar] [CrossRef]
- Shokr, M.E. Field observations and model calculations of dielectric properties of Arctic sea ice in the microwave C-band. IEEE Geosci. Remote 1998, 36, 463–478. [Google Scholar] [CrossRef]
- Michel, B. Ice Mechanics; Laval University Press: Laval, QC, Canada, 1978; pp. 124–136. [Google Scholar]
- Zhang, Y.; Gao, G.; Deng, Y.; Li, Z.; Li, G.; Guo, W. Investigation on ice crystal, density and sediment content in ice at different positions in Bayannaoer section of the Yellow River. Yellow River 2018, 40, 44–48. (In Chinese) [Google Scholar] [CrossRef]
- Gherboudj, I.; Bernier, M.; Hicks, F.; Leconte, R. Physical characterization of air inclusions in river ice. Cold Reg. Sci. Technol. 2007, 49, 179–194. [Google Scholar] [CrossRef]
- Guo, Y.; Xu, S.; Shan, W. Development of a frozen soil dielectric permittivity model and determination of dielectric permittivity variation during the soil freezing process. Cold Reg. Sci. Technol. 2018, 151, 28–33. [Google Scholar] [CrossRef]
- Roth, K.; Schulin, R.; Flühler, H.; Attinger, W. Calibration of time domain reflectometry for water content measurement using a composite dielectric approach. Water Resour. Res. 1990, 26, 2267–2273. [Google Scholar] [CrossRef]
- Alharthi, A.; Lange, J. Soil water saturation: Dielectric determination. Water Resour. Res. 2010, 23, 591–595. [Google Scholar] [CrossRef]
- Herkelrath, W.N.; Hamburg, S.P.; Murphy, F. Automatic, real-time monitoring of soil moisture in a remote field area with time domain reflectometry. Water Resour. Res. 1991, 27, 857–864. [Google Scholar] [CrossRef]
- Fabbri, A.; Fen-Chong, T.; Coussy, O. Dielectric capacity, liquid water content, and pore structure of thawing-freezing materials. Cold Reg. Sci. Technol. 2006, 44, 52–66. [Google Scholar] [CrossRef]
- Overduin, P.P.; Kane, D.L.; van Loon, W.K.P. Measuring thermal conductivity in freezing and thawing soil using the soil temperature response to heating. Cold Reg. Sci. Technol. 2006, 45, 8–22. [Google Scholar] [CrossRef]
- Wang, C.; Lai, Y.; Yu, F.; Li, S. Estimating the freezing-thawing hysteresis of chloride saline soils based on the phase transition theory. Appl. Therm. Eng. 2018, 135, 22–33. [Google Scholar] [CrossRef]
- Duan, C.; Dong, S.; Wang, Z. Study on arctic sea Ice growth based on Logistic curve model. T. Oceanol. Limn. 2021, 4, 1–6. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, G.; Qiao, C.; Yan, Y.; Feng, F.; Wang, L.; Zhang, S.; Chen, Y. Study on model of relations between water content and dielectric constant: Experimental study. Hydrogeol. Eng. Geol. 2016, 43, 7–10. (In Chinese) [Google Scholar] [CrossRef]
- Kawamura, T. Observations of the internal structure of sea ice by X ray computed tomography. J. Geophys. Res. Atmos. 1988, 93, 2243–2350. [Google Scholar] [CrossRef]
- Lieb-Lappen, R.M.; Golden, E.J.; Obbard, R.W. Metrics for interpreting the microstructure of sea ice using X-ray micro-computed tomography. Cold Reg. Sci. Technol. 2017, 138, 24–35. [Google Scholar] [CrossRef]
- Eicken, H.; Bock, C.; Wittig, R.; Miller, H.; Poertner, H.O. Magnetic resonance imaging of sea ice pore fluids: Methods and thermal evolution of pore microstructure. Cold Reg. Sci. Technol. 2000, 31, 207–225. [Google Scholar] [CrossRef]
- Brown, J.R.; Brox, T.I.; Vogt, S.J.; Seymour, J.D.; Skidmore, M.L.; Codd, S.L. Magnetic resonance diffusion and relaxation characterization of water in the unfrozen vein network in polycrystalline ice and its response to microbial metabolic products. J. Magn. Reson. 2012, 225, 17–24. [Google Scholar] [CrossRef]
- Crabeck, O.; Galley, R.; Delille, B.; Else, B.; Geilfus, N.; Lemes, M.; Roches, M.D.; Francus, P.; Tison, J.; Rysgaard, S. Imaging air volume fraction in sea ice using non-destructive X-ray tomography. Cryosphere 2016, 10, 1125–1145. [Google Scholar] [CrossRef]
- Li, Z.; Pu, Y.; Gao, S.; Liao, Q. Images of computerized tomography in nature sea ice in Liaodong Gulf. In Proceedings of the Abstracts of 9th International Symposium on Okhotsk Sea and Sea Ice, Mombetsu, Japan, 6–8 February 1994. [Google Scholar]
- Li, Z.; Pu, Y. Some applications of computerized tomography scanner to sea ice. In Proceedings of the Twelfth International Offshore and Polar Engineering Conference, Kitakyushu, Japan, 26–31 May 2002. [Google Scholar]
- Wang, S.; Li, Z.; Zhang, Y.; Xiu, Y.; Deng, Y.; Li, G. A preliminary study on observations of the fabric of lake ice by CT scanning technique. Hydro. Sci. Cold Zone Eng. 2020, 3, 63–69. (In Chinese) [Google Scholar] [CrossRef]
- Cheng, B.; Vihma, T.; Palo, T.; Nicolaus, M.; Gerland, S.; Rontu, L.; Haapala, J.; Perovich, D. Observation and modelling of snow and sea ice mass balance and its sensitivity to atmospheric forcing during spring and summer 2007 in the Central Arctic. Adv. Polar Sci. 2021, 32, 312–326. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Q.; Tang, M.; Lu, P.; Li, G.; Leppäranta, M.; Huotari, J.; Arvola, L.; Shi, L. Diurnal Cycle Model of Lake Ice Surface Albedo: A Case Study of Wuliangsuhai Lake. Remote Sens. 2021, 13, 3334. [Google Scholar] [CrossRef]



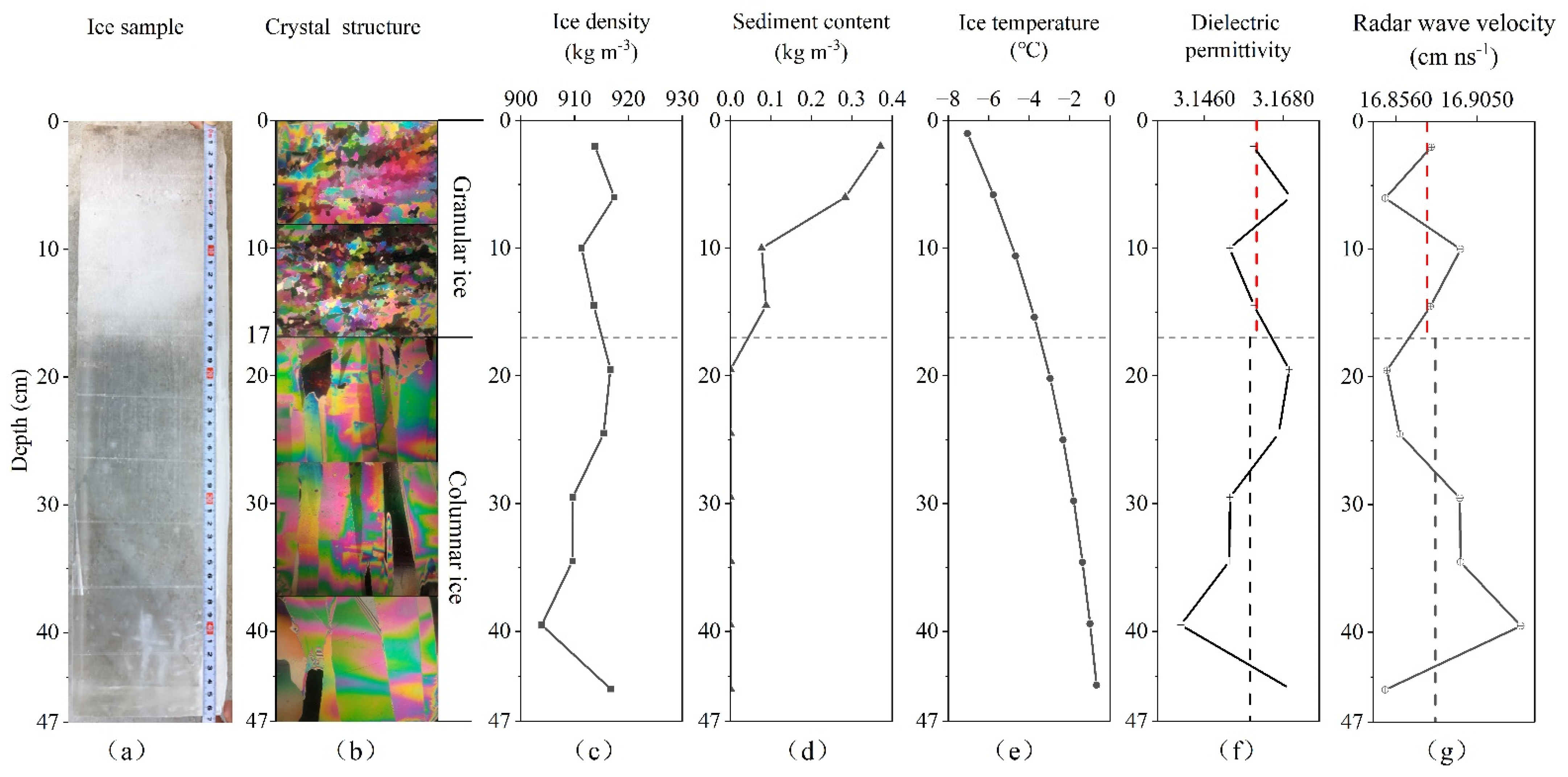


| Crystal Structure | Position of Each Ice Layer Center (cm) | Measured Ice Block Density Including Pure Ice, Sediment, and Air (kg m−3) | Sediment Content per Unit Volume (kg m−3) |
|---|---|---|---|
| Granular ice | 2 | 913.772 | 0.37 |
| 6 | 917.381 | 0.28 | |
| 10 | 911.318 | 0.08 | |
| 14.5 | 913.563 | 0.09 | |
| Columnar ice | 19.5 | 916.643 | 0 |
| 24.5 | 915.418 | 0 | |
| 29.5 | 909.669 | 0 | |
| 34.5 | 909.606 | 0 | |
| 39.5 | 903.880 | 0 | |
| 44.5 | 916.728 | 0 |
| Substance | Density (kg m−3) | Dielectric Permittivity | Radar Wave Velocity (m ns−1) | Source |
|---|---|---|---|---|
| Pure ice | 917 | 3.17 | 0.1685 | [4,9,11,35] |
| Air | 0 | 1 | 0.3000 | [4,9,11,35] |
| Pure water | 1000 | 81 | 0.0333 | [4,11,29,35] |
| Sediment | 1800 | 5.50 | 0.1279 | [35] |
| Coefficients | Air Temperature | Air Temperature + Ice Thickness | ||||||
|---|---|---|---|---|---|---|---|---|
| Warming Process | Cooling Process | Warming Process | Cooling Process | |||||
| GI * | CI * | GI * | CI * | GI * | CI * | GI * | CI * | |
| A | 13.6800 | 13.6800 | 13.6800 | 13.6800 | 13.4550 | 13.4550 | 13.4550 | 13.4550 |
| B | 3.3300 | 3.3300 | 3.3300 | 3.3300 | 3.6500 | 3.6500 | 3.6500 | 3.6500 |
| C1 | 0.033 | 0.032 | 0.061 | 0.060 | −0.892 | −0.921 | −6.813 | −6.798 |
| C2 | 0 | 0 | 0 | 0 | 7.229 | 7.436 | 48.376 | 48.271 |
| C3 | 0 | 0 | 0 | 0 | −16.98449 | −17.48161 | −110.36265 | −110.12702 |
| C4 | 0 | 0 | 0 | 0 | 12.343861 | 12.741714 | 81.956272 | 81.782522 |
| D1 | 0.163 | 0.165 | 0.147 | 0.148 | 4.438 | 4.383 | 0.838 | 0.632 |
| D2 | 0 | 0 | 0 | 0 | −31.810 | −31.345 | −4.076 | −2.504 |
| D3 | 0 | 0 | 0 | 0 | 76.17527 | 74.89003 | 6.54336 | 2.56125 |
| D4 | 0 | 0 | 0 | 0 | −59.670671 | −58.492396 | −2.446005 | 0.906506 |
| Correlation coefficient | 0.7382 | 0.6884 | 0.7389 | 0.6884 | 0.8207 | 0.8210 | 0.8338 | 0.8338 |
| Indicator | No Correction | Correction by Air Temperature | Correction by Air Temperature and Ice Thickness | |
|---|---|---|---|---|
| Cooling process | Correlation coefficient r | 0.97181 | 0.98577 | 0.99164 |
| MSEs | 0.00026 | 0.00016 | 0.00015 | |
| RMSEs | 0.01608 | 0.01249 | 0.01205 | |
| MAEs | 0.01050 | 0.00958 | 0.01003 | |
| Warming process | Correlation coefficient r | 0.97584 | 0.99010 | 0.99192 |
| MSEs | 0.00025 | 0.00013 | 0.00015 | |
| RMSEs | 0.01596 | 0.01132 | 0.01209 | |
| MAEs | 0.01069 | 0.00880 | 0.01004 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Li, C.; Yang, Y.; Zhang, B.; Deng, Y.; Li, G. Physical Mechanism and Parameterization for Correcting Radar Wave Velocity in Yellow River Ice with Air Temperature and Ice Thickness. Remote Sens. 2023, 15, 1121. https://doi.org/10.3390/rs15041121
Li Z, Li C, Yang Y, Zhang B, Deng Y, Li G. Physical Mechanism and Parameterization for Correcting Radar Wave Velocity in Yellow River Ice with Air Temperature and Ice Thickness. Remote Sensing. 2023; 15(4):1121. https://doi.org/10.3390/rs15041121
Chicago/Turabian StyleLi, Zhijun, Chunjiang Li, Yu Yang, Baosen Zhang, Yu Deng, and Guoyu Li. 2023. "Physical Mechanism and Parameterization for Correcting Radar Wave Velocity in Yellow River Ice with Air Temperature and Ice Thickness" Remote Sensing 15, no. 4: 1121. https://doi.org/10.3390/rs15041121
APA StyleLi, Z., Li, C., Yang, Y., Zhang, B., Deng, Y., & Li, G. (2023). Physical Mechanism and Parameterization for Correcting Radar Wave Velocity in Yellow River Ice with Air Temperature and Ice Thickness. Remote Sensing, 15(4), 1121. https://doi.org/10.3390/rs15041121









