Abstract
We studied the characteristics of quasi-two-day wave (QTDW) using the meridional wind in the mesosphere and lower thermosphere (MLT) obtained from a meteor radar over Kototabang (KB, 0.2S, 100.3E) from 2003 to 2012. Atmospheric oscillations have a crucial impact on atmospheric dynamics, which contributes to more accurate space weather forecasting, thus providing a more secure space environment for human space exploration activities such as remote sensing and satellite navigation. QTDWs are typical atmospheric oscillations in the upper stratosphere, mesosphere and lower thermosphere. The occurrence time, amplitudes, periods and vertical wavelengths of QTDW events are analyzed statistically. Data obtained from the TIMED Doppler Interferometer (TIDI), which can measure wind and temperature and is onboard the Thermosphere, Ionosphere, Mesosphere Energetics and Dynamics (TIMED) satellite, are used to analyze the global distribution and spatial structure of QTDWs with different zonal wavenumbers. The characteristics of the QTDWs over KB are compared with the QTDWs at the middle latitudes using the meridional wind data from a meteor radar over Wuhan (114.4E, 30.6N), Beijing (116.5E, 39.9N) and Mohe (121.1E, 50.1N). The amplitudes of the QTDW and spectral analysis are calculated by the least squares fitting method. Our results demonstrate that QTDWs are present almost all year around over KB. The occurrence time, amplitudes, periods and vertical wavelengths of QTDW events with different zonal wavenumbers are determined in this study. We also find that the statistical characteristics of the QTDWs in KB are different from those at middle latitudes. The westward zonal wavenumber −4 (W4) events gradually increase with increasing latitude, whereas westward zonal wavenumbers −1, −2, and −3 (W1, W2 and W3, respectively) events all decrease with increasing latitude.
1. Introduction
Quasi-two-day waves (QTDWs) are planetary waves with a period of approximately 40–60 h and they are typical planetary waves in the mesosphere and lower thermosphere (MLT). The characteristics of QTDWs have been studied by many researchers using observations from ground-based radars and satellites [1,2,3,4] since the first observations of QTDWs were obtained from meteor radar reported by Muller and Sciences [5]. Many studies have focused on the meridional wind because the amplitudes of QTDWs in the meridional wind are much larger than those of zonal wind [6,7]. Meridional wind data were also chosen in this study for the same reason. It is well-acknowledged that the typical seasonal characteristic of QTDWs are the maximum amplitudes of the QTDWs near the summer solstice [8,9,10]. However, the seasonal variations in QTDWs are highly dependent on latitude. Harris and Vincent [11] observed that QTDWs appear almost all year near the equator in the MLT regions using data obtained from medium frequency (MF) radar at the equator. They also found that the amplitudes of QTDWs peaked in July/August and January/February. Kumar, Subrahmanyam, Mathew, Koushik and Ramkumar [6] reported QTDW amplitude maximums in July/August, January/February, and October, which were observed from the equatorial Kototabang (0.2S, 100.3E) and low-latitude Thumba (8.5N, 77E) stations. This conclusion is consistent with a study on the amplitudes of QTDWs in low latitudes measured by MF radar in Tirunelveli (8.7N, 77.8E) and a meteor radar in Thumba (8.5N, 77E) by Rao, et al. [12]. Lima, et al. [13] reported that the amplitudes of QTDWs near the equator were larger than those in low latitudes in the summer, and the amplitudes of QTDWs in January/February were almost the same based on analyzing data from equatorial and low-latitude stations, respectively. The meridional wind detected by the middle-latitude Collm (51.3N, 13.0E) station had much larger amplitudes of QTDWs in summer than those in winter [7,14]. The maximum amplitudes of QTDWs in winter in the middle latitude were also much weaker than those at the equator and low latitudes [7,12,13]. The seasonal characteristics of QTDWs at high latitudes are totally different from their counterparts at low and middle latitudes. Nozawa, et al. [15] observed that QTDWs obtained from MF radar at the high-latitude station Tromsø (69.6N, 19.2E) showed stronger amplitudes in winter than in summer, and the maximum occurred around the winter solstice. The periods of QTDWs in summer were found to be more centralized than in winter by utilizing data from a VHF radar over Collm (51.3N, 13.0E) [7]. Some studies have shown that the vertical wavelengths of QTDWs are also dependent on latitude. For instance, the vertical wavelengths of meridional QTDWs in C. Paulista (22.7S, 45.0W) were approximately 65 km in January/February meanwhile the vertical wavelength of QTDW in Cariri (7.4S, 36.5W) was approximately 40 km [16]. The vertical wavelengths of the QTDW are larger at higher latitudes [7,13,16].
Although these ground-based radars can accurately record the seasonal characteristics of QTDWs, they cannot directly acquire information about the zonal wavenumbers. The zonal wavenumber represents the number of complete waveforms in the same latitude circle. To obtain the zonal wavenumber and the global structure of QTDWs, satellite observations are essential. The most prominent QTDWs are westward waves with a zonal wavenumber of 3 [17,18,19]. QTDWs with a zonal wavenumber 3 are usually present in January/February from approximately 40S to 30N and QTDWs with zonal wavenumbers of 3 and 4 always occur in July/August in the Northern Hemisphere [20,21]. Westward QTDWs with wavenumbers of 2, 3, and 4 are the most common waves, which appear most frequently compared to QTDWs with other zonal wavenumbers [22]. In addition, the westward zonal wavenumber 3 (W3) dominate in the Southern Hemisphere, and westward zonal wavenumbers 2, 3, 4, and 5 (W2, W3, W4 and W5, respectively) are found in the Northern Hemisphere [23,24]. Although the amplitudes of W3 QTDWs are strongest in the Southern Hemisphere, their counterparts in the Northern Hemisphere are weaker than W4 QTDWs [22,25]. Liu, et al. [26] also found that W3 QTDWs are most common at a latitude between 30 40 in both hemispheres in January/February and July/August. However, Tunbridge, Sandford and Mitchell [22] found that W2 QTDWs are present in both hemispheres and the QTDWs in the Southern Hemisphere reach larger peaks than those in the Northern Hemisphere. Even W2 QTDWs are more likely to occur in the Southern Hemisphere [27]. These hemispheric disparities mentioned above may be caused by the differences in the summer easterly jet [28,29]. The summer easterly jet is also a source of instability, which amplifies the westward QTDWs [30,31].
The two well-accepted mechanisms for exciting QTDWs and explaining the seasonal variations in QTDWs are baroclinic/barotropic instability and the normal mode, respectively [9,32]. The normal mode theory considers QTDWs as a representation of the Rossby-gravity normal (3, 0) mode with a westward zonal wavenumber of 3, which was first introduced by Salby [33]. Plumb [34] proposed that baroclinic instability results in a massive intensification of QTDWs. Some researchers agree that these two mechanisms often control the QTDWs concurrently [9]. The quasi-biennial oscillation (QBO) is an oscillation with an approximately 28-month period, and QTDWs are also found to be modulated by QBO [23,26,35,36]. Rao, Ratnam, Vedavathi, Tsuda, Murthy, Sathishkumar, Gurubaran, Kumar, Subrahmanyam and Rao [12] reported that the QBO in QTDWs are more easily observed by MF radar than by meteor radar. QTDWs are also impacted by tides and the solar cycle [20,37].
In the present study, the characteristics of QTDWs were explored by analyzing the meridional wind obtained from the meteor radar over Kototabang (KB, 0.2S, 100.3E). The QTDW events in KB were determined to research their statistical characteristics, such as their amplitude, period and vertical wavelength. The zonal wavenumbers were also calculated to determine the statistics on the characteristics of QTDWs with different wavenumbers using satellite observations. QTDWs observed in different latitudes were compared with those at the equator to study the more complete latitude features by the data obtained from the meteor radars installed at Wuhan (114.4E, 30.6N), Beijing (116.5E, 39.9N) and Mohe (121.1E, 50.1N). This study focused on the seasonal characteristics of QTDWs with different zonal wave numbers. Studying the seasonal characteristics of QTDWs with different wave numbers is more helpful to distinguish the wind patterns in different months. It is also important to further study the excitation and propagation mechanism of QTDWs. Comparison of the QTDW characteristics between the equatorial and middle-latitude regions is also a focus of this study. By analyzing the characteristics of QTDWs at different latitudes, we can further explore the generation mechanism of QTDWs. Through our research, we hope to provide a clearer understanding of the seasonal and long-term characteristics of QTDWs.
2. Materials and Methods
2.1. Meteor Radar
The meteor radars used in the present study were all-sky interferometric meteor radar (SkiYMET) located at KB (0.2°S, 100.3°E), Wuhan (114.4E, 30.6N), Beijing (116.5E, 39.9N) and Mohe (121.1E, 50.1N). The meteor radar over KB, near the geographic equator, runs at a frequency of 37.7 MHz. The maximum power of this meteor radar can reach 13 kW [38]. Usually, approximately 8000–12,000 meteors can be recorded in one day. [39]. Moreover, the meteor radars installed at Wuhan, Beijing and Mohe are controlled by the Institute of Geology and Geophysics, Chinese Academy of Sciences (IGGCAS). These three radars all runs at a frequency of 38.9 MHz, with a maximum power of 7.5 kW in Wuhan and Beijing and 20 kW in Mohe [40]. The daily mean meteor counts in Wuhan and Beijing are approximately 4000–5000, and the radar in Mohe detects 13,000 meteors per day [40]. The meteor radars have a measured altitude of about 70–110 km. The vertical resolution is 2 km and the temporal resolution is 1 h. Hourly meridional wind data between 82 and 96 km from 2003 to 2012 over KB and from 2011 to 2019 over Wuhan, Beijing and Mohe were used in our study to analyze the characteristics of QTDWs in the MLT.
2.2. TIDI
The TIMED Doppler Interferometer (TIDI) is a limb-scanning Fabry–Perot interferometer (FPI) that can perform wind and temperature measurements and is onboard the Thermosphere, Ionosphere, Mesosphere Energetics and Dynamics (TIMED) satellite [41]. The TIDI has four orthogonally orientated telescopes, and thus, it can observe the wind on both sides of the satellite track. The side facing the sun is so called the “warmside” and the side facing away from the sun is called the “coldside” [42]. Furthermore, the warm side neutral wind observed by the TIDI is zonal wind and the cold side neutral wind is meridional wind [43]. The TIDI can measure wind data at four different local solar times on a given day. The TIMED satellite precession rate determines that the TIDI sampling track will cover 24 h in local time every 60 days, which is one satellite’s yaw period [41]. The TIDI wind observations in the MLT are between 70 km and 120 km, with a vertical resolution of 2.5 km. The meridional wind data in an altitude range of 85–105 km from 2003 to 2012 were used to calculate the zonal wavenumbers of QTDWs and the spatial structure of QTDWs with different wavenumbers.
2.3. Methodology
The hourly meridional wind data from the meteor radar over KB from 2003 to 2012 were used to determine the seasonal and long-term variations of QTDW. The central day of the dataset steps from day 8 to day 358, in increments of one day, and the hourly dataset from 7 days before and after the central day are binned to perform spectral analysis using the least squares fitting method [44]. Additionally, the observations in 15 days were more than 240 h (66.7%). The sinusoidal wave period from 30 h to 72 h in 1 h increments was used to calculate the accurate periods of the QTDWs at 90 km. To obtain more detailed information about the QTDWs, the QTDW events in the spectrum were recorded from 2003 to 2012. During the time of the QTDW events, the least squares fitting method was also utilized to obtain a spectrum with an altitude range of 86–96 km. The fitting equation is described as follows:
where A and B are the amplitudes of the QTDWs; σ represents the frequency of QTDWs; C represents the background meridional wind. The maximum amplitudes and phases of the QTDWs are expressed as
where A and B are the amplitudes of the QTDWs; R is the maximum amplitude of the QTDWs; represents the phase of the QTDWs. The vertical wavelength is the height at which a wave travels vertically in a full period. Thus, the vertical wavelength can be calculated by the slope of the phase of the QTDWs at different altitudes.
Regarding the zonal wavenumbers of the QTDWs, the meridional wind data from the TIDI were analyzed by using the least squares fitting method. The fitting equation is expressed as
where A and B are the amplitudes of the QTDWs; σ represents the frequency of QTDWs; s is the zonal wavenumber of the QTDW; and are the UT time and longitudes of the samplings, respectively. C is the background wind. The zonal wavenumber s steps from −6 to 6 were utilized to analyze the accurate zonal wave number of the QTDW events at 90 km from 2003 to 2012.
3. Results
3.1. Statistics on the Seasonal Features
Figure 1 illustrates the decadal meridional wind obtained from meteor radar over KB in the MLT. Figure 1a shows the meridional wind near the equator between 82 km and 96 km from 2003 to 2012. In Figure 1a, it can be seen that there were almost no missing data over the past decade. In addition, the annual oscillations (AO) were significant between approximately 82 km and 88 km. Figure 1b displays the averaged period spectrum of meridional wind at 90 km from 2003 to 2012. QTDWs within a period of approximately 48 h were found to be present almost all year around near the equator, as shown in Figure 1b. The maximum amplitudes peaked in January, February, March, July, August, September, and October, which is consistent with the observations at the equator [6,11,45]. The seasonal variations in the QTDWs at the equator are different from those in the middle and high latitudes [46,47]. The summer easterly jet at the equator appears more often than that in the middle latitudes. Thus, the anomalous summer easterly jet in the equatorial region may be the reason why QTDWs over KB are present almost all year. The summer easterly jet may cause instability, resulting in a massive intensification of the westward QTDWs [30,31].
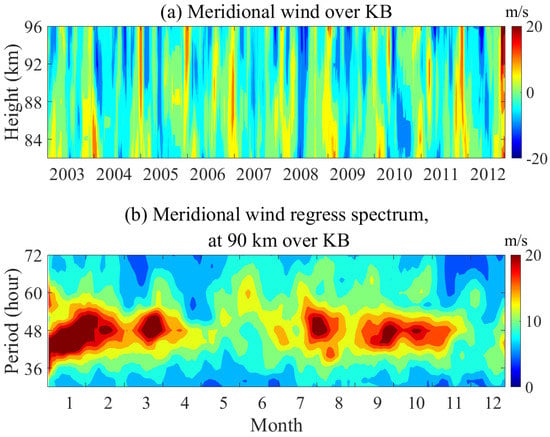
Figure 1.
(a) The meridional wind obtained from meteor radar over KB from 2003 to 2012. (b) The averaged spectrum of meridional wind at 90 km over KB.
To further study the seasonal variations in QTDWs at the equator, the QTDW events over KB from 2003 to 2012 were recorded and chosen to analyze in detail. Figure 2 displays a significant QTDW event in February 2003 over KB. The period spectrum of meridional wind between 82 km and 96 km is shown in Figure 2a. The period of the strongest amplitudes was approximately 52 h at 86 km, which further verifies the validity of this QTDW event over KB. Figure 2b shows the amplitudes of the QTDW between 82 km and 96 km, which peaked at 96 km with the maximum of 39.6 m/s. The phase and vertical wavelength of this event are shown in Figure 2c. The slopes of the phases were calculated as the vertical wavelength of the QTDWs. The vertical wavelength shown in Figure 2c is approximately 23.4 km, which is consistent with the vertical wavelength of the QTDW in the previous studies [48]. Figure 2d illustrates the zonal wavenumber of this QTDW event at 90 km using the meridional wind data obtained from the TIDI. The amplitudes peaked at 2 within a period of 52 h. Thus, the QTDW from day 47 to day 61 in 2003 was a westward zonal wavenumber 2 (W2) wave. Moreover, the maximum amplitudes, the periods of maximum amplitudes, the vertical wavelengths, and the zonal wavenumbers of all QTDW events are recorded in Table, which can be seen from https://www.zenodo.org/record/7589912, accessed on 31 January 2023, similar to the above QTDW event.
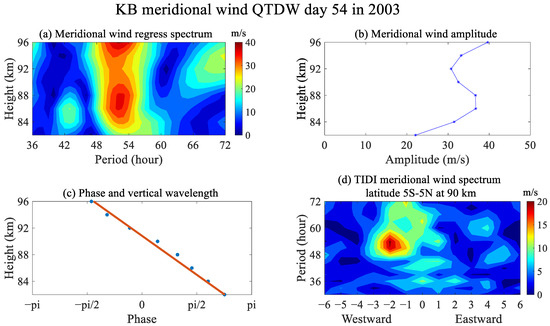
Figure 2.
An example of QTDW events in meridional wind over KB from day 47 to day 61 in 2003. (a) The spectrum of meridional wind between 82 km and 96 km. (b) The amplitude of the QTDW. (c) The phase and the vertical wavelength of the QTDW. (d) The wavenumber spectrum of the TIDI Citation: Sun, R.; Gu, S.-Y.; Dou, X.; Wei, Y.; Qin, Y.; Yang, Z. meridional wind at 90 km.
Every QTDW event was then investigated, as shown in Figure 2. The occurrence dates, periods, amplitudes, vertical wavelengths, and their wave types were all recorded in detail and can be seen at https://www.zenodo.org/record/7589912, accessed on 31 January 2023. Statistical analysis was finally performed to study their seasonal characteristics. Figure 3 shows the zonal wavenumber statistics of QTDW events over KB from 2003 to 2012. It is obvious that the westward zonal wavenumbers 1, 2 and 3 (W1, W2 and W3, respectively) were dominant while the zonal wavenumber −4 (W4) was very rare in QTDW events. It is well-known that the amplitudes of W3 QTDWs are strongest in the Southern Hemisphere and the amplitudes of W4 QTDWs are strongest in the Northern Hemisphere [22,25]. The zonal wavenumber of QTDW events in the equatorial region are somewhat different. At the equator, the number of W2 QTDW incidents was the highest at 40%. At the same time, W3 and W1 QTDW incidents accounted for 31% and 27%, respectively. W4 events were almost absent, accounting for 1% of the total QTDW events.
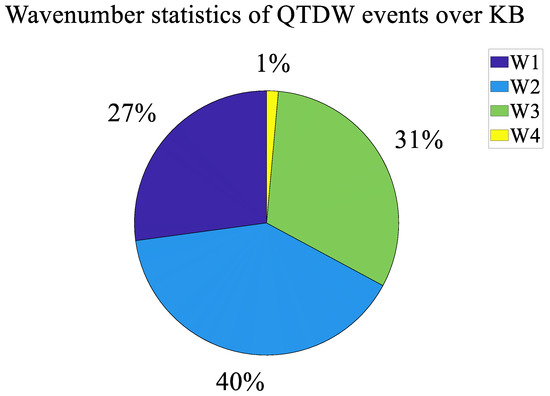
Figure 3.
The wavenumber statistics of QTDW events over KB from 2003 to 2012.
The seasonal variation statistics of QTDW events with different zonal wavenumbers are exhibited in Figure 4. Figure 4 displays the occurrence time, amplitudes, periods and vertical wavelengths of QTDW events over KB from 2003 to 2012. Figure 4a,e,i show the number of W1, W2, and W3 QTDW occurrences per month, respectively. W1 events were present almost all year around, and the highest number of W1 QTDW incidents occurred in September, with seven. This is slightly different from the previous studies, which have suggested that the months with the most frequent events are January/February and July/August. As shown in Figure 4e, W2 events occurred more evenly throughout the year than W1 events. Additionally, W2 events occurred most frequently in February five times. Figure 4i shows the seasonal variation statistic of W3 events over KB. The number of W3 events peaked twice in a year, one in January/February and the other in August, which is consistent with the seasonal variations in other studies [12,13]. As a result, the pattern of W3 events is more in line with the seasonal variation in QTDWs at other stations. This may be because W3 waves have usually been the most prominent QTDWs in other observations [17,18].
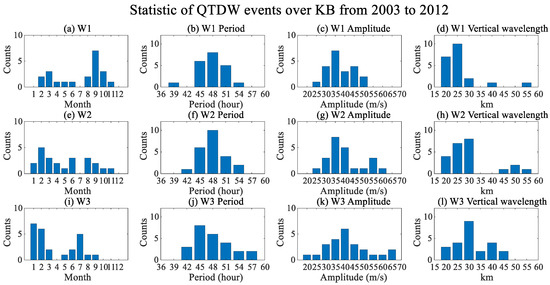
Figure 4.
The statistic of (a) W1, (e) W2, and (i) W3 QTDW events over KB from 2003 to 2012. The periods statistic of (b) W1, (f) W2, and (j) W3 QTDW events over KB from 2003 to 2012. The amplitude statistic of (c) W1, (g) W2, and (k) W3 QTDW events over KB from 2003 to 2012. The vertical wavelength statistics of (d) W1, (h) W2, and (l) W3 QTDW events over KB from 2003 to 2012.
Figure 4b,f,j display the period statistic of QTDW events with different zonal wavenumbers. Figure 4b exhibits the distribution results of the periods of QTDWs over KB from 2003 to 2012. The period distribution of W1 waves ranged from 39 to 54 h, and the periods were mainly concentrated between 45 and 51 h, with the most occurring for 48 h. This is also further evidence that the period of QTDWs is approximately 48 h. Figure 4f shows the period statistics of W2 QTDWs at the equator, which is more concentrated than those of W1 waves. The period distribution of W2 waves is between 42 and 54 h, which is similar to that of the W1 waves. Furthermore, the period of W2 waves is mainly concentrated between 45 and 51 h with most appearing for 48 h. The period statistics of W3 QTDWs are exhibited in Figure 4j and are different from those of W1 and W2 waves. Figure 4j shows periods ranging from 42 h to 57 h, with a maximum of 45 h. Palo, Roble, Hagan and space [20] observe that the periods of the QTDWs were concentrated to approximately 48 h in summer in the Southern Hemisphere, while the periods and the time of occurrence of QTDWs varied more in the Northern Hemisphere. In the present study, we found that the periods of W2 QTDWs were more concentrated than those of W1 and W3 waves, and the maximum periods of W3 QTDWs were smaller than those of W1 and W2 waves.
The amplitudes and vertical wavelengths are also essential statistical indexes of QTDWs. Figure 4c,g,k show the amplitude statistics of QTDW events with different zonal wavenumbers. Figure 4c displays the W1 QTDW distribution of the amplitude over KB from 2003 to 2012. The amplitude distribution of W1 waves ranged from 25 m/s to 50 m/s, and the amplitudes peaked at approximately 35 m/s. Figure 4g displays the amplitude statistics of W2 QTDWs. The amplitudes of W2 QTDW were distributed between 25 m/s and 60 m/s, with a maximum of 35 m/s. The amplitude distribution of W2 QTDW was also similar to that of the W1 waves. Figure 4k shows the amplitude ranging from 20 m/s to 65 m/s, which is more scattered than those of W1 and W2 QTDWs. The maximum amplitude of W3 QTDW was 40 m/s, which is larger than the amplitudes of the W1 and W2 waves. In conclusion, we found that the amplitudes of W3 QTDWs were more scattered than those of W1 and W2 QTDW and the maximum amplitudes of W3 QTDWs were also stronger than the amplitudes of W1 and W2.
Figure 4d,h,l exhibits the vertical wavelength statistic of QTDW incidents with different zonal wavenumbers. Figure 4d displays the vertical wavelengths of W1 QTDWs over KB from 2003 to 2012. The vertical wavelength distribution of W1 waves varied from 20 km to 55 km. The vertical wavelengths were mainly concentrated between 20 km and 25 km with the maximum occurring at 25 km. Larger vertical wavelengths were almost absent in W1 QTDWs. The vertical wavelengths of W2 QTDWs, shown in Figure 4h were distributed between 20 km and 55 km, with the maximum appearing at 30 km. Figure 4l shows the vertical wavelength of W3 QTDWs ranging from 20 km to 45 km, which is more concentrated than those of the W1 and W2 QTDWs. The maximum amplitude of W3 QTDW was 30 km. The ranges of the vertical wavelengths of W1 and W2 were larger than that of W3 QTDWs. In addition, their vertical wavelength peaks were larger. The vertical wavelength distribution of W3 waves was more concentrated, and the vertical wavelength was larger with more QTDW events.
Figure 5 shows the averaged QTDW in meridional wind obtained from the TIDI at 90 km at latitudes 60S to 60N from 2003 to 2012. Figure 5a displays the global distribution of the seasonal variations of W1 QTDWs. There were four peaks in the low latitudes throughout the year, which occurred in February, March, October, and December. The most prominent peak occurred in October and all four peaks range between a latitude of 20S and 20N. The peaks in February and October mostly occurred in the Southern Hemisphere while most of the peaks in March and December occurred in the Northern Hemisphere. As discussed above, the seasonal variations in W1 waves were also different compared to previous studies. It is well-known that there are seasonal variations in QTDW peaks in January/February and July/August [12,13]. Figure 5b exhibits the global distribution of the seasonal variations in W2 QTDWs. W2 waves were present almost all of the year and there were approximately six peaks, with one each in January, February, March, September, October and December. These peaks were also trapped between about 20S and 20N and most of them were symmetrical around the equator. The global distribution of the seasonal variations in W3 QTDWs is shown in Figure 5c. A significant peak appeared in January at latitudes from 60S to 30N, which is consistent with the seasonal variations in previous studies. There were also two weak peaks in July and September near the equator and in the Northern Hemisphere. Figure 5d displays the global distribution of W4 QTDWs. The peak in January occurred in the Southern Hemisphere whereas the peak in July occurred in the Northern Hemisphere.
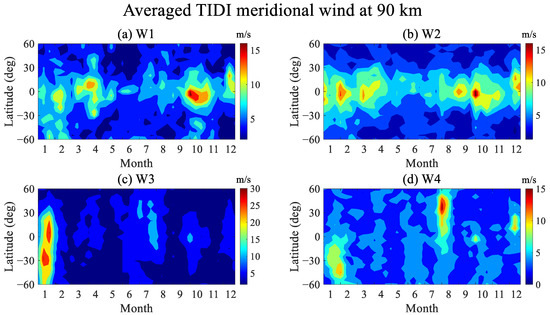
Figure 5.
The averaged TIDI (a) W1, (b) W2, (c) W3 and (d) W4 meridional wind at 90 km at latitudes of 60S to 60N from 2003 to 2012.
Based on the above, the spatial structures of QTDWs, especially in January/February and July/August were studied in further detail. Figure 6 shows the spatial structures of QTDWs with different zonal wavenumbers in meridional wind between 82 km and 96 km at latitudes of 60S to 60N from 2003 to 2012. Figure 6a exhibits the average spatial structure of W1 QTDWs. The amplitudes of W1 were weaker than those of QTDWs with other zonal wavenumbers. As described in Figure 5a, the amplitude of W1 waves in Figure 6a peaked between 20S and 20N. Figure 6b shows the spatial structure of W2 QTDWs, which is similar to the shape of W1 QTDW. The amplitude of W2 waves displayed in Figure 6b also peaked between 20S and 20N, with a maximum of approximately 3 m/s. Regarding W3 and W4 QTDWs, the global distribution in Figure 5c,d indicate the significant features in January/February and July/August. The spatial structure of W3 QTDWs in January and February is shown in Figure 6c with a maximum amplitude of 12 m/s. The significant amplitudes occurred at latitudes from 60S to 30N, which is consistent with the results in Figure 5c. Figure 6d displays the spatial structure of W4 QTDWs in January and February with weaker amplitudes than W3 QTDWs in January and February. Most W4 QTDWs occurred at latitudes from 40S to 20S in the Southern Hemisphere. The spatial structures of W3 and W4 in July and August are shown in Figure 9e,f, respectively. As described in Figure 6e, there were two peaks near the equator and at latitudes between approximately 30N and 50N. Moreover, the spatial structure of the W4 QTDWs in Figure 6f indicates that the maximum amplitudes were distributed at about 40N, with a maximum value of about 6 m/s. As a result, the spatial structures show that most W3 and W4 QTDWs both occurred in January and February in the Southern Hemisphere and in July and August in the Northern Hemisphere, which means occurred in the summer in both hemispheres.
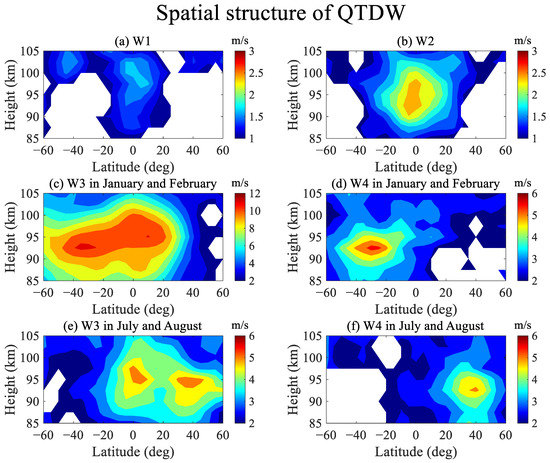
Figure 6.
The spatial structures of (a) W1, (b) W2, and (c) W3 in January and February, (d) W4 in January and February, (e) W3 in July and August, and (f) W4 in July and August QTDWs in meridional wind between 82 km and 96 km at latitudes of 60°S to 60°N from 2003 to 2012.
3.2. QBO Influence
The seasonal variations in QTDWs are discussed in the above results, and then the long-term trend is studied in this section. Figure 7 shows the long-term QTDWs and deseasonalized QTDWs in the mesospheric meridional wind obtained from meteor radar over KB from 2003 to 2012. Figure 7a displays the decadal QTDWs in the mesospheric meridional wind between 82 km and 96 km. The long-term trend of QTDWs is not obvious in Figure 7a. To further study the long-term trend, the deseasonalized QTDWs in the meridional wind are exhibited in Figure 7b. The seasonal variations were eliminated by smoothing the daily mean QTDW over a span of 365 days. The diagram illustrates that the westward and eastward winds alternated for a period of approximately two years, which is referred to as the quasi-biennial oscillation (QBO). The QBO was most significant between approximately 88 km and 96 km with a maximum amplitude of approximately 15 m/s. Furthermore, QTDWs have also been found to be modulated by QBO in some other studies [12,23,35]. The recognized mechanisms of QTDW activation are baroclinic/barotropic instability and the normal mode. Baroclinic/barotropic instability is closely related to the zonal wind shear below the QTDW. Thus, the monthly mean zonal wind at 30 km over KB, which was deseasonalized, is plotted in Figure 7c. The alternating easterlies and westerlies demonstrate the QBO and the amplitude of the QBO was about 30 m/s. The QBO in the zonal wind at 30 km is in phase with the QBO in QTDWs between 82 km and 96 km, which was demonstrated by Koval, et al. [49]. It is reasonable to suspect that the QBO in mesospheric QTDWs is related to the QBO in stratospheric zonal winds, which propagate upwind and excite QTDWs. The QBO signal in zonal winds also modulates the QBO in QTDWs.
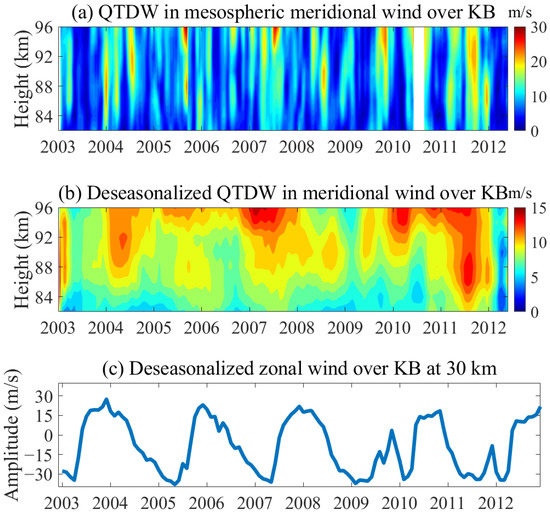
Figure 7.
(a) QTDWs in the mesospheric meridional wind from meteor radar over KB. (b) Deseasonalized QTDWs in mesospheric meridional wind over KB. (c) Amplitudes of deseasonalized monthly mean zonal wind at 30 km from 2003 to 2012.
4. Discussion
The above results of the seasonal variations and the impact of QBO on QTDWs over KB were investigated. The results in Figure 4 show that the most frequent occurrence of W1 QTDW was in September whereas the most frequent occurrence of W2 QTDWs was in February. Moreover, the W3 QTDWs occurred most frequently in January, February and July, which is in line with the previous studies. This finding indicates that the seasonal characteristics of QTDWs are mainly dominated by W3 waves. At the same time, the amplitudes of W3 waves are larger than those of W1 and W2 waves, as shown in Figure 4. This may be also the reason the seasonal characteristics of QTDWs are the same for W3 waves. As for the period, the periods of W3 QTDWs were slightly smaller than those of W1 and W2 QTDWs, which provides a reference for distinguishing the zonal wavenumbers of QTDWs. Waves with longer vertical wavelengths travel more easily into the upper atmosphere. Our finding shows that the ranges of vertical wavelengths of W1 and W2 QTDWs were larger than that of W3 QTDWs. The vertical wavelength peaks were also larger. At the same time, the vertical wavelength distribution of W3 QTDWs was more concentrated. The vertical wavelength of W1 QTDW that appears most frequently was 25 km and the vertical wavelengths of W2 and W3 QTDWs that happened the most often were both 30 km. Thus, the statistical analysis of the zonal wavenumbers of QTDWs in the upper atmosphere would also be interesting, which may be carried out in future studies, and it would be helpful to study the mechanism of the upward propagation of QTDWs.
The characteristics of QTDWs near the equator are different from the QTDWs at other latitudes. Thus, a comparison with QTDWs at middle latitudes is illustrated in Figure 8 and Figure 9. Figure 8 displays the averaged spectrum of the meridional wind at 90 km in Wuhan, Beijing, and Mohe from 2011 to 2019, which is different from the spectrum in KB. Figure 8a shows the averaged spectrum of the meridional wind in Wuhan. The significant largest peak occurred in July and August, and the second peak occurred in January and February, which is consistent with the well-known seasonal variations in QTDWs [7,14]. QTDWs with a period of approximately 48 h were almost not present in other months whereas QTDWs in KB appeared for most of the year. The spectrum of QTDWs in Beijing is plotted in Figure 8b, resembling the spectrum of the QTDWs in Wuhan. The largest peak also occurred in July and August while a much weaker peak occurred in January. Figure 8c shows the spectrum of QTDWs in Mohe, which is at a higher latitude than Wuhan and Beijing. The maximum amplitudes also occurred in July and August; however, there were not any peaks in January and February in Wuhan and Beijing. It can be seen that the amplitude in January and February decreased or even disappeared with the increasing latitude, which is also consistent with the results in Figure 6c. Additionally, the maximum of QTDWs in July over Mohe was weaker than those over Wuhan and Beijing.
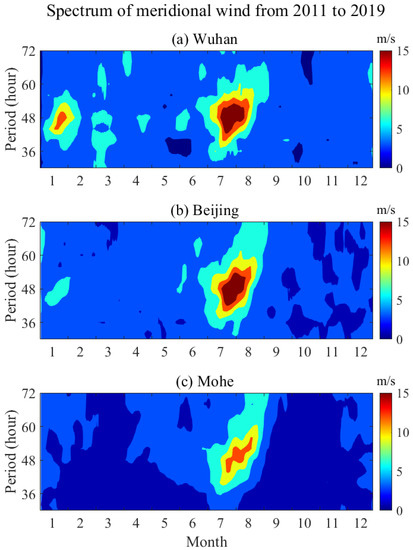
Figure 8.
The averaged spectrum of meridional wind at 90 km over (a) Wuhan, (b) Beijing, and (c) Mohe from 2011 to 2019.
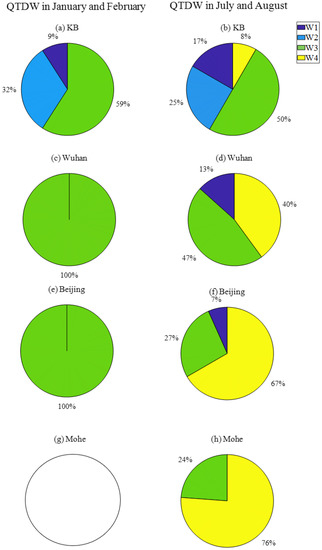
Figure 9.
The wavenumber statistics of QTDW events in January and February over (a) KB from 2003 to 2012, (c) Wuhan, (e) Beijing, and (g) Mohe from 2011 to 2019. The wavenumber statistics of QTDW events in July and August over (b) KB from 2003 to 2012, (d) Wuhan, (f) Beijing, and (h) Mohe from 2011 to 2019. The white color in (g) represents no QTDW events in January and February.
To compare the zonal wavenumbers of QTDW events at the equator and at the middle latitudes, the wavenumber statistics of QTDW events in KB, Wuhan, Beijing and Mohe are displayed in Figure 9. Figure 9a,c,e,g show the QTDW events statistics with different zonal wavenumber in January and February. The W3 events in January and February accounted for the largest portion of QTDW events over KB, accounting for 59% and W2 and W1 events accounting for 32% and 9%, respectively. At the same time, the QTDW events in Wuhan and Beijing were all W3 events in January and February. However, there is no QTDW event in Mohe in January and February, as shown in Figure 9g. Figure 9b,d,f,h display the QTDW event statistics with different zonal wavenumber in July and August. The W3 events in July and August shown in Figure 9b also accounted for the largest portion of QTDW events over KB, accounting for 50%. The W2, W1 and W4 incidents accounted for 25%,17% and 8%, respectively. The W3 events in Wuhan still accounted for the largest proportion, but slightly less than the QTDW events in KB. The number of W4 incidents in Wuhan increased significantly than those in KB, reaching 47%. Both W1 and W2 events also declined in Wuhan. As displayed in Figure 9f, the number of W3 incidents decreased by 27%, and the number of W4 incidents increased by 67%. The W1 events also declined compared to those in KB and Wuhan. Similarly, W3 events continue to decrease and W4 events continued to increase in Mohe. It is easily seen that the W4 events gradually increase with increasing latitude, while W1, W2, and W3 events all decreased with increasing latitude. It also can be seen that the QTDW events at the middle latitudes were dominated by W3 and W4, and W1 and W2 events were more often found in equatorial regions.
5. Conclusions
We studied the characteristics of QTDWs in the mesospheric meridional wind data obtained from meteor radar over KB from 2003 to 2012. The occurrence time, amplitude, period, and vertical wavelength of QTDW events were analyzed statistically. TIDI data were also used in this study to analyze the global distribution and the spatial structure of QTDWs with different zonal wavenumbers. Additionally, meridional wind data obtained from meteor radar in Wuhan, Beijing and Mohe were also analyzed to compare the QTDW events in the equatorial regions and middle latitudes.
The decadal observations in the equatorial mesopause region show that QTDWs are present almost all year around over KB. The QTDW events are all shown in Table and further statistical analysis was carried out to study the seasonal variations and long-term trends of QTDWs. W1, W2, W3, and W4 events were all observed over KB and the occurrence time, amplitudes, periods and vertical wavelengths of QTDW events with different zonal wavenumbers were determined in the present study. The most frequent occurrence of W1 QTDWs was in September whereas the most frequent occurrence of W2 QTDWs was in February. W3 QTDWs occurred most frequently in January, February, and July, which is consistent with previous studies. The periods of W2 QTDWs were more concentrated than those of W1 and W3 waves and the maximum periods of W3 QTDWs were smaller than those of the W1 and W2 QTDWs. The maximum periods in W1 and W2 QTDW were 48 h and the W3 QTDWs peaked at 45 h. Moreover, the amplitudes of W3 QTDWs were more scattered than those of W1 and W2 QTDWs and the maximum amplitudes of W3 QTDWs was stronger than the amplitudes of W1 and W2 QTDWs. The amplitude of W3 QTDWs that occurred most often was 40 m/s while the amplitudes of the W1 and W2 QTDWs that appeared most frequently were both 35 m/s. The statistics show that the ranges of the vertical wavelengths of W1 and W2 QTDWs were larger than that of W3 QTDWs. The vertical wavelength peaks were also larger. At the same time, the vertical wavelength distribution of W3 QTDWs was more concentrated. The vertical wavelength of W1 QTDWs that appeared most frequently was 25 km and the vertical wavelengths of W2 and W3 that occurred most often were both 30 km.
As for the global distribution and spatial structure of QTDWs with different zonal wavenumbers, the W1 and W2 QTDWs were present for almost the whole year between 20S and 20N. The spatial structures show that most W3 and W4 QTDWs were both present in January and February in the Southern Hemisphere and in July and August in the Northern Hemisphere, which means they occurred in the summer in both hemispheres. The QBO variability in the QTDWs over KB was also found in the meridional wind from meteor radar. The QBO in QTDWs was most significant between approximately 88 km and 96 km with a maximum amplitude of approximately 15 m/s. QTDWs have also been found to be modulated by QBO in some other studies [12,23,35]. The QBO in the zonal wind at 30 km is in phase with the QBO in QTDWs between 82 km and 96 km. It is reasonable to conclude that the QBO in mesospheric QTDWs is related to the QBO in stratospheric zonal winds, which propagate upwind and excite QTDWs. The QBO signals in the mesospheric QTDW are modulated by the QBO in zonal winds.
The statistical characteristics of QTDWs over KB are different from those at middle latitudes. The QTDWs over KB are present for almost the whole year; however, the QTDWs at middle latitudes are mainly present in January/February and July/August. The W3 QTDWs in KB usually occur in January and July, while the W1 and W2 QTDWs are present in other months. It was found that the amplitude in January and February decreases or even disappears with increasing latitude. Furthermore, the maximum amplitude of QTDW in July over Mohe is weaker than those over Wuhan and Beijing. Regarding the zonal wavenumber statistics of QTDWs, the W4 events gradually increase with increasing latitude, whereas W1, W2 and W3 events all decrease with increasing latitude.
Author Contributions
Conceptualization, S.-Y.G. and R.S.; software, R.S.; validation, R.S., S.-Y.G. and X.D.; formal analysis, R.S.; investigation, R.S.; resources, S.-Y.G. and X.D.; writing—original draft preparation, R.S.; writing—review and editing, R.S., S.-Y.G., Y.W., Y.Q. and Z.Y.; funding acquisition, S.-Y.G. and X.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (41831071, 42188101).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The Mohe, Beijing and Wuhan meteor radar data are available from http://wdc.geophys.cn/dbList.asp?dType=MetPublish, accessed on 5 September 2022. Data acquisition of meteor wind radar at Kototabang are from http://database.rish.kyoto-u.ac.jp/arch/iugonet/mwr_ktb/index_mwr_ktb.html, accessed on 20 March 2022. The TIDI horizontal winds are obtained at http://timed.hao.ucar.edu/tidi/data.html, accessed on 12 July 2022.
Acknowledgments
This work is funded by the National Natural Science Foundation of China (41831071, 42188101). We acknowledge the use of data from the Chinese Meridian Project. Data acquisition of meteor wind radar at Kototabang has been done by Research Institute for Sustainable Humanosphere (RISH), Kyoto University. Distribution of the data has been partly supported by the IUGONET (Inter-university Upper atmosphere Global Observation NETwork) project (http://www.iugonet.org/, accessed on 20 March 2022) funded by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan. We acknowledge the TIMED/TIDI for providing the wind field data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yue, J.; Wang, W.; Ruan, H.; Chang, L.C.; Lei, J. Impact of the interaction between the quasi-2 day wave and tides on the ionosphere and thermosphere. J. Geophys. Res. Space Phys. 2016, 121, 3555–3563. [Google Scholar] [CrossRef]
- Fröhlich, K.; Pogoreltsev, A.; Jacobi, C. Numerical simulation of tides, Rossby and Kelvin waves with the COMMA-LIM model. Adv. Space Res. 2003, 32, 863–868. [Google Scholar] [CrossRef]
- Chang, L.C.; Palo, S.E.; Liu, H.L. Short-term variability in the migrating diurnal tide caused by interactions with the quasi 2 day wave. J. Geophys. Res. Atmos. 2011, 116, D12112. [Google Scholar] [CrossRef]
- Yang, C.; Li, T.; Lai, D.; Wang, X.; Xue, X.; Dou, X. The Delayed Response of the Troposphere-Stratosphere-Mesosphere Coupling to the 2019 Southern SSW. Geophys. Res. Lett. 2022, 49, e2022GL101759. [Google Scholar] [CrossRef]
- Muller, H.G. A discussion on D and E region winds over Europe-Long-period meteor wind oscillations. Philos. Trans. R. Soc. London Ser. A Math. Phys. Sci. 1972, 271, 585–599. [Google Scholar] [CrossRef]
- Kumar, K.K.; Subrahmanyam, K.V.; Mathew, S.S.; Koushik, N.; Ramkumar, G. Simultaneous observations of the quasi 2-day wave climatology over the low and equatorial latitudes in the mesosphere lower thermosphere. Clim. Dyn. 2018, 51, 221–233. [Google Scholar] [CrossRef]
- Lilienthal, F.; Jacobi, C. Meteor radar quasi 2-day wave observations over 10 years at Collm (51.3°N, 13.0°E). Atmos. Chem. Phys. 2015, 15, 9917–9927. [Google Scholar] [CrossRef]
- Pancheva, D.; Mitchell, N.J.; Manson, A.H.; Meek, C.E.; Jacobi, C.; Portnyagin, Y.; Merzlyakov, E.; Hocking, W.K.; MacDougall, J.; Singer, W.; et al. Variability of the quasi-2-day wave observed in the MLT region during the PSMOS campaign of June–August 1999. J. Atmos. Sol. -Terr. Phys. 2004, 66, 539–565. [Google Scholar] [CrossRef]
- Yue, J.; Liu, H.-L.; Chang, L.C. Numerical investigation of the quasi 2 day wave in the mesosphere and lower thermosphere. J. Geophys. Res. Atmos. 2012, 117, D05111. [Google Scholar] [CrossRef]
- Yang, C.; Ren, B.; Li, G.; Zheng, J. Change of the wintertime SSTA variability over the West Pacific after the mid-1980s: Effect of the increasing El Niño Modoki. J. Geophys. Res. Atmos. 2014, 119, 5204–5225. [Google Scholar] [CrossRef]
- Harris, T.J.; Vincent, R.A. The quasi-two-day wave observed in the equatorial middle atmosphere. J. Geophys. Res. Atmos. 1993, 98, 10481–10490. [Google Scholar] [CrossRef]
- Rao, N.V.; Ratnam, M.V.; Vedavathi, C.; Tsuda, T.; Murthy, B.V.K.; Sathishkumar, S.; Gurubaran, S.; Kumar, K.K.; Subrahmanyam, K.V.; Rao, S.V.B. Seasonal, inter-annual and solar cycle variability of the quasi two day wave in the low-latitude mesosphere and lower thermosphere. J. Atmos. Sol. -Terr. Phys. 2017, 152–153, 20–29. [Google Scholar] [CrossRef]
- Lima, L.M.; Medeiros, A.F.; Buriti, R.A.; Batista, P.P.; Clemesha, B.R.; Takahashi, H. Mesospheric 2-Day waves observed simultaneously in the equatorial and low latitudes regions of Brazil. Rev. Bras. Geofís. 2007, 25, 43–48. [Google Scholar] [CrossRef]
- Jacobi, C.; Hoffmann, P.; Kürschner, D. Trends in MLT region winds and planetary waves, Collm (52°N, 15°E). Ann. Geophys. 2008, 26, 1221–1232. [Google Scholar] [CrossRef]
- Nozawa, S.; Imaida, S.; Brekke, A.; Hall, C.M.; Manson, A.; Meek, C.; Oyama, S.; Dobashi, K.; Fujii, R. The quasi 2-day wave observed in the polar mesosphere. J. Geophys. Res. Atmos. 2003, 108, ACL 3-1–ACL 3-12. [Google Scholar] [CrossRef]
- Araújo, L.R.; Lima, L.M.; Batista, P.P.; Clemesha, B.R.; Takahashi, H. Planetary wave seasonality from meteor wind measurements at 7.4°S and 22.7°S. Ann. Geophys. 2014, 32, 519–531. [Google Scholar] [CrossRef]
- Rodgers, C.; Prata, A.J. Evidence for a traveling two-day wave in the middle atmosphere. J. Geophys. Res. Atmos. 1981, 86, 9661–9664. [Google Scholar] [CrossRef]
- Wu, D.; Hays, P.; Skinner, W.; Marshall, A.; Burrage, M.; Lieberman, R.; Ortland, D.A. Observations of the quasi 2-day wave from the High Resolution Doppler Imager on UARS. Geophys. Res. Lett. 1993, 20, 2853–2856. [Google Scholar] [CrossRef]
- Yang, C.; Li, T.; Smith, A.K.; Dou, X. The response of the Southern Hemisphere middle atmosphere to the Madden–Julian oscillation during austral winter using the Specified-Dynamics Whole Atmosphere Community Climate Model. J. Clim. 2017, 30, 8317–8333. [Google Scholar] [CrossRef]
- Palo, S.E.; Roble, R.G.; Hagan, M. Middle atmosphere effects of the quasi-two-day wave determined from a General Circulation Model. Earth Planets Space 1999, 51, 629–647. [Google Scholar] [CrossRef]
- Gu, S.-Y.; Li, T.; Dou, X.; Wu, Q.; Mlynczak, M.G.; Russell III, J.M. Observations of Quasi-Two-Day wave by TIMED/SABER and TIMED/TIDI. J. Geophys. Res. Atmos. 2013, 118, 1624–1639. [Google Scholar] [CrossRef]
- Tunbridge, V.M.; Sandford, D.J.; Mitchell, N.J. Zonal wave numbers of the summertime 2 day planetary wave observed in the mesosphere by EOS Aura Microwave Limb Sounder. J. Geophys. Res. Atmos. 2011, 116, D11103. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Zhang, S.D.; Yi, F.; Huang, C.M.; Huang, K.M.; Gan, Q.; Gong, Y. Global climatological variability of quasi-two-day waves revealed by TIMED/SABER observations. Ann. Geophys. 2013, 31, 1061–1075. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P.; Siskind, D.E. Climatology of the quasi-2-day waves observed in the MLS/Aura measurements (2005–2014). J. Atmos. Sol. -Terr. Phys. 2018, 171, 210–224. [Google Scholar] [CrossRef]
- Garcia, R.R.; Lieberman, R.; Russell, J.M.; Mlynczak, M.G. Large-scale waves in the mesosphere and lower thermosphere observed by SABER. J. Atmos. Sci. 2005, 62, 4384–4399. [Google Scholar] [CrossRef]
- Liu, G.; England, S.L.; Janches, D. Quasi Two-, Three-, and Six-Day Planetary-Scale Wave Oscillations in the Upper Atmosphere Observed by TIMED/SABER Over ~17 Years During 2002–2018. J. Geophys. Res. Space Phys. 2019, 124, 9462–9474. [Google Scholar] [CrossRef]
- Gu, S.-Y.; Dou, X.-K.; Yang, C.-Y.; Jia, M.; Huang, K.-M.; Huang, C.-M.; Zhang, S.-D. Climatology and Anomaly of the Quasi-Two-Day Wave Behaviors During 2003–2018 Austral Summer Periods. J. Geophys. Res. Space Phys. 2019, 124, 544–556. [Google Scholar] [CrossRef]
- Gu, S.Y.; Liu, H.L.; Pedatella, N.; Dou, X.; Li, T.; Chen, T. The quasi 2 day wave activities during 2007 austral summer period as revealed by Whole Atmosphere Community Climate Model. J. Geophys. Res. Space Phys. 2016, 121, 2743–2754. [Google Scholar] [CrossRef]
- Madhavi, G.; Kishore, P.; Rao, S.; Velicogna, I.; Basha, G. Two-day wave observations over the middle and high latitudes in the NH and SH using COSMIC GPSRO measurements. Adv. Space Res. 2015, 55, 722–731. [Google Scholar] [CrossRef]
- Merzlyakov, E.; Jacobi, C. Quasi-two-day wave in an unstable summer atmosphere-some numerical results on excitation and propagation. Ann. Geophys. 2004, 22, 1917–1929. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P.; Siskind, D.E.; Smith, A.K. Global distribution and variability of quasi 2 day waves based on the NOGAPS-ALPHA reanalysis model. J. Geophys. Res. Space Phys. 2016, 121, 11422–411449. [Google Scholar] [CrossRef]
- Andrews, D.G.; Holton, J.R.; Leovy, C.B. Middle Atmosphere Dynamics; Academic Press: Cambridge, MA, USA, 1987. [Google Scholar] [CrossRef]
- Salby, M.L. The 2-day wave in the middle atmosphere: Observations and theory. J. Geophys. Res. Ocean. 1981, 86, 9654–9660. [Google Scholar] [CrossRef]
- Plumb, R.A. Baroclinic instability of the summer mesosphere: A mechanism for the quasi-two-day wave? J. Atmos. Sci. 1983, 40, 262–270. [Google Scholar] [CrossRef]
- Li, T.; She, C.-Y.; Palo, S.E.; Wu, Q.; Liu, H.-L.; Salby, M.L. Coordinated lidar and TIMED observations of the quasi-two-day wave during August 2002–2004 and possible quasi-biennial oscillation influence. Adv. Space Res. 2008, 41, 1463–1471. [Google Scholar] [CrossRef]
- Yang, C.; Smith, A.K.; Li, T.; Dou, X. The effect of the Madden-Julian oscillation on the mesospheric migrating diurnal tide: A study using SD-WACCM. Geophys. Res. Lett. 2018, 45, 5105–5114. [Google Scholar] [CrossRef]
- Guharay, A.; Batista, P.; Andrioli, V. Study of solar cycle dependence of the quasi-two-day wave in the MLT from an extratropical station. J. Earth Syst. Sci. 2020, 129, 38. [Google Scholar] [CrossRef]
- Batubara, M.; Suryana, R.; Manik, T.; Sitompul, P. Kototabang—West Sumatera meteor radar: System design and initial results of a large scale meteor echo. In Proceedings of the 2011 6th International Conference on Telecommunication Systems, Services, and Applications (TSSA), Denpasar, Indonesia, 20–21 October 2011; pp. 17–21. [Google Scholar] [CrossRef]
- Matsumoto, N.; Shinbori, A.; Riggin, D.M.; Tsuda, T. Measurement of momentum flux using two meteor radars in Indonesia. Ann. Geophys. 2016, 34, 369–377. [Google Scholar] [CrossRef]
- Jia, M.; Xue, X.; Gu, S.; Chen, T.; Ning, B.; Wu, J.; Zeng, X.; Dou, X. Multiyear Observations of Gravity Wave Momentum Fluxes in the Midlatitude Mesosphere and Lower Thermosphere Region by Meteor Radar. J. Geophys. Res. Space Phys. 2018, 123, 5684–5703. [Google Scholar] [CrossRef]
- Killeen, T.L.; Wu, Q.; Solomon, S.C.; Ortland, D.A.; Skinner, W.R.; Niciejewski, R.J.; Gell, D.A. TIMED Doppler Interferometer: Overview and recent results. J. Geophys. Res. Space Phys. 2006, 111, A10S01. [Google Scholar] [CrossRef]
- Dhadly, M.S.; Englert, C.R.; Drob, D.P.; Emmert, J.T.; Niciejewski, R.; Zawdie, K.A. Comparison of ICON/MIGHTI and TIMED/TIDI Neutral Wind Measurements in the Lower Thermosphere. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029904. [Google Scholar] [CrossRef]
- Oberheide, J.; Wu, Q.; Killeen, T.; Hagan, M.; Roble, R.G. A climatology of nonmigrating semidiurnal tides from TIMED Doppler Interferometer (TIDI) wind data. J. Atmos. Sol. -Terr. Phys. 2007, 69, 2203–2218. [Google Scholar] [CrossRef]
- Wu, D.L.; Hays, P.B.; Skinner, W.R. A Least Squares Method for Spectral Analysis of Space-Time Series. J. Atmos. Sci. 1995, 52, 3501–3511. [Google Scholar] [CrossRef]
- Yang, C.; Li, T.; Xue, X.; Gu, S.Y.; Yu, C.; Dou, X. Response of the northern stratosphere to the Madden-Julian oscillation during boreal winter. J. Atmos. Sci. 2019, 124, 5314–5331. [Google Scholar] [CrossRef]
- Merzlyakov, E.; Pancheva, D.; Mitchell, N.; Forbes, J.; Portnyagin, Y.I.; Palo, S.; Makarov, N.; Muller, H. High-and mid-latitude quasi-2-day waves observed simultaneouslyby four meteor radars during summer 2000. Ann. Geophys. 2004, 22, 773–788. [Google Scholar] [CrossRef]
- Ern, M.; Preusse, P.; Kalisch, S.; Kaufmann, M.; Riese, M. Role of gravity waves in the forcing of quasi two-day waves in the mesosphere: An observational study. J. Geophys. Res. Atmos. 2013, 118, 3467–3485. [Google Scholar] [CrossRef]
- Wu, D.L.; Schwartz, M.J.; Waters, J.W.; Limpasuvan, V.; Wu, Q.; Killeen, T.L. Mesospheric Doppler wind measurements from aura microwave limb sounder (MLS). Adv. Space Res. 2008, 42, 1246–1252. [Google Scholar] [CrossRef]
- Koval, A.V.; Gavrilov, N.M.; Didenko, K.A.; Ermakova, T.; Kandieva, K. Numerical simulation of stratospheric QBO impact on the meridional circulation up to the thermosphere. Sci. Rep. 2022, 44, 882. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).