Urban Area Characterization and Structure Analysis: A Combined Data-Driven Approach by Remote Sensing Information and Spatial–Temporal Wireless Data
Abstract
:1. Introduction
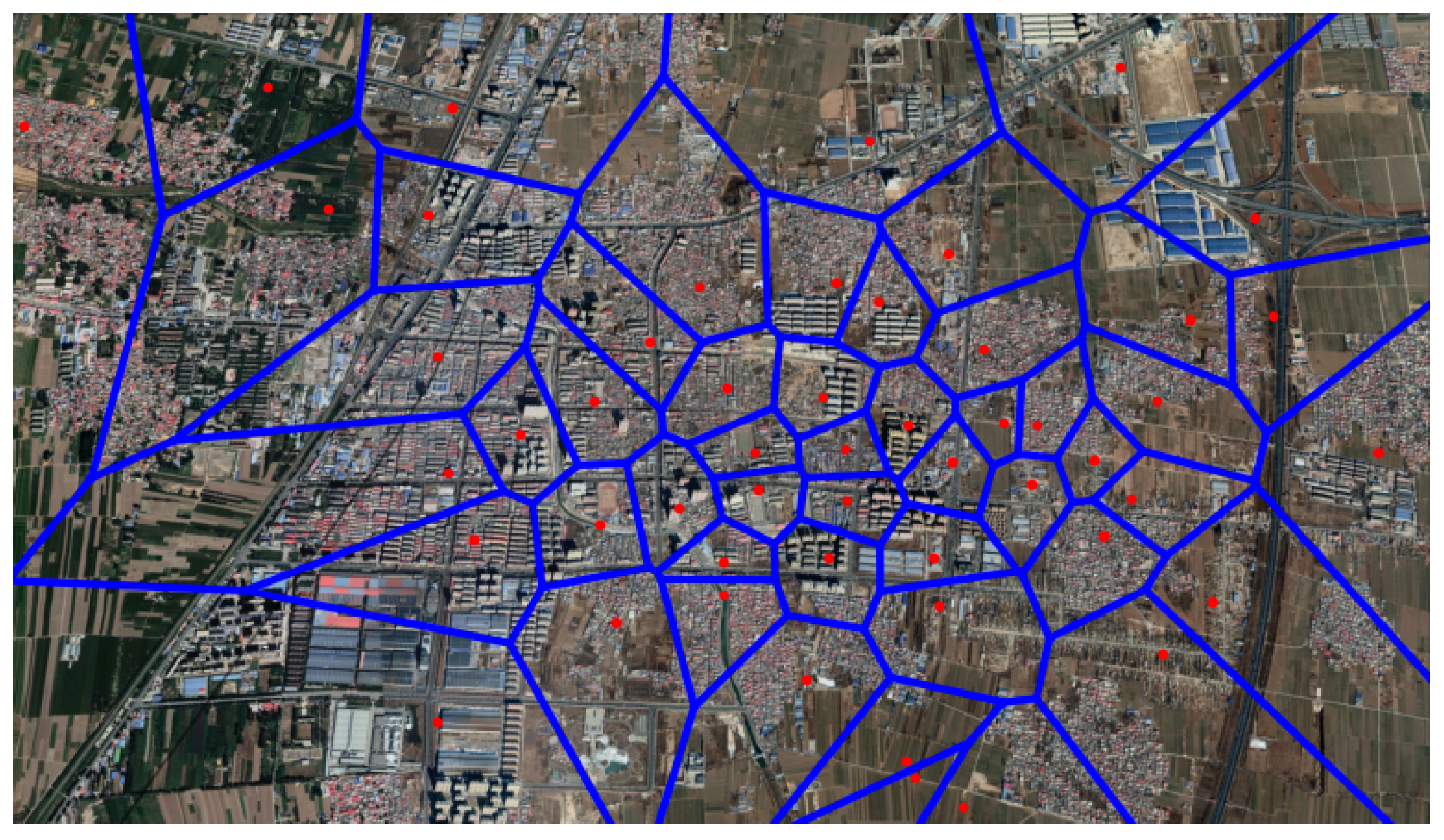
- We adopt Voronoi diagrams to zone urban areas by combining BS locations data and remote sensing images. The Voronoi-diagram-based method can accurately identify activity areas of the users served by BSs.
- We employ an ensemble empirical mode decomposition (EEMD) method to extract period component and trend component of wireless network data, which represent human behavior and activity level, and we use transfer-entropy-based causal structure learning to model urban function structure as a causal directed graph.
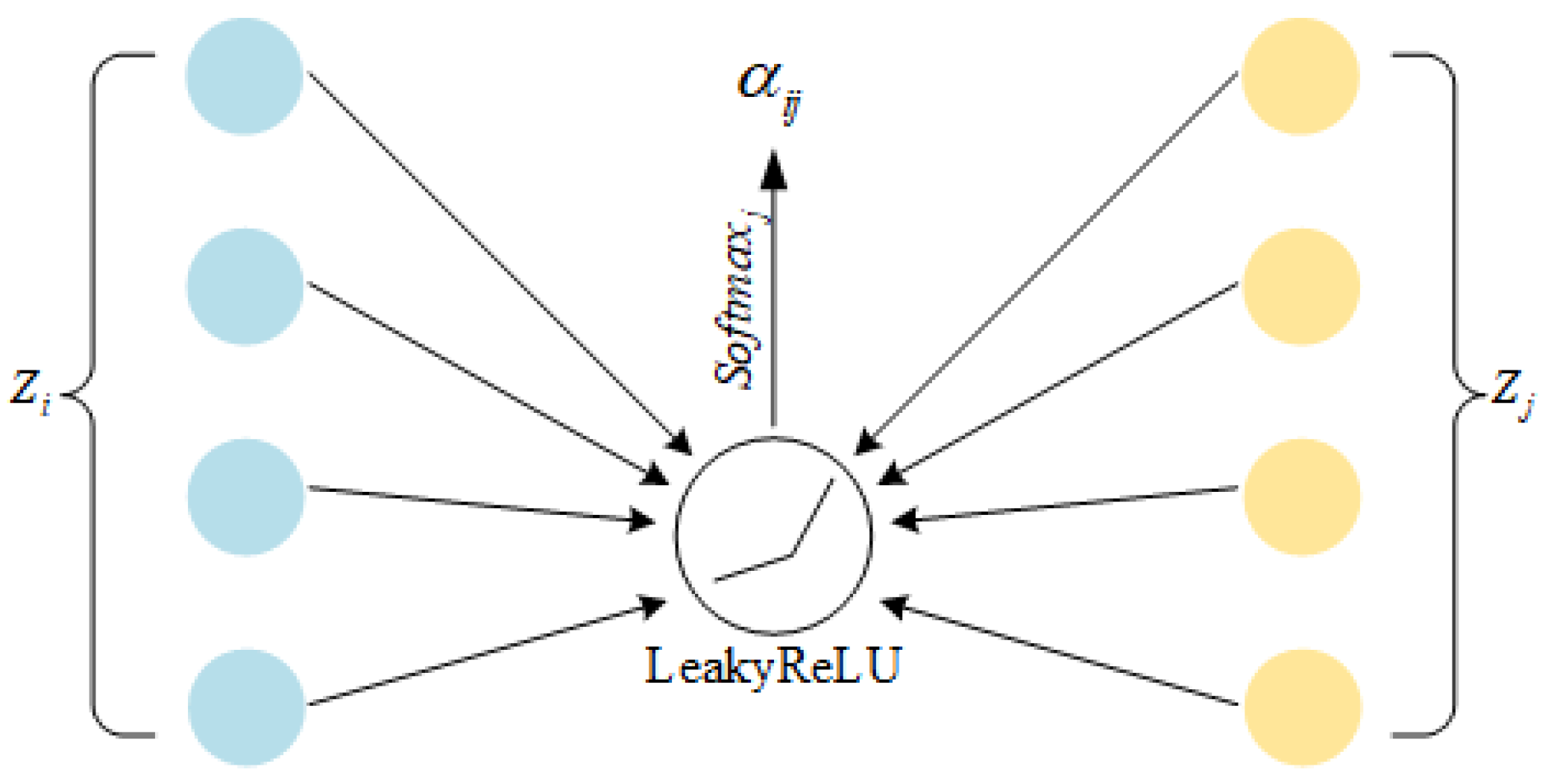
- We design a novel spatiotemporal city computing method based on graph attention network to mine features of urban function structure. The goal of our city computing research is to find an accurate prediction method for urban wireless traffic, which is an important topic in city simulation. Combined with commuting index calculation, the method can provide guidance for urban planning, transportation planning, and urban energy saving. Experimental results prove that the proposed method outperforms other common methods.
2. Materials and Methods
2.1. Dataset and Study Area
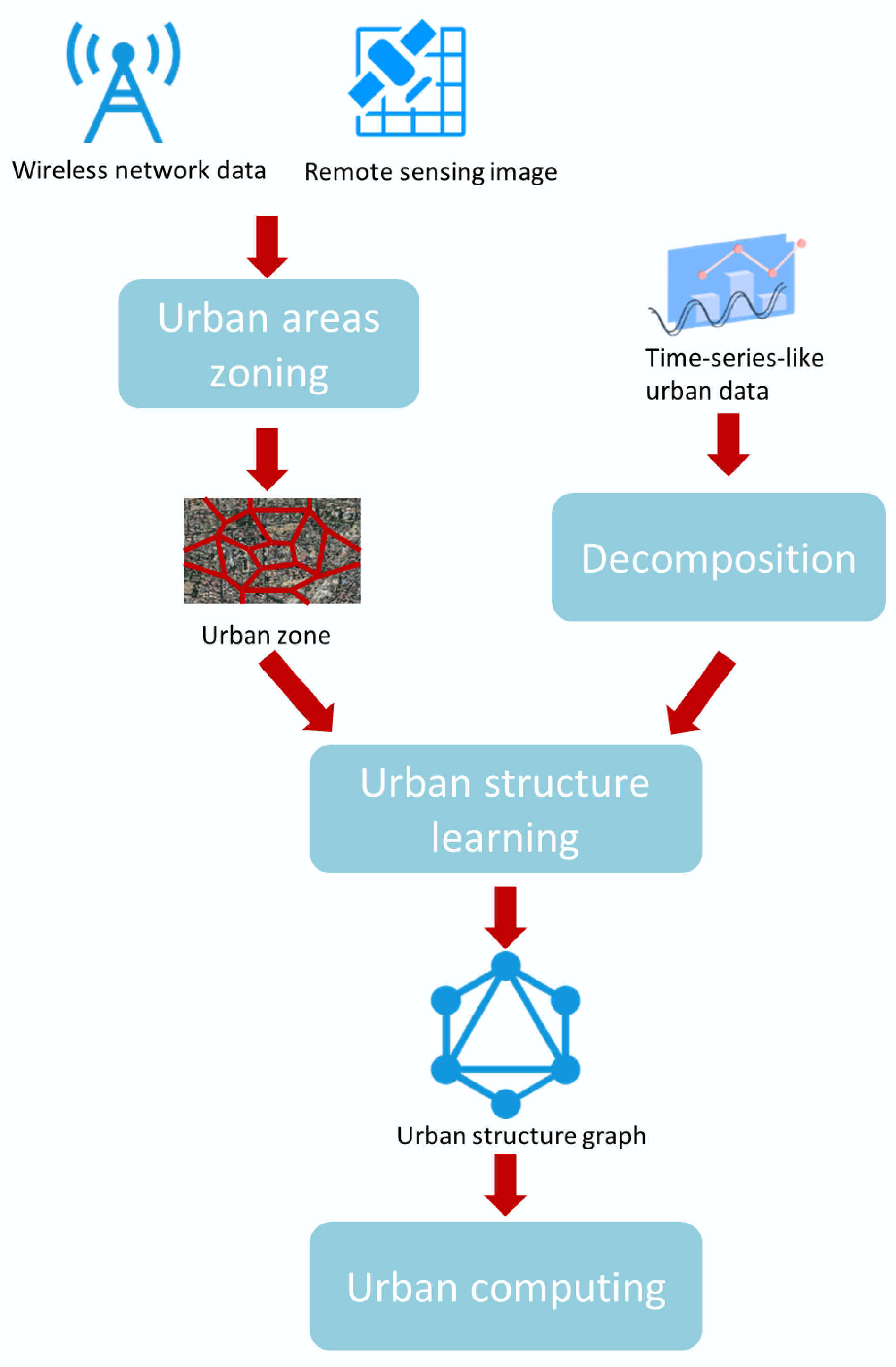
2.2. General Structure of Proposed Method
- Urban areas zoning: The motivation of this paper is to analyze city functions through BS-level wireless network traffic data. Therefore, the first task is to accurately zone BS coverage areas. As a result, an urban remote sensing image is divided into a collection of coverage areas anchored by BSs. To achieve this objective, we propose a Voronoi-diagram-based method, which is detailed in Section 2.3.
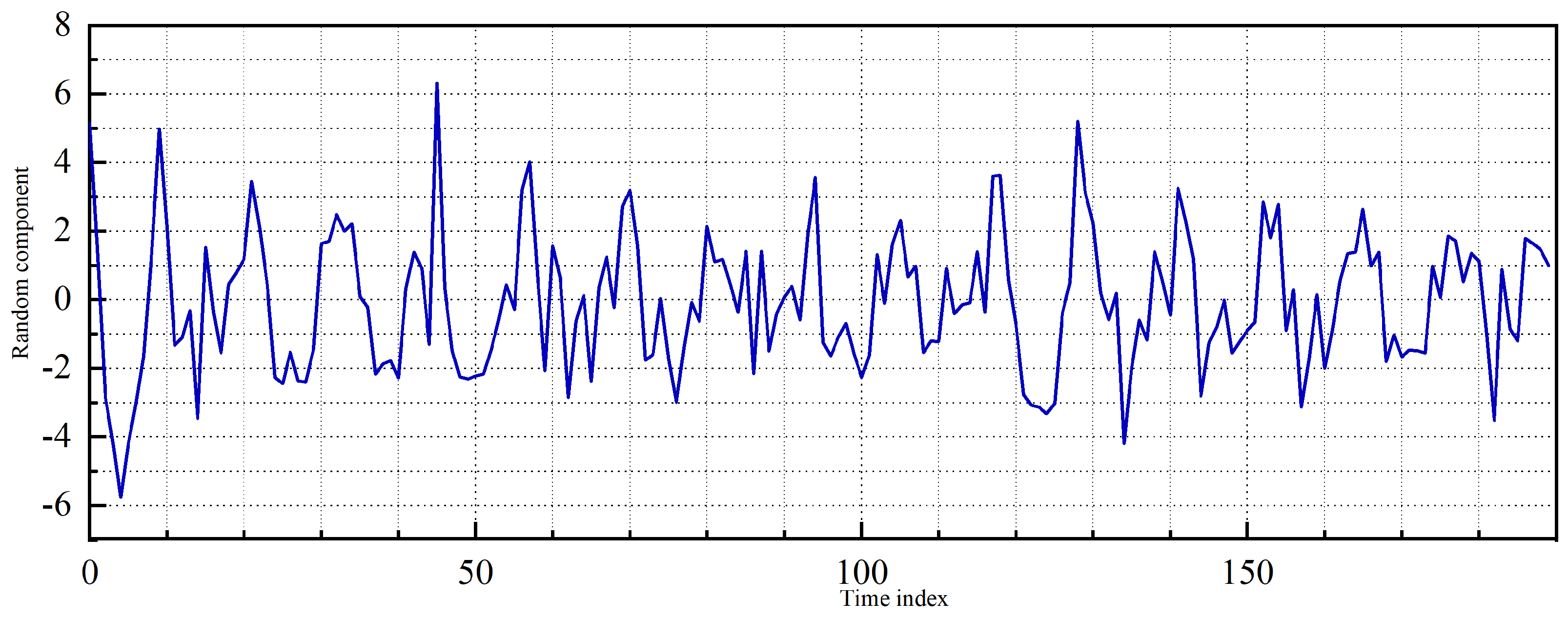
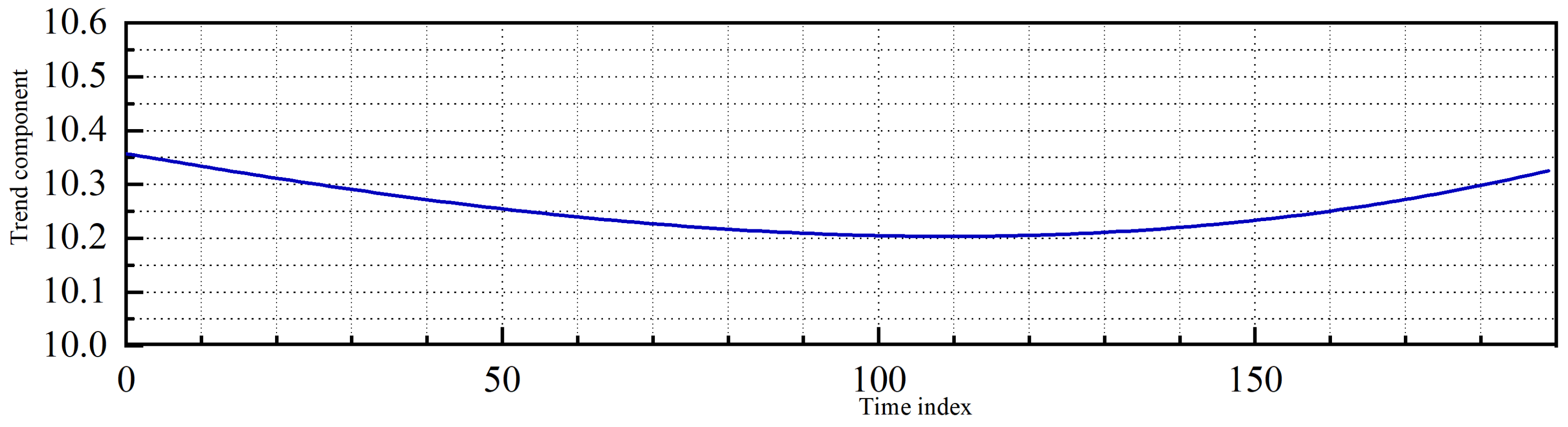
- Wireless network data decomposition: A challenge of analyzing urban function structure through wireless network data is the nonstationarity of the data. Therefore, as preparation for urban function structure learning, we propose an EEMD-based method for decomposing wireless network traffic data. The method decomposes nonstationary traffic time series of each BS into three components (i.e., random component, periodic component, and trend component). Each component represents human behavior at different scales within the BS coverage area. The specific process of the method is described in Section 2.4.1.
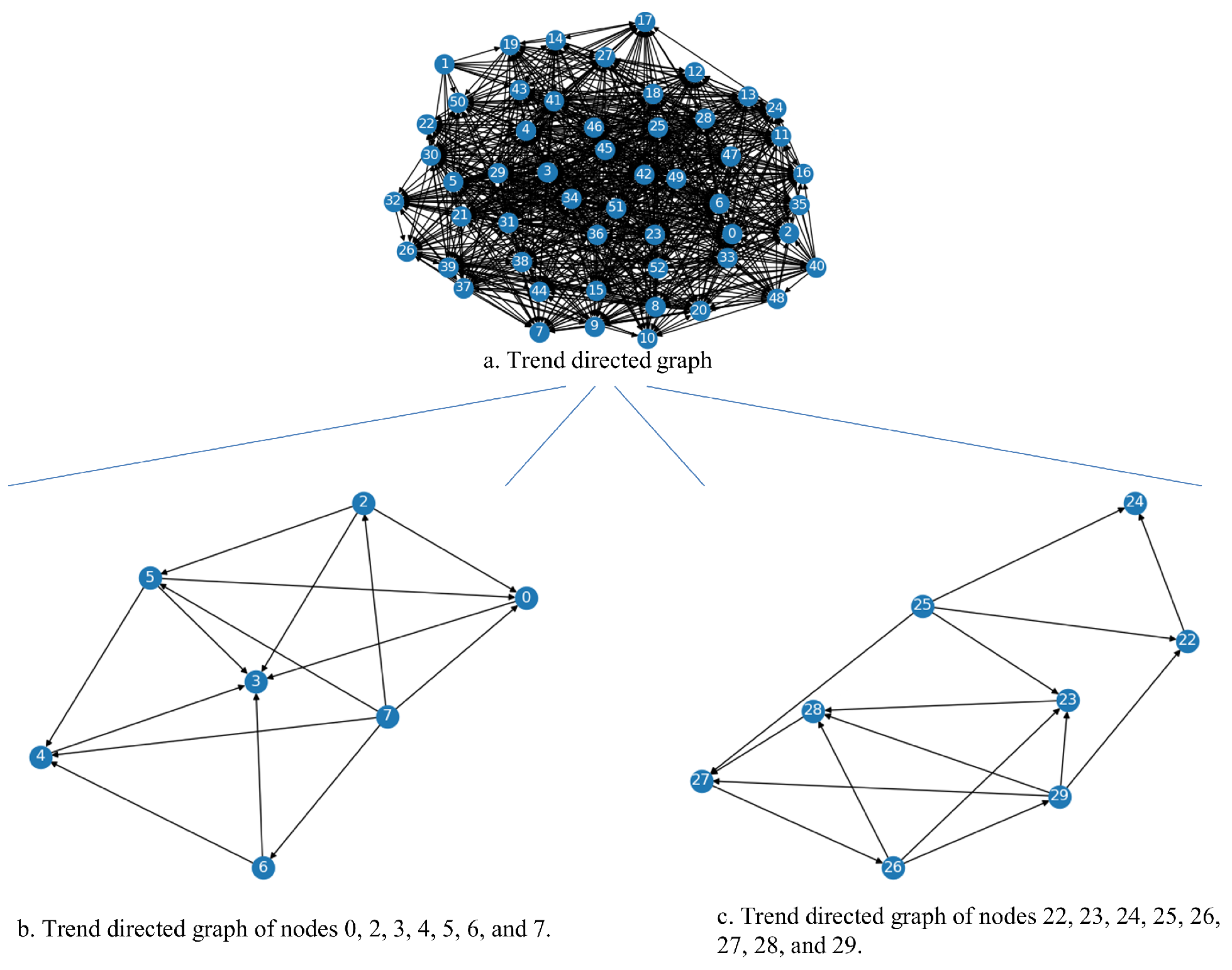
- Urban structure learning: In this module, we model the impacts among different coverage areas as directed causal relationships, and we adopt a VLTE-based causal structure learning method to mine the causal relationships among coverage areas at three components (the specific algorithm is described in Section 2.4.2). As a result, urban function structures at three component scales are modeled as causal directed graphs. This enables visualization of urban function structure.
- Urban computing: The above three modules provide the possibility for structured city simulation. To deal with complex causal directed graphs of urban areas, this paper introduces advanced graph neural network technology to implement spatiotemporal city computing, and we perform wireless network traffic prediction to verify the method. The spatiotemporal city computing method and simulation results are presented in Section 2.5 and Section 3.
2.3. Urban Area Zoning
- Construct the Delaunay triangle network according to control points set B and record the three control points that construct the triangle in T;
- Generate an adjacent triangle set for each control point , that is, is the set of triangles whose vertices have control point ; then sort the triangles in into a clockwise or counterclockwise direction;
- Calculate the external circle center of each triangle in T. Record it as ;
- According to adjacent triangles of each control point, the Voronoi diagram set V are obtained by connecting outer circle centers of these adjacent triangles. The vertices of can be represented by Formula (2). For Voronoi diagrams at the edges of the triangular network, a vertical bisector can be made to intersect with the outline of the figure and form a Voronoi diagram together with the outline.
2.4. Urban Function Structure Learning
2.4.1. Wireless Network Data Decomposition
- The number of extreme and zero crossings must either equal or differ by 1 or 2;
- The envelopes defined by the local maxima and the local minima are symmetrical.
- Initialize and .
- Generate M white noises .
- Perform the jth decomposition on the signal added white noise.
- Set then repeat step 2 if .
- Report then separate from to obtain .
- If still has least 2 extremes then set and repeat the operations from step 2 to step 6, otherwise the decomposition process is finished.
2.4.2. Causal Structure Learning
| Algorithm 1 Causal structure learning. |
2.5. Spatiotemporal City Computing
3. Results
3.1. Urban Area Zoning
3.2. Urban Function Structure
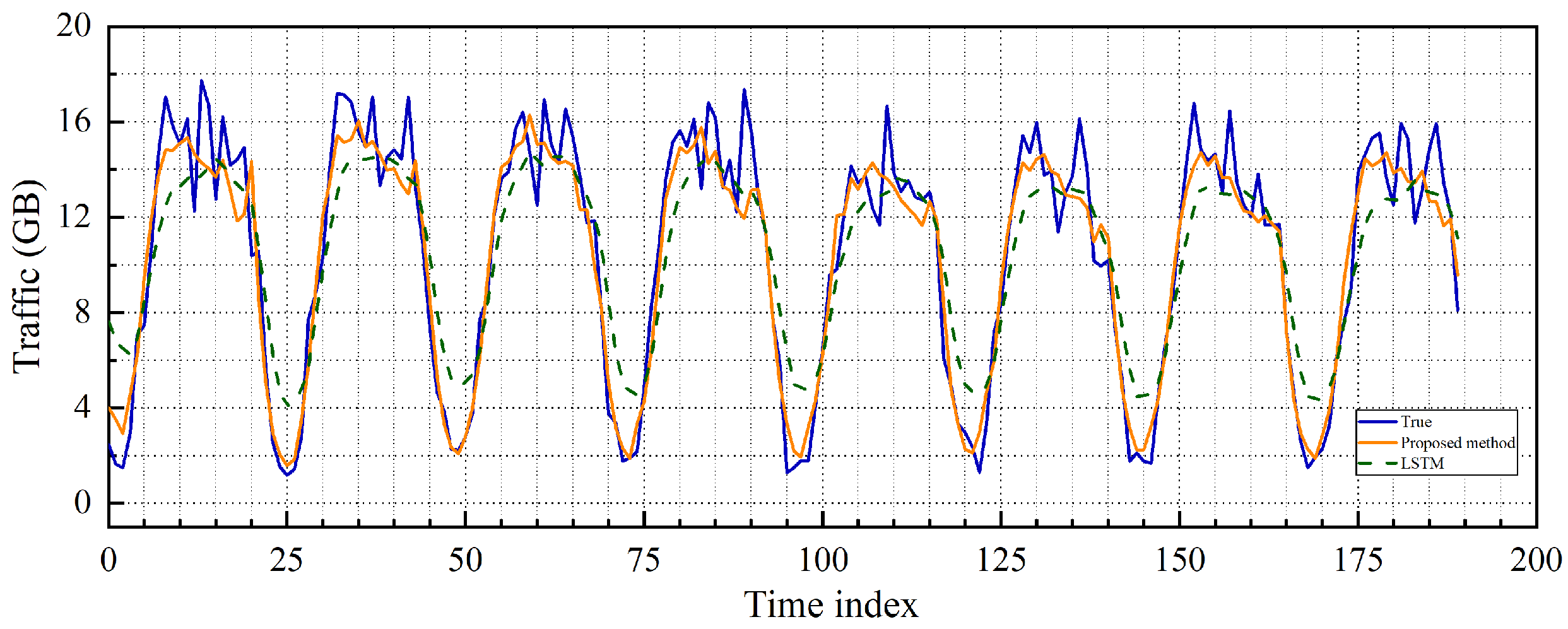
3.3. Spatiotemporal City Computing
- GCN: GCN is a convolutional neural network for graph data [10]. In the simulation of this method, the used graph structure is generated by the urban function structure learning module proposed in this paper.
- LSTM: LSTM is a recurrent neural network with long- and short-term memory capability. In recent years, it is often used to perform time series prediction with the spread of machine learning applications [62].
- ARIMA: ARIMA is a differentially integrated moving average autoregressive model, which is a statistical method commonly used for time series prediction.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, W.; Pickett, S.T.; Cadenasso, M.L. Shifting concepts of urban spatial heterogeneity and their implications for sustainability. Landsc. Ecol. 2017, 32, 15–30. [Google Scholar] [CrossRef]
- Shoemaker, D.A. The Role of Spatial Heterogeneity and Urban Pattern in Modulating Ecosystem Services; North Carolina State University: Raleigh, NC, USA, 2016. [Google Scholar]
- Pickett, S.T.; Cadenasso, M.L.; Childers, D.L.; McDonnell, M.J.; Zhou, W. Evolution and future of urban ecological science: Ecology in, of, and for the city. Ecosyst. Health Sustain. 2016, 2, e01229. [Google Scholar] [CrossRef]
- Borgström, S.; Andersson, E.; Björklund, T. Retaining multi-functionality in a rapidly changing urban landscape: Insights from a participatory, resilience thinking process in Stockholm, Sweden. Ecol. Soc. 2021, 4, 4. [Google Scholar] [CrossRef]
- Elbakidze, M.; Dawson, L.; Milberg, P.; Mikusiński, G.; Hedblom, M.; Kruhlov, I.; Yamelynets, T.; Schaffer, C.; Johansson, K.E.; Grodzynskyi, M. Multiple factors shape the interaction of people with urban greenspace: Sweden as a case study. Urban For. Urban Green. 2022, 74, 127672. [Google Scholar] [CrossRef]
- Shane, D.G. Urban Design since 1945. In A Global Perspective; John Wiley and Sons Ltd.: New York, NY, USA, 2011. [Google Scholar]
- Ortiz-Báez, P.; Cabrera-Barona, P.; Bogaert, J. Characterizing landscape patterns in urban-rural interfaces. J. Urban Manag. 2021, 10, 46–56. [Google Scholar] [CrossRef]
- Vanderhaegen, S.; Canters, F. Mapping urban form and function at city block level using spatial metrics. Landsc. Urban Plan. 2017, 167, 399–409. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Yang, M.; Yin, H. A graph convolutional neural network for classification of building patterns using spatial vector data. ISPRS J. Photogramm. Remote Sens. 2019, 150, 259–273. [Google Scholar] [CrossRef]
- Zhang, K.; Chuai, G.; Zhang, J.; Chen, X.; Si, Z.; Maimaiti, S. DIC-ST: A Hybrid Prediction Framework Based on Causal Structure Learning for Cellular Traffic and Its Application in Urban Computing. Remote Sens. 2022, 14, 1439. [Google Scholar] [CrossRef]
- Gu, J.R.; Chen, X.W.; Yang, H.L. Spatial clustering algorithm on urban function oriented zone. Sci. Surv. Mapp. 2011, 36, 5. [Google Scholar]
- Cheng, J.; Turkstra, J.; Peng, M.; Du, N.; Ho, P. Urban land administration and planning in China: Opportunities and constraints of spatial data models. Land Use Policy 2006, 23, 604–616. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, J.; Yang, R.; Xiao, X.; Xia, J.C. Contribution of urban functional zones to the spatial distribution of urban thermal environment. Build. Environ. 2022, 216, 109000. [Google Scholar] [CrossRef]
- Heiden, U.; Heldens, W.; Roessner, S.; Segl, K.; Esch, T.; Mueller, A. Urban structure type characterization using hyperspectral remote sensing and height information. Landsc. Urban Plan. 2012, 105, 361–375. [Google Scholar] [CrossRef]
- Batty, M.; Longley, P.A. Fractal Cities: A Geometry of Form and Function; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Luck, M.; Wu, J. A gradient analysis of urban landscape pattern: A case study from the Phoenix metropolitan region, Arizona, USA. Landsc. Ecol. 2002, 17, 327–339. [Google Scholar] [CrossRef]
- Zhou, W.; Ming, D.; Lv, X.; Zhou, K.; Bao, H.; Hong, Z. SO–CNN based urban functional zone fine division with VHR remote sensing image. Remote Sens. Environ. 2020, 236, 111458. [Google Scholar] [CrossRef]
- Aubrecht, C.; León Torres, J.A. Evaluating multi-sensor nighttime earth observation data for identification of mixed vs. residential use in urban areas. Remote Sens. 2016, 8, 114. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Levin, N.; Saaroni, H. A spectral based recognition of the urban environment using the visible and near-infrared spectral region (0.4-1.1 μm). A case study over Tel-Aviv, Israel. Int. J. Remote Sens. 2001, 22, 2193–2218. [Google Scholar] [CrossRef]
- Herold, M.; Gardner, M.E.; Roberts, D.A. Spectral resolution requirements for mapping urban areas. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1907–1919. [Google Scholar] [CrossRef]
- Du, S.; Du, S.; Liu, B.; Zhang, X. Context-enabled extraction of large-scale urban functional zones from very-high-resolution images: A multiscale segmentation approach. Remote Sens. 2019, 11, 1902. [Google Scholar] [CrossRef]
- Tu, W.; Hu, Z.; Li, L.; Cao, J.; Jiang, J.; Li, Q.; Li, Q. Portraying urban functional zones by coupling remote sensing imagery and human sensing data. Remote Sens. 2018, 10, 141. [Google Scholar] [CrossRef]
- Cao, R.; Tu, W.; Yang, C.; Li, Q.; Liu, J.; Zhu, J.; Zhang, Q.; Li, Q.; Qiu, G. Deep learning-based remote and social sensing data fusion for urban region function recognition. ISPRS J. Photogramm. Remote Sens. 2020, 163, 82–97. [Google Scholar] [CrossRef]
- He, Y.; Wang, W.; Chen, Y.; Yan, H. Assessing spatio-temporal patterns and driving force of ecosystem service value in the main urban area of Guangzhou. Sci. Rep. 2021, 11, 3027. [Google Scholar] [CrossRef]
- Song, J.; Lin, T.; Li, X.; Prishchepov, A.V. Mapping urban functional zones by integrating very high spatial resolution remote sensing imagery and points of interest: A case study of Xiamen, China. Remote Sens. 2018, 10, 1737. [Google Scholar] [CrossRef]
- Huang, C.; Xiao, C.; Rong, L. Integrating Point-of-Interest Density and Spatial Heterogeneity to Identify Urban Functional Areas. Remote Sens. 2022, 14, 4201. [Google Scholar] [CrossRef]
- Xu, N.; Luo, J.; Wu, T.; Dong, W.; Liu, W.; Zhou, N. Identification and portrait of urban functional zones based on multisource heterogeneous data and ensemble learning. Remote Sens. 2021, 13, 373. [Google Scholar] [CrossRef]
- Zhang, X.; Du, S.; Wang, Q. Hierarchical semantic cognition for urban functional zones with VHR satellite images and POI data. ISPRS J. Photogramm. Remote Sens. 2017, 132, 170–184. [Google Scholar] [CrossRef]
- Chen, W.; Huang, H.; Dong, J.; Zhang, Y.; Tian, Y.; Yang, Z. Social functional mapping of urban green space using remote sensing and social sensing data. ISPRS J. Photogramm. Remote Sens. 2018, 146, 436–452. [Google Scholar] [CrossRef]
- Yunliang, J.; Moxuan, D.; Jing, F.; Shaowen, G.; Yong, L.; Xinqiang, M. Research on identifying urban regions of different functions based on POI data. J. Zhejiang Norm. Univ. 2017, 40, 398–405. [Google Scholar]
- Kang, Y.; Wang, Y.; Xia, Z.; Chi, J.; Jiao, L.; Wei, Z. Identification and classification of Wuhan urban districts based on POI. J. Geomat. 2018, 43, 81–85. [Google Scholar]
- Calabrese, F.; Ferrari, L.; Blondel, V.D. Urban sensing using mobile phone network data: A survey of research. ACM Comput. Surv. (CSUR) 2014, 47, 1–20. [Google Scholar] [CrossRef]
- Novović, O.; Brdar, S.; Mesaroš, M.; Crnojević, V.; Papadopoulos, A.N. Uncovering the relationship between human connectivity dynamics and land use. ISPRS Int. J. Geo Inf. 2020, 9, 140. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Q.; Tu, W.; Mai, K.; Yao, Y.; Chen, Y. Functional urban land use recognition integrating multi-source geospatial data and cross-correlations. Comput. Environ. Urban Syst. 2019, 78, 101374. [Google Scholar] [CrossRef]
- Chang, S.; Wang, Z.; Mao, D.; Liu, F.; Lai, L.; Yu, H. Identifying Urban Functional Areas in China’s Changchun City from Sentinel-2 Images and Social Sensing Data. Remote Sens. 2021, 13, 4512. [Google Scholar] [CrossRef]
- Cools, D.; McCallum, S.C.; Rainham, D.; Taylor, N.; Patterson, Z. Understanding Google location history as a tool for travel diary data acquisition. Transp. Res. Rec. 2021, 2675, 238–251. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, L.; Xu, C.; Ni, J.; Huang, C.; Shen, X. Location privacy-preserving task recommendation with geometric range query in mobile crowdsensing. IEEE Trans. Mob. Comput. 2021, 21, 4410–4425. [Google Scholar] [CrossRef]
- Jiang, H.; Li, J.; Zhao, P.; Zeng, F.; Xiao, Z.; Iyengar, A. Location privacy-preserving mechanisms in location-based services: A comprehensive survey. ACM Comput. Surv. (CSUR) 2021, 54, 1–36. [Google Scholar] [CrossRef]
- Zhang, K.; Chuai, G.; Gao, W.; Liu, X.; Maimaiti, S.; Si, Z. A new method for traffic forecasting in urban wireless communication network. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 66. [Google Scholar] [CrossRef]
- Zhang, K.; Chuai, G.; Gao, W.; Zhang, J.; Liu, X. Traffic-Aware and Energy-Efficiency Network Oriented Spatio-Temporal Analysis and Traffic Prediction. In Proceedings of the 2019 IEEE Globecom Workshops (GC Wkshps), Waikoloa, HI, USA, 9–13 December 2019; IEEE: New York, NY, USA, 2019; pp. 1–6. [Google Scholar]
- Granger, C.W.; Jeon, Y. Long-term forecasting and evaluation. Int. J. Forecast. 2007, 23, 539–551. [Google Scholar] [CrossRef]
- Ning, Y.; Wah, L.C.; Erdan, L. Stock price prediction based on error correction model and Granger causality test. Clust. Comput. 2019, 22, 4849–4858. [Google Scholar] [CrossRef]
- Fortune, S. Voronoi diagrams and Delaunay triangulations. In Handbook of Discrete and Computational Geometry; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017; pp. 705–721. [Google Scholar]
- Epstein, L. Selfish Bin Packing Problems. In Encyclopedia of Algorithms; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Liu, Z.; Liu, H.; Lu, Z.; Zeng, Q. A dynamic fusion pathfinding algorithm using delaunay triangulation and improved a-star for mobile robots. IEEE Access 2021, 9, 20602–20621. [Google Scholar] [CrossRef]
- Liu, X.; Dong, L.; Jia, M.; Tan, J. RETRACTED CHAPTER: Urban Jobs-Housing Zone Division Based on Mobile Phone Data. In Proceedings of the Blockchain and Trustworthy Systems: First International Conference, BlockSys 2019, Guangzhou, China, 7–8 December 2019; Proceedings 1. Springer: Cham, Switzerland, 2020; pp. 534–548. [Google Scholar]
- Zhao, N.; Ye, Z.; Pei, Y.; Liang, Y.C.; Niyato, D. Spatial-temporal attention-convolution network for citywide cellular traffic prediction. IEEE Commun. Lett. 2020, 24, 2532–2536. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2009, 23, 1327–1338. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, X.; Ren, F.; Shao, Z.; Tian, C. Wind speed prediction using a hybrid model of EEMD and LSTM considering seasonal features. Energy Rep. 2022, 8, 8965–8980. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, M.; Yu, Q.; Zhang, H. Comparing the applications of EMD and EEMD on time–frequency analysis of seismic signal. J. Appl. Geophys. 2012, 83, 29–34. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Wen, J.; Sheng, M.; Li, J.; Huang, K. Assisting intelligent wireless networks with traffic prediction: Exploring and exploiting predictive causality in wireless traffic. IEEE Commun. Mag. 2020, 58, 26–31. [Google Scholar] [CrossRef]
- Orzeszko, W. Nonlinear Causality between Crude Oil Prices and Exchange Rates: Evidence and Forecasting. Energies 2021, 14, 6043. [Google Scholar] [CrossRef]
- Lindner, B.; Auret, L.; Bauer, M.; Groenewald, J.W. Comparative analysis of Granger causality and transfer entropy to present a decision flow for the application of oscillation diagnosis. J. Process Control 2019, 79, 72–84. [Google Scholar] [CrossRef]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef]
- Dhifaoui, Z.; Khalfaoui, R.; Abedin, M.Z.; Shi, B. Quantifying information transfer among clean energy, carbon, oil, and precious metals: A novel transfer entropy-based approach. Financ. Res. Lett. 2022, 49, 103138. [Google Scholar] [CrossRef]
- Amornbunchornvej, C.; Zheleva, E.; Berger-Wolf, T. Variable-lag granger causality and transfer entropy for time series analysis. ACM Trans. Knowl. Discov. Data (TKDD) 2021, 15, 67. [Google Scholar] [CrossRef]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph Attention Networks; University of Cambridge: Cambridge, UK, 2017; Volume 1050, p. 20. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. A comparison of ARIMA and LSTM in forecasting time series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; IEEE: New York, NY, USA, 2018; pp. 1394–1401. [Google Scholar]
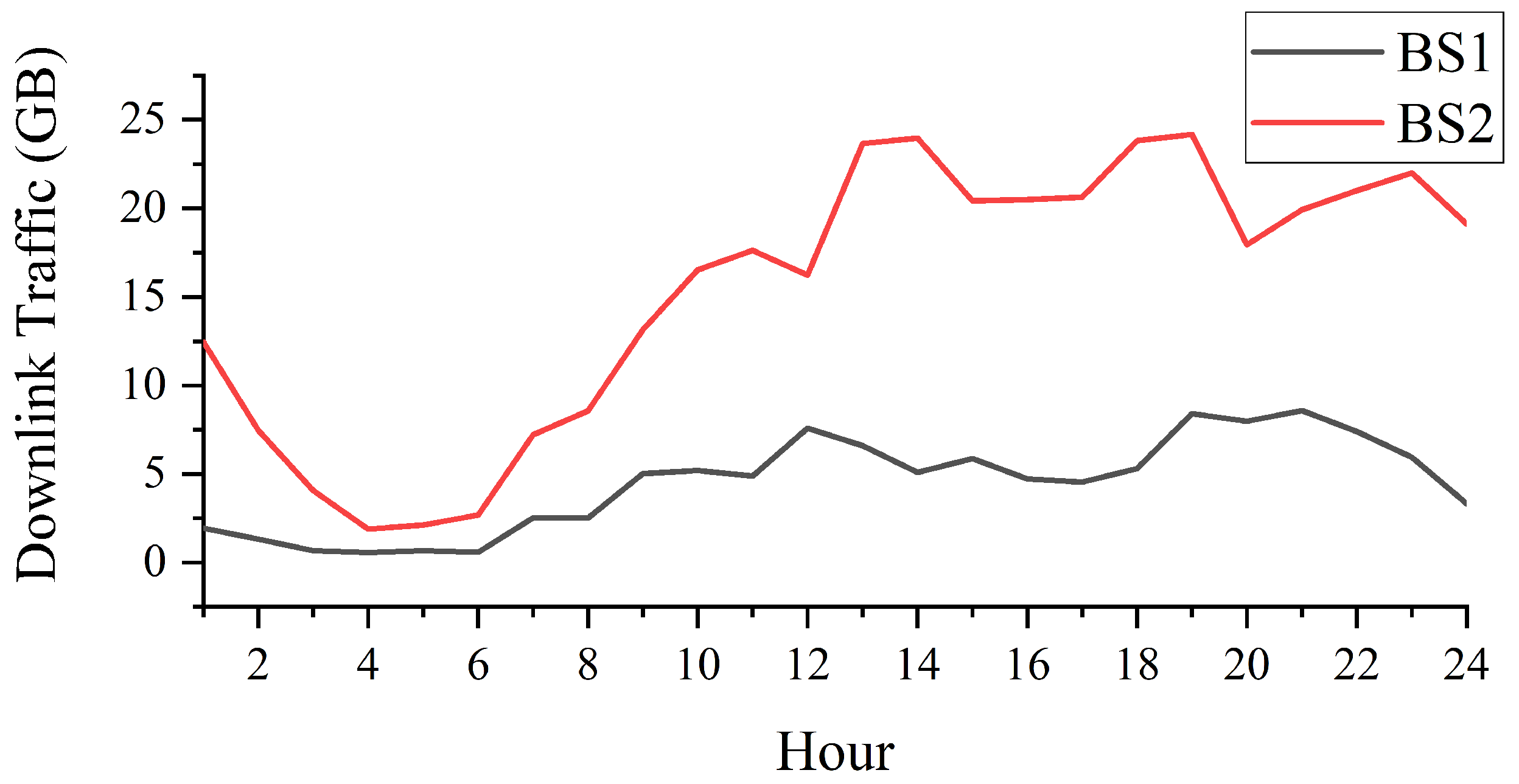
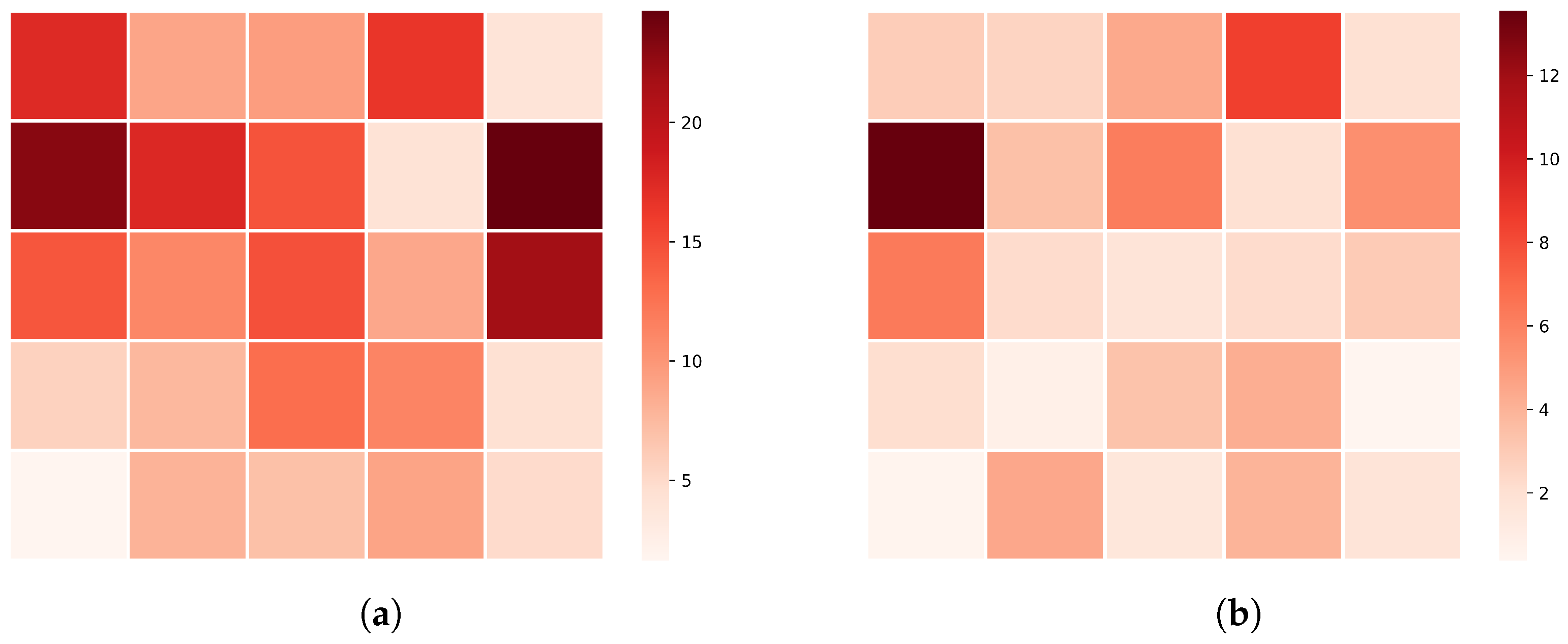




| Time Stamp | eNodeBID | Downlink Traffic (GB) |
|---|---|---|
| 1 July 2019 00:00 | 1 | 2.429 |
| 1 July 2019 01:00 | 1 | 0.9914 |
| 1 July 2019 02:00 | 2 | 2.045 |
| 1 July 2019 03:00 | 2 | 0.2787 |
| ... | ||
| Zone Id | Commuting Index | Zone Id | Commuting Index | Zone Id | Commuting Index |
|---|---|---|---|---|---|
| 1 | 0.14713343 | 18 | 0.6250174 | 35 | −0.905465 |
| 2 | 0.003361332 | 19 | −0.055667 | 36 | −0.970327 |
| 3 | −0.504959471 | 20 | −0.550208 | 37 | −0.576254 |
| 4 | −0.487725772 | 21 | −0.949675 | 38 | −0.860672 |
| 5 | −0.894548963 | 22 | −0.165399 | 39 | −0.561098 |
| 6 | 0.250310568 | 23 | −0.79184 | 40 | −0.558165 |
| 7 | 0.462387708 | 24 | 0.1178097 | 41 | −0.658584 |
| 8 | −0.490481698 | 25 | −0.434763 | 42 | −0.626709 |
| 9 | −0.819941458 | 26 | −0.922275 | 43 | −0.805434 |
| 10 | 1 | 27 | −0.661987 | 44 | −0.33808 |
| 11 | 0.062685314 | 28 | −0.727245 | 45 | −0.621166 |
| 12 | −0.335140768 | 29 | −0.940734 | 46 | 0.0613054 |
| 13 | −0.155702131 | 30 | −0.610347 | 47 | −0.689869 |
| 14 | −0.368456079 | 31 | −0.191953 | 48 | −0.868152 |
| 15 | −0.155143688 | 32 | −0.902722 | 49 | 0.7691417 |
| 16 | −0.66856836 | 33 | −0.444718 | 50 | −0.316654 |
| 17 | −0.669408032 | 34 | −0.55769 | 51 | −0.028517 |
| 52 | −0.541641 |
| Component | Learning Rate | Batch Size | Iterations |
|---|---|---|---|
| Trend | 0.08 | 128 | 800 |
| Period | 0.007 | 64 | 800 |
| Random | 0.01 | 128 | 800 |
| Method | RMSE | MAPE |
|---|---|---|
| Proposed method | 1.535814 | 45.895 |
| GCN | 1.603046 | 55.4792 |
| LSTM | 2.0889 | 55.5947 |
| ARIMA | 3.020975 | 87.8763 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Zhang, K.; Chuai, G.; Gao, W.; Si, Z.; Hou, Y.; Liu, X. Urban Area Characterization and Structure Analysis: A Combined Data-Driven Approach by Remote Sensing Information and Spatial–Temporal Wireless Data. Remote Sens. 2023, 15, 1041. https://doi.org/10.3390/rs15041041
Chen X, Zhang K, Chuai G, Gao W, Si Z, Hou Y, Liu X. Urban Area Characterization and Structure Analysis: A Combined Data-Driven Approach by Remote Sensing Information and Spatial–Temporal Wireless Data. Remote Sensing. 2023; 15(4):1041. https://doi.org/10.3390/rs15041041
Chicago/Turabian StyleChen, Xiangyu, Kaisa Zhang, Gang Chuai, Weidong Gao, Zhiwei Si, Yijian Hou, and Xuewen Liu. 2023. "Urban Area Characterization and Structure Analysis: A Combined Data-Driven Approach by Remote Sensing Information and Spatial–Temporal Wireless Data" Remote Sensing 15, no. 4: 1041. https://doi.org/10.3390/rs15041041
APA StyleChen, X., Zhang, K., Chuai, G., Gao, W., Si, Z., Hou, Y., & Liu, X. (2023). Urban Area Characterization and Structure Analysis: A Combined Data-Driven Approach by Remote Sensing Information and Spatial–Temporal Wireless Data. Remote Sensing, 15(4), 1041. https://doi.org/10.3390/rs15041041






