Abstract
Reducing methane (CH4) emissions from anthropogenic activities is critical to climate change mitigation efforts. However, there is still considerable uncertainty over the amount of fugitive CH4 emissions due to large-scale area sources and heterogeneous emission distributions. To reduce the uncertainty and improve the spatial and temporal resolutions, a new hybrid method was developed combining optical remote sensing (ORS), computed tomography (CT), and inverse-dispersion modeling techniques on the basis of which a multi-path scanning system was developed. It uses a horizontal radial plume mapping path configuration and adapts a Lagrangian stochastic dispersion mode into CT reconstruction. The emission map is finally calculated by using a minimal curvature tomographic reconstruction algorithm, which introduces smooth constraints at each pixel. Two controlled-release experiments of CH4 were conducted with different configurations, showing relative errors of only 2% and 3%. Compared with results from the single-path inverse-dispersion method (5–175%), the new method can not only derive the emission distribution but also obtain a more accurate emission rate. The outcome of this research would bring broad application of the ORS-CT and inverse-dispersion techniques to other gases and sources.
1. Introduction
Climate change represents an urgent and potentially irreversible threat to human societies and the planet. The fast increase of the global temperature is predominantly due to human activity, causing the amount of greenhouse gases (GHGs) in the atmosphere [1]. To mitigate the GHGs emissions, the fastest opportunity is to reduce methane (CH4) emission, which is the second largest contributor to global warming after carbon dioxide (CO2) [2]. Although the concentration of the atmospheric CH4 is lower than CO2, the global warming potential of CH4 is approximately 80 times that of CO2 over a 20-year period and 25 times over a 100-year period, which means it is more efficient in trapping infrared radiation emitted from the earth’s surface than CO2 to cause global warming [3]. The increase in atmospheric CH4 concentration is caused mainly by human activities, which account for more than 60% of total CH4 emissions globally [4]. Main emission sources include industry, agriculture, and waste management activities. In Canada, CH4 emissions account for 14% of total GHGs emissions in 2020. The emissions are largely from fugitive sources in oil and natural gas systems (35%), agriculture (30%), and landfills (27%) [1]. A similar trend can be seen in the United States. To mitigate CH4 emissions, it is essential to accurately monitor the emissions from those sources so that we can assess the effectiveness of various emission reduction measures, identify emission hotspots for targeted treatment, and develop accurate emission inventories.
There is still considerable uncertainty over the amount of fugitive CH4 emissions. A report shows that the Canadian upstream oil and gas CH4 inventory is estimated to be underestimated by a factor of 1.5 [5]. The main issue is that most of the emissions are from area sources or unknown leaks in large areas, which have long been a special challenge for atmospheric monitoring [6]. The quantification difficulties result mainly from their large-scale and non-homogeneous characteristics [7]. First, the source may differ in composition from area to area, leading to spatial and temporal variability across the entire area source [8]. Second, emission rates of sources such as landfills are often influenced by environmental factors, such as atmospheric temperature, humidity, and wind conditions, causing them to keep changing over time, and they show obvious daily and seasonal variabilities [9,10]. Third, some area sources are not flat and have complicated terrain. All these factors lead to large uncertainty in emission quantification. Therefore, to accurately quantify area emissions, a measurement method must provide high spatial and temporal resolutions as well as the ability for continuous and automatic monitoring.
Conventional methods show limitations in dealing with fugitive area sources. Flux chamber and eddy covariance collect data at a point, rendering them not representative for non-homogeneous area sources [10,11]. The flux gradient method is based on the turbulent diffusivity and the vertical gradient of gas concentration. It requires a neutral stability atmosphere, steady-state conditions, and a uniform emission source [7]. The integrated horizontal flux method is a micrometeorological mass balance method, which needs to measure wind speed and gas concentration at different heights around the edges of the source [12]. The deployment of the equipment is too complicated for practical applications. The tracer ratio method has been used in estimating GHGs emissions from landfills [13]. It can provide reasonable results when equipped with mobile sensors. However, it is difficult to implement and labor-intensive, making it not suitable for long-term continuous monitoring. A practical mass balance method based on optical remote sensing (ORS) is solar occultation flux (SOF). It uses a mobile platform to obtain vertical column concentrations along the road around the source, but it needs sunlight and available roads to work. The temporal resolution is also very low. Another ORS-based mass balance method is the vertical radial plume mapping (VRPM) [14]. It derives the concentration distribution on a vertical plane downwind of the source using the multi-path ORS technique and computed tomography (CT) [15]. This method can achieve real-time and continuous monitoring. However, it is difficult to deploy the mirrors on the vertical plane. The measurement is also affected by the wind direction.
A more flexible method is the inverse-dispersion modeling, which back-calculates the emission rates on the basis of the concentration observations at downwind locations from the source [16]. The method simplifies the concentration measurements compared with other approaches. It can use data obtained from point, line, or mobile sensors. It is very suitable for continuous, in situ measurement of emissions from large-scale area sources. However, it assumes idealized airflow. The source should be homogeneous and can be separated from other possible sources [17]. Another issue is that the result is heavily affected by the wind direction which determines the direction of gas plume. The sensors must capture the main gas plume. The method also requires the distance between the sensor and the source (fetch) to be large enough to avoid overestimation [18], but the concentration also decreases with increasing fetch. Another issue with the fetch is that it may not be feasible to deploy the sensor at the required fetch due to terrain, land usage, or other environmental limitations.
All these methods cannot derive emission distribution of the area source. To obtain a two-dimensional (2-D) emission distribution, possible approaches are using sensor network, mobile platform, or multi-path ORS techniques. Multiple fixed-point sensors can form a sensor network to obtain concentrations at different locations. Multiple point concentrations can also be obtained by multi-point survey using sensors mounted on a moving platform [19,20]. The multiple point concentrations can be interpolated to derive the concentration distribution. Network methods usually use multiple low-cost point sensors or monitoring stations, and they can provide only limited spatial or temporal resolutions [21]. Common mobile platforms are vehicles, aircrafts, and satellites. They are used for large spatial scales, including facility to site scale (<1–10 km2), regional scale (10–1000 km2), and global scale (100–1000 km2) [22]. The limitations are related to spatial, temporal resolutions, lowest detection limit, and automatic, continuous monitoring [23]. Long-path ORS sensors can be mounted on a scanner to measure multiple line-integrated-concentrations (PICs) over a surface [24]. It is reported to identify the point leak sources and quantify the leak strength by using an atmospheric dispersion model or a statistical method with a star path geometry over a synthetic area greater than 4 km2 [25,26].
High spatial resolution concentration distribution can be derived by using a CT technique [27]. ORS coupled with CT provides a powerful tool for sensitive mapping of air pollutants throughout kilometer-sized areas in real time [28]. In addition, this technique is non-intrusive so that interferences to the site under investigation are minimal compared with other techniques. The sensors can be deployed around the boundary of the site, making it especially useful for measurements on some sites that are difficult to be accessed. However, ORS-CT application is usually reported to measure the concentration distribution. It is not used to obtain emission distribution in the literature. This situation may result from the difficulty of deploying a multi-path ORS system and the uncertainty with the atmospheric dispersion models. On the basis of the requirement of quantifying fugitive area emission and the review of current measurement techniques, this research proposes a combined method using multi-path ORS, inverse-dispersion modeling, and CT technologies. By adapting the inverse-dispersion modeling technique into CT reconstruction, both emission distribution and concentration distribution can be derived. Compared with a single-path inverse-dispersion method, it can also improve the accuracy by eliminating the influence of varying wind directions and obtaining an optimal result.
2. Materials and Methods
2.1. Combined Method of ORS-CT and Inverse-Dispersion Techniques
The schematic of the new combined method of multi-path ORS, CT reconstruction, and inverse-dispersion techniques is shown in Figure 1.
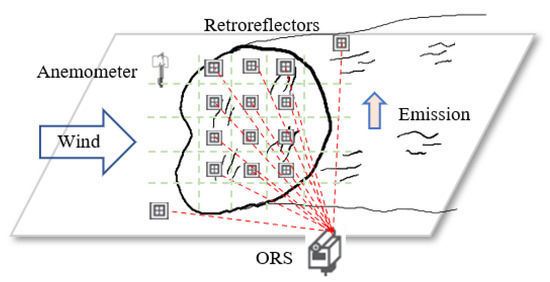
Figure 1.
Schematic of the combined method of ORS-CT and inverse-dispersion techniques.
- (1)
- Data collection
The ORS analyzer emits a beam of light targeting a mirror. By accepting the reflected light, a path integrated concentration (PIC) is measured on the basis of the principle of the absorption of light at characteristic absorption wavelength of the target gas. Multiple PICs are measured by scanning the analyzer targeting different mirrors using a pan-tilt scanner. Meanwhile, the wind data are measured by a three-dimensional (3-D) anemometer, assuming the wind field is horizontally homogeneous.
The mirrors can be distributed inside or along the edges of the measurement area using different path configurations, which also affect the performance of the reconstruction results.
- (2)
- Data processing
After multiple PICs data are collected, the concentration distribution on the measurement plane can be calculated using a CT reconstruction algorithm.
The process to derive the emission distribution using CT technique has not been reported in the literature. In this study, we introduce an atmospheric dispersion model to establish the relationship between emission rates and the measured concentrations. As a result, the emission distribution can be calculated using CT technique similar to the process of calculating concentration distribution. The detailed process will be described in the following section.
2.2. Light Path Configuration
The light path configuration affects the performance of the CT reconstruction. Generally, the performance becomes better with increasing numbers of beams and analyzers. However, the number is usually limited in real applications due to the cost and work of deployment. For ORS-CT, two categories of beam configurations are usually used. One is the overlapped configuration, where the mirrors spread at the edges of the area. In this configuration, at least two or more analyzers are required to generate overlapped beams for successful CT reconstruction (Figure 2a). Another one is a non-overlapped configuration, where the mirrors are distributed into the area. It needs only one analyzer. Therefore, the system cost and complexity can be reduced (Figure 2b).
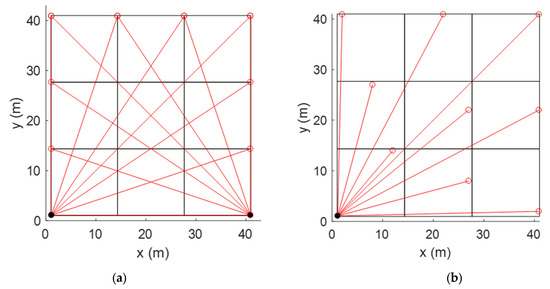
Figure 2.
(a) Overlapped path configuration. (b) Non-overlapped path configuration.
In this research, a non-overlapped configuration of horizontal radial plume mapping (HRPM) is used [29]. HRPM has been applied in landfills for locating hotspots of CH4 emissions and other fugitive area sources, such as oil sands mining sites, carbon capture and storage sites, or tank farms. HRPM divides the site area evenly into sub-grids where mirrors are deployed. There are generally two ways to install a mirror into a grid. One is to put it at the center of the grid, another is to put it at the edge of the grid. Literature shows that the latter configuration has better performance because it maximizes the spread of the optical beams [30].
2.3. Inverse-Dispersion Modeling
The inverse-dispersion technique uses atmospheric dispersion models to calculate the theoretical relationship between a source emission rate and a downwind concentration [16,31]. Assuming downwind concentration C and background concentration Cb are measured, the relationship between the concentration and the source emission rate Q is determined by an atmospheric dispersion model. The emission rate can be inferred on the basis of the model prediction of the ratio of concentration as:
where (C/Q)model is the model predicted relationship. This equation is the basis of the inverse-dispersion technique. It requires a single C measurement with flexibility in the choice of the measurement location.
The key to the inverse-dispersion technique is an accurate and easy-to-use dispersion model to calculate the relationship. The simple Gaussian plume model is not suitable under this on-site condition because of the lack of calibrated dispersion parameters in short-range (<100 m) dispersion [32,33]. A Lagrangian stochastic (LS) dispersion model is used, which has the capability to represent near-field dispersion by explicitly incorporating turbulent velocity statistics in the trajectories of tracer particles [34]. The LS model simulates the dispersion process by releasing a large number of tracer particles and tracing the evolution of tracer velocity and location through a Markov process described by the Langevin equation [35]
where i and j take values of 1, 2, and 3 to represent the three components of the Cartesian coordinates, are the particle’s position and velocity vectors (at along-wind, crosswind, and vertical dictions), respectively, dWj(t) is an incremental Wiener process, which is Gaussian with zero mean and variance of dt, and ai and bi,j are coefficients.
For three-dimensional (3-D), nonstationary, inhomogeneous diffusion in Gaussian turbulence, a simplified solution for the coefficients was given by [34] by making the following assumptions: a stationary, horizontally homogeneous atmosphere, taking the average vertical velocity W = 0 and average crosswind velocity V = 0, with the friction velocity u* and the horizontal velocity fluctuation variance constant with height but allowing the vertical velocity variance to be height-dependent. The detailed formulas of the solutions can be found in [34].
The input parameters include sensor information (laser path configuration), source information (source geometry and strength), atmospheric conditions (mean wind speed and direction, atmospheric temperature, and pressure), and surface layer model described by the Monin–Obukhov similarity theory (MOST). MOST needs the information of surface roughness length (z0), Monin–Obukhov length (L), and friction velocity u*. Using the 3-D sonic anemometer, one can derive these parameters as well as mean variance and covariance data of wind and temperature from the raw wind and temperature data [34].
2.4. Tomographic Reconstruction of Emission Distribution
In the literature, ORS-CT technique is usually used to retrieve 2-D concentration map over an area under investigation. A pixel-based reconstruction algorithm is usually used for ORS-CT application due to the limited path number compared with medical CT application. It divides an area into multiple grid pixels and assigns a value inside each pixel. The path integral is approximated by the sum of the product of the pixel value and the length of the path in that pixel. A system of linear equations can be set up for multiple paths. The inverse problem involves finding the optimal set of pixel concentrations. Traditional pixel-based algorithms are algebraic reconstruction techniques (ARTs), non-negative least square (NNLS), and expectation–maximization (EM) [27,36,37]. These algorithms are suitable for rapid CT reconstruction, but they produce maps with poor spatial resolution, owing to the requirement that the pixel number must not exceed the beam number. Otherwise, they may have a problem of indeterminacy associated with substantially under-determined systems [30]. This problem can be solved by adding smoothness constraints into the inverse problem. One pixel-based smooth algorithm is low third derivative (LTD), which sets the third derivative at each pixel to zero, thus resulting in a new over-determined system of linear equations [38]. In our previous work, a new smooth algorithm of minimal curvature (MC) was developed on the basis of variational interpolation technique, which requires only approximately 65% of the computation time required by the LTD algorithm [39].
In this research, the ORS-CT technique is also used to derive the 2-D emission distribution for the first time. To achieve this goal, we adapt the LS dispersion model into the CT reconstruction process. A smooth CT algorithm is a key part of the method. On the basis of our previous work, a MC algorithm is used for the CT inversion. The process of calculating emission distribution is described in the following steps.
- (1)
- High-resolution grid division is used. The site is divided into N = m × n pixels (21× 21 in this application), as shown in Figure 3. As a result, the number of grids is much larger than the number of paths (3 × 3).
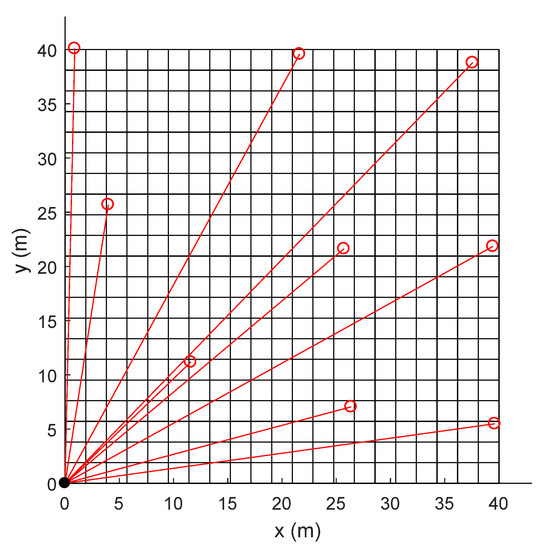 Figure 3. Grid division (21 × 21) of the site for tomographic reconstruction.
Figure 3. Grid division (21 × 21) of the site for tomographic reconstruction.
- (2)
- Establish the relationship between the PICs and the pixel concentrations. The measured PIC is defined as follows:
- (3)
- Establish the relationship between the emission rate and the concentration. The emission map is also divided into high-resolution pixels. For simplification, we use the same division as that for the concentration pixels. The cj is defined as follows:
- (4)
- Use the MC algorithm to introduce additional constraints at each pixel to achieve smooth regularization by using the variational interpolation technique [39]. The idea of the MC algorithm is to minimize the seminorm, which is defined to be equal to the total squares curvature of the underlying concentration distribution. If we use (m, n) to index a pixel located at m-th row and n-th column of the pixels, the discrete total squares curvature is:
There is one prior equation at each pixel. The reconstruction becomes a problem of minimizing the regularization, as follows:
- (5)
- The over-determined system of linear equations is solved by the NNLS optimization algorithm to generate the emission rates [36].
3. Results and Discussions
3.1. The Multi-Path Scanning TDL System
On the basis of the new combined method, a multi-path scanning ORS system was developed (Figure 4).
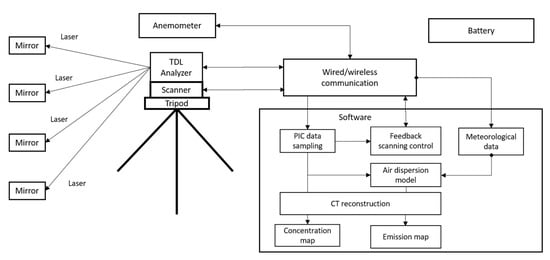
Figure 4.
Schematic of the multi-path scanning TDL system.
Open-path Fourier-transform infrared (OP-FTIR) and open-path tunable diode laser (OP-TDLAS) are two commonly used ORS techniques for gas detection. The OP-FTIR technique has the advantage of measuring multiple gas components simultaneously. The OP-TDLAS technique can measure only one gas component per laser beam with a fixed wavelength. However, it is less expensive and has a faster response (one second per sample) than the OP-FTIR technique (tens of seconds per sample). In addition, it requires a smaller reflection mirror because the diameter of the laser beam is much smaller than the infrared light beam used by the OP-FTIR. The system is designed to be portable and can be easily deployed in a field. For CH4 detection, we use an OP-TDL analyzer (GasFinder3, Boreal Laser Inc., Edmonton, Canada) to save costs, reduce size and weight, and increase the data rate. It has a path length range of 0.5 to 750 m, precision of 2% RSD, and detection limit of 1.2 ppm.m.
The TDL analyzer emits a beam of laser targeting a mirror. By accepting the reflected light, a path-integrated-concentration (PIC) is measured on the basis of the principle of the absorption of light at characteristic absorption wavelength of the target gas. The analyzer is installed on a fast, accurate, and durable pan-tilt scanner (PTU-48E, Teledyne FLIR LLC, Wilsonville, OR, USA) which is mounted on a tripod. The speed of the scanner is 50°/s with a position resolution of 0.003°. Multiple PICs are measured by scanning the analyzer targeting at different mirrors sequentially and periodically.
On the basis of HRPM path configuration, the area source is divided into multiple grids. In each grid, there is a retroreflector installed. Depending on the distance between the reflector and the analyzer, different types of reflectors will be used. For a distance less than 50 m, only a corner cube retroreflector is needed, which can be installed on a metal pole. This installation allows the equipment to be very easily transported and set up in the field. For a distance of more than 50 m, more corner cube retroreflectors are needed to increase the reflection area of the light beam.
Meteorological information, including wind speed, direction, atmospheric temperature, and atmospheric pressure, is obtained through a 3-D sonic anemometer (Young 81000, Campbell Scientific Inc., Logan, USA) with wind speed range of 0 to 40 m/s, wind speed accuracy of ±0.05 m/s, wind direction range of 0.0 to 359.9°, and wind direction accuracy of ±2°. For field application, the system can be powered by 12 VDC battery if the 120–240 VAC is not available. The length of the laser path is measured by a range finder (Scout DX 1000, Bushnell Corporation, Overland Park, KS, USA).
The system software running on a laptop includes a feedback scanning control module, data acquisition module, air dispersion model module, and CT reconstruction module. The scanning logic is controlled automatically by the feedback control module, which communicates with both the TDL analyzer and the scanner through serial communication protocols with a wired cable connection or wireless transmitter and receivers. The scanning control module records the location information of the mirrors and sends commands to the scanner to change its pan and tilt positions. Meanwhile, it also receives the laser intensity information as feedback to ensure the laser is aiming at a mirror. For continuous monitoring application, automatic alignment of the laser is needed to correct accumulated positioning errors or other interferences which may change the locations of the laser or mirrors.
The scanner stops at each path for 10 s when the PIC data of the path is acquired and recorded by the data acquisition module. Meanwhile, ambient temperature, pressure, and wind data are also acquired and recorded. After each cycle of the scan, multiple PICs from all the paths are measured on the basis of which the CT reconstruction algorithm is executed to generate a 2-D concentration distribution on the measurement plane during this scan period. After a long period (e.g., 10 min), the PICs data and wind data are averaged on the basis of which the CT reconstruction algorithm coupled with an atmospheric dispersion model is executed to generate a 2-D emission distribution during the averaging duration.
3.2. Controlled-Release Experiments of CH4
To evaluate the system and the method, controlled-release experiments of CH4 were conducted in Calgary, Canada, in September 2021. The site was an open flat area of 40 m × 40 m, which was divided into 3 × 3 grids. Nine retroreflectors were distributed in each grid at the height of 0.8 m according to HRPM beam configuration. The area sources were simulated by 1/2” PVC pipes. Two releases were conducted. The first one used one area source of 2.2 m × 2.2 m. The second one used two area sources of 1 m × 2.2 m separated in a distance of 12 m. The equipment is shown in Figure 5.

Figure 5.
(a) Area source for Release One. (b) Area sources for Release Two. (c) The multi-path scanning TDL system.
CH4 gas with a purity of 99.97% was released from a high-pressure gas cylinder. The gas flow was controlled by a regulator. The flow rate was monitored by a rotameter. The gas cylinder was connected to the simulated area sources. CH4 gas was emitted from small outlets with a diameter of 0.5 mm, uniformly distributed on the pipes at a distance of 0.5 m to each other. Before and after a release period, the gas cylinder was weighed. The 3-D wind speeds and the atmospheric temperature were measured by the sonic anemometer with a data frequency of 32 Hz and a height of 2 m. A computer program controlled the scanner to target the laser beam at the reflectors sequentially and periodically. At each retroreflector, it stayed for 10 s for data acquisition. Background concentration was measured before each release. The path configurations are shown in Figure 6. Some parameters and PICs are shown in Table 1.
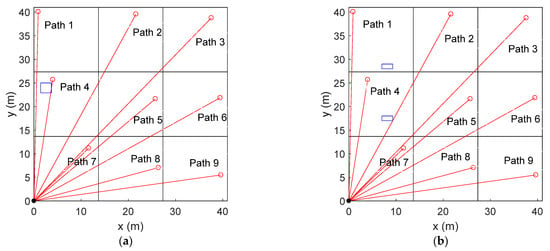
Figure 6.
The source and path configurations: (a) Release One and (b) Release Two. The small rectangles represent area sources.

Table 1.
Parameters of the releases.
3.3. Calculation of Emission Distribution
The distribution of emission rates of the area sources is calculated according to the method described in Section 2.4. The area source is divided into 21 × 21 grids. The same grid division is also used for the concentration map. The concentration of each grid is assumed to be uniform and is represented by a point sensor located at the center of the grid. Therefore, there are 441 small area sources and 441 point sensors. For the LS dispersion model, 50,000 particles were released. The derived emission distributions for Releases One and Two are interpolated and shown in Figure 7a,b.
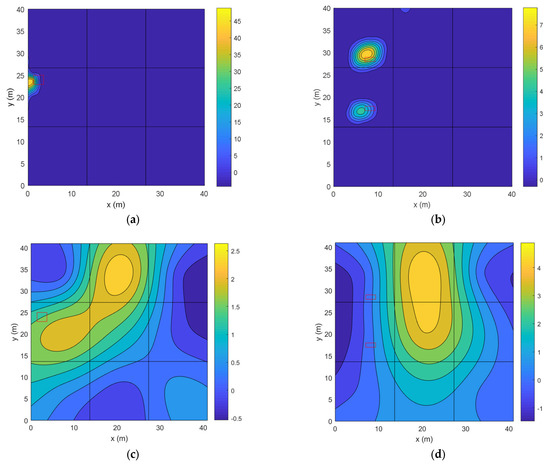
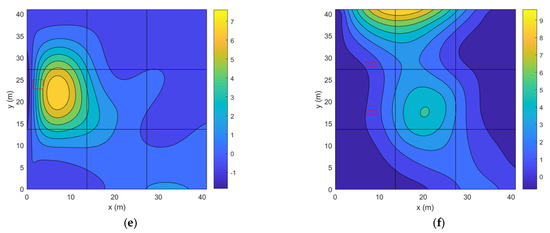
Figure 7.
(a,b) Predicted emission distributions (unit: g/s.m2); (c,d) predicted concentration maps using the NNLS algorithm (unit: g/m3); and (e,f) predicted concentration maps using the MC algorithm (unit: g/m3). The first column shows results for Release One. The second column shows results for Release Two. The rectangular areas are the real area sources. The black lines show 3 × 3 division for the beams.
We can see that the emission sources are successfully located. The distances between the real and predicted source centers for Releases One and Two are 1.8 m and 1.7 m, respectively, which are approximately equal to the length of one grid (1.9 m). The total emission rates can be derived by integrating the emission maps. The results are 0.193 g/s for Release One and 0.194 g/s for Release Two. Compared with the real emission rates, the error is 2% for Release One and 3% for Release Two. These results illustrate that both the source locations and the emission rates are very accurate.
As a comparison, the concentration maps predicted by the NNLS and MC algorithms are also shown. From Figure 7c,d, we can see that the non-smooth NNLS algorithm gives incorrect results on both the source number and locations. In Figure 7e,f, the smooth MC algorithm predicts current source number. However, there are large errors on source locations. In addition, neither algorithm can predict the current size of the sources.
3.4. Comparison with Single-Path Results
The traditional inverse-dispersion method uses one single path to calculate the emission rate of the area source, in which case the location and geometry of the source must be known, and the emission rate of the area source needs to be uniform. Therefore, this method cannot derive the emission rate in real applications. However, for the controlled-release experiments, we can use this method because both the source information and emission rates are known.
The emission rates were calculated on the basis of each observed PIC by using the LS dispersion model with the same dispersion parameters as that used for the CT reconstruction. For Release One, the derived emission rates are 0.52 g/s, 0.17 g/s, 0.11 g/s, 0.39 g/s, and 0.15 g/s according to Paths 2, 3, 4, 7, and 7, respectively. For Release Two, the derived emission rates are 0.38 g/s, 0.24 g/s, 0.24 g/s, 0.21 g/s, 0.22 g/s, and 0.18 g/s according to Paths 3, 4, 6, 7, 8, and 9, respectively. Data from other paths are not valid because there is only a very small or no part of the path passing through the gas plume.
Emission rates from multi-path and single-path methods are shown in Figure 8. We can see the following results. First, the emission rate is overestimated when the path is very close to the emission source. This is an issue of using LS models near the source [18]. The trend is shown from Paths 4 and 5 in Release One and Path 2 in Release Two. The errors are 173%, 105%, and 90%, respectively. Second, the emission rates tend to be underestimated as the path is far away from the source. This may result from the increasing uncertainty in the observation when the fetch becomes large. The uncertainty is due to low concentration and nonideal dispersion. Third, the multi-path approach provides a better result than the single-path method. This is because all data observations on the site are used to derive an optimal result. To conclude, the multi-path scanning approach can not only derive the source distribution but also obtain a more accurate emission rate compared with the single-path method.
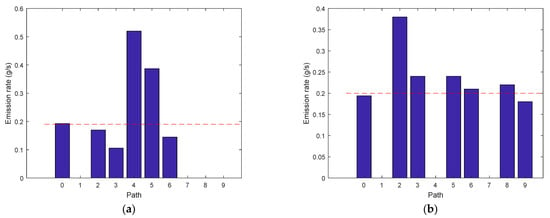
Figure 8.
Emission rates based on multi-path and single-path observations: (a) Release One and (b) Release Two. Path 0 represents result from the multi-path inversion. The horizontal dashed line shows the real emission rate.
3.5. Uncertainty Analysis
The measurement uncertainty of the hybrid method is affected by many factors. (1) The accuracy of the PIC and wind data is determined by the equipment. (2) The performance of the CT reconstruction is affected by the path configuration, underlying distribution, and different reconstruction algorithms. (3) The accuracy of the LS dispersion model is affected by the terrain and atmospheric conditions. Over these factors, the equipment performance is fixed. The performance of MC algorithm has been evaluated in [39], which is also affected by the dispersion model in this study because the outputs of the dispersion model will determine the kernel matrix in the reconstruction. Therefore, the performance of the LS dispersion model will largely affect the overall performance of the hybrid method. However, the model performance is also difficult to evaluate because of the different site environment and continuously varying atmospheric conditions.
To analyze the overall uncertainty of the hybrid method, we studied the performance of the method in a long measurement period. The period was chosen to be when the atmospheric conditions satisfy the assumption of the LS dispersion model, and the wind data are filtered on the basis of the rule that the friction velocity is larger than 0.15 m/s to ensure the data are valid [34]. As a result, the period of Release One configuration lasts from 14:30 to 15:00. The period of Release Two configuration lasts from 15:36 to 16:10. The wind speeds and wind directions for the Release One and Two periods are shown in Figure 9.
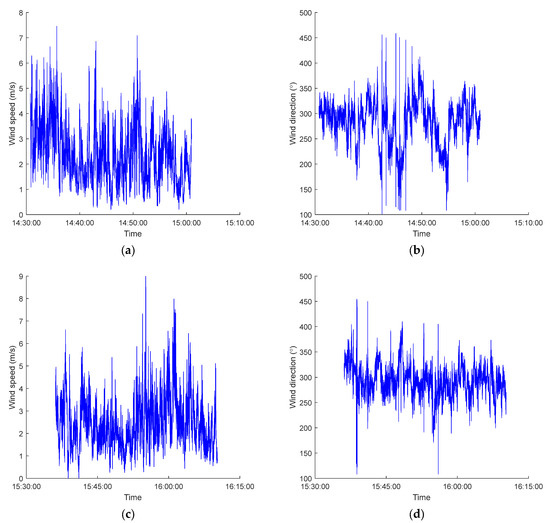
Figure 9.
(a,b) Wind speed and wind direction for Release One period. (c,d) Wind speed and wind direction for Release Two period.
In the Release One period, the mean and standard deviation of wind speed is 2.41 m/s and 1.07 m/s, and the mean and standard deviation of wind direction is 282.02° and 44.18°, respectively. In the Release Two period, the mean and standard deviation of wind speed is 2.51 m/s and 1.08 m/s, and the mean and standard deviation of wind direction is 293.42° and 30.12°, respectively. We can see that the wind direction variation is larger in Release One than that in Release Two.
The emission rate is calculated on the basis of 15 min averaged data. Multiple emission rates are calculated by using a moving window averaging method with a window length of 15 min and a step of 2 min. The calculated mean emission rate of release one period is 0.198 g/s, with a standard deviation of 0.039 g/s. The emission rate errors range from −18.5% to 47.0%, with a mean error of 4.2%. The calculated mean emission rate of release two period is 0.215 g/s, with a standard deviation of 0.021 g/s. The emission rate errors range from −6.9% to 28.3%, with a mean error of 7.5%. From the results we can see that the mean errors are less than 10% in both release periods. Although the mean error is smaller in the Release One period than that in the Release Two period, it has a larger variation. From Figure 9b we can see that this large variation is caused mainly by the large variation of wind direction. To conclude, the hybrid method shows good long-time performance even when the atmospheric conditions are not ideal.
4. Conclusions
High spatial and temporal resolutions are required to accurately quantify emission from fugitive area sources. The single-path inverse-dispersion method is a very flexible method to quantify the emission rate of the area source. However, a single-path approach cannot derive the emission distribution. It also requires the path to be located at a downwind location with sufficient fetch and to pass through the main gas plume, which is affected by the wind direction. To improve the resolutions and performance, this paper develops a new hybrid method that is based on multi-path ORS, inverse-dispersion modeling, and CT techniques to derive the emission map and rate of an area source.
The underlying techniques are important for the successful application of the new method. The OP-TDL ORS technique ensures the fast response of the measurement. The LS dispersion model plays a key role to accurately mimic the air dispersion near the source. The use of smooth tomographic algorithm ensures the accuracy of the CT reconstruction. The number of beams greatly affects the performance of the CT reconstruction. To reduce the cost and deployment complicity, the non-overlapped method of HRPM configuration with only one TDL analyzer was used. If the mirrors are difficult to install inside the area source, overlapped beam configuration with two or more analyzers can be used.
The hybrid method is evaluated through two controlled-release experiments of CH4, showing errors of only 2% and 3% relative to the real values. The results prove the efficiency and advantages of the method. Compared with the single-path approach, it can not only derive the source distribution but also obtain more accurate emission rates.
The method is tested on a flat terrain. In practice, the environment of the site can be complicated. The terrain may not be flat and there may be obstacles, such as buildings and trees. The complicated conditions will affect mainly the applicability of the atmospheric dispersion model. One possible method is to improve the performance of the atmospheric dispersion model to support complex terrain. Furthermore, more advanced techniques, such as computational fluid dynamics (CFD), can be used to calculate the wind field in sites with obstacles. Finally, optimal techniques can also be used to tune the input parameters of the atmospheric dispersion model.
Author Contributions
Conceptualization, S.L. and K.D.; methodology, S.L.; software, S.L.; validation, S.L., Y.L. and K.D.; formal analysis, S.L.; investigation, S.L.; resources, S.L. and Y.L.; data curation, S.L.; writing—original draft preparation, S.L.; writing—review and editing S.L., Y.L. and K.D.; visualization, S.L.; supervision, K.D.; project administration, K.D.; funding acquisition, K.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Sciences and Engineering Research Council (NSERC) of Canada, grant number: RGPIN-2020-05223; John R. Evans Leaders Fund (JELF) and Infrastructure Operating Fund (IOF) from Canada Foundation for Innovation (CFI), grant number: 35468; University Research Grant Committee (URGC) seed grant from University of Calgary grant number: 1050666.
Data Availability Statement
Data and code are available on request by contacting the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- IPCC. FAQ Chapter 1. 2022. Available online: https://www.ipcc.ch/sr15/faq/faq-chapter-1/ (accessed on 21 May 2022).
- Thomas, G.; Sherin, A.P.; Zachariah, E.J. Atmospheric methane mixing ratio in a south Indian coastal city interlaced by wetlands. Procedia Environ. Sci. 2014, 21, 14–25. [Google Scholar] [CrossRef]
- U.S. EPA. Inventory of U.S. Greenhouse Gas Emissions and Sinks, 1990–2014; EPA 403-R-16-002; United States Environmental Protection Agency: Washington, DC, USA, 2016. [Google Scholar]
- U.S. EPA. Methane and Nitrous Oxide Emissions from Natural Sources; EPA 403-R-10-001; United States Environmental Protection Agency: Washington, DC, USA, 2010. [Google Scholar]
- Mackay, K.; Lavoie, M.; Bourlon, E.; Atherton, E.; O’Connell, E.; Bailie, J.; Fougere, C.; Risk, D. Methane emissions from upstream oil and gas production in Canada are underestimated. Sci. Rep. 2021, 11, 8041. [Google Scholar] [CrossRef]
- Schutze, C.; Sauer, U. Challenges associated with the atmospheric monitoring of areal emission sources and the need for optical remote sensing techniques—An open-path Fourier transform infrared (OP-FTIR) spectroscopy experience report. Environ. Earth Sci. 2016, 75, 919. [Google Scholar] [CrossRef]
- Small, C.S.; Chao, S.; Hashisho, Z.; Ulrich, A.C. Emissions from oil sands tailings ponds: Review of tailings pond parameters and emission estimates. J. Pet. Sci. Eng. 2015, 127, 490–501. [Google Scholar] [CrossRef]
- Hu, E.; Babcock, E.L.; Bialkowski, S.E.; Jones, S.B.; Tuller, M. Methods and Techniques for Measuring Gas Emissions from Agricultural and Animal Feeding Operations. Crit. Rev. Anal. Chem. 2014, 44, 200–219. [Google Scholar] [CrossRef]
- Amon, B.; Amon, T.; Boxberger, J.; Alt, C. Emissions of NH3, N2O and CH4 from Dairy Cows Housed in a Farmyard Manure Tying Stall (Housing, Manure Storage, Manure Spreading). Nutr. Cycl. Agroecosys 2001, 60, 103–113. [Google Scholar] [CrossRef]
- Hashisho, Z.; Small, C.C.; Morshed, G. Review of Technologies for the Characterization and Monitoring of VOCs, Reduced Sulphur Compounds and CH4; OSRIN Report No. TR-19; Oil Sands Research and Information Network: Edmonton, AB, Canada, 2012; p. 93. [Google Scholar]
- McGinn, S.M.; Flesch, T.K.; Crenna, B.P.; Beauchemin, K.A.; Coates, T. Quantifying ammonia emissions from a cattle feedlot using a dispersion model. J. Environ. Qual. 2007, 36, 1585–1590. [Google Scholar] [CrossRef]
- Brown, H.A.; Wagner-Riddle, C.; Thurtell, G.W. Nitrous Oxide Flux from a Solid Dairy Manure Pile Measured Using a Micrometeorological Mass Balance Method. Nutr. Cycl. Agroecosys 2002, 62, 53–60. [Google Scholar] [CrossRef]
- Foster-Wittig, T.A.; Thoma, E.D.; Albertson, J.D. Estimation of point source fugitive emission rates from a single sensor time series: A conditionally-sampled Gaussian plume reconstruction. Atmos. Environ. 2015, 115, 101–109. [Google Scholar] [CrossRef]
- Hashmonay, R.A.; Yost, M.G.; Wu, C.F. Computed tomography of air pollutants using radial scanning path-integrated optical remote sensing. Atmos. Environ. 1999, 33, 267–274. [Google Scholar] [CrossRef]
- Herman, G.T. Fundamentals of Computerized Tomography: Image Reconstruction from Projection, 2nd ed.; Springer: New York, NY, USA, 2009; pp. 101–124. [Google Scholar]
- Flesch, T.K.; Wilson, J.D.; Yee, E. Backward-time lagrangian stochastic dispersion models and their application to estimate gaseous emissions. J. Appl. Meteorol. 1995, 34, 1320–1332. [Google Scholar] [CrossRef]
- McGinn, S. Measuring Greenhouse Gas Emissions from Point Sources in Agriculture. Can. J. Soil Sci. 2006, 86, 355–371. [Google Scholar] [CrossRef]
- Gao, Z.; Desjardins, R.L.; Flesch, T.K. Assessment of the uncertainty of using an inverse-dispersion technique to measure methane emissions from animals in a barn and in a small pen. Atmos. Environ. 2010, 44, 3128–3134. [Google Scholar] [CrossRef]
- Barchyn, T.E.; Hugenholtz, C.H. A UAV-based system for detecting natural gas leaks. J. Unmanned Veh. Syst. 2018, 6, 18–30. [Google Scholar] [CrossRef]
- Gonzalez-Valencia, R.; Magana-Rodriguez, F.; Cristobal, J.; Thalasso, F. Hotspot detection and spatial distribution of methane emissions from landfills by a surface probe method. Waste Manag. 2016, 55, 299–305. [Google Scholar] [CrossRef]
- Behera, S.N.; Sharma, M.; Mishra, P.K.; Nayak, P.; Fontaine, B.D.; Tahon, R. Passive measurement of NO2 and application of GIS to generate spatially-distributed air monitoring network in urban environment. Urban Clim. 2015, 14, 396–413. [Google Scholar] [CrossRef]
- Saito, M.; Niwa, Y.; Saeki, T.; Cong, R.; Miyauchi, T. Overview of model systems for global carbon dioxide and methane flux estimates using GOSAT and GOSAT-2 observations. J. Remote Sens. Soc. Jpn. 2019, 39, 50–56. [Google Scholar]
- Allen, G.; Gallagher, M.; Hollingsworth, P.; Illingworth, S.; Kabbabe, K.; Percival, C. Feasibility of Aerial Measurements of Methane Emissions from Landfills; Report—SC130034/R; Environment Agency: Bristol, UK, 2014. [Google Scholar]
- Du, K.; Rood, M.J.; Welton, E.J.; Varma, R.M.; Hashmonay, R.A.; Kim, B.J.; Kemme, M.R. Optical Remote Sensing to Quantify Fugitive Particulate Mass Emissions from Stationary Short-Term and Mobile Continuous Sources: Part I. Method and Examples. Environ. Sci. Technol. 2011, 45, 658–665. [Google Scholar] [CrossRef]
- Alden, C.B.; Ghosh, S.; Coburn, S.; Sweeney, C.; Karion, A.; Wright, R.; Coddington, I.; Rieker, G.B.; Prasad, K. Bootstrap inversion technique for atmospheric trace gas source detection and quantification using long open-path laser measurements. Atmos. Meas. Tech. 2018, 11, 1565–1582. [Google Scholar] [CrossRef]
- Coburn, S.; Alden, C.B.; Wright, R.; Cossel, K.; Baumann, E.; Truong, G.; Gioregetta, F.; Sweeney, C.; Newbury, N.R.; Prasad, K.; et al. Regional trace-gas source attribution using a field-deployed dual frequency comb spectrometer. Optica 2018, 5, 320–327. [Google Scholar] [CrossRef]
- Todd, L.; Ramachandran, G. Evaluation of Optical Source-Detector Configurations for Tomographic Reconstruction of Chemical Concentrations in Indoor Air. Am. Ind. Hyg. Assoc. J. 1994, 55, 1133–1143. [Google Scholar] [CrossRef]
- Dobler, J.T.; Zaccheo, T.S.; Pernini, T.G.; Blume, N.; Broquet, G.; Vogel, F.; Ramonet, M.; Braun, M.; Staufer, J.; Ciais, P.; et al. Demonstration of spatial greenhouse gas mapping using laser absorption spectrometers on local scales. J. Appl. Remote Sens. 2017, 11, 14002. [Google Scholar] [CrossRef]
- Wu, C.F.; Yost, M.G.; Hashmonay, R.A.; Park, D.Y. Experimental evaluation of a radial beam geometry for mapping air pollutants using optical remote sensing and computed tomography. Atmos. Environ. 1999, 33, 4709–4716. [Google Scholar] [CrossRef]
- Hashmonay, R.A. Theoretical evaluation of a method for locating gaseous emission hot spots. J. Air Waste Manag. Assoc. 2008, 58, 1100–1106. [Google Scholar] [CrossRef]
- Harper, L.A.; Denmead, D.T.; Flesch, T.K. Micrometeorological techniques for measurement of enteric greenhouse gas emission. Anim. Feed. Sci. Technol. 2011, 166–167, 227–239. [Google Scholar] [CrossRef]
- Lateb, M.; Meroney, R.N.; Yataghene, M.; Fellouah, H.; Saleh, F.; Boufadel, M.C. On the use of numerical modelling for near-field pollutant dispersion in urban environments—A review. Environ. Pollut. 2016, 208, 271–283. [Google Scholar] [CrossRef]
- U.S. EPA. Selection Criteria for Mathematical Models Used in Exposure Assessments: Atmospheric Dispersion Models; EPA/600/8-91/038; U.S. Environmental Protection Agency: Washington, DC, USA, 1993. [Google Scholar]
- Flesch, T.K.; Wilson, J.D.; Harper, L.A.; Crenna, B.P.; Sharpe, R.R. Deducing Ground-to-Air Emissions from Observed Trace Gas Concentrations: A Field Trial. J. Appl. Meteorol. 2005, 44, 475–484. [Google Scholar] [CrossRef]
- Thomson, D.J. Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 1987, 180, 529–556. [Google Scholar] [CrossRef]
- Lawson, C.L.; Janson, R.J. Solving least squares problems. Soc. Ind. Appl. Math. Phila. 1995, 23, 158–165. [Google Scholar]
- Tsui, B.M.W.; Zhao, X.; Frey, E.C.; Gullberg, G.T. Comparison between ML-EM and WLS-CG algorithms for SPECT image reconstruction. IEEE Trans. Nucl. Sci. 1991, 38, 1766–1772. [Google Scholar] [CrossRef]
- Price, P.N.; Fischer, M.L.; Gadgil, A.J.; Sextro, R.G. An algorithm for real-time tomography of gas concentrations, using prior information about spatial derivatives. Atmos. Environ. 2001, 35, 2827. [Google Scholar] [CrossRef]
- Li, S.; Du, K. A minimum curvature algorithm for tomographic reconstruction of atmospheric chemicals based on optical remote sensing. Atmos. Meas. Tech. 2021, 14, 7355–7368. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).