Deep Learning-Based Emulation of Radiative Transfer Models for Top-of-Atmosphere BRDF Modelling Using Sentinel-3 OLCI
Abstract
1. Introduction
2. Theoretical Background
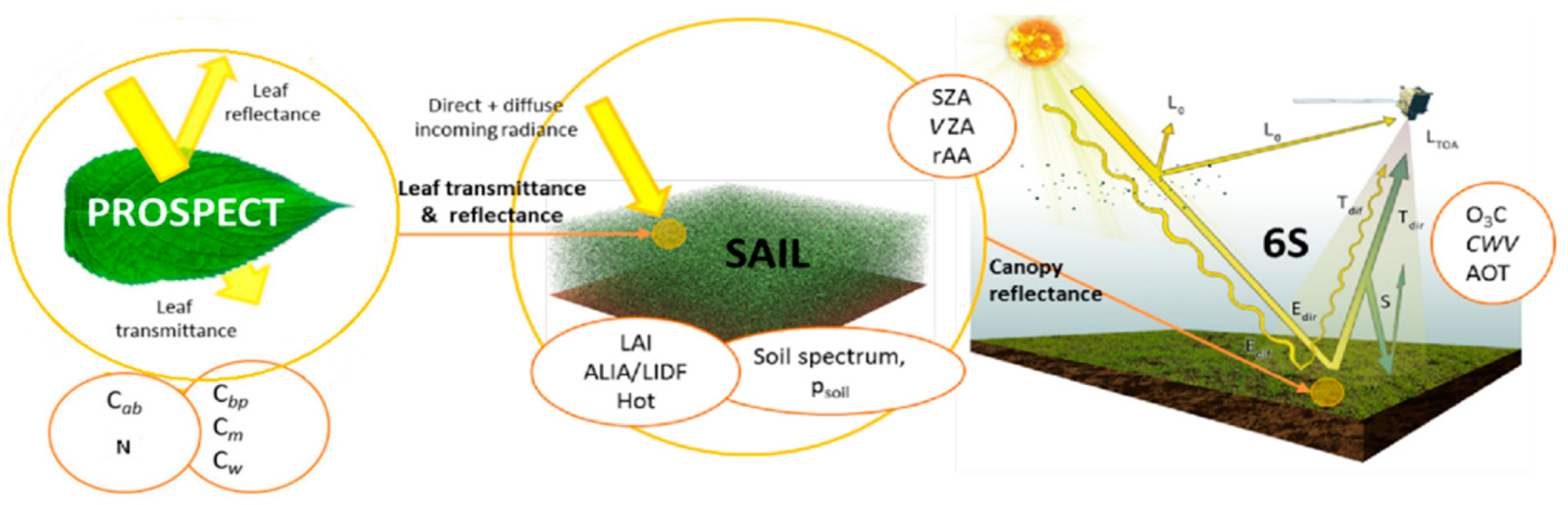
2.1. PROSAIL
2.2. Atmospheric RTM: The 6S Code
2.3. One-Dimensional Convolutional Neural Networks (1D-CNNs)
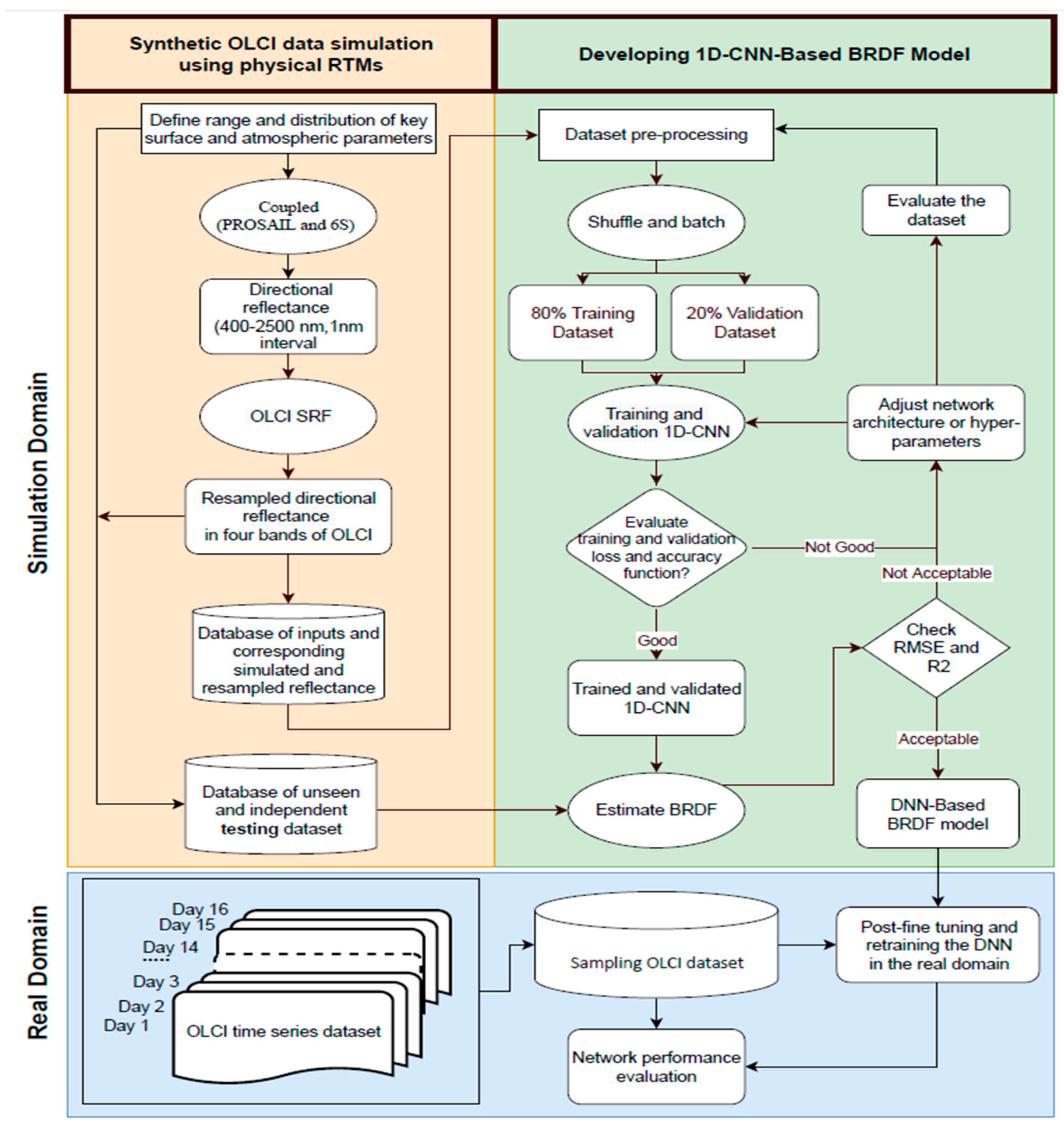
3. Material and Methodology
3.1. PROSAIL and 6S Parameterization to Generate Synthetic OLCI Data
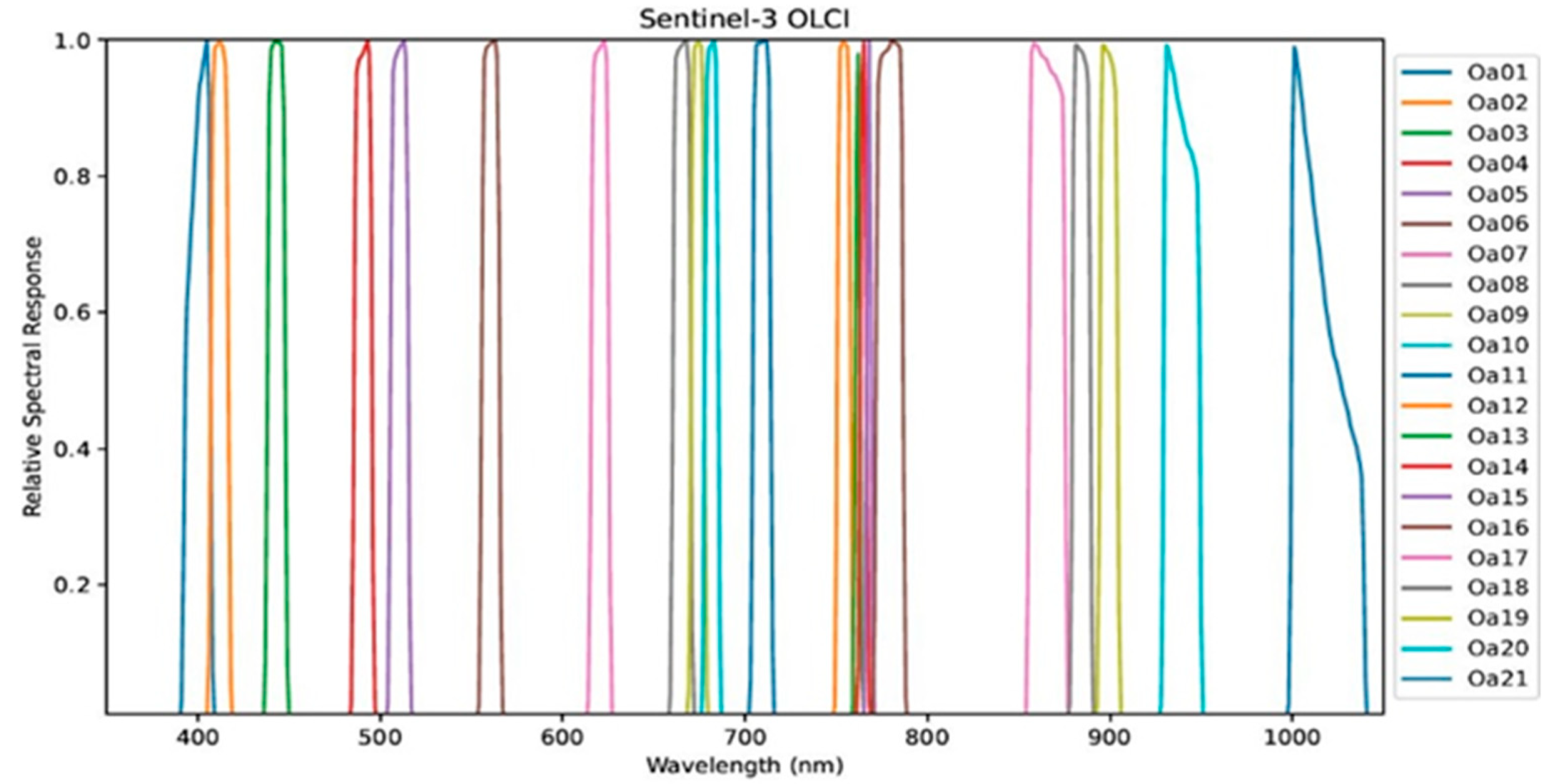
3.2. Real Sentinel 3-OLCI Data for Validation and Application
3.2.1. Collection of OLCI Data for Application in the Real Domain
3.2.2. Sampling of OLCI Data
- To determine the optimal n pixels, the average RMSE between the measured and the estimated reflectance by 1D-CNN in four bands was considered.
- The normalized Difference Vegetation Index (NDVI) of the selected pixels should be greater than 0.5 to cover the dense vegetation areas.
- Geometrical parameters, including VZA, SZA, and RAA values were divided into 10 bins using the histogram analysis of each variable, and then for each bin, a defined number of pixels were chosen randomly.
3.3. 1D-CNN Developing
3.3.1. Data Preprocessing for the 1D-CNN
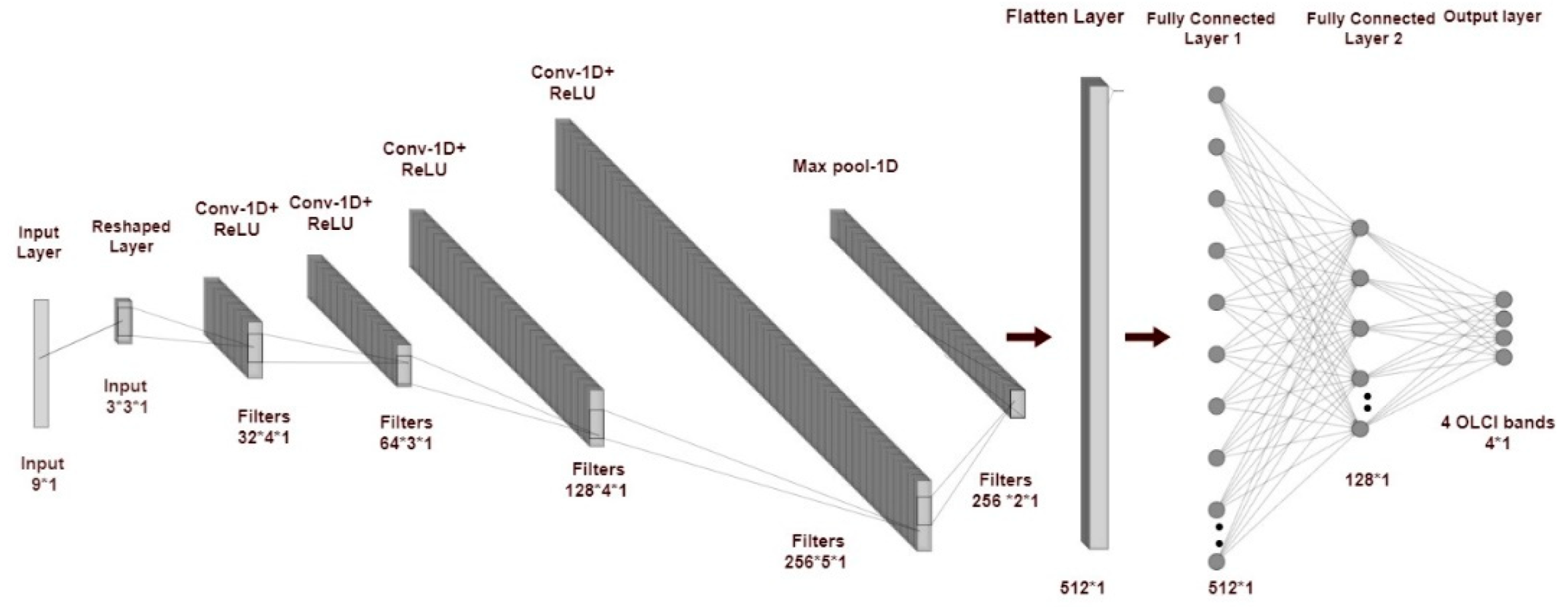
3.3.2. 1D-CNN Architecture Design
3.3.3. 1D-CNN Hyper-Parameter Tuning
3.4. Performance Evaluation
4. Results
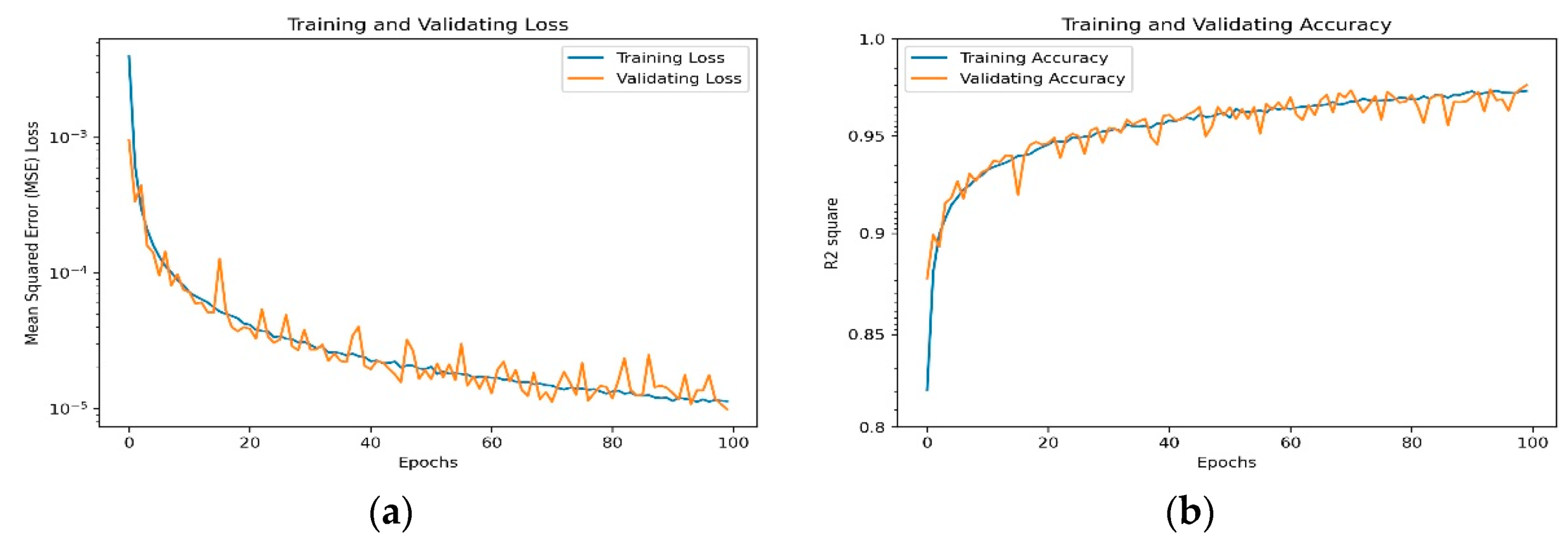
4.1. Network Training and Testing in the Simulation Domain
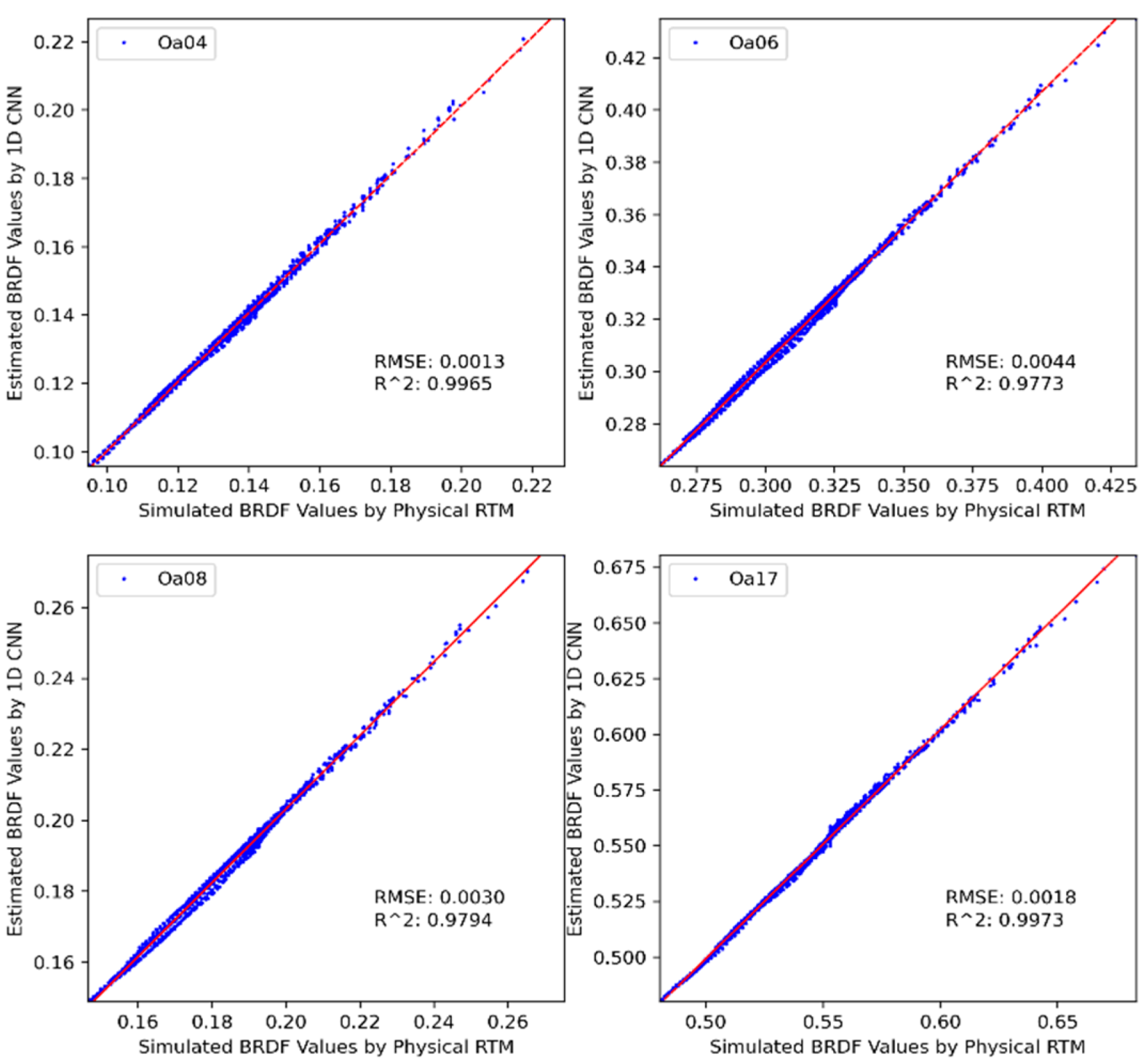
4.2. Simulation Testing Dataset for Network Evaluation
Analysis of Estimation Error
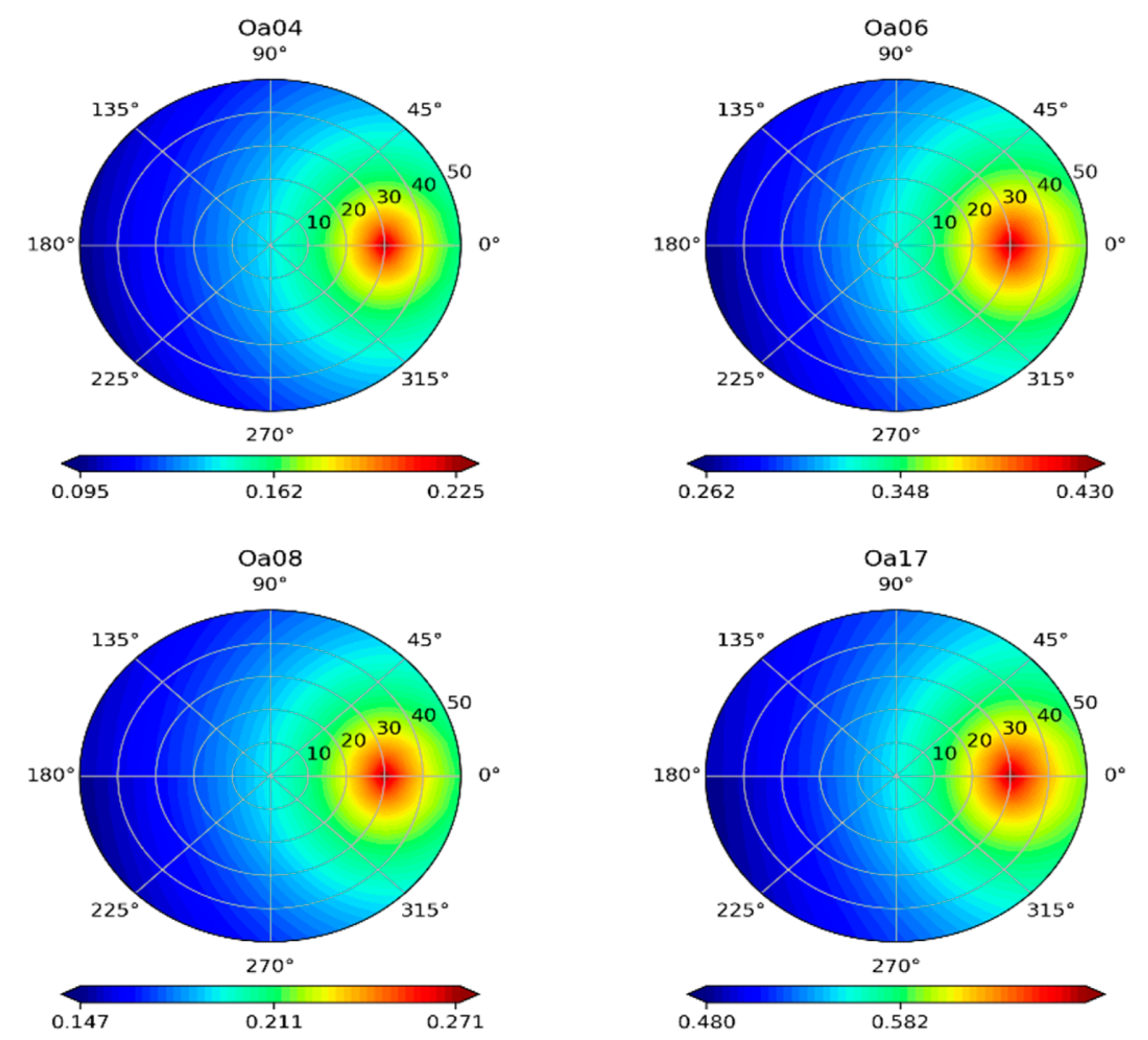
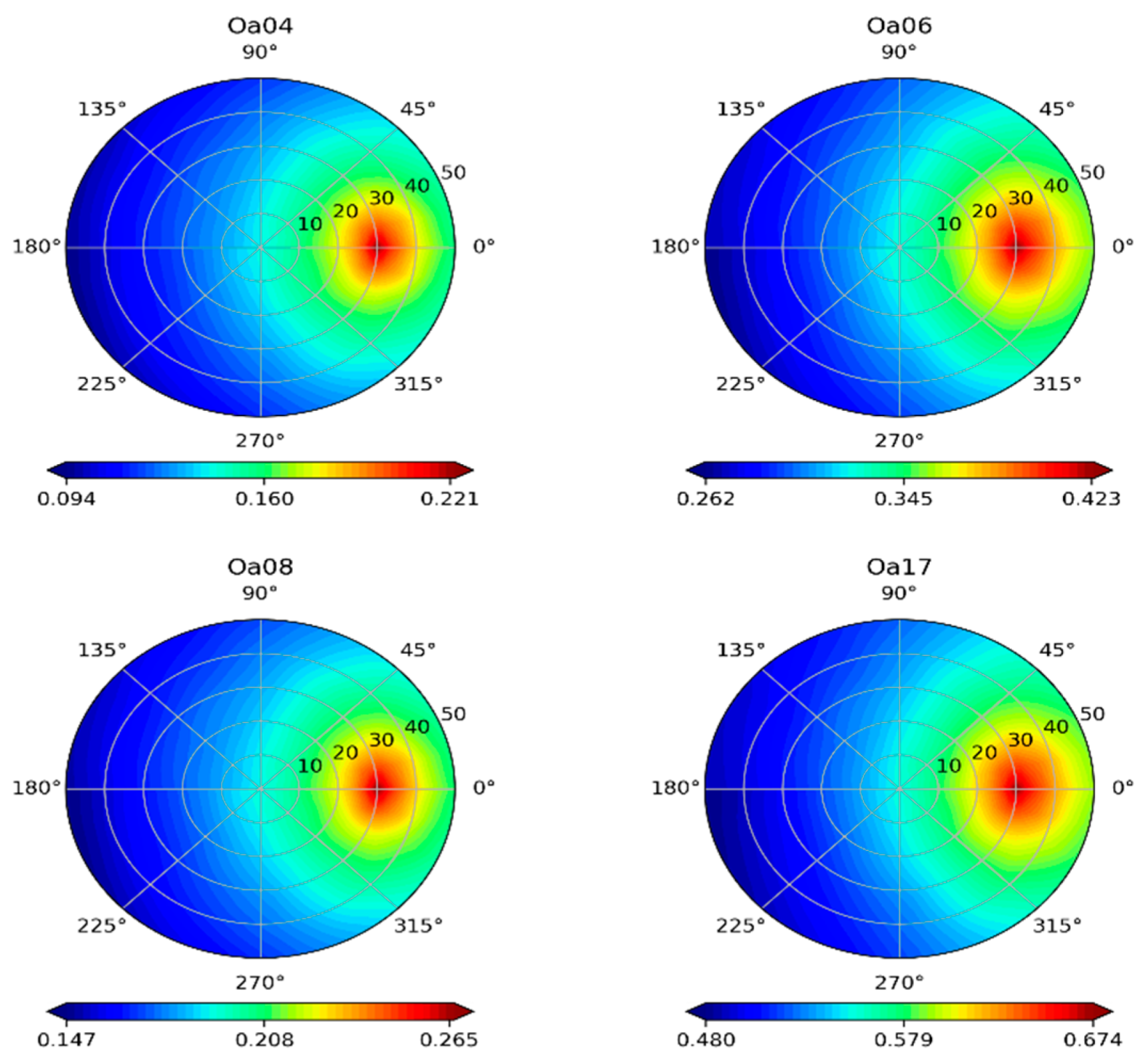
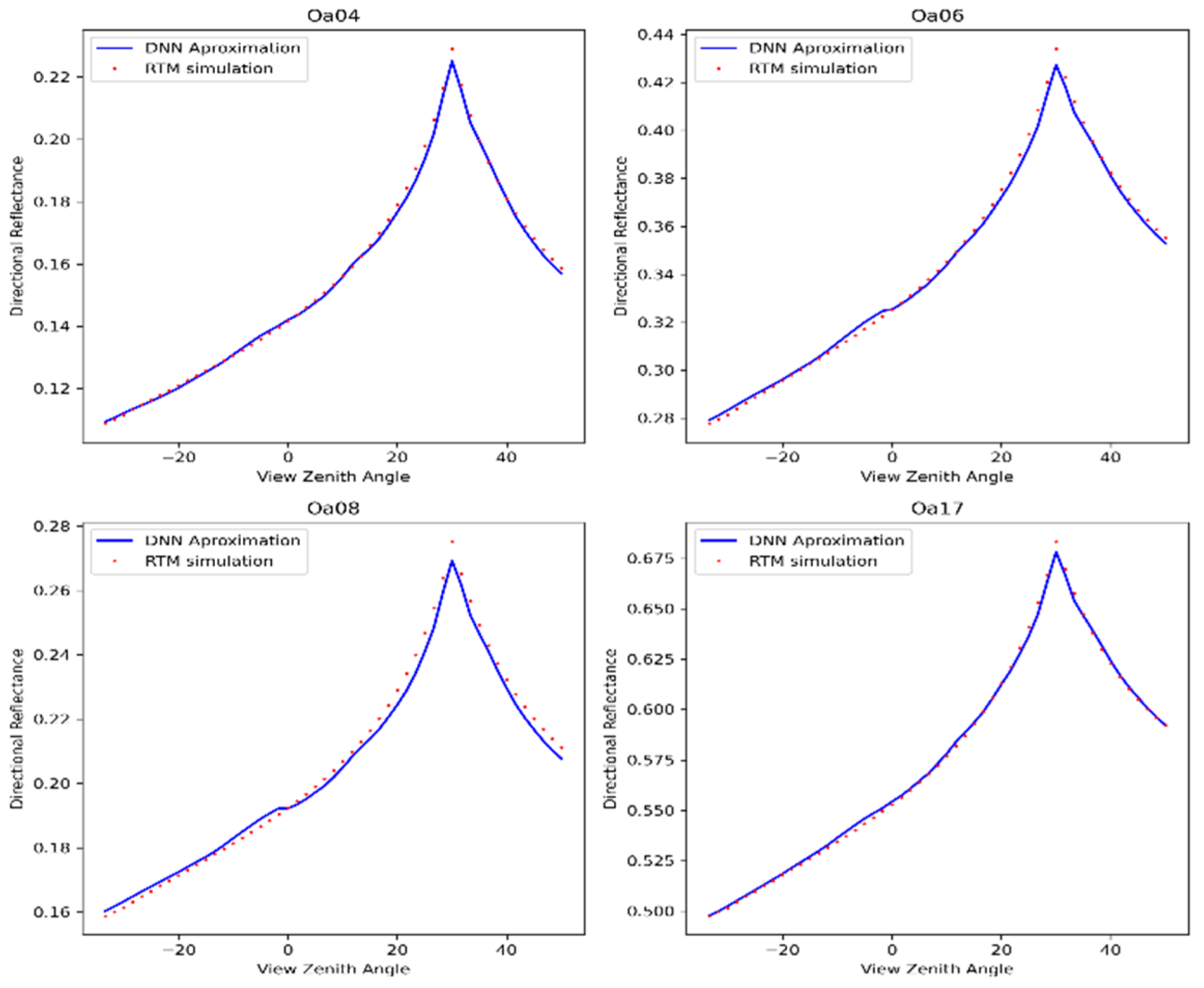
4.3. Comparison of the BRDF Shape in Principal and Cross-Principal Plans
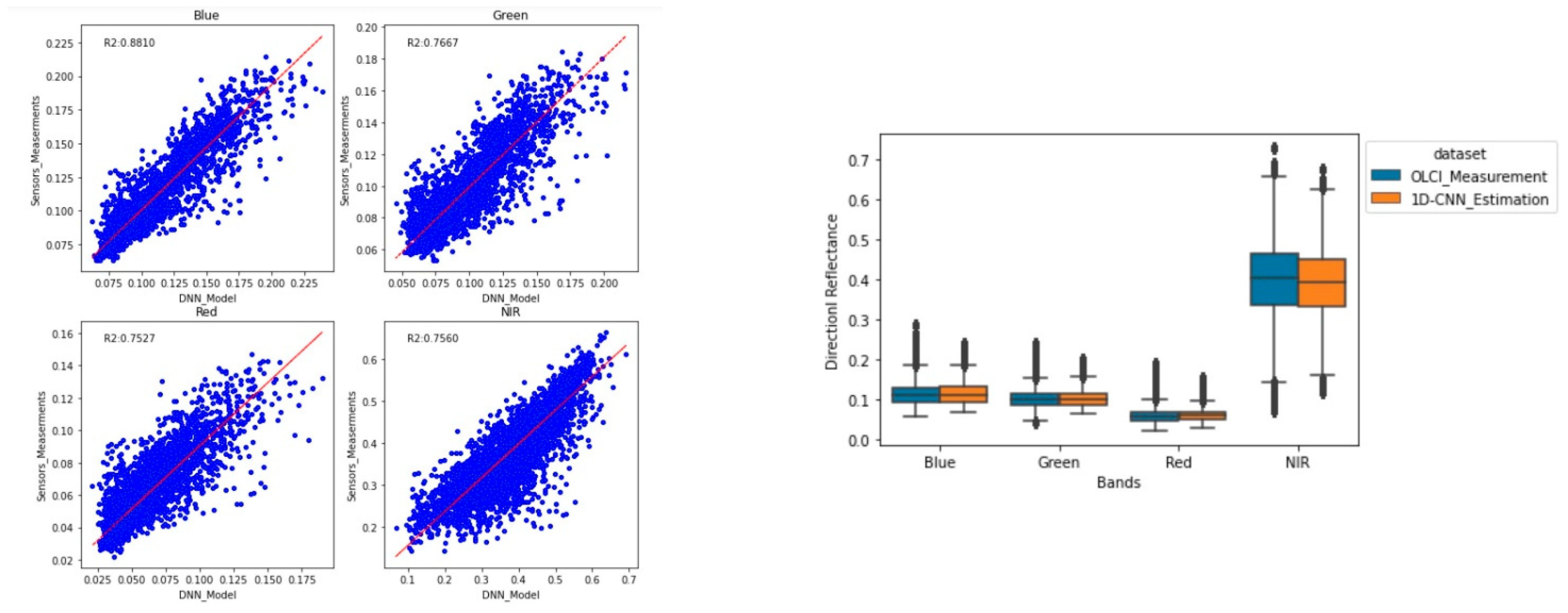
4.4. Application to Real Data
4.5. 1D-CNN Evaluation in the Real Domain
5. Conclusions
6. Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing-definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Latifovic, R.; Cihlar, J.; Chen, J. A comparison of BRDF models for the normalization of satellite optical data to a standard sun-target-sensor geometry. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1889–1898. [Google Scholar] [CrossRef]
- Luo, Y.; Trishchenko, A.P.; Latifovic, R.; Li, Z. Surface bidirectional reflectance and albedo properties derived using a land cover–based approach with Moderate Resolution Imaging Spectroradiometer observations. J. Geophys. Res. Atmos. 2005, 110, 1–17. [Google Scholar] [CrossRef]
- Qi, J.; Cabot, F.; Moran, M.; Dedieu, G. Biophysical parameter estimations using multidirectional spectral measurements. Remote Sens. Environ. 1995, 54, 71–83. [Google Scholar] [CrossRef]
- Guan, Y.; Zhou, Y.; He, B.; Liu, X.; Zhang, H.; Feng, S. Improving Land Cover Change Detection and Classification With BRDF Correction and Spatial Feature Extraction Using Landsat Time Series: A Case of Urbanization in Tianjin, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4166–4177. [Google Scholar] [CrossRef]
- Odongo, V.O. Uncertainty in Reflectance Factors Measured in the Field: Implications for the Use of Ground Targets in Remote Sensing. Master’s Thesis, University of Twente, Enskord, The Netherlands, 2010; p. 103. [Google Scholar]
- Zhang, X.; Jiao, Z.; Zhao, C.; Guo, J.; Zhu, Z.; Liu, Z.; Dong, Y.; Yin, S.; Zhang, H.; Cui, L.; et al. Evaluation of BRDF Information Retrieved from Time-Series Multiangle Data of the Himawari-8 AHI. Remote Sens. 2021, 14, 139. [Google Scholar] [CrossRef]
- Roberts, G. A review of the application of BRDF models to infer land cover parameters at regional and global scales. Prog. Phys. Geogr. 2016, 25, 483–511. [Google Scholar] [CrossRef]
- Roujean, J. A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. Atmos. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Biliouris, D.; Van Der Zande, D.; Verstraeten, W.W.; Stuckens, J.; Muys, B.; Dutré, P.; Coppin, P. RPV Model Parameters Based on Hyperspectral Bidirectional Reflectance Measurementsof Fagus sylvatica L. Leaves. Remote Sens. 2009, 1, 92–106. [Google Scholar] [CrossRef]
- Walthall, C.L.; Norman, J.M.; Welles, J.M.; Campbell, G.; Blad, B.L. Simple equation to approximate the bidirectional reflectance from vegetative canopies and bare soil surfaces. Appl. Opt. 1985, 24, 383–387. [Google Scholar] [CrossRef]
- Laurent, V.C.; Verhoef, W.; Clevers, J.G.; Schaepman, M.E. Estimating forest variables from top-of-atmosphere radiance satellite measurements using coupled radiative transfer models. Remote Sens. Environ. 2011, 115, 1043–1052. [Google Scholar] [CrossRef]
- Strahler, A.H.; Muller, J.; Lucht, W.; Schaaf, C.; Tsang, T.; Gao, F.; Li, X.; Lewis, P.; Barnsley, M.J. MODIS BRDF/albedo product: Algorithm theoretical basis document version 5.0. MODIS Doc. 1999, 23, 42–47. [Google Scholar]
- Scarino, B.R.; Bedka, K.; Bhatt, R.; Khlopenkov, K.; Doelling, D.R.; Smith, W.L., Jr. A kernel-driven BRDF model to inform satellite-derived visible anvil cloud detection. Atmos. Meas. Tech. 2020, 13, 5491–5511. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Sun, Q.; Erb, A.M.; Li, Z.; Schaaf, C.B.; Zhang, X.; Román, M.O.; Scott, R.L.; Zhang, Q.; et al. Evaluation of the VIIRS BRDF, Albedo and NBAR products suite and an assessment of continuity with the long term MODIS record. Remote Sens. Environ. 2017, 201, 256–274. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Ferreira, K.R.; Queiroz, G.R.; Camara, G.; Souza, R.C.M.; Vinhas, L.; Marujo, R.F.B.; Simoes, R.E.O.; Noronha, C.A.F.; Costa, R.W.; Arcanjo, J.S.; et al. Using Remote Sensing Images and Cloud Services on Aws to Improve Land Use and Cover Monitoring. In Proceedings of the 2020 IEEE Latin American GRSS & ISPRS Remote Sensing Conference (LAGIRS), Santiago, Chile, 22–26 March 2020; pp. 558–562. [Google Scholar] [CrossRef]
- Chen, K.; Sun, S.; Li, S.; He, Q. Analysis of water surface area variation of Hanfeng Lake in the Three Gorges Reservoir Area based on Microsoft Planetary Computer. In Proceedings of the 2022 3rd International Conference on Geology, Mapping and Remote Sensing (ICGMRS), Zhoushan, China, 22–24 April 2022; pp. 229–232. [Google Scholar] [CrossRef]
- Campos-Taberner, M.; Moreno-Martínez, Á.; García-Haro, F.J.; Camps-Valls, G.; Robinson, N.P.; Kattge, J.; Running, S.W. Global Estimation of Biophysical Variables from Google Earth Engine Platform. Remote Sens. 2018, 10, 1167. [Google Scholar] [CrossRef]
- Faurtyot, T. Vegetation water and dry matter contents estimated from top-of-the-atmosphere reflectance data: A simulation study. Remote Sens. Environ. 1997, 61, 34–45. [Google Scholar] [CrossRef]
- Guanter, L.; Segl, K.; Kaufmann, H. Simulation of Optical Remote-Sensing Scenes With Application to the EnMAP Hyperspectral Mission. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2340–2351. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, Z.; Dong, Y.; Zhang, H.; Li, Y.; He, D.; Ding, A.; Yin, S.; Cui, L.; Chang, Y. Potential Investigation of Linking PROSAIL with the Ross-Li BRDF Model for Vegetation Characterization. Remote Sens. 2018, 10, 437. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113 (Suppl. S1), S56–S66. [Google Scholar] [CrossRef]
- Vermote, E.F.T.D.; Tanré, D.; Deuzé, J.L.; Herman, M.; Morcrette, J.J.; Kotchenova, S.Y. Second simulation of a satellite signal in the solar spectrum-vector (6SV). 6s User Guide Version 2006, 3, 1–55. [Google Scholar]
- Estévez, J.; Vicent, J.; Rivera-Caicedo, J.P.; Morcillo-Pallarés, P.; Vuolo, F.; Sabater, N.; Camps-Valls, G.; Moreno, J.; Verrelst, J. Gaussian processes retrieval of LAI from Sentinel-2 top-of-atmosphere radiance data. ISPRS J. Photogramm. Remote Sens. 2020, 167, 289–304. [Google Scholar] [CrossRef] [PubMed]
- Verrelst, J.; Sabater, N.; Rivera, J.P.; Muñoz-Marí, J.; Vicent, J.; Camps-Valls, G.; Moreno, J. Emulation of Leaf, Canopy and Atmosphere Radiative Transfer Models for Fast Global Sensitivity Analysis. Remote Sens. 2016, 8, 673. [Google Scholar] [CrossRef]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Efficient RTM-based training of machine learning regression algorithms to quantify biophysical & biochemical traits of agricultural crops. ISPRS J. Photogramm. Remote Sens. 2021, 173, 278–296. [Google Scholar] [CrossRef]
- Vicent, J.; Verrelst, J.; Rivera-Caicedo, J.P.; Sabater, N.; Munoz-Mari, J.; Camps-Valls, G.; Moreno, J. Emulation as an Accurate Alternative to Interpolation in Sampling Radiative Transfer Codes. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4918–4931. [Google Scholar] [CrossRef]
- De Grave, C.; Verrelst, J.; Morcillo-Pallarés, P.; Pipia, L.; Rivera-Caicedo, J.P.; Amin, E.; Belda, S.; Moreno, J. Quantifying vegetation biophysical variables from the Sentinel-3/FLEX tandem mission: Evaluation of the synergy of OLCI and FLORIS data sources. Remote Sens. Environ. 2020, 251, 112101. [Google Scholar] [CrossRef]
- Reyes-Muñoz, P.; Pipia, L.; Salinero-Delgado, M.; Belda, S.; Berger, K.; Estévez, J.; Morata, M.; Rivera-Caicedo, J.P.; Verrelst, J. Quantifying Fundamental Vegetation Traits over Europe Using the Sentinel-3 OLCI Catalogue in Google Earth Engine. Remote Sens. 2022, 14, 1347. [Google Scholar] [CrossRef]
- Sawut, R.; Li, Y.; Liu, Y.; Kasim, N.; Hasan, U.; Tao, W. Retrieval of betalain contents based on the coupling of radiative transfer model and SVM model. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102340. [Google Scholar] [CrossRef]
- Jiao, Q.; Sun, Q.; Zhang, B.; Huang, W.; Ye, H.; Zhang, Z.; Zhang, X.; Qian, B. A Random Forest Algorithm for Retrieving Canopy Chlorophyll Content of Wheat and Soybean Trained with PROSAIL Simulations Using Adjusted Average Leaf Angle. Remote Sens. 2022, 14, 98. [Google Scholar] [CrossRef]
- Trombetti, M.; Riano, D.; Rubio, M.; Cheng, Y.; Ustin, S. Multi-temporal vegetation canopy water content retrieval and interpretation using artificial neural networks for the continental USA. Remote Sens. Environ. 2008, 112, 203–215. [Google Scholar] [CrossRef]
- Krasnopolsky, V.M.; Fox-Rabinovitz, M.S.; Hou, Y.T.; Lord, S.J.; Belochitski, A.A. Accurate and Fast Neural Network Emulations of Model Radiation for the NCEP Coupled Climate Forecast System: Climate Simulations and Seasonal Predictions*. Mon. Weather. Rev. 2010, 138, 1822–1842. [Google Scholar] [CrossRef]
- Morata, M.; Siegmann, B.; Perez-Suay, A.; Garcia-Soria, J.L.; Rivera-Caicedo, J.P.; Verrelst, J. Neural Network Emulation of Synthetic Hyperspectral Sentinel-2-Like Imagery With Uncertainty. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 16, 762–772. [Google Scholar] [CrossRef] [PubMed]
- Verrelst, J.; Caicedo, J.P.R.; Vicent, J.; Pallarés, P.M.; Moreno, J. Approximating Empirical Surface Reflectance Data through Emulation: Opportunities for Synthetic Scene Generation. Remote Sens. 2019, 11, 157. [Google Scholar] [CrossRef]
- Liang, X.; Garrett, K.; Liu, Q.; Maddy, E.S.; Ide, K.; Boukabara, S. A Deep-Learning-Based Microwave Radiative Transfer Emulator for Data Assimilation and Remote Sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8819–8833. [Google Scholar] [CrossRef]
- Duffy, K.; Vandal, T.; Wang, W.; Nemani, R.; Ganguly, A.R. A framework for deep learning emulation of numerical models with a case study in satellite remote sensing. arXiv 2019, arXiv:1910.13408. [Google Scholar] [CrossRef]
- Sinha, R.K.; Pandey, R.; Pattnaik, R. Deep Learning For Computer Vision Tasks: A review. arXiv 2018, arXiv:1804.03928. [Google Scholar] [CrossRef]
- Palaz, D.; Magimai, M.; Collobert, R. Convolutional Neural Networks-based continuous speech recognition using raw speech signal. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; pp. 4295–4299. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Yao, C.; Luo, X.; Zhao, Y.; Zeng, W.; Chen, X. A review on image classification of remote sensing using deep learning. In Proceedings of the 2017 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16 December 2017; Volume 2018, pp. 1947–1955. [Google Scholar] [CrossRef]
- Hoeser, T.; Bachofer, F.; Kuenzer, C. Object Detection and Image Segmentation with Deep Learning on Earth Observation Data: A Review—Part II: Applications. Remote Sens. 2020, 12, 3053. [Google Scholar] [CrossRef]
- Minaee, S.; Boykov, Y.Y.; Porikli, F.; Plaza, A.J.; Kehtarnavaz, N.; Terzopoulos, D. Image Segmentation Using Deep Learning: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3523–3542. [Google Scholar] [CrossRef]
- Raj, A.; Shah, N.A.; Tiwari, A.K.; Martini, M.G. Multivariate Regression-Based Convolutional Neural Network Model for Fundus Image Quality Assessment. IEEE Access 2020, 8, 57810–57821. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2020, 151, 107398. [Google Scholar] [CrossRef]
- Alem, A.; Kumar, S. Transfer Learning Models for Land Cover and Land Use Classification in Remote Sensing Image. Appl. Artif. Intell. 2021, 36, 2014192. [Google Scholar] [CrossRef]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D.D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Verhoef, W. Theory of Radiative Transfer Models Applied in Optical Remote Sensing of Vegetation Canopies; Wageningen University and Research: Wageningen, The Netherlands, 1998; ISBN 90-5485-804-4. [Google Scholar]
- Berger, K.; Atzberger, C.; Danner, M.; D’Urso, G.; Mauser, W.; Vuolo, F.; Hank, T.; Berger, K.; Atzberger, C.; Danner, M.; et al. Evaluation of the PROSAIL Model Capabilities for Future Hyperspectral Model Environments: A Review Study. Remote Sens. 2018, 10, 85. [Google Scholar] [CrossRef]
- Gómez-Dans, J.L.; Lewis, P.E.; Disney, M. Efficient Emulation of Radiative Transfer Codes Using Gaussian Processes and Application to Land Surface Parameter Inferences. Remote Sens. 2016, 8, 119. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanré, D.; Deuze, J.L.; Herman, M.; Morcette, J.-J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Bouroubi, Y.; Batita, W.; Cavayas, F.; Tremblay, N. Ground Reflectance Retrieval on Horizontal and Inclined Terrains Using the Software Package REFLECT. Remote Sens. 2018, 10, 1638. [Google Scholar] [CrossRef]
- Kotchenova, S.Y.; Vermote, E.F. Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data Part II Homogeneous Lambertian and anisotropic surfaces. Appl. Opt. 2007, 46, 4455–4464. [Google Scholar] [CrossRef]
- Lee, C.S.; Yeom, J.M.; Lee, H.L.; Kim, J.-J.; Han, K.-S. Sensitivity analysis of 6S-based look-up table for surface reflectance retrieval. Asia-Pac. J. Atmos. Sci. 2015, 51, 91–101. [Google Scholar] [CrossRef]
- Coppini, F.; Jiang, Y.; Tabti, S. Predictive Models on 1D Signals in a Small-Data Environment; Research Report; IMB—Institut de Mathématiques de Bordeaux: 2021; hal-03211100. Available online: https://hal.inrae.fr/MATHS-ENTREPRISES/hal-03211100v1 (accessed on 9 December 2022).
- Mozaffari, M.H.; Tay, L.-L. A Review of 1D Convolutional Neural Networks toward Unknown Substance Identification in Portable Raman Spectrometer. arXiv 2020, arXiv:2006.10575. [Google Scholar]
- Mele, B.; Altarelli, G. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. Phys. Lett. B 1993, 299, 345–350. [Google Scholar] [CrossRef]
- Le Maire, G.; François, C.; Soudani, K.; Berveiller, D.; Pontailler, J.-Y.; Bréda, N.; Genet, H.; Davi, H.; Dufrêne, E. Calibration and validation of hyperspectral indices for the estimation of broadleaved forest leaf chlorophyll content, leaf mass per area, leaf area index and leaf canopy biomass. Remote Sens. Environ. 2008, 112, 3846–3864. [Google Scholar] [CrossRef]
- Verrelst, J.; Vicent, J.; Rivera-Caicedo, J.P.; Lumbierres, M.; Morcillo-Pallarés, P.; Moreno, J. Global sensitivity analysis of leaf-canopy-atmosphere RTMs: Implications for biophysical variables retrieval from top-of-atmosphere radiance data. Remote Sens. 2019, 11, 1923. [Google Scholar] [CrossRef]
- Available online: https://sentinels.copernicus.eu/documents/247904/4598066/Sentinel-3-OLCI-Land-Handbook.pdf/455f8c88-520f-da18-d744-f5cda41d2d91?t=1664349550631 (accessed on 31 January 2023).
- You, D.; Wen, J.; Liu, Q.; Zhang, Y.; Tang, Y.; Liu, Q.; Xie, H. The Component-Spectra-Parameterized Angular and Spectral Kernel-Driven Model: A Potential Solution for Global BRDF/Albedo Retrieval From Multisensor Satellite Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8674–8688. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; Wocher, M.; Mauser, W.; Hank, T. Model-Based Optimization of Spectral Sampling for the Retrieval of Crop Variables with the PROSAIL Model. Remote Sens. 2018, 10, 2063. [Google Scholar] [CrossRef]
- Sinha, S.K.; Padalia, H.; Dasgupta, A.; Verrelst, J.; Rivera, J.P. Estimation of leaf area index using PROSAIL based LUT inversion, MLRA-GPR and empirical models: Case study of tropical deciduous forest plantation, North India. Int. J. Appl. Earth Obs. Geoinf. 2019, 86, 102027. [Google Scholar] [CrossRef]
- Boren, E.J.; Boschetti, L.; Johnson, D.M. Characterizing the Variability of the Structure Parameter in the PROSPECT Leaf Optical Properties Model. Remote Sens. 2019, 11, 1236. [Google Scholar] [CrossRef]
- Andrieu, B.; Baret, F.; Jacquemoud, S.; Malthus, T.; Steven, M. Evaluation of an Improved Version Model for Simulating Bidirectional of Sugar Beet Canopies of SAIL Reflectance; ©Elsevier Science Inc.: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Féret, J.-B.; François, C.; Gitelson, A.; Asner, G.P.; Barry, K.M.; Panigada, C.; Richardson, A.D.; Jacquemoud, S. Optimizing spectral indices and chemometric analysis of leaf chemical properties using radiative transfer modeling. Remote Sens. Environ. 2011, 115, 2742–2750. [Google Scholar] [CrossRef]
- Sun, J.; Wang, L.; Shi, S.; Li, Z.; Yang, J.; Gong, W.; Wang, S.; Tagesson, T. Leaf pigment retrieval using the PROSAIL model: Influence of uncertainty in prior canopy-structure information. Crop J. 2022, 10, 1251–1263. [Google Scholar] [CrossRef]
- de Sá, N.C.; Baratchi, M.; Hauser, L.; van Bodegom, P. Exploring the Impact of Noise on Hybrid Inversion of PROSAIL RTM on Sentinel-2 Data. Remote Sens. 2021, 13, 648. [Google Scholar] [CrossRef]
- Wang, W.; Ma, Y.; Meng, X.; Sun, L.; Jia, C.; Jin, S.; Li, H. Retrieval of the Leaf Area Index from MODIS Top-of-Atmosphere Reflectance Data Using a Neural Network Supported by Simulation Data. Remote Sens. 2022, 14, 2456. [Google Scholar] [CrossRef]
- Seitz, B.; Mavrocordatos, C.; Rebhan, H.; Nieke, J.; Klein, U.; Borde, F.; Berruti, B. The sentinel-3 mission overview. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 4208–4211. [Google Scholar]
- Jia, W.; Pang, Y.; Tortini, R.; Schläpfer, D.; Li, Z.; Roujean, J.-L. A Kernel-Driven BRDF Approach to Correct Airborne Hyperspectral Imagery over Forested Areas with Rugged Topography. Remote Sens. 2020, 12, 432. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of Deep Learning: Concepts, CNN Architectures, Challenges, Applications, Future Directions; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; Volume 8. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. 3—Data Preprocessing. In Data Mining (Third Edition), 3rd ed.; Han, J., Kamber, M., Pei, J., Eds.; Morgan Kaufmann: Boston, MA, USA, 2012; pp. 83–124. [Google Scholar] [CrossRef]
- Padarian, J.; Minasny, B.; McBratney, A. Using deep learning to predict soil properties from regional spectral data. Geoderma Reg. 2018, 16, e00198. [Google Scholar] [CrossRef]
- Bhatt, D.; Patel, C.; Talsania, H.; Patel, J.; Vaghela, R.; Pandya, S.; Modi, K.; Ghayvat, H. CNN Variants for Computer Vision: History, Architecture, Application, Challenges and Future Scope. Electronics 2021, 10, 2470. [Google Scholar] [CrossRef]
- Yi, D.; Ahn, J.; Ji, S. An Effective Optimization Method for Machine Learning Based on ADAM. Appl. Sci. 2020, 10, 1073. [Google Scholar] [CrossRef]
- Prikaziuk, E.; Yang, P.; van der Tol, C. Google Earth Engine Sentinel-3 OLCI Level-1 Dataset Deviates from the Original Data: Causes and Consequences. Remote Sens. 2021, 13, 1098. [Google Scholar] [CrossRef]





| Parameters | Symbol | Description | Unit | Range | Distribution |
|---|---|---|---|---|---|
| Sun-sensor geometry | SZA | Solar zenith angle | Deg | 10–50 | Uniform |
| VZA | Viewing zenith angle | Deg | 0–60 | Uniform | |
| RAA | Relative azimuth angle | Deg | −185–185 | Uniform | |
| Leaf properties | Chlorophyll a, b content | μg | 3–30 | Uniform | |
| N | Leaf structure parameters | unitless | 1–3 | Uniform | |
| Leaf Carotenoids content | μg | 10 | Fixed value | ||
| Equivalent water thickness | cm | 0.002 | Fixed value | ||
| Dry matter content | g | 0.002 | Fixed value | ||
| Brown pigments | unitless | 0 | Fixed value | ||
| Canopy architecture | LAI | Leaf area index | 0.1–6 | Uniform | |
| Average leaf slope | Deg | 15–60 | Uniform | ||
| Leaf inclination distribution | Deg | 0 | Fixed value | ||
| Hspot | Hot spot parameter | unitless | 0.01–0.9 | Uniform | |
| Dry/Wet soil factor | unitless | 0.5 | Fixed value | ||
| Atmospheric | AOT | Aerosol Optical Thickness | unitless | 0.1–0.5 | Uniform |
| Spectral Bands | Spectral Range (nm) | Center (nm) | Width (nm) | Spatial Resolution (m) |
|---|---|---|---|---|
| Oa04 | 438–448 | 490 | 10 | 300 |
| Oa06 | 555–565 | 560 | 10 | 300 |
| Oa08 | 660–670 | 665 | 10 | 300 |
| Oa017 | 856–876 | 865 | 20 | 300 |
| Layer Type | Layer Configuration | Output Size | Learnable Parameters | ||||
|---|---|---|---|---|---|---|---|
| Filters size | Kernel | Stride | Pad | Channel | Length | ||
| Reshaped input layer | - | - | - | - | 3 | 3 | 0 |
| Conv-1D | 32 | 2 | 1 | 1 | 32 | 4 | (2 × 1 × 3 + 1) × 32 = 224 |
| Conv-1D | 64 | 2 | 1 | 1 | 64 | 3 | (2 × 1 × 32 + 1) × 64 = 4160 |
| Conv-1D | 128 | 2 | 1 | 1 | 128 | 4 | (2 × 1 × 64 + 1) × 128 = 16,512 |
| Conv-1D | 256 | 2 | 1 | 1 | 256 | 5 | (2 × 1 × 128 + 1) × 256 = 65,792 |
| Max-pooling | 2 | 2 | 0 | 256 | 2 | 0 | |
| Flatten | - | 512 | 1 | 0 | |||
| Dense | 512 neurons | - | 512 × 128 + 128 = 65,664 | ||||
| Dense | 128 neurons | - | |||||
| Output layer | 4 neurons | - | 0 | ||||
| Total parameters | - | - | 152,352 | ||||
| Hyper-Parameters | Tested Values | Selected Values |
|---|---|---|
| Learning rate | 0.01, 0.001, 0.0001 | 0.001 |
| Epochs number | 100, 250, 500 | 100 |
| Batch size | 16, 32, 64, 128, 256 | 32 |
| Optimizer | SGD, ADAM, AdaMax | AdaMax |
| Loss function | MAE(L1Loss), MSE | MSE |
| Learning Rate | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Batch Size | 0.01 | 0.001 | 0.0001 | |||||||
| Training Accuracy | Testing Accuracy | Time (Minutes) | Training Accuracy | Testing Accuracy | Time (Minutes) | Training Accuracy | Testing Accuracy | Time (Minutes) | ||
| 16 | 0.997 | 0.560 | 83.62 | 0.997 | 0.942 | 83.05 | 0.998 | 0.925 | 80.53 | |
| 32 | 0.998 | 0.670 | 38.27 | 0.998 | 0.987 | 37.92 | 0.988 | 0.811 | 38.08 | |
| 64 | 0.998 | 0.790 | 20.01 | 0.998 | 0.876 | 20.22 | 0.998 | 0.853 | 20.28 | |
| 128 | 0.998 | 0.910 | 12.37 | 0.999 | 0.925 | 11.47 | 0.997 | 0.864 | 11.51 | |
| 256 | 0.999 | 0.871 | 7.63 | 0.998 | 0.718 | 7.65 | 0.997 | 0.861 | 7.17 | |
| N | LIDFA (°) | Hspot | AOT | SZA (°) | VZA (°) | RAA(°) | ||
|---|---|---|---|---|---|---|---|---|
| 1.5 | 10.5 | 30.5 | 0.3 | 3.5 | 0.15 | 30.5 | 0–50° | −180–180° |
| Spectral Bands | RMSE | |
|---|---|---|
| Oa04 | 0.996 | 0.0013 |
| Oa06 | 0.977 | 0.0044 |
| Oa08 | 0.979 | 0.0030 |
| Oa017 | 0.997 | 0.0018 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ojaghi, S.; Bouroubi, Y.; Foucher, S.; Bergeron, M.; Seynat, C. Deep Learning-Based Emulation of Radiative Transfer Models for Top-of-Atmosphere BRDF Modelling Using Sentinel-3 OLCI. Remote Sens. 2023, 15, 835. https://doi.org/10.3390/rs15030835
Ojaghi S, Bouroubi Y, Foucher S, Bergeron M, Seynat C. Deep Learning-Based Emulation of Radiative Transfer Models for Top-of-Atmosphere BRDF Modelling Using Sentinel-3 OLCI. Remote Sensing. 2023; 15(3):835. https://doi.org/10.3390/rs15030835
Chicago/Turabian StyleOjaghi, Saeid, Yacine Bouroubi, Samuel Foucher, Martin Bergeron, and Cedric Seynat. 2023. "Deep Learning-Based Emulation of Radiative Transfer Models for Top-of-Atmosphere BRDF Modelling Using Sentinel-3 OLCI" Remote Sensing 15, no. 3: 835. https://doi.org/10.3390/rs15030835
APA StyleOjaghi, S., Bouroubi, Y., Foucher, S., Bergeron, M., & Seynat, C. (2023). Deep Learning-Based Emulation of Radiative Transfer Models for Top-of-Atmosphere BRDF Modelling Using Sentinel-3 OLCI. Remote Sensing, 15(3), 835. https://doi.org/10.3390/rs15030835







