Accuracy Analysis and Appropriate Strategy for Determining Dynamic and Quasi-Static Bridge Structural Response Using Simultaneous Measurements with Two Real Aperture Ground-Based Radars

Abstract

Over the past 10 years, ground-based radar interferometry has become a frequently used technology for determining dynamic deflections of bridge structures induced by vehicle passages. When measuring with only one radar device, the so-called Interpretation Error (E_I) considerably rises. When using two radars, it is possible to simultaneously determine, for example, vertical and longitudinal displacements and to eliminate the Interpretation Error. The aim of the article is to establish a suitable strategy for determining dynamic and quasi-static response of bridge structures based on the accuracy analysis of measurement by two radars. The necessary theory for displacements determination by means of two radar devices is presented. This is followed by an analysis of errors when measuring with only one radar. For the first time in the literature, mathematical formulas are derived here for determining the accuracy of the resulting displacements by simultaneous measurement with two radars. The practical examples of bridge structures displacements determination by measuring with two radar devices in the field are presented. The key contribution of the paper is the possibility to estimate and plan in advance the achievable accuracy of the resulting displacements for the given radar configurations in relation to the bridge structure.

1. Introduction

Recently, structural health monitoring (also called bridge health monitoring in bridge engineering) has gradually become an important topic in bridge engineering and bridge management. For example, an interesting study concerning the design of a monitoring system for a prestressed composite box-girder bridge with corrugated steel webs, including the development of the real-time monitoring system, implementation of in-situ experiments, and the analysis of a 3D FEM model is introduced in [1]. The obtained results were used to derive the envelope of warning and critical thresholds, thus enabling effective judgment concerning the safety assessment of the bridge in the operating phase. As another example, the results of structural health monitoring of an extremely skew steel arch railway bridge concerned about different purposes, namely long-term monitoring of the track–bridge interactions, are described in [2].

Over the past 10 years, ground-based radar interferometry with real aperture radar (GB-RAR or GB-InRAR) has become a frequently used technology for determining dynamic deflections of bridge structures induced by vehicle passages [3,4,5,6,7,8]. The goal of these experiments was to obtain experimental data which could be meaningfully used for bridge health monitoring. The radar interferometry method allows to measure real-time deflections for short- and long-term loads in normal traffic (e.g., the passage of vehicles or vice versa standing columns of vehicles or static load tests). Furthermore, it can dynamically capture and detect frequency and amplitude of vibration of the monitored object in the frequency range from approximately 0.0 to 80 Hz. This method provides to determine the deflection size with precision better than 0.1mm. Deflections of a bridge can be simultaneously determined at multiple locations. It is possible to obtain both general and detailed information on the behavior of the structure under its dynamic load. For example, on the bridge of the length of 100 m there is possible to simultaneously monitor up to about 100 points. The basic principles and examples of the use of GB-RAR technology for determining deflection of bridges are given, for example, in [3,4,5,6,7]. An example of the use of GB-RAR technology to determine the deflections of metal rail bridge constructions caused by both temperature changes and vehicle passages (dynamic loads) is presented in [8]. However, this technology is very often also used for monitoring of further objects. For example, the monitoring of communications towers and urban buildings are described in [9,10] and monitoring of water tower reservoirs, factory chimneys, and wind power plant pylons is given in [11]. The joint use of a terrestrial laser scanner (TLS), configured in line scanner mode, and a GB-RAR technology for monitoring of vibration frequencies and oscillation amplitudes of tall structures is presented in [12]. The comparisons of the GB-RAR technology and technology using accelerometers for dynamic monitoring of large structures and for monitoring of bridges are given in [13,14]. A review in the field of GNSS technology use for dynamic structural health monitoring together with other technologies such as accelerometers and RTS (robotic total stations) is presented in [15]. Recent research trends also include [16] presenting a practical framework for urban bridge damage detection and analysis by using three key techniques: terrestrial laser scanning (TLS), ground-based microwave interferometry, and satellite permanent scatterer interferometry synthetic aperture radar (PS-InSAR). A review and future directions of modern bridge monitoring using TLS are in [17]. Further, ref. [18] proposes a methodology for the portfolio-scale detection of structural deformations of bridges via multi-temporal satellite-based differential interferometry (MTInSAR). In [19], a fiber Bragg grating (FBG) liquid-level system based on optical fiber sensors formed by structures with two fixed ends is presented. Such a system is suitable for long-term monitoring of bridges over long distances and does not require suitable environmental conditions, in situ visibility, and intensive labor work. However, it cannot be used to monitor dynamic or horizontal displacements. In contrast, the radar interferometry method is suitable for operational monitoring of both dynamic and horizontal displacements.

This contribution is focused on the measurement of deflections of bridges by two IBIS-FS interferometric radars of the Italian manufacturer IDS—Ingegneria Dei Sistemi. More details about this instrument are, e.g., in [20].

One of the basic shortcomings of the GB-RAR method is that the radar measures only line of site (LOS) displacements in the direction of intent and these are recalculated into the expected direction of displacements. In the case of bridges, the expected direction is usually vertical. The geometry situation is shown in Figure 1.

The assumed (expected) vertical displacement is calculated according to [4]:

d = d_LOS R/H.

(1)

However, the assumption of only a vertical displacement may not be fulfilled and is generally not fulfilled. The reason is, for example, that bridges are often nor horizontal nor straight, and then significant longitudinal or transverse deformation occurs at the same time as a result of torsion during vertical deflection and also vehicles generate usually longitudinal and transverse horizontal forces (e.g., braking forces or centrifugal forces) during their passages. In most cases, the longitudinal or transverse horizontal displacements are much smaller than the vertical ones. In some cases, however, horizontal displacements can become significant compared to vertical displacements. Examples of railway bridges with significant values of transversal horizontal displacements are presented in [21,22]. In [23], errors from the erroneous assumption of only vertical displacements are pointed out. In other words, these are errors from not taking horizontal displacements into account when determining vertical displacements using the GB-RAR method with only one radar. This error from not taking horizontal displacements into account is discussed in more detail in [24], where it is called an Interpretation Error E_I.

The geometric situation clarifying the origin of the Interpretation Error E_I is shown in Figure 2.

In accordance with [24], the Interpretation Error E_I can be expressed as follows:

E_I = (d − s_y)/d.

(2)

Then, the Interpretation Error E_I can be calculated based on the geometry shown in Figure 2 according to the relationship.

$$E_I=\frac{s_x}{s_y}\sqrt{{\left(\frac{R}{H}\right)}^2-1}$$

(3)

Formula (3) therefore gives the relationship between Interpretation Error E_I and the ratios R/H (radar distance from the measured point/radar distance from the measured point in vertical direction) and s_x/s_y (longitudinal or transversal horizontal displacement/vertical displacement). For clarity,

Table 1. Values of the Interpretation Error E_I for R/H and s_x/s_y ratios commonly used in practice.

R/H\sx/sy	0.01	0.04	0.07	0.10	0.15	0.20	0.25	0.30	0.40	0.50
1.00	0%	0%	0%	0%	0%	0%	0%	0%	0%	0%
1.20	1%	3%	5%	7%	10%	13%	17%	20%	27%	33%
1.40	1%	4%	7%	10%	15%	20%	24%	29%	39%	49%
1.60	1%	5%	9%	12%	19%	25%	31%	37%	50%	62%
1.80	1%	6%	10%	15%	22%	30%	37%	45%	60%	75%
2.00	2%	7%	12%	17%	26%	35%	43%	52%	69%	87%
2.50	2%	9%	16%	23%	34%	46%	57%	69%	92%	115%
3.00	3%	11%	20%	28%	42%	57%	71%	85%	113%	141%
3.50	3%	13%	23%	34%	50%	67%	84%	101%	134%	168%
4.00	4%	15%	27%	39%	58%	77%	97%	116%	155%	194%
4.50	4%	18%	31%	44%	66%	88%	110%	132%	175%	219%
5.00	5%	20%	34%	49%	73%	98%	122%	147%	196%	245%
5.50	5%	22%	38%	54%	81%	108%	135%	162%	216%	270%
6.00	6%	24%	41%	59%	89%	118%	148%	177%	237%	296%
7.00	7%	28%	48%	69%	104%	139%	173%	208%	277%	346%
8.00	8%	32%	56%	79%	119%	159%	198%	238%	317%	397%
9.00	9%	36%	63%	89%	134%	179%	224%	268%	358%	447%
10.00	10%	40%	70%	99%	149%	199%	249%	298%	398%	497%

shows the values of the Interpretation Error depending on the ratios R/H and s_x/s_y. With the usual size of the ratio of horizontal displacements to vertical s_x/s_y = 0.10 in practice, the value of Interpretation Error E_I = 23% already at the ratio R/H = 2.50. At the ratio R/H = 5.00, E_I = 49%. With a greater ratio of horizontal to vertical displacements, which can occur in some cases, the E_I values are even significantly larger. The size of the Interpretation Error can therefore take on very significant values and in common practice can completely invalidate the measurement results and lead to erroneous conclusions regarding the health of the tested structure. The most important finding regarding the influence of the Interpretation Error E_I is that, with some exceptions, it is not possible to rely on the results of measuring vertical displacements with only one radar.

It is therefore necessary to design new procedures for measuring and processing the measured LOS displacements in order to detect and determine the actual directions and magnitudes of the real (total) displacements. The ability to measure by two or more radar systems simultaneously would be able to overcome this shortcoming in probably the most effective way. It is also possible to eliminate this shortcoming with the help of a computational model of the bridge. However, in most cases, it is not available, and even so, its options are limited by uncertain boundary conditions and input parameters.

Simultaneous measurements with two radars are mentioned in the commonly available scientific literature only rarely. One of the first articles dealing with the use of two radars for determining bridge displacements is [25]. The first time the principle of calculation of real (total) displacements when measuring with two radars is given in [26]. The issue of time synchronization of measurements, which is crucial for correct calculation of real displacements, is not mentioned there. From the later literature dealing with the determination of 2D/3D displacements by measuring with two or more radars, ref. [27,28] can be cited.

A similar principle for detecting total displacements, but a different technical solution, is presented in [23,29]. The solution consists in the design of a monostatic/bistatic interferometric radar for retrieving the three-dimensional (3D) displacement vector for static and dynamic monitoring of bridges. The monostatic/bistatic technique makes use of a multiple input multiple output (MIMO) interferometric radar equipped with two transponders. Each single transponder consists of an antenna and an amplifier, and it is connected to the radar with a radiofrequency cable.

The aim of the article is to establish a suitable strategy for determining dynamic and quasi-static response of bridge structures based on the accuracy analysis of measurement by two radars. The key contribution of the article is the possibility to estimate and plan in advance the achievable accuracy of the resulting displacements for the given radar configurations in relation to the observed bridge structure. These findings have not been published yet.

2. Method of GB-RAR with Two Interferometric Radars

2.1. Data Processing

Simultaneous measurements with two radars bring up several technical problems that need to be solved. It is mainly a matter of determining the spatial configuration of radars and the measured bridge, which enables calculation of real displacements. Furthermore, time synchronization of both radars causes serious problems as well.

If we assume that the bridge deck moves along two directions (longitudinally and vertically), it is possible to determine the real displacements and their individual components in vertical plane by simultaneous measurement with two radars. The vertical plane is usually located in such a way that it goes through the monitored points on the bridge deck and positions of the both radars. In this case, Figure 3 shows two basic configurations of the positions of the two radars when measuring bridges: (a) the radars measure against each other—at the top, or (b) the radars measure from one side of the bridge—at the bottom. Then, Figure 4 shows geometric relations between LOS displacements and real (total) displacements of a point measured from two different radar positions. The geometric relations are the same for both configurations. The coordinate system used for the components of the total displacement vector has an X axis horizontal (in the direction of the bridge axis) and an Y axis vertical (pointing downwards).

The longitudinal and vertical components of the displacement vector are functions of vertical angles of the radar directions and the measured displacements in these directions (LOS displacements). They can be calculated by Formula (4) [24,26].

$$\begin{array}{ccc}{s}_X& =& \frac{t_1\sin \left({\psi }_2\right)-t_2\sin \left({\psi }_1\right)}{\sin \left({\psi }_2-{\psi }_1\right)}\\ s_Y& =& \frac{-t_1\cos \left({\psi }_2\right)+t_2\cos \left({\psi }_1\right)}{\sin \left({\psi }_2-{\psi }_1\right)}\end{array},$$

(4)

where

$t_1, t_2$ … measured LOS displacements;

${\psi }_1, {\psi }_2$ … vertical angles of the radar directions;

$s_X, s_Y$ … components of the displacement vector (longitudinal and vertical).

Proof. 

Equation (4) can be derived with the aid of well-known property of scalar product of two vectors. If angle $\omega$ of the vectors $\mathit{r}$, $\mathit{s}$ is given in advance, the scalar product of them is

$$\left(\mathit{r}, \mathit{s}\right):={\mathit{r}}^T·\mathit{s}=r_X{s}_X+r_Y{s}_Y=\left|\left|\mathit{r}\right|\right|·\left|\left|\mathit{s}\right|\right|·\cos \omega ,$$

where

$r_X, r_Y$ … coordinates of the vector $\mathit{r}$, ${\mathit{r}}^T=\left[r_X, r_Y\right]$;

$s_X, s_Y$ … coordinates of the vector $\mathit{s}$, ${\mathit{s}}^T=\left[s_X, s_Y\right];$

$\left|\left|\mathit{r}\right|\right|$ … length of the vector $\mathit{r}$;

$\left|\left|\mathit{s}\right|\right|$ … length of the vector $\mathit{s}$;

$\omega$ … angle of the vectors $\mathit{r}$, $\mathit{s}$.

This property of scalar product simplifies if ${\mathit{r}}^T=[\cos \left({\psi }_i\right) , \sin \left({\psi }_i\right)$].

$$s_X{\cos \psi }_i + s_Y{\sin \psi }_{\mathrm{i}}=\left|\left|\mathit{s}\right|\right|·1·{\cos \omega }_i$$

(5)

It is obvious in Figure 4 that the following equality holds:

$${\cos \omega }_i=\frac{t_i}{\left|\left|\mathit{s}\right|\right|}.$$

After using this equality as substitution in Equation (5), further simplification results in:

$$s_X\cos {\psi }_i + s_Y\sin {\psi }_i=t_i .$$

This equality is valid for $i\in \left\{1,2\right\};$ therefore, it is a system of two linear equations for unknowns $s_X, s_Y$.

$$\begin{array}{ccc}\hfill s_X\cos {\psi }_1+ s_Y\sin {\psi }_1& \hfill =& \hfill t_1\\ \hfill s_X\cos {\psi }_2+ s_Y\sin {\psi }_2& \hfill =& \hfill t_2\end{array}$$

(6)

The solution of System (6) results in Formula (4). This proves the correctness of Formula (4) for determining the displacement vector $\left[s_X, s_Y\right]$. □

In this way, it is possible to determine the longitudinal and vertical components of the total (real) displacement of the monitored point. However, since the IBIS Data Viewer software supplied with the radar equipment does not allow the evaluation of multi-radar measurements, it is necessary to export the data (LOS displacements) from the IBIS software and, afterwards, process them by some other suitable software.

A serious limitation of this measurement procedure is the interference of the signals of both radars. Interference was observed for any configuration and position of the radars. More interference occurs when the antennas of the radars are facing each other, but it also depends on the object being observed. Its size also depends on the type of radar. Radar IBIS-FS is generally interfered with less than IBIS-S. The size of the interference is also smaller if the value of NumberOfDeadTonesBetweenTwoSweeps is as small as possible. This value can be found in the ini file stored with the measurement. The value depends on the Sampling Frequency and the Max distance of the measurement.

Interference is expressed by periodic peaks. Their frequency depends on the settings of the radars. If the interference is larger, it needs to be filtered out.

If we wanted to measure without interference, the radars would have to communicate directly with each other, which is not possible with ordinary IBIS-S and IBIS-FS radars.

2.2. Time Synchronization of Two or More Radars

When measuring with two radars, there is a practical problem how to recognize displacements measured at the same time in two different time series of the acquired LOS displacements. Therefore, the time series have to be synchronized to find time correspondence of the acquired LOS displacements. If the measurement is performed for example with sampling rate 200 Hz, then the synchronization must be performed with the appropriate accuracy, i.e., ±0.0025 s.

One possible solution of the synchronization is based on identification of maximum deflection values in the two timeseries [24]. Positions of these maxima presumably correspond to the same moment of acquiring them. Hence the synchronization could be performed simply as a time shift obtained after fitting peaks of the two timeseries. There is a serious disadvantage of this method. Deflection values acquired in both time series may not reach their maxima at the same moment. Fitting the time series is therefore only approximate and may not reach the required accuracy ±0.0025 s.

Due to the above disadvantage, more accurate method of synchronization was designed. This method utilizes system times of operating laptops that control measurement processes of the radars and on which the measured data are stored. Synchronizing the two radars therefore means synchronizing the system time of their operating laptops. The radar operating software obtains the exact time from the laptop’s operating system and saves the measurement start time in a file with the measured values from the radar. By comparing the time data stored in the measurement files, it is therefore possible to identify the measured values that were taken at the same time.

When the laptop is turned on, the operating system gets real time from the Real-Time Clock (RTC) module and then measures time using the processor’s clock signal, which is more accurate than RTC. To keep the deviation from the real time sufficiently small, current operating systems synchronize their clocks with special time servers on the Internet at regular intervals. To do this, the Network Time Protocol (NTP) stated in [30] is used, which allows the clock in a packet network to be synchronized with a variable delay. This NTP protocol can be used to synchronize radars service laptops too. The synchronization is generally described in [31]. Such a synchronization process requires physical interconnection of both operating laptops by Ethernet cable or by wireless communication. The time differences between the laptops can be saved to a file. Using these values, it is then possible to synchronize the measured data (LOS displacements) of both radars.

This method of time synchronization can also be used when synchronizing radar measurements using the GB-RAR method with measurements using other classic methods, for example using accelerometers or photogrammetry.

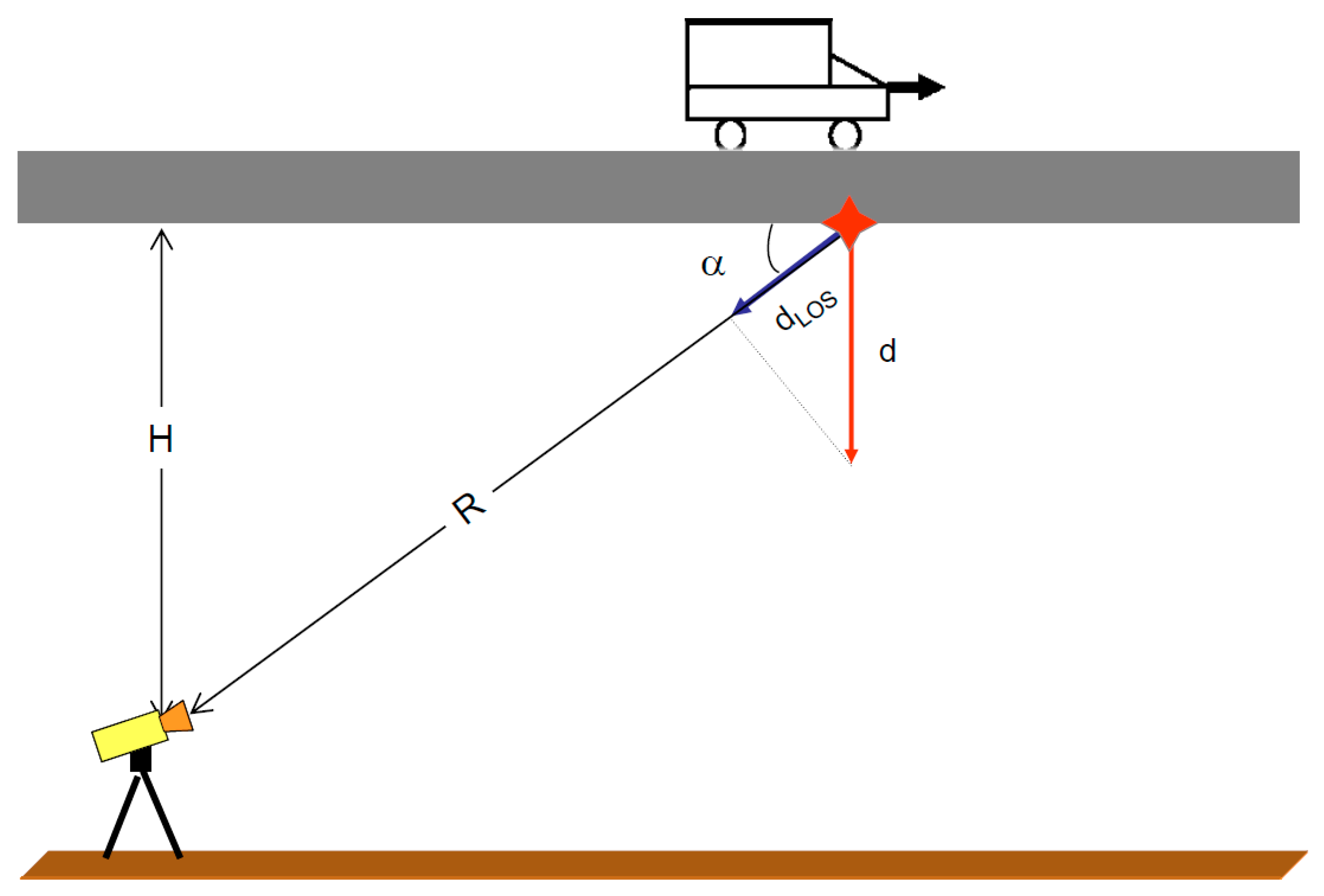
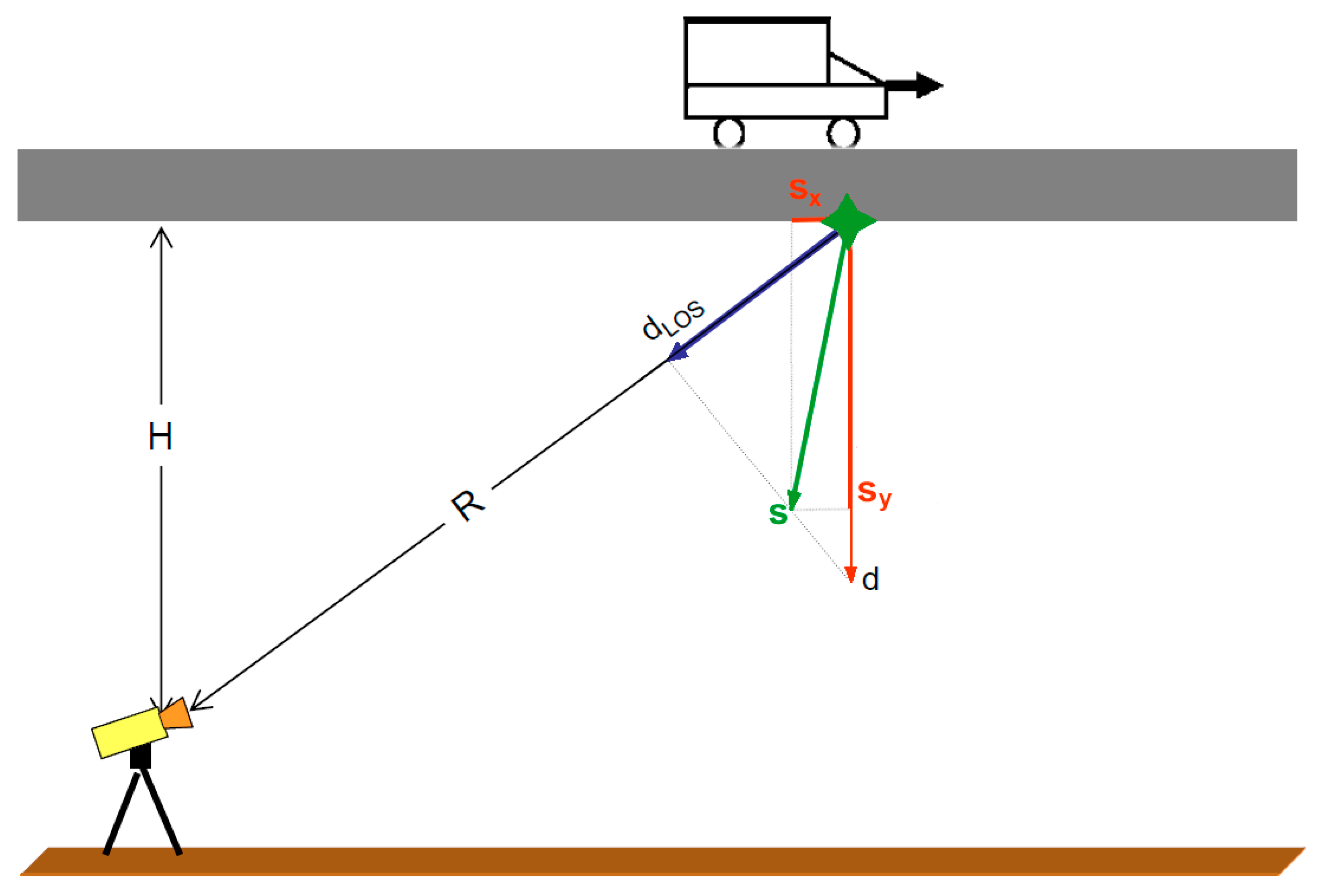
2.3. Accuracy Analysis of Longitudinal and Vertical Component of the Total Displacement

Accuracy analysis of displacements $\left[s_X, s_Y\right]$ stems from Equation (4). Covariance matrix of the displacement vector $\left[s_X, s_Y\right]$ can be estimated using a well-known formula of error propagation, e.g., [32], if precisions of LOS displacements $t_1, t_2$ and radar directions ${\psi }_1, {\psi }_2$ are given in advance. Therefore, prediction of accuracy of the resulting displacements is possible. The prediction is important namely for planning appropriate placements of the radars in the terrain.

The Formula (4) are not suitable for accuracy analysis. Matrix notation is more appropriate. Therefore, the linear system (6) has to be expressed as:

$$\left[\begin{array}{c}{\mathit{r}}_1^T\\ {\mathit{r}}_2^T\end{array}\right]·\mathit{s}=\mathit{t} ,$$

(7)

where

$\mathit{s}$ … column vector of displacement, $\mathit{s}:=\left[s_X, s_Y\right]{ }^T;$

$\mathit{t}$ … column vector of LOS displacement, $\mathit{t}:={[t_1, t_2]}^T$;

${\mathit{r}}_i^T$ … row vector directing from the monitored point to $i$-th radar, $i\in \left\{1, 2\right\};$

$${\mathit{r}}_i^T=\left[\cos \left({\psi }_i\right) ,\sin \left({\psi }_i\right)\right]=\frac{\left[x_i, y_i\right]}{\sqrt{x_i^2+y_i^2}} ,$$

$x_i, y_i$ … coordinates of position of $i$-th radar, $i\in \left\{1, 2\right\}$.

Solution of the matrix Equation (7) is

$$\mathit{s}=\frac{1}{{\mathit{r}}_2^T·{\mathit{r}}_1^{\perp }} \left[\begin{array}{c}-{\mathit{r}}_2^{\perp }, {\mathit{r}}_1^{\perp }\end{array}\right]·\mathit{t} ,$$

(8)

where operator of perpendicularity ${}^{\perp }$ is defined for any 2D vector.

$\mathit{v}=\left[v_X , v_Y\right]\in R^2$ as

$${\mathit{v}}^{\perp }:=\left[-v_Y , v_X\right].$$

Accuracy of angles ${\psi }_1, {\psi }_2$ depends on accuracy of vectors ${\mathit{r}}_1$, ${\mathit{r}}_2,$ as well as on accuracy of radar positions that will be denoted ${\mathit{x}}_i$ for $i\in \left\{1, 2\right\}$.

$$\begin{array}{rrr}\hfill {\mathit{x}}_i& \hfill :=& \hfill {[x_i, y_i]}^T ,\\ \hfill \left|\left|{\mathit{x}}_i\right|\right|& \hfill :=& \hfill \sqrt{x_i^2+y_i^2} . \\ \hfill & \hfill & \hfill \end{array}$$

Coordinates $x_1, y_1, x_2, y_2$ can be measured by standard geodetic methods and accuracy of the coordinates can be easily estimated as well. Therefore, it is suitable to express displacement vector $\mathit{s}$ in terms of coordinates of radar positions ${\mathit{x}}_1$, ${\mathit{x}}_2$. With the aid of substitution,

$${\mathit{r}}_i=\frac{{\mathit{x}}_i}{\left|\left|{\mathit{x}}_i\right|\right|}$$

the final formula for determination of displacement vector can be expressed in concise matrix form:

$$\mathit{s}=\frac{1}{{\mathit{r}}_2^T·{\mathit{r}}_1^{\perp }}[-||{\mathit{x}}_1||{\mathit{x}}_2^{\perp },||{\mathit{x}}_2||{\mathit{x}}_1^{\perp }]·\mathit{t}$$

(9)

Hence, accuracy of positions ${\mathit{x}}_1$, ${\mathit{x}}_2$ of the radars can be used instead of accuracy of angles ${\psi }_1, {\psi }_2$. To determine the accuracy of the displacement vector, it is therefore necessary to know the values of the LOS displacements $t_1, t_2$, the coordinates of the positions of both radars and their accuracy characteristics. It is assumed that these input variables have normal (Gaussian) distribution.

On the contrary, the size of the range resolution area [26], so-called range bin (R_bin) or distance resolution, which can be, for example, ΔR = 0.75m, does not affect the accuracy of determining the displacement vector. This value expresses the uncertainty of the position of the monitored point. It is possible to determine the displacement vector of a point on the bridge very precisely and correctly estimate the accuracy of its determination but, at the same time, it is usually not possible to identify the position of this moving point more precisely than a decimeter resolution allows. This problem is caused not only by the size of the range resolution area ΔR, but also by the different reflectivity of the material and by the complexity (number of details) of the bridge deck construction in the given range resolution area as well.

For the best possible solution to the problem of identifying individual R_bins on the monitored object, it is recommended to create a point cloud of using the laser scanning method. The point cloud must contain both the given object and the positions of both radars during the measurement. Then individual points on the object can be colored according to the distances from the phase centers of the radars at intervals according to the R_bin interface. This identifies the positions of individual R_bins on the monitored object. It means that the corresponding locations on the monitored object will be assigned to the measured LOS displacements. The creation of a point cloud by laser scanning can of course be replaced by any other geodetic method for creating 3D models of objects, such as, e.g., photogrammetry using UAVs (drones) [33,34].

Thus, with regard to the above-mentioned indeterminacy of identifying the position of the moving (targeted) point, determining the accuracy characteristics of the position coordinates of both radars is very problematic, since this indeterminacy affects the position of the origin of the coordinate system in which the position of both radars is determined (see Figure 4). This should be kept in mind for further considerations.

We assume that accuracy characteristics of the LOS displacements $t_1, t_2$ and coordinates of positions of both radars $x_1, y_1, x_2, y_2$ are given in form of block covariance matrix ${\mathit{C}}_{\mathit{u}}$ which is compounded of covariance matrices ${\mathit{C}}_{\mathit{t}}$, ${\mathit{C}}_{xy }$ and zero matrices ${\mathit{O}}_{2,4}$, ${\mathit{O}}_{4,2}$.

$${\mathit{C}}_{\mathit{u}}:=\left[\begin{array}{ccc}{\mathit{C}}_{\mathit{t}} & ,& {\mathit{O}}_{2,4}\\ {\mathit{O}}_{4,2} & ,& {\mathit{C}}_{xy}\end{array}\right].$$

(10)

Here, $\mathit{u}$ stands for vector of input quantities, i.e.,

$$\mathit{u}:=\left[t_1, t_2, x_1, y_1, x_2, y_2\right]$$

(11)

and

${\mathit{C}}_{\mathit{t}}$ … known covariance matrix of LOS displacements $\left[t_1, t_2\right]$;

${\mathit{C}}_{xy}$ … covariance matrix of radar coordinates $\left[x_1, y_1, x_2, y_2\right]$;

${\mathit{O}}_{2,4}$ … zero matrix of type $2\times 4$ (2 rows and 4 columns);

${\mathit{O}}_{4,2}$ … zero matrix of type $4\times 2$ (4 rows and 2 columns).

Covariance matrix of displacement vector $s$ can be computed with the aid of formula of error propagation, (see, e.g., [32], Equation (8a.1.7)).

$${\mathit{C}}_{\mathit{s}}={\mathit{J}}_{\mathit{u}}·{\mathit{C}}_{\mathit{u}}·{\mathit{J}}_{\mathit{u}}^T ,$$

(12)

where

${\mathit{C}}_{\mathit{s}}$	…	covariance matrix of displacement vector s;
${\mathit{C}}_{\mathit{u}}$	…	covariance matrix of components of vector u;
${\mathit{J}}_{\mathit{u}}$	…	Jacobian matrix of mapping $\mathit{u}\mapsto \mathit{s}\left(\mathit{u}\right)$ given by (9); ${\mathit{J}}_{\mathit{u}}:=\frac{\partial \mathit{s}}{\partial \mathit{u}}\left(\widehat{\mathit{u}}\right),\mathit{s}\left(\mathit{u}\right) \cong \mathit{s}\left(\widehat{\mathit{u}}\right)+{\mathit{J}}_{\mathit{u}}·\left(\mathit{u}-\widehat{\mathit{u}}\right),$
$\widehat{\mathit{u}}$	…	vector of measured or approximately computed values of input quantities $t_1, t_2, x_1, y_1, x_2, y_2,$ i.e., $\widehat{\mathit{u}}=:\left[{\widehat{t}}_1, {\widehat{t}}_2, {\widehat{x}}_1, {\widehat{y}}_1, {\widehat{x}}_2, {\widehat{y}}_2\right]=:\left[ {\widehat{\mathit{t}}}_2, {\widehat{\mathit{x}}}_1,{\widehat{\mathit{x}}}_2\right].$

General Formula (12) can be simplified under various presumptions that will be discussed in the following subsections.

2.3.1. The Case When Imprecision of LOS Directions Is Neglected

Assumption that LOS directions was measured without errors means that coordinates $x_1, y_1, x_2, y_2$ were determined flawlessly as well. In such case, covariance matrix ${\mathit{C}}_{\mathrm{xy}}$ would be zero matrix, i.e., ${\mathit{C}}_{\mathrm{xy}}={\mathit{O}}_{4,4}$ and Jacobian matrix ${\mathit{J}}_{\mathit{u}}$ would gain the form

$${\mathit{J}}_{\mathit{u}}=\frac{1}{{\widehat{\mathit{x}}}_2^T·{\widehat{\mathit{x}}}_1^{\perp }}\left[\begin{array}{cccccccc}\left|\left|{\widehat{\mathit{x}}}_1\right|\right| {\widehat{y}}_2& ,& -\left|\left|{\widehat{\mathit{x}}}_2\right|\right| {\widehat{y}}_1& ,& 0,& 0,& 0,& 0\\ -\left|\left|{\widehat{\mathit{x}}}_1\right|\right| {\widehat{x}}_2& ,& \left|\left|{\widehat{\mathit{x}}}_2\right|\right| {\widehat{x}}_1& ,& 0,& 0,& 0,& 0\end{array}\right]$$

Hence, smaller Jacobian matrix

$${\mathit{J}}_{\mathit{t}}:=\frac{\partial \mathit{s}}{\partial \mathit{t}}\left(\widehat{\mathit{t}}\right)=\frac{1}{{\widehat{\mathit{x}}}_2^T·{\widehat{\mathit{x}}}_1^{\perp }}\left[\begin{array}{c}-\left|\left|{\widehat{\mathit{x}}}_1\right|\right| {\widehat{\mathit{x}}}_2^{\perp }, \left|\left|{\widehat{\mathit{x}}}_2\right|\right| {\widehat{\mathit{x}}}_1^{\perp }\end{array}\right]$$

(13)

of type $2\times 2$ can be used instead of ${\mathit{J}}_{\mathit{u}},$ and the formula of error propagation (12) changes to

$${\mathit{C}}_{\mathit{s}}={\mathit{J}}_{\mathit{t}}·{\mathit{C}}_{\mathit{t}}·{\mathit{J}}_{\mathit{t}}^{\mathit{T}}$$

(14)

The resulting covariance matrix ${\mathit{C}}_{\mathit{s}}$ can be graphically visualized by means of mean error ellipse.

Size and orientation of the ellipse, which are associated with the covariance matrix,

$${\mathit{C}}_{\mathit{s}}=:\left[\begin{array}{lll}{c}_{1,1}\hfill & ,\hfill & c_{1,2}\hfill \\ c_{1,2}\hfill & ,\hfill & c_{2,2}\hfill \end{array}\right]$$

can be computed by

$$\begin{array}{c}a=\sqrt{\frac{c_{1,1}+c_{2,2}+D}{2}},\hfill \\ b=\sqrt{\frac{c_{1,1}+c_{2,2}-D}{2}},\hfill \\ \phi =\frac{1}{2}\left(\arctan \left(\frac{2c_{1,2}}{c_{1,1}-c_{2,2}}\right)+\pi \cdot \mathrm{ind}(c_{1,1}-c_{2,2}<0)\right),\hfill \end{array}$$

(15)

where

a	…	main axis size of the ellipse,
b	…	semi axis size of the ellipse,
φ	…	orientation of the main axis (in radians),
D	…	discriminant of the covariance matrix, $D :=\sqrt{{(c_{1,1}-c_{2,2})}^2+4c_{1,2}^2}.$
ind	…	dicator function, $\mathrm{ind}\left(\mathrm{true}\right):=1,\mathrm{ind}\left(\mathrm{false}\right):=0.$

Mean error ellipses of different displacement vectors have the same shape, size and orientation since Jacobian matrix ${\mathit{J}}_{\mathit{t}}$ (13) does not depend on LOS displacements $\left[t_1, t_2\right]$. It is apparent in Figure 5a where the vertical angles of radar directions are assumed to have values ${30}^{\circ }$, ${150}^{\circ }$. Midpoints of the ellipses are located at selected, evenly distributed endpoints of displacement vectors.

2.3.2. The Case When Imprecision of LOS Directions Is Considered

Accuracy characteristics of the all input quantities $t_1, t_2, x_1, y_1, x_2, y_2$ is represented by full covariance matrix ${\mathit{C}}_{\mathit{u}}$ introduced by (10). In this general case, it is convenient to divide Jacobian matrix ${\mathit{J}}_{\mathit{u}}$ into three submatrices and treat it as the block matrix.

$${\mathit{J}}_{\mathit{u}}=:\left[ {\mathit{J}}_{\mathit{t}} , {\mathit{J}}_{xy,1} , {\mathit{J}}_{xy,2} \right]$$

(16)

Submatrix ${\mathit{J}}_{\mathit{t}}$ was introduced in (13), and submatrices ${\mathit{J}}_{xy,1} , {\mathit{J}}_{xy,2}$ can be obtained after derivation of (9) with respect to $x_1, y_1, x_2, y_2$.

$${\mathit{J}}_{xy,\mathrm{i}}:=\left(\left|\left|{\widehat{\mathit{x}}}_{3-i}\right|\right| {\widehat{t}}_{3-i}-\frac{{\widehat{\mathit{x}}}_1^T·{\widehat{\mathit{x}}}_2}{\left|\left|{\widehat{\mathit{x}}}_i\right|\right|}{\widehat{t}}_i \right)\frac{{\widehat{\mathit{x}}}_{3-i}^{\perp }·{({\widehat{\mathit{x}}}_i^{\perp })}^T}{{({\widehat{\mathit{x}}}_2^T·{\widehat{\mathit{x}}}_1^{\perp })}^2}.$$

(17)

Matrix ${\mathit{J}}_{xy,\mathrm{i}}$ evaluated for $i\in \left\{1, 2\right\}$ and for known components of vector $\widehat{\mathit{u}}$ can then be used as submatrix in (16). Thus, Jacobian matrix ${\mathit{J}}_{\mathit{u}}$ can be compiled as (16) orders and entered into formula of error propagation. Finally, the required covariance matrix ${\mathit{C}}_{\mathit{s}}$ can be computed with the aid of known covariance matrix ${\mathit{C}}_{\mathit{u}}$ by means of (12).

The resulting covariance matrix ${\mathit{C}}_{\mathit{s}}$ in the general case can be visualized by means of mean error ellipse as well. Parameters of the ellipses can be computed by Formulae (15). These ellipses are drawn in Figure 5b. Their midpoints are located at endpoints of displacement vectors $\mathit{s}$ as in the previous case. Unlike the previous case, shapes of the ellipses differ since the corresponding covariance matrix ${\mathit{C}}_{\mathit{s}}$ depends on LOS displacement $\mathit{t}$ as can be seen in the expression of Jacobian submatrices (17).

2.3.3. The Case of Placing Radars behind Each Other

It is possible to locate the radars behind each other if the choice to put them under the opposite end of the bridge is not possible. Enough appropriate space under the selected end of the bridge has to be available to direct both radars at the region of interest on the bridge. Accuracy of the displacement depends on the distance of radars because the distance influences difference between the vertical angles of radar directions. Covariance matrix ${\mathit{C}}_{\mathit{s}}$ of the displacement vector can be computed by means of (12) as in the previous cases. Corresponding error ellipses for vertical angles ${10}^{\circ }$, ${30}^{\circ }$ of radar directions are shown in Figure 6.

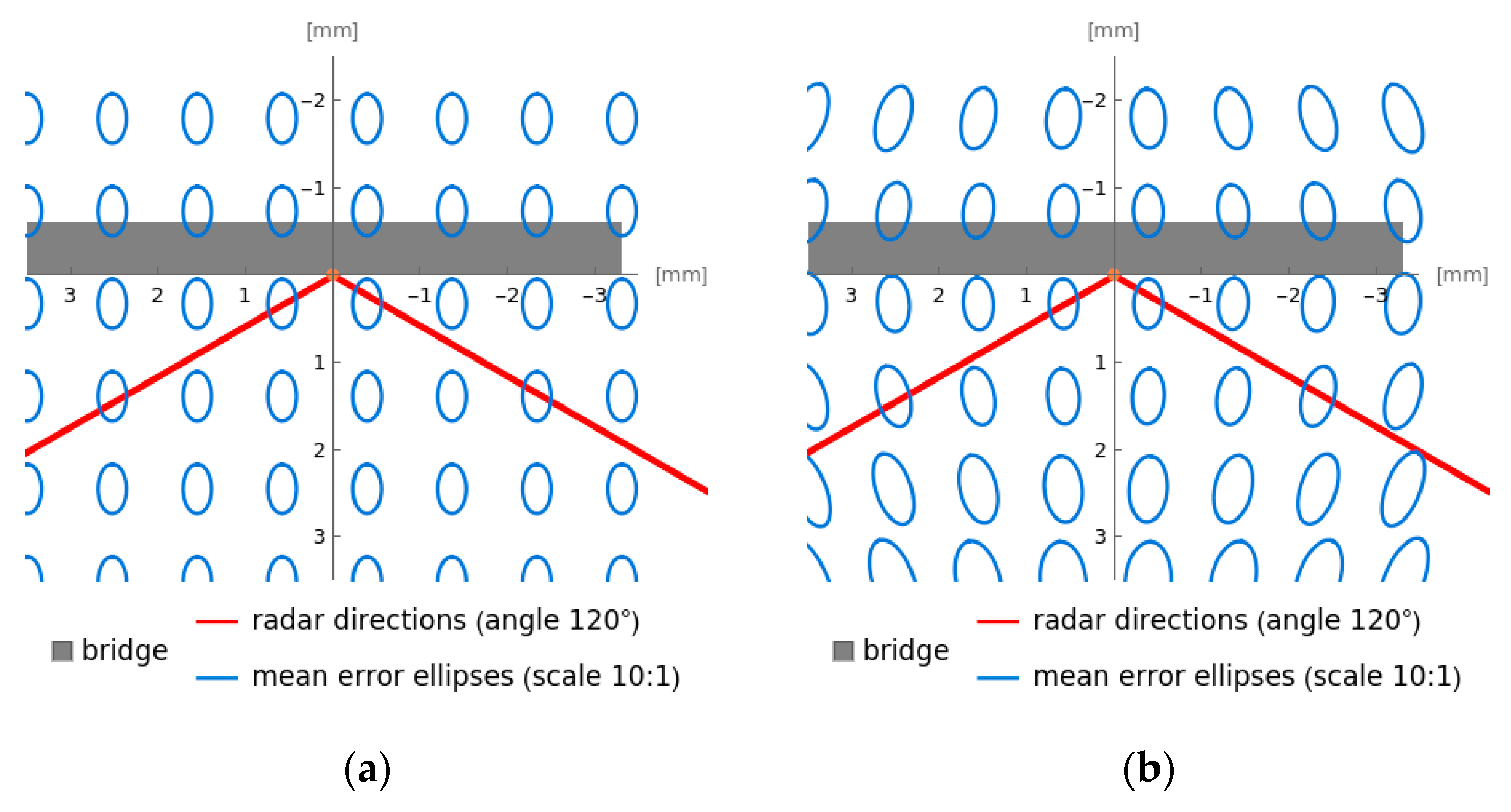
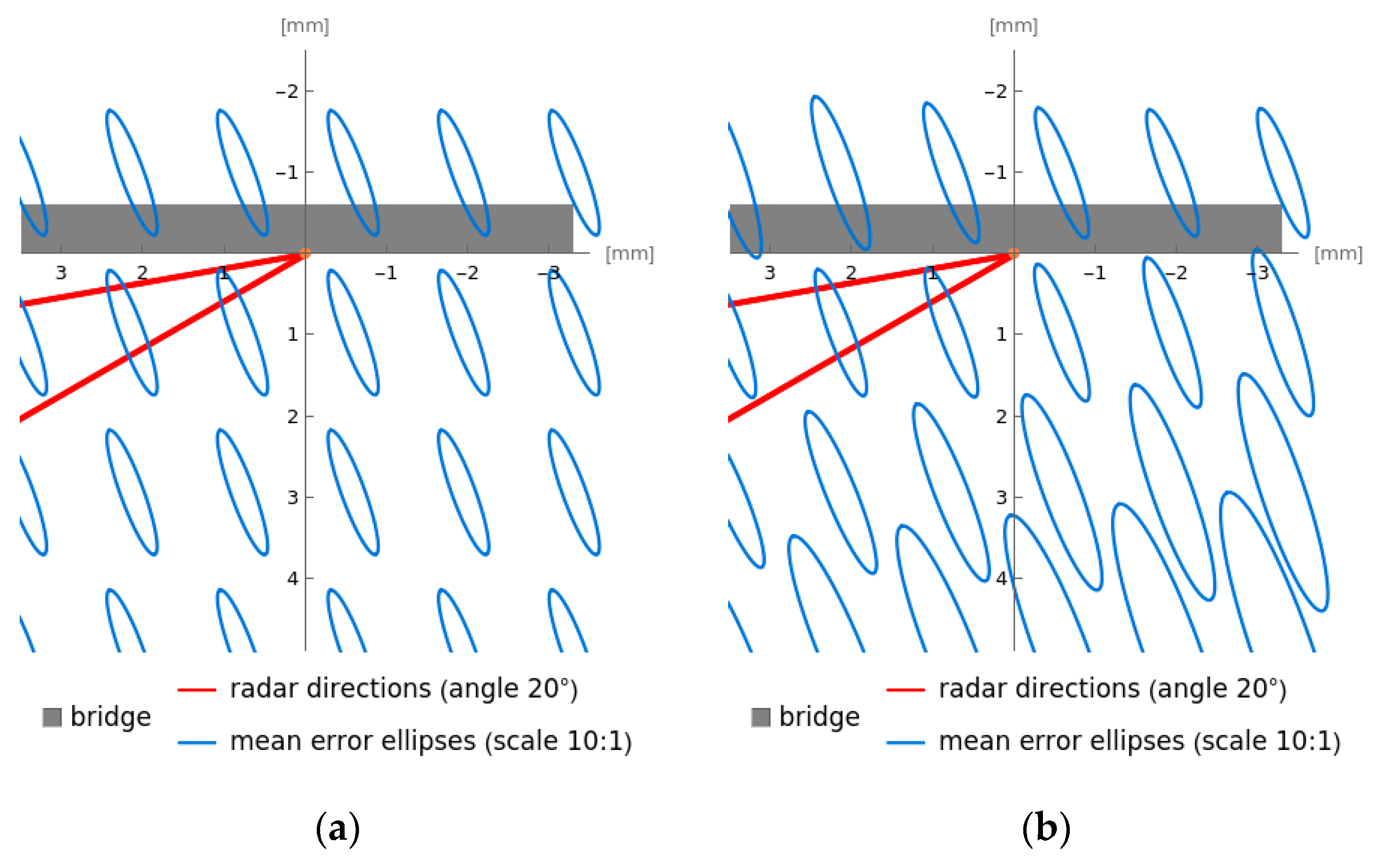
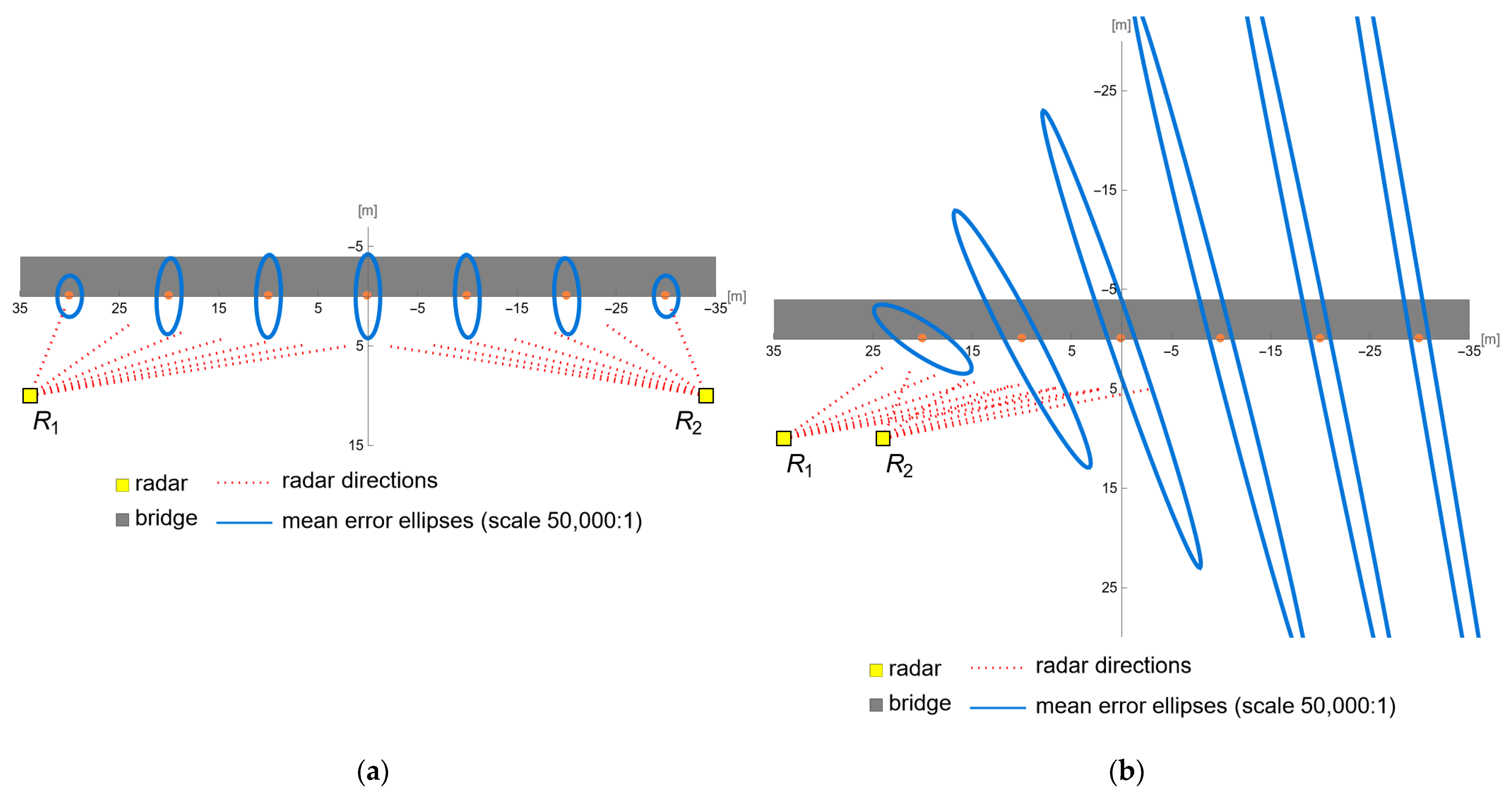
2.3.4. Accuracy Analysis in Different Locations of the Monitored Bridge

The accuracy of determining the displacement vector also depends significantly on the position of the monitored point on the bridge, since this position influences the vertical angles of the radar directions. Graphical representation of the accuracy in Section 2.3.2 and Section 2.3.3 is shown in Figure 7. It is apparent there that Section 2.3.3 when the radars are located behind each other is much less suitable for long bridges than Section 2.3.2. For clarity, the mean error ellipses are drawn for purely vertical displacement $s_Y=5.0 \mathrm{mm}$ and for precision $0.2 \mathrm{m}$ of radar positions (imprecision of LOS directions is considered by precision of radar positions). Other features of this figure are the same as in Figure 5 and Figure 6 (except angles).

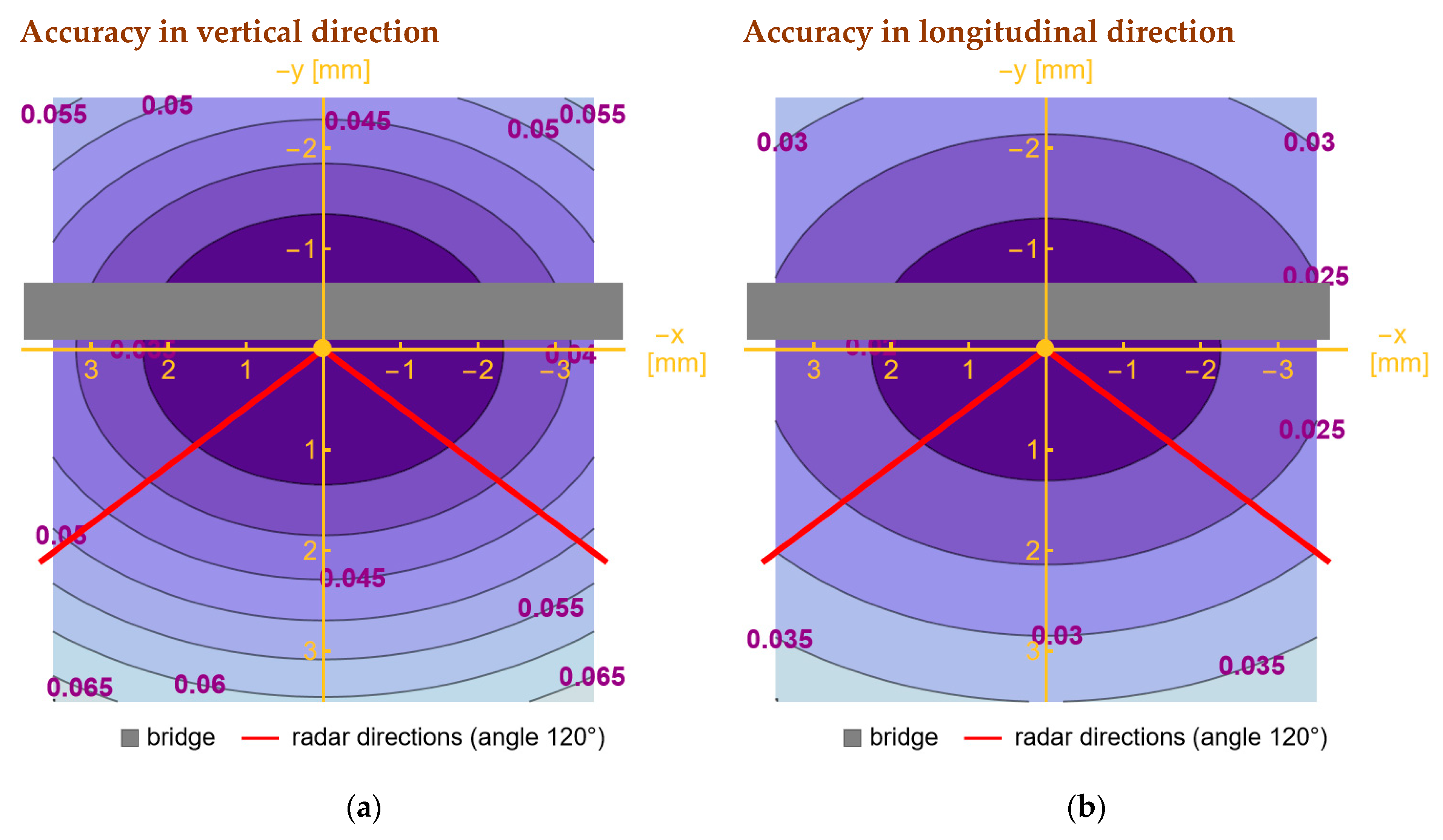
2.3.5. Accuracy Analysis Separately in Vertical and Longitudinal Directions

It is usually required to know the displacement of a point on the bride just in one direction (vertical or longitudinal). Therefore, the precision of the single component of the displacement vector has to be estimated independently of the other. In such a case, marginal probability distribution of the displacement vector has to be evaluated. Since normal (Gaussian) distribution is assumed, diagonal elements of covariance matrix ${\mathit{C}}_{\mathit{s}}$ can be directly used. Thus, longitudinal standard deviation ${\sigma }_x$ and vertical standard deviation ${\sigma }_y$ can be easily obtained as

$${\sigma }_x=\sqrt{c_{1,1}} , {\sigma }_y=\sqrt{c_{2,2}} .$$

(18)

Distribution of values of the standard deviations ${\sigma }_x$, ${\sigma }_y$ is depicted as a contour plot in Figure 8 and Figure 9. Isolines of the contour plot are marked by values in mm of ${\sigma }_x$ (right), resp. ${\sigma }_y$ (left).

2.3.6. Summary of Accuracy Analysis Findings

Accuracy of the displacement vector is characterized by covariance matrix ${\mathit{C}}_{\mathit{s}}$. It was derived for two different cases:

• Imprecision of LOS directions is neglected—covariance matrix ${\mathit{C}}_{\mathit{t}}$ is given (Section 2.3.1).
• Precision of LOS directions is considered—covariance matrices ${\mathit{C}}_{\mathit{t}}$, ${\mathit{C}}_{xy}$ are given (Section 2.3.2).

Evaluation of covariance matrix ${\mathit{C}}_{\mathit{s}}$ in both cases is concisely summarized in the following

Table 2. Summary of the evaluation of covariance matrix ${\mathit{C}}_{\mathit{s}}$.

Case	${\mathit{C}}_{\mathit{s}}$	Substitutions
LOS imprecision neglected	${\mathit{J}}_{\mathit{t}}\cdot {\mathit{C}}_{\mathit{t}}\cdot {\mathit{J}}_{\mathit{t}}^T$	(14), (13)
LOS precision considered	${\mathit{J}}_{\mathit{u}}\cdot {\mathit{C}}_{\mathit{u}}\cdot {\mathit{J}}_{\mathit{u}}^T$	(12), (10), (16), (13), (17)

.

Graphical illustration of accuracy of determining the displacement vector computed by Formula (4) offer Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. Figure 5, Figure 6, Figure 8 and Figure 9 demonstrate how this accuracy depends on the size and direction of the displacement vector (in case when imprecision of LOS directions is considered). Figure 7 demonstrate how this accuracy depends on the difference between the vertical angles of radar directions (on the position of the monitored point on the bridge). It practically means that the accuracy is sensitive to mutual configuration of the radars, the region of interest on the bridge and also on the size and direction of the displacement vector. Therefore, as Figure 7 shows, positioning of the radars at opposite ends of the bridge is more convenient then positioning them behind each other.

2.4. Experimental Measurement in Order to Verify Theory

In order to verify the above theory, experimental measurements of two bridges were carried out. In the first case, it was the arch road bridge over the Labe River in the Valy municipality, Czechia. Here, a configuration of placing the radars against each other was used. In the second case, it was the railway bridge in the Púchov municipality, Slovakia, where the configuration of placing the radars behind each other was used.

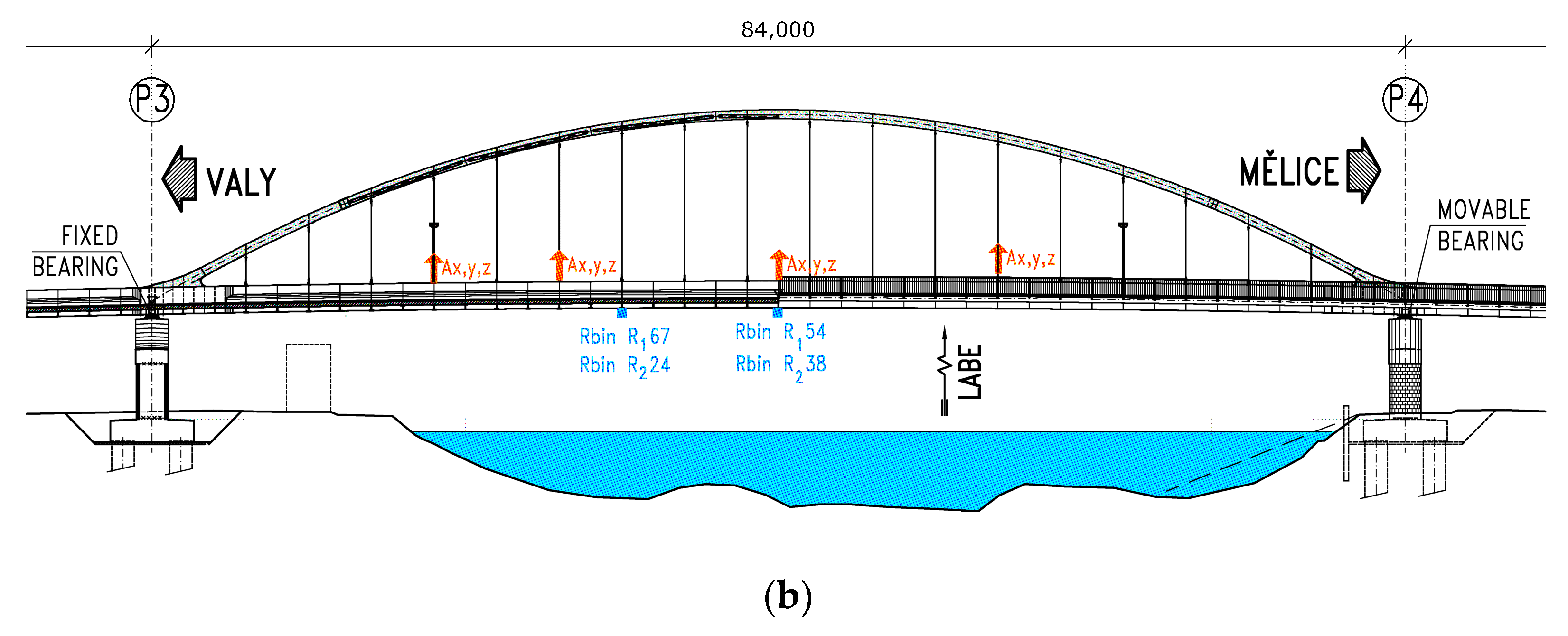
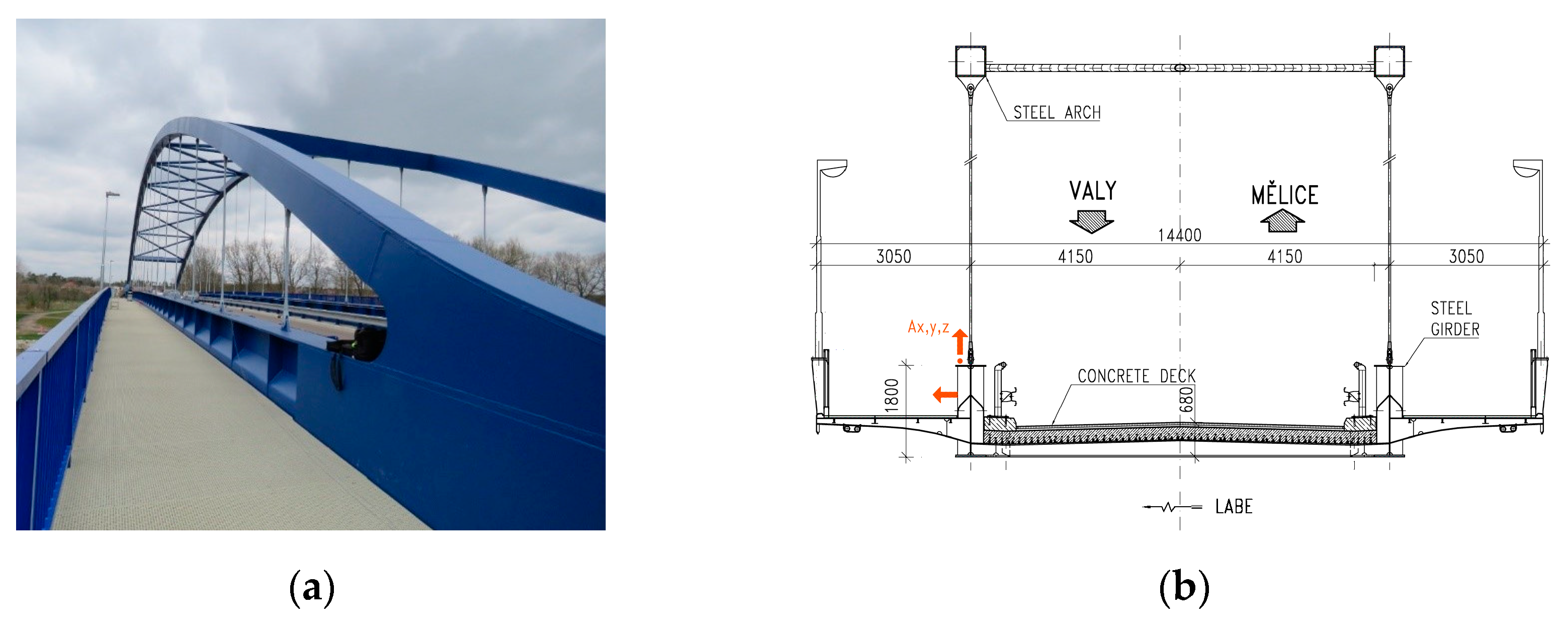
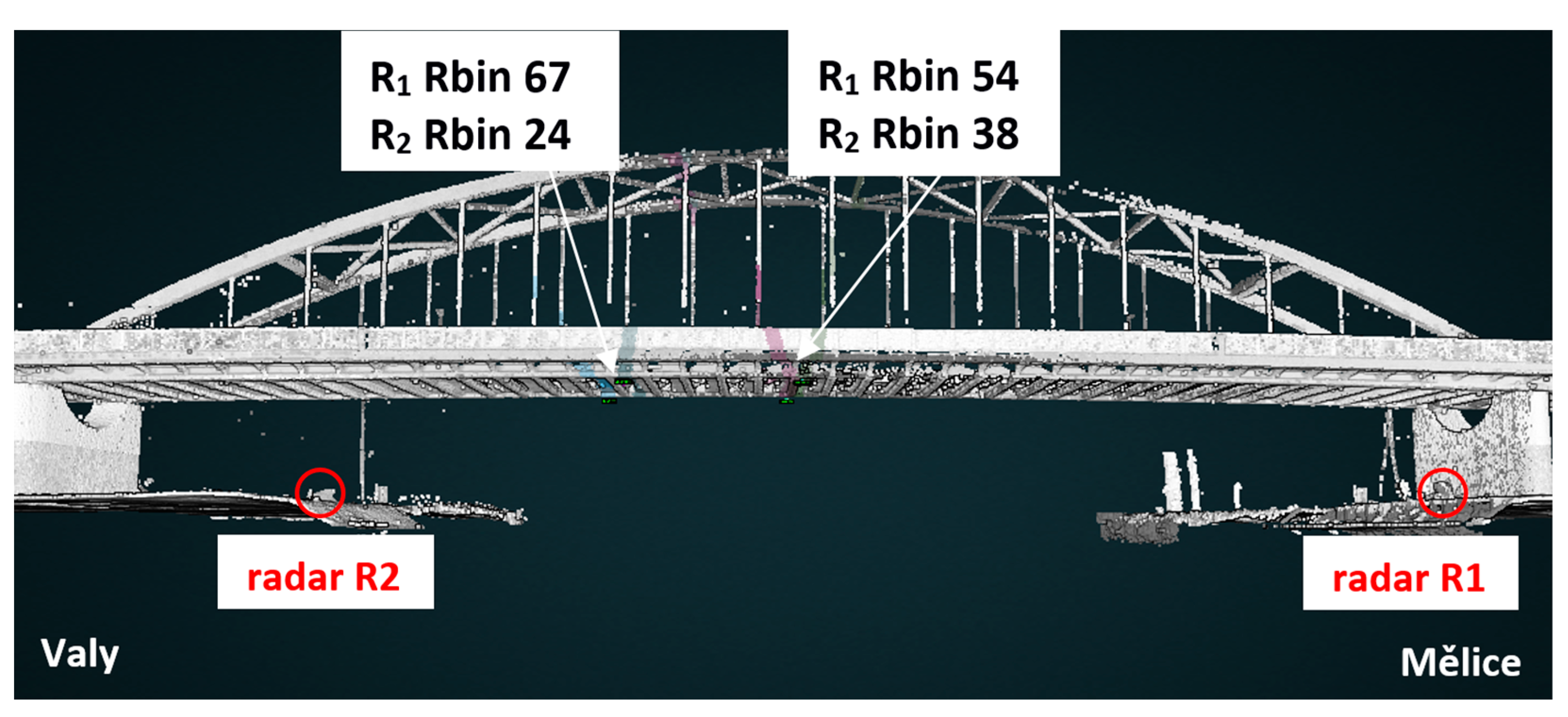
2.4.1. Experimental Measurement of the Arch Road Bridge “Valy”

The first reported example of the experimental dynamic analysis in order to verify theory of the measurement by two radars was performed on the road bridge across the Labe River at Valy municipality in Czechia that was put into operation in June 2020 (Figure 10).

Basic objective of the experiment, that was carried out in mid-August 2020, was to verify the new approach to measure dynamic response of a bridge by radar interferometry utilizing two synchronized radars. The vibrations of the bridge were observed concurrently by both radar interferometry and classical approach realized by high-sensitive piezoelectric accelerometers. Additionally, the fundamental natural frequencies were also evaluated.

Description of the Observed Bridge

The observed structure is the bridge with five spans 23.1 m, 31.5 m, 84.0 m, 31.5 m and 23.1 m long. The main load-bearing structure is formed by a five-span continuous tied-arch, this structural system is also called the Langer beam (Figure 10).

A steel-concrete composite bridge deck is spanned between two identical I-shaped steel main girders in the bridge cross-section (Figure 11). The lost formwork made from ultra-high performance concrete (UHPC) was used for the deck concreting. The steel crossbeams are coupled with the concrete deck using the shear connectors. The main girders have constant height 1.80 m, and the width of their bottom and top flange is 600 mm. The web is covered on both sides by the 8 mm thick steel protective shroud. The concrete deck thickness including the lost formwork is 250 mm. The road width between crash barriers is 6.50 m. Bridge walkways are located on cantilevers outside the main girders and their width is 2.50 m. The total width of the whole bridge cross-section is 13.90 m.

The dimensions 600 mm × 600 mm of the welded square box cross-section of the arch are uniform along the whole arch span, except the short part in the connection to the girder on arch ends (Figure 11). The steel bar-type arch hangers (Figure 11) are made of S460. The main girders, crossbeams, and the arches are made of S355.

Used Radar Interferometry Equipment

Two radars’ IBIS Italian manufacturer Ingegneria Dei Sistemi (IDS) were used for the measurements. Radar R1: IDS Radar IBIS—FS Plus, radar R2: IDS Radar IBIS—RU 172. In both cases, IBIS-ANT3-H17V15 antennas were used. More details on radar settings are in

Table 3. Settings of used radars (bridge Valy).

	R1: Radar IBIS—FS Plus	R2: Radar IBIS—RU 172
Sampling frequency	200 Hz	199.2 Hz 1
Signal range (max. distance)	75 m	70 m
Rbin (range resolution area)	0.75 m	0.75 m

¹ The set value was 200 Hz; the actual value (corrected by the radar control software) was 199.2 Hz.

.

During the measurements, climatic conditions were recorded using a data logger and a video recording of the traffic on the road on the bridge was taken. The local situation and position of the radars were mapped by detailed terrestrial laser scanning and subsequently a 3D model was processed.

Used Standard Measuring Equipment

To verify the vibration of the main bridge span measured by the radars the bridge dynamic behavior was observed also by eight piezoelectric acceleration transducers Brüel & Kjær Type 8344 (Figure 12). The working range of these sensors is from 0.2 Hz to 3 kHz. These transducers are very suitable for the dynamic experiments performed on bridges because the lower frequency limit of their working frequency range is low enough and they have very high sensitivity of approximately 2500 mV/g. The expanded uncertainty of the measured acceleration was ±4.5% for the used accelerometers in the frequency range of 0.8 Hz to 200 Hz. A coverage factor k = 2 was used.

The sensors were connected via cables to the 8-channel data acquisition station SIRIUS Type 6ACC-2ACC+ made by DEWESoft. All channels have their own 2 × 24-bit A/D converter (so called DualCore) that allows to measure with dynamic range up to 160 dB. All A/D converters are mutually synchronized due to ensuring simultaneous measurement on all active channels.

During the experiment, the used sampling frequency of the recording data was 256 Hz and the length of the records was the same as for the radar interferometry due to the simultaneous measurements.

The sensors were attached using neodymium magnets to the left main steel beam in the cross-section of the 4th hanger (vertical vibration), the 6th hanger (vertical vibration and horizontal transversal vibration), in the middle of the span (vertical vibration and horizontal both transversal and longitudinal vibration) and in the cross-section of the 13th hanger (vertical vibration and horizontal transversal vibration).

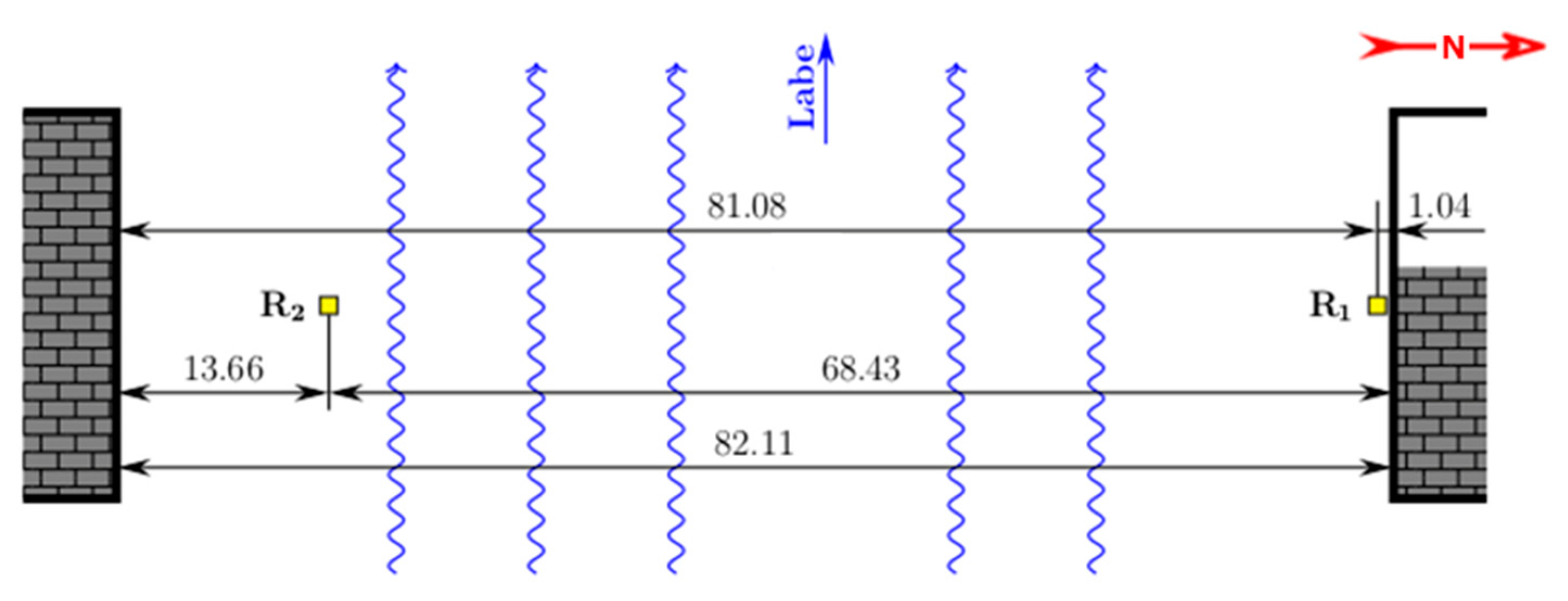
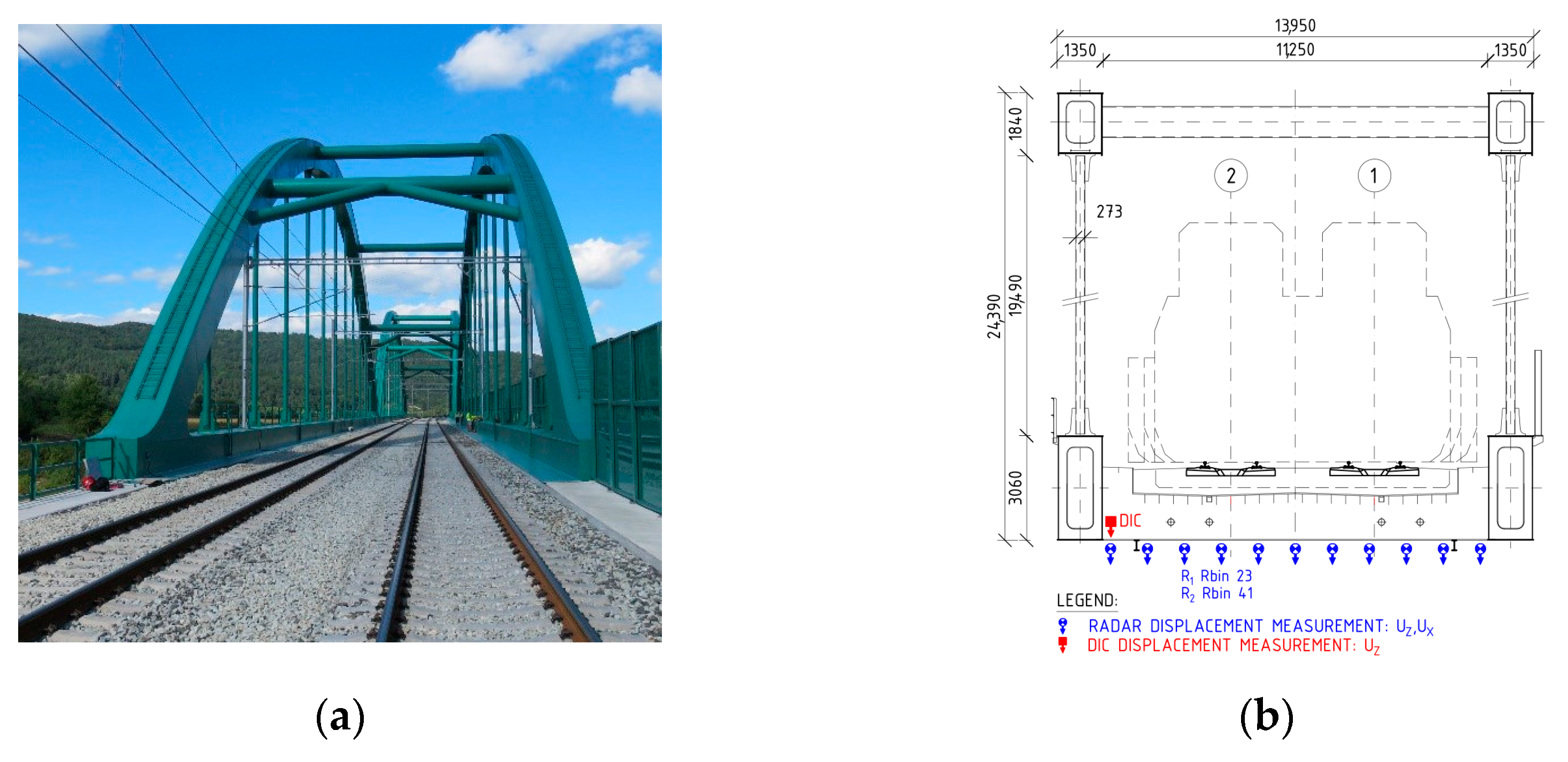
Measurement Configuration

The measurement was performed during normal road traffic on 13 August 2020 in the period from 10:00 am to 11:00 am simultaneously with the standard measuring equipment described in Section “Used standard measuring equipment” and with the radar interferometry equipment described in Section “Used radar interferometry equipment”. Climatic conditions during the measurement: temperature 25.1–26.3 °C, humidity 51.0–55.4%, wind speed 0–1 m/s in a variable direction.

The standard road traffic was not restricted during the experiment. It means that the bridge vibrations measured during the bridge observation were induced only by vehicles passing over the bridge deck and by movement of random pedestrian groups over sidewalks. In addition, vibrations of the bridge were intentionally caused by an organized group of people walking over the bridge several times during the measurements. The walking of pedestrians was generally synchronized. The step frequency was controlled by a metronome, and it was selected to achieve resonance with some fundamental natural frequency of the bridge deck.

The dynamic measurement of the bridge was performed with two interferometric radars simultaneously. Radar R1 was located on the right bank of the river Labe (near the Mělice municipality) by the foot of the bridge support approximately in the axis of the bridge deck. Radar R2 was located on the left bank (near the Valy municipality) closer to the river. The vertical tilt of both radars was determined experimentally to cover the maximum length of the main bridge span and to avoid significant mutual interference of the radar signal. A view of the steel crossbeams of the bridge from the position of the R2 radar is shown in Figure 13. The crossbeams served as natural signal reflectors. A top view of the location of radars under the third (main) span of the bridge is shown in Figure 14.

Significant maxims were selected on the range profiles (SNR profiles) of both radars (Figure 15), which correspond to the positions of the steel crossbeams of the bridge structure. These selected maxims determine the selection of R_bins for evaluation. Only those R_bins that have sufficient signal strength on both radars were selected. Selected R_bins (crossbeams) are highlighted in Figure 16.

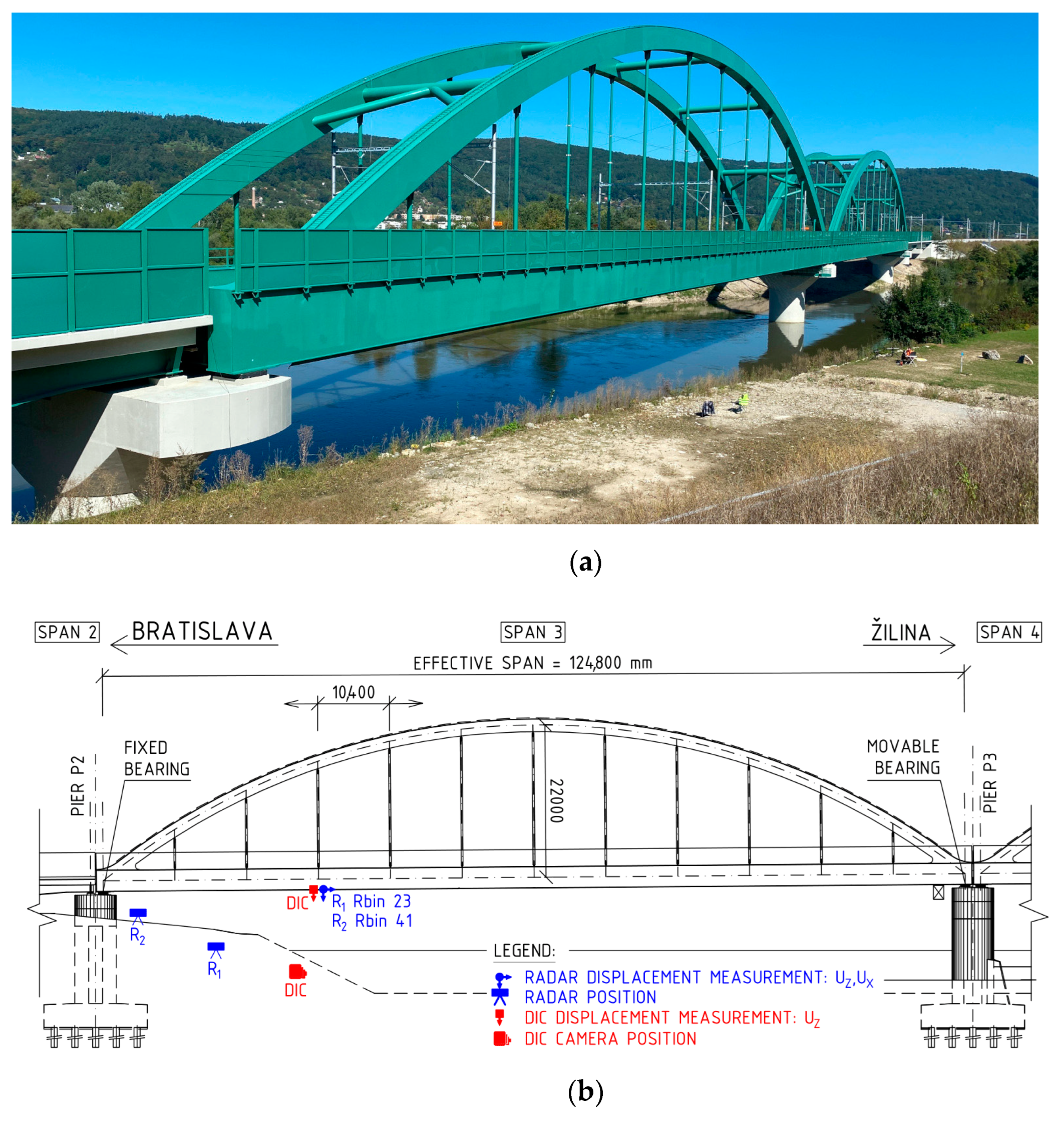
2.4.2. Experimental Measurement of the Railway Bridge “Púchov”

The second reported example of the experimental dynamic analysis in order to verify theory of the measurement by two radars was carried out on the new railway steel arch bridge in Púchov municipality. There were used three different methods. The first one was the usual experimental approach realized only by highly sensitive piezoelectric accelerometers because the standard sensors for determination of relative vertical deflection of the bridge deck could not be installed under the bridge due to the deep water. The other two methods were new approaches to dynamic measurement—ground-based radar interferometry (GBRI) with ground-based real aperture radar (GB-RAR) performed by two synchronized IBIS interferometric radars and photogrammetry method with digital image correlation (DIC), these ones were applied to the measurement of deflection of the superstructure of the bridge. The experiment was carried out in September 2021 on the superstructure BS2 which is a part of the new railway bridge across the Váh River at the Púchov municipality in Slovakia (Figure 17 and Figure 18).

The main purpose of the performed experimental analysis was to determine the dynamic properties of the bridge to verify the results of numerical simulations of the bridge structure before its opening and also to verify applicability of two new approaches GB-RAR and DIC for measurements of the bridge dynamic behavior.

Description of the Observed Bridge

The observed bridge structure is the system of six independent simply supported load-bearing structures with spans 30.6 m, 30.6 m, 124.8 m, 124.8 m, 30.6 m, and 30.6 m long, which are separated by expansion joints. The experiment was performed only on the third superstructure named BS2 (Figure 17 and Figure 18) that is identical with the fourth one, named BS3.

The steel superstructure BS2 is a simply supported through tied-arch structure with the span length of 124.8 m. This structural system is also called the Langer beam. The observed structure BS2 is the double-track railway bridge with the continuous ballasted bed. The bridge deck is orthotropic with crossbeams and stringers. The axial distance of the main girders is 12.60 m, and it is constant along the whole length of the structure. The main welded box-girders are 3.0 m high.

Both arches are in the shape of a circle. The rise of the arches is 22.0 m. The dimensions 1.15 m and 1.71 m of the welded square box cross-section of the both arches are uniform along the whole arch span except for the short part at the connection to the rigid beams on the arch ends (Figure 18). The main beams are supported by the vertical steel bar-type hangers.

During the experiment, the observed dynamic response of the superstructure BS2 was induced by the test train (Figure 19a) that crossed the bridge at different speeds in both directions. The railway vehicles standardly used in the bridge region were selected for the dynamic load test. The bridge vibrations were measured in the course of twenty-two passages of the test train moving in both directions at its different speeds varying from 5 to 100 km per hour.

Used Standard Measuring Equipment

The vibration of the main beams was measured in the course of the experiment by piezoelectric acceleration transducers Brüel & Kjær Type 8344 (Figure 19b). These transducers are the same ones used in the previous example. Likewise, the used data acquisition station, and the connection of the sensors were the same as in the first example.

The scope of the experimental analysis using standard measuring equipment was greater than is described in this paper. However, the selected set of eight accelerometers of type 8344 was used to fulfill the goal of the reported experiment. The accelerometers that measured the bridge vibration in the vertical direction were placed on the top flange of both main beams (Figure 19b) in the first quarter, in the middle and in the third quarter of the span of the structure BS2. The last two accelerometers measured transverse vibrations on the left main beam.

Used Radar Interferometry Equipment

Two synchronized radars were applied for contactless observation of the dynamic deflections on the studied horizontal bearing structure BS2 (Figure 20). The positions of the both radars are marked in Figure 21.

The radar R1 was of type IDS Radar IBIS—FS Plus with antenna IBIS-ANT3-H17V15 (Figure 20a), and the radar R2 was of type IDS Radar IBIS—RU 172 with antenna IBIS-ANT5-H12V39 (Figure 20b).

A bottom view on the bridge deck of the structure BS2 with the steel crossbeams from the position of the radar R1 is shown in Figure 20a. The crossbeams served for both radars as natural signal reflectors.

The sampling frequency was set at 200 Hz on both radars. However, the actual value of the sampling frequency on the radar R2 corrected by the radar control software was 199.2 Hz. More details about settings of radars are in

Table 4. Settings of used radars (bridge Púchov).

	R1: Radar IBIS—FS Plus	R2: Radar IBIS—RU 172
Sampling frequency	200 Hz	199.2 Hz 1
Signal range (max. distance)	100 m	120 m
Rbin (range resolution area)	0.75 m	0.75 m
Vertical tilt of the radar	0.0°	53.9° 1

¹ The R2 radar was tilted more upwards to avoid interference between the radars. This resulted in weak reflections from more distant Rbins, which could not be evaluated by the R2 radar.

.

During the performed experiment, climatic conditions were recorded using a data logger and video records of the test train passages over the bridge were taken. The local situation and position of both radars were mapped by detailed terrestrial laser scanning, and subsequently, a 3D model was processed (Figure 21).

Used Photogrammetric Digital Image Correlation Equipment

The photogrammetric digital image correlation (DIC) is the optical method that was used, as well as GB-RAR, for contactless measurement of the dynamic deflections on the studied superstructure BS2 (Figure 22).

The photogrammetric DIC system produced by Correlated Solutions, Inc. enables potentially 2D or 3D measurements. In the course of the realized experiment, the 2D-DIC system was applied, and two active cameras (Figure 22a) were used to measure the displacement in vertical plane at three selected points on the bridge deck, which were placed in the first quarter, in the middle and in the third quarter of the span of the structure BS2. The steel boards painted by white color and by a black contrasting speckle pattern (Figure 22b) were fixed at the selected observed points on the bottom surface of the bridge deck to improve obtained results.

The sampling frequency of DIC was set at 10 Hz. The evaluation of the experimental results was realized in software VIC-2D produce by Correlated Solutions, Inc. The expanded uncertainty of the measured vertical displacement was ±0.03 mm.

3. Results

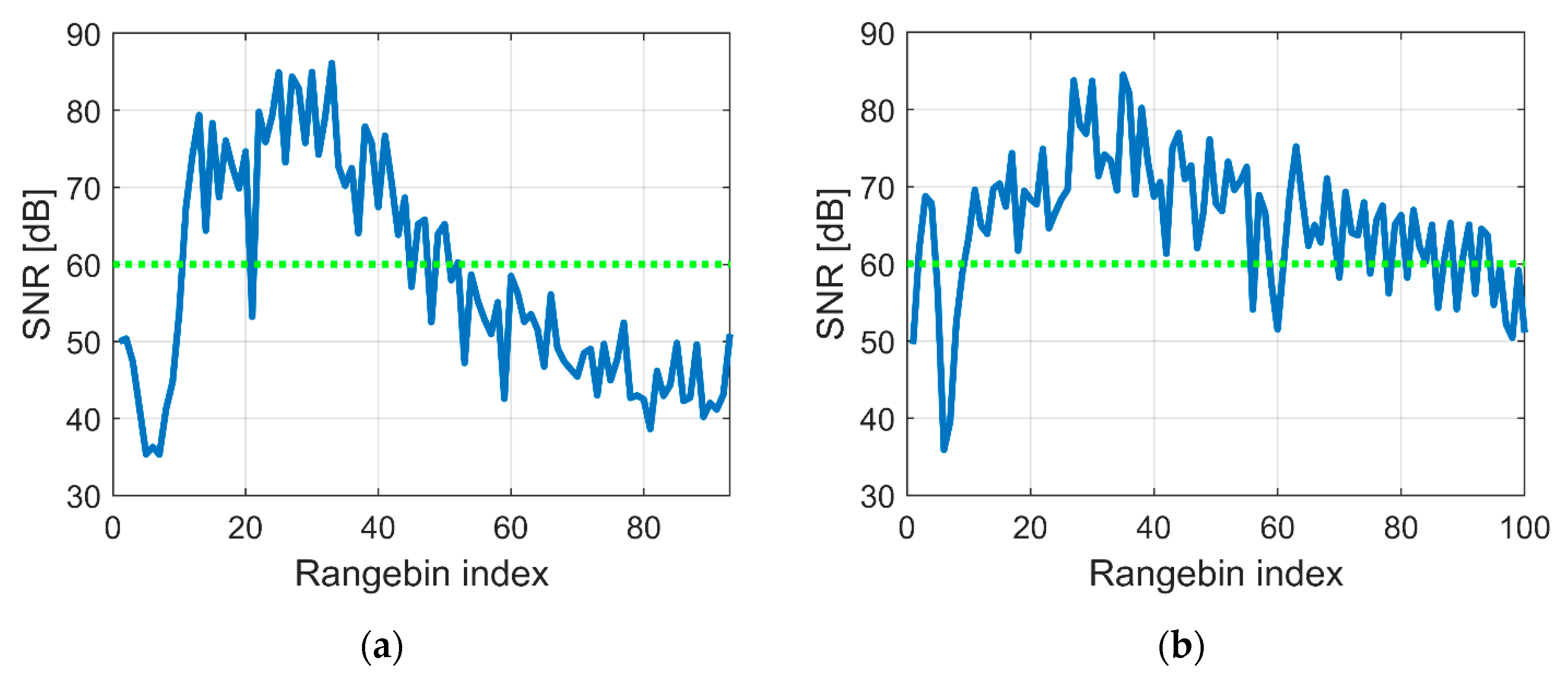
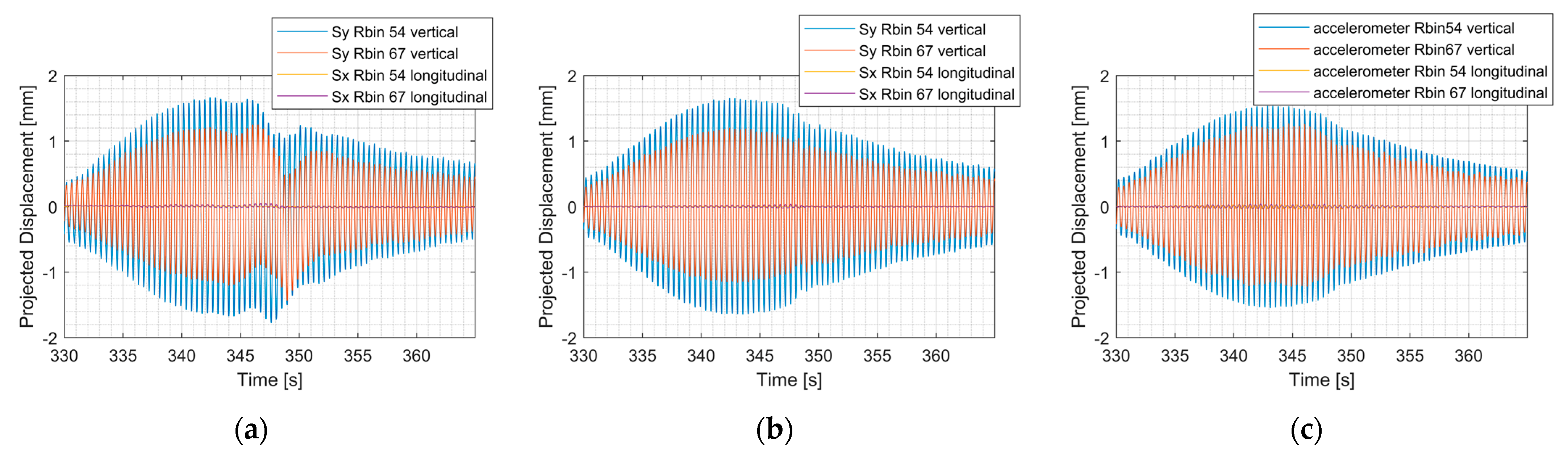
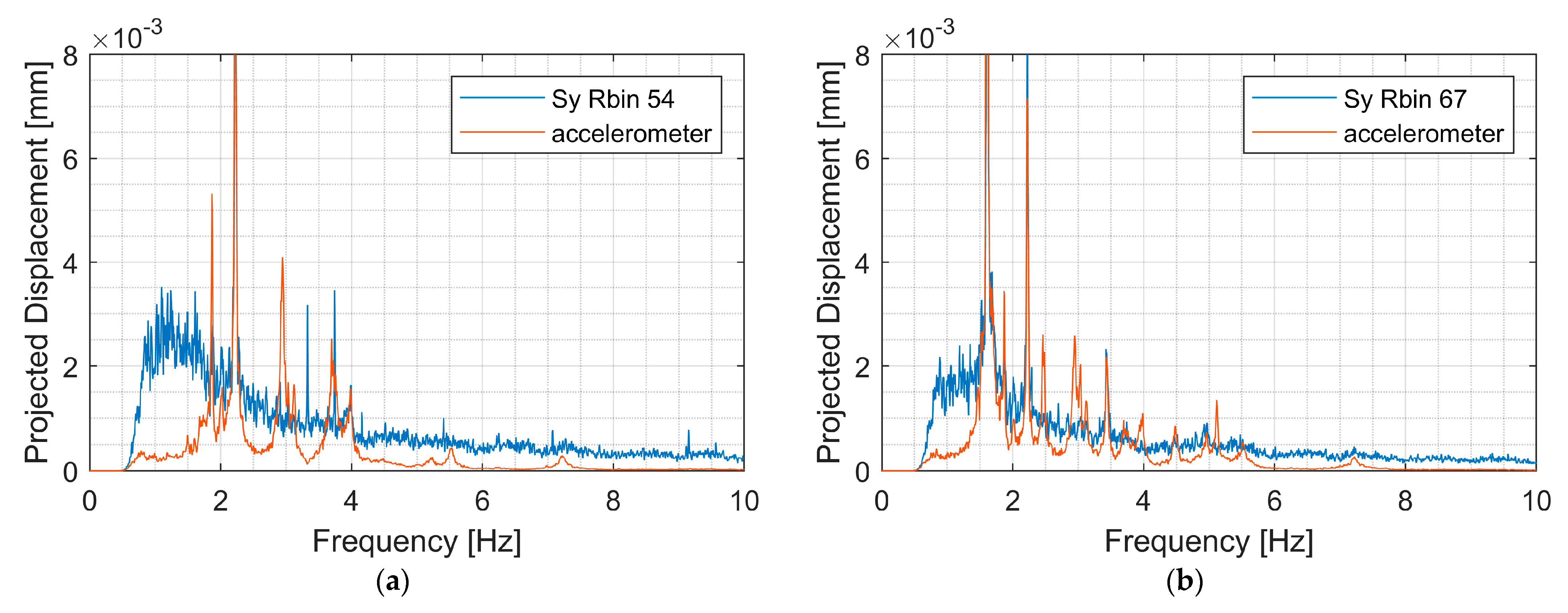
3.1. Tests on the Bridge “Valy”

On the bridge “Valy”, the dynamic behavior in two locations was evaluated, in the middle of the third bridge span and in its one third. In Figure 16, they are labeled as R1 Rbin 54 and R1 Rbin 67. The radar measurements were compared with the results of accelerometers that observed both vertical acceleration and longitudinal acceleration of the bridge at the same locations as the radar. Acceleration was converted to the displacement using double integration in the time domain by application of Simpson’s 3/8 rule, e.g., [35]. In order to compare mutually the displacements measured by the radars and accelerometers, it was necessary to filter out the quasi-static component of the displacements (frequencies between 0 and 0.3 Hz) from the data obtained by the radars, which the used accelerometers of type 8344 cannot capture due to their working frequency range. These displacements without the quasi-static component are labeled dynamic displacements.

For comparison of the results obtained from the measurements performed by only one radar with the experiment carried out by two radars, the displacements evaluated from the original radar measurements including the quasi-static component are also shown in Figure 23. All the vertical and longitudinal displacements calculated by combination of the measured data by both R1 and R2 radars (by Formula (4)) are labeled Sy and Sx in the followed figures (in accordance with Figure 4).

Two time periods were evaluated for the purposes of this article. Vehicle passage in the direction from Mělice to Valy and bridge movements caused by a group of pedestrians walking at regular pace. Figure 23a,c show the vertical displacements including the quasi static component determined by Formula (1) separately from data measured by radars R1 and R2. The longitudinal and vertical displacements including the quasi static component which were calculated by relationship (4) using combination of the data measured by both radars are depicted in Figure 23b,d. Figure 24a,d,g,j then show a comparison of corresponding vertical and longitudinal dynamic displacements calculated using combination of both radar measurements with the ones converted from the observed acceleration data.

It was necessary to correct the vertical displacement obtained from the acceleration data (Figure 24d,j) because of the different positions of the Rbin 67 and the accelerometer (see Figure 10b). It was realized based on the bridge measured mode shapes.

The larger relative differences between the horizontal displacements measured by radar interferometry and accelerometers compared to the differences between the vertical displacements in Figure 24d,j are caused by the very low values of the measured horizontal displacements but also by the different positions of the points observed by accelerometers and radar interferometry in the bridge cross-section (see Figure 10b). In this case, the difference could not be compensated due to the lack of information on cross-sectional properties.

Several statistical tests were performed to prove reliability of the previous results. Confidence probability was set up to custom value 95%. Standard deviation of vertical and longitudinal displacements were computed separately with the aid of covariance matrix as (18) states. Coordinates of radar positions were assumed to be measured with accuracy 0.2 m. Imprecision of LOS displacements were picked up from IBIS Data Viewer software. Standard deviation of LOS displacement measured by radar R1 and R2 was 0.035 mm and 0.031 mm, respectively. Precision of the accelerometers was estimated by a qualified expert. Standard deviation in spatial domain of the accelerometer measurement was assumed to have value 0.02 mm. Confidence intervals for differences of radar and accelerometer measurements are shown in Figure 24b,c,e,f,h,i,k,l. The confidence intervals drawn there seem to be constant. They should be influenced by magnitude of the displacements since covariance matrix ${\mathit{C}}_{\mathit{s}}$ (12) depends on the LOS displacements. Nevertheless, the displacements are so small and so similar in the considered time interval that variability of the bounds (0.01 μ) is in this case below graphical resolution of the figures.

Statistical tests for both components of displacement vector were performed too. Confidence ellipse for probability 95% was used instead of confidence interval. Parameters of the confidence ellipses were evaluated with the aid of covariance matrices that correspond to two used points on the bridge (two steel crossbeams of the bridge structure relevant to Rbin R1 54, and Rbin R1 67). The same data that were shown in Figure 24b,c,e,f were used to create point clusters overlayed by the 95% confidence ellipses. The results of the overlays are shown in Figure 25.

Figure 26 shows the effect of the quasi static components on the total displacement. In this case, the dynamic displacement is mainly induced by the regular pace of a group of pedestrians, and the quasi static component is then caused by the concurrent passage of a vehicle across the bridge. This effect of the quasi static component cannot be registered by accelerometers due to the low limit of their effective frequency range. However, it can be detected by the radar measurements and this fact is the demonstrable benefit of the experiment realized by radar interferometry compared to the one performed by accelerometers. This example also illustrates that it is often not possible to simply compare displacements from radar measurements with displacements from accelerometer ones and that it can be sometimes important to filter out the quasi static component from the data measured by the radars.

To determine the natural frequencies of the observed bridge, a frequency analysis was performed using a discrete Fourier transform (DFT), e.g., [36]. A measurement section of 1035s was used for the calculation. The results of the analysis are the frequency spectra (the periodograms) drawn in Figure 27, which also shows a comparison with the ones evaluated from the accelerometers. Figure 27 shows that radar measurements contain more noise than accelerometer ones and thus cannot detect higher natural frequencies. However, the lower ones have generally the essential importance. In Figure 27, there are also detectable several distinct frequencies (e.g., 3.32 Hz) that are probably the effect of the interference between the signals of both radars.

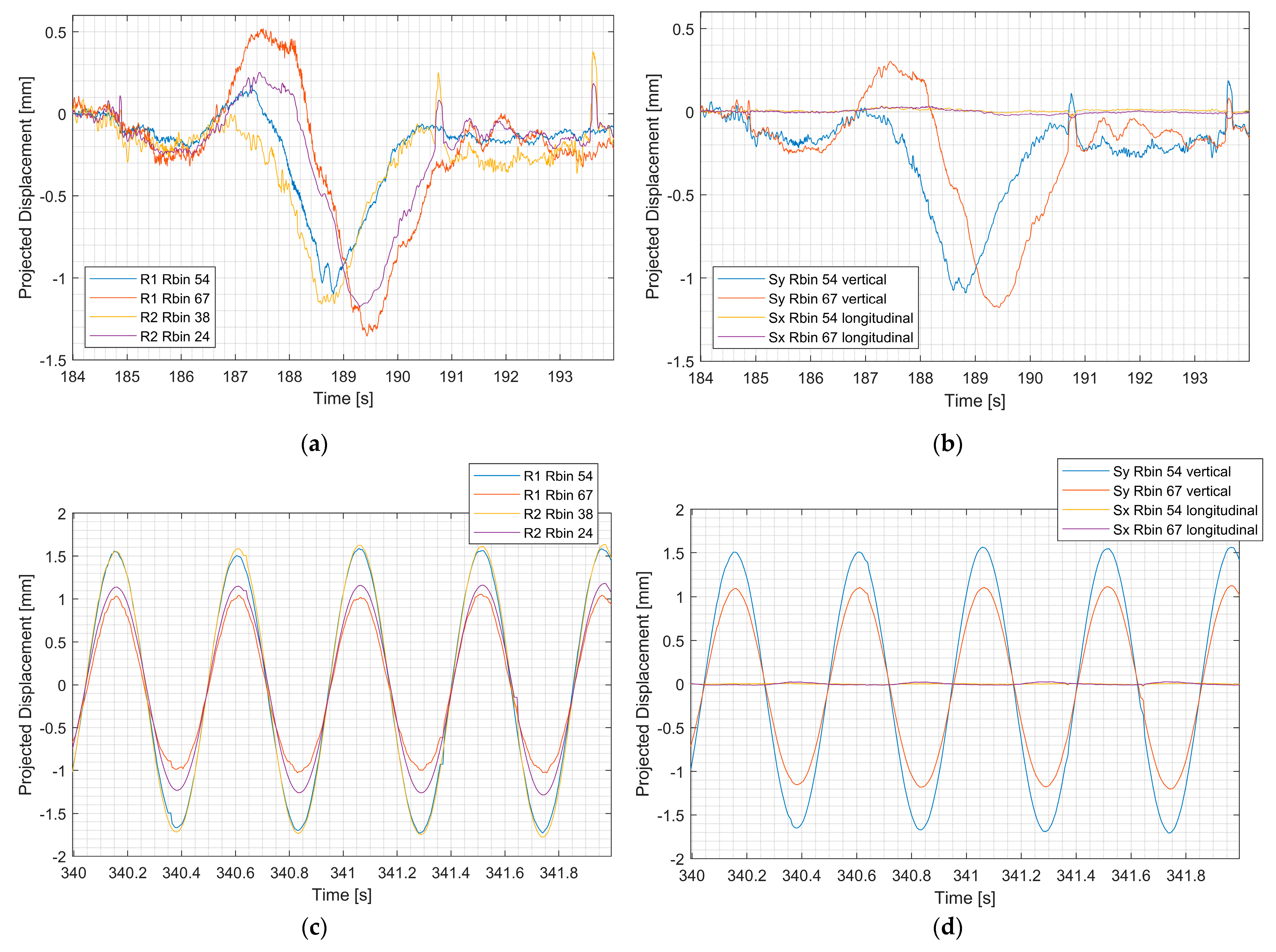
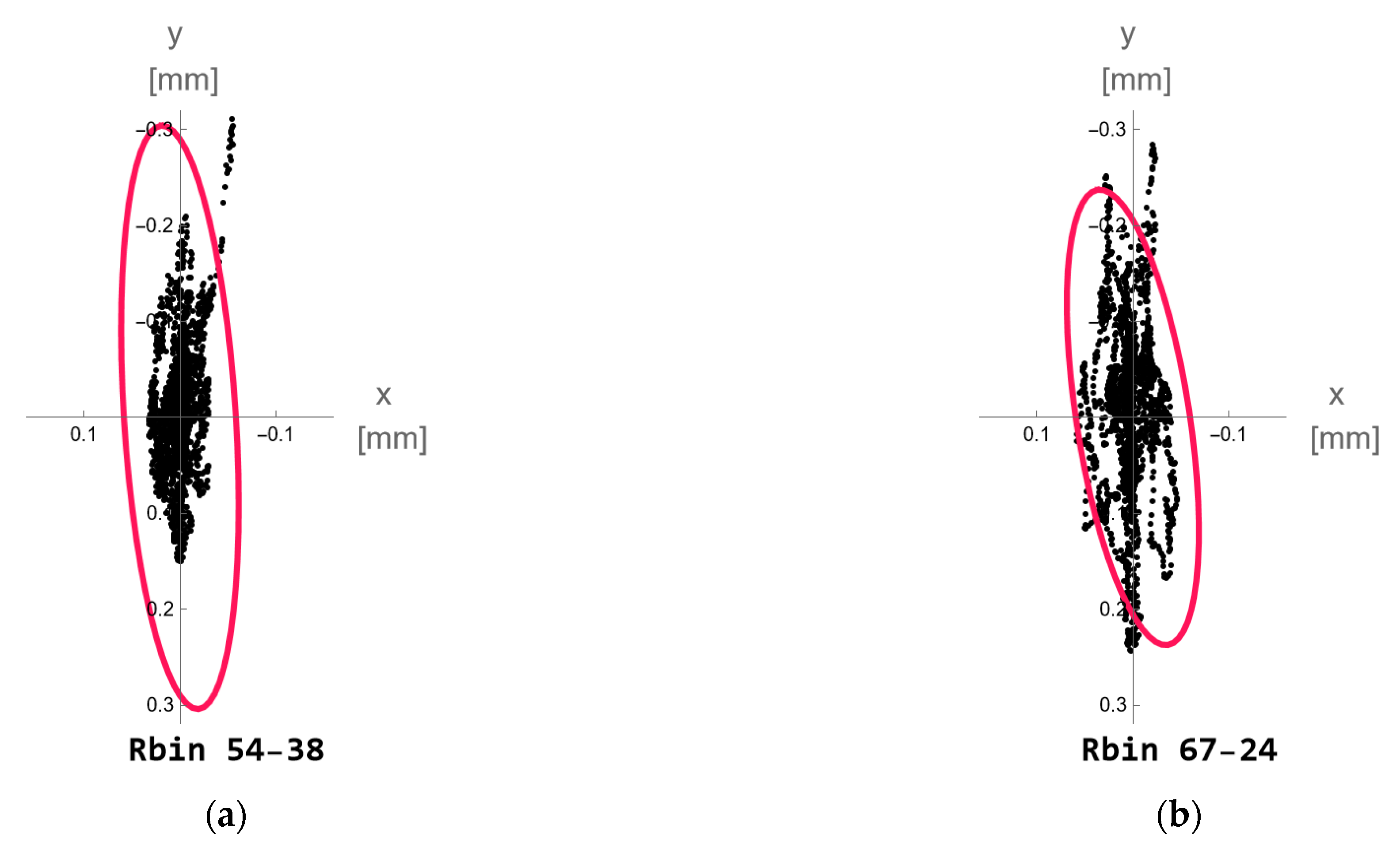
3.2. Tests on the Bridge “Púchov”

On the bridge in Púchov, only one point (crossbeam) in the 1st quarter of the bridge was evaluated from the data measured by both radars (Figure 21) for the purposes of this article. This crossbeam corresponds to Rbins R1 23 and R2 41. Comparing radar measurements with accelerometer ones is not appropriate in this case, because accelerometers do not detect the quasi static component of motion that is dominant in the observed bridge dynamic response to the used dynamic load. For this reason, the photogrammetric digital image correlation (DIC) method was chosen to compare the results of the radar measurement with the results of some other experimental method.

Figure 28a–c show comparisons of the separately calculated (1) vertical displacements that were measured by radars R1 and R2 with the vertical (Sy) displacements calculated by combination of both radar measurements of these radars (4) and with results of the DIC measurement at the same location. At the 2nd row is the comparisons of vertical displacements biases between radar (Sy) and DIC measurements with the confidence intervals. In this case, the influence of the displacement magnitudes on the magnitude of the confidence intervals is significant. This is due to the larger magnitudes of these displacements compared to the bridge “Valy”. Considering that the radars are positioned one behind the other, the magnitude of the confidence intervals at minimum displacements are approximately twice as compared to the intervals in the case of radars positioned opposite each other (compare Figure 24 and Figure 28).

4. Discussion

The main reason for the necessity of using two or more interferometric radars for determining the deflections of bridge structures by the GB-RAR method is the existence of the so-called Interpretation Error E_I (2). This error occurs as a result of assumption about an expected direction of the bridge displacement whenever the expected direction differs from the direction of real total displacement. In common practice, the E_I error can take on values in the tens of % of the magnitude of the determined displacement. In the case of inappropriate geometrical configuration of the radar position and the monitored point, the E_I can acquire unacceptable values, even more than 100%, as shown in Table 1. It is therefore necessary to perform measurements with at least two radar devices that can eliminate the E_I error. This means that when measuring with two radars, a detailed accuracy analysis of determining the total displacements (vertical and longitudinal) according to (4) has to be developed.

The basic requirement for measuring with two radars is the accurate synchronization of the resulting time series of the measured values of LOS displacements acquired by both radars. Commonly used approaches to synchronization that are based on the coincidence of maximal displacement values or, respectively, the correlation of entire time series, are unsatisfactory in general case. Therefore, a new method of time synchronization using the interconnection of service laptops is proposed in this paper. The method can be used even if the maximum displacements occur at different times, which may be caused by a different position of the radar in relation to the monitored object. Other measurement methods, e.g., accelerometric or DIC, can be synchronized by the proposed method as well.

The actual analysis of the accuracy of determining the resulting total displacements according to (4) is performed analytically. The derived mathematical formulae have not been published anywhere yet. The resulting accuracy in determining the total displacements depends on the geometry of the configuration of the radars relative to each other and relative to the position of the point whose displacement is being determined. The configuration is actually given by the LOS inclinations. Furthermore, it depends on the accuracy of determination of these inclinations, the size of LOS displacements and the accuracy of determination of LOS displacements.

If the accuracy of determining the LOS directions is neglected when calculating the accuracy of determining the resulting total displacements, the resulting accuracy will not depend on the size of the LOS displacements. This fact is clearly demonstrated in Figure 5 and Figure 6. However, the accuracy of determining the LOS directions have to be considered in practice.

The influence of the geometry of the mutual configuration of the radars was investigated for two basic radar positions. It turned out that placing the radars opposite each other is much more advantageous than placing the radars one behind the other in terms of the resulting accuracy of the determined total displacements. This fact is clearly demonstrated by comparing Figure 5 and Figure 6, respectively Figure 7a,b.

The influence of the geometry of the radar configuration relative to the position of the point whose displacement is being determined is clearly demonstrated in Figure 7. When the radars are placed opposite each other, the lowest accuracy of determining the resulting total displacements is in the middle of the bridge deck. However, this may not apply exactly in practice, because points on the edge of the bridge deck may have a lower-quality (weaker) reflected signal from a more distant radar. In this case, geometrical and physical influences act against each other. When placing the radars one behind the other, the resulting accuracy decreases significantly as the distance between the monitored point and the radars increases.

Furthermore, mathematical formulae were derived for separate analysis in the vertical and longitudinal directions. Here, too, it was confirmed that the resulting accuracy is significantly lower when the radars are placed one behind the other.

In order to verify the derived mathematical formulae for accuracy of total displacements (Table 2), experimental measurements were carried out in two locations. In the case of the “Valy” road bridge, radars were placed opposite each other, and the results are compared with accelerometric measurements. In the case of the “Púchov” railway bridge, the placement of radars one behind the other was used and the results are compared with the DIC photogrammetric method.

When comparing the differences in the magnitudes of vertical displacements determined independently from the measurements by single radars according to (1), it should be kept in mind that these differences also include Interpretation Errors E_I (Figure 23a,c and Figure 28a–c). These E_I errors are generally different for both radars, and therefore, the resulting vertical displacements cannot be simply averaged.

By comparison of the biases between the total displacements determined from the radar measurements (4) and the displacements from the accelerometric measurement with the calculated confidence intervals and ellipses, it was verified that the expected accuracy of the synchronized measurement by two radars corresponds to the achieved accuracy (Figure 24 and Figure 25). A similar comparison with the same conclusion, this time with displacements from a DIC photogrammetric measurement is demonstrated in Figure 28. It was also verified that the accuracy of their determination decreases with large displacements. This is also demonstrated in Figure 28 and confirms the theoretical findings illustrated in Figure 5b and Figure 6b.

At the same time, it was demonstrated in Figure 26 that it is usually not possible to directly compare displacements determined by radar measurements (GB-RAR) with displacements determined by accelerometric measurements. The reason is that the displacements determined by radar measurements contain both a dynamic and a quasi-static component. However, depending on the parameters of the accelerometers used, the quasi-static component may not be present in the displacements evaluated from the accelerometer measurement or its magnitude may be comparable with influence of some negative side effects on measured data.

More generally, if an existing bridge is investigated, whatever reliable experimental information is important especially when the reliability and aptness of its FEM model should be validated.

Each bridge structure is unique, and the arrangement of the experiment is therefore influenced by the specific parameters of the particular bridge, on which the experimental analysis should be carried out and by the possibilities of the individual experimental methods that are available for the bridge behavior observation.

Each of the experimental method has its advantages and disadvantages. The advantages of ground-based radar interferometry compared with standard experimental methods usually used for displacement observation (such as relative displacement transducers, geodetic methods, digital image correlation method (DIC), inclinometers, or accelerometers) are listed below.

Radar interferometry is suitable for operational rapid use to monitor dynamic and quasi-static displacements. It is thus possible to perform either short-term measurements in the order of a few minutes or long-term measurements in the order of hours, a maximum of a few days. During long-term measurements, problems arise with the stabilization of the radar position and with the continuous storage of a large amount of acquired data.

The application of radar interferometry is particularly beneficial in parts of the bridge deck where it is not possible to place a standard relative displacement transducer. Further, where it is possible to place the radars below the longitudinal axis of the horizontal load-bearing structure and where there are no obstacles (trees or pillars, for example) preventing radar signal propagation.

It is convenient to apply radar interferometry when the measured displacements are particularly large. Radar interferometry is able to measure bridge deflections in the greater range than standard relative displacement transducers that are based on LVDT sensors (±25 mm, for example).

If it is necessary to specify the bridge deflection during the load test, radar interferometry measures it directly unlike accelerometers or inclinometers, where the deflection is evaluated based on the integration of the measured data.

The sampling frequency on contemporary radars can be set up to 200 Hz. This means that the bridge vibration captured by these radars can be applied to investigate the bridge dynamic behavior in the frequency range from 0.0 Hz to about 80 Hz. This frequency range is sufficient for most potential experimental dynamic tasks implemented on bridges and it is larger than the frequency ranges of standard relative displacement transducers.

Both the static and the quasi-static component of the displacement in the observed point on the monitored bridge deck that is induced by the test load can be observed and recorded by radar interferometry. This experimental approach can, therefore, be applied among others to determine the dynamic coefficient. In most cases, the value of the dynamic coefficient is influenced by the vibration components, which correspond to its lowest natural frequencies, and radar interferometry is able to capture them accurately enough.

Radar interferometry observes the vibration of the bridge deck in the displacement measure. This is convenient for the investigation of the lowest natural frequencies and their associated mode shapes, especially on bridges with large spans, whose fundamental natural frequencies are low and, thus, the level of bridge vibration in the acceleration scale is usually low.

The proportion of frequency components of displacements for higher natural frequencies is usually smaller in the recorded vibration compared to the lowest ones; therefore, the application of radar interferometry for the investigation of higher natural frequencies is limited by the level of induced vibration of the observed bridge and by the parameters of the measured signal (e.g., noise level).

The mode shapes of the bridge structure can be investigated by radar interferometry in the structure sector only that is covered by the signal of both radars. When the radars are relocated to various positions during the experiment (for example, in the case of a continuous span bridge into its different spans), it is possible to evaluate the mode shapes in these various separate sectors of the structure, but the parts of the mode shapes obtained in this way are not linked to each other by a unified scale and phase.

All the above-mentioned findings should be kept in mind during the practical measurement of displacements of bridge structures using the GB-RAR method.

5. Conclusions

Until this time, bridge management has been based mostly on periodical visual inspections. However, bridge engineering brings different situations when it is necessary to verify reliability of a bridge structure by an experiment and alternatively the aptness or accuracy of its FEM model. The experiment is carried out, e.g., in the form of a standard static load test, static load test study, experimental modal analysis, standard dynamic load test or dynamic test study.

Radar interferometry being performed using two radars can be applied for measurement of the static and also dynamic displacements in both vertical and horizontal longitudinal directions concurrently in multiple points on bridge decks in the central part of bridge spans. The uncertainties of the measured displacements vary from hundredths, tenths to ones of millimeters, depending on the conditions and the arrangement of a specific experiment. The accuracy of 0.01 mm stated by the radar manufacturer applies only to LOS displacements. The sampling frequency on contemporary radars can be set up to 200 Hz. This means that the bridge vibration captured by these radars can be applied to investigate the bridge dynamic behavior in the frequency range from 0.0 Hz to about 80 Hz.

The aim of the article was to establish a suitable strategy for determining dynamic and quasi-static response of bridge structures based on the accuracy analysis of measurement by two interferometric radars. The use of simultaneous measurement by two radars is necessary to eliminate the so-called Interpretation Error E_I that occurs, with exceptions, when measuring with only one radar. The example in Figure 23a can be used to concretely illustrate the significance of the Interpretation Error E_I in practice. At 187.4 s, the single radars determined a vertical deflection of 0.50 mm (Rbin R1 67) and 0.20 mm (Rbin R2 24). By combining both radar measurements, a vertical deflection of 0.27 mm was determined (Figure 23b). The influence of the Interpretation Error when determining vertical displacements separately by single radars is therefore +46% (radar R1) and −35% (radar R2) in this particular case.

Specific methodology was designed in this article to fulfill two main requirements:

• to highlight necessity of simultaneous usage of two interferometric radars to eliminate the Interpretation Error;
• to achieve the highest possible accuracy in determining the resulting total displacements.

The methodology therefore consists of the following steps:

• description of the current state and analysis of Interpretation Errors E_I when measuring with single radar (see the Section 1);
• presentation of the principles of measurement by two radars with the accuracy analysis of the resulting displacements (see the Section 2.1, Section 2.2 and Section 2.3);
• verification of the results in practice by experimental measurement (see the Section 2.4 and Section 3);
• discussion of the findings and their summary in the Section 4 and Section 5.

For this purpose, analysis of the accuracy of determining the total displacements of bridge structures by simultaneous measuring with two interferometric radars was derived for the first time in the literature. The accomplished results have been verified by practical measurements and demonstrated by practical achievements. Several discussed findings for practice resulting from accuracy analysis were reached. The most important insight from them is that placing radars opposite each other is much more suitable than placing radars behind each other.

The key contribution of this paper is the possibility to estimate and plan in advance the achievable accuracy of the resulting displacements for the given radar configurations in relation to the bridge structure. The derived formulas for the resulting accuracy of the determined displacements can be used in advance to model and calculate the achievable accuracy. This will make it possible to determine the optimal measurement strategy with two interferometric radars and thereby reduce the financial costs of performing measurement and monitoring works.

The next development trend will probably be towards the use of more radars and combining more different measurement methods.