Estimation of Moist Atmospheric Profiles from Refraction and Attenuation Measurements by Using Centimeter and Millimeter Wave Links between LEO Satellites
Abstract
1. Introduction
2. Principles and Methods
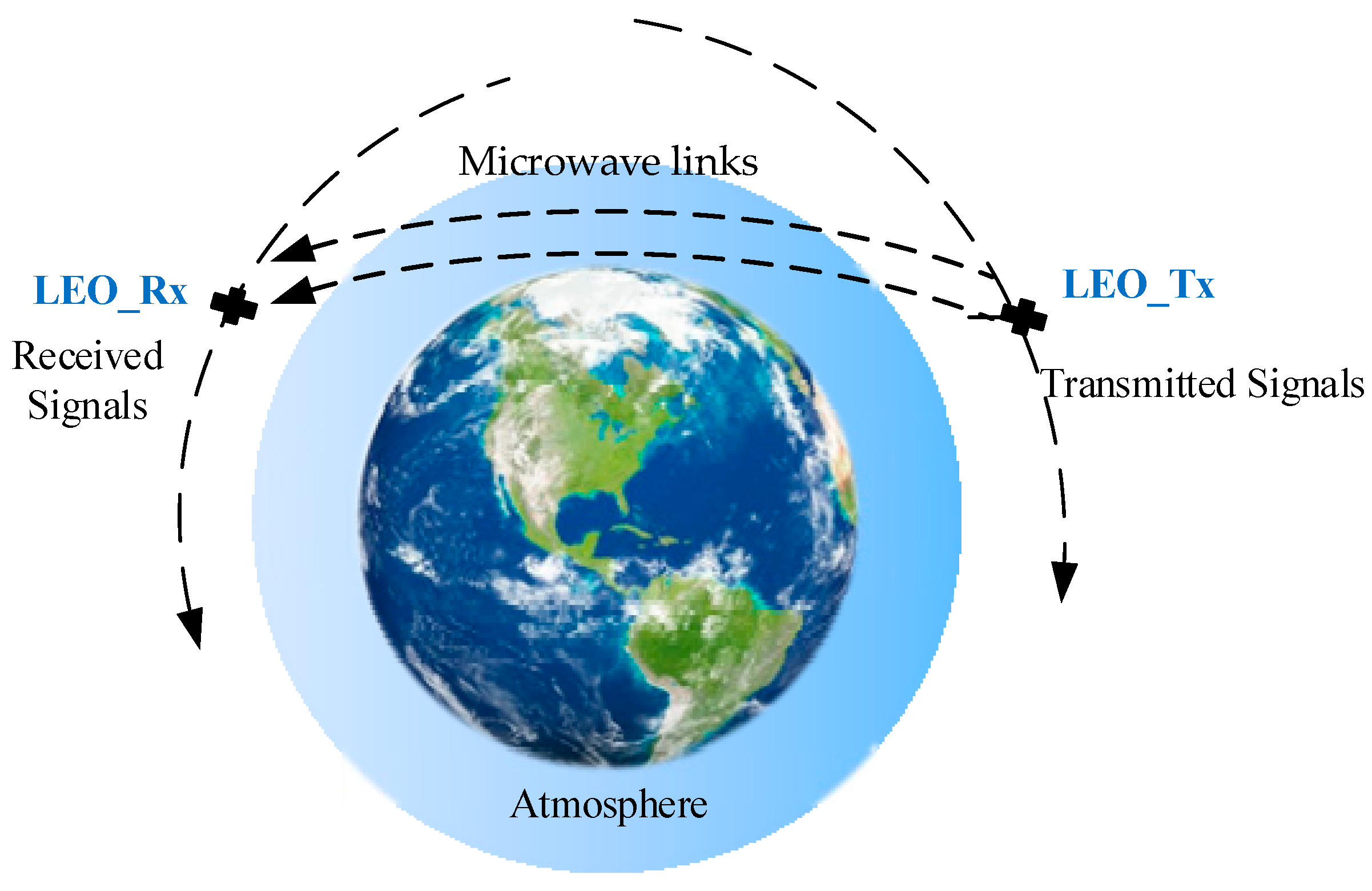
2.1. Measurement Theory
2.2. Double Differential Absorption Approach
2.3. Forward Propagation Model
3. Results
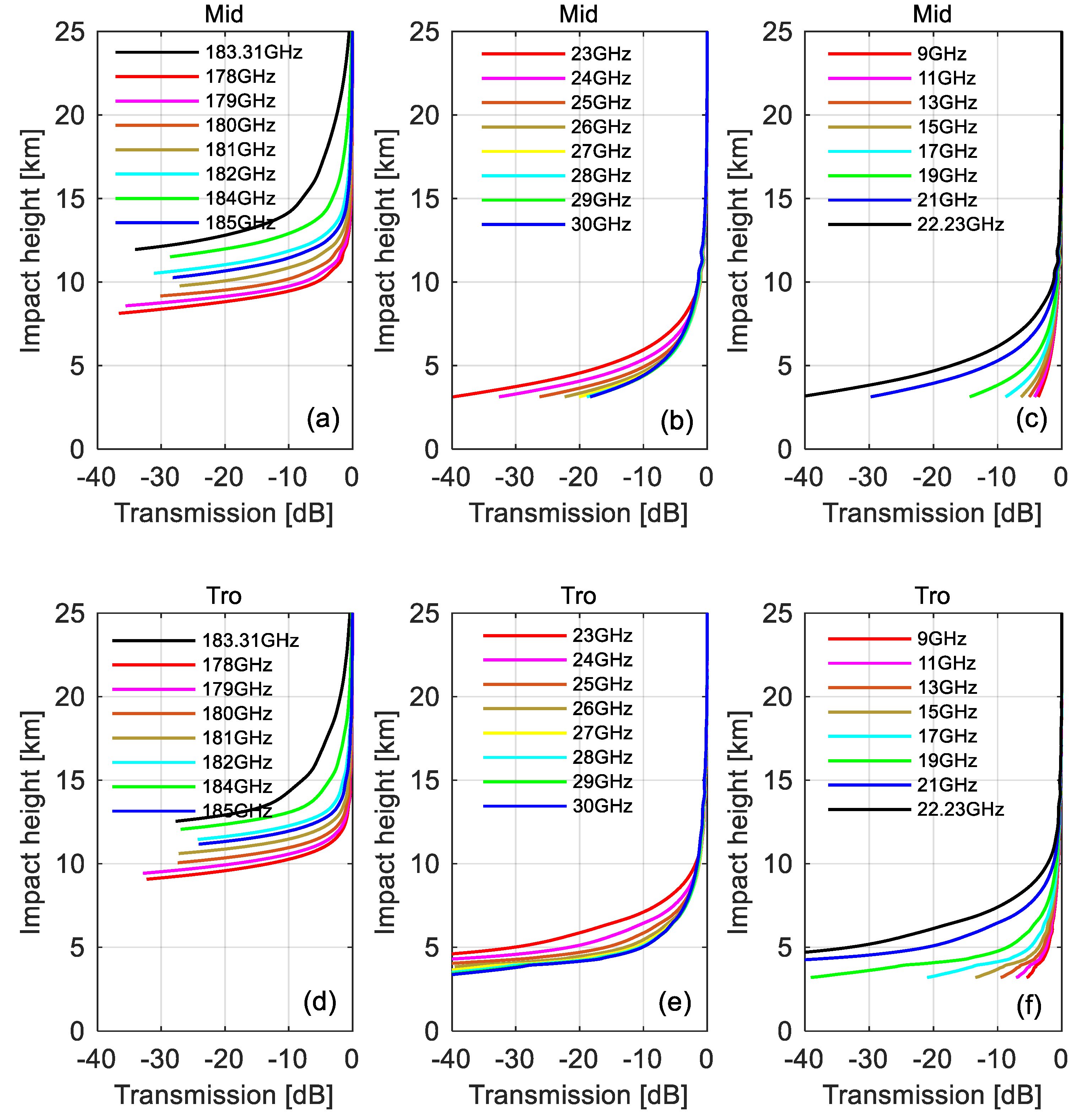
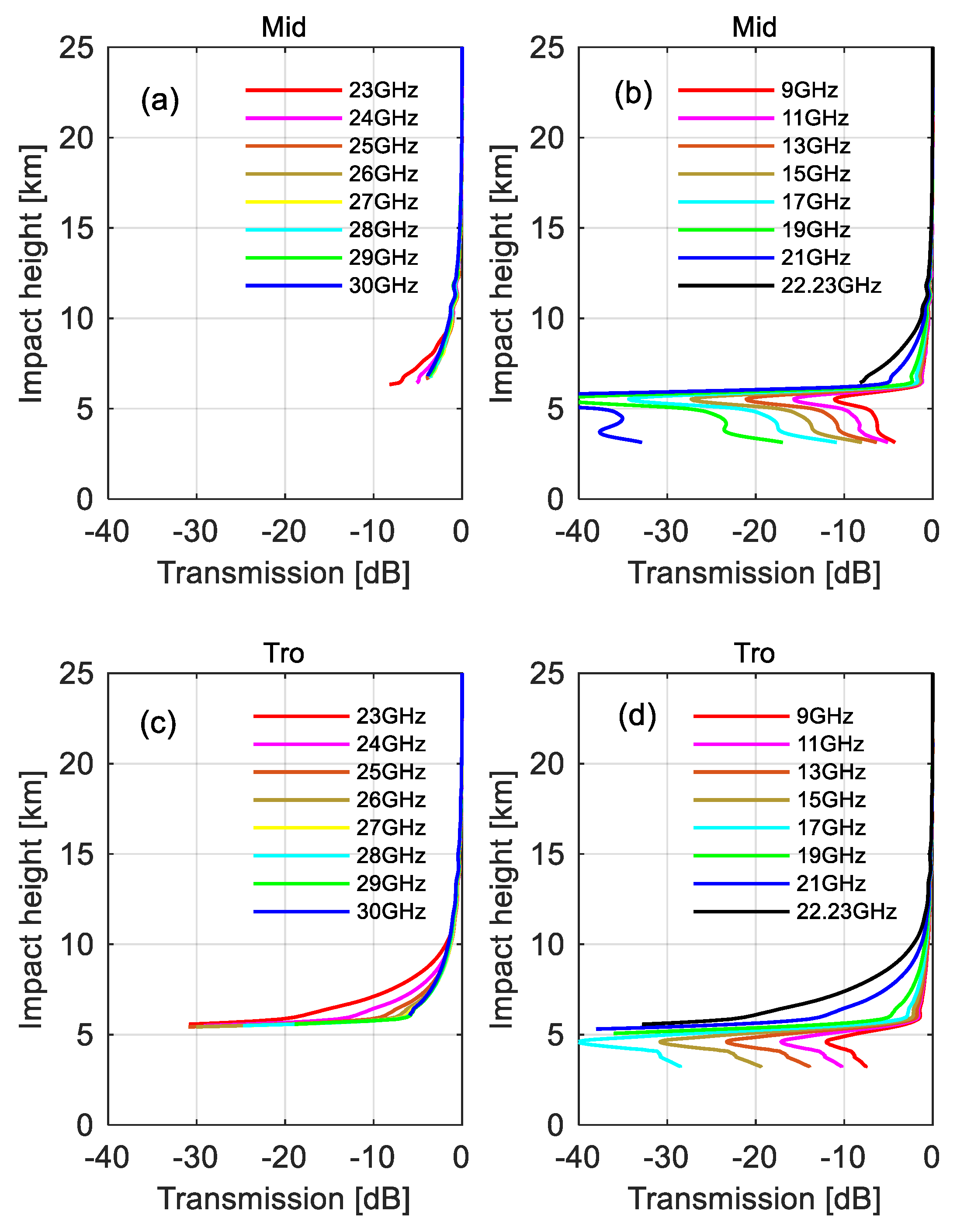
3.1. Signal Attenuation Properties
3.1.1. Transmission Profiles
3.1.2. Ratio of Frequency Pair
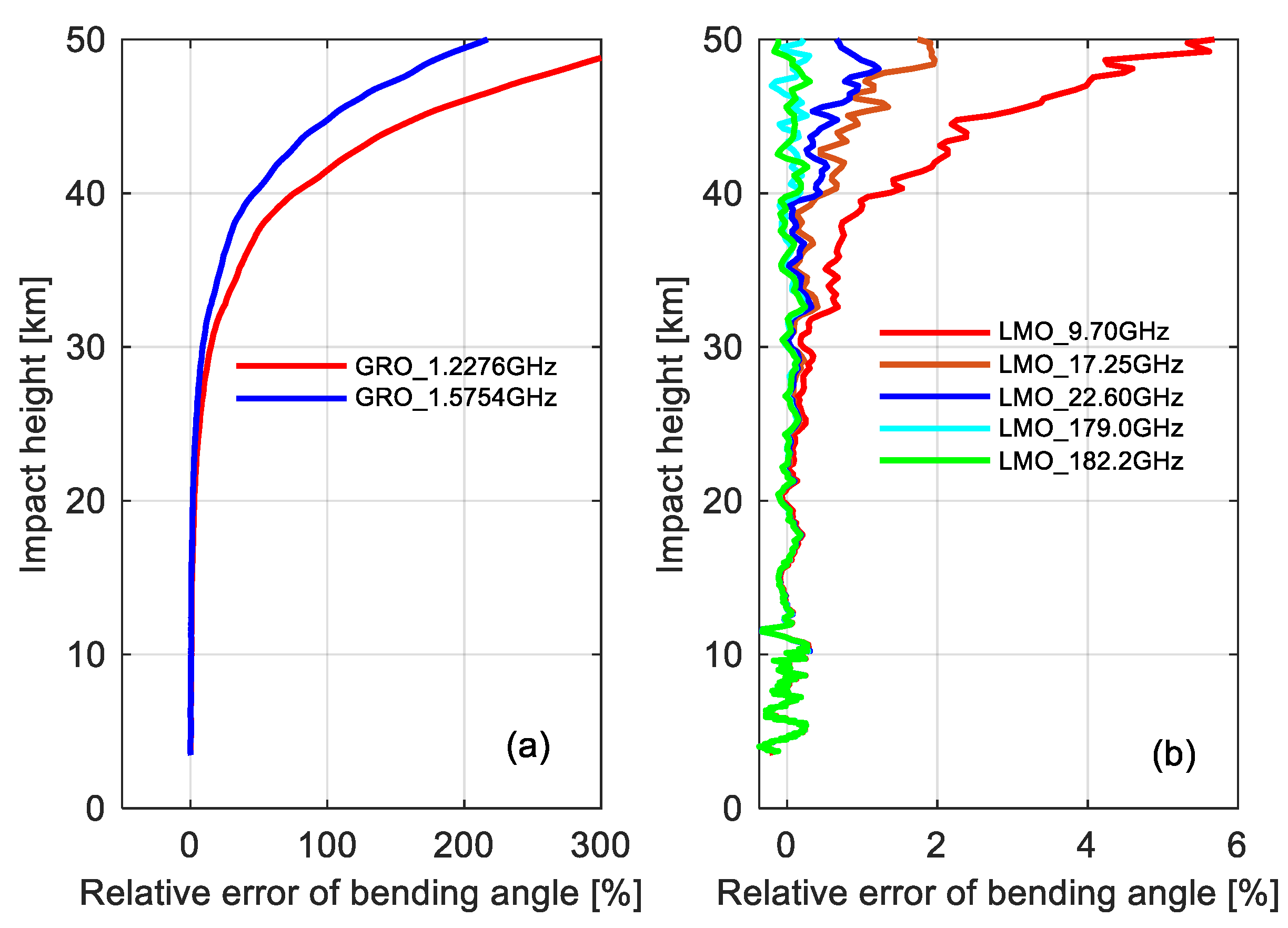
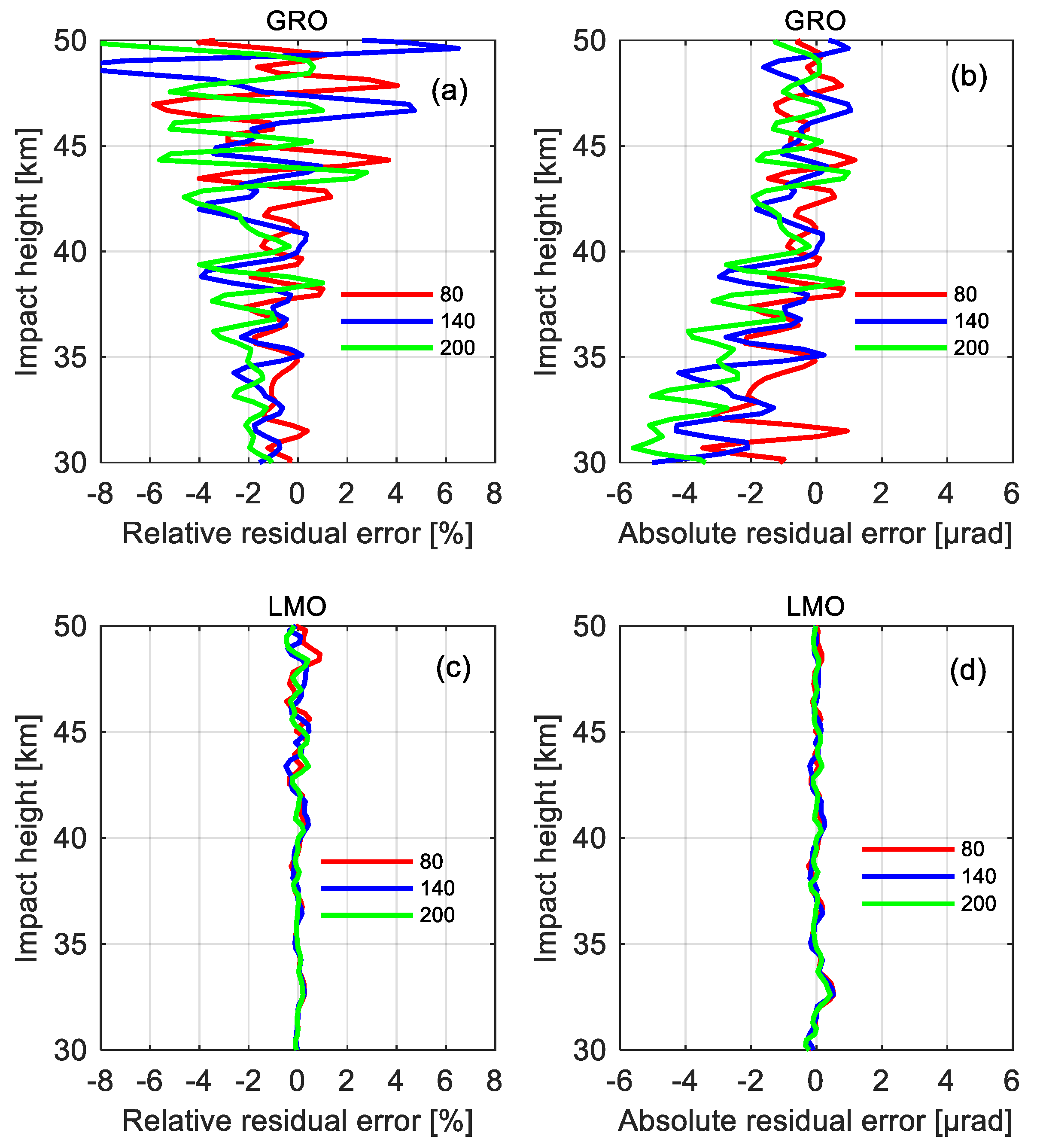
3.2. Signal Propagation Comparison with GRO
3.3. Detection Performance of Different Frequency Combinations
3.3.1. Frequencies Setting
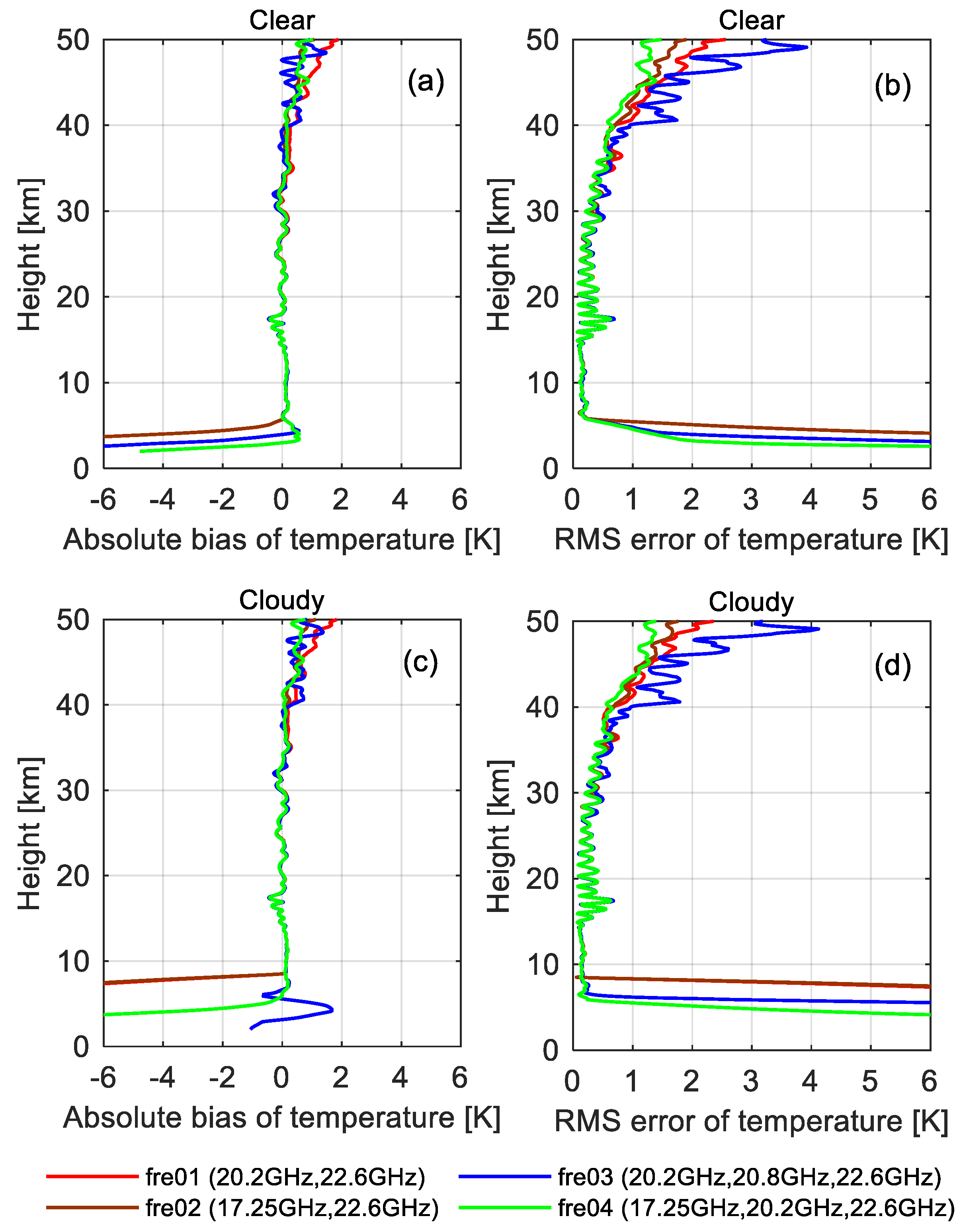
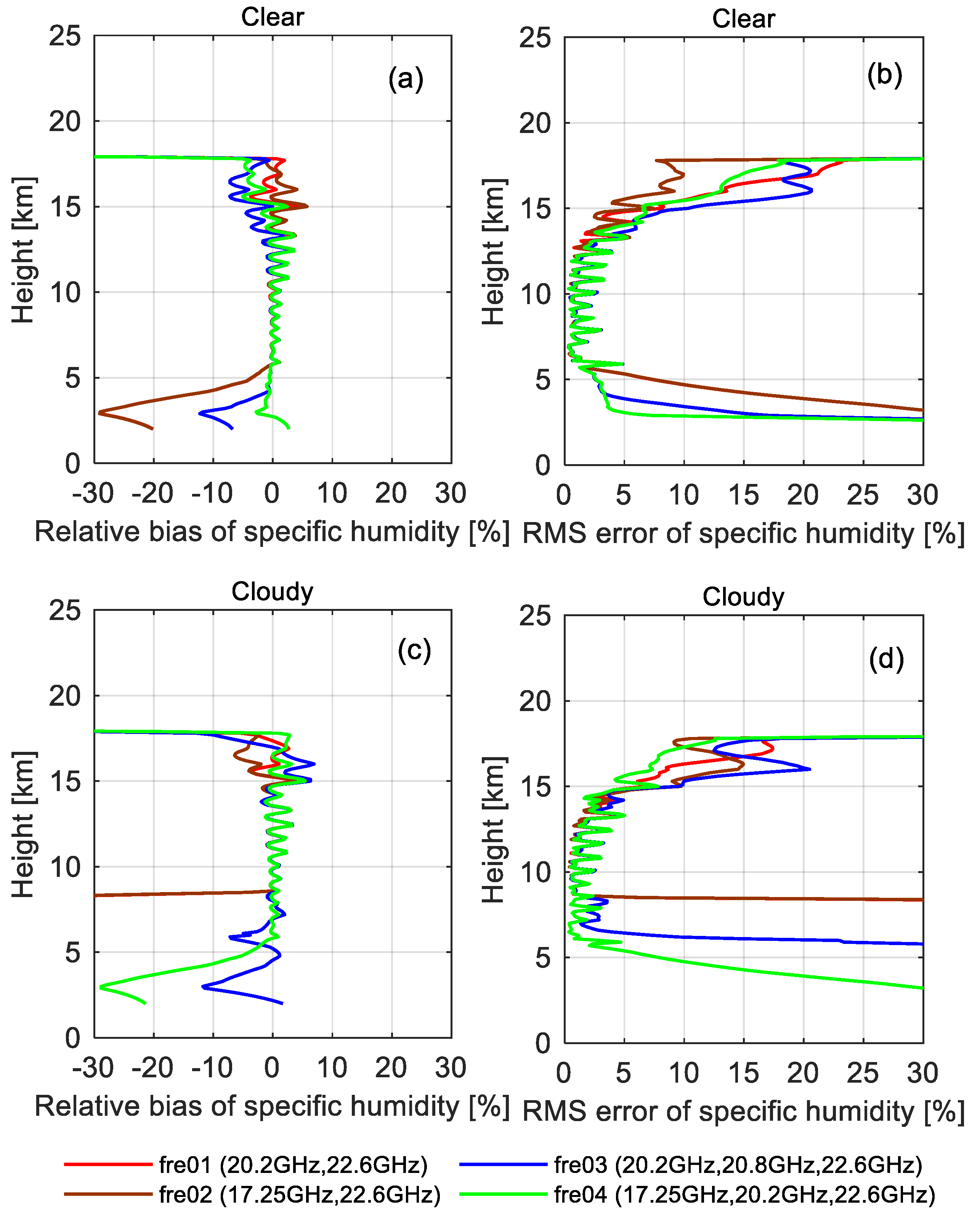
3.3.2. K Band
3.3.3. X+K Band
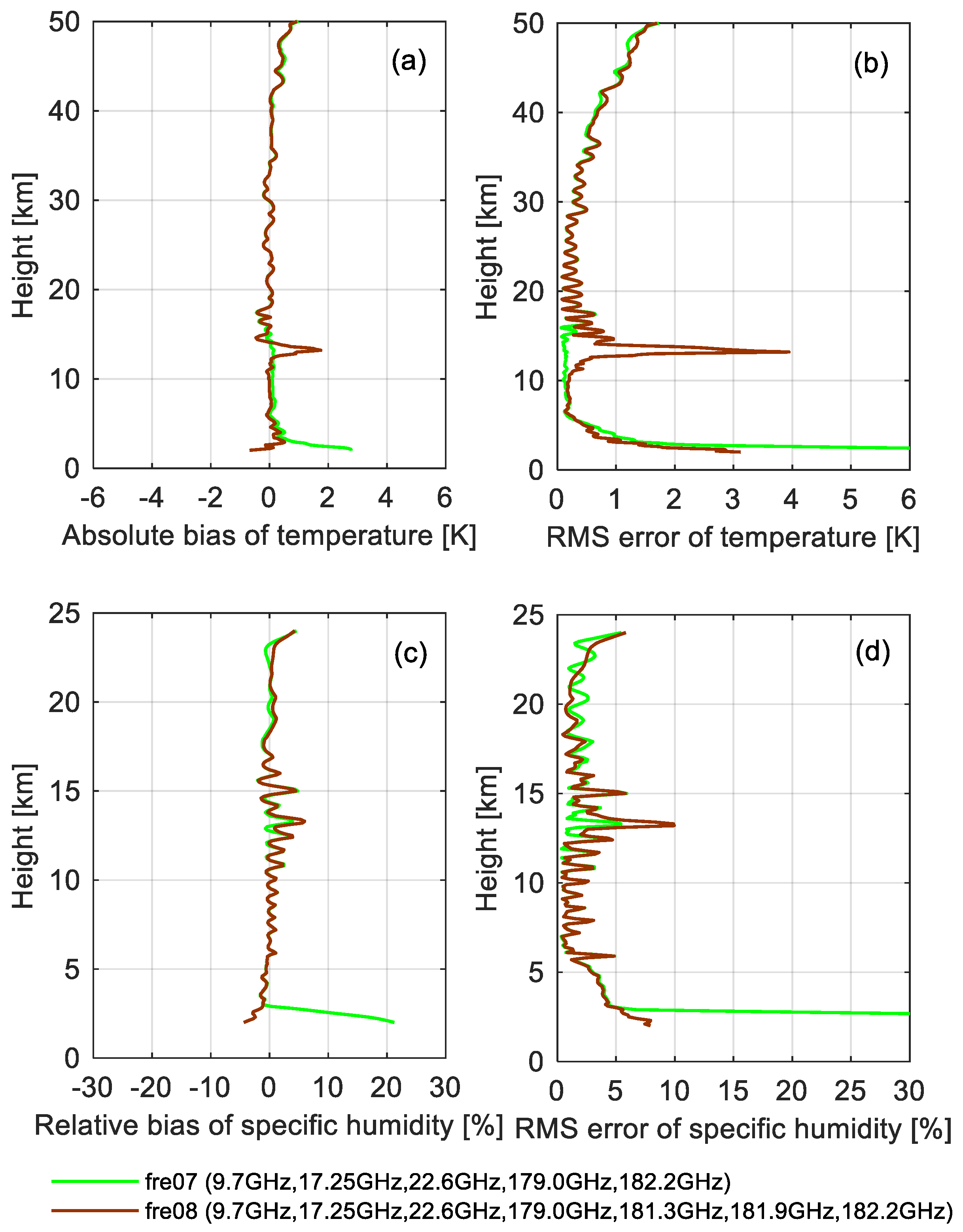
3.3.4. X+K+M Band
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, Y. Impact of human activities on climate system: An interpretation of Chapter III of WGI report of IPCC AR6. Trans. Atmos. Sci. 2021, 44, 654–657. [Google Scholar]
- Kursinski, E.R.; Syndergaard, S.; Flittner, D.; Feng, D.; Hajj, G.; Herman, B.; Ward, D.; Yunck, T. A microwave occultation observing system optimized to characterize atmospheric water, temperature, and geopotential via absorption. J. Atmos. Ocean. Technol. 2002, 19, 1897–1914. [Google Scholar] [CrossRef]
- Schweitzer, S.; Kirchengast, G.; Schwaerz, M.; Fritzer, J.; Gorbunov, M.E. Thermodynamic state retrieval from microwave occultation data and performance analysis based on end-to-end simulations. J. Geophys. Res. Atmos. 2011, 116, D10301. [Google Scholar] [CrossRef]
- Shine, K.P.; Sinha, A. Sensitivity of the Earth’s climate to height dependent changes in the water vapor mixing ratio. Nature 1991, 354, 382–384. [Google Scholar] [CrossRef]
- He, Y.; Zhu, X.; Sheng, Z.; He, M.; Feng, Y. Observations of Inertia Gravity Waves in the Western Pacific and Their Characteristic in the 2015/2016 Quasi-biennial Oscillation Disruption. J. Geophys. Res. Atmos. 2022, 127, e2022JD037208. [Google Scholar] [CrossRef]
- Ward, D.M.; Kursinski, E.R.; Otarola, A.C.; Stovern, M.; McGhee, J.; Young, A.; Hainsworth, J.; Hagen, J.; Sisk, W.; Reed, H. Retrieval of water vapor using ground-based observations from a prototype ATOMMS active centimeter- and millimeter-wavelength occultation instrument. Atmos. Meas. Tech. 2019, 12, 1955–1977. [Google Scholar] [CrossRef]
- Ji, Q.; Zhu, X.; Sheng, Z.; Tian, T. Spectral Analysis of Gravity Waves in the Martian Thermosphere during Low Solar Activity Based on MAVEN/NGIMS Observations. Astrophys. J. 2022, 938, 97. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Ward, D.M.; Otarola, A.C.; McGhee, J.; Stovern, M.; Sammler, K.; Reed, H.; Erickson, D.; McCormick, C.; Griggs, E. Atmospheric profiling via satellite to satellite occultations near water and ozone absorption lines for weather and climate. In Proceedings of the SPIE 9881, Earth Observing Missions and Sensors: Development, Implementation, and Characterization IV, New Delhi, India, 2 May 2016. [Google Scholar]
- Zhang, J.; Ji, Q.Q.; Sheng, Z.; He, M.Y.; He, Y.; Zuo, X.J.; He, Z.F.; Qin, Z.L.; Wu, G.Y. Observation based climatology Martian atmospheric waves perturbation Datasets. Sci. Data 2023, 10, 9. [Google Scholar] [CrossRef]
- Yunck, T.P.; Hajj, G.A.; Kursinski, E.R.; LaBrecque, J.A.; Lowe, S.T.; Watkins, M.M.; McCormick, C. AMORE: An autonomous constellation concept for atmospheric and ocean observation. Acta Astronaut. 2000, 46, 355–364. [Google Scholar] [CrossRef]
- Ware, R.; Exner, M.; Feng, D.; Gorbunov, M.; Hardy, K.; Herman, B.; Kuo, Y.; Meehan, T.; Melbourne, W.; Rocken, C.; et al. GPS sounding of the atmosphere from low earth orbit: Preliminary results. Bull. Am. Meteorol. Soc. 1996, 77, 19–40. [Google Scholar] [CrossRef]
- Hajj, G.A.; Kursinski, E.R.; Romans, L.J.; Bertiger, W.I.; Leroy, S.S. A technical description of atmospheric sounding by GPS occultation. J. Atmos. Solar-Terr. Phys. 2002, 64, 451–469. [Google Scholar] [CrossRef]
- Liu, C.L.; Kirchengast, G.; Zhang, K.; Norman, R.; Li, Y.; Zhang, S.C.; Fritzer, J.; Schwaerz, M.; Wu, S.Q.; Tan, Z.X. Quantifying residual ionospheric errors in GNSS radio occultation bending angles based on ensembles of profiles from end-to-end simulations. Atmos. Meas. Tech. 2015, 8, 2999–3019. [Google Scholar] [CrossRef]
- Yunck, T.P.; Liu, C.H.; Ware, R.J. A History of GPS Sounding. Terr. Atmos. Ocean. Sci. 2000, 11, 1–20. [Google Scholar] [CrossRef]
- Wickert, J.; Reigber, C.; Beyerle, G.; Konig, R.; Marquardt, C.; Schmidt, T.; Grunwaldt, L.; Galas, R.; Meehan, T.K.; Melbourne, W.G.; et al. Atmosphere sounding by GPS radio occultation: First results from CHAMP. Geophys. Res. Lett. 2001, 28, 3263–3266. [Google Scholar] [CrossRef]
- Ho, S.-p.; Yue, X.; Zeng, Z.; Ao, C.O.; Huang, C.-Y.; Kursinski, E.R.; Kuo, Y.-H. Applications of COSMIC Radio Occultation Data from the Troposphere to Ionosphere and Potential Impacts of COSMIC-2 Data. Bull. Am. Meteorol. Soc. 2014, 95, ES18–ES22. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, Y.; Bai, W.; Xia, J.; Tan, G.; Cheng, C.; Du, Q.; Wang, X.; Zhao, D.; Tian, Y.; et al. Validation of Preliminary Results of Thermal Tropopause Derived from FY-3C GNOS Data. Remote Sens. 2019, 11, 1139. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System. J. Geophys. Res. Atmos. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Wang, X.; Lu, D.R. Retrieval of water vapor profiles with radio occultation measurements using an artificial neural network. Adv. Atmos. Sci. 2005, 22, 759–764. [Google Scholar] [CrossRef]
- Feng, D.D.; Syndergaard, S.; Herman, B.M.; Kursinski, E.R.; Yunck, T.P.; Romberg, F.W. Deriving atmospheric water vapor and ozone profiles from active microwave occultation measurements. Sens. Syst. Next-Gener. Satell. IV 2001, 4169, 299–308. [Google Scholar] [CrossRef]
- Fu, N.; Guo, P.; Wu, M.; Huang, Y.; Hu, X.; Hong, Z. The Two-Parts Step-by-Step Ionospheric Assimilation Based on Ground-Based/Spaceborne Observations and Its Verification. Remote Sens. 2019, 11, 1172. [Google Scholar] [CrossRef]
- Liu, C.L.; Kirchengast, G.; Syndergaard, S.; Kursinski, E.R.; Sun, Y.Q.; Bai, W.H.; Du, Q.F. A review of low Earth orbit occultation using microwave and infrared-laser signals for monitoring the atmosphere and climate. Adv. Space Res. 2017, 60, 2776–2811. [Google Scholar] [CrossRef]
- Herman, B.M.; Feng, D.; Flittner, D.; Kursinski, E.R.; Syndergaard, S.; Ward, D. An overview of the university of Arizona ATOMS project. In Occultations for Probing Atmosphere and Climate; Kirchengast, G., Foelsche, U., Steiner, A.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 189–200. [Google Scholar]
- Palmer, P.I.; Barnett, J.J.; Eyre, J.R.; Healy, S.B. A nonlinear optimal, estimation inverse method for radio occultation measurements of temperature, humidity, and surface pressure. J. Geophys. Res. Atmos. 2000, 105, 17513–17526. [Google Scholar] [CrossRef]
- Poli, P.; Joiner, J.; Kursinski, E.R. 1DVAR analysis of temperature and humidity using GPS radio occultation refractivity data. J. Geophys. Res. Atmos. 2002, 107, 14–20. [Google Scholar] [CrossRef]
- Healy, S.B.; Eyre, J.R. Retrieving temperature, water vapour and surface pressure information from refractive-index profiles derived by radio occultation: A simulation study. J. Roy. Meteorol. Soc. 2000, 126, 1661–1683. [Google Scholar] [CrossRef]
- Li, Y.; Kirchengast, G.; Scherllin-Pirscher, B.; Schwaerz, M.; Nielsen, J.K.; Ho, S.-p.; Yuan, Y.-b. A New Algorithm for the Retrieval of Atmospheric Profiles from GNSS Radio Occultation Data in Moist Air and Comparison to 1DVar Retrievals. Remote Sens. 2019, 11, 2729. [Google Scholar] [CrossRef]
- Schweitzer, S. Atmosphere and Climate Explorer mission ACE+: Humidity and temperature retrieval performance analysis. Master’s Thesis, Institute for Geophysics Astrophysics and Meteorology, University of Graz, Graz, Austria, 2004. [Google Scholar]
- Kirchengast, G.; Schweitzer, S. Climate benchmark profiling of greenhouse gases and thermodynamic structure and wind from space. Geophys. Res. Lett. 2011, 38, 142–154. [Google Scholar] [CrossRef]
- Proschek, V.; Kirchengast, G.; Schweitzer, S. Greenhouse gas profiling by infrared-laser and microwave occultation: Retrieval algorithm and demonstration results from end-to-end simulations. Atmos. Meas. Tech. 2011, 4, 2035–2058. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Ward, D.; Stovern, M.; Otarola, A.C.; Young, A.; Wheelwright, B.; Stickney, R.; Albanna, S.; Duffy, B.; Groppi, C.; et al. Development and testing of the Active Temperature, Ozone and Moisture Microwave Spectrometer (ATOMMS) cm and mm wavelength occultation instrument. Atmos. Meas. Tech. 2012, 5, 439–456. [Google Scholar] [CrossRef]
- Benzon, H.H.; Høeg, P. Wave optics-based LEO-LEO radio occultation retrieval. Radio Sci. 2016, 51, 589–602. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Hardy, K.R.; Romans, L.J.; Schofield, J.T. Observing tropospheric water-vapor by radio occultation using the global positioning system. Geophys. Res. Lett. 1995, 22, 2365–2368. [Google Scholar] [CrossRef]
- Fjeldbo, G.; Kliore, A.J.; Eshlemen, V.R. Neutral atmosphere of venus as studied with mariner-v radio occultation experiments. Astron. J. 1971, 76, 123. [Google Scholar] [CrossRef]
- Syndergaard, S. Modeling the impact of the Earth’s oblateness on the retrieval of temperature and pressure profiles from limb sounding. J. Atmos. Solar-Terr. Phys. 1998, 60, 171–180. [Google Scholar] [CrossRef]
- Li, Y.; Yuan, Y.; Wang, X. Assessments of the Retrieval of Atmospheric Profiles from GNSS Radio Occultation Data in Moist Tropospheric Conditions Using Radiosonde Data. Remote Sens. 2020, 12, 2717. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific Publishing: Singapore, 2000; pp. 43–61. [Google Scholar]
- Liebe, H.J. An updated model for millimeter wave-propagation in moist air. Radio Sci. 1985, 20, 1069–1089. [Google Scholar] [CrossRef]
- Liebe, H.J.; Hufford, G.A.; Cotton, M.G. Propagation modeling of moist air and suspended water/ice particles at frequencies below 1000 GHz. In Proceedings of the NATO/AGARD Wave Propagation Panel, 52nd Meeting, Mallorca, Spain, 17–20 May 1993. [Google Scholar]
- Larsen, G.B.; Kirchengast, G.; Bernath, P. Science Objectives and Observational Requirements of The ACCURATE Mission Concept; Technical Report DMI/ESA-IRDAS/ObsReq/Oct2009; Danish Meteorology Institute: Copenhagen, Denmark, 2009. [Google Scholar]




| GRO | LMO | ||
|---|---|---|---|
| Frequency (GHz) | Wavelength(cm) | Frequency (GHz) | Wavelength(cm) |
| L1 = 1.5754 | 19.03 | Fre1 = 9.7 | 3.0906 |
| L2 = 1.2276 | 24.42 | Fre2 = 17.25 | 1.7379 |
| Fre3 = 22.6 | 1.4841 | ||
| Fre4 = 179.0 | 0.1675 | ||
| Fre5 = 182.2 | 0.1648 | ||
| Group | Wavelength | Band | Frequencies (GHz) | Number of Frequencies |
|---|---|---|---|---|
| fre01 | Centimeter wave | K | 20.2, 22.6 | 2 |
| fre02 | Centimeter wave | K | 17.25, 22.6 | 2 |
| fre03 | Centimeter wave | K | 20.2, 20.8, 22.6 | 3 |
| fre04 | Centimeter wave | K | 17.25, 20.2, 22.6 | 3 |
| fre05 | Centimeter wave | X+K | 9.7, 17.25, 22.6 | 3 |
| fre06 | Centimeter wave | X+K | 9.7, 13.5, 17.25, 20.2, 22.6 | 5 |
| fre07 | Centimeter and millimeter wave | X+K+M | 9.7, 17.25, 22.6, 179.0, 182.2 | 5 |
| fre08 | Centimeter and millimeter wave | X+K+M | 9.7, 17.25, 22.6, 179.0, 181.3, 181.9, 182.2 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, X.; Lyu, D. Estimation of Moist Atmospheric Profiles from Refraction and Attenuation Measurements by Using Centimeter and Millimeter Wave Links between LEO Satellites. Remote Sens. 2023, 15, 391. https://doi.org/10.3390/rs15020391
Zhang Z, Wang X, Lyu D. Estimation of Moist Atmospheric Profiles from Refraction and Attenuation Measurements by Using Centimeter and Millimeter Wave Links between LEO Satellites. Remote Sensing. 2023; 15(2):391. https://doi.org/10.3390/rs15020391
Chicago/Turabian StyleZhang, Zhihua, Xin Wang, and Daren Lyu. 2023. "Estimation of Moist Atmospheric Profiles from Refraction and Attenuation Measurements by Using Centimeter and Millimeter Wave Links between LEO Satellites" Remote Sensing 15, no. 2: 391. https://doi.org/10.3390/rs15020391
APA StyleZhang, Z., Wang, X., & Lyu, D. (2023). Estimation of Moist Atmospheric Profiles from Refraction and Attenuation Measurements by Using Centimeter and Millimeter Wave Links between LEO Satellites. Remote Sensing, 15(2), 391. https://doi.org/10.3390/rs15020391





