Densifying and Optimizing the Water Level Series for Large Lakes from Multi-Orbit ICESat-2 Observations
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
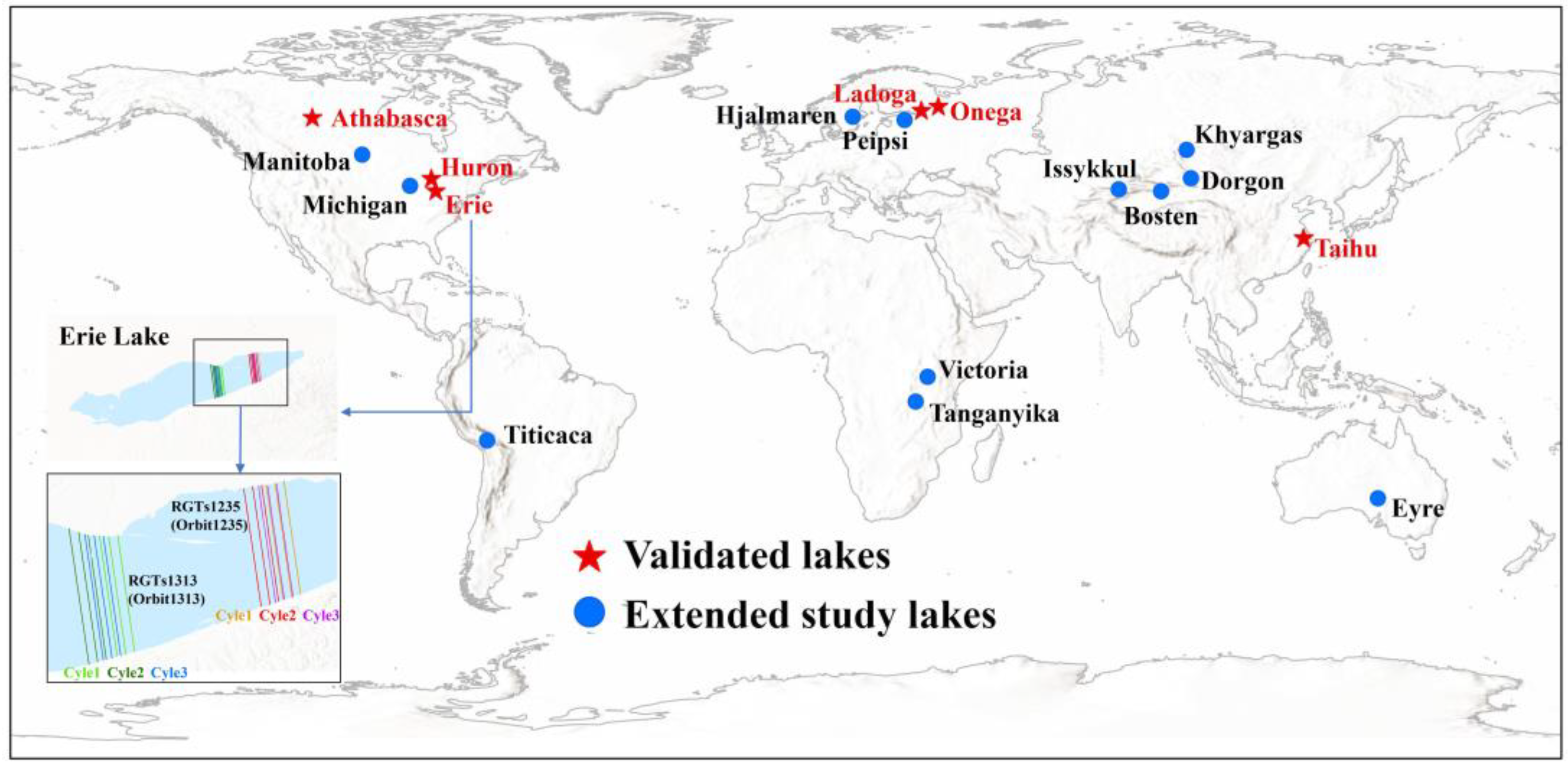
2.1.1. Study Area and Lake Selection
2.1.2. ICESat-2 Altimetry Data
2.1.3. Auxiliary Data
2.2. Methods
2.2.1. Preprocessing of Lake Level Derived from ICESat-2
2.2.2. Densification by Synthesizing Multi-Orbit Data
2.2.3. Kalman Filtering Optimization
2.2.4. Evaluation Metrics
3. Results and Discussion
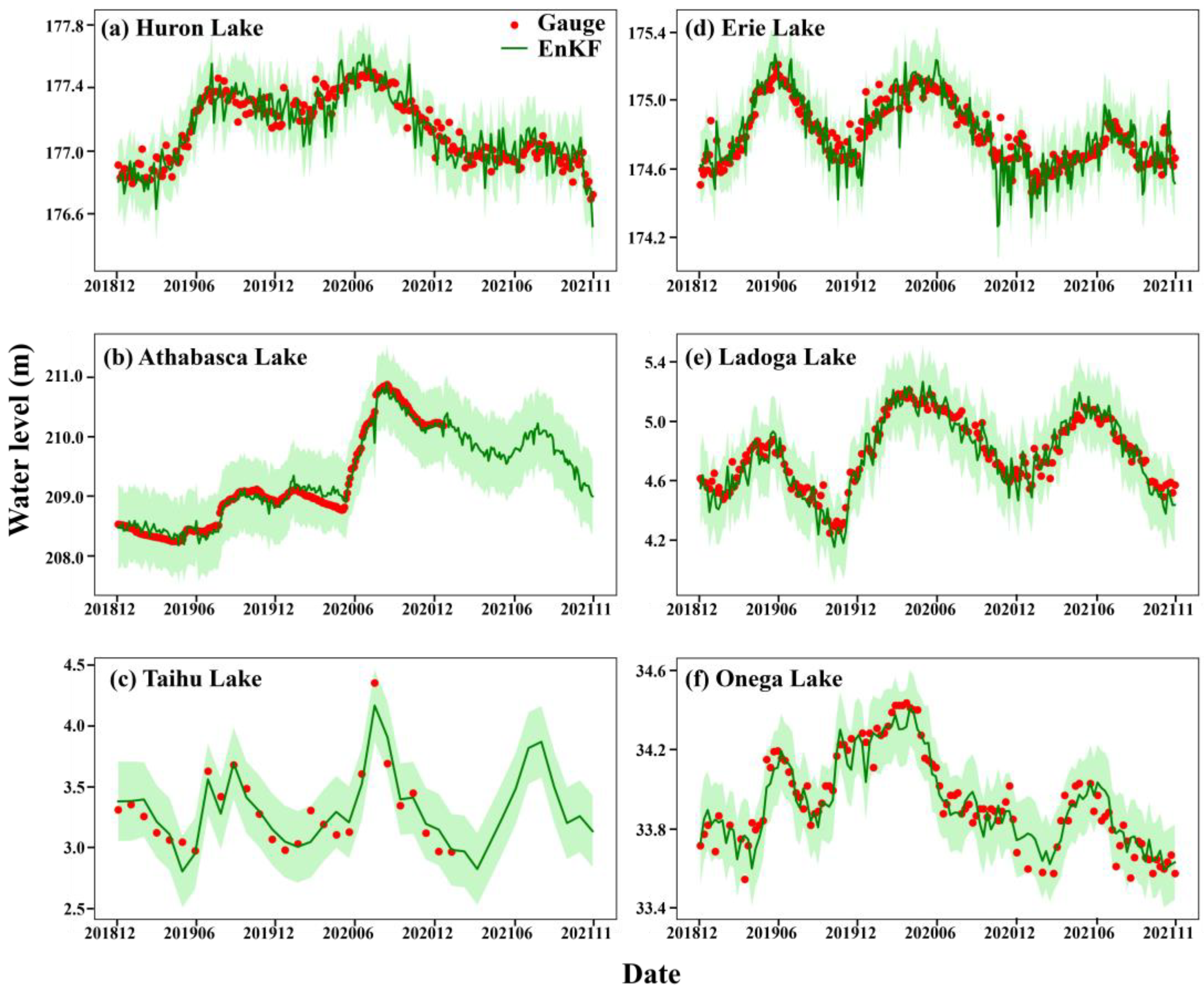
3.1. Validation of Lake Water Level Time Series
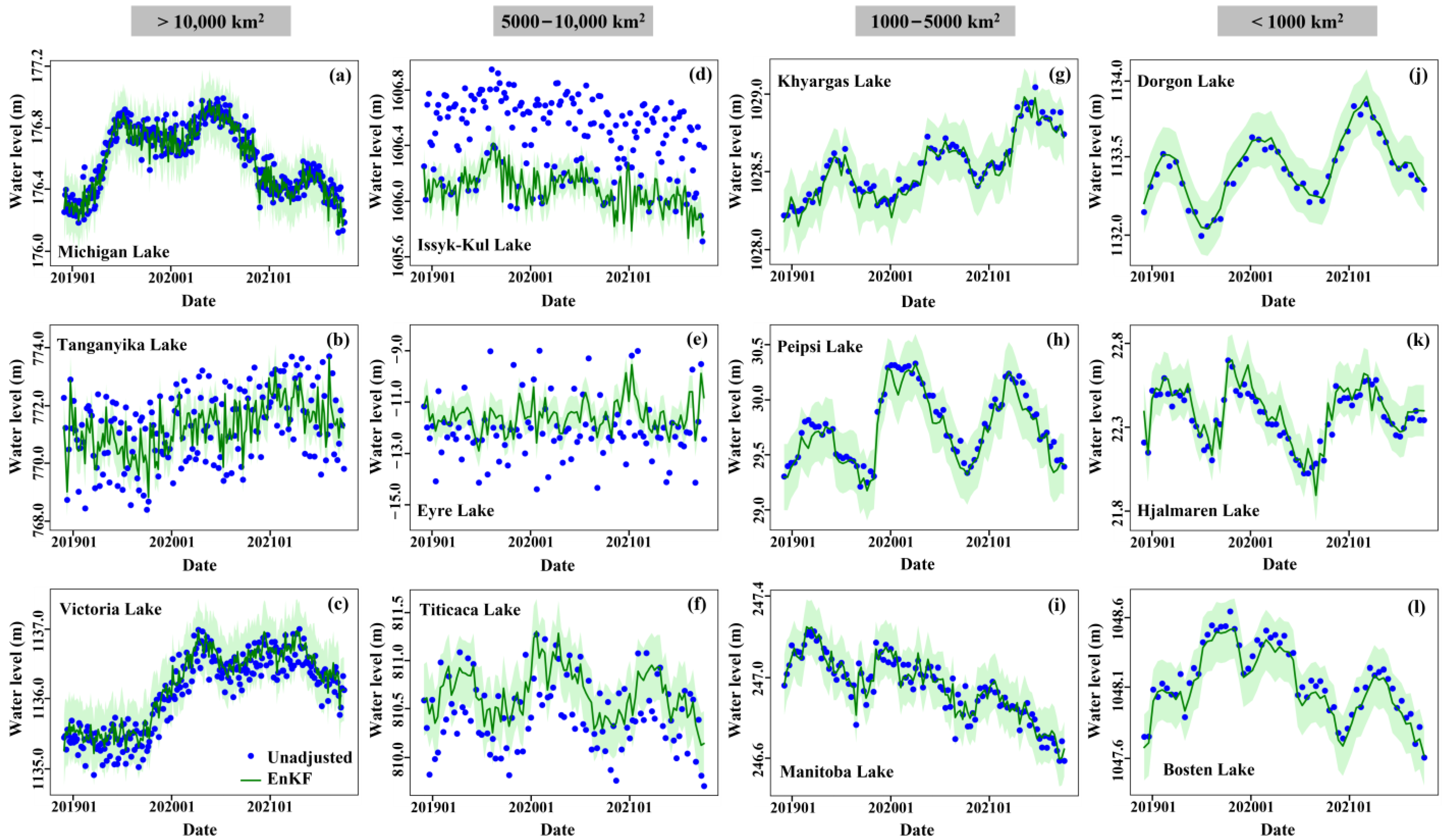
3.2. Lake Level Time Series Synthesized by Multi-Orbit ICESat-2 Footprints
3.3. Comparison of Different Filter Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crétaux, J.F.; Arsen, A.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Maisongrande, P. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Richards, K.; Ke, L.; Hien Phan, V. Accelerated lake expansion on the Tibetan Plateau in the 2000s: Induced by glacial melting or other processes? Water Resour. Res. 2014, 50, 3170–3186. [Google Scholar] [CrossRef]
- Schwatke, C.; Dettmering, D.; Bosch, W.; Seitz, F. DAHITI–an innovative approach for estimating water level time series over inland waters using multi-mission satellite altimetry. Hydrol. Earth Syst. Sci. 2015, 19, 4345–4364. [Google Scholar] [CrossRef]
- Busker, T.; de Roo, A.; Gelati, E.; Schwatke, C.; Adamovic, M.; Bisselink, B.; Cottam, A. A global lake and reservoir volume analysis using a surface water dataset and satellite altimetry. Hydrol. Earth Syst. Sci. 2019, 23, 669–690. [Google Scholar] [CrossRef]
- Li, X.; Long, D.; Huang, Q.; Han, P.; Zhao, F.; Wada, Y. High-temporal-resolution water level and storage change data sets for lakes on the Tibetan Plateau during 2000–2017 using multiple altimetric missions and Landsat-derived lake shoreline positions. Earth Syst. Sci. Data 2019, 11, 1603–1627. [Google Scholar] [CrossRef]
- Papa, F.; Crétaux, J.F.; Grippa, M.; Robert, E.; Trigg, M.; Tshimanga, R.M.; Calmant, S. Water resources in Africa under global change: Monitoring surface waters from space. Surv. Geophys. 2022, 43, 1–51. [Google Scholar]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Thomas, T.C. The Ice, Cloud, and Land Elevation Satellite–2 Mission: A global geolocated photon product derived from the advanced topographic laser altimeter system. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef]
- Thomas, T.C.; Luthcke, S.B.; Pennington, T.A.; Nicholas, J.B.; Rowlands, D.D. ICESat-2 Precision Orbit Determination. Earth Space Sci. 2021, 8, e2020EA001496. [Google Scholar] [CrossRef]
- Bae, S.; Helgeson, B.; James, M.; Magruder, L.; Sipps, J.; Luthcke, S.; Thomas, T. Performance of ICESat-2 precision pointing determination. Earth Space Sci. 2021, 8, e2020EA001478. [Google Scholar] [CrossRef]
- Ryan, J.C.; Smith, L.C.; Cooley, S.W.; Pitcher, L.H.; Pavelsky, T.M. Global characterization of inland water reservoirs using ICESat-2 altimetry and climate reanalysis. Geophys. Res. Lett. 2020, 47, e2020GL088543. [Google Scholar] [CrossRef]
- Cooley, S.W.; Ryan, J.C.; Smith, L.C. Human alteration of global surface water storage variability. Nature 2021, 591, 78–81. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Zhang, H.; Tao, S.; Ao, Z.; Song, C.; Chave, J.; Fang, J. Decadal Lake Volume Changes (2003–2020) and Driving Forces at a Global Scale. Remote Sens. 2022, 14, 1032. [Google Scholar] [CrossRef]
- Luo, S.; Song, C.; Ke, L.; Zhan, P.; Fan, C.; Liu, K.; Zhu, J. Satellite laser altimetry reveals a net water mass gain in global lakes with spatial heterogeneity in the early 21st century. Geophys. Res. Lett. 2022, 49, e2021GL096676. [Google Scholar] [CrossRef]
- Xu, N.; Ma, Y.; Wei, Z.; Huang, C.; Li, G.; Zheng, H.; Wang, X.H. Satellite observed recent rising water levels of global lakes and reservoirs. Environ. Res. Lett. 2022, 17, 074013. [Google Scholar] [CrossRef]
- Xu, N.; Zheng, H.; Ma, Y.; Yang, J.; Liu, X.; Wang, X. Global estimation and assessment of monthly lake/reservoir water level changes using ICESat-2 ATL13 Products. Remote Sens. 2021, 13, 2744. [Google Scholar] [CrossRef]
- Scherer, D.; Schwatke, C.; Dettmering, D.; Seitz, F. ICESat-2 Based River Surface Slope and Its Impact on Water Level Time Series from Satellite Altimetry. Water Resour. Res. 2022, 58, e2022WR032842. [Google Scholar] [CrossRef]
- Han, W.; Huang, C.; Gu, J.; Hou, J.; Zhang, Y.; Wang, W. Water Level Change of Qinghai Lake from ICESat and ICESat-2 Laser Altimetry. Remote Sens. 2022, 14, 6212. [Google Scholar] [CrossRef]
- Lao, J.; Wang, C.; Nie, S.; Xi, X.; Wang, J. Monitoring and Analysis of Water Level Changes in Mekong River from ICESat-2 Spaceborne Laser Altimetry. Water 2022, 14, 1613. [Google Scholar] [CrossRef]
- Liu, C.; Hu, R.; Wang, Y.; Lin, H.; Zeng, H.; Wu, D.; Shao, C. Monitoring water level and volume changes of lakes and reservoirs in the Yellow River Basin using ICESat-2 laser altimetry and Google Earth Engine. J. Hydro-Environ. Res. 2022, 44, 53–64. [Google Scholar] [CrossRef]
- Narin, O.G.; Abdikan, S. Multi-temporal analysis of inland water level change using ICESat-2 ATL-13 data in lakes and dams. Environ. Sci. Pollut. Res. 2022, 1–13. [Google Scholar] [CrossRef]
- Xie, J.; Li, B.; Jiao, H.; Zhou, Q.; Mei, Y.; Xie, D.; Fu, Y. Water Level Change Monitoring Based on a New Denoising Algorithm Using Data from Landsat and ICESat-2: A Case Study of Miyun Reservoir in Beijing. Remote Sens. 2022, 14, 4344. [Google Scholar] [CrossRef]
- Zhang, C.; Lv, A.; Zhu, W.; Yao, G.; Qi, S. Using multisource satellite data to investigate lake area, water level, and water storage changes of terminal lakes in ungauged regions. Remote Sens. 2021, 13, 3221. [Google Scholar] [CrossRef]
- Madson, A.; Sheng, Y. Automated Water Level Monitoring at the Continental Scale from ICESat-2 Photons. Remote Sens. 2021, 13, 3631. [Google Scholar] [CrossRef]
- Yuan, C.; Gong, P.; Bai, Y. Performance assessment of ICESat-2 laser altimeter data for water-level measurement over lakes and reservoirs in China. Remote Sens. 2020, 12, 770. [Google Scholar] [CrossRef]
- Chen, T.; Song, C.; Luo, S.; Ke, L.; Liu, K.; Zhu, J. Monitoring global reservoirs using ICESat-2: Assessment on spatial coverage and application potential. J. Hydrol. 2022, 604, 127257. [Google Scholar] [CrossRef]
- Shu, S.; Liu, H.; Beck, R.A.; Frappart, F.; Korhonen, J.; Lan, M.; Xu, M.; Yang, B.; Huang, Y.J.H.; Sciences, E.S. Evaluation of historic and operational satellite radar altimetry missions for constructing consistent long-term lake water level records. Hydrol. Earth Syst. Sci. 2021, 25, 1643–1670. [Google Scholar] [CrossRef]
- Thakur, P.K.; Garg, V.; Kalura, P.; Agrawal, B.; Sharma, V.; Mohapatra, M.; Kalia, M.; Aggarwal, S.P.; Calmant, S.; Ghosh, S.J.A.i.S.R. Water level status of Indian reservoirs: A synoptic view from altimeter observations. Adv. Space Res. 2021, 68, 619–640. [Google Scholar] [CrossRef]
- Wang, X.; Gong, P.; Zhao, Y.; Xu, Y.; Cheng, X.; Niu, Z.; Luo, Z.; Huang, H.; Sun, F.; Li, X.J.R.S.o.E. Water-level changes in China’s large lakes determined from ICESat/GLAS data. Remote Sens. Environ. 2013, 132, 131–144. [Google Scholar] [CrossRef]
- Jasinski, M.; Stoll, J.; Hancock, D.; Robbins, J.; Nattala, J.; Morison, J.; Parrish, C. Algorithm Theoretical Basis Document (ATBD) for along Track Inland Surface Water Data, Release 005. 2021. Available online: https://nsidc.org/sites/default/files/icesat2_atl13_atbd_r005_0.pdf (accessed on 1 January 2022).
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the volume and age of water stored in global lakes using a geo-statistical approach. Nat. Commun. 2016, 7, 1–11. [Google Scholar] [CrossRef]
- Höhle, J.; Höhle, M. Accuracy assessment of digital elevation models by means of robust statistical methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Ocean. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Katzfuss, M.; Stroud, J.R.; Wikle, C.K. Understanding the ensemble Kalman filter. Am. Stat. 2016, 70, 350–357. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. ASME J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Mitchell, H.L. Ensemble kalman filtering. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2005, 131, 3269–3289. [Google Scholar] [CrossRef]


| Name | Unadjusted/EnKF | |||||
|---|---|---|---|---|---|---|
| Area (km2) | R 1 | RMSE 2 | MAE 3 | NSE 4 | CV 5 | |
| Huron | 59,399.30 | 0.846/0.875 | 0.126/0.108 | 0.094/0.084 | 0.639/0.732 | 0.133/0.125 |
| Erie | 25,767.79 | 0.857/0.881 | 0.109/0.098 | 0.079/0.071 | 0.623/0.694 | 0.122/0.117 |
| Athabasca | 7528.73 | 0.986/0.990 | 0.136/0.116 | 0.104/0.093 | 0.971/0.979 | 0.339/0.338 |
| Ladoga | 17,444.01 | 0.881/0.959 | 0.155/0.078 | 0.117/0.064 | 0.556/0.886 | 6.219/5.505 |
| Taihu | 2329.14 | 0.984/0.912 | 0.341/0.340 | 0.335/0.314 | −0.147/−0.143 | 11.394/10.480 |
| Onega | 9961.85 | 0.906/0.929 | 0.121/0.087 | 0.098/0.069 | 0.738/0.863 | 0.660/0.620 |
| Name | Country | Continent | Longitude | Latitude | Area (km2) | Elevation (m) | Number of Orbits | Densified Ratio * |
|---|---|---|---|---|---|---|---|---|
| Dorgon | Mongolia | Asia | 93.431 | 47.709 | 370.35 | 1128 | 6 | 4 |
| Hjalmaren | Sweden | Europe | 15.770 | 59.239 | 474.39 | 24 | 11 | 8 |
| Bosten | China | Asia | 87.040 | 41.969 | 961.84 | 1050 | 8 | 6 |
| Khyargas | Mongolia | Asia | 93.311 | 49.179 | 1383.23 | 1029 | 11 | 7 |
| Peipsi | Russia | Europe | 27.545 | 58.547 | 3489.00 | 28 | 12 | 8 |
| Manitoba | Canada | North America | −98.645 | 50.904 | 4751.05 | 245 | 14 | 10 |
| Issyk-Kul | Kyrgyzstan | Asia | 77.266 | 42.441 | 6195.93 | 1601 | 18 | 14 |
| Titicaca | Bolivia | South America | −69.354 | −15.882 | 8002.51 | 3815 | 13 | 9 |
| Eyre | Australia | Oceania | 137.305 | −28.597 | 8026.70 | −15 | 11 | 8 |
| Tanganyika | Congo | Africa | 29.886 | −6.224 | 32,826.65 | 767 | 18 | 14 |
| Michigan | America | North America | −86.757 | 44.007 | 57,726.84 | 175 | 42 | 29 |
| Victoria | Uganda | Africa | 32.911 | −1.099 | 67,166.22 | 1134 | 28 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Song, C.; Zhan, P.; Fan, C. Densifying and Optimizing the Water Level Series for Large Lakes from Multi-Orbit ICESat-2 Observations. Remote Sens. 2023, 15, 780. https://doi.org/10.3390/rs15030780
Chen T, Song C, Zhan P, Fan C. Densifying and Optimizing the Water Level Series for Large Lakes from Multi-Orbit ICESat-2 Observations. Remote Sensing. 2023; 15(3):780. https://doi.org/10.3390/rs15030780
Chicago/Turabian StyleChen, Tan, Chunqiao Song, Pengfei Zhan, and Chenyu Fan. 2023. "Densifying and Optimizing the Water Level Series for Large Lakes from Multi-Orbit ICESat-2 Observations" Remote Sensing 15, no. 3: 780. https://doi.org/10.3390/rs15030780
APA StyleChen, T., Song, C., Zhan, P., & Fan, C. (2023). Densifying and Optimizing the Water Level Series for Large Lakes from Multi-Orbit ICESat-2 Observations. Remote Sensing, 15(3), 780. https://doi.org/10.3390/rs15030780







