A Method for Long-Term Target Anti-Interference Tracking Combining Deep Learning and CKF for LARS Tracking and Capturing
Abstract
1. Introduction
- We propose the LTAT method to achieve the designated AUV’s long-term pixel position information, integrating deep learning and online learning ideas. This effectively solves the inevitable tracking loss problem caused by complex sea conditions during long-term tracking.
- We optimize and anticipate the AUV’s position via CKF to lessen the influence of interfering data on position.
- We use pixel position information and binocular camera data to obtain the AUV’s coordinates in the camera coordinate system and estimate its orientation. We obtain the relative positions between the end of LARS and the AUV by calculating the coordinate transformation relationship.
- We design the motion trajectory of the end of the LARS using a five-polynomial interpolation method. We use the discrete PID method to control the motion trajectory of the LARS. Based on our proposed system, the complete process of LARS tracking and capturing AUV is virtually verified via a physical simulation system.
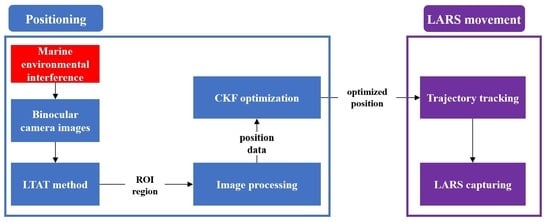
2. Unmanned LARS Tracking and Capturing System
2.1. Pixel Coordinates Acquisition of AUV
2.1.1. Theoretical Background
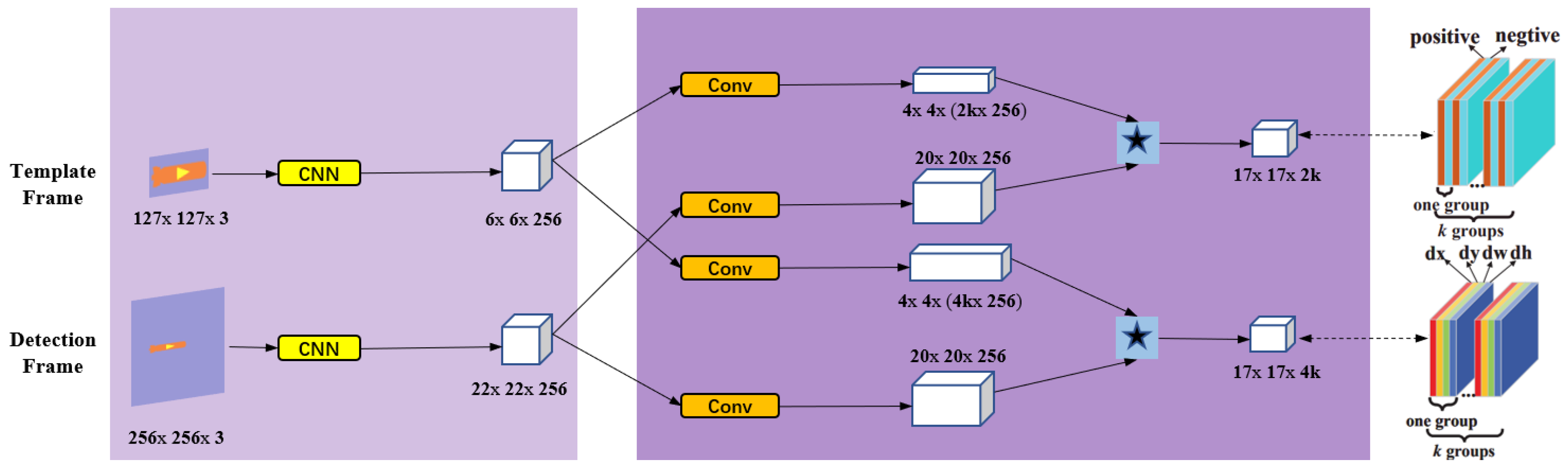
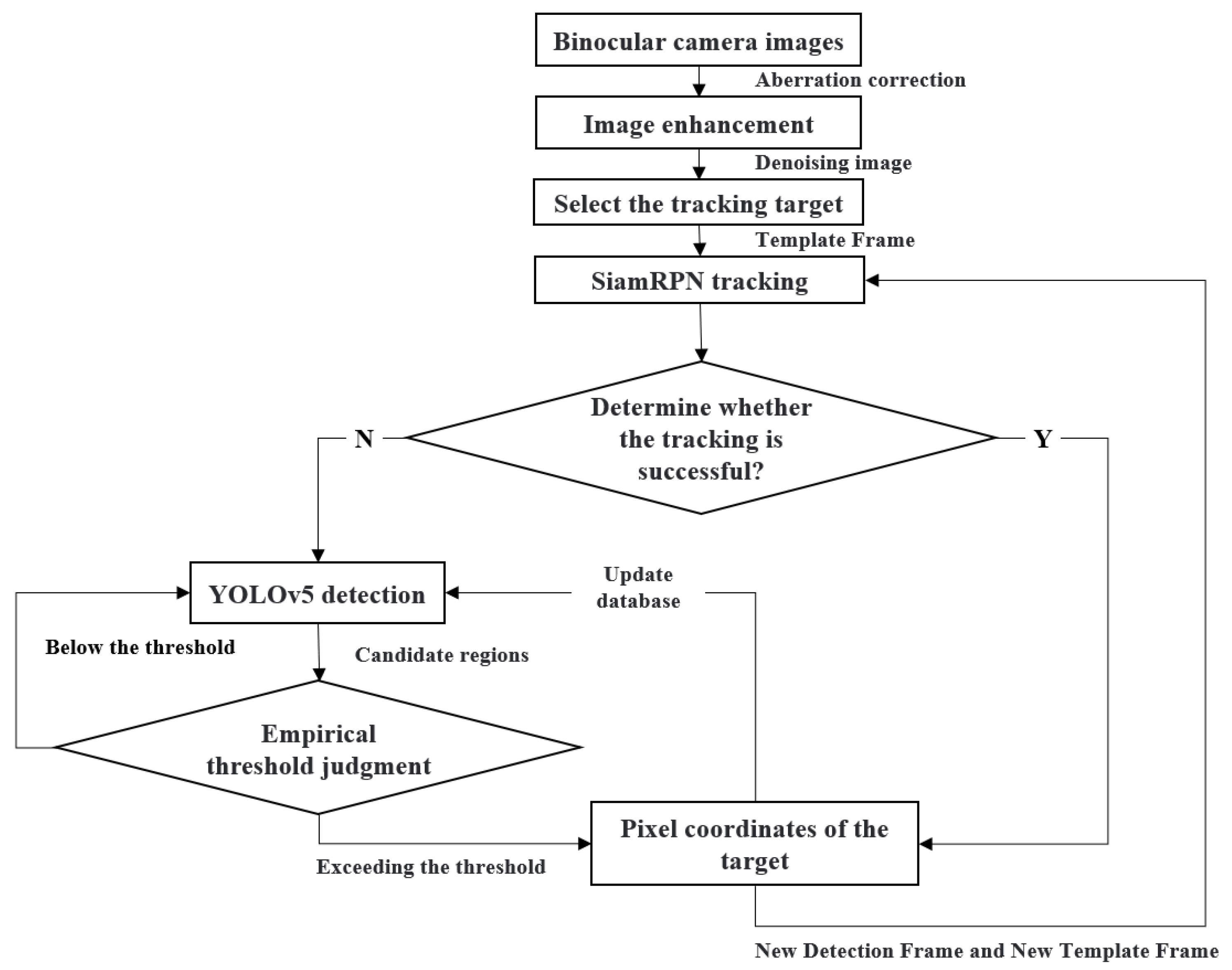
2.1.2. Long-Term Target Anti-Interference Tracking Method
2.2. AUV Position and Orientation Estimation
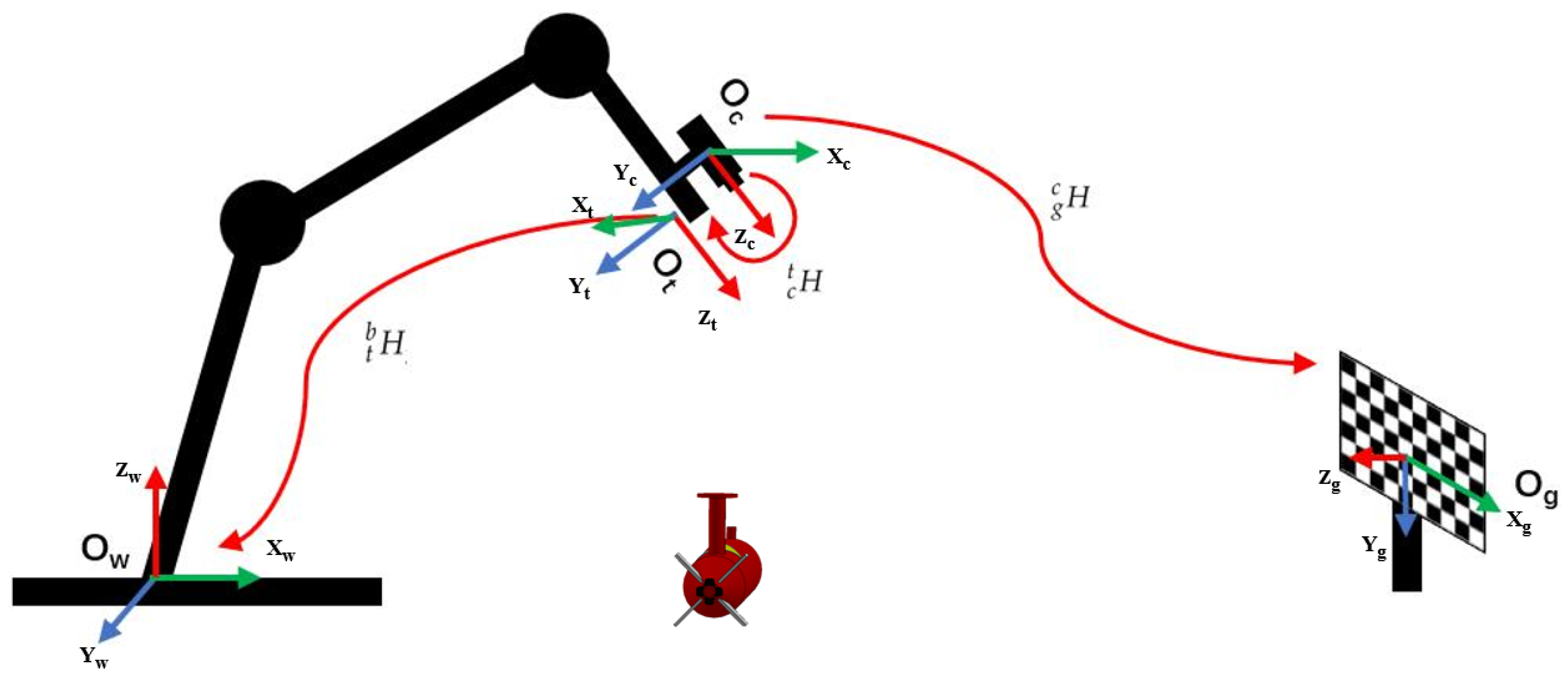
2.2.1. Coordinate System Conversion Relationship
2.2.2. Orientation Measurement Method
2.3. Position Optimization Based on CKF
2.4. LARS Control
3. Simulation and Experimental Results
3.1. Experimental Design of Simulation
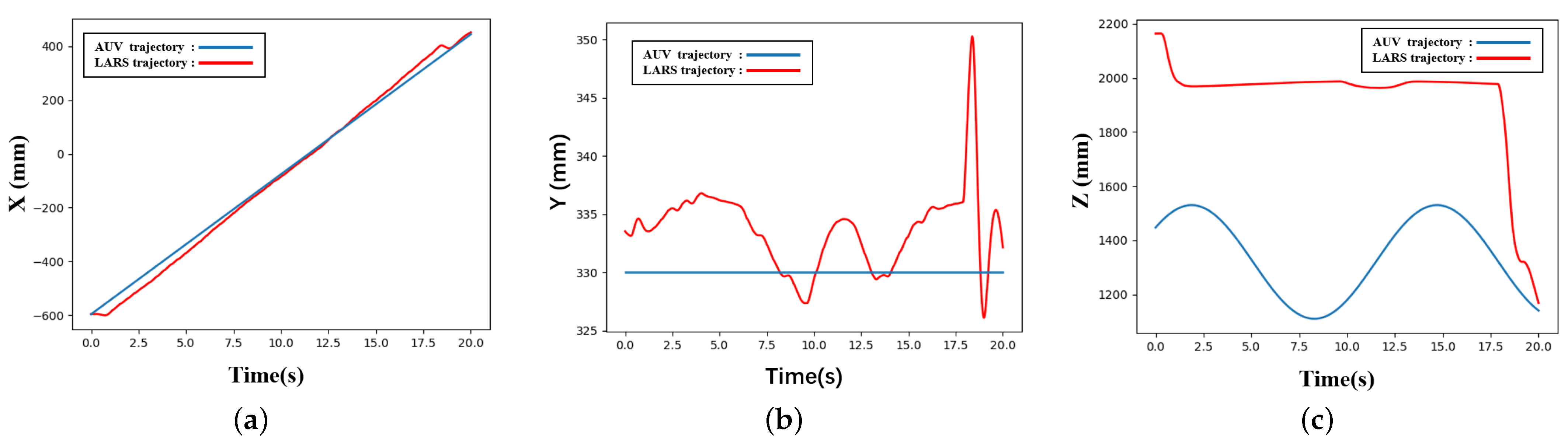
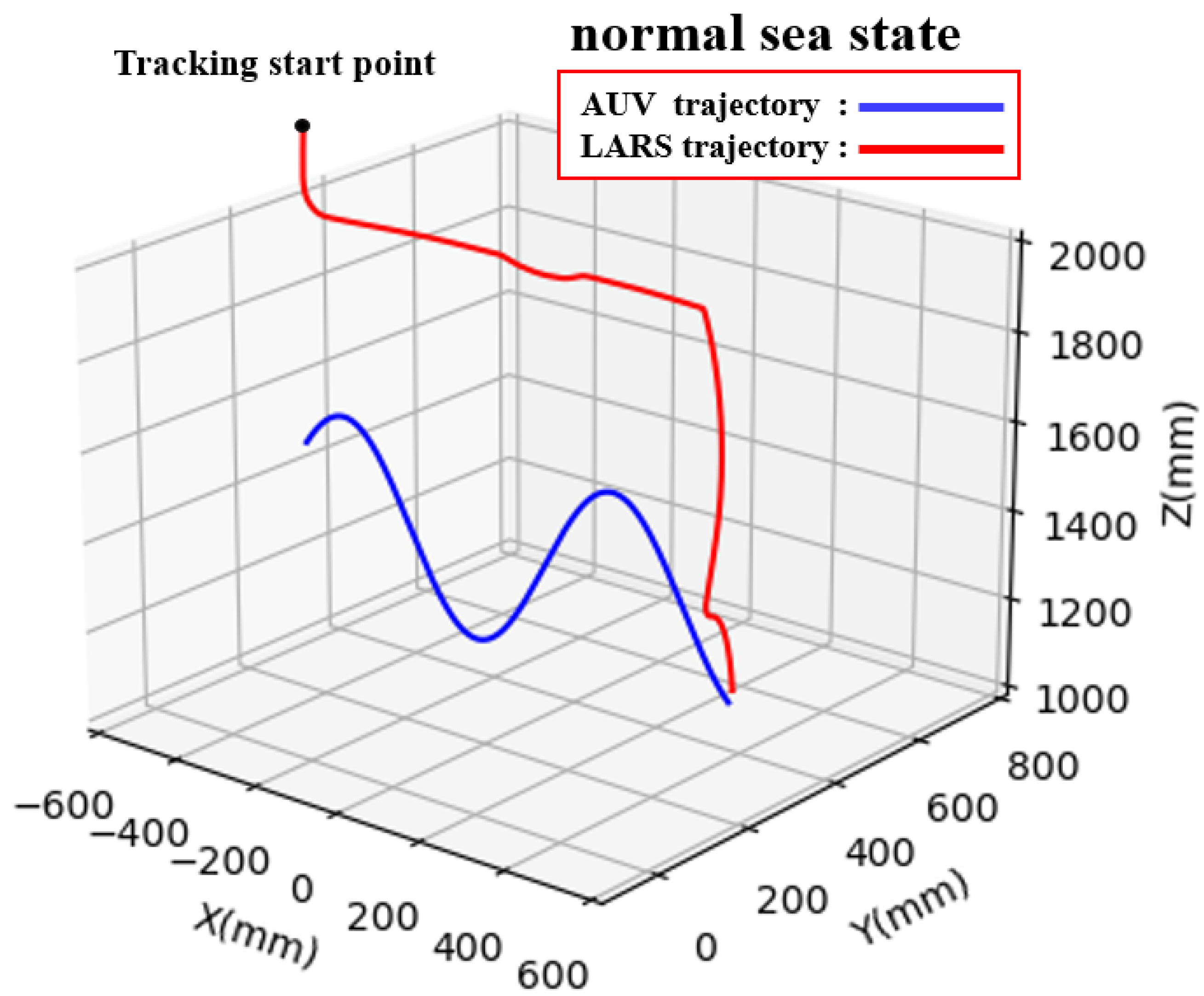
- First, we set LARS to be in an initial state, and we executed the end of LARS to obtain the image data. The image data’s simulated scene includes normal driving and bad sea conditions and similar interference. We mainly simulated severe sea conditions for the most common wave coverage interference. By reviewing the relevant literature [42,43], we found that the primary interference in the recovery process was the smaller ships during the simultaneous advance of the two ships, which exists in the direction of heave. Therefore, we set the AUV to perform sine wave movement on the Z axis, make a uniform linear motion on the X axis, and ensure that it is in a fixed position on the Y axis;
- Second, we used a binocular camera to obtain ocean images, and then we used the LTAT method to track the specified AUV in the image. We used the tracking results to calculate the AUV’s position, as well as its pitch and yaw angles;
- Finally, we regulated the end of LARS to follow the AUV’s position trajectory in accordance with the position results, avoiding collision with the AUV in the process. We operated the LARS to capture the AUV when it sinks on the Z axis.
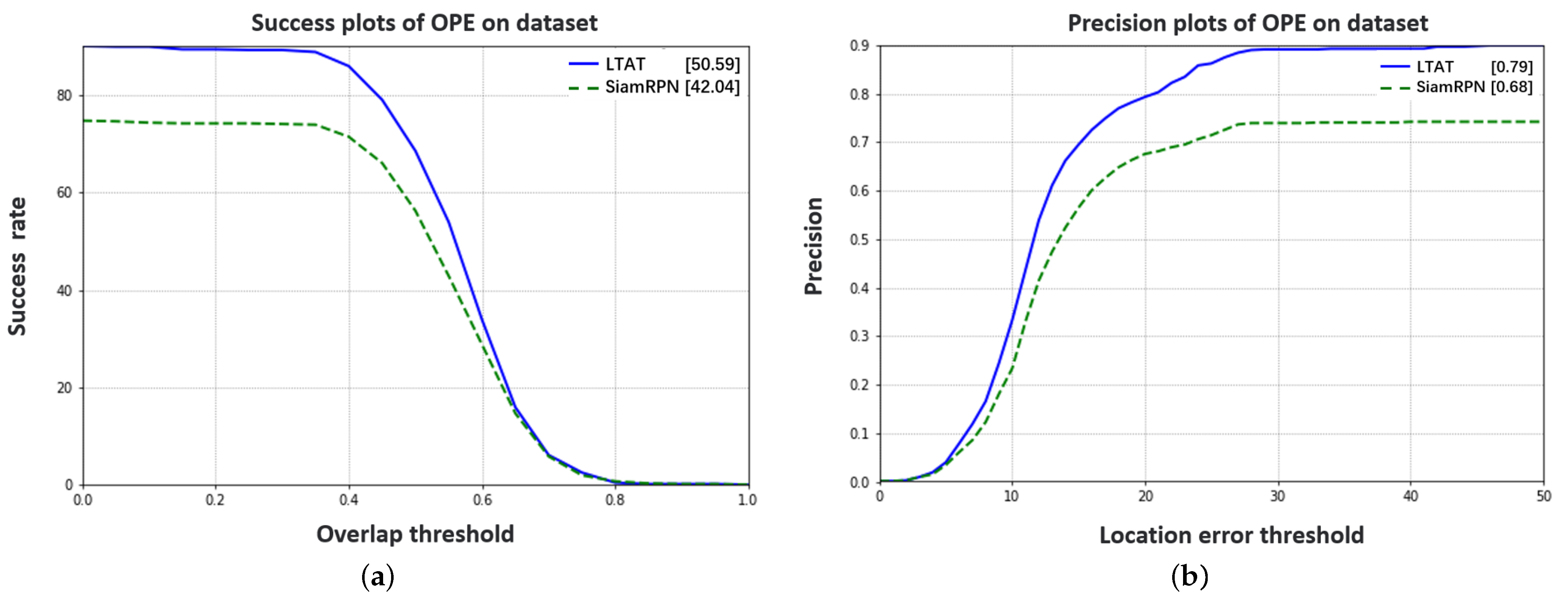
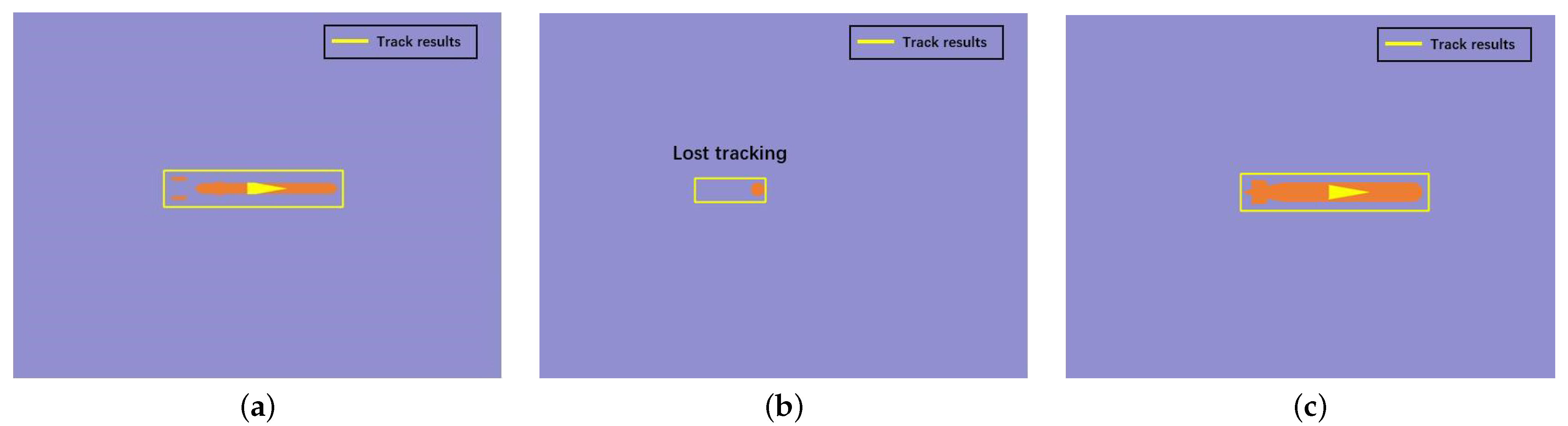
3.2. Long-Term Target Anti-Interference Tracking Experiment
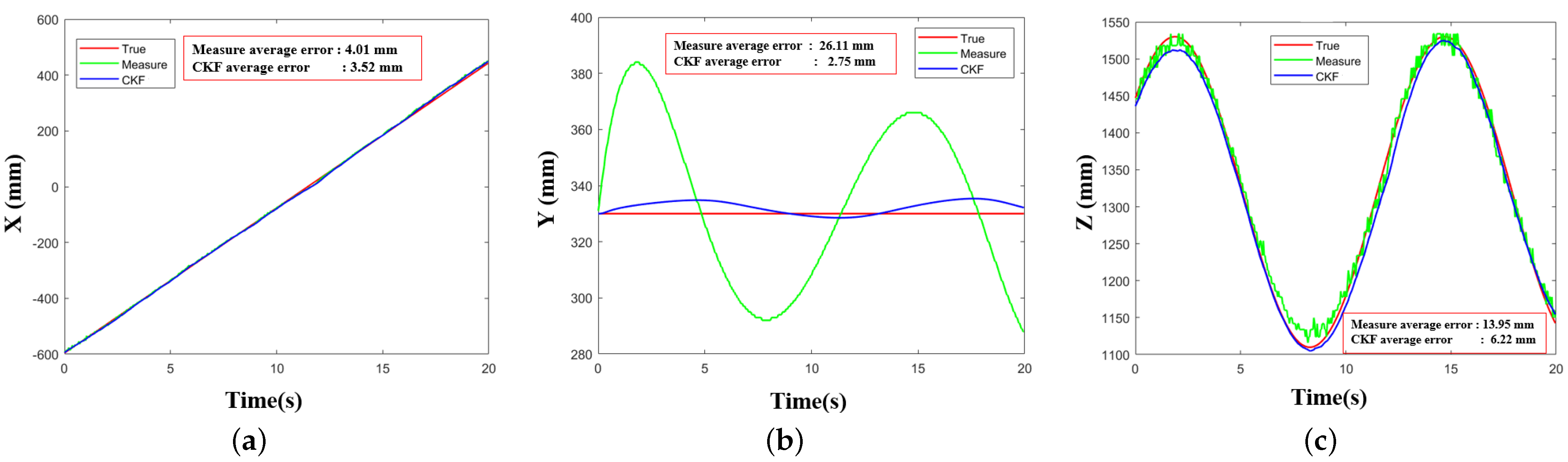
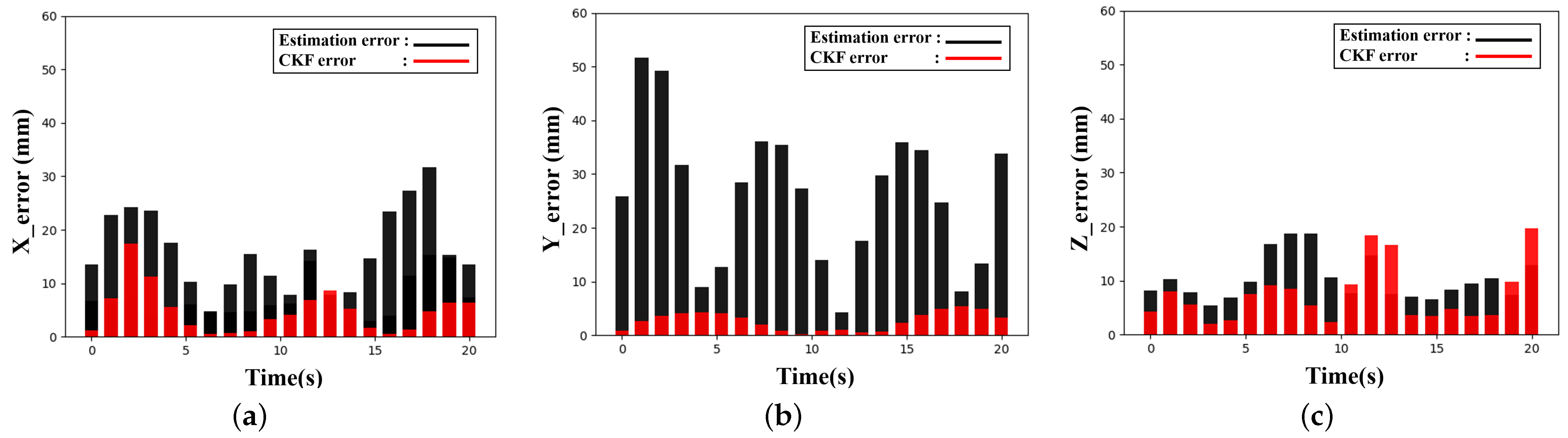
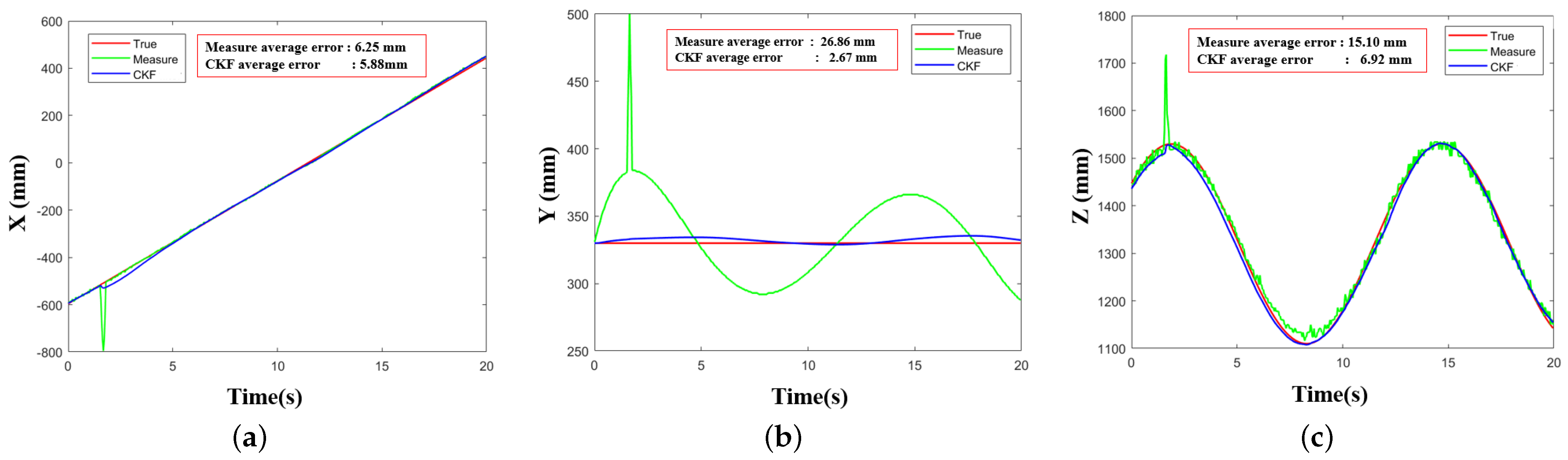
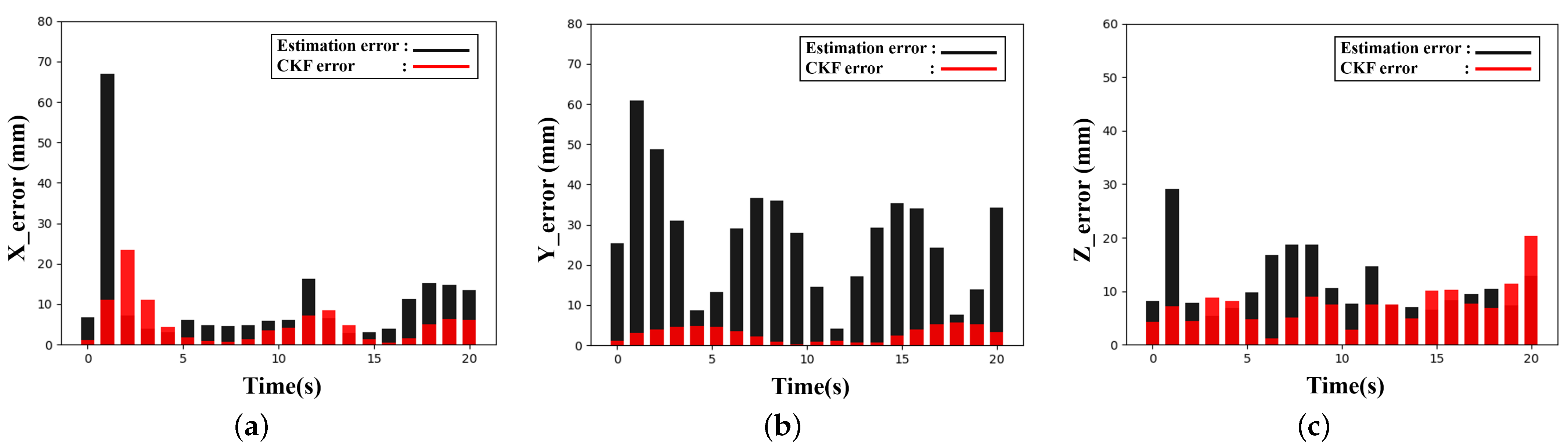
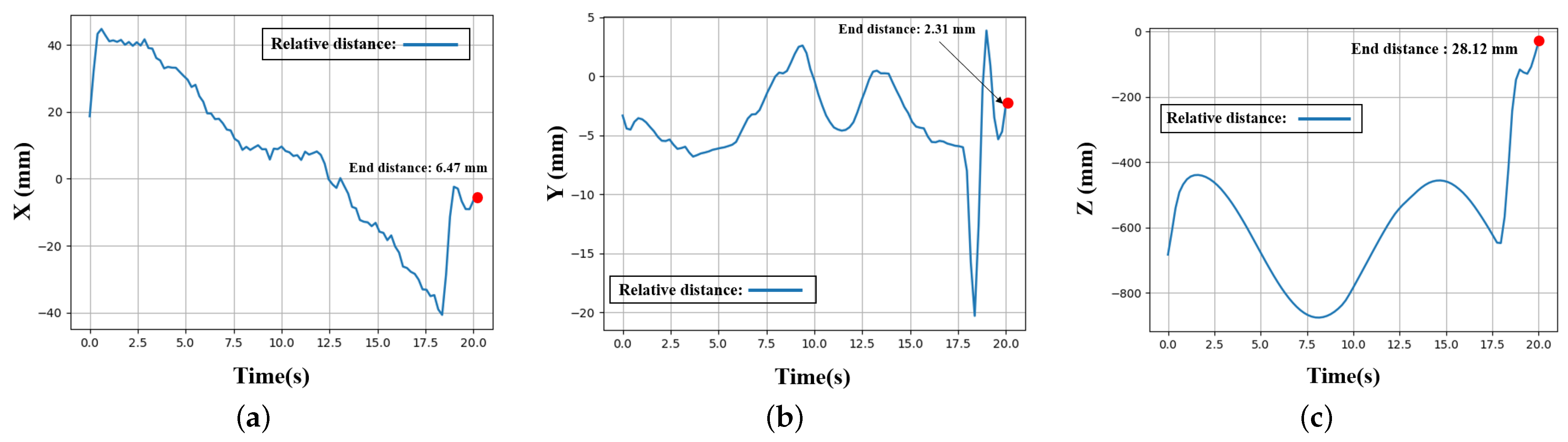
3.3. Relative Position and Orientation Estimation Experiments
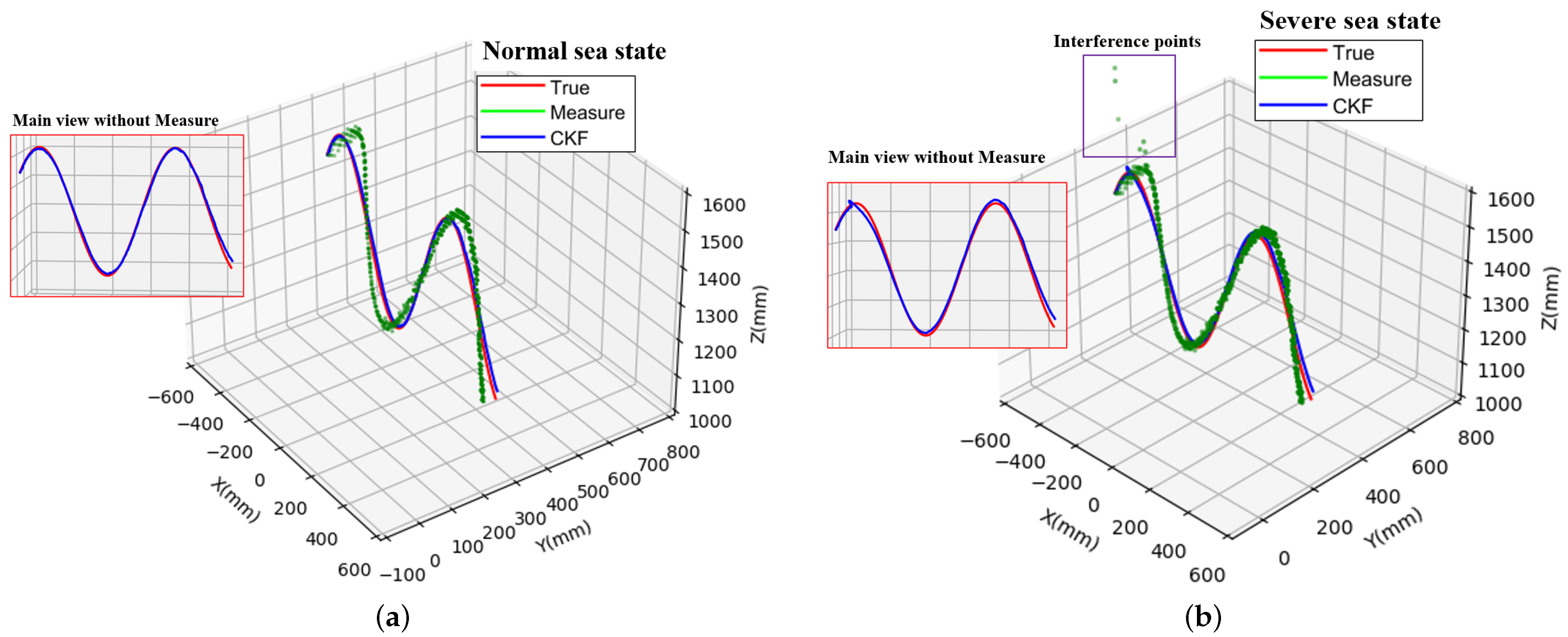
3.4. LARS Tracking Trajectory
4. Discussion
4.1. Performance Analysis of LTAT Method
4.2. Analysis of Position Estimation Method
4.3. Constraint and Improvement of Control Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AUV | Autonomous underwater vehicles |
| CKF | Cubature Kalman filter |
| EKF | Extended Kalman filter |
| GPU | Graphics processing unit |
| INS | Inertial navigation system |
| IMU | Inertial Measurement Unit |
| LARS | Launch and recovery system |
| LTAT | Long-term target anti-interference tracking |
| OPE | One-pass evaluation |
| PID | Proportion integration differentiation |
| ROS | Robot operating system |
| SiamRPN | Siamese region proposal network |
| UKF | Unscented Kalman filter |
| UWB | Ultra-Wide Band |
| VIO | Visual-Inertial Odometry |
| YOLO | You Only Look Once |
References
- Caruso, F.; Tedesco, P.; Della Sala, G.; Palma Esposito, F.; Signore, M.; Canese, S.; Romeo, T.; Borra, M.; Gili, C.; de Pascale, D. Science and Dissemination for the UN Ocean Decade Outcomes: Current Trends and Future Perspectives. Front. Mar. Sci 2022, 9, 863647. [Google Scholar] [CrossRef]
- Mabus, R. Autonomous Undersea Vehicle Requirement for 2025; Chief of Naval OPERATIONS Undersea Warfare Directorate: Washington, DC, USA, 2016. [Google Scholar]
- Zhang, F.; Marani, G.; Smith, R.N.; Choi, H.T. Future trends in marine robotics [tc spotlight]. IEEE Robot. Autom. Mag. 2015, 22, 14–122. [Google Scholar] [CrossRef]
- Zacchini, L.; Ridolfi, A.; Allotta, B. Receding-horizon sampling-based sensor-driven coverage planning strategy for AUV seabed inspections. In Proceedings of the 2020 IEEE/OES Autonomous Underwater Vehicles Symposium (AUV), St. Johns, NL, Canada, 30 September–2 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Mattioli, M.; Bernini, T.; Massari, G.; Lardeux, M.; Gower, A.; De Baermaker, S. Unlocking Resident Underwater Inspection Drones or AUV for Subsea Autonomous Inspection: Value Creation between Technical Requirements and Technological Development. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2022. [Google Scholar]
- Wang, C.; Mei, D.; Wang, Y.; Yu, X.; Sun, W.; Wang, D.; Chen, J. Task allocation for Multi-AUV system: A review. Ocean Eng. 2022, 266, 112911. [Google Scholar] [CrossRef]
- Liang, X.; Dong, Z.; Hou, Y.; Mu, X. Energy-saving optimization for spacing configurations of a pair of self-propelled AUV based on hull form uncertainty design. Ocean Eng. 2020, 218, 108235. [Google Scholar] [CrossRef]
- Zhang, B.; Xu, W.; Lu, C.; Lu, Y.; Wang, X. Review of low-loss wireless power transfer methods for autonomous underwater vehicles. IET Power Electron. 2022, 15, 775–788. [Google Scholar] [CrossRef]
- Heo, J.; Kim, J.; Kwon, Y. Technology development of unmanned underwater vehicles (UUVs). J. Comput. Commun. 2017, 5, 28. [Google Scholar] [CrossRef]
- Rong, Z.; Chuanlong, X.; Zhong, T.; Tao, S. Review on the Platform Technology of Autonomous Deployment of AUV by USV. Acta Armamentarii 2020, 41, 1675. [Google Scholar]
- Meng, L.; Lin, Y.; Gu, H.; Su, T.C. Study on the mechanics characteristics of an underwater towing system for recycling an Autonomous Underwater Vehicle (AUV). Appl. Ocean Res. 2018, 79, 123–133. [Google Scholar] [CrossRef]
- Sarda, E.I.; Dhanak, M.R. Launch and recovery of an autonomous underwater vehicle from a station-keeping unmanned surface vehicle. IEEE J. Ocean. Eng. 2018, 44, 290–299. [Google Scholar] [CrossRef]
- Sarda, E.I.; Dhanak, M.R. A USV-based automated launch and recovery system for AUVs. IEEE J. Ocean. Eng. 2016, 42, 37–55. [Google Scholar] [CrossRef]
- Haiting, Z.; Haitao, G.; Yang, L.; Guiqiang, B.; Lingshuai, M. Design and Hydrodynamic Analysis of Towing Device of the Automated Recovery of the AUV by the USV. In Proceedings of the 2018 IEEE International Conference on Information and Automation (ICIA), Wuyishan, China, 11–13 August 2018; pp. 416–421. [Google Scholar]
- Zhang, G.; Tang, G.; Huang, D.; Huang, Y. Research on AUV Recovery by Use of Manipulator Based on Vision Servo. In Proceedings of the The 32nd International Ocean and Polar Engineering Conference, Shanghai, China, 5–10 June 2022. [Google Scholar]
- Kebkal, K.; Mashoshin, A. AUV acoustic positioning methods. Gyroscopy Navig. 2017, 8, 80–89. [Google Scholar] [CrossRef]
- Maurelli, F.; Krupiński, S.; Xiang, X.; Petillot, Y. AUV localisation: A review of passive and active techniques. Int. J. Intell. Robot. Appl. 2022, 6, 246–269. [Google Scholar] [CrossRef]
- Wu, Y.; Lim, J.; Yang, M.H. Online Object Tracking: A Benchmark. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New York, NY, USA, 15–17 June 2013. [Google Scholar]
- Zhu, Z.; Wu, W.; Zou, W.; Yan, J. End-to-End Flow Correlation Tracking With Spatial-Temporal Attention. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New York, NY, USA, 15–17 June 2018. [Google Scholar]
- Wang, T.; Zhao, Q.; Yang, C. Visual navigation and docking for a planar type AUV docking and charging system. Ocean Eng. 2021, 224, 108744. [Google Scholar] [CrossRef]
- Wu, D.; Zhu, H.; Lan, Y. A Method for Designated Target Anti-Interference Tracking Combining YOLOv5 and SiamRPN for UAV Tracking and Landing Control. Remote Sens. 2022, 14, 2825. [Google Scholar] [CrossRef]
- Pham, M.T.; Courtrai, L.; Friguet, C.; Lefèvre, S.; Baussard, A. YOLO-Fine: One-stage detector of small objects under various backgrounds in remote sensing images. Remote Sens. 2020, 12, 2501. [Google Scholar] [CrossRef]
- Liu, S.; Xu, H.; Lin, Y.; Gao, L. Visual Navigation for Recovering an AUV by Another AUV in Shallow Water. Sensors 2019, 19, 1889. [Google Scholar] [CrossRef]
- Meng, L.; Lin, Y.; Gu, H.; Su, T.C. Study on dynamic docking process and collision problems of captured-rod docking method. Ocean Eng. 2019, 193, 106624. [Google Scholar] [CrossRef]
- Szczotka, M. AUV launch & recovery handling simulation on a rough sea. Ocean Eng. 2022, 246, 110509. [Google Scholar]
- Li, B.; Yan, J.; Wu, W.; Zhu, Z.; Hu, X. High performance visual tracking with siamese region proposal network. In Proceedings of the IEEE conference on computer vision and pattern recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8971–8980. [Google Scholar]
- Chen, X.; He, K. Exploring simple siamese representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 15750–15758. [Google Scholar]
- Zuo, M.; Zhu, X.; Chen, Y.; Yu, J. Survey of Object Tracking Algorithm Based on Siamese Network. J. Phys. 2022, 2203, 12035. [Google Scholar] [CrossRef]
- Benjumea, A.; Teeti, I.; Cuzzolin, F.; Bradley, A. YOLO-Z: Improving small object detection in YOLOv5 for autonomous vehicles. arXiv 2021, arXiv:2112.11798. [Google Scholar]
- Jiang, P.; Ergu, D.; Liu, F.; Cai, Y.; Ma, B. A Review of Yolo algorithm developments. Procedia Comput. Sci. 2022, 199, 1066–1073. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, C.; Dai, Y.; Feng, X.; Ma, Y.; Li, Q. Dual-View Stereovision-Guided Automatic Inspection System for Overhead Transmission Line Corridor. Remote Sens. 2022, 14, 4095. [Google Scholar]
- Auger, F.; Hilairet, M.; Guerrero, J.M.; Monmasson, E.; Orlowska-Kowalska, T.; Katsura, S. Industrial applications of the Kalman filter: A review. IEEE Trans. Ind. Electron. 2013, 60, 5458–5471. [Google Scholar] [CrossRef]
- Kim, T.; Park, T.H. Extended Kalman filter (EKF) design for vehicle position tracking using reliability function of radar and lidar. Sensors 2020, 20, 4126. [Google Scholar] [CrossRef]
- Jin, Z.; Zhao, J.; Chakrabarti, S.; Ding, L.; Terzija, V. A hybrid robust forecasting-aided state estimator considering bimodal Gaussian mixture measurement errors. Int. J. Electr. Power Energy Syst. 2020, 120, 105962. [Google Scholar] [CrossRef]
- Mazaheri, A.; Radan, A. Performance evaluation of nonlinear Kalman filtering techniques in low speed brushless DC motors driven sensor-less positioning systems. Control Eng. Pract. 2017, 60, 148–156. [Google Scholar] [CrossRef]
- Kulikov, G.Y.; Kulikova, M.V. Do the cubature and unscented Kalman filtering methods outperform always the extended Kalman filter? IFAC-PapersOnLine 2017, 50, 3762–3767. [Google Scholar] [CrossRef]
- Wan, M.; Li, P.; Li, T. Tracking maneuvering target with angle-only measurements using IMM algorithm based on CKF. In Proceedings of the 2010 International Conference on Communications and Mobile Computing, Shenzhen, China, 12–14 April 2010; IEEE: Piscataway, NJ, USA, 2010; Volume 3, pp. 92–96. [Google Scholar]
- Arasaratnam, I.; Haykin, S. Cubature kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Shen, C.; Zhang, Y.; Tang, J.; Cao, H.; Liu, J. Dual-optimization for a MEMS-INS/GPS system during GPS outages based on the cubature Kalman filter and neural networks. Mech. Syst. Signal Process. 2019, 133, 106222. [Google Scholar] [CrossRef]
- Naing, W.W.; Thanlyin, M.; Aung, K.Z.; Thike, A. Position Control of 3-DOF Articulated Robot Arm using PID Controller. Int. J. Sci. Eng. Appl. 2018, 7, 254–259. [Google Scholar]
- Bi, M. Control of Robot Arm Motion Using Trapezoid Fuzzy Two-Degree-of-Freedom PID Algorithm. Symmetry 2020, 12, 665. [Google Scholar] [CrossRef]
- Xie, N.; Iglesias, G.; Hann, M.; Pemberton, R.; Greaves, D. Experimental study of wave loads on a small vehicle in close proximity to a large vessel. Appl. Ocean Res. 2019, 83, 77–87. [Google Scholar] [CrossRef]
- Kashiwagi, M.; Endo, K.; Yamaguchi, H. Wave drift forces and moments on two ships arranged side by side in waves. Ocean Eng. 2005, 32, 529–555. [Google Scholar] [CrossRef]

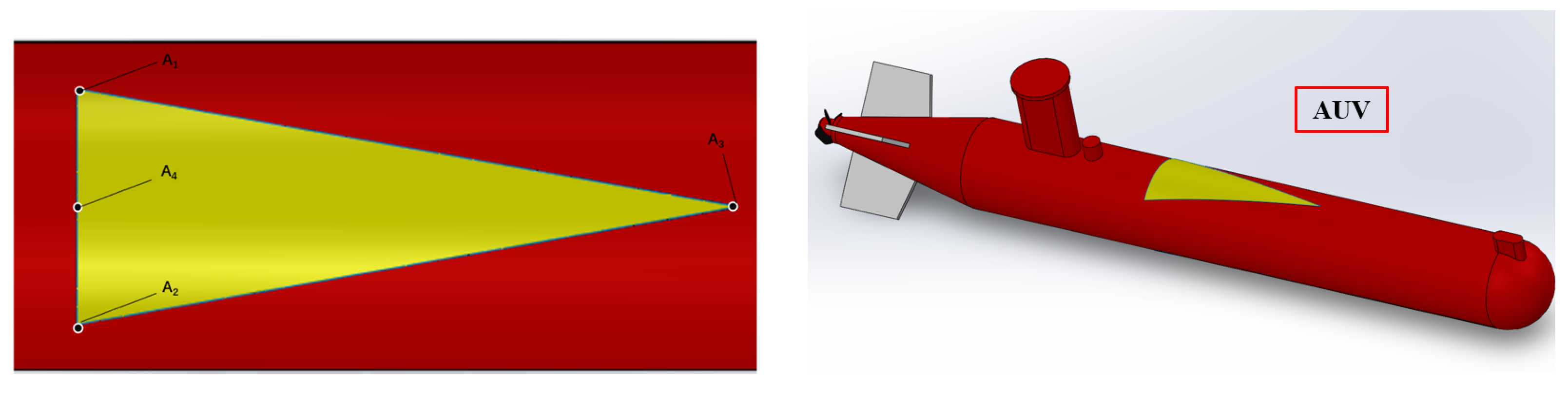

| Weight | Diameter | Length |
|---|---|---|
| 47 kg | 200 mm | 1.8 m |
| Set the Angle | 15 | 20 | 30 |
|---|---|---|---|
| Pitch angle | 14.7891 | 20.8188 | 33.4522 |
| Set the Angle | −30 | 0 | 30 |
|---|---|---|---|
| Yaw angle | −29.5647 | −0.0124 | −29.6427 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, T.; Situ, W.; Yang, W.; Zeng, W.; Wang, Y. A Method for Long-Term Target Anti-Interference Tracking Combining Deep Learning and CKF for LARS Tracking and Capturing. Remote Sens. 2023, 15, 748. https://doi.org/10.3390/rs15030748
Zou T, Situ W, Yang W, Zeng W, Wang Y. A Method for Long-Term Target Anti-Interference Tracking Combining Deep Learning and CKF for LARS Tracking and Capturing. Remote Sensing. 2023; 15(3):748. https://doi.org/10.3390/rs15030748
Chicago/Turabian StyleZou, Tao, Weilun Situ, Wenlin Yang, Weixiang Zeng, and Yunting Wang. 2023. "A Method for Long-Term Target Anti-Interference Tracking Combining Deep Learning and CKF for LARS Tracking and Capturing" Remote Sensing 15, no. 3: 748. https://doi.org/10.3390/rs15030748
APA StyleZou, T., Situ, W., Yang, W., Zeng, W., & Wang, Y. (2023). A Method for Long-Term Target Anti-Interference Tracking Combining Deep Learning and CKF for LARS Tracking and Capturing. Remote Sensing, 15(3), 748. https://doi.org/10.3390/rs15030748