Abstract
The differential interferometric synthetic aperture radar (DInSAR) method is based on phase variation between the complex value of pixels of timely separated scenes in interferometric SAR pairs. This phase variation has five components: surface topography, curvature of planet’s surface, terrain displacement, volume scatterers, and atmospheric propagation effects. The terrain displacement is the main product of the DInSAR method, while the last two effects are unpredictable and bring inaccuracy into the terrain displacement measurements. In this work, the propagation conditions in the troposphere and ionosphere were studied during two DInSAR measurements examining the Zagreb 22 March 2020 earthquake, with terrain raising of up to +3 cm at the epicenter. For the troposphere, the vertical profile of the modified refraction index, which incorporates local curvature change with height, was reconstructed using aerological balloon probing data. Ionospheric conditions were determined based on total electron content (TEC) calculated from the Croatian positioning system (CROPOS) and global navigation satellite system (GNSS) reference stations’ measurements. One of the DInSAR measurements was conducted in unfavorable tropospheric refractive conditions, which resulted in an overall bias of −2 cm. The variability of propagation conditions indicates the need for examining the atmospheric propagation effects when calculating terrain displacements using the DInSAR method. The results of DInSAR indicate slight displacements, comparable with the amplitude of atmospheric variations, and should therefore be approached with caution.
1. Introduction
Several geodynamic processes could produce terrain displacements: volcanic eruptions, earthquakes, landslides, surface subsidence, avalanches, glacier movements, flooding sedimentation, dune displacements, etc. Observation, detection, and relatively precise measurements of these phenomena are available today thanks to the synthetic aperture radar (SAR), which is mainly satellite-borne. Due to the high velocity of the radar platform, the radar antenna (aperture) changes its position rapidly during the period between emitting and receiving a radar impulse, producing an effect of synthetic enlargement of the aperture, which results with much better resolution of the radar image [1,2]. During March 2020, both Sentinel-1A and Sentinel-1B SAR satellites were active, and their data are used in this work. The differential interferometry SAR (DInSAR) is based on a pair of SAR images: the reference image and the complex conjugate secondary image (amplitudes and phases of the SAR image are converted in the form of complex numbers) to achieve the phase variation between them [2,3].
The influence of the atmosphere on the propagation of SAR radio waves is not negligible, and is difficult to predict [4]. In the mid-1990s, some of the first publications on atmospheric artifacts on DInSAR [5,6,7] identified spatial and temporal variations in the atmospheric condition as their main causes. Sentinel-1 satellites orbit the Earth at the altitude of 693 km, at the edge between the thermosphere and exosphere, and the signals of their SAR instruments must pass twice through the thermosphere, mesosphere, stratosphere, and troposphere. The thermosphere and upper mesosphere (defined by the temperature profile) coincide with the layers of the ionosphere (defined by the content of charged particles) [8]. The lower mesosphere and stratosphere can be considered stable in terms of refractive conditions for radio waves, but the ionosphere and troposphere are highly variable; the ionosphere due to charged particles, and troposphere due to water vapor content [9]. At the global level, regular measurements are performed for the troposphere and ionosphere, and based on their results, the current propagation conditions in these two atmospheric layers can be reconstructed and investigated [8,10,11,12,13]. Detection of unfavorable refractive conditions in the troposphere and ionosphere would suggest additional caution in interpreting the terrain displacements measured using the DInSAR method.
Impact of tropospheric and ionospheric effects on DInSAR measurements and its corrections have been studied in numerous recent scientific papers [14,15,16,17,18,19,20,21]. Murray, Bekaert, and Lohman [22] determined that the quality of estimated tropospheric delay is related to local properties of the troposphere and the spatial and temporal scale of the observed area, as well as the spatiotemporal resolution and accuracy of the applied correction method. The overview of tropospheric correction requirements and approaches is nicely outlined and described in the papers by Liu, Zeng, and Zhang [21] and Milczarek, Kopec, and Glabicki [18]. Three main requirements for a tropospheric correction method to be effective are highlighted in [21] as: (1) it should account for different components in the troposphere [6,23,24,25,26], (2) the time difference between the acquisition of SAR images and atmospheric data should be minimal or as close as possible [16,27], and (3) the spatial scale of the correction should capture changes in tropospheric delay in the horizontal direction [26]. Furthermore, tropospheric and ionospheric correction techniques based on DInSAR can generally be categorized as [18]: (1) empirical [28,29,30,31,32,33,34], (2) based on weather models [21,35,36,37], (3) based on spectrometer data [38,39], or (4) based on GNSS data [40,41].
A catastrophic geodynamic event, the earthquake that took place on 22 March 2020 with the epicenter on the southeast slope of the Medvednica mountain near Zagreb, the capital of Croatia, was observed using two SAR interferometric pairs, with Sentinel-1B (11 and 23 March 2020) and with Sentinel-1A (17 and 29 March 2020). The geological setting, tectonics overview, and the seismicity of the observed area can be found in the work of Markusic et al. [42]. The observed line-of-sight (LOS) terrain displacements in the vicinity of the epicenter were about 3 cm [42], which is close to the absolute error of the DInSAR method with Sentinel-1 instruments [43]. The relatively low absolute value of the terrain displacement actuated detailed research of the atmospheric refractive conditions during the days of the SAR acquisitions, especially in the troposphere and ionosphere, the two atmospheric layers with dominant effects on the propagation of the SAR signals.
In this paper, we analyzed the tropospheric and ionospheric refractive conditions corresponding to the aforementioned Sentinel-1A and Sentinel-1B acquisitions. Determined atmospheric conditions proved to be useful in explaining the bias between the displacements calculated by DInSAR processing of two subsequent image pairs.
2. Materials and Methods
2.1. Error Sources in Differential Interferometry SAR
The phase variation between SAR interferometric images could be transformed into terrain displacement (if the displacement occurs in the interval between reference and secondary image acquisition) using technological availability of very accurate determination of the satellite positions during the acquisition of the reference image and secondary image [3,13,44,45,46,47].
The phase variation between the reference and secondary image depends on five components [3,43]:
where is the topographic phase, which came into existence due to the surface topography; is the flat Earth phase derived from the curvature of the planet’s surface; is the phase component that came into existence if any terrain displacement occurred; is the phase difference due to atmospheric (radio refraction) effects; is the unpredictable influence of the volume scatterers on the surface and the different look angles.
The noise term is greatly reduced on the Sentinel-1 SAR due to the use of terrain observation with a progressive scan (TOPSAR) mode instead of older ScanSAR technologies. TOPSAR provides the same coverage but with a nearly uniform radar signal parameters, both distributed target ambiguity ratio (DTAR) and signal to noise ratio (SNR) [43].
The goal of the DInSAR method is the determination of the terrain displacement so that Equation (1) could be expressed to obtain :
The topographic phase and the flat Earth phase (2) are proportional to the slant range displacements shown in Figure 1. In fact, both are geometrically determined as [3]:
where (as shown in Figure 1) is the location of satellite taking reference image, is the location of satellite taking secondary image, is the perpendicular baseline between S1 and S2 successive acquisition points, is the range measured from the S1, is the ground altitude difference due to actual terrain (relief), is the acquisition (incidence) angle for a particular image pixel, is the wavelength of radar wave, the central frequency of the Sentinel-1 SAR is 5.405 GHz, which means a wavelength of 5.55 cm in space (slightly less in the atmosphere due to the refractive index), is the change in R due to the vertical displacement of the surface.

Figure 1.
The basic geometry of DInSAR.
With precise knowledge of the satellite positions and times of acquisition at S1 and S2 in Figure 1, it is possible to compute and correct both topographic and flat Earth influences. This procedure is called the “interferogram flattening”. That way, the right side of Equation (2) is ready for use. However, the left side of Equation (2) still has two non-negligible terms: the atmospheric (refractive index profile) and unpredictable surface scatterers . The atmospheric influence appears as a low-frequency spatial variation of the computed in the last row of Equation (3).
In order to be suitable for the displacement computing by Equation (2), both images of the interferometric pair should have strong similarities, i.e., the images in the interferometric pair must have a significant amount of coherence [48]. Estimation of the coherence between the master and the slave image is estimated as the quantitative measure of the phase information quality in the interferometric pair. Low-coherence values indicate that the phase information may not be usable, because the weak coherences usually produce poor results during the unwrapping phase in the DInSAR processing.
2.2. Atmospheric Refractive Conditions
The mesosphere and the stratosphere have refractive index profiles [8] which are stable enough to preserve the refractive profiles during the acquisition of both SAR images in the interferometric pair, resulting in no phase difference due to the influence of these two atmospheric layers. The refractive stability of the stratosphere was confirmed over the Adriatic [10] and Alpine [49] regions in two studies that used the standard aerological balloon probing technique for altitudes up to 40 km. The studies have shown that in the observed areas, the vertical profile of the stratospheric refractive index was on the brink of subrefraction, but very stable, starting from the tropopause up to the highest altitudes reached by aerological balloons.
The troposphere, as the lowest atmospheric layer, contains almost all the atmospheric water vapor, the most variable ingredient of the atmosphere with a strong influence on electromagnetic propagation. The signal path through the troposphere, though relatively short (twice 10–12 km; 67 μs to 80 μs), can introduce heavy phase disturbances to the SAR signal.
In the ionosphere, at heights between 50 km and 2000 km, the free electrons and ions are present in quantities sufficient to affect the propagation of radio waves. The ionosphere is also very variable and causes phase advance of the signal. Unfortunately, there is no simple, deterministic model of the refractive index profile for the entire atmosphere. The atmospheric phase screen (APS), the faulty phase shift in the interferometric pair caused by atmospheric refractive conditions [14,50], cannot be determined quantitatively, due to the lack of appropriate rocket atmospheric soundings up to the satellite orbits. Instead, the regular sounding of the troposphere and ionosphere should be used qualitatively to determine and examine the anomalies in the vertical profile of the refractive index in these two observed layers.
2.2.1. Determination of the Tropospheric Refractive Conditions
Tropospheric refractive conditions depend on vertical profiles of air temperature, total air pressure, and humidity of the air [4]. The profile of the air humidity has the greatest effect, due to the dipole structure of the water molecule. During decades of atmospheric radio propagation research, several empirical equations for refractive conditions were developed [12,51]. All these equations use measurements of air pressure (total or water vapor pressure), air temperature, and humidity (absolute, relative, or specific humidity). Some of the equations are applicable to surface measurements only, due to the relatively narrow temperature range. An equation with a wide enough temperature range (−100 °C to +50 °C) was developed by the Naval Research Laboratory [52], in the form of refractive index n determination:
where the thermodynamic air temperature (T) and total air pressure (p) come from the aerology sounding data (hydrogen-filled balloons with ceiling up to 40 km). The humidity of the air was determined in the “wet” term of the Equation (4) with y, a function of relative humidity (rh) of the air:
and the relative humidity could be computed as a ratio of partial pressure of water vapor pressure (e) to saturated vapor pressure (es):
The constant values in Equations (7) and (8) are the pressure of the saturated water vapor at 0 °C = 6.11 hPa, the latent temperature of vaporization = 2.5 × 106 J kg−1 and the gas constant of the water vapor = 461.5 J K−1 kg−1. All of the variables in Equations (4)–(8) are available from aerological balloon soundings. These soundings take place in regular intervals at 6:00, 12:00, 18:00, and 24:00 UTC, simultaneously, all over the world (many countries contribute with just one or two soundings daily). The nearest aerological station to the observed Zagreb earthquake area is the Zagreb Maksimir station, with World Meteorological Organization (WMO) index 14,240, where measurements are conducted at 12:00 and 24:00 UTC.
In order to describe refractive conditions in the atmosphere (normal or anomaly, so-called ANAPROPs), the curvature of the radio propagation path has to be considered too in the ratio of height over surface and radii of the Earth (h/Re), producing the modified refraction index M [52,53]:
Even though M is a dimensionless physical quantity, it is usually referred to in so-called “M units”. The vertical gradient of the M is used to describe refractive conditions, normal or three types of anomalous propagation conditions, ANAPROPS (Table 1). The commonly used units of the vertical gradient of the modified refraction index are M [dimensionless]/km, but one has to be aware that its variability is significant over much a smaller height range than a kilometer.

Table 1.
Types of radio propagation [52,53].
2.2.2. Determination of Ionospheric Refractive Conditions
The ionospheric refraction causes the group delay and phase advance proportional to the level of ionization, quantified by the total electron content (TEC):
where Ne is the number of electrons on the signal path between the satellite and ground, with a cross-section of 1 m2 [54]. The ionospheric sounding used to determine the number of electrons can be conducted using ionosondes, satellite in situ measurements, and global navigation satellite systems (GNSSs) signals [11]. The ionospheric error, expressed as an error in calculated distance between the satellite and the observed ground ΔIS, is calculated using Equation (11):
The frequency f used in Sentinel-1 SAR is 5.405 GHz, while GNSSs use several frequencies in the L band. As GNSS-derived ionospheric data are captured by a limited number of GNSS receivers, in the areas between the received signals’ paths, the state of ionosphere needs to be defined. It can be executed either by normalizing the values of measured ionospheric errors and interpolating in the areas between, or by driving an ionospheric model with such locally available data [55]. In this research, we used a single-layer model of ionosphere, located at a height of 350 km, where the ionization level (which affects the signal propagation) is the highest [56]. All the slant values of ionospheric error were translated to vertical values on locations where the signals crossed the 350 km height layer, in order to be comparable and useful for interpolation. The translation of slant values to vertical ones, and vice versa, is conducted using a mapping function. As the satellite elevation El (complementary to incidence angle θ) lowers down from the zenith towards the horizon, the signal path through the ionosphere gets longer, and the ionospheric error increases from the zenith value by the factor of MI:
with Re being the Earth radius and hI the height of 350 km [56].
In SAR-related literature, the ionospheric error is usually defined by equations that express the amount of phase error [29,57], but for clarity and comparison with the amount of DInSAR calculated displacements, in this paper we quantified the ionospheric error with distance error ΔIS instead.
If the level of ionization in the area of interest would be equal in the periods of taking a pair of SAR images to be used for differential interferometry, the ionosphere would not affect the measurement quality. However, that is rarely the case, as the ionosphere is dynamic and prone to spatial and temporal changes. The ionization of the ionosphere changes diurnally, seasonally, with solar and geomagnetic activity, and with geomagnetic coordinates. For a location of interest there is no spatial change, and DInSAR is usually calculated from subsequent satellite passes that occur at the same local time, twelve days apart. Therefore, diurnal and seasonal variations can also be neglected, and geomagnetic conditions remain the main driver of possible ionospheric variations.
During March 2020, the 11-year solar activity cycle was in its minimum, between solar cycles 24 and 25, and the geomagnetic field was not affected by coronal mass ejections. In such a middle-latitude location and quiet ionospheric conditions, the GNSS-derived ionospheric data (such as global or local ionospheric maps) can be used to assess the ionospheric delay of the Sentinel-1 SAR signal [57]. As Sentinel-1 satellites orbit the Earth, they are located within the top layers of the ionosphere. On top of that, the ionospheric error, calculated from GNSS signals originating from medium-earth orbit, contains the contribution of the topside ionosphere situated above the Sentinel-1 satellites, which has a share of 15–20%. Due to the higher frequency of Sentinel-1 signals compared to the L-band GNSS and L-band SAR signals, the contribution of ionospheric error for Sentinel-1 signals is an order of magnitude lower, so the topside ionosphere error contribution is usually neglected [57].
3. Results
3.1. Tropospheric Refractive Conditions
The aerological soundings are very useful, because any sudden change in telemetrically measured data (temperature, dew point, geopotential, or air pressure) is reported as a “significant level” which could signal an anomalous propagation [49]. Using methods for determining refractive conditions in the lower layers of the atmosphere, as described in Equations (4)–(8), we have researched the vertical profiles of the refraction index for radio waves, computed from aerological probing data. Data were obtained from the Atmospheric Soundings Website, University of Wyoming, College of Engineering, Department of Atmospheric Sciences (http://weather.uwyo.edu/upperair/sounding.html, accessed on 20 September 2022). Measured data are presented in Appendix A at the end of the article in Table A1, Table A2, Table A3 and Table A4, corresponding to the aerological measurements nearest to the time of SAR measurements used in this research. Along with the available measurement data, Table A1, Table A2, Table A3 and Table A4 contain the data computed within the scope of this research, including modified refraction index M, refractive index n, vertical gradient of the modified refraction index dM/dh, and the type of refraction.
3.1.1. Tropospheric Refractive Conditions for the Sentinel-1A Interferometric Pair
During the aerological sounding on 17 March 2020 at 12:00 UTC (13:00 locally), which was the closest in time to the acquisition of the first image of the Sentinel-1A interferometric pair that started on 16:50 UTC that day, almost normal refractive conditions prevailed all over the troposphere and stratosphere up to the height of 31,803 m above ground (data available in Table A1). Figure 2a depicts the vertical profile of the modified refraction index M for radio waves. The profile shows the almost linear dependence of the modified refraction index, according to the height through the troposphere. Figure 2b shows the vertical profile of the modified refraction index gradient (dM/dh in Table A1). The only exception in refractive conditions is a layer with slightly subrefractive conditions (dM/dh = 160.08 km−1), which lies between the heights of 1171 m and 1467 m above the ground. The wind data, which are not applicable for the calculations within the scope of this paper, are preserved to illustrate relatively calm conditions all over the heights of up to 32 km above ground. According to the 17 March 2020 12:00 UTC soundings, the upper boundary of the troposphere was at 10,909 m. The stratospheric modified refraction index was stable on the brink of subrefractive conditions, which is consistent with the model of the standard atmosphere [8] and findings of a research with the same methodology [10].
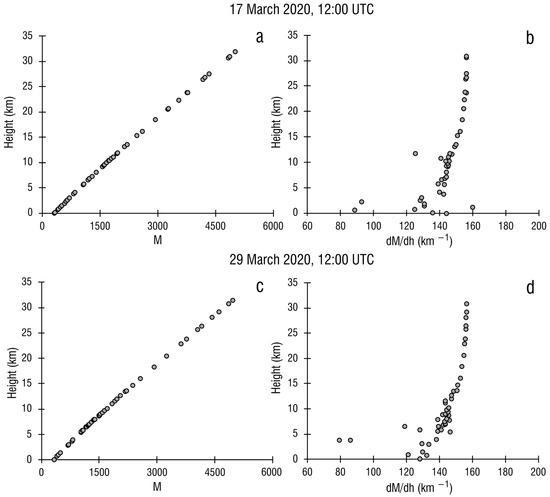
Figure 2.
Tropospheric refractive conditions during aerological probing over Zagreb, Croatia, nearest in time to the acquisition of the Sentinel-1A pair of images: (a) vertical profile of the modified refraction index on 17 March 2020, 12:00 UTC; (b) vertical profile of the modified refraction index gradient on 17 March 2020, 12:00 UTC; (c) vertical profile of the modified refractive index on 29 March 2020 at 12:00 UTC; (d) vertical profile of the modified refraction index gradient on 29 March 2020, 12:00 UTC.
The tropospheric refraction profile shows expected variations of the gradient of the modified refraction index (Figure 2b,d and Figure 3b,d) mostly due to the variability of moisture in the troposphere (water vapor pressure e in Appendix A; Table A1, Table A2, Table A3 and Table A4). The same information is available graphically in thermodynamic diagrams in Figure 4 and Figure 5, where the small difference between air temperature and dew point represents the moist layer.
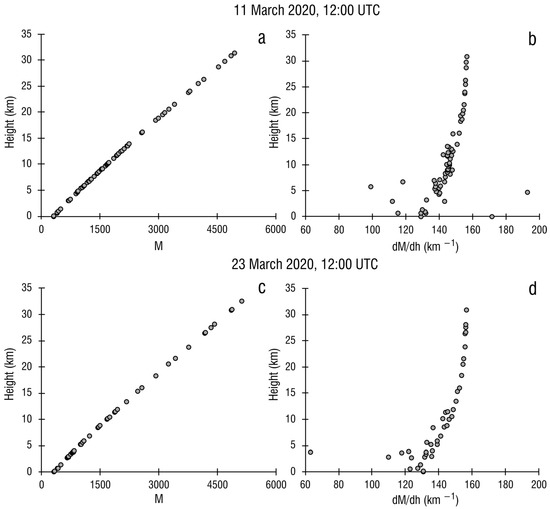
Figure 3.
Tropospheric refractive conditions during aerological probing over Zagreb, Croatia, nearest in time to the acquisition of the Sentinel-1B pair of images: (a) vertical profile of the modified refraction index on 11 March 2020, 12:00 UTC; (b) vertical profile of the modified refraction index gradient on 11 March 2020, 12:00 UTC; (c) vertical profile of the modified refraction index on 23 March 2020 at 12:00 UTC; (d) vertical profile of the modified refraction index gradient on 23 March 2020, 12:00 UTC.
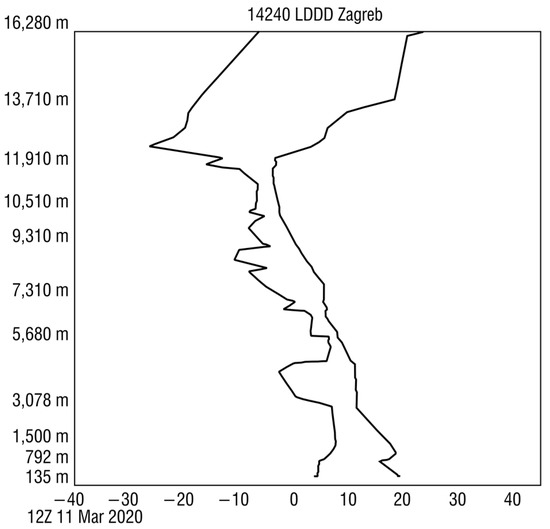
Figure 4.
Vertical profiles of air temperature (right) and dew point (left) based on probing data over Zagreb, Croatia, on 11 March 2020, 12:00 UTC. The right solid black curve is profile of the air temperature while left black solid curve is the dewpoint profile, heights at which significant differences in temperature profiles occur compared to the standard atmosphere (so-called “significant levels”) are marked (source: University of Wyoming website, URL http://weather.uwyo.edu/upperair/sounding.html, accessed on 20 September 2022).
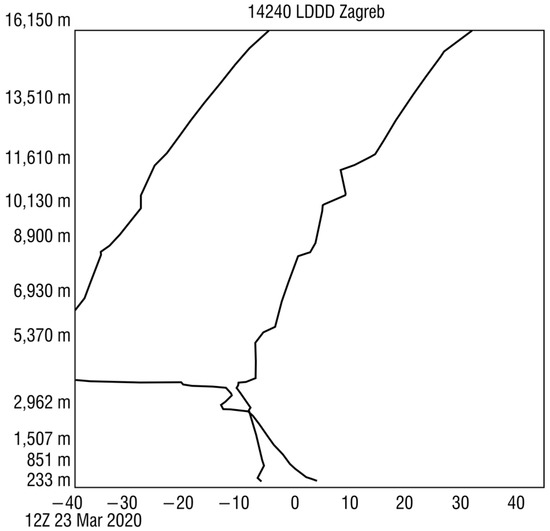
Figure 5.
Vertical profiles of air temperature (right) and dew point (left) based on probing data over Zagreb, Croatia, on 23 March 2020, 12:00 UTC. The right solid black curve is profile of the air temperature while left black solid curve is the dewpoint profile, heights at which significant differences in temperature profiles occur compared to the standard atmosphere (so-called “significant levels”) are marked (source: University of Wyoming website, URL http://weather.uwyo.edu/upperair/sounding.html, accessed on 20 September 2022).
The second image of the Sentinel-1A interferometric pair was acquired on 29 March 2020 16:50 UTC and the closest aerological sounding occurred at the Zagreb Maksimir station on 12:00 h UTC. The refractive conditions computed from the measurements show normal refractive conditions all the way up to 31,451 m above ground (data available in Table A2). Figure 2c depicts the change in the modified refraction index M with height, and Figure 2d depicts the vertical gradient of the modified refraction index. The descriptions are almost identical to the situation depicted in Figure 2a,b. Please note the two layers with almost superrefractive refraction at levels between 3653 m and 3847 m. Such conditions are not uncommon, especially in the lower half of the troposphere, and were recorded in some earlier works [10,49]. The upper boundary of the troposphere was at 11,202 m, slightly higher than on 17 March.
3.1.2. Tropospheric Refractive Conditions for the Sentinel-1B Interferometric Pair
The Sentinel-1B interferometric pair was acquired under more unfavorable meteorological conditions in the troposphere which resulted in less standard vertical profiles of the refraction indexes. The first image of the Sentinel-1B interferometric pair was acquired on 11 March 2020 at 16:50 UTC. The aerological probing nearest in time to that image took place on the same day, at 12:00 UTC (data available in Table A3). The vertical profile of the modified refraction index and its gradient show usual variability in the lower half of the troposphere, but still inside the boundaries of the normal refraction (Figure 3a,b). The exception from normal conditions existed in two layers where a refraction anomaly, the subrefraction, was detected. One was a shallow surface layer, and the other one was an elevated layer between 4745 m and 4814 m, at the upper boundary of the dry air layer. An examination of the Figure 4, based on the data from the Table A3, shows that a layer of exceptionally dry air was present between 3335 m and 4814 m with an elevated subrefractive layer at the upper boundary. Strong NNW wind was present over the upper half of the troposphere. The air in the stratosphere was dry, as expected in the standard model of the atmosphere [8].
The second image of the Sentinel-1B interferometric pair was acquired on 23 March 2020 at 16:50 and the aerological probing nearest in time to that image took place on the same day at 12:00 UTC (data available in Table A4). The refractive conditions of the probing are depicted in Figure 3c,d. They were mostly within boundaries of normal conditions, with the exception of a superrefractive layer between 3806 m and 3841 m. Figure 5 shows that this superrefraction is tied to the lower boundary of unusually dry air above 3714 m height.
In the lower part of the stratosphere, the vertical profile of the modified refractive index M for radio waves and its gradient with height showed stable and predictable refractive conditions [10], still normal, but very close to the subrefraction (Figure 2 and Figure 3). These findings are consistent with the standard model of the atmosphere and confirm the negligible influence of the stratosphere on DInSAR errors [11,12].
The refractive conditions’ variability was caused mostly by sudden changes of the moisture profile. These phenomena are characteristic in thermodynamically complex situations, especially in the lower half of the troposphere. The exact refraction conditions (normal or ANAPROP) are determined by the value of the vertical gradient of modified refraction index dM/dh. Figure 2b,d and Figure 3b,d confirm that the troposphere, even though it is a relatively thin atmospheric layer, can introduce variability in the modified refraction index gradient. However, the tropospheric refractive conditions were normal for the Sentinel-1A pair, but showed subrefraction and superrefraction for the Sentinel-1B images. Diagrams in Figure 4 and Figure 5 show an overview of the vertical profile of the moisture and reveal the presence of layers with sudden differences of the air temperature and dew points marking the layers of the ANAPROP refraction conditions.
3.2. Ionospheric Refractive Conditions
To evaluate geomagnetic conditions in the observed area during the InSAR measurements, the geomagnetic K indices [58], which represent the disturbance of geomagnetic field which affects the state of ionosphere, were analyzed. The Chambon la Foret observatory is situated on a latitude of 48.025°N, similar to the observed area, and for 15–18 h UTC on the dates 11, 17, 23, and 29 March 2020 had K index values of 1, 1, 2, and 3, respectively. Such values represent low ionospheric activity, with some variations towards the end of the month, and slightly higher geomagnetic activity during the acquiring of the second Sentinel-1A image. The Lonjsko polje geomagnetic observatory’s (situated very close to the earthquake epicenter at coordinates 45.41°N 16.66°E) K index data in the periods of interest were very similar, with values of 1, 2, 2, and 3 for 11, 17, 23, and 29 March 2020, respectively [59]. The global Dst index for the observed time and dates had values of 7 nT, −10 nT, −11 nT, and −11 nT [60,61]. Dst indices also confirm the quiet state of the ionosphere. The value on the 11 March, when the first Sentinel-1B image was taken, differs from the rest of the values, but as Dst is a global index, it does not necessarily represent the local geomagnetic and ionospheric conditions [60].
As shown in Equation (11), the ionospheric error is frequency dependent, so the ionization of the ionosphere can be determined using GNSS signals on two frequencies. In this paper we used receiver independent exchange format (RINEX) data [62] from CROPOS reference GNSS stations in Čakovec (CAKO) and Zagreb (ZAGR), containing the GPS and GLONASS dual frequency L band (L1 and L2) data generated in the time of Sentinel-1 InSAR measurements. The Ciraolo calibration [63] was applied to RINEX observation and navigation files to calculate calibrated Slant TEC (STEC) for each satellite visible from a GNSS station. STEC values from satellites with an elevation angle lower than 20° were discarded to mitigate the signal multipath errors.
As GNSS satellites travel across the sky, their azimuth and elevation angles constantly change in respect to the ground location of interest, and are different to the azimuth and elevation angles of the Sentinel-1 satellites. To calculate the ionospheric conditions over the observed area, the calibrated STEC derived from GNSS measurements was divided by MI to calculate the vertical equivalent TEC (VTEC) on the coordinates of ionospheric pierce points (IPPs), i.e., the points where signals crossed the 350 km height. After such normalization, the ionospheric error, expressed as on 5.405 GHz using Equation (11), was interpolated between the locations of IPPs, revealing the ionospheric conditions in the observed area.
Figure 6 presents the interpolated vertical ionospheric distance errors for a single crossing of the 5.405 GHz signal through the ionosphere in the time of acquiring each Sentinel-1A and Sentinel-1B SAR image. From Figure 6, the state of the ionosphere in the observed area can be evaluated and compared between image pairs. As expected, the ionization was higher towards the Equator, and above the earthquake area it equaled around 10 cm for the first three observed periods. On 29 March 2020 the ionization was overall higher, reaching up to 20 cm, increasing the potential for the biased results for the Sentinel-1A pair. Figure 7 presents the difference between the vertical single ionospheric crossing errors for Sentinel-1A and Sentinel-1B DInSAR pairs. Depending on those values, the degradation of DInSAR results for each image pair can be assessed.
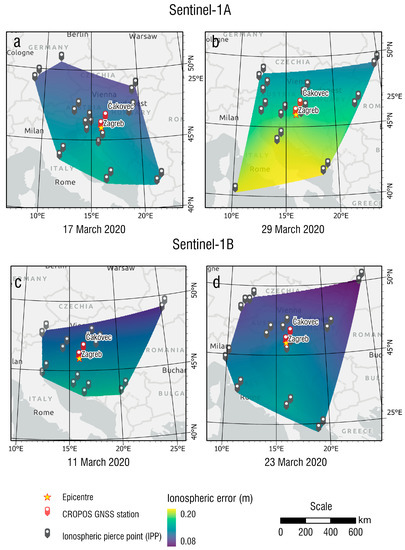
Figure 6.
Vertical single ionospheric crossings interpolated between IPPs at the time of taking Sentinel-1A images for a DInSAR pair (a,b) and Sentinel-1B images for a DInSAR pair (c,d).
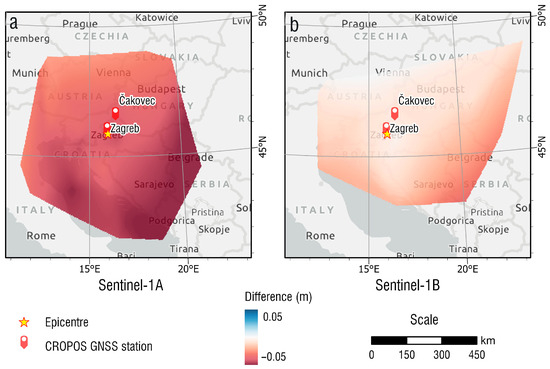
Figure 7.
Difference between vertical single ionospheric crossing errors for Sentinel-1A (a) and Sentinel-1B (b) DInSAR pairs.
Looking at the ionosphere, the Sentinel-1A pair was more influenced by the changes in the ionization between the two images, while between the images of the Sentinel-1B pair, there was no noticeable change in ionization in the observed area. To transform the presented VTEC into an ionosphere-induced Sentinel-1 DInSAR distance error, the Sentinel-1 elevation should be taken into account; multiplying the vertical ionospheric error by the factor of MI, with further multiplication by the factor of two to represent the two crosses of the SAR signal through the ionosphere on its way towards the Earth and back to the satellite after reflection [63]. In the analyzed SAR images, the Zagreb earthquake area was located on the eastern part of the middle Sentinel-1 interferometric wide (IW) burst IW2. The corresponding incidence angle equaled 40–41 degrees, with a complementary elevation angle of 49–50 degrees. As both image pairs were taken during the ascending passes, and the Sentinel-1 antennas are always pointing right, the satellites were positioned to the west of the observed area. Therefore, the Sentinel-1 SAR signals’ IPPs were also located to the west of the Zagreb area, above north-eastern Italy.
Both the observed area and the locations of Sentinel-1 IPPs were situated in middle latitudes, where the ionosphere is less dynamic than in polar and equatorial latitudes and no high gradients are expected, except in case of extreme geomagnetic conditions [29]. Therefore, the difference in ionospheric conditions at the time of recording of each InSAR image of the DInSAR pair could introduce a bias in the observed DInSAR image, but not the ionospheric features of local character. Considering the higher variation in ionization between the images, Sentinel-1A DInSAR0-based displacements were more prone to ionospheric bias.
3.3. DInSAR Displacements during Observed Atmospheric Conditions
The main sources of errors in the determination of the displacement of terrain by the DInSAR method are phase decorrelation, atmospheric effects, difficulties due to phase unwrapping, and, in much smaller effects, errors in the baseline and digital elevation model (DEM) [48]. Weakly correlated and unwrapped pixels usually produce high-frequency spatial changes in the final displacements, presented as false local liftings or sinkings, so they have to be further filtered to be interpreted correctly [3,48]. The atmospheric effects, on the other hand, are usually spread over large areas as a false low-frequency spatial displacement, sometimes connected with meteorological orographic effects [16,48].
Coherence for both the Sentinel-1A and Sentinel-1B pairs is estimated and presented in Figure 8a,b. As expected, urban areas have significantly higher coherence than forest areas. However, the epicenter of the Zagreb 22 March 2020 earthquake, marked in Figure 8 with a yellow star, was located in such a forested and mountainous area that the coherence around the epicenter was poor, suggesting that caution be exercised with the interpretation of displacement results.
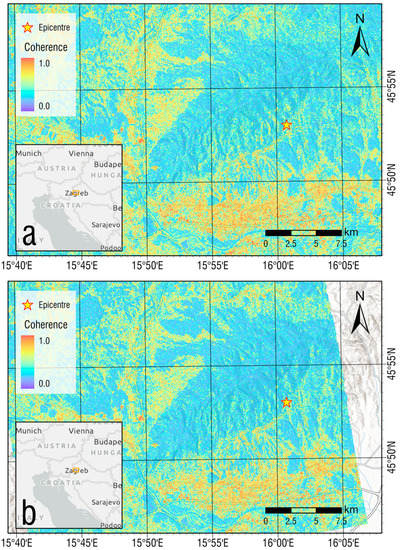
Figure 8.
Estimated coherence for: (a) Sentinel-1A interferometric pair (17 and 29 March 2020); (b) Sentinel-1B interferometric pair (11 and 23 March 2020).
The line-of-sight (LOS) displacement results are only accurate and reliable if the coherence between the interferometric pair is high. Figure 9 shows the masking of the displacement according to the coherence on both the Sentinel-1A pair (17 and 29 March 2020) and the Sentinel-1B pair (11 and 23 March 2020) for coherence masks with γ > 0.0, γ > 0.3, and γ > 0.6. LOS displacements with strong coherence, as shown in the Figure 9e,f, are considered the most reliable, but leave vast gaps in the displacement data.
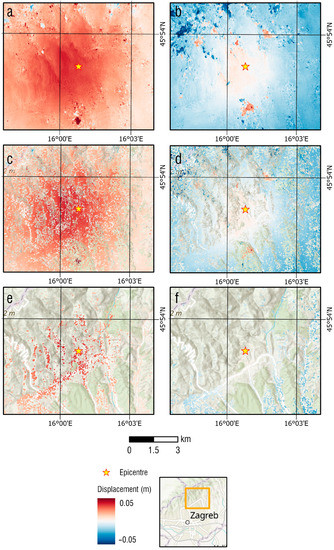
Figure 9.
Line-of-sight displacements on the interferometric pairs of Sentinel-1A images (first column: (a,c,e)) taken on 17 March and 29 March and Sentinel-1B images (second column: (b,d,f)) taken on 11 and 23 March 2020. First row (a,b) represents displacements without regard of the coherence between them (γ > 0.0); second row (c,d) represents displacements masked to appear for medium coherences γ > 0.3; third row (e,f) represents displacements masked to appear for strong coherences γ > 0.6.
Atmospheric effects on DInSAR terrain displacements are best studied if the coherence, as a source of error, is not present [14]. Figure 9a,b shows the high influence of coherence-associated errors, appearing as localized spots with pronounced displacement, to the final displacement calculation. As Figure 9e,f lacks most of the DInSAR displacement data, Figure 9c,d represents the best option for analysis of the effects introduced to DInSAR measurements, due to the atmospheric refraction conditions. Figure 9c, based on Sentinel-1A data, shows positive DInSAR LOS displacement in the area close to the epicenter, and almost no displacement in the areas at the edges of the figure. Figure 9d, based on Sentinel-1B data, depicts a similar difference between the displacements in the epicenter and the displacements at the edges of the shown area, but with a −2 cm offset if compared to Figure 9c. The consequence of the offset in the Figure 9d is that there are virtually no displacements in the epicenter area, and false negative displacement is present at the edges. As influences of other error sources were minimized, these differences in the results of DInSAR terrain displacements closest in time to the earthquake can be associated with the difference in atmospheric refractive conditions at the time of acquisition of SAR images. The Sentinel-1A interferometric pair was acquired in favorable tropospheric refractive conditions, but the ionospheric ionization changed between the acquisition of the two images. The Sentinel-1B interferometric pair had almost no ionospheric influence, but the tropospheric ANAPROP conditions were opposite in the two images of the interferometric pair, with subrefraction appearing in the vertical refraction profile closest to the first image, and superrefraction appearing in the vertical refraction profile closest to the second image.
4. Discussion
In the absence of a vertical profile of the refraction index for radio waves of the C-band for the entire atmosphere, it is worth focusing on the two layers of the atmosphere where the changes in the vertical profile of the refraction index appear to be the largest: the ionosphere and the troposphere. We were able to base our research on regular geophysical measurements of the troposphere and ionosphere. Despite the fact that they do not represent a comprehensive refraction model for the entire atmosphere [8], they were still able to provide objective warnings of the occurrences of strong anomalous phenomena.
The tropospheric vertical profile of the refraction index can be obtained from aerological balloon soundings. The advantage of this approach is that the refraction profile is accurate. On the other hand, balloon soundings were conducted from aerological stations located at some distance from the area covered by the DInSAR scene. In addition, the time of the balloon sounding does not coincide with the time of acquisition of the satellite image. This can be partially compensated by a mathematical model of atmospheric dynamics, whereby the state of the atmosphere at the desired moment above the observed area is calculated from the nearest meteorological measurements. Several authors have successfully used the weather research and forecasting model (WRF) for this purpose [21,64].
In the case of the interferometric pair obtained from the Sentinel-1B satellite, the occurrences of anomalous refractions of different signs coincided in such a way that their effects added up, leading to a bias of −2 cm in the wider area of the interferometric scene around the earthquake epicenter (Figure 9b). Both elevated phenomena of anomalous refraction are quite pronounced: subrefraction at 4745 m 11 March 2020 (Table A3), and superrefraction at 3806 mm which appeared on the sounding of 23 March 2020 (Table A4). In such cases, the qualitative analysis of the vertical profile of the refractive index indicates possible errors of the DInSAR method due to refraction in the troposphere. From the tropospheric influence on DInSAR point of view, it is advisable to avoid SAR pairs acquired in such conditions if alternative pairs are available.
Regarding the ionosphere, as the GNSS data are collected continuously, with multi-GNSS receivers receiving the signals from dozens of satellites, the temporal and spatial resolutions of such ionospheric data are sufficient for the recognition of ionospheric conditions during DInSAR pair acquisition, even in severe ionospheric conditions. However, if all the observed DInSAR pairs would be affected by such conditions, then the correction of ionospheric effects should be applied. In the case of disturbed ionospheric conditions with steep ionization gradients, which usually appear in times of higher solar activity and in low or high latitudes, the split-spectrum method of mitigation of ionospheric errors [29] or the range group-phase delay difference method [28] of mitigation of ionospheric errors should be used to compensate for the ionospheric effects on SAR interferograms, even though the reliable tools that would utilize such methods and allow the input of locally acquired TEC data are yet to be developed.
5. Conclusions
To investigate the tropospheric and ionospheric refraction conditions and their influence on the DInSAR LOS displacements, we analyzed two subsequent Sentinel-1B (11 and 23 March 2020) and Sentinel-1A (17 March and 29 March) pairs related to the Zagreb earthquake that took place on 22 March 2020. The interferometric pair, acquired by Sentinel-1A, had similar tropospheric refractive conditions in both images, which is desirable. The ionospheric ionization was higher in the second image, introducing difference in the ionospheric signal propagation and possible bias. The interferometric pair, acquired by Sentinel-1B, had significant differences in the refractive profiles of the atmosphere due to the unusually dry upper half of the troposphere with a sharp gradient in humidity on the day of the second acquisition. The ionospheric conditions for Sentinel-1B were similar for both SAR images of the pair. The difference in the refractive conditions between the two produced DInSAR measurements produced an offset between the calculated LOS displacements. In the case of ground displacements with small magnitudes, reaching only few centimeters, which is close to the absolute error of the DInSAR method applied on Sentinel-1 SAR satellites, a study of the refractive conditions in the troposphere and the ionosphere produces important information about the quality of the particular interferometric pair.
Author Contributions
Conceptualization, M.V., J.V. and I.R.; methodology, M.V. and J.V.; analysis, M.V. and J.V.; data curation, M.V., J.V. and I.R.; writing—original draft preparation, M.V. and J.V.; writing—review and editing, M.V., J.V. and I.R.; visualization, M.V. and I.R., funding acquisition, J.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
We are thankful to Croatian State Geodetic Administration for providing us with RINEX data of CROPOS reference GNSS stations. We are thankful to Chambon la Foret (CLF) magnetic observatory staff for providing the local K index data, calculated and made available by the Bureau Central de Magnétisme Terrestre (BCMT) of France. We are thankful to the Department of Geophysics, Faculty of Science, University of Zagreb for providing the local K index data of Lonjsko Polje Observatory.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
- Height over the ground;
- Modified refraction index M (dimensionless) computed by Equation (9);
- Refraction index n (dimensionless) computed by Equation (4);
- Water vapor pressure e;
- Total air pressure p;
- Air temperature T;
- Dew point Td;
- Wind speed Ws;
- Wind direction Wd (in geographic degrees);
- The vertical gradient of the modified refraction index dM/dh (dimensions km−1);
- The type of the refraction is determined in accordance with Table 1 (norm—normal refraction conditions, subrf—subrefractions and SUPER—for superrefractive conditions in the layer).
Vertical gradient of the modified refraction index dM/dh was computed using finite differences and represents the value between current and the next level (rows in a table), which is why these values are not present in the last rows of the Table A1, Table A2, Table A3 and Table A4.

Table A1.
Aerological soundings data and refractive profiles on 17 March 2020 at meteorological station Zagreb Maksimir (WMO index 14240).
Table A1.
Aerological soundings data and refractive profiles on 17 March 2020 at meteorological station Zagreb Maksimir (WMO index 14240).
| Height [m] | M | n | e [hPa] | P [hPa] | t [°C] | td [°C] | Ws [ms−1] | Wd [°] | dM/dh [km−1] | Refraction |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 313.63 | 1.000313630 | 5.2 | 1014.0 | 16.8 | −2.2 | 1 | 100 | 143.97 | norm |
| 118 | 330.62 | 1.000312094 | 5.2 | 1000.0 | 14.8 | −2.2 | 2 | 210 | 135.87 | norm |
| 643 | 401.96 | 1.000301009 | 5.2 | 939.0 | 9.8 | −2.2 | 88.51 | norm | ||
| 770 | 413.20 | 1.000292310 | 4.2 | 925.0 | 9.8 | −5.2 | 4 | 20 | 124.83 | norm |
| 1171 | 463.25 | 1.000279403 | 3.5 | 881.0 | 7.6 | −7.4 | 160.08 | subrf | ||
| 1467 | 510.63 | 1.000280311 | 5.0 | 850.0 | 5.4 | −2.6 | 9 | 25 | 130.91 | norm |
| 1897 | 566.93 | 1.000269101 | 4.6 | 806.0 | 2.2 | −3.8 | 130.78 | norm | ||
| 2243 | 612.17 | 1.000260019 | 4.4 | 772.0 | 0.6 | −4.4 | 92.63 | norm | ||
| 2538 | 639.50 | 1.000241034 | 2.0 | 744.0 | −0.5 | −14.5 | 128.35 | norm | ||
| 3026 | 702.14 | 1.000227058 | 1.2 | 700.0 | −4.1 | −21.1 | 5 | 345 | 129.19 | norm |
| 3810 | 803.42 | 1.000205250 | 0.1 | 633.0 | −8.3 | −45.3 | 142.5 | norm | ||
| 4121 | 847.74 | 1.000200743 | 0.4 | 608.0 | −9.9 | −31.9 | 139.8 | norm | ||
| 5597 | 1054.08 | 1.000175351 | 0.3 | 500.0 | −21.7 | −34.7 | 10 | 310 | 143.03 | norm |
| 5745 | 1075.25 | 1.000173285 | 0.4 | 490.0 | −22.7 | −32.7 | 139.1 | norm | ||
| 6540 | 1185.83 | 1.000159050 | 0.1 | 439.0 | −28.3 | −43.3 | 141.21 | norm | ||
| 6804 | 1223.11 | 1.000154882 | 0.1 | 423.0 | −30.5 | −47.5 | 143.18 | norm | ||
| 7207 | 1280.82 | 1.000149321 | 0.1 | 400.0 | −33.9 | −47.9 | 12 | 305 | 143.95 | norm |
| 8066 | 1404.47 | 1.000138108 | 0.1 | 353.0 | −41.9 | −46.6 | 144 | norm | ||
| 9147 | 1560.13 | 1.000124051 | 0.0 | 300.0 | −51.3 | −59.3 | 11 | 325 | 145.12 | norm |
| 9366 | 1591.91 | 1.000121448 | 0.0 | 290.0 | −53.3 | −60.3 | 144.15 | norm | ||
| 9500 | 1611.23 | 1.000119730 | 0.0 | 284.0 | −54.3 | −64.3 | 145.23 | norm | ||
| 9915 | 1671.50 | 1.000114845 | 0.0 | 266.0 | −57.7 | −62.2 | 144.88 | norm | ||
| 10,297 | 1726.84 | 1.000110211 | 0.0 | 250.0 | −60.5 | −65.5 | 17 | 320 | 145.71 | norm |
| 10,322 | 1730.49 | 1.000109936 | 0.0 | 249.0 | −60.7 | −65.7 | 143.78 | norm | ||
| 10,786 | 1797.20 | 1.000103798 | 0.0 | 231.0 | −61.9 | −67.9 | 14 | 310 | 140.67 | norm |
| 11,092 | 1840.25 | 1.000098806 | 0.0 | 220.0 | −59.5 | −75.5 | 145.31 | norm | ||
| 11,687 | 1926.71 | 1.000091851 | 0.0 | 200.0 | −60.5 | −79.5 | 7 | 300 | 147.35 | norm |
| 11,749 | 1935.84 | 1.000091247 | 0.0 | 198.0 | −60.9 | −80.9 | 125.32 | norm | ||
| 11,812 | 1943.74 | 1.000089256 | 0.0 | 196.0 | −57.1 | −82.1 | 146.01 | norm | ||
| 13,107 | 2132.82 | 1.000075021 | 0.0 | 160.0 | −52.3 | −85.3 | 149.12 | norm | ||
| 13,537 | 2196.94 | 1.000071631 | 0.0 | 150.0 | −52.9 | −85.9 | 10 | 305 | 150.01 | norm |
| 15,235 | 2451.65 | 1.000059755 | 0.0 | 115.0 | −55.7 | −87.7 | 150.67 | norm | ||
| 16,127 | 2586.05 | 1.000054111 | 0.0 | 100.0 | −54.1 | −88.1 | 2 | 230 | 152.42 | norm |
| 18,397 | 2932.04 | 1.000043711 | 0.0 | 70.0 | −56.9 | −88.9 | 5 | 310 | 153.61 | norm |
| 20,527 | 3259.24 | 1.000036501 | 0.0 | 50.0 | −57.5 | −89.5 | 2 | 90 | 154.41 | norm |
| 20,641 | 3276.84 | 1.000036203 | 0.0 | 49.1 | −57.9 | −89.9 | 154.35 | norm | ||
| 22,303 | 3533.37 | 1.000031799 | 0.0 | 37.8 | −53.5 | −89.5 | 155.13 | norm | ||
| 23,759 | 3759.24 | 1.000029077 | 0.0 | 30.1 | −54.7 | −89.7 | 156.03 | norm | ||
| 23,797 | 3765.17 | 1.000029041 | 0.0 | 30.0 | −54.7 | −89.7 | 3 | 30 | 155.56 | norm |
| 26,407 | 4171.18 | 1.000025281 | 0.0 | 20.0 | −51.5 | −88.5 | 5 | 80 | 155.85 | norm |
| 26,739 | 4222.92 | 1.000024897 | 0.0 | 19.0 | −50.9 | −88.9 | 156.07 | norm | ||
| 27,457 | 4334.98 | 1.000024231 | 0.0 | 17.0 | −53.1 | −89.1 | 156.22 | norm | ||
| 30,618 | 4828.80 | 1.000021774 | 0.0 | 10.4 | −52.7 | −89.7 | 156.39 | norm | ||
| 30,897 | 4872.44 | 1.000021611 | 0.0 | 10.0 | −51.5 | −88.5 | 4 | 175 | 156.42 | norm |
| 31,803 | 5014.16 | 1.000021089 | 0.0 | 8.7 | −49.1 | −87.1 | ----- | ----- |

Table A2.
Aerological soundings data and refractive profiles on 29 March 2020 at meteorological station Zagreb Maksimir (WMO index 14240).
Table A2.
Aerological soundings data and refractive profiles on 29 March 2020 at meteorological station Zagreb Maksimir (WMO index 14240).
| Height [m] | M | n | e [hPa] | P [hPa] | t [°C] | td [°C] | Ws [ms−1] | Wd [°] | dM/dh [km−1] | Refraction |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 323.26 | 1.000323260 | 8.0 | 999.0 | 15.8 | 3.8 | 1 | 170 | 128.01 | norm |
| 642 | 405.44 | 1.000304646 | 6.7 | 925.0 | 9.2 | 1.2 | 3 | 235 | 132.35 | norm |
| 903 | 439.98 | 1.000298209 | 6.4 | 896.0 | 6.6 | 0.6 | 121.11 | norm | ||
| 1335 | 492.30 | 1.000282705 | 5.2 | 850.0 | 3.8 | −2.2 | 3 | 355 | 129.53 | norm |
| 2874 | 691.65 | 1.000240432 | 2.9 | 700.0 | −9.5 | −10.1 | 5 | 340 | 133.57 | norm |
| 3018 | 710.88 | 1.000237054 | 2.8 | 687.0 | −10.3 | −10.3 | 129.43 | norm | ||
| 3653 | 793.07 | 1.000219549 | 1.9 | 632.0 | −14.9 | −15.2 | 79.03 | norm | ||
| 3677 | 794.96 | 1.000217671 | 1.6 | 630.0 | −15.3 | −17.2 | 85.95 | norm | ||
| 3847 | 809.57 | 1.000205591 | 0.3 | 616.0 | −14.3 | −35.3 | 138.03 | norm | ||
| 5397 | 1023.51 | 1.000176181 | 0.2 | 500.0 | −24.1 | −39.1 | 8 | 350 | 146.29 | norm |
| 5455 | 1032.00 | 1.000175565 | 0.3 | 496.0 | −24.5 | −36.5 | 139.04 | norm | ||
| 5737 | 1071.21 | 1.000170501 | 0.2 | 477.0 | −26.9 | −40.9 | 127.94 | norm | ||
| 5798 | 1079.01 | 1.000168724 | 0.1 | 473.0 | −27.1 | −49.1 | 140.91 | norm | ||
| 6380 | 1161.02 | 1.000159360 | 0.2 | 436.0 | −30.1 | −41.1 | 118.82 | norm | ||
| 6413 | 1164.94 | 1.000158099 | 0.1 | 434.0 | −30.1 | −49.1 | 139.45 | norm | ||
| 6662 | 1199.66 | 1.000153726 | 0.0 | 419.0 | −31.3 | −55.3 | 142.19 | norm | ||
| 6815 | 1221.42 | 1.000151465 | 0.1 | 410.0 | −32.1 | −50.1 | 143.58 | norm | ||
| 6997 | 1247.55 | 1.000149021 | 0.1 | 400.0 | −33.5 | −49.5 | 11 | 310 | 143.47 | norm |
| 7372 | 1301.35 | 1.000143946 | 0.1 | 379.0 | −36.5 | −46.5 | 143.01 | norm | ||
| 7725 | 1351.83 | 1.000139005 | 0.1 | 360.0 | −39.7 | −52.7 | 145.87 | norm | ||
| 7878 | 1374.15 | 1.000137304 | 0.1 | 352.0 | −41.3 | −49.3 | 138.69 | norm | ||
| 7975 | 1387.60 | 1.000135525 | 0.0 | 347.0 | −41.9 | −63.9 | 144.19 | norm | ||
| 8642 | 1483.78 | 1.000126986 | 0.0 | 314.0 | −47.3 | −61.3 | 145.33 | norm | ||
| 8726 | 1495.99 | 1.000126008 | 0.0 | 310.0 | −47.9 | −55.9 | 141.75 | norm | ||
| 8790 | 1505.06 | 1.000125030 | 0.0 | 307.0 | −48.3 | −62.3 | 143.99 | norm | ||
| 8947 | 1527.67 | 1.000122991 | 0.0 | 300.0 | −48.9 | −56.9 | 14 | 330 | 143.35 | norm |
| 9327 | 1582.14 | 1.000117801 | 0.0 | 283.0 | −50.9 | −69.9 | 145.04 | norm | ||
| 9655 | 1629.71 | 1.000113875 | 0.0 | 269.0 | −53.1 | −65.1 | 144.25 | norm | ||
| 10,127 | 1697.80 | 1.000107861 | 0.0 | 250.0 | −54.9 | −67.9 | 15 | 320 | 145.43 | norm |
| 11,079 | 1836.25 | 1.000096847 | 0.0 | 215.0 | −59.1 | −74.1 | 14 | 315 | 143.58 | norm |
| 11,537 | 1902.01 | 1.000090701 | 0.0 | 200.0 | −57.1 | −82.1 | 7 | 295 | 143.47 | norm |
| 11,965 | 1963.42 | 1.000084915 | 0.0 | 187.0 | −53.5 | −85.5 | 147.31 | norm | ||
| 12,576 | 2053.42 | 1.000078988 | 0.0 | 170.0 | −53.9 | −85.9 | 147.17 | norm | ||
| 13,387 | 2172.78 | 1.000071021 | 0.0 | 150.0 | −50.3 | −86.3 | 8 | 300 | 148.27 | norm |
| 13,563 | 2198.88 | 1.000069489 | 0.0 | 146.0 | −49.7 | −86.7 | 150.33 | norm | ||
| 14,674 | 2365.89 | 1.000062072 | 0.0 | 123.0 | −52.9 | −87.9 | 150.83 | norm | ||
| 16,017 | 2568.46 | 1.000053791 | 0.0 | 100.0 | −52.1 | −88.1 | 4 | 335 | 152.48 | norm |
| 18,317 | 2919.16 | 1.000043391 | 0.0 | 70.0 | −54.1 | −89.1 | 7 | 300 | 153.64 | norm |
| 20,467 | 3249.49 | 1.000036171 | 0.0 | 50.0 | −53.5 | −90.5 | 7 | 240 | 154.70 | norm |
| 22,798 | 3610.09 | 1.000030804 | 0.0 | 34.7 | −55.7 | −91.7 | 155.13 | norm | ||
| 23,737 | 3755.76 | 1.000029051 | 0.0 | 30.0 | −54.9 | −90.9 | 5 | 290 | 155.48 | norm |
| 25,667 | 4055.84 | 1.000026121 | 0.0 | 22.2 | −52.5 | −89.5 | 155.85 | norm | ||
| 26,347 | 4161.81 | 1.000025331 | 0.0 | 20.0 | −53.1 | −90.1 | 3 | 265 | 156.04 | norm |
| 28,013 | 4421.77 | 1.000023729 | 0.0 | 15.4 | −56.5 | −92.5 | 156.10 | norm | ||
| 29,144 | 4598.32 | 1.000022712 | 0.0 | 12.9 | −52.7 | −89.7 | 156.35 | norm | ||
| 30,777 | 4853.63 | 1.000021641 | 0.0 | 10.0 | −53.7 | −90.7 | 11 | 230 | 156.45 | norm |
| 31,451 | 4959.08 | 1.000021273 | 0.0 | 9.0 | −54.3 | −90.3 | ----- | ----- |

Table A3.
Aerological soundings data and refractive profiles on 11 March 2020 at meteorological station Zagreb Maksimir (WMO index 14240).
Table A3.
Aerological soundings data and refractive profiles on 11 March 2020 at meteorological station Zagreb Maksimir (WMO index 14240).
| Height [m] | M | n | e [hPa] | P [hPa] | t [°C] | td [°C] | Ws [ms−1] | Wd [°] | dM/dh [km−1] | Refraction |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 318.33 | 1.000318330 | 7.2 | 1001.0 | 17.2 | 2.2 | 3 | 210 | 171.68 | subrf |
| 12 | 320.39 | 1.000318506 | 7.4 | 1000.0 | 17.6 | 2.6 | 2 | 225 | 129.18 | norm |
| 658 | 403.84 | 1.000300534 | 6.2 | 926.0 | 11.2 | 0.2 | 132.15 | norm | ||
| 669 | 405.29 | 1.000300257 | 6.2 | 925.0 | 11.2 | 0.2 | 5 | 300 | 115.57 | norm |
| 732 | 412.57 | 1.000297646 | 6.4 | 918.0 | 12.6 | 0.6 | 129.30 | norm | ||
| 972 | 443.60 | 1.000290996 | 6.6 | 892.0 | 13.0 | 1.0 | 131.80 | norm | ||
| 1377 | 496.98 | 1.000280791 | 6.2 | 850.0 | 10.2 | 0.2 | 11 | 330 | 129.95 | norm |
| 2955 | 702.05 | 1.000238115 | 3.5 | 700.0 | −2.9 | −7.4 | 15 | 310 | 143.40 | norm |
| 2966 | 703.63 | 1.000237968 | 3.5 | 699.0 | −2.9 | −7.3 | 112.07 | norm | ||
| 3335 | 744.99 | 1.000221395 | 1.9 | 667.0 | −4.5 | −15.5 | 132.50 | norm | ||
| 4381 | 883.58 | 1.000195763 | 0.9 | 583.0 | −9.5 | −23.5 | 139.81 | norm | ||
| 4622 | 917.27 | 1.000191616 | 1.0 | 565.0 | −10.7 | −22.7 | 140.42 | norm | ||
| 4745 | 934.55 | 1.000189585 | 1.0 | 556.0 | −11.5 | −22.5 | 193.13 | subrf | ||
| 4814 | 947.87 | 1.000192072 | 1.7 | 551.0 | −12.3 | −16.8 | 138.35 | norm | ||
| 5354 | 1022.58 | 1.000182002 | 1.4 | 513.0 | −16.1 | −18.5 | 137.61 | norm | ||
| 5557 | 1050.52 | 1.000178071 | 1.3 | 500.0 | −17.5 | −19.9 | 25 | 340 | 139.80 | norm |
| 5753 | 1077.92 | 1.000174699 | 1.2 | 487.0 | −19.1 | −20.6 | 98.99 | norm | ||
| 5799 | 1082.47 | 1.000172027 | 0.9 | 484.0 | −19.3 | −24.3 | 137.94 | norm | ||
| 5922 | 1099.44 | 1.000169686 | 0.8 | 476.0 | −19.9 | −24.9 | 141.00 | norm | ||
| 6515 | 1183.05 | 1.000160195 | 0.7 | 439.0 | −24.9 | −27.4 | 137.71 | norm | ||
| 6749 | 1215.28 | 1.000155687 | 0.5 | 425.0 | −26.1 | −29.9 | 118.52 | norm | ||
| 6800 | 1221.32 | 1.000153720 | 0.4 | 422.0 | −26.1 | −34.1 | 143.48 | norm | ||
| 7078 | 1261.21 | 1.000149964 | 0.4 | 406.0 | −28.1 | −33.1 | 137.05 | norm | ||
| 7187 | 1276.15 | 1.000147791 | 0.3 | 400.0 | −28.5 | −35.5 | 29 | 330 | 140.48 | norm |
| 7703 | 1348.63 | 1.000139259 | 0.2 | 372.0 | −31.1 | −42.1 | 143.75 | norm | ||
| 8210 | 1421.52 | 1.000132550 | 0.1 | 346.0 | −35.5 | −47.5 | 146.84 | norm | ||
| 8311 | 1436.35 | 1.000131523 | 0.1 | 341.0 | −36.3 | −44.3 | 143.71 | norm | ||
| 8620 | 1480.76 | 1.000127420 | 0.1 | 326.0 | −39.1 | −52.1 | 145.04 | norm | ||
| 8984 | 1533.55 | 1.000123062 | 0.1 | 309.0 | −42.1 | −53.1 | 148.01 | norm | ||
| 9094 | 1549.83 | 1.000122072 | 0.1 | 304.0 | −43.1 | −47.9 | 145.07 | norm | ||
| 9187 | 1563.32 | 1.000120961 | 0.1 | 300.0 | −43.9 | −49.9 | 34 | 325 | 145.32 | norm |
| 9716 | 1640.20 | 1.000114788 | 0.0 | 277.0 | −48.3 | −55.3 | 146.04 | norm | ||
| 9981 | 1678.90 | 1.000111883 | 0.0 | 266.0 | −50.5 | −55.5 | 146.41 | norm | ||
| 10,129 | 1700.57 | 1.000110317 | 0.0 | 260.0 | −51.7 | −54.3 | 144.64 | norm | ||
| 10,254 | 1718.65 | 1.000108772 | 0.0 | 255.0 | −52.5 | −58.5 | 146.30 | norm | ||
| 10,387 | 1738.10 | 1.000107341 | 0.0 | 250.0 | −53.3 | −57.6 | 33 | 330 | 146.29 | norm |
| 11,169 | 1852.50 | 1.000098967 | 0.0 | 221.0 | −58.7 | −61.6 | 146.58 | norm | ||
| 11,667 | 1925.50 | 1.000093781 | 0.0 | 204.0 | −61.7 | −67.7 | 145.03 | norm | ||
| 11,787 | 1942.90 | 1.000092341 | 0.0 | 200.0 | −61.9 | −73.9 | 34 | 330 | 145.00 | norm |
| 11,818 | 1947.40 | 1.000091974 | 0.0 | 199.0 | −61.9 | −74.9 | 147.45 | norm | ||
| 12,006 | 1975.12 | 1.000090178 | 0.0 | 193.0 | −63.1 | −72.1 | 32 | 330 | 142.41 | norm |
| 12,407 | 2032.22 | 1.000084321 | 0.0 | 181.0 | −58.7 | −88.7 | 145.58 | norm | ||
| 12,655 | 2068.32 | 1.000081485 | 0.0 | 174.0 | −57.7 | −85.7 | 148.40 | norm | ||
| 12,988 | 2117.74 | 1.000078624 | 0.0 | 165.0 | −59.1 | −85.1 | 147.41 | norm | ||
| 13,503 | 2193.65 | 1.000073679 | 0.0 | 152.0 | −58.3 | −87.3 | 145.97 | norm | ||
| 13,587 | 2205.92 | 1.000072761 | 0.0 | 150.0 | −57.5 | −87.5 | 26 | 350 | 145.13 | norm |
| 13,936 | 2256.57 | 1.000068618 | 0.0 | 142.0 | −52.1 | −88.1 | 151.00 | norm | ||
| 16,026 | 2572.16 | 1.000056078 | 0.0 | 102.0 | −61.5 | −89.5 | 148.48 | norm | ||
| 16,157 | 2591.62 | 1.000054971 | 0.0 | 100.0 | −59.3 | −89.3 | 17 | 340 | 152.01 | norm |
| 18,407 | 2933.63 | 1.000043731 | 0.0 | 70.0 | −57.1 | −89.1 | 3 | 330 | 153.07 | norm |
| 18,846 | 3000.83 | 1.000042008 | 0.0 | 65.3 | −56.9 | −89.9 | 153.60 | norm | ||
| 19,538 | 3107.12 | 1.000039654 | 0.0 | 58.5 | −58.1 | −90.1 | 153.04 | norm | ||
| 19,916 | 3164.97 | 1.000038158 | 0.0 | 55.1 | −55.3 | −89.3 | 154.17 | norm | ||
| 20,537 | 3260.71 | 1.000036401 | 0.0 | 50.0 | −56.3 | −90.3 | 2 | 200 | 154.43 | norm |
| 21,563 | 3419.15 | 1.000033759 | 0.0 | 42.5 | −57.5 | −90.5 | 154.91 | norm | ||
| 23,777 | 3762.12 | 1.000029131 | 0.0 | 30.0 | −56.5 | −90.5 | 4 | 125 | 155.43 | norm |
| 24,057 | 3805.64 | 1.000028691 | 0.0 | 28.7 | −57.3 | −90.3 | 155.39 | norm | ||
| 25,467 | 4024.73 | 1.000026411 | 0.0 | 23.0 | −52.7 | −89.7 | 155.82 | norm | ||
| 26,367 | 4164.97 | 1.000025351 | 0.0 | 20.0 | −53.5 | −89.5 | 4 | 20 | 156.05 | norm |
| 28,738 | 4534.97 | 1.000023104 | 0.0 | 13.8 | −55.1 | −90.1 | 156.16 | norm | ||
| 29,803 | 4701.28 | 1.000022209 | 0.0 | 11.7 | −49.5 | −87.5 | 156.38 | norm | ||
| 30,837 | 4862.98 | 1.000021571 | 0.0 | 10.0 | −49.1 | −87.1 | 6 | 80 | 156.48 | norm |
| 31,381 | 4948.11 | 1.000021293 | 0.0 | 9.2 | −50.3 | −88.3 | ----- | ----- |

Table A4.
Aerological soundings data and refractive profiles on 23 March 2020 at meteorological station Zagreb Maksimir (WMO index 14240).
Table A4.
Aerological soundings data and refractive profiles on 23 March 2020 at meteorological station Zagreb Maksimir (WMO index 14240).
| Height [m] | M | n | e [hPa] | P [hPa] | t [°C] | td [°C] | Ws [ms−1] | Wd [°] | dM/dh [km−1] | Refraction |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 321.85 | 1.000321850 | 3.4 | 1014.0 | 2.2 | −7.8 | 6 | 10 | 130.66 | norm |
| 110 | 336.22 | 1.000318950 | 3.2 | 1000.0 | 0.4 | −8.6 | 8 | 55 | 130.70 | norm |
| 617 | 402.49 | 1.000305621 | 2.9 | 938.0 | −4.7 | −9.7 | 122.70 | norm | ||
| 728 | 416.11 | 1.000301814 | 2.8 | 925.0 | −5.5 | −10.5 | 10 | 15 | 127.33 | norm |
| 1384 | 499.63 | 1.000282342 | 2.1 | 850.0 | −11.3 | −14.1 | 13 | 25 | 129.07 | norm |
| 2649 | 662.91 | 1.000247017 | 1.1 | 718.0 | −21.7 | −21.9 | 123.46 | norm | ||
| 2773 | 678.22 | 1.000242859 | 0.9 | 706.0 | −22.5 | −24.3 | 109.79 | norm | ||
| 2839 | 685.47 | 1.000239747 | 0.7 | 700.0 | −22.5 | −27.5 | 20 | 45 | 131.61 | norm |
| 2944 | 699.28 | 1.000237072 | 0.6 | 690.0 | −23.3 | −28.3 | 135.47 | norm | ||
| 3321 | 750.36 | 1.000228963 | 0.6 | 655.0 | −26.5 | −28.1 | 132.38 | norm | ||
| 3600 | 787.29 | 1.000222090 | 0.5 | 630.0 | −28.7 | −30.8 | 117.87 | norm | ||
| 3714 | 800.73 | 1.000217632 | 0.2 | 620.0 | −29.1 | −39.1 | 132.25 | norm | ||
| 3806 | 812.90 | 1.000215358 | 0.2 | 612.0 | −29.5 | −39.5 | 63.18 | SUPER | ||
| 3841 | 815.11 | 1.000212073 | 0.0 | 609.0 | −27.9 | −55.9 | 122.09 | norm | ||
| 3948 | 828.17 | 1.000208334 | 0.0 | 600.0 | −26.9 | −61.9 | 135.88 | norm | ||
| 5200 | 998.29 | 1.000181890 | 0.0 | 503.0 | −33.3 | −68.3 | 139.16 | norm | ||
| 5247 | 1004.83 | 1.000181051 | 0.0 | 500.0 | −33.5 | −68.5 | 17 | 15 | 135.11 | norm |
| 5606 | 1053.34 | 1.000173198 | 0.0 | 475.0 | −33.9 | −69.9 | 132.72 | norm | ||
| 5846 | 1085.19 | 1.000167368 | 0.0 | 459.0 | −32.9 | −71.9 | 139.17 | norm | ||
| 6807 | 1218.93 | 1.000150231 | 0.0 | 400.0 | −36.5 | −72.5 | 8 | 360 | 141.24 | norm |
| 8354 | 1437.44 | 1.000125862 | 0.0 | 319.0 | −41.5 | −77.5 | 136.49 | norm | ||
| 8483 | 1455.04 | 1.000123209 | 0.0 | 313.0 | −40.1 | −78.1 | 143.12 | norm | ||
| 8777 | 1497.12 | 1.000119131 | 0.0 | 300.0 | −40.7 | −77.7 | 13 | 350 | 144.88 | norm |
| 10,007 | 1675.32 | 1.000104221 | 0.0 | 250.0 | −45.7 | −78.7 | 13 | 340 | 146.27 | norm |
| 10,114 | 1690.97 | 1.000103072 | 0.0 | 246.0 | −46.3 | −79.3 | 142.51 | norm | ||
| 10,475 | 1742.42 | 1.000097845 | 0.0 | 233.0 | −44.1 | −81.1 | 147.73 | norm | ||
| 11,321 | 1867.40 | 1.000090003 | 0.0 | 205.0 | −49.5 | −83.5 | 10 | 290 | 143.91 | norm |
| 11,487 | 1891.29 | 1.000087831 | 0.0 | 200.0 | −48.1 | −84.1 | 13 | 305 | 145.25 | norm |
| 11,860 | 1945.47 | 1.000083450 | 0.0 | 189.0 | −46.1 | −84.1 | 148.68 | norm | ||
| 13,387 | 2172.50 | 1.000070741 | 0.0 | 150.0 | −49.1 | −86.1 | 9 | 305 | 150.31 | norm |
| 15,286 | 2457.93 | 1.000058028 | 0.0 | 112.0 | −52.1 | −88.1 | 151.02 | norm | ||
| 16,027 | 2569.84 | 1.000053601 | 0.0 | 100.0 | −50.9 | −87.9 | 6 | 285 | 152.51 | norm |
| 18,337 | 2922.14 | 1.000043231 | 0.0 | 70.0 | −52.7 | −89.7 | 4 | 280 | 153.73 | norm |
| 20,497 | 3254.20 | 1.000036171 | 0.0 | 50.0 | −53.5 | −90.5 | 3 | 350 | 154.52 | norm |
| 21,581 | 3421.70 | 1.000033483 | 0.0 | 42.2 | −55.1 | −90.1 | 154.93 | norm | ||
| 23,777 | 3761.93 | 1.000028941 | 0.0 | 30.0 | −52.7 | −89.7 | 7 | 55 | 155.62 | norm |
| 26,397 | 4169.64 | 1.000025311 | 0.0 | 20.0 | −52.5 | −89.5 | 7 | 175 | 155.80 | norm |
| 26,594 | 4200.34 | 1.000025082 | 0.0 | 19.4 | −51.9 | −88.9 | 156.02 | norm | ||
| 27,521 | 4344.96 | 1.000024163 | 0.0 | 16.8 | −53.3 | −90.3 | 155.95 | norm | ||
| 28,084 | 4432.76 | 1.000023572 | 0.0 | 15.4 | −50.1 | −88.1 | 156.28 | norm | ||
| 30,844 | 4864.10 | 1.000021592 | 0.0 | 10.1 | −48.1 | −87.1 | 156.54 | norm | ||
| 30,917 | 4875.53 | 1.000021561 | 0.0 | 10.0 | −48.3 | −86.3 | 16 | 125 | 156.49 | norm |
| 32,549 | 5130.92 | 1.000020727 | 0.0 | 7.8 | −48.1 | −87.1 | ----- | ----- |
References
- Chen, K.-S. Principles of Synthetic Aperture Radar Imaging: A System Simulation Approach; CRC Press: Boca Raton, FL, USA, 2016; Volume 2. [Google Scholar]
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Ferretti, A.; Monti-Guarnieri, A.; Prati, C.; Rocca, F.; Massonnet, D. Insar Principles: Guidelines for SAR Interferometry Processing and Interpretation; ESA Publications TM-19: Frascati, Italy, 2007. [Google Scholar]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer: Dordrecht, The Netherlands, 2001. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. Solid Earth 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Goldstein, R. Atmospheric limitations to repeat-track radar interferometry. Geophys. Res. Lett. 1995, 22, 2517–2520. [Google Scholar] [CrossRef]
- American Institute of Aeronautics and Astronautics. Guide to Reference and Standard Atmosphere Models (G-003B-2004); American Institute of Aeronautics and Astronautics: Reston, Virginia, USA, 2004. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration. National Aeronautic and Space Administration; United States Air Force. U.S. Standard Atmosphere; NOAA: Washington, DC, USA, 1976; p. 227. [Google Scholar]
- Viher, M.; Prtenjak, M.T. A multi-year study of radio-wave refractivity profiles above the Adriatic Sea up to an altitude of 40 km. Meteorol. Z. 2012, 21, 365–370. [Google Scholar] [CrossRef] [PubMed]
- Zolesi, B.; Cander, L.R. Ionospheric Prediction and Forecasting; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- International Telecommunication Union. Recommendation ITU-R P.453-14 (08/19) The radio refractive index: Its formula and refractivity data, P Series, Radiowave Propagation; International Telecommunication Union: Geneva, Switzerland, 2019. [Google Scholar]
- Villarini, G.; Krajewski, W.F. Review of the Different Sources of Uncertainty in Single Polarization Radar-Based Estimates of Rainfall. Surv. Geophys. 2010, 31, 107–129. [Google Scholar] [CrossRef]
- Darvishi, M.; Cuozzo, G.; Bruzzone, L.; Nilfouroushan, F. Performance Evaluation of Phase and Weather-Based Models in Atmospheric Correction with Sentinel-1Data: Corvara Landslide in the Alps. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1332–1346. [Google Scholar] [CrossRef]
- Gomba, G.; Cong, X.Y.; Eineder, M. Correction of Ionospheric and Tropospheric Path Delay For L-Band Interferograms. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 310–313. [Google Scholar]
- Hu, Z.B.; Mallorqui, J.J. An Accurate Method to Correct Atmospheric Phase Delay for InSAR with the ERA5 Global Atmospheric Model. Remote Sens. 2019, 11, 1969. [Google Scholar] [CrossRef]
- Mathew, J.; Majumdar, R.; Kumar, K.V. Estimating the Atmospheric Phase Delay for Quantifying Co-Seismic Deformation Using Repeat Pass Differential Sar Interferometry: Observations From 20th April 2013 Lushan (China) Earthquake. In Proceedings of the ISPRS Technical Commission VIII Symposium, Hyderabad, India, 9–12 December 2014; pp. 57–64. [Google Scholar]
- Milczarek, W.; Kopec, A.; Glabicki, D. Estimation of Tropospheric and Ionospheric Delay in DInSAR Calculations: Case Study of Areas Showing (Natural and Induced) Seismic Activity. Remote Sens. 2019, 11, 621. [Google Scholar] [CrossRef]
- Qian, F.M.; Chen, G.; Lu, J.; Chen, X.M.; Lou, L.S.; Jiang, T.; Liu, W.; Wang, S. Correcting method of slant-range error for the TH-2 satellites. Remote Sens. Lett. 2021, 12, 194–201. [Google Scholar] [CrossRef]
- Zhu, M.; Zeng, Q.M.; Jiao, J. Quantitative assessment to the impact of InSAR ionospheric and tropospheric corrections on source parameter modelling: Application to the 4th nuclear test, North Korea. Geophys. J. Int. 2021, 224, 86–99. [Google Scholar] [CrossRef]
- Liu, Q.; Zeng, Q.; Zhang, Z. Evaluation of InSAR Tropospheric Correction by Using Efficient WRF Simulation with ERA5 for Initialization. Remote Sens. 2023, 15, 273. [Google Scholar] [CrossRef]
- Murray, K.D.; Bekaert, D.P.S.; Lohman, R.B. Tropospheric corrections for InSAR: Statistical assessments and applications to the Central United States and Mexico. Remote Sens. Environ. 2019, 232, 111326. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Hooper, A.; Wright, T.J. A spatially variable power law tropospheric correction technique for InSAR data. J. Geophys. Res. Solid Earth 2015, 120, 1345–1356. [Google Scholar] [CrossRef]
- Doin, M.P.; Lasserre, C.; Peltzer, G.; Cavalié, O.; Doubre, C. Corrections of stratified tropospheric delays in SAR interferometry: Validation with global atmospheric models. J. Appl. Geophys. 2009, 69, 35–50. [Google Scholar] [CrossRef]
- Fattahi, H.; Amelung, F. InSAR bias and uncertainty due to the systematic and stochastic tropospheric delay. J. Geophys. Res. Solid Earth 2015, 120, 8758–8773. [Google Scholar] [CrossRef]
- Parker, A.L.; Biggs, J.; Walters, R.J.; Ebmeier, S.K.; Wright, T.J.; Teanby, N.A.; Lu, Z. Systematic assessment of atmospheric uncertainties for InSAR data at volcanic arcs using large-scale atmospheric models: Application to the Cascade volcanoes, United States. Remote Sens. Environ. 2015, 170, 102–114. [Google Scholar] [CrossRef]
- Kim, J.-R.; Lin, S.-Y.; Yun, H.-W.; Tsai, Y.-L.; Seo, H.-J.; Hong, S.; Choi, Y. Investigation of Potential Volcanic Risk from Mt. Baekdu by DInSAR Time Series Analysis and Atmospheric Correction. Remote Sens. 2017, 9, 138. [Google Scholar]
- Brcic, R.; Parizzi, A.; Eineder, M.; Bamler, R.; Meyer, F. Estimation and compensation of ionospheric delay for SAR interferometry. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 2908–2911. [Google Scholar]
- Gomba, G.; Parizzi, A.; De Zan, F.; Eineder, M.; Bamler, R. Toward Operational Compensation of Ionospheric Effects in SAR Interferograms: The Split-Spectrum Method. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1446–1461. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Chen, C. Measurement and mitigation of the ionosphere in L-band Interferometric SAR data. In Proceedings of the IEEE National Radar Conference–Proceedings, Arlington, VA, USA, 10–14 May 2010; pp. 1459–1463. [Google Scholar]
- Xu, X.; Sandwell, D.T.; Tymofyeyeva, E.; Gonzalez-Ortega, A.; Tong, X. Tectonic and anthropogenic deformation at the cerro prieto geothermal step-over revealed by sentinel-1A insar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5284–5292. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Walters, R.J.; Wright, T.J.; Hooper, A.J.; Parker, D.J. Statistical comparison of InSAR tropospheric correction techniques. Remote Sens. Environ. 2015, 170, 40–47. [Google Scholar] [CrossRef]
- Lin, Y.N.N.; Simons, M.; Hetland, E.A.; Muse, P.; Dicaprio, C. A multiscale approach to estimating topographically correlated propagation delays in radar interferograms. Geochem. Geophys. Geosystems 2010, 11, Q09002. [Google Scholar] [CrossRef]
- Tymofyeyeva, E.; Fialko, Y. Mitigation of atmospheric phase delays in InSAR data, with application to the eastern California shear zone. J. Geophys. Res. Solid Earth 2015, 120, 5952–5963. [Google Scholar] [CrossRef]
- Löfgren, J.S.; Björndahl, F.; Moore, A.W.; Webb, F.H.; Fielding, E.J.; Fishbein, E.F. Tropospheric correction for InSAR using interpolated ECMWF data and GPS zenith total delay from the Southern California integrated GPS network. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 4503–4506. [Google Scholar]
- Gong, W.; Meyer, F.; Webley, P.W.; Morton, D.; Liu, S. Performance analysis of atmospheric correction in InSAR data based on the Weather Research and Forecasting Model (WRF). In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 2900–2903. [Google Scholar]
- Jolivet, R.; Grandin, R.; Lasserre, C.; Doin, M.P.; Peltzer, G. Systematic InSAR tropospheric phase delay corrections from global meteorological reanalysis data. Geophys. Res. Lett. 2011, 38, L17311. [Google Scholar] [CrossRef]
- Li, Z.; Fielding, E.J.; Cross, P.; Preusker, R. Advanced InSAR atmospheric correction: MERIS/MODIS combination and stacked water vapour models. Int. J. Remote Sens. 2009, 30, 3343–3363. [Google Scholar] [CrossRef]
- Li, Z.; Muller, J.P.; Cross, P.; Albert, P.; Fischer, J.; Bennartz, R. Assessment of the potential of MERIS near-infrared water vapour products to correct ASAR interferometric measurements. Int. J. Remote Sens. 2006, 27, 349–365. [Google Scholar] [CrossRef]
- Cheng, S.; Perissin, D.; Lin, H.; Chen, F. Atmospheric delay analysis from GPS meteorology and InSAR APS. J. Atmos. Sol.-Terr. Phys. 2012, 86, 71–82. [Google Scholar] [CrossRef]
- Zhu, W.; Ding, X.L.; Jung, H.S.; Zhang, Q.; Zhang, B.C.; Qu, W. Investigation of ionospheric effects on SAR Interferometry (InSAR): A case study of Hong Kong. Adv. Space Res. 2016, 58, 564–576. [Google Scholar] [CrossRef]
- Markušić, S.; Stanko, D.; Korbar, T.; Belić, N.; Penava, D.; Kordić, B. The Zagreb (Croatia) M5.5 Earthquake on 22 March 2020. Geosciences 2020, 10, 252. [Google Scholar] [CrossRef]
- Braun, A.; Veci, L. TOPS Interferometry Tutorial; SkyWatch Space Applications Inc.: Paris, France, 2020. [Google Scholar]
- Crosetto, M.; Monserrat, O.; Cuevas, M.; Crippa, B. Spaceborne Differential SAR Interferometry: Data Analysis Tools for Deformation Measurement. Remote Sens. 2011, 3, 305–318. [Google Scholar] [CrossRef]
- Zhu, C.H.; Wang, C.S.; Zhang, B.C.; Qin, X.Q.; Shan, X.J. Differential Interferometric Synthetic Aperture Radar data for more accurate earthquake catalogs. Remote Sens. Environ. 2021, 266, 11. [Google Scholar] [CrossRef]
- Zebker, H.A.; Rosen, P.A.; Goldstein, R.M.; Gabriel, A.; Werner, C.L. On The Derivation of Coseismic Displacement-Fields Using Differential Radar Interferometry–The Landers Earthquake. J. Geophys. Res. Solid Earth 1994, 99, 19617–19634. [Google Scholar] [CrossRef]
- Dalla Via, G.; Crosetto, M.; Crippa, B. Resolving vertical and east-west horizontal motion from differential interferometric synthetic aperture radar: The L’Aquila earthquake. J. Geophys. Res. Solid Earth 2012, 117, 14. [Google Scholar] [CrossRef]
- Ferretti, A. Satellite InSAR Data: Reservoir Monitoring from Space; Earthdoc: London, UK, 2014. [Google Scholar]
- Viher, M. A study of the modified refraction indices over the Alpine and sub-Alpine region. Meteorol. Z. 2006, 15, 625–630. [Google Scholar] [CrossRef]
- Susaki, J.; Maeda, N.; Akatsuka, S. Estimation of phase delay due to precipitable water for DInSAR-based land deformation monitoring. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, IV-2/W4, 477–484. [Google Scholar] [CrossRef]
- International Radio Consultative Committee. Recommendations and reports of the CCIR, 1986; International Radio Consultative Committee: Dubrovnik, Croatia, 1986; p. 19. [Google Scholar]
- Patterson, W.; Hattan, C.; Hitney, H.; Paulus, R.; Lindem, G. Engineer’s Refractive Effects Prediction System (EREPS) Version 3.0; Naval Command Control and Ocean Surveillance Center Rdt and E Division: San Diego, CA, USA, 1994. [Google Scholar]
- Bech, J.; Codina, B.; Lorente, J. Forecasting weather radar propagation conditions. Meteorol. Atmos. Phys. 2007, 96, 229–243. [Google Scholar] [CrossRef]
- Klobuchar, J.A.; Kunches, J.M. Comparative range delay and variability of the earth’s troposphere and the ionosphere. GPS Solut. 2003, 7, 55–58. [Google Scholar] [CrossRef]
- Vuković, J.; Kos, T. Locally adapted NeQuick 2 model performance in European middle latitude ionosphere under different solar, geomagnetic and seasonal conditions. Adv. Space Res. 2017, 60, 1739–1750. [Google Scholar] [CrossRef]
- RTCA. DO-229C Minimum Operational Performance Standards for Global Positioning System/Wide Area Augmentation System Airborne Equipment; RTCA: Washington, DC, USA, 2001. [Google Scholar]
- Liao, W.T.; Tseng, K.H.; Lee, I.T.; Liibusk, A.; Lee, J.C.; Liu, J.Y.; Chang, C.P.; Lin, Y.C. Sentinel-1 interferometry with ionospheric correction from global and local TEC maps for land displacement detection in Taiwan. Adv. Space Res. 2020, 65, 1447–1465. [Google Scholar] [CrossRef]
- Bartels, J. The standardized index, Ks, and the planetary index, Kp. IATME Bull. 1949, 97, 0001. [Google Scholar]
- Mandic, I.; Vujic, E.; Heilig, B.; Pelajic, I.; Herak, D. Recent Efforts Toward the Establishment of the Lonjsko Polje Geomagnetic Observatory. Acta Geophys. 2016, 64, 1311–1339. [Google Scholar] [CrossRef]
- Sugiura, M. Hourly Values of Equatorial Dst for the IGY; Pergamon Press: Oxford, UK, 1964; pp. 7–45. [Google Scholar]
- Nose, M.; Sugiura, M.; Kamei, T.; Iyemori, T.; Koyama, Y. Dst Index. WDC for Geomagnetism, Kyoto: 2015. Available online: https://doi.org/10.17593/14515-74000 (accessed on 11 October 2022).
- Gurtner, W.; Estey, L. RINEX: The Receiver Independent Exchange Format Version 2.11; Astronomical Institute, University of Bern: Bern, Switzerland, 2007. [Google Scholar]
- Ciraolo, L.; Azpilicueta, F.; Brunini, C.; Meza, A.; Radicella, S.M. Calibration errors on experimental slant total electron content (TEC) determined with GPS. J. Geod. 2007, 81, 111–120. [Google Scholar] [CrossRef]
- Prtenjak, M.T.; Horvat, I.; Tomazic, I.; Kvakic, M.; Viher, M.; Grisogono, B. Impact of mesoscale meteorological processes on anomalous radar propagation conditions over the northern Adriatic area. J. Geophys. Res. Atmos. 2015, 120, 8759–8782. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).