Abstract
The official launch of the Chinese BeiDou Navigation Satellite System with global coverage (BDS-3) presents significant opportunities for various applications, including precision agriculture and autonomous driving, among others. With its global spatial coverage and hybrid space constellation comprising geosynchronous Earth orbit (GEO), inclined geosynchronous orbit (IGSO), and medium Earth orbit (MEO) satellites, BDS can significantly contribute to various GNSS remote sensing applications that require real-time, precise water surface height measurements with high temporal and spatial resolution, such as in tidal monitoring. In this paper, we propose a carrier-phase-based method for BDS Reflectometry (BDS-R) to precisely retrieve real-time water surface height. Firstly, the BDS-R altimetry method is introduced, along with a detailed explanation of the data processing procedures. Secondly, a quality control method tailored to the characteristics of low-cost BDS devices is developed. Thirdly, a land altimetry experiment is conducted to evaluate the precision of BDS-R and analyze the specific contribution of the BDS hybrid constellation. Finally, a water surface altimetry experiment validates the real-time monitoring capabilities for low-cost BDS-R. The results indicate that low-cost BDS-R can achieve real-time centimeter-level water level monitoring with a temporal resolution of 1 s in lakefront environments. The performance of BDS-R can be significantly improved by the BDS hybrid constellation, particularly IGSOs. It is concluded that low-cost BDS-R has great potential for promoting ground-based GNSS remote sensing applications.
1. Introduction
Global navigation satellite system (GNSS) reflectometry (GNSS-R), which was first envisioned in 1993 [1], has been proved to be an effective remote sensing tool to support emerging remote sensing applications, such as monitoring water levels [2,3,4,5,6], snow thickness [7,8,9], sea ice condition [10,11], sea waves and breeze [12,13,14,15], and soil moisture [16,17,18], etc. GNSS-R altimetry uses direct and reflected GNSS signals to address the issue of sea-level monitoring, tidal warning, and reservoir level monitoring, etc. For coastal zones, ground-based GNSS-R devices have unique advantages. Due to the ubiquity of GNSS signals, it can support altimetry with high spatial and temporal resolutions. Compared with satellite altimetry, GNSS-R still works well when the land is contaminated within the sensing footprint [19].
The ground-based GNSS-R technique relies on precisely calculating the time delay between direct and reflected GNSS signals to obtain the water surface height. This can be achieved through several data sources, such as code phase [20,21], carrier phase [22] and signal-to-noise ratio (SNR) [23,24]. The GNSS-R technique based on carrier phase measurements can achieve high precision and temporal resolution results, provided that the integer ambiguity is resolved accurately. The corresponding device requires two antennas to segregate the direct and reflected signals into different links: one upwards right-hand circular polarization (RHCP) antenna is used to receive direct signals, and one downward left-hand circular polarization (LHCP) antenna is used to receive reflected signals. High-precision altimetry involves two primary steps: firstly, resolving the integer ambiguity of the carrier phase to determine the time delays between direct and reflected signals and, secondly, determining the relative height from the reflected surface to the antenna based on geometric relationships.
The receiver utilized for carrier phase processing can be customized, as demonstrated in [22,25]. However, the customized devices often come with a high price tag or limited accessibility to the general public, which hinders the development of low-cost GNSS applications. An alternative method involves the utilization of dual positioning receivers, which has been extensively studied. Löfgren et al. [26,27] proposed a GNSS tide gauge that employs two positioning receivers and antennas. This hardware configuration can not only handle the integer ambiguity of the carrier phase, but also extract the interference power of the signal, so that the two height-measuring methods can complement each other effectively. The corresponding experiment achieved a temporal resolution of 5 s for sea surface monitoring through carrier-phase processing. For this configuration, Wang et al. [28] further improved the single-difference and double-difference algorithms to achieve a time resolution of 1 s. Bao et al. [29] introduced an external atomic clock to improve data precision and temporal resolution. Liu et al. proposed the continuous phase tracking algorithm [30], which enhanced the GNSS-R performance under rough seas. Notice that in these works mentioned above, certain high-quality devices are experimentally utilized, such as choke-ring antennas of AR10, AR20, AT504, receivers of GRX1200, AT504, JAVAD Quattro-G3D, and an atomic clock, in order to alleviate the workload of resolving integer ambiguity, the key part of carrier-phase processing. Unfortunately, the use of expensive devices also restricts the popularity of applications.
Low-cost GNSS receivers have the advantage of being affordable, but they suffer from hardware performance limitations such as increased observation noise [31]. Many low-cost receivers only support single frequency observations, which is not conducive to forming observation combinations used in cycle slip detection and integer ambiguity resolution. Additionally, low-cost antennas have poorer multipath suppression capabilities [32]. It is beneficial to extract signal interference power, but not conducive to resolving integer ambiguities. Although there have been many studies on low-cost GNSS-R in recent years, such as [6,23,24,33], they mainly focus on GNSS multipath reflectometry. For low-cost GNSS-R, obtaining real-time, high temporal resolution results remains challenging, especially in complex environments such as coastal areas and lakefronts.
Previous research has primarily focused on GPS and high-quality devices. However, with the official launch of BeiDou Navigation Satellite System with global coverage (BDS-3), the number of observable satellites for the B1I and B3I signals has increased to 45 [23]. This abundance of single-frequency observations can alleviate the challenge of integer ambiguity resolution for low-cost devices, while the hybrid constellation can provide unique contributions to position dilution of recision (PDOP). It is expected that the increased number of satellites and improved PDOP could significantly enhance the performance of GNSS-R [3,5,34]. In this study, we configured a set of low-cost BeiDou Navigation Satellite System Reflectometry (BDS-R) devices and conducted experimental assessments of land and water surface altimetry based on single-frequency (B1I) signals. We adopted two U-Blox F9P receivers and two off-the-shelf antennas, worth about USD 620 in total. The receiver is capable of supporting BDS dual-frequency signals, which means that the cost can be further reduced by opting for a single-frequency receiver. In data processing, Kalman filtering (KF) and relative positioning algorithms were employed alongside two easily implementable quality control (QC) methods to ensure the real-time reliability of the BDS-R results. Ultimately, we explored the specific contributions of both inclined geosynchronous orbit (IGSO) and geostationary Earth orbit (GEO) satellites of the BDS hybrid constellation in terms of SNR, multipath interference, and overall solutions.
This paper is structured as follows: Section 2 provides a detailed explanation of the principles of BDS-R and outlines the data processing strategy used for calculating reflector height on an epoch-by-epoch basis; Section 3 starts with describing two altimetry experiment and ends with a comparison of experimental results using the BDS-R and GPS Reflectometry (GPS-R), which primarily assesses the contribution of the BDS hybrid constellation to BDS-R and evaluates the real-time performance of low-cost BDS-R for water-level altimetry; Section 4 discusses characteristics, problems, and ways to improve our work; and Section 5 summarizes this paper.
2. Methodology
Currently, retrieving water surface height with high temporal resolution in real time using low-cost GNSS-R equipment poses a challenge. To overcome these obstacles, this study employs a four-step data processing procedure (see Figure 1). Firstly, the double difference (DD) observation equations are formulated based on BDS code, carrier-phase observations, and virtual observations, with the latter primarily being utilized for QC purposes. Secondly, real-time calculation of the baseline vector between two antennas is performed using the KF. Thirdly, reliable results are selected by screening the horizontal component of the baseline vector against known truth values. Finally, based on geometric principles, dependable baseline vectors are utilized to compute the water surface elevation for the current epoch. Further details will be discussed later in this paper and the numbers in brackets in Figure 1 represent the equations in this paper.
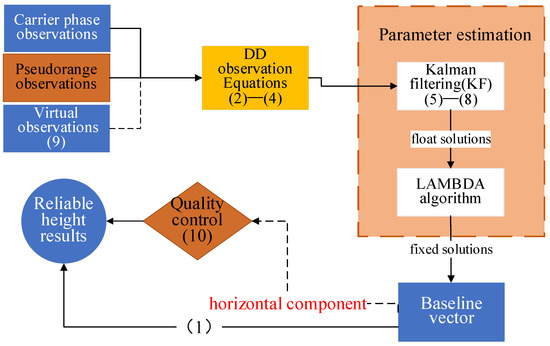
Figure 1.
Processing flow of real-time precise altimetry by BDS-R. The numbers in brackets represent the equations in this paper.
2.1. Geometry of BDS-R
The BDS-R adopted the relative positioning GNSS-R configuration [27] to retrieve water surface height. The device comprises two vertically mounted antennas (see Table 1 for parameters), one RHCP and one LHCP, with their phase centers aligned along the local vertical (refer to Figure 2). While the RHCP antenna receives direct signals, the LHCP antenna captures reflected signals. This is due to the right-hand circular polarization of GNSS satellite carrier signals. When reflection occurs, the portion of the signal is converted into left-hand circularly polarized waves, particularly when the satellite elevation angle exceeds the Brewster angle (approximately 8° for sea water) [35,36]. The two antennas are then connected to two low-cost GNSS receivers (U-Blox F9P, https://www.u-blox.com/en/product/zed-f9p-module (accessed on 1 April 2022), about USD 240 each), individually. In this way, BDS code and carrier-phase data from the two receivers can be incorporated to obtain the relative position between the two antennas.

Table 1.
Antenna performance parameters.
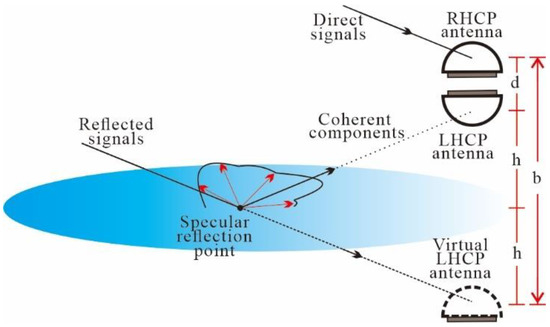
Figure 2.
The BDS-R geometry. It consists of two antennas, one right-hand circular polarized and one left-hand circular polarized, mounted back-to-back, so that the two-phase centers are aligned vertically. The red scattered signals represent the incoherent components.
Figure 2 depicts the simple geometry of BDS-R altimetry. The scattered signals can be divided into two: coherent and incoherent components. The coherent components can be considered as specular reflection on a smooth surface [30]. According to the specular reflection, the LHCP antenna receiving the reflected signal can be considered as the mirror point of a virtual LHCP antenna below the reflecting surface. Therefore, the baseline result from the relative positioning is the distance between the phase centers of the virtual LHCP and the RHCP antennas, and will change as the variation of the reflection interface height changes. Clearly, the height of the real LHCP antenna from the reflector can be simply written as:
where b is the baseline vector of the phase centers of the virtual LHCP and the RHCP antennas, obtained via relative positioning, which is discussed in Section 2.2. d is the actual distance between the phase centers of the LHCP-RHCP antennas, which can be accurately set up in advance.
It should be noted that the coherent components decrease when the water surface becomes rough, which may result in discontinuous or even unusable carrier phase of the reflected signal. Therefore, this configuration is more suitable for environments with less wind and waves.
2.2. Date Processing Model
For short baselines of a few meters, the double difference (DD) model can effectively mitigate the impact of tropospheric and ionospheric delays as well as multipath effects, while preserving the integer nature of carrier phase ambiguities. This facilitates an accurate baseline solution and, thus, we adopt DD observations as our fundamental data processing observation.
Firstly, the baseline vector b in Equation (1) is obtained using Kalman Filter (KF) with double-differenced (DD) observations on BDS B1I:
where denote the notation for single difference between virtual LHCP and RHCP antennas, is the notation for the between-satellite single difference. is the wavelength of the carrier. is the DD code observation expressed in meters, and is the DD carrier phase expressed in cycles. is the DD geometry distance in meters, and is the DD carrier phase ambiguity in cycles. and are the combined effect of DD observational noise and multipath effects for code and carrier phase, respectively.
Take the state vector at epoch k as the combination of baseline vector and DD integer ambiguities ( is the number of satellites):
The linearized DD observation equations in the matrix form can be expressed as follows:
where is the correction vector of , is the observed-minus-computed observation vector, is the design matrix, and refers to the DD observational noise vector combined with multipath effects. Then, can be estimated epoch-by-epoch in KF with two steps.
- (a)
- Time update.
We recursively obtain the predicted value of and its covariance matrix by the following equation:
where and stand for the predicted and the estimated vectors. is the covariance matrix. denotes the process noise. Considering water surface changes nearby the tested lake, we add a process noise of normal distribution for the baseline vector b:
- (b) State update.
The predicted and its covariance can be improved to derive the best estimated with the newly coming in DD observation at epoch k as follows:
with
where is gain matrix, is innovation sequence, and is identity matrix. is the covariance matrix of the observations at epoch decided by the empirical elevation angle weighting model [37], where the code and phase weight ratio is set to 300.
With the completion of the calculation, we can obtain the results of the positional parameters and the corresponding residuals of the DD observations. The residual () validation is also an essential step, and we use 4 times the standard deviation to rule out possible effects of abnormal observations. It is noted that we can only obtain the ambiguity float solution based on Equations (5)–(8). Then, we fix the integer ambiguity by the conventional least-square ambiguity decorrelation adjustment (LAMBDA) algorithm [38,39]. At this point, the baseline vector is obtained epoch-wise and, then, its length b can be taken into Equation (1) to compute the height of the reflecting surface.
2.3. Quality Control Methods
Owing to the special geometry of LHCP-RHCP antennas, the horizontal component of the baseline theoretically should be zero (or another known value). This kind of geometric constraint has been utilized in some improved algorithms such as [40] and has proven that it can greatly improve the performance of real-time altimetry. In our data processing, we propose two simple and effective strategies to make full use of this geometric constraint.
The first versatile strategy is to deal with the geometric constraint in the observation domain, namely, taking the baseline horizontal component as a virtual observation. In our data processing model, the following virtual observation equation is added to DD observation Equation (4) for every epoch:
where and donate the east and north component of baseline vector , respectively. is the residual of the virtual observation. The left-hand side of the equation represents the observed value of the baseline horizontal component. Since this theoretical value is zero in our experimental configuration, we assign a corresponding value of zero to the observation quantity. It is worth noting that too large a variance of virtual observation will lead to insufficient geometric constraints and reduce the quality improvement effect. If the variance value is too small, the KF will be unstable. The empirical variance of the virtual observations is given as in this study, which is about 1 to 2 orders of magnitude smaller than that of the carrier phase observation.
The second QC method simply takes the geometric constraint as a rule-out criterion for the baseline results. Considering that the precisions of the baseline vertical and horizontal components are interrelated, we can use the horizontal component performance to judge the reliability of the vertical component estimation. More precisely, an acceptable solution should conform to the following equation:
where is the threshold for the horizontal component of the baseline. We will discuss the QC method in land altimetry experiments and discuss the virtual observation in water surface altimetry experiments.
3. Experimental Results and Analysis
The experimental results are divided into two parts based on two different datasets: the land altimetry experiment and the water surface altimetry experiment.
3.1. Land Altimetry Experiment
To evaluate the performance of low-cost BDS-R, as well as the QC strategy, we conducted a land altimetry experiment. In this experimental environment, the receiver-to-ground height can be accurately obtained in advance, and the satellite visibility is good. Firstly, we describe the experimental environment, including experiment setup and GNSS constellation conditions. Then, the quality of the direct and reflected signals are evaluated based on SNR. After that, the measurement noise and multipath effect are evaluated by the carrier phase residuals. Finally, the experimental results are compared and discussed under different constellation configurations.
3.1.1. Experiment Environment
We selected an open and flat ground to deploy the experimental device, located at the northwest corner of a plastic runway in Zhengzhou, China. The data were collected from 00:45 to 3:45 (GPST), 1 April 2022, with a sampling interval of 1 s. Considering the measurement noises and Brewster angle, the satellite elevation cutoff angle was set to 15° to exclude particularly noisy data. The distance between the nominal phase centers of the two antennas was set at 0.211 m, while the phase center height of the LHCP antenna from the ground was 0.727 m, measured by a laser rangefinder. Figure 3 shows the location, equipment, and pre-set configuration parameters of the experiment.

Figure 3.
Land altimetry experiment environment and configuration. (a) The site was located at the northwest corner of a plastic runway at 113.57°E, 34.81°N; (b) The two antennas were mounted vertically back-to-back on the same bolt and connected to the two receivers; (c) The distance between the nominal phase centers of the two antennas was set at 0.211 m, while the phase center height of the LHCP antenna from the ground was 0.727 m, measured by a laser rangefinder.
3.1.2. Analysis of Constellations and BDS Data
Table 2 compares the satellite visibility and the corresponding PDOP, VDOP, and HDOP values for five constellation configurations, where the first four are all within BDS constellations. We can conclude that, over the 3 h, IGSOs and GEOs of BDS considerably contributed to the DOPs, owing to their unique coverage performance in China. IGSOs contribute more to VDOP, and GEOs contribute more to HDOP. Therefore, it is worthwhile to explore, specifically, the merits of IGSOs and GEOs in BDS-R. Meanwhile, GPS is better than MEO alone.

Table 2.
Mean level statistics of five constellations.
SNR can be used to describe the strength and quality of GNSS signal reception, and it is worth noting the SNR of the reflected signals from the device. Figure 4 shows the SNR of BDS as a function of elevation angle, and the mean value is fitted. Figure 5 demonstrates some SNR samples of B1I signals from GEO (C02), IGSO (C09), MEO (C30), and GPS (G27) satellites. It can be observed that the reflected signal has two different characteristics. On the one hand, the SNR of the reflected signal is overall lower than that of the direct signal. The SNR of direct signals generally fluctuate within the range of 35 to 52 dB-Hz most of the time, while the SNR of the reflected signal generally fluctuate within the range of 25 to 45 dB-Hz most of the time, and are below 20 dB-Hz for some epochs. The average difference between two SNR is about 7.16 dB-Hz. On the other hand, with the increase in elevation angle, the SNR of the reflected signal is not strictly increasing, and there is oscillation in the process.
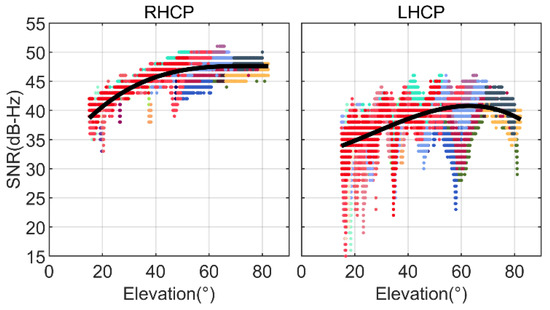
Figure 4.
SNR variation of B1I signals with respect to elevation angle is depicted, with different satellites distinguished by varying colors. The average fitting line is represented by the black curve.
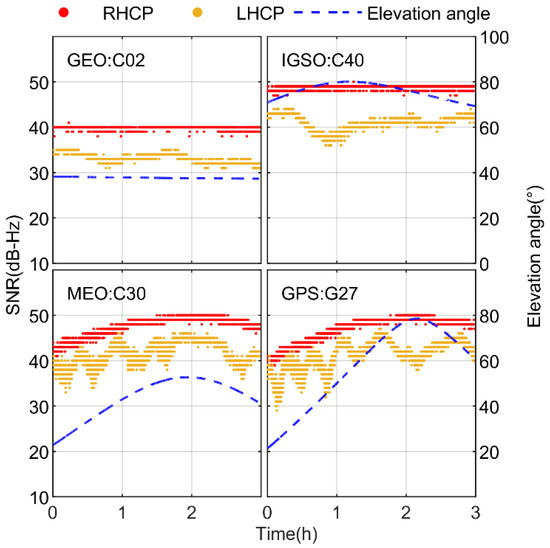
Figure 5.
Some SNR samples of B1I signals from GEO (C02), IGSO (C09), and MEO (C30, C46), and SNR of L1C/A signals from GPS (G27) satellites. The red color represents the SNR observations received by the RHCP antenna, the orange color represents the SNR observations received by the LHCP antenna, and the blue dashed line represents the satellite elevation angle.
The multipath effect is another aspect that we were interested in. Figure 6 shows the DD carrier phase residuals of all available satellites. Due to the specific background selected, complex multipaths from the surrounding environment were rare. The multipath of residual reaction mainly came from the interference effect of direct signal and reflected signal. On the one hand, the residuals of GEOs were still not zero at the time average of 3 h, which may be caused by the multipath effect on the GEOs or the stable geometric multipath effect. On the other hand, the high elevation characteristic of IGSOs minimized the residual RMS value.
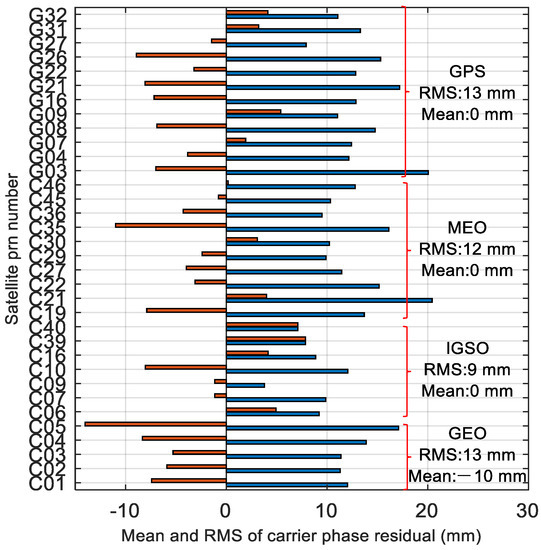
Figure 6.
The mean and RMS value of DD residuals of all the available satellites, respectively. The red is the mean value, and the blue is the RMS value.
The analysis of SNR and residuals shows that the experiment is still affected by multiple paths, especially reflected signals. For the carrier phase, when the ambiguity is correctly fixed, high-precision altimetry results can be obtained. In our experimental configuration, the potential effect of the strong multipath was to reduce the fixed rate of integer ambiguity. In addition to using DD observations to reduce the influence of multipath, our data processing also included two measures: firstly, the SNR threshold (30 dB-Hz) was set in the data preprocessing stage to ensure the reliability of the observations and secondly, the residual validation was carried out to reduce the influence of abnormal observations on the results.
3.1.3. Results and Analysis
The receiver-to-ground height solutions were derived individually from the five configurations of satellite constellations listed in Table 2. The height errors without QC, and their statistics, are shown in Figure 7 and Table 3. We retained the fixed solutions (blue line) as well as the float solutions (red line).
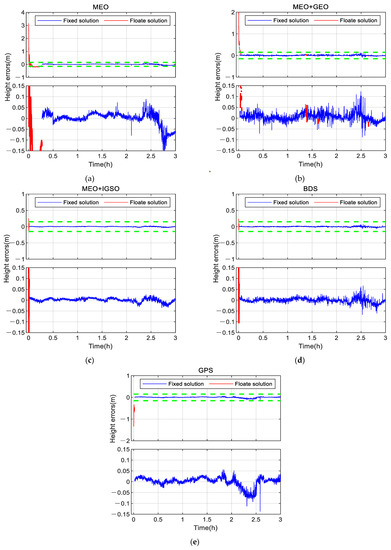
Figure 7.
The corresponding time series of the height errors for the GNSS-R based on five satellite constellation configurations. Each figure is divided into upper and lower parts. The lower part is the enlarged display within the range of the green dotted line of the top half (−0.15 m to 0.15 m). The blue line represents the fixed solution errors, the red line represents the float solution errors. No QC was used for this data set. (a) Height errors based on MEO constellation; (b) Height errors based on MEO plus GEO constellation; (c) Height errors based on MEO plus IGSO constellation; (d) Height errors based on BDS constellation; (e) Height errors based on GPS constellation.

Table 3.
Statistics of fixed rate and fixed solutions height errors.
Figure 7c performs the best in the first four of BDS constellation configurations, which demonstrates that IGSOs play a prominent role in improving the precision of BDS MEO constellation. The contribution of GEOs was less than that of IGSOs, by comparing Figure 7b,c. According to the previous analysis, IGSOs usually have a higher elevation angle compared to GEOs (see Figure 5). Higher elevation angles can obtain more left-hand components of reflected signals [35,36], so IGSOs are more conducive to obtaining high-quality reflected signals. At the same time, IGSOs contributed more to the VDOP value than GEOs, which is very favorable for the experimental configuration we adopted, considering that the precision of the height results is more related to the positioning precision of the vertical direction. In addition, GPS was somehow better than MEOs of BDS. due to its preferable satellite visibility and fixed rate.
Note that, except for the short initialization (around 38 s for BDS) in Figure 7, there are some float point solutions (red line) retained when their errors are within 0.1 m. Likewise, there may have a few fixed solutions being ruled out because their errors exceed 0.1 m, such as a small period after 2.5 h in Figure 7a,e. Hereafter, we only focus on the IGSO-included constellations of BDS and GPS for comparison. What is more, we will see the QC performance of identifying outliers, with the threshold set as 10 cm (upper panel in Figure 8) or 5 cm (lower panel in Equation (10)) in real-time processing.
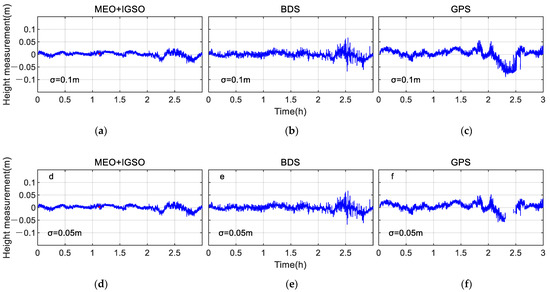
Figure 8.
The corresponding time series of the height errors within [−0.15 m, 0.15 m] after QC. σ is the threshold value of the horizontal baseline in Equation (10). (a) Height errors based on MEO plus IGSO constellation when = 0.1 m; (b) Height errors based on BDS constellation when σ=0.1 m; (c) Height errors based on GPS constellation when σ = 0.1 m; (d) Height errors based on MEO plus IGSO constellation when σ = 0.05 m; (e) Height errors based on BDS constellation when σ=0.05 m; (f) Height errors based on GPS constellation when σ = 0.05 m.
Figure 8 and Table 4 confirm the efficacy of the QC method from two perspectives. Firstly, it accurately identifies all outliers in both fixed and float solutions. Secondly, with a mere 0.3% false rejection rate for BDS-R solutions, the QC method effectively distinguishes real-time processing solutions with centimeter-level precision. We can conclude that the presented QC method, under the tested installation deployment, will be beneficial for real-time altimetry, even in other challenging environments. It is worth noting that our threshold value is obtained through experience, and that the specific value may be related to the DOP value and experimental configuration to some extent. At the same time, too strict a threshold (0.05 m) might lead to discontinuity, such as in Figure 8f. Therefore, a dynamic adaptive threshold needs to be further studied.

Table 4.
Statistics of correct and incorrect elimination rates of QC.
The performance of low-cost BDS-R was evaluated by a land altimetry experiment, while exploring the contributions of IGSOs and GEOs. It concluded that BDS-R can achieve real-time centimeter-level land altimetry with 1 s temporal resolution, and that IGSOs play a prominent role in improving the precision of BDS-R. It can be concluded that, if good satellite visibility is available, a fixed rate of over 90% (or even 99.6%) and centimeter-level real-time land altimetry precision can be achieved for low-cost BDS-R.
3.2. Water Surface Altimetry Experiment
The land altimetry experiment demonstrated the potential of low-cost BDS-R, which is based on omnidirectional azimuth observations. However, in water surface altimetry, the azimuth angle is always limited due to terrain and other environmental factors and the water level is constantly changing. Therefore, there are two differences between the water surface and the land altimetry experiments. Firstly, we added elevation and azimuth masks to resist multipath effects from the surrounding environment. Secondly, since there is almost no change in the water level of the selected lake, we used a lifting platform to simulate water level change by changing the height of the antenna.
3.2.1. Experiment Environment
The same low-cost BDS-R device was installed over a lake in Zhengzhou, China. Two antennas are mounted on the lifting platform, and the latter were fixed on a wooden deck at the northeast corner of the lake, a place selected to maximize the reflecting water surface as well as the satellite visibility (see Figure 9). Again, the distance between the nominal phase centers of the two antennas was set at 0.211 m. Unfortunately, there was no water level gauge nearby. The data were collected from 2:30 to 4:30 (GPST), 28 October 2022, with a sampling interval of 1 s. The lake surface was smooth on that day and the wind speed was merely 2–4 m/s. Therefore, several platform lifts were designed to achieve a total height change of 20 cm with different testing speeds (see Figure 10). Firstly, a speed of 4 cm/min was inserted, starting at 0.5 h and 1 h individually, and lasting for 5 min for each. Then, a faster speed of 20 cm/min was applied at 1.5 h. Finally, 20, 26.6, and 4 cm/min were used for three consecutive ups and downs.

Figure 9.
Water surface altimetry experiment environment. (a) The site was located on a wooden deck on the northeast corner of the lake at 113.56°E, 34.81°N; (b) the two antennas were mounted vertically back-to-back on a lifting platform and connected to the two receivers; (c) the distance between the two nominal phase centers was set at 0.211 m and the phase center height of the LHCP antenna from the water surface was between 1.4 m and 1.6 m (controlled by the lifting platform).
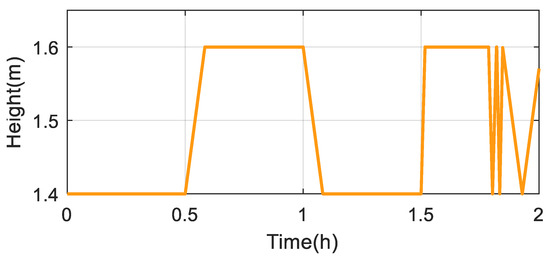
Figure 10.
The height of the water surface simulated by the lifting platform.
As in the land altimetry experiment, the elevation cutoff angle was set to 15°. In addition, there were two ranges suffering from serious multipath effects in the experimental environment. The first was about 10°–90° in azimuth, northeast of the lake, where the LHCP antenna was sheltered by the wooden deck. The second was 160°–200° in azimuth, right towards the south, where a tall half-circle building blocked parts of the GNSS signals for both antennas (see Figure 9). Therefore, we applied an azimuth mask of 10°–90° for the first area and a 30° elevation mask for the second area.
With the two masks set to the challenging lakeside environment, satellite visibility deteriorated as expected. In Figure 11, there are only five visible GPS satellites on average. However, about 16 BDS satellites still can been seen, which suggests BDS-R is more favorable in challenging environments due to the regional coverage characteristics of IGSOs and GEOs in Asia.
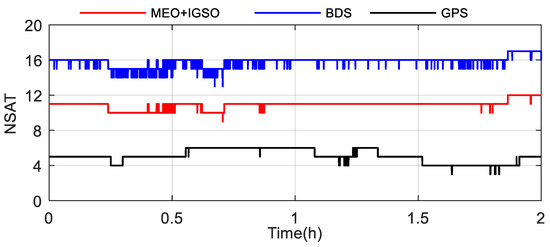
Figure 11.
Comparison of the number of visible satellites in the water surface altimetry experiment after the application of angle masks. One azimuth mask for the northeast direction to exclude this region (from 10° to 90° azimuth) and one elevation mask for the south direction (from 160° to 200° azimuth) to exclude elevation below 30°.
3.2.2. Results and Analysis
Figure 12 shows the water surface heights under the three constellation conditions. Figure 12a,b are the height results without and with QC (Equation (9)), respectively. Table 5 also provides the statistics of the associated fixed rates as well as the standard deviation (STD) of the obtained height errors.
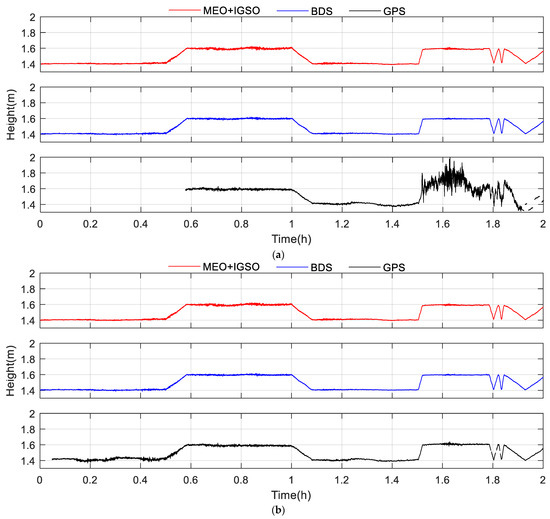
Figure 12.
Time series of water surface height measurements of low-cost BDS-R. (a) The height results without QC. (b) The height results are improved by adding the virtual observations, as in Equation (9).

Table 5.
Statistics of carrier phase ambiguity fixed rate and STD of the obtained height errors.
We can see that the movements of the platform are all reflected by the height results variations, although no water level gauge was available to confirm the average water surface height. Moreover, the height variations from 1.4 to 1.6 m are also consistent with the initial phase center of LHCP antenna measured by laser rangefinder (about 1.4 m above the water surface) and the 20 cm lift settings of the platform.
The QC method of adding virtual observations significantly improved the GPS-based results under a relatively complex environment. The fixed rate was increased from 70% to more than 97%, and the STD of the obtained height errors was reduced from 5 cm to 1 cm (see Table 5). These improvements considerably shortened the GPS-based heights gap in the first 0.5 h, and stabilized the dramatically noisy heights starting from 1.5 h in Figure 12. For BDS-R, the improvement by QC does not seem to be obvious, because the original results have worked so well. It is expected that QC will also improve the performance of BDS-R in more complex environments.
From Table 5, we can see that the low-cost BDS-R can achieve a fixed rate of more than 99% with a standard deviation of less than 1 cm. The results based on the entire BDS constellation are slightly better than the results based on the MEO plus IGSO satellites. This is the opposite of the result of the land altimetry, which may be due to the fact that the complex environment drastically reduced the number of visible satellites. Nevertheless, both of them can realize real-time centimeter-level water-level monitoring with 1 s temporal resolution.
Figure 13 shows the errors of obtained height after QC, which were obtained by subtracting the expected displacement from the obtained height. It can be seen that BDS-R realized the real-time monitoring of water surface height changes with a time resolution of 1 s. Large errors occurred at the inflection point of water surface height change, but it still did not exceed 0.05 m. During the 2 h test period, the carrier phase ambiguity fixed rate was 99.9% and the STD of the obtained height errors was less than 1 cm. The results of the above analyses show that the low-cost BDS-R proposed in this paper can be expected to achieve real-time water level monitoring.
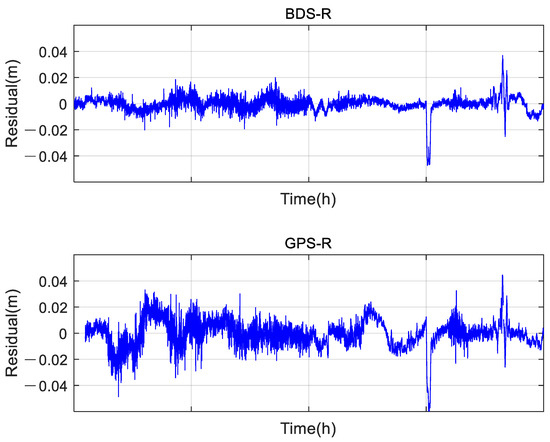
Figure 13.
Time series of the residuals of heights after subtracting the expected displacement.
4. Discussion
The current work shows that low-cost BDS-R could be a feasible and cost-effective method for real-time precise altimetry, which has key advantages compared with other water-level monitoring methods. The georeferenced centimeter-level real-time altimetry solutions could support various geophysical and remote sensing applications, especially in terms of increasing the density of the water level monitoring network and short-term rapid warning, etc.
It is noted that our experiments were conducted in land and lakefront environments, where the surface is relatively smooth and conducive to the continuous phase tracking of the reflected signals [41]. Therefore, the current research is more suitable for use in environments with water level changes but that are not accompanied by significant water surface fluctuations, such as reservoirs, lakes, and coastal environments with breakwaters. However, in the coastal environment, the coherent components of scattered signals on rough sea surfaces gradually decrease and even become unavailable. Studies have shown that the reflected signal has sufficient coherence when the wind and wave are lower than 6 m/s and 1.5 m, respectively [42]. Zhang et al. [43] further verified the feasibility of carrier phase altimeter measurement by BDS B1I and B3I single-frequency signals under the condition of wind speed 7–11 m/s, and the time resolution of the result was 6 min. The proposed method uses multiple satellites in the same epoch. Although strict phase tracking is not required for each satellite, continuous phase tracking is still an important factor affecting the fixed rate. Sea level altimetry in coastal environment still needs further verification and improvement. Thus, one of our future works should be focused on this issue.
In addition to the effect of surface roughness, there are other multipath effects, especially in terms of possible reflections from the rear lobes of low-cost antennas. These can potentially affect the results, including the precision and integer ambiguity fixed rate. How to further weaken the impact of strong multipath brought by low-cost equipment, is also a problem that we need to further study.
In this paper, we focus on B1I signals for low-cost single-frequency devices, and theoretically B3I signals can provide the same number of observations and have a larger bandwidth, which may be beneficial to resist water surface roughness. In addition, signals from BDS-2 will become progressively unavailable outside Asia, so the common frequency (1575.42 or 1176.45 MHz) signals will be the new option, such as B1C, E1, and L1 signals. It is expected that the multi-systems interoperation at the common frequencies could contribute to the performance improvement in low-cost GNSS-R technique outside of Asia, which will also be investigated in our future work.
5. Conclusions
In the context of the official operation of BDS-3 in 2020, we studied the feasibility of low-cost BDS-R for emerging water surface altimetry applications. Firstly, we introduced the BDS-R principle and the corresponding data processing model. Then, we tested the low-cost BDS-R on land surface altimetry with a known height value, and the individual contributions of three different types of satellites in the BDS hybrid constellation were characterized in detail. The results show that centimeter-level height measurement can be achieved in open-sky and flat situations using the developed low-cost single-frequency BDS-R device. On the other hand, it found that the BDS hybrid constellation, especially the IGSOs, can make significant contributions to the performance of BDS-R. This is because the high elevation angle of IGSOs increases the left-hand component of the reflected signal and improves the quality of the reflected signal. At the same time, an improvement in VDOP can also improve the precision in the vertical direction, which is beneficial for altimetry.
Thereafter, we assessed the real-time performance of low-cost BDS-R to support water surface altimetry. On the one hand, low-cost BDS-R can clearly reflect the changes of water surface height in real time with a carrier phase ambiguity fixed rate of 99.9% at the 1 s temporal resolution. The trend of water surface variation is consistent with the actual height variations, and the corresponding STD of the obtained height errors is less than 1 cm. On the other hand, continuous changes in water surface height up to 26.6 cm/min can be precisely monitored.
Author Contributions
Conceptualization, K.D. and L.D.; methodology, K.D. and P.Z.; validation, K.D., Z.L. and K.D.; investigation, L.D. and P.Z.; resources, P.Z and Z.L.; data curation, K.D.; writing—original draft preparation, K.D.; writing—review and editing, L.D., P.Z., Z.Z. and Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by State Key Laboratory of Geodesy and Earth’s Dynamics, Innovation Academy for Precision Measurement Science and Technology, CAS, Wuhan 430077, China (SKLGED2023-3-5) and the National Natural Science Foundation of China (42204041).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Martin-Neira, M. A Passive Reflectometry and Interferometry System (PARIS): Application to Ocean Altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Martin-Neira, M.; Caparrini, M.; Font-Rossello, J.; Lannelongue, S.; Vallmitjana, C.S. The PARIS Concept: An Experimental Demonstration of Sea Surface Altimetry Using GPS Reflected Signals. IEEE Trans. Geosci. Remote Sens. 2001, 39, 142–150. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, L.; Meng, W.; Gu, Q.; Han, Y.; Hong, Z. Feasibility of Code-Level Altimetry Using Coastal BeiDou Reflection (BeiDou-R) Setups. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4130–4140. [Google Scholar] [CrossRef]
- Larson, K.; Löfgren, J.; Haas, R. Coastal Sea Level Measurements Using a Single Geodetic GPS Receiver. Adv. Space Res. 2013, 51, 1301–1310. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Y.; Gao, F.; Guo, P.; Wang, X.; Niu, X.; Wu, M.; Fu, N. Sea Surface Height Estimation by Ground-Based BDS GEO Satellite Reflectometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5550–5559. [Google Scholar] [CrossRef]
- Rodriguez Alvarez, N.; Bosch, X.; Camps, A.; Ramos-Perez, I.; Valencia, E.; Park, H.; Vall-llossera, M. Water Level Monitoring Using the Interference Pattern GNSS-R Technique. In Proceedings of the GPS Snow Sensing: Results from the EarthScope Plate Boundary Observatory, Vancouver, BC, Canada, 24–29 July 2011; pp. 2334–2337. [Google Scholar]
- Larson, K.; Geremia-Nievinski, F. GPS Snow Sensing: Results from the EarthScope Plate Boundary Observatory. GPS Solut. 2013, 17, 41–52. [Google Scholar] [CrossRef]
- Zhang, S.; Dai, K.; Nan, Y.; Zhang, Q.; Qu, W.; Li, Z.; Zhao, Y. Preliminary Research on GNSS-MR for Snow Depth. Wuhan Daxue Xuebao Xinxi Kexue Ban Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 234–240. [Google Scholar] [CrossRef]
- Rodriguez Alvarez, N.; Aguasca, A.; Valencia, E.; Bosch, X.; Ramos-Perez, I.; Park, H.; Camps, A.; Vall-llossera, M. Snow Monitoring Using GNSS-R Techniques. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 4375–4378. [Google Scholar]
- Fabra Cervellera, F. GNSS-R as a Source of Opportunity for Remote Sensing of the Cryosphere. Ph.D. Thesis, Universitat Politècnica de Catalunya, Catalonia, Spain, 2013. [Google Scholar]
- Komjathy, A.; Maslanik, J.; Zavorotny, V.U.; Axelrad, P.; Katzberg, S.J. Sea Ice Remote Sensing Using Surface Reflected GPS Signals. In Proceedings of the IGARSS 2000. IEEE 2000 International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment. Proceedings (Cat. No.00CH37120), Honolulu, HI, USA, 24–28 July 2000; Volume 7, pp. 2855–2857. [Google Scholar]
- Rius, A.; Nogués-Correig, O.; Ribó, S.; Cardellach, E.; Oliveras, S.; Valencia, E.; Park, H.; Tarongí, J.; Camps, A.; Marel, H.; et al. Altimetry with GNSS-R Interferometry: First Proof of Concept Experiment. GPS Solut. 2012, 16, 231–241. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Gommenginger, C.; Gleason, S.T.; Srokosz, M.; Galdi, C.; Bisceglie, M. Analysis of GNSS-R Delay-Doppler Maps from the UK-DMC Satellite over the Ocean. Geophys. Res. Lett. 2009, 36, L02608. [Google Scholar] [CrossRef]
- Germain, O.; Ruffini, G.; Soulat, F.; Caparrini, M.; Chapron, B.; Silvestrin, P. The Eddy Experiment: GNSS-R Speculometry for Directional Sea-roughness Retrieval from Low Altitude Aircraft. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Garrison, J.; Voo, J.; Yueh, S.; Grant, M.; Fore, A.; Haase, J. Estimation of Sea Surface Roughness Effects in Microwave Radiometric Measurements of Salinity Using Reflected Global Navigation Satellite System Signals. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1170–1174. [Google Scholar] [CrossRef]
- Masters, D. Surface Remote Sensing Applications of GNSS Bistatic Radar: Soil Moisture and Aircraft Altimetry. Ph.D. Thesis, University of Colorado Boulder, Boulder, CO, USA, 2004. [Google Scholar]
- Zhang, S.; Wang, T.; Wang, L.; Zhang, J.; Peng, J.; Liu, Q. Evaluation of GNSS-IR for Retrieving Soil Moisture and Vegetation Growth Characteristics in Wheat Farmland. J. Surv. Eng. 2021, 147, 04021009. [Google Scholar] [CrossRef]
- Rodriguez Alvarez, N.; Bosch, X.; Camps, A.; Vall-llossera, M.; Valencia, E.; Marchan, J.; Ramos-Perez, I. Soil Moisture Retrieval Using GNSS-R Techniques: Experimental Results over a Bare Soil Field. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3616–3624. [Google Scholar] [CrossRef]
- Vignudelli, S.; Birol, F.; Benveniste, J.; Raynal, M.; Roinard, H. Satellite Altimetry Measurements of Sea Level in the Coastal Zone. Surv. Geophys. 2019, 40, 1319. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Gleason, S.; Cardellach, E.; Camps, A. Tutorial on Remote Sensing Using GNSS Bistatic Radar of Opportunity. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–45. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Domenech, E.; Pascual, D.; Martín, F.; Rius, A.; Ribo, S.; Benito, J.; Andres-Beivide, A.; Saameno, P.; et al. Optimization and Performance Analysis of Interferometric GNSS-R Altimeters: Application to the PARIS IoD Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1436–1451. [Google Scholar] [CrossRef]
- Martin-Neira, M.; Colmenarejo, P.; Ruffini, G.; Serra, C. Altimetry Precision of 1 Cm over a Pond Using the Wide-Lane Carrier Phase of GPS Reflected Signals. Can. J. Remote Sens. 2002, 28, 394–403. [Google Scholar] [CrossRef]
- Liu, Z.; Du, L.; Zhou, P.; Liu, Z.; Zhang, Z.; Xu, Z. BDS/GNSS Multipath Reflectometry (BDS/GNSS-MR) Based Altimetry with New Signals: Initial Assessment and Comparison. Adv. Space Res. 2021, 69, 282–291. [Google Scholar] [CrossRef]
- Rodrigues, E.; Kasser, M. Limnimétrie par réflectométrie GNSS à faible coût. Geomatik Schweiz 2014, 8, 349–354. [Google Scholar] [CrossRef]
- Treuhaft, R.; Lowe, S.; Zuffada, C.; Chao, Y. 2-Cm GPS Altimetry over Crater Lake. Geophys. Res. Lett. 2001, 22, 4343–4346. [Google Scholar] [CrossRef]
- Löfgren, J.; Haas, R.; Johansson, J. High-Rate Local Sea Level Monitoring with a GNSS-Based Tide Gauge. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3616–3619. [Google Scholar]
- Löfgren, J.; Haas, R.; Johansson, J. Monitoring Coastal Sea Level Using Reflected GNSS Signals. Adv. Space Res. 2011, 47, 213–220. [Google Scholar] [CrossRef]
- Wang, N.; Bao, L.; Gao, F. Improved Water Level Retrieval from Epoch-by-Epoch Single and Double Difference GNSS-R Algorithms. Acta Geod. Et Cartogr. Sin. 2016, 45, 795–802. [Google Scholar] [CrossRef]
- Bao, L.; Wang, N.; Gao, F. Improvement of Data Precision and Spatial Resolution of CGNSS-R Altimetry Using Improved Device with External Atomic Clock. IEEE Geosci. Remote Sens. Lett. 2015, 13, 207–211. [Google Scholar] [CrossRef]
- Liu, W.; Beckheinrich, J.; Semmling, M.; Ramatschi, M.; Vey, S.; Wickert, J.; Hobiger, T.; Haas, R. Coastal Sea-Level Measurements Based on GNSS-R Phase Altimetry: A Case Study at the Onsala Space Observatory, Sweden. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5625–5636. [Google Scholar] [CrossRef]
- Nie, Z.; Liu, F.; Gao, Y. Real-Time Precise Point Positioning with a Low-Cost Dual-Frequency GNSS Device. GPS Solut 2019, 24, 9. [Google Scholar] [CrossRef]
- Biagi, L.; Grec, F.-C.; Negretti, M. Low-Cost GNSS Receivers for Local Monitoring: Experimental Simulation, and Analysis of Displacements. Sensors 2016, 16, 2140. [Google Scholar] [CrossRef]
- Williams, S.; Bell, P.; McCann, D.; Cooke, R.; Sams, C. Demonstrating the Potential of Low Cost GPS Units for the Remote Measurement of Tides and Water Levels Using Interferometric Reflectometry. J. Atmos. Ocean. Technol. 2020, 37, 1925–1935. [Google Scholar] [CrossRef]
- Zhang, Y.; Binbin, L.; Luman, T.; Qiming, G.; Yanling, H.; Hong, Z. Phase Altimetry Using Reflected Signals From BeiDou GEO Satellites. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1410–1414. [Google Scholar] [CrossRef]
- Löfgren, J. Local Sea Level Observations Using Reflected GNSS Signals. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2014. [Google Scholar]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS Signals from the Ocean with Wind Remote Sensing Application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; Shen, Y.; Gao, Y.; Wang, M. Site-Specific Unmodeled Error Mitigation for GNSS Positioning in Urban Environments Using a Real-Time Adaptive Weighting Model. Remote Sens. 2018, 10, 1157. [Google Scholar] [CrossRef]
- Chang, X.-W.; Yang, X.; Zhou, T. MLAMBDA: A Modified LAMBDA Method for Integer Least-Squares Estimation. J. Geod. 2005, 79, 552–565. [Google Scholar] [CrossRef]
- Teunissen, P. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Löfgren, J.; Haas, R. Sea Level Measurements Using Multi-Frequency GPS and GLONASS Observations. J. Adv. Signal Process. 2014, 2014, 50. [Google Scholar] [CrossRef]
- Helm, A. Ground-Based GPS Altimetry with the L1 OpenGPS Receiver Using Carrier Phase Delay Observations of Reflected GPS Signals. Sci. Tech. Rep. Geoforschungszentrum Potsdam. 2008, 8. [Google Scholar] [CrossRef]
- Cardellach, E.; Li, W.; Rius, A.; Semmling, M.; Wickert, J.; Zus, F.; Ruf, C.; Buontempo, C. First Precise Spaceborne Sea Surface Altimetry With GNSS Reflected Signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 13, 102–112. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, L.; Meng, W.; Qin, J.; Sheng, Z.; Yang, S. Evaluation of Shore-Based Sea Surface Altimetry Based on Beidou Satellite Reflection Signals. J. Beijing Univ. Aeronaut. Astronaut. 2022, 49, 999–1008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).