Deep Clouds on Jupiter

Abstract

Jupiter’s atmospheric water abundance is a highly important cosmochemical parameter that is linked to processes of planetary formation, weather, and circulation. Remote sensing and in situ measurement attempts still leave room for substantial improvements to our knowledge of Jupiter’s atmospheric water abundance. With the motivation to advance our understanding of water in Jupiter’s atmosphere, we investigate observations and models of deep clouds. We discuss deep clouds in isolated convective storms (including a unique storm site in the North Equatorial Belt that episodically erupted in 2021–2022), cyclonic vortices, and northern high-latitude regions, as seen in Hubble Space Telescope visible/near-infrared imaging data. We evaluate the imaging data in continuum and weak methane band (727 nm) filters by comparison with radiative transfer simulations, 5 micron imaging (Gemini), and 5 micron spectroscopy (Keck), and conclude that the weak methane band imaging approach mostly detects variation in the upper cloud and haze opacity, although sensitivity to deeper cloud layers can be exploited if upper cloud/haze opacity can be separately constrained. The cloud-base water abundance is a function of cloud-base temperature, which must be estimated by extrapolating 0.5-bar observed temperatures downward to the condensation region near 5 bar. For a given cloud base pressure, the largest source of uncertainty on the local water abundance comes from the temperature gradient used for the extrapolation. We conclude that spatially resolved spectra to determine cloud heights—collected simultaneously with spatially-resolved mid-infrared spectra to determine 500-mbar temperatures and with improved lapse rate estimates—would be needed to answer the following very challenging question: Can observations of deep water clouds on Jupiter be used to constrain the atmospheric water abundance?

1. Introduction

Aerosol particles in the atmospheres of giant planets can be roughly divided into categories of “clouds” and “hazes,” although these terms are difficult to quantitatively define. West et al. [1] used definitions based on opacity and vertical structure, with “haze” referring to layers with low optical depth $\tau$ and possibly extended vertical structure (high particle-to-gas scale height ratio, $H_p/H_g$). They used “cloud” to refer to regions with high $\tau$ and low $H_p/H_g$. Particle origins could also be used to distinguish clouds and hazes, with clouds formed by the condensation of volatile heavy element gas species such as water vapor, and hazes from products of chemistry driven by energy input from solar ultraviolet, auroral precipitation and heating, atmospheric electrical phenomena, cosmic rays, etc. The different origins of particles lead to an altitude-based definition, with hazes formed at pressure levels near and above the tropopause that can be reached by external energy inputs, and with clouds formed below the tropopause, where warmer air laden with volatiles mixes upward to the condensation levels of various species.

The distinction between hazes as higher-altitude phenomena and clouds as lower-altitude phenomena becomes blurred in the ice giants. Several analyses have suggested that extended hazes (in the opacity/vertical structure sense) were found in Neptune’s troposphere [2,3], supported by analysis of more recent infrared spectroscopic data [4]. Irwin et al. [5] found that hazes (in the origin sense) mix into the tropospheres of Uranus and Neptune and interact with clouds, serving as condensation nuclei and modifying the single-scattering albedo of cloud particles. This ice giant finding is relevant to the case of the gas giants Jupiter and Saturn, where haze and cloud interaction have been discussed as mechanisms to suppress the infrared spectral signatures of ammonia ice [6] or to drive color changes in anticyclonic vortices such as Oval BA [7,8]. In Neptune’s atmosphere, compact bright clouds (in the origin sense) are composed of CH${}_4$ ice condensed at high altitudes, extending into the lower stratosphere (making them hazes in the altitude sense [9,10]). Methane comprises the highest-altitude condensation clouds on Uranus and Neptune, but in the warmer atmospheres of Jupiter and Saturn, remote sensing in the visible/near-infrared wavelength regime can detect sunlight scattered back from cloud decks of ammonia, ammonium hydrosulfide, and water (in order of increasing pressure level). Distinguishing the depths of these cloud layers, especially when multiple layers are present, is a challenging feat.

In the discussion of deep clouds inferred from imaging data in this paper, as well as deep clouds identified spectroscopically in the companion paper Bjoraker et al. [11] in this Special Issue, we conceive of deep clouds as anything within the NH${}_4$SH and H${}_2$O condensation region. We also refer to an upper cloud/haze layer, which we conceive as a combination of aerosols from NH${}_3$ condensation, plus upper tropospheric hazes of possible photochemical origin. This categorization allows us to focus on water clouds, which are the deepest clouds potentially detectable in Jupiter’s atmosphere in reflected sunlight. The next deepest layers of thermodynamically expected condensation (KCl, ZnS) are not found until several hundred bar [12]. Rayleigh scattering and gas opacity limit sunlight penetration depths to about 20–50 bar even in the absence of other aerosols [13,14].

Identifying deep water clouds is valuable for two reasons: they are intimately connected to atmospheric circulation and heat transport via moist convection, and their depth provides a lower limit on the abundance of water in the atmosphere. Deep clouds have been identified in rare cases using imaging data (particularly using 727-nm imaging filters, as discussed in Section 2), although most of the planet’s aerosol opacity is dominated by cloud and haze particles at $p<1$ bar. Remote sensing in the 5-µm infrared window has also been exploited to resolve spectral lines of well-mixed gases such as CH${}_3$D, which can sense deep cloud levels. Bjoraker et al. [11] used this approach to identify cloud opacity in the 4–7 bar range. The deep cloud levels can be used to constrain the water abundance at the location of the observed cloud, because saturation is implied at or below the level where cloud opacity is located. Any local water abundance must still be regarded as a lower limit to the bulk atmospheric abundance, given numerous observational and theoretical findings that volatile species in giant planet atmospheres are depleted (with respect to bulk atmospheric abundances) to vertical levels significantly deeper than their cloud bases, e.g., [4,15,16,17,18].

Water abundance is commonlyreferenced to the protosolar O/H ratio of 5.4$\times {10}^{-4}$ from Asplund et al. [19], corresponding to an atmospheric H${}_2$O/H${}_2$ volume mixing ratio of 1.1$\times {10}^{-3}$, or an atmospheric concentration (or mole fraction) of 9.3 $\times {10}^{-4}$ in Jupiter’s atmosphere depending on the assumptions of other gas mixing ratios. Both Asplund et al. [19] and Asplund et al. [20] give the same photospheric ratios of O/H, N/H, and S/H (for elements that form clouds in Jupiter’s troposphere), but the two papers differ in the corrections for solar evolution that convert from photospheric to protosolar abundances. In this work, we use a protosolar correction of +0.04 dex [19,21], although Asplund et al. [20] reviews more recent work with corrections falling between +0.064 dex for the solar model of Vinyoles et al. [22] to as low as +0.03 dex.

The cloud-height approach is one of several approaches that have been followed in the quest to measure Jupiter’s water abundance. The sole in situ measurement is from the Galileo Probe mass spectrometer [16,23], giving a low result of 0.46× protosolar O/H, but influenced by compositional perturbations from the 5-µm hot spot at the probe entry site [24,25]. The Microwave Radiometer (MWR [26]) on the Juno orbiter [27] constrains the water abundance to 1–5× protosolar in the equatorial region [18], with further analysis and laboratory data expected to extend this determination to other latitudes in the near future [28,29]. The depth of lightning flashes was used as a constraint on O/H (using similar reasoning to the cloud-height approach, [30,31]), but the possibility of flashes extending below the water condensation level [32] means that flash depth does not directly relate to water abundance at the lightning site. Even the suggestion that $\ge 1\times$ protosolar water is needed so that mixed-phase cloud particles can achieve sufficient charge separation [33] is called into question by very shallow lightning detected in Juno night-side imaging, which has been explained by hypothetical mushballs composed of mixed-phased condensates with high ammonia concentration [32,34,35]. Direct spectroscopic measurements of water vapor concentration find very low mole fractions [11,36], but this could result from the same dynamical effects [37,38,39] governing the trend in ammonia from microwave remote sensing of Jupiter, which finds depletion of ammonia at depths greatly exceeding the ammonia condensation level [15,17,18,40]. Measurements of CO in the troposphere have also been used as a constraint on the O/H ratio at the deep quench level for thermochemical conversion between H${}_2$O and CO [41,42,43,44], but in addition to measurement uncertainties on CO, this method is sensitive to differences in the treatment of mixing and the choice of chemical network reactions and reaction rates [45,46,47,48,49]. Although our study was originally conceived as a way to narrow the uncertainty on Jupiter’s atmospheric O/H ratio, we ultimately find that the problem remains challenging, such that a range of simultaneous observations from the visible to the mid-infrared would be needed to truly derive tight constraints on O/H using the cloud-height approach. Even then, only lower limits on O/H can be established using measurements of cloud tops rather than cloud bases, unless the vertical thickness of the cloud layer can be separately determined.

We present new results on the multi-level distribution of Jupiter’s clouds, on how uncertainties in Jupiter’s temperature structure propagate to uncertainties in the O/H ratio at the cloud base, and how future spectro-imaging observations at high spatial resolution might make progress on our understanding of deep clouds. In Section 2, we use Hubble Space Telescope (HST) and Gemini North ground-based imaging data to identify deep clouds on Jupiter. This includes radiative transfer calculations characterizing the degeneracy between upper cloud opacity and the pressure level of deep clouds observed using the HST weak methane band filter (Section 2.3) and a description of specific features such as non-convecting deep clouds, a “stealth superstorm” driving intermittent convective eruptions throughout 2021–2022, deep clouds in cyclonic vortices, and a broad region north of 45°N that has a shift in the depth of cloud opacity. In Section 3, we calculate cloud base pressure levels for a suite of temperature conditions that span the full range of published data. In Section 4 and Section 5, we apply the results of the radiative transfer and cloud condensation models to specific areas of interest, discuss how the results to date constrain the atmospheric water abundance (particularly as applied to the cloud-top pressures derived in Bjoraker et al. [11]), and recommend directions for future studies to advance our knowledge of Jupiter’s deep cloud structure.

2. Imaging Deep Jovian Clouds with HST

Imaging observations of Jupiter, particularly those at high spatial resolution, provide useful constraints on the distribution of deep clouds on Jupiter. This section covers the data and the diagnostics used to constrain deep clouds in HST data, which follows approaches previously used for Galileo and Cassini imaging observations. Section 2.2 focuses on examples of deep clouds in three specific areas of interest: convective storms, non-convective deep clouds, and deep clouds at high latitudes. In Section 2.3, we quantitatively interpret Jupiter imaging data using a radiative-transfer modeling study.

2.1. Imaging Data

Visible/UV/near-IR observations were performed with the UVIS channel of the WFC3 instrument [50] on the Hubble Space Telescope. The FQ727N filter on WFC3, which samples the reflectivity in the 727-nm weak methane absorption band, is key to identifying and mapping deep clouds on Jupiter. Methane-band (and continuum) quad filters were included in the design for WFC3 with the primary intention of supporting studies of giant planet atmospheres [51].

Thermal infrared imaging was performed with the NIRI instrument [52] at the Gemini North telescope. We used the M’-band filter with a central wavelength of 4.7 µm, although we also generically refer to images at this wavelength as 5-µm images because the M’ filter is situated within the broad 5-µm window where thermal radiation from the 2–11 bar region of Jupiter’s troposphere can escape to space [11,53,54].

Figure 1 presents an overview of imaging data acquired 21–23 May, 2022 in various filters, along with composites and filter ratios. Channels have been scaled to maximize contrast (see color bars). Data were taken close in time to the Juno perijove 42 pass (diffraction-limited resolution was 300 km for HST at 727 nm and 575 km for Gemini at 4.7 µm). Data in panels B, D, E, and F are corrected for limb darkening (Minnaert k = 0.98 for 727 nm, 0.999 for other HST filters). Panel A is shown with natural limb darkening, and panel C is stretched by the 0.4 power to emphasize faint detail. Ratios in panel G are based on data without limb-darkening correction. Frames taken at different times were remapped to a common time point to reconstruct the full-disk image in each composite. See Supplemental Figures S1–S12 in SM1 for enlargements.

2.1.1. HST Imaging Programs

HST data used in this study are listed in Table 1. Although the majority of HST data are from WFC3, one figure shows an RGB composite map taken with the WFPC2 instrument in 2007. Figure 1 presents data taken near the time of Juno PJ 42. PJ stands for perijove, the Jupiter periapsis portion of the Juno orbit when atmospheric science observations are conducted. Continuum and 727-nm filter data were used to compare with radiative-transfer forward models discussed in Section 2.3. HST and Gemini data taken near Juno’s PJ 19 [55,56,57] are used in Section 4.1 to validate the interpretation of the radiative transfer modeling. HST/WFC3 data from some other epochs are also discussed, but many more epochs are not shown and merit additional detailed investigation in future work.

2.1.2. HST Data Processing

Jupiter maps result from images that have gone through several stages of processing, as described in detail in [55]. These stages involve cleaning of cosmic ray artifacts, correction of geometric distortion, photometric calibration to $I/F$ (reflectivity) units [4], and navigation to transform the data to latitude/longitude coordinates on Jupiter. (Planetographic latitudes are used in this paper unless otherwise noted.) Corrections for fringing (etaloning) artifacts in the narrow-band filters at $\lambda >700$ nm were performed [58]. The WFC3 pipeline now includes time-dependent photometric calibration [59].

Processing of the WFPC2 data was discussed in Asay-Davis et al. [60].

2.1.3. Gemini Imaging Data and Data Processing

Figure 1C presents M-band (4.7 µm) imaging data taken with the NIRI camera at Gemini Observatory. The data were taken near Juno PJ 42 on 23 May 2022 between 14:39 and 14:50, using a four-position mosaic. To approach the diffraction limit of the telescope, individual 0.3-sec exposures were coadded in a lucky-imaging approach described in Wong et al. [55]. To assist in comparison with HST imaging in Figure 1 taken almost four Jupiter rotations earlier, refer to individual features marked on the images at the two time-points in the Supplementary Material. Gemini data presented in later figures were taken near Juno PJs 19 and 29.

2.1.4. Cloud Depths from Imaging

A wide range of filters across the visible spectrum have been used to constrain cloud vertical structure. Because structure varies significantly on short length scales, the high resolution provided by spacecraft (and HST) imaging data is required, particularly within discrete features. For constraining the deepest clouds, a filter pair measuring the reflectivity in the 727-nm weak methane band plus reflectivity in a nearby continuum wavelength are most effective [55,61,62]. Prior works have visually represented the resulting cloud depth information in two ways, for which we adopt specific convenience labels in this work:

CH${}_4$ composites, or CH${}_4$-band cloud depths maps (e.g., Figure 1B). These are a standard type of color composite image, where the red/green/blue channels of the composite are used to display, respectively, the deep-probing continuum/weak CH${}_4$ band (727 nm) / strong CH${}_4$ band (889 nm). Examples of CH${}_4$-band depth maps from Galileo Orbiter data are shown in Figure 6 of Banfield et al. [61] and Figures 1 and 2 of Gierasch et al. [63]. Examples from Cassini data are shown in Figures 2 and 3 of Porco et al. [62] for Jupiter, and Figure 4 of Sayanagi et al. [64] for Saturn.

In this paper, we use either 631-nm or 750-nm filters as “continuum” reference filters for the weak methane band at 727 nm. Neither filter provides a perfect continuum reference. The WFC3 FQ750N filter is officially the continuum filter for FQ727N [50], but its use is complicated by the presence of NH${}_3$ gas absorption within its bandpass [14]; see Section 2.3 below. The disadvantage of the F631N filter is the greater wavelength shift compared to 727 nm (13% rather than 3% for 750 nm), which allows particle properties to influence the relative reflectances.

CM7 is an abbreviation used in this article for the ratio of the continuum to methane 727-nm reflectivity:

$$\mathrm{CM}7=\frac{I/F_{\mathrm{cont}.}}{I/F_{727}}$$

(1)

The CM7 ratio is useful for distinguishing deep clouds from upper clouds in Jupiter’s atmosphere (e.g., Figure 1G). Continuum filters reach an optical depth of 1 (for two-way scattering/absorption of sunlight back to the observer) near 6–10 bar in an aerosol-free atmosphere [65], while the weak CH${}_4$-band filter near 727 nm reaches two-way $\tau$ = 1 near 3 bar, and the strong CH${}_4$-band filter near 889 nm reaches two-way $\tau$ = 1 near 300–500 mbar [61]. When the vertically integrated aerosol opacity has a stronger contribution from deep clouds, CH${}_4$ absorption in the in 727-nm bandpass limits the response in the weak methane-band filter, so the CM7 ratio is higher. Low values of CM7 correspond to cloud structures dominated by upper-level opacity, or structures with very high upper-level opacity such that both filters are insensitive to any deeper clouds. The CM7 ratio is sensitive to the relative weighting between upper opacity and deep opacity in the column, but the ratio is insensitive to the total amount of opacity.

The CM7 ratio was used in Figure 5.9 of West et al. [66] to identify deep clouds in a region of active moist convection. The imaging data constrained the deep clouds to lie at pressures of 3 bar or deeper, leading West et al. [66] to conclude that the clouds must be composed of water, since NH${}_3$ and NH${}_4$SH cannot condense as deep in the atmosphere. The CM7 ratio safely avoids division by zero because even in locations with no condensation clouds, Jupiter’s reflectivity is nonzero due to Rayleigh scattering and scattering by low-opacity hazes at high altitudes. The continuum wavelength used in the ratio varies, depending on the filters available at a given observation time.

Quantitative interpretation of cloud depth using narrow-band imaging data requires radiative transfer analysis, as described in Section 2.3. However, qualitative information can be derived from simple visual comparison, as a demonstration of the cloud depth information content in the data.

2.2. Settings of Deep Clouds

Deep clouds on Jupiter—whether identified using the red appearance in CH${}_4$-band composites, high CM7 ratios, or CH${}_3$D line widths in high-resolution 5-µm spectroscopy [11]—are often located in three distinct settings: isolated moist convective storms, cyclonic vortices, and a large region north of 45°N with distinct cloud structure. In this section, we discuss specific observations of deep clouds in each of these three settings.

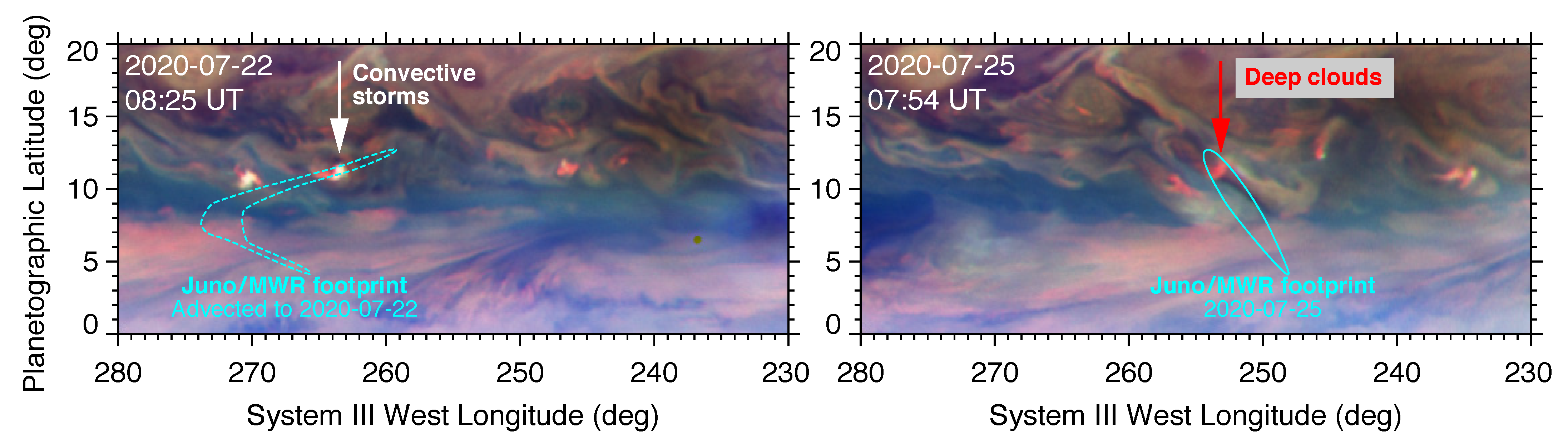
2.2.1. Deep Cloud Setting 1: Moist Convective Storms

The cloud structure in moist convective systems has been investigated on Jupiter for decades. Gierasch et al. [63] used Galileo imaging data to identify a two-component cloud structure in a region of active moist convection: (1) deep water clouds juxtaposed with (2) thick convective towers reaching high altitudes. Night-side imaging detected lightning within the cloud complex, confirming its moist-convective nature. The cloud structure was derived from CH${}_4$-composite maps.

Imai et al. [56] identified a third component of the cloud structure in active moist convective regions: cloud clearings (Figure 2). As with Gierasch et al. [63], Imai et al. [56] combined lightning detections with CH${}_4$-band cloud depth maps, but in this case, the lightning came from localized signals detected by Juno in the microwave/radio wavelength regime, and the cloud depth maps came from HST imaging data.

Galileo night-side imaging found lightning flashes in the North Equatorial Belt (NEB) among other locations (e.g., Storm 15 in Figures 3 and 4 of Little et al. [67]). Around the time of Juno’s perijove 28 in July 2020, HST imaging revealed a series of deep clouds in the NEB, but Juno did not detect lightning near the deep clouds. HST images three days prior (Figure 3, left) showed deep clouds juxtaposed with tall/thick convective towers and cloud clearings (the three-component cloud structure characteristic of active moist convection). However, by the time Juno scanned the same deep clouds, the tall/thick cloud towers had disappeared, suggesting that moist convective activity had ended. Three days is long enough to observe significant evolution in a moist convective storm, although denser temporal sampling would be needed to fully characterize timescales of storm evolution. The 10-hour cadence of the Cassini Jupiter-approach time series (see Figure 3 of Porco et al. [62]) confirms three days to be the approximate timescale for the decay of a convective storm eruption in the region to the northwest of the Great Red Spot (GRS). As with Figure 3, compact deep clouds remained after the decay of tall convective towers. Isolated compact deep clouds may commonly persist for a longer time than active convective outbreaks.

In 2021 and early 2022, typical isolated convective storms in the NEB such as those in Figure 3 died out, except at a single active latitude that drifted around the planet at a constant speed [69,70]. Figure 4 shows the cloud structure around the active longitude in May 2022, near Juno perijove 42 (PJ 42). Juno MWR measurements of lightning activity near the same active longitude several months prior (near perijove 38) suggest that storms near the active longitude are moist-convective in nature, yet the cloud structure in Figure 4 is not fully consistent with the three-component moist convective cloud structure. Specifically, deep clouds (red in a CH${}_4$ composite) are largely absent near the active longitude, whereas typical moist-convective storms feature deep clouds and tall, thick clouds with roughly equal feature sizes and areal coverage. Reflectivity in the strong methane band (889 nm) is also not particularly strong relative to nearby cloud features, suggesting weak convection that does not extend to high tropospheric levels. There is no clear explanation why convection in the NEB in 2021–2022 exhibits the long-term behavior typical of a large superstorm while the cloud structure is barely consistent with moist convection and the cloud tops do not reach the same heights typical of other moist-convective regions.

2.2.2. Deep Cloud Setting 2: Cyclonic Vortices

Deep clouds detected within some cyclonic vortices may be examples of clouds formed without strong moist convective activity. Cyclonic vortices are known to transform between different morphologies: a “barge” morphology characterized by a distinct, smooth elliptical outline (e.g., Figure 5) and turbulent morphology with a less distinct peripheral boundary and a more chaotic and filamentary appearance [55,72,73,74]. Cyclone morphology transformations have been studied from the Voyager era to the Juno era [75,76,77]. The visual appearance of cyclones suggests that the folded filamentary morphology coincides with active moist convection, while the smooth-edged “barge” morphology indicates an absence of active moist convection. Figure 5 supports this interpretation because the large barge-type cyclone at the center of the map lacks key elements of convective cloud structure (tall/thick cloud towers and deep clearings), while folded filamentary cyclones have all three components of convective cloud structure [55]. Additionally, Wong et al. [55] linked clusters of lightning sferics detected by Juno MWR to folded filamentary regions (FFRs), while the barge in Figure 5A is not accompanied by a cluster of lightning signals. Some lightning directly to the north is found much closer to regions exhibiting the three-component cloud structure signature of moist convection. Bolton et al. [57] analyzed MWR scans of this particular barge, finding a density inversion layer somewhere in the 3–6 bar range. The observation of a deep central cloud suggests that convection in the water cloud layer is taking place, but perhaps the density inversion layer represents strong convective inhibition (CIN [78]), preventing the moist convective process from rising up to the upper troposphere, as seen in FFRs.

A barge in the South Equatorial Belt was imaged by HST/WFPC2 in 2007 (Figure 5B), revealing a compact central red cloud in RGB composite (pseudo true color) images [79]. Deep clouds can appear red in RGB composites because Rayleigh scattering limits the penetration depth of sunlight at short wavelengths. The barge with the central red cloud erupted into a convective outbreak several days after the WFPC2 observations, leading to global-scale changes in cloud color at that latitude.

The creation of deep isolated clouds, particularly within non-convective cyclonic vortices, may indicate the development of conditions favoring moist convective initiation (e.g., a buildup of convective available potential energy, or CAPE [80]). Thus, deep clouds may precede moist convective outbreaks in cyclones, as well as persisting after them (as in the isolated convective storms shown in Figure 3).

Figure 6 presents an enlargement of a southern hemisphere region from Figure 1. Two cyclones are seen in different states: C45 has a smooth cigar-shaped outline with homogeneous internal cloud coverage (a “cloudy oval” state), and C34 has a folded filamentary cloud structure typical of active moist convection. The cloud structure state of C45 differs from barges because it has significant cloud opacity throughout its interior, but it shares the smooth outline of barges, unbroken by active moist convective filaments, towers, and clearings. The cloudy oval state of C45 resembles that of a named cyclone at 24°S, the South Temperate Belt Ghost, which was observed transitioning through a convective outbreak into an FFR state [76]. Hueso et al. [77] reported on two cyclones near 31°S, DS6 and DS7. DS7 (also known as Clyde’s Spot [81]) transitioned between a barge-like state and an FFR state, while DS6 transitioned between a barge-like state and a smooth-outlined but cloudy state, like the cyclone C45 in Figure 6. Although it is clear that the difference between the FFR state and both of the smooth-outline cyclone states (barge and cloudy oval states) is active moist convection, it is not clear whether the cyclone’s internal structure or its interactions with surrounding cloud layers explains the differences between barge states (Figure 5) and cloudy oval states (Figure 6). Deep clouds have been seen within cyclones in FFR and barge states, but the high opacity of upper-level clouds in the cloudy oval cyclone state prevents detection of any deeper clouds that may lie beneath the upper aerosol layer.

2.2.3. Deep Cloud Setting 3: The Northern High Latitudes

Past studies of Jupiter’s cloud structure have naturally concentrated on low latitudes, where the view from Earth is least distorted. However, recent attention has been drawn to the high latitudes, particularly in the northern hemisphere, due to the data coming from Juno on its polar orbit (Figure 7).

Figure 8 shows a systematic difference in cloud properties above and below 45°N in observations taken in 2020. Specifically, the CM7 ratio is higher north of 45°N, which could be interpreted as deeper clouds. The presence of moist convection and thus water clouds is confirmed by numerous detections of lightning sferics from Juno/MWR data [82] north of 45°N. The dramatic drop in sferic detection rate south of 45°N requires further analysis, because spatial coverage is not uniform over the map area shown in Figure 8. The cloud structure boundary near 45°N persisted into 2022, as shown by the data in Figure 1.

Interpreting the observations requires careful attention to two questions: Could the 45°N boundary be explained by differences in viewing geometry (i.e., a higher slant angle approaching the pole)? Is there an opacity change in the upper tropospheric layer, the deep cloud layer, or both?

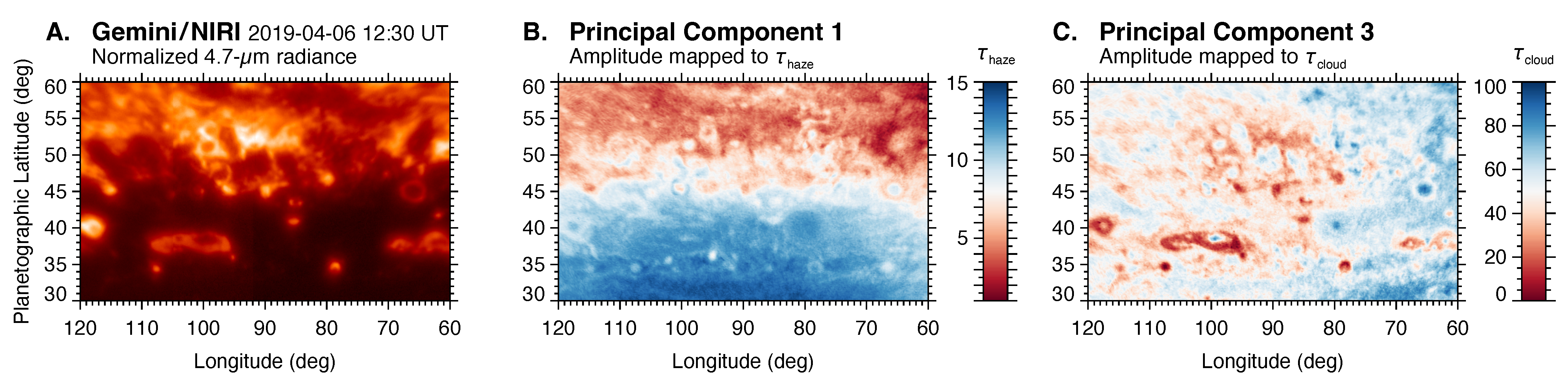
• Viewing geometry: The boundary near 45°N cannot be solely an effect of viewing geometry, based on the data in Figure 1. The CM7 ratio (Figure 1G) increases at high emission/incidence angles, raising the possibility that the 45°N boundary may be a viewing effect. However, at any fixed latitude, the CM7 ratio only increases noticeably at emission angles greater than $\sim 65$°, whereas the distinct high-latitude region begins at a much lower emission angle (roughly equivalent to the planetographic latitude). Secondly, the enhanced contribution from hazes at high viewing angles, combined with increased haze densities approaching the auroral region, should increase the 727 nm reflectivity more than the continuum, so we would expect the CM7 ratio to actually decrease towards the poles as a geometric effect. Therefore, there is strong evidence that the observed CM7 enhancement north of 45°N represents a physical change to the aerosol structure. This is further supported by evidence for a brightness enhancement of the region in at 4.7 µm in Figure 1, Figure 7, Figure 8, as well as Figure 20 in Section 4.1.
• Separating upper/deep cloud opacity contributions. Although high CM7 values may suggest deeper clouds north of 45°N, radiative transfer modeling is needed to confirm whether upper and lower cloud opacity effects can be separated (next section). The role of upper cloud/haze opacity can be seen immediately in the 727-nm frame itself, which is darker north of 45°N, even after Minnaert correction (Figure 1E, Figure 8B). The drop in continuum reflectivity is less pronounced. The 5-µm images show enhanced thermal emission, but this wavelength is sensitive to integrated cloud opacity in both deep and shallow layers. Overall, qualitative analysis suggests a significant depletion of upper cloud/haze opacity, coupled with moderate deep cloud opacity (because even 5-µm bright regions in the high northern latitudes are not as bright as in low-latitude locations such as hot spots in the NEB).

2.3. Radiative Transfer Modeling

Remote sensing imaging data can cover a global-scale area, at spatial resolutions as fine as $\sim 230$ km on Jupiter (near solar opposition), which the previous section showed is important for the study of deep clouds. Mapping the CM7 ratio (Equation (1)) in imaging data is a powerful way to identify and characterize areas and features with differences in cloud structure. Spatially resolved spectroscopy spanning the 727-nm feature has more power to derive full vertical profiles of aerosol properties, e.g., [14,84,85]. However, imaging data at fine spatial resolution can be obtained rapidly on a global scale, a capability that is not yet matched by imaging spectrometers with seeing limited resolutions of >1200 km (which averages across regions with heterogeneous cloud properties). Both imaging and spectroscopic approaches are valuable, but maximizing the return of useful vertical information on aerosol structure from imaging data requires simplifying assumptions in aerosol distributions, along with honest characterization of unavoidable systematic sources of error inherent to the more limited spectral information content available from imaging.

To better understand the vertical information that can be extracted from high-resolution imaging in 727-nm and continuum filters, we performed an exploratory radiative transfer study. The main goal of the study was to understand the amount of information available on the pressure levels of deep clouds. Recognizing that a full aerosol structure retrieval on inhomogeneous regions with small deep cloud features is underconstrained by a simple pair of narrow-band filters, we chose a forward-modeling approach to study the problem. We chose an aerosol layer framework guided by prior spectroscopic studies in the visible wavelength region, informed by the classic aerosol structure of West et al. [1,66], which contains the deep condensation clouds of interest (NH${}_4$SH, H${}_2$O), along with haze distributed in multiple upper layers. Figure 9 schematically illustrates the individual aerosol layers in our model framework. Of key importance is the upper cloud/haze layer, which we conceptualize as a combination of NH${}_3$ condensation clouds and upper tropospheric hazes, with variable opacity. Two additional haze layers as described below were kept fixed in all model cases: a thin stratospheric haze and a vertically and optically thin layer of absorbing “chromophore” particles. The results of our study will show that there is valuable—but degenerate—information about the deep cloud levels in the spectrum, because the upper cloud/haze layer dominates the information content at these wavelengths.

We use the SUNBEAR code to forward-model a range of aerosol structures as they would be observed across the Jovian disk. The SUNBEAR (Spectra from Ultraviolet to Near-infrared with the BErkeley Atmospheric Retrieval) code is described in Molter et al. [87] and has been applied previously (but without the catchy name) to the atmospheres of Titan, Uranus, and Neptune [4,40,88,89,90,91,92]. It uses the discrete ordinates method to solve the radiative transfer equation [92,93], and treats processes important at visible wavelengths such as Rayleigh scattering, Rayleigh polarization, and Raman scattering [94,95,96,97,98,99,100]. However, Fry and Sromovsky [65] argued that these effects are not significant longward of UV wavelengths, so computational efficiency was increased by disabling these options in our study of red/near-IR wavelengths. The correlated-k approach [101] is used for gas absorption, with methane coefficients from Karkoschka and Tomasko [102] and ammonia coefficients from Irwin et al. [103]. Ammonia absorption was modeled using a vertical profile roughly consistent with Li et al. [17] and de Pater et al. [15] at $p\ge$ 500 mbar, decreasing with altitude to a concentration of 10${}^{-12}$ near the tropopause (consistent with the 80-mbar value retrieved from UV spectroscopy [104]). The model extended from a lower boundary of 26 bar to an upper boundary at 0.2 mbar, with an adaptive grid of 130 layers providing balanced vertical resolution in log-pressure space.

We wish to use CM7 values across the disk of Jupiter to interpret cloud depths, but the CM7 photometric ratio is also affected by viewing geometry. Specifically, the 727-nm reflectivities come from shallower depths when there is a greater slant angle for incoming solar radiation and outgoing scattered light, and the atmospheric scale height changes with latitude due to Jupiter’s rotation and oblateness. To test the influence of geometrical effects on the observed CM7 ratio, we performed radiative transfer model calculations over the grid of values shown in Figure 10.

Reflectivities in continuum and 727-nm filters were calculated for each point in the geometric grid. A series of six aerosol structure frameworks were tested until one was found that could approximate the reflectivities, limb darkening, and CM7 values in the HST observations (Figure 1). This adopted framework (Figure 9 and Table 2) had deep clouds placed below a “crème-brûlée” upper cloud/haze layer, with parameters broadly consistent with several recent radiative transfer analyses of spectral data in the visible range [65,84,85,86]. Crème-brûlée models get their name from an upper tropospheric haze structure that has an optically thin absorbing layer overlying an optically thicker layer with conservative scattering. We performed calculations to quantify the effect of a limited number of variables: opacity in the upper cloud/haze layer, opacity in the deep cloud layer, and pressure level of the deep cloud layer.

The rationale for parameter choices (Table 2) is as follows:

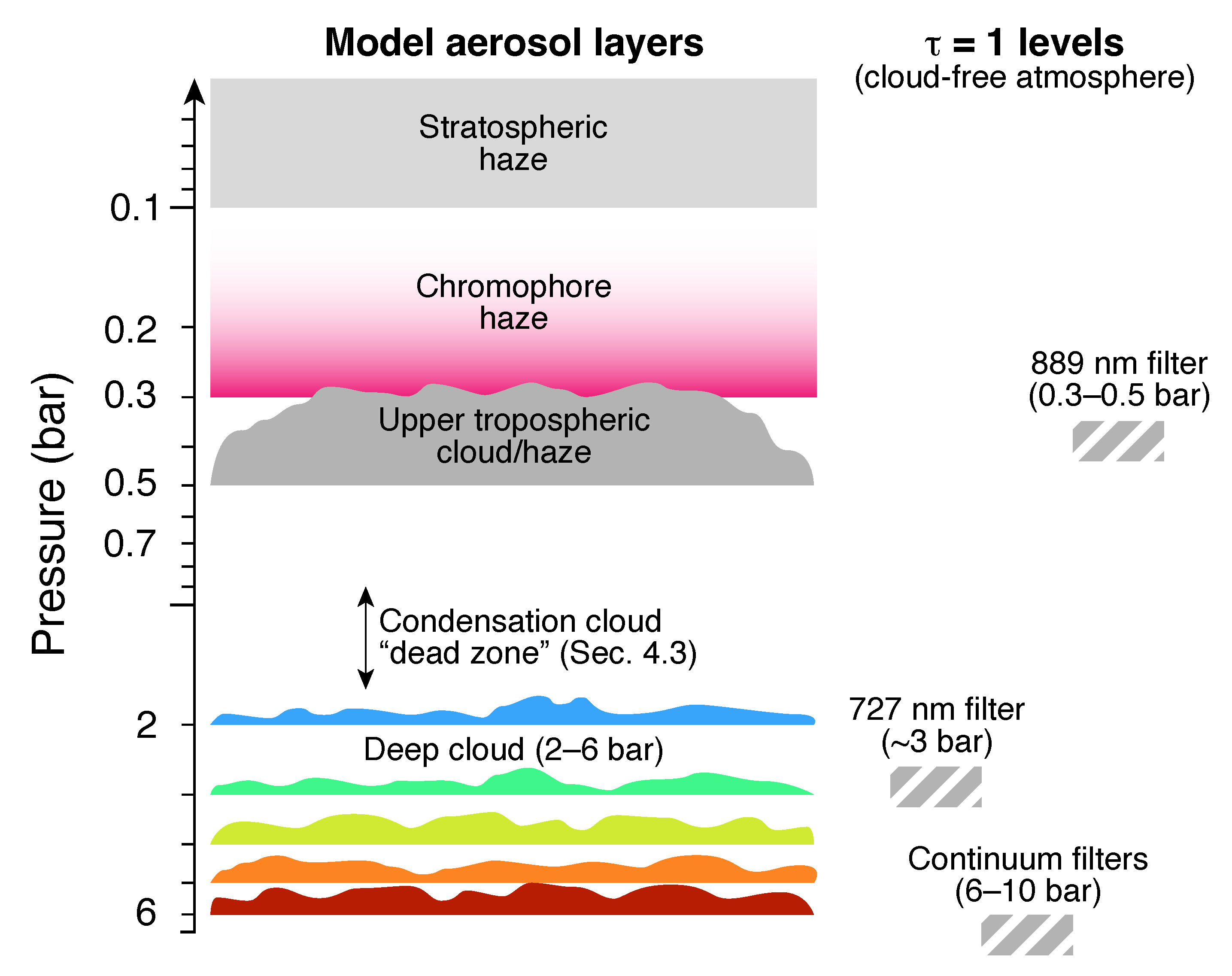
• Stratospheric haze: A vertically extended but optically thin upper layer of small non-absorbing particles is required to match center-to-limb curves at high incidence and/or emission angles. Parameters for this layer were held fixed for all calculations shown in this paper. Values were chosen to broadly match values found in several recent works that used constraints provided by spectroscopy and/or zonal-mean center-to-limb brightness variation [65,85,86]. These works found spatially variable stratospheric haze parameters, but to simplify our investigation into deep clouds using only continuum and 727-nm narrowband filters, we kept stratospheric haze parameters fixed in all model runs.
• Chromophore haze: A thin layer of small absorbing particles in the upper troposphere; the crème-brûlée crust. Parameters for this layer were held fixed for all calculations. The layer is moderately compact in the vertical direction. The index of refraction set to 1.4 + i0.1, generally consistent with the chromophore material characterized by Carlson et al. [105], which was an irradiated product of C${}_2$H${}_2$ and NH${}_3$ successfully used to model Jupiter’s visible-wavelength spectrum in recent work [14,65,84,85,86]. Other chromophore candidates have similar absorption characteristics, and it is difficult to identify Jupiter’s chromophores based on the planet’s spectrum alone [66,106,107].
• Upper tropospheric cloud/haze: A non-absorbing cloud/haze layer in the upper troposphere; the custard part of the crème-brûlée. We chose representative particle characteristics with some haze-like properties (moderately small radius, puffy distribution with large $H_p/H_g$ across the vertical layer), but with relatively large optical depths that might be more consistent with condensation clouds. A large $H_p/H_g$ within the uppermost high-opacity layer has been suggested going back to the earliest analyses of methane absorption in the visible/near-IR spectral range [108,109]. Our simple treatment of the uppermost high-opacity layer is meant to simulate more complex but degenerate mixtures haze/cloud opacity bounded between the ammonia cloud base and the tropopause. Absorption was modeled as being concentrated in the fixed chromophore layer, so the index of refraction of this upper tropospheric cloud/haze layer was fixed at 1.4 + i10${}^{-8}$. The base pressure level $p_{\mathrm{base}}$ of this layer was found to have minimal influence compared to the total opacity, when $p_{\mathrm{base}}$ was varied over the 300–800 mbar range (keeping the fractional scale height fixed at 1 and the low-pressure cutoff fixed at 300 mbar). The variable parameter for this layer was total optical depth ${\tau }_{\mathrm{haze}}$ (tested at 1, 3, 5, 10, and 15).
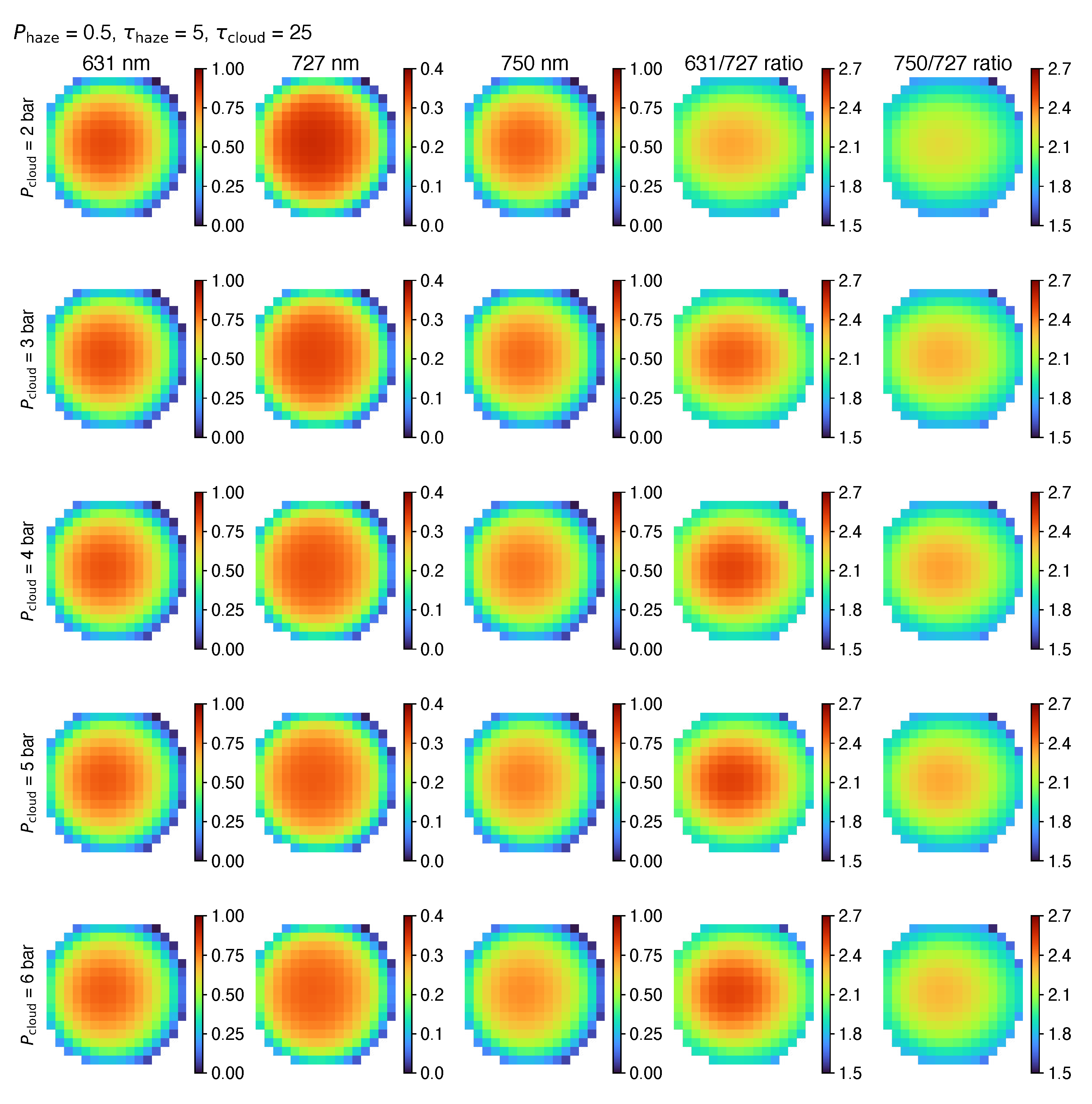
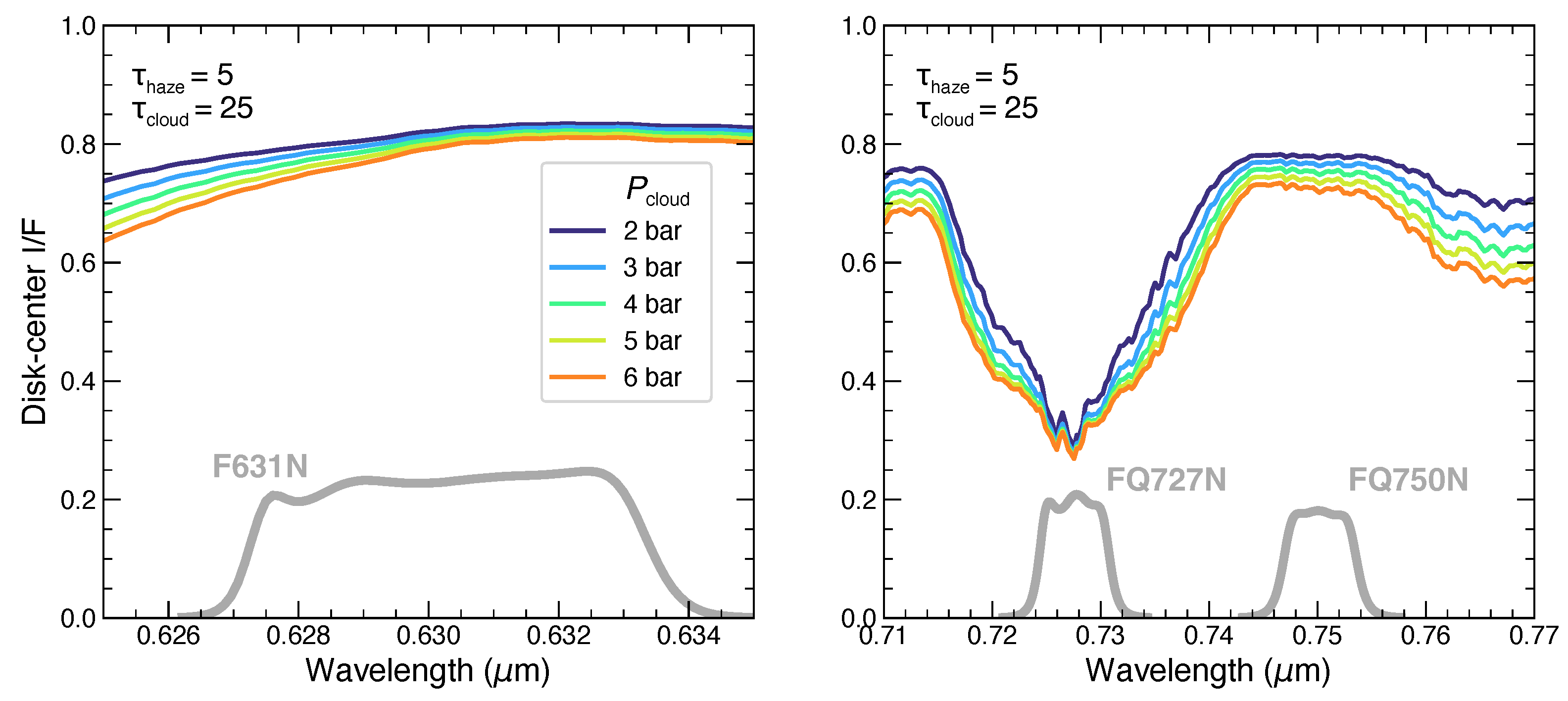
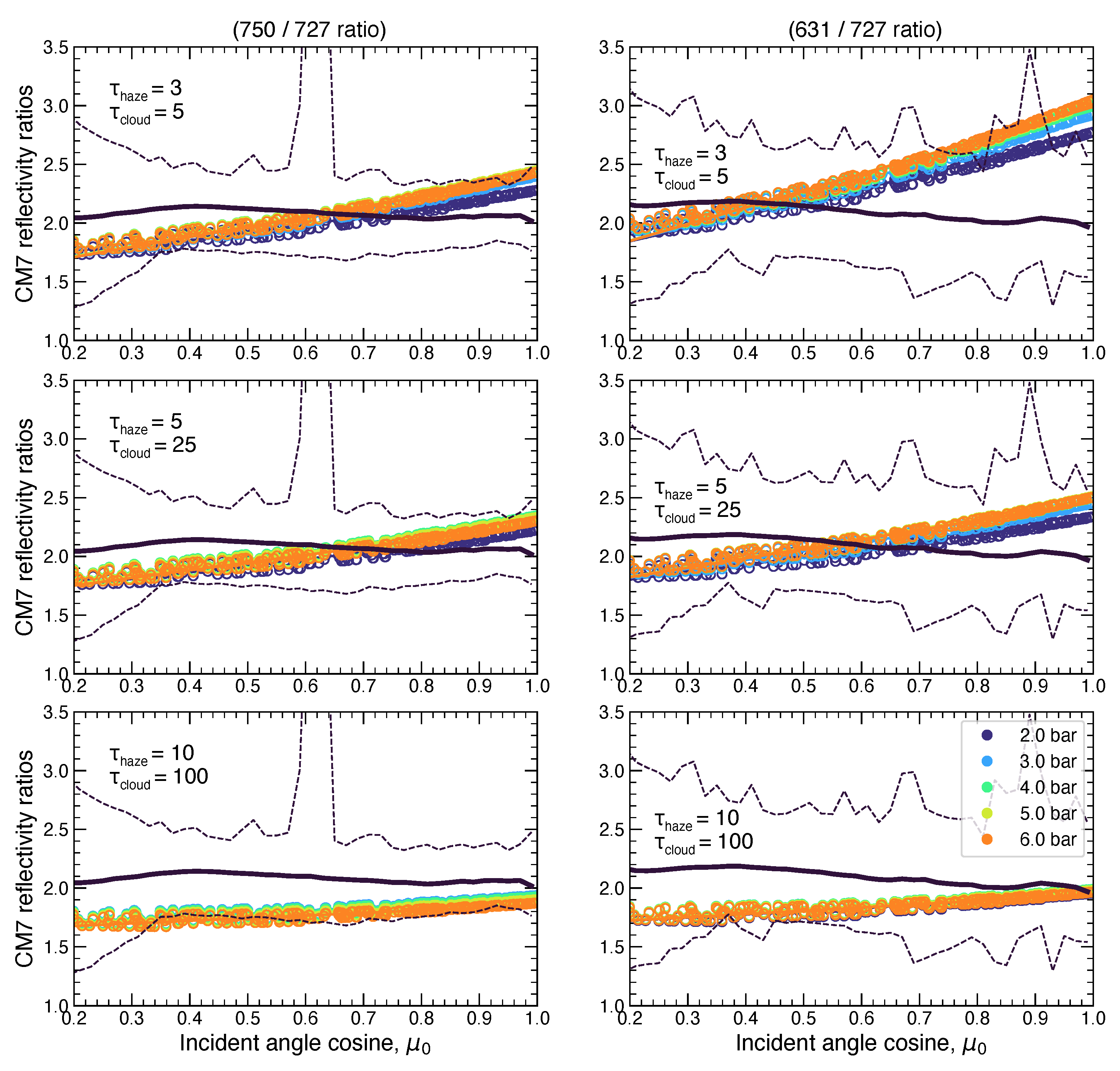
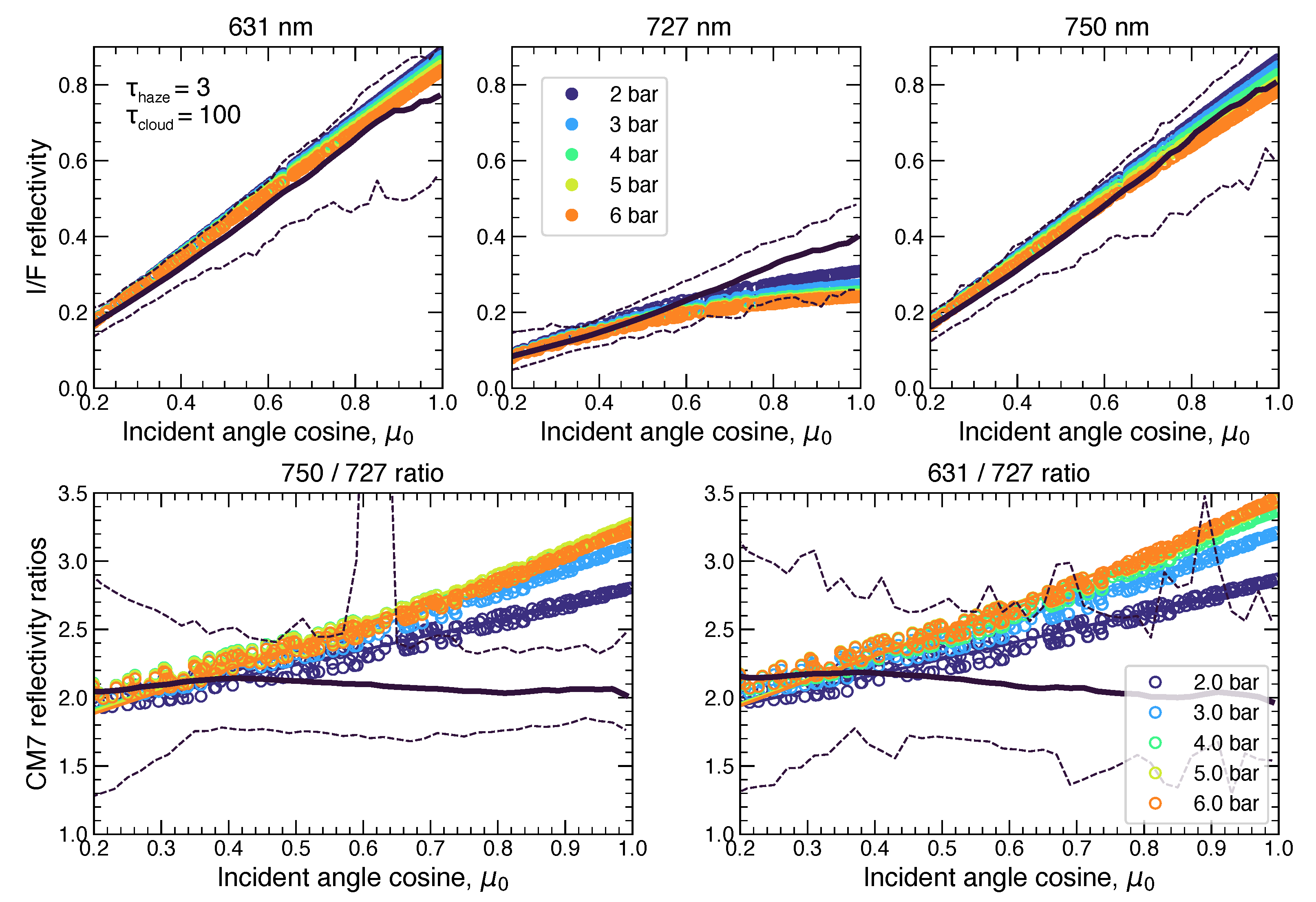
• Deep cloud: This layer was intended to simulate NH${}_4$SH or H${}_2$O cloud opacity. To simulate a vertically-compact condensation cloud layer, we distributed the aerosol opacity above a variable cloud base with fractional scale height 0.1 and a low-pressure cutoff of $p_{\mathrm{top}}=0.9\times p_{\mathrm{base}}$. Although $p_{\mathrm{cloud}}$ is the model parameter, at high optical depths, it is really the cloud top that is significant, but for the vertically compact clouds assumed in the model, these agree to within 10%. The variable parameters for this layer were cloud base level $p_{\mathrm{cloud}}$ (tested at 2, 3, 4, 5, and 6 bar) and total optical depth ${\tau }_{\mathrm{cloud}}$ (tested at 0, 5, 25, and 100).

The total number of model states is $5\times 5\times 3$ + 5 = 80 model parameter combinations, evaluated over 224 spatial grid points (less than $16\times 16$ because Jupiter is not square), or 17,920 states. Figure 11 demonstrates how model output varies over the geometrical grid and over the range of $p_{\mathrm{cloud}}$ values, for cases fixed at ${\tau }_{\mathrm{haze}}=5$ and ${\tau }_{\mathrm{cloud}}=25$. Similar plots for other ${\tau }_{\mathrm{haze}}$ and ${\tau }_{\mathrm{cloud}}$ states (not shown) can be generated using data files included in Supplemental Materials SM2.

Figure 11 shows the simulated Jupiter disk for a given cloud structure state, but this type of output is difficult to compare with observations where cloud structure is clearly variable over the disk. To better compare with the data, we sampled the Jovian disk in Figure 1 to calculate mean, maximum, and minimum values of reflectivities and CM7 ratios as a function of incidence angle cosine ${\mu }_0$. The observational data (reflectivities in 727-nm and continuum filters) are shown in black in Figure 12 (solid for the mean and dashed for the extrema at each ${\mu }_0$ bin). Model output shown as colored symbols span the full geometrical grid and 15 model states, as indicated by legends in the panels. Figures S13–S17 in SM1 show all the other model states for comparison, but the states shown in Figure 12 span the full range of the observed $I/F$ data (i.e., the colored dots span the range between the dashed black curves).

Some conclusions can be drawn already from the limb-darkening curves in Figure 12 before proceeding to discussing CM7 ratios.

The minimum reflectivities in the observations (lower dashed black lines in Figure 12 corresponding to the data in Figure 1) are best fit by the row with ${\tau }_{\mathrm{haze}}=3$ and ${\tau }_{\mathrm{cloud}}=5$. Figures S13–S17 show that no other cloud structure provides a better fit to the minimum reflectivities: lower ${\tau }_{\mathrm{haze}}$ produces values of $I/F_{727}$ much lower than the observations, except if ${\tau }_{\mathrm{cloud}}$ at 2 bar is increased to compensate, but that then drives $I/F_{\mathrm{cont}.}$ too high. Higher ${\tau }_{\mathrm{haze}}$ produces values of $I/F_{727}$ higher than the observations, even with ${\tau }_{\mathrm{cloud}}=0$. One red flag is that modeled $I/F_{631}$ and $I/F_{750}$ do not both fit the lower dashed line in Figure 12 for any singular model. This could be an artifact of modeling the chromophore haze with a constant $n_i$ as a function of wavelength. The observations require a minimum optical depth of 8 (distributed among the upper cloud/haze and the lower cloud decks (at least for the assumed particle size distributions)).

The mean $I/F$ values (solid black lines in Figure 12) are best fit by the middle row with ${\tau }_{\mathrm{haze}}=5$ and ${\tau }_{\mathrm{cloud}}=25$. Here, the model suggests some sensitivity to the deep cloud base level $p_{\mathrm{cloud}}$ (with colored points shifting from blue to orange as cloud level increases from 2 to 6 bar). For 727 and 750 nm, the mean $I/F$ center-to-limb curve is best fit when the deep cloud opacity is located at 2 bar.

The modeled $I/F$ at 631 nm behaves as would be expected for a continuum wavelength: it has sensitivity to the opacity of the deep cloud layer, but almost no sensitivity to the deep cloud pressure level. The sensitivity to the cloud base level in the 750-nm filter is somewhat surprising, given the official title of the FQ750N filter, “7270 continuum” [50]. Continuum filters near 750 nm were also used on Galileo and Cassini imaging systems [110,111]. Figure 5 of Sromovsky et al. [14] suggests that ammonia absorption at 750 nm may complicate the use of this filter as a continuum reference for 727 nm. In both Figure 11 and Figure 12, $I/F$ at 750 nm decreases as $p_{\mathrm{cloud}}$ increases, consistent with gas absorption in the bandpass. Figure 13 shows the model spectra across the filter bandpasses, for a single disk-center case with ${\tau }_{\mathrm{haze}}=5$ and ${\tau }_{\mathrm{cloud}}=25$. Although the spectrum does exhibit nice continuum behavior over most of the 631-nm filter bandpass, the spectral proximity to the 619-nm methane band introduces some sensitivity to deep cloud pressure level in the blue end of the bandpass.

Finally, the bottom row of Figure 12 provides the best match to the maximum $I/F$ center-to-limb curve for the three filters, with ${\tau }_{\mathrm{haze}}=10$ and ${\tau }_{\mathrm{cloud}}=100$. Despite the high upper cloud/haze opacity, some sensitivity to $p_{\mathrm{cloud}}$ remains due to the very high value of ${\tau }_{\mathrm{cloud}}=100$ required to match the maximum reflectivities. Better fits are found for $p_{\mathrm{cloud}}=2$ bar than for deep clouds at higher pressures, so it is possible that a model with more freedom might prefer clouds within the 1–2 bar region. However, we did not test this type of cloud structure because cloud condensation efficiency is reduced at this level, according to theoretical arguments discussed in Section 3.

No attempt has been made in this work to fit differences in cloud structure within different latitude bands. In a global sense, best fit mean and minimum/maximum center-to-limb reflectivity curves are consistent with variation in the upper cloud/haze opacity from ${\tau }_{\mathrm{haze}}=3$ to 10, along with variation in deeper cloud opacity over a wider range of values and some sensitivity to the pressure level of the deep cloud.

For the best-fit cases (minimum, mean, and maximum $I/F$ vs. ${\mu }_0$) in Figure 12, we plotted the corresponding CM7 values in Figure 14.

The simulated CM7 values for moderate incidence angles (${\mu }_0>$ 0.4) for the best-fit aerosol structures lie within the minimum/maximum observed CM7 envelope (dashed lines). In this sense, the modeled aerosol structures are Jupiter-like.

Consider first the bottom row, for the case of ${\tau }_{\mathrm{haze}}=10$ and ${\tau }_{\mathrm{cloud}}=100$ best matching the maximum $I/F$ values in Figure 12. This case also best matches the minimum CM7 values across the disk, validating the interpretation that low CM7 corresponds to high opacity in the upper cloud/haze layer. The high upper cloud/haze opacity renders the CM7 ratio completely insensitive to $p_{\mathrm{cloud}}$. Some sensitivity to deep cloud opacity starts to appear at lower ${\tau }_{\mathrm{haze}}$ (middle row).

A degeneracy can be seen between the $p_{\mathrm{cloud}}$ and ${\tau }_{\mathrm{haze}}$ parameters in Figure 14. Moving the deep cloud level upwards (decreasing $p_{\mathrm{cloud}}$, colors going from orange to blue) acts to lower the CM7 ratio. However, increasing the opacity in the upper layer also lowers CM7 (top row toward bottom row).

Taken together, the three rows show that although the CM7 ratio may be sensitive to the deep cloud level, the sensitivity to upper cloud/haze opacity dominates, and deep clouds can only be distinguished in regions where the upper cloud/haze opacity is near its minimum value. Minimum cloud/haze opacity is found where the $I/F$ values for all filters are the lowest (Figure 12), and where CM7 is the highest. So the best place to distinguish deep clouds on Jupiter would be a location that is dark overall, with small regions where CM7 increases in discrete features located within a broad area with low ${\tau }_{\mathrm{haze}}$. In Figure 1, Figure 3 and Figure 8, these conditions are seen to apply very well at high northern latitudes and in the NEB. Figure 15 shows simulated $I/F$ and CM7 for a case that is still marginally consistent with the observations and that provides maximum sensitivity to cloud depth: the ${\tau }_{\mathrm{haze}}=3$ and ${\tau }_{\mathrm{cloud}}=100$ case.

The ${\tau }_{\mathrm{haze}}=3$ and ${\tau }_{\mathrm{cloud}}=100$ case is Jupiter-like because it still fits within the $I/F$ minimum/maximum envelope for the data in Figure 1. This case provides maximum sensitivity to $p_{\mathrm{cloud}}$ at disk center: when the cloud base goes from 2 to 6 bar, $\Delta \mathrm{CM}7>0.6$ for the 631/727 ratio, and $\Delta \mathrm{CM}7>0.4$ for the 750/727 ratio. This sensitivity to $p_{\mathrm{cloud}}$ is similar to the sensitivity to ${\tau }_{\mathrm{haze}}$ in a different case (${\tau }_{\mathrm{cloud}}=0$; see top rows of Figures S19 and S20), where increasing ${\tau }_{\mathrm{haze}}$ from 3 to 5 gives $\Delta \mathrm{CM}7<-0.6$ for the 631/727 ratio, and $\Delta \mathrm{CM}7<-0.2$ for the 750/727 ratio. If regions of Jupiter can be identified where the upper layer opacity is inferred to remain constant (perhaps by exploiting the correlation between CM7 ratios and 889-nm $I/F$ in imaging data, or by resolved spectroscopic observations), then variation in CM7 can be attributed to the deep cloud layer. Comparison of Figure 14 (top row) and Figure 15 reveals a serious degeneracy even in this low ${\tau }_{\mathrm{haze}}$ case, between deep cloud opacity and deep cloud pressure level. The degeneracy is worse for the 750/727 ratio, but for the 631/727 ratio, the CM7 vs. ${\mu }_0$ curves have only a weak dependence on ${\tau }_{\mathrm{cloud}}$ for $p_{\mathrm{cloud}}=2$ bar. Imaging data seem to be minimally capable of distinguishing between 2-bar and deeper clouds (under some conditions), which would be sufficient to rule out NH${}_4$SH composition (but not sufficient to place meaningful limits on the O/H ratio).

Although trends in the simulated data allow valuable conclusions to be drawn, the main conclusion is that variation in upper-layer cloud/haze opacity is the dominant control, such that deep cloud properties can only be constrained if the upper-layer opacity is separately measured by additional data. Beyond the challenges presented by this degeneracy, there are deficiencies in the fidelity of our aerosol model framework. One issue is that the 631-nm reflectivity is anomalously high compared to the longer-wavelength filters, a possible effect of inaccurate assumptions for the chromophore haze layer in the model. The issues with modeled 631-nm $I/F$ can be seen in the top row of Figure 12, where a model in our framework matching the minimum observed $I/F$ at 631 nm produces $I/F$ far too low at the other wavelengths. Excessive 631-nm $I/F$ means that no CM7 values in our models actually match the lowest observed CM7 values (lower dashed curves in Figure 14) at the disk center.

The second red flag is the slope of the CM7 vs. ${\mu }_0$ curve, which is positive in the model but flat or slightly decreasing in the observations. Examination of the middle column of Figure 12 suggests that the CM7 slope mismatch is due to the wrong limb darkening behavior at 727 nm in the simulations. No other models tested in this work were able to achieve better matches to both the 727-nm limb darkening and overall reflectivity.

Although improved models of deep cloud reflectivity may be attempted in the future—preferably with additional information from visible-wavelength spectroscopy—the model presented here provides a reasonably close approximation to Jupiter’s reflectivity at 727 nm and adjacent continuum wavelengths, sufficient for demonstrating the strong degeneracy between the effects of upper and lower cloud opacity on the observed results.

Table 1. HST Jupiter observations used in this study.

Start Time (UT)	Program	HST Instruments and Filters Used	Figure Numbers
2022-05-22 23:32	GO-16913	WFC3/UVIS: F395N, F502N, F631N, FQ727N, FQ750N, FQ889N	Figure 1, Figure 4, Figure 6 and Figures S1–S12
2019-04-06 10:39	GO-15665	WFC3/UVIS: F631N, FQ727N, FQ889N	Figure 2, Figure 5, Figures 19 and 20
2020-07-22 08:19	GO-16053	WFC3/UVIS: F631N, FQ727N, FQ889N	Figure 3
2007-05-11 12:16	GO-10782	WFPC2/PC1: F410M, F502N, F673N	Figure 5
2020-09-15 16:33	GO-16074	WFC3/UVIS: F395N, F502N, F631N, FQ727N, FQ889N	Figure 8

Table 1. HST Jupiter observations used in this study.

Start Time (UT)	Program	HST Instruments and Filters Used	Figure Numbers
2022-05-22 23:32	GO-16913	WFC3/UVIS: F395N, F502N, F631N, FQ727N, FQ750N, FQ889N	Figure 1, Figure 4, Figure 6 and Figures S1–S12
2019-04-06 10:39	GO-15665	WFC3/UVIS: F631N, FQ727N, FQ889N	Figure 2, Figure 5, Figures 19 and 20
2020-07-22 08:19	GO-16053	WFC3/UVIS: F631N, FQ727N, FQ889N	Figure 3
2007-05-11 12:16	GO-10782	WFPC2/PC1: F410M, F502N, F673N	Figure 5
2020-09-15 16:33	GO-16074	WFC3/UVIS: F395N, F502N, F631N, FQ727N, FQ889N	Figure 8

Table 2. Aerosol model framework and key parameters. Opacity in each layer is bounded between $p_{\mathrm{top}}$ and $p_{\mathrm{base}}$, distributed following the particle-to-gas scale height ratio $H_p/H_g$. Particle sizes follow gamma distributions with variance 0.1 and mean particle sizes as listed in the table. Particles are modeled as Mie scatterers with indices of refraction $n_r+i{n}_i$. Particles with $n_i\le {10}^{-8}$ behave as conservative scatterers, with numerical stability provided by $n_i$ > 0.

Parameter	Stratospheric Haze	Chromophore Haze	Upper Cloud/Haze	Deep Cloud
$p_{\mathrm{top}}$	1 mbar	100 mbar	300 mbar	0.9 × $p_{\mathrm{base}}$
$p_{\mathrm{base}}$	100 mbar	300 mbar	500 mbar	variable: 2, 3, 4, 5, 6 bar
$H_p/H_g$	1	0.3	1	0.1
$\tau$ at 700 nm	0.1	0.15	variable: 1, 3, 5, 10, 15	variable: 0, 5, 25, 100
r (µm)	0.2	0.2	0.5	2
$n_r$	1.4	1.4	1.4	1.4
$n_i$	${10}^{-8}$	0.01	${10}^{-8}$	${10}^{-8}$

Table 2. Aerosol model framework and key parameters. Opacity in each layer is bounded between $p_{\mathrm{top}}$ and $p_{\mathrm{base}}$, distributed following the particle-to-gas scale height ratio $H_p/H_g$. Particle sizes follow gamma distributions with variance 0.1 and mean particle sizes as listed in the table. Particles are modeled as Mie scatterers with indices of refraction $n_r+i{n}_i$. Particles with $n_i\le {10}^{-8}$ behave as conservative scatterers, with numerical stability provided by $n_i$ > 0.

Parameter	Stratospheric Haze	Chromophore Haze	Upper Cloud/Haze	Deep Cloud
$p_{\mathrm{top}}$	1 mbar	100 mbar	300 mbar	0.9 × $p_{\mathrm{base}}$
$p_{\mathrm{base}}$	100 mbar	300 mbar	500 mbar	variable: 2, 3, 4, 5, 6 bar
$H_p/H_g$	1	0.3	1	0.1
$\tau$ at 700 nm	0.1	0.15	variable: 1, 3, 5, 10, 15	variable: 0, 5, 25, 100
r (µm)	0.2	0.2	0.5	2
$n_r$	1.4	1.4	1.4	1.4
$n_i$	${10}^{-8}$	0.01	${10}^{-8}$	${10}^{-8}$

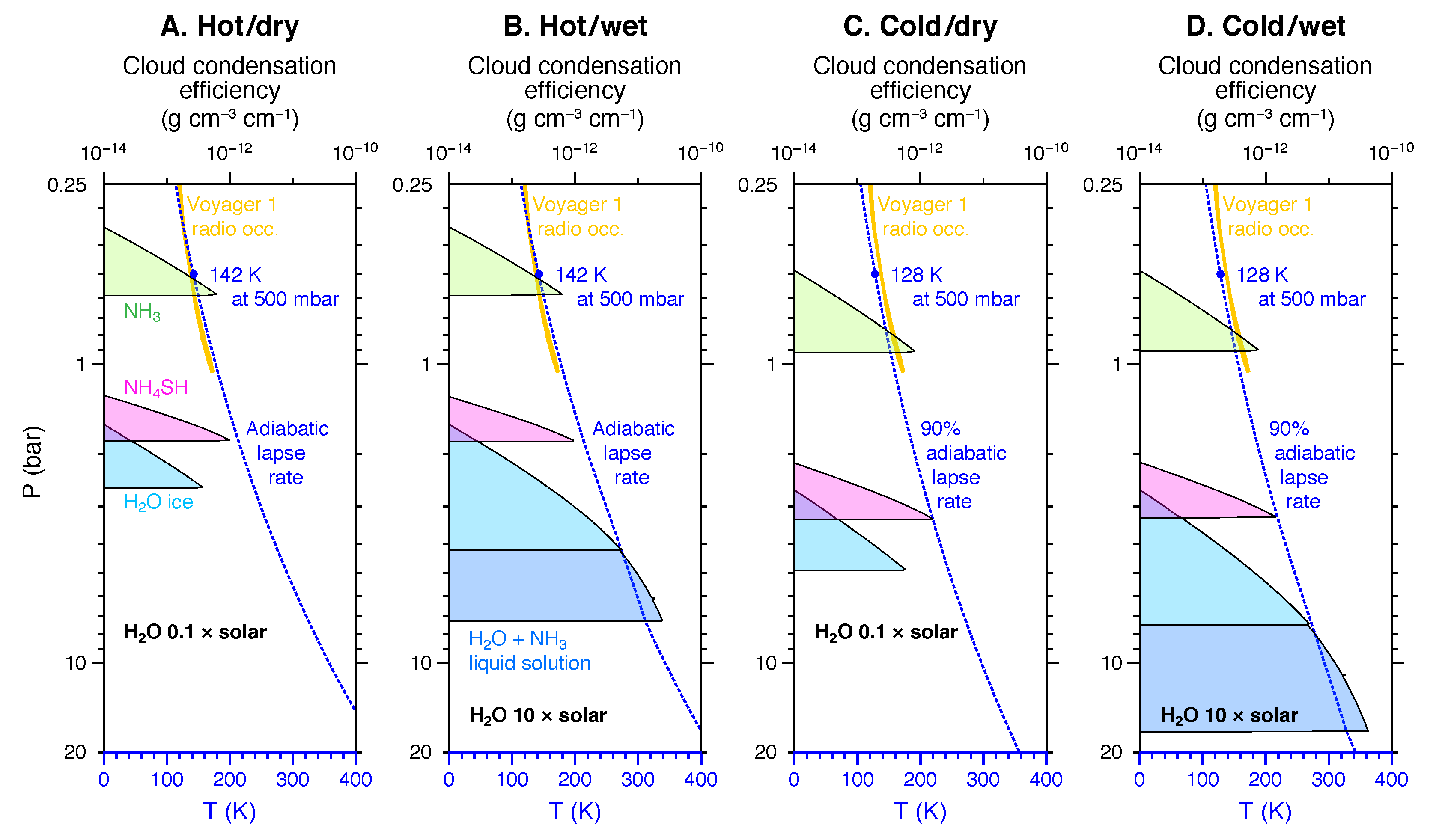
3. The Water Cloud Level and the Oxygen Abundance

We use an equilibrium cloud condensation model (ECCM) to relate cloud base pressure levels to atmospheric composition and thermal structure. Previous work using ECCMs to explain observed constraints on cloud base levels in terms of volatile abundances (particularly the H${}_2$O abundance) has focused on the effect of atmospheric composition, with a fixed pressure-temperature boundary condition, e.g., [112,113]. We consider how conclusions also depend on the thermal structure of the atmosphere by exploring a range of temperatures and lapse rates consistent with the range of values found from remote sensing and the Galileo Probe. Lapse rate $\mathsf{\Gamma }$ is defined as

$$\mathsf{\Gamma }=-\frac{dT}{dz},$$

(2)

with expressions for its calculation given in Weidenschilling and Lewis [114] and Atreya and Romani [115].

3.1. The ECCM Model

Equilibrium cloud condensation models based on the formalism of Weidenschilling and Lewis [114] have been used by many research groups over the years. The model is initialized at a deep level and calculates the changes in pressure, temperature, and composition at higher levels assuming hydrostatic equilibrium and an adiabatic temperature profile. The gas composition is the same at each level as it is in the level below, until volatile saturation is reached, at which point the condensed material remains where it forms and only the gas component is carried to the level above.

Our particular implementation is described in Atreya and Romani [115], with revisions to the cloud density formalism as described in Wong et al. [113]. Specifically, there is an error in the original Weidenschilling and Lewis [114] formalism for calculating cloud densities. The model naturally calculates a “cloud condensation efficiency” $R_x$ for volatile species x. The cloud density $D_x$ in units of mass per unit volume depends on the cloud condensation efficiency and the strength of the updraft that produces condensation:

$$D_x=R_x{w}_{*}{t}_d=R_{x}L,$$

(3)

where the updraft velocity scale is $w_{*}$, the updraft time scale is $t_d$, and their product is interpreted as an updraft length scale, L (see Section 2 of [113]). Under the formalism of the ECCM, condensed material accumulates at the level where it condenses, so a smaller column of air perturbed upward will produce a lower cloud density than a larger column of air in an updraft. ECCM calculations of “cloud densities” using the erroneous Weidenschilling and Lewis [114] formula, e.g., [116,117] have implicitly assumed that the updraft length scale is equal to the gas pressure scale height $H_g$ at every level of the atmosphere. Scale height is a quantity that increases from 21 km at 0.5 bar to 63 km at 20 bar in the Galileo Probe entry site [118], because $H_g=RT/\mu g$. Although it is likely that $L=H_g$ in some cases, there may be many more cases where $L<H_g$ and perhaps some where $L>H_g$. The best way to visualize ECCM output is to plot cloud condensation efficiency $R_x$ itself, in units of mass per unit volume per unit length (allowing the reader to convert to cloud density depending on the relevant value of the updraft length scale L). Alternately, cloud density could be plotted along with an explicit statement of the value of L used in the calculation. Wong et al. [113] demonstrated broad consistency between ECCM cloud densities and measured terrestrial densities in fresh cirrus clouds (with $L\sim$ 10–200 m) and fresh cumulus clouds (with $L\sim$ 1–6 km).

Cloud condensation efficiency calculated using ECCMs gives a useful estimate of the pressure level of the cloud base, given the initial atmospheric composition and temperature/pressure chosen. In Figure 16, we show model cases for four end-member conditions. The temperature profile end members are a stable/cold profile (128 K at 500 mbar and a lapse rate 90% of the adiabatic rate) and a neutral/warm profile (142 K and fully adiabatic). The composition end members shown have water abundances of 0.1 and 10 times the protosolar abundance of Asplund et al. [19].

The initial condition for composition in each model run was set to mixing ratios of He/H${}_2$ = 0.157 (from Galileo Probe [23,119]), CH${}_4$/H${}_2$ = $2.37\times {10}^{-3}$ (from Galileo Probe [16]), NH${}_3$/H${}_2$ = $4\times {10}^{-4}$ (from Juno [18]), H${}_2$S/H${}_2$ = $7.80\times {10}^{-5}$ (matching the 2.7×solar enrichments of water and ammonia from Juno [18] and consistent with the Galileo Probe value [16]), Ar/H${}_2$ = $1.82\times {10}^{-5}$, and Ne/H${}_2$ = $2.24\times {10}^{-5}$ (both from Galileo Probe [120]).

3.2. Thermal Structure and Water Cloud Levels

Only four model runs are shown in Figure 16. To fully map the dependence of the water condensation level on water abundance and atmospheric temperature structure, we calculated cloud structures for a range of conditions. Temperatures at the 500-mbar level ranged from 128 K to 142 K in steps of 1 K (15 values), and water abundances ranged from 0.01 to 22.28×solar, in 22 steps evenly spaced in the square root of the protosolar enrichment value. (Due to this grid definition, the 0.1 and 10 × protosolar cases in Figure 16 are actually 0.102 and 10.1 × protosolar.) The array of test values was run for both adiabatic and 90% adiabatic lapse rates. The mixing ratios of other gases besides water vapor were initialized to the same values in every model calculation.

The thermal parameter space was chosen to cover the range of published conditions estimated for Jupiter’s atmosphere. Simon-Miller et al. [122] retrieved temperatures at the 500-mbar level from Voyager IRIS and Cassini CIRS infrared spectra, finding latitudinal variation over the 128–138 K range (with the coldest values of $T\le$ 132 K only found north of 55°N for Voyager or in the EZ for Cassini). Using Cassini CIRS and ground-based TEXES spectra, Fletcher et al. [123] found 500-mbar temperatures in the range of 134–142 K. The Voyager 1 radio occultation temperatures at 500 mbar were 137.4 K and 136.4 K for ingress and egress, respectively [121], within the range of the infrared retrievals. The Galileo Probe temperature was 132.8 K at 500 mbar [118], also within the infrared range.

The two lapse rates chosen span the values retrieved from Galileo Probe data. Magalhães et al. [124] estimated a stability of 0.2 K/km, corresponding to a lapse rate of about 90% of the 1.94 K/km dry adiabatic lapse rate. A statically stable troposphere is also consistent with expectations from latent heat of cloud condensation [125,126] and models of atmospheric flow [7,127,128,129,130,131,132]. However, static stability varied vertically in the Galileo Probe profile, between about 90% and 100% of the adiabatic lapse rate (even becoming statically unstable at some levels, which Magalhães et al. [124] suggested may be due to molecular weight compensation of the thermal gradient), so we also ran ECCM cases for 100% of the moist adiabatic lapse rate as our warm end-member profile. Using dry adiabats would lead to even warmer temperatures at 5 bar, but the atmosphere would be conditionally unstable to moist convection in saturated conditions. The 90% and 100% adiabatic cases should therefore cover the range of uncertainty in the deep thermal structure of Jupiter, which has unknown vertical, horizontal, and temporal variability.

The results of the suite of model calculations are shown in Figure 17. For a given water cloud base pressure level on the x-axis—or lifting condensation level (LCL)—contours of water abundance vary depending on the thermal structure in the atmosphere. The temperature at 500 mbar is given on the y-axis, with the two panels covering the lapse rate end members: statically stable or neutrally stable atmospheres. For example, a water cloud base at 5 bar is consistent with a range of water abundances from 0.15 to 3 × protosolar O/H. The full 14 K range of 500-mbar temperatures extrapolates down to a 43 K range (from 247 K to 290 K) at the 5-bar level, accounting for the range in lapse rate from 90% to 100% of the wet adiabatic rate.

The wide range of thermal/compositional conditions capable of setting the water LCL at a particular pressure level is significant for two reasons. First, it underscores the importance of obtaining accurate measurements of Jupiter’s atmospheric temperatures. Pressure-level constraints on deep clouds would be much more powerful if combined with simultaneous knowledge of the temperatures at that location, even if measured only at the 500-mbar level. In the previous example of a water cloud base at 5 bar, adding knowledge that the local 500-mbar temperature is $135\pm 1$ K constrains the water abundance to a tighter range of 0.3 to 1.8× protosolar O/H, depending on the stability of the atmosphere. Although detailed measurements of static stability are available only at the Galileo Probe site, Juno MWR observations provide some qualitative constraints on its spatial variation. Density profiles of discrete vortices suggest weaker stratification in an anticyclone compared to a cyclone [57], particularly near the water condensation region. Secondly, the range of conditions consistent with cloud condensation at a given level provides a way of quantifying the uncertainty that applies to estimates of O/H based on cloud depth.

3.3. Thermal Structure and the Upper Clouds

To identify the pressure level below which no other clouds besides water could form, we must also examine how the thermal structure affects the cloud bases of the NH${}_3$ and NH${}_4$SH layers. Lifting condensation levels from ECCM calculations are shown in Figure 18 for fixed NH${}_3$/H${}_2$ and H${}_2$S/H${}_2$ volume mixing ratios. The deepest possible NH${}_4$SH cloud base, at 3.2 bar, is possible only with a stable temperature gradient and a very low 500-mbar temperature near 128 K, found only in the special case of latitudes poleward of 70°N in Voyager IRIS retrievals [122]. In retrievals from Cassini CIRS observations, both Simon-Miller et al. [122] and Fletcher et al. [123] found the coldest 500-mbar temperatures in the equatorial zone, with $T_{500\mathrm{mbar}}\ge$ 133 K. That temperature would set a limit of 2.7 bar as the deepest level where the composition of an observed cloud could be either NH${}_4$SH or water.

4. Results

4.1. Information Content of the Imaging Data

In Section 2, we identified several examples where imaging data strongly suggest the detection of deep clouds, but radiative transfer modeling found that photometry in the continuum and weak methane band filters contained a strong degeneracy between deep cloud level and upper cloud/haze opacity. Although the original intent of this work was to use imaging data to measure deep cloud levels, it now appears that additional spectroscopic information would be required to break the degeneracy between upper and lower layer properties. In order to motivate future observational studies, we attempted to link the imaging data and the radiative transfer modeling using principal components analysis (PCA) to validate that the information content in the multispectral data is sufficient to constrain deep cloud properties. PCA is often used to reduce the number of variables in a dataset, such as to reduce a spectral data cube into a map described by a small number of orthogonal spectral vectors. We instead use PCA to transform the observed variables into orthogonal variables and test how closely these empirical orthogonal variables track the physically based variables in the radiative transfer model. Figure 19 illustrates the steps followed, which are as follows:

• We construct maps near the time of Juno’s perijove 19, encompassing the northern region with active moist convection studied by Imai et al. [56] and the northern barge studied by Bolton et al. [57], where deep clouds have been suggested in Figure 2 and Figure 5.
• We perform PCA to characterize the spatial variation in terms of new empirical orthogonal components, constrained by three input variables: the CM7 ratio, the incidence angle cosine ${\mu }_0$, and the $I/F$ at 631 nm.
• We test whether the resulting three orthogonal components might translate to physical constraints on the upper and deep aerosol layers. Specifically, we test a scaling where the maps of the amplitudes of PCs 1–3 across the domain (panels G–I of Figure 19) are normalized to span the range of cloud layer properties in the radiative transfer model shown in Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15.
• For each map pixel, we convert the PC amplitudes to values of ${\tau }_{\mathrm{haze}}$, ${\tau }_{\mathrm{cloud}}$, and $p_{\mathrm{cloud}}$ to set radiative transfer model parameter values, using the PCA results to simulate $I/F$ values at 631 and 727 nm (and the corresponding CM7 ratios).

The inputs to the PCA included the two independent measurements of aerosol opacity (631-nm and 727-nm images), along with the ${\mu }_0$ plane to characterize the limb darkening (which is needed to distinguish effects of geometry from cloud layer properties). Very similar PC amplitude maps were produced whether the input variables were CM7 ratio and $I/F$ at 631 nm (as shown in Figure 19) or simply 631 and 727-nm $I/F$. The remarkably strong (but qualitative) match between the reconstructed $I/F$ and CM7 maps and the equivalent observations validates our hypothesis that the variability in the data is well described in terms of ${\tau }_{\mathrm{haze}}$, ${\tau }_{\mathrm{cloud}}$, and $p_{\mathrm{cloud}}$.

Some discrete features with local maxima in CM7 are highlighted in the second row of the figure. Near 51°N, a pair of compact features are candidates for deep clouds: they have high CM7 and significant reflectivity at 631 nm. Just to the northeast (not circled) is another high-CM7 region, but it does not have strong reflectivity at 631 nm, suggesting a thin but perhaps deep cloud. These three features appear red in the CH${}_4$-composite image (Figure 2). The circled features have high amplitude in PC2 (interpreted as being deep) and in PC3 (interpreted as having high opacity in the deep layer). In PC1 (interpreted as upper haze/cloud opacity), the features are local minima, again suggesting a degeneracy between opacity in the upper and deep cloud levels. A different type of region near 45°N has locally high CM7 but low reflectivity in both 631 and 727-nm filters. The high CM7 is reflected in a high PC2 amplitude, while both PC1 and PC3 (mapping to $\tau$ in the two cloud/haze layers) have low values. The interpretation of the central cloud within the “Bolton barge” [57] near 39°N and 100°W as a deep feature (Figure 5) is supported by the analysis. The CM7 of the central cloud is locally high, but it is barely visible at 727 nm against a background of significant upper cloud/haze opacity. In contrast, the surrounding barge area is dark at 631 nm. PC 3 has some of its lowest values (lowest ${\tau }_{\mathrm{cloud}}$) over the whole map domain within the barge, while the feature is almost invisible in PC 1 (no change in ${\tau }_{\mathrm{haze}}$ relative to the surroundings). The Bolton barge central cloud does not have the cloud structure of active moist convection, since there are no clearings penetrating the upper cloud/haze layer, nor tall/thick convective towers. This is consistent with the absence of intense lightning activity (Figure 5).

Comparison of panels G and I suggests that the cloud structure transition near 45°N (see Figure 20) is mainly due to a drop in upper cloud opacity. There is a significant decrease in PC 1 amplitude north of 45°N, while PC 3 (${\tau }_{\mathrm{cloud}}$) tends to vary locally over small length scales without a widespread change near 45°N. The deep clouds are not consistently deeper or thinner north of this boundary, but the upper cloud/haze layer has a systematic difference on either side of the boundary. This may explain why the 4.7-µm brightness is higher north of 45°N (Figure 1C), but not as high as in discrete low-latitude regions such as 5-µm hot spots.

Figure 19 reveals some deficiencies with the PCA-guided reconstruction analysis. The deficiencies provide a warning not to over-interpret quantitative scaling of the data, but they do not alter the main conclusions. One deficiency is the reconstructed limb darkening. The reconstructed 631-nm frame has very little limb darkening compared to panel A. On the other hand, the reconstructed 727-nm frame has too much limb darkening compared to the data. The limb darkening deficiencies could come from both the PCA-reconstruction approach, as well as the radiative transfer model suite itself. Because PCA creates orthogonal basis functions to characterize the spatial variability, it seems that limb darkening was concentrated into PC 2 and removed from PC 1. Thus, PC 3 may map to ${\tau }_{\mathrm{cloud}}$ as we hypothesized, but PC 1 actually maps to a combination of limb darkening + ${\tau }_{\mathrm{haze}}$. Figure 12 and Figure 15 also suggest discrepancies between model and observed center-to-limb curves (especially for 727 nm). The PCA-guided reconstruction was naively performed by mapping the PC amplitudes to the full range of cloud parameters tested in the radiative transfer modeling effort, which was designed to cover the full range of values over Jupiter’s disk. Within the smaller spatial domain of Figure 19, it might have been more appropriate to scale to a more limited range of cloud parameters, although the choice of parameter range would likely not affect our qualitative conclusions.

Future work to refine the modeling approach might produce better results, but caution should be taken due to the upper-/lower-layer opacity degeneracy. Still, the analysis suggests that deep clouds do influence the reflectivity ratios in 727 nm and the continuum and that the high spatial resolution achieved with HST and Gemini (in the 300–500 km range) is needed to isolate compact deep features.

4.2. The O/H Ratio from Deep Clouds

Some of the best constraints on deep cloud levels come from high-resolution spectroscopy at 5 µm [11,44,136]. Section 3.2 described how the cloud base pressure level, or LCL, maps to an H${}_2$O volume mixing ratio for a given temperature structure. Retrievals of cloud-top pressure levels ($p_{\mathrm{top}}$)—like those from 5-µm spectroscopy—can only give lower limits on the local atmospheric water abundance, because $p_{\mathrm{top}}$ < LCL for any cloud of finite vertical thickness. For the purpose of constraining atmospheric water abundance, the most useful (i.e., largest) lower limits come from the deepest cloud tops.

In Bjoraker et al. [11], $p_{\mathrm{top}}$ for deep clouds was measured in the 3–7 bar range, independent of the opacity of upper clouds at $p\le$ 2 bar. Cloud-top pressure was retrieved from the spectra using a power-law function of the equivalent width of the CH${}_3$D line, for a fully-opaque cloud layer. Although figures in Bjoraker et al. [11] at times show $p_{\mathrm{top}}$ in the range of 7–11 bar, these values were not interpreted as fully opaque clouds at $p>$ 7 bar; rather, the values were taken to indicate partially-opaque cloud opacity somewhere in the 3–7 bar range. In order to best relate $p_{\mathrm{top}}$ from spectroscopy to the O/H ratio, we focus on three types of features with deep clouds retrieved in Bjoraker et al. [11], plus the GRS with deep clouds from Bjoraker et al. [44], as described in

Table 3. Details of spectroscopically detected deep cloud regions (corresponding to the yellow bars in Figure 21 and the grey boxes in Figure 22).

Feature Type	${\mathit{p}}_{\mathbf{top}}$ (bar)	${\mathit{T}}_{500}\mathbf{mbar}$ (K)	Bjoraker et al. [11] Figure Numbers	Latitudes
FFRs	7	131.7–134.2 (South), 131.5–133.9 (North)	4, 6, 11, 14	55°S–57°S, 42°N–48°N
NEB cyclones	5–6.5	133.1–140.5	19, 21, 23, 24	17°N–19°N
Rossby plumes	5.5–6.5	133.0–139.1	20, 22, 25, 26	6°N–9°N
GRS	4–6	133.0–136.0	–	22°S

.

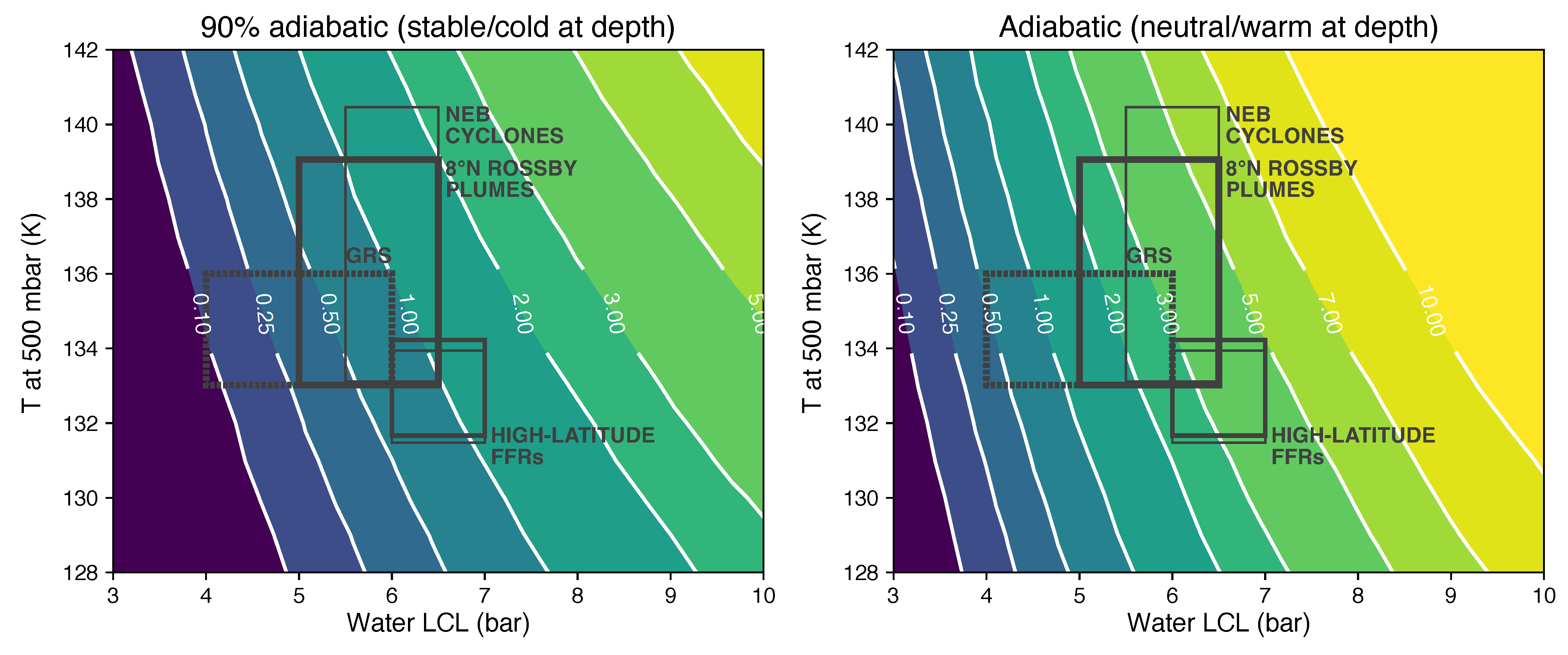
• Folded filamentary regions (FFRs). The CH${}_4$-composite map in Figure 7 of Bjoraker et al. [11] shows a FFR structure (extending from 290°W to the eastern edge of the map at 260°W) where deep clouds were retrieved in the 55°–57°S range. In the north, the spectral slit also intersected an FFR, but the full 42°–48°N range featuring deep clouds also includes areas outside the FFR.
• NEB cyclones. Cloud tops in the 5–6.5 bar range were retrieved for some areas in the 17°–19°N range (Figures 19, 21, 23, and 24 in Bjoraker et al. [11]). The CH${}_4$-composite base map shows cyclonic vortices at the locations of these deep clouds, similar to other cyclones at this latitude that may have generated mesoscale waves [137,138]. The vortices are considered to be non-convecting because the CH${}_4$-composite maps do not show tall/thick convective towers. Figure 24 of Bjoraker et al. [11] shows that the two cyclones have water vapor concentrations differing by a factor of 2, but very similar deep cloud top pressures, which validates the premise that the CH${}_3$D equivalent width is impacted by cloud opacity rather than by opacity in the extended wings of water vapor lines.
• Rossby plumes. Cloud tops in the 5.5–6.5 bar range were retrieved at select positions along a scan covering 6°–9°N (Figures 20, 22, 25, and 26 in Bjoraker et al. [11]). The deep clouds seem to be linked to the Rossby wave system [25,139,140] that produces 5 µm hot spots at the wave trough [141] and plumes of enhanced ammonia at the wave crests [142]. Cloud tops from 5.5 to 6.5 bar were retrieved under a range of varying upper cloud opacity (Figure 22 of Bjoraker et al. [11]).
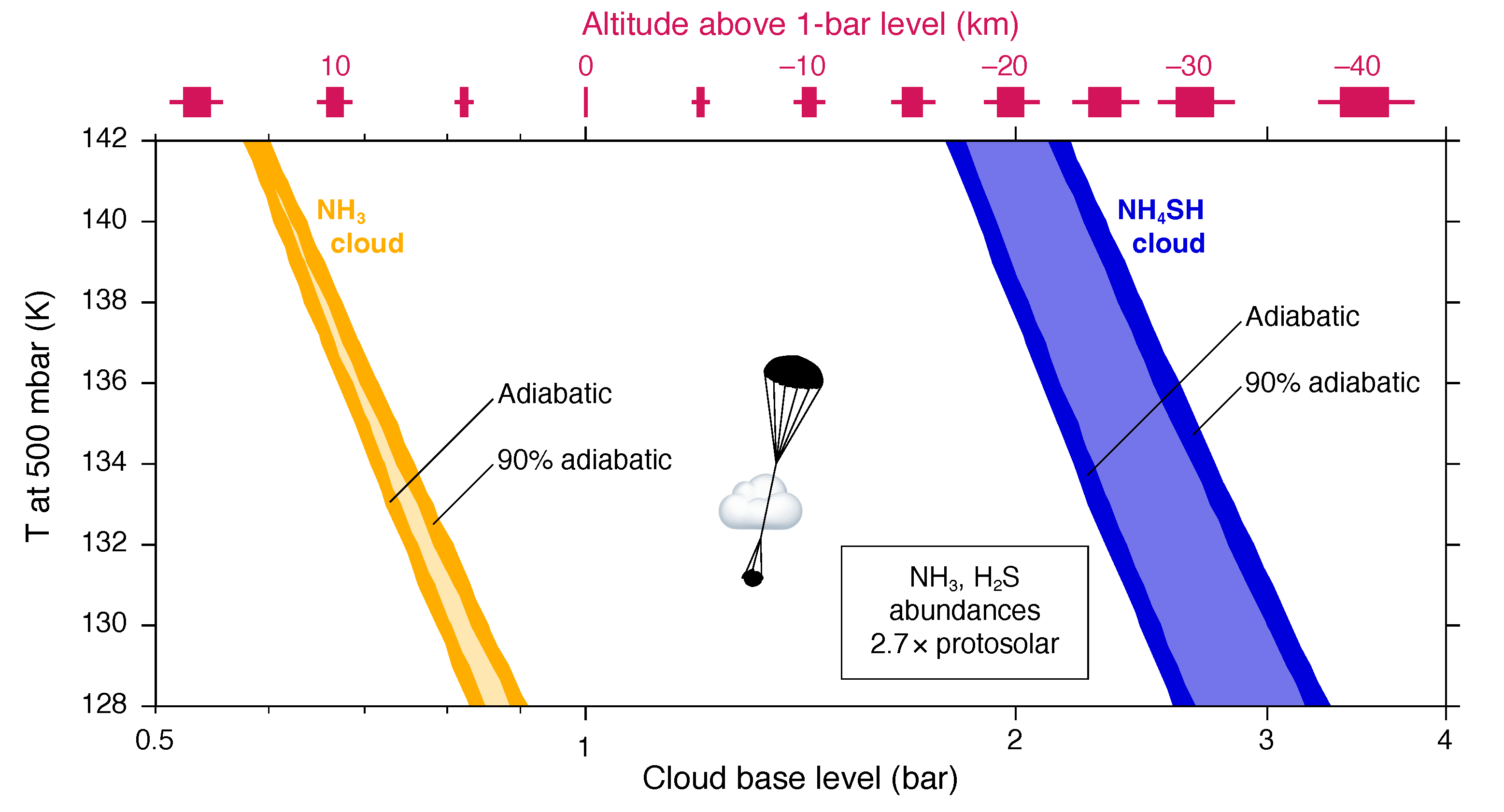
• Great Red Spot. Bjoraker et al. [44] found cloud tops in the 4–6 bar range within the GRS, based on spectra with long integration times to achieve signal-to-noise ratios sufficient to measure the CH${}_3$D line shape through upper-layer cloud opacity ${\tau }_{\mathrm{haze}}\sim 4$ at 4.7 $\mathsf{\mu }$m. Temperatures at 500 mbar range from 133 K from TEXES at Gemini North [143] to 136 K from Cassini CIRS [144], encompassing the value of 134 K from Voyager IRIS [145].

Atmospheric temperatures in the upper troposphere are time-variable [146], but temperatures were not measured simultaneously with the deep cloud measurements in Bjoraker et al. [11], so 500-mbar temperature ranges in Table 3 span the full range bounded by three published zonal mean temperature datasets (Figure 21). These were mid-infrared temperature retrievals from Voyager IRIS measurements in 1979 [122], from Cassini CIRS measurements in 2000-2001 [122], and from the TEXES instrument mounted at the Gemini North observatory in 2017 [143]. We used the scatter between the datasets at each latitude to provide an estimate of the range of temperatures appropriate to the spectroscopically derived deep cloud tops and included $\pm 1$ K arbitrarily-assigned measurement uncertainty to account for potential differences in calibration (about half the formal retrieval uncertainty for temperature at this level in Fletcher et al. [143]) and potential systematic errors from aerosols affecting retrievals of temperature at $p>400$ mbar [72].

We can combine the cloud top pressure ranges, and the corresponding 500-mbar temperatures at the relevant latitudes, to narrow the parameter range in Figure 17 and provide narrower constraints on the atmospheric O/H abundance. Figure 22 shows the same O/H abundance curves with “cloud box” overlays corresponding to the deep cloud $p_{\mathrm{top}}$ and $T_{500}$ information from Table 3.

The strictest upper limit is O/H > 0.5 × protosolar. This comes from the lower-left corners of the cloud boxes lying furthest to the right in the left panel (stable profile) of Figure 22. The lower left corners correspond to the lowest zonal mean temperatures at that latitude (from [122,143]), and the lowest $p_{\mathrm{top}}$ for the feature, from the spectroscopic data [11]. Atmospheric O/H < 0.5 × protosolar would be inconsistent with the data for the cyclones (in both the NEB and the high-latitude FFRs), unless 500-mbar temperatures were significantly colder than the range of zonal mean temperatures derived to date, or cloud top pressures retrieved in [11] were biased to greater pressures than the actual cloud tops. Cyclone 500-mbar temperatures should actually be somewhat higher than their surroundings, not lower (Figure 12 in [55]), so the upper limit of O/H > 0.5 × protosolar is a robust value. In case Jupiter’s deep temperature structure is less stable and follows a wet adiabatic profile (right panel of Figure 22), the lower left corners of the cloud boxes give a lower limit of O/H > 2 × protosolar.

The Great Red Spot is an interesting case because it is a discrete feature with 500-mbar temperatures consistently in the 133–136 K range over decades of observations [143,144,145]. Since it is an anticyclone, its static stability should be weaker than the surroundings on theoretical grounds [8,131,132], placing its lapse rate closer to adiabatic (right panel of Figure 22). Cyclones, on the other hand, should have static stability stronger than their surroundings, with abundances closer to the contours in the left panel of the figure.

Following the theoretical arguments that lapse rates should be closer to adiabatic in anticyclones, and more stable than the surroundings in cyclones [7,8,131,132], we can perhaps reduce the uncertainty based on deep lapse rate (i.e., the difference between left and right panels of Figure 17 and Figure 22). Reading abundances derived from cyclones from the stable left panel, and abundances from the adiabatic right panel for the anticyclonic GRS, we find values near the centers of the cloud boxes close to the O/H 1–2 × protosolar contours. These abundances apply just to the cloud tops. Significantly deeper cloud bases, for vertically extended clouds, would require greater abundances. Additionally, if there is a deep sub-cloud gradient in water mixing ratio [37] (as has been found for ammonia [15,17,142]), the true atmospheric water abundance would be greater still.

4.3. Pressure Levels of the Upper Clouds

Equilibrium models feature a cloud condensation “dead zone” near 1 bar (Figure 16 and Figure 18). At this level, ammonia ice cannot condense because Jupiter’s observed temperatures are too warm for condensation of NH${}_3$ in its observed atmospheric abundance (from in situ mass spectrometry and microwave remote sensing [15,16,17,18,142]). Ammonia condensation is even more impossible at 1 bar, if numerous observations of depleted ammonia (relative to the deep atmospheric abundance) at levels deeper than 1 bar are taken into account (e.g., [11,15,16,136,147,148,149]).

Pink curves in Figure 16 show the condensation efficiency of NH${}_4$SH as a function of pressure level, which decreases by two orders of magnitude over a vertical range of about 1/3 of a pressure scale height ($H_g\sim 30$ km). Although the NH${}_4$SH cloud base may vary depending on temperature (as summarized in Figure 18), some 10 km above this level, cloud condensation of saturation-limited vapor is only 1% as efficient as at the equilibrium cloud base level. Although NH${}_4$SH condensed at deeper levels may be lofted up into the dead zone, it does not efficiently form there.

5. Discussion

Our radiative transfer analysis of HST imaging data in the 727-nm weak methane band and nearby continuum wavelengths suggests that data at these wavelengths do have sensitivity to deep clouds, even in the presence of an upper cloud/haze layer with significant opacity. However, quantitative interpretation of cloud depths is difficult based on imaging in these two filters alone, because the CM7 color ratio is also very sensitive to the opacity in the upper layer. There have been very few reports deriving the pressure levels of deep clouds from imaging. Banfield et al. [61] and West et al. [66] analyzed Galileo observations of cloud features with very high CM7 ratios in the GRS turbulent wake region, originally estimating a depth of 4 bar but revising the estimate to $p_{\mathrm{top}}$ > 2.75 bar in the later work, which included careful treatment of upper-layer opacity. Deep clouds from Cassini imaging data were discussed by [62], but without assigning pressure levels. Li et al. [13] identified deep clouds (high CM7 ratio) inside 5-µm hot spots in Cassini imaging data, finding $p_{\mathrm{top}}$ < 3 bar based on the gas-only opacity in the 727-nm filter. These deep clouds seen within 5-µm hot spots drifted with a fast speed of 170 m s${}^{-1}$ eastward, a similar wind speed found by the Galileo Probe at 3 bar [150], which Li et al. [13] used to imply a depth of 3 bar for the deep cloud. Under expected temperature conditions at the 8°N latitude of the 5-µm hot spots (Figure 22), a 3-bar cloud is too deep to be composed of NH${}_4$SH (Figure 18). The conclusion of Li et al. [13] that these deep clouds within hot spots must be water clouds is robust across the range of temperature constraints found in previous works.

Jupiter’s high latitudes—particularly the region north of about 45°N—are darker overall at visible/near-infrared wavelenths, and brighter at 5 µm. Belts at lower latitudes have high 5-µm emission and darker visible/near-infrared reflectance, but with a higher degree of inhomogeneity. The difference seems to be primarily an effect of reduced upper cloud/haze opacity, which is more uniform than deep cloud opacity. The reduced upper cloud/haze opacity and the increased lightning frequency found in Juno data [82,151] could be related. Lightning is a marker of moist convection, and Guillot et al. [35,37] suggested that strong moist convection may cause strong depletion of ammonia mixing ratios through mixed-phase water/ammonia condensation in “mushballs.” Increased convective activity may result in more widespread ammonia depletion, in turn reducing the efficiency of upper cloud condensation. This hypothesis is generally supported by the increased lightning frequency in belts [152] and patterns consistent with lower ammonia mixing ratio in belts relative to adjacent zones, spanning 6 bar [11] to 440 mbar [153] levels.

More accurate measurements of deep cloud pressure levels will require improvements in remote sensing data. The imaging data presented here show spatial variations down to the HST resolution limit of about 230 km. However, the analysis shows that filter imaging is not sufficient to break degeneracies between upper and lower cloud layer opacity and pressure level, and our basic analysis did not even allow other cloud properties to vary, like particle scale height, particle single scattering albedo, or ammonia volume mixing ratio (significant near 750 nm). Spectral data spanning the 727-nm methane band and nearby continuum wavelengths is needed, but at spatial resolutions that are not achievable by ground-based visble spectro-imaging systems currently in use, e.g., [84,85]. Visible-wavelength adaptive optics would enable high spatial resolution spectra, if a wide enough field of view can be corrected: Jupiter’s diameter is typically 35–50", and guide stars for wavefront sensing would cover additional area. Although analyses using limb darkening curves can make up for the lack of spectral coverage in imaging data [65,86], these approaches are difficult to apply to longitudinally variable cloud properties in compact features.

Narrowing the cloud boxes in Figure 22 would also require advances in remote sensing, permitting simultaneous measurement of cloud top pressure level and 500-mbar temperatures. The TEXES spectrometer has the capability to conduct this kind of simultaneous spectroscopic observation, if the right observing modes are selected. Anticipated radio occultation data from Juno will deliver new constraints on the temperatures above 500 mbar [154]. However, even with perfect knowledge of the 500-mbar temperature, Figure 22 shows that the uncertain deep temperature structure leads to a factor of four range in O/H abundance corresponding to a specific LCL. Future theoretical and/or observational constraints on the thermal structure at $p>500$ mbar would provide the greatest advance in the ability to link $p_{\mathrm{cloud}}$ and O/H.

Constraining Jupiter’s atmospheric composition—particularly its O/H ratio—is important for models of the planet’s interior structure, evolution, and formation [155,156,157,158].

The Galileo Probe Nephelometer measured an apparent thin condensation cloud with a well-defined base near 1.34 bar [133]. This mysterious cloud layer is located directly in the cloud condensation dead zone. Atreya et al. [112] explained the pressure level of this cloud layer in terms of condensation of NH${}_4$SH with greatly depleted local concentrations of NH${}_3$ and H${}_2$S. However, Wong et al. [113] used an updated cloud density method in the ECCM to show that the observed density of the observed cloud layer is very high given the low NH${}_4$SH condensation efficiency described above. The observed density—if explained in terms of condensation alone—would require a huge updraft length scale of L = 10 km (Equation (3)). Retrievals based on visible and infrared spectroscopic data from Galileo NIMS, Cassini CIRS, and VLT MUSE have also found cloud opacity between 1 and 2 bar [84,159,160,161,162]. Interestingly, these retrievals share the characteristic that the aerosol models applied did not have an imposed constraint that cloud layers were located outside of the thermodynamic dead zone.

Clouds in the 1-bar dead zone suggest that our knowledge of cloud physics in the NH${}_3$-H${}_2$S system is in need of improvement. The microphysics of NH${}_4$SH is poorly understood; it is a precipitate of a gas-phase reaction of NH${}_3$ and H${}_2$S. If this reaction is inhibited until high levels of disequilibrium (similar to supersaturation), it could be possible to achieve more efficient condensation within the dead zone found in equilibrium models. Another possibility is that other compounds are formed from the reaction of NH${}_3$ and H${}_2$S [15,112,163]. Previous suggestions that ammonia hydrates NH${}_3·$H${}_2$O or 2NH${}_3·$H${}_2$O may produce tenuous clouds below the NH${}_3$ ice cloud [155,164] were discounted by Weidenschilling and Lewis [114], and these hydrates are not included in most modern ECCM codes, particularly as updated Jovian atmospheric parameters led to lower temperatures and lower water partial pressures at this level of the atmosphere. An exception is the mushball scenario in Guillot et al. [35], where the low availability of water in the dead zone (due to saturation-limited vapor) can be overcome by advection of condensed water from below, via strong convective updrafts. Adsorption of NH${}_3$ into the advected water aerosols [165] can then lead to build-up of NH${}_3·$H${}_2$O liquid and solid phases. Alternative chemistry in the NH${}_3$-H${}_2$S system remains an appealing hypothesis for explaining widespread cloud opacity in the 1–2 bar region, since mushball formation should be limited just to isolated areas of strong moist convection.

6. Conclusions

In Bjoraker et al. [11] and this paper, we took a detailed look at deep clouds in Jupiter’s atmosphere, with the goal of relating deep cloud levels to the O/H abundance in the atmosphere. We highlight areas where improvements in observational and theoretical data may someday help reach this goal.

The water cloud base pressure (LCL) is a function of the temperature and the O/H abundance. We examined the full range of temperature at 500 mbar (the upper boundary condition), and the range of temperature lapse rates consistent with observations and theory, and found that the large uncertainty in temperatures means that constraints on O/H from water LCL are very loose.

• Deep cloud tops at 5–7 bar from spectroscopic data [11] provide a strict upper limit of O/H > 0.5 × protosolar. Values closer to the means (for 500-mbar temperature and cloud top pressure) correspond to O/H > 1–4 × protosolar.
• Over the full range of temperatures considered, clouds at 3 bar or deeper in almost all cases must be water clouds (too deep to be NH${}_4$SH).

We analyzed HST data in continuum and weak methane band filters (including their ratio, CM7) to constrain deep clouds in the Juno era. A similar approach has been used previously with data from Galileo and Cassini. We used the SUNBEAR code to perform forward model calculations to identify conditions under which meaningful constraints on deep clouds could be placed.

• A layer of cloud and haze in an upper layer (p < 1 bar) has a strong effect on CM7 and filter reflectivities. This upper layer had $\tau \ge 3$ over all locations in a full-disk image of Jupiter.
• No results from 727-nm and continuum filter reflectivities alone can conclusively determine deep cloud levels, because changes in the opacity of the upper layer are degenerate with properties of the deep cloud layer.

We used CH${}_4$-band composite maps to show deep clouds in different contexts around the planet:

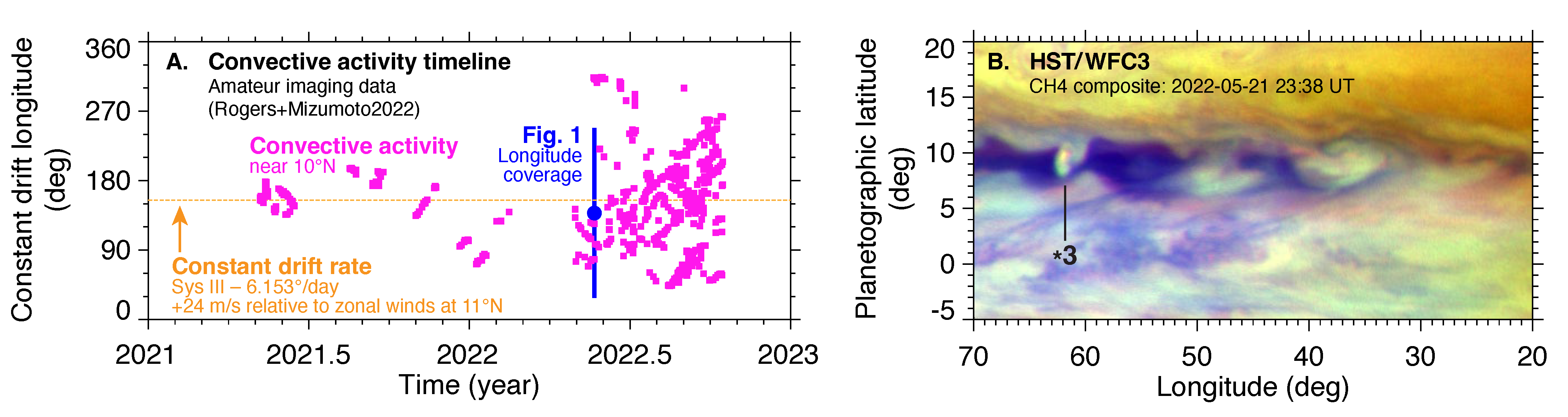
• During the 2021–2022 period, convective activity in the NEB first shut off, then resumed at a single “stealth superstorm” longitude that drifted around the planet at a constant speed (about $-6.153$°/day in System III). Activity at the stealth superstorm longitude had both similarities and differences to large convective superstorms seen on Jupiter and Saturn: it continued for many months and drifted at a constant speed like a superstorm, but it had modest vertical extent and did not always show the three-component cloud structure consistent with active moist convection.
• We identified a region north of 45°N seen to have unique cloud structure at several epochs within the Juno era, although a full time-series analysis was not performed. The region has elevated and roughly uniform/homogeneous 5-µm brightness compared to other regions, and it is darker at visible/near-infrared wavelengths, with a high CM7 ratio. A PCA analysis supports the interpretation that this region has reduced upper cloud/haze opacity, but similar deep cloud opacity and distribution as at other latitudes. The same region has enhanced lightning frequency in Juno data [82,151].
• Deep clouds are sometimes seen without evidence of active moist convection. In some cases, these deep clouds may precede convective outbreaks or persist after them. Compact central clouds can sometimes be seen within non-convecting cyclonic vortices (i.e., vortices without turbulent filamentary cloud structure or intense lightning activity).

The understanding of deep clouds on Jupiter—and their implications for the convective process and the atmospheric O/H abundance—could be advanced by improvements in remote sensing data:

• Future work to determine the pressure level of deep clouds from imaging data in the weak methane band would benefit from simultaneous spectroscopy to characterize the vertical distribution of opacity over multiple levels. However, current ground-based spectroscopic instrumentation in the 600–900 nm range is seeing-limited, without the ability to resolve features at the $\sim 260$ km scales detectable with HST. Full-disk spectroscopic observations at HST spatial resolution is not yet technologically feasible, but advances in adaptive optics could eventually lead to a better understanding of deep clouds on Jupiter.
• Much tighter O/H constraints in the future could be achieved by combining high-resolution spectra at 5 $\mathsf{\mu }$m to measure deep cloud top levels, with simultaneous resolved mid-infrared temperature retrievals. This is technologically feasible with instrumentation such as TEXES, although such an effort would benefit from simultaneous imaging at higher spatial resolution to characterize the effects of horizontal inhomogeneity.
• The current uncertainty in the deep lapse rate (between 500 mbar and the water cloud base) leads to an uncertainty with a factor of about four in the O/H abundance derived from water cloud pressure levels, even in best-case scenarios when simultaneous infrared deep cloud level and 500-mbar temperature retrievals are both available. There is currently no clear pathway toward better observational constraints on the deep lapse rate, but improvements in analysis of existing data and theoretical models might lead to the next advance. In particular, submillimeter and microwave observations are sensitive to temperature as well as composition (mainly ammonia), so efforts to somehow disentangle these degenerate properties would have high potential value.