Abstract
Cloud properties are essential for the Clouds and the Earth’s Radiant Energy System (CERES) Project, enabling accurate interpretation of measured broadband radiances, providing a means to understand global cloud-radiation interactions, and constituting an important climate record. Producing consistent cloud retrievals across multiple platforms is critical for generating a multidecadal cloud and radiation record. Techniques used by CERES for retrievals from measurements by the MODerate-Resolution Imaging Spectroradiometer (MODIS) on Terra and Aqua platforms are adapted for the application to radiances from the Visible Infrared Imaging Radiometer Suite (VIIRS) on the Suomi National Polar-orbiting Partnership to continue the CERES record beyond the MODIS era. The algorithm adjustments account for spectral and channel differences, use revised reflectance models, and set new thresholds for detecting thin cirrus clouds at night. Cloud amounts from VIIRS are less than their MODIS counterparts by 0.016 during the day and 0.026 at night, but trend consistently over the 2012–2020 period. The VIIRS mean liquid water cloud fraction differs by ~0.01 from the MODIS amount. The average cloud heights from VIIRS differ from the MODIS heights by less than 0.2 km, except the VIIRS daytime ice cloud heights, which are 0.4 km higher. The mean VIIRS nonpolar optical depths are 17% (1%) larger (smaller) than those from MODIS for liquid (ice) clouds. The VIIRS cloud hydrometeor sizes are generally smaller than their MODIS counterparts. Discrepancies between the MODIS and VIIRS properties stem from spectral and spatial resolution differences, new tests at night, calibration inconsistencies, and new reflectance models. Many of those differences will be addressed in future editions.
1. Introduction
The Clouds and the Earth’s Radiant Energy System (CERES) Project [1] is a long-term satellite-based effort to monitor the Earth’s radiative energy budget and cloud properties for climate studies. The primary measurements utilized by CERES are broadband radiances recorded by the CERES scanners [2] and multispectral narrowband radiances taken by an imaging radiometer on the same orbiting platform. Cloud properties determined from the latter are key variables used to convert the former into broadband shortwave and longwave fluxes at the surface, top-of-the atmosphere (TOA), and specified levels within the atmosphere. Together, the resulting parameters allow the study of radiation–cloud interactions and their trends at various time and space scales.
The initial CERES measurements began in March 1998 using the Tropical Rainfall Measuring Mission (TRMM) satellite, which carried two CERES scanners and the 5-channel Visible and InfraRed Scanner (VIRS). The TRMM was in a 35°-inclined orbit that provided complete diurnal coverage between roughly 45°N and 45°S over the course of 45 days. Global coverage commenced in March 2000 with the CERES broadband scanners on the Terra platform complemented by narrowband radiances measured by the MODerate-resolution Imaging Spectroradiometer (MODIS; see [3]). Terra is in a Sun-synchronous orbit with a descending node equator crossing time (ECT) of 10:30 local time. It was followed in July 2002 by Aqua, which carried the same complement of instruments in a Sun-synchronous orbit with a 13:30 ascending node ECT. Although TRMM and VIRS lasted for more than 17 years, the TRMM CERES scanner had electronic problems and acquired only 11 months of usable data. As of this writing, the CERES scanners and the MODIS on Terra and Aqua continue taking measurements, well past their expected lifetimes.
Outgoing radiation and cloud fields can vary systematically over the diurnal cycle from one region to another (e.g., [4,5]), so that measurements taken at only a few local times can result in biased means when averaged over a 24-h period (e.g., [6]). To minimize any potential diurnal bias due to sampling at four local times, CERES incorporated nonpolar (60°N–60°S) hourly (Edition 4) and 3-hourly (Editions 2 and 3) geostationary satellite narrowband radiances and cloud properties derived therefrom [7]. These are used to help estimate the corresponding hourly or 3-hourly broadband fluxes between the Sun-synchronous CERES broadband measurements [8]. The narrowband-based broadband flux estimates are normalized to the CERES scanner broadband fluxes to ensure consistency among the various geostationary satellites and between the narrowband estimates and CERES measurements [9,10].
To create a continuous climate record of the Earth’s radiation budget and clouds, the CERES Project planned to put additional broadband scanners on later satellites carrying narrowband imagers similar to MODIS in orbits with the same ECTs as Aqua and/or Terra. To that end, the CERES instruments were launched on the Suomi National Polar-orbiting Partnership (SNPP) in 2011, and on the first Joint Polar Satellite System satellite, NOAA-20, in 2018. Both satellites have nominal ECTs at ~13:30 LT, providing diurnal consistency with Aqua, and carry the Visible Infrared Imaging Radiometer Suite (VIIRS; see [11]), which has many channels similar to those on MODIS. CERES scanners were not deployed on later satellites with Terra-like orbits. As of this writing, both SNPP and NOAA-20 are providing data that overlap with those from Aqua. Assuming that the CERES instruments on Aqua fail first, those on SNPP and/or NOAA-20 will continue monitoring the cloud and radiation system into the future.
Having similar instruments in nearly the same orbits, however, does not ensure consistency in the retrieved parameters. Any dissimilarities in the calibrations, spectral bands, spatial resolution, and processing among the sensors must also be understood and mitigated to provide a stable continuous record. Szewczyk et al. [12] and Smith et al. [13] examined the relative calibrations among the CERES broadband scanning radiometers on Terra, Aqua, and SNPP, and determined ways to put all three onto the same radiometric scale. As a first step to minimizing errors due to spatial resolution and model selection between the SNPP and Aqua broadband fluxes, Su et al. [14] estimated the sensitivity of the derived fluxes to differences in the SNPP and Aqua scanner field of view sizes and to differences between the cloud properties retrieved from the VIIRS and MODIS radiances. Although consistent in ECT to within 5 min, the SNPP orbit is 119 km higher than Aqua’s. Thus, the SNPP CERES scanner field of view is significantly greater than its Aqua counterpart and covers a wider swath of the Earth. There are also differences between the imagers on Aqua and SNPP. Although many of the MODIS channels are matched with VIIRS channels to some extent, others are missing. Additionally, the VIIRS pixel resolution is either 375 m (Ix channels) or 750 m (Mx channels) compared to 1 km for most MODIS channels. The VIIRS pixel size remains relatively constant with an increasing viewing zenith angle (VZA), while the MODIS pixel size continuously increases as a function of sec(VZA). These differences can impact the retrieved cloud properties, which constitute an independent climate record and help convert the CERES broadband radiances to fluxes.
The CERES data processing system comprises several sequential subsystems that, for the most part, are downstream of the cloud retrieval subsystem, which ultimately affects the radiative fluxes derived from the observed broadband radiances [15,16]. Because the instrument calibrations, algorithms, and auxiliary data are continuously examined and improved, timely incorporation of such refinements can introduce anomalies and spurious trends in the long-term record. To avoid such impacts, the CERES processing system was designed to operate with a fixed set of calibrations, algorithms, and auxiliary data until a major change to one of those components occurs in a critical subsystem. When that happens, a new version of the system is employed and all of the satellite data over the entire record are reanalyzed with it. Each version for a given satellite is designated as an Edition and assigned a number. Notable, but less comprehensive, changes having minor effects on particular subsystems are identified by adding a lower-case letter or other indicator to the Edition number. The data for that Edition are not reprocessed from the beginning, but only from the time when the minor change is introduced, on the assumption that the change is not considered detrimental to the long-term record. The current cloud algorithms for MODIS, designated as Ed4, are applied to both Terra and Aqua.
The CERES MODIS Ed4 cloud mask [17] and retrieval algorithms [16] were adapted for application to the SNPP VIIRS radiances. Those adaptations constitute the CERES SNPP VIIRS Ed1a cloud retrieval system, CV1S. For brevity, the CERES MODIS Ed4 and SNPP VIIRS Ed1a are referred to as CM4 and CV1S, respectively. An “A” is appended to CM4 when referring to those parameters derived from Aqua MODIS data using the Ed4 algorithms. The CV1S retrieval algorithms were applied to VIIRS data taken from 1 January 2012 to 30 June 2021, resulting in a record of 9.5 years.
This paper summarizes the changes made to the CM4 cloud mask and the retrieval process and their impact. Section 2 provides a review of the input data and the major changes made to CM4 to create CV1S. Some CV1S results and comparisons with their Aqua CM4 (CM4A) counterparts are presented in Section 3. Discussion of the CV1S results and some comparisons with other data sources are given in Section 4, followed by the concluding remarks in Section 5. Part II of this paper [18] provides an evaluation of several cloud parameters with cloud properties derived from satellite-borne lidar measurements.
2. Materials and Methods
2.1. Data
The input data consist of VIIRS radiances and an array of ancillary datasets and models used to estimate the expected cloud-free spectral radiances and to simulate cloudy sky radiances for different heights, optical depths, and hydrometeor sizes for both ice and liquid water clouds. Other data are used for evaluating the results.
2.1.1. VIIRS Radiances
For CV1S, CERES ingests a 16-channel subset of the 22-channel SNPP VIIRS Collection-1 Level 1B geo-located and calibrated radiance data. From 2012 through 2015, the data were obtained from the NASA Land Science Investigator-led Processing System (SIPS) product, which employed the nominal calibrations. Beginning in January 2016, the data have been provided by the NASA Land Product Evaluation and Algorithm Testing Element (PEATE). The PEATE VIIRS calibrations from [19] are used for all channels. As indicated in Table 1, the CV1S cloud mask and retrieval algorithms use 10 and 7 VIIRS channels, respectively, compared to 12 and 8 for CM4. For cross-platform consistency and to facilitate the processing, notation, and description, CERES uses a common channel-numbering system different from those used for either MODIS or VIIRS. For the solar and thermal channels, the radiance parameters are given as the reflectance ρk and brightness temperature Tk, respectively, where the subscript k denotes the CERES channel number. The CERES numbering system is given in Table 1 along with the acronyms used as reference names, the central wavelengths, and the radiance parameter variable names. Unless otherwise noted, the CERES channel numbers will be used. To achieve pixel-size consistency among the employed wavebands, four I-channel, 375-m resolution radiances nearest the center of each 750-m M-channel pixel are averaged to obtain a radiance equivalent to a nominal 750-m resolution pixel. The 750-m VIIRS data are sampled every eighth pixel and every other scan line to yield a nominal resolution of 6 km × 1.5 km, or ~9 km2.

Table 1.
Spectral Channels Used in CERES Cloud Retrievals.
Because of the various sources, there are slightly different calibrations for some of the VIIRS channels before and after the source switch. According to the unpublished intercalibration plots developed according to the methods of [20], and found at the NASA SATCORPS Satellite Calibration Page (https://satcorps.larc.nasa.gov/cgi-bin/site/showdoc?mnemonic=SAT_CALIB_USER, accessed on 21 March 2022), the PEATE VIS gain is 1.5% greater than its SIPS counterpart. The PEATE gain for the 0.48-µm channel is 2.6% higher than that for the SIPS data. There is essentially no difference in the radiances between the two datasets for the 1.24-µm and 1.61-µm channels and for all of the thermal channels.
While the channels common to MODIS and VIIRS are similar, there are instrument differences that must be resolved to achieve consistency. For example, Figure 1 shows the spectral response functions (SRF) for the Aqua MODIS (blue) and SNPP VIIRS (red) channels corresponding to CERES channels 1 (Figure 1a) and 3 (Figure 1b), respectively. The VIIRS wavebands are broader than, and encompass, their MODIS counterparts with the centers shifted slightly to shorter wavelengths.
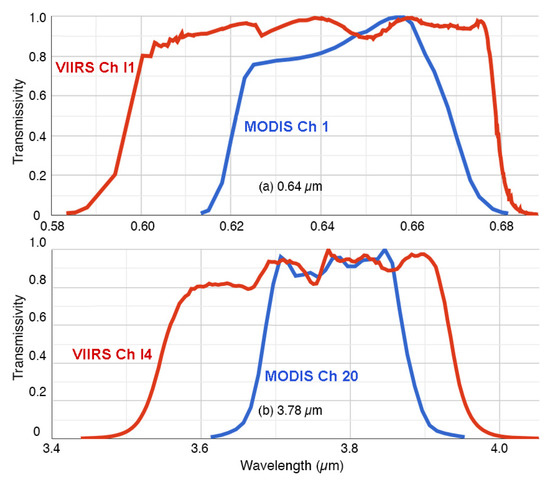
Figure 1.
Spectral response functions for CERES channels (a) 1 and (b) 3 used in cloud detection and retrieval algorithms.
In addition to its higher resolution, the VIIRS pixel size varies minimally with the increasing scan angle (SA) or VZA, unlike MODIS pixels. Combinations of sub-pixels are used to produce the operational pixels recorded by VIIRS. The number of sub-pixels used for each pixel decreases at SA = 32° and again at 43°, so that instead of the pixel area rising monotonically with VZA, it suddenly decreases at SA = 32° and again at 43° to the nadir resolution or even higher [21]. Thus, while the MODIS pixel size has increased by a factor of five at SA = 53°, the VIIRS pixel size has risen by less than 50%. This characteristic is likely to cause some differences between the VIIRS and MODIS cloud property retrievals.
2.1.2. Ancillary Input
The ancillary data used in the cloud mask and retrievals are the same as those employed for CM4. These include global surface skin temperature, surface wind speed, and atmospheric temperature, ozone, and humidity profiles, as well as total precipitable water vapor taken from the CERES Meteorology, Ozone, and Aerosol (MOA) dataset. Reanalyses from version 5.4 of the Global Modeling Assimilation Office (GMAO) Global Earth Observing System Model Version 5.41 (GMAO-G541), an update of the versions described by [22], provide the MOA with algorithm-consistent estimates of surface skin temperature and the vertical profiles of temperature, humidity, and ozone throughout the CV1S record. The native GMAO-G541 vertical profiles are available at a nominal horizontal resolution of 0.5° × 0.625° every 3 h, while surface skin temperature Ts is provided hourly at the same resolution. Total column water vapor values are taken over ocean by the Special Sensor Microwave Imager product at a 25 km resolution [23]. The CERES MOA interpolates all data to an hourly resolution and degrades the spatial grid to the 1° × 1° CERES nested grid for the vertical profiles, while retaining the native GMAO-G541 surface skin temperature time and space resolutions.
The ancillary and clear-sky radiance data are, for the most part, the same as those for CM4 [17]. The main exception is for channel 2a (1.60 µm), which is used instead of channel 2b, because the cloud optical properties for the VIIRS 2.26-µm channel differ significantly from those of the MODIS 2.13-µm channel. A set of normalized bidirectional reflectance models were developed for channel 2a using the same approach as [17] for water surfaces, [24] for snow-free land surfaces, and [25] for snow-covered surfaces. A starting clear-sky albedo map with a resolution of 10′ was developed for channel 2a using one year of data from Terra MODIS. That map, which provides the clear-sky albedos that are converted to reflectances for any given set of solar zenith, viewing zenith, and relative azimuth angles, is updated with VIIRS measurements using the same procedure employed by [17].
The change in channels and channel filter functions used in the CERES algorithms affect the atmospheric transmission and cloud optical properties, so that each instrument requires different sets of cloud model lookup tables (LUTs) and atmospheric attenuation parameters. Atmospheric absorption is computed in the same manner as in CM4, except new coefficients were computed for each channel using the VIIRS SRFs. Additionally, the technique used to estimate ozone and water vapor absorption in the VIS channel for CM4 and Aqua Edition 2 [24] was replaced with a different approach in CV1S. The new method computes the water vapor and ozone optical depths between the TOA and specified levels in the atmosphere using LUTs of normalized optical depths computed for a given SRF. The inputs include the total column ozone and water vapor amounts. Similarly, the cloud reflectance model LUTs were recomputed for channels 1, 2a, 3, and 7 using the VIIRS SRFs. This change is discussed in Section 2.2.3.
2.2. Changes to the CM4 Algorithms for Application to VIIRS, CV1S
The CERES algorithms have two main components: pixel scene identification or cloud mask, and cloud and surface property retrievals.
2.2.1. Cloud Mask Changes
The CERES CM4 cloud mask is described by [17] and outlined in detail with flow charts (https://satcorps.larc.nasa.gov/CERES_algorithms, accessed on 12 February 2022). It is employed for CV1S scene identification, but was altered due to the reduced number of channels and the use of 1.64 µm instead of 2.13 µm in CV1S. Those alterations include the elimination of some tests that rely on the missing channels, and substitution of channels in other tests. Those changes to the mask were guided by and adjusted based on comparisons of the CM4 and initial CV1S scene identification results for matching images with the goal of satellite-to-satellite consistency. For example, in the daytime and twilight cloud detection sequences, tests using 2.1 µm (see flow charts) were revised by simply replacing all 2.1-µm parameters with their 1.6-µm counterparts. Tests using brightness temperature differences (BTDij, where i and j are channel numbers) between the 11 µm and the 6.7 and 13.3 µm channels were either eliminated altogether or replaced with tests employing BTD45 or the 1.6-µm reflectance. Similarly, for night-time detection, tests using BTD35, BTD34, BTD45, and the difference between the clear-sky temperature Tcs and T4 were developed to replace those using channels 11 and 12. In all cases, new thresholds were developed for the revised or eliminated tests by examining the imagery.
A change was made to reduce overestimates of thin cirrus at night over ocean in moist atmospheres. Alterations were made to a set of thresholds used to determine if a pixel is truly cloud-free after all of the D tests were negative for clouds [17]. For CM4, an otherwise clear pixel is changed to cloudy if
Tcs − T4 > 2.5 K or BTD45 > 2.0 K.
This test was changed to the following for CV1S:
Tcs − T4 > 2.5 K or (BTD45 > 2.5 K and BTD34 > 4.0 K).
This test adjustment represents a potential source of inconsistency between CM4 and CV1S.
2.2.2. Cloud Retrieval Changes
The CM4 retrieval algorithms consist primarily of the Visible Infrared Shortwave-infrared Split-window Technique (VISST) for daytime snow-free conditions, the Shortwave-infrared Infrared Near-infrared Technique (SINT) for daytime over snow and ice surfaces, and the Shortwave-infrared Infrared Split-window Technique (SIST) for night-time and near-terminator conditions. Additional algorithms, to provide alternative information and additional secondary parameters, are also included. For CV1S, many of the CM4 algorithms were used without any changes. Some of the procedures, however, were altered to account for channel differences and to correct some of the coding errors found in CM4. The latter include indexing errors in the 1.24-µm reflectance LUTs for both ice and liquid water clouds; the use of a default surface skin temperature when the MOA and retrieved temperatures differed by more than 10 K (affects extremely high land values); and the overwriting of the CM4 opaque ice cloud-top height with the Edition 2 value. New LUTs were developed (see below), eliminating the CM4 1.24-µm LUT errors. No default values are used to replace extremely high surface skin temperatures, and the Ed4 opaque ice cloud-top heights are no longer overwritten by a lower value. Other notable changes are described below.
2.2.3. Liquid Cloud Reflectance LUTs
The CM4 water droplet cloud reflectance LUTs were created using optical properties based on the central wavelength of the SRF. In the central wavelength approach [26], the indices of refraction from [27,28] for each wavelength specified in the SRF were convolved with the SRF to obtain an effective index of refraction that corresponds to the effective central wavelength. From this, the bulk scattering properties were computed for each droplet and ice crystal size distribution adopted by [26], and used to compute the reflectance LUTs employing an adding-doubling technique. Although this method may work well for relatively uniform SRFs and minimally varying refractive indices, it can introduce some significant errors for more variable wavebands.
A more accurate technique, the spectral properties integral (SPI) method, first computes the single-scattering properties: extinction efficiency Qe, asymmetry parameter g, and single-scatter albedo ϖ0, for each hydrometeor size distribution at every wavelength in the SRF. These are used to compute the bulk scattering properties for the band by integrating over the channel and weighting by the SRF and the incoming solar radiance spectrum to obtain the band-reflected radiance. That is the method used for ice crystal reflectance LUTs for both CM4 [29] and for ice crystals and water droplets in CV1S.
For CV1S liquid clouds, the optical properties for each droplet size and wavelength were computed using Mie scattering calculations with the spectral refractive indices from [26] for droplet size distributions having an effective variance of 0.1. To provide a flexible database of optical properties, the calculations were performed for a total of 2821 wavelengths and 3000 droplet size bins for droplet radii between 0 and 300 µm. The discrete ordinates (DISORT) radiative transfer method was utilized with the bulk scattering properties to compute the reflectance for every angle combination, optical depth COD, and droplet effective radius CER. DISORT computations produced reflectance LUTs for channels 1, 2a, 3, and 7 at the same angular, CER, and COD nodes used for CM4. In general, the resulting bulk scattering properties reduce the retrieved water droplet effective radius, CERw, by 0.5–1.0 µm relative to the CM4 values.
2.2.4. Infrared Cirrus Cloud Height
Two components of the CM4 retrieval code rely on having the CO2 channel, channel 12 (13.3 µm), which is not available on VIIRS. In CM4, the modified CO2 absorption technique (MCAT; see [30,31]) used a pair of 11.0 and 13.3-µm radiances along with the MOA sounding and Ts to retrieve cloud-top heights, pressures, temperatures, and optical depths that serve as alternate values to those derived with either the VISST or SIST and as a seed for a multi-layer detection and retrieval algorithm. For CV1S, the MCAT, as used in CM4 [16], was further modified by replacing the CO2 channel with the SPW channel, CERES channel 5 (12.0 µm). The mechanics of the retrieval using the 11 and 12-µm channels are the same as those of the original MCAT and the output cloud-top height CTHM is used in the same manner as in CM4 to adjust the standard cloud effective height CEH when certain conditions are met [16]. Because the technique relies heavily on BTD45, it is designated the brightness temperature-difference method (BTM). The BTM is only applied when the surface skin temperature Ts ≥ 263 K, the surface pressure ps ≥ 825 hPa, BTD45 ≥ 0.5 K, and the surface snow cover is zero. The BTM cloud-top pressure must be less than 600 hPa before it is considered valid.
2.2.5. Multi-Layer Cloud Retrievals
When a valid BTM retrieval occurs, the MCAT multilayer retrieval method [32] is applied to the pixel, if there is a significant difference between the MCAT and VISST/SIST optical depths and the former value is no greater than 2.0. For CV1S, the retrieval approach is the same as that used for the MCAT multilayer retrieval method [16], except channel 5 radiances are employed instead of those from channel 12. The multilayer products in CM4 and CV1S are experimental and, while included in the standard CERES Single-Scanner Footprint cloud properties [33], are to be used with caution. Further details about the multilayer products will be discussed in detail in a future publication.
3. Results
Consistency with CM4A is a critical goal for CERES as the VIIRS products are expected to completely replace those from MODIS in the future and should be as much like them as possible.
In the process of performing comparisons of the two datasets, it was determined that the approach for averaging cloud properties, as in [16,17] causes a VZA-dependent bias in monthly and longer-term means. For CM4A, the monthly mean regional cloud amounts and properties were computed by summing the values of a particular parameter for all pixels that correspond to the region for the month, then dividing this by the number of pixels. Although this approach will produce a valid average, it may not be the most representative value of the monthly mean due to reduced sampling at higher VZAs and the dependence of a particular parameter average on VZA.
For example, the size of the MODIS footprint and mean cloud amount increases with rising VZA [17]. The increased field of view reduces the number of pixels that fall within a given 1° × 1° region relative to the number at the nadir. Thus, the contribution of the high-VZA overpasses to the monthly average will be smaller than the low-VZA overpasses. This would be a random effect if there were no dependence of the parameter on VZA. However, for those parameters that vary systematically with VZA, the skewed sampling will introduce a low-VZA bias. In the case of MODIS, the mean cloud fraction would be underestimated because cloud fraction CF is significantly higher at VZA = 60° than at 30° [16]. For VIIRS, the VZA-sampling dependence is minimized by the relatively constant footprint size, which is actually smaller than that at the nadir for some angles beyond 30° [21].
Daily daytime and night-time means are first computed based on the local time for each region in order to properly compare the CV1S and CM4A mean cloud properties and to minimize the biasing due to VZA dependencies. These are then used to compute the monthly, annual, and multiannual averages. The differences between the earlier approach and the method used here are significant for Aqua, but less so for VIIRS. For example, the mean global VIIRS and Aqua daytime cloud amounts determined from the earlier method are essentially the same. As shown in the following subsection, the global mean CM4A cloud fraction exceeds its CV1S counterpart when the daily averaging technique is employed.
3.1. Cloud Amount
The distributions of the 2013 mean cloud fractions from CV1S, CF(V), and their regional differences with CF from CM4A, CF(M), are plotted in Figure 2. The global CF patterns are very similar during the day (Figure 2a) and night (Figure 2b), except in the polar regions (latitudes poleward of 60°N or S). In nonpolar areas (equatorward of 60°N or S), CF generally appears to be greater at night. Overall, the global mean CF(V) increases by 0.02 from day to night, despite the nearly 0.03 drop in polar cloudiness. During the day, CF(V) is generally 0.01–0.02 less than the CF(M) (Figure 2c), except over some desert areas and some tropical littorals. The non-polar positive differences occur in areas affected by seasonal dust and smoke outbreaks (e.g., around tropical west Africa and the maritime continent). The greatest negative differences (dark green, light blue) are in the tropical marine trade cumulus areas and over central Greenland. On average, the daytime CF(M) is 0.013 greater than the CV1S cloud fraction. At night (Figure 2d), the differences over tropical oceans and large portions of the permanent sea ice and snow areas are strongly negative, while the CF(V) exceeds the CF(M) over many land areas, particularly where desert and tundra prevail. In the nocturnal global mean, the CF(V) is 0.025 less than the CF(M). Over the polar regions, the large negative and positive regional differences cancel out to some degree but the mean difference is still significant at −0.020. The wide regional variability and increased negative differences in those cold regions at night are likely due to the lack of CERES channels 11 and 12 on the VIIRS and the reduced sensitivity in the VIIRS I4 band at very low temperatures relative to that of the MODIS channel 20.
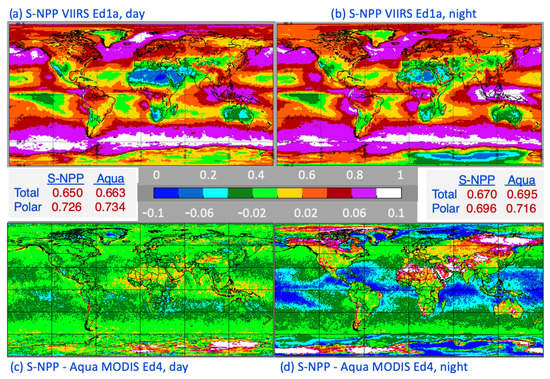
Figure 2.
Mean 2013 cloud fractions from CV1S for (a) day and (b) night with the differences between CV1S and CM4 for (c) day and (d) night.
Figure 3 shows the time series of the CF from CM4A (blue) and CV1S (green) as 12-month running means between 2012 and 2020. Note the different scales in each plot. During daytime in nonpolar regions (Figure 3a), the average difference between the two datasets is relatively constant around −0.015. The trends for these 9 years are −0.7 and −0.5%/decade for CV1S and CM4A, respectively. Over polar areas, the CF differences vary between −0.004 to −0.014 (Figure 3b). Here, the CF trends are positive at 1.6 and 1.5%/decade for VIIRS and MODIS, respectively. Over the entire globe (Figure 3c), the daytime time series are very similar to those over nonpolar regions, with the differences averaging around −0.015, and yielding trends in the CF(V) and CF(M) of −0.4 and −0.2%/decade, respectively. As indicated in Figure 2c, the differences are not uniform across the globe, but vary with latitude and surface type.
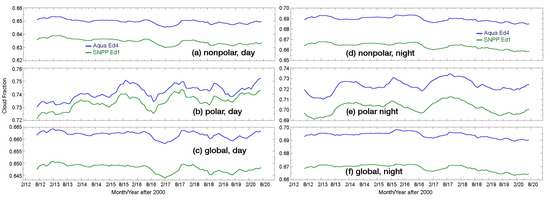
Figure 3.
Time series of 12-month running mean cloud amount during daytime (left) and at night (right) over nonpolar (top), polar areas (middle row), and the globe (bottom) for Aqua Ed4 (blue) and SNPP Ed1a (green). Note the scale differences among the plots.
At night (Figure 3, right), the differences appear fairly constant with time at all latitudes. Over the nonpolar regions (Figure 3d), the CF(V) is 0.025 less than the CF(M), while the V1S and CM4A trends of −0.9 and −0.7 %/decade reflect a slight divergence with time. The difference over the polar areas (Figure 3e) begins around 0.018 and ends around 0.025, resulting in a mean difference of 0.022. Because of the CM4A calibration change, the CF(M) polar trends are unreliable. Nocturnal cloud detection was unaffected by the 2016 change in VIIRS data because only its solar channels were altered. For this period, the CF trends are evident day and night with decreasing (rising) cloudiness in the nonpolar (polar) regions. A decrease is apparent when the whole Earth is considered (Figure 3f).
Table 2 summarizes the mean cloud fractions from Aqua and VIIRS for the period, 2012–2020. During the daytime, the VIIRS averages are 0.016 less than Aqua over all marine areas and 0.013 less over land regions. Overall, the means differ by −0.015 during the day. At night, the discrepancies are more substantial, with mean differences of around –0.041 over oceans. Over land, the nocturnal differences are positive over nonpolar regions and are essentially zero over polar regions. For all surfaces over the globe, the night-time 9-year difference, CF(V) − CF(M), is −0.026.

Table 2.
Mean cloud amounts from Aqua Ed4 and SNPP Ed1a for 2012–2020.
Since the VIIRS pixel footprint changes little with VZA compared to that of MODIS, it is important to determine the differences, if any, in the properties as a function of VZA. Figure 4 plots the average global cloud fractions from CM4A and CV1S for 2013. Mean CF increases with VZA for both retrievals during the day and night, but less so for CV1S than for CM4A. On average, the CF rises by 11% from near to the nadir to VZA = 65° for CV1S compared to 14% for CM4A. Thus, the nearly constant pixel size appears to have reduced the tendency for increasing cloudiness, perhaps by offering views of more clear areas between clouds. However, the increasing cloudiness with VZA cannot be eliminated by simply changing the pixel size, because the vertical extent of the clouds blocks views of the breaks between clouds when viewed off-nadir.
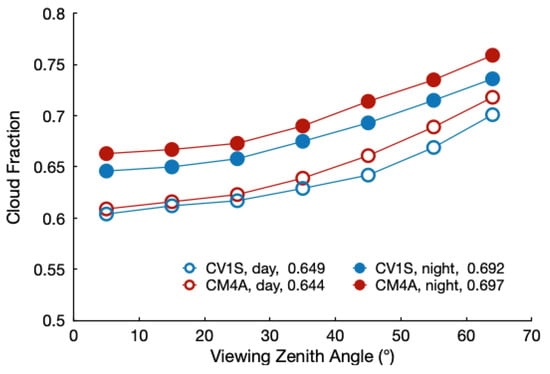
Figure 4.
Mean 2013 global cloud fractions as a function of VZA for Aqua CM4 and CV1S.
3.2. Cloud Phase
The 2013 mean CV1S liquid cloud amount, CFw, and the differences with CM4A are presented in Figure 5. The CFw from CV1S (Figure 5a) is greatest over the marine areas under the subtropical highs, the midlatitudes, and the Arctic. It is least over desert areas, including Antarctica. The daytime liquid cloud amount differences, CV1S-CM4A, in Figure 5c reveal that CV1S generally classifies fewer tropical pixels as water clouds compared to CM4A. Over the midlatitudes and polar regions, the differences flip, so that more clouds are classified as liquid by CV1S than by CM4A. As listed in the table in Figure 5, the mean difference in the CFw during the day is −0.005 for the globe as a whole, but is 0.034 over polar areas. The daytime CV1S ice cloud amounts Cfi over polar regions are 0.052 less than their CM4A counterparts, while the global mean CV1S CFi is 0.014 less than the CM4 average.
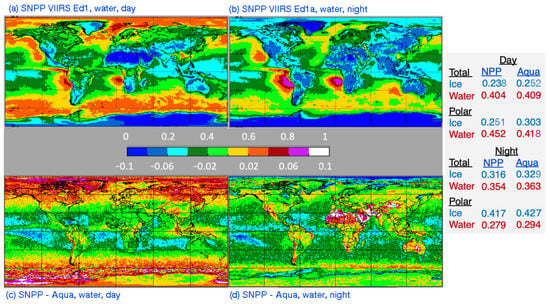
Figure 5.
Mean 2013 liquid cloud amounts from CV1S for (a) day and (b) night and the differences between CV1S and CM4A for (c) day and (d) night. The table lists the average liquid and ice cloud amounts for the globe and polar regions only.
At night, the CV1S liquid cloud amounts (Figure 5b) are less than the CM4A means over most oceanic areas, with the greatest absolute differences in the trade cumulus realm (Figure 5d). The CV1S liquid clouds exceed the Aqua values over mountainous and arid regions. In polar areas, the differences in liquid cloud amount are −0.015 compared to −0.009 over the entire Earth. The VIIRS ice cloud amounts (table in Figure 5) are less than their Aqua counterparts. These lower amounts for each phase reflect the overall smaller CV1S nocturnal cloud amount. The global liquid fraction relative to the total amount is the same for both datasets: 62% and 53% for day and night, respectively.
The time series in Figure 6 reveal that at the beginning of the SNPP period, the CV1S liquid cloud fractions are ~0.008 less than those from Aqua during the daytime (Figure 6a), but converge to within 0.002 of the CM4A amounts in 2016 and thereafter. At night (Figure 6b), the CFw from CV1S rises from ~0.351 in 2012 to ~0.356 in 2014, before slowly decreasing down to ~0.352 in 2018. The CM4A liquid fraction is ~0.016 greater than its SNPP counterpart, then converges with CV1S and decreases after 2014. That decrease is due, in part, to problems with the Aqua MODIS channel 29 in the Collection 5 dataset. That channel is employed in the nocturnal phase selection algorithm. The MODIS Collection 6.1 data were used for CM4 starting in 2016, so the CM4A averages decreased slightly after 2015 and the difference between CV1S and CM4A is relatively constant thereafter at ~0.010. Thus, the variation in the night-time phase differences is due mainly to problems with MODIS than with CV1S. The daytime phase selection also uses the troublesome channel 29 data, but much less frequently than at night, so there is less impact during the day. The ice fraction variations complement the liquid cloud results. The daytime CFi from Ed4 remains fairly steady at ~0.253, with a slight rising trend (Figure 6c). The CV1S CFi is constant at ~0.238 until 2016 when it drops to ~0.235, increasing the difference between CM4A and CV1S. At night (Figure 6d), the mean CFi from CV1S decreases slightly in 2014 but remains between 0.312 and 0.317 throughout the record. The CM4A jumps from 0.328 to 0.334 in 2015 and does not return, again reflecting the impact of the change in MODIS datasets.

Figure 6.
Global 12-month running mean liquid water (left) and ice (right) cloud fractions of total cloud amount from CM4A (blue) and CV1S (green).
The liquid phase fraction averages for the whole period are summarized in Table 3. In general, the results in Figure 5 are quite representative of the 9-year means. Over nonpolar ocean, the CV1S mean CFw during daytime is 0.012 less than its CM4A counterpart, while over polar ocean, the CV1S liquid fraction is 0.032 greater than CFw from CM4A. At night, when the VIIRS total cloud fraction is reduced relative to CM4A, the nonpolar ocean difference is −0.023. Globally, theCV1S CFw means over land for CV1S is 0.004 and 0.015 greater than those from CM4A, for day and night, respectively. For all surfaces, the respective day and night differences in global mean liquid cloud fraction are −0.005 and −0.011.

Table 3.
Same as Table 2, except for the liquid water cloud amount.
Over nonpolar regions, the CFw accounts for 62% of the total cloud cover during the day for both products. However, the CV1S CFw makes up 64% of the total over the polar areas compared to 59% for CM4A. Overall, the difference in relative water cloud fraction is −0.7% during the day. At night, the liquid fraction relative to the whole differs by less than 1% everywhere for the two satellites. Thus, the greatest inconsistency in phase selection is over the polar regions during the daytime.
Globally, CFi accounts for 47.0% and 47.5% of the total nocturnal cloud fraction for CV1S and CM4A, respectively. During the day, the corresponding percentages are 36.4 and 38.0. The mean daytime nonpolar CFi amounts for the period are 0.244 and 0.233, respectively, for CM4A and CV1S, while at night, the corresponding averages are 0.314 and 0.298.
3.3. Standard Cloud Height, Pressure, and Temperature
In this section, all parameters are related because the cloud effective temperature CET is used to ascertain the cloud effective height CEH, and the height, in turn, is used to select the pressure. The effective cloud height derived from VIIRS should be at an altitude somewhere between the top and the base of the cloud. This corresponds to the mean radiating temperature of the cloud. For water clouds, the level of CET is usually within a few meters to 100 m of the top. For cirrus clouds, it can be close to the cloud base or near the cloud-top depending on the cloud density and physical thickness. For water clouds, the true cloud-top height CTH is estimated based on a small adjustment to the effective height, while for optically thin ice clouds, it is determined as a function of CET and COD or cloud emissivity [24]. For CM4, a new parameterization based on [34] was implemented to estimate the CTH for opaque ice clouds. However, a coding error overwrote the results of the new parameterization in the final version of CM4 and it needs to be applied by the user [16]. That issue was corrected for CV1S. The cloud base height CBH is estimated as the difference between the CTH and cloud thickness CDH, which is estimated from CET, COD, and the cloud phase using various empirical formulae as described by [16]. Cloud base temperature and pressure are found from the soundings based on CBH. The results here focus primarily on the cloud effective height since it is determined in the same manner for each satellite.
Figure 7 maps the 2013 mean water cloud effective heights for both CM4A and CV1S. During the day, CV1S (Figure 7a) yields patterns in CEH that are quite similar to those for CM4A (Figure 7c), although the former heights are, on average, greater than the latter values by 0.08 km. The most obvious discrepancies are seen over many land areas and over the equatorial convergence zones. The nocturnal distributions are similar, but again, the mean CEH from CV1S (Figure 7b) exceeds that from CM4A (Figure 7d) by 0.17 km. The most obvious differences are found over the Southern Ocean.
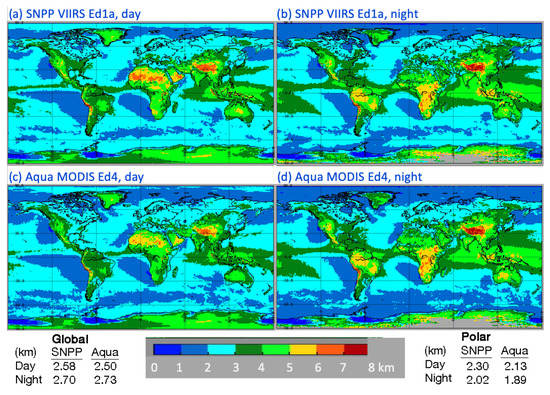
Figure 7.
Mean 2013 daytime water cloud effective heights from SNPP Ed1a during (a) day and (b) night, and from CM4A for (c) day and (d) night.
For ice clouds (Figure 8), daytime CEH(V) varies zonally for the most part (Figure 8a), much like CEH(M) (not shown). CEH(V) exceeds CEH(M) everywhere, except over tropical land (Figure 8c). At night (Figure 8b), CEH(V) is significantly less than CEH(M) over all tropical surfaces, but is greater than CEH(M) for most regions poleward of 30° latitude (Figure 8d). On average, for 2013, the CEH(V) is 0.51 km greater than CEH(M) over all areas during the day, while the two mean heights differ by only −0.05 km at night.
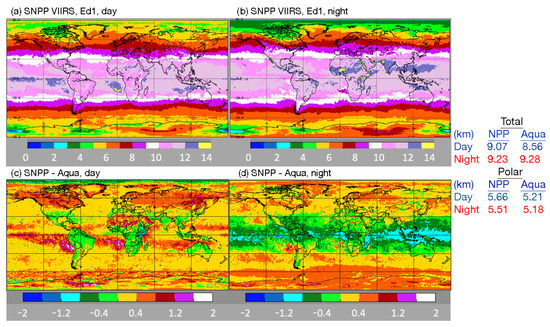
Figure 8.
Mean 2013 ice cloud effective heights from CV1S during (a) day and (b) night, and the CV1S minus CM4A differences for (c) day and (d) night.
The time series of cloud effective heights are given in 12-month running global means in Figure 9. Daytime liquid cloud heights (Figure 9a) from SNPP closely track those from Aqua, with an offset of ~0.15 km. Both have a slight downward trend. Similar behavior is seen at night (Figure 9b) with a starting difference of ~0.11 km ending at ~0.13 km. The downward trend is also quite evident. During the day, the average ice cloud heights from CV1S follow their CM4A counterparts very closely, with an offset of ~0.50 km (Figure 9c). Both curves exhibit a slight upward trend. This trend is more apparent at night, when the two averages increase over the period and differ from ~−0.07 km to −0.01 km over the period (Figure 9d). The variable ice cloud differences probably arise from the change in phase fractions at night due to the Aqua channel issues mentioned above.
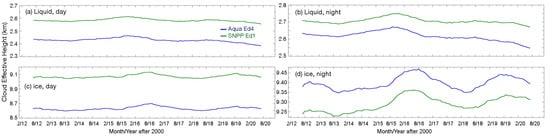
Figure 9.
Same as Figure 6, except for the mean liquid (top) and ice (bottom) cloud effective height for day (left) and night (right).
Table 4 summarizes the means for the 9-y period. The magnitudes of the liquid cloud effective height differences are greater over land than over water during the day and vice versa during the night. Differences over the polar regions are nearly identical to those over other areas during the day and somewhat larger at night. The global mean CEH difference during the day is 0.15 km. The CM4A ice clouds are higher (lower), on average, than their CV1S counterparts during the night (day), consistent with the plots in Figure 9. Globally, CV1S ice cloud effective heights are 0.41 km higher than those from CM4A during the day, but 0.11 km lower than their Aqua counterparts at night. The sources for these differences are objects of further discussion.

Table 4.
Same as Table 2, except for the mean cloud effective height (km).
3.4. Standard Daytime Cloud Optical Depth, Effective Hydrometeor Size Based on a 3.74-µm Channel
The 2013 global distributions of SNPP Ed1a daytime mean cloud optical depths are shown in Figure 10 along with their differences relative to the Aqua Ed4 means. The average CV1S liquid water optical depth, CODw(V), is greatest over the midlatitudes and polar regions (Figure 10a). CODi(V) peaks in the areas of tropical deep convection and in the midlatitude storm tracks (Figure 10c). For liquid clouds, CODw(V) exceeds CODw(M) by 6 or more over much of the polar snow and ice areas (Figure 10b), but differs from CODw(M) by less than 1.5 over most of the nonpolar oceans. Over many land areas, the CODw(V) exceeds the CM4A mean. For ice clouds, CODi(V) < CODi(M) over most regions. Positive differences are seen over the Southern Ocean and near the Russian–Mongolian border (Figure 10d). Smaller CODi(V) values over snow and ice are due to a replacement of the reflectance LUT used in the 1.24-µm CM4A retrievals, calibration differences (see Section 4), and discrepancies in the clouds selected as ice (e.g., Table 3).
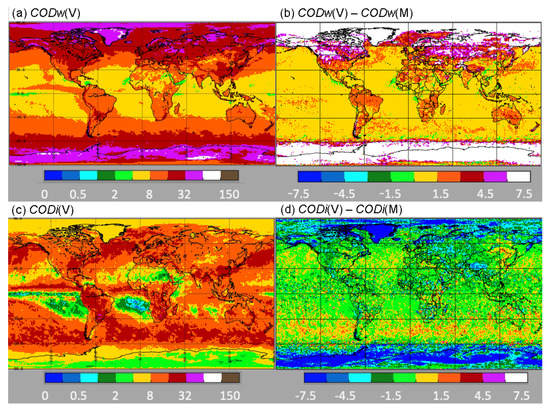
Figure 10.
Mean 2013 daytime cloud (a) CV1S liquid cloud optical depth and (b) difference in the optical depth, CODw(V) − CODw(M), for liquid clouds, (c) CV1S ice cloud optical depth and (d) difference in the optical depth for ice clouds.
Figure 11 plots the nonpolar running mean optical depths. The mean CODw(V) is ~1.8 greater than CODw(M) before 2016 (Figure 11a), when COD(V) rises by roughly 0.6. The rise is more pronounced for ice clouds (Figure 11b). Both the ice and water COD(V) means drop slightly after 2017. The increase in COD(V) after 2015 is due entirely to the calibration change effected by the switch from SIPS to the PEATE data. No increase is observed for COD(V) in the polar regions (not shown). Since the 1.24-µm channel data are mostly used to retrieve COD(V), there was no calibration change to drive the post-2015 increase.
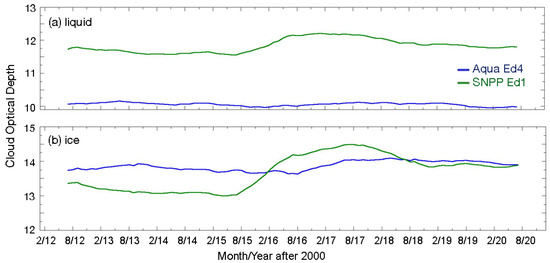
Figure 11.
Nonpolar 12-month running mean daytime cloud optical depth from CM4A and CV1S for (a) water and (b) ice clouds.
The mean differences between the two datasets can be quantified from the average optical depths given in Table 5 for the period, 2012–2020. Over nonpolar ocean and land, the CODw(V) averages are 1.4 and 3.1 greater than CODw(M). For all nonpolar regions, CODw(V) is 1.8 or about 18% greater than the CM4A mean. This can be contrasted with the nonpolar CODi(V), which is 0.2 less than its CM4A equivalent. The liquid and ice COD differences over the polar zones are 8.7 and −4.1, respectively. That is, the polar COD(V) means are 43% greater and 31% less than the respective liquid and ice cloud COD(M) values.

Table 5.
Same as Table 2, except for the daytime mean cloud optical depths.
The regional averages of the CV1S cloud droplet effective radius CERw for 2013 are plotted in Figure 12, along with the differences between the VIIRS and Aqua means. Overall, the relative distribution of VIIRS CERw (Figure 12a) is quite similar to that for Ed4 (not shown, e.g., see Figure 15 of [16]). Yet, the magnitudes are clearly not the same as seen in Figure 12b. Negative differences of 1.0 µm or greater are common over nonpolar ocean areas, while positive differences are evident over Greenland, Alaska, Siberia, north Africa, and Antarctica.
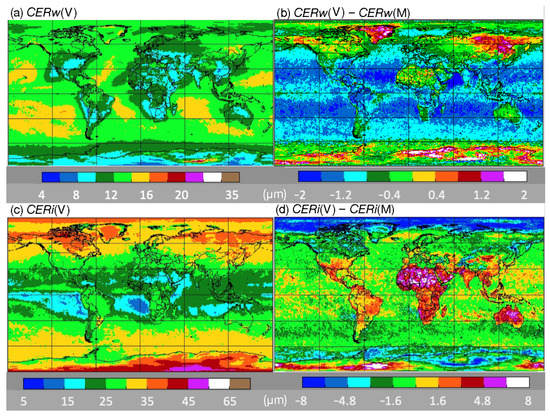
Figure 12.
Same as Figure 10, except for the daytime cloud hydrometeor effective radii.
Ice crystal effective radius CERi means from CV1S are plotted in Figure 12c along with the regional CERi(V) − CERi(M) differences in Figure 12d. Much like their droplet counterparts, the VIIRS CERi regional averages are distributed in patterns similar to the CM4A values with a mostly zonal decrease from the poles to the tropics (Figure 12c). Superimposed on that zonal pattern are deviations resulting from climatological circulation patterns, such as the intertropical convergence zone (e.g., ~5°N in the Pacific Ocean) and those induced by the positioning of landmasses (e.g., the west coasts of southern continents). Again, the magnitudes vary with small differences over ice-free water and large negative differences over the Arctic Ocean and parts of Antarctica and the Southern Ocean (Figure 12d). Over land equatorward of 45° latitude, CERi(V) exceeds CERi(M) by up to 6 µm. The largest differences occur where ice clouds are sparse.
The time series of nonpolar mean CER (not shown) indicate that the differences between CER(V) and CER(M) are relatively constant at −1.1 µm and −0.5 µm throughout the 9 years for water and ice clouds, respectively. For liquid clouds, the mean difference over the polar regions is much smaller than that over the nonpolar regions. A slight upward trend, evident in CERw(V) and CERw(M), is primarily due to clouds over nonpolar areas (not shown).
Table 6 lists the CER averages from Aqua CM4A and CV1S for 2012–2020. Overall, the CERw(V) and CERi(V) means are 1.1 and 0.8 µm less than those from Aqua, respectively. These global differences are mainly driven by clouds over the nonpolar oceans where the VIIRS CERw and CERi means are 1.2 µm and 0.9 µm, respectively; smaller than the CM4A averages. Over the polar regions, the mean CERi(V) is 1.8 µm less than CERi(M); it exceeds CERi(M) by 0.8 µm over nonpolar land.

Table 6.
Same as Table 2, except for the daytime mean cloud droplet and ice crystal effective radii (µm).
Table 7 shows the mean liquid and ice cloud water paths, CWPw and CWPi, respectively, from CM4A and CV1S for cloudy pixels only, over the period 2012–2020. To obtain the total CWPw or CWPi, the results would need to be multiplied by the cloud fraction. Here, the cloud water path CWP is computed under the assumption that the retrieved effective size represents the cloud as a whole. Alternatively, CWPw can be estimated by multiplying the result of Equation (3) by 0.83 [35] using the assumption that the retrieved CERw represents only the top layer of the cloud and the droplet size increases adiabatically with height in the cloud. The adiabatic assumption is more accurate in many areas (e.g., [36]). Over nonpolar areas, the CWPw(V) is ~14% greater than the CWPw(M), but this difference jumps to 81% over the polar regions due to the large COD differences there. That polar difference yields a global overestimate of ~30% for CWPw(V) relative to CWPw(M).
CWP = 0.67 CER × COD,

Table 7.
Same as Table 2, except for the daytime mean liquid and ice cloud water path (gm−2) over cloudy areas only.
Overall, the mean CWPi values are very close, with the greatest absolute difference in CWPi of −41% over polar land and the smallest discrepancy, 6%, over nonpolar land. Over oceans, the VIIRS CWPi is ~8% greater than its Aqua counterpart. Globally, the CWPi from CM4A exceeds that from CV1S by 4%.
The mean 2013 microphysical parameters are plotted in Figure 13 as a function of VZA for all surfaces together. Figure 13a plots the mean COD values as a function of VZA for SNPP and Aqua. Optical depth from VIIRS tends to vary less with VZA than its Aqua counterparts. For liquid water clouds (solid symbols), the CODw(V) curve drops with increasing VZA until rising again for VZA > 55°. The change with VZA is only −7% between 0 and 70° for the CV1S mean optical depths over all surfaces, compared to 22% for CM4A. For ice clouds (open symbols), however, the decrease in CODi(V) is ~13% compared to 22% for CODi(M). The smaller drop with VZA for VIIRS is likely due to VIIRS smaller pixel size at the more oblique angles relative to that from Aqua MODIS, since the optical depth tends to decrease with increasing pixel size (e.g., Table 16 of [37]). Note that the polar and nonpolar results are included in the VZA average and there is only pixel-weighted averaging, so the means computed from the curves in Figure 13 are unlikely to match those in Table 5.
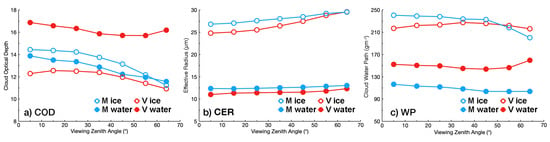
Figure 13.
Global mean cloud microphysical properties from CM4A (denoted by M) and CV1S (denoted by V) for 2013. (a) cloud optical depth, (b) Cloud hydrometeor effective radius, and (c) cloud water path.
The mean CER is plotted as a function of VZA in Figure 13b for the 2013 CV1S and CM4A retrievals. Unlike the optical depth variations, the VIIRS CER increases more with VZA than its MODIS counterpart. In this plot, CERw rises by ~12% for VIIRS compared to ~5% for CM4. Likewise, CERi increases by 19% for CV1S, while it changes by +10% for CM4A. This larger change in CERi with VZA from the VIIRS retrievals is surprising given the smaller pixel size.
The opposing dependencies of CER and COD on VZA also tend to compensate each other when used to compute CWP. Figure 13c shows the mean 2013 CWPw and CWPi from CV1S and Aqua as functions of VZA. The curve for CWPw(V) is relatively flat with a minimal decrease up to VZA = 55°, but jumps by +11% in the last VZA bin. This bump at the end follows the less dramatic rises in both COD and CER at the same point. Conversely, the mean CWPw(M) decreases almost monotonically from 0° to 64°, an overall drop of 11%. The mean CWPi(M) falls off more at the higher angles, resulting in a 17% drop relative to the nadir. The CWPi(V) curve is very flat, changing by only 4% with a maximum at 35°. Note, the values in Figure 13c may differ from those in Table 7 because of the different geographical weighting in calculating the means.
3.5. Alternative Products
The CERES project has a long-term perspective that includes adding new cloud properties to the SSF as they become available. These alternate products are currently not utilized in the operational determination of broadband fluxes in any of the CERES processing subsystems. However, they are included in the SSF for experimental purposes and further scientific analysis as they become more mature. Some have already been employed in various studies (e.g., [38,39]). As they improve, some or all of these parameters may become part of the standard CERES processing, if they enhance the accuracy of the CERES flux products.
3.5.1. Alternate Cloud-Top Height
The BTM, used to provide an alternative estimate of CTH, is applied only when its retrieved temperature corresponds to a pressure that is less than 600 hPa and, at least, 100 hPa less than the pressure from the standard retrieval. Thus, it is mostly applicable to ice clouds. Figure 14 maps the distributions of 2013 daytime mean cloud-top heights from Aqua CM4 MCAT, CV1S BTM, and the CV1S standard retrieval (CTH). Overall, the standard retrieval (Figure 14c) yields the highest cloud-tops in the nonpolar regions, 10.8 km, on average, compared to MCAT with 9.5 km (Figure 14a), and BTM with 10.5 km (Figure 14b). Over polar regions, the BTM produces the highest cloud-tops. Similar results are found at night (not shown). It should be noted that there are some sampling differences among the methods and the BTM result sometimes substitutes for the standard value. Nevertheless, a clear discontinuity exists between the MODIS and VIIRS alternative cloud-top height product due to changes from switching from 13.3-µm to 12.0-µm in the alternate retrieval. The channel differences will need to be resolved in future editions.
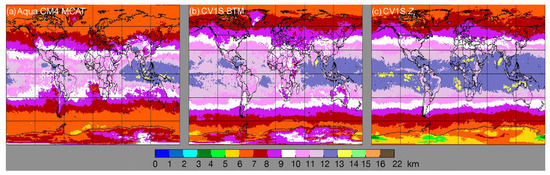
Figure 14.
Mean 2013 cloud-top heights from (a) Aqua CM4 MCAT, (b) CV1S BTM, and (c) CV1S standard retrieval for ice clouds.
3.5.2. Alternative Cloud Hydrometeor Sizes
Figure 15 plots the global distribution of the 2013 daytime CER means, CER7 and CER2, derived from the 1.24-µm (left) and 1.61-µm (right) reflectances, respectively. These may be compared with the standard retrievals in Figure 12a,c based on 3.78-µm reflectances. The relative distributions of the mean liquid water droplet radii at 1.24 µm (Figure 15a) and 1.60 µm (Figure 15b) are very similar, and, in turn, are not unlike those in Figure 12a; however, the magnitudes are quite different. Except for the littoral areas under the subtropical highs or around Antarctica and in the Arctic Ocean, CER7w tends to be less than CER2w. In nearly all cases, the CERw from 3.74 µm is smaller than its alternative counterparts.
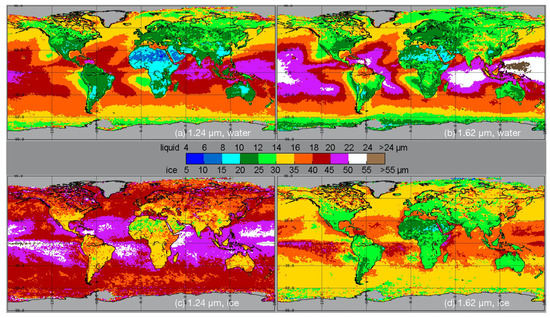
Figure 15.
SNPP VIIRS Ed1a 2013 mean CER for liquid water clouds at (a) 1.24 µm and (b) 1.62 µm, and for ice clouds at (c) 1.24 µm and (d) 1.62 µm, 2013.
For ice clouds, CER7i in Figure 15c greatly exceeds CER2i in Figure 15d. In turn, the latter is significantly larger than CERi. Although the magnitudes are quite different, the patterns in Figure 15c,d are similar, except for some notable discrepancies between CERi in Figure 12c and CER2i and CER7i. For example, CER2i and CER7i increase westward from the coastal areas under the subtropical highs, while CERi remains relatively constant or even decreases to the west in some areas.
The time series of the alternative values in Figure 16 show discontinuities in 2016 for both the liquid (Figure 16a) and ice cloud (Figure 16b) CER7 averages for CV1S. Increases after the beginning of 2016 may be attributed to the switch in the VIS calibration, which changed the COD(V). The CER7w(V) means are much closer to those from CM4A than their ice counterparts. Similarly, CER2w from VIIRS (Figure 16c) is much closer to CER2w from Aqua after 2016, despite the spectral channel differences. For ice clouds, CER2i(V) shows no increase after 2016 and parallels CER2i(M) through the whole period (not shown).
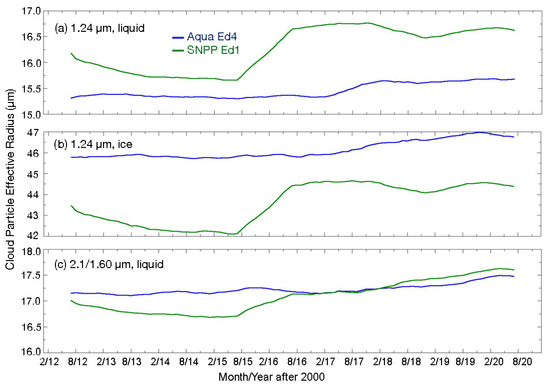
Figure 16.
Same as Figure 11, except for the CER retrieved using the 1.24-µm channel for (a) liquid, CER7w, and (b) ice clouds, CER7i, and (c) 2.1 or 1.6-µm for liquid clouds, CER2w.
Globally for the 2012–2020 period, CER7w and CER2w are 16.2 µm and 18.1 µm, respectively, compared to 15.6 µm and 18.1 µm for CM4A. CER7i(V) and CER2i(V) are 43.6 µm and 33.7 µm, values smaller than the 46.3 µm and 38.8 µm from CM4A. The nonpolar averages are nearly the same as the global means. The global averages of CSV1 CER7 (1.24 µm) are 3.5 µm and 16.6 µm greater than those from the standard retrieval for liquid and ice clouds (Table 6), respectively. The corresponding differences for CER2 are 5.4 µm and 6.7 µm. These differences are substantial and require further analysis.
3.5.3. Multilayer Cloud Fraction and Layer Properties
The multilayer (ML) identification algorithm for ice clouds over water clouds is applied to every cloudy VIIRS pixel and returns a flag indicating the pixel is multilayer cloud, convective or thick cloud, single-layer (SL) cloud, or clear. Detection and retrieval of the ML cloud parameters relies on the BTM for CV1S and is, therefore, likely to yield different results than the MCAT used for CM4. On average, the CV1S ML cloud fractions are roughly one-third of those from CM4A data during daytime and less than half their CM4A counterparts at night (Figure S1, Table S1). The upper layer clouds from CV1S are 1.3 km and 2.0 km higher than the Aqua results during the day and night, respectively (Figure S2, Table S2). Conversely, the mean lower-layer cloud heights from VIIRS are ~0.6 km less than the CM4A means. The multilayer infrared optical depth, cloud effective water droplet size, and the effective ice crystal radius are also retrieved for both the lower and upper layers, respectively. The multilayer products are considered experimental in both CM4 and CV1S, and are not expected to detect all multilayer clouds, or to be without false detections. Rather, these products serve as an initial database for exploring the quality of the results, for initial studies of the impact of multilayer clouds on the radiation budget, and for the development of more refined methods for multilayer cloud diagnosis and retrieval. Since this is a rarely used product, to date, details of the results and a brief discussion of the differences in two of the products can be found in the Supplemental Material.
4. Discussion
Comparisons of the CV1S results with those from CM4A are valuable for validating the CV1S data because of the desired consistency, and because a considerable amount of validation has been performed for the CERES MODIS cloud products as reported in [16,17,40]. Nevertheless, additional comparisons lend more confidence to the quality of the CERES VIIRS cloud properties. Some of these are described below along with a discussion of the sources of some inconsistencies among the various parameters. More in-depth evaluations of the selected cloud properties can be found in [18].
4.1. Calibration
Calibration variations and errors are often a source of uncertainty in imager-based cloud retrievals. The changes in the VIIRS calibrations in the CSV1 dataset were noted in Section 2.1.1 and their impacts on the cloud retrievals were discussed in Section 3. Differences in calibration between the VIIRS channels and their Aqua MODIS counterparts could also affect the consistency between the retrieved cloud parameters. Long after NPP VIIRS Ed1 processing began, scaling factors were developed using nearly simultaneous nadir overpass data from NPP VIIRS and Ed1 following the methods of [20]. The results, found on the SatCORPS Calibration Page, reveal that to match the Aqua C5 reflectances, the VIIRS values must be reduced by 0.3% and 3.2% for the 0.65-µm and 1.24-µm channels, respectively. For the Aqua C6.1 reflectances used after 2015, the same VIIRS channel reflectances need to be decreased by 1.2% and 3.2%, respectively. Solar channels used only for the mask agreed to within 3–4% for the C5 data and within 1% for the C6.1 data.
The VIIRS 3.79-µm channel tends be colder than its Aqua C5 counterpart by an average of 3.3 K at 220 K and 0.5 K at 290 K during the night. This improves for the Aqua C6.1 data with VIIRS being warmer by 1.0 K at 220 K and 0.3 K colder at 290 K. For both datasets, the VIIRS brightness temperature is essentially constant at ~212 K for all Aqua temperatures less than ~212 K, similar to that seen for Terra C5 data [41]. For the C6.1 data, VIIRS is warmer by 1.1 K and 0.3 K at 220 K and 290 K, respectively, at 11.0 µm and is greater than Aqua by 0.4 K and 0.0 K at 12.0 µm. The absolute differences are similar or smaller for the C5 data. The absolute differences for the 8.59-µm channel are all less than 0.3 K.
4.2. Cloud Fraction and Phase
From the above comparisons, it is clear that the CV1S cloud amounts are mostly consistent with their Aqua counterparts, but are slightly smaller during the daytime and more so at night. The differences vary regionally and with surface type (e.g., Figure 2). An examination of the impact of employing Equation (2) in CV1S to reduce over-detection of thin cirrus clouds revealed that the nocturnal VIIRS-MODIS differences over the tropical oceans are mainly due to that added test. The large negative biases over tropical oceans seen in Figure 2d were not obvious in the preprocessing testing due to the use of the original averaging method. Changing to the approach employed here revealed the bias resulting from the application of Equation (2). It is clear that other, more cirrus-specific tests should replace that test in future Editions. Further alterations of the CERES cloud mask and auxiliary data (e.g., surface emissivity) would need to be made to ameliorate other regional discrepancies, to more closely align the VIIRS and MODIS results. The calibration differences also likely contribute to the cloud mask differences, probably more so at night when the 3.79 µm channel plays a large role in the mask. A more detailed analysis of the clouds that are missed is provided in [18].
During the daytime, the CERES nonpolar VIIRS-MODIS differences are roughly twice the magnitude of their MODIS VIIRS Cloud Mask (MVCM) counterparts [42]. At night, the MVCM nonpolar cloud fractions differ by −0.009, roughly one-third that of the CV1S-CM4A differences. This discrepancy in the two approaches is likely due to the MVCM having been designed specifically to achieve intersatellite consistency, while the CV1S is simply an adaptation of the CM4 cloud mask to account for some of the channel differences, and also to reduce known cloud detection uncertainties found in the CM4A validation studies. Again, developing optimal thresholds for each of the common channels is needed, and the test represented by Equation (2) should be eliminated. Additional discussion and comparisons to other datasets are provided by [18].
The mean nonpolar retrievals of ice and liquid cloud phase amounts from CV1S are close to those from CM4A, but with less water and ice cloud coverage, primarily due to the clouds missed in the CV1S mask. The breakdown of the cloud phase is similar to that determined from VIIRS by the NASA MODIS and SNPP VIIRS climate data record continuity cloud properties (CLDPROP) algorithms [43]. The mean daytime 2012–2020 nonpolar CLDPROP ice and liquid phase cloud amounts from VIIRS are ~0.22 and ~0.41, values that are as close to the corresponding amounts from CV1S as they are to the MODIS CLDPROP averages. The daytime CV1S global total cloud fraction and relative amounts of liquid and ice clouds are near the center of the range in those same parameters from various satellite cloud retrievals [44].
4.3. Cloud Heights
The CV1S-CM4A liquid water cloud effective height differences in Table 4 are likely due to several factors, including pixel resolution, slight discrepancies in phase selection, differences in the clouds that were detected, and possibly, calibration. An increasing pixel size tends to yield lower cloud heights [37]. This may be due to a smaller ratio of partly cloudy pixels to overcast pixels at higher resolutions, with detection of more of the coldest cloud-tops. This appears to be borne out in the change of CEH with VZA (not shown). For CSV1, the 2013 mean daytime CEHw and CEHi rise by 0.07 km and 0.39 km, respectively, from near to the nadir to the highest angle views. The corresponding increases for CM4A are 0.15 km and 0.56 km. The smaller pixels appear to yield higher cloud-tops. Clouds that are missed by the scene identification tend to be those presenting the lowest contrast with the surface as viewed by the satellite. Thus, small optical depth clouds and those lowest in the atmosphere, particularly at night, will most likely be classified as clear. Since CM4A has fewer nocturnal water clouds classified as clear relative to CV1S [18], the average CV1S water cloud heights should be greater than their MODIS counterparts. This tendency is exacerbated at night with the application of Equation (2).
The average CEHi(V)–CEHi(M) differences are positive during the day and negative at night. Missed percentages of ice clouds are similar for CM4A and CV1S for both day and night [18,40], so factors other than resolution and detection differences are probably responsible. The lack of the CO2 channel on VIIRS could account for the lower CEHi(V) at night. During the day, the BTM likely worked better to produce greater ice cloud altitudes because the heights from the VISST were available to remove all of the low ones computed with the BTM. Both the CM4 MCAT and CV1S BTM benefitted from the independent information from the VIS channel during the day. At night, the MCAT provides additional information that can be compared with the SIST results, but the SIST and BTM both employed BTD45, so there is actually no truly independent data available to change the SIST heights. Thus, it is possible that the MCAT detects higher clouds in enough pixels to yield higher mean effective heights for ice clouds at night.
4.4. Cloud Optical Depth, Effective Hydrometeor Size, and Water Path
The standard COD, CER, and CWP products from CM4 and CERES MODIS Edition 2 have all been evaluated against various surface and airborne observations as discussed by [16] and [45], respectively. It is expected that those evaluations are applicable to the CV1S data, when the CV1S-CM4A differences are taken into account. For example, since CERw(V) < CERw(M), the biases in CERw(M), found in some comparisons of CM4 retrievals with other data (e.g., [16,45,46,47,48,49]), will be reduced slightly because of the smaller values retrieved from VIIRS.
The mean CV1S-CM4A difference in COD for both liquid and ice clouds is due to several factors. These include calibration disparities, slightly smaller VIIRS cloud fractions, discrepancies in the cloud phase selections, and the higher-resolution VIIRS pixels. Changes in the VIIRS data source and calibrations after 2015 produced a ~0.8 rise in nonpolar mean cloud τ for an average VIS-channel gain rise of 1.5%. The pre-2015 CV1S-CM4A VIS gain difference is ~0.3% compared to a mean COD difference of ~1.1 for all nonpolar clouds. After 2015, the gain difference of ~1.4% is accompanied by a mean nonpolar COD difference of ~1.5. This suggests that approximately one-third of the optical depth difference is due to unnormalized VIIRS calibrations. The gradual decrease in COD from CV1S after 2018 in Figure 11 results from a slowly decreasing VIIRS VIS gain relative to that of CM4A. Much greater differences in COD are found for water clouds over polar regions. They are likely to depend more on the larger calibration discrepancies found in the VIIRS and MODIS 1.24-µm channels. This would give rise to larger COD differences that would increase further because the mean COD is already large compared to that over nonpolar areas and the surface albedo is quite large. Both of those factors enhance the change in COD for a given change in reflectance (e.g., [50]).
The higher spatial resolution of the VIIRS channels likely produces greater CODs than for MODIS because average COD decreases with rising pixel size. This is primarily true for liquid clouds, due to the heterogeneity of the internal structure and the non-linear relationship between τ and the reflectance. For example, [37] found that the mean CODw dropped from 20.2 for 1-km pixels to 18.9 and 17.6 for 2-km and 4-km MODIS pixels, respectively, while CODi showed negligible changes with decreasing resolution. Thus, a significant fraction of the mean CODw bias could be due to the resolution differences. This effect is evident in Figure 13a, which shows the CV1S and CM4A liquid water curves diverging for VZA > 35°. The smaller cloud fractions for liquid water clouds could lead to a higher mean COD if the missing cloudy pixels all had very low optical depths. Finally, discrepancies between the CV1S and CM4A phase selections might depend on COD and, therefore, could result in systematic differences in the average COD. This last possibility is probably only a small component of the overall COD differences between the two datasets.
Although [47] found good agreement between surface and CM4A retrievals of CODw over Barrow, Alaska, the optical depths over most snow-covered areas in the polar regions from CM4A are probably too high, especially for thin clouds [17]. This is due mainly to the uncertainty in the 1.24-µm clear-sky reflectance over snow, which is relatively high and quite variable. Thus, it is reasonable to conclude that the CV1S COD values, especially those for liquid clouds, are overestimated over snow/ice surfaces. Obtaining more realistic values over the full range of COD could be obtained by applying a hybrid retrieval using reflectances measured at longer wavelengths for smaller optical depths and the 1.24-µm reflectances for optically thicker clouds.
In addition to being relatively consistent with the nonpolar CM4A retrievals of COD, on average, the microphysical properties are similar to those from other observations. For example, the CV1S nonpolar mean CODw is ~1.5 less than its CLDPROP counterpart of ~13.3, but CV1S CODi is approximately 1.5 greater than the CODi of 12.2 from CLDPROP. These differences could arise for a variety of reasons, including calibration, use of overcast pixels (non-edge pixels) only in the CLDPROP averaging, discrepancies in the ice cloud model optical properties, and possible differences in the phase selections for particular clouds.
The differences between the VIIRS and Aqua retrievals of CER are likely due to a variety of factors. For liquid clouds, the main discrepancy is the use of the new LUTs for VIIRS, which yield smaller values of CERw compared to those from the old LUTs. Another major source for the discrepancies is the inadvertent use of the smaller Aqua SIR solar constant for VIIRS. It produces a greater reflectance and, hence, yields a lower value of retrieved CERw. Using the correct VIIRS SIR solar constant accounts for about a third of the difference. The remaining difference is likely due to the LUT changes. For ice clouds, the small VIIRS-MODIS disagreement probably results from differences in ice cloud selection.
The VIIRS CLDPROP 9-y average nonpolar estimates of CER from the VIIRS 3.74-µm channel are ~14.2 µm and ~23.0 µm for liquid and ice water, respectively. These means can be compared to the corresponding CV1S averages from Table 6: 12.9 µm and 26.3 µm. The differences may be due to discrepancies in sampling, as only 70% of the pixels identified as liquid water by the CLDPROP algorithms had CERw retrievals at 3.74 µm. For CER2, the CLDPROP means are ~14.5 µm and ~30.3 µm for liquid and ice, respectively, compared to 17.1 µm and 33.8 µm from CV1S. The larger CERES values may be due to differences in the indices of the refraction used by the two algorithms, to different sampling, and errors in the retrievals, as discussed in the next section. In addition, for ice particularly, there are differences in the optical properties of the assumed ice crystal models used for the CV1S and CLDPROP LUTs. The CLDPROP results do not include CER7.
Although the calibration of the 1.24-µm channel did not vary when the VIIRS data source changed in 2015, CER7 and CER2 both increased after 2015 (Figure 16). This change is most likely due to the jump in COD at the same time.
4.5. Hydrometeor Size Estimates from Alternate Wavelengths
Discrepancies in the patterns and, perhaps, the magnitudes of the three distinct VIIRS CER averages in Figure 12 and Figure 15 may be due, in part, to differences among the cloudy pixels that yielded a CER solution at a given wavelength. For example, over ocean, the mean CER7w is based on 64% of the pixels having a CERw retrieval. For ice clouds, that fraction reduces to 53%. Likewise, at 1.61 µm, those amounts are 59% and 77%, respectively. Thus, some of the differences in magnitude and pattern could be due to the alternative retrievals being successful for only a certain portion of the total sample.
To explore that idea further, histograms of CER were generated from retrievals in all three channels for intervals of increasing COD. Examples of those histograms are provided in Figure S3 for liquid clouds, respectively, over COD ranges of 1–2 and 16–32. For liquid water clouds, it was found that for all optical depths, CERw has an almost log-normal distribution for both land and water scenes, whereas CER7w and CER2w are nearly linearly distributed with maxima near the high end over ocean and near the low end for land surfaces. As COD increases, the maximum CER7w and CER2w gradually decrease, while the probability distributions slowly approach the log-normal shape and the fraction of alternative retrievals relative to the 3.74-µm retrievals increases. For COD between four and eight and above, the histograms are essentially log-normal. Therefore, the data were plotted and averaged for COD < 6 and for COD ≥ 6.
The resulting histograms in Figure 17 are similar to those in Figure S3. At 1.24 µm, the CERw distribution for COD < 6 is relatively flat over water surfaces with a weak peak around 17 µm (Figure 17a). For the greater COD range (Figure 17b), the maximum is near 11 µm and the distribution is nearly log-normal. The CER2w histogram is less flat for the small COD interval with a weak maximum of ~13 µm (Figure 17c). This contrasts with the nearly log-normal histogram for the upper COD range (Figure 17d). The probability distributions for CERw are nearly log-normal for the upper (Figure 17f) and lower (Figure 17e) ranges. For COD < 6, the respective liquid CER means for the 1.24, 1.60, and 3.74-µm channels are 18.8, 17.7, and 12.9 µm, compared to 13.8, 14.4, and 12.9 µm for the upper range. The fractions of the CERw retrievals represented by those numbers are, respectively, 41 and 36.4% for CER7w and CER2w for the lower COD interval, and 90 and 85% for the higher optical depths.

Figure 17.
Probability distributions of CV1S liquid water droplet effective radii from (a,b) 1.24 µm, (c,d) 1.60 µm, and (e,f) 3.74 µm for optical depth, τ, ranges; left: 0–6 and right: 6–150, April 2013.
Similar results are found for ice clouds, although more reasonable values of CER2i are found for lower optical depths than for those retrieved at 1.24 µm. Histograms of CER for the same range of COD as in Figure S3, but for ice clouds, are presented in Figure S4. At low optical depths, CERi has a mostly log-normal distribution except for a significant bump around 10 µm, which is due to using a default value of CERi in order to retrieve COD. As COD increases, the relative magnitude of the default maximum steadily decreases as the 3-channel retrievals become more successful. The probability distributions for CER7i behave much like those for liquid water, but have more pronounced maxima in the lowest COD ranges. At 1.60 µm, however, a more normal or log-normal type of distribution is found for some lower COD intervals. Excepting the default maximum in 3.74-µm probability distributions, the histograms for 1.24 µm and 1.61-µm CERi retrievals become increasingly like their 3.74-µm counterparts as COD increases, although some significant differences remain for 1.24 µm.
This is borne out in Figure 18, which shows that the histograms of ice CERi for COD ≤ 6 and COD > 6 are somewhat different from those for water clouds, even after omitting the default peak for CERi seen in Figure 18e. Without that peak, the frequency distribution of CERi in Figure 18e would be similar to its CER2i counterpart (Figure 18c) in the low COD range. This similarity does not extend to CER7i in Figure 18a. For the larger COD interval, both the 3.78-µm (Figure 18f) and 1.61-µm histograms (Figure 18d) tighten up. The mode for the latter is less than that for the former. The CER7i frequency distribution (Figure 18b) takes on a more log-normal form, but has a longer tail than that seen for the other wavelengths. The CER7i means are 47.5 and 36.7 µm, respectively, for the lower and higher COD range, compared to 22.5 and 32.8 µm at 3.75 µm. The corresponding CER2i averages are 34.8 and 29.3 µm. Relative to the number of 3.74-µm retrievals (including the default values), the fraction retrieved at 1.60 µm rises from 61% for COD < 6 to 97% at the upper COD end, compared to a rise from 41 to 89% for CER7i.
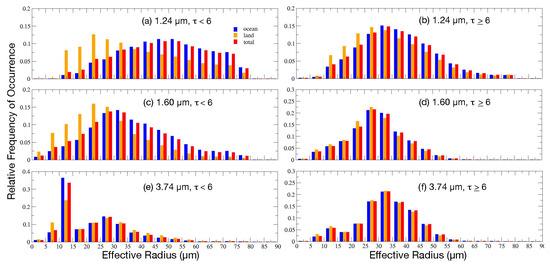
Figure 18.
Same as Figure 17, except for the ice clouds.
These results suggest that the NIR retrievals at low optical depths are subject to significant uncertainties, a result found by [51] for stratiform water clouds. These uncertainties include errors in surface and aerosol reflectances, which are less important as the cloud becomes opaque. The behavior of the reflectances at these wavelengths is also critical.
Reflectances ρ7 at 1.24 µm (top) and ρ2 at 1.60 µm (bottom) taken from the CSV1 water droplet LUTs are plotted against the VIS reflectance in Figure 19 over a range of ρ7 and CERw values at SZA = 45.6° and VZA = 31.8°. The plots in each row are for different relative azimuth angles (RAZ) that increase from left to right. A relative azimuth angle of 0° is in the forward scatter direction, while 180° is in the backscatter direction. For a given value of COD, the reflectances ρ decrease at both wavelengths in a mostly monotonic fashion with CERw except at very low values of CERw. In Figure 19a–c, the ρ7 curve for CER = 2 µm falls below those for larger radii over most of the COD range. Its drop increases as RAZ rises. Coincidentally, the separation of the curves for CER = 4–8 µm also decreases with the rising RAZ, increasing the uncertainty in the retrievals for smaller radii. The separation between the curves for ρ7 for all values of CERw is smaller than that for ρ2 (Figure 19d–f), indicating that CER2w should be less uncertain than CER7w for a given retrieval. However, for both wavelengths, the curve separation is minimal for COD ≤ 4, indicating that the retrievals at those optical depths will be highly uncertain, a conclusion borne out by the observations.
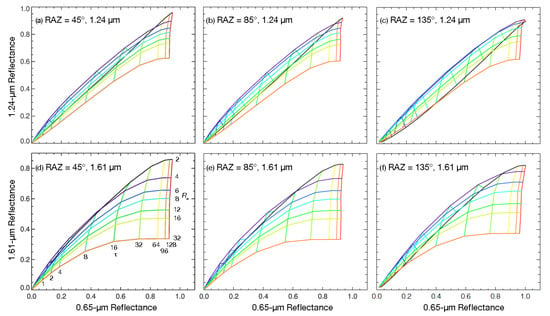
Figure 19.
Model liquid water cloud NIR reflectance versus VIS reflectance from CV1S LUTs at SZA = 45.6°, VZA = 31.8° for range of COD, and CERw, denoted as τ and Re, respectively. (a–c) 1.24-µm and (d–f) 1.61-µm reflectances for RAZ = 45° (left column), RAZ = 85° (center column), and RAZ = 135° (right column).
The behavior of the ice cloud curves (Figure 20) is quite similar, but the reduced separation is more extreme at 1.24 µm for COD < 8 (Figure 20a–c). This would introduce even greater uncertainty into the ice retrievals, which could help explain the small fraction of retrieved pixels and larger average values for those pixels that were retrieved. The iteration used to solve for CER and COD simultaneously begins with the largest value of CER in the LUT. If it finds a solution for a large CER, and the error in the reflectance calculated from the assumed optical depth does not decrease significantly for a smaller CER, then the iteration stops. When the reflectance curves are very close, or the dependence is not monotonic, the larger CER value is more likely to be selected. For larger optical depths, the spread in curves is even greater than that seen for the water droplet model, especially for channel 2 (Figure 20d–f). This greater range could explain why the CER2i results yield a more normal histogram (Figure 18c) than that for CER2w (Figure 17c).
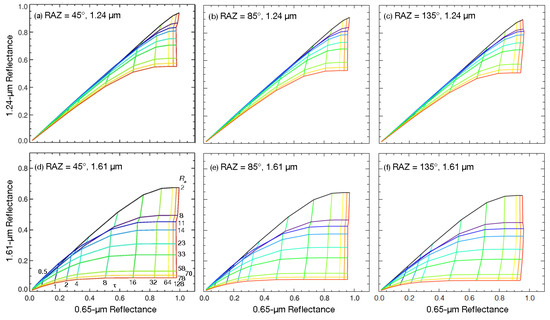
Figure 20.
Same as Figure 19, except for the ice clouds.
From these analyses, it is clear that the CER can be quite uncertain if the cloud is thin. A value of COD > 6 is recommended as a conservative threshold for yielding an accurate retrieval for these alternate wavelengths. The exact COD threshold value at either alternative wavelength depends on the phase, the angles, and likely, the surface characteristics. Retrievals at each wavelength correspond to a certain thickness at the top of the cloud. As the wavelength increases, the representative thickness decreases. Thus, CER at 3.78 µm may correspond to the top 3–8 optical depth at the cloud-top. Depending on CER and the viewing and illumination angles (e.g., [52]), CER2 can represent the true value for optical depths as great as 40 and 10–20 for liquid and ice clouds, respectively. The corresponding maxima for retrievals of CER7 can be up to 64–128 and ~100. Thus, CER7 probably provides little additional information about the effective radius, except when COD exceeds ~20, the optical depths for which the retrieval is most accurate. Likewise, CER2 does not provide much additional information about optically thin clouds, which are more suited for 3.74-µm retrievals. Thus, when carefully used, the three retrievals should be valuable for gaining an understanding about the cloud’s vertical structure for optically thick clouds.
5. Conclusions
The goal of CERES is to develop and use cloud and radiation datasets to monitor the Earth’s radiation budget and its interactions with clouds and aerosols. This climate data record requires results that are consistent across platforms and instruments. In many respects, the initial cloud properties derived from the analysis of the SNPP VIIRS radiances, referred to here as CSV1, are consistent with their CERES Ed4 Aqua MODIS, or CM4A, counterparts. The trends in the averages of a given parameter are generally the same, except for those parameters affected by calibration changes such as the switch from MODIS Collection 5 to Collection 6.1, which impacted some of the thermal infrared channels, or the change in the source for the VIIRS data that altered some of the solar channel calibrations. Other differences in mean values can be explained by changes in cloud reflectance models, resolution differences, and an unrepresentative solar constant value for the VIIRS 3.8-µm channel. Still other issues causing differences are the lack of certain channels on VIIRS that were used by MODIS for phase selection over polar regions. Data users should be cautious when employing the polar cloud optical depths from both VIIRS and MODIS, as they are likely overestimated in many cases, particularly for liquid water clouds. It is not clear how much the current inconsistencies between the two datasets affect the radiative fluxes derived from the application of the cloud properties to the process converting the CERES radiances to fluxes.
While many of the discrepancies are understood, further improvement of the consistency between the MODIS and VIIRS retrievals will require additional research and analysis that should lead to changes in the analysis algorithms and input data for the detection and retrieval systems for both instruments. Normalization of the calibrations is a crucial first step. Improvement of the VIIRS scene identification scheme to detect more clouds, especially at night, is also a key component of any revision. To improve the retrieval of cloud optical depth over snow and ice, a near-infrared channel other than 1.24 µm is recommended for clouds that are not optically thick. The 1.24-µm snow reflectances are highly variable and much greater than those at the 2.13 and 1.61-µm wavelengths and, thus, the retrievals are more susceptible to uncertainties in the clear-sky albedos. Better phase detection could be accomplished if multilayer clouds could be confidently detected. The liquid water phase is often determined for optically thin ice clouds over lower water clouds. The current multilayer methods employed experimentally in CERES have not yet been proven reliable. Retrievals of cloud effective hydrometeor sizes using near-infrared channels should be limited to optical depth ranges that yield singular solutions and have the sensitivity of hydrometeor size to non-negligible changes in reflectance. These suggested improvements, and others, should enhance the consistency and accuracy of future CERES cloud datasets. In the meantime, the CERES SNPP VIIRS Ed1a cloud properties should be quite useful for cloud and radiation analyses, particularly when the differences relative to the MODIS datasets are known and taken into account.
Validation of the CERES products is a continuing effort. The comparisons presented here comprise only a partial assessment of the results. More comprehensive and quantitative analyses using active sensor data as “cloud truth” are presented in Part II [18]. That study, and others, should lead to improvements in future editions of CERES cloud properties. Those future editions will extend the CERES SNPP record beyond June 2021.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs15030578/s1, Figure S1: Mean 2013 daytime multilayer cloud fraction from CERES SNPP VIIRS (left) and Aqua (right) retrievals for day (top) and night (bottom). Figure S2: Same as Figure S1, except for the daytime multilayer cloud-top height for the upper and lower layers. Figure S3: Probability distributions of CSV1 liquid water droplet effective radii from (a,b) 1.24 µm, (c,d) 1.60 µm, and (e,f) 3.74 µm for optical depth ranges; left: 1–2 and right: 16–32, April 2013. Figure S4: Same as Figure S3, except for the ice clouds. Table S1: Mean multilayer cloud fraction from Aqua Ed4 and SNPP Ed1a, 2013. Table S2: Mean multilayer cloud-top height (km) for the upper and lower layers from Aqua Ed4 and SNPP Ed1a, 2013.
Author Contributions
Conceptualization, P.M.; methodology, P.M., Q.Z.T., S.S.-M., G.H., F.-L.C. and P.Y.; software, S.S.-M., Q.Z.T., Y.C., G.H., P.W.H., R.A.S. and F.-L.C.; validation, P.M., C.R.Y. and S.S.-M.; formal analysis, P.M. and S.S.-M.; investigation, P.M. and S.S.-M.; resources, S.S.-M. and Y.C.; data curation, S.S.-M. and R.A.S.; writing—original draft preparation, P.M.; writing—review and editing, S.S.-M., W.L.S.J., Q.Z.T., C.R.Y. and G.H.; visualization, P.M., S.S.-M., G.H. and Y.C.; supervision, P.M. and W.L.S.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Aeronautics and Space Administration through the CERES Project.
Data Availability Statement
The CERES SSF data are available at the NASA LaRC Atmospheric Sciences Data Center (https://asdc.larc.nasa.gov/project/CERES, accessed on 11 December 2022).
Acknowledgments
This study was supported by the NASA CERES program. We thank Norman Loeb and Seiji Kato at NASA LaRC for their discussions during the development of the algorithms. Dave Doelling and his team provided the calibrations discussed here.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Wielicki, B.A.; Barkstrom, B.R.; Harrison, E.F.; Lee, R.B., III; Smith, G.L.; Cooper, J.E. Clouds and the Earth’s Radiant Energy System (CERES): An Earth Observing System Experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef]
- Priestley, K.J.; Smith, G.L.; Thomas, S.; Cooper, D.; Lee, R.B.; Walikainen, D.; Hess, P.; Szewcyk, P.; Wilson, R. Radiometric performance of the CERES Earth radiation budget climate record sensors on the EOS Aqua and Terra spacecraft through April 2007. J. Atmos. Ocean. Technol. 2011, 28, 3–21. [Google Scholar] [CrossRef]
- Barnes, W.L.; Pagano, T.S.; Salomonson, V.V. Prelaunch characteristics of the Moderate Resolution Imaging Spectroradiometer (MODIS) on EOS-AM1. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1088–1100. [Google Scholar] [CrossRef]
- Minnis, P.; Harrison, E.F. Diurnal variability of regional cloud and clear-sky radiative parameters derived from GOES data, Part II: November 1978 cloud distributions. J. Clim. Appl. Meteorol. 1984, 23, 1012–1031. [Google Scholar] [CrossRef]
- Minnis, P.; Harrison, E.F. Diurnal variability of regional cloud and clear-sky radiative parameters derived from GOES data, Part III: November 1978 radiative parameters. J. Clim. Appl. Meteorol. 1984, 23, 1032–1052. [Google Scholar] [CrossRef]
- Brooks, D.R.; Harrison, E.F.; Minnis, P.; Suttles, J.T.; Kandel, R.S. Development of algorithms for understanding the temporal and spatial variability of the Earth’s radiation balance. Rev. Geophys. 1986, 24, 422–438. [Google Scholar] [CrossRef]
- Minnis, P.; Nguyen, L.; Palikonda, R.; Heck, P.W.; Spangenberg, D.A.; Doelling, D.R.; Ayers, J.K.; Smith, W.L., Jr.; Khaiyer, M.M.; Trepte, Q.Z.; et al. Near-real time cloud retrievals from operational and research meteorological satellites. In Remote Sensing of Clouds and the Atmosphere XIII, Proceedings of the SPIE, Cardiff, UK, 15–18 September 2008; SPIE: London, UK, 2008; Volume 7107, pp. 19–26. [Google Scholar] [CrossRef]
- Doelling, D.R.; Loeb, N.G.; Keyes, D.F.; Nordeen, M.L.; Morstad, D.; Nguyen, C.; Wielicki, B.A.; Young, D.F.; Sun, M. Geostationary enhanced temporal interpolation for CERES flux products. J. Atmos. Ocean. Technol. 2013, 30, 1072–1090. [Google Scholar] [CrossRef]
- Young, D.F.; Minnis, P.; Gibson, G.G.; Doelling, D.R.; Wong, T. Temporal interpolation methods for the clouds and Earth’s Radiant Energy System (CERES) Experiment. J. Appl. Meteorol. 1998, 37, 572–590. [Google Scholar] [CrossRef]
- Doelling, D.R.; Sun, M.; Nguyen, L.T.; Nordeen, M.L.; Haney, C.O.; Keyes, D.F.; Mlynczak, P.E. Advances in geostationary-derived longwave fluxes for the CERES synoptic (SYN1deg) product. J. Atmos. Ocean. Technol. 2016, 33, 503–521. [Google Scholar] [CrossRef]
- Hillger, D.; Kopp, T.; Lee, T.; Lindsey, D.; Seaman, C.; Miller, S.; Solberg, J.; Kidder, S.; Bachmeier, S.; Jasmin, T.; et al. First-light imagery from Suomi NPP VIIRS. Bull. Am. Meteorol. Soc. 2013, 93, 1019–1029. [Google Scholar] [CrossRef]
- Szewczyk, P.; Walikainen, D.R.; Smith, N.; Thomas, S.; Priestley, K.J. Improving consistency of the ERB record measured by CERES scanners aboard Terra/Aqua/S-NPP satellites. In Remote Sensing of Clouds and the Atmosphere XXII; SPIE: London, UK, 2017; Volume 10424, p. 1042401. [Google Scholar] [CrossRef]
- Smith, N.; Thomas, S.; Shankar, M.; Priestley, K.; Loeb, N.; Walikainen, D. Assessment of on-orbit variations of the Clouds and the Earths Radiant Energy System (CERES) FM5 instrument. In Earth Observing Missions and Sensors: Development, Implementation, and Characterization V; SPIE: London, UK, 2018; Volume 1078119. [Google Scholar] [CrossRef]
- Su, W.; Liang, L.; Miller, W.F.; Sothcott, V.E. The effects of different footprint sizes and cloud algorithms on the top-of-atmosphere radiative flux calculation from the Clouds and the Earth’s Radiant Energy System (CERES) instrument on Suomi National Polar-orbiting Partnership (NPP). Atmos. Meas. Tech. 2017, 10, 4001–4011. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Barkstrom, B.R.; Baum, B.A.; Charlock, T.P.; Green, R.N.; Kratz, D.P.; Lee, R.B.; Minnis, P.; Smith, G.L.; Young, D.F.; et al. Clouds and the Earth’s Radiant Energy System (CERES): Algorithm overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1127–1141. [Google Scholar] [CrossRef]
- Minnis, P.; Sun-Mack, S.; Yost, C.R.; Chen, Y.; Smith, W.L., Jr.; Chang, F.-L.; Heck, P.W.; Arduini, R.F.; Trepte, Q.Z.; Ayers, K.; et al. CERES MODIS cloud product retrievals for Edition 4, Part I: Algorithm changes to CERES MODIS. IEEE Trans. Geosci. Remote Sens. 2021, 58, 2744–2780. [Google Scholar] [CrossRef]
- Trepte, Q.Z.; Minnis, P.; Sun-Mack, S.; Yost, C.R.; Chen, Y.; Jin, Z.; Chang, F.-L.; Smith, W.L., Jr.; Bedka, K.M.; Chee, T.L. Global cloud detection for CERES Edition 4 using Terra and Aqua MODIS data. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9410–9449. [Google Scholar] [CrossRef]
- Yost, C.R.; Minnis, P.; Sun-Mack, S.; Smith, W.L., Jr.; Trepte, Q.Z. VIIRS Edition 1 cloud properties for CERES. Part 2: Evaluation with CALIPSO. Remote Sens. 2022. submitted. Available online: https://satcorps.larc.nasa.gov/projects/PMinnis/ (accessed on 11 December 2022).
- Xiong, X.; Butler, J.; Chiang, K.; Efremova, B.; Fulbright, J.; Lei, N.; McIntire, J.; Oudrari, H.; Sun, J.; Wang, Z.; et al. VIIRS on-orbit calibration methodology and performance. J. Geophys. Res. Atmos. 2014, 119, 5065–5078. [Google Scholar] [CrossRef]
- Doelling, D.R.; Wu, A.; Xiong, X.; Scarino, B.R.; Bhatt, R.; Haney, C.O.; Morstad, D.; Gopalan, A. The radiometric stability and scaling of Collection 6 Terra- and Aqua-MODIS VIS, NIR, and SWIR spectral bands. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4520–4535. [Google Scholar] [CrossRef]
- Lee, T.E.; Miller, S.D.; Schueler, C.; Miller, S. NASA MODIS previews NPOEES VIIRS capabilities. Weather Forecast. 2006, 21, 649–655. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Todling, R.; Bacmeister, S.; Takacs, L.; Liu, H.-C.; Gu, W.; Sienkiewicz, M.; Koster, R.D.; Gelaro, R.; et al. The GEOS-5 Data Assimilation System—Documentation of Versions 5.0.1, 5.1.0, and 5.2.0; Technical Report Series on Global Modeling and Data Assimilation; NASA/TM-2008-104606; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2008; Volume 27, p. 118.
- Alishouse, J.C.; Snyder, S.A.; Vongsathorn, J.; Ferraro, R.R. Determination of oceanic total precipitable water from the SSM/I. IEEE Trans. Geosci. Remote Sens. 1990, 28, 811–816. [Google Scholar] [CrossRef]
- Minnis, P.; Sun-Mack, S.; Young, D.F.; Heck, P.W.; Garber, D.P.; Chen, Y.; Spangenberg, D.A.; Arduini, R.F.; Trepte, Q.Z.; Smith, W.L., Jr.; et al. CERES Edition-2 cloud property retrievals using TRMM VIRS and Terra and Aqua MODIS data, Part I: Algorithms. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4374–4400. [Google Scholar] [CrossRef]
- Chen, Y.; Minnis, P.; Sun-Mack, S.; Arduini, R.F.; Trepte, Q.Z. Clear-sky and surface narrowband albedo datasets derived from MODIS data. In Proceedings of the 13th Conference on Atmospheric Radiation, Portland, OR, USA, 27 June–2 July 2010; p. 9. Available online: https://ams.confex.com/ams/13CldPhy13AtRad/webprogram/Paper170890.html (accessed on 11 December 2022).
- Minnis, P.; Garber, D.P.; Young, D.F.; Arduini, R.F.; Takano, Y. Parameterization of reflectance and effective emittance for satellite remote sensing of cloud properties. J. Atmos. Sci. 1998, 55, 3313–3339. [Google Scholar] [CrossRef]
- Hale, G.M.; Querry, M.R. Optical constants of water in the 200-nm to 200-µm wavelength region. Appl. Opt. 1973, 12, 555–563. [Google Scholar] [CrossRef] [PubMed]
- Warren, S.G. Optical constants of ice from ultraviolet to the microwave. Appl. Opt. 1984, 23, 1206–1225. [Google Scholar] [CrossRef]
- Yang, P.; Kattawar, G.W.; Hong, G.; Minnis, P.; Hu, Y.X. Uncertainties associated with the surface texture of ice particles in satellite-based retrieval of cirrus clouds: Part II. Effect of particle surface roughness on retrieved cloud optical thickness and effective particle size. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1948–1957. [Google Scholar] [CrossRef]
- Chang, F.-L.; Minnis, P.; Lin, B.; Khaiyer, M.; Palikonda, R.; Spangenberg, D. A modified method for inferring cloud top height using GOES-12 imager 10.7- and 13.3-µm data. J. Geophys. Res. 2010, 115, D06208. [Google Scholar] [CrossRef]
- Chang, F.-L.; Minnis, P.; Ayers, J.K.; McGill, M.J.; Palikonda, R.; Spangenberg, D.A.; Smith, W.L., Jr.; Yost, C.R. Evaluation of satellite-based upper-troposphere cloud-top height retrievals in multilayer cloud conditions during TC4. J. Geophys. Res. 2010, 115, D00J05. [Google Scholar] [CrossRef]
- Chang, F.-L.; Minnis, P.; Sun-Mack, S.; Nyugen, L.; Chen, Y. On the satellite determination of multi-layered multi-phase cloud properties. In Proceedings of the 13th Conference on Atmospheric Radiation, Portland, OR, USA, 27 June–2 July 2010; p. 6. Available online: https://ams.confex.com/ams/pdfpapers/171180.pdf (accessed on 11 December 2022).
- CERES. CERES_SSF_Terra-Aqua_Edition4A Data Products Catalog. Available online: https://ceres.larc.nasa.gov/documents/DPC/DPC_current/pdfs/DPC_SSF-Ed4_R5V1.pdf (accessed on 17 June 2014).
- Minnis, P.; Yost, C.R.; Sun-Mack, S.; Chen, Y. Estimating the physical top altitude of optically thick ice clouds from thermal infrared satellite observations using CALIPSO data. Geophys. Res. Lett. 2008, 35, L12801. [Google Scholar] [CrossRef]
- Bennartz, R. Global assessment of marine boundary layer cloud droplet number concentration from satellite. J. Geophys. Res. 2007, 112, D02201. [Google Scholar] [CrossRef]
- Dong, X.; Minnis, P. Chapter 8: Stratus, stratocumulus, and remote sensing. In Fast Physics in Large Scale Atmospheric Models: Parameterization, Evaluation, and Observations; Liu, Y., Kollias, P., Donner, L., Eds.; AGU-Wiley Publ.: Hoboken, NJ, USA, 2022; in press. [Google Scholar]
- Minnis, P.; Bedka, K.; Trepte, Q.; Yost, C.R.; Bedka, S.T.; Scarino, B.; Khlopenkov, K.; Khaiyer, M.M. A Consistent Long-Term Cloud and Clear-Sky Radiation Property Dataset from the Advanced Very High Resolution Radiometer (AVHRR). Climate Algorithm Theoretical Basis Document (C-ATBD), CDRP-ATBD-0826 AVHRR Cloud Properties—NASA, NOAA CDR Program. 19 September 2016; 159p. Available online: https://www1.ncdc.noaa.gov/pub/data/sds/cdr/CDRs/AVHRR_Cloud_Properties_NASA/AlgorithmDescription_01B-30b.pdf (accessed on 11 December 2022).
- Painemal, D.; Minnis, P.; Sun-Mack, S. The impact of horizontal heterogeneities, cloud fraction, and cloud dynamics on warm cloud effective radii and liquid water path from CERES-like Aqua MODIS retrievals. Atmos. Chem. Phys. 2013, 13, 9997–10003. [Google Scholar] [CrossRef]
- Painemal, D.; Greenwald, T.; Cadeddu, M.; Minnis, P. First extended validation of satellite microwave liquid water path with ship-based observations of marine low clouds. Geophys. Res. Lett. 2016, 43, 6563–6570. [Google Scholar] [CrossRef]
- Yost, C.R.; Minnis, P.; Sun-Mack, S.; Chen, Y.; Smith, W.L., Jr. CERES MODIS cloud product retrievals for Edition 4, Part II: Comparisons to CloudSat and CALIPSO. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3695–3724. [Google Scholar] [CrossRef]
- Sun-Mack, S.; Minnis, P.; Chen, Y.; Doelling, D.R.; Scarino, B.; Haney, C.O.; Smith, W.L., Jr. Calibration changes to Terra MODIS Collection-5 radiances for CERES Edition 4 cloud retrievals. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6016–6032. [Google Scholar] [CrossRef] [PubMed]
- Frey, R.A.; Ackerman, S.A.; Holz, R.E.; Dutcher, S.; Griffith, Z. The Continuity MODIS-VIIRS Cloud Mask. Remote Sens. 2020, 12, 3334. [Google Scholar] [CrossRef]
- Platnick, S.; Meyer, K.; Wind, G.; Holz, R.E.; Amarasinghe, N.; Hubanks, P.A.; Marchant, B.; Dutcher, S.; Veglio, P. The NASA MODIS-VIIRS continuity cloud optical properties products. Remote Sens. 2021, 13, 2. [Google Scholar] [CrossRef]
- Stubenrauch, C.; Rossow, W.B.; Kinne, S.; Ackerman, S.; Cesana, G.; Chepfer, H.; Getzewich, B.; DiGirolamo, L.; Guignard, A.; Heidinger, A.; et al. Assessment of global cloud datasets from satellites: Project and database initiated by the GEWEX Radiation Panel. Bull. Am. Meteorol. Soc. 2013, 94, 1031–1049. [Google Scholar] [CrossRef]
- Minnis, P.; Sun-Mack, S.; Chen, Y.; Khaiyer, M.M.; Yi, Y.; Ayers, J.K.; Brown, R.R.; Dong, X.; Gibson, S.C.; Heck, P.W.; et al. CERES Edition-2 cloud property retrievals using TRMM VIRS and Terra and Aqua MODIS data, Part II: Examples of average results and comparisons with other data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4401–4430. [Google Scholar] [CrossRef]
- Xi, B.; Dong, X.; Minnis, P.; Sun-Mack, S. Comparison of marine boundary layer cloud properties from CERES-MODIS Edition 4 and DOE ARM AMF measurements at the Azores. J. Geophys. Res. 2014, 119, 9509–9529. [Google Scholar] [CrossRef]
- Dong, X.; Xi, B.; Qiu, S.; Minnis, P.; Sun-Mack, S.; Rose, F. A radiation closure study of Arctic stratus cloud microphysical properties using the collocated satellite-surface data and Fu-Liou radiative transfer model. J. Geophys. Res. 2016, 121, 10175–10198. [Google Scholar] [CrossRef]
- Painemal, D.; Spangenberg, D.; Smith, W.L., Jr.; Minnis, P.; Cairns, B.; Moore, R.H.; Crosbie, E.; Robinson, C.; Thornhill, K.L.; Winstead, E.L.; et al. Evaluation of satellite retrievals of liquid clouds from the GOES-13 imager and MODIS over the midlatitude North Atlantic during the NAAMES campaign. Atmos. Meas. Tech. 2021, 14, 6633–6646. [Google Scholar] [CrossRef]
- Zhang, Z.; Dong, X.; Xi, B.; Song, H.; Ma, P.-L.; Ghan, S.; Platnick, S.; Minnis, P. Intercomparisons of marine boundary layer cloud properties from two MODIS products, ground-based retrievals, and a GCM over the ARM Azores site. J. Geophys. Res. 2017, 122, 2351–2365. [Google Scholar] [CrossRef]
- Dong, X.; Minnis, P.; Xi, B.; Sun-Mack, S.; Chen, Y. Comparison of CERES-MODIS stratus cloud properties with ground-based measurements at the DOE ARM Southern Great Plains site. J. Geophys. Res. 2008, 113, D03204. [Google Scholar] [CrossRef]
- Zhang, Z.; Platnick, S. An assessment of differences between cloud effective particle radius for marine water clouds from three MODIS spectral bands. J. Geophys. Res. 2011, 116, D20215. [Google Scholar] [CrossRef]
- Chang, F.L.; Li, Z. Estimating the vertical variation of cloud droplet effective radius using multispectral near-infrared satellite measurements. J. Geophys. Res. 2002, 107, D15. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).