Mutual Interference Mitigation of Millimeter-Wave Radar Based on Variational Mode Decomposition and Signal Reconstruction
Abstract
1. Introduction
- According to the broadband frequency characteristics of the interference, the VMD method with quasi-orthogonal decomposition characteristics can effectively decompose the interference energy into different decomposed modes, thus reducing the energy of the interference in each mode and helping to improve SIR through the interference mitigation process in decomposed modes.
- With the narrowband characteristics of VMD, the linear frequency-modulated (LFM) like interference can be decomposed into sub-band components that have a limited time-support region. This is beneficial in interference detection and signal reconstruction.
- For multi-target scenes, targets in different ranges can be separated into different decomposed modes based on the nature of narrowband filter banks of VMD. As a result, the number of targets in each mode can be reduced and signal reconstruction can be realized by the linear prediction model with low complexity.
2. Related Work and Research Motivation
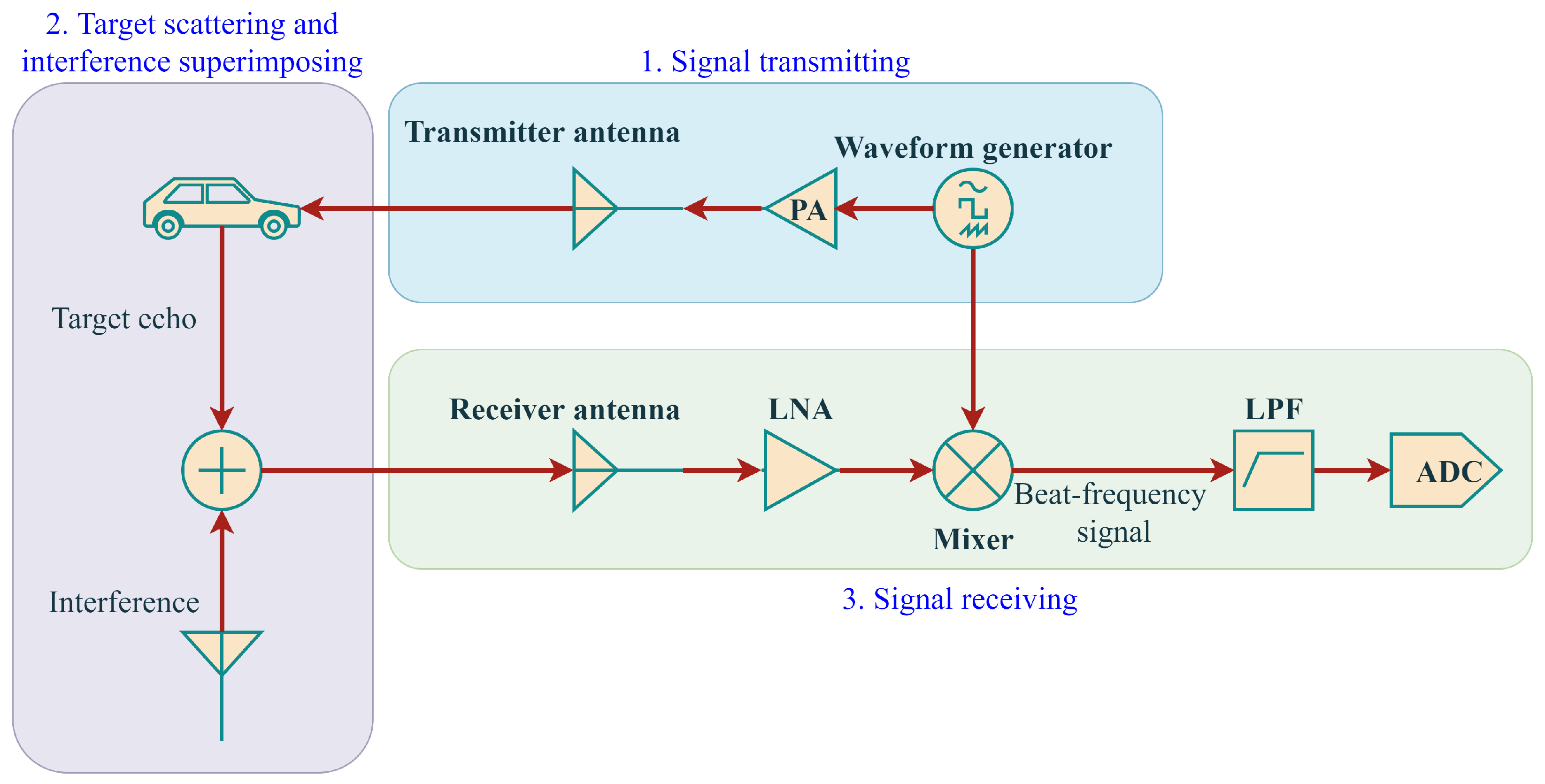
3. Signal Model with Mutual Interference
- The target echo is a single-frequency and small-power sinusoid.
- The interference is a broadband and large-power signal.
4. Interference Mitigation Method
4.1. Introduction to Variational Mode Decomposition
- Firstly, for each mode , compute the associated analytic signal by using the Hilbert transform.
- Secondly, for each mode , shift the mode’s frequency spectrum to baseband, by mixing with an exponential tuned to the respective estimated center frequency.
- Finally, the bandwidth is estimated through the squared -norm of the gradient.
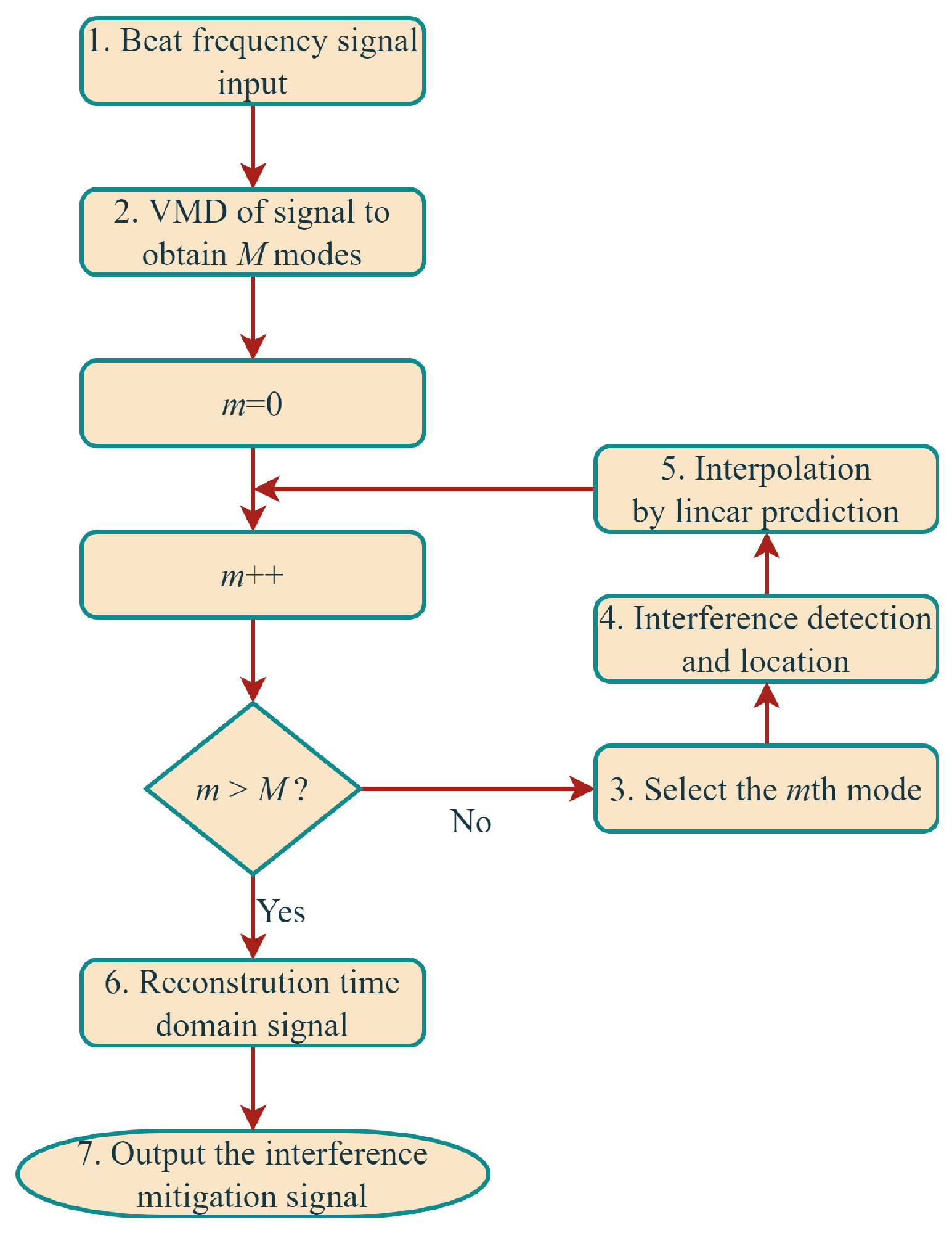
4.2. Interference Mitigation Realization
- Signal input step.The received signal with interference is dechirped in the radar receiver to obtain the beat frequency signal, and the beat frequency signal is the input of the interference mitigation algorithm.
- Signal decomposition step.VMD is used to obtain the narrowband modes of the beat frequency signal. There are total M modes.
- Mode selection step.Interference mitigation is performed on each decomposed mode. For one interference mitigation process, a decomposed mode needs to be selected.
- Interference detection and location step.For each mode, the interference is detected and located by means of a constant false alarm rate (CFAR) detector [40].
- Signal recovery step.Based on the results of interference location, the signal at the interference points is removed and replaced by interpolation values via an AR model as shown in (15) in each mode.
- Signal reconstruction step.Repeat steps 3 to 5 until all modes have been processed. Then, the beat frequency signal is reconstructed according to (14) to obtain an interference-free time domain signal.
- Signal output step.The interference-free signal is output and will be used as input for subsequent radar signal processing.
5. Numerical Simulation Results
5.1. Simulation Description
5.2. Performance Evaluation Methodology
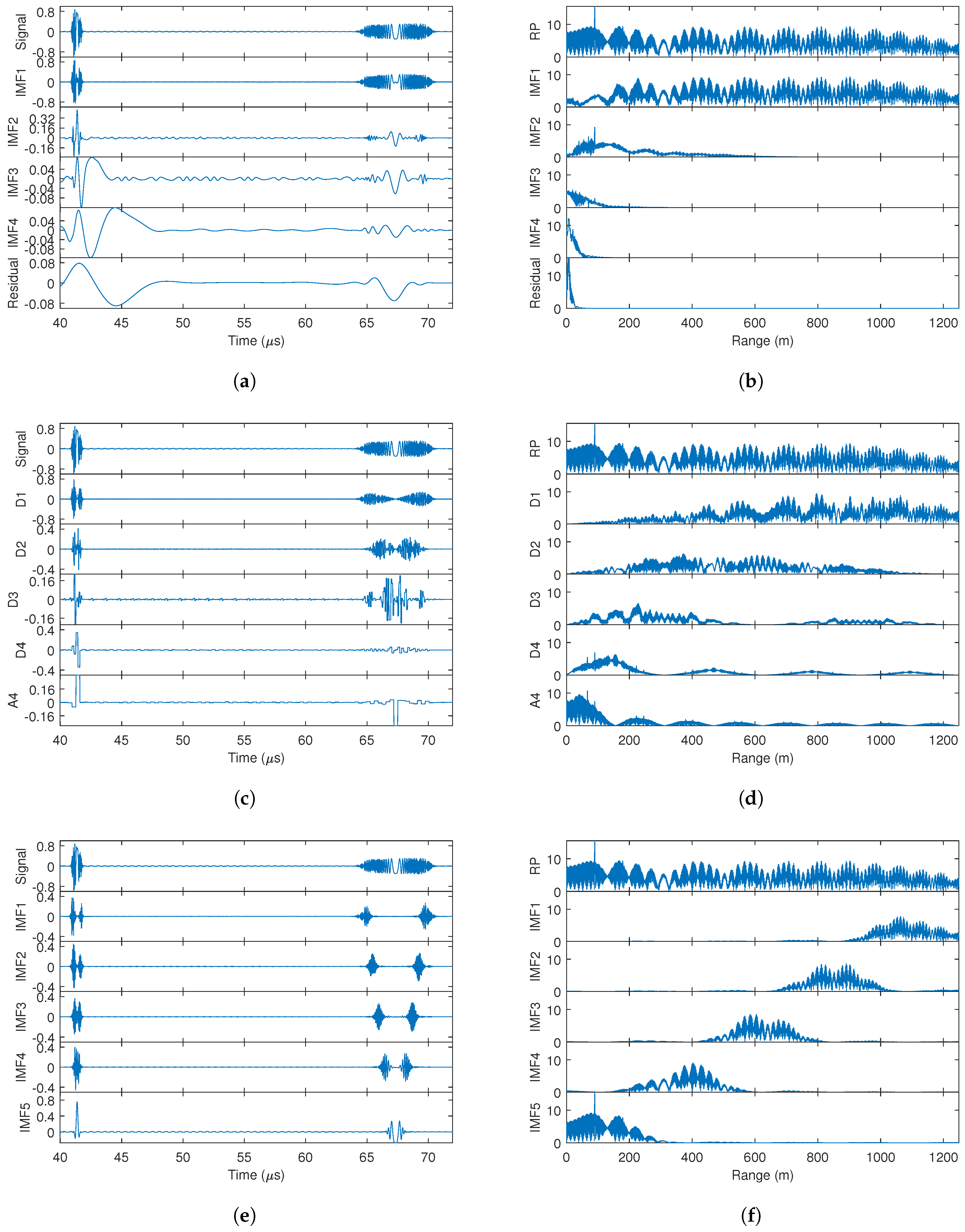
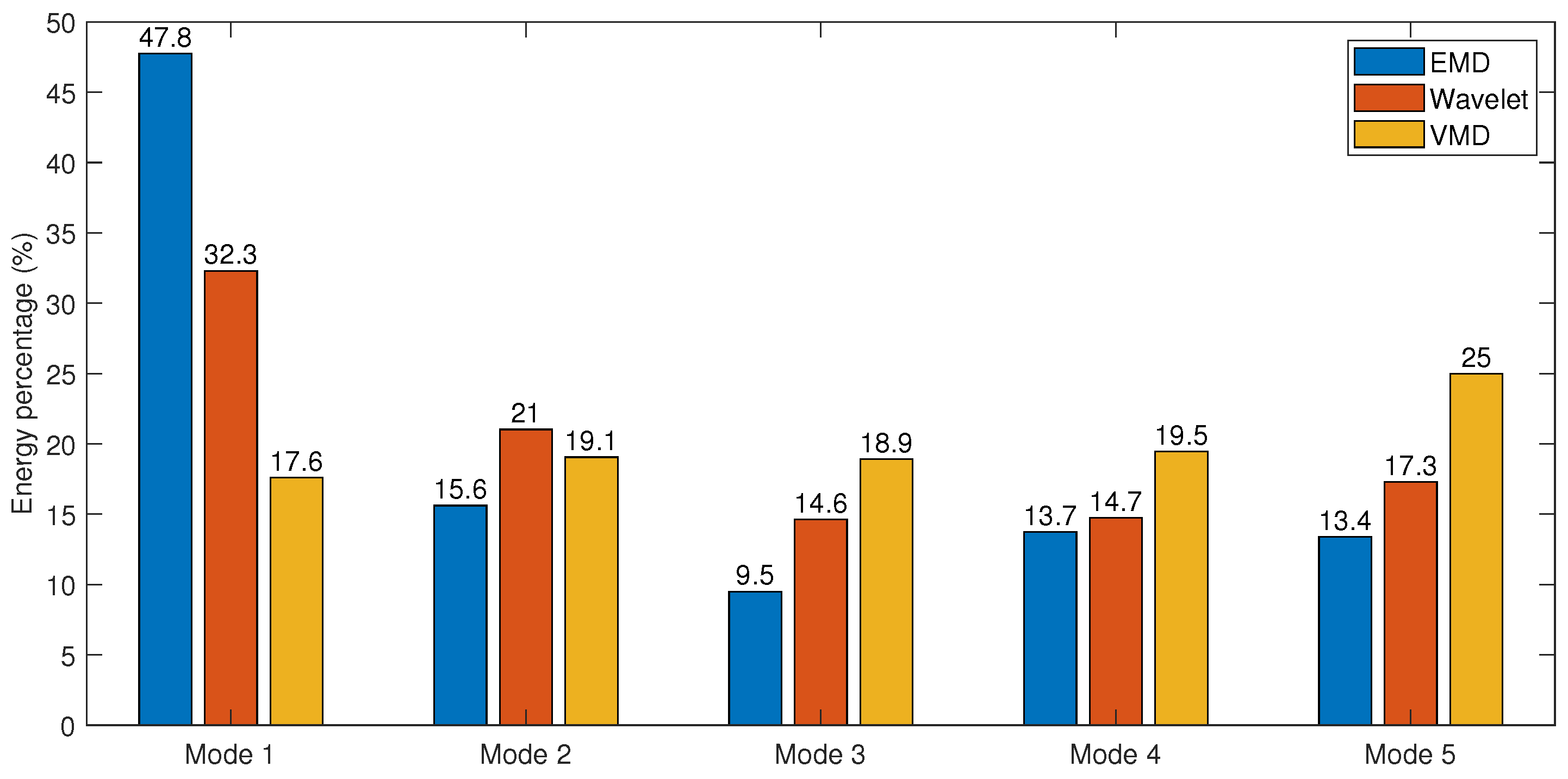
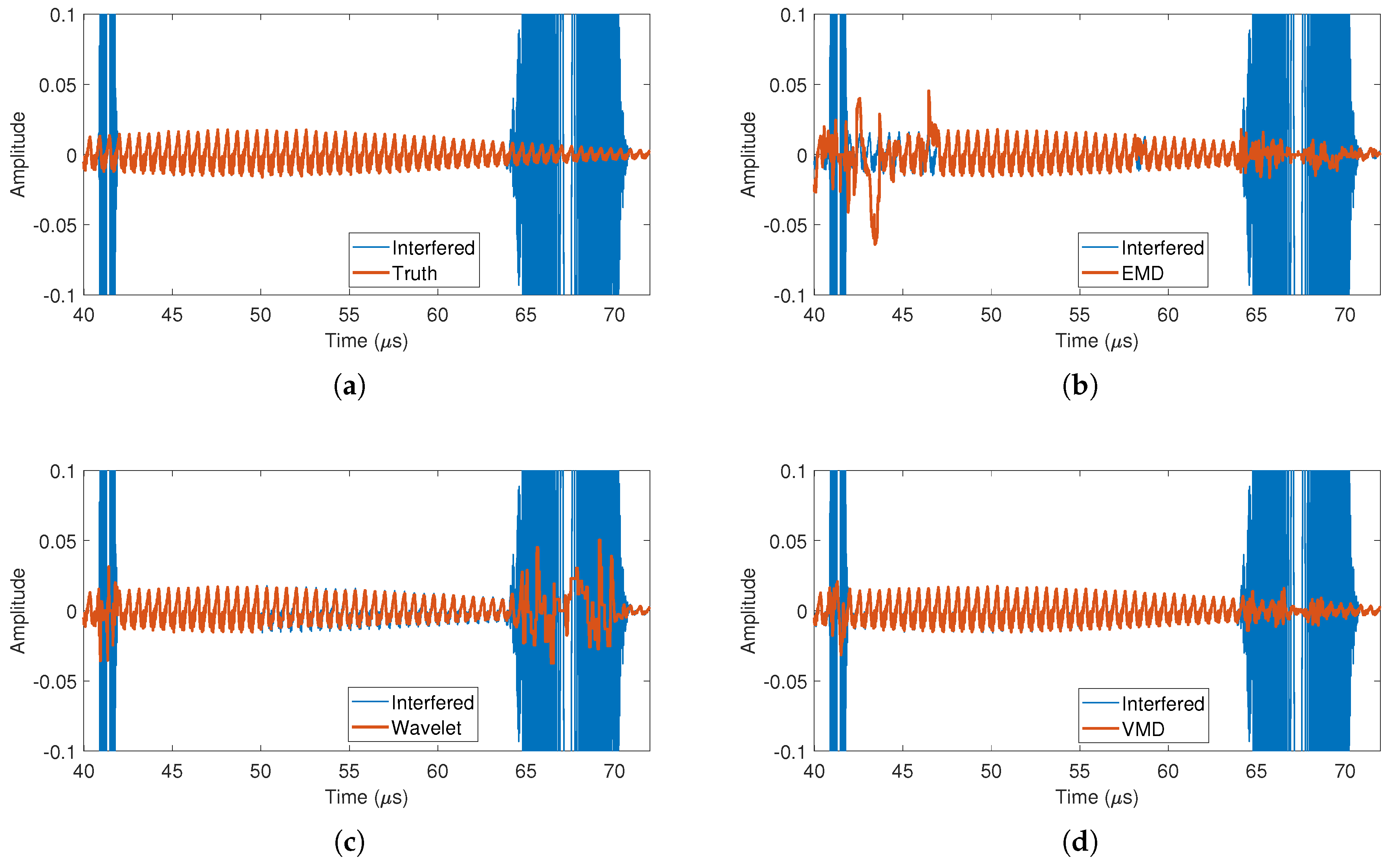
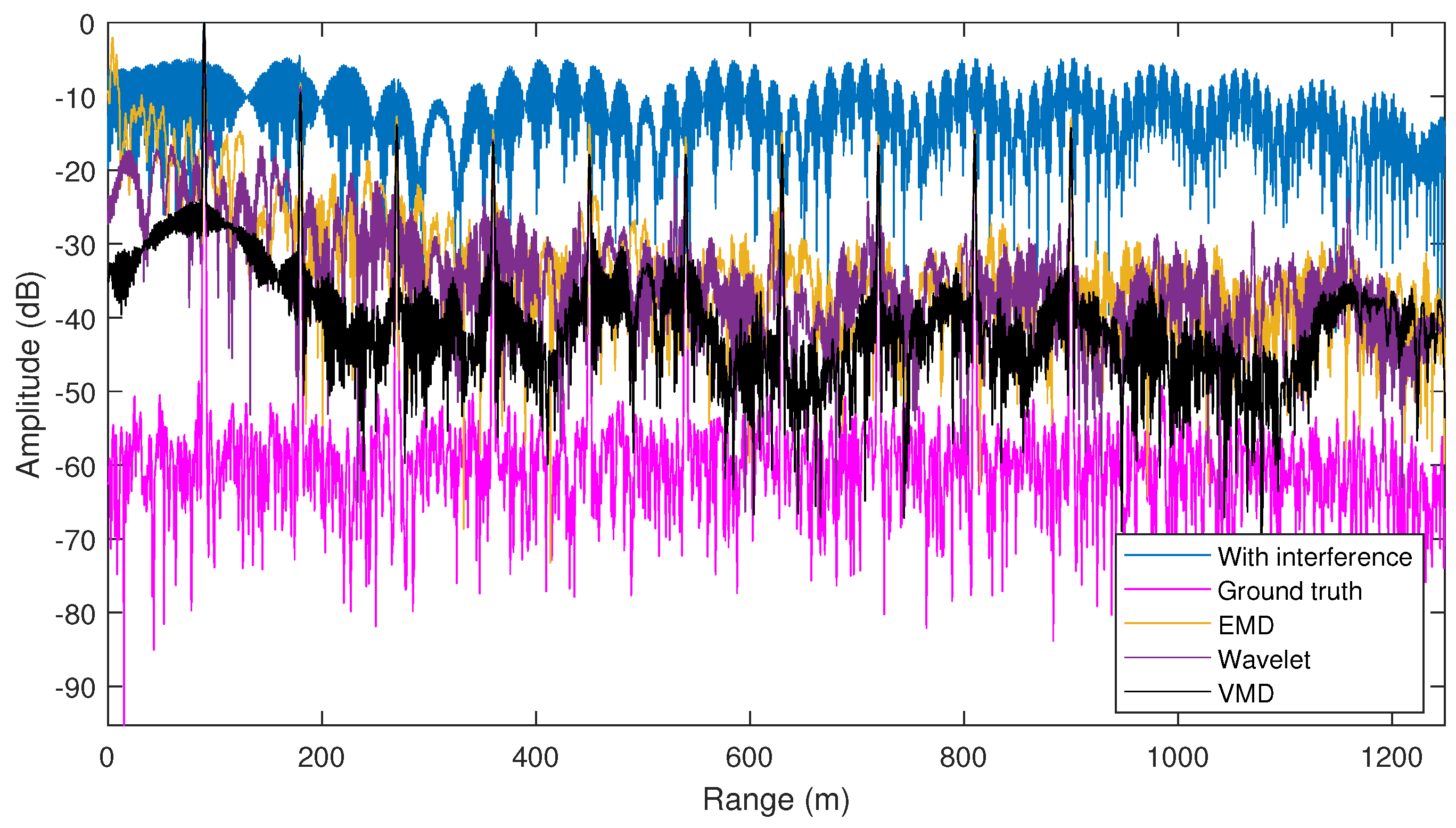
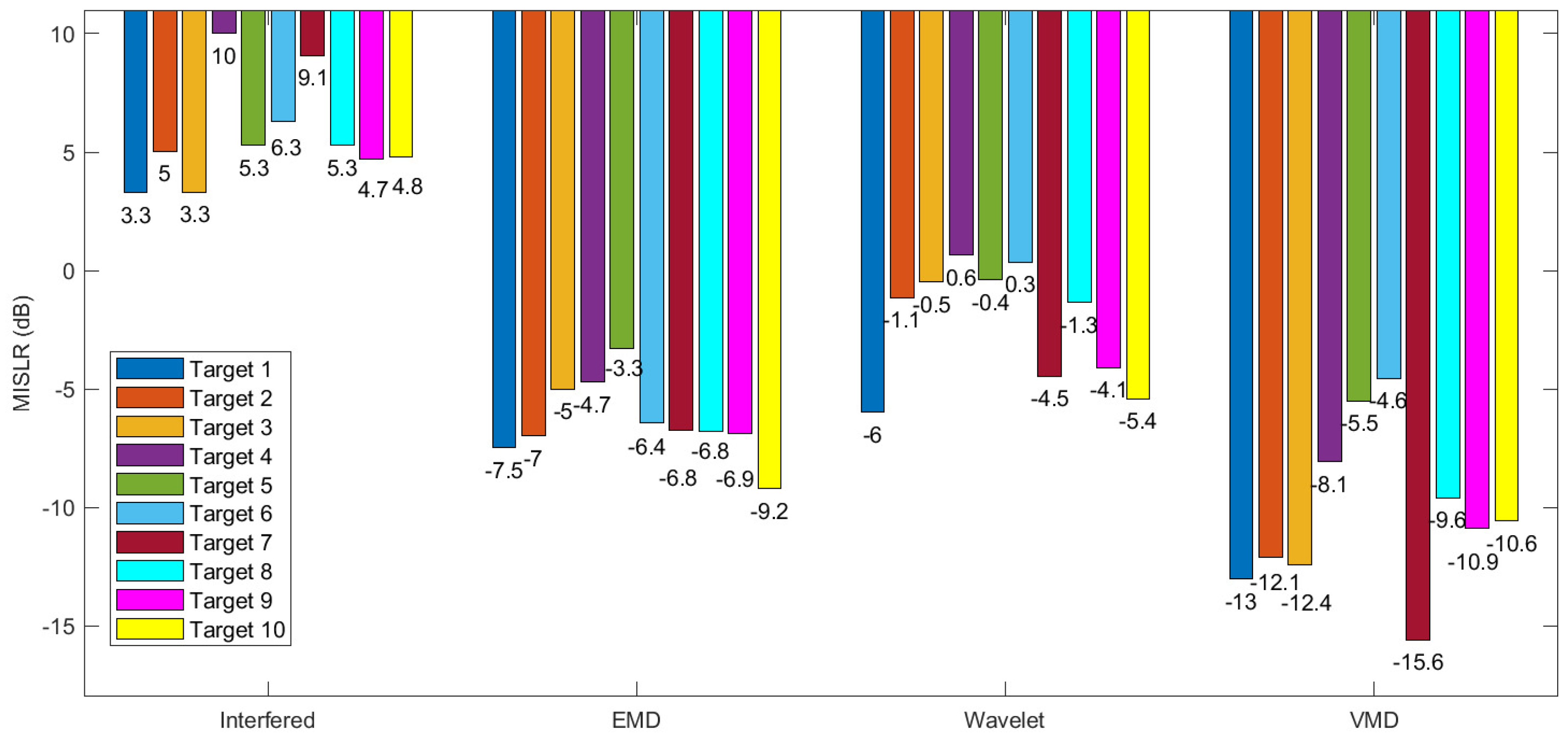
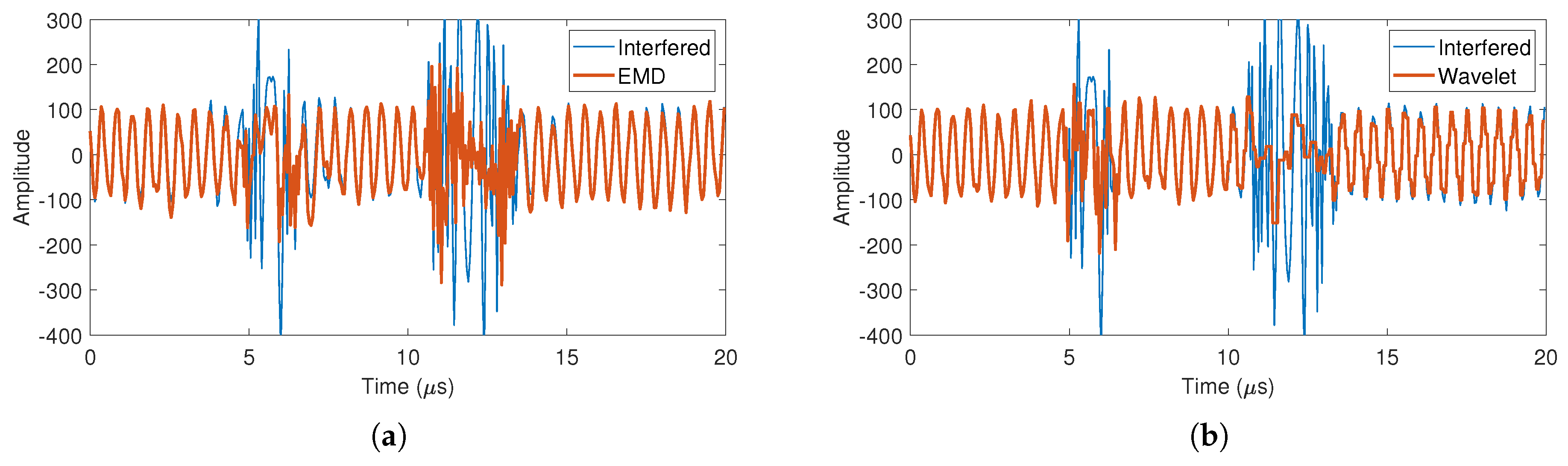
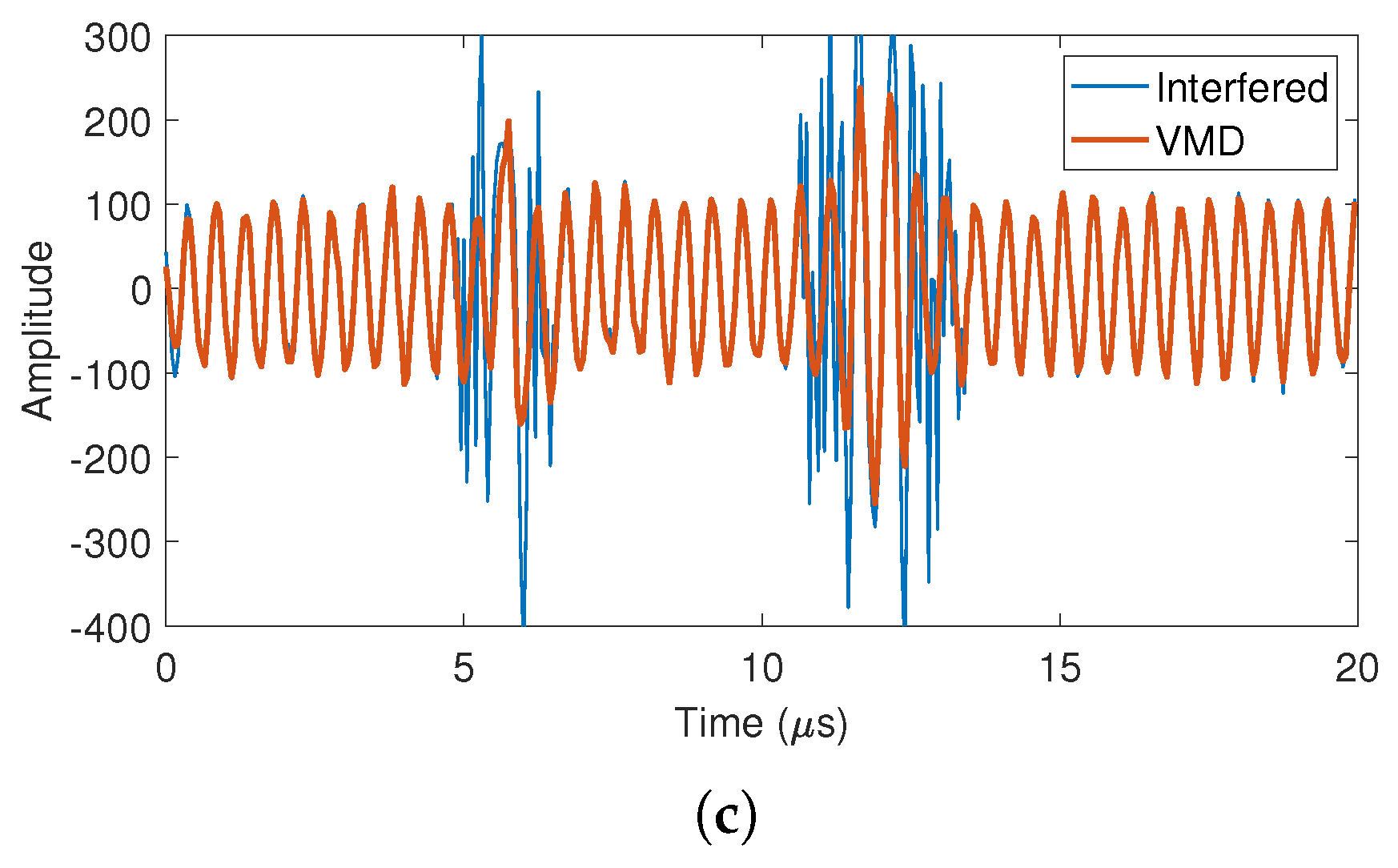
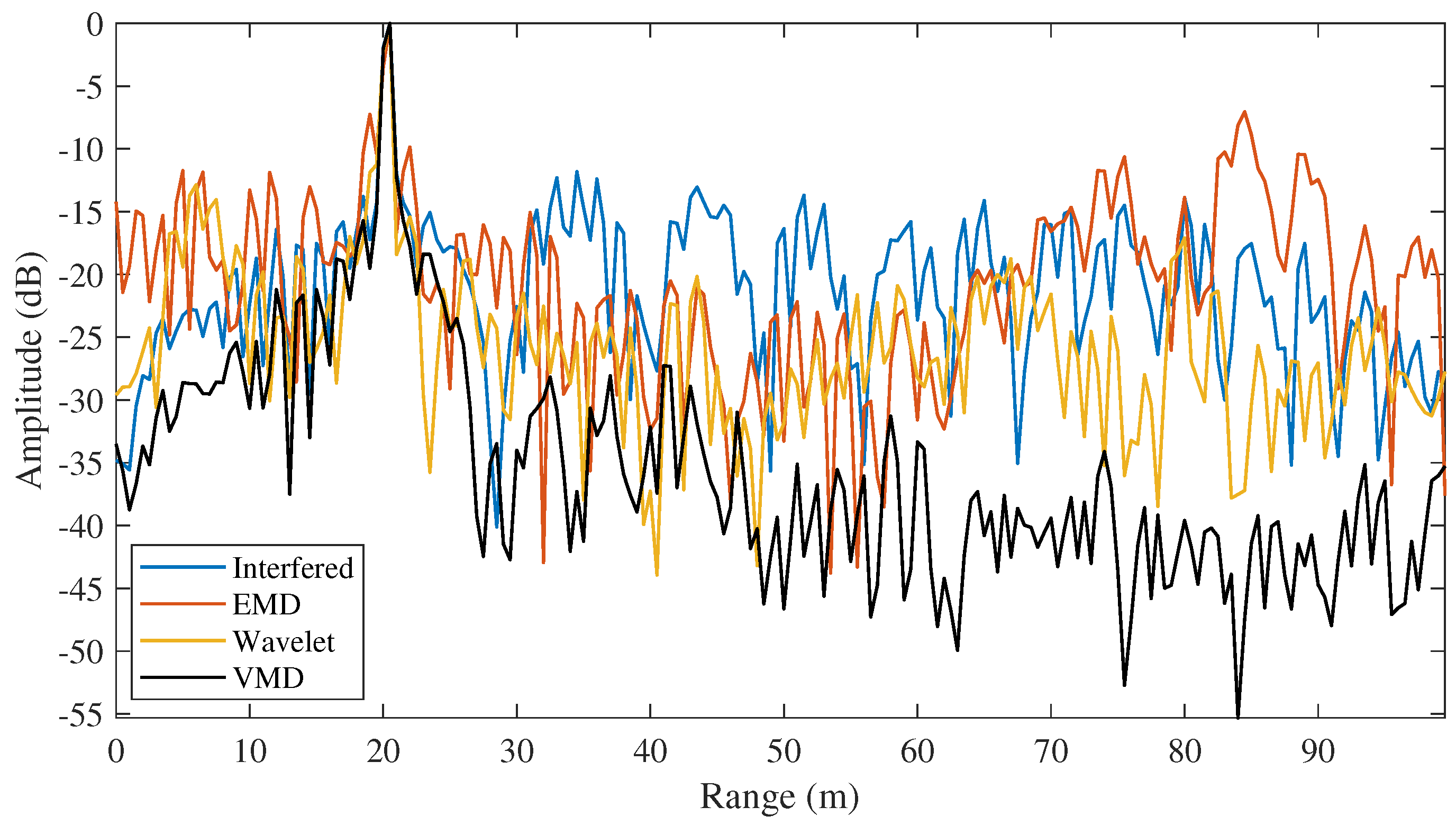
5.3. Simulation Results
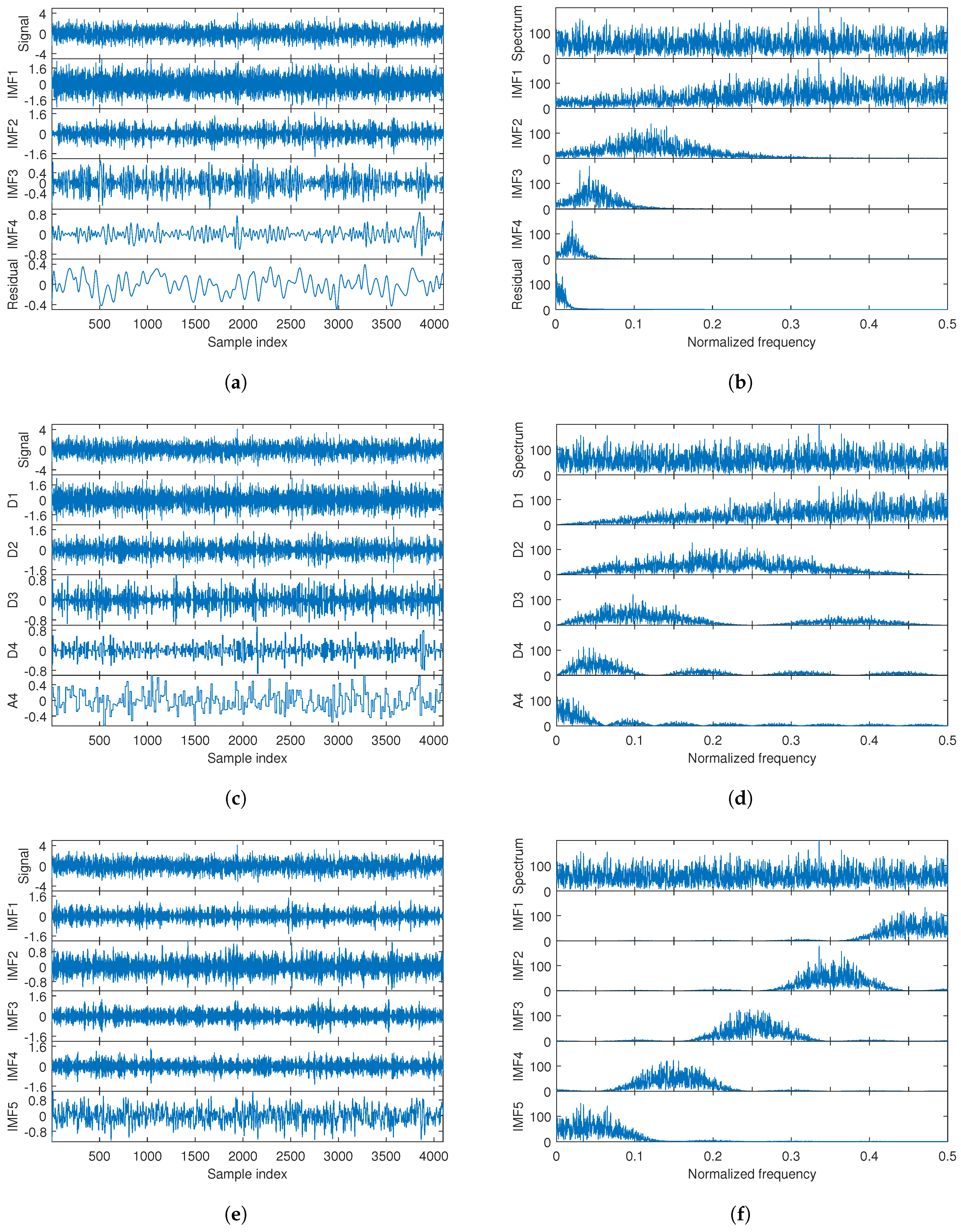
- Results of EMD.It can be seen from the decomposition results of the RP that IMF1 contains most of the frequency components, as shown in Figure 5b. Although IMF2 occupies about half of the low-frequency band, there is still a large frequency overlap between IMF1 and IMF2. This decomposition feature makes the interference components and most of the target echoes to be contained in IMF1. The decomposition results in the time domain also show that the waveform of IMF1 is similar to the original signal. In this case, the interference mitigation based on EMD does not gain benefit in the decomposition process.
- Results of wavelet.The wavelet decomposition results are similar to those of EMD, where most of the interference and target echo components are decomposed into Detail 1 and Detail 2 signals, as shown in Figure 5c,d. This also makes it impossible to obtain better interference mitigation based on this decomposition result.
- Results of VMD.Based on the quasi-orthogonal and band-limited decomposition characteristics of VMD, the interfered echo signal is decomposed to obtain approximately uniform range sections in RP, as shown in Figure 5f. Such decomposition brings two benefits: the first benefit is that the interference power is uniformly decomposed into different IMFs. According to (7), the interference is characterized as an LFM signal in the beat frequency signal. When the interference is decomposed into different narrowband IMFs, it is correspondingly decomposed into different time segments in the time domain, as shown in Figure 5e. The second benefit is that targets at different distances are uniformly decomposed into different IMFs, and each target is basically decomposed into a unique IMF due to the quasi-orthogonality of VMD. As a result of the above benefits, the support area of the interference in time domain becomes smaller for each IMF, which contributes to the computational reduction in the linear prediction model. In addition, the number of targets in each IMF is reduced, which contributes to the reconstruction of target echoes by using a lower-order model.
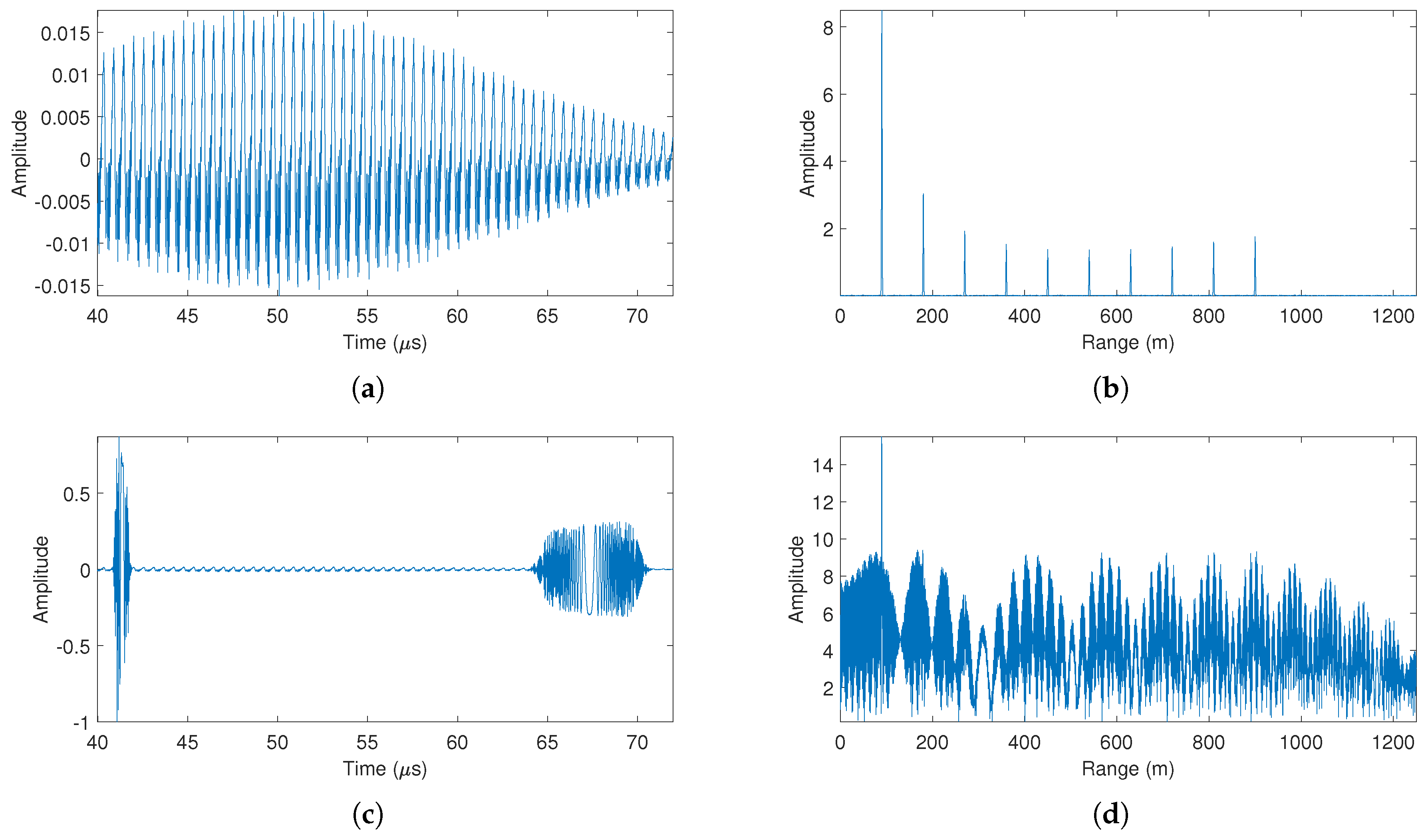
6. Real Experiment Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.; Wang, X.; Huang, D.; Fang, X.; Zhou, M.; Zhang, Y. MRPT: Millimeter-Wave Radar-based Pedestrian Trajectory-Tracking for Autonomous Urban Driving. IEEE Trans. Instrum. Meas. 2021, 71, 1–17. [Google Scholar] [CrossRef]
- Hasch, J.; Topak, E.; Schnabel, R.; Zwick, T.; Weigel, R.; Waldschmidt, C. Millimeter-wave technology for automotive radar sensors in the 77 GHz frequency band. IEEE Trans. Microw. Theory Tech. 2012, 60, 845–860. [Google Scholar] [CrossRef]
- Saponara, S.; Greco, M.S.; Gini, F. Radar-on-chip/in-package in autonomous driving vehicles and intelligent transport systems: Opportunities and challenges. IEEE Signal Process. Mag. 2019, 36, 71–84. [Google Scholar] [CrossRef]
- Neri, B.; Saponara, S. Advances in technologies, architectures, and applications of highly-integrated low-power radars. IEEE Aerosp. Electron. Syst. Mag. 2012, 27, 25–36. [Google Scholar] [CrossRef]
- Bilik, I.; Longman, O.; Villeval, S.; Tabrikian, J. The rise of radar for autonomous vehicles: Signal processing solutions and future research directions. IEEE Signal Process. Mag. 2019, 36, 20–31. [Google Scholar] [CrossRef]
- Munoz-Ferreras, J.M.; Perez-Martinez, F.; Calvo-Gallego, J.; Asensio-Lopez, A.; Dorta-Naranjo, B.P.; Blanco-del Campo, A. Traffic Surveillance System Based on a High-Resolution Radar. IEEE Trans. Geosci. Remote. Sens. 2008, 46, 1624–1633. [Google Scholar] [CrossRef]
- Dogru, S.; Marques, L. Pursuing Drones With Drones Using Millimeter Wave Radar. IEEE Robot. Autom. Lett. 2020, 5, 4156–4163. [Google Scholar] [CrossRef]
- Roos, F.; Bechter, J.; Knill, C.; Schweizer, B.; Waldschmidt, C. Radar sensors for autonomous driving: Modulation schemes and interference mitigation. IEEE Microw. Mag. 2019, 20, 58–72. [Google Scholar] [CrossRef]
- Sun, S.; Petropulu, A.P.; Poor, H.V. MIMO radar for advanced driver-assistance systems and autonomous driving: Advantages and challenges. IEEE Signal Process. Mag. 2020, 37, 98–117. [Google Scholar] [CrossRef]
- Yamada, H.; Kobayashi, T.; Yamaguchi, Y.; Sugiyama, Y. High-resolution 2D SAR imaging by the millimeter-wave automobile radar. In Proceedings of the 2017 IEEE Conference on Antenna Measurements & Applications (CAMA), Tsukuba, Japan, 4–6 December 2017; pp. 149–150. [Google Scholar] [CrossRef]
- Brooker, G.M. Mutual interference of millimeter-wave radar systems. IEEE Trans. Electromagn. Compat. 2007, 49, 170–181. [Google Scholar] [CrossRef]
- Kim, G.; Mun, J.; Lee, J. A peer-to-peer interference analysis for automotive chirp sequence radars. IEEE Trans. Veh. Technol. 2018, 67, 8110–8117. [Google Scholar] [CrossRef]
- Pirkani, A.; Norouzian, F.; Hoare, E.; Cherniakov, M.; Gashinova, M. Automotive interference statistics and their effect on radar detector. IET Radar Sonar Navig. 2022, 16, 9–21. [Google Scholar] [CrossRef]
- Overdevest, J.; Jansen, F.; Laghezza, F.; Uysal, F.; Yarovoy, A. Uncorrelated Interference in 79 GHz FMCW and PMCW Automotive Radar. In Proceedings of the 2019 20th International Radar Symposium (IRS), Ulm, Germany, 26–28 June 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Alland, S.; Stark, W.; Ali, M.; Hegde, M. Interference in Automotive Radar Systems: Characteristics, Mitigation Techniques, and Current and Future Research. IEEE Signal Process. Mag. 2019, 36, 45–59. [Google Scholar] [CrossRef]
- Goppelt, M.; Blöcher, H.L.; Menzel, W. Analytical investigation of mutual interference between automotive FMCW radar sensors. In Proceedings of the 2011 German Microwave Conference, Darmstadt, Germany, 14–16 March 2011; pp. 1–4. [Google Scholar]
- Nozawa, T.; Makino, Y.; Takaya, N.; Umehira, M.; Takeda, S.; Wang, X.; Kuroda, H. An anti-collision automotive FMCW radar using time-domain interference detection and suppression. In Proceedings of the International Conference on Radar Systems, Belfast, UK, 23–26 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Rameez, M.; Dahl, M.; Pettersson, M.I. Autoregressive Model-Based Signal Reconstruction for Automotive Radar Interference Mitigation. IEEE Sens. J. 2020, 21, 6575–6586. [Google Scholar] [CrossRef]
- Wu, J.; Yang, S.; Lu, W.; Liu, Z. Iterative modified threshold method based on EMD for interference suppression in FMCW radars. IET Radar Sonar Navig. 2020, 14, 1219–1228. [Google Scholar] [CrossRef]
- Lee, S.; Lee, J.Y.; Kim, S.C. Mutual Interference Suppression Using Wavelet Denoising in Automotive FMCW Radar Systems. IEEE Trans. Intell. Transp. Syst. 2021, 22, 887–897. [Google Scholar] [CrossRef]
- Norouzian, F.; Pirkani, A.; Hoare, E.; Cherniakov, M.; Gashinova, M. Phenomenology of automotive radar interference. IET Radar Sonar Navig. 2021, 15, 1045–1060. [Google Scholar] [CrossRef]
- Neemat, S.; Krasnov, O.; Yarovoy, A. An interference mitigation technique for FMCW radar using beat-frequencies interpolation in the STFT domain. IEEE Trans. Microw. Theory Tech. 2018, 67, 1207–1220. [Google Scholar] [CrossRef]
- Eslami Nazari, M.; Huang, W.; Zhao, C. Radio Frequency Interference Suppression for HF Surface Wave Radar Using CEMD and Temporal Windowing Methods. IEEE Geosci. Remote Sens. Lett. 2020, 17, 212–216. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, F.; Zhao, C.; He, C. Radio Frequency Interference Mitigation in High-Frequency Surface Wave Radar Based on CEMD. IEEE Geosci. Remote Sens. Lett. 2017, 14, 764–768. [Google Scholar] [CrossRef]
- Zhou, F.; Xing, M.; Bai, X.; Sun, G.; Bao, Z. Narrow-Band Interference Suppression for SAR Based on Complex Empirical Mode Decomposition. IEEE Geosci. Remote Sens. Lett. 2009, 6, 423–427. [Google Scholar] [CrossRef]
- Díez-García, R.; Camps, A.; Park, H. On the Potential of Empirical Mode Decomposition for RFI Mitigation in Microwave Radiometry. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Ramasubramanian, K.; Instruments, T. Using a complex-baseband architecture in FMCW radar systems. Tex. Instrum. 2017, 19, 1–9. [Google Scholar]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Vetterli, M.; Herley, C. Wavelets and filter banks: Theory and design. IEEE Trans. Signal Process. 1992, 40, 2207–2232. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive radars: A review of signal processing techniques. IEEE Signal Process. Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Skolnik, M.I. Introduction to Radar Systems; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Upadhyay, A.; Pachori, R.B. Instantaneous voiced/non-voiced detection in speech signals based on variational mode decomposition. J. Frankl. Inst. 2015, 352, 2679–2707. [Google Scholar] [CrossRef]
- Lahmiri, S. Intraday stock price forecasting based on variational mode decomposition. J. Comput. Sci. 2016, 12, 23–27. [Google Scholar] [CrossRef]
- Smruthy, A.; Suchetha, M. Real-Time Classification of Healthy and Apnea Subjects Using ECG Signals With Variational Mode Decomposition. IEEE Sens. J. 2017, 17, 3092–3099. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Du, W. Research on Fault Diagnosis of Gearbox with Improved Variational Mode Decomposition. Sensors 2018, 18, 3510. [Google Scholar] [CrossRef]
- Toth, M.; Meissner, P.; Melzer, A.; Witrisal, K. Performance Comparison of Mutual Automotive Radar Interference Mitigation Algorithms. In Proceedings of the 2019 IEEE Radar Conference, Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Chan, Y.; Lavoie, J.; Plant, J. A parameter estimation approach to estimation of frequencies of sinusoids. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 214–219. [Google Scholar] [CrossRef]
- Richards, M.A. Fundamentals of Radar Signal Processing; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Davis, M.S.; Lanterman, A.D. Minimum integrated sidelobe ratio filters for MIMO radar. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 405–416. [Google Scholar] [CrossRef]
- Chatzitheodoridi, M.E.; Taylor, A.; Rabaste, O. A Mismatched Filter for Integrated Sidelobe Level Minimization over a Continuous Doppler Shift Interval. In Proceedings of the 2020 IEEE Radar Conference, Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar] [CrossRef]





| Target Index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Range (m) | 90 | 180 | 270 | 360 | 450 | 540 | 630 | 720 | 810 | 900 |
| Velocity (m/s) | 2.7 | 3.0 | 3.3 | 3.6 | 3.8 | 4.1 | 4.4 | 4.7 | 5.0 | 5.2 |
| Parameter | Victim | Interferer1 | Interferer2 |
|---|---|---|---|
| Operating frequency (GHz) | 77 | 77 | 77 |
| Sweep bandwidth (MHz) | 300 | 600 | 600 |
| Sweep time (μs) | 100 | 10 | 50 |
| Sweep direction | Up | Down | Up |
| IF sampling frequency (MHz) | 50 | - | - |
| Method List | Running Time of Signal Decomposition (ms) | Running Time of Interference Detection and Mitigation (ms) | Total Running Time (ms) |
|---|---|---|---|
| EMD | 47 | 412.9 | 459.9 |
| Wavelet | 38.9 | 28.3 | 67.2 |
| VMD | 192.2 | 749.9 | 942.1 |
| VMD (parallel) | 191.1 | 126.7 | 317.8 |
| Radar Parameters | Victim | Interferer1 | Interferer2 |
|---|---|---|---|
| Operating frequency (GHz) | 77 | 77 | 77 |
| Sweep bandwidth (MHz) | 300 | 300 | 500 |
| Sweep time (μs) | 20 | 20 | 20 |
| Sweep direction | Up | Down | Up |
| Pulse repetition time (PRT) (μs) | 30 | 43 | 61 |
| Sampling frequency (MHz) | 20 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Feng, B.; Zhang, W. Mutual Interference Mitigation of Millimeter-Wave Radar Based on Variational Mode Decomposition and Signal Reconstruction. Remote Sens. 2023, 15, 557. https://doi.org/10.3390/rs15030557
Li Y, Feng B, Zhang W. Mutual Interference Mitigation of Millimeter-Wave Radar Based on Variational Mode Decomposition and Signal Reconstruction. Remote Sensing. 2023; 15(3):557. https://doi.org/10.3390/rs15030557
Chicago/Turabian StyleLi, Yanbing, Bo Feng, and Weichuan Zhang. 2023. "Mutual Interference Mitigation of Millimeter-Wave Radar Based on Variational Mode Decomposition and Signal Reconstruction" Remote Sensing 15, no. 3: 557. https://doi.org/10.3390/rs15030557
APA StyleLi, Y., Feng, B., & Zhang, W. (2023). Mutual Interference Mitigation of Millimeter-Wave Radar Based on Variational Mode Decomposition and Signal Reconstruction. Remote Sensing, 15(3), 557. https://doi.org/10.3390/rs15030557






