Automatic Horizon Picking Using Multiple Seismic Attributes and Markov Decision Process
Abstract
1. Introduction
2. Review of the Markov Decision Process
2.1. 5-Tuple <>
2.2. The Markov Decision Process
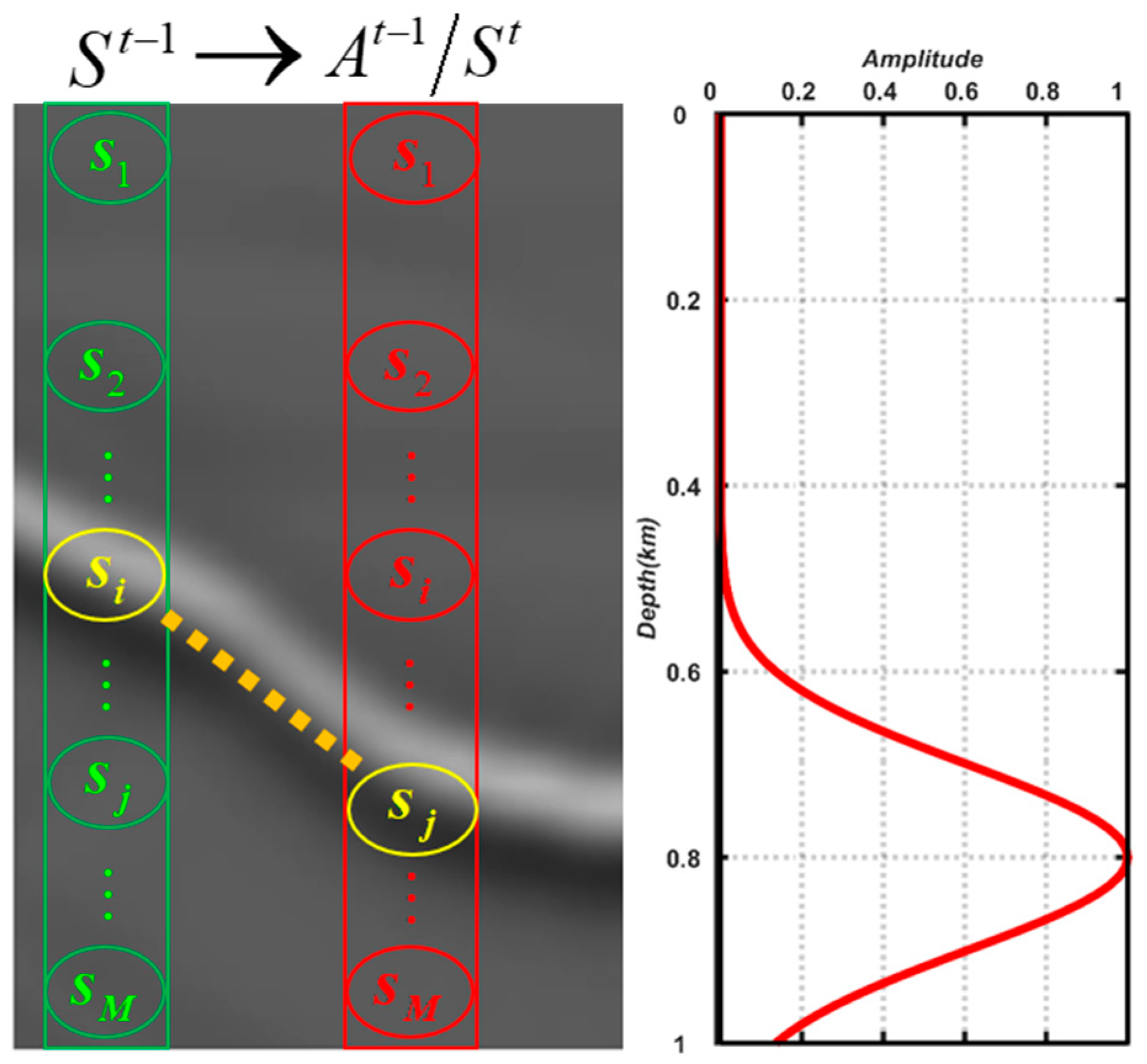
3. Formulation of Horizon Picking with MDP
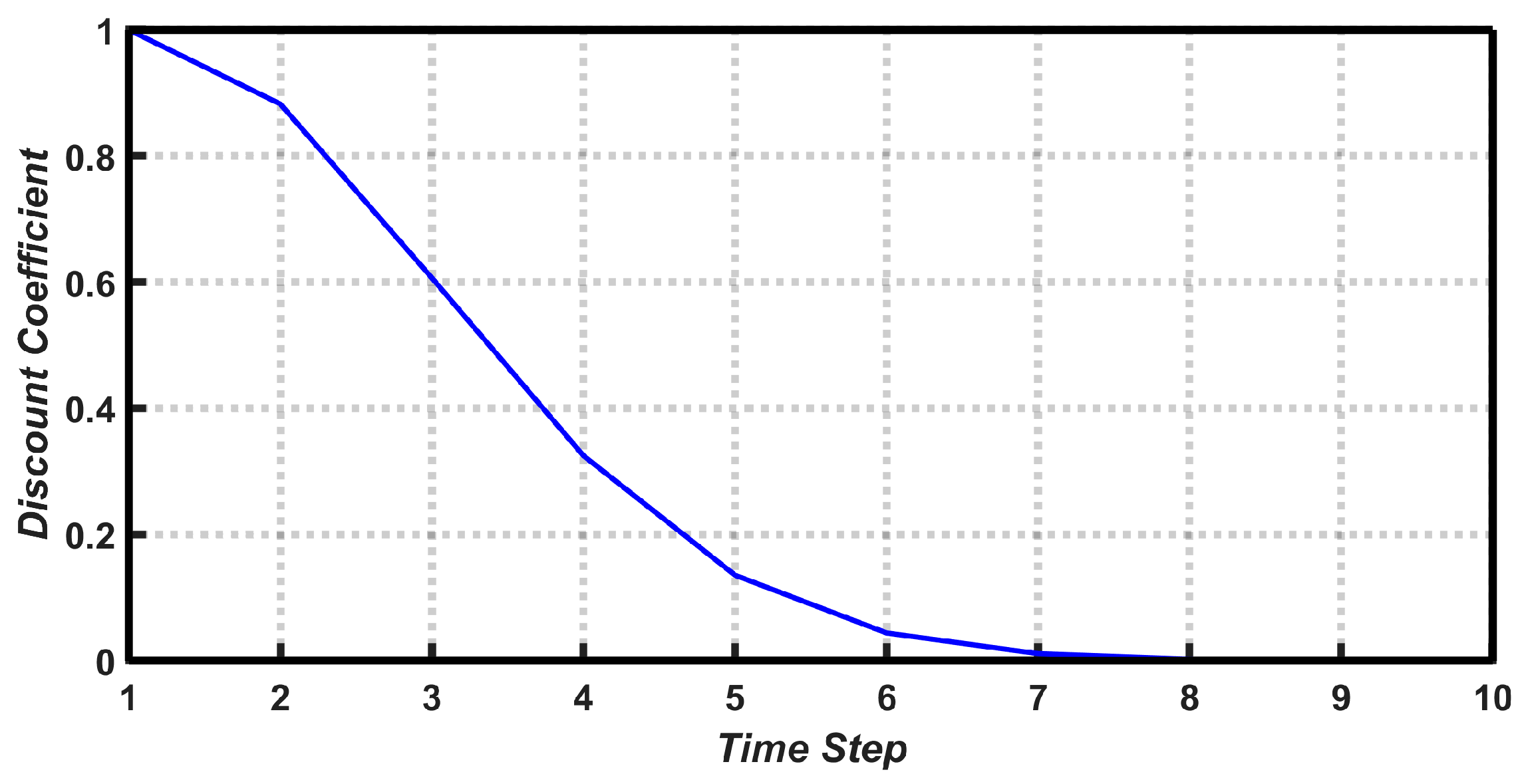
4. An Effective Scheme for Horizon Picking
5. Numerical Examples
5.1. A Local Layered Model
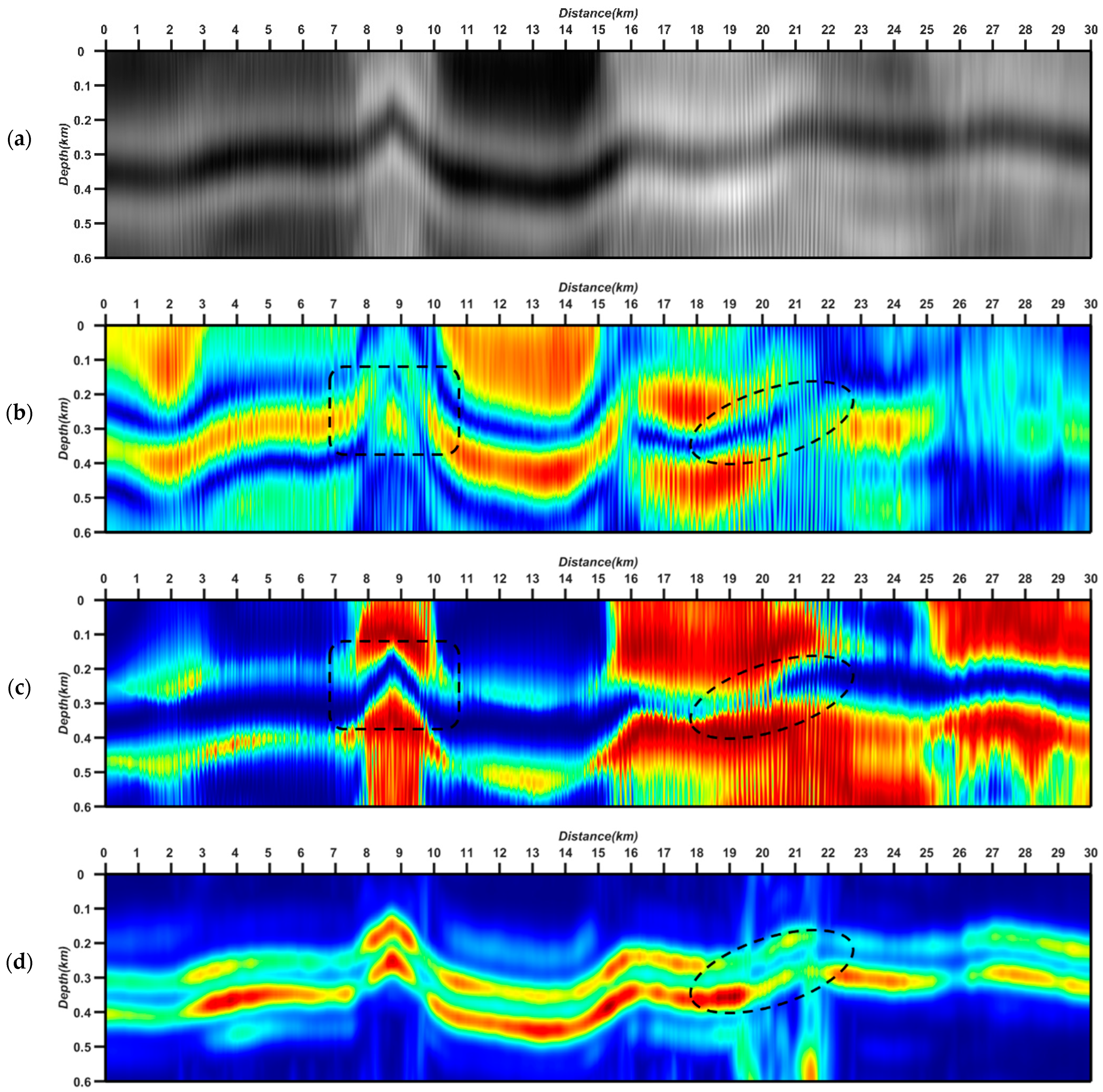
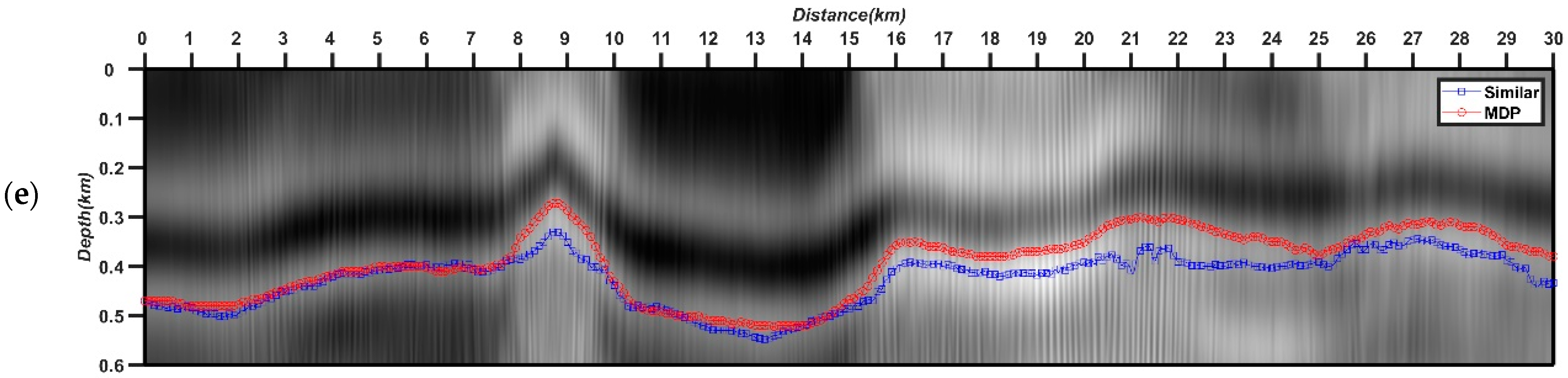
5.2. The North Sea F3 Field Data
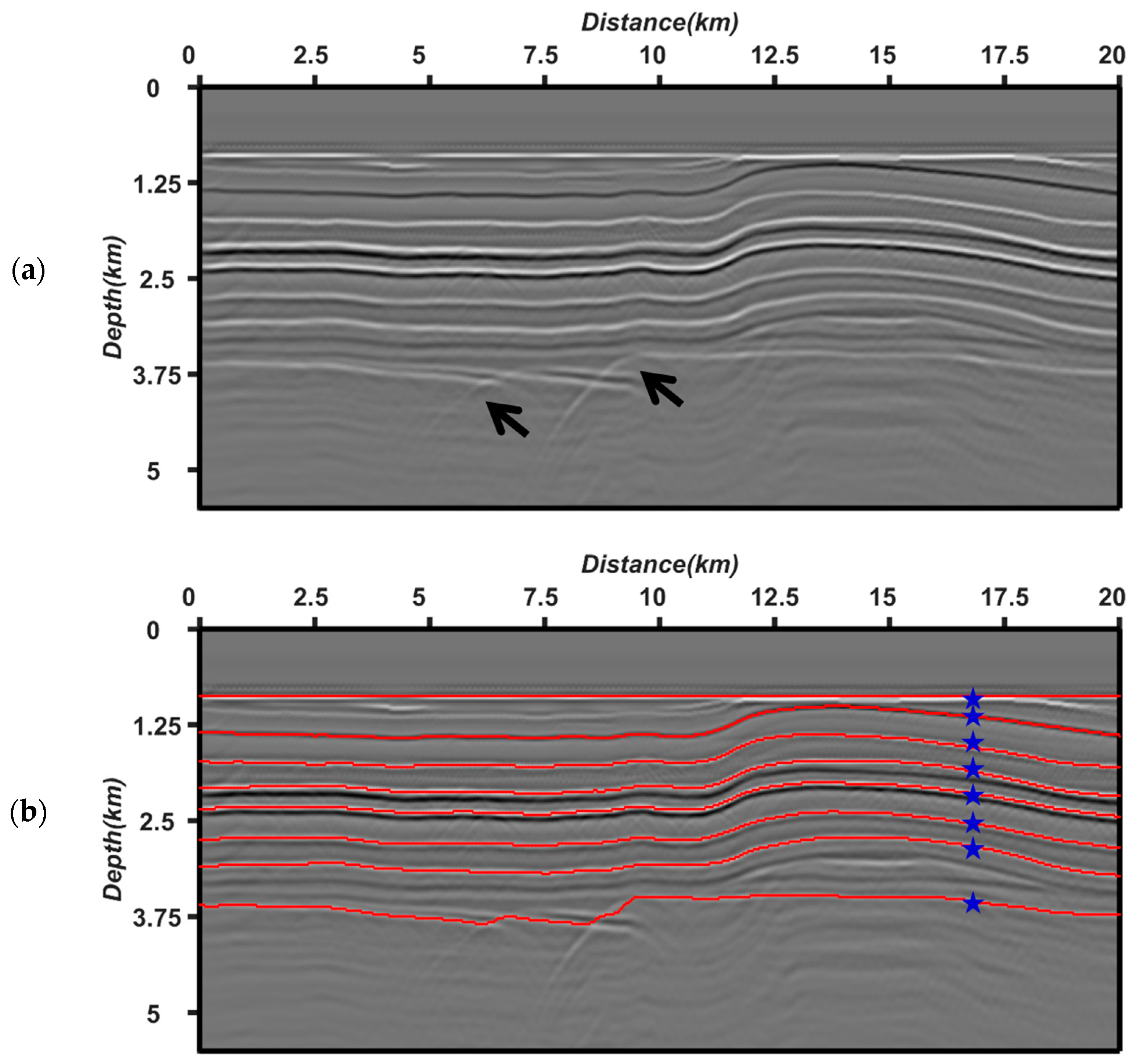
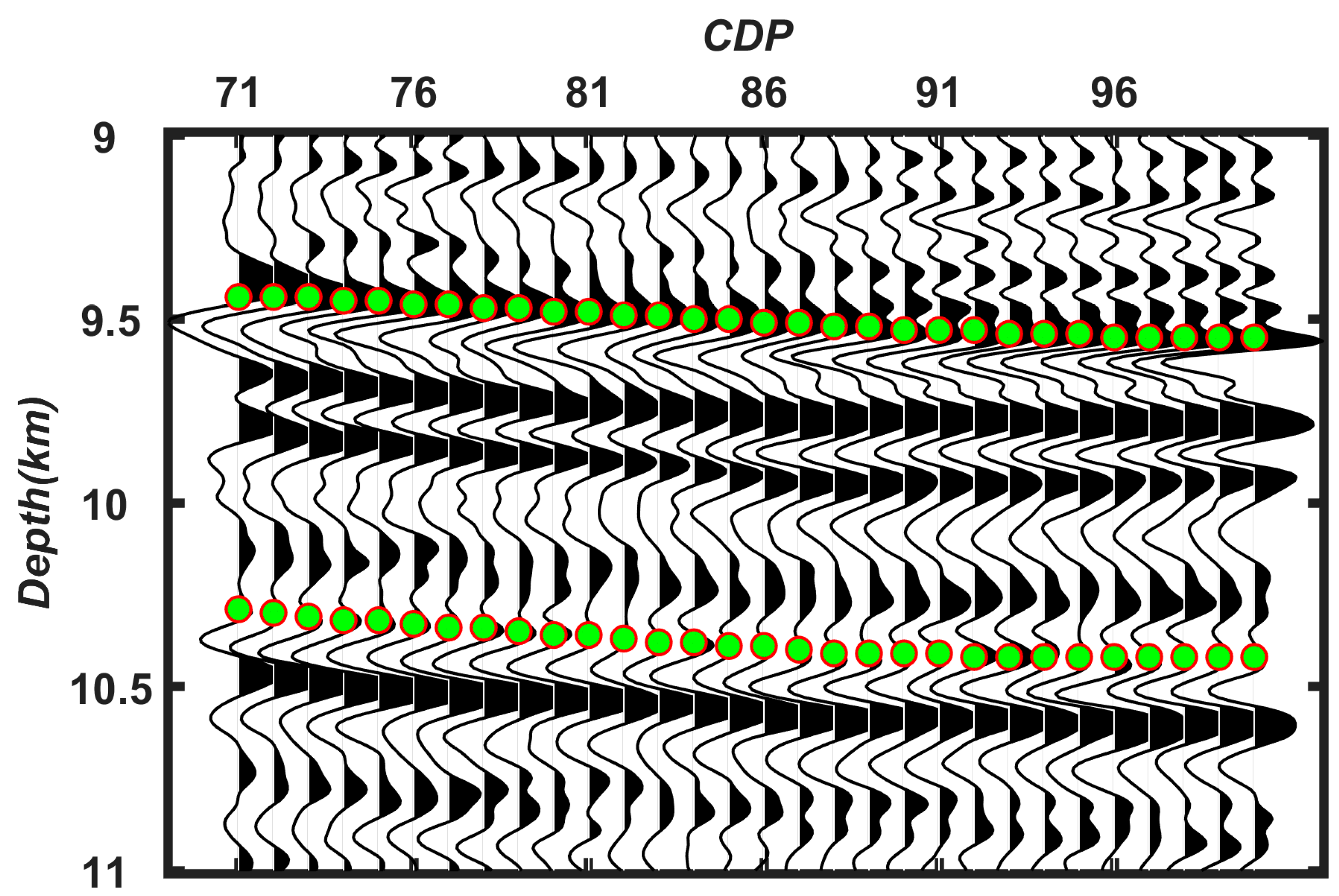
5.3. The Overthrust Model for Picking Multiple Horizons
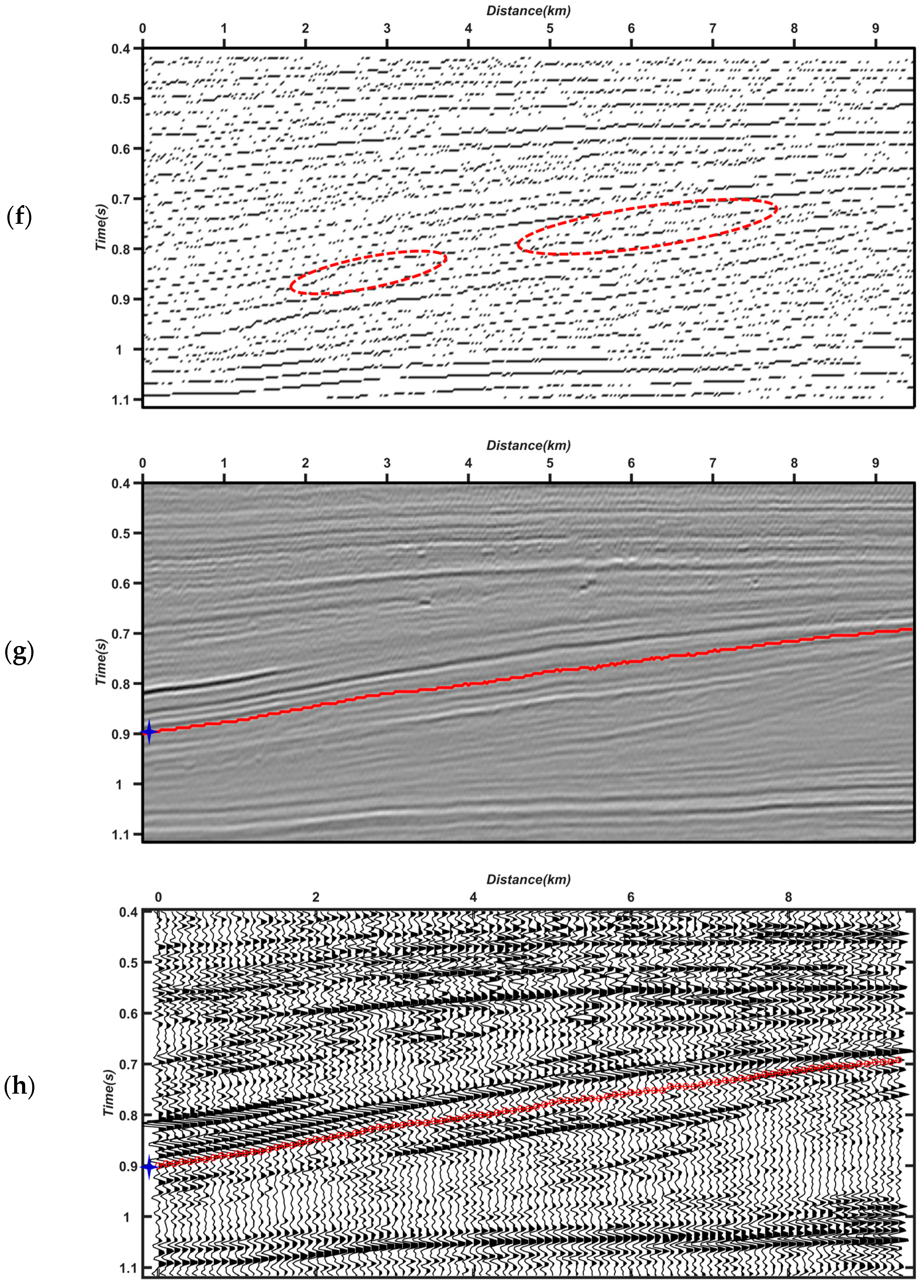
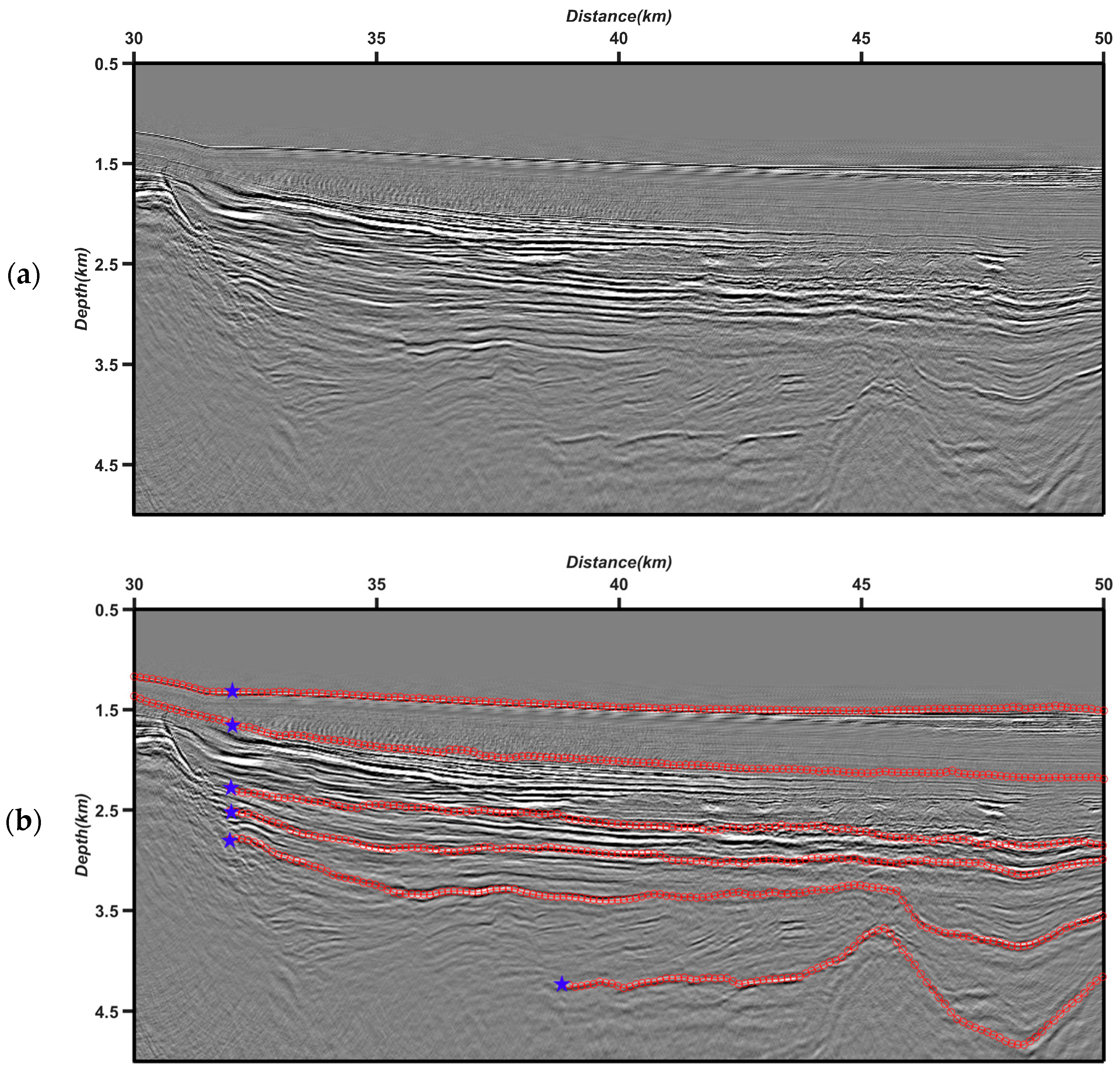
5.4. The Field Data for Picking Multiple Horizons
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Howard, R.E. Method for Attribute Tracking in Seismic Data. U.S. Patent No. 5,1991,056-066, 8 October 1991. [Google Scholar]
- Zeng, H.; Backus, M.M.; Barrow, K.T.; Tyler, N. Stratal slicing—Part 1: Realistic 3D seismic model. Geophysics 1998, 63, 502–513. [Google Scholar] [CrossRef]
- Stark, T.J. Unwrapping instantaneous phase to generate a relative geologic time volume. In 73rd Annual International Meeting, SEG, Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 2003; pp. 1707–1710. [Google Scholar] [CrossRef]
- Wu, X.; Zhong, G. Generating a relative geologic time volume by 3D graph-cut phase unwrapping method with horizon and unconformity constraints. Geophysics 2012, 77, O21–O34. [Google Scholar] [CrossRef]
- Dossi, M.; Forte, E.; Pipan, M. Automated reflection picking and polarity assessment through attribute analysis: Theory and application to synthetic and real ground-penetrating radar data. Geophysics 2015, 80, H23–H35. [Google Scholar] [CrossRef]
- Forte, E.; Dossi, M.; Pipan, M.; Ben, A.D. Automated phase attribute-based picking applied to reflection seismic. Geophysics 2016, 81, V141–V150. [Google Scholar] [CrossRef]
- Marfurt, K.; Kirlin, R.; Farmer, S.; Bahorich, M. 3-D seismic attributes using a semblance-based coherency algorithm. Geophysics 1998, 63, 1150–1165. [Google Scholar] [CrossRef]
- Lacaze, F.; Valding, T. Autopicking Velocity by Path-Integral Optimization and Surface Fairing. In 79th Annual International Meeting, SEG Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 2009; pp. 2592–2596. [Google Scholar] [CrossRef]
- Zou, G.; Ji, R.; Liu, W.; Zhang, J. Horizon auto-tracking technology based on the waveform similarity for the coalmining area seismic data. In Proceedings of the 2013 2nd International Symposium on Instrumentation and Measurement, Sensor Network and Automation (IMSNA), Toronto, ON, Canada, 23–24 December 2013; pp. 236–242. [Google Scholar]
- Gersztenkorn, A.; Marfurt, K.J. Eigenstructure-based coherence computations as an aid to 3-D structural and stratigraphic mapping. Geophysics 1999, 64, 1468–1479. [Google Scholar] [CrossRef]
- Bakker, P. Image Structure Analysis for Seismic Interpretation. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2002. [Google Scholar]
- Lomask, J.; Guitton, A.; Fomel, S.; Claerbout, J.; Valenciano, A.A. Flattening without picking. Geophysics 2006, 71, P13–P20. [Google Scholar] [CrossRef]
- Lomask, J.; Guitton, A. Volumetric flattening: An interpretation tool. Lead. Edge 2007, 26, 888–897. [Google Scholar] [CrossRef]
- Parks, D. Seismic Image Flattening as a Linear Inverse Problem. Master’s Thesis, Colorado School of Mines, Golden, CO, USA, 2010. [Google Scholar]
- Wu, X. Directional structure-tensor-based coherence to detect seismic faults and channels. Geophysics 2017, 82, A13–A17. [Google Scholar] [CrossRef]
- Wu, X.; Fomel, S. Least-squares horizons with local slopes and multigrid correlations. Geophysics 2018, 83, IM29–IM40. [Google Scholar] [CrossRef]
- Di, H.; Gao, D.; AlRegib, G. 3D dip vector-guided auto-tracking for weak seismic reflections: A new tool for shale reservoir visualization and interpretation. Interpretation 2018, 6, SN47–SN56. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, B. Automatic horizon picking using multiple seismic attributes. In 88th Annual International Meeting, SEG Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 2018; pp. 1683–1688. [Google Scholar]
- Gogia, R.; Singh, R.; de Groot, P.; Gupta, H.; Srirangarajan, S.; Phirani, J.; Ranu, S. Tracking 3D seismic horizons with a new hybrid tracking algorithm. Interpretation 2020, 8, SQ39–SQ45. [Google Scholar] [CrossRef]
- Li, S.; Zhao, J.; Zhang, H.; Bi, Z.; Qu, S. A Novel Horizon Picking Method on Sub-Bottom Profiler Sonar Images. Remote Sens. 2020, 12, 3322. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, B.; Lin, T.; Cao, D. Seismic horizon picking by integrating reflector dip and instantaneous phase attributes. Geophysics 2020, 85, O37–O45. [Google Scholar] [CrossRef]
- Zhang, B.; Qi, J.; Lou, Y.; Fang, H.; Cao, D. Generating seismic horizon using multiple seismic attributes. IEEE Geosci. Remote Sens. Lett. 2020, 18, 979–983. [Google Scholar] [CrossRef]
- Zhao, J.; Li, S.; Zhao, X.; Feng, J. A Comprehensive Horizon-Picking Method on Subbottom Profiles by Combining Envelope, Phase Attributes, and Texture Analysis. Earth Space Sci. 2020, 7, e2019EA000680. [Google Scholar] [CrossRef]
- Admasu, F.; Tönnies, K.D. Model-based Approach to Automatic 3D Seismic Horizon Correlation across Faults. In Proceedings of the Simulation und Visualisierung 2004 (SimVis), Magdeburg, Germany, 4–5 March 2004; pp. 239–250. [Google Scholar]
- Bondár, I. Seismic horizon detection using image processing algorithms. Geophys. Prospect. 1992, 40, 785–800. [Google Scholar] [CrossRef]
- Aurnhammer, M.; Tonnies, K.D. A genetic algorithm for automated horizon correlation across faults in seismic images. IEEE Trans. Evol. Comput. 2005, 9, 201–210. [Google Scholar] [CrossRef]
- Pauget, F.; Lacaze, S.; Valding, T. A global approach in seismic interpretation based on cost function minimization. In 79th Annual International Meeting, SEG Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 2009; pp. 2592–2596. [Google Scholar]
- Hoyes, J.; Cheret, T. A review of global interpretation methods for automated 3D horizon picking. Lead. Edge 2011, 30, 38–47. [Google Scholar] [CrossRef]
- Hong, Z.; Su, M.; Qian, F.; Han, Q. Global seismic horizon interpretation based on data mining—A new tool for seismic geomorphologic study. Interpretation 2020, 8, T131–T140. [Google Scholar] [CrossRef]
- Wu, X.; Hale, D. Automatically interpreting all faults, unconformities, and horizons from 3D seismic images. Interpretation 2016, 4, T227–T237. [Google Scholar] [CrossRef]
- Jin, S.; Chen, S.; Wei, J.; Li, X. Automatic seismic event tracking using a dynamic time warping algorithm. J. Geophys. Eng. 2017, 14, 1138–1149. [Google Scholar] [CrossRef]
- Bugge, A.J.; Erik, L.J.; Evensen, A.K.; Faleide, J.I.; Clark, S. Automatic extraction of dislocated horizons from 3D seismic data using nonlocal trace matching. Geophysics 2019, 84, IM77–IM86. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, B.; Fang, H.; Cao, D.; Wang, K.; Huo, Z. Simulating the procedure of manual seismic horizon picking. Geophysics 2021, 86, O1–O12. [Google Scholar] [CrossRef]
- Yan, S.; Wu, X. Seismic horizon extraction with dynamic programming. Geophysics 2021, 86, 51–62. [Google Scholar] [CrossRef]
- Harrigan, E.; Kroh, J.R.; Sandham, W.A.; Durrani, T.S. Seismic horizon picking using an artificial neural network. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA, USA, 23–26 March 1992; pp. 105–108. [Google Scholar]
- Huang, K. Hopfield neural network for seismic horizon picking. In 75th Annual International Meeting, SEG, Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 1997; pp. 562–565. [Google Scholar] [CrossRef]
- Huang, K. Neural network for seismic horizon picking. In IEEE International Joint Conference on Neural Networks Proceedings; IEEE World Congress on Computational Intelligence: Anchorage, AK, USA, 1998; Volume 3, pp. 1840–1844. [Google Scholar]
- Leggett, M.; Sandham, W.A.; Durrani, T.S. Automated 3-D Horizon Tracking and Seismic Classification Using Artificial Neural Networks; Springer: Cham, The Netherlands, 2003; pp. 31–44. [Google Scholar]
- Peters, B.; Granek, J.; Haber, E. Multi-resolution neural networks for tracking seismic horizons from few training images. Interpretation 2019, 7, SE201–SE213. [Google Scholar] [CrossRef]
- Waldeland, A.U.; Jensen, A.C.; Gelius, L.-J.; Solberg, A.H.S. Convolutional neural networks for automated seismic interpretation. Lead. Edge 2018, 37, 529–537. [Google Scholar] [CrossRef]
- Shi, Y.; Wu, X.; Fomel, S. SaltSeg: Automatic 3D salt segmentation using a deep convolutional neural network. Interpretation 2019, 7, SE113–SE122. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, B.; Lin, T.; Cao, D.; Lou, Y. Semiautomated seismic horizon interpretation using the encoder-decoder convolutional neural network. Geophysics 2019, 84, B403–B417. [Google Scholar] [CrossRef]
- Yang, L.; Sun, Z. Seismic horizon tracking using a deep convolutional neural network. J. Pet. Sci. Eng. 2020, 187, 106709. [Google Scholar] [CrossRef]
- Tschannen, V.; Delescluse, M.; Ettrich, N.; Keuper, J. Extracting horizon surfaces from 3D seismic data using deep learning. Geophysics 2020, 85, N17–N26. [Google Scholar] [CrossRef]
- Zhang, K.; Lin, N.; Zhang, D.; Zhang, J.; Yang, J.; Tian, G. Automatic tracking for seismic horizons using convolution feature analysis and optimization algorithm. J. Pet. Sci. Eng. 2021, 208, 109441. [Google Scholar] [CrossRef]
- Huang, K.; Chang, W.; Lin, C. Self-organizing neural network for picking seismic horizons. In 60th Annual International Meeting, SEG Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 1990; pp. 313–316. [Google Scholar]
- Shi, Y.; Wu, X.; Fomel, S. Waveform embedding: Automatic horizon picking with unsupervised deep learning. Geophysics 2020, 85, WA67–WA76. [Google Scholar] [CrossRef]
- Wald, A. Foundations of a general theory of sequential decision functions. Econometrica. J. Econom. Soc. 1947, 15, 279–313. [Google Scholar] [CrossRef]
- Shapley, L.S. Stochastic games. Proc. Natl. Acad. Sci. USA 1953, 39, 1095–1100. [Google Scholar] [CrossRef]
- Bellman, R.A. Markovian decision process. J. Math. Mech. 1957, 6, 679–684. [Google Scholar] [CrossRef]
- Howard, R.A. Dynamic Programming and Markov Processes; John Wiley: Hoboken, NJ, USA, 1960. [Google Scholar]
- Blackwell, D. Discrete dynamic programming. Ann. Math. Stat. 1962, 33, 719–726. [Google Scholar] [CrossRef]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Barto, A.G.; Sutton, R.S.; Watkins, C. Learning and Sequential Decision Making; University of Massachusetts: Amherst, MA, USA, 1989. [Google Scholar]
- Littman, M.L. Algorithms for Sequential Decision-Making; Brown University: Rhode Island, RI, USA, 1996. [Google Scholar]
- Read, P.; Lermit, J. Bio-energy with carbon storage (BECS): A sequential decision approach to the threat of abrupt climate change. Energy 2005, 30, 2654–2671. [Google Scholar] [CrossRef]
- Bertsekas, D. Dynamic Programming and Optimal Control: Volume I; Athena Scientific: Belmont, MA, USA, 2012. [Google Scholar]
- Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Ma, Y.; Fei, T.; Luo, Y. A new insight into automatic first-arrival picking based on reinforcement learning. In 81st EAGE Conference and Exhibition, Expanded Abstracts; European Association of Geoscientists and Engineers: Houten, The Netherlands, 2019; pp. 1–5. [Google Scholar]
- Luo, F.; Feng, B.; Wang, H. Automatic first-arrival picking method via intelligent Markov optimal decision processes. J. Geophys. Eng. 2021, 18, 406–417. [Google Scholar] [CrossRef]
- Sutton, R.S. Generalization in reinforcement learning: Successful examples using sparse coarse coding. In Advances in Neural Information Processing Systems; MIT Press: Denver, CO, USA, 1996; pp. 1038–1044. [Google Scholar]
- Wu, C.; Wang, H.; Feng, B.; Sheng, S. RTM angle gathers based on the Combining Local and Global (CLG) optical flow method and wavefield decomposition method. Chin. J. Geophys. 2021, 64, 1375–1388. (In Chinese) [Google Scholar] [CrossRef]
- Wu, C.; Wang, T.; Wang, H.; Luo, F.; Xu, P. Improving the quality of Common-Image Gathers using DTW and Local Similarity. In 89th SEG Annual International Meeting, Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 2019; pp. 4336–4340. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.; Feng, B.; Song, X.; Wang, H.; Xu, R.; Sheng, S. Automatic Horizon Picking Using Multiple Seismic Attributes and Markov Decision Process. Remote Sens. 2023, 15, 552. https://doi.org/10.3390/rs15030552
Wu C, Feng B, Song X, Wang H, Xu R, Sheng S. Automatic Horizon Picking Using Multiple Seismic Attributes and Markov Decision Process. Remote Sensing. 2023; 15(3):552. https://doi.org/10.3390/rs15030552
Chicago/Turabian StyleWu, Chengliang, Bo Feng, Xiaonan Song, Huazhong Wang, Rongwei Xu, and Shen Sheng. 2023. "Automatic Horizon Picking Using Multiple Seismic Attributes and Markov Decision Process" Remote Sensing 15, no. 3: 552. https://doi.org/10.3390/rs15030552
APA StyleWu, C., Feng, B., Song, X., Wang, H., Xu, R., & Sheng, S. (2023). Automatic Horizon Picking Using Multiple Seismic Attributes and Markov Decision Process. Remote Sensing, 15(3), 552. https://doi.org/10.3390/rs15030552





