Next Article in Journal
Vertically Resolved Global Ocean Light Models Using Machine Learning
Previous Article in Journal
VQ-InfraTrans: A Unified Framework for RGB-IR Translation with Hybrid Transformer
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 24
10.3390/rs15245662
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A First Step towards Meteosat Third Generation Day-2 Precipitation Rate Product: Deep Learning for Precipitation Rate Retrieval from Geostationary Infrared Measurements

by
Leo Pio D’Adderio
,
Daniele Casella
*,
Stefano Dietrich
,
Giulia Panegrossi
and
Paolo Sanò
National Research Council of Italy, Institute of Atmospheric Sciences and Climate (CNR-ISAC), 00133 Rome, Italy
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(24), 5662; https://doi.org/10.3390/rs15245662
Submission received: 12 October 2023 / Revised: 21 November 2023 / Accepted: 1 December 2023 / Published: 7 December 2023
(This article belongs to the Section Environmental Remote Sensing)
Browse Figures
Versions Notes

Abstract

:
The estimate of precipitation from satellite measurements is an indirect estimate if compared to rain gauges or disdrometer measurements, but it has the advantage of complete coverage over oceans, mountainous regions, and sparsely populated areas where other sources of precipitation data (e.g., weather radar) are unavailable or unreliable. Among the satellite-based precipitation estimates, geostationary (GEO) data ensure the highest spatial and temporal resolution. At the same time, the IR/VIS channels deployed on GEO satellites have lower capabilities than microwave (MW) channels in characterizing the cloud structure. Machine learning (ML) techniques can be considered a powerful tool to overcome the limitations related to the physical relationship between IR/VIS channels and precipitation estimation. This study describes the development of a convolutional neural network (U-Net) to retrieve the precipitation rate using IR measurements only from the Meteosat Second Generation (MSG) satellite. Its performances are evaluated through a comparison with H SAF and NASA operational products (e.g., H60B or H03B and IMERG-E, respectively), of which the algorithms are based on different principles. The results highlight a lower error in precipitation rate estimates for the U-Net with respect to the other products but also some issues in correctly estimating the more intense precipitation (>5 mmh−1). On the other hand, the precipitation detection capabilities of the U-Net outperform the H SAF products for lower precipitation rate, while IMERG-E shows the best performance regardless of the precipitation regime. Furthermore, the U-Net is able to account for and correct the parallax displacement that affects the measurement as the satellite viewing angle increases.

1. Introduction

Precipitation is a crucial component of global hydrological and energy cycles and its measurement is a key feature in a many research topics, such as the management of water resources, hydrology, climate studies, weather forecasts, and natural hazards.
Despite its fundamental role in many contexts of economic and social life on Earth, precipitation estimation still has many problems to overcome in order to meet the needs of operational monitoring applications and the ones of hydrological and climate research. The large spatial and temporal variability of precipitation makes it one of the most difficult atmospheric parameters to accurately retrieve (from satellites and from the ground) since many factors have to be considered in the estimation process: its composition in terms of hydrometeor phase (liquid, solid, and mixed phase), densities and sizes, and problems in the conversion of radiometric measurements into quantitative precipitation estimates [1,2,3,4,5]. In addition, the validation of the precipitation estimates has issues because independent reference data are affected by relatively large errors due to different sources [6].
Rain gauge measurements are the only available direct measurements of precipitation. However, they are punctual measurements affected by errors (e.g., effects of wind and evaporation, dependence on precipitation rate values, etc.) and suffer from their spatial distribution, often being too sparse over land (especially in polar areas and in mountainous and sparsely populated regions) to resolve rainfall intensity variability and almost non-existent over the oceans [7,8]. On the other hand, ground-based weather radars provide indirect measurements of precipitation covering a larger area than rain gauge networks but are affected by uncertainties related to the conversion of reflectivity to precipitation intensity (e.g., calibration, range effects, beam-blocking, clutter, etc.). Both instrument types are inadequate for precipitation monitoring globally and highlight the need to rely on satellite-based observations, which represent the most promising approach for obtaining estimates of global precipitation.
In this perspective, the key role of satellite-borne sensors in estimating precipitation is evident, being the only instruments able to provide global observations. Although important advances have been since the first measurements in the 1970s, quantitative precipitation estimations still pose several problems since the relation between the surface precipitation rate and satellite-based observations is very complex and strongly dependent on the type of precipitation. Remote sensing of precipitation from satellites is largely based on the observation of some cloud top properties (e.g., cloud cover and cloud-top temperatures) in visible (VIS) or infrared (IR) images, or by analyzing the effects (absorption and scattering) of rain drops or large ice particles on microwave (MW) radiation. The two techniques are different in several aspects. Spaceborne passive microwave (PMW) observations from Low Earth Orbit (LEO) satellite systems have great capabilities in estimating precipitation and are very effective for retrieving instantaneous precipitation with greater precision than the VIS/IR technique because precipitating clouds are semi-transparent for MW radiation. However, precipitation retrieval based on PMW has to overcome some limitations, for example the inability to resolve the extreme variability of precipitation both temporally (the re-visiting time of a LEO is not high) and spatially (the PMW spatial resolution is low if compared to VIS/IR). Retrieval techniques based on IR measurements from geostationary (GEO) satellites are suitable for retrieving continuous precipitation due to the higher temporal sampling frequency coupled to the higher spatial resolution than PMW. Many previous uses of IR measurements for precipitation retrieval (e.g., [9,10,11,12,13,14]) have been based on the relationship between the cloud top temperature, estimated from the brightness temperature (TB) of the IR thermal channel around 10.8 µm and the surface precipitation rate following the idea that the cloud that generates the precipitation has a colder top [15,16]. However, this method is not always adequate for rainfall retrieval [17,18] and the use of retrieval techniques based on only IR cloud-top temperature was therefore considered not highly reliable, leading to the development of techniques combining IR and PMW measurements [19,20,21].
The measurement of optical and microphysical cloud parameters, such as the cloud optical thickness, the cloud effective particle radius, and the cloud liquid water content, obtained from multispectral data of new generation satellite systems, has made it possible to overcome these limitations [22,23,24] and to reconsider the potential of IR retrieval. The improvement of the resolution of the spectral data obtained with the Spinning Enhanced Visible and Infrared Instrument (SEVIRI) of the second generation Meteosat geostationary system (MSG), enabling the retrieval of optical and microphysical properties of the clouds, has allowed the improvement of the performance of the IR algorithms [23]. The combination of the brightness temperatures and brightness temperature differences was introduced to provide enhanced information on the clouds’ characteristics [17,25,26,27]. However, it should be noted that most of these techniques rely on the relationship between cloud parameters and precipitation processes. This procedure is highly complex, and there is an indirect (and nonlinear) relationship between the surface precipitation intensity and the physical characteristics of cloud-tops, depending on the rain systems and the climatological regimes [28,29,30,31]. Moreover, the conceptual physical models generate a limited number of parametric relationships between cloud optical parameters and precipitation [17,32], which does not allow any further development of this kind of approach.
In this context, the use of machine learning (ML) techniques has proven to be effective in overcoming these limitations. These approaches are widely adopted in Earth observation because of their ability to approximate, with optimal accuracy, imperfectly known functions, such as the relationships between satellite observations and atmospheric geophysical variables [17,29,32,33,34,35,36,37,38,39]. A fundamental characteristic of these techniques is that the training process eliminates the need for a well-defined physical or numerical model that describes the relationships between the input and the output parameters, allowing the identification of these relationships during the learning phase. It should be also added that the ML approaches, unlike the parametric ones, do not have limitations on the number of predictor variables as they can manage all available information.
An important aspect, linked to the great increase in the available data, is the possibility of using large observational datasets in the training and testing phases of ML systems. These datasets, built matching coincident IR (or MW) satellite observations, rainfall reference measurements, and other ancillary data, allow us to reduce the limitations present in previous approaches, based uniquely on simulations (e.g., a cloud-resolving model coupled with a radiative transfer model) affected by some physical assumptions (e.g., the microphysical scheme of the cloud model, the emissivity of the background surface, the scattering properties of the ice hydrometeors, etc.).
Several studies have highlighted the potential of various ML techniques in exploiting satellite IR data for surface precipitation retrieval. For example, the PERSIANN-CNN model [40], based on a convolutional neural network (CNN), estimates the precipitation rate using infrared and water vapor channels from geostationary satellites. Wang et al. (2020) [39] proposed a satellite rainfall estimation algorithm based on a CNN technique, using satellite IR imageries from the Geostationary Operational Environmental Satellite. On the other hand, Gorooh et al. (2022) [29] developed a CNN algorithm using satellite passive microwave TBs (from the GPM Microwave Imager (GMI) of the GPM Core Observatory (GPM-CO)) combined with IR TBs from geostationary satellites (from NOAA Climate Prediction Center) to instantaneously map surface precipitation intensities. The random forest (RF) approach was used in several other studies. Kühnlein et al. (2014) [17] presented a rainfall retrieval algorithm based on satellite-derived information on cloud-top height, cloud-top temperature, cloud phase, and cloud water path retrieved from MSG SEVIRI data using the RF technique. More recently, Zhang et al. (2021) [32] proposed a new rainfall retrieval technique based on RF using the Advanced Himawari Imager-8 infrared spectrum data and the NCEP operational Global Forecast System forecast information. Li et al. (2021) [41] presented a ML-based regression model using the RF method to derive quantitative precipitation estimations from Fengyun-4 Advanced Geostationary Radiation Imager observations, in conjunction with cloud and physical parameters (from ERA5), and taking three rainstorm events over South China to discuss the proposed model. A performance analysis of different ML approaches was presented by [42], who compared four ML algorithms (random forests (RF), neural networks (NNET), averaged neural networks (AVNNET), and support vector machines) for the prediction of rainfall areas and rainfall rates over Germany, using MSG SEVIRI data, and highlighted the considerable importance of determining suitable predictors for rainfall. Kingsley et al. (2021) [43] proposed a rain area detection scheme, over southwestern Kenya, using a gradient-based adaptive technique applied to IR brightness temperature data of the MSG satellite. It has to be highlighted that the algorithms described above have been developed over small regions around the globe (ranging from 5° × 5° to 30° × 50° at most). This can be considered a crucial point to improve the performances of a neural network since the smaller the area the easier for a ML-based algorithm to be representative of the seasonal and climatological variability of the precipitation.
This paper presents the results of a preliminary study carried out within the EUMETSAT Satellite Application Facility for Operational Hydrology and Water Management (H SAF) towards the development of a new GEO-LEO multispectral precipitation retrieval algorithm based on a ML approach, providing instantaneous precipitation rate maps in Near Real-Time (NRT) from Meteosat Third Generation (MTG) Flexible Combined Imager (FCI) IR/VIS measurements [44]. The study was based on SEVIRI data instead of MTG FCI data due to the unavailability of a large dataset of MTG FCI simulated radiances required for the development of a ML approach. The ML algorithm has been trained using as reference the precipitation rates as observed by the GPM-CO’s Dual-Frequency Precipitation Radar (DPR) and GMI combined product 2B-CMB [45,46]. This study represents a first step for the development of the MTG day-2 algorithm, which will include, in its final version, the integration of MW measurements. Furthermore, the ML-based approach marks a clear change in development of the H SAF GEO/LEO precipitation products, which are currently based on the rapid update blending technique [20], used for both MSG SEVIRI products (P-IN-SEVIRI (H03B) and P-IN-SEVIRI-PMW (H60B)) and for the upcoming day-1 product for MTG FCI. The main aim of this study is to evaluate the performances of the algorithm (based on ML approach) with respect to both H SAF (i.e., H60B and H03B) and NASA (IMERG Early Run) MW/IR precipitation rate operational products.
This paper is structured as follows: Section 2 presents an overview of instruments, data, and products used in the study, as well as the description of the methodology used to develop the algorithm; Section 3 shows the results obtained by applying the algorithm to an independent dataset, while the discussion of the performances together with the conclusions are depicted in Section 4.

2. Materials and Methods

In the first part of this Section, the data and the products considered are illustrated together with a short description of the instruments from which they are derived. The second part of Section describes the methodology adopted.

2.1. Data and Products Used

In the following, an overview of data and products used in the study is outlined: in particular, the MSG SEVIRI and the GPM-CO measurements are utilized to train and test the neural network architecture, and the operational MW/IR precipitation rate products (i.e., H SAF products H03B and H60B and the NASA GPM product IMERG Early Run) are used in a comparative analysis to evaluate the performances of the developed network.

2.1.1. MSG SEVIRI Measurements

The SEVIRI radiometer [47] is the main instrument on-board MSG operating at about 36,000 km altitude. The geostationary satellite considered in this study (Meteosat-10) is located at 0°N, 0°E, providing data over the full disc area (−80°E/+80°E, −80°N/+80°N). SEVIRI is a passive instrument that focuses on detecting the radiation emitted and reflected by the ground and atmospheric components (i.e., gases, cloud particles, precipitation, etc.). The detectors are sensitive to twelve bands distributed among the VIS (channels VIS 0.6 μm and VIS 0.8 μm), near-infrared (channel NIR 1.6 μm), IR (channels IR 3.9 to IR 13.4 μm—for a total of eight channels), and High Resolution Visible (channel HRV 0.75 μm) channels. Table 1 shows the twelve SEVIRI channel properties. The data are provided every 15 min with spatial resolutions ranging from 1 km for the HRV channel to 3 km for the VIS-NIR-IR channels at the sub-satellite point (i.e., at 0°N, 0°E) and decreasing moving away from the sub-satellite point.
In the presence of clouds, the radiation measured by SEVIRI is representative of different cloud characteristics. In this study, we used three IR SEVIRI channels, namely channel 5 (6.25 μm in an absorption band of water vapor), channel 9 (10.8 μm in the thermal window), and channel 11 (13.4 μm in a CO2 absorption band).

2.1.2. The GPM-CO DPR and GMI

The GPM-CO Dual-frequency Precipitation Radar (DPR) and the GPM Microwave Imager (GMI) are the most advanced instruments for the retrieval of precipitation from satellite [48]. The DPR operating at both the Ka- (35 GHz) and Ku-band (13.6 GHz) is the first dual-frequency spaceborne precipitation radar. The dataset used for this study was created when the DPR data were provided through three scanning modes: matched scan, normal scan, and high-sensitivity scan. Currently (i.e., from December 2021), the data are provided in one scanning mode: the full scan. The swath of Ka- and Ku-band radars are 120 and 245 km wide, respectively, while a spatial sampling of 5 km is provided both at the Ka- and at Ku-band. The Ku-band radar normal scan (used for this study) covers the full swath, with 49 angle bins with a vertical resolution of 125 m.
The GMI is a total power conically scanning MW radiometer, measuring radiation in 13 channels, with 10 channels in dual-polarization (V and H) at five central frequencies (10.65, 18.70, 36.5, 89.0, and 166.0 GHz) and 3 channels in single-polarization (V), at 23.8, 183 ± 3, and 183 ± 7 GHz. The GMI swath is 904 km wide, and the spatial resolution ranges from about 4 km × 7 km at the high frequency (>89 GHz), 8 km × 14 km at 36.5 GHz, to 19 km × 32 km at 10 GHz (see [49] for further details). The DPR swath overlaps the central region of the GMI swath. The GMI frequencies have been selected for optimally detecting the wide spectrum of precipitation type and intensities. In particular, the high-frequency channels at 166 GHz and 183.31 GHz are well suited for the detection of light liquid precipitation and snowfall [50,51].
The NASA GPM combined DPR-GMI product (i.e., 2B-CMB) [45,46] combines reflectivity measured by the DPR and brightness temperatures by the GMI, provided only for the matched and normal scan. In this study, the 2B-CMB product (V06A) surface precipitation rate (surfPrecipTotRate variable over the normal scan (i.e., the full DPR swath) has been used as a reference.

2.1.3. H SAF GEO/LEO MW/IR Products

The H SAF P-IN-SEVIRI (H03B) product [20] (operational until 31 January 2023) provides an instantaneous precipitation rate at SEVIRI spatial and temporal resolution over the MSG full disc area. It exploits a collection of time and space overlapping overpasses from SEVIRI IR images and surface precipitation rate estimates derived from LEO PMW radiometers. The precipitation rate products used are the H SAF Level 2 products H01 (precipitation rate from the Special Sensor Microwave Imager/Sounder—SSMIS; [52,53]) and H02B (precipitation rate from the Advanced Microwave Sounding Unit/Microwave Humidity Sounder—AMSU/MHS; [54]). The matching between the IR TBs at 10.8 μm and the precipitation rates builds a look-up table of geo-located relationships between the two quantities, updated as new input datasets (matched PMW precipitation rate and SEVIRI IR measurements) are available in the processing chain. This method is called the “Rapid Update” (RU) blending technique [55]. In particular, the PMW-derived precipitation rate pixels are coupled with time and space-coincident TB data, using a 10 min maximum allowed time offset between the pixel acquisition times and a maximum space offset of 10 km between the pixels coordinates. The data within a box 2.5° wide, as well as the eight surrounding boxes (to provide a fairly smooth transition between neighboring boxes), are used to update the relationship curve between the IR TBs and the precipitation rates. In order to build an ensemble of coincident IR-TBs and precipitation intensities that is statistically significant, the RU can look up to 24 h before the current observation to reach a minimum (75%) box coverage and a minimum number of coincident observations in each box. Thus, the RU technique requires an initial start-up time (~24 h) to allow for establishing meaningful initial relationships all over the considered area.
The H SAF P-IN-SEVIRI-PMW (H60B) product can be considered as an evolution of P-IN-SEVIRI (H03B) (it became operational after the discontinuation of H03B occurred on 31 January 2023). As for H03B, the H60B outputs are provided at the SEVIRI spatial and temporal resolution and always over the full disc area. It is based on the RU techniques but, unlike H03B, the precipitation rates used in the H60B algorithm are obtained from all the available PMW radiometers of the GPM constellation (currently SSMIS, AMSU/MHS, Advanced Microwave Scanning Radiometer 2—AMSR2, Advanced Technology Microwave Sounder—ATMS, and GPM Microwave Imager—GMI). In addition, a dedicated module for the precipitation estimate of convective clouds is present in the operational chain: NEFODINA [56]. NEFODINA uses multispectral information from SEVIRI channels at 10.8, 6.2, and 7.3 μm in order to detect and monitor convective processes and relies on the high temporal repeat cycle of the MSG satellite. Information coming from the IR window channel at 10.8 μm and WV absorption bands (at 6.2 μm and 7.3 μm) are statistically combined to create an accurate detection-and-tracking procedure for Convective Objects. Indeed, the H60B production chain identifies convective areas and computes different relationships between IR TBs and precipitation rates for convective and for stratiform clouds.

2.1.4. The NASA GPM IMERG Product

The Integrated Multi-satellitE Retrievals for GPM (IMERG) is the main official GPM MW/IR product delivered by NASA [19], providing the surface precipitation rate on a 0.1° × 0.1° regular grid every 30 min combining geostationary IR and PMW data of the GPM constellation satellites. The IMERG processing steps include (1) the CMORPH Kalman Filter for quality-weighted time interpolation (“morphing”) of PMW estimates following cloud motion vectors, (2) the PERSIANN-CCS for retrieving PMW-calibrated IR estimates, and (3) the TRMM Multi-satellite Precipitation Analysis products (TMPA) for inter-satellite calibration and monthly gauge adjustment [57]. The IMERG system is processed in three different runs (Early (E), Late (L), and Final (F)) depending on user requirements (in terms of data latency and accuracy) and on the rain gauge networks used for calibration [58]. IMERG-E data are provided about 4 h after the nominal observation time and are mostly directed to users needing quick information related to potential flood or landslide warnings; on the other hand, IMERG-L data are distributed with roughly 14 h latency for agricultural forecasting or drought monitoring purposes. Approximately 3 months after the observation, the final cycle is run to create the IMERG-F data, after the reception of the monthly gauge analysis of the Global Precipitation Climatology Centre (GPCC) [59]. Note that both IMERG-E and IMERG-L runs, considering climatological gauge data for bias adjustment, use only some of the IMERG processing steps, while monthly GPCC gauge analyses feed the IMERG-F run; therefore, the estimates of IMERG-F run are supposed to be the most reliable and accurate [19].
For this study, IMERG-E (V06B) data are used. This choice is justified by the requirement of NRT timeliness (<4 h) of the H SAF products, fulfilled only by IMERG-E. Nevertheless, deep differences remain between the two approaches since the IMERG-E and H SAF products considered here use both GEO IR observations and PMW-based precipitation rate estimates as inputs, while the ML-based algorithm presented in this study uses only GEO IR observations as inputs.

2.1.5. Ancillary Data

Some ancillary data are used during the training phase. Namely, latitude and longitude (provided within the MSG SEVIRI data), from which the surface type is derived (from ESA CCI map). In addition, the cloud top height (CTH, GEO v2021) as estimated by the Nowcasting SAF (NWC SAF) software is also used [60].

2.2. Deep Learning Applied to Satellite Data

This sub-Section is dedicated to the description of the ML approach used to develop the algorithm and of the dataset used to train the neural network. Namely, the ML approach used is the U-Net [61], a convolutional neural network (CNN) architecture chosen because of its capacity to preserve the spatial relationships among the objects.

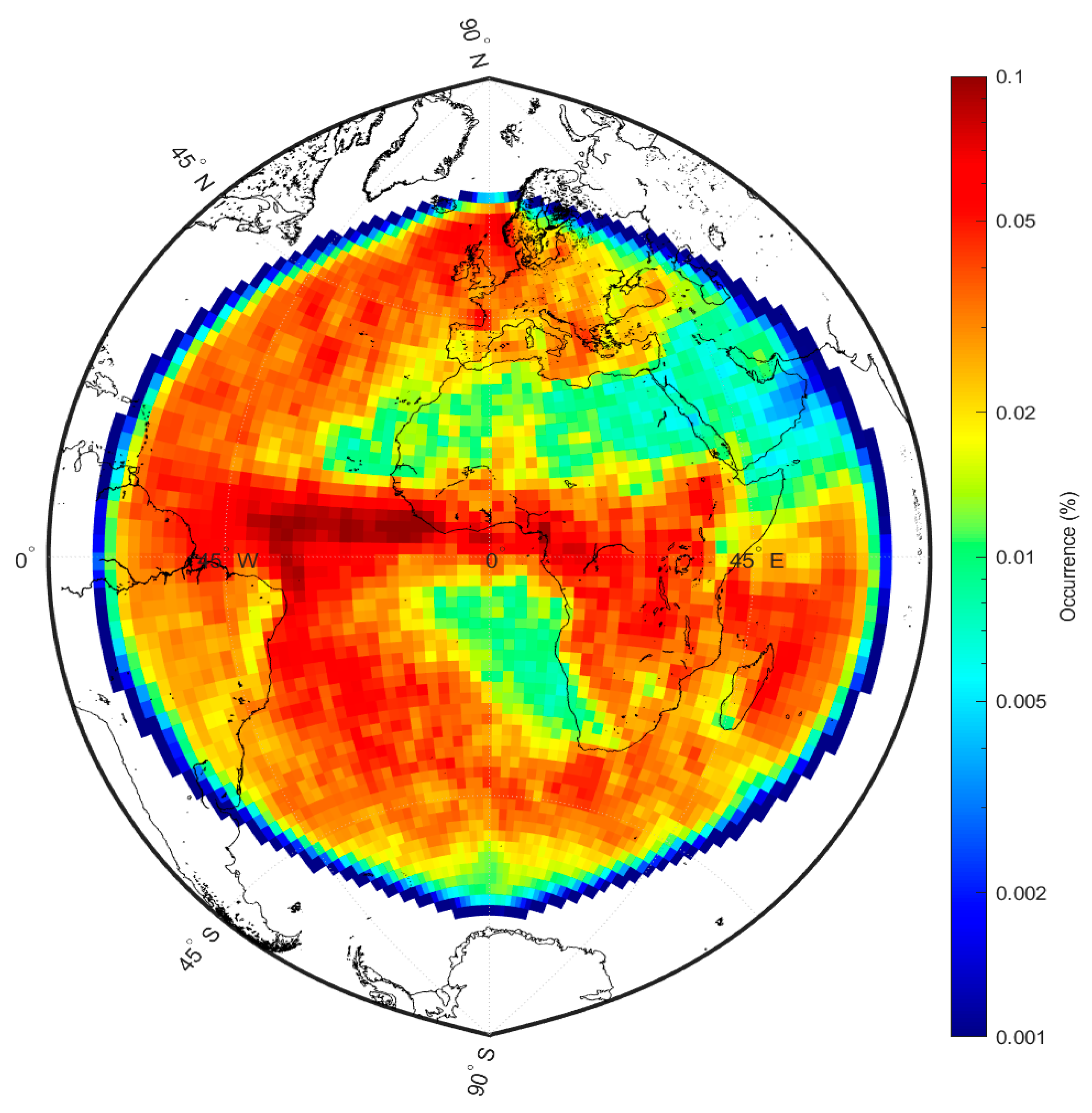
2.2.1. Building Datasets for Learning and Test Phase

The first step in developing a ML approach is to build a reliable dataset to be used for the learning process. The development of a ML-based algorithm involves two main phases: the training phase and the test phase. Within the training phase, a validation process is applied in order to provide a first guess about the reliability of the training network. Once the training phase is completed and the optimal network configuration is set, the test phase can take place. Consequently, in order to complete the whole process, three datasets are needed: the training (TRD), the validation (VD), and the test (TD) dataset.
Both TRD and VD have been built matching the SEVIRI TBs and the DPR-GMI surface precipitation rate coupling each SEVIRI pixel to the closest, in space and time, DPR footprint, i.e., within a maximum distance of 5 km (approximately equal to the DPR footprint size) and a maximum time difference of 7.5 min (half the SEVIRI 15 min temporal resolution). Both TRD and VD are provided at the SEVIRI IR spatial resolution. In particular, nine parameters (i.e., the input parameters) have been coupled with the surfPrecipTotRate variable of the DPR-GMI 2B-CMB product (i.e., the target parameter). The nine input parameters are the following: the three SEVIRI channels mentioned in Section 2.1.1, their difference (i.e., TB ch5-TB ch9 and TB ch9-TB ch11), and the four ancillary parameters described in Section 2.1.5 (i.e., latitude, longitude, surface type, and CTH).
The full disc image has been divided into boxes of 48 × 48 pixel size. The boxes are oversampled, with an 8 pixel step both latitude and longitude in order to avoid the padding issue (see Section 2.2.2), while their size is related to the U-Net depth. In addition, all the pixels within a box have to satisfy the following condition:
l a t 2 + l o n 2 ≤ 65 °
This choice is related to the progressive worsening of the SEVIRI spatial resolution moving away from the sub-satellite point (see also Figure 1). A further check is carried out on the quality of both input and target parameters by excluding SEVIRI images where at least one pixel corresponds to an outlier or a fill value. The matching between the input and the target parameters has been made for the whole year (2017). The TRD consists of boxes where at least one pixel reported a precipitation rate exceeding 5 mmh−1; only 20% of the boxes with no significant precipitation (with no pixels exceeding 5 mmh−1) were included in the TRD. The same method was applied to build the VD; to ensure the independence of the two datasets, they have been populated with different DPR orbits and the boxes included on one dataset were automatically excluded from the other. This led to having two 4D matrices (or tensors) with a size of 48x48xNVARxNIMAGE where NVAR and NIMAGE indicate the number of variables (nine input and one target) and the number of images considered, respectively. The value of NIMAGE is 713,302 for the TRD and 767,259 for the VD.
Figure 1 reproduces the distribution over the MSG full disc of the images included in the TRD. The distribution shows a peak of occurrence on the Equatorial area, while a uniform distribution can be noted in the remaining part of the full disc. The desert areas (i.e., Sahara desert and Arabian Peninsula) are the zones with the lowest occurrence, as well as a part of the South East Atlantic ocean. It has to be highlighted that, being the condition defined in (1) to be satisfied, the images on the edge of the full disc are not included in the TRD and VD.
On the other hand, the TD has been built in a different way. Once the training phase is completed, the U-Net is applied to the SEVIRI image, which has been filtered out by the condition specified in Equation (1) and the output (i.e., the estimated precipitation rate) is stored. This is made for all the SEVIRI acquisitions between the 10th and the 14th of each month from July 2020 to June 2021 for a total of 60 days and 5760 acquisitions. Then, the estimated precipitation rate is matched with the reference (i.e., the surfPrecipTotRate of 2B-CMB product) and averaged at the IMERG resolution (i.e., 0.1° × 0.1°). The same matching is performed for H03B and H60B, as well as for IMERG-E.

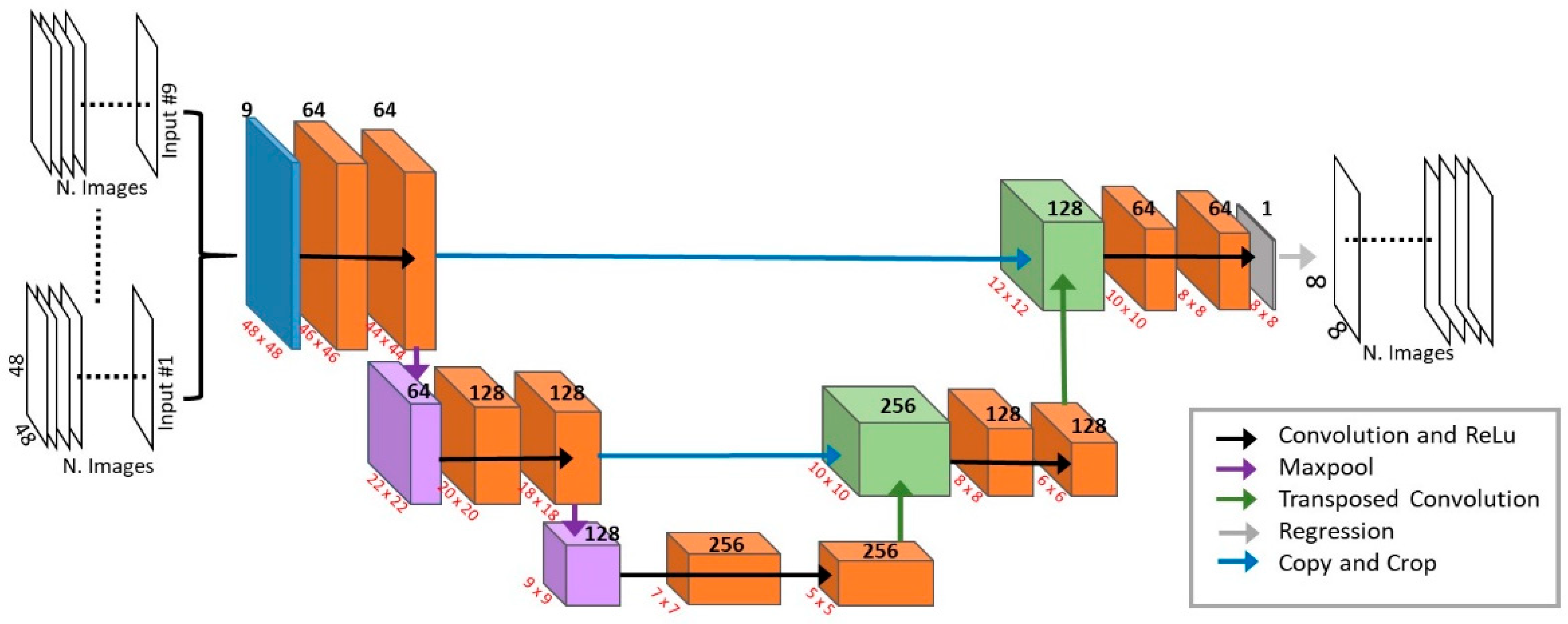
2.2.2. U-Net Configuration and Setting

The U-Net [61] convolutional network architecture has been selected for this study. This type of architecture has proven to be particularly suitable as it allows us to preserve the spatial relationships among the objects. The U-Net belongs to the family of the convolutional neural network (CNN). A CNN typically has three kinds of layers: convolutional layers, pooling layers, and fully connected layers.
A convolutional layer is the main building block of a CNN. It contains a set of filters (a filter is generally smaller than a given image), the parameters of which are changed throughout the training. Each filter convolves with the image and creates an activation map, scanning the image in height and width. In addition, a convolutional layer includes a ReLU (Rectified Linear Unit), an activation function used to introduce non-linearity into the network, allowing it to learn more complex functions. The pooling layer down-samples feature maps by indicating the presence of features in patches of the feature map. Common pooling methods are average pooling and max pooling, which summarize the average presence and the most activated presence of a feature, respectively. The fully connected layer is the last layer in the CNN, taking as input the output of the convolutional and pooling layers. The goal of a fully connected layer is to tune the weight parameters to create a stochastic likelihood representation of each class in which the input image is classified (see [37,39,62,63,64] for further details).
However, the use of a regular CNN does not preserve the information regarding the position of an object in the image (as the U-Net does) but only detects its presence. In the case of segmentation (i.e., when each pixel of an image is labeled with a corresponding class), both pieces of information (classification and localization) are necessary. Consequently, the U-Net is structured in two branches: one with a contraction path (the encoder) aimed at capturing the objects in the image and one (the decoder) with a symmetrical expansion path that allows their precise localization [61]. To rebuild the spatial relationships, an up-sample of the image is required in order to convert a low-resolution image to a high-resolution image. Transposed Convolution, the most preferred choice for this purpose, learns parameters through back propagation to convert a low-resolution image to a high-resolution image.
During the training process, the network hyperparameters are optimized. They can be divided into model hyperparameters that define the U-Net structure and training algorithm hyperparameters that influence the speed and the quality of the training process. Different hyperparameters can be set in order to obtain the most accurate and generalizable U-Net. During this study, the hyperparameter optimization involved firstly the optimization of the network structure, including the optimal setting of: (1) the encoder depth; (2) the number of network filters, that represents the number of output channels for the first encoder stage; (3) the use of max pooling layers instead of mean pooling; (4) the use of batch normalization layers; and (5) the use of 0-padding in the convolutional layers. The final U-Net is composed of two encoder stages, with 64 network filters in the first stage. Moreover, it makes use of max pooling and does not include any batch normalization layer or 0-padding. In particular, the 0-padding option consists of adding zero values at the edge of each image in order to perform the convolution even on the edge of the image. This corresponds to a modification of the input values on one hand, but, on the other hand, it ensures that the output feature images will have the same size as the input feature images. Not applying the “zero padding option”, a convolution layer returns an output feature image that is smaller than the input feature image. In particular, since the size of the input image used in this study is 48 × 48, the size of the output image, after many convolution and transposed convolution layers, is 8 × 8. Figure 2 summarizes what is described above highlighting the layers associated with each stage with a schematic representation of input and output images. It is worth noting that the U-Net structure illustrated in Figure 2 (together with the hyperparameter settings described above) is not a generic representation of the U-Net structure but is customized for the aim of this study.

3. Results

The evaluation of the performances of the U-Net is obtained by applying it to the TD (independent from the training dataset) and calculating the error statistics with respect to the DPR-GMI precipitation rates, used as reference. The same procedure has been applied and the same error statistics have been calculated for the other products (i.e., the two H SAF products H03B and H60B and the NASA official product IMERG) in order to perform a comparison between the results obtained for the U-Net and these operational products. The performances are evaluated at six different spatial grid sizes (from 0.1° × 0.1°, the IMERG grid size, up to 1° × 1°) and both in terms of continuous and categorical statistical scores. Namely, the continuous statistical scores considered are the mean error (ME), the mean absolute error (MAE), the root mean square error (RMSE), and the Pearson correlation coefficient (CC). On the other hand, the categorical scores are the probability of detection (POD), the false alarm ratio (FAR), and the critical success index (CSI). For a detailed description of both continuous and categorical scores, refer to [65]. In addition, the capability of the U-Net in estimating and taking into account the parallax displacement is also evaluated.

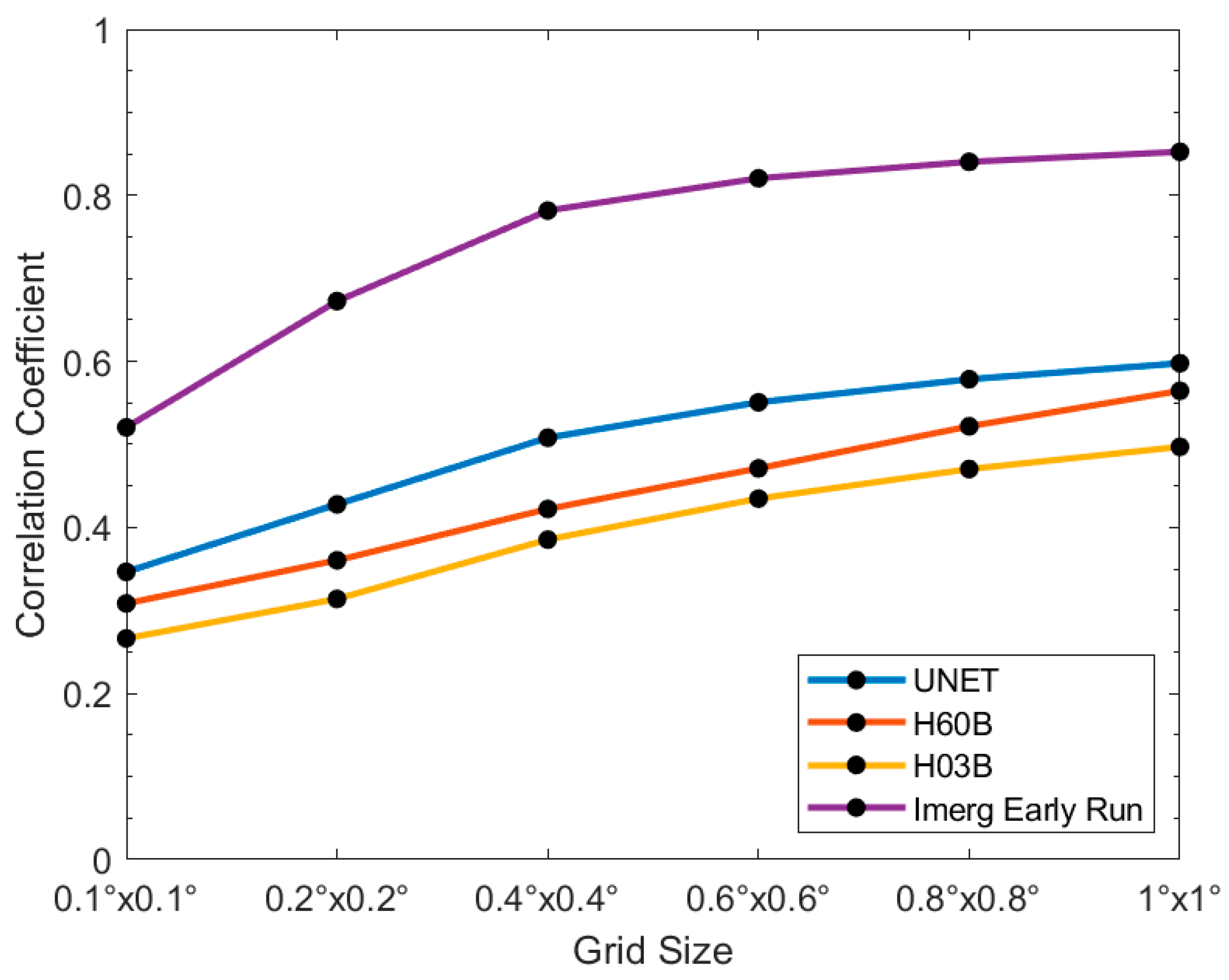
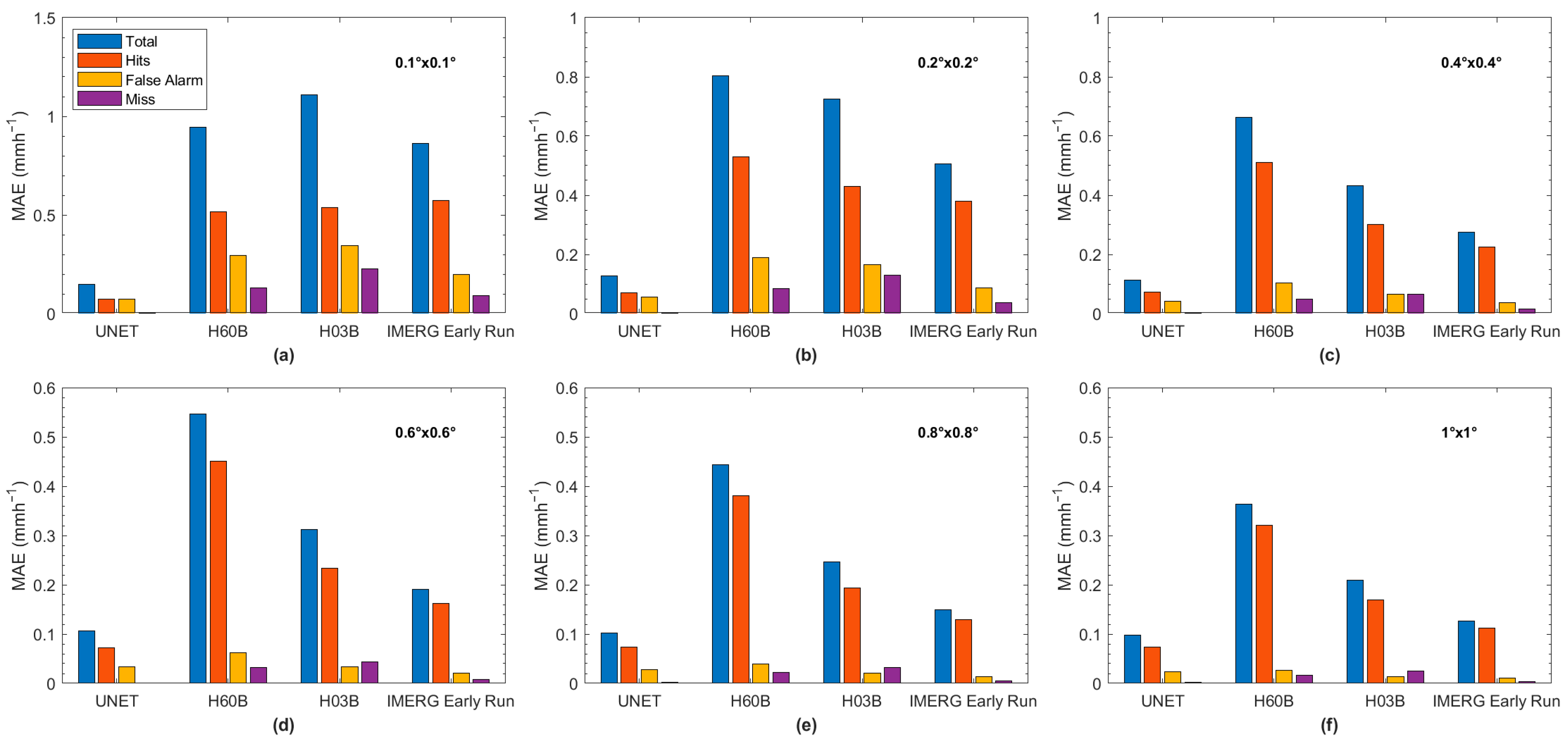
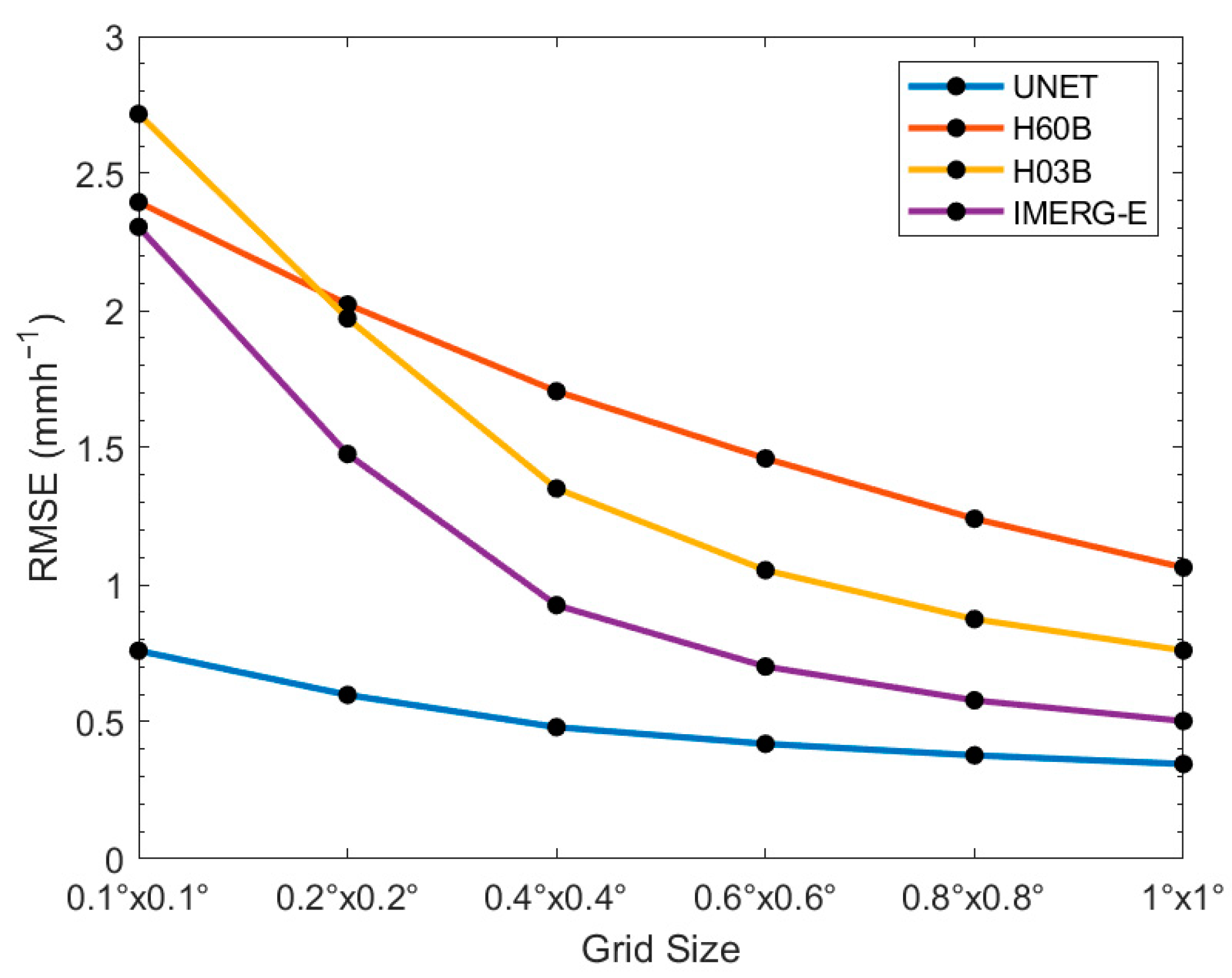
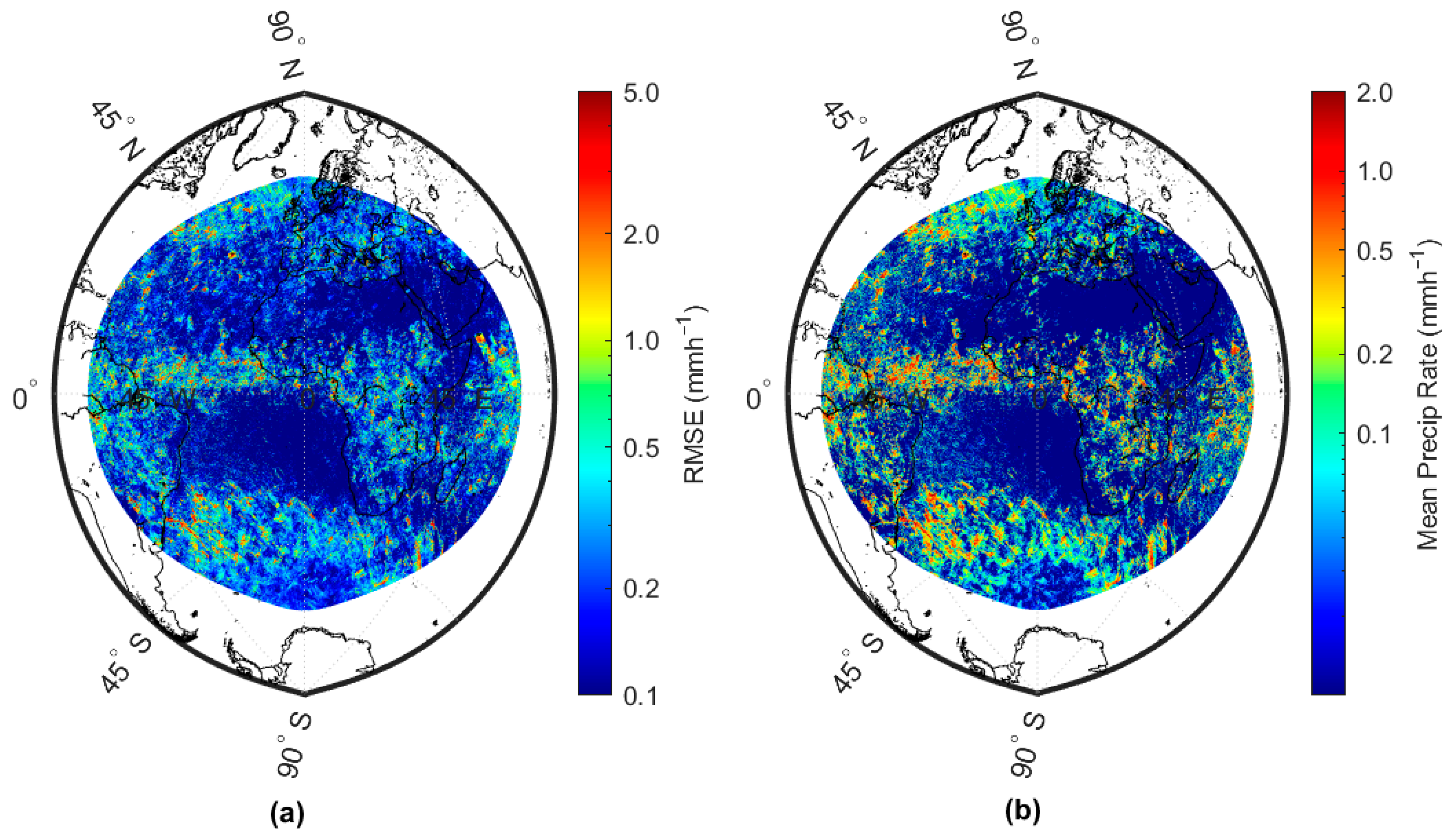
3.1. Precipitation Rate Quantitative Analysis

Figure 3 shows the CC at the six grid sizes considered, for the U-Net and the three products considered. The correlation increases as the grid size increases for all products. In addition, the U-Net shows higher CC values than both H03B and H60B at all the grid sizes reaching 0.60 at 1° × 1°. The best performances in terms of CC are obtained by IMERG-E.
The MAE provides an indication about the average magnitude of estimation errors in a given dataset and therefore is a scalar measure of its accuracy, with values ranging between 0 (perfect score) and infinity. It is calculated by eliminating the pixel pairs (i.e., the reference and the estimation) both corresponding to no rain (i.e., 0 and 0 mmh−1, respectively). Figure 4 shows the MAE at different grid sizes and the contribution of hits, false alarms, and miss pixel pairs to the total MAE. The decomposition of total MAE aims to quantify the contribution to the total error for the cases where each satellite product wrongly detects or not the precipitation, as well as for the cases where both satellite products and reference detect precipitation. All the products show a decrease in MAE from fine to coarse grid size, with the U-Net reporting the lowest values regardless of the grid size. The contribution of hits, false alarm, and miss components does not show a univocal behavior among the different products, and their relative contribution changes at the different grid size. The contribution of miss cases to the MAE is null or extremely low for the U-Net, highlighting that the precipitation fraction lost because of missed precipitation is negligible. This is true also for IMERG-E, which shows decreasing miss contribution values as the grid size increases. Furthermore, for all products except H03B, the miss contribution is always lower than hits and false alarms contributions. H03B shows a higher contribution of misses with respect to the false alarms at grid sizes greater than 0.4° × 0.4°.
With respect to the MAE, the root mean square error (RMSE) is much more sensitive to large errors and could be misleading in presence of outliers, which can make the RMSE increase dramatically. Figure 5 shows the trend of the RMSE at the six grid sizes considered. The RMSE decreases as the grid size increases because of the smoothing of co-location errors and of the spatial averaging of the precipitation peaks and outliers. In Figure 5, the U-Net has the lowest RMSE at all grid sizes among the products considered. IMERG-E shows the lower RMSE at all grid sizes excluding the U-Net, followed by H03B and H60B. The only exception to this trend is the 0.1 × 0.1 grid, where H60B shows a lower RMSE than H03B.
A specific analysis on the U-Net results has been dedicated to identifying the areas where larger errors occur. To this end, the RMSE spatial distribution over the study area has been evaluated (Figure 6). Figure 6a shows larger RMSE values over the equatorial zone and over the north and south Atlantic Ocean. These are the areas where higher values of precipitation intensity are registered (Figure 6b). This could partially explain the larger error, evidencing some difficulties in estimating high precipitation rates. At the same time, it has to be taken into account also the degradation of the MSG SEVIRI spatial resolution moving away from the sub-satellite point that could have an impact on the U-Net performance, when applied to the TD, and can be an issue during the learning phase. In addition, Figure 6b highlights that higher mean precipitation rate values occurring at the edge of the TD area (other than on the equatorial zone), where the degradation of spatial resolution plays a role. The combination of the two issues could result in higher RMSE values.
Summarizing the results shown in this Section, it has to be highlighted that RMSE and MAE are smaller for the U-Net than for IMERG-E, while IMERG-E shows a higher correlation coefficient at all grid sizes. This is a direct consequence of the underestimation of the intense precipitation rates from the U-Net, which will be discussed in the next Section.

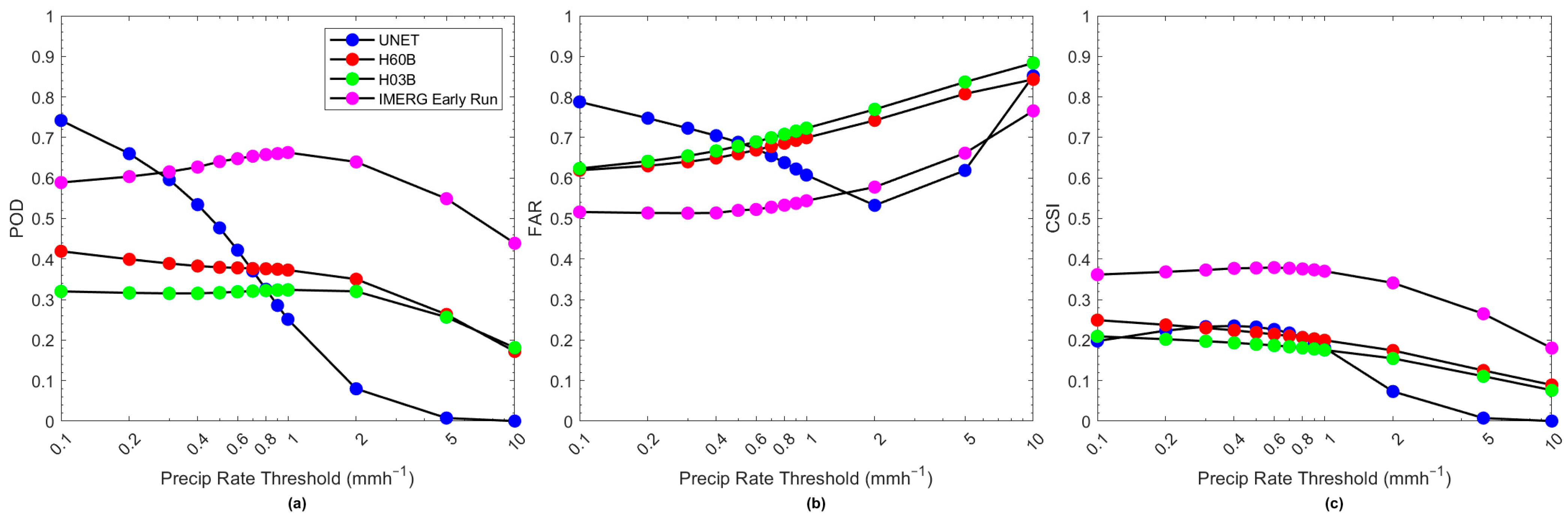
3.2. Precipitation Rate Detection Analysis

The U-Net approach has a great advantage in that the trained network is able to distinguish the precipitating areas from the not precipitating areas, other than to estimate the precipitation rate. This is related to the fact that the input data include both precipitating and not precipitating areas. This enables the U-Net to recognize the precipitating areas and to estimate the precipitation rate on one hand, and on the other hand, to recognize the areas where there is no precipitation. In order to investigate the detection skills of the U-Net, some categorical scores have been calculated, namely the POD, FAR, and CSI. All these three scores range between 0 and 1, with 1 being the perfect score for the POD and CSI, and 0 being the perfect score for FAR. Different precipitation rate thresholds have been applied, while these scores have been calculated only for the 0.1° × 0.1° grid size. The thresholds are applied to both the reference and the estimate, i.e., a correct detection occurs only if both the reference and the estimate at a given pixel have values greater than the threshold. Figure 7 shows the trend of the POD (Figure 7a), FAR (Figure 7b), and CSI (Figure 7c) with respect to the precipitation rate thresholds. For the U-Net, H03B, and H60B, the POD decreases, moving from lower to higher precipitation rate thresholds with higher values (more than 0.9) for the U-Net at very low precipitation rates (Figure 7a). IMERG-E instead shows a maximum value of the POD around 1 mmh−1. Moving towards higher precipitation rates, the U-Net shows worse performances, with IMERG-E outperforming all the other products. It is worth noting that at very high precipitation rate thresholds, all the products evidence a lower capacity in correctly detecting the precipitating areas. The FAR (Figure 7b) shows a decreasing trend up to 2 mmh−1 for the U-Net, followed by increasing values at higher precipitation rates. On the other hand, for all the other products the FAR decreases, moving from a 0 to 0.1 mmh−1 threshold to constantly increase for higher precipitation rate thresholds. It has to be highlighted that all products show an FAR greater than 50% for all the thresholds, with values higher than 70% for precipitation rates higher than 10 mmh−1. In general, this analysis reveals critical issues for all the algorithms in correctly locating the more intense precipitation areas. IMERG-E seems to be the algorithm with less strong issues as it generally shows the lowest FAR and highest POD. The U-Net algorithm shows critical issues for both the very low rates of precipitation (between 0 and 0.1 mmh−1) and for the moderate to intense rates (greater than 1 mmh−1). The CSI (Figure 7c), summarizing the information from the POD and FAR, highlights that IMERG-E is the best product in detecting precipitation, while the U-Net shows a maximum at 0.4 mmh−1, outperforming the H SAF products at mid-low precipitation rate thresholds (0.2–0.8 mmh−1). It is worth noting that the new H SAF MW/IR product H60B, currently operational, outperforms the previous H03B which has been superseded.
A very important difference between the U-Net and the other products is the lack of MW-base estimates, which are crucial not only for the estimation of the intense precipitation rates but also for delineating the very low precipitation patterns.
The mean error (ME) quantifies the overestimation and the underestimation with respect to the reference. Table 2 shows the percent ME calculated as follows:
M E % = 1 N ∑ i = 1 N ( E i − R e f i ) R e f ¯
where Ei is the estimate precipitation rate (i.e., the output of the U-Net, H60B, H03B, and IMERG-E, respectively), Refi is the reference precipitation rate (i.e., the 2B-CMB precipitation rate product), and R e f ¯ is the mean reference precipitation rate. Table 2 presents the percent mean error for three different thresholds: 0, 1, and 10 mmh−1. In this computation, the threshold acts for the selection of the areas, i.e., the mean precipitation rate and the mean error are evaluated only in areas where both the estimates and the reference (i.e., the DPR-GMI) retrieved a precipitation rate higher than the threshold. It is clear from Table 2 that all considered products overestimate the rainfall rates globally (for a 0 mmh−1 threshold); however, the U-Net shows the lowest mean error. For the highest threshold (10 mmh−1), all products underestimate the precipitation rates. This is coherent with the results shown in Figure 7, where the POD for the intense precipitation is relatively low (e.g., around 50% and 0% for the IMERG-E and U-Net products, respectively). Above the 1 mmh−1 threshold, IMERG-E shows a very low positive ME% (around 5%), while all other products underestimate precipitation. Table 2 evidences that the U-Net severely underestimates the mid and high precipitation rates, with respect to the other products. This issue is particularly relevant also because the MTG day-2 product is meant to provide support to operational hydrology and severe weather monitoring.

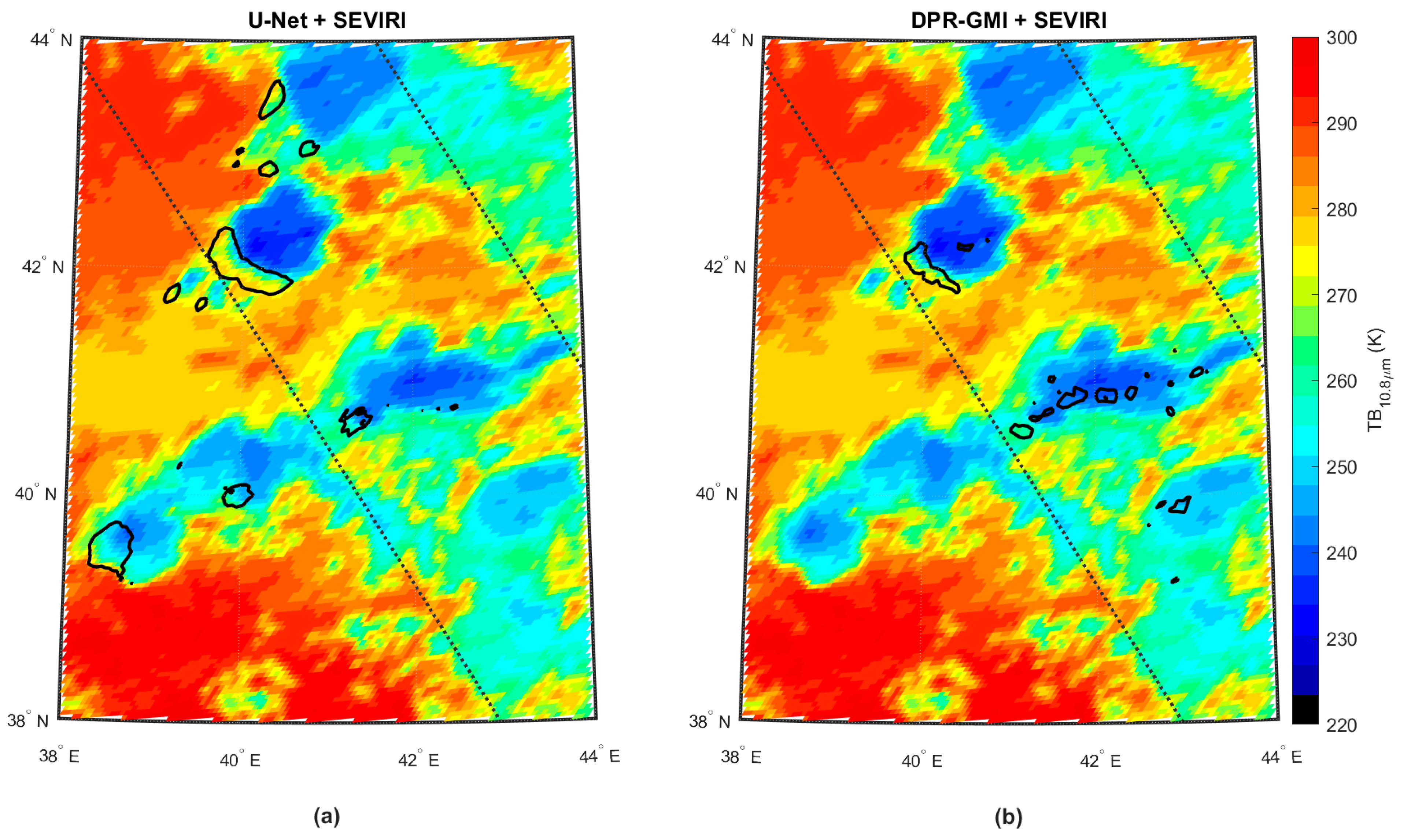
3.3. Parallax Displacement Error

One important issue that has to be accounted for in GEO IR-based precipitation estimates is the displacement of satellite data due to the parallax error (particularly severe at large viewing angles and for high clouds). If one out of the two sources of parallax error is well known (i.e., the viewing angle which is a function of latitude and longitude), the second one (i.e., the cloud height) has to be estimated. Even if the cloud height was estimated with high accuracy and the cloud was correctly displaced in its real location, it would not be easy to replace the “hole” left by this correction. A very significant result obtained is that the trained U-Net is able to correct (or at least mitigate) the parallax error without being trained against a dataset already corrected for parallax displacement. Figure 8 shows the cloud structure (red to blue colormap, with the blue representing the coldest and highest clouds) and the areas with the maximum precipitation rates based on the U-Net and on the DPR-GMI 2B-CMB product (black lines, indicating the 95th percentile of the precipitation rate for each product). The U-Net locates the areas with the maximum precipitation rates shifted with respect to the areas with the lowest MSG TBs (Figure 8a), but they are displaced to the southwest. This is in excellent agreement with the maximum precipitation areas detected by DPR-GMI (affected by a negligible cloud parallax error—Figure 8b).
As a comparative test, a simple parallax correction tool has been developed. The SEVIRI data used in the TDR have been corrected by applying a shift Δx to each pixel and channel proportional to the CTH as
Δ x = C T H ⋅ t a n ( θ )
where θ is the MSG satellite viewing angle. The direction of the shift was defined by the azimuth of MSG. This correction has been used to build a new training dataset that has been exploited for training an additional U-Net, with the same architecture and hyperparameter of the U-Net used within this study. The precipitation rates predicted by the two U-Nets have been compared with the reference DPR precipitation in the TD. The results showed how the not-parallax-corrected U-Net outperformed the parallax-corrected U-Net in terms of accuracy (RMSE, MAE) and detection of precipitation (POD, FAR, CSI). This evidences the great potentialities and capabilities of the U-Net in correcting the parallax displacement.

4. Discussion

The algorithm performance has been evaluated through an independent DPR-GMI dataset and compared to the performance obtained by the MW/IR operational H SAF program products (i.e., the currently operational H60B and the previous H03B operational until 31 January 2023) and by the IMERG Early Run (V06B) (the NASA GPM official product). The metrics used to quantify the error in the precipitation rate estimation (i.e., MAE and RMSE) show lower values of the U-Net than the other products at all the grid sizes considered (e.g., the U-Net RMSE never exceeds 1 mmh−1, while the lowest values for the other products are obtained by IMERG-E ranging between 2.2 and 0.55 mmh−1). On the other hand, the metrics used to verify the detection of the precipitating areas (i.e., POD, FAR, and CSI) show better performances of the U-Net with respect to the H SAF products only for some precipitation rate regimes (0.2–0.6 mmh−1), with two main issues at very low (especially in the 0–0.1 mmh−1 range) and at moderate to high precipitation rates. The first issue is related to very high values of the POD and FAR caused by an enlargement of the low precipitation areas (blurring effect) with respect to the DPR-GMI reference. This problem also affects the other products considered but is more severe for the U-Net. However, the quantitative error statistics of the U-Net are not strongly impacted by the large number of false alarms as the MAE due to false alarms (see Figure 4) and the ME% (for rainfall rates greater than 0 mmh−1, see Table 2) are relatively low. The second issue is related to the difficulty of the U-Net in estimating higher precipitation rates. This issue is particularly relevant in heavy rainfall monitoring and flood warning applications. One reason for this difficulty could lie in the undersampling of moderate to high precipitation rates. This was partially mitigated in the building of the TRD by putting a threshold on the precipitation rate (i.e., only boxes with at least one pixel > 5 mmh−1 have been selected) and selecting a small fraction (20%) of the remaining images (i.e., images with very low or null precipitation rates). Moreover, the U-Net algorithm is based only on IR observations, while the other products exploit PMW estimates from several PMW radiometers. It is well known that the PMW precipitation retrieval algorithms are affected by substantially lower errors than combining VIS/IR and MW data (e.g., IMERG-E, H60B) because MW radiation penetrates clouds interacting with all liquid and ice cloud vertical layers, while precipitating clouds are completely opaque to VIS/IR radiation. Despite the large use of PMW observations, the other products show similar but less severe issues, i.e., the IMERG-E and H SAF products show issues both in the detection of very low precipitation (POD < 65% and FAR > 58% at 0 mmh−1) and in the estimate of intense rainfall (POD < 55% and FAR > 75% at 10 mmh−1). It has to be also highlighted that the precipitation detection capability of IMERG-E is better than the U-Net (and H SAF products) regardless of the precipitation regime.

5. Conclusions

In this study, a convolutional neural network-based algorithm has been developed by exploiting the U-Net architecture to estimate the precipitation rate from MSG SEVIRI measurements. The precipitation rate values provided by the DPR-GMI combined product (i.e., 2B-CMB) have been taken as references during the training phase. At the same time, the algorithm provides its output over the full disc area. The algorithm accuracy has been tested using an independent dataset of DPR-GMI measurements and the performances compared with one of three algorithms: (1) the MW/IR operational H SAF program product (H60B), (2) the previous H SAF product (H03B), and (3) the IMERG Early Run (V06B) product from NASA GPM. The analysis of the MAE and RMSE show lower values for the U-Net than for the other products for all the grid sizes considered. Conversely the POD, FAR, and CSI, used to verify the detection of the precipitating areas, show that the U-Net has better performances then the H SAF products only in the precipitation rate regime between 0.2 mmh−1 and 0.6 mmh−1, with two main issues at very low (especially in the 0–0.1 mmh−1 range) and at moderate to high precipitation rates. Moreover, for all precipitation regimes, the precipitation detection capability of IMERG-E is better than the U-Net and H SAF products.
In spite of these problems, the performances of the -Net do not appreciably differ with respect to what is present in the literature for IR-only algorithms, even if the study area is much larger compared to other studies. Based on our knowledge, this is the first deep learning-based study trying: (1) to estimate the precipitation rate by using only IR channels (and CTH variable) and, (2) to consider, as the study area, the whole full disc observed by a geostationary satellite and, (3) to apply a single ML-based module to both detect and estimate the precipitation rate. It is worth noting that the development of an algorithm applicable to the full disc area entails a number of problems to be faced. Above everything, an MSG image is a snapshot of different seasons, different times of the day, and different precipitation regimes. Other studies on ML-based approaches using geostationary data [32,41,66] to estimate the precipitation rate show slightly better statistical scores, but they are applied over small regions. On the other hand, one of the more promising results obtained from this study is that the U-Net, other than detecting and estimating the precipitation rate, is also able to correctly locate the precipitating area accounting for the parallax displacement. This allows us to address an issue that is generally treated with a dedicated module.
The U-Net algorithm can be considered as a first guess module of the future H SAF MTG day-2 product; however, further development is needed. Both the issues evidenced by this study, the overestimation of the low rate and underestimation of the intense rates, could be caused by the smoothing effect of convolutional neural networks. This effect has been observed in other deep learning applications and has been addressed by some authors by using the conditional Generative Adversarial Network approach [66] which will be tested in the future version of the algorithm. Moreover, the use of short sequences of MSG images could provide valuable information that can be exploited by deep learning models using proper architectures (e.g., recurrent and Long-Short Term Memory neural networks). Finally, this study evidences the need for synergic use of the PMW and IR data, which has been proven to give very promising results [26,63].

Author Contributions

Conceptualization, L.P.D., D.C. and P.S.; methodology, L.P.D., D.C. and P.S.; software, L.P.D., P.S. and D.C.; formal analysis, L.P.D., D.C. and P.S.; investigation, L.P.D., D.C. and P.S.; data curation, L.P.D.; writing—original draft preparation, L.P.D., D.C. and P.S.; writing—review and editing, L.P.D., D.C., P.S., G.P. and S.D.; visualization, L.P.D. and D.C.; supervision, G.P. and S.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the EUMETSAT Satellite Application Facility for Hydrology and Water Management (H SAF) Third Continuous Development and Operation Phase (CDOP-3). H-SAF Agreement H-SAF_CDOP-3 Prot. 0001479 28-03-2107.

Data Availability Statement

The MSG SEVIRI dataset is available through the Eumetsat Data Store https://data.eumetsat.int/ (last access 15 March 2023). The DPR-GMI data can be downloaded from https://storm.pps.eosdis.nasa.gov/storm/after user registration (last access 15 March 2023).

Acknowledgments

The authors express sincere gratitude to Davide Melfi and Claudio Giorgi, who were directly involved in the design and development of the H SAF products H60 and H03, as well as to the H SAF management.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

List of Acronyms

AcronymDefinitionAcronymDefinition
AMSUAdvanced Microwave Sounding UnitMLMachine Learning
AMSR2Advanced Microwave Scanning Radiometer 2MHSMicrowave Humidity Sounder
ATMSAdvanced Technology Microwave SounderMSGMeteosat geostationary system Second Generation
AVNNETAveraged Neural NetworkMTGMeteosat Third Generation
CCPearson correlation coefficientNASANational Aeronautics and Space Administration
CNNconvolutional neural networkNCEPNational Centers for Environmental Prediction
CSICritical Success IndexNNETNeural Network
CTHCloud Top HeightNOAANational Oceanic and Atmospheric Administration
DPRDual-Frequency Precipitation RadarNRTNear Real-Time
ESAEuropean Space AgencyNWC SAFNowcasting SAF
FARFalse Alarm RatioPMWPassive MicroWave
FCIFlexible Combined ImagerPODProbability of Detection
GEOGeostationaryRFRandom Forest
GMIGPM Microwave ImagerRMSERoot Mean Square Error
GPCCGlobal Precipitation Climatology CentreSEVIRISpinning Enhanced Visible and Infrared Instrument
GPMGlobal Precipitation Measurement MissionSSMISSpecial Sensor Microwave Imager/Sounder
GPM-COGPM Core ObservatorySTDStandard Deviation
H SAFHydrology SAFTBBrightness Temperature
HRVHigh Resolution VisibleTDTest Dataset
IMERGIntegrated Multi-satellitE Retrievals for GPMTRDTraining Dataset
IRInfraredVDValidation Dataset
LEOLow Earth OrbitVISVisible
MAEMean Absolute Error

References

  1. Iturbide-Sanchez, F.; Boukabara, S.-A.; Chen, R.; Garrett, K.; Grassotti, C.; Chen, W.; Weng, F. Assessment of a Variational Inversion System for Rainfall Rate Over Land and Water Surfaces. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3311–3333. [Google Scholar] [CrossRef]
  2. Kidd, C.; Bauer, P.; Turk, J.; Huffman, G.J.; Joyce, R.; Hsu, K.-L.; Braithwaite, D. Intercomparison of High-Resolution Precipitation Products over Northwest Europe. J. Hydrometeorol. 2012, 13, 67–83. [Google Scholar] [CrossRef]
  3. Kidd, C.; Matsui, T.; Chern, J.; Mohr, K.; Kummerow, C.; Randel, D. Global Precipitation Estimates from Cross-Track Passive Microwave Observations Using a Physically Based Retrieval Scheme. J. Hydrometeorol. 2016, 17, 383–400. [Google Scholar] [CrossRef]
  4. Levizzani, V.; Cattani, E. Satellite Remote Sensing of Precipitation and the Terrestrial Water Cycle in a Changing Climate. Remote Sens. 2019, 11, 2301. [Google Scholar] [CrossRef]
  5. Sorooshian, S.; AghaKouchak, A.; Arkin, P.; Eylander, J.; Foufoula-Georgiou, E.; Harmon, R.; Hendrickx, J.M.H.; Imam, B.; Kuligowski, R.; Skahill, B.; et al. Advanced Concepts on Remote Sensing of Precipitation at Multiple Scales. Bull. Am. Meteorol. Soc. 2011, 92, 1353–1357. [Google Scholar] [CrossRef]
  6. Kirstetter, P.-E.; Hong, Y.; Gourley, J.J.; Chen, S.; Flamig, Z.; Zhang, J.; Schwaller, M.; Petersen, W.; Amitai, E. Toward a Framework for Systematic Error Modeling of Spaceborne Precipitation Radar with NOAA/NSSL Ground Radar–Based National Mosaic QPE. J. Hydrometeorol. 2012, 13, 1285–1300. [Google Scholar] [CrossRef]
  7. Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, How Much of the Earth’s Surface Is Covered by Rain Gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef]
  8. Hong, Y.; Tang, G.; Ma, Y.; Huang, Q.; Han, Z.; Zeng, Z.; Yang, Y.; Wang, C.; Guo, X. Remote Sensing Precipitation: Sensors, Retrievals, Validations, and Applications. In Observation and Measurement; Li, X., Vereecken, H., Eds.; Ecohydrology; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–23. ISBN 978-3-662-47871-4. [Google Scholar]
  9. Ebert, E.E.; Manton, M.J. Performance of Satellite Rainfall Estimation Algorithms during TOGA COARE. J. Atmos. Sci. 1998, 55, 1537–1557. [Google Scholar] [CrossRef]
  10. Negri, A.J. A TRMM-Calibrated Infrared Rainfall Algorithm Applied over Brazil. J. Geophys. Res. 2002, 107, 8048. [Google Scholar] [CrossRef]
  11. Scofield, R.A.; Kuligowski, R.J. Status and Outlook of Operational Satellite Precipitation Algorithms for Extreme-Precipitation Events. Weather Forecast. 2003, 18, 1037–1051. [Google Scholar] [CrossRef]
  12. Lahuerta, J.A.; Lliso, L.; Ripodas, P. Algorithm Theoretical Basis Document for the Precipitation Product Processors of the NWC/GEO 2021. Available online: https://www.nwcsaf.org/Downloads/GEO/2021/Documents/Scientific_Docs/NWC-CDOP3-GEO-AEMET-SCI-ATBD-Precipitation_v1.0.1.pdf (accessed on 18 November 2023).
  13. Lahuerta, J.A.; Lliso, L.; Ripodas, P. Scientific and Validation Report for the Precipitation Product Processors of the NWC/GEO 2022. Available online: https://www.nwcsaf.org/Downloads/GEO/2021/Documents/Scientific_Docs/NWC-CDOP3-GEO-AEMET-SCI-VR-Precipitation_v2.0.1.pdf (accessed on 18 November 2023).
  14. Karagiannidis, A.; Lahuerta, J.A.; Calbet, X.; Lliso, L.; Lagouvardos, K.; Kotroni, V.; Ripodas, P. Efficiency of the NWC SAF Version 2021 CRRPh Precipitation Product: Comparison against Previous NWC SAF Precipitation Products and the Influence of Topography. Climate 2023, 11, 34. [Google Scholar] [CrossRef]
  15. Arkin, P.A.; Meisner, B.N. The Relationship between Large-Scale Convective Rainfall and Cold Cloud over the Western Hemisphere during 1982–84. Mon. Weather. Rev. 1987, 115, 51–74. [Google Scholar] [CrossRef]
  16. Adler, R.F.; Negri, A.J. A Satellite Infrared Technique to Estimate Tropical Convective and Stratiform Rainfall. J. Appl. Meteor. 1988, 27, 30–51. [Google Scholar] [CrossRef]
  17. Kühnlein, M.; Appelhans, T.; Thies, B.; Nauß, T. Precipitation Estimates from MSG SEVIRI Daytime, Nighttime, and Twilight Data with Random Forests. J. Appl. Meteorol. Climatol. 2014, 53, 2457–2480. [Google Scholar] [CrossRef]
  18. Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of Near-Real-Time Precipitation Estimates from Satellite Observations and Numerical Models. Bull. Amer. Meteor. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
  19. Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.-L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Integrated Multi-Satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In Satellite Precipitation Measurement; Levizzani, V., Kidd, C., Kirschbaum, D.B., Kummerow, C.D., Nakamura, K., Turk, F.J., Eds.; Advances in Global Change Research; Springer International Publishing: Cham, Switzerland, 2020; Volume 67, pp. 343–353. ISBN 978-3-030-24567-2. [Google Scholar]
  20. Mugnai, A.; Casella, D.; Cattani, E.; Dietrich, S.; Laviola, S.; Levizzani, V.; Panegrossi, G.; Petracca, M.; Sanò, P.; Di Paola, F.; et al. Precipitation Products from the Hydrology SAF. Nat. Hazards Earth Syst. Sci. 2013, 13, 1959–1981. [Google Scholar] [CrossRef]
  21. Ricciardelli, E.; Cimini, D.; Di Paola, F.; Romano, F.; Viggiano, M. A Statistical Approach for Rain Intensity Differentiation Using Meteosat Second Generation–Spinning Enhanced Visible and InfraRed Imager Observations. Hydrol. Earth Syst. Sci. 2014, 18, 2559–2576. [Google Scholar] [CrossRef]
  22. Nauss, T.; Kokhanovsky, A.A. Assignment of Rainfall Confidence Values Using Multispectral Satellite Data at Mid-Latitudes: First Results. Adv. Geosci. 2007, 10, 99–102. [Google Scholar] [CrossRef]
  23. Thies, B.; Nauß, T.; Bendix, J. Precipitation Process and Rainfall Intensity Differentiation Using Meteosat Second Generation Spinning Enhanced Visible and Infrared Imager Data. J. Geophys. Res. 2008, 113, D23206. [Google Scholar] [CrossRef]
  24. Cattani, E.; Torricella, F.; Laviola, S.; Levizzani, V. On the Statistical Relationship between Cloud Optical and Microphysical Characteristics and Rainfall Intensity for Convective Storms over the Mediterranean. Nat. Hazards Earth Syst. Sci. 2009, 9, 2135–2142. [Google Scholar] [CrossRef]
  25. Lazri, M.; Ameur, S. A Satellite Rainfall Retrieval Technique over Northern Algeria Based on the Probability of Rainfall Intensities Classification from MSG-SEVIRI. J. Atmos. Sol. Terr. Phys. 2016, 147, 106–120. [Google Scholar] [CrossRef]
  26. Feidas, H.; Giannakos, A. Classifying Convective and Stratiform Rain Using Multispectral Infrared Meteosat Second Generation Satellite Data. Theor. Appl. Climatol. 2012, 108, 613–630. [Google Scholar] [CrossRef]
  27. Thies, B.; Nauss, T.; Bendix, J. Discriminating Raining from Non-Raining Clouds at Mid-Latitudes Using Meteosat Second Generation Daytime Data. Atmos. Chem. Phys. 2008, 8, 2341–2349. [Google Scholar] [CrossRef]
  28. Kidd, C.; Huffman, G. Global Precipitation Measurement: Global Precipitation Measurement. Met. App 2011, 18, 334–353. [Google Scholar] [CrossRef]
  29. Gorooh, V.A.; Asanjan, A.A.; Nguyen, P.; Hsu, K.; Sorooshian, S. Deep Neural Network High Spatiotemporal Resolution Precipitation Estimation (Deep-STEP) Using Passive Microwave and Infrared Data. J. Hydrometeorol. 2022, 23, 597–617. [Google Scholar] [CrossRef]
  30. Levizzani, V.; Schmetz, J.; Lutz, H.J.; Kerkmann, J.; Alberoni, P.P.; Cervino, M. Precipitation Estimations from Geostationary Orbit and Prospects for METEOSAT Second Generation. Meteorol. Appl. 2001, 8, 23–41. [Google Scholar] [CrossRef]
  31. Levizzani, V. Satellite Rainfall Estimates: New Perspectives for Meteorology and Climate from the EURAINSAT Project. Ann. Geophys. 2003, 46, 363–372. [Google Scholar] [CrossRef]
  32. Zhang, Y.; Wu, K.; Zhang, J.; Zhang, F.; Xiao, H.; Wang, F.; Zhou, J.; Song, Y.; Peng, L. Estimating Rainfall with Multi-Resource Data over East Asia Based on Machine Learning. Remote Sens. 2021, 13, 3332. [Google Scholar] [CrossRef]
  33. Sanò, P.; Panegrossi, G.; Casella, D.; Marra, A.C.; Di Paola, F.; Dietrich, S. The New Passive Microwave Neural Network Precipitation Retrieval (PNPR) Algorithm for the Cross-Track Scanning ATMS Radiometer: Description and Verification Study over Europe and Africa Using GPM and TRMM Spaceborne Radars. Atmos. Meas. Tech. 2016, 9, 5441–5460. [Google Scholar] [CrossRef]
  34. Sanò, P.; Panegrossi, G.; Casella, D.; Marra, A.; D’Adderio, L.; Rysman, J.; Dietrich, S. The Passive Microwave Neural Network Precipitation Retrieval (PNPR) Algorithm for the CONICAL Scanning Global Microwave Imager (GMI) Radiometer. Remote Sens. 2018, 10, 1122. [Google Scholar] [CrossRef]
  35. Boukabara, S.-A.; Krasnopolsky, V.; Stewart, J.Q.; Maddy, E.S.; Shahroudi, N.; Hoffman, R.N. Leveraging Modern Artificial Intelligence for Remote Sensing and NWP: Benefits and Challenges. Bull. Am. Meteorol. Soc. 2019, 100, ES473–ES491. [Google Scholar] [CrossRef]
  36. Boukabara, S.-A.; Krasnopolsky, V.; Penny, S.G.; Stewart, J.Q.; McGovern, A.; Hall, D.; Ten Hoeve, J.E.; Hickey, J.; Allen Huang, H.-L.; Williams, J.K.; et al. Outlook for Exploiting Artificial Intelligence in the Earth and Environmental Sciences. Bull. Am. Meteorol. Soc. 2021, 102, E1016–E1032. [Google Scholar] [CrossRef]
  37. Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.; Tiede, D.; Aryal, J. Evaluation of Different Machine Learning Methods and Deep-Learning Convolutional Neural Networks for Landslide Detection. Remote Sens. 2019, 11, 196. [Google Scholar] [CrossRef]
  38. Prakash, N.; Manconi, A.; Loew, S. Mapping Landslides on EO Data: Performance of Deep Learning Models vs. Traditional Machine Learning Models. Remote Sens. 2020, 12, 346. [Google Scholar] [CrossRef]
  39. Wang, C.; Xu, J.; Tang, G.; Yang, Y.; Hong, Y. Infrared Precipitation Estimation Using Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8612–8625. [Google Scholar] [CrossRef]
  40. Sadeghi, M.; Asanjan, A.A.; Faridzad, M.; Nguyen, P.; Hsu, K.; Sorooshian, S.; Braithwaite, D. PERSIANN-CNN: Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks–Convolutional Neural Networks. J. Hydrometeorol. 2019, 20, 2273–2289. [Google Scholar] [CrossRef]
  41. Li, X.; Yang, Y.; Mi, J.; Bi, X.; Zhao, Y.; Huang, Z.; Liu, C.; Zong, L.; Li, W. Leveraging Machine Learning for Quantitative Precipitation Estimation from Fengyun-4 Geostationary Observations and Ground Meteorological Measurements. Atmos. Meas. Tech. 2021, 14, 7007–7023. [Google Scholar] [CrossRef]
  42. Meyer, H.; Kühnlein, M.; Appelhans, T.; Nauss, T. Comparison of Four Machine Learning Algorithms for Their Applicability in Satellite-Based Optical Rainfall Retrievals. Atmos. Res. 2016, 169, 424–433. [Google Scholar] [CrossRef]
  43. Kingsley, K.K.; Maathuis, B.H.P.; Hoedjes, J.C.B.; Rwasoka, D.T.; Retsios, B.V.; Su, B.Z. Rain Area Detection in South-Western Kenya by Using Multispectral Satellite Data from Meteosat Second Generation. Sensors 2021, 21, 3547. [Google Scholar] [CrossRef]
  44. Holmlund, K.; Grandell, J.; Schmetz, J.; Stuhlmann, R.; Bojkov, B.; Munro, R.; Lekouara, M.; Coppens, D.; Viticchie, B.; August, T.; et al. Meteosat Third Generation (MTG): Continuation and Innovation of Observations from Geostationary Orbit. Bull. Am. Meteorol. Soc. 2021, 102, E990–E1015. [Google Scholar] [CrossRef]
  45. Grecu, M.; Olson, W.S.; Munchak, S.J.; Ringerud, S.; Liao, L.; Haddad, Z.; Kelley, B.L.; McLaughlin, S.F. The GPM Combined Algorithm. J. Atmos. Ocean. Technol. 2016, 33, 2225–2245. [Google Scholar] [CrossRef]
  46. Li, Z.; Wright, D.B.; Hartke, S.H.; Kirschbaum, D.B.; Khan, S.; Maggioni, V.; Kirstetter, P.-E. Toward a Globally-Applicable Uncertainty Quantification Framework for Satellite Multisensor Precipitation Products Based on GPM DPR. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
  47. Schmetz, J.; Pili, P.; Tjemkes, S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. Supplement to An Introduction to Meteosat Second Generation (MSG): SEVIRI CALIBRATION. Bull. Am. Meteorol. Soc. 2002, 83, 992. [Google Scholar] [CrossRef]
  48. Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (GPM) Mission for Science and Society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef] [PubMed]
  49. Draper, D.W.; Newell, D.A.; Wentz, F.J.; Krimchansky, S.; Skofronick-Jackson, G.M. The Global Precipitation Measurement (GPM) Microwave Imager (GMI): Instrument Overview and Early On-Orbit Performance. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3452–3462. [Google Scholar] [CrossRef]
  50. Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
  51. Panegrossi, G.; Rysman, J.-F.; Casella, D.; Marra, A.; Sanò, P.; Kulie, M. CloudSat-Based Assessment of GPM Microwave Imager Snowfall Observation Capabilities. Remote Sens. 2017, 9, 1263. [Google Scholar] [CrossRef]
  52. Sanò, P.; Casella, D.; Mugnai, A.; Schiavon, G.; Smith, E.A.; Tripoli, G.J. Transitioning From CRD to CDRD in Bayesian Retrieval of Rainfall From Satellite Passive Microwave Measurements: Part 1. Algorithm Description and Testing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4119–4143. [Google Scholar] [CrossRef]
  53. Casella, D.; Panegrossi, G.; Sanò, P.; Dietrich, S.; Mugnai, A.; Smith, E.A.; Tripoli, G.J.; Formenton, M.; Di Paola, F.; Leung, W.-Y.H.; et al. Transitioning From CRD to CDRD in Bayesian Retrieval of Rainfall From Satellite Passive Microwave Measurements: Part 2. Overcoming Database Profile Selection Ambiguity by Consideration of Meteorological Control on Microphysics. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4650–4671. [Google Scholar] [CrossRef]
  54. Sanò, P.; Panegrossi, G.; Casella, D.; Di Paola, F.; Milani, L.; Mugnai, A.; Petracca, M.; Dietrich, S. The Passive Microwave Neural Network Precipitation Retrieval (PNPR) Algorithm for AMSU/MHS Observations: Description and Application to European Case Studies. Atmos. Meas. Tech. 2015, 8, 837–857. [Google Scholar] [CrossRef]
  55. Turk, F.J.; Rohaly, G.; Hawkins, J.; Smith, E.A.; Marzano, F.S.; Mugnai, A.; Levizzani, V. Meteorological Applications of Precipitation Estimation from Combined SSM/I, TRMM and Geostationary Satellite Data. In Microwave Radiometry and Remote Sensing of the Earth’s Surface and Atmosphere; Pampaloni, P., Paloscia, S., Eds.; CRC Press: Boca Raton, FL, USA, 2000; pp. 353–363. ISBN 978-0-367-44744-1. [Google Scholar]
  56. De Leonibus, L.; Rosci, P.; Zauli, F. Nefodina: A Tool for Automatic Detection of Severe Convective Phenomena. In Proceedings of the SAF Training Workshop Nowcsting and Very Short Range Forecasting, Madrid, Spain, 9–11 December 1998. [Google Scholar]
  57. Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeor. 2007, 8, 38–55. [Google Scholar] [CrossRef]
  58. Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.-L.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG) 2020. Available online: https://gpm.nasa.gov/sites/default/files/2020-05/IMERG_ATBD_V06.3.pdf (accessed on 18 November 2023).
  59. Schneider, U.; Ziese, M.; Meyer-Christoffer, A.; Finger, P. Global Precipitation Analysis Products of the GPCC 2015. Available online: https://opendata.dwd.de/climate_environment/GPCC/PDF/GPCC_intro_products_v2015.pdf (accessed on 18 November 2023).
  60. Le Gleau, H. Algorithm Theoretical Basis Document for the “Precipitation Product” Processors of the NWC/GEO 2019. Available online: https://www.nwcsaf.org/Downloads/GEO/2018/Documents/Scientific_Docs/NWC-CDOP2-GEO-AEMET-SCI-ATBD-Precipitation_v2.1.pdf (accessed on 18 November 2023).
  61. Ronnerberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. 2015. Available online: https://link.springer.com/chapter/10.1007/978-3-319-24574-4_28 (accessed on 18 November 2023).
  62. Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
  63. Zhu, W.; Ma, Y.; Zhou, Y.; Benton, M.; Romagnoli, J. Deep Learning Based Soft Sensor and Its Application on a Pyrolysis Reactor for Compositions Predictions of Gas Phase Components. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2018; Volume 44, pp. 2245–2250. ISBN 978-0-444-64241-7. [Google Scholar]
  64. Alkhelaiwi, M.; Boulila, W.; Ahmad, J.; Koubaa, A.; Driss, M. An Efficient Approach Based on Privacy-Preserving Deep Learning for Satellite Image Classification. Remote Sens. 2021, 13, 2221. [Google Scholar] [CrossRef]
  65. Nurmi, P. Recommendations on the Verification of Local Weather Forecasts. ECMWF Tech. Memo. 430, 19 pp. Available online: https://www.ecmwf.int/en/elibrary/11401-recommendations-verificationlocal-weather-forecasts (accessed on 18 November 2023).
  66. Kim, Y.; Hong, S. Hypothetical Ground Radar-Like Rain Rate Generation of Geostationary Weather Satellite Using Data-to-Data Translation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4103414. [Google Scholar] [CrossRef]
Remotesensing 15 05662 g001
Figure 1. Spatial distribution of the images included in the TRD.
Figure 1. Spatial distribution of the images included in the TRD.
Remotesensing 15 05662 g001
Remotesensing 15 05662 g002
Figure 2. Representation of the U-Net structure designed within this study. In the figure, the network operators (or layers) are represented by arrows of different colors (see the legend for details). The colored boxes show the feature and spatial dimensions at each layer, indicating with red and bold black numbers the spatial and feature dimensions, respectively.
Figure 2. Representation of the U-Net structure designed within this study. In the figure, the network operators (or layers) are represented by arrows of different colors (see the legend for details). The colored boxes show the feature and spatial dimensions at each layer, indicating with red and bold black numbers the spatial and feature dimensions, respectively.
Remotesensing 15 05662 g002
Remotesensing 15 05662 g003
Figure 3. Pearson correlation coefficient at different spatial grid sizes (i.e., from 0.1° × 0.1° to 1° × 1°) for the four different products considered.
Figure 3. Pearson correlation coefficient at different spatial grid sizes (i.e., from 0.1° × 0.1° to 1° × 1°) for the four different products considered.
Remotesensing 15 05662 g003
Remotesensing 15 05662 g004
Figure 4. Mean absolute error (MAE) at different spatial grid sizes (i.e., from 0.1° × 0.1° to 1° × 1°) for the four different products considered. Each bar shows, for each product, the total MAE, as well as the hits, false alarm, and miss contribution to the total, respectively. Panel (a) shows the results for 0.1° × 0.1°, panel (b) for 0.2° × 0.2°, panel (c) for 0.4° × 0.4°, panel (d) for 0.6° × 0.6°, panel (e) for 0.8° × 0.8° and panel (f) for 1° × 1° spatial grid, respectively. The subplots do not have the same y-scale because of the difference in the MAE values depending on the grid size. This allows us to better highlight the hits, false alarm, and miss relative contribution.
Figure 4. Mean absolute error (MAE) at different spatial grid sizes (i.e., from 0.1° × 0.1° to 1° × 1°) for the four different products considered. Each bar shows, for each product, the total MAE, as well as the hits, false alarm, and miss contribution to the total, respectively. Panel (a) shows the results for 0.1° × 0.1°, panel (b) for 0.2° × 0.2°, panel (c) for 0.4° × 0.4°, panel (d) for 0.6° × 0.6°, panel (e) for 0.8° × 0.8° and panel (f) for 1° × 1° spatial grid, respectively. The subplots do not have the same y-scale because of the difference in the MAE values depending on the grid size. This allows us to better highlight the hits, false alarm, and miss relative contribution.
Remotesensing 15 05662 g004
Remotesensing 15 05662 g005
Figure 5. Trend of RMSE at the six spatial grid sizes considered (i.e., from 0.1° × 0.1° to 1° × 1°) and for the four different products considered.
Figure 5. Trend of RMSE at the six spatial grid sizes considered (i.e., from 0.1° × 0.1° to 1° × 1°) and for the four different products considered.
Remotesensing 15 05662 g005
Remotesensing 15 05662 g006
Figure 6. RMSE spatial distribution (panel a) and mean precipitation rate (panel b) over the full disc area, calculated at 0.1° × 0.1° grid size.
Figure 6. RMSE spatial distribution (panel a) and mean precipitation rate (panel b) over the full disc area, calculated at 0.1° × 0.1° grid size.
Remotesensing 15 05662 g006
Remotesensing 15 05662 g007
Figure 7. Trend of (a) POD, (b) FAR, and (c) CSI for the four products considered as a function of different precipitation rate thresholds.
Figure 7. Trend of (a) POD, (b) FAR, and (c) CSI for the four products considered as a function of different precipitation rate thresholds.
Remotesensing 15 05662 g007
Remotesensing 15 05662 g008
Figure 8. Snapshot in the northeast region of the full disc captured at 16:30 UTC of 12 July 2020. The cloud structure is depicted by the SEVIRI TB at 10.8 µm and represented by the colormap from red to blue. The most intense precipitating area detected by (a) U-Net and (b) by DPR-GMI are shown by black lines (95th percentile of the precipitation rate). The dashed lines indicate the DPR swath limits.
Figure 8. Snapshot in the northeast region of the full disc captured at 16:30 UTC of 12 July 2020. The cloud structure is depicted by the SEVIRI TB at 10.8 µm and represented by the colormap from red to blue. The most intense precipitating area detected by (a) U-Net and (b) by DPR-GMI are shown by black lines (95th percentile of the precipitation rate). The dashed lines indicate the DPR swath limits.
Remotesensing 15 05662 g008
Table 1. SEVIRI MSG channels properties.
Table 1. SEVIRI MSG channels properties.
Channel NumberCentral Wavelength (μm)Spectral DomainMain Gas Absorber or Window
10.653VISWindow
20.81VISWindow
31.64NIRWindow
43.90IRWindow
56.25WVWater Vapor
67.35WVWater Vapor
78.70IRWindow
89.66IROzone
910.80IRWindow
1012.0IRWindow
1113.4IRCarbon Dioxide
12(0.4–1.1)HRVWindow/WV
Table 2. Percent mean error (ME%) calculated for each precipitation product and for different precipitation rate thresholds.
Table 2. Percent mean error (ME%) calculated for each precipitation product and for different precipitation rate thresholds.
Percent Mean Error (%)
DPR-GMI Threshold (mmh−1)U-NetH60BH03BIMERG-E
016.6117.025.859.3
1−78.2−49.0−47.75.8
10−91.8−69.5−69.1−33.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

D’Adderio, L.P.; Casella, D.; Dietrich, S.; Panegrossi, G.; Sanò, P. A First Step towards Meteosat Third Generation Day-2 Precipitation Rate Product: Deep Learning for Precipitation Rate Retrieval from Geostationary Infrared Measurements. Remote Sens. 2023, 15, 5662. https://doi.org/10.3390/rs15245662

AMA Style

D’Adderio LP, Casella D, Dietrich S, Panegrossi G, Sanò P. A First Step towards Meteosat Third Generation Day-2 Precipitation Rate Product: Deep Learning for Precipitation Rate Retrieval from Geostationary Infrared Measurements. Remote Sensing. 2023; 15(24):5662. https://doi.org/10.3390/rs15245662

Chicago/Turabian Style

D’Adderio, Leo Pio, Daniele Casella, Stefano Dietrich, Giulia Panegrossi, and Paolo Sanò. 2023. "A First Step towards Meteosat Third Generation Day-2 Precipitation Rate Product: Deep Learning for Precipitation Rate Retrieval from Geostationary Infrared Measurements" Remote Sensing 15, no. 24: 5662. https://doi.org/10.3390/rs15245662

APA Style

D’Adderio, L. P., Casella, D., Dietrich, S., Panegrossi, G., & Sanò, P. (2023). A First Step towards Meteosat Third Generation Day-2 Precipitation Rate Product: Deep Learning for Precipitation Rate Retrieval from Geostationary Infrared Measurements. Remote Sensing, 15(24), 5662. https://doi.org/10.3390/rs15245662

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop