Delineation of Backfill Mining Influence Range Based on Coal Mining Subsidence Principle and Interferometric Synthetic Aperture Radar
Abstract
:1. Introduction
2. Materials and Methods
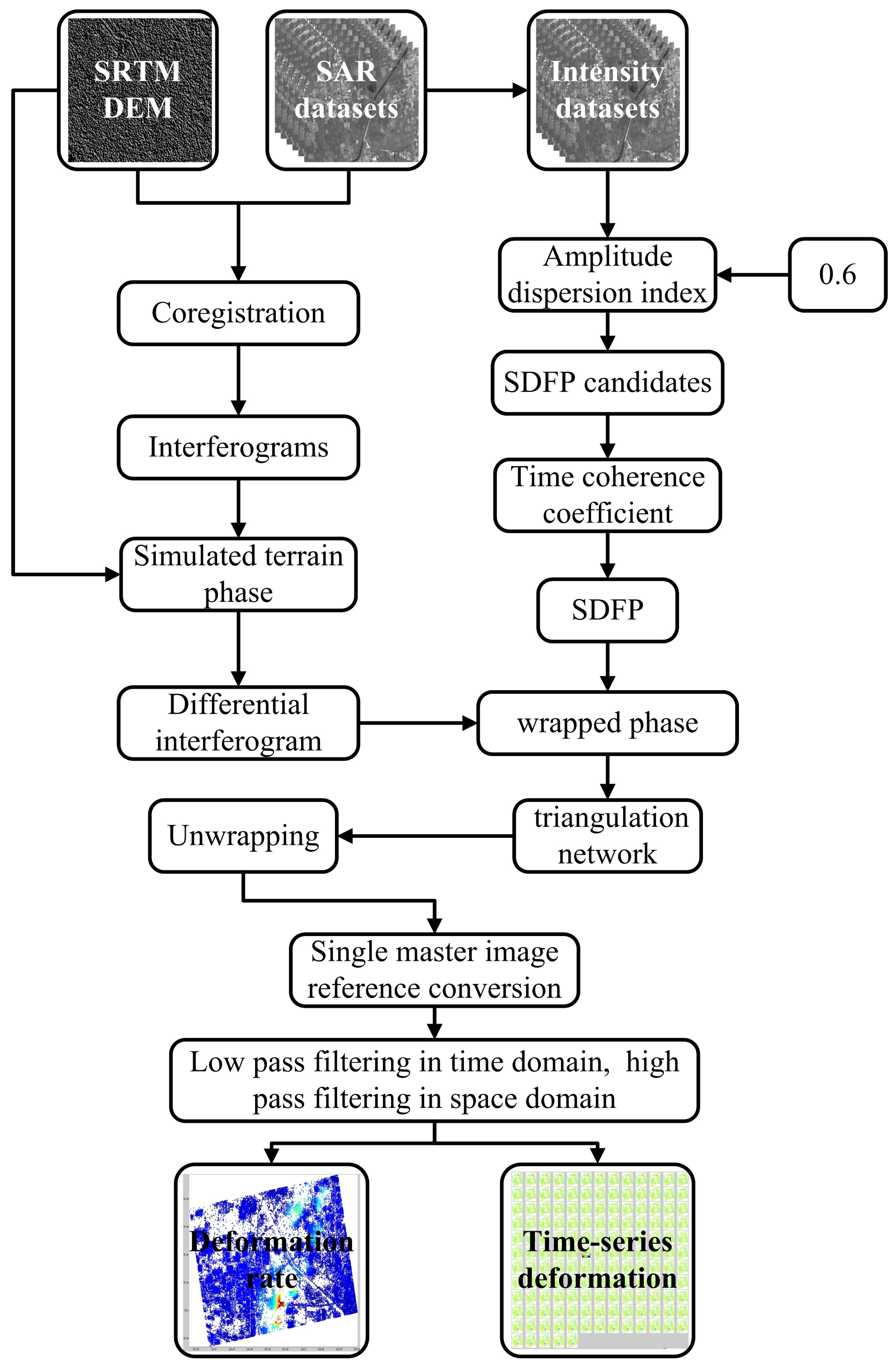
2.1. Principle of StaMPS-SBAS Technology
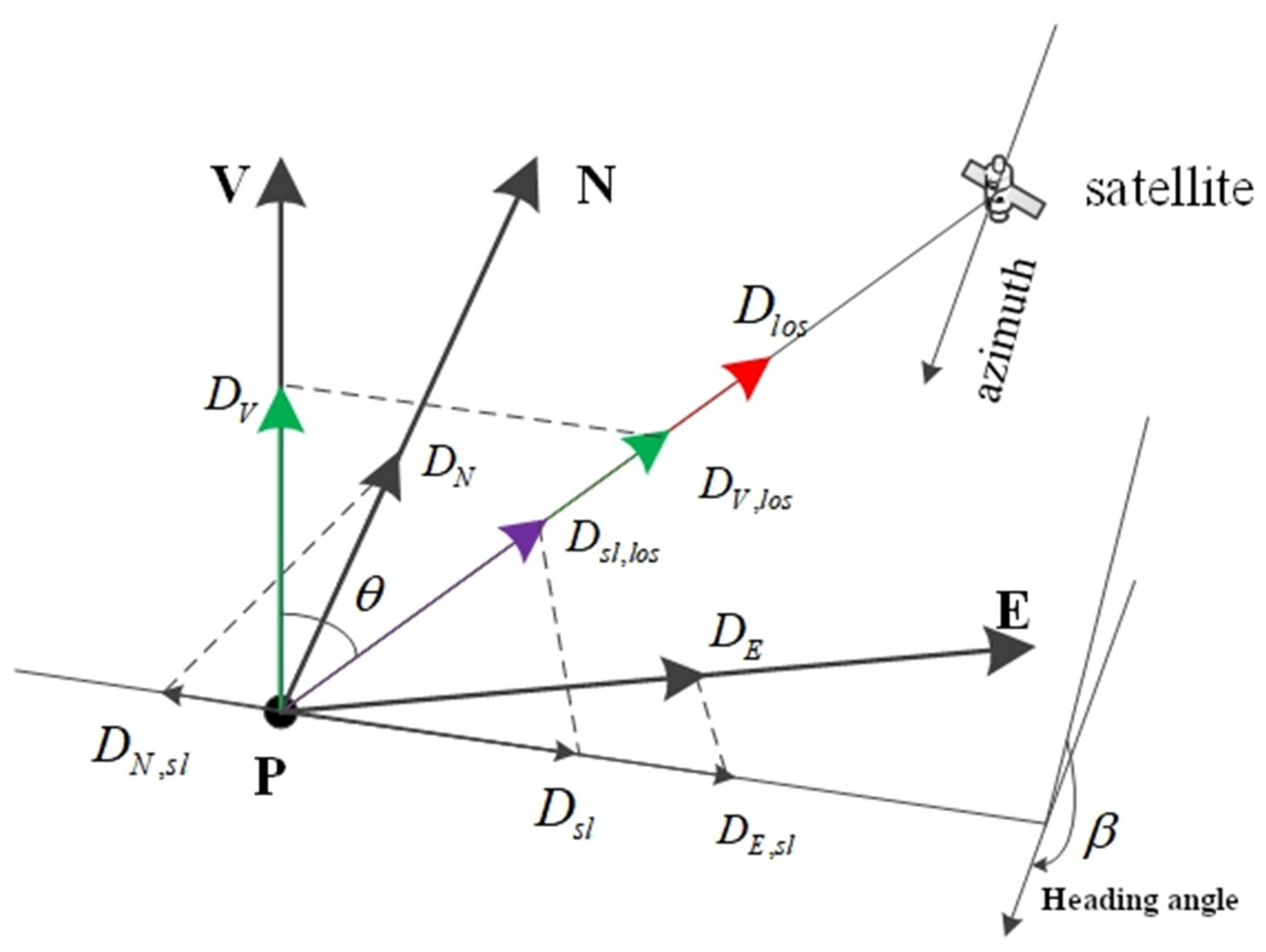
2.2. Principle of Three-Dimensional Deformation Decomposition
2.3. Study Area Overview and InSAR Data Preparation
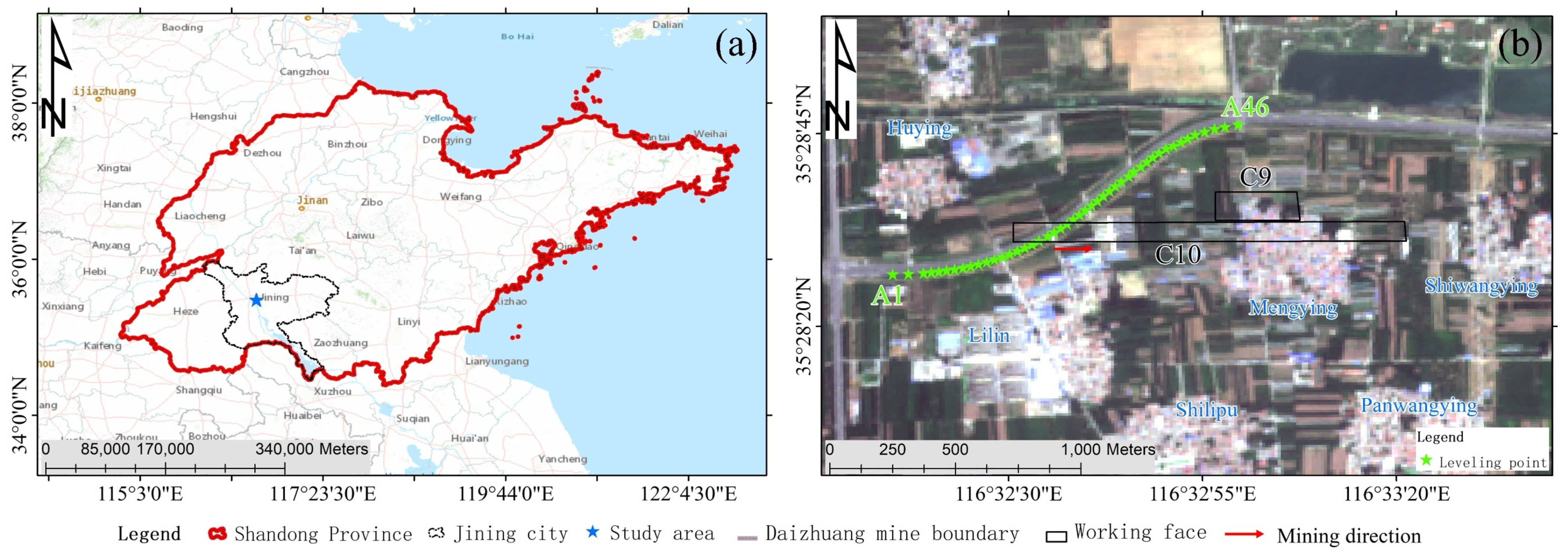
2.3.1. Study Area Overview
2.3.2. InSAR Data Preparation
3. Results
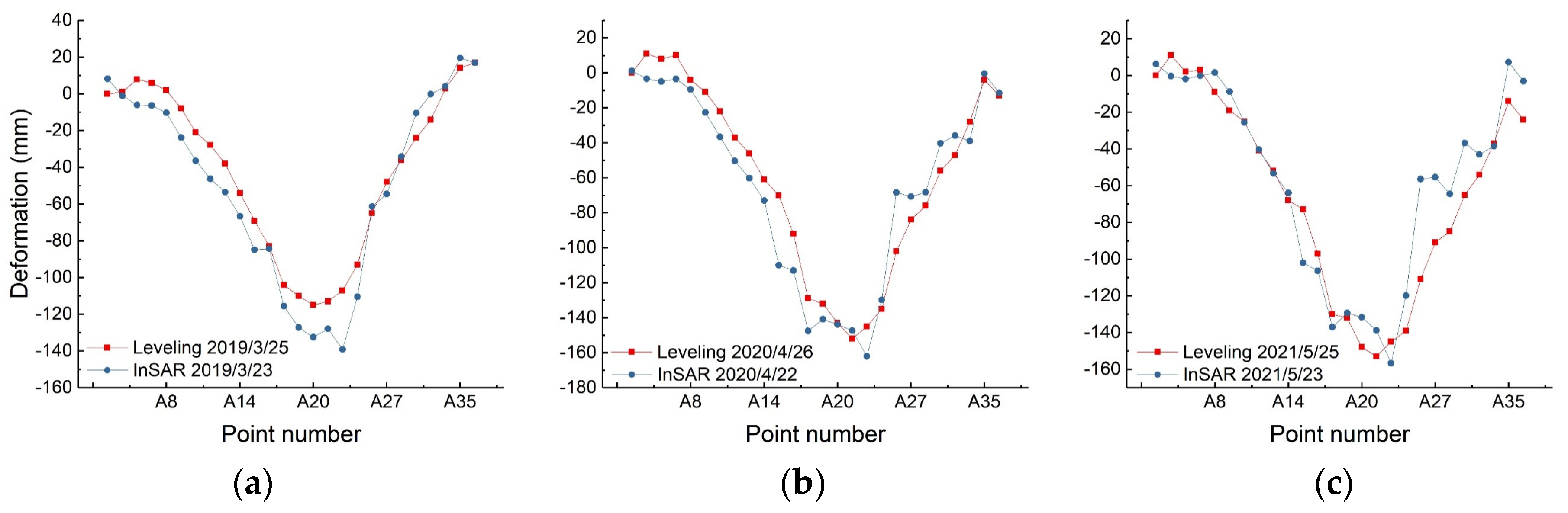
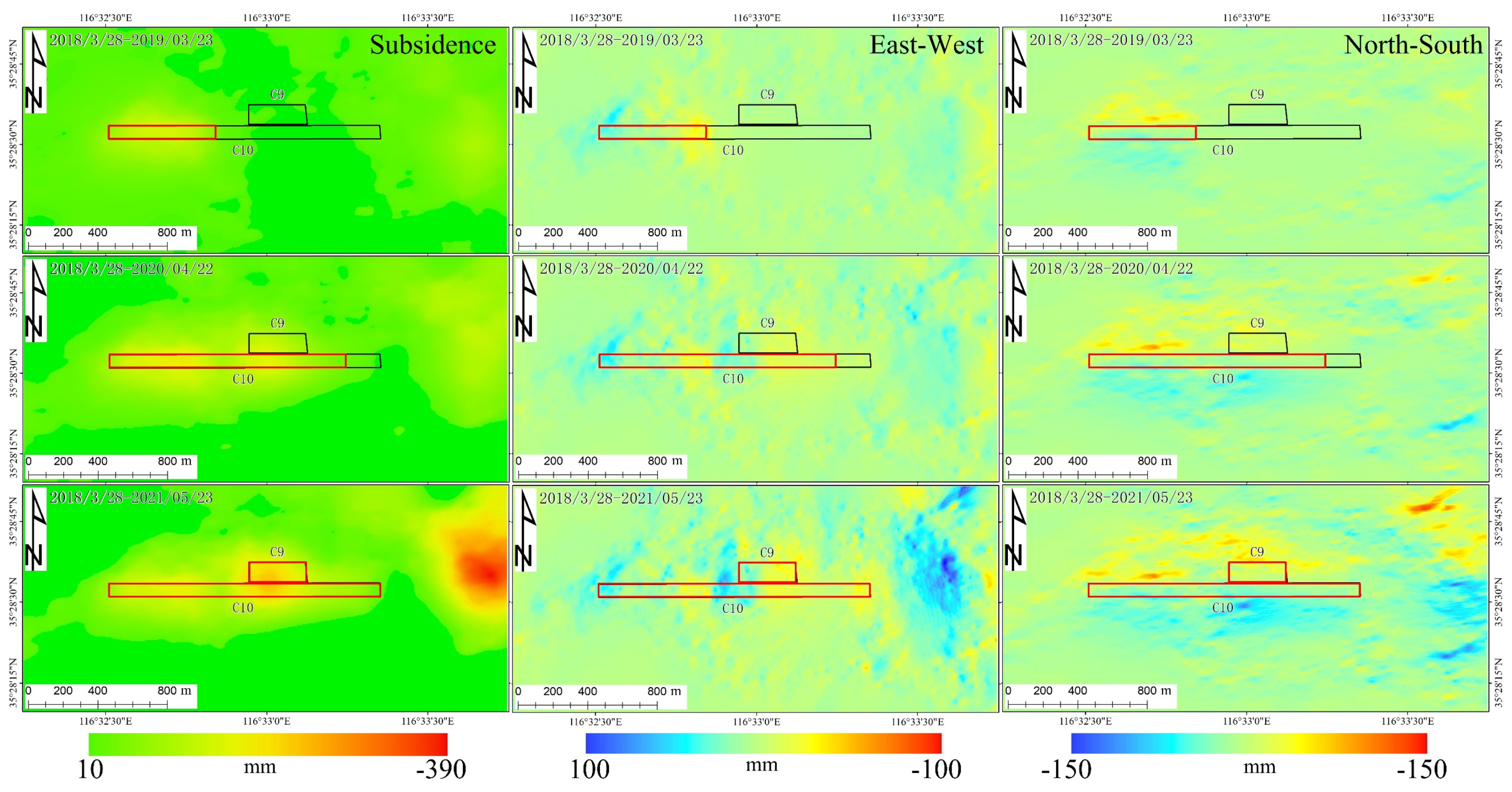
3.1. SBAS Monitoring Results
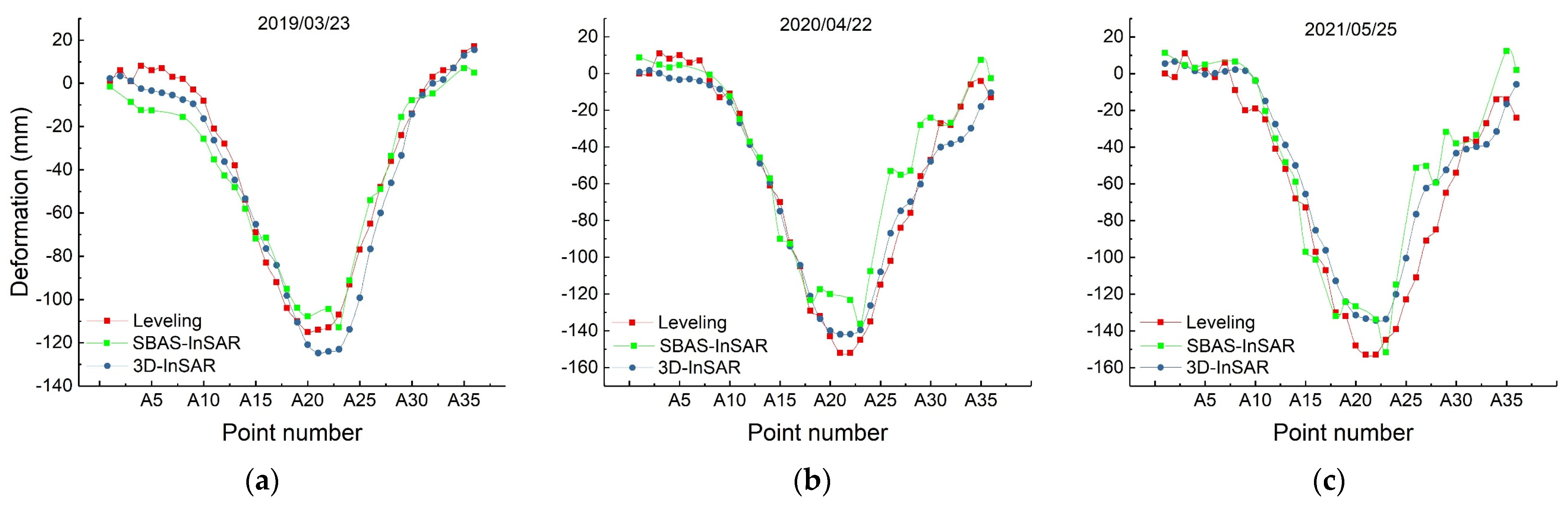
3.2. Three-Dimensional Deformation Inversion Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- BP. BP Statistical Review of World Energy 2018; British Petroleum Company: London, UK, 2018. [Google Scholar]
- Chen, B.; Li, Z.; Yu, C.; Fairbairn, D.; Kang, J.; Hu, J.; Liang, L. Three-dimensional time-varying large surface displacements in coal exploiting areas revealed through integration of SAR pixel offset measurements and mining subsidence model. Remote Sens. Environ. 2020, 240, 111663. [Google Scholar] [CrossRef]
- Pawluszek-Filipiak, K.; Borkowski, A. Monitoring mining-induced subsidence by integrating differential radar interferometry and persistent scatterer techniques. Eur. J. Remote Sens. 2021, 54, 18–30. [Google Scholar] [CrossRef]
- Declercq, P.-Y.; Dusar, M.; Pirard, E.; Verbeurgt, J.; Choopani, A.; Devleeschouwer, X. Post Mining Ground Deformations Transition Related to Coal Mines Closure in the Campine Coal Basin, Belgium, Evidenced by Three Decades of MT-InSAR Data. Remote Sens. 2023, 15, 725. [Google Scholar] [CrossRef]
- Emad, M.Z. Numerical modelling approach for mine backfill. Sādhanā 2017, 42, 1595–1604. [Google Scholar] [CrossRef]
- Raffaldi, M.J.; Seymour, J.B.; Richardson, J.; Zahl, E.; Board, M. Cemented paste backfill geomechanics at a narrow-vein underhand cut-and-fill mine. Rock Mech. Rock Eng. 2019, 52, 4925–4940. [Google Scholar] [CrossRef] [PubMed]
- Hasan, A.; Karrech, A.; Chareyre, B. Evaluating force distributions within virtual uncemented mine backfill using discrete element method. Int. J. Geomech. 2017, 17, 06016042. [Google Scholar] [CrossRef]
- Mo, S.; Canbulat, I.; Zhang, C.; Oh, J.; Shen, B.; Hagan, P. Numerical investigation into the effect of backfilling on coal pillar strength in highwall mining. Int. J. Min. Sci. Technol. 2018, 28, 281–286. [Google Scholar] [CrossRef]
- Akkaya, U.G.; Cinku, K.; Yilmaz, E. Characterization of strength and quality of cemented mine backfill made up of lead-zinc processing tailings. Front. Mater. 2021, 8, 740116. [Google Scholar] [CrossRef]
- Cavusoglu, I.; Yilmaz, E.; Yilmaz, A.O. Sodium silicate effect on setting properties, strength behavior and microstructure of cemented coal fly ash backfill. Powder Technol. 2021, 384, 17–28. [Google Scholar] [CrossRef]
- Fenn, D.; du Kanda, A.; Dukhan, D. Determining settlement rates and surface stability using in situ density of backfill as a proxy for displacement. J. South. Afr. Inst. Min. Metall. 2015, 115, 1035–1043. [Google Scholar] [CrossRef]
- Ren, H.; Xiao, W.; Zhao, Y.; Hu, Z. Land damage assessment using maize aboveground biomass estimated from unmanned aerial vehicle in high groundwater level regions affected by underground coal mining. Environ. Sci. Pollut. Res. 2020, 27, 21666–21679. [Google Scholar] [CrossRef]
- State Administration of Work Safety; State Administration of Coal Mine Safty; National Energy Administration; National Railway Administration of the People’s Republic of China. Regulations for Coal Pillar Retention and Coal Mining for Buildings, Water Bodies, Railways and Main Roadways; The State Council: Beijing, China, 2017.
- Li, J.; Wang, L. Mining subsidence monitoring model based on BPM-EKTF and TLS and its application in building mining damage assessment. Environ. Earth Sci. 2021, 80, 396. [Google Scholar] [CrossRef]
- Guo, W.B.; Liu, Y.X.; Li, X.S. Fuzzy Custering Analysis of Mining Induced Damages of Buildings. J. Min. Saf. Enginneing 2007, 3, 288–292. [Google Scholar]
- Chomacki, L.; Rusek, J.; Słowik, L. Machine Learning Methods in Damage Prediction of Masonry Development Exposed to the Industrial Environment of Mines. Energies 2022, 15, 3958. [Google Scholar] [CrossRef]
- Chomacki, L.; Rusek, J.; Słowik, L. Selected Artificial Intelligence Methods in the Risk Analysis of Damage to Masonry Buildings Subject to Long-Term Underground Mining Exploitation. Minerals 2021, 11, 958. [Google Scholar] [CrossRef]
- Zheng, M.; Deng, K.; Fan, H.; Huang, J. Monitoring and analysis of mining 3D deformation by multi-platform SAR images with the probability integral method. Front. Earth Sci. 2019, 13, 169–179. [Google Scholar] [CrossRef]
- Antonielli, B.; Sciortino, A.; Scancella, S.; Bozzano, F.; Mazzanti, P. Tracking Deformation Processes at the Legnica Glogow Copper District (Poland) by Satellite InSAR—I: Room and Pillar Mine District. Land 2021, 10, 653. [Google Scholar] [CrossRef]
- Fialko, Y.; Simons, M.; Agnew, D. The complete (3-d) surface displacement field in the epicentral area of the 1999 m w 7.1 hector mine earthquake, california, from space geodetic observations. Geophys. Res. Lett. 2001, 28, 3063–3066. [Google Scholar] [CrossRef]
- Nematollah, G.; Yo, F. Using InSAR for evaluating the accuracy of locations and focal mechanism solutions of local earthquake catalogues. Geophys. J. Int. 2022, 230, 607–622. [Google Scholar] [CrossRef]
- Nardò, S.; Ascione, A.; Mazzoli, S.; Terranova, C.; Vilardo, G. PS-InSAR data analysis: Pre-seismic ground deformation in the 2009 L′Aquila earthquake region. Boll. Di Geofis. Teor. Ed Appl. 2020, 61, 41–56. [Google Scholar] [CrossRef]
- Lu, Z.; Fielding, E.; Patrick, M.R.; Trautwein, C.M. Estimating lava volume by precision combination of multiple baseline spaceborne and airborne interferometric synthetic aperture radar: The 1997 eruption of okmok volcano, alaska. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1428–1436. [Google Scholar]
- Bountos, N.I.; Papoutsis, I.; Michail, D.; Anantrasirichai, N. Self-Supervised Contrastive Learning for Volcanic Unrest Detection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Anantrasirichai, N.; Biggs, J.; Albino, F.; Bull, D. A deep learning approach to detecting volcano deformation from satellite imagery using synthetic datasets. Remote Sens. Environ. 2019, 230, 111179. [Google Scholar] [CrossRef]
- Li, Q.Y.; Wang, Y. Research on Deformation Law of Deep Excavation Supporting Structures in Beijing Metro Station. Adv. Mater. Res. 2011, 243, 2338–2344. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, Z.F.; Zhu, J.J.; Hu, J.; Wang, Y.J.; Li, P.X.; Chen, G. Retrieving three-dimensional displacement fields of mining areas from a single InSAR pair. J. Geod. 2015, 89, 17–32. [Google Scholar] [CrossRef]
- Fan, H.D.; Cheng, D.; Deng, K.Z.; Chen, B.Q.; Zhu, C.G. Subsidence monitoring using d-insar and probability integral prediction modelling in deep mining areas. Surv. Rev. 2015, 47, 438–445. [Google Scholar] [CrossRef]
- Modeste, G.; Doubre, C.; Masson, F. Time evolution of mining-related residual subsidence monitored over a 24-year period using InSAR in southern Alsace, France. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102392. [Google Scholar] [CrossRef]
- Chatterjee, R.S.; Lakhera, R.C.; Dadhwal, V.K. InSAR coherence and phase information for mapping environmental indicators of opencast coal mining: A case study in Jharia Coalfield, Jharkhand, India. Can. J. Remote Sens. 2010, 36, 361–373. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F.L. Permanent scatterers in sar interferometry. ieee trans geosci remot sen. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential sar interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, 96–106. [Google Scholar] [CrossRef]
- Zheng, M.; Deng, K.; Fan, H.; Du, S.; Zou, H. Monitoring and analysis of mining 3D time-series deformation based on multi-track SAR data. Int. J. Remote Sens. 2019, 40, 1409–1425. [Google Scholar] [CrossRef]
- Witkowski, W.T.; Łukosz, M.; Guzy, A.; Hejmanowski, R. Estimation of Mining-Induced Horizontal Strain Tensor of Land Surface Applying InSAR. Minerals 2021, 11, 788. [Google Scholar] [CrossRef]
- Puniach, E.; Gruszczynski, W.; Stoch, T.; Mrocheń, D.; Ćwiąkała, P.; Sopata, P.; Pastucha, E.; Matwij, W. Determination of the coefficient of proportionality between horizontal displacement and tilt change using UAV photogrammetry. Eng. Geol. 2023, 312, 106939. [Google Scholar] [CrossRef]

| (a) | (b) | (c) | Mean Value | |
|---|---|---|---|---|
| MaxD | 40.2 | 39.9 | 54.6 | 44.9 |
| MinD | 0.2 | 0.8 | 0.4 | 0.5 |
| StD | 9.2 | 9.0 | 12.7 | 10.3 |
| (a) | (b) | (c) | Mean Value | |
|---|---|---|---|---|
| MaxD | 22.3 | 23.7 | 34.4 | 26.8 |
| MinD | 0.1 | 0.7 | 0.5 | 0.4 |
| StD | 5.4 | 5.4 | 7.8 | 6.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Zheng, M.; Li, H.; Chen, Y.; Guo, G.; Su, Z.; Huo, W. Delineation of Backfill Mining Influence Range Based on Coal Mining Subsidence Principle and Interferometric Synthetic Aperture Radar. Remote Sens. 2023, 15, 5618. https://doi.org/10.3390/rs15235618
Yuan Y, Zheng M, Li H, Chen Y, Guo G, Su Z, Huo W. Delineation of Backfill Mining Influence Range Based on Coal Mining Subsidence Principle and Interferometric Synthetic Aperture Radar. Remote Sensing. 2023; 15(23):5618. https://doi.org/10.3390/rs15235618
Chicago/Turabian StyleYuan, Yafei, Meinan Zheng, Huaizhan Li, Yu Chen, Guangli Guo, Zhe Su, and Wenqi Huo. 2023. "Delineation of Backfill Mining Influence Range Based on Coal Mining Subsidence Principle and Interferometric Synthetic Aperture Radar" Remote Sensing 15, no. 23: 5618. https://doi.org/10.3390/rs15235618
APA StyleYuan, Y., Zheng, M., Li, H., Chen, Y., Guo, G., Su, Z., & Huo, W. (2023). Delineation of Backfill Mining Influence Range Based on Coal Mining Subsidence Principle and Interferometric Synthetic Aperture Radar. Remote Sensing, 15(23), 5618. https://doi.org/10.3390/rs15235618






