Abstract
The International GNSS Service analysis centers provide orbit products of GPS satellites with weekly, daily, and sub-daily latency. The most frequent ultra-rapid products, which include 24 h of orbits derived from observations and 24 h of orbit predictions, are vital for real-time applications. However, the predicted part of the ultra-rapid orbits is less accurate than the estimated part and has deviations of several decimeters with respect to the final products. In this study, we investigate the potential of applying machine-learning (ML) and deep-learning (DL) algorithms to further enhance physics-based orbit predictions. We employed multiple ML/DL algorithms and comprehensively compared the performances of different models. Since the prediction errors of the physics-based propagators accumulate with time and have sequential characteristics, specific sequential modeling algorithms, such as Long Short-Term Memory (LSTM), show superiority. Our approach shows promising results with average improvements of 47% in 3D RMS within the 24-h prediction interval of the ultra-rapid products. In the end, we applied the orbit predictions improved by LSTM to kinematic precise point positioning and demonstrated the benefits of LSTM-improved orbit predictions for positioning applications. The accuracy of the station coordinates estimated based on these products is improved by 16% on average compared to those using ultra-rapid orbit predictions.
1. Introduction
The Global Navigation Satellite System (GNSS) satellites are substantial for the engineering and science community. Accurate predictions of GNSS satellite orbits and clocks, along with Earth rotation parameters (EOPs), are essential for many real-time positioning applications, such as real-time navigation and early warning systems [1,2,3,4]. Presently, orbit predictions are typically obtained using physics-based orbit propagators, relying on precise initial states of the space object and good knowledge of the orbital forces. The deterministic models cannot perfectly describe the changing perturbing forces, which is one of the major remaining challenges for orbit prediction. As a result, errors in orbit predictions accumulate over time. At the same time, the demand for real-time positioning is presently increasing [5,6,7], which inspires further investigations on improving GNSS orbit predictions.
Motivated by the rapid expansion of computing power and the considerable data volume in recent years, more and more scientists have applied machine learning (ML) and deep learning (DL) in geoscience [8,9], geophysics [10] and geodesy [11]. More specifically, some studies try to improve orbit prediction using ML/DL approaches (In this study, the term ML refers to methods from classical tree-based methods to simple neural networks. DL refers to deep neural networks with advanced mechanisms such as convolutional and recurrent units). Convolutional Neural Networks (CNN) have been applied to improve the accuracy of an orbit prediction model [12]. The orbit errors were computed based on the broadcast ephemerides and converted into an image-like format to be fed into a CNN model. Improvements in all orbit types of GPS and Beidou constellations have been reported. The back propagation neural network has been applied to a similar question and results in beneficial improvements [13]. Several studies focus on low Earth orbit (LEO) satellites because the impacts of non-gravitational perturbing forces, gravitational anomalies, and imperfect shape modeling are more significant than in other types of orbits, resulting in substantial errors in the physics-based orbit propagators [14]. The performance of the Support Vector Machine (SVM) on the orbit prediction of LEO satellites has been tested in a simulation-based environment [15], and then is applied to publicly available Two-Line Element (TLE) files [16]. These two studies conclude that SVM can improve position and velocity accuracy when the data volume is sufficient. A time-delay neural network has been built up for LEO satellites, which reduces errors in tracking LEO satellite positions and effectively improves a vehicle’s navigation performance [17]. However, all the mentioned studies modeled the satellite orbits with the accuracy of dozens of meters or even kilometers. They did not study the feasibility of ML/DL algorithms for further improving the orbit prediction with accuracy at the sub-meter level.
In this study, we investigate the potential of ML/DL methods for improving the orbit prediction products at the centimeter level theoretically in hindcast experiments. To this end, we concentrate on the products provided by the German Research Center for Geosciences (GFZ), which is an International GNSS Service (IGS) analysis center (AC) focusing on GPS satellites. GFZ provides three types of GNSS orbit products with weekly (final products), daily (rapid products), and sub-daily (ultra-rapid products) latency [18]. Among them, ultra-rapid products are most important for real-time applications because they provide orbit predictions for the next 24 h as well as the estimated orbits of the last 24 h. However, the accuracy of the predictions in ultra-rapid products degrades significantly over time due to the limitations of the physics-based orbital propagator, such as imperfect initial states and an insufficient model of solar radiation pressure [19]. In addition, the uncertainties in the applied EOPs may also degrade the accuracy of the ultra-rapid products [20]. As a result, the differences between the ultra-rapid predictions and final products vary from a few centimeters to meters. In contrast, the final products, which are estimated in an unconstrained condition and used to define the reference frame, have the highest quality with an accuracy of around [21]. Overall, if we consider the final products as the reference, the differences between the ultra-rapid and final products mainly indicate the errors caused by the limitations of the physics-based orbit propagators.
Inspired by the success of ML/DL in sequence predictions and the time-series characteristics of the satellite orbits, we applied ML/DL algorithms to model differences between ultra-rapid and final orbit products, which investigates the potential to further enhance the quality of physics-based orbit predictions at the centimeter level. In this context, we combined the advantages of physics-based and data-driven methods. Another emphasis of this study is the detailed comparison of different ML/DL algorithms applied to orbit prediction, which can provide a reference for further investigations. Moreover, we also validated the enhanced ultra-rapid products by employing them in kinematic precise point positioning (PPP) to investigate the potential benefits of LSTM-improved orbit predictions for positioning applications. This study focused on hindcast experiments to investigate the potential theoretically. Some potential efforts to put this pipeline into operational use are also discussed at the end.
2. Data
We used the ultra-rapid [22] and final [23] products provided by GFZ, which is an IGS analysis center. We used these data rather than the official IGS products since GFZ provides ultra-rapid products eight times per day, as shown in Figure 1, allowing us to have a relatively larger number of samples, which is beneficial for data-driven methods to obtain better generalizability. Furthermore, using the products provided by one AC rather than the official combined solutions can avoid a potential impact of the combination strategy [24], which means the differences between the ultra-rapid and final products are mainly caused by the deficiencies of the used orbit forces model. We considered each ultra-rapid product as one sample, the 24-h observations of which were considered to be inputs, whereas the 24-h predictions were considered to be targets (Figure 1). The products from January 2019 to April 2021 were used (205,281 valid samples), the sampling rate of which is 15 min. To monitor the training process and evaluate the model independently, the data samples were randomly divided into training, validation, and test sets with proportions of 70% (144,075), 15% (30,873) and 15% (30,873). All the proposed models were trained on the same training samples, and all the results reported were based on the same test set to obtain a fair comparison.

Figure 1.
The schematic diagram of the GFZ 3-hourly ultra-rapid orbit products.
3. Methodology
3.1. Overview
Figure 2 shows an overview of the pipeline designed for this study. First, we generated the differences between the ultra-rapid and final orbit products in the radial, along-track, cross-track (RSW) frame [25]. The RSW frame is satellite-fixed, and the individual components are less correlated. The gravitational impacts are better separated in the RSW frame, whereas the non-gravitational perturbing forces are only isolated to a lesser degree. Each single ultra-rapid product (Figure 2) served as one sample. The RSW differences within the 24-h observation interval served as input features, whereas the RSW differences within the 24-h prediction interval of the same product were targets. To achieve the best performance, we trained three models to predict RSW differences individually. Therefore, the input sequences had a length of 95 and three features (R, S, W differences) at each epoch, whereas the output sequences had the same length but only one component at each epoch. The input-output pairs were fed into multiple ML/DL algorithms for supervised regression.
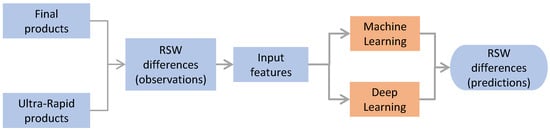
Figure 2.
Graphical representation of the pipeline in this study.
3.2. Data Preprocessing
3.2.1. Generating Orbit Differences
We first aligned each ultra-rapid product to the corresponding final product based on GPS time. Then, we transformed the Earth-centered Earth-fixed (ECEF) coordinates into the Earth-centered inertial (ECI) frame by considering EOPs. The transformation was realized using the following equation [25,26,27]:
where and denote the satellites’ position vectors in the ECI and ECEF frames, respectively. and are the precession and nutation matrices. denotes the Earth’s rotation angle relating to . and are the rotation matrices describing polar motion. All the EOPs are provided by the International Earth Rotation and Reference Systems Service (IERS) regularly [26]. After converting the satellite orbits into the ECI system, we computed the orbit errors between the ultra-rapid () and the final products ():
Then, we can transform the orbit errors into the RSW frame [25]:
where , , are the three normal unit vectors in the RSW frame. and denote the position and velocity in the inertial frame, respectively. denotes the transformation matrix. denotes the error vector in the RSW frame. For Equations (3)–(7), the velocity in the ECI frame is necessary. Since the original products do not provide any information about the velocities, we computed them using numerical differentiation:
where is the time difference between two adjacent epochs, which is 15 in our case. However, we did not have any information about the velocity at the very beginning and end of each ultra-rapid product as indicated in Equation (8), which means we obtained a sequence with a length of 190 instead of 192.
3.2.2. Feature Standardization
Then, we standardized the features to simplify the optimization process in the ML/DL algorithms and improved their performance [28]. Since our data are temporal deviations accumulating with time, as shown in Figure 3, we computed the ensemble mean values and standard deviations of each feature at each individual time epoch:
where and denote the original and standardized ith feature at the time epoch t. The ensemble mean and standard deviation of the ith feature at the epoch t over all training samples are denoted by and . The standardizing approach was realized using StandardScaler in scikit-learn [29]. We first determined 95 scalers for each feature to deal with the input epochs individually, and 95 scalers for the target based on the training set. Later, these scalers were applied to the validation and test sets.
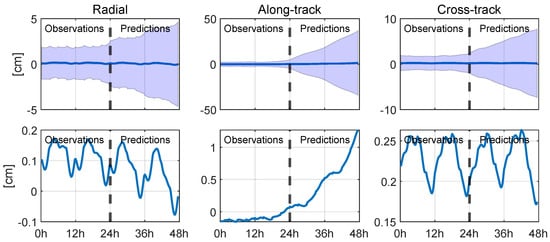
Figure 3.
The mean orbit differences of the GPS constellations with 1- intervals (top) and the zoomed-in version of only the mean orbit differences (bottom).
This standardization strategy was applied to all the input features (RSW differences). Figure 4 shows 30 randomly selected examples of the RSW differences and corresponding standardized RSW differences. The first column shows the radial errors, where we can find that the proposed standardization clearly reduces the magnitudes while keeping the major features. The severe accumulation problem of along-track errors is clearly reduced.
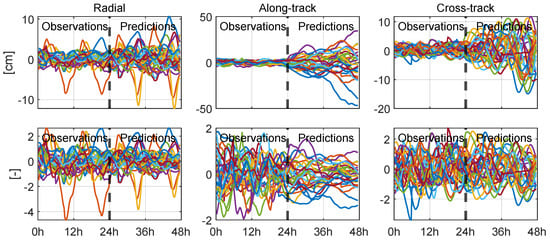
Figure 4.
Thirty randomly selected samples of radial, along-track, cross-track differences (top) and corresponding standardized unitless differences (bottom) of the GPS constellation.
3.3. Machine-Learning and Deep-Learning Algorithms
This section introduces the principles of the employed ML/DL algorithms. For clarity, we categorize the tree-based model and multilayer perceptron as ML models and the other neural networks with convolutional or recurrent mechanisms as DL models. For the ML models, the input features were reshaped from (95, 3) into (285, 1) to meet their requirements since they cannot consider the sequential relationship between input epochs.
3.3.1. Tree-Based Models
The first category of the tested ML methods are the tree-based models, from which many geodetic studies profited due to their reasonable performance and good interpretability [30,31,32]. We investigated Decision Tree (DT; [33]) and Random Forest (RF; [34]). A DT consists of nodes, branches, and leaves. At each node, the data are split into two groups and fed into branches based on specific criteria. The target at the root node is split into targets at the sub-nodes, which are pursued with the lowest loss value. This process goes on until the dataset is split into its smallest parts. RF is an ensemble of multiple tree-based predictors. The data are randomly split into subsets, which are then processed separately in different DTs. Therefore, the individual trees are less correlated, and the ensemble forest can provide better generalizability. The final results are then obtained by averaging the results of the individual trees. In this study, we implemented the tree-based models using scikit-learn [29] with the hyperparameters tuned using Bayesian search [35,36].
3.3.2. Multilayer Perceptron
The multilayer perceptron (MLP; [37]) model has been applied to different geodetic time series [38,39]. An MLP has an input layer, an output layer, and multiple hidden layers whose number of neurons can be arbitrarily chosen. Data in an MLP flows in a forward direction from the input to the output layer. The hidden layers consist of neurons with ReLU activation functions: . The results of each layer are passed to the next one. The outputs of a neural network are compared with the corresponding labels to compute the loss function. The weights are adjusted accordingly in the backward direction based on the partial gradients of the loss function from the output layer to the input layer.
3.3.3. Convolutional Neural Networks
A convolutional neural network (CNN; [40]) is a specific type of neural network that uses convolution in place of matrix multiplication in some layers. CNN-based models can be applied to time-series data using the 1D convolutional operation. In this study, we designed a CNN model as shown in Figure 5 with the detailed architecture shown in Table A1 realized using TensorFlow [41]. After two 1D convolutional layers, we use a flattening layer to convert the 2D vector (sequence and feature) into a 1D vector. Then, a fully connected layer with 64 hidden neurons and activation function tanh is applied to increase the non-linearity further. In the end, an output layer is applied.
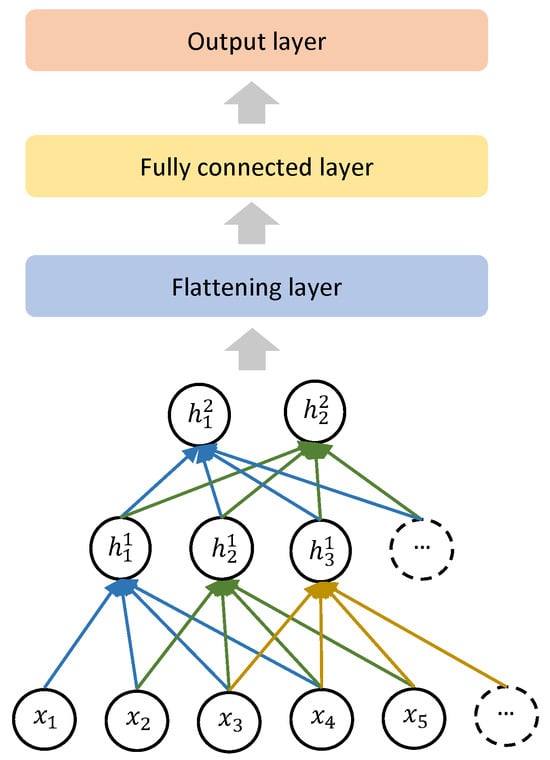
Figure 5.
The schematic representation of the CNN model used in this study. The inputs and hidden states are denoted using x and h, respectively.
3.3.4. Recurrent Neural Networks
The major shortcoming of the traditional MLP for time-series modeling is that they are not designed to incorporate sequential information properly. As a result, the performance of the traditional MLP in analyzing a long time series is imperfect. One of the historic DL models for processing sequential data is the Recurrent Neural Network (RNN; [42]). The key idea of RNN is that the hidden state at epoch t is related to the external signals and previous state. Two well-known difficulties in training an RNN model are the gradient vanishing problem when the gradients are too small or the gradient exploding problem when the gradients are too big [43,44]. To mitigate this problem, the Long Short-Term Memory (LSTM; [45]) has been introduced, which is one of the most used RNN variants. The LSTM neuron contains four gates: input gate (), forget gate (), output gate (), and cell state (). Equation (10)–(14) show the complete mathematical representation of an LSTM neuron:
where and are trainable weight matrices whereas are biases. The subscripts denote the time epoch t of the ith neuron within a layer. The sigmoid and the hyperbolic tangent activation functions are denoted by and tanh, respectively. The element-wise product is represented by ⊙. In this study, all the RNN architectures were combined with the LSTM neurons since their performance on predicting geodetic time series has been demonstrated [46,47,48,49].
A clear limitation of the original RNN architecture for our purpose is that the outputs at earlier epochs do not sense the latter hidden states. Since the 24-h orbit predictions should be related to the whole 24-h orbit observations, we should summarize all the information contained within the first 24 h and use them to predict the differences in the next 24 h. Multiple architectures exist that can provide sequential predictions by summarizing all the information in the input sequence. In this study, we considered three options, as shown in Figure 6.
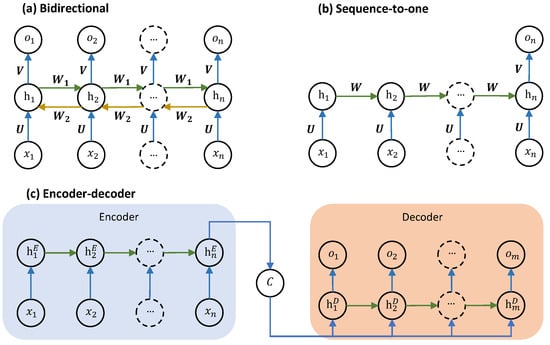
Figure 6.
The schematic representations of the three architectures of RNNs used in this study. The inputs and outputs are denoted by x and o, respectively. The hidden states are denoted by h, with the context denoted by C. The trainable weights are represented by .
The first option is bidirectional modeling (biLSTM; Figure 6a). The bidirectional modeling includes additional connections from the latter hidden states to the foregone hidden states, which is not feasible for real-time monitoring applications. However, if the entire input sequence precedes the target sequence, we can use the bidirectional architecture to let all the outputs sense the whole input sequence. The second architecture is called sequence-to-one modeling (LSTM-s2o; Figure 6b), which only has one output at the end of the sequence. This architecture is usually used to summarize a sequence and give one fixed-size representation as output. In this study, we used this architecture first to summarize the information contained in the orbit differences of the 24-h observations and then fed the output vector into two fully connected layers to predict the orbit differences in the following 24-h predictions. Figure 6c shows the third solution using an encoder-decoder architecture (EDLSTM; [50,51]). In the encoder, the input features are fed into an RNN model and generate a context vector , which summarizes the whole input sequence and serves as input features of the decoder model. The context vector will be copied m times to fit the length of the output sequence.
3.3.5. Combination of CNN and LSTM
Combining CNN and LSTM is beneficial for processing a sequence of images [52]. Presently, the idea of combining CNN and LSTM is becoming more noticeable in time-series prediction as well. The motivation is that the one-dimensional CNN layers focus on local areas and can extract high-level features. Then, LSTM layers can obtain these features and capture the long-term dependency. In this study, we also designed a model to combine the advantages of these two principles, as shown in Figure 7.
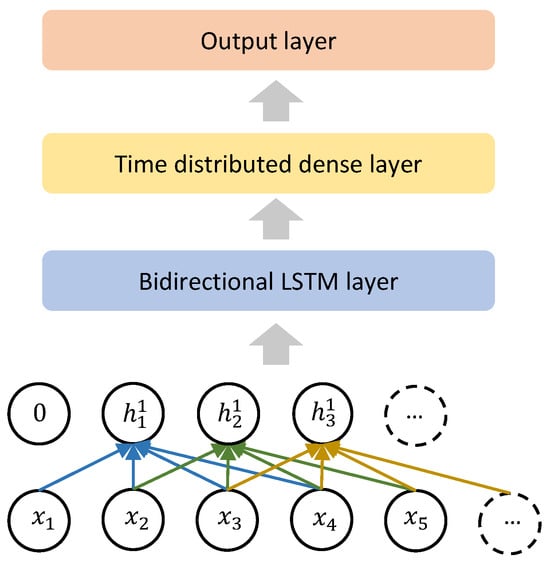
Figure 7.
Combination of CNN and bidirectional LSTM.
First, we treated the problem as a sequence-to-sequence problem, as shown in Figure 6a. We kept the sequence length the same with the help of the padding option [28]. After several 1D CNN layers, we connected the outputs to the LSTM layers, which means the different channels were considered to be different features in the LSTM layers. Since the high-level features extracted by the CNN layers usually do not contain all information of the whole sequence, the bidirectional LSTM was preferred for our purpose. To this end, each hidden state of the LSTM layer contains the information of the whole input time series and is fed into different dense layers to obtain the outputs.
3.4. Evaluation Metrics
We evaluated our results in two aspects: (a) the ensemble average of all test samples at individual time epochs () and (b) the temporal average of an individual test sample (). To evaluate the performances of our methods numerically, we defined three different evaluation metrics as follows:
where y, , and denote the original differences between ultra-rapid and final products, predicted differences using the models, and reduced differences. The subscripts denote the time epoch t of the ith sample. The number of samples and sequence length are denoted by N and S. The positive ratio () describes the proportion of samples that our approach improves.
3.5. Kinematic Precise Point Positioning Using Improved Orbits
The kinematic PPP was performed using Bernese V5.2 [53] with state-of-the-art parameterization without ambiguity resolution due to the lack of phase biases. All the settings and input data except for orbit products were kept the same for the three experiments to keep consistency: The GFZ final clock and ERP products were used [23]. We estimated 2-h tropospheric zenith delays and 24-h tropospheric gradients with an a priori model [54]. The necessary ionosphere models were downloaded from the Center for Orbit Determination in Europe (CODE; [55]) to compute the higher-order ionosphere corrections [56]. Following the standard setting in Bernese GNSS data processing, an elevation cutoff angle of 3 degrees was applied to the kinematic PPP processing.
To compare the impact of the three orbit products, we used 24-h arc lengths from GFZ final estimated orbits, GFZ ultra-rapid predicted orbits, and LSTM-improved predicted orbits. In the end, we estimated kinematic station coordinates and clock offsets jointly for every epoch, namely epoch-wise station coordinates in the zero-difference and PPP modes. To perform the analysis for a full year, we retrained the LSTM-s2o model, using data from 2017 to 2020, and applied the model to the data in 2021. We generated three solutions of station coordinates in 2021 using final estimations, ultra-rapid predictions, and LSTM-improved predictions of GPS orbit products, respectively. The estimated coordinates with a temporal resolution of 30 were then compared to the IGS weekly SINEX solution of GNSS station coordinates products [57].
4. Results and Discussion
In this section, we comprehensively report and discuss the performance of different ML/DL algorithms. First, we will compare the different LSTM architectures to determine the most suitable one. Then, we will compare the performance of all the other ML/DL approaches and demonstrate the suitability of LSTM-s2o for our purpose. Ultimately, we will report the results of kinematic PPP to the benefits of LSTM-improved orbit predictions for positioning applications.
4.1. Comparison of Different LSTM Architectures
Figure 8 shows the of the improved orbits using the four LSTM models compared to the original ultra-rapid orbit predictions. The statistics of the absolute improvements of are shown in Table 1. The LSTM-s2o model has the best performance with maximum 3D improvements of with the average improvements close to 10 . The maximum relative improvement is remarkable and reaches 73% with an average relative improvement of 47%. As a result, the improved orbit predictions can keep the difference under 10 for up to 10 h. The LSTM-s2s perform worse than all the other architectures, especially in the first epochs, since the outputs on the first few output epochs do not sense the information of later input epochs, which is unreasonable for our purpose. On the other hand, the outputs on the latter epochs contain more information about the input sequence. Therefore, the performance of LSTM-s2s in the later epochs becomes better.
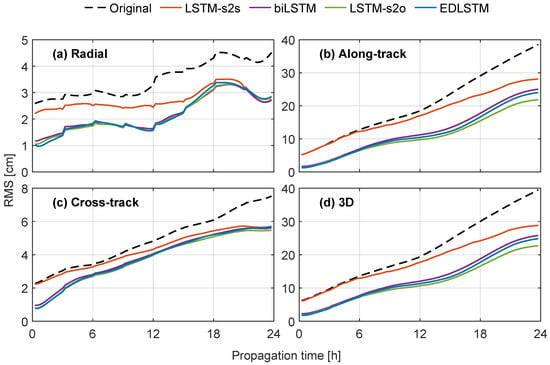
Figure 8.
[cm] of the differences between the orbit products enhanced using the four LSTM-based models and the final orbit products. The differences between the original ultra-rapid and final products are shown as reference.

Table 1.
The maximum, average, and minimal absolute improvements of [cm] of the three different LSTM architectures regarding the original ultra-rapid . The best performances are highlighted in bold.
We notice that the LSTM-s2o slightly outperforms other candidates. The potential reason for the worse performance of the biLSTM model is its limited performance in describing long-term correlation. If the time gap between input and output epochs is long, the correlations between the sequences decrease because of multiplications of multiple weight matrices. Due to the orbital period of around 12 h for GPS satellites, the outputs should have a high correlation to the inputs at 12 h (48 epochs) before, which is relatively long and challenging for the biLSTM network. On the contrary, the EDLSTM should perform better than the LSTM-s2o since it takes a similar final output of the LSTM layers but considers it to be a context vector rather than an input vector for fully connected layers. In the decoder, the sequential relationship between the epochs of the output sequence is also considered. In our experiments, however, the EDLSTM shows slightly lower performance than the LSTM-s2o model. A possible explanation is the overfitting issue. We have 144,075 training samples. However, the EDLSTM model has more trainable parameters due to the additional LSTM layers in the decoder (Table A1). Although the DL models can usually keep good generality with more trainable parameters than training samples, they may perform worse for certain complicated tasks.
We also studied the performance of the models on individual samples. Figure 9 shows the relative improvements of using the four LSTM-based models with the positive ratio shown in Table 2. They demonstrate again that the sequence-to-sequence architecture is, for our purpose, inferior, and all the other methods provide similar results. The other three models benefit from the periodicities of the GPS satellites and provide positive impacts on the radial components for about 90% of the test samples. The along-track component is the most important and challenging because of its large magnitude caused by error accumulation over time. Overall, the three models can provide positive 3D improvements to more than 75% of the test samples. The reason for the negative impact on certain samples is that some of the original products already have relatively low , and the errors of our models are more significant than the original differences between ultra-rapid and final products. With a low original value, a small negative impact can cause a large relative value. Our later analysis of the application of the enhanced orbit predictions demonstrates that the cases with negative impacts are not critical for the overall orbit quality.
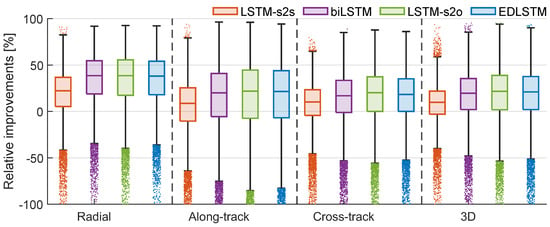
Figure 9.
Relative improvements of using the four LSTM-based models regarding the original ultra-rapid [%]. The edges of each box are the upper and lower quartiles. The data points that exceed 1.5 interquartile ranges are denoted using dots. The four groups show the improvements of radial, along-track, cross-track, and 3D .

Table 2.
The positive ratio of the relative improvements using the four different LSTM-based models regarding the original ultra-rapid errors [%]. The best performances are highlighted in bold.
4.2. Comparison of Machine-Learning and Deep-Learning Models
In this section, we summarize the results of the applied ML/DL models. Based on previous analysis, we only include the LSTM-s2o as the representation of LSTM-based models since it had the best performance. Furthermore, we also added some CNN layers before the LSTM layers to build the CNNLSTM model, which can explicitly extract high-level features from the original inputs (RSW coordinates). Figure 10 shows the behavior of the of the improved orbits using the six models compared to the differences between the original ultra-rapid and final orbits with the statistics of the absolute improvements of shown in Table 3. Overall, the DL models outperform the ML models because of their higher capacity. The LSTM model still demonstrates superiority because of its sequential modeling characteristics. DT shows only minor improvements with maximum improvements of 3D of only 9 because of its relatively basic principle. RF is an ensemble of multiple DTs and therefore provides more improvements with maximum improvements of reaching . MLP, CNN, and CNNLSTM show comparable results, indicating that we do not clearly benefit from the 1D CNN layers.
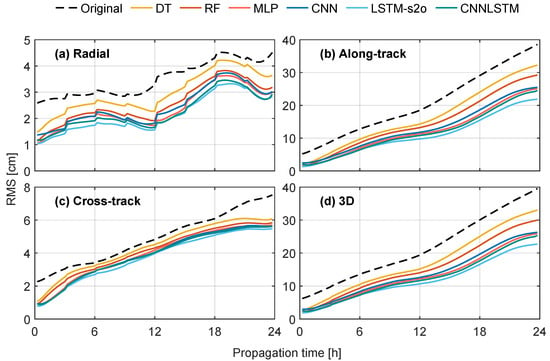
Figure 10.
[cm] of the differences between the orbits enhanced using the six ML/DL models and the final orbits. The differences between the original ultra-rapid and final products are shown as reference.

Table 3.
The maximum, average, and minimal absolute improvements of [cm] of the different ML/DL models regarding the original ultra-rapid . The best performances are highlighted in bold.
Figure 11 shows the relative improvements of using the six selected ML/DL models with the positive ratio shown in Table 4. The DL models generally provide more significant improvements with higher median values. However, the higher complexities of the DL models result in larger interquartile ranges, which means the improvements are less stable. This issue is expected to be mitigated if we include more training data. CNNLSTM has a more compact box with a higher positive ratio, which implies that extracting high-level features can make our predictions more stable. As a cost, it may not significantly reduce gross errors.
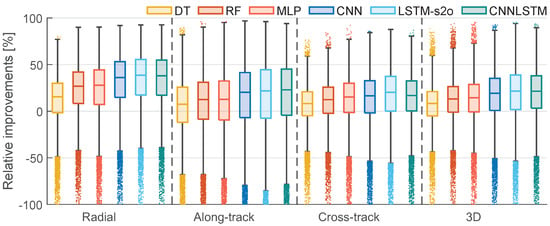
Figure 11.
Relative improvements of using the six ML/DL models regarding the original ultra-rapid [%]. The edges of each box are the upper and lower quartiles, respectively. The data points that exceed 1.5 interquartile ranges are denoted using dots. The four groups show the improvements of radial, along-track, cross-track, and 3D , respectively.

Table 4.
The positive ratio of the relative improvements using the six ML/DL models [%]. The best performances are highlighted in bold.
4.3. Precise Point Positioning Using LSTM-Improved Orbits
After proving the abilities of ML/DL approaches to model the differences between the ultra-rapid and final products, we analyzed the potential benefits of LSTM-improved orbit predictions for positioning applications. For this purpose, we generated the LSTM-improved orbits by adding differences predicted by the LSTM-s2o model to the corresponding ultra-rapid orbit predictions. Then, we performed kinematic PPP to evaluate the impact. We selected ten globally distributed IGS stations, as shown in Figure 12 to avoid potential latitude-based biases. The observation files were downloaded from CDDIS [58].
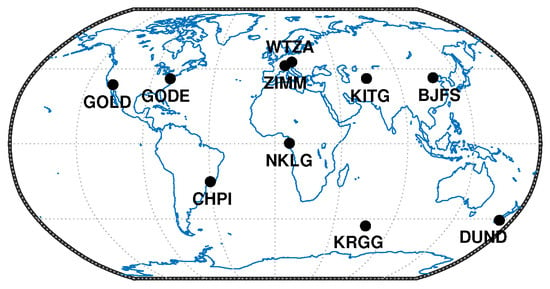
Figure 12.
The positions of the ten selected IGS stations.
Figure 13 shows the daily RMS of the estimated station coordinates regarding a reference for 2021 using the three different orbit products after removing outliers with daily RMS larger than ten times the median RMS. On average, about three days per year (less than 1%) were detected as outliers and excluded from further analysis. For all the components, the station coordinates using LSTM-improved orbit predictions outperform those using ultra-rapid predictions in both accuracy and precision. The boxes of the LSTM-improved orbits are significantly more compact than those using ultra-rapid orbits and with lower upper boundaries. The largest errors are in the up component due to their sensitivity to the satellite orbits [59], where our method provides consistent improvements of more than 10%. The lowest improvement of our method occurs in the east component of the NKLG station with relative improvements of 7%. One potential reason is its equatorial location, where the GPS orbit errors are mainly projected into the north and up directions. Moreover, the impact of the float ambiguity solution used in our processing is another potential reason. The results indicate the efficiency of the LSTM-s2o model in reducing the errors of ultra-rapid products. Considering the annual average RMS, the LSTM-improved orbits have lower errors at all ten stations with an average improvement of 16%, which indicates that the proposed method can provide improvements that are beneficial for positioning applications.
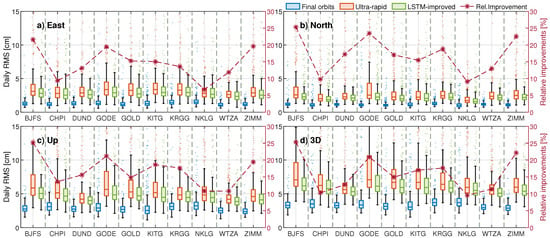
Figure 13.
The daily RMS [cm] of the station coordinates estimated using kinematic PPP with different orbit products for 2021. The box charts (left y-axis) show the RMS of the station coordinates using final, ultra-rapid, and LSTM-improved orbits. The black dashed line (right y-axis) indicates the relative improvements of the average RMS using LSTM-improved orbits compared to those using ultra-rapid orbit products.
5. Conclusions and Outlook
In this study, we applied different ML/DL algorithms to model the differences between the GPS ultra-rapid and final orbit products. The differences within the 24-h observation interval of the ultra-rapid products are used as input features, while the differences within the 24-h prediction interval of the same ultra-rapid products serve as targets for the ML/DL models. In this context, the ML/DL models capture the non-linear relationship between the 24-h observations and the 24-h predictions. Our analysis shows that all the studied ML/DL models can stably model the differences and achieve significant improvements in orbit predictions. Comparing the performance of different methods, we conclude that the LSTM models are the most suitable because of the time-series characteristic of the satellite orbits. The LSTM model with sequence-to-one modeling achieves the best performance with a maximum absolute improvement of 16.8 cm and averaged relative improvements over 45% in the aspect of . Additionally, it achieves stable improvements for more than 76% of test samples, which proves the sufficient generalization of the proposed method. The improved GPS orbits have an accuracy better than 10 cm over 10 h, which is 2.5 times longer than the original ultra-rapid orbits (4 h). We then applied the LSTM-improved orbits to estimate the coordinates of ten IGS stations globally and compared the results with the estimated coordinates using final and ultra-rapid orbits. The coordinates using LSTM-improved orbits are more accurate than those using ultra-rapid orbits by 16%. The results proved the potential benefits of the orbits enhanced by ML/DL methods for geodetic applications.
This study demonstrated the potential of applying data-driven ML/DL models to correct the systematic errors of the physics-based orbit propagators. The promising results revealed the prospect of combining the physics-based orbit propagator and the data-driven ML/DL algorithms to improve precise orbit predictions further. With the help of ML/DL algorithms, the limitations of the physics-based orbit propagator can be reduced to a certain degree. Moreover, the benefits of improved orbit predictions for positioning applications have been demonstrated. However, we should emphasize that the proposed method cannot be operationally applied due to the lack of high-quality references (final product) in this setting. In the future, combining the proposed methods with physics-based propagators for orbit predictions with time horizons longer than one day appears to be promising. In this case, we can benefit from the overlap of ultra-rapid orbit products and rapid orbit products and enhance the orbit predictions for the later epochs. One of the examples is the 5-day orbit prediction products provided by CODE [60]. We may benefit from their 1-day overlap with rapid products and enhance the orbit predictions for the next four days. As a result, the improved orbit predictions can be generated operationally and contribute to real-time applications.
Author Contributions
J.G. implemented the experiments with a focus on the deep-learning algorithms, generated plots, and drafted the manuscript. C.R. implemented the experiments with a focus on machine-learning algorithms. E.S. proposed and advised this study. K.C. advised this study and processed the kinematic PPP. M.K.S. advised this study. B.S. and M.R. supervised this study. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The used GFZ ultra-rapid and final orbit products can be found at https://doi.org/10.5880/GFZ.1.1.2020.004 and https://doi.org/10.5880/GFZ.1.1.2020.002, accessed on 3 May 2022. The used GFZ clock and ERP products can be found at https://doi.org/10.5880/GFZ.1.1.2020.002, accessed on 3 May 2022. The used transformation matrices between ITRF and ICRF can be found at https://hpiers.obspm.fr/eop-pc/index.php?index=matrice, accessed on 1 November 2021. The used ionosphere can be found at http://ftp.aiub.unibe.ch/CODE/IONO/, accessed on 11 May 2022. The used IGS weekly SINEX solution of GNSS station coordinates can be found at https://doi.org/10.5067/GNSS/gnss_igssnx_001, accessed on 17 May 2022.
Acknowledgments
We thank Lukas Müller for checking the Bernese settings.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Model Architectures
The detailed implementations of the used deep-learning models are described in Table A1.

Table A1.
Architectures of the used deep-learning models. The order follows the description in Section 3.3.
Table A1.
Architectures of the used deep-learning models. The order follows the description in Section 3.3.
| Model | Layer | Output Shape | Number of Parameters |
|---|---|---|---|
| CNN | Conv1D | (None, 92, 16) | 208 |
| Conv1D | (None, 89, 16) | 1040 | |
| Flatten | (None, 1424) | 0 | |
| Dense | (None, 64) | 91,200 | |
| Dense | (None, 95) | 6175 | |
| LSTM-s2s | LSTM | (None, 95, 128) | 67,584 |
| LSTM | (None, 95, 64) | 49,408 | |
| LSTM | (None, 95, 32) | 12,416 | |
| TimeDistributed(Dense) | (None, 95, 32) | 1056 | |
| TimeDistributed(Dense) | (None, 95, 1) | 33 | |
| biLSTM | Bidirectional(LSTM) | (None, 95, 256) | 135,168 |
| Bidirectional(LSTM) | (None, 95, 128) | 164,352 | |
| Bidirectional(LSTM) | (None, 95, 64) | 41,216 | |
| TimeDistributed(Dense) | (None, 95, 32) | 2080 | |
| TimeDistributed(Dense) | (None, 95, 1) | 33 | |
| LSTM-s2o | LSTM | (None, 95, 128) | 67,584 |
| LSTM | (None, 95, 64) | 49,408 | |
| LSTM | (None, 32) | 12,416 | |
| Dense | (None, 128) | 4224 | |
| Dense | (None, 95) | 12,255 | |
| EDLSTM | LSTM | (None, 95, 128) | 67,584 |
| LSTM | (None, 128) | 131,584 | |
| RepeatVector | (None, 95, 128) | 0 | |
| LSTM | (None, 95, 64) | 49,408 | |
| TimeDistributed(Dense) | (None, 95, 64) | 4160 | |
| TimeDistributed(Dense) | (None, 95, 1) | 65 | |
| CNNLSTM | Conv1D | (None, 95, 4) | 52 |
| Conv1D | (None, 95, 8) | 136 | |
| Conv1D | (None, 95, 16) | 528 | |
| Bidirectional(LSTM) | (None, 95, 60) | 11,280 | |
| Bidirectional(LSTM) | (None, 95, 25) | 8400 | |
| Bidirectional(LSTM) | (None, 95, 14) | 2016 | |
| TimeDistributed(Dense) | (None, 95, 1) | 15 |
References
- Shi, J.; Wang, G.; Han, X.; Guo, J. Impacts of satellite orbit and clock on real-time GPS point and relative positioning. Sensors 2017, 17, 1363. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Liao, X.; Li, B.; Yang, L. Modeling of the GPS satellite clock error and its performance evaluation in precise point positioning. Adv. Space Res. 2018, 62, 845–854. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Gong, X. Improved method for the GPS high-precision real-time satellite clock error service. GPS Solut. 2022, 26, 136. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Xiao, J. Estimating GNSS satellite clock error to provide a new final product and real-time services. GPS Solut. 2024, 28, 17. [Google Scholar] [CrossRef]
- Hauschild, A.; Montenbruck, O. Precise real-time navigation of LEO satellites using GNSS broadcast ephemerides. Navig. J. Inst. Navig. 2021, 68, 419–432. [Google Scholar] [CrossRef]
- Montenbruck, O.; Kunzi, F.; Hauschild, A. Performance assessment of GNSS-based real-time navigation for the Sentinel-6 spacecraft. GPS Solut. 2022, 26, 12. [Google Scholar] [CrossRef]
- Müller, L.; Chen, K.; Möller, G.; Rothacher, M.; Soja, B.; Lopez, L. Real-time navigation solutions of low-cost off-the-shelf GNSS receivers on board the Astrocast constellation satellites. Adv. Space Res. 2023. [Google Scholar] [CrossRef]
- Bergen, K.J.; Johnson, P.A.; Maarten, V.; Beroza, G.C. Machine learning for data-driven discovery in solid Earth geoscience. Science 2019, 363, eaau0323. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Yu, S.; Ma, J. Deep learning for geophysics: Current and future trends. Rev. Geophys. 2021, 59, e2021RG000742. [Google Scholar] [CrossRef]
- Butt, J.; Wieser, A.; Gojcic, Z.; Zhou, C. Machine learning and geodesy: A survey. J. Appl. Geod. 2021, 15, 117–133. [Google Scholar] [CrossRef]
- Pihlajasalo, J.; Leppäkoski, H.; Ali-Löytty, S.; Piché, R. Improvement of GPS and BeiDou extended orbit predictions with CNNs. In Proceedings of the 2018 European Navigation Conference (ENC), Gothenburg, Sweden, 14–17 May 2018; pp. 54–59. [Google Scholar] [CrossRef]
- Chen, H.; Niu, F.; Su, X.; Geng, T.; Liu, Z.; Li, Q. Initial results of modeling and improvement of BDS-2/GPS broadcast ephemeris satellite orbit based on BP and PSO-BP neural networks. Remote. Sens. 2021, 13, 4801. [Google Scholar] [CrossRef]
- Kiani, M. Simultaneous approximation of a function and its derivatives by Sobolev polynomials: Applications in satellite geodesy and precise orbit determination for LEO CubeSats. Geod. Geodyn. 2020, 11, 376–390. [Google Scholar] [CrossRef]
- Peng, H.; Bai, X. Improving orbit prediction accuracy through supervised machine learning. Adv. Space Res. 2018, 61, 2628–2646. [Google Scholar] [CrossRef]
- Peng, H.; Bai, X. Machine learning approach to improve satellite orbit prediction accuracy using publicly available data. J. Astronaut. Sci. 2020, 67, 762–793. [Google Scholar] [CrossRef]
- Mortlock, T.; Kassas, Z.M. Assessing machine learning for LEO satellite orbit determination in simultaneous tracking and navigation. In Proceedings of the 2021 IEEE Aerospace Conference (50100), Big Sky, MT, USA, 6–13 March 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Johnston, G.; Riddell, A.; Hausler, G. The International GNSS Service. In Springer Handbook of Global Navigation Satellite Systems; Springer International Publishing: Cham, Switzerland, 2017; pp. 967–982. [Google Scholar] [CrossRef]
- Duan, B.; Hugentobler, U.; Chen, J.; Selmke, I.; Wang, J. Prediction versus real-time orbit determination for GNSS satellites. GPS Solut. 2019, 23, 1–10. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, C.; Xu, T.; Chang, G.; Moraleda, A.H. Impacts of Earth rotation parameters on GNSS ultra-rapid orbit prediction: Derivation and real-time correction. Adv. Space Res. 2017, 60, 2855–2870. [Google Scholar] [CrossRef]
- IGS Products. Available online: https://igs.org/products/#orbits_clocks (accessed on 24 November 2012).
- Männel, B.; Brandt, A.; Nischan, T.; Brack, A.; Sakic, P.; Bradke, M. GFZ Ultra-Rapid Product Series for the International GNSS Service (IGS); GFZ Data Services: Potsdam, Germany, 2020. [Google Scholar] [CrossRef]
- Männel, B.; Brandt, A.; Nischan, T.; Brack, A.; Sakic, P.; Bradke, M. GFZ Final Product Series for the International GNSS Service (IGS); GFZ Data Services: Potsdam, Germany, 2020. [Google Scholar] [CrossRef]
- Griffiths, J. Combined orbits and clocks from IGS second reprocessing. J. Geod. 2019, 93, 177–195. [Google Scholar] [CrossRef]
- Rothacher, M. Orbits of Satellite Systems in Space Geodesy; lnstitut ftlr Geodlsie mid Photogrammetrie: Zurich, Switzerland, 1992; Volume 46. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions (2010); Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt, Germany, 2010. [Google Scholar]
- Montenbruck, O.; Gill, E. Satellite Orbits: Models, Methods and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Crocetti, L.; Schartner, M.; Soja, B. Discontinuity Detection in GNSS Station Coordinate Time Series Using Machine Learning. Remote. Sens. 2021, 13, 3906. [Google Scholar] [CrossRef]
- Jing, W.; Zhao, X.; Yao, L.; Di, L.; Yang, J.; Li, Y.; Guo, L.; Zhou, C. Can terrestrial water storage dynamics be estimated from climate anomalies? Earth Space Sci. 2020, 7, e2019EA000959. [Google Scholar] [CrossRef]
- Kiani Shahvandi, M.; Gou, J.; Schartner, M.; Soja, B. Data Driven Approaches for the Prediction of Earth’s Effective Angular Momentum Functions. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 6550–6553. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees; Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery; Routledge: New York, NY, USA, 2011; Volume 1, pp. 14–23. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Močkus, J. On bayesian methods for seeking the extremum. In Proceedings of the Optimization Techniques IFIP Technical Conference, Novosibirsk, Russia, 1–7 July 1974; Marchuk, G.I., Ed.; Springer: Berlin/Heidelberg, Germany, 1975; pp. 400–404. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; Pereira, F., Burges, C., Bottou, L., Weinberger, K., Eds.; Curran Associates, Inc.: New York, NY, USA, 2012; Volume 25. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Hoboken, NJ, USA, 1994. [Google Scholar]
- Schuh, H.; Ulrich, M.; Egger, D.; Müller, J.; Schwegmann, W. Prediction of Earth orientation parameters by artificial neural networks. J. Geod. 2002, 76, 247–258. [Google Scholar] [CrossRef]
- Li, F.; Kusche, J.; Rietbroek, R.; Wang, Z.; Forootan, E.; Schulze, K.; Lück, C. Comparison of data-driven techniques to reconstruct (1992–2002) and predict (2017–2018) GRACE-like gridded total water storage changes using climate inputs. Water Resour. Res. 2020, 56, e2019WR026551. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: tensorflow.org (accessed on 1 March 2021).
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 16–21 June 2013; pp. 1310–1318. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Gou, J.; Kiani Shahvandi, M.; Hohensinn, R.; Soja, B. Ultra-short-term prediction of LOD using LSTM neural networks. J. Geod. 2023, 97, 52. [Google Scholar] [CrossRef]
- Kiani Shahvandi, M.; Soja, B. Small geodetic datasets and deep networks: Attention-based residual LSTM Autoencoder stacking for geodetic time series. In Proceedings of the 7th International Conference on Machine Learning, Optimization, and Data Science, Grasmere, UK, 4–8 October 2021. [Google Scholar] [CrossRef]
- Kiani Shahvandi, M.; Soja, B. Inclusion of data uncertainty in machine learning and its application in geodetic data science, with case studies for the prediction of Earth orientation parameters and GNSS station coordinate time series. Adv. Space Res. 2022, 70, 563–575. [Google Scholar] [CrossRef]
- Tang, J.; Li, Y.; Ding, M.; Liu, H.; Yang, D.; Wu, X. An ionospheric TEC forecasting model based on a CNN-LSTM-attention mechanism neural network. Remote. Sens. 2022, 14, 2433. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 October 2014. pp. 3104–3112.
- Donahue, J.; Anne Hendricks, L.; Guadarrama, S.; Rohrbach, M.; Venugopalan, S.; Saenko, K.; Darrell, T. Long-term recurrent convolutional networks for visual recognition and description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2625–2634. [Google Scholar]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software, version 5.2; Astronomical Institute, University of Bern: Bern, Switzerland. [CrossRef]
- Böhm, J.; Heinkelmann, R.; Schuh, H. Short note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Dach, R.; Schaer, S.; Arnold, D.; Kalarus, M.S.; Prange, L.; Stebler, P.; Villiger, A.; Jäggi, A. CODE Final Product Series for the IGS; Astronomical Institute, University of Bern: Bern, Switzerland, 2020. [Google Scholar] [CrossRef]
- Chen, K.; Xu, T.; Yang, Y. Robust combination of IGS analysis center GLONASS clocks. GPS Solut. 2017, 21, 1251–1263. [Google Scholar] [CrossRef]
- IGS. International GNSS Service, GNSS Final Cumulative Combined Set of Station Coordinates Product, Greenbelt, MD, USA: NASA Crustal Dynamics Data Information System (CDDIS). 2022. Available online: https://cddis.nasa.gov/Data_and_Derived_Products/GNSS/gnss_igssnx.html (accessed on 16 May 2022).
- Noll, C.E. The crustal dynamics data information system: A resource to support scientific analysis using space geodesy. Adv. Space Res. 2010, 45, 1421–1440. [Google Scholar] [CrossRef]
- Santerre, R. Impact of GPS satellite sky distribution. Manuscripta Geod. 1991, 16, 28–53. [Google Scholar]
- Lutz, S.; Beutler, G.; Schaer, S.; Dach, R.; Jäggi, A. CODE’s new ultra-rapid orbit and ERP products for the IGS. GPS Solut. 2016, 20, 239–250. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).