A Satellite Observational Study of Topographical Effects on Daytime Shallow Convective Clouds
Abstract
1. Introduction
2. Study Area, Data, and Methods
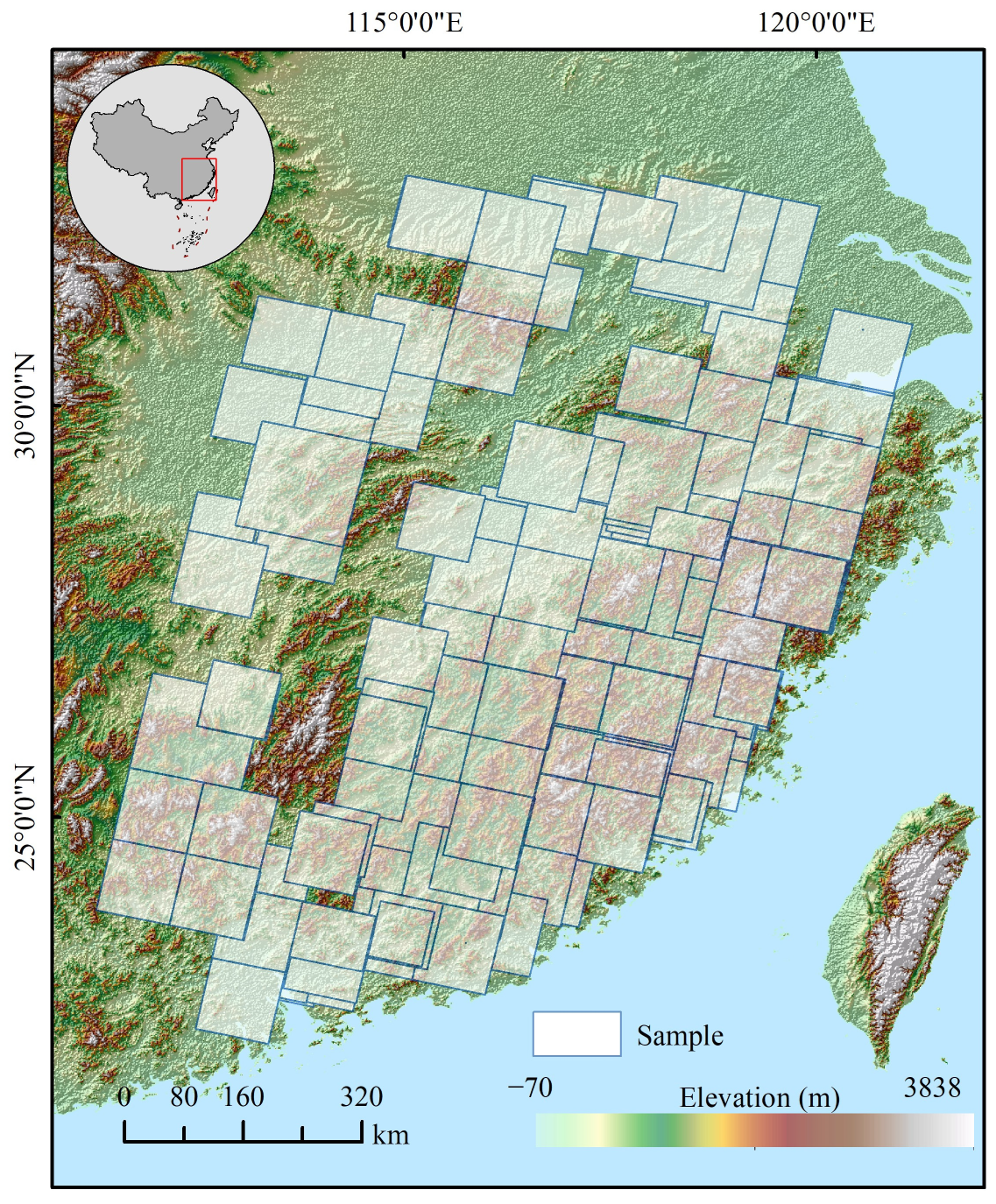
2.1. Study Area
2.2. Data
2.3. Cloud Identification Method
3. Results and Discussion
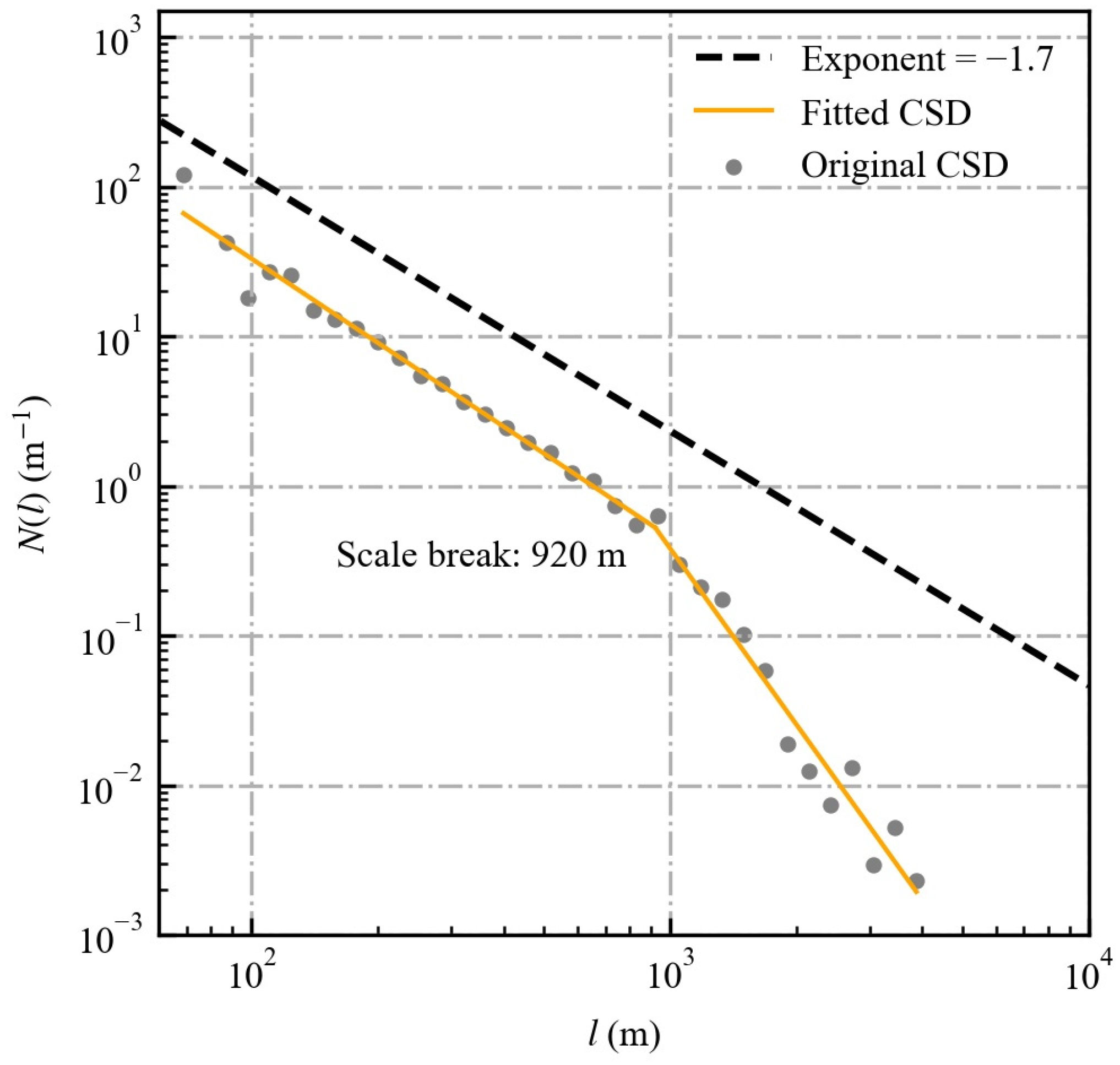
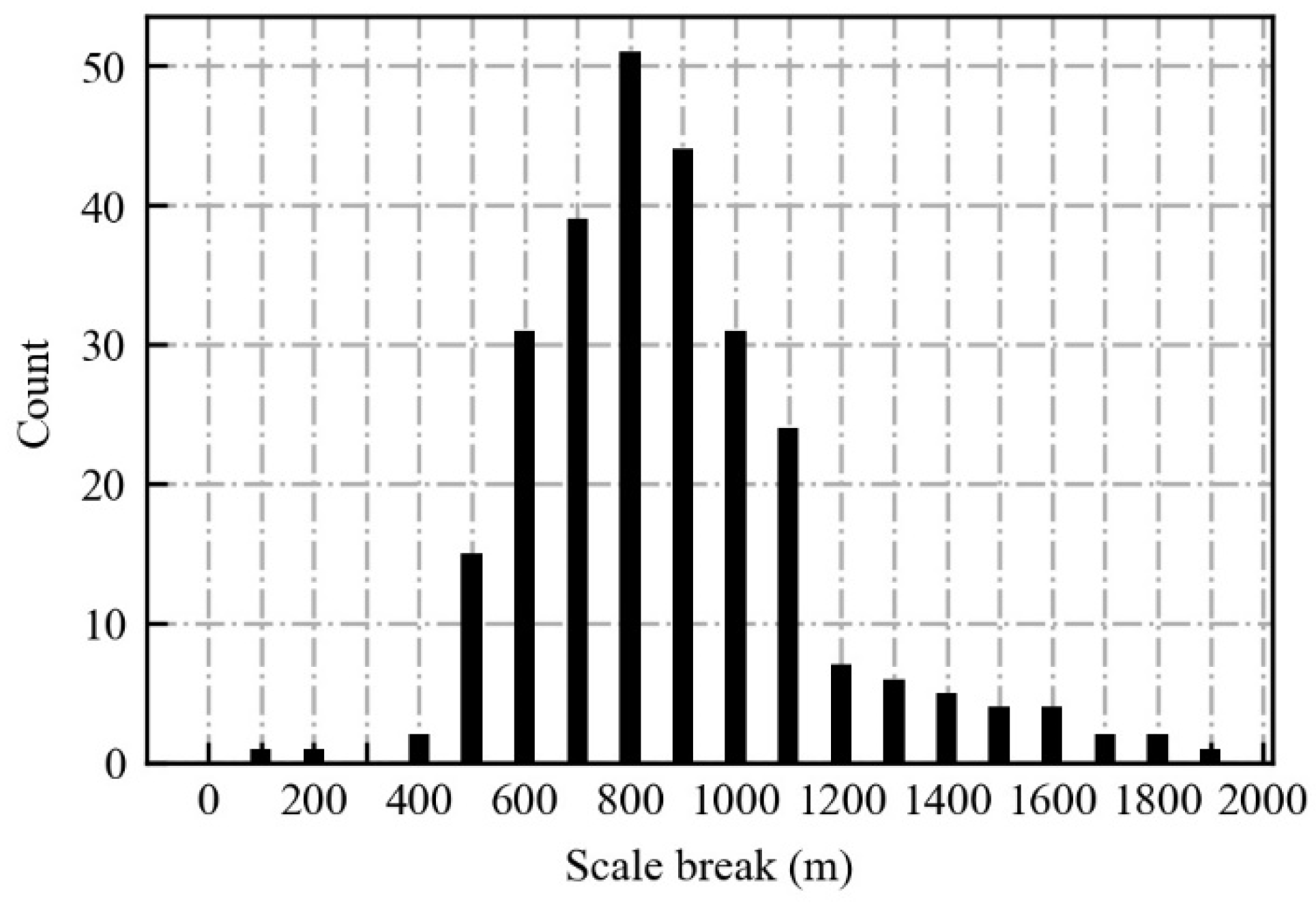
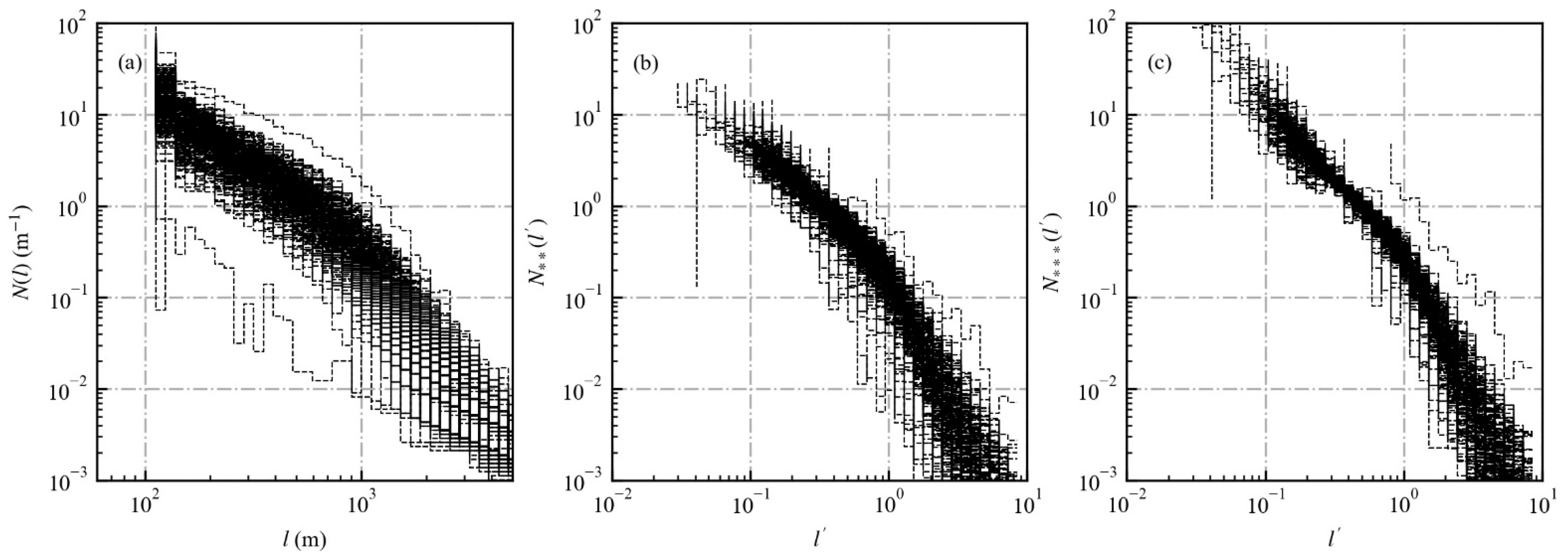
3.1. Cloud Size Distribution
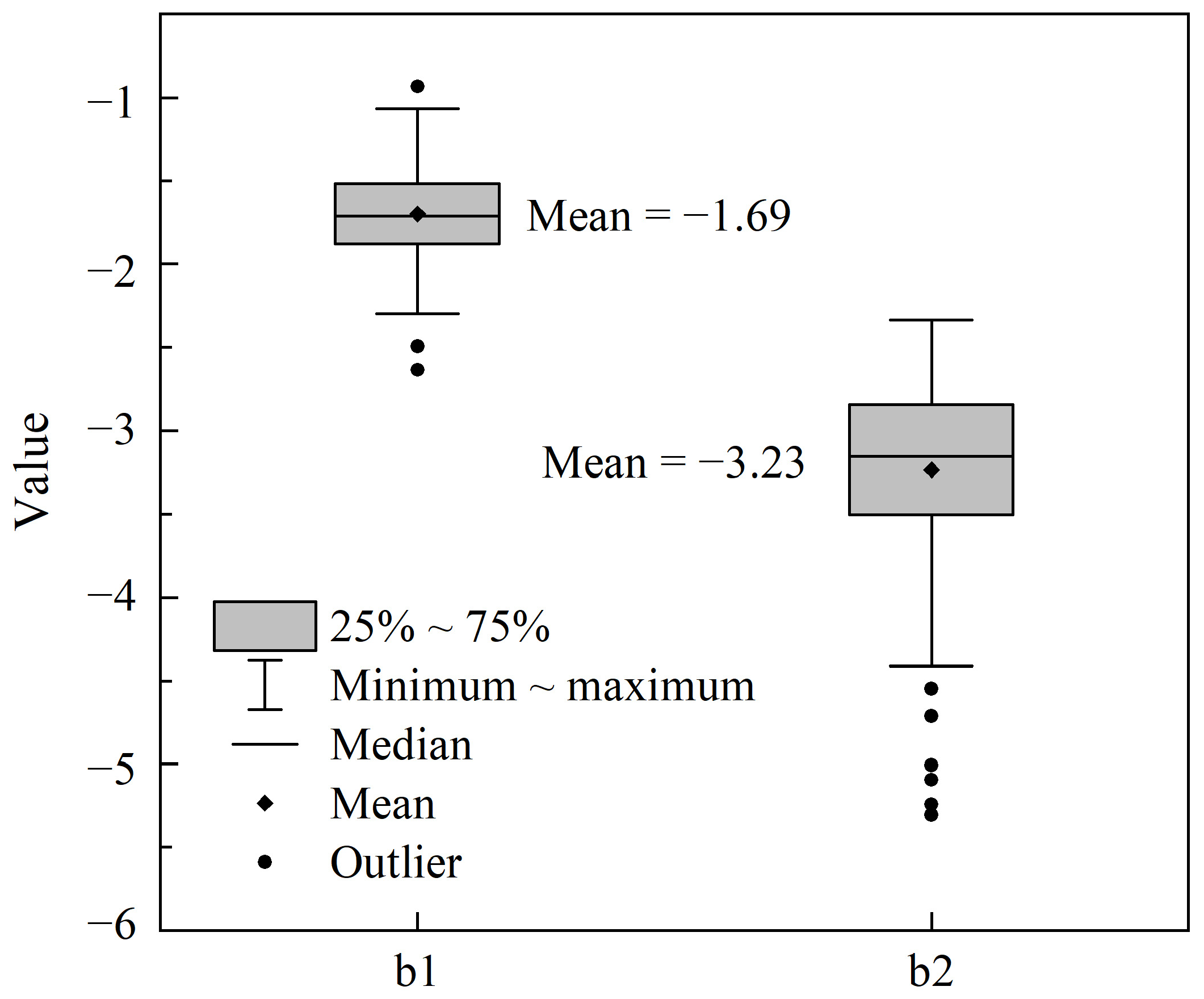
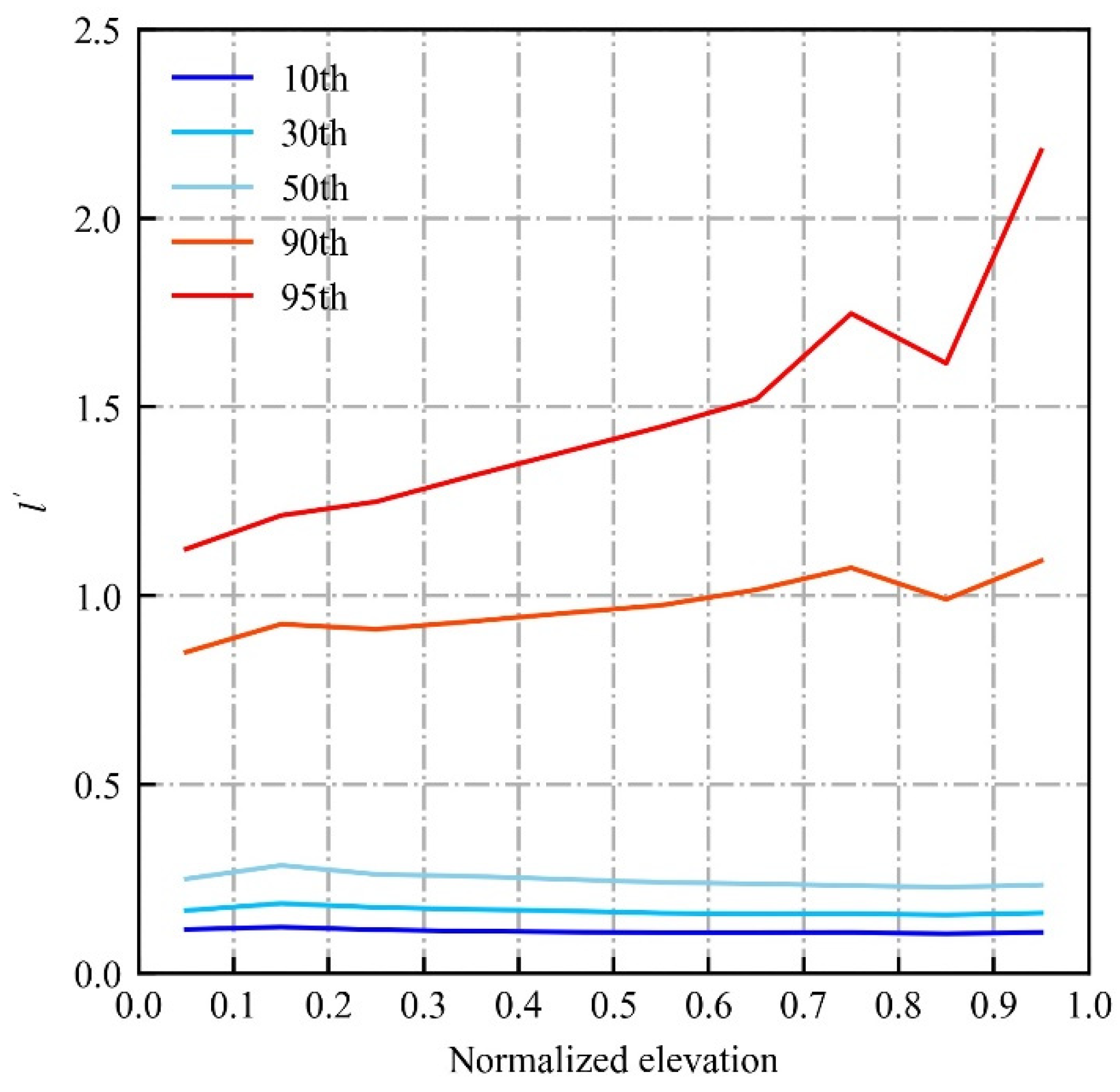
3.2. The Variation of Cloud Numbers and Sizes with the Elevation
3.3. Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Warren, S.G.; Hahn, C.J.; London, J.; Chervin, R.M.; Jenne, R.L. Global Distribution of Total Cloud Cover and Cloud Type Amounts Ocean; NCAR Technical Notes; University Corporation for Atmospheric Research: Boulder, CO, USA, 1988. [Google Scholar]
- Dror, T.; Koren, I.; Altaratz, O.; Heiblum, R.H. On the Abundance and Common Properties of Continental, Organized Shallow (Green) Clouds. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4570–4578. [Google Scholar] [CrossRef]
- Warren, S.G.; Hahn, C.J.; London, J.; Chervin, R.M.; Jenne, R.L. Global Distribution of Total Cloud Cover and Cloud Type Amounts Land; NCAR Technical Notes; University Corporation for Atmospheric Research: Boulder, CO, USA, 1986. [Google Scholar]
- Tian, J.; Zhang, Y.; Klein, S.A.; Wang, L.; Öktem, R.; Romps, D.M. Summertime Continental Shallow Cumulus Cloud Detection Using GOES-16 Satellite and Ground-Based Stereo Cameras at the DOE ARM Southern Great Plains Site. Remote Sens. 2021, 13, 2309. [Google Scholar] [CrossRef]
- Bony, S.; Stevens, B.; Frierson, D.M.W.; Jakob, C.; Kageyama, M.; Pincus, R.; Shepherd, T.G.; Sherwood, S.C.; Siebesma, A.P.; Sobel, A.H.; et al. Clouds, circulation and climate sensitivity. Nat. Geosci. 2015, 8, 261–268. [Google Scholar] [CrossRef]
- Fast, J.D.; Berg, L.K.; Alexander, L.; Bell, D.; D’Ambro, E.; Hubbe, J.; Kuang, C.; Liu, J.; Long, C.; Matthews, A.; et al. Overview of the HI-SCALE Field Campaign: A New Perspective on Shallow Convective Clouds. Bull. Am. Meteorol. Soc. 2019, 100, 821–840. [Google Scholar] [CrossRef]
- Berg, L.K.; Kassianov, E.I.; Long, C.N.; Mills, D.L. Surface summertime radiative forcing by shallow cumuli at the Atmospheric Radiation Measurement Southern Great Plains site. J. Geophys. Res. 2011, 116, D01202. [Google Scholar] [CrossRef]
- Chen, G.; Xue, H.; Feingold, G.; Zhou, X. Vertical transport of pollutants by shallow cumuli from large eddy simulations. Atmos. Chem. Phys. 2012, 12, 11319–11327. [Google Scholar] [CrossRef]
- Fu, S.; Rotunno, R.; Chen, J.; Deng, X.; Xue, H. A large-eddy simulation study of deep-convection initiation through the collision of two sea-breeze fronts. Atmos. Chem. Phys. 2021, 21, 9289–9308. [Google Scholar] [CrossRef]
- Richter, I.; Tokinaga, H. An overview of the performance of CMIP6 models in the tropical Atlantic: Mean state, variability, and remote impacts. Clim. Dyn. 2020, 55, 2579–2601. [Google Scholar] [CrossRef]
- Bauer, P.; Thorpe, A.; Brunet, G. The quiet revolution of numerical weather prediction. Nature 2015, 525, 47–55. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Mccaa, J.R.; Grenier, H. A New Parameterization for Shallow Cumulus Convection and Its Application to Marine Subtropical Cloud-Topped Boundary Layers. Part I: Description and 1D Results. Mon. Weather. Rev. 2003, 132, 864–882. [Google Scholar] [CrossRef]
- Neggers, R.A.J. A Dual Mass Flux Framework for Boundary Layer Convection. Part II: Clouds. J. Atmos. Sci. 2009, 66, 1489–1506. [Google Scholar] [CrossRef]
- Neggers, R.A.J. Exploring bin-macrophysics models for moist convective transport and clouds. J. Adv. Model. Earth Syst. 2015, 7, 2079–2104. [Google Scholar] [CrossRef]
- Neggers, R.A.J.; Jonker, H.J.J.; Siebesma, A.P. Size Statistics of Cumulus Cloud Populations in Large-Eddy Simulations. J. Atmos. Sci. 2003, 60, 1060–1074. [Google Scholar] [CrossRef]
- Guo, X.; Li, Y.; Cao, L.; Endo, S.; Wu, X.; Zhang, G.J.; Liu, Y.; Lu, C. Improving Parameterization of Entrainment Rate for Shallow Convection with Aircraft Measurements and Large-Eddy Simulation. J. Atmos. Sci. 2016, 73, 761–773. [Google Scholar] [CrossRef]
- de Rooy, W.C.; Bechtold, P.; Fröhlich, K.; Hohenegger, C.; Jonker, H.; Mironov, D.; Pier Siebesma, A.; Teixeira, J.; Yano, J.-I. Entrainment and detrainment in cumulus convection: An overview. Q. J. R. Meteorol. Soc. 2013, 139, 1–19. [Google Scholar] [CrossRef]
- Drueke, S.; Kirshbaum, D.J.; Kollias, P. Environmental sensitivities of shallow-cumulus dilution—Part 1: Selected thermodynamic conditions. Atmos. Chem. Phys. 2020, 20, 13217–13239. [Google Scholar] [CrossRef]
- Plank, G.V. The Size Distribution of Cumulus Clouds in Representative Florida Populations. J. Appl. Meteorol. 1969, 8, 46–67. [Google Scholar] [CrossRef]
- Neggers, R.A.J.; Duynkerke, P.G.; Rodts, S.M.A. Shallow cumulus convection: A validation of large-eddy simulation against aircraft and Landsat observations. Q. J. R. Meteorol. Soc. 2003, 129, 2671–2696. [Google Scholar] [CrossRef]
- Xue, H.; Feingold, G. Large-Eddy Simulations of Trade Wind Cumuli: Investigation of Aerosol Indirect Effects. J. Atmos. Sci. 2006, 63, 1605–1622. [Google Scholar] [CrossRef]
- Mieslinger, T.; Horváth, Á.; Buehler, S.A.; Sakradzija, M. The Dependence of Shallow Cumulus Macrophysical Properties on Large-Scale Meteorology as Observed in ASTER Imagery. J. Geophys. Res. Atmos. 2019, 124, 11477–11505. [Google Scholar] [CrossRef]
- Stevens, B. Atmospheric Moist Convection. Annu. Rev. Earth Planet. Sci. 2005, 33, 605–643. [Google Scholar] [CrossRef]
- Kirshbaum, D.; Adler, B.; Kalthoff, N.; Barthlott, C.; Serafin, S. Moist Orographic Convection: Physical Mechanisms and Links to Surface-Exchange Processes. Atmosphere 2018, 9, 80. [Google Scholar] [CrossRef]
- Whiteman, C.D. Mountain Meteorology: Fundamentals and Applications; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Markowski, P.; Richardson, Y. Convection Initiation. In Mesoscale Meteorology in Midlatitudes; Wiley-Blackwell: West Sussex, UK, 2010; pp. 183–199. [Google Scholar]
- Demko, J.C.; Miao, Q.; Geerts, B. Pressure Perturbations and Upslope Flow over a Heated, Isolated Mountain. Mon. Weather. Rev. 2008, 136, 4272–4288. [Google Scholar] [CrossRef][Green Version]
- Banta, M.R. Daytime Boundary-Layer Evolution over Mountainous Terrain.Part I: Observations of the Dry Circulations. Mon. Weather. Rev. 1983, 112, 340–356. [Google Scholar] [CrossRef]
- Lu, G.; Ren, Y.; Fu, S.; Xue, H. Statistics of Isolated Deep Convection Initiation and Its Relation to Topography in the North China Area. J. Geophys. Res. Atmos. 2023, 128, e2022JD037949. [Google Scholar] [CrossRef]
- Geerts, B.; Demko, J.C. A Numerical Study of the Evolving Convective Boundary Layer and Orographic Circulation around the Santa Catalina Mountains in Arizona. Part I: Circulation without Deep Convection. Mon. Weather. Rev. 2010, 138, 1902–1922. [Google Scholar] [CrossRef][Green Version]
- Panosetti, D.; Böing, S.; Schlemmer, L.; Schmidli, J. Idealized Large-Eddy and Convection-Resolving Simulations of Moist Convection over Mountainous Terrain. J. Atmos. Sci. 2016, 73, 4021–4041. [Google Scholar] [CrossRef]
- Rotach, M.W.; Wohlfahrt, G.; Hansel, A.; Reif, M.; Wagner, J.; Gohm, A. The World is Not Flat: Implications for the Global Carbon Balance. Bull. Am. Meteorol. Soc. 2014, 95, 1021–1028. [Google Scholar] [CrossRef]
- Ensle, F.; Heinzel, J.; Koch, B. Evaluating height differences between global digital surface models and icesat heights at footprint geolocation. In Proceedings of the 9th International Symposium on Surface Models for Geosciences (GIS), Ostrava, Czech Republic, 23–25 January 2012; pp. 37–47. [Google Scholar]
- Qiu, S.; Zhu, Z.; He, B. Fmask 4.0: Improved cloud and cloud shadow detection in Landsats 4–8 and Sentinel-2 imagery. Remote Sens. Environ. 2019, 231, 111205. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Gomez-Chova, L.; Camps-Valls, G.; Calpe-Maravilla, J.; Guanter, L.; Moreno, J. Cloud-Screening Algorithm for ENVISAT/MERIS Multispectral Images. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4105–4118. [Google Scholar] [CrossRef]
- Irish, R.R.; Barker, J.L.; Goward, S.N.; Arvidson, T. Characterization of the Landsat-7 ETM Automated Cloud-Cover Assessment (ACCA) Algorithm. Photogramm. Eng. Remote Sens. 2006, 72, 1179–1188. [Google Scholar] [CrossRef]
- Pilgrim, C. Piecewise-regression (aka segmented regression) in Python. J. Open Source Softw. 2021, 6, 3859. [Google Scholar] [CrossRef]
- Muggeo, V.M.R. Estimating regression models with unknown break-points. Stat. Med. 2003, 22, 3055–3071. [Google Scholar] [CrossRef] [PubMed]
- Dawe, J.T.; Austin, P.H. Statistical analysis of an LES shallow cumulus cloud ensemble using a cloud tracking algorithm. Atmos. Chem. Phys. 2012, 12, 1101–1119. [Google Scholar] [CrossRef]
- Heus, T.; Seifert, A. Automated tracking of shallow cumulus clouds in large domain, long duration large eddy simulations. Geosci. Model Dev. 2013, 6, 1261–1273. [Google Scholar] [CrossRef]
- Fu, S.; Rotunno, R.; Xue, H. Convective updrafts near sea-breeze fronts. Atmos. Chem. Phys. 2022, 22, 7727–7738. [Google Scholar] [CrossRef]
- Banta, R.M.; Barker Schaaf, C. Thunderstorm Genesis Zones in the Colorado Rocky Mountains as Determined by Traceback of Geosynchronous Satellite Images. Mon. Weather. Rev. 1987, 115, 463–476. [Google Scholar] [CrossRef]


| Band Number | Band Name | Wavelength (μm) | Resolution (m) | Sensor |
|---|---|---|---|---|
| 2 | Blue | 0.4520.512 | 30 | OLI |
| 3 | Green | 0.5330.590 | 30 | OLI |
| 4 | Red | 0.6360.673 | 30 | OLI |
| 5 | NIR | 0.8510.879 | 30 | OLI |
| 6 | SWIR1 | 1.5661.651 | 30 | OLI |
| 7 | SWIR2 | 2.1072.294 | 30 | OLI |
| 10 | TIR | 10.6011.19 | 100 | TIRS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Fu, S.; Liu, J.; Shang, R.; Luo, Y. A Satellite Observational Study of Topographical Effects on Daytime Shallow Convective Clouds. Remote Sens. 2023, 15, 5542. https://doi.org/10.3390/rs15235542
Xu G, Fu S, Liu J, Shang R, Luo Y. A Satellite Observational Study of Topographical Effects on Daytime Shallow Convective Clouds. Remote Sensing. 2023; 15(23):5542. https://doi.org/10.3390/rs15235542
Chicago/Turabian StyleXu, Guoqiang, Shizuo Fu, Jane Liu, Rong Shang, and Yuanyuan Luo. 2023. "A Satellite Observational Study of Topographical Effects on Daytime Shallow Convective Clouds" Remote Sensing 15, no. 23: 5542. https://doi.org/10.3390/rs15235542
APA StyleXu, G., Fu, S., Liu, J., Shang, R., & Luo, Y. (2023). A Satellite Observational Study of Topographical Effects on Daytime Shallow Convective Clouds. Remote Sensing, 15(23), 5542. https://doi.org/10.3390/rs15235542







