Abstract
Remote sensing has emerged as a promising tool for monitoring water quality (WQ) in aquatic ecosystems. This study evaluates the effectiveness of remote sensing in assessing WQ parameters in Cajititlán and Zapotlán lakes in the state of Jalisco, Mexico. Over time, these lakes have witnessed a significant decline in WQ, necessitating the adoption of advanced monitoring techniques. In this research, satellite-based remote sensing data were combined with ground-based measurements from the National Water Quality Monitoring Network of Mexico (RNMCA). These data sources were harnessed to train and evaluate the performance of six distinct categories of machine learning (ML) algorithms aimed at estimating WQ parameters with active spectral signals, including chlorophyll-a (Chl-a), turbidity, and total suspended solids (TSS). Various limitations were encountered during the study, primarily due to atmospheric conditions and cloud cover. These challenges affected both the quality and quantity of the data. However, these limitations were overcome through rigorous data preprocessing, the application of ML techniques designed for data-scarce scenarios, and extensive hyperparameter tuning. The superlearner algorithm (SLA), which leverages a combination of individual algorithms, and the multilayer perceptron (MLP), capable of handling complex and non-linear problems, outperformed others in terms of predictive accuracy. Notably, in Lake Cajititlán, these models provided the most accurate predictions for turbidity (r2 = 0.82, RMSE = 9.93 NTU, MAE = 7.69 NTU), Chl-a (r2 = 0.60, RMSE = 48.06 mg/m3, MAE = 37.98 mg/m3), and TSS (r2 = 0.68, RMSE = 13.42 mg/L, MAE = 10.36 mg/L) when using radiometric data from Landsat-8. In Lake Zapotlán, better predictive performance was observed for turbidity (r2 = 0.75, RMSE = 2.05 NTU, MAE = 1.10 NTU) and Chl-a (r2 = 0.71, RMSE = 6.16 mg/m3, MAE = 4.97 mg/m3) with Landsat-8 radiometric data, while TSS (r2 = 0.72, RMSE = 2.71 mg/L, MAE = 2.12 mg/L) improved when Sentinel-2 data were employed. While r2 values indicate that the models do not exhibit a perfect fit, those approaching unity suggest that the predictor variables offer valuable insights into the corresponding responses. Moreover, the model’s robustness could be enhanced by increasing the quantity and quality of input variables. Consequently, remote sensing emerges as a valuable tool to support the objectives of WQ monitoring systems.
1. Introduction
Water resources provide ecosystem services of high natural and economic value for the population in general. Consequently, more than 40% of human settlements are located near coastal regions and on the shores of lotic and lentic resources [1,2]. Unfortunately, this makes these bodies of water more susceptible to pollution and overexploitation. In this way, WQ monitoring has become the most suitable strategy to evaluate sustainability in water management practices [3,4]. In recent years, there has been an increase in continuous monitoring campaigns for WQ parameters in various Latin American countries [5]. These initiatives aim to comprehend and proactively address WQ degradation by analyzing data collected during monitoring campaigns.
Conventional monitoring determines the WQ parameters by collecting samples in the field and their subsequent analysis in the laboratory. This is why it becomes a highly precise technique, but its complexity increases when working in large bodies of water. Consequently, the work is laborious and time-consuming, which results in an increase in costs that governments in many poor or developing countries cannot afford [6]. In addition, the sampling points may be limited due to restricted access in sectors with irregular topographies. Therefore, the accuracy and precision of the data may be compromised, including by in situ sampling error or laboratory analysis error. Hence, conventional methods cannot easily identify temporal and spatial variations of WQ parameters. Consequently, it is not possible to represent the complete state of the water surface and thus an obstacle prevents the monitoring and management of the quality of water masses [1,5,6,7].
On the other hand, advances in space science, cloud computing and ML contribute to the development of new techniques to work with natural resource management. For instance, satellites have built-in optical and thermal sensors that measure reflected electromagnetic radiation. This information is used to evaluate WQ with high spectral and spatial resolution [2,8]. Remote sensing as a technique to monitor WQ has been used since the 1970s, so that, since that decade, studies with methodological approaches have been developed to take advantage of the advantages offered by satellites [9]. The satellite radiometers used up to now are designed for the observation of the ocean and the terrestrial surface; therefore, they are not suitable for observing continental waters [10,11]. However, the fine spatial resolution of terrestrial sensors enables the acquisition of acceptable results for monitoring WQ parameters [4,12].
The literature review underscores the increasing utilization of Landsat-8 and Sentinel-2 sensors, highlighting their remarkable advantages in terms of fine spatial and temporal resolution [13,14]. Landsat-8, for instance, provides data at 16-day intervals, roughly equivalent to 22 annual images, depending on the location, while Sentinel-2 captures images every 5 days, resulting in approximately 73 images annually. These attributes have played a pivotal role in yielding highly promising results in the remote detection of WQ parameters within continental water bodies [15,16,17,18].
Nevertheless, a significant challenge for these studies has been the limitation in accessing sufficient training data for ML models [2,19]. The acquisition of satellite images is constrained by adverse climatic factors, such as persistent cloud cover or precipitation, which hinder the capture of surface water reflectance values [20]. The pressing need for an adequate quantity of training data materializes as a substantial challenge in this research domain. To address this data limitation, several studies employ the k-Fold-Cross-Validation technique to maximize the use of limited data and build robust models [18]. It is heartening to note that the relationship between the reflected light from specific parameters and their field-measured concentrations has proven to be an effective avenue for generating promising results in predictive models [21].
Furthermore, to overcome the shortage of training data for ML models, several studies opt to incorporate in situ data from monitoring activities available through open-access portals of national water and environmental agencies across diverse nations [19]. For instance, Papenfus et al. [22] employed data from the United States Environmental Protection Agency’s Water Quality Portal to facilitate remote sensing of Chl-a in lakes and reservoirs within the United States. Similarly, other data sources include the European Environment Agency (EEA) Waterbase portal in Europe, the Global Freshwater Quality Database (GEMStat) at a global scale, and Canada’s Open Government Portal [19].
In Latin America, studies such as that by Rodríguez López et al. [23] used in situ data from Dirección General de Aguas de Chile to estimate Chl-a concentration using Landsat-8 and obtained r2 values ranging from 0.64 to 0.93 when testing various neural networks. In Brazil, Bettencourt et al. [24] estimated turbidity and Chl-a through in situ data from the National Agency of Waters (ANA-Hidroweb). In Argentina, Germán et al. [25] estimated Chl-a levels using Sentinel-2 satellite data in conjunction with in situ measurements obtained from a monitoring program conducted by the Ministry of Water, Environment, and Public Services of the province of Córdoba. Their findings revealed an r2 of 0.77. In Mexico, Otto et al. [26] used data from the RNMCA together with Landsat radiometric data as input variables to develop empirical models and estimate turbidity in Lake Chapala; the authors obtained an r2 of 0.7. Similarly, Torres Vera [27], based on data from the RNMCA, developed an ML model to estimate TSS in Lake Chapala using Landsat images; the r2 obtained was 0.81. Another significant work was conducted by Arias Rodríguez et al. [5], where the authors evaluated an extreme learning machine (ELM), a support vector regression, and a linear regression to estimate Chl-a, turbidity, TSS, and Secchi disk depth in the lakes of the Mexican territory (Chapala, Cuitzeo, Patzcuaro, Yuriria, and Catemaco). They integrated in situ measurements of the RNMCA with data from Landsat-8, Sentinel-3, and Sentinel-2, and reported that the atmospherically corrected Sentinel-3 data and ELM models performed better, particularly for turbidity (r2 = 0.7). This illustrates the remarkable evolution in the application of remote sensing technologies for WQ monitoring in Latin American countries while emphasizing the innovative strategies employed to address the challenges in this research field.
Despite the vast scientific literature dedicated to WQ monitoring through remote sensing techniques, the global environment remains a complex and evolving system, as emphasized by Sagan et al. [8]. In light of this understanding, dependence solely on existing research becomes inadequate and occasionally unfeasible. To tackle this challenge, it is essential to engage in continuous research and monitoring of water bodies that have not undergone comprehensive analysis.
This situation is exemplified in the case of lakes Cajititlán and Zapotlán, distinguished by their unique geography, hydrology, surrounding land use, and environmental conditions, rendering them particularly pertinent to this study. Each water body constitutes a distinct system, and solutions effective in one may not be directly applicable in the other. The diversity and distinctiveness of these ecosystems underscore the necessity of data collection and the generation of specific contextual information for future water research and management projects [14]. Furthermore, both lakes hold ecological and touristic significance within the country, as their waters are employed for agricultural irrigation and recreational purposes [28,29].
In the perspective of developing countries like Mexico, budget constraints often limit the resources allocated for water management [30]. Accessing advanced equipment, such as hyperspectral sensors or drones equipped with high-resolution multispectral cameras, can pose a significant challenge due to financial restrictions [31,32]. In this context, the study’s primary objective is to introduce an innovative and cost-effective solution for monitoring WQ in Lakes Cajititlán and Zapotlán. By breaking new ground, the aim is to contribute to filling the critical gap in the field of remote sensing studies, where these particular bodies of water have remained largely unexplored. To achieve this goal, a wide range of ML algorithms were systematically evaluated, distinguishing the best performing ones to ensure the effectiveness and robustness of the method. By addressing this research gap, this work advances the understanding and management of WQ, thereby establishing a valuable precedent for future studies in similar ecological contexts.
Utilizing the data made available by the National Water Commission (CONAGUA) and delivering a pragmatic management tool for these bodies of water, a valuable resource was provided that serves the interests of both the scientific community and the local population. In the present day, society assumes a pivotal role in the decision-making processes related to water resource management [33]. There is a growing demand for robust tools that streamline the acquisition of pertinent information concerning WQ in these natural resources. Such information is indispensable for preempting environmental challenges, including water pollution, and proactively mitigating these issues [34].
This study involved correlating radiometric data from Landsat-8 and Sentinel-2 with WQ parameters characterized by an active spectral signal. While existing methods from the literature were employed, the uniqueness of this research is corroborated by the examination of water bodies that had not previously been monitored by remote sensing. Furthermore, the advantage lies in the availability of RNMCA data from 2009 to the present, which effectively increases the volume of input data for training ML algorithms.
The effectiveness of eight state-of-the-art ML algorithms spanning various categories was evaluated, introducing a broader range compared to previous studies using RNMCA data. The scope of hyperparameter adjustment was expanded through grid search techniques to enhance the model performance. The first category of algorithms encompasses ensemble methods, where the Gradient Boosting Regressor was considered for its capacity to amalgamate the predictive prowess of multiple decision trees. This attribute renders it particularly adept at capturing the intricate and interrelated dynamics inherent in WQ parameters [35]. Concomitantly, the Random Forest Regressor, a model that harnesses an ensemble of decision trees, was engaged to deliver precise predictions [36]. Furthermore, the SLA was leveraged to enhance predictive performance. The SLA operates by stacking the outputs of individual estimators and utilizing a regressor to compute the final prediction, harnessing the collective strength of each constituent estimator [37]. The second category encompasses neural networks, where the MLP assumes a pivotal role. The MLP, renowned for its proficiency in apprehending intricate relationships, excels at modeling non-linear dependencies between WQ input and output variables more effectively than conventional linear regression models [21,38]. Within the third category, regularization techniques were incorporated, with particular emphasis on the Ridge regression algorithm. Ridge regression, through the introduction of a penalty term, effectively mitigates the risk of overfitting in linear regression models [36]. The fourth category, consisting of instance-based methods, introduced the K-Neighbors Regressor. This algorithm relies on the similarity between data points to make predictions, rendering it well-suited for the estimation of WQ parameters [35]. In the fifth category, decision trees were comprehensively explored for their inherent interpretability and effectiveness [21]. Finally, the sixth category extended the evaluation to encompass other algorithms, such as Support Vector Machines, renowned for their distinctive capabilities in modeling intricate and non-linear relationships [36].
The thorough investigation of these diverse ML algorithms underlines the primary objective of the study: to identify the most effective approach for addressing the intricate and nonlinear characteristics inherent to WQ parameters [21]. Additionally, the strategic adjustment of hyperparameters, encompassing broad ranges, played a pivotal role in enhancing the predictive model’s performance. This comprehensive analysis ensures that the results are not only robust but also capable of meeting the complex challenges posed by WQ parameter estimation.
2. Materials and Methods
2.1. Description of the Study Area
Lake Cajititlán is located in the municipality of Tlajomulco de Zúñiga in the state of Jalisco, Mexico at the geographic coordinates: 20.41543° in latitude and −103.335317° in longitude. It has a length of 7.5 km, a width of 2.0 km and a depth of 2.5 m [39]. Lake Zapotlán is located in the south of the State of Jalisco at the geographic coordinates: 19.755395° in latitude and −103.483733° in longitude. It has an approximate area of 16.73 km2 and an average depth of 4.5 m. Figure 1 shows the location of the lakes with their respective monitoring points managed by the RNMCA.

Figure 1.
Location map of the Cajititlán and Zapotlán lakes with the water quality sampling points administered by the RNMCA.
2.2. Lake Water Quality Data
The in situ data were acquired from the platform of the Jalisco State Water Commission through the open data service of the WQ system of the RNMCA [40]. Three optically active parameters (Chl-a, turbidity and TSS) were selected, which interact with light and change the energy spectrum of the radiation reflected from water bodies, so that they can be measured with remote sensors. The RNMCA uses the 10200-H extraction method described in the American Public Health Association to measure Chl-a [41]. Turbidity is measured by the nephelometry method referred to in NMX-AA-038-SCFI-2001 [42]. The TSS are determined by the procedures of the Mexican standard NMX-AA-034-SCFI-2015 [43].
2.3. Satellite Data
The reflectance values of the Landsat-8 and Sentinel-2 images of the pixels where the fixed monitoring points are established were extracted (Figure 1). Matching satellite products were identified within a tolerance of ±3 days based on in situ monitoring dates [5,44]. The RNMCA has in situ data spanning from 2009 to the present. Consequently, data filtering was performed based on satellite image availability. Landsat-8 data, consisting of L2 surface reflectance level images, are available from April 2013 to the present date. In parallel, the Sentinel-2 images used in this study belonged to surface reflectance level 2A and have been accessible since March 2017. For Cajititlán, 33 Landsat-8 and 36 Sentinel-2 images were matched, and for Zapotlán 19 Landsat-8 and 32 Sentinel-2 images.
The Landsat-8 and Sentinel-2 images were obtained and processed on the Google Earth Engine (GEE) platform, which is powered by Google’s cloud infrastructure and uses a JavaScript programming language, as well as on the platform from Google Colaboratory using the Earth Engine Python API using the geemap library [45]. Numerous images showed cloud cover over the monitoring points, posing a significant challenge in acquiring accurate lake surface reflectance values. To mitigate this issue, specialized functions that operate in the BQA bands for Landsat-8 and the QA60 band for Sentinel-2 were employed. These functions, as suggested by studies conducted by Braaten et al. [46,47], Kochenour et al. [47], and Vanhellemont et al. [48], provided instrumental in the identification and removal of pixels affected by shadows and clouds within the images. This meticulous process aimed to eliminate values that do not correspond to the true surface reflectance of the lake water mirror, ensuring the generation of a dataset without serious alteration and suitable for training ML algorithms. [46,47,48]. Detailed descriptions of the Landsat-8 and Sentiel-2 satellite products can be reviewed in Table A1 and Table A2 of Appendix A.
2.4. Machine Learning Models
Eight regression algorithms from six different categories were evaluated to develop the predictive models (Table 1). The open-source Python resources available in the Scikit-learn library were used and executed in the Google Colaboratory environment that uses Google cloud servers [35].

Table 1.
Categories of the regression algorithms used in the study.
In the study, the use of the MLP feedforward was prioritized due to its ability to model non-linear and complex phenomena. This supervised learning algorithm learns a function by training on a data set, where m is the number of dimensions for the input and o is the number of dimensions for the output. Given a set of features and an objective y it can learn a nonlinear function approximator for classification or regression [35,49].
2.4.1. Data Processing and Algorithm Training
The process was developed by running code in the Python programming language. It began with the identification of the numerical variables that correspond to the satellite reflectance and the concentration values of the WQ parameter to be predicted. Non-numeric values were removed, and a data distribution analysis was performed using the method of Shapiro and Wilk [50] with a 95% confidence interval. Outliers were identified and eliminated using the pandas library boxplot graph and the interquartile range method (IQR) [51]. A correlation analysis matrix was also constructed using Pandas in Python, employing the Pearson correlation coefficient (R) to assess the spectral bands of the sensors that exhibited the strongest correlation with the WQ parameters. This analysis enabled to pinpoint the specific wavelengths where the parameters demonstrated their highest peak of reflected energy [5].
A Pipeline was created that includes three phases. In the first phase, the data are divided randomly, identifying the predictor variables and the response variable. In this way, 80% of the data was selected for training and 20% for validation. For each of the ML algorithms, in the second phase, the training data were scaled and in the third phase, by implementing the Exhaustive Feature Selector class from the mlxtend library, the spectral bands of Landsat-8 and Sentinel-2 were selected as most relevant input variables. All possible combinations were sampled and evaluated with a cross-validation of 8 folds for Landsat-8 and 12 folds for Sentinel-2, matching numbers according to the number of bands analyzed [52].
With the processed data, the hyperparameter adjustment was performed, so the optimal values were identified by testing different possibilities through an exhaustive search with the grid search method. In this way, the models were trained, and their respective errors were estimated using the Repeated k-Fold-Cross-Validation validation method. In the end, the new model was fitted with all of the training data and with the best hyperparameters found.
To illustrate the flow of the methodology on data processing and algorithm training, a diagram is provided in Figure 2.
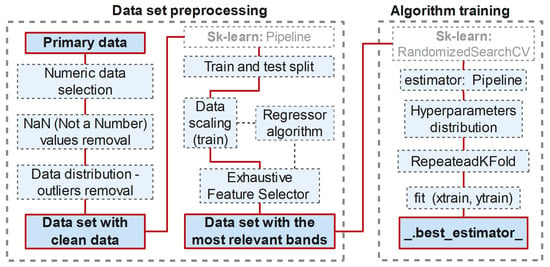
Figure 2.
Workflow for data processing and training of ML algorithms.
2.4.2. Model Validation
The Repeated k-Fold-Cross-Validation method divided the training observations into n folds (sets) of the same size, repeating the cross-validation procedure with different randomization. The metrics used were: the Root Mean Square Error (RMSE), the Mean Absolute Error (MAE), and the coefficient of determination (r2) that corresponds to the proportion of the total variance. They can be defined as follows [35]:
where is the estimated value, is the observed value and is the number of samples.
3. Results
3.1. Data Preprocessing and Evaluation
The presence of cloudiness in the satellite images considerably reduced the number of coincident records between the radiometric data and the in situ data. A total of 34 low-quality satellite products affected by the presence of clouds in the total surface of the lakes were identified, therefore, they do not contain water reflectance information and were discarded for the study. Of these 34 images, 8 Landsat-8 and 16 Sentinel-2 images were identified for Lake Cajititlán, while for Lake Zapotlán there were 6 Landsat-8 and 4 Sentinel-2 images. On the other hand, there were images that presented cloudiness, only in some sampling points; therefore, they were corrected by means of masks that eliminated the pixels of clouds and shadows, keeping only the pixels with reflectance values of the surface of the lake water. In the final dataset, a total of 128 records were retained for the CA parameters in Cajitilán when using Landsat-8, while 98 records remained when Sentinel-2 was employed. For Zapotlán, 78 records were obtained for both Landsat-8 and Sentinel-2. It is worth noting that these records represent the data that aligned with the in situ monitoring. From these records, some extreme outliers of certain parameters were removed, so the number of records used to train the algorithms is variable. A comprehensive breakdown of the specific record counts employed for algorithm training is provided in Supplementary Table S1.
Figure 3 shows an example of cloud mask application for the Landsat-8 image of Lake Cajititlán, working with the combination of true color bands L8-b4 - L8-b3 - L8-b2 to identify clouds and bodies of water.
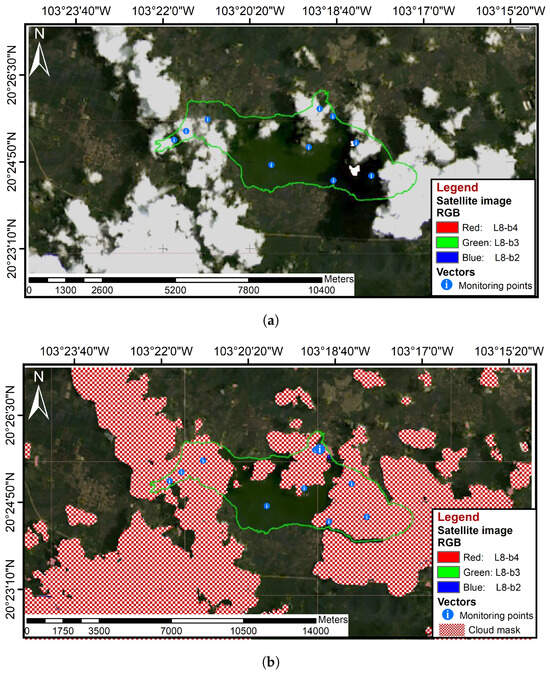
Figure 3.
Application of cloud masks to Landsat-8 images of Lake Cajititlán. (a) Original image with cloudiness. (b) Image with cloud mask.
Radiometric data from Landsat-8 and Sentinel-2 were matched with data from the RNMCA creating a separate dataset for each lake. The normality test of Shapiro and Wilk [50] with a confidence interval of 95% reported that the data of the WQ parameters and the radiometric data of the Landsat-8 and Sentinel-2 images do not follow a normal distribution. The statistical results can be reviewed in Table A3–Table A5 of the Appendix A. For Lake Cajititlán, a broader distribution of the Chl-a data was evidenced, varying from a minimum value of 0.34 mg/m3 and to a maximum value of 1387.59 mg/m3. In the case of turbidity, the range was between 9 NTU and 140 NTU, and for TSS, between 10 mg/L and 170 mg/L. On the other hand, for Lake Zapotlán, the distribution of the data for the parameters was found in a lower range than in Cajititlán. Thus, the ranges were: Chl-a between 0.30 mg/m3 and 81 mg/m3, TSS between 7 mg/L and 64 mg/L, and turbidity between 3.70 NTU and 100 NTU. For a more complete analysis, the distribution of the variables was graphically represented in a boxplot, as shown in Figure 4. Consequently, extreme outliers that were far from the mean were identified, mainly in the Chl-a data sets in Lake Cajititlán (Figure 4a) and turbidity in Lake Zapotlán (Figure 4b).
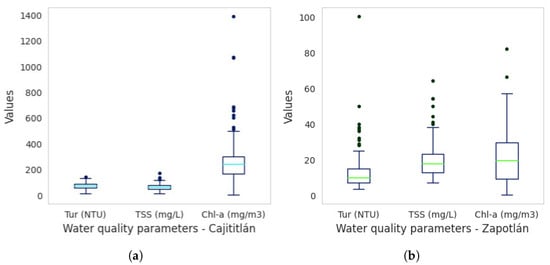
Figure 4.
Distribution of the data set of water quality parameters for (a) Cajititlán, and (b) Zapotlán.
Figure 5 shows the analysis of the distribution of the Landsat-8 and Sentinel-2 radiometric data for the Cajititlán and Zapotlán lakes. The Landsat-8 images were generated by OLI sensors that measure the visible (VIS), near-infrared (NIR), and short-wavelength infrared (SWIR) regions of the spectrum. For its part, the Sentinel-2 images were generated by a multispectral instrument, which samples 13 VIS and NIR spectral bands at 10 m, red edge and SWIR at 20 m, and atmospheric bands at 60 m of spatial resolution in a wide strip with a global review frequency of 5 days. Thus, a larger interquartile range was reported for Sentinel-2, thus demonstrating a wider range in the distribution of this data set. Additionally, positive asymmetric biases are recorded for all the Landsat-8 and Sentinel-2 spectral bands, demonstrating that there are high reflectance values that move away from the majority concentration of the data. On the other hand, a greater number of outliers are recorded in the Landsat-8 (Figure 5a) and Sentinel-2 (Figure 5c) radiometric data for Lake Cajititlán, which are far from each other. Likewise, for Lake Zapotlán, there were fewer outliers in the Sentinel-2 (Figure 5d) and Landsat-8 radiometric data (Figure 5b), so that the range of dispersion of values is more adjusted except for L8-b5.
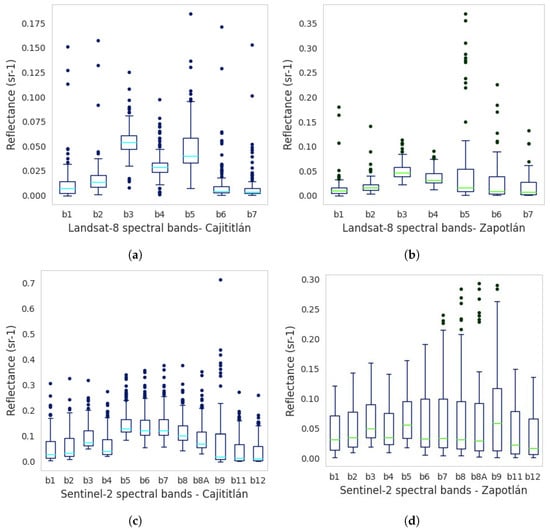
Figure 5.
Distribution of radiometric data (a) Landsat-8 Cajititlán, and (b) Landsat-8 Zapotlán, (c) Sentinel-2 Cajititlán and (d) Sentinel-2 Zapotlán.
Figure 6 shows the heat map of the correlation matrix between the RNMCA values with the radiometric data of the Landsat-8 and Sentinel-2 spectral bands for the Cajititlán and Zapotlán lakes. According to this exploratory analysis, in Lake Cajititlán better correlations are reported between the in situ values of the RNMCA and the radiometric data of L8-b3 (green), L8-b4 (red) from the VIS and L8-b5 from the NIR. TSS registered the highest correlation coefficients, R = 0.68 in L8-b5, R = 0.55 in L8-b3 and R = 0.52 in L8-b4. Sentinel-2 showed slightly better correlations between RNMCA and S2-b5 (Red Edge 1), S2-b6 (Red Edge 2), S2-b7 (Red Edge 3) and S2-b8 (NIR1), where Chl- a presented the best record with coefficients of R = 0.33 in S2-b6 and S2-b7, R = 0.31 in S2-b8 and R = 0.30 in S2-b5. On the other hand, for Lake Zapotlán, the best correlation records between the RNMCA and the Landsat-8 radiometric data occurred in L8-b3 and L8-b4 of the VIS. Turbidity was the parameter with the highest correlation values, R = 0.69 in L8-b3 and R = 0.57 in L8-b4. Likewise, the correlation between the RNMCA and the radiometric data from Sentinel-2 reported slightly better results in S2-b1 (aerosol), S2-b2 (blue), S2-b3 (green), S2-b4 (red) and S2- b5 (NIR). Turbidity was the parameter with the highest correlation values R = 0.36 in S2-b1, S2-b3 and S2-b5; R = 0.33 in S2-b2; and R = 0.31 in S2-b4. Consequently, the best correlations of the RNMCA data with the spectral bands in the spectral range of the VIS and NIR are evident. However, there are other wavelengths that maintain weaker correlations but can be identified by ML models and find patterns to improve predictive performance [4,21,38]. The combinations of spectral bands selected as predictors for each ML algorithm are presented in Table S1 of the Supplementary Material.
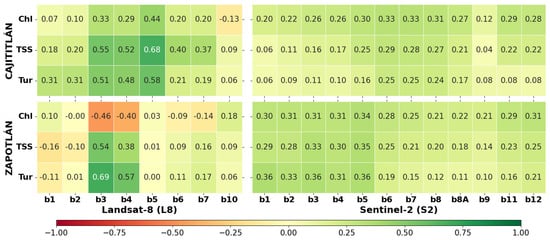
Figure 6.
Heat map of the correlation matrix between the RNMCA values with the Landsat-8 and Sentinel-2 spectral bands for the Cajititlán and Zapotlán lakes.
3.2. Performance of Machine Learning Models
The best performances for the modeling were identified by comparing the r2 values. In each of the lakes, the best results for the prediction of TSS, turbidity and Chl-a were found based on the ML algorithms and radiometric data evaluated. Figure 7a shows the results for Lake Cajititlán. It is observed that the Landsat-8 radiometric data were the most appropriate input variables to develop the ML predictive models. For example, for turbidity r2 values between 0.64 and 0.82 were obtained, for TSS r2 were between 0.42 and 0.68, and for Chl-a r2 were between 0.34 and 0.60. Likewise, the models that presented the best performance were the MLP with r2 between 0.58 and 0.78 and SLA with r2 between 0.60 and 0.82, while the lowest performance was reported by the DTR with r2 between 0.36 and 0.70. In the case of the models developed with Sentinel-2 radiometric data for turbidity, r2 values between 0.14 and 0.57 were obtained, for TSS they reached a range of r2 between 0.15 and 0.61, and for Chl-a the r2 comprised results between 0.10 and 0.45. For this case, the most acceptable performances were achieved with the Ridge models with r2 between 0.47 and 0.54, SLA with r2 between 0.14 and 0.61, and MLP with r2 between 0.24 and 0.55.
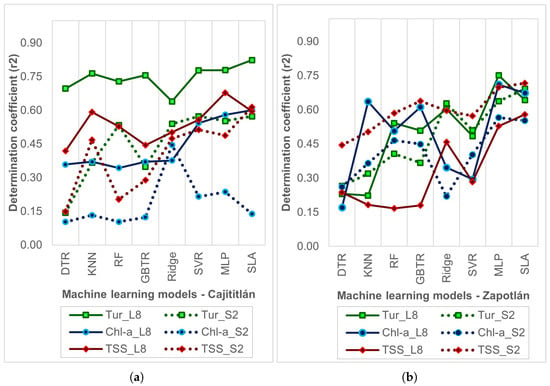
Figure 7.
Assessment of the predictive capabilities of ML models for (a) Lake Cajititlán and (b) Lake Zapotlán. The models are identified by distinct symbols and colors, with green denoting turbidity, red representing TSS, and blue signifying Chl-a. Furthermore, solid lines correspond to models developed using Landsat-8 data (L8), while dashed lines correspond to models utilizing Sentinel-2 data (S2).
On the other hand, Figure 7b shows the results for the WQ prediction of Lake Zapotlán. It is observed that the results were more varied, not identifying a strong trend for any of the satellite products evaluated. Although, if a general average is analyzed for all ML models, r2 = 0.44 is reported for Landsat-8 data models and r2 = 0.49 for Sentiel-2 data models. These averages for each of the lakes, in fusion of the ML models, WQ parameters and satellite products can be seen in Table A6 and Table A7 of the Appendix A. In Lake Zapotlán, the predictive capacity for turbidity with the Landsat-8 models reached r2 values between 0.22 and 0.75, while the Sentinel-2 models registered r2 between 0.27 and 0.69, lower values compared to those found in the lake Cajititlán. The same trend is observed for TSS with Landsat-8, this is, the r2 vary between 0.18 and 0.58 while for Sentinel-2 the r2 values are between 0.45 and 0.72. Finally, it is also observed that for Chl-a the values of r2 are between 0.17 and 0.71 for Landsat-8 models, and r2 between 0.22 and 0.57 for Sentinel-2 models. Another difference with what was found in Lake Cajititlán is that the MLP and SLA models were the best predictors for the Landsat-8 models, while the lowest performance was for DTR (r2 between 0.17 and 0.23). In the case of the Sentinel-2 models, the MLP (r2 between 0.57 and 0.70) and SLA (r2 between 0.55 and 0.72) reached the best predictive capacity, and the DTR (r2 between 0.26 and 0.45) reported the lowest performance. The difference found with the Sentinel-2 and Landsat-8 data is evident since the modeled algorithms varied in each of the lakes according to the approach, the hyperparameters, and the size of the training sample.
The r2 in general does not present a perfect adjustment; however, the values close to the unit explain that the predictive variables have the tendency to provide valuable information about the response. Full validation of the ML models showing the error metrics, r2, best algorithm, predictor spectral bands, and WQ parameters for each lake are shown in Table S1 of the Supplementary Material.
According to the results of the Repeated k-Fold-Cross-Validation, the best predictive models for TSS, Chl-a, and turbidity in each of the lakes were selected. In this way, Figure 8 presents the scatter diagrams of the residuals (in situ values vs. predicted values) for the in situ data of the WQ parameters that result from the best selected models. In the context of Lake Cajititlán, the SLA models developed using Landsat-8 radiometric data displayed superior performance for predicting turbidity, with r2 = 0.82, RMSE = 9.93 NTU, and MAE = 7.69 NTU (Figure 8a). For Chl-a, r2 = 0.60, RMSE = 48.06 mg/m3 and MAE = 37.98 mg/m3 were observed (Figure 8c). The MLP model, trained with Landsat-8 radiometric data, delivered the best results for TSS prediction, yielding r2 = 0.68, RMSE = 13.42 mg/L and MAE = 10.36 mg/L (Figure 8e). Conversely, Lake Zapotlán exhibited distinct results, with the MLP models trained with Landsat-8 radiometric data outperforming other models. Turbidity prediction achieved r2 = 0.75, RMSE = 2.05 NTU, and MAE = 1.10 NTU (Figure 8b) while Chl-a prediction displayed an r2 = 0.71, RMSE = 6.16 mg/m3 and MAE = 4.97 mg/m3 (Figure 8d). In the case of TSS, the SLA model, trained with Sentinel-2 radiometric data, produced the best results, with an r2 = 0.72, RMSE = 2.71 mg/L and MAE = 2.12 mg/L (Figure 8f).
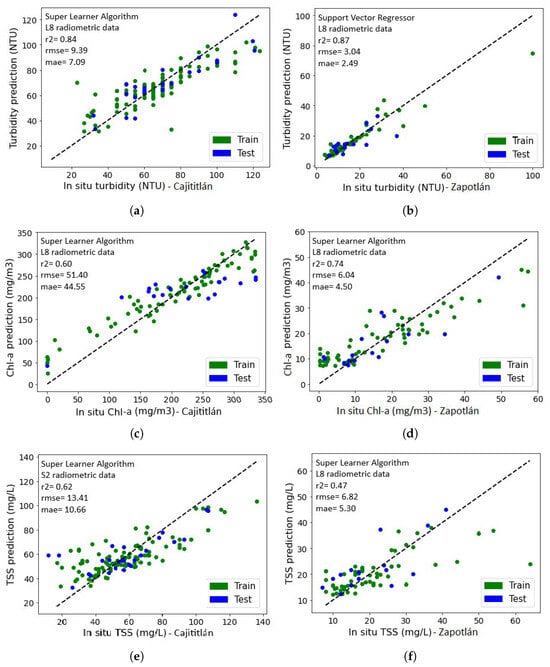
Figure 8.
Distribution of the residuals for the ML models with the best performance in the prediction of the WQ parameters: (a) Turbidity in Cajititlán, (b) Turbidity in Zapotlán, (c) Chl-a in Cajititlán, (d) Chl-a in Zapotlán, (e) TSS in Cajititlán. (f) TSS in Zapotlán.
3.3. Water Quality Parameter Predictions
The best-performing ML models were used to predict the WQ parameters. The input data for the model were obtained from the Landsat-8 image of collection 2 and level 2 dated 10 November 2022. This image was not part of the training of the algorithms and was the most current available on the Earth Engine Data Catalog. Figure 9a,c show the qualitative analysis of the Landsat-8 image in natural color (combination: L8-b4, L8-b3, L8-b2), where a greenish coloration is observed for the two Lakes, being more intense in Lake Cajititlán. In addition, it is possible to perceive color variations in the water mirror of each lake, so that the variation in the spatial distribution of the WQ parameters is evident. Likewise, the spectral signatures of the sampling points of Lake Cajititlán showed high peaks at L8-b3 and L8-b5 (Figure 9b). This indicates a predominance of green color and energy in the NIR region, as shown in Figure 9a. For Lake Zapotlán, it is observed that the highest values of reflected energy are in the green region (L8-b3) as seen in Figure 9d. In general, when comparing the reflectance between the lakes, it is observed that the highest values are found in Lake Cajititlán and this is in accordance with the values of the WQ parameters in situ, where it is evident that there is a higher concentration of Chl-a, TSS, and turbidity in this lake.
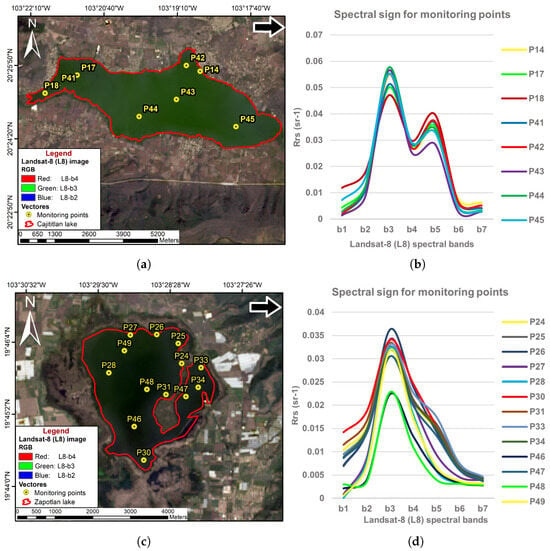
Figure 9.
Landsat-8 image in natural color for lakes (a) Cajititlán and (c) Zapotlán. Spectral signal for the monitoring points managed by the RNMC for (b) Cajititlán and (d) Zapotlán.
The morphology of the lakes varies over time depending on several factors. Therefore, for the results of the predictions of the WQ parameters, the water mirror was delimited according to the optical information of the selected Landsat-8 image. For this, the combination of bands was used: L8-b6, L8-b5, and L8-b4 of vegetation analysis. Consequently, the pixels of the lake that represent vegetation on the shores of the two lakes and floating aquatic plants were eliminated, as is the case of Zapotlán, which has a considerable area of the water mirror covered by Eichhornia crassipes and Typha latifolia L. In this way, the input data for the prediction of WQ parameters were only pixels of the water surface, eliminating pixels of vegetation.
Figure 10 depicts the spatial distribution of Chl-a, SST, and turbidity on the water surface based on predictions generated by the best-performing ML models evaluated. It was evident that the concentrations of water quality parameters in Lake Cajititlán (Figure 10a) exceeded those observed in Lake Zapotlán (Figure 10b), indicating higher contamination levels in Cajititlán. In this context, lake Cajititlán was classified as a lake in a hypereutrophic state, according to the Carlson and Simpson [53] Trophic Status Index for Chl-a . The spatial distribution of Chl-a oscillates between 90 mg/m3 and 302 mg/m3, and the largest surface area of the water mirror is above 200 mg/m3. TSS levels range between 45.7 mg/L and 71 mg/L and according to the standards by CONAGUA [54] in the RNMCA, these values correspond to surface waters with low TSS content, that means generally natural conditions that favor the conservation of aquatic communities and unrestricted agricultural irrigation. Turbidity registers values in a range of 48 mg/L and 84 mg/L, these values are derived from the presence of high levels of suspended particles and algae according to the values recorded in the previous parameters. On the other hand, the spatial distribution of Chl-a in Lake Zapotlán classified the lake as mesotrophic where the concentrations were lower with values between 8 mg/m3 and 25 mg/m3. Likewise, in the highest concentrations, with values ranging between 25 mg/m3 and 40 mg/m3, the lake is classified as eutrophic. TSS levels were recorded between 11 mg/L and 17.5/L and according to CONAGUA [54] standards, these are excellent waters with particularly good quality. The turbidity of the lake presented low values that oscillate between 1.76 NTU and 12.46 NTU.
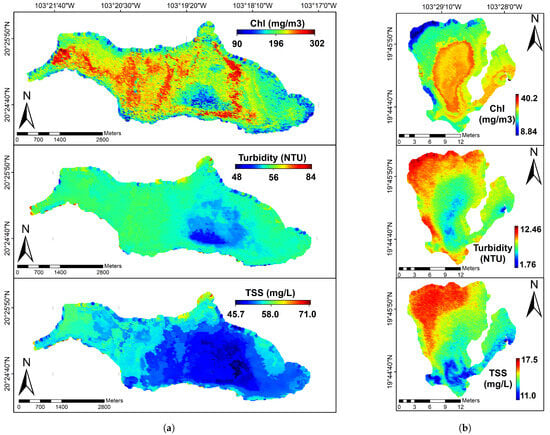
Figure 10.
Spatial distribution maps for the estimation of Chl-a, TSS and turbidity with radiometric data from Landsat-8 10 November 2022). Results for Lake Cajititlán in the left column (a) and Zapotlán in the right column (b).
4. Discussion
4.1. Data Processing
Limited access to training data for ML algorithms was a notable challenge in this study. While the study had access to a substantial database from the RNMCA, aligning it with the acquisition data of satellite images proved to be a complex task. As a result, Landsat-8 and Sentinel-2 imagery was chosen, as these sensors offered lower temporal resolution compared to others and were suitable for capturing data from the relatively small continental water bodies under study. This choice aligns with common practices in the field, as documented in the literature review by Chen et al. [38], Yang et al. [14], Sagan et al. [8] and Topp et al. [4].
Subsequent to data acquisition, thorough data processing played a pivotal role. On one hand, the in situ data analysis revealed that the observed values did not conform to a normal distribution. Furthermore, the identification and removal of extreme outliers became essential to prevent their negative influence on the performance of ML algorithms. Outliers, as noted by Najah et al. [21], possess the potential to distort descriptive statistics such as mean and standard deviation, consequently leading to inaccurate predictions by the models. On the other hand, satellite data introduced limitations, primarily attributed to atmospheric conditions. The presence of clouds acted as a barrier, obstructing the retrieval of reflectance values from the water’s surface [20]. Accurate predictive model development and validation depends on the availability of WQ data that aligns with uncontaminated reflectance data. When cloud cover affects reflectance data, it complicates the process of model calibration and validation, as noted by Gulati and Sharma [55] and Gholizadeh et al. [1]. Consequently, this study opted to eliminate pixels corresponding to cloud or shadow values. This was achieved by employing masking functions to identify and exclude such pixels, in line with recommendations from previous studies, such as Kochenour [56]. However, alternative methods, such as image reconstruction, warrant further exploration to potentially recover information and thereby increase the dataset available for training the predictive models [57,58].
The disparities in the correlations of WQ parameters between lakes Cajititlán and Zapotlán may be attributed to variations in factors such as the physical and chemical composition of the water in each lake. Parameters like Chl-a concentration, turbidity, and TSS have a direct impact on how light is reflected on the water’s surface [4]. Additionally, rapid changes in water conditions could be influenced by factors like water flow, seasonality, and nearby pollution sources [14]. The geographical and topographical features of the surrounding region also play a significant role. Factors like vegetation, latitude, and altitude can affect the interaction of light with the water [1]. Moreover, disparities were observed in parameter-sensor correlations, with Landsat-8 exhibiting a more suitable spectral range for certain parameters. These findings underscore the necessity of accounting for the heterogeneity of water bodies and sensor characteristics when interpreting correlations in WQ studies utilizing satellite data. It highlights the complexity of WQ monitoring and the importance of evaluating the specific conditions of each lake to obtain accurate results [59].
4.2. ML Models Performance
The atmospheric effects and optical complexities observed in Lakes Cajititlán and Zapotlán had a noticeable impact on the quality of the input data used for the ML models. These limitations affected the scale and robustness of the models and are consistent with findings from other studies [1,8,14]. The optical complexities of these lakes were evident in the concentration values of WQ parameters, with Lake Cajititlán showing higher contamination levels compared to Lake Zapotlán. The quality of the radiometric data was also affected during cloud masking, where some shadow pixels remained unremoved, leading to alterations in the reflectance values of the water surface, as reported in other studies [4,20,57,58].
To address these challenges, the authors recommend developing models tailored to each specific body of water and adjusting hyperparameters based on the quality of the input data obtained during processing [2,38]. Choosing the right ML algorithms can be challenging due to the wide array of options available. Key considerations for selection include the quantity and quality of the available data. This is particularly relevant in fields like medicine, ecology, or geoscience, where data collection can be resource-intensive and may have ethical constraints [35,36]. To overcome limited datasets, researchers often turn to ML techniques specifically designed for such scenarios. These techniques aim to optimize ML models to deliver the best possible performance with the available data [21]. In this study, k-Fold-Cross-Validation was used to evaluate and enhance model performance, a technique previously employed by researchers such as Blix et al. [60], even with smaller training datasets. For extremely limited data, some researchers like Arias et al. [7] opt for leave-one-out cross-validation (LOOCV), although this approach demands substantial computational resources.
While some investigations [1,14] focus on using only visible (VIS) and near-infrared (NIR) spectral regions due to their empirical and semi-analytical modeling capabilities, this study initially leveraged all the spectral bands from Landsat-8 and Sentinel-2 satellites. This approach enabled access to information across a wide range of wavelengths, offering a more comprehensive view of the water surface and its characteristics [4,5]. Subsequently, the exhaustive feature selector was employed for feature selection to identify the most representative predictor bands [52]. This process aimed to assess the contributions of different spectral regions to the model, leading to the use of optimal spectral band combinations. Conclusively, the study did not definitively establish the most suitable spectral bands to use, as various models employing different combinations depending on the lake and the parameter being estimated. This ongoing challenge highlights the complexity of applying remote sensing in WQ detection. For instance, in the case of Chl-a, Zhang and Han [61] reported a strong correlation between Landsat-8 bands 1 and 4 and their combinations, while Kim et al. [62] used Landsat-8 bands 1 and 2, in addition to a ratio of band 2 to band 4. A more recent study by Arias et al. [5] used data from the RNMCA and used all Landsat-8 bands. On the other hand, for TSS and turbidity, several studies have been found that report a good correlation between the first five Landsat bands [1,12]. Lim and Choi [63] built multiple regression models to recover TSS from b2 and b5 of Landsat-8. In this way, the alternatives that can be used to define the input data for ML models are evidenced. What could be determined is that ML algorithms can produce models that capture complex and non-linear relationships between remotely sensed reflectance and WQ parameters [38].
To ensure the robustness of the models, a critical aspect involves randomizing the selection of training data and subsequently fine-tuning the hyperparameters of the ML algorithms, as recommended in prior research [64,65]. It is worth noting that hyperparameter tuning requires meticulous analysis and incurs a significant computational cost due to the multitude of alternatives that must be tested using GridSearch. Furthermore, the evaluation through cross-validation is imperative [66,67]. Among the ML models assessed, Support SVR and Ridge linear models demand calibration of fewer hyperparameters compared to their counterparts. The models that exhibited the highest performance were the SLA and the MLP. The MLP, being an artificial neural network model, uses backpropagation to adjust the weights between neurons, resulting in enhancing prediction accuracy. Its ability to handle complex and non-linear datasets provides it with a distinct advantage over other ML models [35,36]. In the case of the SLA, its superior performance can be attributed to its strategy of combining predictions from multiple models that individually demonstrated the best performance. Notably, the MLP and Ridge models were frequently selected due to their capacity to contribute to a diverse ensemble that can enhance individual predictions. This diversity is vital because if all combined models are too similar to one another, they may not effectively complement each other [64].
In summary, the prediction outcomes of this study are consistent with previous research conducted by Otto et al. [26], Torres [27], and Arias et al. [5], who investigated different water bodies. However, this study’s distinct contribution lies in the evaluation of eight ML algorithms, introducing greater variability and overall performance improvement. The increased data overlap and performance enhancements achieved in this study highlighted the potential of remote sensing supported by ML techniques in the domain of WQ monitoring.
4.3. Prediction of WQ Parameters and Practical Application
This study presents a significant contribution in the field of WQ monitoring in aquatic bodies, specifically in the Cajititlán and Zapotlán lakes in the state of Jalisco, Mexico. One of the main distinguishing features of this work is that these lakes, which until now had remained largely unexplored in terms of remote sensing WQ monitoring, have been the subject of extensive analysis. This approach is essential in the current context, since, despite the extensive scientific literature dedicated to remote sensing techniques, our planet continues to be a dynamic and complex system in constant evolution [68]. Therefore, exclusive reliance on existing studies has proven insufficient and impractical [4]. Assessment of these lakes, which face continued deterioration in WQ over time, becomes an essential task.
The predictive ML models developed in this study open the door to new possibilities. The MLP and SLA algorithms, which were noted for their high performance, presented a promising approach for WQ monitoring in these lakes. These results have significant practical implications. First of all, the study highlights the importance of the integration of these techniques in the RNMCA. Since there are water bodies that have been excluded from monitoring campaigns due to certain limitations [5], the application of remote sensing supported by ML can expand the scope of analysis and contribute to the advancement of environmental monitoring efforts [2]. This integration would not only be beneficial in improving monitoring coverage but can also serve as an important precedent for early decision making. By enabling remote analysis of contamination, these techniques provide valuable information before physical site visits are made, which can be essential in proactive decision making [14]. In a broader social context, these techniques have direct relevance to society. By involving the community in assessing WQ and monitoring water bodies, citizen participation is encouraged, and greater awareness is promoted about the importance of conserving these resources. This collaboration between the community and researchers can empower society by providing them with the tools and knowledge necessary to actively participate in activities related to WQ preservation [2].
5. Conclusions
Working with historical data from the RNMCA, which conducts long-term monitoring campaigns spanning from 2009 to the present, has facilitated the development of a useful database for the study. Despite facing limitations stemming from atmospheric factors and occasional satellite data mismatches, this dataset has proven to be helpful for the development of ML models. To address these challenges, extensive hyperparameter tuning was performed and the widely used k-Fold-Cross-Validation technique was applied in data-limited scenarios. As a result, the ML models exhibited varying predictive capacities, with the MLP and SLA algorithms demonstrating superior performance, yielding valuable insights into the spatial distribution of Chl-a, SST, and turbidity in Lakes Cajititlán and Zapotlán.
Underscoring the significance of remote sensing, the study revealed that only through a qualitative analysis of spectral signatures within satellite images was it possible to identify heightened light reflection in the green and near-infrared wavelengths, a telltale sign of the greenish coloration characteristic of eutrophic waters in Lake Cajititlán.
Within this context, the study meticulously developed models that showcase the highest predictive capabilities. Importantly, these models were fine-tuned to accommodate the unique characteristics of each lake. The inability to generalize findings arises from the differences in water composition, topography, and various other environmental factors that distinguish the two lakes. This research has, therefore, generated invaluable data for the comprehensive analysis of these lakes, hitherto untouched in the realm of WQ monitoring through remote sensing. Consequently, this study lays the groundwork for future research endeavors in a rapidly growing field that has garnered the attention of both researchers and water management authorities.
The outcomes of the study also underscore the immense potential of integrating remote sensing techniques into the monitoring campaigns conducted by the RNMCA. This expansion offers the possibility of including more water bodies in monitoring efforts that were previously excluded due to a range of limitations. Furthermore, it sets a promising precedent for advancing environmental monitoring practices, ultimately facilitating more informed and timely decision making in water resource management.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs15235505/s1, Table S1: Validation Metrics for ML Models: Lake-Specific Results, Satellite Data, Hyperparameters, and Best Band Predictors.
Author Contributions
Conceptualization, V.Z.-G. and B.S.-R.; methodology F.H.V.-G.; formal analysis, K.J.G.-T., F.Z.-M. and B.S.-R.; investigation, F.H.V.-G. and K.J.G.-T.; writing—original draft preparation, F.H.V.-G.; writing—review and editing V.Z.-G., B.S.-R. and F.Z.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by a student scholarship awarded by the National Council of Humanities, Sciences and Technologies (CONAHCYT)—Mexico.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy restrictions.
Acknowledgments
We thank the United Stated Geological Service (USGS) and the European Space Agency (ESA) for providing the necessary Landsat-8 and Sentinel-2 images for the spectral data adquisition for this study. We are further grateful to the Comision Estatal del Agua (CONAGUA) for providing the field water quality measurements through the National Water Quality Monitoring Network (RNMCA). Finally, we would like to thank the Consejo Nacional de Ciencia y Tecnología (CONAHCYT) for the support through the student maintenance scholarship.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| WQ | Water Quality |
| ML | Machine Learning |
| RNMCA | National Water Quality Monitoring Network |
| TSS | Total Suspended Solids |
| Chl-a | Chlorophyll-a |
| MLP | Multilayer Perceptron |
| SLA | Super Learner Algorithm |
| GEE | Google Earth Engine |
| MRSE | Mean Square Error |
| MAE | Mean Absolute Error |
| r2 | Coefficient of Determination |
| L8 | Landsat-8 |
| S2 | Sentinel-2 |
| VIS | Visible |
| NIR | Near Infrared |
| SWIR | Short Wavelength Infrared |
Appendix A

Table A1.
Characteristics of Landsat-8 satellite products.
Table A1.
Characteristics of Landsat-8 satellite products.
| Band | Sensor | Wavelength (µm) | Spatial Resolution (m) | Radiometric Resolution |
|---|---|---|---|---|
| 1—Ultra blue (Coastal Aerosol) | OLI | 0.43–0.45 | 30 | 16 bits |
| 2—Blue | OLI | 0.45–0.51 | 30 | 16 bits |
| 3—Green | OLI | 0.53–0.59 | 30 | 16 bits |
| 4—Red | OLI | 0.64–0.67 | 30 | 16 bits |
| 5—Near infrared (NIR) | OLI | 0.85–0.88 | 30 | 16 bits |
| 6—Shortwave infrared (SWIR1) | OLI | 1.57–1.65 | 30 | 16 bits |
| 7—Shortwave infrared (SWIR2) | OLI | 2.11–2.29 | 30 | 16 bits |
| 8—Panchromatic | OLI | 0.52–0.90 | 15 | 16 bits |
| 9—Cirrus | OLI | 1.36–1.38 | 30 | 16 bits |
| 10—Thermal infrared 1 | TIRS | 10.60–11.19 | 100 | 16 bits |
| 11—Thermal infrared 2 | TIRS | 11.50–12.51 | 100 | 16 bits |

Table A2.
Characteristics of Sentinel-2 satellite products.
Table A2.
Characteristics of Sentinel-2 satellite products.
| S2A | S2B | ||||
|---|---|---|---|---|---|
| Band | Central Wavelength (nm) | Band Width (nm) | Central Wavelength (nm) | Band Width (nm) | Spatial Resolution (m) |
| 1—Coastal aerosol | 443.9 | 27 | 442.3 | 45 | 60 |
| 2—Blue | 496.6 | 98 | 492.1 | 98 | 10 |
| 3—Green | 560.0 | 45 | 559 | 46 | 10 |
| 4—Red | 664.5 | 38 | 665 | 39 | 10 |
| 5—Vegetation red edge | 703.9 | 19 | 703.8 | 20 | 20 |
| 6—Vegetation red edge | 740.2 | 18 | 739.1 | 18 | 20 |
| 7—Vegetation red edge | 782.5 | 28 | 779.7 | 28 | 20 |
| 8—NIR | 835.1 | 145 | 833 | 133 | 10 |
| 8a—Vegetation red edge | 864.8 | 33 | 864 | 32 | 20 |
| 9—Water vapor | 945.0 | 26 | 943.2 | 27 | 60 |
| 10—SWIR - cirrus | 1373.5 | 75 | 1376.9 | 76 | 60 |
| 11—SWIR | 1610.4 | 141 | 1613.7 | 143 | 20 |
| 12—SWIR | 2185.7 | 238 | 2202.4 | 242 | 20 |

Table A3.
Water Quality Parameters—Descriptive Statistics and Shapiro-Wilk Test.
Table A3.
Water Quality Parameters—Descriptive Statistics and Shapiro-Wilk Test.
| Lake | Parameter | Count | Mean | Std | Min | 25% | 50% | 75% | Max | Statistic | p-Value (95%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TSS | 252.00 | 63.71 | 24.28 | 10.00 | 48.00 | 62.50 | 76.00 | 170.00 | 0.98 | 1.64 × 10−3 | |
| Cajititlán | Tur | 252.00 | 71.71 | 24.23 | 9.00 | 55.00 | 70.00 | 88.13 | 140.00 | 0.98 | 1.38 × 10−3 |
| Chl-a | 252.00 | 241.46 | 154.87 | 0.34 | 166.25 | 239.18 | 299.89 | 1387.59 | 0.76 | 6.36 × 10−19 | |
| TSS | 153.00 | 19.58 | 9.67 | 7.00 | 13.00 | 18.00 | 23.00 | 64.00 | 0.86 | 5.74 × 10−11 | |
| Zapotlán | Tur | 153.00 | 12.99 | 10.54 | 3.70 | 7.30 | 10.00 | 15.00 | 100.00 | 0.63 | 5.15 × 10−18 |
| Chl-a | 153.00 | 21.20 | 14.82 | 0.30 | 10.11 | 19.43 | 28.44 | 81.78 | 0.94 | 7.17 × 10−6 |

Table A4.
Landsat-8 radiometric data set—Descriptive Statistics and Shapiro-Wilk Test.
Table A4.
Landsat-8 radiometric data set—Descriptive Statistics and Shapiro-Wilk Test.
| Lake | Parameter | Count | Mean | Std | Min | 25% | 50% | 75% | Max | Statistic | p-Value (95%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| L8-b1 | 129 | 0.0130 | 0.0210 | 0.00004 | 0.0020 | 0.0076 | 0.0144 | 0.15 | 0.53 | 1.36 × 10−18 | |
| L8-b2 | 129 | 0.0183 | 0.0197 | 0.0010 | 0.0087 | 0.0137 | 0.0205 | 0.16 | 0.54 | 2.40 × 10−18 | |
| L8-b3 | 129 | 0.0554 | 0.0164 | 0.0081 | 0.0471 | 0.0543 | 0.0611 | 0.13 | 0.93 | 4.13 × 10−6 | |
| Cajititlán | L8-b4 | 129 | 0.0309 | 0.0154 | 0.0012 | 0.0235 | 0.0287 | 0.0335 | 0.10 | 0.89 | 1.65 × 10−8 |
| L8-b5 | 129 | 0.0477 | 0.0269 | 0.0075 | 0.0331 | 0.0400 | 0.0583 | 0.18 | 0.86 | 1.52 × 10−9 | |
| L8-b6 | 129 | 0.0113 | 0.0217 | 0.0003 | 0.0030 | 0.0044 | 0.0093 | 0.17 | 0.45 | 6.42 × 10−20 | |
| L8-b7 | 129 | 0.0092 | 0.0181 | 0.0005 | 0.0025 | 0.0034 | 0.0076 | 0.15 | 0.42 | 2.02 × 10−20 | |
| L8-b10 | 129 | 23.87 | 3.94 | 11.15 | 21.36 | 24.18 | 26.77 | 31.16 | 0.97 | 4.13 × 10−3 | |
| L8-b1 | 78 | 0.0174 | 0.0296 | 0.0001 | 0.0049 | 0.0095 | 0.0162 | 0.18 | 0.49 | 5.78 × 10−15 | |
| L8-b2 | 78 | 0.0219 | 0.0203 | 0.0034 | 0.0105 | 0.0162 | 0.0229 | 0.14 | 0.67 | 5.66 × 10−12 | |
| L8-b3 | 78 | 0.0521 | 0.0208 | 0.0224 | 0.0383 | 0.0468 | 0.0579 | 0.11 | 0.88 | 1.62 × 10−6 | |
| Zapotlán | L8-b4 | 78 | 0.0374 | 0.0195 | 0.0119 | 0.0259 | 0.0307 | 0.0454 | 0.09 | 0.88 | 1.68 × 10−6 |
| L8-b5 | 78 | 0.0596 | 0.0923 | 0.0007 | 0.0088 | 0.0158 | 0.0546 | 0.37 | 0.63 | 8.57 × 10−13 | |
| L8-b6 | 78 | 0.0303 | 0.0446 | 0.0008 | 0.0029 | 0.0083 | 0.0390 | 0.23 | 0.68 | 1.06 × 10−11 | |
| L8-b7 | 78 | 0.0193 | 0.0262 | 0.0007 | 0.0024 | 0.0071 | 0.0272 | 0.13 | 0.71 | 4.00 × 10−11 | |
| L8-b10 | 78 | 23.27 | 4.03 | 8.63 | 20.89 | 24.34 | 26.47 | 29.13 | 0.90 | 2.10 × 10−5 |

Table A5.
Sentinel-2 radiometric data set—Descriptive statistics and Shapiro-Wilk Test.
Table A5.
Sentinel-2 radiometric data set—Descriptive statistics and Shapiro-Wilk Test.
| Lake | Parameter | Count | Mean | Std | Min | 25% | 50% | 75% | Max | Statistic | p-Value (95%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S2-b1 | 128 | 0.0572 | 0.0613 | 0.0035 | 0.0127 | 0.0284 | 0.0790 | 0.31 | 0.79 | 2.76 × 10−12 | |
| S2-b2 | 128 | 0.0634 | 0.0600 | 0.0091 | 0.0203 | 0.0341 | 0.0928 | 0.33 | 0.79 | 3.75 × 10−12 | |
| S2-b3 | 128 | 0.1017 | 0.0558 | 0.0508 | 0.0624 | 0.0739 | 0.1206 | 0.32 | 0.80 | 5.55 × 10−12 | |
| S2-b4 | 128 | 0.0694 | 0.0586 | 0.0209 | 0.0279 | 0.0402 | 0.0878 | 0.27 | 0.77 | 6.13 × 10−13 | |
| Cajititlán | S2-b5 | 128 | 0.1547 | 0.0575 | 0.0856 | 0.1162 | 0.1289 | 0.1658 | 0.34 | 0.80 | 4.55 × 10−12 |
| S2-b6 | 128 | 0.1449 | 0.0648 | 0.0554 | 0.1048 | 0.1205 | 0.1628 | 0.36 | 0.85 | 3.23 × 10−10 | |
| S2-b7 | 128 | 0.1461 | 0.0674 | 0.0575 | 0.1036 | 0.1216 | 0.1640 | 0.38 | 0.85 | 4.28 × 10−10 | |
| S2-b8 | 128 | 0.1242 | 0.0639 | 0.0419 | 0.0851 | 0.1005 | 0.1401 | 0.38 | 0.84 | 1.24 × 10−10 | |
| S2-b8A | 128 | 0.1004 | 0.0690 | 0.0313 | 0.0555 | 0.0690 | 0.1172 | 0.35 | 0.80 | 8.03 × 10−12 | |
| S2-b9 | 128 | 0.0738 | 0.1126 | 0.0003 | 0.0091 | 0.0192 | 0.1100 | 0.71 | 0.66 | 6.99 × 10−16 | |
| S2-b11 | 128 | 0.0471 | 0.0604 | 0.0015 | 0.0050 | 0.0136 | 0.0676 | 0.27 | 0.74 | 1.16 × 10−13 | |
| S2-b12 | 128 | 0.0423 | 0.0553 | 0.0009 | 0.0043 | 0.0118 | 0.0600 | 0.26 | 0.74 | 8.44 × 10−14 | |
| S2-b1 | 79 | 0.0421 | 0.0330 | 0.0007 | 0.0129 | 0.0314 | 0.0709 | 0.12 | 0.88 | 3.30 × 10−6 | |
| S2-b2 | 79 | 0.0476 | 0.0344 | 0.0090 | 0.0188 | 0.0342 | 0.0768 | 0.14 | 0.88 | 2.42 × 10−6 | |
| S2-b3 | 79 | 0.0633 | 0.0362 | 0.0180 | 0.0344 | 0.0491 | 0.0890 | 0.16 | 0.89 | 3.42 × 10−6 | |
| S2-b4 | 79 | 0.0501 | 0.0361 | 0.0091 | 0.0222 | 0.0345 | 0.0745 | 0.14 | 0.87 | 7.48 × 10−7 | |
| Zapotlán | S2-b5 | 79 | 0.0660 | 0.0399 | 0.0178 | 0.0326 | 0.0553 | 0.0947 | 0.16 | 0.91 | 5.45 × 10−5 |
| S2-b6 | 79 | 0.0613 | 0.0537 | 0.0049 | 0.0182 | 0.0324 | 0.0982 | 0.19 | 0.86 | 5.85 × 10−7 | |
| S2-b7 | 79 | 0.0656 | 0.0629 | 0.0042 | 0.0175 | 0.0333 | 0.0984 | 0.24 | 0.83 | 4.25 × 10−8 | |
| S2-b8 | 79 | 0.0637 | 0.0683 | 0.0034 | 0.0152 | 0.0312 | 0.0943 | 0.28 | 0.79 | 2.84 × 10−9 | |
| S2-b8A | 79 | 0.0645 | 0.0725 | 0.0017 | 0.0121 | 0.0293 | 0.0917 | 0.29 | 0.78 | 2.01 × 10−9 | |
| S2-b9 | 79 | 0.0781 | 0.0802 | 0.0005 | 0.0125 | 0.0584 | 0.1164 | 0.29 | 0.85 | 1.60 × 10−7 | |
| S2-b11 | 79 | 0.0439 | 0.0430 | 0.0007 | 0.0071 | 0.0214 | 0.0773 | 0.15 | 0.85 | 2.54 × 10−7 | |
| S2-b12 | 79 | 0.0353 | 0.0346 | 0.0012 | 0.0060 | 0.0163 | 0.0652 | 0.13 | 0.85 | 2.01 × 10−7 |

Table A6.
Means of the coefficient of determination (r2) for the modeling results for Lake Cajititlán, as a function of CA parameters, ML models and satellite products.
Table A6.
Means of the coefficient of determination (r2) for the modeling results for Lake Cajititlán, as a function of CA parameters, ML models and satellite products.
| ML Models | Tur-L8 | Chl-a-L8 | TSS-L8 | Mean for Models | Tur-S2 | Chl-a-S2 | TSS-S2 | Mean for Models |
|---|---|---|---|---|---|---|---|---|
| DTR | 0.70 | 0.36 | 0.42 | 0.49 | 0.14 | 0.10 | 0.15 | 0.13 |
| KNN | 0.76 | 0.37 | 0.59 | 0.58 | 0.37 | 0.13 | 0.47 | 0.32 |
| RF | 0.73 | 0.34 | 0.53 | 0.53 | 0.53 | 0.10 | 0.20 | 0.28 |
| GBTR | 0.76 | 0.37 | 0.44 | 0.52 | 0.35 | 0.12 | 0.29 | 0.25 |
| Ridge | 0.64 | 0.38 | 0.50 | 0.51 | 0.54 | 0.45 | 0.47 | 0.49 |
| SVR | 0.78 | 0.54 | 0.56 | 0.63 | 0.57 | 0.22 | 0.51 | 0.43 |
| MLP | 0.78 | 0.58 | 0.68 | 0.68 | 0.55 | 0.24 | 0.49 | 0.43 |
| SLA | 0.82 | 0.60 | 0.60 | 0.67 | 0.57 | 0.14 | 0.61 | 0.44 |
| Mean for WQ parameters | 0.75 | 0.44 | 0.54 | - | 0.45 | 0.19 | 0.40 | 0.35 |
| General mean | 0.58 | 0.35 |
The table displays the horizontal averages for the ML models and the vertical averages for the CA parameters. The overall average corresponds to the average of all ML models for each set of satellite data (Landsat-8 and Sentinel-2).

Table A7.
Means of the coefficient of determination (r2) for the modeling results for Lake Zapotlán, as a function of CA parameters, ML models and satellite products.
Table A7.
Means of the coefficient of determination (r2) for the modeling results for Lake Zapotlán, as a function of CA parameters, ML models and satellite products.
| ML Models | Tur-L8 | Chl-a-L8 | TSS-L8 | Mean for Models | Tur-S2 | Chl-a-S2 | TSS-S2 | Mean for Models |
|---|---|---|---|---|---|---|---|---|
| DTR | 0.23 | 0.17 | 0.24 | 0.21 | 0.27 | 0.26 | 0.45 | 0.32 |
| KNN | 0.22 | 0.64 | 0.18 | 0.35 | 0.32 | 0.37 | 0.50 | 0.40 |
| RF | 0.54 | 0.51 | 0.17 | 0.41 | 0.41 | 0.47 | 0.59 | 0.49 |
| GBTR | 0.51 | 0.61 | 0.18 | 0.43 | 0.37 | 0.45 | 0.64 | 0.49 |
| Ridge | 0.60 | 0.35 | 0.46 | 0.47 | 0.63 | 0.22 | 0.60 | 0.48 |
| SVR | 0.48 | 0.29 | 0.28 | 0.35 | 0.51 | 0.40 | 0.57 | 0.50 |
| MLP | 0.75 | 0.71 | 0.53 | 0.66 | 0.64 | 0.57 | 0.70 | 0.63 |
| SLA | 0.64 | 0.67 | 0.58 | 0.63 | 0.69 | 0.55 | 0.72 | 0.65 |
| Mean for WQ parameters | 0.50 | 0.49 | 0.33 | - | 0.48 | 0.41 | 0.59 | 0.49 |
| General mean | 0.44 | 0.49 |
The table displays the horizontal averages for the ML models and the vertical averages for the CA parameters. The overall average corresponds to the average of all ML models for each set of satellite data (Landsat-8 and Sentinel-2).
References
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef]
- Giardino, C.; Brando, V.E.; Gege, P.; Pinnel, N.; Hochberg, E.; Knaeps, E.; Reusen, I.; Doerffer, R.; Bresciani, M.; Braga, F.; et al. Imaging Spectrometry of Inland and Coastal Waters: State of the Art, Achievements and Perspectives. Surv. Geophys. 2019, 40, 401–429. [Google Scholar] [CrossRef]
- Spyrakos, E.; O’Donnell, R.; Hunter, P.D.; Miller, C.; Scott, M.; Simis, S.G.; Neil, C.; Barbosa, C.C.; Binding, C.E.; Bradt, S.; et al. Optical types of inland and coastal waters. Limnol. Oceanogr. 2018, 63, 846–870. [Google Scholar] [CrossRef]
- Topp, S.N.; Pavelsky, T.M.; Jensen, D.; Simard, M.; Ross, M.R.V. Research Trends in the Use of Remote Sensing for Inland Water Quality Science: Moving Towards Multidisciplinary Applications. Water 2020, 12, 169. [Google Scholar] [CrossRef]
- Rodríguez, L.F.A.; Duan, Z.; Torres, J.D.D.; Hazas, M.B.; Huang, J.; Kumar, B.U.; Tuo, Y.; Disse, M. Integration of Remote Sensing and Mexican Water Quality Monitoring System Using an Extreme Learning Machine. Sensors 2021, 21, 4118. [Google Scholar] [CrossRef]
- Ritchie, J.; Zimba, P.; Everitt, J. Remote sensing techniques to assess water quality. Photogramm. Eng. Remote Sens. 2003, 69, 695–704. [Google Scholar] [CrossRef]
- Rodríguez, L.F.A.; Duan, Z.; Sepúlveda, R.; Martinez, S.I.M.; Disse, M. Monitoring Water Quality of Valle de Bravo Reservoir, Mexico, Using Entire Lifespan of MERIS Data and Machine Learning Approaches. Remote Sens. 2020, 12, 1586. [Google Scholar] [CrossRef]
- Sagan, V.; Peterson, K.T.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, B.A.; Maalouf, S.; Adams, C. Monitoring inland water quality using remote sensing: Potential and limitations of spectral indices, bio-optical simulations, machine learning, and cloud computing. Earth-Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Ritchie, J.C.; Schiebe, F.R.; McHenry, R.J. Remote sensing of suspended sediments in surface waters. Photogramm Eng. Remote Sens. 1976, 42, 1539–1545. [Google Scholar]
- Papa, F.; Frappart, F. Surface Water Storage in Rivers and Wetlands Derived from Satellite Observations: A Review of Current Advances and Future Opportunities for Hydrological Sciences. Remote Sens. 2021, 13, 4162. [Google Scholar] [CrossRef]
- Cretaux, J.F.; Calmant, S.; Papa, F.; Frappart, F.; Paris, A.; Berge-Nguyen, M. Inland surface waters quantity monitored from remote sensing. Surv. Geophys. 2023, 44, 1519–1552. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Cui, Y.; Yan, S. Consistency of Suspended Particulate Matter Concentration in Turbid Water Retrieved from Sentinel-2 MSI and Landsat-8 OLI Sensors. Sensors 2021, 21, 1662. [Google Scholar] [CrossRef] [PubMed]
- Chawla, I.; Karthikeyan, L.; Mishra, A.K. A review of remote sensing applications for water security: Quantity, quality, and extremes. J. Hydrol. 2020, 585, 124826. [Google Scholar] [CrossRef]
- Yang, H.; Kong, J.; Hu, H.; Du, Y.; Gao, M.; Chen, F. A Review of Remote Sensing for Water Quality Retrieval: Progress and Challenges. Remote Sens. 2022, 14, 1770. [Google Scholar] [CrossRef]
- Abdelal, Q.; Assaf, M.N.; Al-Rawabdeh, A.; Arabasi, S.; Rawashdeh, N.A. Assessment of Sentinel-2 and Landsat-8 OLI for Small-Scale Inland Water Quality Modeling and Monitoring Based on Handheld Hyperspectral Ground Truthing. J. Sensors 2022, 2022, 4643924. [Google Scholar] [CrossRef]
- Caballero, I.; Roca, M.; Santos Echeandía, J.; Bernárdez, P.; Navarro, G. Use of the Sentinel-2 and Landsat-8 Satellites for Water Quality Monitoring: An Early Warning Tool in the Mar Menor Coastal Lagoon. Remote Sens. 2022, 14, 2744. [Google Scholar] [CrossRef]
- Hafeez, S.; Wong, M.S.; Abbas, S.; Asim, M. Evaluating Landsat-8 and Sentinel-2 Data Consistency for High Spatiotemporal Inland and Coastal Water Quality Monitoring. Remote Sens. 2022, 14, 3155. [Google Scholar] [CrossRef]
- Leggesse, E.S.; Zimale, F.A.; Sultan, D.; Enku, T.; Srinivasan, R.; Tilahun, S.A. Predicting Optical Water Quality Indicators from Remote Sensing Using Machine Learning Algorithms in Tropical Highlands of Ethiopia. Hydrology 2023, 10, 110. [Google Scholar] [CrossRef]
- Rodríguez, L.F.A.; Tüzün, U.F.; Duan, Z.; Huang, J.; Tuo, Y.; Disse, M. Global Water Quality of Inland Waters with Harmonized Landsat-8 and Sentinel-2 Using Cloud-Computed Machine Learning. Remote Sens. 2023, 15, 1390. [Google Scholar] [CrossRef]
- Skakun, S.; Wevers, J.; Brockmann, C.; Doxani, G.; Aleksandrov, M.; Batič, M.; Frantz, D.; Gascon, F.; Gómez-Chova, L.; Hagolle, O.; et al. Cloud Mask Intercomparison eXercise (CMIX): An evaluation of cloud masking algorithms for Landsat 8 and Sentinel-2. Remote Sens. Environ. 2022, 274, 112990. [Google Scholar] [CrossRef]
- Ahmed, A.N.; Othman, F.B.; Afan, H.A.; Ibrahim, R.K.; Fai, C.M.; Hossain, M.S.; Ehteram, M.; Elshafie, A. Machine learning methods for better water quality prediction. J. Hydrol. 2019, 578, 124084. [Google Scholar] [CrossRef]
- Papenfus, M.; Schaeffer, B.; Pollard, A.I.; Loftin, K. Exploring the potential value of satellite remote sensing to monitor chlorophyll-a for US lakes and reservoirs. Environ. Monit. Assess. 2020, 192. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez López, L.; Usta, D.B.; Duran Llacer, I.; Alvarez, L.B.; Yépez, S.; Bourrel, L.; Frappart, F.; Urrutia, R. Estimation of Water Quality Parameters through a Combination of Deep Learning and Remote Sensing Techniques in a Lake in Southern Chile. Remote Sens. 2023, 15, 4157. [Google Scholar] [CrossRef]
- Bettencourt, P.; Wasserman, J.C.; Ferreira Dias, F.; Alves, P.R.; Bernardino Bezerra, D.; Américo Santos, C.; Perez Zotes, L.; Barros, S.R. Remote Sensing Applied to the Evaluation of Spatial and Temporal Variation of Water Quality in a Coastal Environment, Southeast Brazil. J. Geogr. Inf. Syst. 2019, 11, 500–521. [Google Scholar] [CrossRef]
- Germán, A.; Shimoni, M.; Beltramone, G.; Rodríguez, M.I.; Muchiut, J.; Bonansea, M.; Scavuzzo, C.M.; Ferral, A. Space-time monitoring of water quality in an eutrophic reservoir using SENTINEL-2 data - A case study of San Roque, Argentina. Remote Sens. Appl. Soc. Environ. 2021, 24, 100614. [Google Scholar] [CrossRef]
- Otto, P.; Rodríguez, R.V.; Keesstra, S.; Becerril, E.L.; de Anda, J.; Mena, L.H.; del Real Olvera, J.; de Jesús Díaz Torres, J. Time Delay Evaluation on the Water-Leaving Irradiance Retrieved from Empirical Models and Satellite Imagery. Remote Sens. 2019, 12, 87. [Google Scholar] [CrossRef]
- Vera, M.A.T. Mapping of total suspended solids using Landsat imagery and machine learning. Int. J. Environ. Sci. Technol. 2023, 20, 11877–11890. [Google Scholar] [CrossRef]
- CONAGUA. Actualización de la Disponibilidad Media Anual de Agua en el Acuífero Cajititlán (1403), Estado de Jalisco; Subdirección General Técnica Gerencia de Aguas Subterráneas: Ciudad de México, Mexico, 2020.
- Instituto Nacional de Estadística y Geografía (INEGI). Cuenca hidrológica Laguna de Zapotlán. Humedales 2019, 8, 32. [Google Scholar]
- Morán-Valencia, M.; Flegl, M.; Güemes-Castorena, D. A state-level analysis of the water system management efficiency in Mexico: Two-stage DEA approach. Water Resour. Ind. 2023, 29, 100200. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. Water quality retrieval from PRISMA hyperspectral images: First experience in a turbid lake and comparison with sentinel-2. Remote Sens. 2020, 12, 3984. [Google Scholar] [CrossRef]
- Mbongowo, M. Use of Hyperspectral Remote Sensing to Estimate Water Quality. In Processing and Analysis of Hyperspectral Data; Chen, J., Song, Y., Li, H., Eds.; IntechOpen: Rijeka, Croatia, 2019; Chapter 6. [Google Scholar] [CrossRef]
- Anderson, E.P.; Jackson, S.; Tharme, R.E.; Douglas, M.; Flotemersch, J.E.; Zwarteveen, M.; Lokgariwar, C.; Montoya, M.; Wali, A.; Tipa, G.T.; et al. Understanding rivers and their social relations: A critical step to advance environmental water management. Wiley Interdiscip. Rev. Water 2019, 6, e1381. [Google Scholar] [CrossRef]
- Caro Borrero, A.; Carmona Jiménez, J.; Figueroa, F. Water resources conservation and rural livelihoods in protected areas of central Mexico. J. Rural Stud. 2020, 78, 12–24. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Botón, C.C.; Pérez, D.C.; CasanovaMateo, C.; Ghimire, S.; Prada, E.C.; Gutierrez, P.A.; Deo, R.C.; Sanz, S.S. Machine learning regression and classification methods for fog events prediction. Atmos. Res. 2022, 272, 106157. [Google Scholar] [CrossRef]
- Lemaitre, G. sklearn.ensemble.StackingRegressor. 2023. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.StackingRegressor.html (accessed on 21 April 2023).
- Chen, Y.; Song, L.; Liu, Y.; Yang, L.; Li, D. A Review of the Artificial Neural Network Models for Water Quality Prediction. Appl. Sci. 2020, 10, 5776. [Google Scholar] [CrossRef]
- Caro Becerra, J.L.; Vizcaíno Rodríguez, L.A.; Michel Parra, J.G.; Mayoral Ruiz, P.A.; Reyes Barragán, J.L. The Importance of Informative Data Base of the Wetlands in the Lake Cajititlán, Previous Step for the Proposal as a Ramsar Site. In Water Availability and Management in Mexico; Otazo Sánchez, E.M., Navarro Frómeta, A.E., Singh, V.P., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 233–245. [Google Scholar] [CrossRef]
- CEA-Jalisco. Datos Abiertos del Sistema de Calidad del Agua. 2022. Available online: https://www.ceajalisco.gob.mx/contenido/datos_abiertos/ (accessed on 16 March 2022).
- APHA. Standard Methods for the Examination of Water and Wastewater; Water Environmental Federation: Alexandria, VA, USA, 1985. [Google Scholar]
- Secretaría de Economía. NMX-AA-038-SCFI-2001. Análisis de agua—Determinación de turbiedad en aguas naturales, residuales y residuales tratadas—Método de prueba (Cancela a la NMX-AA038-1981). Official Gazette of the Federation, 1 August 2001; p. 15.
- Secretaría de Economía. NMX-AA-034-SCFI-2015. Análisis de agua—Medición de sólidos y sales disueltas en aguas naturales, residuales y residuales tratadas—Método de prueba (Cancela a la NMX-AA-034-SCFI-2001). Official Gazette of the Federation, 16 October 2015; p. 16.
- Kutser, T.; Paavel, B.; Verpoorter, C.; Ligi, M.; Soomets, T.; Toming, K.; Casal, G.; Zhang, Y.; Giardino, C.; Li, L.; et al. Remote Sensing of Black Lakes and Using 810 nm Reflectance Peak for Retrieving Water Quality Parameters of Optically Complex Waters. Remote Sens. 2016, 8, 497. [Google Scholar] [CrossRef]
- Attard, G. An Intro to the Earth Engine Python API. 2023. Available online: https://developers.google.com/earth-engine/tutorials/community/intro-to-python-api (accessed on 13 February 2023).
- Braaten, J. Sentinel-2 Cloud Masking with s2cloudless. 2023. Available online: https://developers.google.com/earth-engine/tutorials/community/sentinel-2-s2cloudless (accessed on 25 February 2023).
- Kochenour, C. Remote Sensing with Google Earth Engine. 2020. Available online: https://calekochenour.github.io/remote-sensing-textbook/03-beginner/chapter12-cloud-masking.html (accessed on 17 April 2022).
- Vanhellemont, Q.; Ruddick, K. Atmospheric correction of metre-scale optical satellite data for inland and coastal water applications. Remote Sens. Environ. 2018, 216, 586–597. [Google Scholar] [CrossRef]
- Nair, J.P.; Vijaya, M. River water quality prediction and index classification using machine learning. J. Phys. Conf. Ser. 2022, 2325, 012011. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Vinutha, H.P.; Poornima, B.; Sagar, B.M. Detection of outliers using interquartile range technique from intrusion dataset. Adv. Intell. Syst. Comput. 2018, 701, 511–518. [Google Scholar]
- Raschka, S. MLxtend: Providing machine learning and data science utilities and extensions to Python’s scientific computing stack. J. Open Source Softw. 2018, 3, 638. [Google Scholar] [CrossRef]
- Carlson, R.E.; Simpson, J. A coordinator’s guide to volunteer lake monitoring methods. N. Am. Lake Manag. Soc. 1996, 96, 305. [Google Scholar]
- CONAGUA. Red Nacional de Monitoreo de la Calidad del Agua. 2020. Available online: http://dgeiawf.semarnat.gob.mx:8080/ibi_apps/WFServlet?IBIF_ex=D3_R_AGUA05_03&IBIC_user=dgeia_mce&IBIC_pass=dgeia_mce (accessed on 19 October 2021).
- Gulati, S.; Sharma, S. Challenges and Responses Towards Sustainable Future Through Machine Learning and Deep Learning. In Data Visualization and Knowledge Engineering: Spotting Data Points with Artificial Intelligence; Hemanth, J., Bhatia, M., Geman, O., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 151–169. [Google Scholar] [CrossRef]
- Kachroud, M.; Trolard, F.; Kefi, M.; Jebari, S.; Bourrié, G. Water quality indices: Challenges and application limits in the literature. Water 2019, 11, 361. [Google Scholar] [CrossRef]
- Ravishankar, S.; Ye, J.C.; Fessler, J.A. Image Reconstruction: From Sparsity to Data-Adaptive Methods and Machine Learning. Proc. IEEE 2020, 108, 86–109. [Google Scholar] [CrossRef]
- Wang, G.; Ye, J.C.; Mueller, K.; Fessler, J.A. Image Reconstruction is a New Frontier of Machine Learning. IEEE Trans. Med Imaging 2018, 37, 1289–1296. [Google Scholar] [CrossRef] [PubMed]
- Wagle, N.; Acharya, T.D.; Lee, D.H. Comprehensive Review on Application of Machine Learning Algorithms for Water Quality Parameter Estimation Using Remote Sensing Data. Sensors Mater. 2020, 32, 3879–3892. [Google Scholar] [CrossRef]
- Blix, K.; Pálffy, K.; Tóth, V.R.; Eltoft, T. Remote Sensing of Water Quality Parameters over Lake Balaton by Using Sentinel-3 OLCI. Water 2018, 10, 1428. [Google Scholar] [CrossRef]
- Zhang, C.; Han, M.I.N. Mapping chlorophyll-a concentration in Laizhou Bay using Landsat 8 OLI data. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Kim, S.I.; Kim, H.C.; Hyun, C.U. High Resolution Ocean Color Products Estimation in Fjord of Svalbard, Arctic Sea using Landsat-8 OLI. Korean J. Remote Sens. 2014, 30, 809–816. [Google Scholar] [CrossRef]
- Lim, J.; Choi, M. Assessment of water quality based on Landsat 8 operational land imager associated with human activities in Korea. Environ. Monit. Assess. 2015, 187, 384. [Google Scholar] [CrossRef]
- Rodrigo, J.A. Machine Learning con Python y Scikitlearn. 2023. Available online: https://cienciadedatos.net/documentos/py06_machine_learning_python_scikitlearn (accessed on 18 April 2023).
- Zhang, X. Chapter Machine Learning. In A Matrix Algebra Approach to Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2020; pp. 223–440. [Google Scholar]
- Tougui, I.; Jilbab, A.; El Mhamdi, J. Impact of the choice of cross-validation techniques on the results of machine learning-based diagnostic applications. Healthc. Inform. Res. 2021, 27, 189–199. [Google Scholar] [CrossRef]
- Louargant, M.; Jones, G.; Faroux, R.; Paoli, J.N.; Maillot, T.; Gée, C.; Villette, S. Unsupervised Classification Algorithm for Early Weed Detection in Row-Crops by Combining Spatial and Spectral Information. Remote Sens. 2018, 10, 761. [Google Scholar] [CrossRef]
- Muller Karger, F.E.; Hestir, E.; Ade, C.; Turpie, K.; Roberts, D.A.; Siegel, D.; Miller, R.J.; Humm, D.; Izenberg, N.; Keller, M.; et al. Satellite sensor requirements for monitoring essential biodiversity variables of coastal ecosystems. Ecol. Appl. 2018, 28, 749–760. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).