A Partial Point Cloud Completion Network Focusing on Detail Reconstruction
Abstract
:1. Introduction
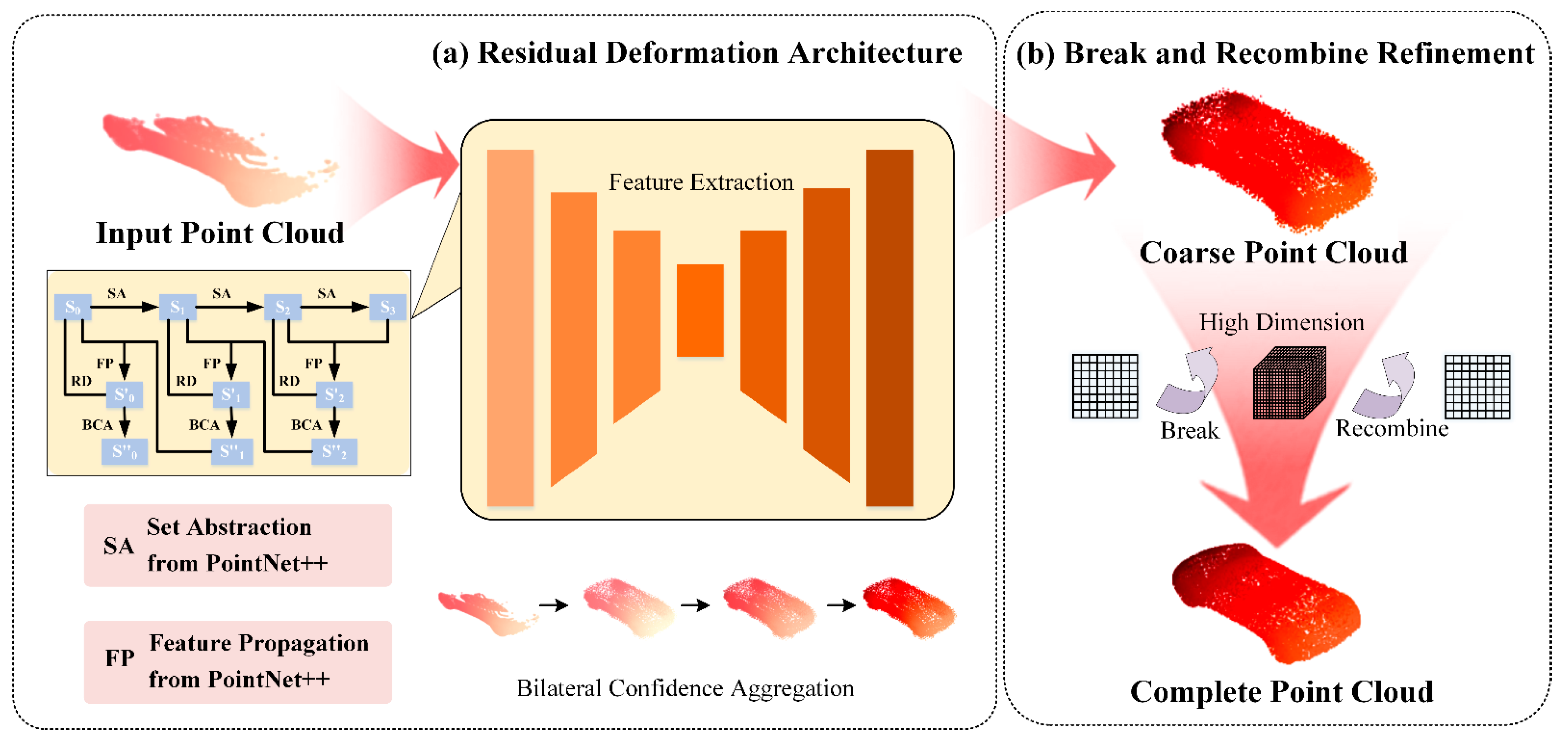
- It proposes a residual deformation architecture to regulate the learning direction of the network and reduce noise, ensuring the accuracy of the structure.
- It designs the break and recombines refinement for high dimensional internal processing, achieving deep fusion and optimization, and recovering point cloud details.
- It designs a bidirectional confidence aggregation unit to guide the recovery of point details by considering the confidence levels of updates and resets during moving path predictions.
- The experiments demonstrate that our network has an enhanced effect on details and suppressed noise, achieving effective end-to-end point cloud completion.
2. Methods
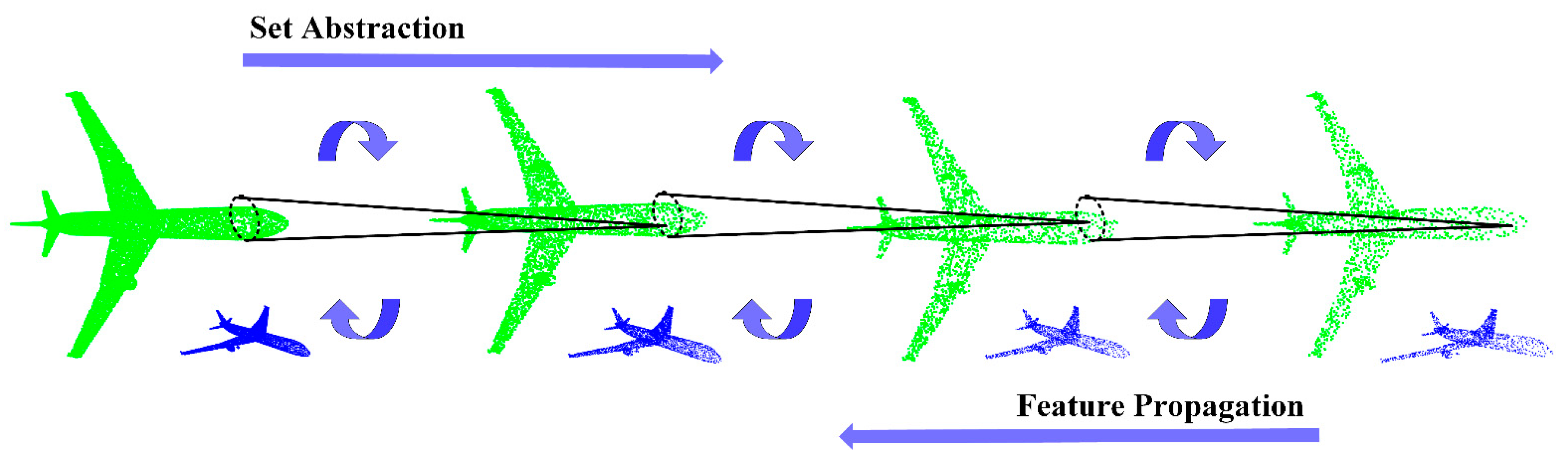
2.1. Residual Deformation Architecture
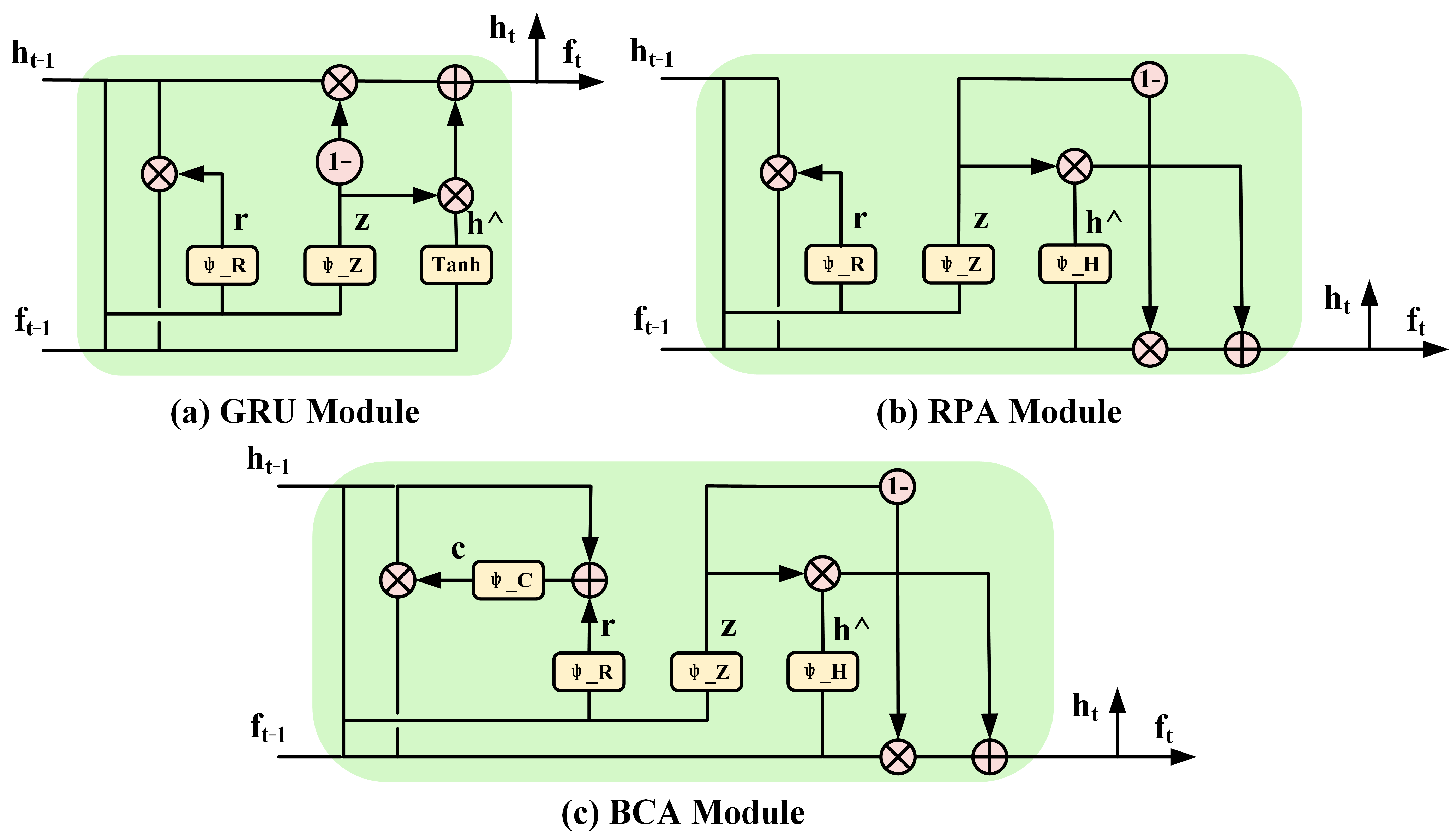
2.2. Bilateral Confidence Aggregation Unit
2.3. Break and Recombine Refinement
2.4. Loss Function
3. Results
3.1. Setup
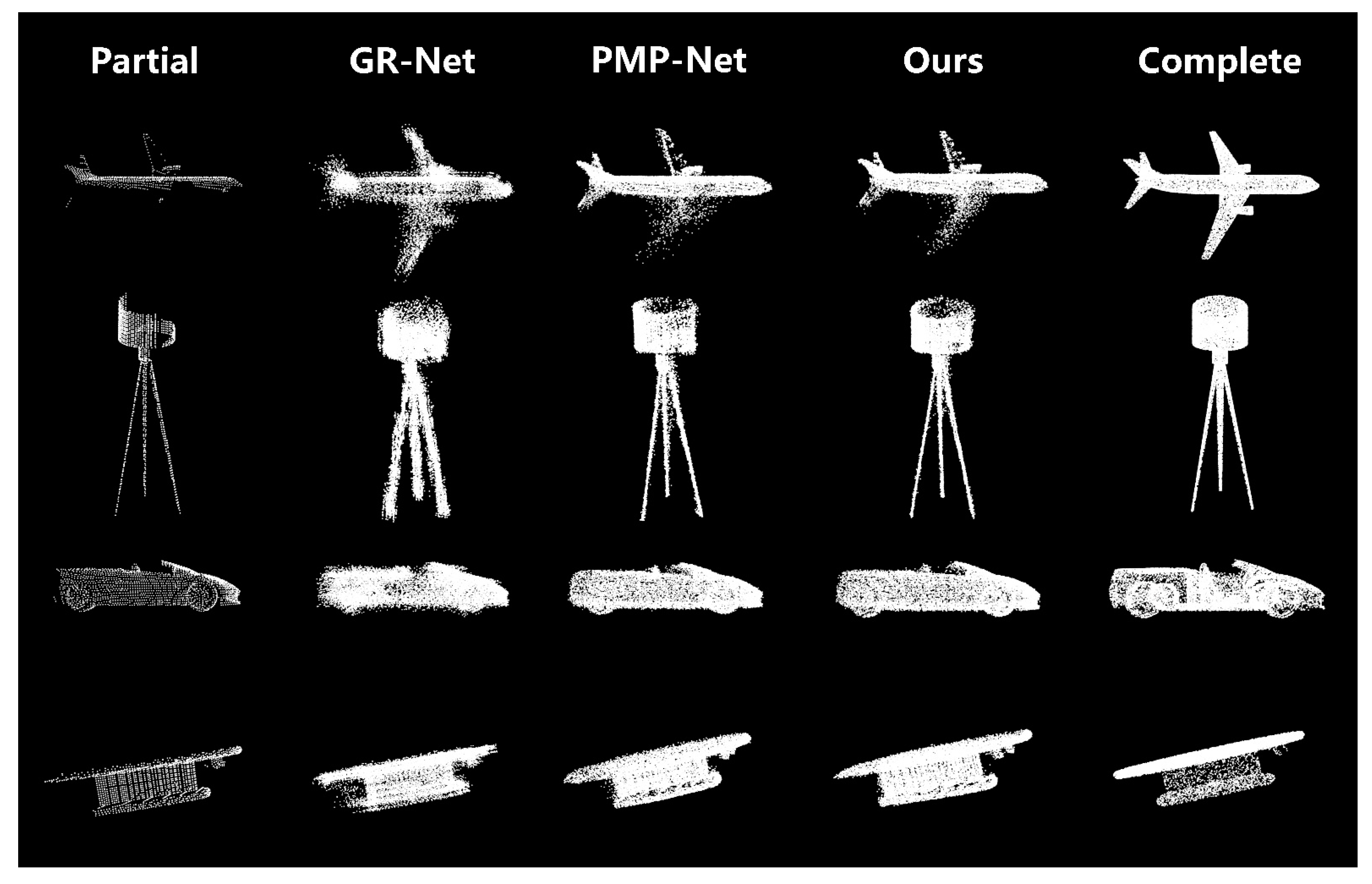
3.2. Results of Comparative Experiments
3.2.1. ShapeNet
3.2.2. Complete3D
3.3. Results of Ablation Experiments
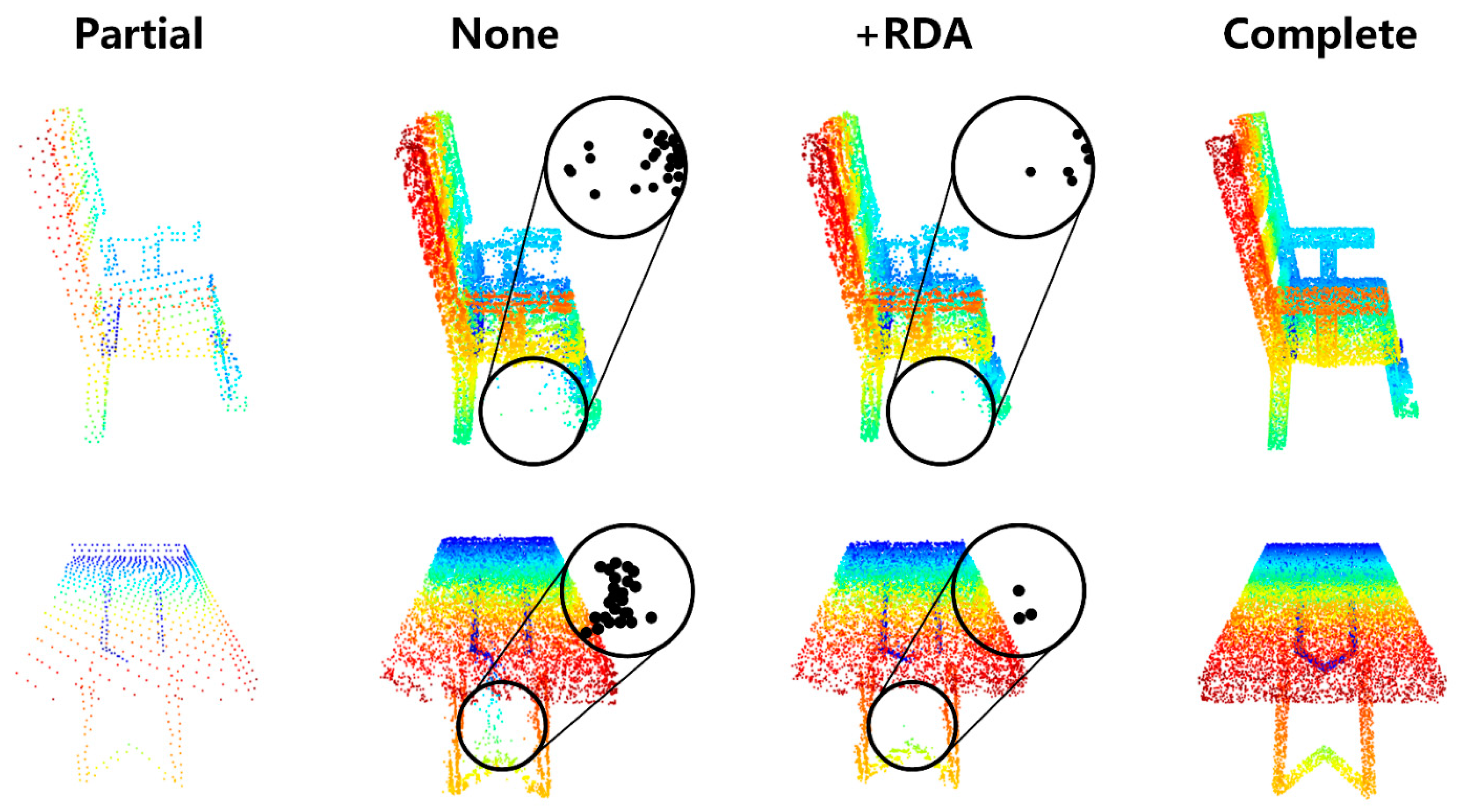
3.3.1. Residual Deformation Architecture
3.3.2. Bilateral Confidence Aggregation Unit
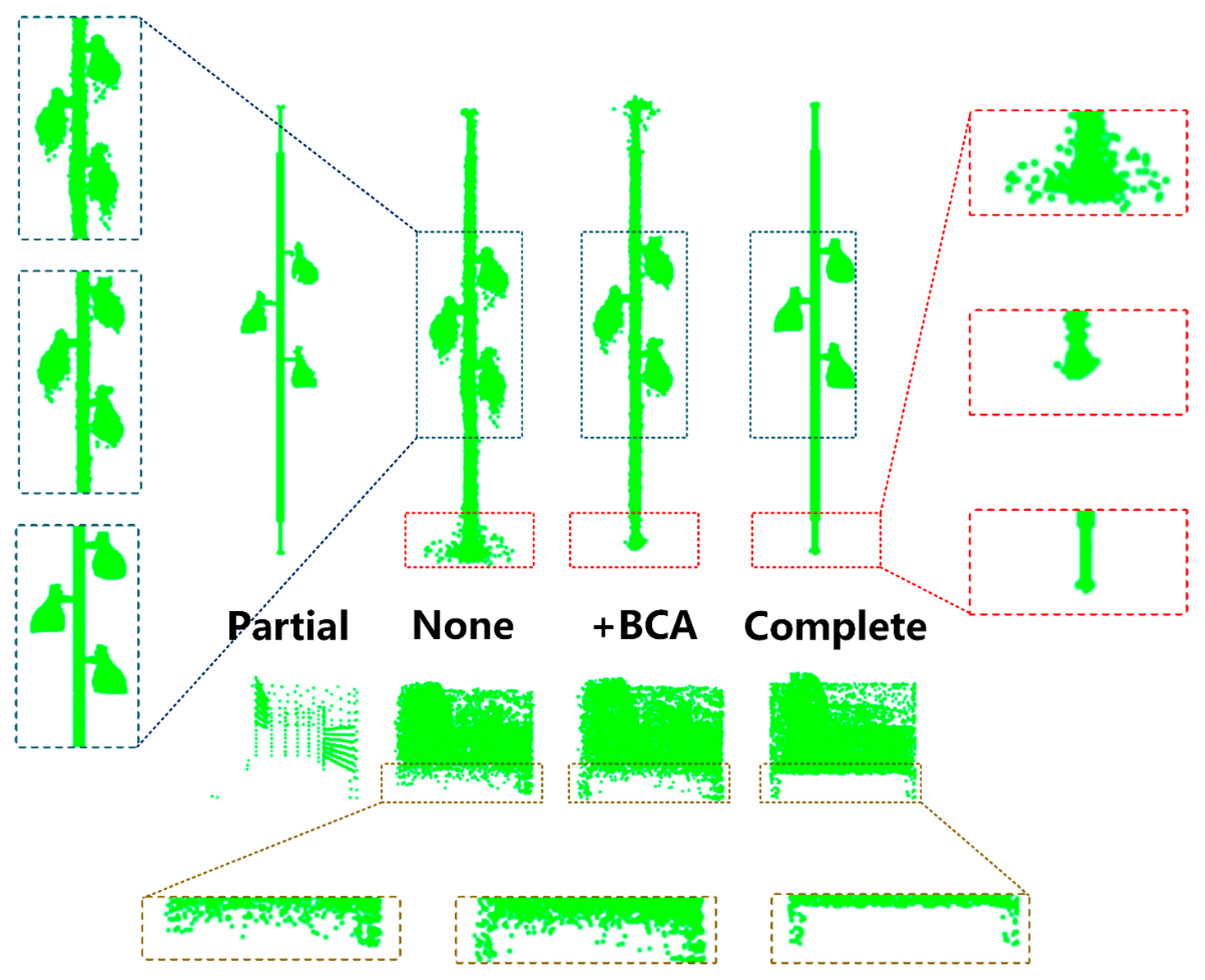
3.3.3. Break and Recombine Refinement
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xia, Y.; Xia, Y.; Li, W.; Song, R.; Cao, K.; Stilla, U. ASFM-Net: Asymmetrical Siamese Feature Matching Network for Point Completion. arXiv 2021, arXiv:2104.09587v2. [Google Scholar]
- Cai, Y.; Lin, K.Y.; Zhang, C.; Wang, Q.; Wang, X.; Li, H. Learning a Structured Latent Space for Unsupervised Point Cloud Completion. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 5533–5543. [Google Scholar]
- Huang, H.; Chen, H.; Li, J. Deep Neural Network for 3D Point Cloud Completion with Multistage Loss Function. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 4604–4609. [Google Scholar]
- Manuele, S.; Gianpaolo, P.; Francesco, B.; Tamy, B.; Paolo, C. High Dynamic Range Point Clouds for Real-Time Relighting. Comput. Graph. Forum 2019, 38, 513–525. [Google Scholar]
- Gurumurthy, S.; Agrawal, S. High Fidelity Semantic Shape Completion for Point Clouds Using Latent Optimization. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019; pp. 1099–1108. [Google Scholar]
- Boulch, A.; Marlet, R. POCO: Point Convolution for Surface Reconstruction. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 6292–6304. [Google Scholar]
- Chen, Z.; Long, F.; Qiu, Z.; Yao, T.; Zhou, W.; Luo, J.; Mei, T. AnchorFormer: Point Cloud Completion from Discriminative Nodes. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 13581–13590. [Google Scholar]
- Yuan, W.; Khot, T.; Held, D.; Mertz, C.; Hebert, M. PCN: Point Completion Network. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 728–737. [Google Scholar]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
- Xie, H.; Yao, H.; Zhou, S.; Mao, J.; Sun, W. GRNet: Gridding Residual Network for Dense Point Cloud Completion. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph CNN for Learning on Point Clouds. ACM Trans. Graph. 2019, 38, 146. [Google Scholar] [CrossRef]
- Tchapmi, L.P.; Kosaraju, V.; Rezatofighi, H.; Reid, I.; Savarese, S. TopNet: Structural Point Cloud Decoder. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 383–392. [Google Scholar]
- Li, S.; Gao, P.; Tan, X.; Wei, M. ProxyFormer: Proxy Alignment Assisted Point Cloud Completion with Missing Part Sensitive Transformer. arXiv 2023, arXiv:2302.14435. [Google Scholar]
- Ma, C.; Chen, Y.; Guo, P.; Guo, J.; Wang, C.; Guo, Y. Symmetric Shape-Preserving Autoencoder for Unsupervised Real Scene Point Cloud Completion. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 13560–13569. [Google Scholar]
- Hong, S.; Yavartanoo, M.; Neshatavar, R.; Lee, K.M. ACL-SPC: Adaptive Closed-Loop System for Self-Supervised Point Cloud Completion. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 9435–9444. [Google Scholar]
- Zhang, J.; Zhang, H.; Vasudevan, R.; Johnsom-Roberson, M. HyperPC: Hyperspherical Embedding for Point Cloud Completion. arXiv 2023, arXiv:2307.05634. [Google Scholar]
- Tan, H. Visualizing Global Explanations of Point Cloud DNNs. In Proceedings of the 2023 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 2–7 January 2023; pp. 4730–4739. [Google Scholar]
- Li, S.; Ye, Y.; Liu, J.; Guo, L. VPRNet: Virtual Points Registration Network for Partial-to-Partial Point Cloud Registration. Remote Sens. 2022, 14, 2559. [Google Scholar] [CrossRef]
- Wen, X.; Li, T.; Han, Z.; Liu, Y. Point Cloud Completion by Skip-Attention Network with Hierarchical Folding. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1936–1945. [Google Scholar]
- Zong, D.; Sun, S.; Zhao, J. ASHF-Net Adaptive Sampling and Hierarchical Folding. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; pp. 3625–3632. [Google Scholar]
- Zhang, W.; Yan, Q.; Xiao, C. Detail Preserved Point Cloud Completion via Separated Feature Aggregation. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Zhao, Y.; Birdal, T.; Deng, H.; Tombari, F. 3D Point Capsule Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 1009–1018. [Google Scholar]
- Xia, Z.; Liu, Y.; Zhu, X.; Ma, Y.; Li, Y.; Hou, Y.; Qiao, Y. SCPNet: Semantic Scene Completion on Point Cloud. arXiv 2023, arXiv:2023.06884. [Google Scholar]
- Wei, M.; Zhu, M.; Zhang, Y.; Sun, J.; Wang, J. Cyclic Global Guiding Network for Point Cloud Completion. Remote Sens. 2022, 14, 3316. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, J.; Wu, Q.; Fan, L.; Yuan, C. A Coarse-to-Fine Algorithm for Matching and Registration in 3D Cross-Source Point Clouds. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 2965–2977. [Google Scholar] [CrossRef]
- Huang, Z.; Yu, Y.; Xu, J.; Ni, F.; Le, X. PF-Net: Point Fractal Network for 3D Point Cloud Completion. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 7659–7667. [Google Scholar]
- Yang, Y.; Feng, C.; Shen, Y.; Tian, D. FoldingNet: Point Cloud Auto-Encoder via Deep Grid Deformation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 206–215. [Google Scholar]
- Pan, L. ECG: Edge-aware Point Cloud Completion with Graph Convolution. IEEE Robot. Autom. Lett. 2020, 5, 4392–4398. [Google Scholar] [CrossRef]
- Achlioptas, P.; Diamanti, O.; Mitliagkas, I.; Guibas, L. Learning Representations and Generative Models for 3D Point Clouds. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 40–49. [Google Scholar]
- Pan, L.; Chen, X.; Cai, Z.; Zhang, J.; Liu, Z. Variational Relational Point Completion Network. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 8520–8529. [Google Scholar]
- Wang, X.; Ang, M.H.; Lee, G.H. Cascaded Refinement Network for Point Cloud Completion. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 787–796. [Google Scholar]
- Tang, J.; Gong, Z.; Yi, R.; Xie, Y.; Ma, L. LAKe-Net: Topology-Aware Point Cloud Completion by Localizing Aligned Keypoints. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 1716–1725. [Google Scholar]
- Wen, X. PMP-Net: Point Cloud Completion by Learning Multi-step Point Moving Paths. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 7439–7448. [Google Scholar]
- Chung, J.; Culcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Lei, T.; Zhang, Y. Training RNNs as Fast as CNNs. arXiv 2017, arXiv:1709.02755. [Google Scholar]
- Mittal, H.; Okorn, B.; Jangid, A.; Held, D. Self-Supervised Point Cloud Completion via Inpainting. arXiv 2021, arXiv:2111.10701. [Google Scholar]
- Liu, M.; Sheng, L.; Yang, S.; Shao, J.; Hu, S.M. Morphing and Sampling Network for Dense Point Cloud Completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Huang, Z.; Wang, X.; Wei, Y.; Huang, L.; Shi, H.; Liu, W.; Huang, T.S. CCNet: Criss-Cross Attention for Semantic Segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Charles, R.Q.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5105–5114. [Google Scholar]


| Model | Folding-Net | Top-Net | PCN | GR-Net | PMP-Net | BCA-Net |
|---|---|---|---|---|---|---|
| Airplane | 9.49 | 7.61 | 5.50 | 6.45 | 5.50 | 5.19 |
| Cabinet | 15.80 | 13.31 | 22.70 | 10.37 | 11.10 | 10.79 |
| Car | 12.61 | 10.90 | 1063 | 9.45 | 9.62 | 9.51 |
| Chair | 15.55 | 13.82 | 8.70 | 9.41 | 9.47 | 9.13 |
| Lamp | 16.41 | 14.44 | 11.00 | 7.96 | 6.89 | 6.62 |
| Sofa | 15.97 | 14.78 | 11.34 | 10.51 | 10.74 | 10.95 |
| Table | 13.65 | 11.22 | 11.68 | 8.44 | 8.77 | 8.03 |
| Watercraft | 14.99 | 11.12 | 8.59 | 8.04 | 7.19 | 7.26 |
| Overall | 14.31 | 12.15 | 9.64 | 8.83 | 8.66 | 8.43 |
| Time | - | - | - | 0.020 | 0.016 | 0.018 |
| Model | Folding-Net | PCN | Top-Net | SA-Net | GR-Net | CRN | PMP-Net | BCA-Net |
|---|---|---|---|---|---|---|---|---|
| Airplane | 1.28 | 0.98 | 0.73 | 0.53 | 0.61 | 0.40 | 0.39 | 0.26 |
| Cabinet | 2.34 | 2.27 | 1.88 | 1.45 | 1.69 | 1.32 | 1.47 | 1.35 |
| Car | 1.49 | 1.24 | 1.29 | 0.78 | 0.83 | 0.83 | 0.86 | 0.71 |
| Chair | 2.57 | 2.51 | 1.98 | 1.37 | 1.22 | 1.06 | 1.02 | 1.20 |
| Lamp | 2.18 | 2.27 | 1.46 | 1.35 | 1.02 | 1.00 | 0.93 | 0.87 |
| Sofa | 2.13 | 2.03 | 1.63 | 1.42 | 1.49 | 1.29 | 1.24 | 0.99 |
| Table | 2.07 | 2.03 | 1.49 | 1.18 | 1.01 | 0.92 | 0.85 | 1.35 |
| Watercraft | 1.15 | 1.17 | 0.88 | 0.88 | 0.87 | 0.58 | 0.58 | 0.49 |
| Overall | 1.91 | 1.82 | 1.45 | 1.12 | 1.06 | 0.92 | 0.92 | 0.90 |
| Model | Overall CD | Time (ms) |
|---|---|---|
| +None | 8.64 | 1.6 |
| +Res*1 | 8.62 | 1.6 |
| +Res*2 | 8.61 | 1.7 |
| +Res*3 | 8.60 | 1.7 |
| Model | Air-Plane | Cabinet | Car | Chair | Lamp | Sofa | Table | Water-Craft | Overall |
|---|---|---|---|---|---|---|---|---|---|
| Ori | 6.05 | 11.13 | 9.62 | 9.53 | 7.50 | 10.82 | 8.36 | 7.42 | 8.72 |
| +GRU | 5.37 | 11.00 | 9.71 | 9.48 | 6.82 | 11.16 | 8.25 | 7.39 | 8.65 |
| +RPA | 5.26 | 11.04 | 9.54 | 9.37 | 6.85 | 11.21 | 8.20 | 7.33 | 8.60 |
| +BCA | 5.34 | 10.81 | 9.57 | 9.34 | 6.84 | 11.14 | 8.22 | 7.41 | 8.58 |
| Model | Air-Plane | Cabinet | Car | Chair | Lamp | Sofa | Table | Water-Craft | Overall | |
|---|---|---|---|---|---|---|---|---|---|---|
| CD | None | 5.34 | 10.81 | 9.57 | 9.34 | 6.84 | 11.14 | 8.22 | 7.41 | 8.58 |
| +BR | 5.19 | 10.79 | 9.51 | 9.13 | 6.62 | 10.95 | 8.03 | 7.26 | 8.43 | |
| FS | None | 0.820 | 0.534 | 0.540 | 0.622 | 0.766 | 0.508 | 0.688 | 0.719 | 0.650 |
| +BR | 0.836 | 0.543 | 0.552 | 0.634 | 0.773 | 0.513 | 0.700 | 0.730 | 0.660 |
| Model | None | + RDA | +BCA | +BR |
|---|---|---|---|---|
| Δt (s) | - | 0.001 | 0.001 | <0.001 |
| Time (s) | 0.016 | 0.017 | 0.018 | 0.018 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, M.; Sun, J.; Zhang, Y.; Zhu, M.; Nie, H.; Liu, H.; Wang, J. A Partial Point Cloud Completion Network Focusing on Detail Reconstruction. Remote Sens. 2023, 15, 5504. https://doi.org/10.3390/rs15235504
Wei M, Sun J, Zhang Y, Zhu M, Nie H, Liu H, Wang J. A Partial Point Cloud Completion Network Focusing on Detail Reconstruction. Remote Sensing. 2023; 15(23):5504. https://doi.org/10.3390/rs15235504
Chicago/Turabian StyleWei, Ming, Jiaqi Sun, Yaoyuan Zhang, Ming Zhu, Haitao Nie, Huiying Liu, and Jiarong Wang. 2023. "A Partial Point Cloud Completion Network Focusing on Detail Reconstruction" Remote Sensing 15, no. 23: 5504. https://doi.org/10.3390/rs15235504
APA StyleWei, M., Sun, J., Zhang, Y., Zhu, M., Nie, H., Liu, H., & Wang, J. (2023). A Partial Point Cloud Completion Network Focusing on Detail Reconstruction. Remote Sensing, 15(23), 5504. https://doi.org/10.3390/rs15235504






