ISHS-Net: Single-View 3D Reconstruction by Fusing Features of Image and Shape Hierarchical Structures

Abstract

The reconstruction of 3D shapes from a single view has been a longstanding challenge. Previous methods have primarily focused on learning either geometric features that depict overall shape contours but are insufficient for occluded regions, local features that capture details but cannot represent the complete structure, or structural features that encode part relationships but require predefined semantics. However, the fusion of geometric, local, and structural features has been lacking, leading to inaccurate reconstruction of shapes with occlusions or novel compositions. To address this issue, we propose a two-stage approach for achieving 3D shape reconstruction. In the first stage, we encode the hierarchical structure features of the 3D shape using an encoder-decoder network. In the second stage, we enhance the hierarchical structure features by fusing them with global and point features and feed the enhanced features into a signed distance function (SDF) prediction network to obtain rough SDF values. Using the camera pose, we project arbitrary 3D points in space onto different depth feature maps of the CNN and obtain their corresponding positions. Then, we concatenate the features of these corresponding positions together to form local features. These local features are also fed into the SDF prediction network to obtain fine-grained SDF values. By fusing the two sets of SDF values, we improve the accuracy of the model and enable it to reconstruct other object types with higher quality. Comparative experiments demonstrate that the proposed method outperforms state-of-the-art approaches in terms of accuracy.

1. Introduction

Three-dimensional shape reconstruction is a core problem in computer vision and computer graphics. With the development of deep learning technology, image-based 3D reconstruction has attracted wide attention [1]. Images contain rich 3D shape information, but directly reconstructing 3D shapes from a single image is a highly challenging task [2]. Three-dimensional shapes can be modeled using various representation methods, commonly including explicit representation, implicit representation, and structural representation. Explicit representation, such as point clouds, can accurately represent three-dimensional point coordinates but lack surface topology information [3]; meshes can represent surface topology but have limitations due to fixed topology [4]. Implicit representation, such as implicit functions, can represent any topology structure [5] but require post-processing to generate surfaces. Structural representation can represent the overall structure of shapes [6] but is weak in modeling local geometric details. Therefore, an important focus of current research is how to effectively combine the advantages of various representation methods [7].

In the task of 3D reconstruction, another key issue is how to extract shape features (such as global features, local features and structural features) from images. Global features can represent the overall contour of shapes but are insufficient in representing occluded regions [1]; local features can express details but cannot represent the complete structure [8]; structural features can represent part relationships but need to be predefined [9]. To address this issue, some methods attempt to combine different features. For example, Tang et al. [10] first predict object skeleton points, then generate base images, and finally optimize vertices using graph convolutional networks. Mao et al. [11] use structural features to guide global shape generation and refine with local features. These methods have somewhat improved reconstruction quality but still have room for improvement [12].

This paper proposes a novel method for 3D reconstruction that combines the structural and geometric features of objects and predicts the reconstruction using a Signed Distance Function (SDF) for representation. Specifically, the method consists of two key modules. The first module is used to extract the structural features of objects from single-view images. This module adopts an encoder-decoder structure, where the encoder consists of a convolutional network that learns the global features from the images. The decoder recursively decodes the output of the encoder to reconstruct the hierarchical component structure of the object [6]. The decoder contains multiple node classifiers and decoders to determine the type of each node and perform decoding. Leaf nodes are decoded as bounding box parameters, symmetric nodes are decoded as symmetric parameters and a child node, and connecting nodes are decoded as two child nodes. By decoding step by step, the entire hierarchical structure can be recovered. After training, the encoder can map images to the structural feature space. The second module is used for the implicit reconstruction of the geometric structure of objects. This module first combines the structural features learned by the encoder with the global features extracted from the image and inputs them into a multilayer perceptron to predict the coarse SDF values [5] of the sampled points, representing the global geometric shape. At the same time, using a convolutional network, it extracts multi-scale local features from the image, combines them with the coordinate features of the points themselves, and inputs them into another multilayer perceptron to predict the fine SDF values [8] of the sampled points, representing the detailed geometric structure. Finally, we combine the predicted SDF values from both modules to obtain the final SDF value. The Marching Cubes algorithm [13] is then used to extract the isosurfaces as the display mesh.

Building on the aforementioned analysis, this paper presents the following contributions dedicated to enhancing the accuracy of single-view 3D reconstruction:

(1)

Extracting hierarchical structure features from input images and encoding them into fixed-length vectors using graph neural networks, which provide strong structural priors about symmetries, connections, and compositional relationships between object parts. This enables the reconstruction of complete shapes, even for occluded regions.

(2)

Fusing the hierarchical structure features with global image features through concatenation and multilayer perceptrons to emphasize structural knowledge. This allows for predicting preliminary global SDF values that establish the overall topological structure and global geometry of the shape, thereby avoiding any missing or discontinuous phenomena in slender and small-volume areas.

(3)

Employing multi-scale local features extracted using convolutional neural networks to predict detailed SDF values for recovering intricate surface details. The local features focus on representing local patches and fine-grained geometry. Fusing the predicted global and local SDF values through summation to obtain the complete SDF representation of the 3D shape. The comprehensive integration of structural and geometric clues enables the reconstruction of high-fidelity 3D shapes, significantly enhancing the results.

2. Related Work

Explicit representation reconstruction. Explicit representation methods directly represent 3D shapes using structures such as point clouds and triangular meshes, which can clearly express the geometric information of the target shape. The results obtained from these methods can be directly used for visualization and subsequent processing. Point clouds are one of the most direct explicit representation methods. Early point cloud processing networks such as PointNet [3] and PointNet++ [14] address the issue of unordered point clouds by applying symmetric functions to model irregular point clouds directly. In the reconstruction task, FoldingNet [15] folds point clouds into a 2D structure and then recovers the 3D coordinates through unfolding, achieving the conversion from point clouds to meshes. A point cloud rendering technique [16], GenMesh [17], can directly reconstruct point clouds from a single viewpoint image. These methods can effectively preserve the geometric structural information of point clouds. However, point clouds themselves do not represent surfaces and lack topological information, requiring additional processing to form closed meshes [18]. Triangular meshes, as the most detailed explicit structure representation, are also widely used in reconstruction tasks. Early template deformation methods such as Pixel2Mesh [19] use graph convolutional networks to progressively deform a spherical template mesh to approximate the target shape. With the development of explicit rendering techniques, rendering loss has also been introduced into these methods, such as tex2shape [20], to make the reconstructed results more realistic. Some subsequent works also attempt to represent the target shape by deforming multiple basic shapes and combining them to improve the flexibility of topology [21]. Face-swapping methods [22] reconstruct facial shapes by deforming only the facial region. In addition, differentiable rendering techniques [23,24,25] have achieved good results in directly reconstructing triangular meshes from multiple viewpoint images. These methods can represent both the geometry and topology information of shapes simultaneously. The main advantage of explicit representation is its intuitive and easy operation. However, it has certain limitations in representing the topological structure of shapes, is not suitable for representing complex shapes, and has limited reconstruction quality. Additionally, point clouds require post-processing to form closed surfaces, which also limits their applications.

Implicit representation reconstruction. Implicit representation methods commonly describe shapes using implicit functions. These functions include occupancy functions and signed distance functions [8,24,26,27]. These methods can represent shapes with arbitrary topology and have flexible structures. Early methods like IM-Net [28] combined with autoencoders generally mapped various inputs to implicit functions. These global methods have weak modeling capabilities for details. Subsequently, methods were proposed to enhance details using local features [29], such as extracting features from point clouds [30] or images [31], to improve the reconstruction quality of local details. Voxelized inputs also help capture global geometric information [32]. NeRF [33] introduced volume rendering techniques in the implicit function framework and successfully reconstructed scene-level results from multiple viewpoint images. Follow-up methods [34,35] based on NeRF utilized signed distance functions for high-quality surface modeling and rendering. The flexible topological structure and the ability to represent complex shapes are the greatest advantages of implicit representation methods. They can provide continuous representation, facilitating network optimization and shape interpolation. However, the results are not intuitive and require extraction to obtain explicit meshes, which limits their applications. There is also room for improvement in detail modeling and rendering.

Structural representation reconstruction. Structural representation methods typically use simple basic shapes to describe the overall structure of the target shape [36,37]. These methods focus more on the high-level semantic information of shapes. Early structural representation methods [38] generated multiple basic shapes as components in a sequential manner through recursive networks and combined them to form the overall shape. These methods have limited control over component details. Subsequent works began to separate shape structure and geometric representation, such as learning independently in structural space and geometric space using variational autoencoders [39]. Recent works combined basic shapes with neural implicit functions, which can represent the structure and reconstruct smooth surfaces [40]. Semantic program networks [41] represent structures as program statements and use transformer networks for modeling. Structural representation methods have the main advantage of representing global structures well. However, they have limited control over local geometric details, require a large amount of additional structural annotation as supervision, and have higher method complexity, which limits their application range.

Feature fusion reconstruction. Feature fusion methods attempt to combine the advantages of different representation methods and perform fusion modeling of multi-source information. One type of method is to blend mesh representation and implicit function representation, utilizing the editability of explicit meshes and the flexible topology of implicit functions [42]. Another type of method is to fuse image features, point cloud features, voxel features, etc., within the implicit function framework to comprehensively use local and global information for more refined modeling [32]. Feature fusion can leverage the strengths of different representation methods and obtain richer shape information. However, it is more complex to implement, requiring the handling of conversions and fusion between different representations [43].

Based on the above-related work, although the implicit surface representation method excels in mesh reconstruction and effectively captures detailed surface information, its performance in terms of structural integrity is poor, especially in areas with occlusion, thinness, and complex connection structures. Therefore, complete structure reconstruction remains a challenging task. On the other hand, structure-based approaches have the capability to comprehend the compositional structure of an object from its image and reconstruct its complete structural shape. However, objects with similar structures may exhibit significant differences in appearance, and such methods are not adept at accurately reconstructing intricate details. Therefore, this paper proposes a single-view 3D reconstruction method that extracts and enhances hierarchical structural features from images, integrates them with global features, and enables the model to reconstruct both fine mesh surfaces and complete hierarchical structures, thereby achieving superior reconstruction quality.

3. Methods

In this work, we aim to recover both the global integrity and fine surface details of the 3D structure from a single image. The input to our proposed method includes the image and a set of predefined 3D points in space. The output is the signed distance function (SDF) values of the predefined points. As illustrated in Figure 1, the SDF characterizes a 3D object by computing the shortest distance from any point in space to the object’s surface. The SDF takes negative values inside the object, positive values outside, and zeros on the surface. By predicting the SDF values of sampled points, we can recover the continuous implicit field to represent the object’s 3D structure. Our proposed method achieves remarkable results in preserving sharp features and details while maintaining watertight topology. The effectiveness of our approach is demonstrated through extensive experiments on various objects and scenes.

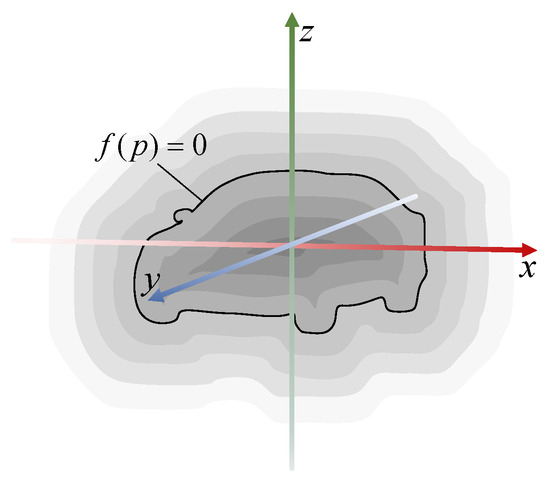
Figure 1. Illustration of SDF. A point p(x, y, z) is outside the surface if $f(p)>0$, inside if $f(p)<0$, and on the surface if $f(p)=0$.

3.1. Overview

This section introduces a network model consisting of two networks that facilitate the reconstruction of 3D shapes from a single image. The first network extracts the hierarchical structure of the object from the input 2D image and encodes it as a fixed-length implicit vector (root code), which can be decoded to represent the structural composition of the corresponding 3D shape. The second network extracts global features from the 2D image, combines them with point features and the implicit vector that carries hierarchical structure information, and predicts the SDF_global value of the sampled point. Subsequently, it extracts multi-scale local features of the sampled point, combines them with point features, and predicts the SDF_local value of the sampled point. Finally, the SDF_global and SDF_local values are fused to determine the final SDF value, and the faces with an SDF value of 0 are extracted to form the final generated 3D model surface. Figure 2 illustrates the overall network structure of this approach.

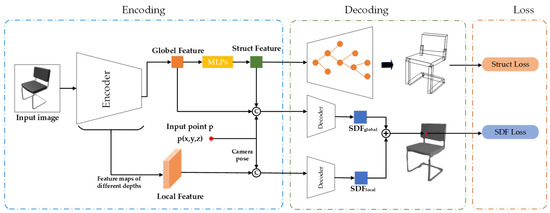
Figure 2. The proposed framework based on a deep model for 3D reconstruction.

The training process consists of two stages, as illustrated in Figure 2. In the first stage (top row), the input image passes through a CNN to extract features and predict an oriented bounding box that captures the structural information of the object. In the second stage (bottom row), additional 3D point coordinates p are input and projected onto the feature map based on camera parameters to obtain local features. The global image feature and local point feature are then used to predict a global SDF and local SDF, respectively. The final SDF result is obtained by fusing the global and local SDF predictions. This two-stage approach allows our model to leverage both holistic image understanding and fine-grained local context for accurate and detailed 3D shape reconstruction from a single image.

In the test process, our goal is to reconstruct the mesh structure of the object without decoding the hierarchical features. The inputs are the image and a set of predefined 3D points in space. The global image features and structure features are used to predict a global SDF, while the local features at each point predict a refined local SDF. The final SDF value at each point is obtained by summing the global and local SDF predictions. This combined SDF field is then converted into a mesh surface using the Marching Cubes algorithm [13]. The high-quality mesh reconstruction results validate the effectiveness of fusing global and local information in our method.

3.2. Structural Features Extraction

We improved the structural reconstruction network proposed by GRASS and developed a framework for converting feature vectors extracted from input images into a hierarchical 3D structure. Figure 2 illustrates the structure reconstruction network framework. We utilized ResNet50 to extract global features from the input image and encoded these features using an encoder to produce a hidden vector $V_r$ called the root code, representing the structural features. Here, $V_r=f_{struct}(G)$. After inputting the global feature $G$ into the structural network $f_{struct}$, we obtain the $V_r$. The global feature $G$ is derived from $[G,L_{depth}]=f_{en}(x)$. $f_{en}$ represent the encoding network. $x$ denotes the input image, $L_{depth}$ represents a collection of feature maps at different depths, i.e., $L_{depth}=\{l_1,l_2,\cdots ,l_n\}$, where $l_n$ represents the feature map at the nth depth.

By decoding $V_r$, a hierarchical tree-like structure is obtained, and the hierarchical structure consists of three node types: leaf nodes, connection nodes, and symmetry nodes (such as rotation, translation, and mirror symmetry). To recursively classify and decode the nodes, we employed the structural reconstruction recursive neural network, which utilized a node classifier and different node decoders based on their category. This process continued until no further decoding could be performed, which occurred when reaching the leaf nodes of the tree structure. These leaf nodes correspond to the parameters of the directed bounding boxes for each component.

The decoder employs a Recursive Neural Network (RvNN) to decode features extracted from RGB images. As shown in Figure 3, this process continues recursively until all leaf nodes are reached, which can then be further decoded into directed bounding box parameters. During decoding, the relationships between parts in internal nodes are decoded into two types: connection relationships and symmetry relationships. Consequently, each node is decoded using one of the following three decoders based on its type:

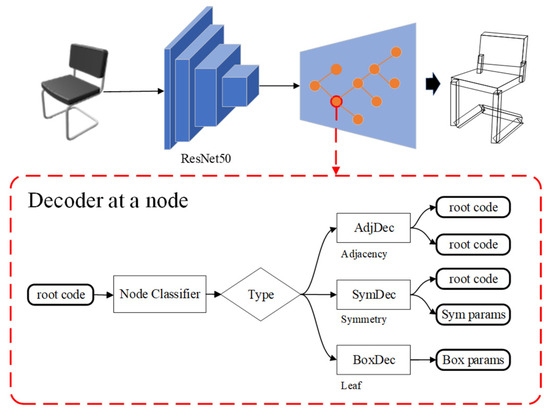
Figure 3. The network architecture for structure reconstruction.

(1) Connection Relationship Decoder (Decoder AdjDec): Segments the parent node $V_{parent}$ (Initially, the parent node $V_{parent}=V_r$) into two child nodes, $V_{child1}$ and $V_{child2}$, using a mapping function:

$$[V_{child1} V_{child2}]=\tanh (W_{ad}·V_{parent}+b_{ad})$$

(1)

here, $W_{ad}\in {ℝ}^{2n\times n}$, $b_{ad}\in {ℝ}^{2n}$, n = 80 represents the dimensions of non-leaf nodes. The child nodes $V_{child1}$ and $V_{child2}$ obtained after decoding are respectively used as new root nodes $V_r$. A new decoder type is performed and recursively selected for decoding.

(2) Symmetry Relationship Decoder (Decoder SymDec): This decoder decodes the symmetry group (including rotation, translation, and mirror symmetry) into a symmetry generator (a node vector $V_{child}$) and a symmetry parameter vector s:

$$[V_{child} s]=\tanh (W_{sd}·V_{parent}+b_{sd})$$

(2)

here, $W_{sd}\in {ℝ}^{(n+m)\times n}$, $b_{sd}\in {ℝ}^{m+n}$, m = 8 represents the symmetry parameters, including the symmetry type (1D); the number of repetitions during rotation or translation (1D) and the symmetry plane, rotation axis, or position and displacement for translation used for mirror symmetry (6D). After decoding, $V_{child}$ is obtained and used as a new $V_{parent}$. Then, a new decoder type is recursively selected for decoding.

(3) Directed Bounding Box Decoder (Decoder BoxDec): This decoder maps a leaf node to a 12D directed bounding box parameterization $x$, which includes the center coordinates, coordinate axes, and dimensions of the bounding box:

$$[x]=\tanh (W_{lb}·V_{parent}+b_{lb})$$

(3)

here, $W_{lb}\in {ℝ}^{12\times n}$, $b_{lb}\in {ℝ}^{12}$.

3.3. SDF Prediction with Structural Features

For a 3D space point $p\left(x, y, z\right)$, our approach is to predict the SDF value of that point. The SDF prediction module consists of two processes: global SDF prediction based on global and structural features, and local SDF prediction based on local features. Prediction of SDF based on global features provides coarse SDF, represented as SDF_global. Prediction of SDF based on local features provides fine SDF, represented as SDF_local.

After the training of the structure encoding-decoding network is completed, the root vector $V_r$ is obtained as the input for the SDF_global prediction phase. Therefore, the entire SDF prediction network is as follows:

$$F_{SDF}=f_{global}(G,V_r,p)+f_{local}(L_p,p)$$

among them, $[G,L_{depth}]=f_{en}(x)$ and $V_r=f_{struct}(G)$. $f_{global}$ and $f_{local}$ respectively represent global SDF and local SDF, $L_p=(p|L_{depth})$ represents the input point. $L_p=(p|L_{depth})$ represents the local feature of point $p$, which is mapped to the corresponding point on the feature depth map $L_{depth}$ through camera parameters.

Prediction of SDF_global value: As shown in Figure 2, the input image is initially fed into a ResNet-50 to extract global features. These features are then fused with hierarchical structure features represented by a fixed-length hidden vector obtained in Section 3.2, thereby enhancing the hierarchical structure features in the global features. During feature fusion, we use the Deep SDF method proposed by Park et al. [5]., which is a direct neural network regression method for SDF. It concatenates the position of any point $p\left(x, y, z\right)$ in 3D space with the shape embedding extracted from depth images or point clouds and then uses an auto-decoder to obtain the corresponding SDF value. The auto-decoder’s structure is optimized for each object by optimizing the shape embedding. In our preliminary experiments, a multilayer perceptron is utilized to map the given point $p\left(x, y, z\right)$ to a higher-dimensional feature space. Subsequently, the resulting high-dimensional features are concatenated with the global features and the hidden vector containing structural features, respectively, for regression of the SDF_global value.

Prediction of SDF_local values: As illustrated in Figure 4, ResNet50 is employed as the encoder for the module responsible for global and local feature extraction. Starting with a 3D point $p\left(x, y, z\right)\in {ℝ}^3$, we project it onto a 2D image to obtain a corresponding point $q\left(u, v\right)\in {ℝ}^2$ using the camera parameters. Subsequently, we locate the corresponding position of $q\left(u, v\right)$ in the four feature submaps of ResNet50, which possess dimensions of 256, 512, 1024, and 2048, respectively. By concatenating these feature maps, we create a local feature vector with a dimension of 3840. Since the feature maps of the later layers are smaller than the original image, we employ bilinear interpolation to adjust them to the original size and extract the adjusted feature at position $q\left(u, v\right)$.

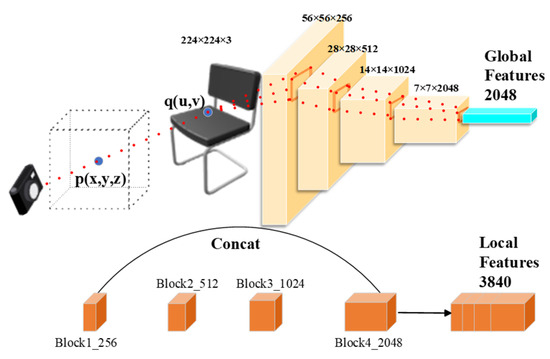
Figure 4. The architecture of the SDF Prediction Network.

The final signed distance field (SDF) value is determined by combining the predicted values of SDF_global and SDF_local. A comparison between the results achieved with and without the utilization of the local feature extraction technique is presented in Figure 5. While a network that solely relies on global features can successfully predict the overall shape, it lacks the ability to generate intricate details. By incorporating the local feature extraction, the missing details can be recovered through the prediction of residual SDF.

Figure 5. The results of shape reconstruction. (a) Input image; (b) Reconstruction result without local features; (c) Reconstruction result with local features.

3.4. Loss Function

In this study, there are two independent networks: one for obtaining structural encoding and the other for SDF prediction. Specifically, the hierarchical structure reconstruction network acquires the hierarchical structure encoding of 3D shapes independently without providing feedback to the SDF prediction network during training. These two networks undergo independent training processes with distinct loss functions.

During the reconstruction of the hierarchical structure from 2D images, we introduce three types of losses to constrain the reconstruction process. Our loss function consists of three components: (i) mean squared error (MSE) between reconstructed directed bounding boxes, (ii) MSE between symmetry information in the hierarchical structure, and (iii) cross-entropy loss (MAE) for node classification. The loss function is defined as follows:

$$Loss=\frac{1}{n_b}{\displaystyle \sum _{i=1}^{n_b}{(\widehat{B}o{x}_i-Bo{x}_i)}^2}+\frac{1}{n_s}{\displaystyle \sum _{i=1}^{n_s}{(\widehat{S}y{m}_i-Sy{m}_i)}^2}+\frac{1}{n_c}{\displaystyle \sum _{i=1}^{n_c}(\widehat{C}a{t}_i)·\log (\widehat{C}a{t}_i)}$$

(4)

here, $n_b$, $n_s$, and $n_c$ represent the number of bounding boxes, symmetric nodes, and total nodes in the hierarchical structure of each 3D model, respectively. Meanwhile, $\widehat{B}o{x}_i$, $\widehat{S}y{m}_i$, and $\widehat{C}a{t}_i$ are used to represent the predicted positions of the bounding boxes, symmetric parameters, and node classifications, respectively.

Our approach involves the regression of continuous SDF values instead of establishing a binary classification problem like IMNET (e.g., determining if a point is inside or outside of the shape). A weighted loss function is utilized to ensure that the network prioritizes the recovery of details near the isosurface $S_0$ and inside the shape. The loss function can be defined as follows:

$$L_{SDF}={\displaystyle \sum _{p}m\left|f(I,p)-SD{F}^I(p)\right|, m=\left\{\begin{array}{l}{m}_1, SD{F}^I(p)<\sigma \\ m_2, other\end{array}\right.}$$

(5)

here, $f(I,p)$ represents the input to the network with image $I$ and 3D point $p\left(x, y, z\right)$, while $SD{F}^I\left(p\right)$ denotes the ground truth SDF value, $m_1$ and $m_2$ are different weights for a given threshold $\sigma$.

3.5. Surface Reconstruction

To generate implicit planes, we first define a dense three-dimensional grid with a resolution of 256 × 256 × 256. The point cloud samples are placed within this grid, and the SDF value is predicted for each point in the grid. Once we have obtained the SDF values for every point in the dense grid, we utilize the Marching Cubes algorithm [13] to produce corresponding planes on the iso-surface, where the SDF value is zero.

4. Results

All training processes were conducted using the ShapeNet Core dataset [44]. The hierarchical structure data were obtained from the PartNet dataset, which is based on ShapeNet Core. We select three representative categories (chair, table and airplane) to show the comparison results. Among them, the chair category has a complex topology, and the 3D model often has holes, so we chose the chair to visualize the effect of comparison with other methods Our method achieved complete structures and details, outperforming state-of-the-art methods in both evaluation metrics and actual observations.

4.1. Experimental Datasets

(1)

PartNet [9] (Hierarchical Reconstruction Network Dataset):

For the hierarchical reconstruction network, we utilized the dataset proposed by PartNet. This dataset enhances the data by incorporating a recursively hierarchical organization of fine-grained parts for each shape. It comprises 22,369 3D shapes spanning 24 shape categories. Each shape consists of seven folders, providing specific information in PartNet. In this paper, we primarily focused on the “obbs” folder, which contains comprehensive shape-oriented bounding box (obb) data for each model. This includes original part obbs, adjacent part relationships, and symmetry parameters. By processing this data, we obtained corresponding hierarchical structure feature vectors.

(2)

ShapeNet [44] (SDF Prediction Network Dataset):

To generate our training dataset for the SDF prediction network, we employed the R²N² approach [1]. This involved capturing 3D data and generating 2D rendering images using Blender 2.79 software. We utilized 24 random camera viewpoints, aligning with the viewing angle of human eyes. The rendered images had a size of 137 × 137, and we saved the camera parameters during the rendering process. Although our method is capable of regressing SDF values for inputs at any position, thus allowing for reconstruction results of any resolution, we focused solely on the sampling points located on the object surface during the training process. For this purpose, we obtained SDF data and labels by Gaussian sampling 32,768 points near the object surface. Throughout the training process, we employed a weighted sampling strategy to randomly select 2048 points for loss calculation and weight updating. We selected 13 common categories from the ShapeNetCore dataset as our data source. After filtering out erroneous models, we obtained a total of 36,303 3D models, with 28,909 models used for training our method and 7394 models used for model testing. The quantities of different categories in the dataset can be found on the ShapeNet dataset website.

4.2. Implementation Details

This paper conducted experiments using a GPU for acceleration, with the following configuration: Ubuntu 18.06 64-bit operating system, Intel(R) i9-10900K @ 3.70GHz, NVIDIA RTX 3090Ti 24GB, CUDA 11.6, CUDNN 10.2, and Tensorflow 1.15 as the deep learning framework. The training process of the single-view 3D reconstruction network in this paper is divided into two stages: training of the hierarchical structure reconstruction network and training of the SDF prediction network with Structural Features. With our hardware and software environment, it takes about 70 h to complete the training of our network.

(1) Training of the Hierarchical Structure Reconstruction Network: In this stage, hierarchical structure features are extracted from image features, requiring separate training. The image features are extracted using the ResNet-50 feature extraction network and then encoded into root node features using a multilayer perceptron (MLP). The root node features are used to reconstruct the structure through a Recursive Neural Network (RvNN), which classifies each node to determine its type. For leaf nodes, directed bounding box values are regressed; for symmetric nodes, symmetric parameters are regressed, and two child nodes are generated for connecting nodes. During the decoding process, the node classification network is recursively called to determine the appropriate decoder for each node until the corresponding directed bounding box leaf node can be decoded, resulting in the reconstruction of the entire hierarchical structure. Throughout the iterative optimization process of structure reconstruction, the root node gradually extracts hierarchical structural information from image features for subsequent mesh reconstruction. Stochastic Gradient Descent (SGD) is employed to optimize the structure reconstruction network and train the RvNN decoder using Backpropagation Through Time (BPTT).

(2) Training of the SDF Prediction Network: In this stage, the parameters for extracting root node hierarchical structure features from image features are fixed to ensure stability. The resulting root node hierarchical structure features are then concatenated with the original image features and used to reconstruct a rough mesh structure of the object. The feature maps of each ResNet-50 network block are upsampled to match the size of the original image, and the camera parameters are utilized to determine the position of each sampled point on the feature map, resulting in 1 × 1 local features with channel sizes of 256, 512, 1024, and 2048, respectively. After concatenating the local features, a 1 × 1 Convolutional layer is used to reduce the dimensionality to 1024. The camera parameters can be predicted from the input image. To better demonstrate the effectiveness of the SDF prediction network in fusing structural features, the network is trained using ground truth camera parameters. The position information of the sampled points $p\left(x, y, z\right)$ is mapped to a high-dimensional feature space of dimension 512 using an MLP and then concatenated with the global and local features. The global shape and local detailed shape are decoded by two different MLP networks, and the final predicted SDF value is obtained by combining the decoded results. The hyperparameters of the loss function are set to m₁ = 1, m₂ = 4, and δ = 0.1. The Adam optimizer is used to update the weights during training, with a learning rate of 1 × 10⁻⁴ and a batch size of 48.

During the testing phase, the first step involves determining the camera parameters based on a given 2D image. This paper utilizes ground truth camera parameters in experiments and pre-sets 256³ uniformly dense sampling points in space to output SDF values in standard space. Through the transformation of spatial positions using the image and camera parameters, hierarchical structure features, global features, and local features are obtained. The hierarchical structure features and global features are concatenated to reconstruct the rough shape of the object, while the local features are used to reconstruct the detailed shape of the object. The final predicted SDF value is obtained by summing the reconstructed global SDF and local SDF. Finally, the Marching Cubes algorithm [13] is employed to extract the zero-value surface and reconstruct the mesh shape.

4.3. Evaluation Metrics

(1) Earth Mover’s Distance (EMD) is a distance metric utilized in this paper to assess the similarity between two distributions: the predicted point cloud (S₁) and the ground truth point cloud (S₂). It can comprehensively evaluate the quality of the reconstructed model. EMD is defined as follows:

$$EMD(S_1,S_2)=\underset{\phi :S_1\to S_2}{\min }{\displaystyle \sum _{x\in S_1}{‖x-\phi (x)‖}_2}.$$

(6)

(2) Chamfer Distance (CD) is a metric for calculating the average shortest point-to-point distance between a generated point cloud and a ground truth point cloud. It can effectively evaluate the detail difference between the reconstructed model and the ground truth model. In this paper, the symmetric CD is computed, where the first term minimizes the distance between the generated point clouds (S₁) and ground truth point clouds (S₂), and the second term ensures that the generated point cloud covers the ground truth points. Smaller values of both CD and EMD signify better performance. Hence, CD is defined as:

$$CD(S_1,S_2)=\frac{1}{\left|S_1\right|}{\displaystyle \sum _{x\in S_1}\underset{y\in S_2}{\min }{‖x-y‖}_2^2+}\frac{1}{\left|S_2\right|}{\displaystyle \sum _{y\in S_2}\underset{x\in S_1}{\min }{‖y-x‖}_2^2.}$$

(7)

(3) The Intersection over Union (IoU) evaluation metric, originally used in 2D image recognition tasks, is extended to represent the voxel overlap ratio in 3D space. It provides an intuitive quantification of the overlap between the reconstructed result and the ground truth model, enabling the evaluation of reconstruction accuracy. The IoU is calculated using the following formula:

$$IoU=\frac{{\displaystyle \sum _{i,j,k}[V(p(i,j,k)>t)V(y(i,j,k))]}}{{\displaystyle \sum _{i,j,k}[V(V(p(i,j,k)>t))+V(y(i,j,k))]}}.$$

(8)

here, the final output of any voxel $p\left(i, j, k\right)$ complies with the Bernoulli distribution $\left[1-p\left(i, j, k\right), p\left(i, j, k\right)\right]$, where $y\left(i,j,k\right)$ is the ground truth of the voxel represented by 0 and 1, $V(\cdot )$ is the indicator function, and $t$ is the threshold for voxelization. In the case of IoU, a higher value signifies better reconstruction quality achieved by the model.

(4) The F-Score is the harmonic mean of precision and recall, which is suitable for comprehensively evaluating the quality of reconstruction results, especially for tasks that need to balance accuracy and completeness. Therefore, F-Score is defined as:

$$F-Score(d)=\frac{2P(d)R(d)}{P(d)+d}.$$

(9)

here, $P$ represents precision, $R$ signifies recall, and $d$ denotes the given threshold.

4.4. Experimental Results and Comparative Analysis

The experiments conducted on the structural reconstruction network primarily focus on evaluating training effectiveness from a subjective standpoint. Specifically, we assess whether the hierarchical structure corresponding to a single view conforms to human visual expectations, thereby achieving optimal training outcomes. The results of our analysis are presented in Figure 6.

Figure 6. Results of Structure Reconstruction.

In this paper, we compare our method with popular methods for single-view 3D reconstruction, including AtlasNet [21], Pixel2mesh [19], IMNET [45], 3DN [46], Occ-Net [8], DISN [29], D²IM-NET [47], Ladybird [48], and 3PSDF [49]. AtlasNet, Pixel2mesh, and 3DN generate reconstructed surfaces. AtlasNet and Pixel2Mesh create fixed-topology meshes from 2D images, while 3DN deforms a template mesh to reconstruct the model. IMNET, OccNet, DISN, Ladybird, D2IM-NET, 3PSDF, and our method generate implicit surfaces. IMNET and OccNet reconstruct surfaces by predicting whether a point is inside or outside the object, i.e., determining the sign of the SDF. On the other hand, DISN, Ladybird, D2IM-NET, 3PSDF, and our method reconstruct the surface by predicting the SDF value of the point. We evaluate our model using CD distance, EMD distance, IoU, and F-Score on the ShapeNet Chair dataset. However, for OccNet, we only compare the IoU due to scale inconsistency with our method. To calculate the corresponding evaluation metrics, we transform the generated meshes into point clouds and voxel data. As demonstrated in the results presented in Table 1 and Table 2, our method outperforms previous methods in all evaluation metrics.

Table 1. Quantitative results on ShapeNet core for various methods. Metrics are CD (×0.001, The smaller, the better ↓), EMD (×100, The smaller, the better ↓) and IoU (%, The larger the better ↑). CD and EMD are computed on 2048 points. (The best results are shown in bold.)

		Atlas Net	Pixel2Mesh	3DN	IMNET	OccNet	DISN	D2IM-NET	Ladybird	3PSDF	Ours
EMD ↓	chair	3. 86	3.52	4.45	3.01	2.70	2.62	-	2.60	-	2.50
	table	3.98	3.52	3.94	3.39	2.35	3.07	-	2.82	-	2.63
	airplane	3.39	2.98	3.30	2.90	2.75	2.45	-	2.48	-	2.37
CD ↓	chair	13.21	11.13	17.53	11.27	7.67	7.54	7.99	7.08	12.29	6.14
	table	18.08	15.61	14.05	17.82	10.57	13.29	11.31	9.97	16.54	8.27
	airplane	5.98	6.10	6.75	12.65	7.70	9.01	7.95	5.85	9.48	7.82
IoU ↑	chair	25.7	40.2	34.4	52.2	50.2	54.9	53.04	55.3	-	56.43
	table	23.3	31.2	31.3	45.0	70.9	47.9	54.75	48.6	-	54.89
	airplane	39.2	51.5	54.3	55.4	54.7	61.7	55.53	60.0	-	63.21

Table 2. F-Score for varying threshold (% of reconstruction volume side length).

Threshold Value	0.50%	1%	2%	5%	10%	20%
3DCNN	0.064	0.295	0.691	0.935	0.984	0.997
IMNet	0.063	0.286	0.673	0.922	0.977	0.995
DISN	0.079	0.327	0.718	0.943	0.984	0.996
3PSDF	0.002	0.010	0.026	0.074	0.216	0.669
D2IM-NET	0.001	0.004	0.010	0.044	0.187	0.647
Ours	0.067	0.324	0.754	0.965	0.996	0.99996

Based on the comparison results, our method extracts global hierarchical structure information from the image and reconstructs the complete structure, even in areas that are not visible from the viewing angle. Our method reconstructs the parts more comprehensively, adhering to the constraints of hierarchical structure features, thereby avoiding any missing or discontinuous phenomena in slender and small-volume areas. By comparing the results shown in Figure 7, our method not only accurately reconstructs the overall shape of the chair but also avoids overfitting in detail-rich areas such as holes and effectively restores detailed information. The ground truth (GT) models depicted in Figure 7 are obtained from the 3D models in the ShapeNet dataset, which correspond to the rendered images. In order to ensure numerical consistency during the generation of the signed distance function (SDF) labels, we carried out a uniform alignment and scaling of the dataset’s data. The GT models shown in Figure 7 are the result of these preprocessing steps. In comparison to the GT model, our method can reconstruct the complete structure of the target with a high level of fidelity. However, it still exhibits certain limitations in cases where the chair exhibits uncommon topological structures (e.g., the fourth chair in Figure 7) or intricate texture details (e.g., the seventh chair in Figure 7). Despite these limitations, our model has demonstrated a remarkable improvement in terms of structural integrity and overall performance, approaching the quality of the GT model.

Figure 7. Single-view reconstruction results of various methods, where “GT” denotes ground truth shapes.

4.5. Ablation Study

Ablation experiments were conducted to assess the impact of each module on the final reconstruction results, aiming to evaluate the contribution of individual components. The following ablation experiments were designed:

• Exp1(ISHS-Net): ResNet50 was used as the feature extraction network. Hierarchical structural features were combined with global features, and global and local SDF values were predicted through two branches before being added together.
• Exp2: Only global and local features were fused without extracting hierarchical structural features.
• Exp3: VGG16 replaced the feature extraction network in the ISHS-Net model.
• Exp4: Hierarchical structural features and global image features were fused without considering the local feature branch.
• Exp5: The hierarchical structure features were concatenated with global and local features, respectively, and then the global features with hierarchical structure features and the local features with hierarchical structure features were fused together.

Qualitative and quantitative comparison results are presented in Table 3 and Table 4, as well as Figure 8. The CD distance, EMD distance, and F-Score demonstrate that our method produces reconstructed 3D models with greater similarity to the real models in spatial comparison. The fusion of hierarchical structural features and global image features achieves superior results in terms of IoU. The absence of hierarchical structure feature fusion results in reconstructed details with discontinuities, missing parts, and incompleteness, compromising the integrity of the structure. ResNet, with its residual structures, is more effective in integrating deep and shallow structure information, resulting in better reconstruction effects on details compared to VGG. The omission of local features prevents the model from capturing the chair’s intricate details. The integration of hierarchical structural information with global features is crucial as it primarily focuses on approximating the object’s overall structure. However, when combined with local features, it may interfere with the extraction of detailed local information, potentially affecting the final reconstruction quality.

Table 3. The influence of each module on the CD, EMD, IoU.

	Exp1 (ISHS-Net)	Exp2	Exp3	Exp4	Exp5
EMD ↓	6.14	7.92	6.84	11.05	6.76
CD ↓	2.50	2.65	2.83	3.27	2.68
IoU ↑	0.56	0.52	0.57	0.46	0.55

Table 4. The influence of each module on the F-Score.

Threshold value	0.5%	1%	2%	5%	10%	20%
Exp1 (ISHS-Net)	0.067	0.324	0.754	0.965	0.996	0.99996
Exp2	0.059	0.297	0.717	0.954	0.993	0.99976
Exp3	0.066	0.317	0.750	0.960	0.994	0.99986
Exp4	0.040	0.218	0.619	0.921	0.988	0.99990
Exp5	0.063	0.307	0.740	0.960	0.995	0.99991

Figure 8. Qualitative results of our method using different settings. The label ‘GT’ denotes the ground truth shapes.

5. Discussion, Limitation and Future Work

In this section, we analyze the key factors that affect the ISHS-Net’s performance and need to be considered in practical applications.

This paper proposes a network that integrates hierarchical structural features and SDF implicit surfaces for reconstructing 3D shapes from single views. The key innovation lies in modeling both the overall structural information and detailed surface features of 3D shapes to enhance reconstruction quality. Specifically, the main contributions are:

(1)

We extract and represent hierarchical structural information from global image features through an encoder-decoder model. The encoder encodes object structure as a latent vector, and the decoder decodes it to obtain the compositional tree structure.

(2)

We fuse the hierarchical structure features with other global image features to emphasize structural information. The fused features are decoded into rough SDF values that estimate distances from 3D sampling points to the surface.

(3)

We determine the projection and feature maps of 3D sampling points based on image viewpoint and use their local features to predict fine-grained SDF values that accurately capture surface details. The integration of rough and fine SDF predictions enables improved 3D reconstruction quality, especially for intricate shape details.

Compared to previous methods relying solely on either global shape features or local surface features, a key advantage of this paper is effectively utilizing both structural knowledge and geometric clues simultaneously for 3D shape modeling and reconstruction, aggregating complementary information from different aspects to significantly enhance the results. Extensive experiments on shape reconstruction benchmarks demonstrate the superiority of the proposed approach over current state-of-the-art techniques in terms of both qualitative visual quality and quantitative evaluation metrics.

Despite the substantial progress made, single-view 3D shape reconstruction remains a highly challenging task with several open problems. Some key limitations of the current method are:

(1)

The approach relies heavily on part-level hierarchical annotations of the shape dataset for training. This requires additional labor-intensive data preprocessing and limits the applicability of the method to datasets without such hierarchical labels. An important direction is exploring unsupervised or weakly-supervised methods to learn intrinsic compositional structures of 3D objects from single-view observations.

(2)

The reconstruction results still lack surface texturing, material properties, and color information. While the SDF representation focuses primarily on geometry, incorporating capabilities to predict texture maps or spatially-varying bidirectional reflectance distribution function (SVBRDF) parameters could significantly enhance the results to recover photo-realistic 3D shapes.

(3)

The training data consists of synthesized images with a clean background. However, real-world images often contain complex environments and occluding objects. Augmenting the training data diversity by compositing rendered shapes onto real image backgrounds could improve the generalization ability and robustness of the method.

(4)

The current pipeline requires pre-estimated camera parameters as input. An end-to-end integration with differentiable camera projection modules could make the entire reconstruction framework fully single-view.

Based on the above analysis, future work can build on the ideas proposed in this paper to further address the limitations, enhance the reconstruction quality and robustness, expand the applicability to less constrained scenarios, and move the field closer toward practical utility. Three-dimensional shape reconstruction from images has wide applications in robotics, autonomous driving, virtual reality, etc. With the rapid development of deep neural networks, learning-based single-view reconstruction methods have emerged as a promising direction and have gained increasing research attention recently. This paper provides useful insights that could inform further progress in this important field.