NO2 Concentration Estimation at Urban Ground Level by Integrating Sentinel 5P Data and ERA5 Using Machine Learning: The Milan (Italy) Case Study
Abstract
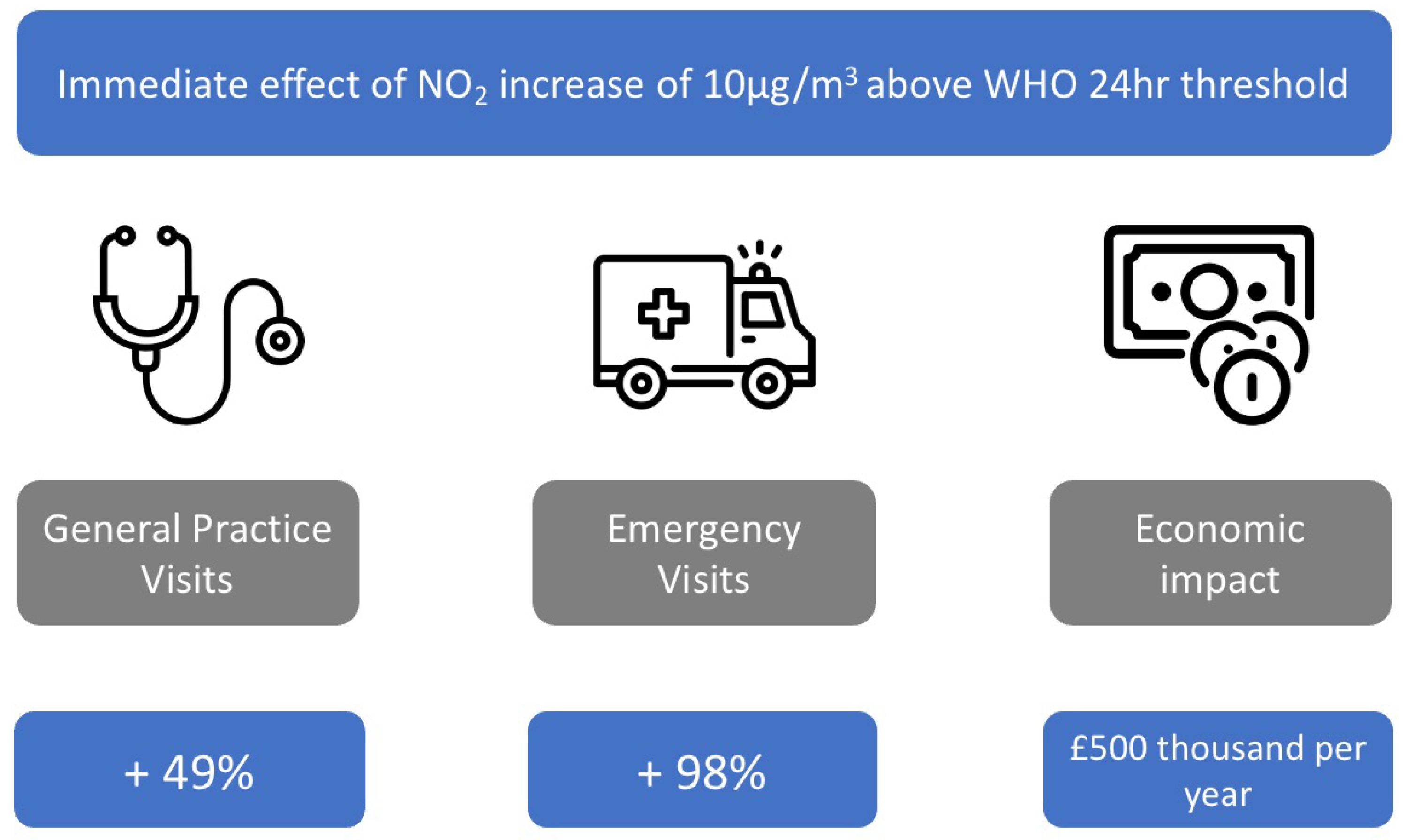
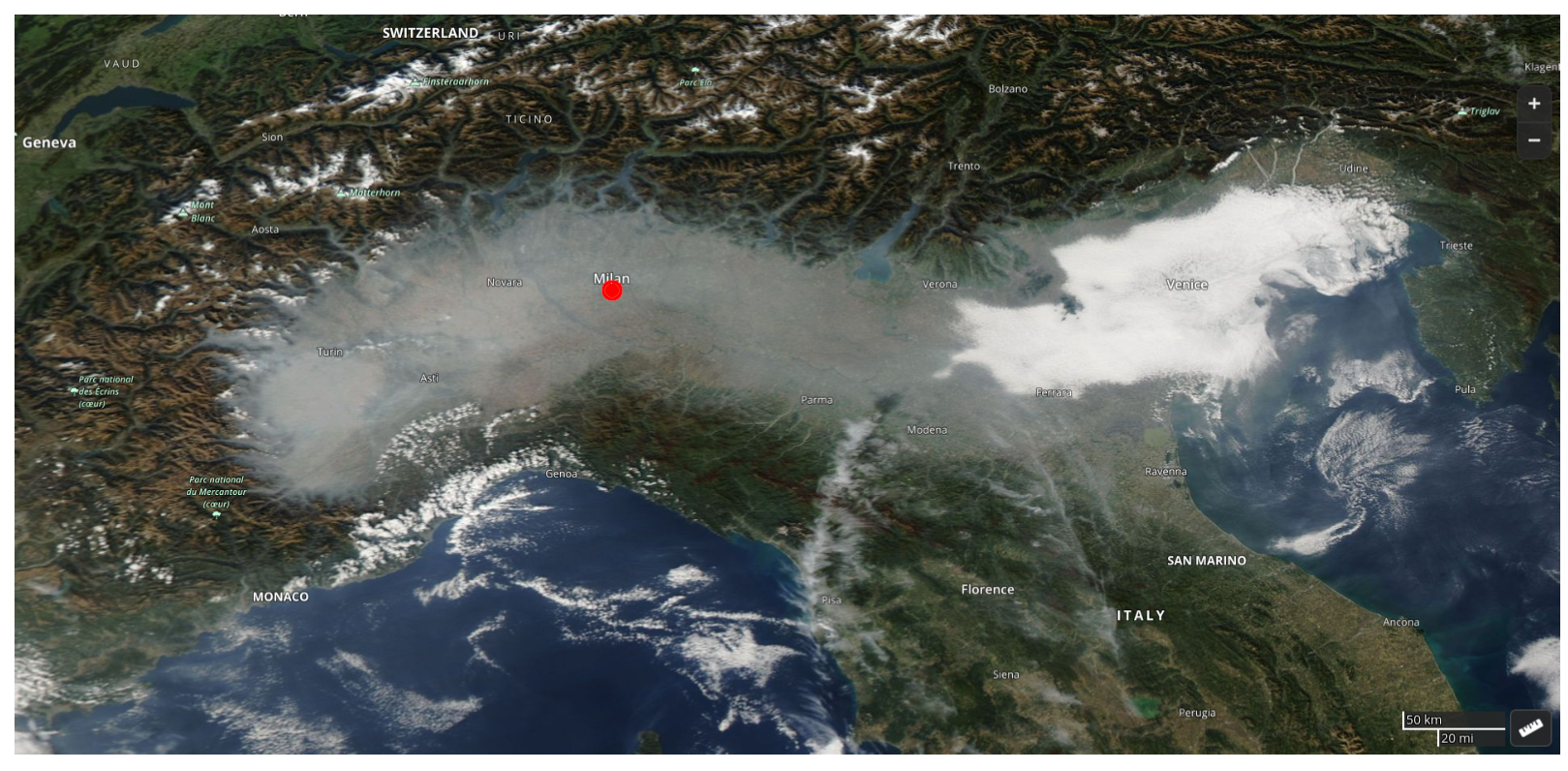
:1. Introduction
2. Materials and Methods
2.1. Data Description
2.1.1. Sentinel-5P Data
- The Copernicus Open Access Hub (https://scihub.copernicus.eu, accessed on 30 October 2023), which provides free access to Sentinel-5P data and other Copernicus data products.
- The S5P Data Portal (https://data-portal.s5p-pal.com, accessed on 30 October 2023), provides access to Sentinel-5P data and related information, such as product specifications and documentation.
- The ESA Earth Observation Data Services (https://www.copernicus.eu/en/access-data/dias, accessed on 30 October 2023), where the Data and Information Access Services (DIAS) provide access to a wide range of Earth observation data, as well as processing and analysis services.
- Ground-based validation: Sentinel-5P data was compared to data from ground-based stations that measure nitrogen dioxide column density. The ground-based stations use a variety of different measurement techniques, such as Dobson spectrophotometers and MAX-DOAS instruments.
- Aircraft validation: Sentinel-5P data was also compared to data from aircraft campaigns that measure nitrogen dioxide column density. The aircraft campaigns use a variety of different measurement techniques, such as in situ instruments and remote sensing instruments.
- Intercomparison with other satellites: Sentinel-5P data were also compared to data from other satellites that measure nitrogen dioxide column density, such as OMI and GOME-2.
- Internal consistency checks: The Sentinel-5P mission team checks the internal consistency of the Sentinel-5P data to identify any anomalies. For instance, the team verifies whether the data align with established physical correlations among various atmospheric components.
- Trend analysis: The Sentinel-5P mission team analyzes trends in the Sentinel-5P data to identify any systematic errors. For example, the team checks to see if the data are showing trends that are consistent with other known trends, such as the trend of decreasing nitrogen dioxide emissions in Europe.
- Intercomparison with models: The Sentinel-5P mission team compares their data to data from atmospheric models. The atmospheric models are based on our understanding of the physics of the atmosphere, and they can be used to predict the distribution of nitrogen dioxide and other atmospheric constituents.
2.1.2. ERA5 Data
2.1.3. ARPA Data
- Pre-deployment calibration: Before each sensor is deployed, it is calibrated in a laboratory using a known concentration of NO. This ensures that the sensor is measuring NO accurately.
- Field calibration: After each sensor is deployed, it is calibrated in the field using a portable NO calibrator. This ensures that the sensor is still measuring NO accurately in the field environment.
- Data quality checks: ARPA Lombardia performs regular data quality checks on the NO2 measurements. These checks include looking for outliers and inconsistencies in the data.
- Collocation studies: ARPA Lombardia conducts collocation studies by placing two or more sensors at the same location. The measurements from the different sensors are compared to ensure that they are consistent.
- Interlaboratory comparisons: ARPA Lombardia participates in interlaboratory comparisons to compare the measurements from its NO sensors to the measurements from other laboratories. These comparisons help to ensure that ARPA Lombardia’s NO sensors are measuring NO accurately compared to other sensors.
2.1.4. Additional Data
2.1.5. Processing and Training Pipeline
- Linear Regression:
- Spline linear regression;
- Krigging linear regression.
- Machine Learning:
- Random Forest (RF);
- Support Vector Regression (SVR);
- Decision Trees Regression (DTR);
- Gradient Tree Boosting (GTB);
- Multi-layer Perceptron Regressor (MLPR).
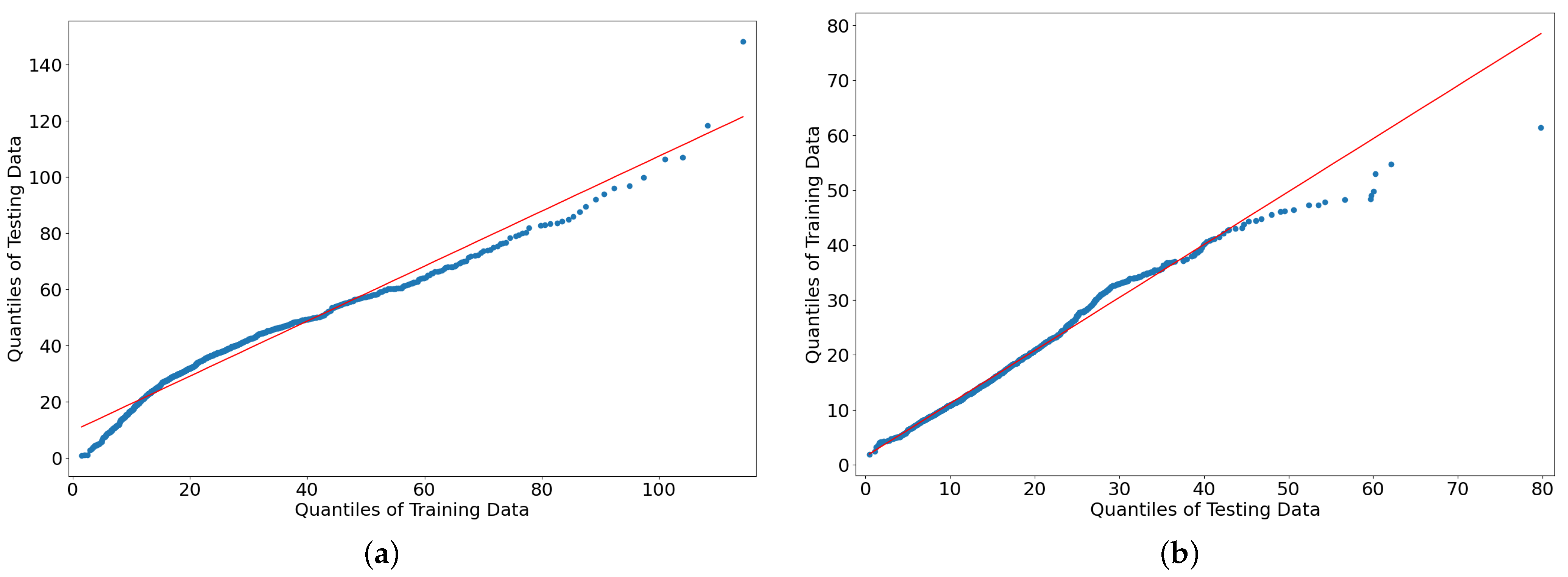
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AQG | Air Quality Guidelines |
| ARPA | Agenzia Regionale per la Protezione dell’Ambiente: |
| Regional Agency for Environmental Protection | |
| API | Application Programming Interface |
| C3S | Copernicus Climate Change Service |
| COVID-19 | Coronavirus Infectious Disease 2019 |
| DEM | Digital elevation model |
| DIAS | Data and Information Access Services |
| DIAS | Data and Information Access Services |
| DTR | Decision Trees Regression |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| EEA | European Environmnet Agency |
| ERA5 | European ReAnalysis 5 |
| ESA | European Space Agency |
| EU | European Union |
| GTB | Gradient Tree Boosting) |
| IFS | Integrated Forecasting System |
| JRA-55 | Japanese 55-year Reanalysis |
| LEO | Low Earth Orbit |
| LMICs | Low- Medium-Income Countries |
| MCM | Metropolitan City of Milan |
| ML | Machine Learning |
| MLPR | Multi-layer Perceptron Regressor |
| NASA | National Aeronautics and Space Administration |
| NGA | National Geospatial-Intelligence Agency |
| NLR | Netherlands Aerospace Centre |
| NO | Nitrogen dioxide |
| NRMSE | Normalised Root Mean Squared Error |
| NSO | Netherlands Space Office |
| OMI | Ozone Measurement Instrument |
| PRIN | Project of National Interest |
| RF | Random Forest |
| RMSE | Root Mean Squared Error |
| SDGs | Sustainable Development Goals |
| SRTM | Shuttle Radar Topography Mission |
| SVR | Support Vector Regression |
| TROPOMI | TROPOspherical Measurement Instrument |
| TVCD | Tropospheric Vertical Column Density |
| USGS | United States Geological Survey |
| UN | United Nations |
| UK | United Kingdom |
| UTC | Coordinated Universal Time |
| UV | Ultra Violet |
| WHO | World Health Organization |
Appendix A
| Model | Hyperparameters |
|---|---|
| SVR | C = 0.7 |
| Epsilon = 0.015 | |
| MLPR | Hidden layer sizes = 8000 |
| Learning rate = Constant | |
| Learning rate init = 0.001 | |
| Max iter = 1000 |
References
- Mebrahtu, T.F.; Santorelli, G.; Yang, T.C.; Wright, J.; Tate, J.; McEachan, R.R. The effects of exposure to NO2, PM2.5 and PM10 on health service attendances with respiratory illnesses: A time-series analysis. Environ. Pollut. 2023, 333, 122123. [Google Scholar] [CrossRef]
- Song, J.; Wang, Y.; Zhang, Q.; Qin, W.; Pan, R.; Yi, W.; Xu, Z.; Cheng, J.; Su, H. Premature mortality attributable to NO2 exposure in cities and the role of built environment: A global analysis. Sci. Total Environ. 2023, 866, 161395. [Google Scholar] [CrossRef]
- United Nations. The 17 Goals; SDGS; UN: New York, NY, USA, 2021. [Google Scholar]
- CAF. Sustainable Development Goals and Air Pollution. 2023. Available online: https://www.cleanairfund.org/news-item/sustainable-development-goals/ (accessed on 4 September 2023).
- European Commission. EU Air Quality Standards; European Union: Brussels, Belgium, 2023. [Google Scholar]
- CENELEC. CEN—CEN/TC 264. 2023. Available online: https://standards.cencenelec.eu/ (accessed on 15 September 2023).
- Pinder, R.W.; Klopp, J.M.; Kleiman, G.; Hagler, G.S.W.; Awe, Y.; Terry, S. Opportunities and challenges for filling the air quality data gap in low- and middle-income countries. Atmos. Environ. 2019, 215, 116794. [Google Scholar] [CrossRef]
- NASA. NASA Earth Science | Science Mission Directorate. 2023. Available online: https://science.nasa.gov/earth-science (accessed on 6 September 2023).
- De Vries, J.; Voors, R.; Ording, B.; Dingjan, J.; Veefkind, P.; Ludewig, A.; Kleipool, Q.; Hoogeveen, R.; Aben, I. TROPOMI on ESA’s Sentinel 5p Ready for Launch and Use. In Proceedings of the Fourth International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2016), Paphos, Cyprus, 4–8 April 2016; Volume 9688, p. 96880B. [Google Scholar]
- NASA. Earth Atmosphere. 2023. Available online: https://www.grc.nasa.gov/www/k-12/airplane/atmosphere.html# (accessed on 20 September 2023).
- NASA. Troposphere | NASA Space Place—NASA Science for Kids. 2023. Available online: https://spaceplace.nasa.gov/troposphere/en/ (accessed on 20 September 2023).
- Oxoli, D.; Cedeno Jimenez, J.R.; Brovelli, M.A. Assessment of Sentinel-5P Performance for Ground-Level Air Quality Monitoring: Preparatory Experiments over the COVID-19 Lockdown Period. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2020, XLIV-3/W1-2020, 111–116. [Google Scholar] [CrossRef]
- KNMI; SRON; DLR; European Union. TROPOMI—L2. 2021. Available online: http://www.tropomi.eu/data-products/level-2-products (accessed on 19 September 2023).
- Grzybowski, P.T.; Markowicz, K.M.; Musiał, J.P. Estimations of the Ground-Level NO2 Concentrations Based on the Sentinel-5P NO2 Tropospheric Column Number Density Product. Remote Sens. 2023, 15, 378. [Google Scholar] [CrossRef]
- Cedeno Jimenez, J.R.; Pugliese Viloria, A.D.J.; Brovelli, M.A. Estimating Daily NO2 Ground Level Concentrations Using Sentinel-5P and Ground Sensor Meteorological Measurements. ISPRS Int. J.-Geo-Inf. 2023, 12, 107. [Google Scholar] [CrossRef]
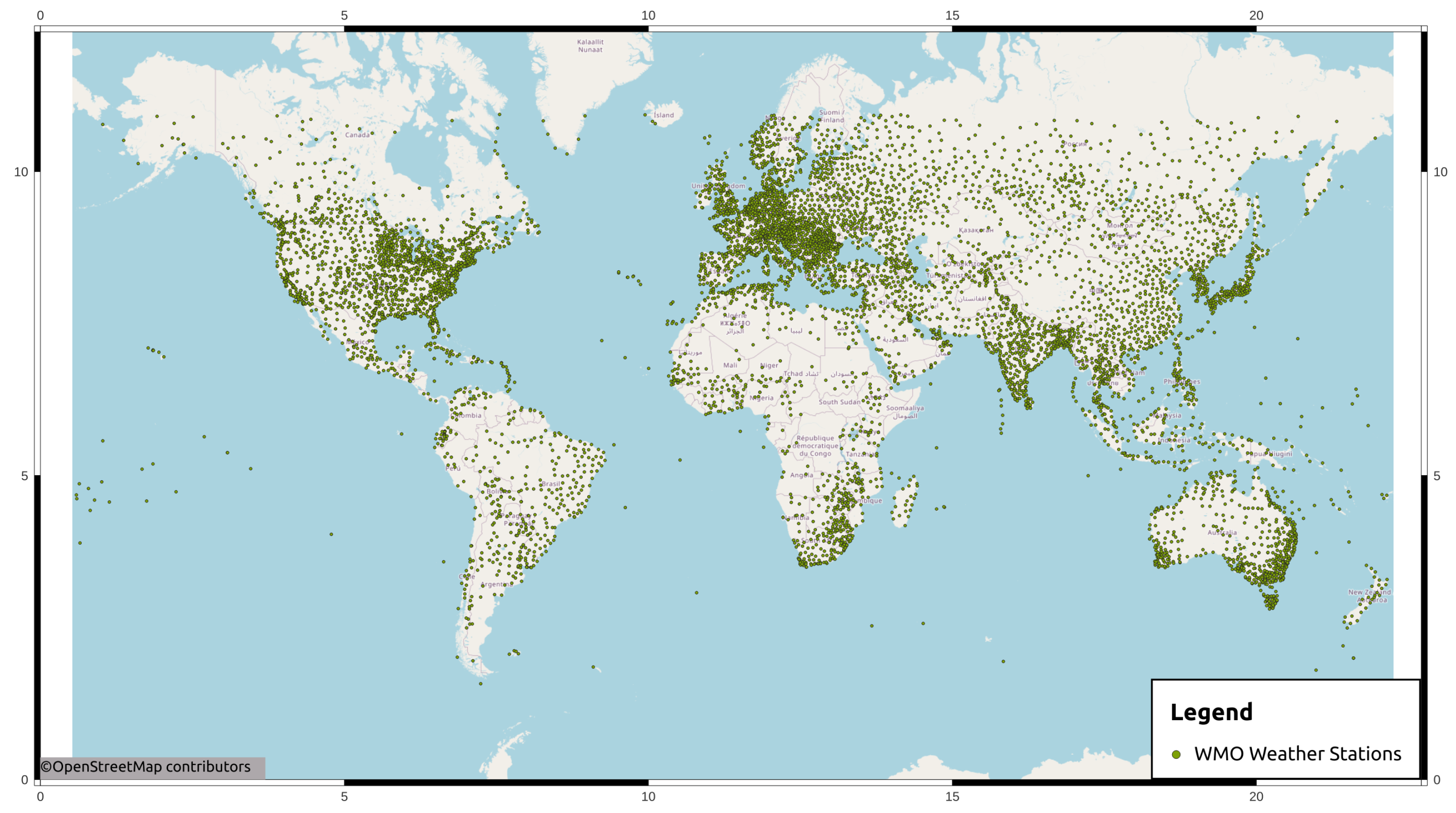
- WMO; Dixon, L. WMO Weather Stations—Overview. 2020. Available online: https://www.arcgis.com/home/item.html?id=c3cbaceff97544a1a4df93674818b012 (accessed on 24 October 2022).
- CMM. La Popolazione e il Territorio. 2023. Available online: https://www.cittametropolitana.mi.it/sviluppo_economico/saperne_di_piu/MIinCIFRE/Popolazioneeterritorio.html (accessed on 20 September 2023).
- JRC. FACT SHEET: Po River Basin. 2023. Available online: https://water.jrc.ec.europa.eu/pdf/po-fs.pdf (accessed on 20 September 2023).
- World Bank. World Bank Country and Lending Groups—World Bank Data Help Desk. 2023. Available online: https://datahelpdesk.worldbank.org/knowledgebase/articles/906519-world-bank-country-and-lending-groups (accessed on 19 September 2023).
- Farsiabi, M. Essays on Health Care Expenditures and Quality of the Environment; Wayne State University: Detroit, MI, USA, 2021. [Google Scholar]
- European Commission. Level-0 Processing and Products. 2021. Available online: https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-5p/products-algorithms/level-0 (accessed on 12 August 2023).
- Kramer, H.J. Copernicus: Sentinel-5P (Precursor—Atmospheric Monitoring Mission); Copernicus: Sentinel-5P—Satellite Missions— eoPortal Directory: Paris, France, 2022; Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/c-missions/copernicus-sentinel-5p (accessed on 20 September 2023).
- Langen, J.; Meijer, Y.; Veihelmann, B.; Ingman, P. Copernicus Sentinels 4 and 5 Mission Requirements Traceability Document. 2017. Available online: https://sentinels.copernicus.eu/documents/247904/2506504/Copernicus-Sentinels-4-and-5-Mission-Requirements-Traceability-Document.pdf/b15b6786-88cd-4f1d-a67e-a1da70ed595b?t=1531155774000 (accessed on 13 October 2023).
- ESA. Validation—Sentinel-5P Technical Guide—Sentinel Online. 2023. Available online: https://copernicus.eu/technical-guides/sentinel-5p/validation (accessed on 13 October 2023).
- Copernicus EU. Climate Reanalysis | Copernicus. 2023. Available online: https://climate.copernicus.eu/climate-reanalysis (accessed on 23 September 2023).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Setchell, H. ECMWF Reanalysis v5. 2020. Available online: https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5 (accessed on 23 September 2023).
- ARPA Lombardia. Rete di Monitoraggio della Qualità dell’Aria. 2023. Available online: https://www.arpalombardia.it/temi-ambientali/aria/rete-di-rilevamento/ (accessed on 24 September 2023).
- ARPA Lombardia. Rapporto Qualità dell’Aria in Lombardia. 2022. Available online: https://www.arpalombardia.it/agenda/notizie/2023/qualita-dell-aria-2022-in-lombardia-trend-costante-per-pm10-e-migliorano-i-livelli-no2/ (accessed on 24 September 2023).
- Pierce, A.M.; Loría-Salazar, S.M.; Holmes, H.A.; Gustin, M.S. Investigating horizontal and vertical pollution gradients in the atmosphere associated with an urban location in complex terrain, Reno, Nevada, USA. Atmos. Environ. 2019, 196, 103–117. [Google Scholar] [CrossRef]
- Wu, M.; Zhang, G.; Wang, L.; Liu, X.; Wu, Z. Influencing Factors on Airflow and Pollutant Dispersion around Buildings under the Combined Effect of Wind and Buoyancy—A Review. Int. J. Environ. Res. Public Health 2022, 19, 12895. [Google Scholar] [CrossRef]
- Sun, H.; Wang, J.; Sheng, L.; Jiang, Q. A Comparative Study on Four Methods of Boundary Layer Height Calculation in Autumn and Winter under Different PM2.5 Pollution Levels in Xi’an, China. Atmosphere 2023, 14, 728. [Google Scholar] [CrossRef]
- CMM. Territorio e Comuni. 2023. Available online: https://www.cittametropolitana.mi.it/portale/territorio/index.html (accessed on 3 November 2023).
- Volovici, V.; Syn, N.L.; Ercole, A.; Zhao, J.J.; Liu, N. Steps to avoid overuse and misuse of machine learning in clinical research | Nature Medicine. Nat. Med. 2022, 28, 1996–1999. [Google Scholar] [CrossRef]
- Shi, C.; Lu, W.; Song, R. Breaking the curse of nonregularity with subagging—Inference of the mean outcome under optimal treatment. J. Mach. Learn. Res. 2020, 21, 176:7122–176:7188. [Google Scholar]
- Van Der Heijden, M.; Miedema, D.M.; Waclaw, B.; Veenstra, V.L.; Lecca, M.C.; Nijman, L.E.; Van Dijk, E.; Van Neerven, S.M.; Lodestijn, S.C.; Lenos, K.J.; et al. Spatiotemporal regulation of clonogenicity in colorectal cancer xenografts. Proc. Natl. Acad. Sci. USA 2019, 116, 6140–6145. [Google Scholar] [CrossRef] [PubMed]
- Gholap, T.B.; Salokhe, R.V.; Ghadage, G.V.; Mane, S.V.; Bajaj, D.K.; Sahoo, D. Computational Aerodynamics of an AK-47 Rifle’s 7.82 mm Bullet in Proximity to a Near Wall. In Proceedings of the 2021 IEEE Pune Section International Conference (PuneCon), Pune, India, 16–19 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zeng, X.; Yi, P.; Hong, Y.; Xie, L. Continuous-Time Distributed Algorithms for Extended Monotropic Optimization Problems. arXiv 2016, arXiv:1608.01167. [Google Scholar] [CrossRef]
- Scikit-Learn Developers. Sklearn-Ensemble-StackingRegressor. 2023. Available online: https://scikit-learn/stable/modules/generated/sklearn.ensemble.StackingRegressor.html (accessed on 25 September 2023).
- Auzzi, R.; Giveon, A. Superpartner spectrum of minimal gaugino-gauge mediation. J. High Energy Phys. 2011, 2011, 3. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; Massachusetts Institute of Technology: London, UK, 2012. [Google Scholar]
- Li, M.; Wu, Y.; Bao, Y.; Liu, B.; Petropoulos, G.P. Near-Surface NO2 Concentration Estimation by Random Forest Modeling and Sentinel-5P and Ancillary Data. Remote Sens. 2022, 14, 3612. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Haque, M. Evidence on the Impact of Winter Heating Policy on Air Pollution and Its Dynamic Changes in North China. Sustainability 2019, 11, 2728. [Google Scholar] [CrossRef]
- Chi, Y.; Fan, M.; Zhao, C.; Yang, Y.; Fan, H.; Yang, X.; Yang, J.; Tao, J. Machine learning-based estimation of ground-level NO2 concentrations over China. Sci. Total Environ. 2022, 807, 150721. [Google Scholar] [CrossRef] [PubMed]
- Jeong, U.; Hong, H. Assessment of Tropospheric Concentrations of NO2 from the TROPOMI/Sentinel-5 Precursor for the Estimation of Long-Term Exposure to Surface NO2 over South Korea. Remote Sens. 2021, 13, 1877. [Google Scholar] [CrossRef]
- Griffin, D.; Zhao, X.; McLinden, C.A.; Boersma, F.; Bourassa, A.; Dammers, E.; Degenstein, D.; Eskes, H.; Fehr, L.; Fioletov, V.; et al. High-Resolution Mapping of Nitrogen Dioxide With TROPOMI: First Results and Validation Over the Canadian Oil Sands. Geophys. Res. Lett. 2019, 46, 1049–1060. [Google Scholar] [CrossRef] [PubMed]






| 2019 | 2020 | 2019 | 2020 | |
|---|---|---|---|---|
| mean | 0.72 | 0.76 | 0.74 | 0.79 |
| median | 0.75 | 0.79 | 0.78 | 0.83 |
| standard deviation | 0.11 | 0.15 | 0.12 | 0.14 |
| Meteorological Variable | Pearson Correlation () |
|---|---|
| Sentinel-5P NO | 0.83 |
| Current Values 1 | |
| Temperature | −0.68 |
| Surface solar radiation | −0.63 |
| Surface thermal radiation | 0.14 |
| Surface pressure | 0.31 |
| Total precipitation | −0.05 |
| Wind direction | −0.020 |
| Wind speed | 0.20 |
| Prior Values 2 | |
| Temperature | 0.70 |
| Surface solar radiation | −0.65 |
| Surface thermal radiation | 0.19 |
| Surface pressure | 0.31 |
| Total precipitation | −0.12 |
| Wind direction | 0.18 |
| Wind speed | −0.19 |
| Whole Period | Value (µg/m) | |
| Mean | 26.95 | |
| Median | 20.33 | |
| Minimum | 2.75 | |
| Maximum | 107.57 | |
| Standard Deviation | 18.45 | |
| Training Period | Chronological Splitting (µg/m) | Random Splitting (µg/m) |
| Mean | 28.38 | 25.09 |
| Median | 21.41 | 19.35 |
| Minimum | 2.75 | 0.10 |
| Maximum | 107.57 | 134.17 |
| Standard Deviation | 19.45 | 18.29 |
| Testing Period | Chronological Splitting (µg/m) | Random Splitting (µg/m) |
| Mean | 19.90 | 26.83 |
| Median | 17.12 | 19.87 |
| Minimum | 7.57 | 1.09 |
| Maximum | 58.54 | 114.24 |
| Standard Deviation | 9.06 | 20.30 |
| Regression Method | RMSE (Training Average MCM) | RMSE (Training Separate Sensors) |
|---|---|---|
| B-spline Linear Regression | 6.54 | 7.31 |
| Krigging Linear Regression | 5.73 | 8.00 |
| Random Forest | 6.28 | 8.22 |
| Decision Trees Regression | 8.45 | 13.42 |
| Support Vector Regression | 5.56 | 7.53 |
| Gradient Tree Boosting | 6.05 | 8.61 |
| Multi-layer Perceptron Regression | 6.04 | 7.38 |
| Voting (SVR + MLPR) | 6.02 | 8.12 |
| Stacking (SVR + MLPR) | 5.97 | 8.06 |
| RF feature selection + Voting (SVR + MLPR) | 5.53 | 7.24 |
| Chronological Extraction | Random Extraction | ||||
|---|---|---|---|---|---|
| Sensor ID | Measure | Current Model | Only Satellite | Current Model | Only Satellite |
| 5504 | NRMSE (%) | 81.46 | 82.52 | 59.90 | 69.41 |
| RMSE (µg/m) | 9.68 | 9.80 | 13.83 | 16.02 | |
| 5507 | NRMSE (%) | 64.38 | 61.55 | 46.00 | 61.00 |
| RMSE (µg/m) | 6.89 | 6.59 | 11.10 | 14.72 | |
| 5517 | NRMSE (%) | 92.56 | 114.15 | 50.52 | 64.44 |
| RMSE (µg/m) | 6.77 | 8.35 | 10.56 | 13.48 | |
| 5520 | NRMSE (%) | 288.44 | 285.14 | 75.02 | 73.49 |
| RMSE (µg/m) | 8.86 | 8.76 | 9.28 | 9.09 | |
| 5531 | NRMSE (%) | 77.84 | 93.04 | 52.42 | 61.11 |
| RMSE (µg/m) | 6.04 | 7.22 | 10.06 | 11.73 | |
| 5534 | NRMSE (%) | 92.63 | 86.52 | 52.51 | 53.43 |
| RMSE (µg/m) | 6.17 | 5.76 | 9.62 | 9.79 | |
| 5547 | NRMSE (%) | 68.46 | 73.37 | 45.92 | 61.01 |
| RMSE (µg/m) | 6.87 | 7.37 | 11.14 | 14.80 | |
| 5548 | NRMSE (%) | 235.02 | 204.44 | 63.68 | 62.82 |
| RMSE (µg/m) | 4.57 | 3.98 | 7.11 | 7.02 | |
| 5549 | NRMSE (%) | 86.40 | 95.93 | 50.97 | 62.41 |
| RMSE (µg/m) | 4.17 | 4.63 | 7.31 | 8.95 | |
| 5554 | NRMSE (%) | 196.28 | 194.27 | 46.36 | 63.46 |
| RMSE (µg/m) | 7.03 | 6.96 | 8.17 | 11.19 | |
| 5609 | NRMSE (%) | 95.03 | 94.21 | 57.35 | 67.02 |
| RMSE (µg/m) | 6.73 | 6.68 | 8.62 | 10.07 | |
| 9999 | NRMSE (%) | 125.59 | 127.32 | 79.31 | 84.08 |
| RMSE (µg/m) | 8.77 | 8.89 | 11.98 | 12.70 | |
| 10279 | NRMSE (%) | 76.15 | 72.91 | 47.01 | 55.65 |
| RMSE (µg/m) | 7.46 | 7.14 | 10.35 | 12.26 | |
| Sensor ID | SD Chronological Extraction | SD Random Extraction | Test Data Size (Days) |
|---|---|---|---|
| 5504 | 11.88 | 23.09 | 160 |
| 5507 | 10.71 | 24.13 | 161 |
| 5517 | 7.32 | 20.91 | 156 |
| 5520 | 3.07 | 12.37 | 67 |
| 5531 | 7.76 | 19.20 | 164 |
| 5534 | 6.66 | 18.32 | 161 |
| 5547 | 10.04 | 24.26 | 157 |
| 5548 | 1.94 | 11.17 | 69 |
| 5549 | 4.83 | 14.35 | 69 |
| 5554 | 3.58 | 17.63 | 70 |
| 5609 | 7.09 | 15.03 | 164 |
| 9999 | 6.98 | 15.11 | 147 |
| 10279 | 9.80 | 22.03 | 150 |
| Sensor ID | Pearson Correlation () | R |
|---|---|---|
| 5504 | 0.83 | 0.70 |
| 5507 | 0.90 | 0.81 |
| 5517 | 0.86 | 0.74 |
| 5520 | 0.89 | 0.80 |
| 5531 | 0.86 | 0.74 |
| 5534 | 0.91 | 0.83 |
| 5547 | 0.89 | 0.80 |
| 5548 | 0.85 | 0.73 |
| 5549 | 0.86 | 0.75 |
| 5554 | 0.89 | 0.80 |
| 5609 | 0.86 | 0.75 |
| 9999 | 0.74 | 0.55 |
| 10279 | 0.90 | 0.81 |
| Mean | 0.87 | 0.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cedeno Jimenez, J.R.; Brovelli, M.A. NO2 Concentration Estimation at Urban Ground Level by Integrating Sentinel 5P Data and ERA5 Using Machine Learning: The Milan (Italy) Case Study. Remote Sens. 2023, 15, 5400. https://doi.org/10.3390/rs15225400
Cedeno Jimenez JR, Brovelli MA. NO2 Concentration Estimation at Urban Ground Level by Integrating Sentinel 5P Data and ERA5 Using Machine Learning: The Milan (Italy) Case Study. Remote Sensing. 2023; 15(22):5400. https://doi.org/10.3390/rs15225400
Chicago/Turabian StyleCedeno Jimenez, Jesus Rodrigo, and Maria Antonia Brovelli. 2023. "NO2 Concentration Estimation at Urban Ground Level by Integrating Sentinel 5P Data and ERA5 Using Machine Learning: The Milan (Italy) Case Study" Remote Sensing 15, no. 22: 5400. https://doi.org/10.3390/rs15225400
APA StyleCedeno Jimenez, J. R., & Brovelli, M. A. (2023). NO2 Concentration Estimation at Urban Ground Level by Integrating Sentinel 5P Data and ERA5 Using Machine Learning: The Milan (Italy) Case Study. Remote Sensing, 15(22), 5400. https://doi.org/10.3390/rs15225400







