Applications of Deep Learning-Based Super-Resolution Networks for AMSR2 Arctic Sea Ice Images
Abstract
:1. Introduction
- (1)
- By analyzing the characteristics of passive microwave imagery and sea ice scenes, this study selects four state-of-the-art MISR networks, namely EDVR, PFNL, RBPN, and RRN. These networks are effectively applied to AMSR2 passive microwave imagery, resulting in a four-fold improvement in spatial resolution. It provides new ideas for improving the spatial resolution of passive microwave images, which enables a more accurate analysis of the Arctic sea ice.
- (2)
- The optimal length of the input image sequence of four MISR networks in different frequency bands is given. Additionally, the performances of each MISR network are evaluated at its respective optimal input sequence length for different frequency bands of passive microwave images. These findings offer valuable recommendations for selecting the appropriate MISR networks in different frequency bands of passive microwave imagery.
- (3)
- The quantification of the various impact factors on SR performance is also discussed in this paper. These impact factors include differences in sea ice concentration across different seasons, the influence of different magnitudes of sea ice motion, and the influence of different polarization modes of the images. By analyzing these factors, a deeper understanding of their effects on MISR performance is gained. This analysis provides insights into optimizing MISR algorithms for passive microwave sea ice imagery.
2. Materials
2.1. AMSR2 Images and Data Processing
2.2. Sea Ice Products
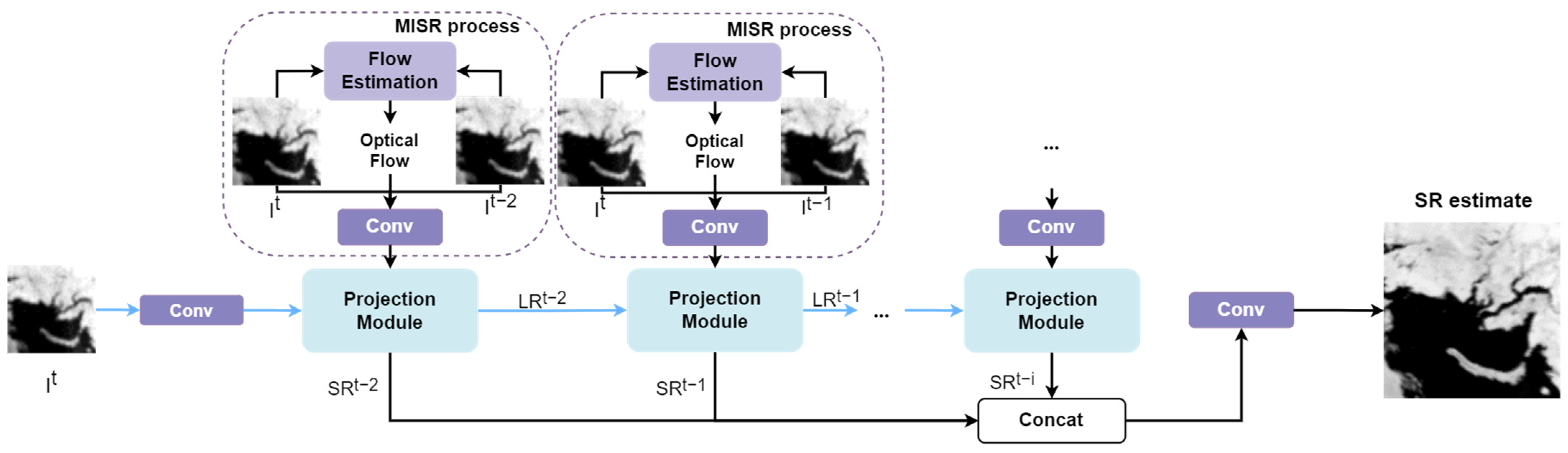
3. SR Networks
4. Results
4.1. Parameters Setting
4.2. Evaluation Criterion
4.3. SR Results
4.3.1. Optimal Image Sequence Length and Best Network for Images at Different Frequencies
4.3.2. Comparison of SR Results in Different Seasons
4.3.3. Comparison of SR Results with Different Ice Motion Velocity
4.3.4. Comparison of Different Polarization Modes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Comiso, J.C.; Parkinson, C.L.; Gersten, R.; Stock, L. Accelerated Decline in the Arctic Sea Ice Cover. Geophys. Res. Lett. 2008, 35, L01703. [Google Scholar] [CrossRef]
- Huntemann, M.; Heygster, G.; Kaleschke, L.; Krumpen, T.; Mäkynen, M.; Drusch, M. Empirical Sea Ice Thickness Retrieval during the Freeze-up Period from SMOS High Incident Angle Observations. Cryosphere 2014, 8, 439–451. [Google Scholar] [CrossRef]
- Haarpaintner, J.ö.; Spreen, G. Use of Enhanced-Resolution QuikSCAT/SeaWinds Data for Operational Ice Services and Climate Research: Sea Ice Edge, Type, Concentration, and Drift. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3131–3137. [Google Scholar] [CrossRef]
- Sommerkorn, M.; Hassol, S.J. Arctic Climate Feedbacks: Global Implications. In Arctic Climate Feedbacks: Global Implications; WWF International Arctic Programme: Washington, DC, USA, 2009. [Google Scholar]
- Bintanja, R.; van Oldenborgh, G.J.; Drijfhout, S.S.; Wouters, B.; Katsman, C.A. Important Role for Ocean Warming and Increased Ice-Shelf Melt in Antarctic Sea-Ice Expansion. Nat. Geosci. 2013, 6, 376–379. [Google Scholar] [CrossRef]
- Aagaard, K.; Carmack, E.C. The Role of Sea Ice and Other Fresh Water in the Arctic Circulation. J. Geophys. Res. Ocean. 1989, 94, 14485–14498. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Parkinson, C.L. Arctic Sea Ice Variability and Trends, 1979–2010. Cryosphere 2012, 6, 881–889. [Google Scholar] [CrossRef]
- Turner, J.; Bracegirdle, T.J.; Phillips, T.; Marshall, G.J.; Hosking, J.S. An Initial Assessment of Antarctic Sea Ice Extent in the CMIP5 Models. J. Clim. 2013, 26, 1473–1484. [Google Scholar] [CrossRef]
- Boé, J.; Hall, A.; Qu, X. September Sea-Ice Cover in the Arctic Ocean Projected to Vanish by 2100. Nat. Geosci. 2009, 2, 341–343. [Google Scholar] [CrossRef]
- Burek, K.A.; Gulland, F.M.; O’Hara, T.M. Effects of Climate Change on Arctic Marine Mammal Health. Ecol. Appl. 2008, 18, S126–S134. [Google Scholar] [CrossRef]
- Laidre, K.L.; Stirling, I.; Lowry, L.F.; Wiig, Ø.; Heide-Jørgensen, M.P.; Ferguson, S.H. Quantifying the Sensitivity of Arctic Marine Mammals to Climate-Induced Habitat Change. Ecol. Appl. 2008, 18, S97–S125. [Google Scholar] [CrossRef]
- Lee, S.-W.; Song, J.-M. Economic Possibilities of Shipping Though Northern Sea Route1. Asian J. Shipp. Logist. 2014, 30, 415–430. [Google Scholar] [CrossRef]
- Peeken, I.; Primpke, S.; Beyer, B.; Gütermann, J.; Katlein, C.; Krumpen, T.; Bergmann, M.; Hehemann, L.; Gerdts, G. Arctic Sea Ice Is an Important Temporal Sink and Means of Transport for Microplastic. Nat. Commun. 2018, 9, 1505. [Google Scholar] [CrossRef] [PubMed]
- Xian, Y.; Petrou, Z.I.; Tian, Y.; Meier, W.N. Super-Resolved Fine-Scale Sea Ice Motion Tracking. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5427–5439. [Google Scholar] [CrossRef]
- Liu, X.; Feng, T.; Shen, X.; Li, R. PMDRnet: A Progressive Multiscale Deformable Residual Network for Multi-Image Super-Resolution of AMSR2 Arctic Sea Ice Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4304118. [Google Scholar] [CrossRef]
- Duan, S.-B.; Han, X.-J.; Huang, C.; Li, Z.-L.; Wu, H.; Qian, Y.; Gao, M.; Leng, P. Land Surface Temperature Retrieval from Passive Microwave Satellite Observations: State-of-the-Art and Future Directions. Remote Sens. 2020, 12, 2573. [Google Scholar] [CrossRef]
- Lindsay, R.W.; Rothrock, D.A. Arctic Sea Ice Leads from Advanced Very High Resolution Radiometer Images. J. Geophys. Res. 1995, 100, 4533. [Google Scholar] [CrossRef]
- Spreen, G.; Kaleschke, L.; Heygster, G. Sea Ice Remote Sensing Using AMSR-E 89-GHz Channels. J. Geophys. Res. Ocean. 2008, 113, C02S03. [Google Scholar] [CrossRef]
- Wernecke, A.; Kaleschke, L. Lead Detection in Arctic Sea Ice from CryoSat-2: Quality Assessment, Lead Area Fraction and Width Distribution. Cryosphere 2015, 9, 1955–1968. [Google Scholar] [CrossRef]
- Zhang, F.; Pang, X.; Lei, R.; Zhai, M.; Zhao, X.; Cai, Q. Arctic Sea Ice Motion Change and Response to Atmospheric Forcing between 1979 and 2019. Int. J. Climatol. 2022, 42, 1854–1876. [Google Scholar] [CrossRef]
- Meier, W.N.; Markus, T.; Comiso, J.C. AMSR-E/AMSR2 Unified L3 Daily 12.5 Km Brightness Temperatures, Sea Ice Concentration, Motion & Snow Depth Polar Grids, Version 1 2018. Available online: http://nsidc.org/data/AU_SI12/versions/1 (accessed on 13 November 2023).
- Backus, G.E.; Gilbert, J.F. Numerical Applications of a Formalism for Geophysical Inverse Problems. Geophys. J. Int. 1967, 13, 247–276. [Google Scholar] [CrossRef]
- Backus, G.; Gilbert, F. The Resolving Power of Gross Earth Data. Geophys. J. Int. 1968, 16, 169–205. [Google Scholar] [CrossRef]
- Wang, P.; Bayram, B.; Sertel, E. A Comprehensive Review on Deep Learning Based Remote Sensing Image Super-Resolution Methods. Earth-Sci. Rev. 2022, 232, 104110. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Hoi, S.C.H. Deep Learning for Image Super-Resolution: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3365–3387. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, X.; Tian, Y.; Wang, W.; Xue, J.-H.; Liao, Q. Deep Learning for Single Image Super-Resolution: A Brief Review. IEEE Trans. Multimed. 2019, 21, 3106–3121. [Google Scholar] [CrossRef]
- Petrou, Z.I.; Xian, Y.; Tian, Y. Towards Breaking the Spatial Resolution Barriers: An Optical Flow and Super-Resolution Approach for Sea Ice Motion Estimation. ISPRS J. Photogramm. Remote Sens. 2018, 138, 164–175. [Google Scholar] [CrossRef]
- Hu, W.; Zhang, W.; Chen, S.; Lv, X.; An, D.; Ligthart, L. A Deconvolution Technology of Microwave Radiometer Data Using Convolutional Neural Networks. Remote Sens. 2018, 10, 275. [Google Scholar] [CrossRef]
- Hu, W.; Li, Y.; Zhang, W.; Chen, S.; Lv, X.; Ligthart, L. Spatial Resolution Enhancement of Satellite Microwave Radiometer Data with Deep Residual Convolutional Neural Network. Remote Sens. 2019, 11, 771. [Google Scholar] [CrossRef]
- Hu, T.; Zhang, F.; Li, W.; Hu, W.; Tao, R. Microwave Radiometer Data Superresolution Using Image Degradation and Residual Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8954–8967. [Google Scholar] [CrossRef]
- Li, Y.; Hu, W.; Chen, S.; Zhang, W.; Guo, R.; He, J.; Ligthart, L. Spatial Resolution Matching of Microwave Radiometer Data with Convolutional Neural Network. Remote Sens. 2019, 11, 2432. [Google Scholar] [CrossRef]
- Liu, H.; Ruan, Z.; Zhao, P.; Dong, C.; Shang, F.; Liu, Y.; Yang, L.; Timofte, R. Video Super-Resolution Based on Deep Learning: A Comprehensive Survey. Artif. Intell. Rev. 2022, 55, 5981–6035. [Google Scholar] [CrossRef]
- Salvetti, F.; Mazzia, V.; Khaliq, A.; Chiaberge, M. Multi-Image Super Resolution of Remotely Sensed Images Using Residual Attention Deep Neural Networks. Remote Sens. 2020, 12, 2207. [Google Scholar] [CrossRef]
- Arefin, M.R.; Michalski, V.; St-Charles, P.-L.; Kalaitzis, A.; Kim, S.; Kahou, S.E.; Bengio, Y. Multi-Image Super-Resolution for Remote Sensing Using Deep Recurrent Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops 2020, Seattle, WA, USA, 14–19 June 2020; pp. 206–207. [Google Scholar]
- Wang, X.; Chan, K.C.K.; Yu, K.; Dong, C.; Change Loy, C. EDVR: Video Restoration With Enhanced Deformable Convolutional Networks. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Long Beach, CA, USA, 14–20 June 2019. [Google Scholar]
- Yi, P.; Wang, Z.; Jiang, K.; Jiang, J.; Ma, J. Progressive Fusion Video Super-Resolution Network via Exploiting Non-Local Spatio-Temporal Correlations. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; IEEE: Seoul, Republic of Korea, 2019; pp. 3106–3115. [Google Scholar]
- Haris, M.; Shakhnarovich, G.; Ukita, N. Recurrent Back-Projection Network for Video Super-Resolution. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 14–20 June 2019; pp. 3892–3901. [Google Scholar]
- Isobe, T.; Zhu, F.; Jia, X.; Wang, S. Revisiting Temporal Modeling for Video Super-Resolution. arXiv 2020, arXiv:2008.05765. [Google Scholar]
- Imaoka, K.; Maeda, T.; Kachi, M.; Kasahara, M.; Ito, N.; Nakagawa, K. Status of AMSR2 Instrument on GCOM-W1. In Earth Observing Missions and Sensors: Development, Implementation, and Characterization II; SPIE: St Bellingham, WA, USA, 2012; Volume 8528, pp. 201–206. [Google Scholar]
- Du, J.; Kimball, J.S.; Jones, L.A.; Kim, Y.; Glassy, J.; Watts, J.D. A Global Satellite Environmental Data Record Derived from AMSR-E and AMSR2 Microwave Earth Observations. Earth Syst. Sci. Data 2017, 9, 791–808. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Chen, N.; Zhang, X.; Cosh, M.H.; Wang, W. Satellite Surface Soil Moisture from SMAP, SMOS, AMSR2 and ESA CCI: A Comprehensive Assessment Using Global Ground-Based Observations. Remote Sens. Environ. 2019, 231, 111215. [Google Scholar] [CrossRef]
- Oki, T.; Imaoka, K.; Kachi, M. AMSR Instruments on GCOM-W1/2: Concepts and Applications. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 1363–1366. [Google Scholar]
- Cui, H.; Jiang, L.; Du, J.; Zhao, S.; Wang, G.; Lu, Z.; Wang, J. Evaluation and Analysis of AMSR-2, SMOS, and SMAP Soil Moisture Products in the Genhe Area of China. J. Geophys. Res. Atmos. 2017, 122, 8650–8666. [Google Scholar] [CrossRef]
- Kachi, M.; Hori, M.; Maeda, T.; Imaoka, K. Status of Validation of AMSR2 on Board the GCOM-W1 Satellite. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 110–113. [Google Scholar]
- Maeda, T.; Imaoka, K.; Kachi, M.; Fujii, H.; Shibata, A.; Naoki, K.; Kasahara, M.; Ito, N.; Nakagawa, K.; Oki, T. Status of GCOM-W1/AMSR2 Development, Algorithms, and Products. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XV, Prague, Czech Republic, 19–22 September 2011; SPIE: St Bellingham, WA, USA, 2011; Volume 8176, pp. 183–189. [Google Scholar]
- Imaoka, K.; Kachi, M.; Fujii, H.; Murakami, H.; Hori, M.; Ono, A.; Igarashi, T.; Nakagawa, K.; Oki, T.; Honda, Y.; et al. Global Change Observation Mission (GCOM) for Monitoring Carbon, Water Cycles, and Climate Change. Proc. IEEE 2010, 98, 717–734. [Google Scholar] [CrossRef]
- Tschudi, M.W.N.; Meier, J.S.; Stewart, C.F.; Maslanik, J. Polar Pathfinder Daily 25 Km EASE-Grid Sea Ice Motion Vectors, 4th ed.; National Snow and Ice Data Center Address: Boulder, CO, USA, 2019. [Google Scholar]
- Emery, W.J.; Fowler, C.W.; Maslanik, J. Satellite Remote Sensing. Oceanogr. Appl. Remote Sens. 1995, 23, 367–379. [Google Scholar]
- Thorndike, A.S.; Colony, R. Sea Ice Motion in Response to Geostrophic Winds. J. Geophys. Res. Ocean. 1982, 87, 5845–5852. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, R.M. Applied Geostatistics; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Charbonnier, P.; Blanc-Feraud, L.; Aubert, G.; Barlaud, M. Deterministic Edge-Preserving Regularization in Computed Imaging. IEEE Trans. Image Process. 1997, 6, 298–311. [Google Scholar] [CrossRef]
- Lai, W.-S.; Huang, J.-B.; Ahuja, N.; Yang, M.-H. Fast and Accurate Image Super-Resolution with Deep Laplacian Pyramid Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2599–2613. [Google Scholar] [CrossRef]
- Lai, W.-S.; Huang, J.-B.; Ahuja, N.; Yang, M.-H. Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE: Piscataway, NJ, USA; pp. 5835–5843. [Google Scholar]
- Chan, K.C.K.; Zhou, S.; Xu, X.; Loy, C.C. BasicVSR++: Improving Video Super-Resolution With Enhanced Propagation and Alignment. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 5972–5981. [Google Scholar]
- Tian, Y.; Zhang, Y.; Fu, Y.; Xu, C. TDAN: Temporally-Deformable Alignment Network for Video Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 3360–3369. [Google Scholar]
- Tang, C.C.L.; Ross, C.K.; Yao, T.; Petrie, B.; DeTracey, B.M.; Dunlap, E. The Circulation, Water Masses and Sea-Ice of Baffin Bay. Prog. Oceanogr. 2004, 63, 183–228. [Google Scholar] [CrossRef]
- Stroeve, J.; Notz, D. Changing State of Arctic Sea Ice across All Seasons. Environ. Res. Lett. 2018, 13, 103001. [Google Scholar] [CrossRef]
- Takeda, H.; Milanfar, P.; Protter, M.; Elad, M. Super-Resolution Without Explicit Subpixel Motion Estimation. IEEE Trans. Image Process. 2009, 18, 1958–1975. [Google Scholar] [CrossRef]
- Brox, T.; Malik, J. Large Displacement Optical Flow: Descriptor Matching in Variational Motion Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 500–513. [Google Scholar] [CrossRef]
- Kwok, R.; Rothrock, D.A. Variability of Fram Strait Ice Flux and North Atlantic Oscillation. J. Geophys. Res. Ocean. 1999, 104, 5177–5189. [Google Scholar] [CrossRef]







| Frequency (GHz) | Sampling Interval (km) | Polarization | Footprint (Along-Scan × Along-Track) (km) |
|---|---|---|---|
| 6.925/7.3 | 10 | V/H | 35 × 62 |
| 10.65 | 10 | V/H | 24 × 42 |
| 18.7 | 10 | V/H | 14 × 22 |
| 23.8 | 10 | V/H | 15 × 26 |
| 36.5 | 10 | V/H | 7 × 12 |
| 89 | 5 | V/H | 3 × 5 |
| Frequency (GHz) | Length of the Input Image Sequence | MISR Network | |||
|---|---|---|---|---|---|
| EDVR | PFNL | RBPN | RRN | ||
| 18.7 | 3 | 31.56/0.8779 | 39.58/0.9624 | 40.65/0.9491 | 41.53/0.9435 |
| 5 | 36.09/0.9325 | 39.81/0.9639 | 40.82/0.9504 | 41.69/0.9745 | |
| 7 | 35.21/0.9305 | 40.44/0.9674 | 40.86/0.9522 | 41.78/0.9750 | |
| 9 | 35.64/0.9322 | - | 40.22/0.9492 | 41.74/0.9747 | |
| 36.5 | 3 | 31.56/0.8297 | 37.10/0.9208 | 38.09/0.9254 | 38.73/0.9395 |
| 5 | 35.27/0.8965 | 37.27/0.9232 | 38.51/0.9311 | 38.88/0.9411 | |
| 7 | 35.04/0.8948 | 36.63/0.9155 | 38.55/0.9312 | 39.06/0.9434 | |
| 9 | 35.24/0.8911 | - | 37.98/0.9249 | 38.91/0.9417 | |
| 89 | 3 | 36.50/0.8879 | 36.54/0.8862 | 37.18/0.8935 | 37.73/0.9057 |
| 5 | 39.64/0.9501 | 36.62/0.8879 | 37.26/0.8953 | 37.72/0.9057 | |
| 7 | 41.69/0.9505 | 36.57/0.8866 | 37.15/0.8931 | 38.00/0.9115 | |
| 9 | 41.56/0.9491 | - | 37.12/0.8924 | 37.99/0.9113 | |
| Frequency (GHz) | Seasons | MISR Network | |||
|---|---|---|---|---|---|
| EDVR | PFNL | RBPN | RRN | ||
| 18.7 | Winter | 39.05/0.9540 | 40.28/0.9641 | 42.87/0.9741 | 42.97/0.9769 |
| Spring | 36.84/0.9394 | 38.27/0.9515 | 40.97/0.9687 | 41.09/0.9759 | |
| Summer | 34.57/0.9237 | 36.16/0.9394 | 40.66/0.9715 | 41.00/0.9710 | |
| Autumn | 37.04/0.9435 | 38.34/0.9552 | 42.04/0.9738 | 42.05/0.9761 | |
| 36.5 | Winter | 36.08/0.9085 | 37.32/0.9224 | 38.16/0.9219 | 39.05/0.9531 |
| Spring | 34.79/0.8915 | 36.32/0.9123 | 37.30/0.9241 | 38.94/0.9373 | |
| Summer | 34.38/0.8928 | 35.77/0.9114 | 36.85/0.9196 | 38.38/0.9360 | |
| Autumn | 35.83/0.8932 | 37.12/0.9160 | 37.58/0.9223 | 39.19/0.9435 | |
| 89 | Winter | 43.07/0.9628 | 37.95/0.9160 | 38.77/0.9230 | 39.52/0.9342 |
| Spring | 41.12/0.9487 | 36.53/0.8905 | 37.04/0.8952 | 37.69/0.9092 | |
| Summer | 40.98/0.9424 | 35.96/0.8706 | 36.56/0.8811 | 37.34/0.8989 | |
| Autumn | 41.36/0.9481 | 36.06/0.8742 | 36.68/0.8821 | 37.45/0.9036 | |
| Frequency (GHz) | Date | MISR Framework | |||
|---|---|---|---|---|---|
| EDVR | PFNL | RBPN | RRN | ||
| 18.7 | 25 February | 43.47/0.9716 | 44.64/0.9769 | 44.77/0.9794 | 46.85/0.9842 |
| 10 June | 36.97/0.9044 | 37.81/0.9494 | 38.96/0.9326 | 39.12/0.9474 | |
| 3 July | 36.33/0.9016 | 37.57/0.9308 | 38.66/0.9323 | 38.76/0.9400 | |
| 19 November | 42.21/0.9527 | 43.13/0.9735 | 43.84/0.9752 | 45.24/0.9795 | |
| 36.5 | 25 February | 42.45/0.9734 | 43.02/0.9649 | 43.19/0.9660 | 43.37/0.9678 |
| 10 June | 37.75/0.9071 | 38.75/0.9279 | 38.87/0.9540 | 39.09/0.9513 | |
| 3 July | 35.96/0.8849 | 37.81/0.9254 | 38.17/0.9251 | 38.28/0.9255 | |
| 19 November | 40.74/0.9530 | 42.29/0.9617 | 42.07/0.9555 | 42.34/0.9573 | |
| 89 | 25 February | 45.32/0.9731 | 43.43/0.9655 | 44.21/0.9703 | 45.17/0.9728 |
| 10 June | 44.88/0.9691 | 43.28/0.9655 | 43.78/0.9510 | 43.97/0.9603 | |
| 3 July | 43.91/0.9658 | 41.61/0.9387 | 41.89/0.9483 | 42.06/0.9400 | |
| 19 November | 44.03/0.9649 | 41.67/0.9445 | 42.00/0.9503 | 42.45/0.9588 | |
| Frequency | Date | MISR Network | |||
|---|---|---|---|---|---|
| EDVR | PFNL | RBPN | RRN | ||
| 18 | 15 February | 39.36/0.9404 | 40.49/0.9494 | 42.33/0.9665 | 43.20/0.9720 |
| 22 March | 38.41/0.9311 | 39.96/0.9494 | 40.89/0.9597 | 41.16/0.9605 | |
| 36 | 15 February | 41.49/0.9504 | 41.65/0.9527 | 42.24/0.9542 | 42.45/0.9577 |
| 22 March | 40.41/0.9430 | 41.48/0.9496 | 42.11/0.9497 | 42.44/0.9511 | |
| 89 | 15 February | 43.71/0.9662 | 43.21/0.9597 | 42.61/0.9499 | 43.21/0.9596 |
| 22 March | 43.11/0.9637 | 42.17/0.9482 | 41.60/0.9378 | 42.72/0.9549 | |
| Polarization | MISR Network | |||
|---|---|---|---|---|
| EDVR | PFNL | RBPN | RRN | |
| H | 37.54/0.9697 | 41.92/0.9846 | 42.70/0.9757 | 43.38/0.9878 |
| V | 41.97/0.9812 | 45.96/0.9896 | 46.38/0.9798 | 47.30/0.9915 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, T.; Jiang, P.; Liu, X.; Ma, X. Applications of Deep Learning-Based Super-Resolution Networks for AMSR2 Arctic Sea Ice Images. Remote Sens. 2023, 15, 5401. https://doi.org/10.3390/rs15225401
Feng T, Jiang P, Liu X, Ma X. Applications of Deep Learning-Based Super-Resolution Networks for AMSR2 Arctic Sea Ice Images. Remote Sensing. 2023; 15(22):5401. https://doi.org/10.3390/rs15225401
Chicago/Turabian StyleFeng, Tiantian, Peng Jiang, Xiaomin Liu, and Xinyu Ma. 2023. "Applications of Deep Learning-Based Super-Resolution Networks for AMSR2 Arctic Sea Ice Images" Remote Sensing 15, no. 22: 5401. https://doi.org/10.3390/rs15225401
APA StyleFeng, T., Jiang, P., Liu, X., & Ma, X. (2023). Applications of Deep Learning-Based Super-Resolution Networks for AMSR2 Arctic Sea Ice Images. Remote Sensing, 15(22), 5401. https://doi.org/10.3390/rs15225401





