Performance of Common Scene Stacking Atmospheric Correction on Nonlinear InSAR Deformation Retrieval
Abstract
:1. Introduction
2. Methodology
2.1. Common Scene Stacking
2.2. Improved Time Series Analysis Method for nonlinear Deformation History
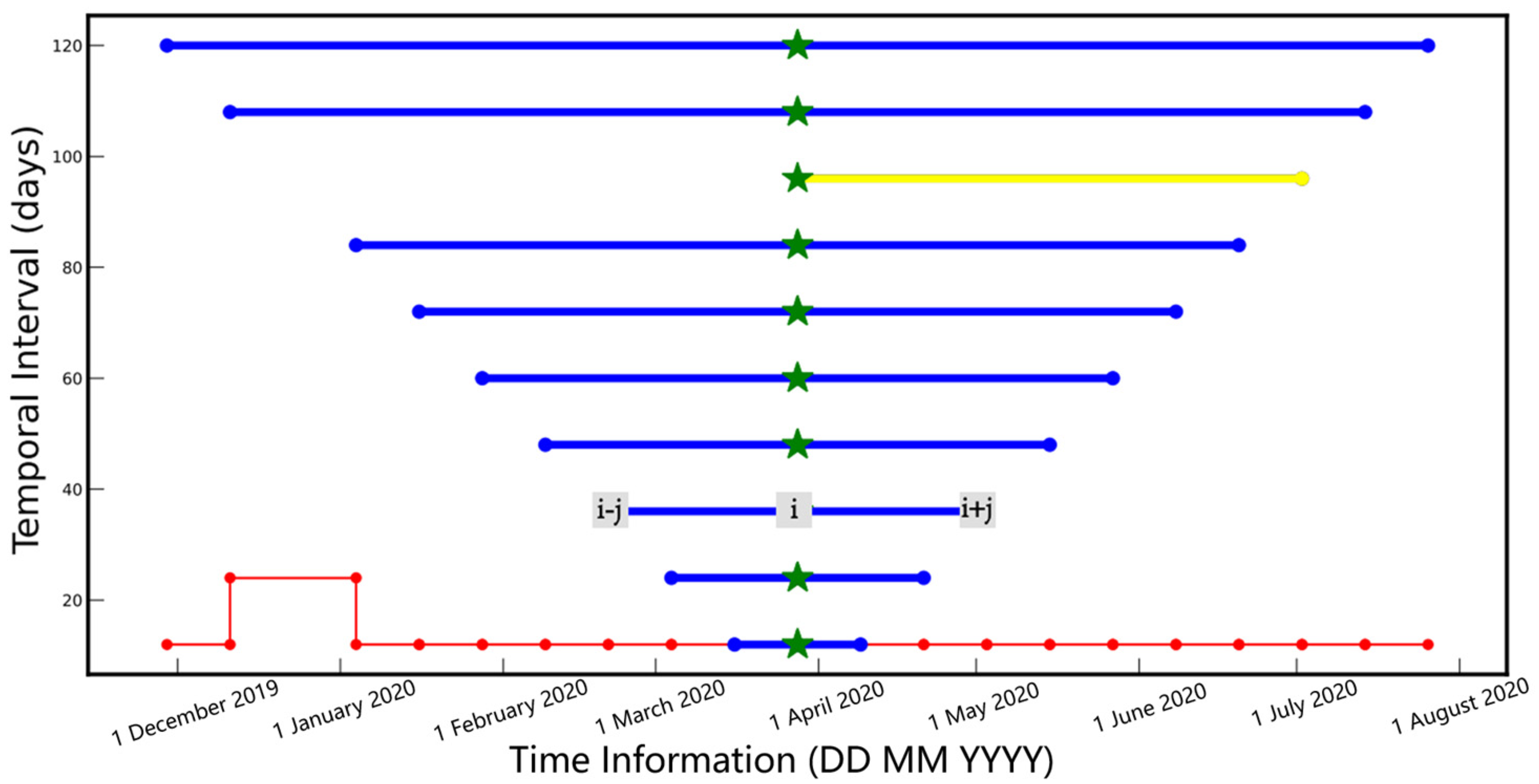
2.3. Numerical Experiments
2.3.1. Forward Modeling for the Earthquake Cycle
2.3.2. Performance Evaluation of the Inversion Results
2.3.3. D-InSAR Processing
3. Results
3.1. Validation with a Synthetic Dataset
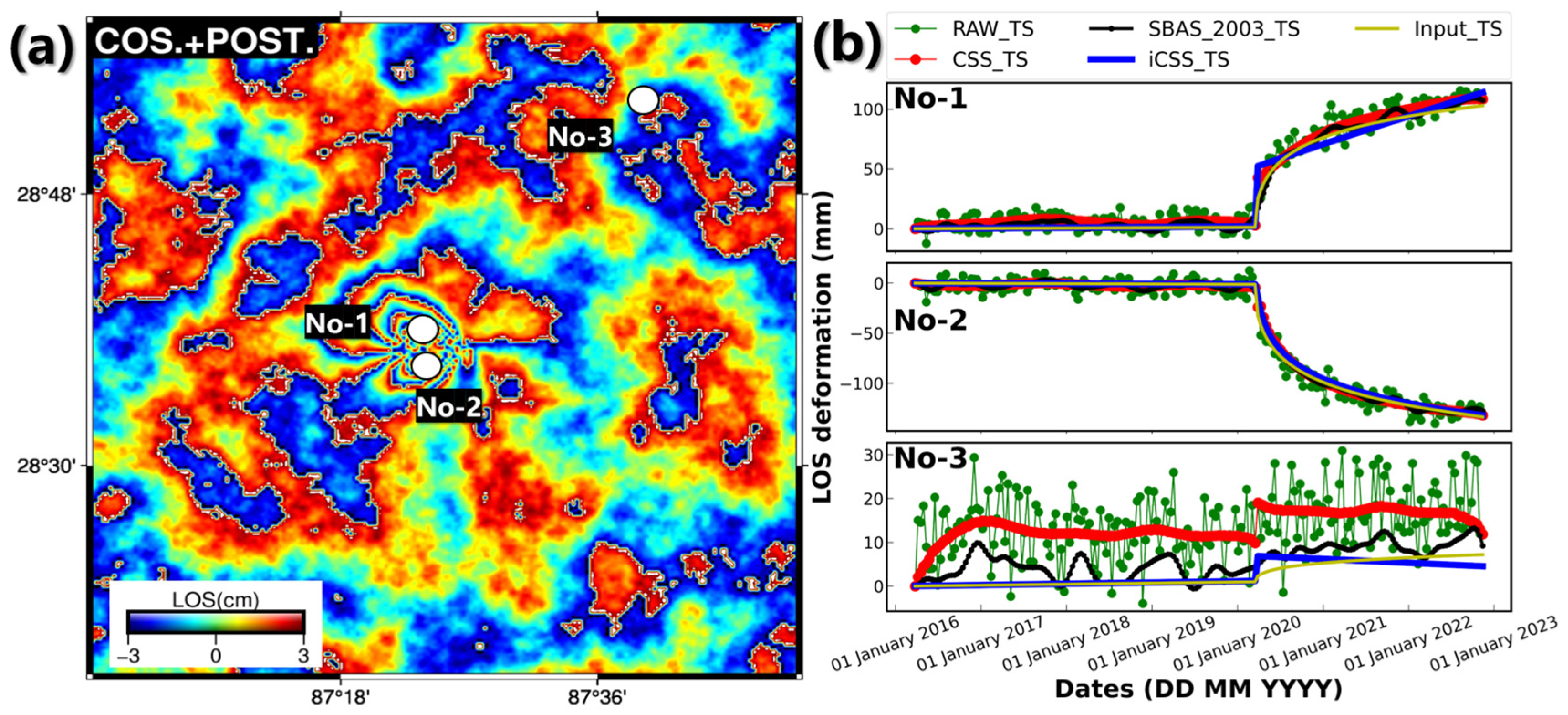
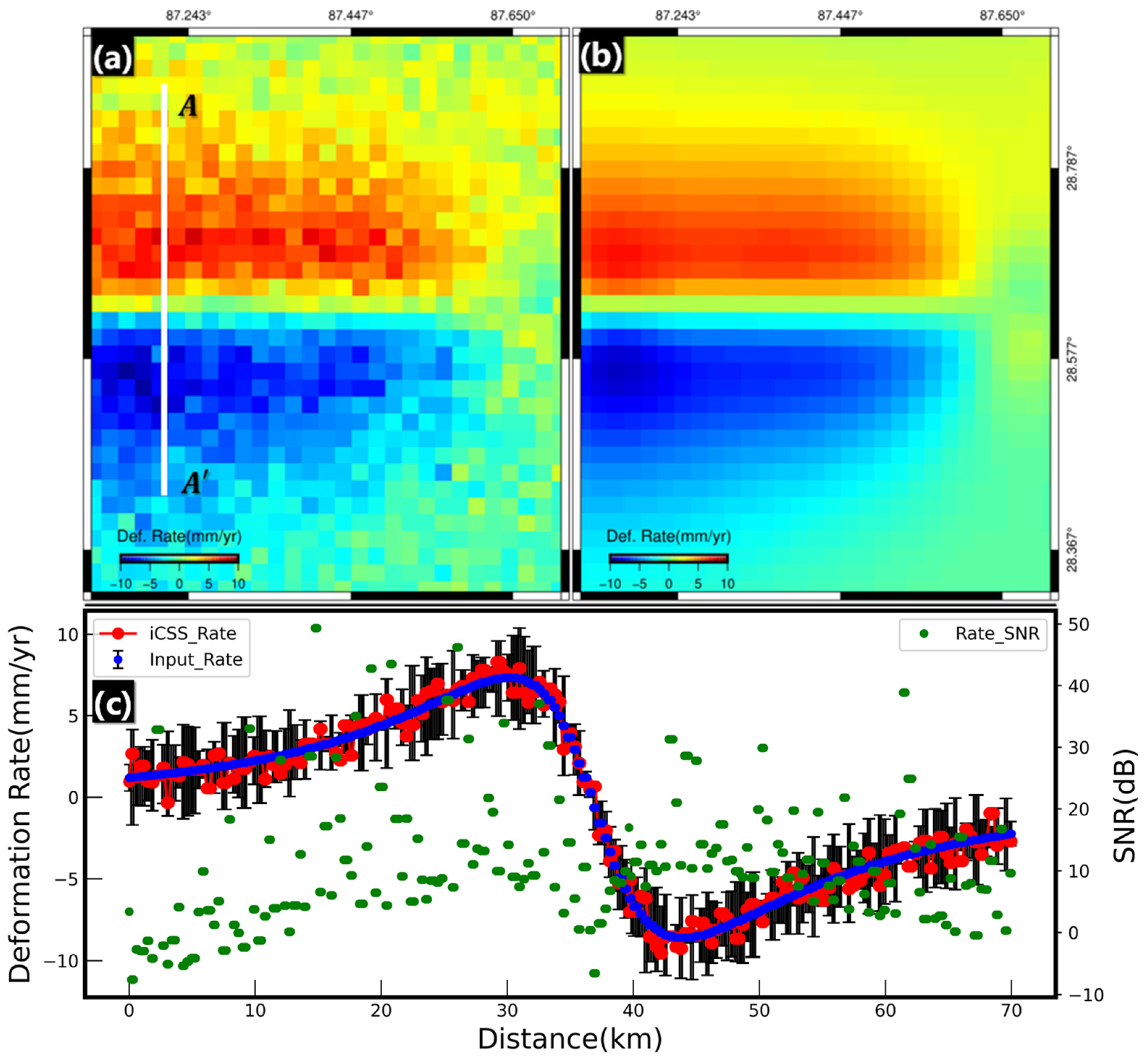
3.2. A Case Study on the 2020 Mw 5.7 Dingjie Earthquake
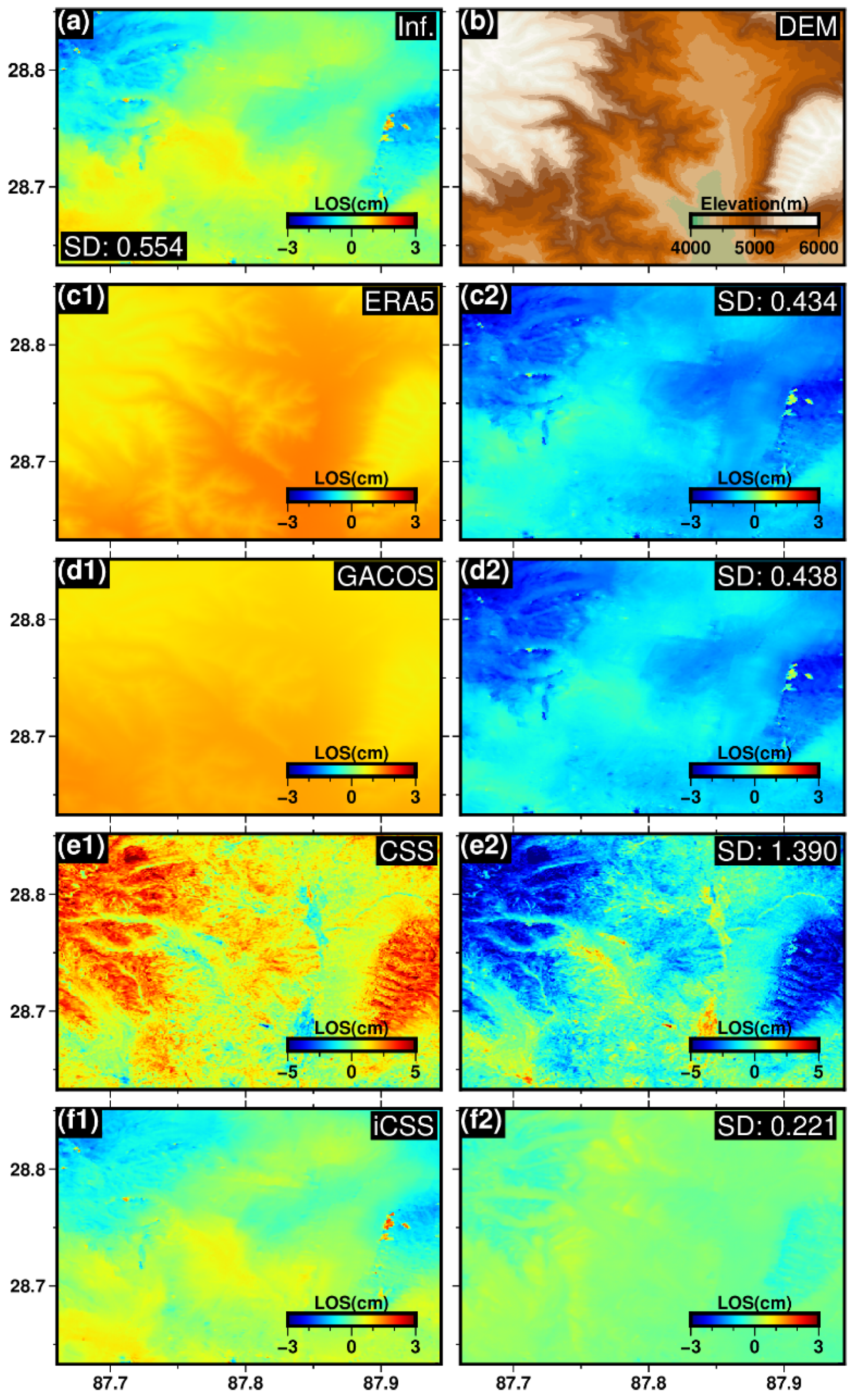
4. Discussion
5. Conclusions
- The CSS method does perform excellently for APS retrieval with abundant interferograms, which has been validated with the ERA5 APS simulation for application in southern Tibet.
- With the iterative way proposed in this study, iCSS can also be applicable for the estimation of cos- and/or postseismic deformation in time series analysis.
- Our proposed method (iCSS) has effectively addressed the weak APS constraint issue for edge SAR acquisitions in an iterative strategy in practical applications.
- For regions showing seasonal APS distributions, we suggest intentionally choosing SAR data with low APS effects as edge SAR data in the InSAR network.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping Small Elevation Changes over Large Areas: Differential Radar Interferometry. J. Geophys. Res. 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Ge, L.; Rizos, C.; Han, S.; Zebker, H. Mining Subsidence Monitoring Using the Combined InSAR and GPS Approach. In Proceedings of the 10th International Symposium on Deformation Measurements, Orange, CA, USA, 19–22 March 2001; pp. 1–10. [Google Scholar]
- Samsonov, S.V.; Feng, W.; Fialko, Y. Subsidence at Cerro Prieto Geothermal Field and Postseismic Slip along the Indiviso Fault from 2011 to 2016 RADARSAT-2 DInSAR Time Series Analysis. Geophys. Res. Lett. 2017, 44, 2716–2724. [Google Scholar] [CrossRef]
- Dong, J.; Liao, M.; Xu, Q.; Zhang, L.; Tang, M.; Gong, J. Detection and Displacement Characterization of Landslides Using Multi-Temporal Satellite SAR Interferometry: A Case Study of Danba County in the Dadu River Basin. Eng. Geol. 2018, 240, 95–109. [Google Scholar] [CrossRef]
- Samsonov, S.V.; Feng, W.; Peltier, A.; Geirsson, H.; d’Oreye, N.; Tiampo, K.F. Multidimensional Small Baseline Subset (MSBAS) for Volcano Monitoring in Two Dimensions: Opportunities and Challenges. Case Study Piton de La Fournaise Volcano. J. Volcanol. Geotherm. Res. 2017, 344, 121–138. [Google Scholar] [CrossRef]
- Feng, W.; Samsonov, S.; Almeida, R.; Yassaghi, A.; Li, J.; Qiu, Q.; Li, P.; Zheng, W. Geodetic Constraints of the 2017 Mw7.3 Sarpol Zahab, Iran Earthquake, and Its Implications on the Structure and Mechanics of the Northwest Zagros Thrust-Fold Belt. Geophys. Res. Lett. 2018, 45, 6853–6861. [Google Scholar] [CrossRef]
- Ghorbani, Z.; Khosravi, A.; Maghsoudi, Y.; Mojtahedi, F.F.; Javadnia, E.; Nazari, A. Use of InSAR Data for Measuring Land Subsidence Induced by Groundwater Withdrawal and Climate Change in Ardabil Plain, Iran. Sci. Rep. 2022, 12, 13998. [Google Scholar] [CrossRef]
- Hooper, A.; Segall, P.; Zebker, H. Persistent Scatterer Interferometric Synthetic Aperture Radar for Crustal Deformation Analysis, with Application to Volcán Alcedo, Galápagos. J. Geophys. Res. Solid Earth 2007, 112, B07407. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.Ö.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 Mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic Aperture Radar Interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Agram, P.S.; Simons, M. A Noise Model for InSAR Time Series. J. Geophys. Res. Solid Earth 2015, 120, 2752–2771. [Google Scholar] [CrossRef]
- Goldstein, R. Atmospheric Limitations to Repeat-Track Radar Interferometry Been Unduly Disturbed during the Time Between. Geophys. Res. Lett. 1995, 22, 2517–2520. [Google Scholar] [CrossRef]
- Tarayre, H.; Massonnet, D. Atmospheric Propagation Heterogeneities Revealed by ERS-1 Interferometry. Geophys. Res. Lett. 1996, 23, 989–992. [Google Scholar] [CrossRef]
- Gray, A.L.; Mattar, K.E.; Sofko, G. Influence of Ionospheric Electron Density Fluctuations on Satellite Radar Interferometry. Geophys. Res. Lett. 2000, 27, 1451–1454. [Google Scholar] [CrossRef]
- Zebker, A.; Rosen, P.A.; Hensley, S. Atmospheric Effects in Interferometric Synthetic Aperture Radar Surface Deformation and Topographic Maps. J. Geophys. Res. Solid Earth 1997, 102, 151. [Google Scholar] [CrossRef]
- Samsonov, S.V.; Trishchenko, A.P.; Tiampo, K.; González, P.J.; Zhang, Y.; Fernández, J. Removal of Systematic Seasonal Atmospheric Signal from Interferometric Synthetic Aperture Radar Ground Deformation Time Series. Geophys. Res. Lett. 2014, 41, 6123–6130. [Google Scholar] [CrossRef]
- Ding, X.L.; Li, Z.W.; Zhu, J.J.; Feng, G.C.; Long, J.P. Atmospheric Effects on InSAR Measurements and Their Mitigation. Sensors 2008, 8, 5426–5448. [Google Scholar] [CrossRef]
- Li, Z.; Cao, Y.; Wei, J.; Duan, M.; Wu, L.; Hou, J.; Zhu, J. Time-Series InSAR Ground Deformation Monitoring: Atmospheric Delay Modeling and Estimating. Earth Sci. Rev. 2019, 192, 258–284. [Google Scholar] [CrossRef]
- Li, Z.; Duan, M.; Cao, Y.; Mu, M.; He, X.; Wei, J. Mitigation of Time-Series InSAR Turbulent Atmospheric Phase Noise: A Review. Geod. Geodyn. 2022, 13, 93–103. [Google Scholar] [CrossRef]
- Cavalié, O.; Doin, M.P.; Lasserre, C.; Briole, P. Ground Motion Measurement in the Lake Mead Area, Nevada, by Differential Synthetic Aperture Radar Interferometry Time Series Analysis: Probing the Lithosphere Rheological Structure. J. Geophys. Res. Solid Earth 2007, 112, B03403. [Google Scholar] [CrossRef]
- Chaabane, F.; Avallone, A.; Tupin, F.; Briole, P.; Maître, H. A Multitemporal Method for Correction of Tropospheric Effects in Differential SAR Interferometry: Application to the Gulf of Corinth Earthquake. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1605–1615. [Google Scholar] [CrossRef]
- Webley, P.W.; Bingley, R.M.; Dodson, A.H.; Wadge, G.; Waugh, S.J.; James, I.N. Atmospheric Water Vapour Correction to InSAR Surface Motion Measurements on Mountains: Results from a Dense GPS Network on Mount Etna. Phys. Chem. Earth 2002, 27, 363–370. [Google Scholar] [CrossRef]
- Puysségur, B.; Michel, R.; Avouac, J.P. Tropospheric Phase Delay in Interferometric Synthetic Aperture Radar Estimated from Meteorological Model and Multispectral Imagery. J. Geophys. Res. Solid Earth 2007, 112, B05419. [Google Scholar] [CrossRef]
- Li, Z.; Muller, J.P.; Cross, P.; Fielding, E.J. Interferometric Synthetic Aperture Radar (InSAR) Atmospheric Correction: GPS, Moderate Resolution Imaging Spectroradiometer (MODIS), and InSAR Integration. J. Geophys. Res. Solid Earth 2005, 110, B03410-1. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Blewitt, G. Global Comparisons of ERA5 and the Operational HRES Tropospheric Delay and Water Vapor Products With GPS and MODIS. Earth Sp. Sci. 2021, 8, e2020EA001417. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Wang, Y.; Chang, L.; Feng, W.; Samsonov, S.; Zheng, W. Topography-Correlated Atmospheric Signal Mitigation for InSAR Applications in the Tibetan Plateau Based on Global Atmospheric Models. Int. J. Remote Sens. 2021, 42, 4364–4382. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Price, E.J. Phase Gradient Approach to Stacking Interferograms. J. Geophys. Res. Solid Earth 1998, 103, 30183–30204. [Google Scholar] [CrossRef]
- Wright, T.; Parsons, B.; Fielding, E. The North Anatolian Interferometry Fault by Satellite Radar. Anatolia 2001, 28, 2117–2120. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Schmidt, D.A.; Bürgmann, R. Time-Dependent Land Uplift and Subsidence in the Santa Clara Valley, California, from a Large Interferometric Synthetic Aperture Radar Data Set. J. Geophys. Res. Solid Earth 2003, 108, 2416. [Google Scholar] [CrossRef]
- Samsonov, S.; Oreye, N. Multidimensional Time-Series Analysis of Ground Deformation from Multiple InSAR Data Sets Applied to Virunga Volcanic Province. Geophys. J. Int. 2012, 191, 1095–1108. [Google Scholar] [CrossRef]
- Shirzaei, M.; Bürgmann, R. Topography Correlated Atmospheric Delay Correction in Radar Interferometry Using Wavelet Transforms. Geophys. Res. Lett. 2012, 39, L01305. [Google Scholar] [CrossRef]
- Tymofyeyeva, E.; Fialko, Y. Mitigation of Atmospheric Phase Delays in InSAR Data, with Application to the Eastern California Shear Zone. J. Geophys. Res. Solid Earth 2015, 120, 5952–5963. [Google Scholar] [CrossRef]
- Tymofyeyeva, E.; Fialko, Y. Geodetic Evidence for a Blind Fault Segment at the Southern End of the San Jacinto Fault Zone. J. Geophys. Res. Solid Earth 2018, 123, 878–891. [Google Scholar] [CrossRef]
- Xu, X.; Sandwell, D.T.; Tymofyeyeva, E.; Gonzalez-Ortega, A.; Tong, X. Tectonic and Anthropogenic Deformation at the Cerro Prieto Geothermal Step-over Revealed by Sentinel-1A Insar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5284–5292. [Google Scholar] [CrossRef]
- Xu, X.; Sandwell, D.T.; Klein, E.; Bock, Y. Integrated Sentinel-1 InSAR and GNSS Time-Series Along the San Andreas Fault System. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022579. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Liu, Z. Reduction of Atmospheric Effects on InSAR Observations Through Incorporation of GACOS and PCA Into Small Baseline Subset InSAR. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Liu, H.; Xie, L.; Zhao, G.; Ali, E.; Xu, W. A Joint InSAR—GNSS Workflow for Correction and Selection of Interferograms to Estimate High-Resolution Interseismic Deformations. Satell. Navig. 2023, 4, 14. [Google Scholar] [CrossRef]
- Zebker, M.S.; Chen, J.; Hesse, M.A. Robust Surface Deformation and Tropospheric Noise Characterization from Common-Reference Interferogram Subsets. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5210914. [Google Scholar] [CrossRef]
- Samsonov, S.V.; Oreye, N.; Samsonov, S. V Multidimensional Small Baseline Subset (MSBAS) for Two-Dimensional Deformation Analysis: Case Study Mexico City. Can. J. Remote Sens. 2017, 43, 318–329. [Google Scholar] [CrossRef]
- Liu, F.; Elliott, J.R.; Craig, T.J.; Hooper, A.; Wright, T.J. Improving the Resolving Power of InSAR for Earthquakes Using Time Series: A Case Study in Iran. Geophys. Res. Lett. 2021, 48, e2021GL093043. [Google Scholar] [CrossRef]
- Okada, Y. Internal Deformation Due to Shear and Tensile Faults in a Half-Space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar] [CrossRef]
- Emardson, T.R.; Simons, M.; Webb, F.H. Neutral Atmospheric Delay in Interferometric Synthetic Aperture Radar Applications: Statistical Description and Mitigation. J. Geophys. Res. Solid Earth 2003, 108, 2231. [Google Scholar] [CrossRef]
- Lohman, R.B.; Simons, M. Some Thoughts on the Use of InSAR Data to Constrain Models of Surface Deformation: Noise Structure and Data Downsampling. Geochem. Geophys. Geosystems 2005, 6, Q01007. [Google Scholar] [CrossRef]
- Richards, M. Fundamentals of Radar Signal Processing; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Feng, W.; Omari, K.; Samsonov, S.V. An Automated Insar Processing System: Potentials and Challenges. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3209–3210. [Google Scholar] [CrossRef]
- Feng, C.H.; Yan, Y.T.; Feng, W.P.; Wang, Y.Q.; Chen, D.Q.; Wu, C.Y. Seismogenic Fault of the 2020 Mw6. 3 Yutian, Xinjiang Earthquake Revealed from InSAR Observations and Its Implications for the Growth of the Rift in the North Tibet. Acta Geophys. Sin. 2022, 65, 2844–2856. [Google Scholar] [CrossRef]
- Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. Open Radar Interferometry Software for Mapping Surface Deformation. EOS Trans. Am. Geophys. Union 2011, 92, 234. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar Interferogram Filtering for Geophysical Applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Phase Unwrapping for Large SAR Interferograms: Statistical Segmentation and Generalized Network Models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Chen, S.; Chen, K. Source Model and Tectonic Implications of the 2020 Dingri MW5.7 Earthquake Constrained by InSAR Data. Earthquake 2021, 41, 116–128. [Google Scholar] [CrossRef]
- Jónsson, S.; Zebker, H.; Segall, P.; Amelung, F. Fault Slip Distribution of the 1999 Mw 7.1 Hector Mine, California, Earthquake, Estimated from Satellite Radar and GPS Measurements. Bull. Seismol. Soc. Am. 2002, 92, 1377–1389. [Google Scholar] [CrossRef]
- Barbot, S.; Fialko, Y.; Bock, Y. Postseismic Deformation Due to the Mw 6.0 2004 Parkfield Earthquake: Stress-Driven Creep on a Fault with Spatially Variable Rate-and-State Friction Parameters. J. Geophys. Res. Solid Earth 2009, 114, B07405. [Google Scholar] [CrossRef]
- Emry, E.L.; Wiens, D.A.; Garcia-Castellanos, D. El Mayor-Cucapah (Mw 7.2) earthquake: Early near-field postseismic deformation from InSAR and GPS observations. J. Geophys. Res. Solid Earth 2014, 119, 3076–3095. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]







| Station Index | Noise Level (mm) | Deformation Model # | APS RMSE (mm) | Recovery Rate (Cos.) (%) |
|---|---|---|---|---|
| 1 | 10 mm | Linear | 0.91 | / |
| Cos. | 0.44 | 95.8 | ||
| Cos. + Post. | 4.20 | 50.4 | ||
| 2 | 20 mm | Linear | 0.38 | / |
| Cos. | 1.39 | 95.1 | ||
| Cos. + Post. | 2.82 | 74.4 | ||
| 3 | 50 mm | Linear | 4.07 | / |
| Cos. | 1.36 | 39.6 | ||
| Cos. + Post. | 5.23 | 0 |
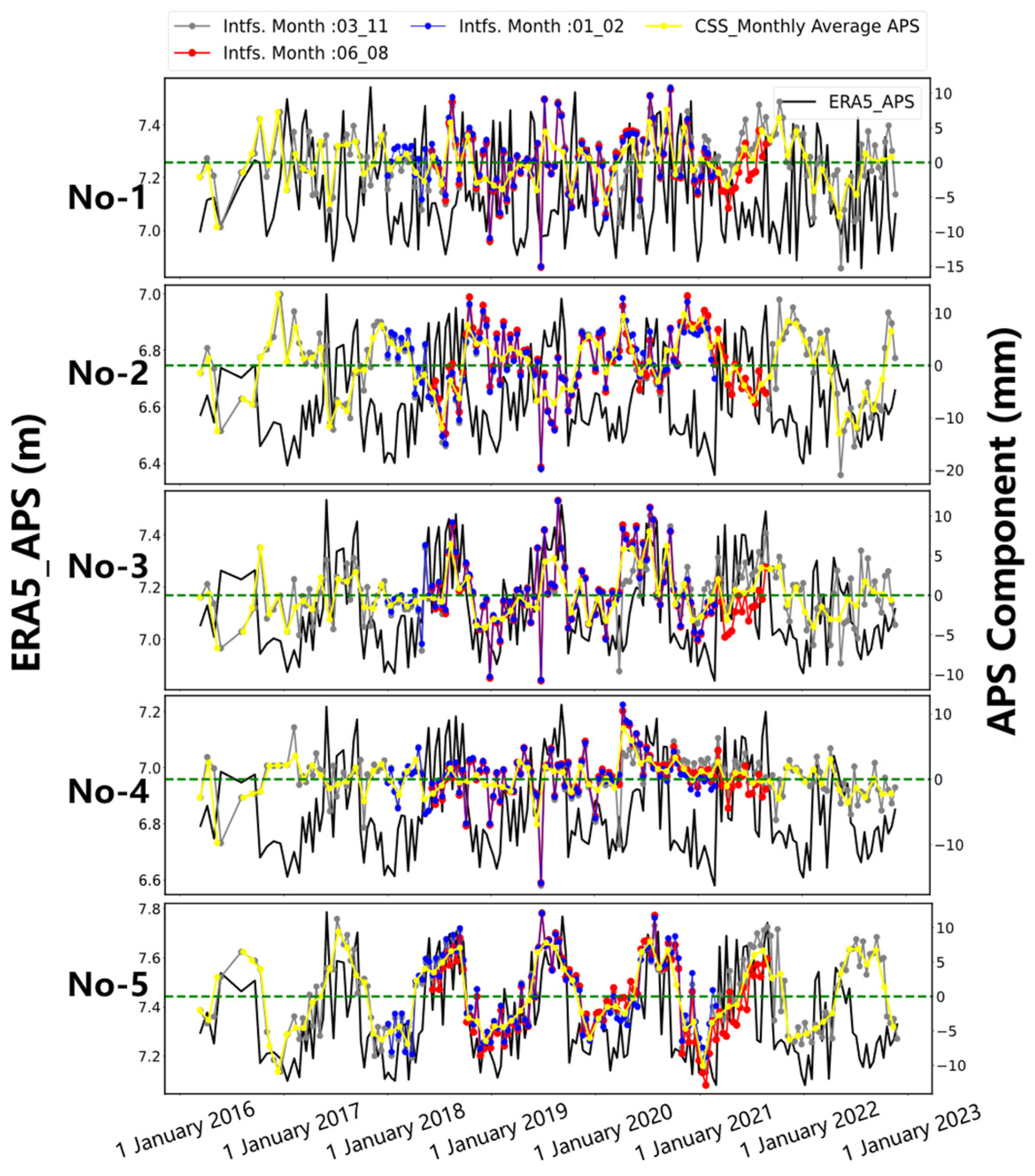
| Station Index | Elevation (m) | Data Period | Difference * | Month of APS Component Maximum | Month of APS Component Minimum |
|---|---|---|---|---|---|
| 1 | 4795 | March 2016–November 2022 | 3.026 | 07 | 03 |
| June 2018–August 2021 | 2.856 | 09 | 03 | ||
| January 2018–February 2021 | 2.876 | 09 | 03 | ||
| 2 | 5299 | March 2016–November 2022 | 3.936 | 07 | 04 |
| June 2018–August 2021 | 3.953 | 12 | 05 | ||
| January 2018–February 2021 | 3.881 | 07 | 03 | ||
| 3 | 4730 | March 2016–November 2022 | 2.811 | 07 | 04 |
| June 2018–August 2021 | 2.996 | 07 | 03 | ||
| January 2018–February 2021 | 2.968 | 07 | 03 | ||
| 4 | 4850 | March 2016–November 2022 | 2.279 | 06 | 01 |
| June 2018–August 2021 | 2.563 | 04 | 02 | ||
| January 2018–February 2021 | 2.637 | 04 | 03 | ||
| 5 | 4307 | March 2016–November 2022 | 2.603 | 07 | 04 |
| June 2018–August 2021 | 2.961 | 07 | 05 | ||
| January 2018–February 2021 | 2.642 | 07 | 05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Feng, W.; Xu, X.; Samsonov, S. Performance of Common Scene Stacking Atmospheric Correction on Nonlinear InSAR Deformation Retrieval. Remote Sens. 2023, 15, 5399. https://doi.org/10.3390/rs15225399
Zhang Z, Feng W, Xu X, Samsonov S. Performance of Common Scene Stacking Atmospheric Correction on Nonlinear InSAR Deformation Retrieval. Remote Sensing. 2023; 15(22):5399. https://doi.org/10.3390/rs15225399
Chicago/Turabian StyleZhang, Zhichao, Wanpeng Feng, Xiaohua Xu, and Sergey Samsonov. 2023. "Performance of Common Scene Stacking Atmospheric Correction on Nonlinear InSAR Deformation Retrieval" Remote Sensing 15, no. 22: 5399. https://doi.org/10.3390/rs15225399
APA StyleZhang, Z., Feng, W., Xu, X., & Samsonov, S. (2023). Performance of Common Scene Stacking Atmospheric Correction on Nonlinear InSAR Deformation Retrieval. Remote Sensing, 15(22), 5399. https://doi.org/10.3390/rs15225399







