Software-Defined Satellite Observation: A Fast Method Based on Virtual Resource Pools

Abstract

In recent years, the proliferation of remote sensing satellites has dramatically increased the demands of Earth observation and observing efficiency. Designing a promising satellite resource scheduling method is a pivotal way to meet the requirements of this scenario. However, with hundreds or more satellites involved, the existing optimization methods struggle to address the NP-hard resource scheduling problem effectively. In this paper, an approach named software-defined satellite observation (SDSO) is proposed. First, adopting the new design ideology, we define a unified specification based on a discrete spatial grid to describe the observation capability of all satellites. The observation resources are virtualized using the virtual resource pool technique and then stored in the database in advance, implementing on-demand acquisition for observation resources. Next, we designed a model of the remote sensing satellite resource scheduling problem based on a virtual resource pool and designed a solution method for searching information within the virtual resource pool. Finally, the experimental results show that the computational efficiency of the proposed SDSO methodology has a substantial advantage over the traditional methods. Meanwhile, with the growing number of satellites involved in scheduling, there is only a slight degradation in the execution performance of our method, while the time complexity of optimization-based approaches increases exponentially.

1. Introduction

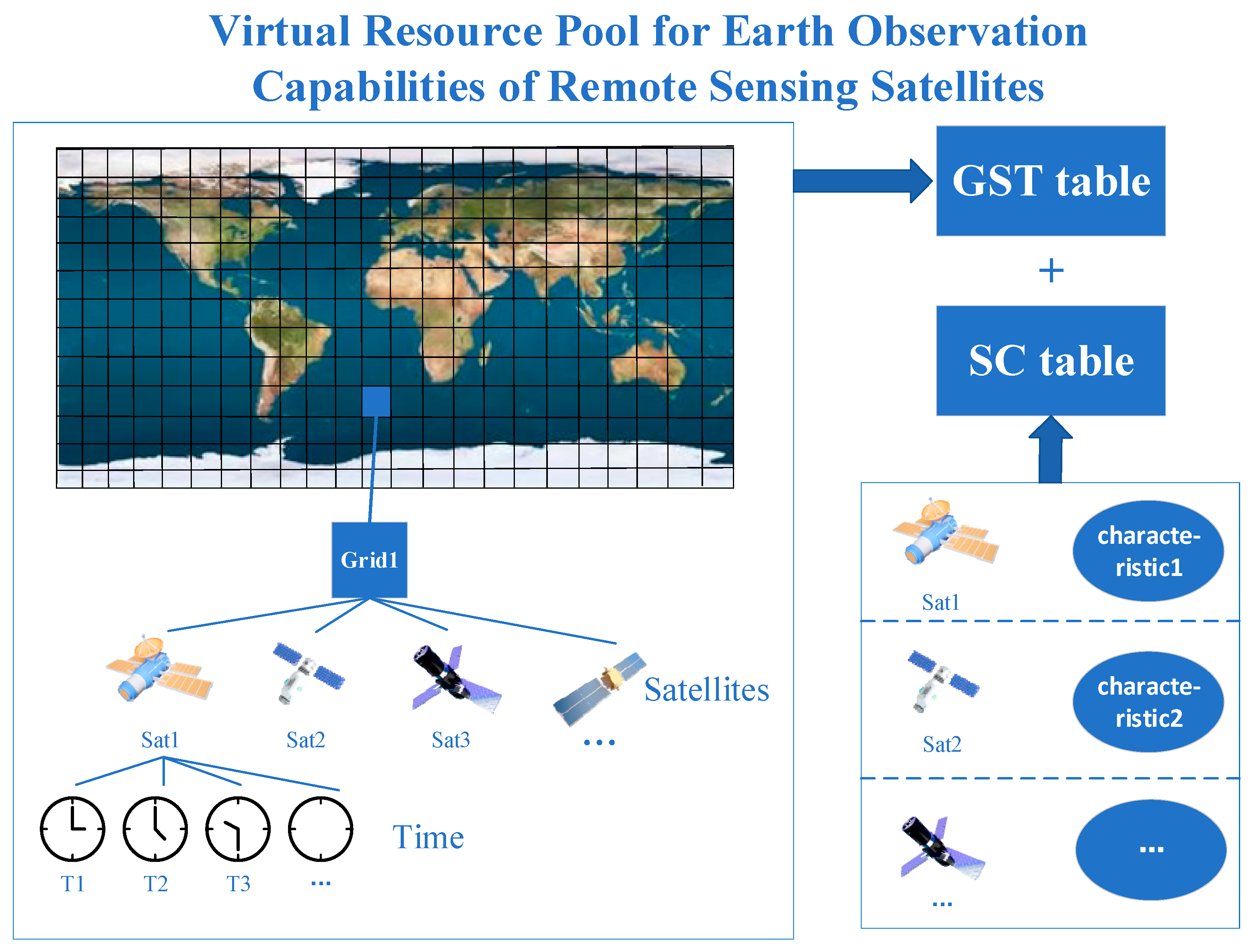
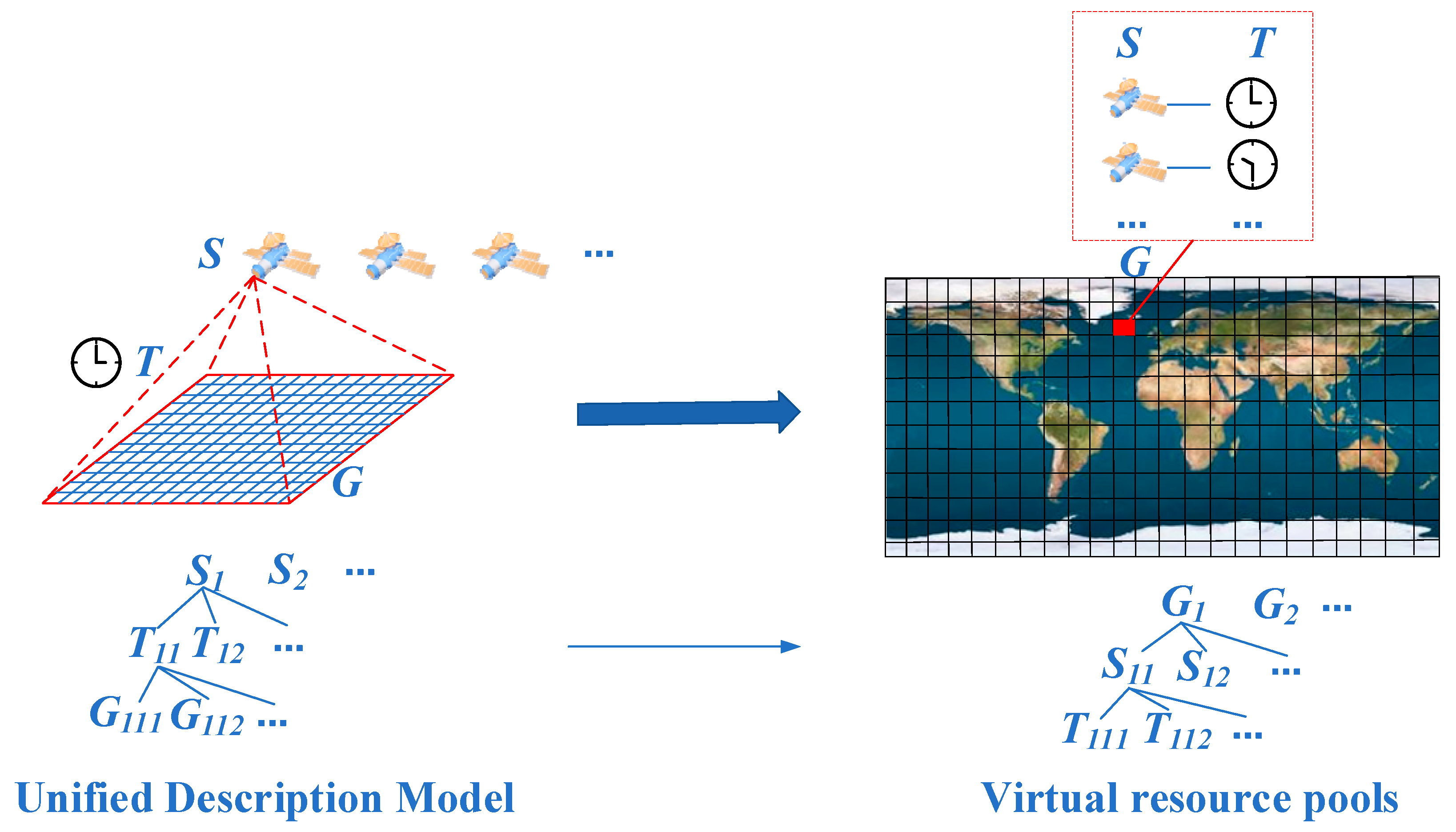
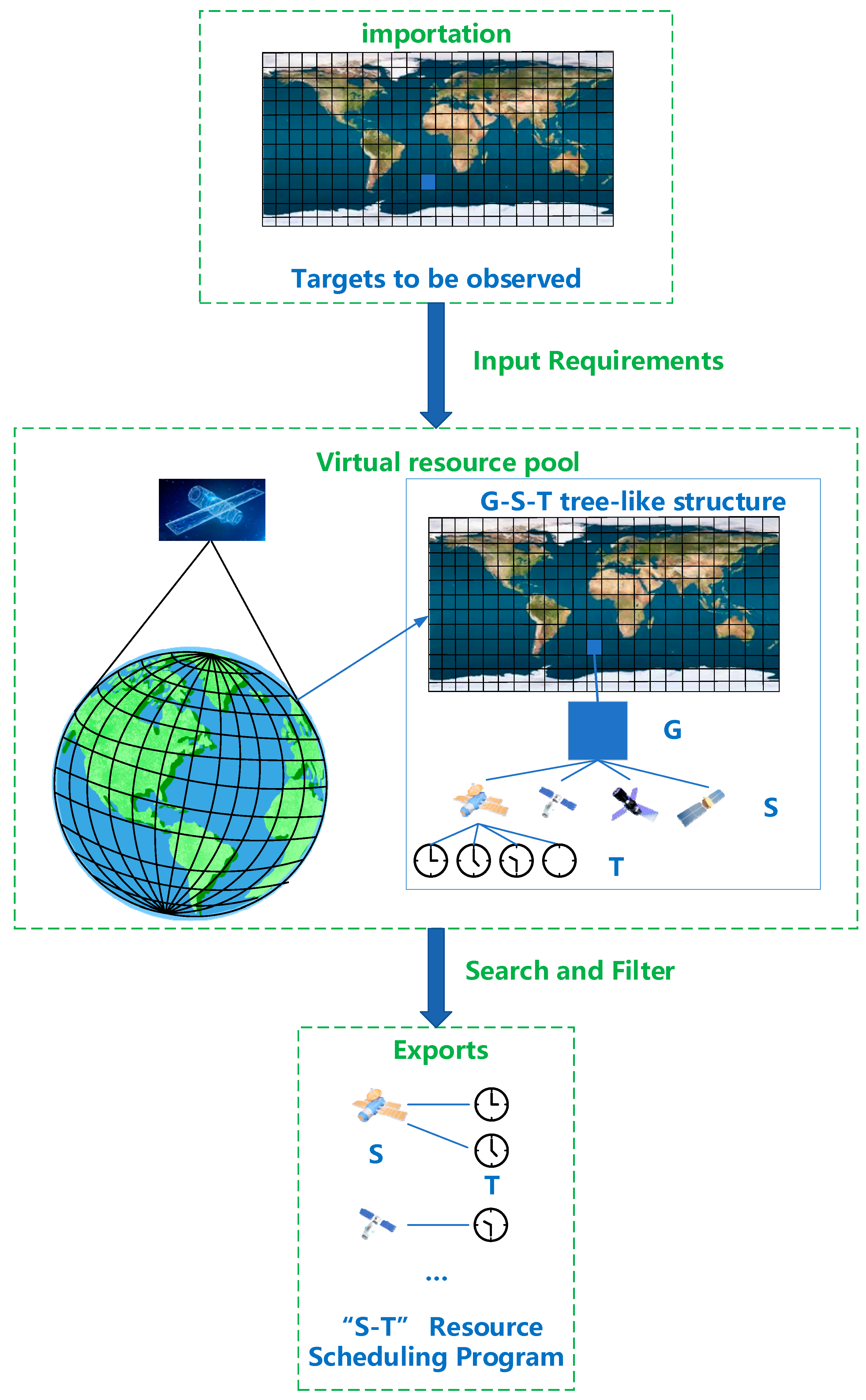
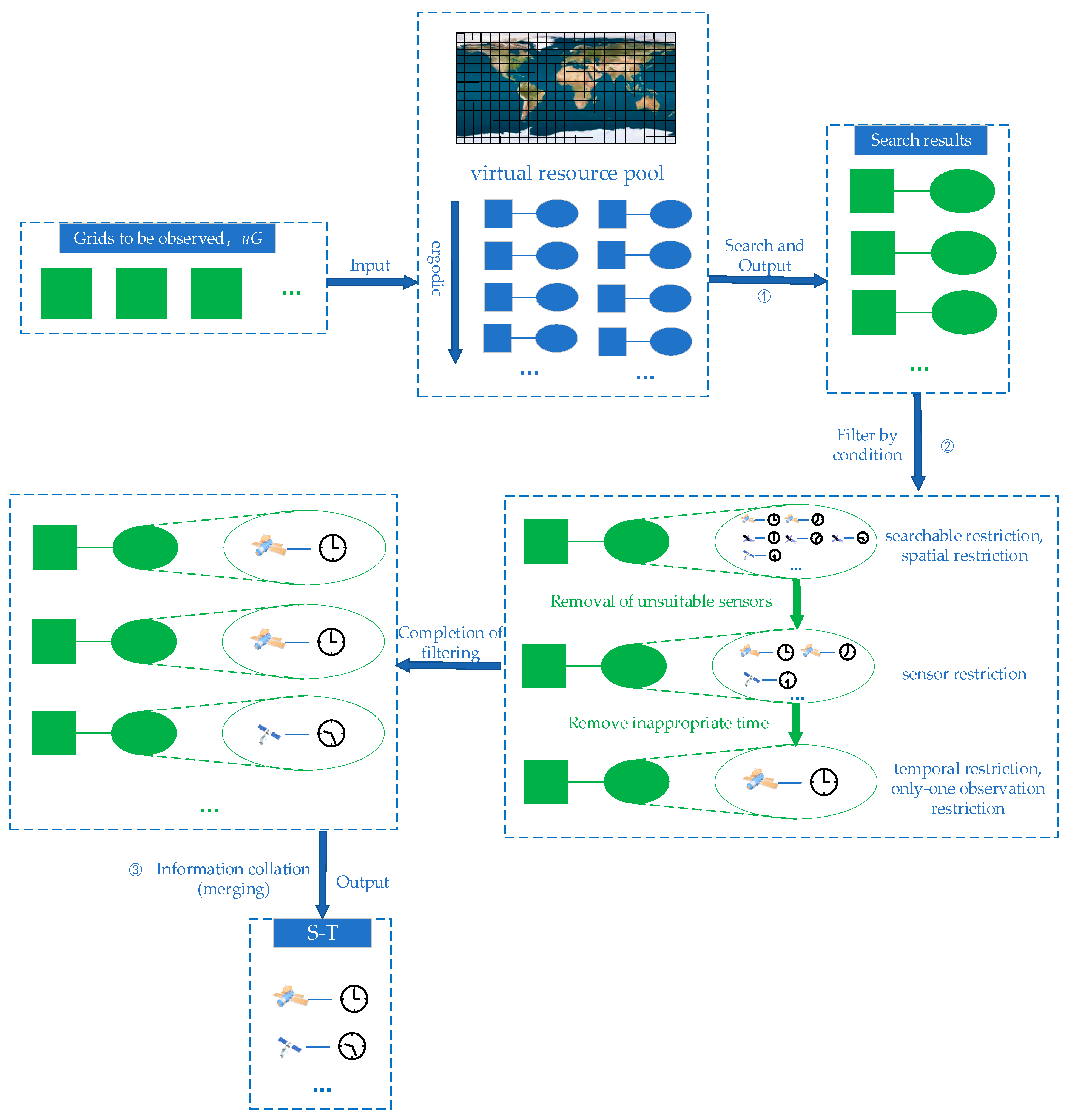
1.1. Background and Current State of Research

A remote sensing satellite is a kind of artificial Earth satellite that observes ground, sea, or air targets in its orbit and obtains target information through its payload such as on-board photoelectric remote sensing devices. The classic type of remote sensing satellite uses imaging equipment, such as visible light cameras, infrared cameras, or synthetic aperture radar to acquire images of specified targets on the ground according to the needs of business users. Due to their unique advantages, including their long operation time, wide observation range, lack of airspace and national boundary restrictions, and lack of personnel safety issues, remote sensing satellites have been widely applied to battlefield situational monitoring, land resource surveys, agricultural yield estimation, marine environment monitoring, urban land use planning, natural disaster forecasting, and disaster assessment. Consequently, a large number of remote sensing satellites have been launched, constructing satellite constellations. A constellation usually consists of several satellites configured according to certain rules. Remote sensing satellite constellations can achieve continuous monitoring of an area of Earth’s surface at any time. They play a significant role in improving the timeliness and integrity of satellite data for Earth observation and more complex application scenarios. Hence, the construction of remote sensing satellite constellations is valued by many countries. With the rapidly increasing demands of space exploration, the number of remote sensing satellites has increased dramatically in recent years. According to the existing known satellite launch and networking plans, this proliferation trend will be maintained long into the future. The number of remote sensing satellites is bound to reach thousands in orders of magnitude. In addition, several well-established giant constellations of low-orbit artificial satellites such as Starlink and OneWeb, which contain huge numbers of satellites, have already emerged. Theoretically, if remote sensors are attached to a giant constellation with thousands of satellites, it will become a giant remote sensing satellite constellation. At present, in remote sensing technology application fields such as military applications and disaster monitoring, which have very strict requirements for immediacy, the current remote sensing satellite observation resource scheduling system cannot yet meet the demand for minute- or even second-level responses in target observation.

In light of the growing number of remote sensing satellites and the requirements of high frequency, quantity, and low latency, it is imperative to investigate observation resource scheduling. Observation resource scheduling addresses the optimization problem of maximizing the control benefits of spacecraft by modeling the observation missions and available resources, driven by the needs of remote sensing satellite fleet users [1]. Through the reasonable allocation of Earth observation resources, the multiple coverage opportunities of multiple satellites can collaborate to achieve the best observing efficiency and reduce operation costs. Currently, the observation resource scheduling problem, as a combinatorial optimization problem, explodes in solution space with the rapid increase in the number of satellites and tasks. Effectively finding the optimal solution for this problem is still a great challenge.

Remote sensing satellite observation resource scheduling and mission planning technology is currently being developed by many scholars and space practitioners. Many studies have investigated and verified actual satellite observation systems. There are two main components of resource scheduling technology: the scheduling model and the scheduling algorithm. The scheduling model is the first step in the process of solving the mission scheduling problem. It is an important factor in determining the problem description, guiding the algorithm design, and influencing the complexity of the problem. Remote sensing satellite mission scheduling is a classical combinatorial optimization problem with NP-hard (non-deterministic polynomial-hard) characteristics [1], in which it needs to decide the order of mission execution and allocate satellites simultaneously. Faced with this problem, researchers have tried to find solutions from classical optimization models. The related scheduling models can be divided into resource-oriented task sequencing models and task-oriented resource allocation models depending on the decision object in the model [2].

A typical model among the solutions to satellite observation scheduling problems is the task sequencing model. The decision variables mainly represent the sequence of resources to execute tasks, reflecting the temporal logic and capacity constraints in the process of successive task execution. The existing studies related to task sequencing models can be divided into three categories: the vehicle routing problem (VRP), the graph theory model, and the workshop scheduling model. The vehicle path planning model is one of the first models used to address the remote sensing satellite mission scheduling problem [3]. It treats satellites as vehicles and mission targets as cities to be visited. Bianchessi et al. [4] applied the algorithm to a multi-satellite, multi-track mission scheduling scenario. Guo [5] solved the mission scheduling problem under sequestration capacity constraints. The graph-theoretic model describes the temporal order and conflict relationships among satellite missions by means of points and lines. Gabrel et al. [6], Bianchessi et al. [7], and Chen et al. [8] abstract the satellite resource scheduling problem as a directed acyclic graph model. For the multi-star scheduling problem, Xu et al. [9] establish a graph theory model based on a minimum spanning tree. Zhang et al. [10] and Wang et al. [11] constructed a graph-theoretic model with hierarchical optimization. The drawback of such models is that it is difficult to carry problem descriptions with compound task constraints for complex scenarios. Another class of models is the shop floor scheduling model. The related study was first introduced by Hall et al. [12]. This type of model has a clearer description of the constraints for satellite area target imaging. Subsequently, Cordeau et al. [3], Li et al. [13], and Gu et al. [14] pointed out that the process of remote sensing satellites performing tasks can be viewed as a process of distributing processes among different types of machines. In this process, satellites and ground stations are considered as machines, and imaging tasks and digital transmission tasks are considered as processes to be completed. In addition, Xiao et al. [15] designed a two-stage task scheduling framework to integrate the satellite imaging task with the output per-task scheduling. As for the problems concerning task sequencing, it is prone to lose high-quality solutions due to the high complexity of the problem constraints and the exponential time c complexity.

Another satellite observation resource scheduling model is the resource allocation model. This is a model oriented towards mission demands, guiding resource allocation decisions for mission execution. In this model, the visible time window (VTW) of the satellite to the observed target is considered as the resource to be dispatched, and therefore the model is also called the VTW allocation model. Bensana et al. [16], Gabrel [17], Jin et al. [18], Wang et al. [19], Liu et al. [20], and Jang et al. [21] expressed the VTWs selected by remote sensing satellites to perform the tasks in terms of 0–1 decision variables. The VTWs represented by 0–1 variables in these studies contain both satellite payload information and mission execution time, reflecting the order of satellite missions, and are more concise. Several subsequent authors have made more improvements based on this model. Lemaître et al. [22], He et al. [23], Mok et al. [24], Chu et al. [25], and Song et al. [26] considered the specific start moment of the mission while deciding the mission execution order and scheduling the mission based on the earliest start principle. On the other hand, Li et al. [27] and Liu et al. [28] scheduled missions based on imaging quality, while Kim et al. [29] focused on the side-view imaging mode in the SAR constellation imaging scheduling problem. These decoding processes above are applicable to agile remote sensing satellite scheduling. However, they are rule-based decoding approaches, so the exploration capability in larger solution spaces deteriorates and the time cost becomes higher for complex constraint cases. Lemaître et al. [22], She et al. [30], Chen et al. [31], and Frank et al. [32] used 0–1 variables to represent the task VTW while indicating the start moment of the task by an integer variable. Niu et al. [33] and Chen et al. [34] computed nonlinear pose transition time constraints on this basis. Multiple decision models such as these that use 0–1 variables for the visible time window of the satellite performing the task and integer variables for the task start time have better model completeness compared to the previous rule-based decoding process. Wang et al. [19], Valicka et al. [35], Nag et al. [36], Zhu et al. [37], He et al. [38], and Li et al. [39] discretized the visible time windows of remote sensing satellite imaging or number transmission missions. They directly decide the start and end time of the mission through 0–1 variables. This model has a smaller number of decision variables and a more concise model. Similarly to the multiple decision model, the discretized assignment model is also free from the influence of heuristic rules and can guarantee the diversity of solutions under complex constraints. However, it expands the solution space of the problem, which, in turn, makes the solving difficulty increase. Another feature of the discretization model is that the granularity of discretization can be controlled, and finding a reasonable granularity of discretization also helps to improve the effectiveness of the model.

There are many studies on polygonal coverage optimization problems in the field of sensing. Manhboubi et al. [40] developed algorithms to achieve the goal of increasing the area covered by a mobile sensor network and used K-means clustering techniques to improve the performance of the algorithms in terms of energy consumption and convergence time. This method can effectively solve the problem in mobile sensor coverage scenarios. Yakovlev et al. [41] addressed the problem of maximum coverage for service siting when both the demand area and the service area are arbitrarily shaped. The authors modeled the problem and solve it using computer techniques. Vaccaro et al. [42] investigated the problem of optimal area coverage using distributed sensing techniques. The authors formulated the problem as an optimization problem with a time-varying constant function and gave a gradient descent optimization algorithm. This method is effective in meeting the desired map resolution. These methods can effectively solve the problem in mobile sensor coverage scenarios, but they are based on the assumption that sensors can move freely without obstacles. Remote sensing satellite sensors, unlike mobile sensors, are not free to move in three dimensions due to strong physical constraints such as orbits. Therefore, the solution space of the remote sensing satellite problem is different from that of the mobile sensor problem.

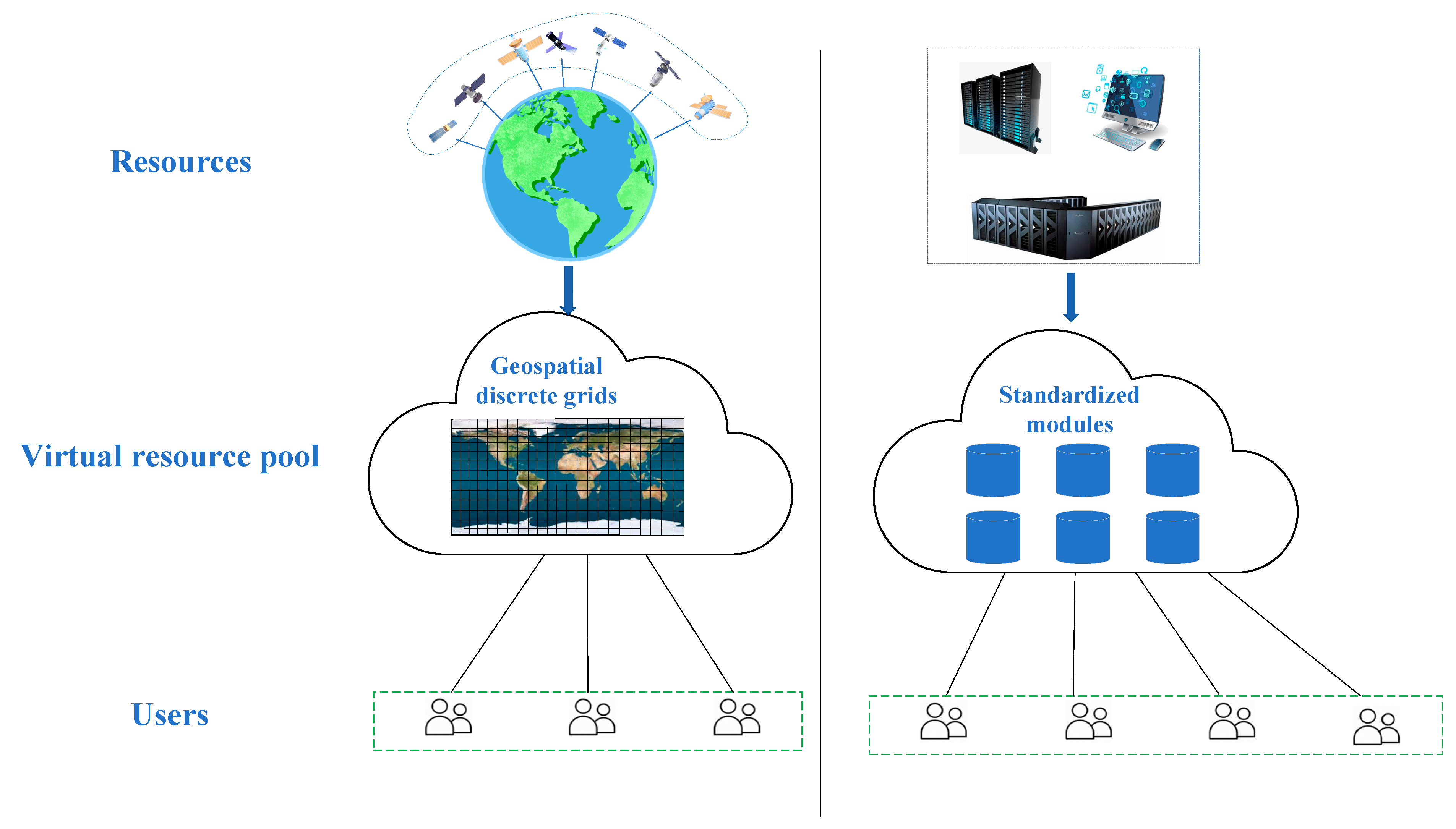
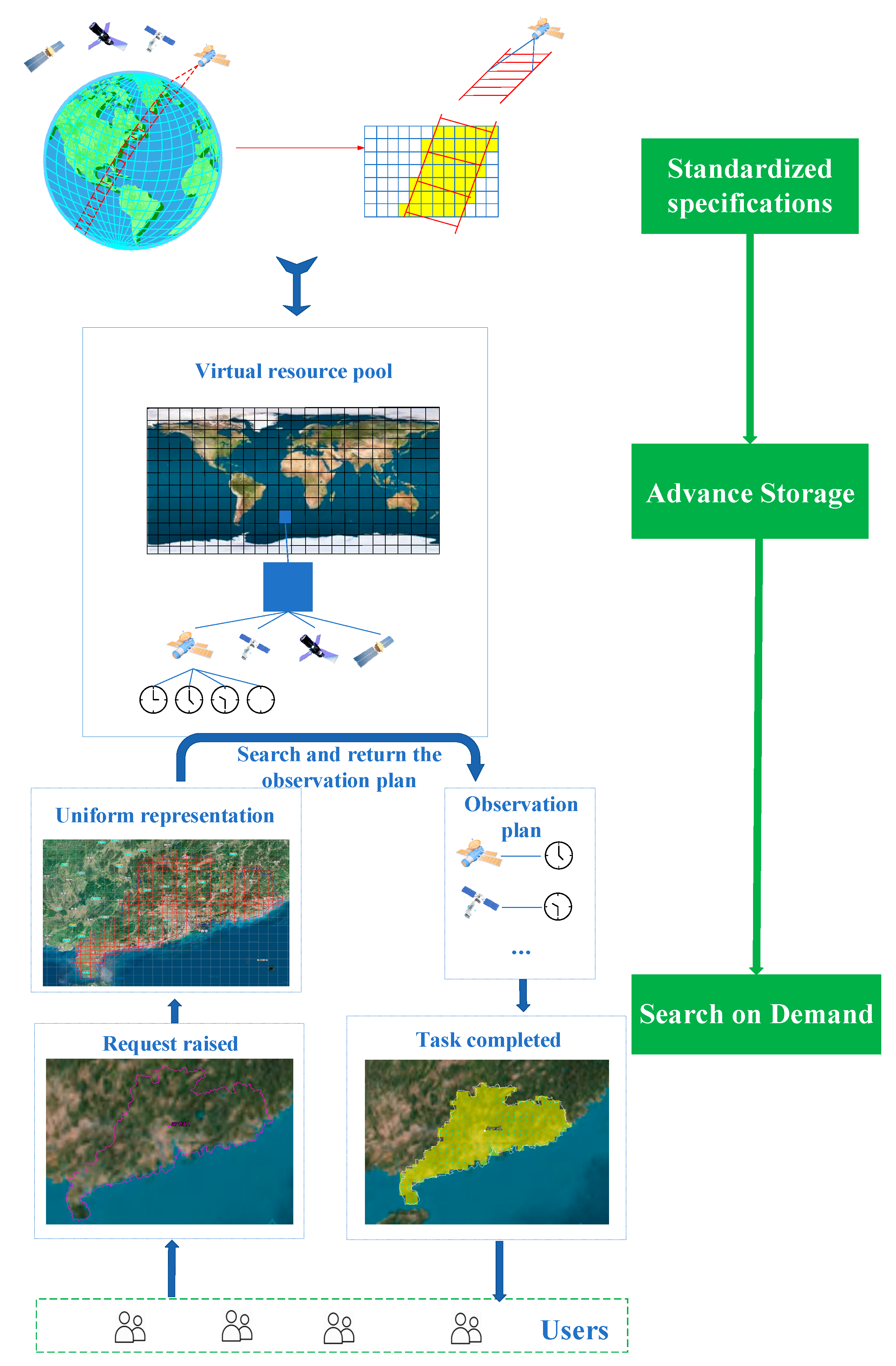
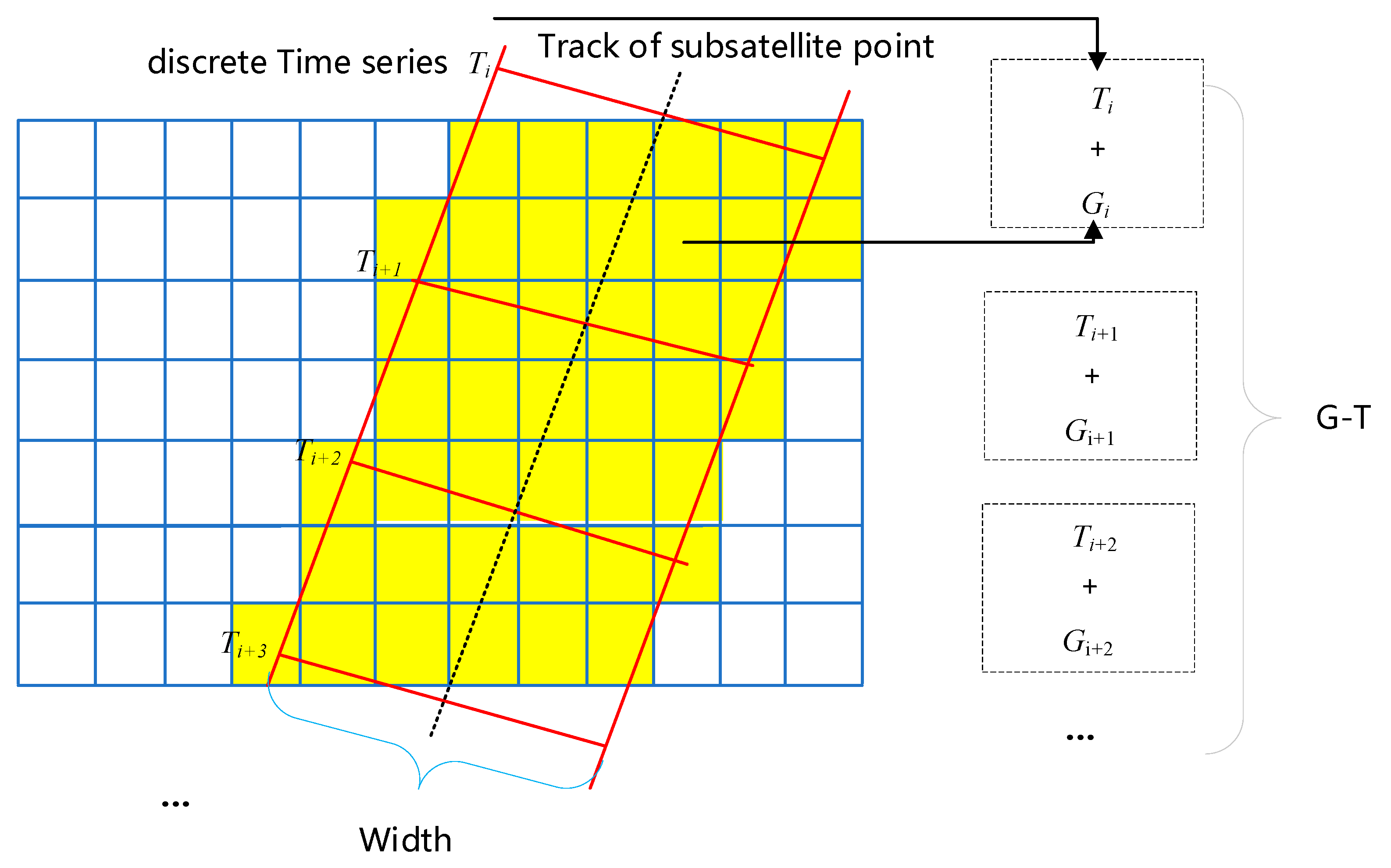
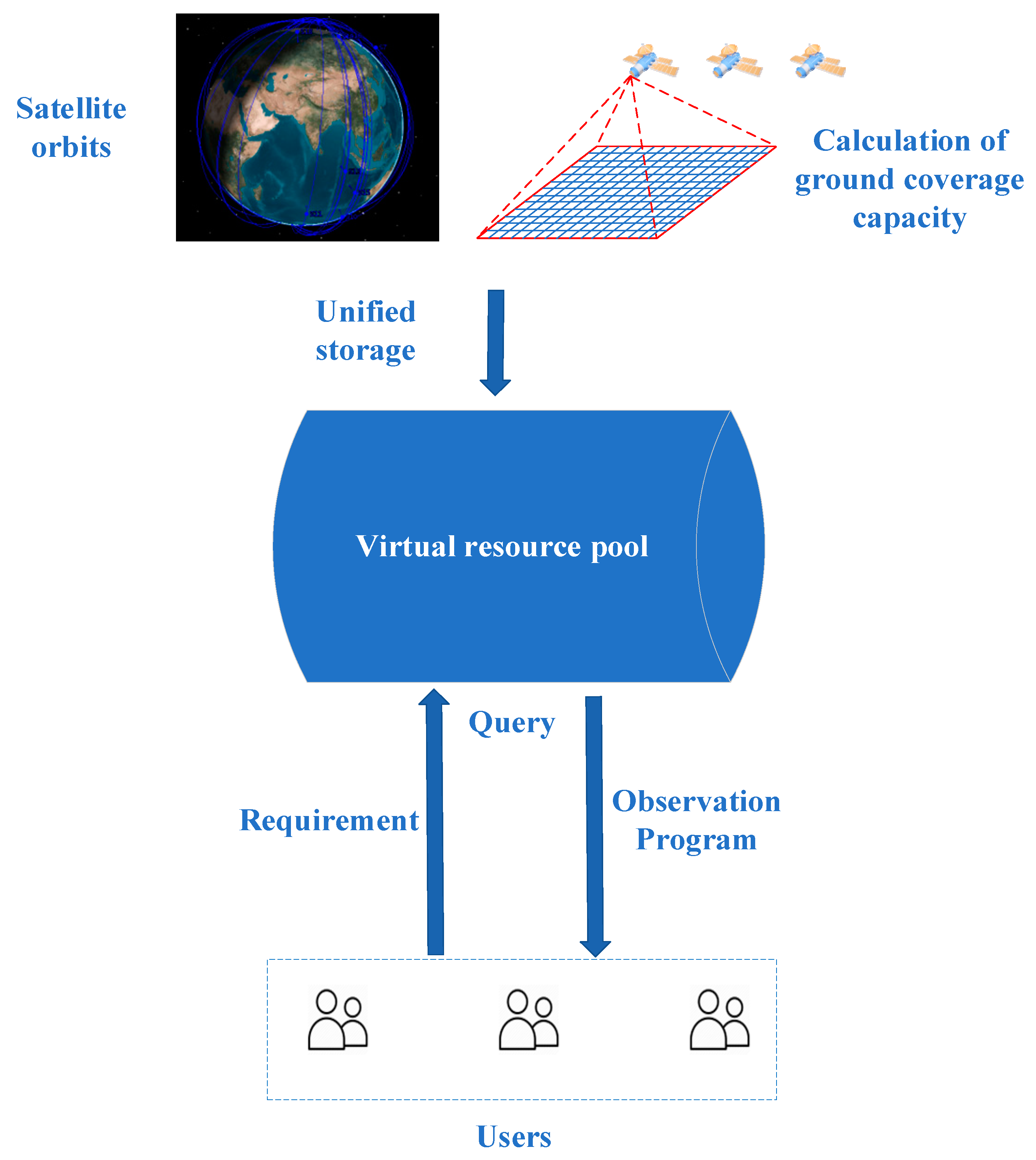
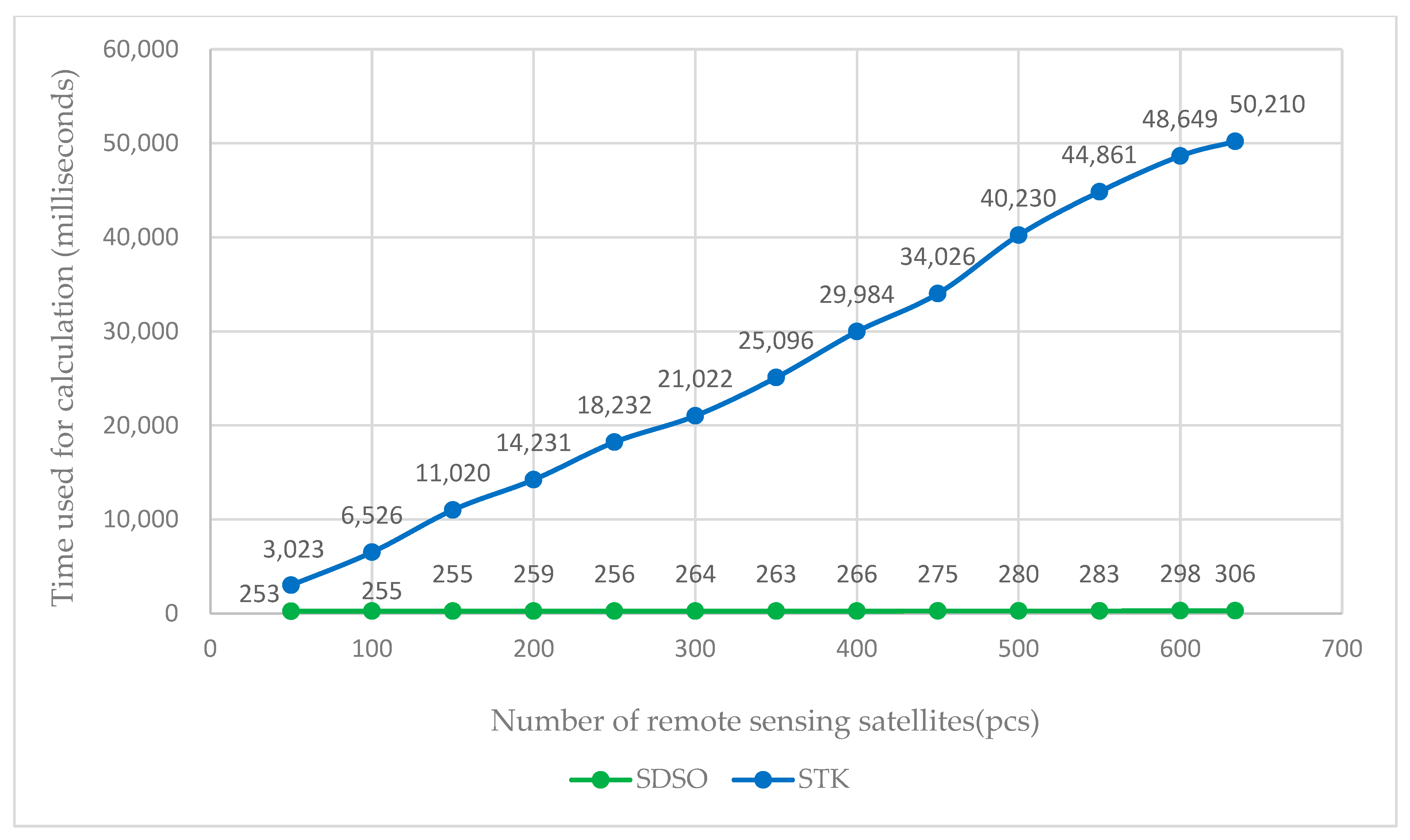
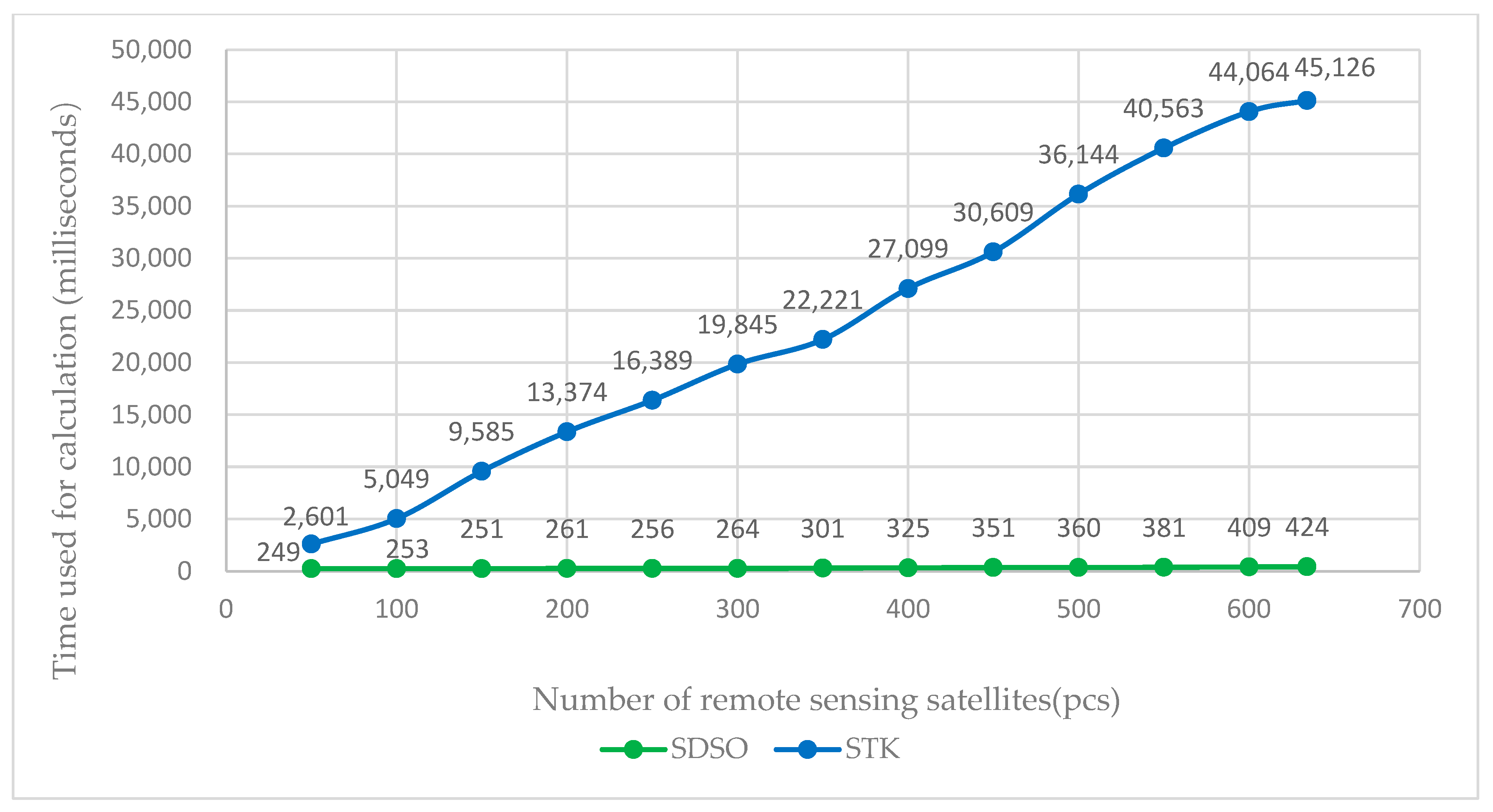
Overall, through the analysis of various models of satellite observation resource scheduling problems established by researchers and their solution algorithms, the shortcomings of existing research can be summarized. First, the existing solution schemes show an exponential increase in the computational complexity, and a sharp decrease in the solution efficiency as the number of satellite resources continues to increase. This is mainly due to the inconsistency in specifying satellite observation capabilities, necessitating the calculation of each satellite’s observation capacity for every target before scheduling resources. The number of times this calculation process is performed also increases significantly. Therefore, it is difficult for existing solution schemes to meet the rapid scheduling of remote sensing satellite resources of hundreds or even thousands in number. In practical application, this leads to the serious phenomenon of satellite “idling” and insufficient effective utilization, resulting in a waste of resources. Second, there is a lack of a set of general modeling and solution techniques to meet the comprehensive control needs of diverse remote sensing satellites. Despite similar modeling principles in terms of mission visibility and satellite resource allocation in time, space, and frequency domains, current models for remote sensing satellite mission scheduling still struggle with compatibility issues.

1.2. Contribution

(1)

This paper proposes a new methodology, namely, software-defined satellite observation (SDSO), to address the challenge in observation resource scheduling problem with a large amount of remote sensing satellites.

(2)

To address the inconsistency in describing remote sensing satellites’ ground coverage capabilities, we established a unified model for this purpose.

(3)

In order to realize the storage of Earth observation capabilities of remote sensing satellites, we designed the logical structure of the virtual resource pool of Earth observation capabilities of remote sensing satellites. This structure reduces query calculations while maintaining data integrity.

(4)

We developed a method to solve the multi-star, multi-task planning problem, utilizing search and filtering based on the unified description model and virtual resource pool. Experimental results demonstrate the method’s high computational efficiency, which remains stable and largely unaffected by the number of remote sensing satellites.

2. Methods

2.1. Framework of SDSO

Given the NP-hardness, the resource scheduling and mission planning of remote sensing satellites remain unresolved challenges, especially with hundreds or thousands of satellites. To overcome this challenge, we introduce a novel SDSO methodology, illustrated in Figure 1 with an analogy to cloud computing. Unlike optimization-based solutions, SDSO adopts the concept of resource virtualization from cloud computing. It decomposes the Earth observation capabilities into standardized units. Using the theoretical framework of Earth segmentation grid and satellite orbit prediction methods, a virtual resource pool with satellite capacities is constructed through a database system. The virtual resource pool is the basis for matching observation resources and user demands. It contains the observation capabilities of all remote sensing satellites, which allows users to obtain the required observation data from the virtual resource pool directly. Finally, the large-scale resource scheduling problem is addressed using database query techniques based on the virtual resource pool. This approach offers a new feasible solution for the efficient and cooperative scheduling of a massive number of remote sensing satellites.

The principle of SDSO is shown in Figure 2. It has three parts: unified specification, advanced storage, and search on demand, which form the research framework of SDSO. First, unified specification is defined to describe the observation capability of remote sensing satellites. It addresses the issues of inconsistent specifications and units in traditional path + row + time point sequence schemes, which have led to underutilization of satellite resources. Essentially, it employs a set of models and consistent specifications to uniformly describe the ground coverage capacities of various satellite types. The observation capabilities of different remote sensing satellites are abstracted into discrete minimum units based on uniform specifications. This forms the foundation for establishing a virtual resource pool and enables unified management and access to a vast array of diversified satellite resources.

For the second part, we established a virtual resource pool by using a database platform to store the Earth observation capabilities of remote sensing satellites. Its aim is to centralize storage and manage a large array of remote sensing satellite resources, enabling efficient fulfillment of user requirements. This involves dividing the global two-dimensional surface into individual spatial grids. Then, using the unified description model, each satellite’s observation capability is quantified into a spatial grid with associated time information. Each spatial grid contains coverage data from all satellites. Thus, a “satellite observation resource pool” is established to store all satellite observation resource information, which provides a basis for rapid remote sensing satellite resource scheduling by means of search.

Finally, we designed a query-based method to solve the remote sensing satellite resource scheduling problem. Specifically, a model based on the virtual resource pool for the remote sensing satellite Earth observation resource scheduling was established. Meanwhile, we designed an efficient solution method that operates by directly searching within the virtual resource pool. This process, an efficient resource scheduling computation, involves converting the target area into a collection of spatial grids, searching for coverage in the virtual resource pool, and filtering and merging query results under various constraints.

Figure 2 illustrates more details about the above three components. In fact, since the virtual resource pool has information on the Earth coverage of all satellites, a large number of satellite resources can be considered as a virtual satellite. A virtual satellite indicates the observation capability of all the satellites that have been deposited into the virtual resource pool. Through further exploration, the virtual satellite can be used to accomplish resource scheduling tasks in different scenarios. In this work, we verified the effectiveness of SDSO by conducting experiments that demonstrate the great potential of efficiently achieving a promising observation solution with abundant satellites.

2.2. The Unified Description of the Observation Capability of Remote Sensing Satellites

Coordinating the diverse array of remote sensing satellites, each with varying orbits, widths, resolutions, sensors, and control modes, poses a significant challenge, particularly as we consider both current and future satellites. At present, the Track of subsatellite point + Width + Time (TWT) method is used to describe the observation capability. A key drawback of this method is the lack of a uniform unit for measuring the observation capability of remote sensing satellites. This would result in each satellite’s observation capability being calculated once for each target, or resource scheduling could not begin. Both the subsatellite point trajectory and the width are variables that change with the satellite. The varying orbital altitudes, angles, and sensor widths of remote sensing satellites substantially add to the computational complexity. Therefore, the existing method of describing the surface coverage capability of remote sensing satellites is difficult to efficiently utilize abundant distinct remote sensing satellites.

To address these issues, we established a unified description for the observation capabilities of remote sensing satellites. This method takes the multi-scale two-dimensional Earth segmentation grid and discrete time code as the basic units for the unified description of the observation capability of remote sensing satellites. First, we divide the two-dimensional surface of the Earth into a number of spatial grids such that any region on the Earth’s surface can be described by a collection of grids. The discrete spatial grid with time information is then used to describe the coverage of remote sensing satellites over a period of time, as shown in Figure 3. Compared with the traditional method, the advantage of the proposed description method is that it can realize the unified characterization of multiple types and large numbers of remote sensing satellite resources with consistent specifications. The grid-based method describing remote sensing satellite observation capability directly uses the spatial grid to visually demonstrate the coverage. The process of determining the coverage target is to search whether the corresponding grid exists in the set of grids describing the observation capability of some individual remote sensing satellites without the need for complex topological calculations. Therefore, it can be easily adapted to the user’s observation needs, providing an opportunity for mission-intensive scenarios.

The basic elements of the method for a unified description of the observation capability of remote sensing satellites consist of two components, space and time. In this method, the coverage capacity of a satellite in a certain operating state can be expressed as in Equation (1).

$$Sat\to \left\{\begin{array}{l}(G_1,T_1)\\ (G_2,T_2)\\ \dots \\ (G_i,T_i)\\ \dots \\ (G_n,T_n)\end{array}\right.$$

(1)

where Sat means a satellite in some operating state, G_i means a collection of spatial grids, and T_i means discrete time. On the spatial side, each spatial grid set G_i represents the location of a specified region. On the time side, [T₁, T_n] is the time interval of the satellite observation capability being described. It is discretized into multiple time points according to time steps T_step.

$$\left\{\begin{array}{l}{T}_1,T_2,\dots ,T_n\in [T_1,T_n]\\ \forall i\in [1,n-1],T_{i+1}-T_i=T_{step}\end{array}\right.$$

(2)

This “G-T” structure makes it possible to clearly express which position is being covered by a particular satellite at what time. The relationship between this method and the traditional “TWT” description is shown in Figure 4.

Many global grid partitioning schemes have been proposed to realize one-to-one geographic location description in multiple levels. The grid division scheme used in the experiments of this paper is Google Earth [43], which takes the whole 180° × 360° area of the sphere as the parent node of a quadtree, gradually divides it into four, and stores them in order according to the level.

2.3. Virtual Resource Pool for Earth Observation Capabilities of Remote Sensing Satellites

To uniformly manage and offer standardized observation services utilizing diverse remote sensing satellite resources, it is essential to virtualize these resources. On one hand, there are several influencing factors on observation capability necessary to be considered. Remote sensing satellite resources have some unique characteristics as follows. Satellites are subject to the strict physical constraints of orbits and their observation capabilities have a rather strong spatial and temporal correlation. The types of sensors carried by different remote sensing satellites and their operating status also differ. On the other hand, remote sensing satellite resources for user demand also have unique characteristics; the user demand focusing the remote sensing satellite fleet on the target, visible or not, in space and time has more stringent requirements, and in different scenarios, it is appropriate for the use of satellite resources to achieve the observation effect to also be different. Finally, attributes such as the type, resolution, and operating status of the sensors also affect the fulfillment of the observation task. Therefore, the core problem is how to integrate remote sensing satellite resources and efficiently interface with user requirements.

To address this issue, we created a virtual resource pool that integrates the Earth observation capabilities of remote sensing satellites. Remote sensing satellite resources are virtualized and stored for searching based on observation needs. It is important to note that the creation of the virtual resource pool is based solely on the status of the resources, not on specific observation requirements. This process involves only the allocation of storage space for the virtual resource pool, without impacting resource scheduling time, thereby realizing the “more space for less time” concept in SDSO theory.

2.3.1. Virtual Resource Pool for Remote Sensing Satellite Observation Capabilities

The virtual resource pool of remote sensing satellite Earth observation capabilities is formed by virtualizing all satellite observation resources with uniform specifications. It takes the spatial grid as the basic unit for describing the Earth observation capability, and then encodes the observations of all satellites into grids that cover the whole surface of the Earth. The virtual resource pool thus contains the global coverage of all remote sensing satellites. The resource scheduling problem, whatever the observational need, can be solved by means of searching the virtual resource pool. The conceptual schematic of the virtual resource pool storing remote sensing satellite observation capability is shown in Figure 5. In general, the establishment of a virtual resource pool is an important method for integrating a large number of diversified satellite resources and efficiently matching user requirements.

2.3.2. Model Description of the Virtual Resource Pool

The virtual resource pool consists of two parts named the GST table and SC table, shown in Figure 6. The GST table has the spatial grid code as the primary key. It records the covered status of each grid covering the globe for a specified time period. The coverage of a grid is described by the remote sensing satellites as well as the time of coverage. The logical relationship (G-S-T) between the grid code (G), satellite (S) and time (T) codes presents a tree structure. The SC table has the satellite number as the primary key. It records the characteristics of all remote sensing satellites. The information of the SC table consists of the numbers of all remote sensing satellites as well as their set of characteristics (containing sensor type, resolution, operating status, etc.). The information of the GST table and SC table is related through satellite numbers.

The purpose of this design is to improve the search efficiency and to ensure that the search efficiency is not significantly affected by the number of satellites. The GST table of the virtual resource pool is keyed to the global spatial grid. The search is performed by traversing the global spatial grid once based on the set of grids of the target to be observed. Since the number of global spatial grids under a defined grid hierarchy is fixed, the number of satellites does not affect the computational volume of this traversal. The increase in the number of satellites only results in more information being contained in each grid. The subsequent data processing steps involve a very small fraction of the data volume compared to the first traversal, so the increase in the number of satellites does not significantly reduce the computational efficiency.

In order to facilitate the description of the logical structure of the virtual resource pool, the following notations were made: all variables named i, j, k, l, m and n appearing below take on natural numbers; the forms denoted by “<>” appearing in the following are key–value pairs. The concept of key–value pairs comes from computer science and can be expressed simply as <key, value>. The key is the keyword that uniquely identifies a key–value pair, and the value is the value associated with the key.

The virtual resource pool consists of two parts, the GST table and the SC table. These two parts are denoted as GST^S and SC^S. The logical structure of GST^S and SC^S (i.e., the logical structure of the virtual resource pool) is shown in

Table 1. Virtual resource pool logical structure and internal variables (GST table).

Name	Description	Structure	Detail
$GS{T}^{\mathrm{S}}$	GST table	Set	$GS{T}^{\mathrm{S}}=\{GS{T}_1,GS{T}_2,\dots ,GS{T}_{n_1}\}$
$GS{T}_i$	Information about the coverage of a grid	Key and value	$GS{T}_i=<G_i,S{T}_i^{\mathrm{S}}>$
$G_i$	The code of the grid	Single value	/
$S{T}_i^{\mathrm{S}}$	Coverage of the grid by all satellites	Set	$S{T}_i^{\mathrm{S}}=\{S{T}_{i1},S{T}_{i2},\dots ,S{T}_{i{n}_2}\}$
$S{T}_{ij}$	Coverage of the grid by a satellites	Key and value	$S{T}_{ij}=<S_{{}_{ij}}^{\mathrm{GST}},T_{ij}^{\mathrm{S}}>$
$S_{{}_{ij}}^{\mathrm{GST}}$	Number of the satellite	Single value	/
$T_{ij}^{\mathrm{S}}$	All times	Set	$T_{ij}^{\mathrm{S}}=\{T_{ij1},T_{ij2},\dots ,T_{ij{n}_3}\}$
$T_{ijk}$	The code of time	Single value	/
$S{C}^{\mathrm{S}}$	SC table	Set	$S{C}^{\mathrm{S}}=\{S{C}_1,S{C}_2,\dots ,S{C}_{n_4}\}$
$S{C}_i$	Characteristics of a satellite	Key and value	$S{C}_i=<S_I^{\mathrm{SC}},C_i>$
$S_i^{\mathrm{SC}}$	Number of the satellite	Single value	/
$C_i$	Characteristics of the satellite	Sequences	$C_i=(C_i^{\mathrm{Typ}},C_i^{\mathrm{Re}s})$
$C_i^{\mathrm{Typ}}$	The type of the sensor	Single value	/
$C_i^{\mathrm{Re}s}$	Resolution	Single value	/

.

It should be emphasized that since all satellites in the GST and SC tables must correspond one to one. Therefore, the following constraint relationships must be satisfied:

$$\left\{\begin{array}{l}\forall S_i^{\mathrm{SC}},\exists S_{jk}^{\mathrm{GST}}=S_i^{\mathrm{SC}}\\ \forall S_{ij}^{\mathrm{GST}},\exists S_k^{\mathrm{SC}}=S_{ij}^{\mathrm{GST}}\end{array}\right.$$

(3)

2.3.3. Relationship between Virtual Resource Pool and the Unified Description

The virtual resource pool is established by storing all the satellites that have undergone unified description. Since the process of storing the coverage capacity of each remote sensing satellite into the virtual resource pool is the same, this section describes the process of storing the coverage capacity of a particular remote sensing satellite into the virtual resource pool. In addition, the unified storage process can be carried out before the user’s demand, and thus the key to build the virtual resource pool is to ensure the completeness of the information rather than the rapidity of the calculation process.

The difference between the unified description model and the virtual resource pool model is the difference in the primary key. The unified description model uses satellites (S) as the primary key to describe the coverage capabilities of individual satellites. The virtual resource pool uses the spatial grid (G) as the primary key to describe the coverage of each grid in global space. Therefore, the process of storing satellite information into the virtual resource pool is the process of converting the same information from the former to the latter, as shown in Figure 7.

Therefore, the process of storing a satellite’s information into the virtual resource pool can be summarized as follows: for each G-T group of a satellite, traverse the global grid code of the virtual resource pool to find the spatial grid corresponding to the G; then store the T and S information as the values corresponding to the primary key of the spatial grid into the virtual resource pool, and repeat this process until all the grids have gone through the process described above. The coverage and capacity information of Sat are completely stored into the primary table. The coverage information of S, a satellite resource, is completely deposited into the GST table. Then the characteristic information of Sat is stored in the SC table, which completes the storage of the satellite Sat. Finally, all the satellites are stored in the virtual resource pool in the same way.

Following the steps described above, we construct a virtual resource pool containing information on the coverage capabilities of all satellites over time. The content of the virtual resource pool is periodically updated as needed to realize the preservation of information for all satellites and all time periods.

2.4. Remote Sensing Satellite Observation Resource Scheduling Methodology

To deal with the scheduling of Earth observation resources from remote sensing satellites, we designed an effective methodology according to specific emergency applications with multi-scenario and diversified user observation needs. As mentioned earlier, the virtual resource pool is a tool for integrating satellite resources and docking user demands. The virtual resource pool contains satellite observation resources, allowing users to query according to their needs. Based on the virtual resource pool, the proposed method was developed with user demand as input and scheduling scheme as output, aiming to complete all scheduling tasks as early as possible. The problem model takes the query and screening based on the virtual resource pool as the main solution means. This computational approach is very efficient and does not lead to the inability to solve the resource scheduling problem for a large number of remote sensing satellites due to the exponential growth of computational efficiency with the growth of the number of remote sensing satellites. The model can also be adapted to a variety of different application scenarios by adjusting the processing method of the query results.

2.4.1. Problem Model

The satellite resource scheduling model, based on the SDSO concept, utilizes the virtual resource pool of remote sensing satellites’ Earth observation capabilities. It is a large-scale scheduling model that relies on the unified description model and virtual resource pool. It takes observation demand as input, satellite number + time (S-T) used to complete the task as output, and completes the scheduling task as early as possible as the goal. The execution flow of the model is shown in Figure 8, which is characterized by describing the solution process of the resource scheduling problem as the search and screening process of the linear table data. Compared with the traditional resource scheduling model, the solution speed is greatly accelerated, and it has a very obvious advantage in the calculation speed of hundreds of satellite resource scheduling problems. Additionally, according to different application scenarios, different data screening programs can be designed that have a greater potential for complex application scenarios. In the following section, the model is described and the algorithm is introduced.

The following section describes the inputs, outputs, constraints and optimization objectives in the model of the remote sensing satellite resource scheduling problem based on virtual resource pooling.

Table 2. Virtual resource pool logical structure and internal variables (SC table).

Name	Meaning	Structure	Detail
$u{G}^{\mathrm{S}}$	A set of spatial grids for the area to be observed	Set	$u{G}^{\mathrm{S}}=\{u{G}_1,u{G}_2,\dots ,u{G}_{n_5}\}$
$typ$	Types of sensors to be used	Single value	$typ\in \{0,1\}$
$res$	Resolution of the sensor to be used	Single value	$res\in \{1,2,3,4,5\}$
$T^I$	Time requirements for completion of observation tasks	Interval	$T^{\mathrm{I}}=[T_{\mathrm{Start}},T_{\mathrm{End}}]$
$rS{T}^{\mathrm{S}}$	Output results in “S-T” framework	Set	$rS{T}^{\mathrm{S}}=\{rS{T}_1,rS{T}_2,\dots ,rS{T}_{n_6}\}$
$rS{T}_i$	Start-up reference time of a satellite	Key and value	$rS{T}_i=<r{S}_i,r{T}_i^{\mathrm{S}}>$
$r{T}_i^{\mathrm{S}}$	Start-up reference time set	Set	$r{T}_i^{\mathrm{S}}=\{r{T}_{i1},r{T}_{i2},\dots ,r{T}_{i{n}_7}\}$
$r{T}_{ij}$	Start-up reference time	Single value	/

shows the information about the variables related to the problem model. The model is explained in detail in the following section.

(1)

Inputs

The model input is the user requirement, and the general observation task requirement input contains three pieces of information. The first piece of information is the spatial location of the target to be observed. The position information is described using discrete spatial grid codes, following the conversion rules from latitude and longitude, as outlined in Section 3.2. These codes are utilized as input. The set is denoted as uG^S. The second piece of information is the time horizon for the completion of the observation task, expressed as an interval, T^I. The third piece of information is the requirement for satellite characteristics. Such requirements are varied in real scenarios and will not be studied in depth for the time being. As a simplified model only two variables are considered as examples, sensor type typ and resolution res.

(2)

Outputs

The output is the observation program and the result of the calculation. It is simply described as an S-T model, meaning “which satellites start working at which times” in order to accomplish all observation tasks. It is represented as a set rST^S. Its details are presented in Table 2.

(3)

Restriction

In this model, there are a total of five restrictions to be considered. They are temporal restriction, searchable restriction, spatial restriction, sensor restriction and only-one observation restriction. The implication of the temporal restriction is that all start-up reference times need to meet the time requirements for the completion of observation tasks. The temporal restriction is shown as

$$\forall rS{T}_i\in rS{T}^{\mathrm{S}},\forall r{T}_i^{\mathrm{S}}\in rS{T}_i,\forall r{T}_{ij}\in r{T}_i^{\mathrm{S}},r{T}_{ij}\in T^{\mathrm{I}}$$

(4)

The searchable restriction is the restriction that best characterizes the resource scheduling problem model under the SDSO idea. It means that all contents in the output must be existing contents in the virtual resource pool. Following this restriction, the observation resource scheduling problem solution is identified as a search process based on the virtual resource pool. The restriction is expressed as

$$\begin{array}{l}\forall rS{T}_i=<r{S}_i,r{T}_i^{\mathrm{S}}>\in rS{T}^{\mathrm{S}},\exists GS{T}_j=<G_j,S{T}_j^{\mathrm{S}}>\in GS{T}^{\mathrm{S}},\\ \exists S{T}_{jk}=<S_{jk}^{GST},T_{jk}^{\mathrm{S}}>\in S{T}_j^{\mathrm{S}},r{S}_i=S_{jk}^{GST}\end{array}.$$

(5)

The spatial restrain implies that all spatial grids contained in the input must be observed, denoted as

$$\begin{array}{l}\forall u{G}_i\in u{G}^{\mathrm{S}},\exists rS{T}_j\in rST,\exists S{T}_{kl}\in S{T}_k^{\mathrm{S}}\in GS{T}_k=<G_k,S{T}_k^{\mathrm{S}}>,\\ rS{T}_j\mathrm{and}S{T}_{kl}\mathrm{meet}\mathrm{the}\mathrm{searchable}\mathrm{restriction}\\ G_k=u{G}_i\end{array}.$$

(6)

The sensor restriction is that all sensors in the result must conform to the input user requirements, denoted as

$$\begin{array}{l}\forall r{S}_i\in rS{T}_i\in rS{T}^{\mathrm{S}},\exists S_j^{\mathrm{SC}}\in S{C}_j\in S{C}^{\mathrm{S}}\\ r{S}_i=S_j^{\mathrm{SC}},C_j^{typ}=typ,C_j^{res}\le res\end{array}.$$

(7)

The only-one observation restriction means that each grid of the region to be observed needs to be observed only once, without having to be observed multiple times. It is denoted as

$$\begin{array}{l}\forall u{G}_i\in u{G}^{\mathrm{S}},\forall u{G}_j\in u{G}^{\mathrm{S}},i\ne j,\\ \exists rS{T}_k,rS{T}_l\in rST,\exists S{T}_{mn}\in S{T}_m^{\mathrm{S}}\in GS{T}_m,\exists S{T}_{op}\in S{T}_o^{\mathrm{S}}\in GS{T}_o\\ rS{T}_k\mathrm{and}S{T}_{mn}\mathrm{meet}\mathrm{the}\mathrm{searchable}\mathrm{restriction}\\ rS{T}_l\mathrm{and}S{T}_{op}\mathrm{meet}\mathrm{the}\mathrm{searchable}\mathrm{restriction}\\ G_m\ne G_o\end{array}.$$

(8)

(4)

Target

SDSO oftentimes involves abundant satellite resources where, “how to complete all observation tasks earlier” is the most likely concern of users. Therefore, the target is set to the moment when the last observation task is started. The earlier this moment is, the earlier all observation tasks will be completed.

$$\begin{array}{l}{T}_{\mathrm{finish}}=\max \{r{T}_{11},\dots ,r{T}_{ij},\dots ,r{T}_{n_7{n}_8}\}\\ \min T_{\mathrm{finish}}\end{array}.$$

(9)

2.4.2. Solution to Remote Sensing Satellite Resource Scheduling Problem Based on Virtual Resource Pooling

Through the virtual resource pool, the scheduling of remote sensing satellite resource is transformed into an information querying process, which makes the on-demand scheduling of resources fast. The schedule just needs to find the required part of information in the virtual resource pool and then simply filter and merge this information according to the demand. The flowchart is shown in Figure 9.

It can be noted that the developed method is divided into three steps: search, screening and merging. Since the research content of this paper aims to propose a new problem-solving idea, the specific algorithms used for the search and screening process are not discussed in detail. The specifics of these three steps are described below.

(1)

Searching

This step performs a traversal search of the GST table targeting the set of spatial grids uG^S of the region to be observed. The key of each GST_i in the GST table is the grid code G_i, so the search process can be described as finding all GST_i such that

$$\forall u{G}_j\in u{G}^{\mathrm{S}},\exists G_i\in GS{T}_i,G_i=u{G}_j$$

(10)

The result in this step is sure to meet searchable restriction and spatial restriction. All GST_i form the set of search results Step₁.

(2)

Screening

The information in Step₁ will be filtered in this step. The purpose of screening is to remove the information in Step₁ that does not meet the requirements. The aim of this paper is to present a new problem-solving idea, so the model is simplified as an example to explain the idea. The simplified screening process is divided into two parts: sensor screening and time screening.

The purpose of sensor screening is to sift out the information that does not meet the requirements of sensor attributes. Screening is performed for each S_ij^GST in ST_ij in ST_i^S in GST_i. Delete the information that does not meet the requirements based on the SC table. If S_ij^GST does not meet the characteristic requirements, trace back upwards to find the GST_i in which it is located and delete it from the set Step₁ in which it is located. The result obtained in this step is sure to meet the sensor restriction.

The purpose of time screening is to remove information entries that do not meet time requirements. That is, filtering is performed for each T_ijk. In order to meet the goal, all the times under the same T_ij^S are put together and sorted, selecting the earliest time that meets the time constraints and then deleting the others. The result of this step is sure to meet temporal restriction and only-one observation restriction. Once the five restrictions are met, the result of this part of the process is defined as Step₂.

(3)

Merging

The purpose of the merging is to transform the results of the searching and screening into valid information. Since the output of resource scheduling should be information about which satellites are selected and when these satellites are switched on to accomplish the observing task, the grid-related information is actually not ultimately needed. The process of merging is to ignore the grid information and merge the same sensor information as a reference for resource scheduling.

All GST_i in Step₂ are key–value pairs, and the key G_i represents the spatial grid, which is non-referential information. Therefore, this part of the information is ignored and the ST_ij in all ST_i^S are extracted to form a new set containing only S-T. The key S_ij^GST of all ST_ij in this set is the required satellite, and all values belonging to the same key are combined to form a new key value for output, rST_i (detailed information is provided in Table 2). All rST_i form the set rST^S.

At this point, the computational process from input to output is described. The process consists almost entirely of searching and screening, which is a process of screening from a large amount of information to a small amount of information, so there is no exponential time complexity. This is an important reason why the SDSO idea can quickly solve the resource scheduling problem for a large number of satellites.

3. Experiments and Results

3.1. Environment and Data

3.1.1. Environment

We constructed a SDSO simulation platform to verify the performance of SDSO proposed in this paper, shown in Figure 10. It has the functions of spatial grid calculation, virtual resource pool data entry, querying according to needs, and data organization.

Table 3. Hardware conditions of the experiment.

Conditions	Details
Processing unit	12th Gen Intel(R) Core(TM) i5-12500 3.00 GHz
RAM	16 GB

and

Table 4. Software conditions of the experiment.

Conditions	Details
Operating system	Windows11 64-bit
Development tool	Visual Studio 2017
Programming language	C++
Interface framework	Qt 5.12.5
Database	MongoDB 5.0

show the hardware and software conditions of the simulation experiment.

3.1.2. Data and Data Sources

(1)

Satellites’ orbits and width of sensors

The satellite orbit data used in the experiment were obtained from https://www.space-track.org/ (19 March 2023). The orbits of the five satellites used in the first part of the experiment were selected from the Gaofen series satellites, and the widths were set by ourselves. Their number in The North American Aerospace Defense Command (NORAD), widths, and ID are shown in

Table 5. Information on the satellites used in the first part of the experiment.

Satellites’ ID	NORAD	Width
S1	43616	20 km
S2	43259	30 km
S3	43262	40 km
S4	39150	50 km
S5	40118	60 km

. The time step for depositing into the virtual resource pool was set to 1 s.

The source of orbital data for the 634 satellites required for the second part of the experiment was https://www.space-track.org/#catalog (12 July 2023), where TLE orbital data were searched for all satellites with the name “OneWeb”. The satellites were numbered from OW001 to OW634 according to the NORAD number in increasing order (this data source can search a total of 635 satellites, but the orbital data of the satellite with the NORAD number of 48969 was not in line with the common sense of the error and deleted). Each satellite simulation added sensors according to their number, with the first 317 set to a 20 km width and a 40 km width set after the first 317. These two widths maintained the ratio of 1:1, regardless of the number of satellites selected for the experiment, aiming to keep the selected satellites in the above ratio of sensor width.

(2)

Targets to be observed and time requirements

The same regional target was used for the first part of the experiment and for the large area fast coverage in the second part of the experiment. This target is the region where Guangdong Province is located, as shown in Figure 11. Regarding the timing, the timeframe for Part I is 1 November 2022 at 4:00 a.m. to 4 November 2022 at 4:00 a.m. The timeframe for Part II of the large area rapid coverage experiment is 1 May 2023 at 4:00 a.m. to 2 May 2023 at 4:00 a.m.

Twelve points were selected for the multi-target rapid observation experiment in the second part of the experiment. Their latitude and longitude where they are located are shown in Figure 12 and

Table 6. Latitude and longitude of the 12 targets.

Target Number	Longitude	Latitude	Target Number	Longitude	Latitude
1	126.7	45.8	7	125.4	43.7
2	117.3	38.8	8	112.7	37.8
3	109.2	34.2	9	119.0	32.1
4	115.9	28.6	10	113.0	28.3
5	108.5	23.0	11	113.4	23.3
6	106.7	26.5	12	104.3	36.7

. The time frame of the multi-target rapid observation experiment is the same as that of the large area rapid coverage experiment.

The motion target tracking experiment simply simulated the flight path of an airplane that maintains a speed of approximately 800 km/h. The starting point is Chengdu and the end point is Shanghai. Nine targets were set on the flight path, and the targets at points other than the start and end points were required to be observed once within 3 min. The start and end points were allowed to be observed once within 1 h. The intention was to simulate the process of tracking a fast-moving target by observing the specified path points seven times in a four-hour period. The locations of these points and the time intervals at which they must be observed are shown in Figure 13 and

Table 7. Information on the satellites used in the last part of the experiment.

Number of the Point	Location (Longitude, Latitude)	Time Interval
1	104.2, 30.7	1 May 2023 11:00:00–12:00:00
2	106.7, 30.7	1 May 2023 12:17:00–12:20:00
3	109.2, 30.7	1 May 2023 12:37:00–12:40:00
4	113.8, 31.1	1 May 2023 13:20:00–13:23:00
5	116.2, 31.1	1 May 2023 13:30:00–13:33:00
6	118.7, 31.1	1 May 2023 14:01:00–14:04:00
7	121.5, 31.1	1 May 2023 14:20:00–15:00:00

(in ascending order from origin to destination). In Figure 13, the blue line in the diagram simulates the flight path of a commercial aircraft, the red square grid represents this route, and the solid red squares indicate points that need to be observed on time.

3.2. Methods and Procedures

After validating the effectiveness of SDSO, we proceeded to test it in simulation scenarios to determine the extent of efficiency improvement it could achieve. The experiment was divided into two parts. The first one was carried out to study the accuracy of the calculation in order to verify its feasibility. This experiment took the region where Guangdong Province is located as an observation target, and calculated the visibility of a single satellite to this target in a specified time period. Five remote sensing satellites in actual orbits with different widths were selected for five simulation experiments. The Satellite Tool Kit (STK) software and the SDSO simulation experiment program were used to calculate the coverage of the observation target satellite by satellite, and then the two groups of results were compared. Thus, the feasibility of the principle of SDSO was verified.

The second experiment was to observe the computational efficiency of SDSO with different numbers of satellites and in different scenarios. Using the OneWeb constellation, which is a constellation of quite a lot of satellites currently available in orbit (containing a total of 634 satellites), we simulated the installation of a sensor with a fixed width for each satellite to mimic a constellation of remote sensing satellites. The same resource scheduling simulation experiments were performed with the SDSO simulation program and STK, respectively. The main focus was on the time they consumed to accomplish each task. The task was designed as three different scenarios: large area fast coverage, multi-target fast observation, and moving target tracking. It should be noted that the height of the target to be observed was not taken into account in this study since it was modeled on the two-dimensional Earth’s surface.

(1)

Large area fast coverage

Input a regional target that is required to achieve complete coverage of the region in one pass. With this in mind, design the S-T observation program with the goal of the earliest possible completion time of the observation task. Focus on the time required to complete the task.

(2)

Multi-target fast observation

Select a number of point targets as the targets to be observed, with the requirement of realizing a complete observation of all point targets. Again, with the goal of the earliest time to accomplish the mission, calculate the S-T observation program. Focus on the time required for the calculation.

(3)

Moving target tracking

This scenario simulates the tracking of a complete motion path completed by multiple observations in a short period of time. Multiple point targets containing temporal constraints are selected to form a sequence of points used to model the predicted outcome of the motion path of a moving target. It is required to utilize the implementation to complete a single observation of all points while satisfying the temporal constraints of each point. Compute the output S-T observation scheme. Focus on the time required for the computation.

After performing the experiments for the three scenarios using 634 satellites, the number of satellites was then gradually reduced from 600 to 50 in groups of 50 for the same experiments. Each set of experiments aims to determine the computation time. Observe how the computational efficiency of the two scenarios, STK and SDSO, changes as the satellite size changes.

3.3. Results

3.3.1. Results of Feasibility Verification Experiments

Table 8. Results of the calculation of the time of visibility to the target using STK and the SDSO Simulation Program. The dates in the table omit the year and month and are indicated by a number preceding the time for a specific day in November 2022.

Satellite ID	SDSO Simulation Program (Date Start Time—End Time)	STK (Date Start Time—End Time)
S1	3 18:19:35–03 18:20:38	3 18:19:37–03 18:20:38
S2	3 14:52:35–03 14:53:12	3 14:52:35–03 14:53:12
S3	1 14:37:02–01 14:37:38	1 14:37:02–01 14:37:37
	2 15:00:44–01 15:01:14	2 15:00:43–02 15:01:11
	3 03:00:36–03 03:01:08	3 03:00:38–03 03:01:08
	4 03:25:36–04 03:26:12	4 03:25:39–04 03:26:13
S4	2 14:22:43–02 14:23:30	2 14:22:42–02 14:23:31
	4 02:46:16–04 02:47:20	4 02:46:18–04 02:47:20
S5	1 14:06:25–01 14:07:19	1 14:06:25–01 14:07:18
	2 14:26:14–02 14:26:25	2 14:26:16–02 14:26:25
	3 02:24:04–03 02:24:40	3 02:24:04–03 02:24:40
	4 02:44:54–04 02:45:40	4 02:44:57–04 02:45:41

shows the visible time to the target calculated by the SDSO simulation experiment program and STK for each of the five satellites. The time representation format is “date + hour, minute and second”, and the year and month are all November 2022. Since the time step of the virtual resource pool created by the experiment is 1 s, the accuracy of the results of the experiment is also 1 s.

The parts of the calculations where the results are the same are indicated by bolded numbers. However, some of the calculation results have deviations (the maximum deviation is 3 s). There are two main reasons for analyzing the deviation. First, the time step for storing data in the virtual resource pool in the experiment was 1 s, so it was not possible to recognize a difference of less than 1 s. For example, the computed results of S3 and S4 both have 1 s deviation due to this reason. This deviation is completely controllable. It can be minimized by choosing a smaller time step when building the virtual resource pool. Second, in order to ensure that the targets were fully included in the computation, the grid was fitted to a slightly larger region than the actual regional targets (as reflected in Figure 12). This led to the fact that the time range calculated via the SDSO simulation may be slightly larger (i.e., starting earlier and ending later) than that calculated via STK, which occurs in the results of S1, S3, S4, and S5. This deviation is affected by the grid hierarchy and is also controllable.

Overall, the results of the two calculations are basically in agreement. The results of the STK calculations verify the correctness of the results of the simulation calculations of SDSO. It can be considered that the feasibility of SDSO as a principle has been verified through the experiment.

3.3.2. Results of Multi-Scenario Simulation Experiments

(1)

Comparison of computation time curves for three scenarios

Figure 14, Figure 15 and Figure 16 show the time profiles of the three scenarios of large area fast coverage, multi-target fast observation, and moving target tracking, respectively. The two lines in each figure represent STK and SDSO, respectively. The horizontal axis is the number of available remote sensing satellites and the vertical axis is the time required for computation. In the following, these three experiments are referred to as Group I, Group II, and Group III, respectively. Focusing on the time consumed for computation, the results of the three sets of experiments have obvious similarities. It can be found that in the experiment of scheduling 634 satellites, the time consumed by the SDSO is much smaller than that of STK. By observing the trend of the curves, it can also be found that the growth rate of the time consumed by the SDSO is significantly smaller than that of STK as the number of available remote sensing satellites rises.

From the results, it can be found that the computation time and the number of satellites show an almost linear relationship. The reason why the computation time rises with the number of satellites can be further analyzed. It is found that the main source of time consumed by STK is divided into two parts. The first part of the time is used to calculate the visible time window of each satellite for each target to be observed. The second part of time is used for mission planning. Due to the large number of satellites and targets in this experiment, the first part of the time occupies a significant portion. The number of computations in the first part is determined by the product of the number of satellites and the number of targets to be observed. This is the reason why the computation time grows linearly. This proves the sophistication of the SDSO idea to first standardize the description specification and store the satellite coverage capacity in advance, thus saving the first part of the computation time.

Table 9. The ratio of the time consumed by the two approaches and the time-growth multiplier.

Experimental Group	The Ratio of the Time Consumed by the Two Approaches	The Time-Growth Multiplier (SDSO)	The Time-Growth Multiplier (STK)
Group I	20.37	1.92	37.25
Group II	164.08	1.21	16.63
Group III	106.43	1.70	17.35

organizes the ratio of the time consumed by STK to the time consumed by the SDSO for the simulated resource scheduling computation experiments on the 634 satellites for the three scenarios (referred to as the ratio of the time consumed by the two approaches) and the multiplier of the time consumed by the computation of the 634 satellites to the time consumed by the computation of the 50 satellites (referred to as the time-growth multiplier). It can be seen that SDSO takes significantly less time than STK for each task, and the time growth rate of SDSO is much smaller than that of STK.

(2)

Calculated results of the scheduling scheme for the three scenarios

To make the experiment complete,

Table 10. Resource scheduling solution for large-area fast coverage scenarios.

Satellites’ ID	Start-Up Reference Time
OW006	1 May 2023 4:28:30–1 May 2023 4:29:10
OW010	1 May 2023 4:12:40–1 May 2023 4:13:10
OW168	1 May 2023 6:00:20–1 May 2023 6:00:50
OW169	1 May 2023 4:17:00–1 May 2023 4:18:00
OW174	1 May 2023 5:29:30–1 May 2023 5:29:50
OW175	1 May 2023 4:25:10–1 May 2023 4:25:20 1 May 2023 4:25:40–1 May 2023 4:25:50
OW182	1 May 2023 4:33:10–1 May 2023 4:33:40
OW183	1 May 2023 4:11:00–1 May 2023 4:11:10 1 May 2023 4:11:30–1 May 2023 4:11:40
OW193	1 May 2023 4:03:20–1 May 2023 4:03:50
OW194	1 May 2023 5:10:10–1 May 2023 5:10:20
OW195	1 May 2023 5:26:00–1 May 2023 5:26:30
OW215	1 May 2023 5:23:20–1 May 2023 5:23:30
OW266	1 May 2023 6:24:00–1 May 2023 6:25:10
OW292	1 May 2023 6:12:20–1 May 2023 6:12:50
OW297	1 May 2023 6:31:00–1 May 2023 6:31:40
OW309	1 May 2023 4:15:20–1 May 2023 4:16:30
OW318	1 May 2023 4:31:30–1 May 2023 4:32:10
OW320	1 May 2023 4:04:40–1 May 2023 4:05:20
OW325	1 May 2023 4:21:40–1 May 2023 4:22:40
OW328	1 May 2023 4:06:10–1 May 2023 4:06:50
OW330	1 May 2023 4:09:20–1 May 2023 4:09:50
OW336	1 May 2023 4:18:30–1 May 2023 4:19:30
OW399	1 May 2023 5:53:30–1 May 2023 5:53:40
OW432	1 May 2023 9:29:30–1 May 2023 9:29:40
OW436	1 May 2023 5:34:40–1 May 2023 5:35:40
OW456	1 May 2023 5:46:20–1 May 2023 5:46:40
OW457	1 May 2023 6:13:30–1 May 2023 6:14:10
OW544	1 May 2023 6:31:50–1 May 2023 6:31:60
OW557	1 May 2023 8:08:50–1 May 2023 8:09:00
OW581	1 May 2023 7:08:10–1 May 2023 7:08:50
OW587	1 May 2023 7:21:20–1 May 2023 7:22:30
OW589	1 May 2023 7:12:30–1 May 2023 7:13:10
OW590	1 May 2023 7:26:20–1 May 2023 7:27:10

,

Table 11. Resource scheduling solution for the multi-target rapid observation scenarios.

Satellites’ ID	Start-Up Reference Time
OW166	1 May 2023 4:38:40
OW190	1 May 2023 7:34:30
OW266	1 May 2023 6:20:10
OW320	1 May 2023 4:00:30
OW330	1 May 2023 4:08:10
OW331	1 May 2023 4:45:00
OW336	1 May 2023 4:19:00
OW363	1 May 2023 6:14:30
OW364	1 May 2023 4:45:00
OW437	1 May 2023 4:56:00
OW587	1 May 2023 7:20:30
OW618	1 May 2023 4:21:40

and

Table 12. Resource scheduling solution for motion target tracking scenarios.

Satellites’ ID	Start-Up Reference Time
OW409	1 May 2023 11:11:50
OW531	1 May 2023 12:18:00
OW034	1 May 2023 12:39:40
OW254	1 May 2023 13:22:30
OW489	1 May 2023 13:32:30
OW030	1 May 2023 14:03:10
OW515	1 May 2023 14:51:40

show the computational results of the SDSO simulation program for each of the three scenario scheduling schemes. These results were verified by STK.

4. Discussion

4.1. Efficiency of SDSO Ideas in Solving Observation Resource Scheduling Problems

As a query-based solution to the observation resource scheduling problem, the proposed SDSO shows promising computational efficiency. Moreover, the time consumed by computation does not increase significantly with the growth of the number of satellites involved in resource scheduling. To a certain extent, our proposed SDSO provides a feasible alternative for the unified management and cooperative scheduling of a large number of satellites in the future. It is expected that the efficient resource dispatching of hundreds or even thousands of remote sensing satellite resources can be carried out within an acceptable time to solve the demands of huge number and complex scenes. Meanwhile, it also provides rapid observation methods for some urgent satellite application scenarios, such as natural disaster monitoring and military reconnaissance.

4.2. Research on Accuracy Needs to Continue

SDSO is derived from the idea of “space for time”, i.e., the storage space occupied by the virtual resource pool is exchanged for the efficiency of resource scheduling computation. In this paper, the simulation experiments verified the effectiveness of our proposed methodology with a controlled loss of precision. When building a virtual resource pool, the spatial grid level and the time step will have an impact on the accuracy. Higher accuracy may mean lower efficiency, so the related research on accuracy and efficiency needs to be continued in the future.

4.3. Future Perspectives on SDSO Applications

SDSO employs virtual resource pool as a tool to implement centralized management of satellite resources. The virtual resource pool can accommodate a large number of satellites with different types of information. On one hand, the observation capabilities of all existing remote sensing satellites can be presented in a more intuitive way through the design of the visualization interface. Accordingly, people can obtain more effective information, which can enable the discovery of the possible waste of satellite resources in time, thus providing help for the construction of a large number of remote sensing satellite constellations. On the other hand, the idea of SDSO may be used in more fields to solve some NP-HARD problems. For instance, a unified description of surveillance camera observation capabilities for streets, combined with the creation of virtual resource pools, could yield valuable insights and regulations for urban planning.

5. Conclusions

Given the rapid increase in the number of remote sensing satellites and the challenges faced by existing methods in efficiently addressing large-scale observation resource scheduling, this work introduces a new solution ideology called SDSO. Specifically, we first defined an uniform specification, which is used to virtualize and store the remote sensing satellite resources, establishing a virtual resource pool. Next, to efficiently schedule the satellite resource, we designed a fast method based on query technique in a database. During the second phase, it retrieves and filters necessary information from the virtual resource pool based on specific requirements. Finally, we conducted simulation experiments via STK toolkit. The empirical results demonstrate that the proposed SDSO outperforms traditional optimization algorithms in terms of computational efficiency. In addition, as the number of remote sensing satellites involved in scheduling grows, there is just a slight decrease in computational efficiency. Rapid growth in the number of remote sensing satellites is a foreseeable trend, and SDSO provides an effective solution to the problem of resource scheduling for the large number of remote sensing satellites that will inevitably occur in the future.