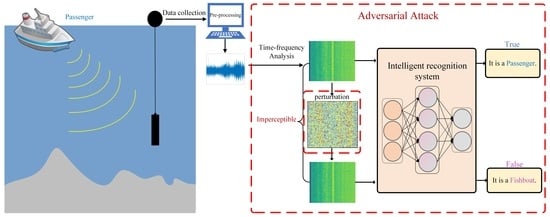
Adversarial Attacks in Underwater Acoustic Target Recognition with Deep Learning Models
Abstract
:1. Introduction
- To the best of our knowledge, this is the first instance of visualizing the extracted features of Transformer-based models for underwater acoustic target recognition, which are believed to perceive spatial structures differently through the use of MHSA rather than convolution operations.
- This is also the first time to introduce adversarial attacks in the area of underwater acoustic target recognition. Based on the real-world underwater acoustic dataset, we generated the adversarial spectrograms by adding a well-designed perturbation on the input time–frequency representation to successfully attack the state-of-the-art (SOTA) deep learning networks for underwater acoustic target recognition, which demonstrates their vulnerability under adversarial attacks. Moreover, we also analyzed how the adversarial attacks influenced the decision-making process of these models through visualization.
- From the perspective of underwater acoustic signal preprocessing, experimental results demonstrate that using the MFCC feature or normalizing time–frequency spectrograms with a standard deviation of 1 can potentially improve the adversarial robustness.
2. Related Work
3. Preliminaries
3.1. CNN Models
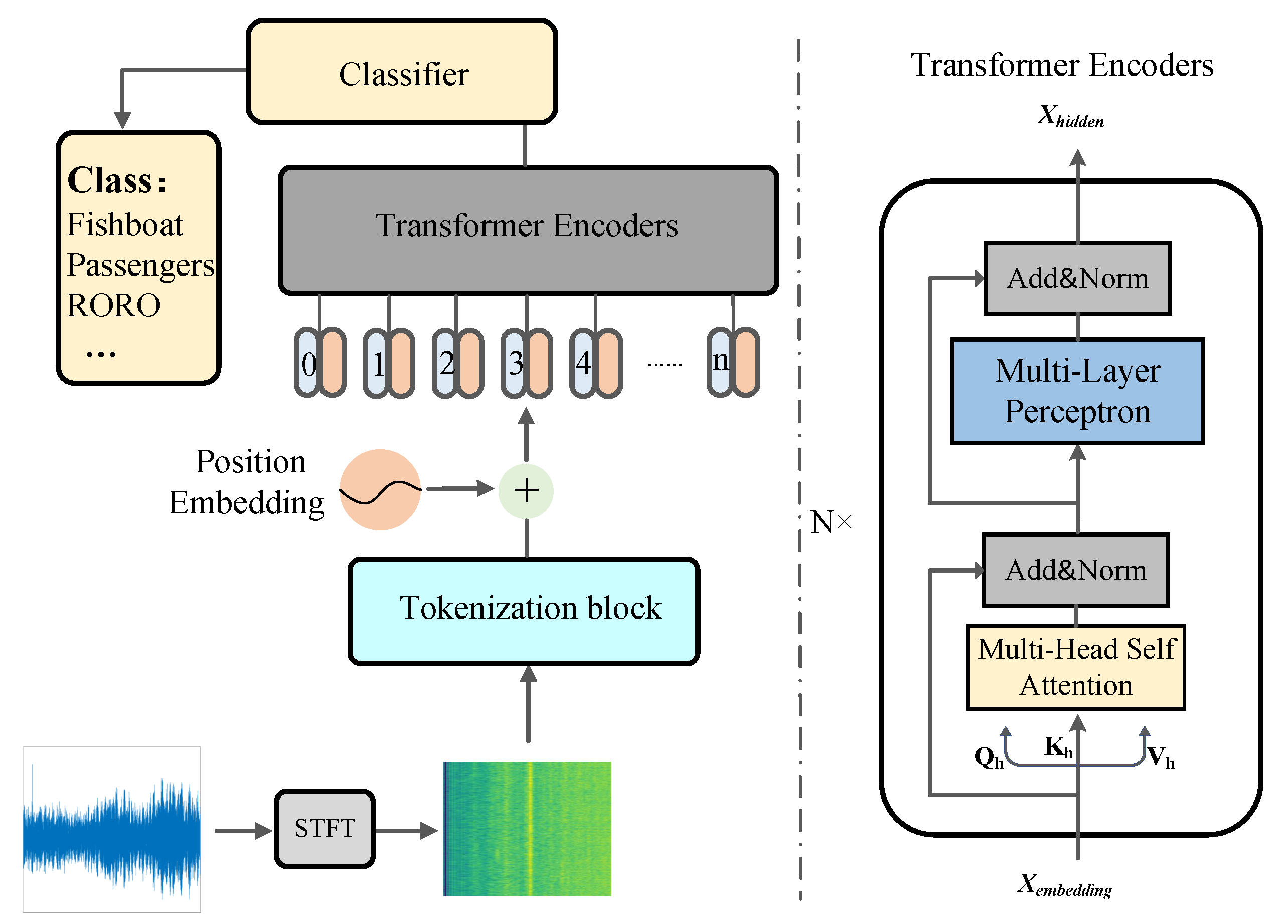
3.2. Transformer Models
4. Methodology
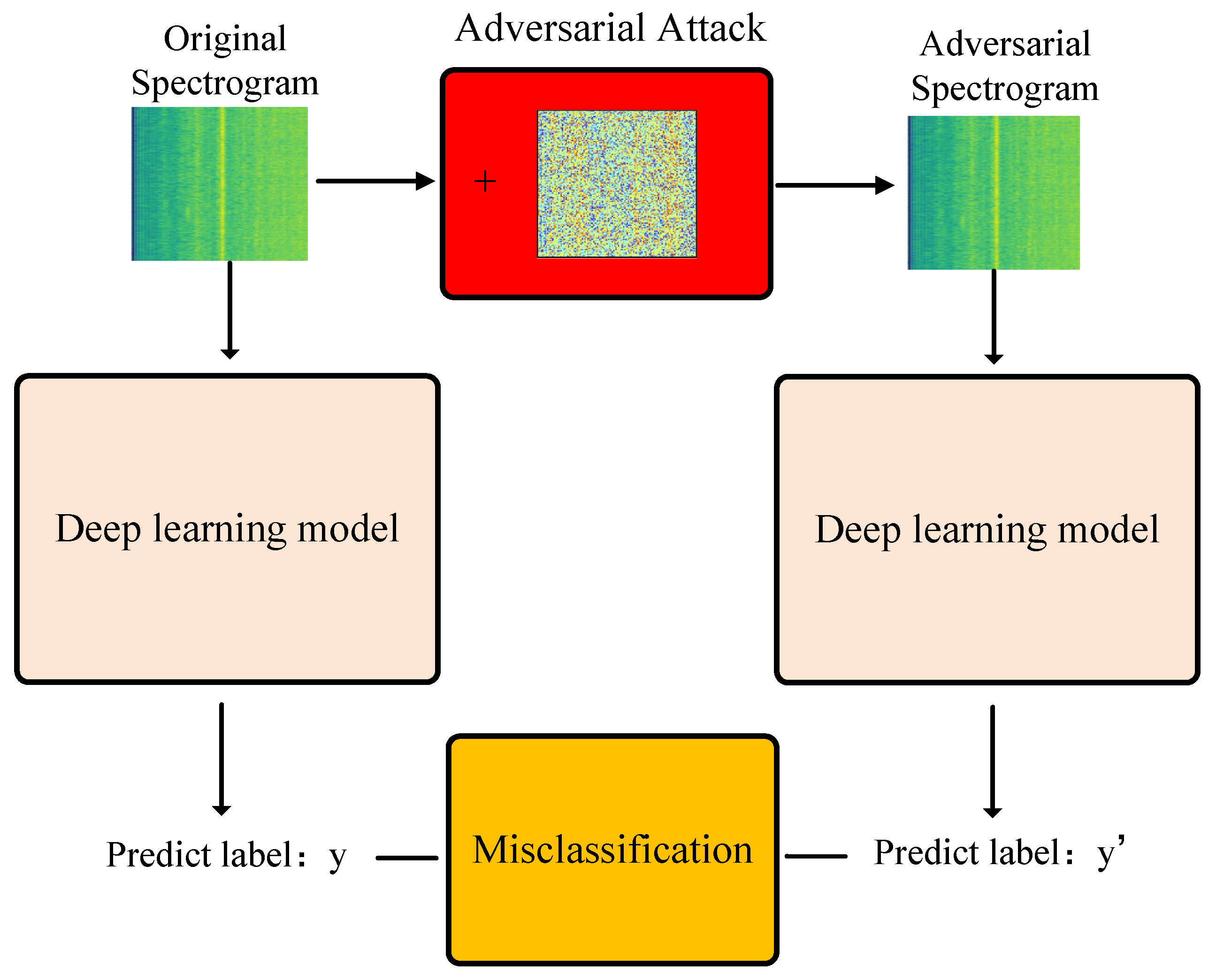
4.1. Adversarial Attack
4.1.1. Fast Gradient Sign Method
4.1.2. Project Gradient Descent
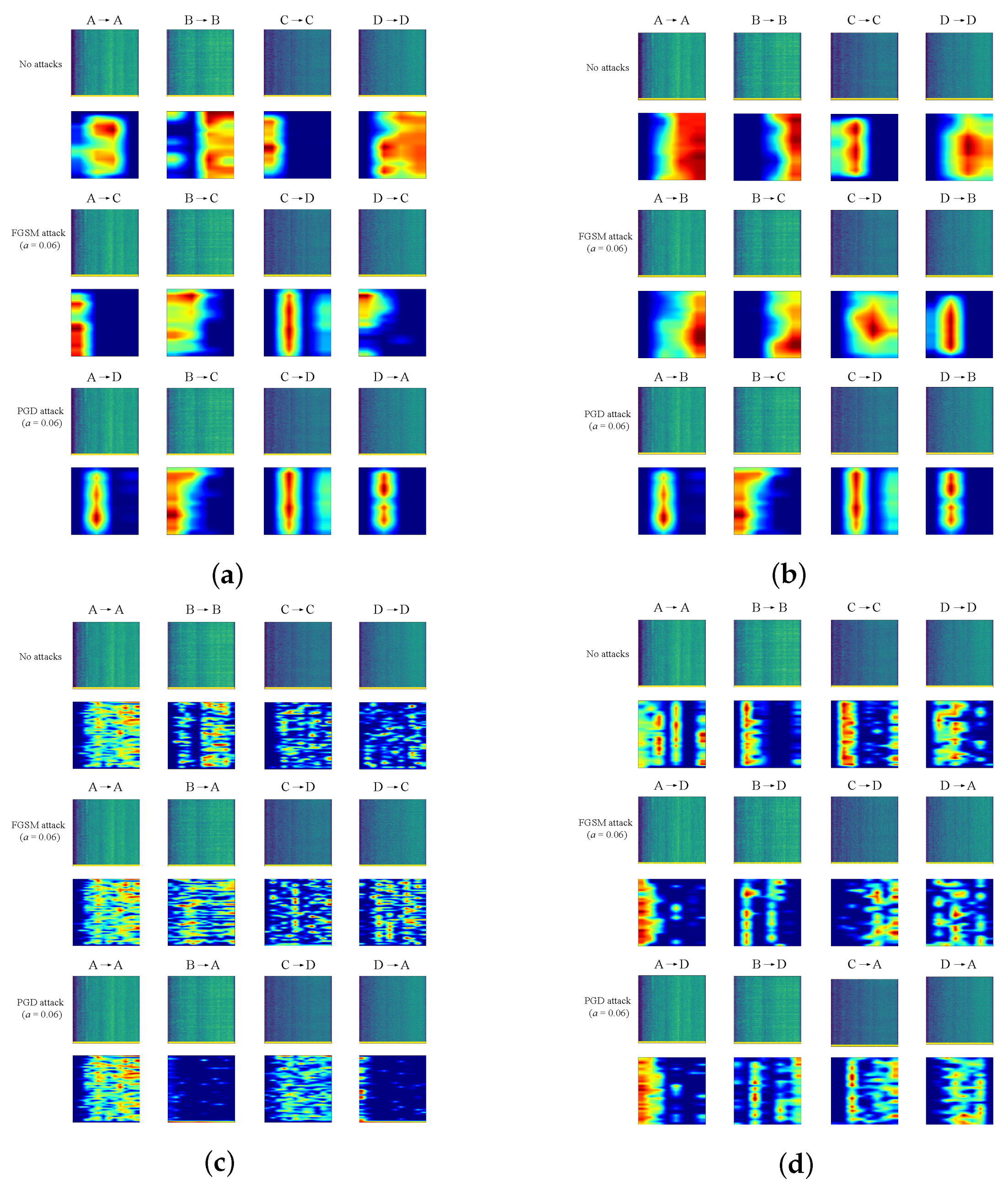
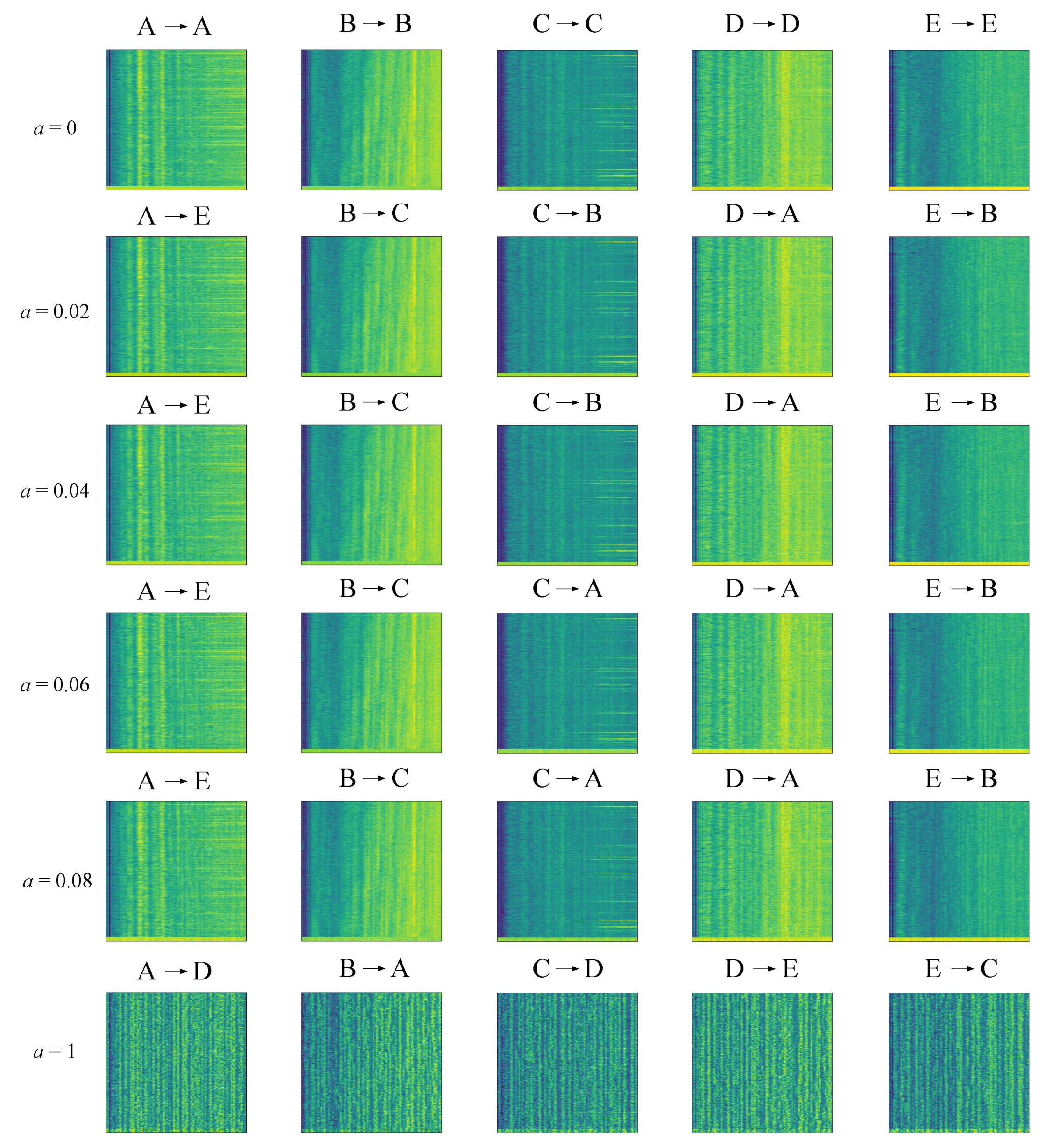
4.2. GradCAM Visualization
5. Experimental Setups and Implementation Details
5.1. Datasets
5.2. Implementation
- UATRT [10]: UATRT is a modified Transformer based on hierarchical tokenization to extract discriminative features for underwater acoustic target recognition.
6. Experimental Results and Discussion
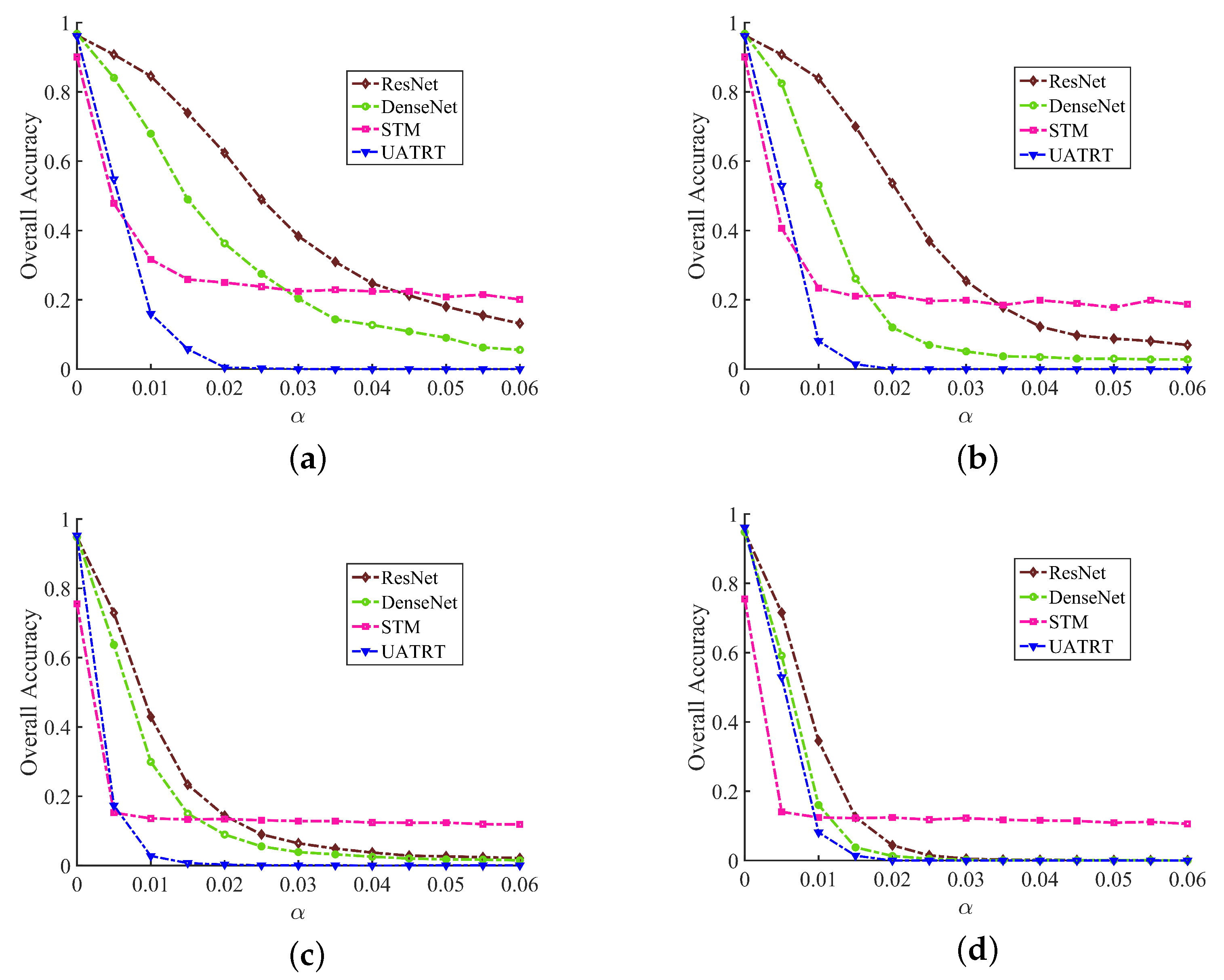
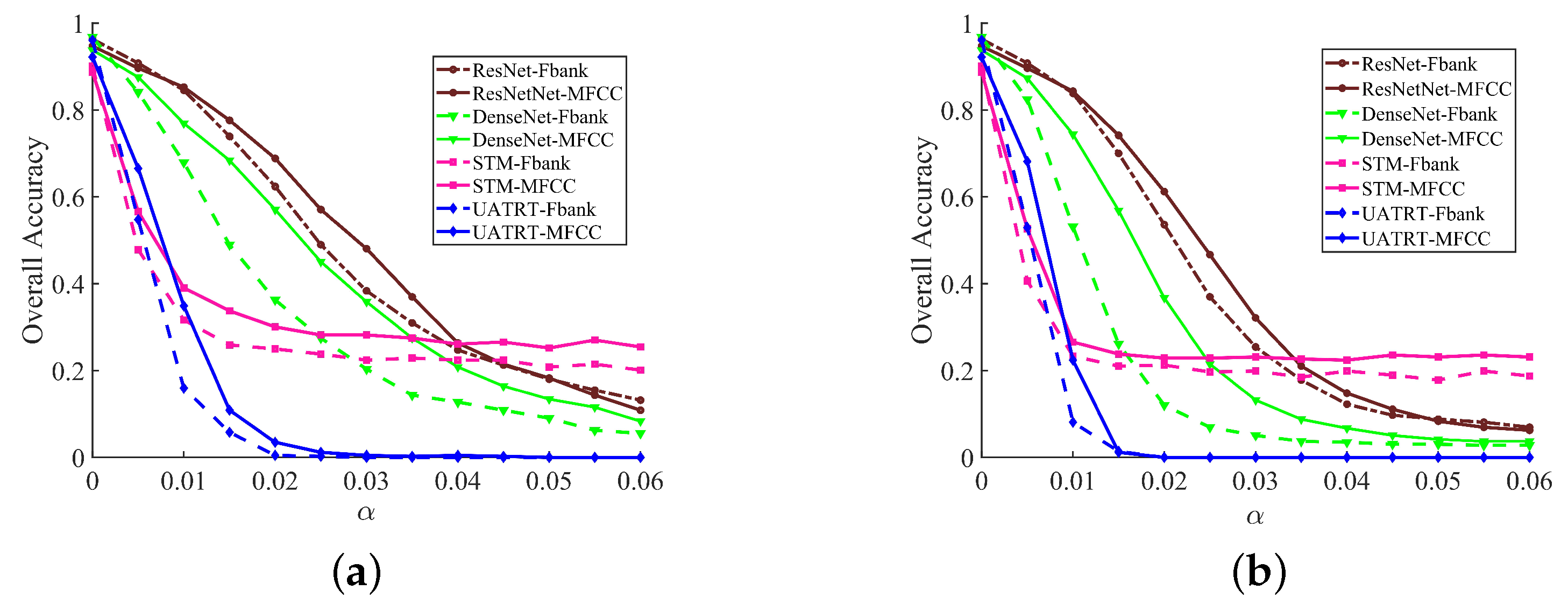
6.1. Attack Performance under Different Perturbations
6.2. Attack Performance under Different Features
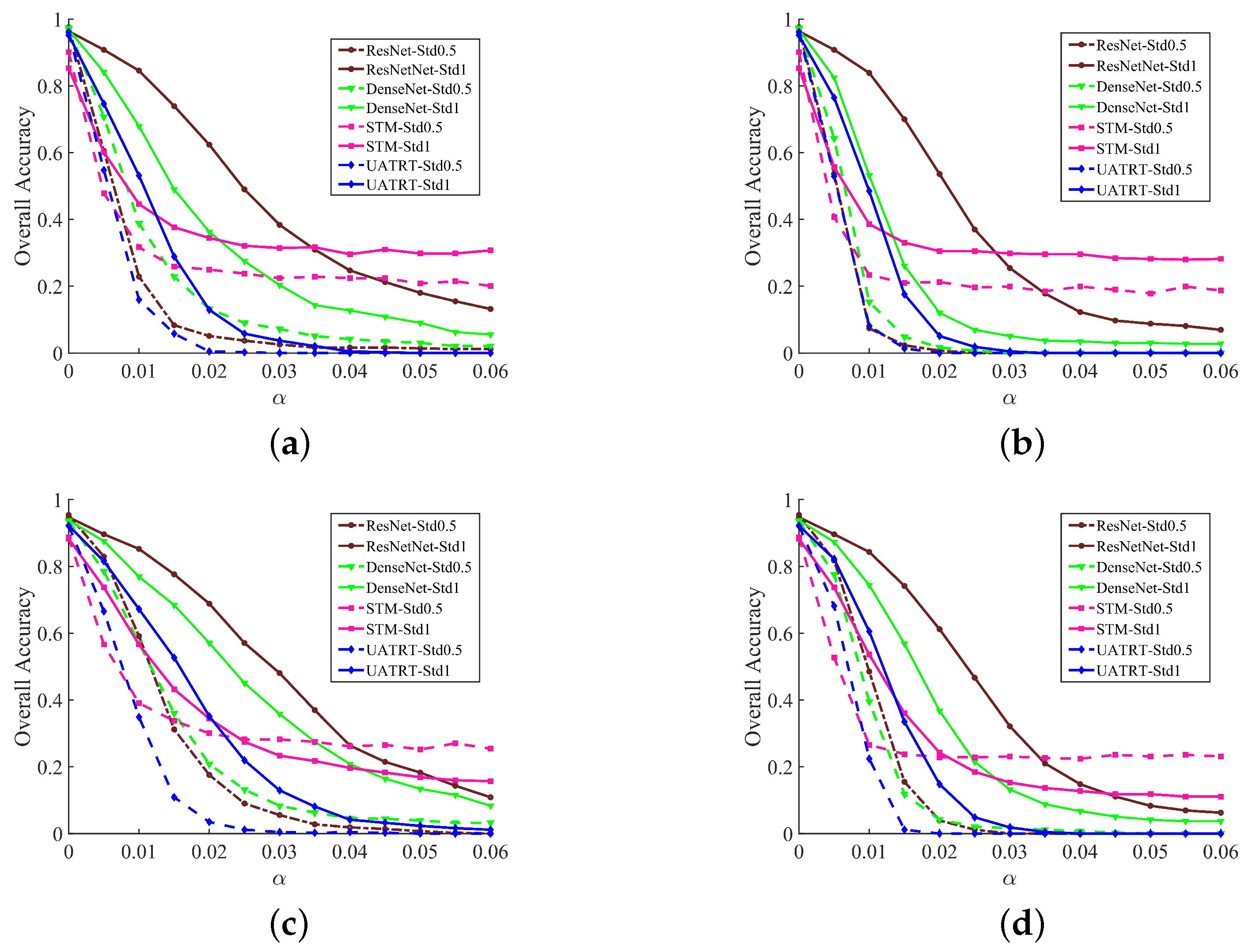
6.3. Attack Performance under Different Normalization Methods
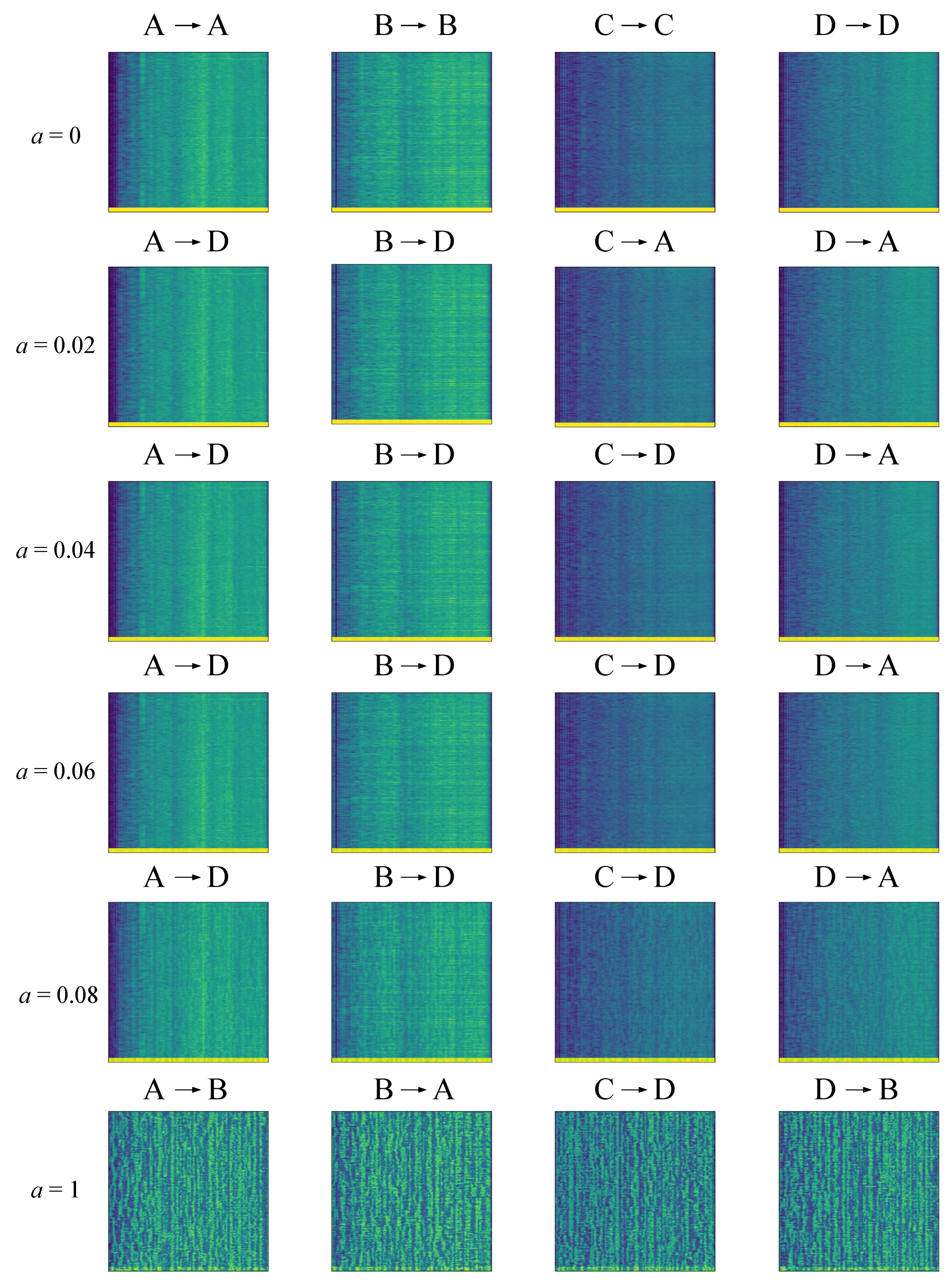
6.4. Heatmap Visualization with Adversarial Attacks
6.5. Evaluation of Adversarial Attacks
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, N.; He, M.; Sun, J.; Wang, H.; Zhou, L.; Chu, C.; Chen, L. IA-PNCC: Noise processing method for underwater target recognition convolutional neural network. Comput. Mater. Contin. 2019, 58, 169–181. [Google Scholar] [CrossRef]
- Steiniger, Y.; Kraus, D.; Meisen, T. Survey on deep learning based computer vision for sonar imagery. Eng. Appl. Artif. Intell. 2022, 114, 105157. [Google Scholar] [CrossRef]
- Barbu, M. Acoustic Seabed and Target Classification Using Fractional Fourier Transform and Time-Frequency Transform Techniques. Ph.D. Thesis, University of New Orleans, New Orleans, LA, USA, 2006. [Google Scholar]
- Sendra, S.; Lloret, J.; Jimenez, J.M.; Parra, L. Underwater acoustic modems. IEEE Sens. J. 2015, 16, 4063–4071. [Google Scholar] [CrossRef]
- Luo, X.; Chen, L.; Zhou, H.; Cao, H. A Survey of Underwater Acoustic Target Recognition Methods Based on Machine Learning. J. Mar. Sci. Eng. 2023, 11, 384. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, X.; Yu, Y.; Niu, L. Deep learning-based recognition of underwater target. In Proceedings of the 2016 IEEE International Conference on Digital Signal Processing (DSP), Beijing, China, 16–18 October 2016; pp. 89–93. [Google Scholar]
- Chen, Y.; Xu, X. The research of underwater target recognition method based on deep learning. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–5. [Google Scholar]
- Sun, Q.; Wang, K. Underwater single-channel acoustic signal multitarget recognition using convolutional neural networks. J. Acoust. Soc. Am. 2022, 151, 2245–2254. [Google Scholar] [CrossRef]
- Doan, V.S.; Huynh-The, T.; Kim, D.S. Underwater Acoustic Target Classification Based on Dense Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1500905. [Google Scholar] [CrossRef]
- Feng, S.; Zhu, X. A Transformer-Based Deep Learning Network for Underwater Acoustic Target Recognition. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 1505805. [Google Scholar] [CrossRef]
- Li, P.; Wu, J.; Wang, Y.; Lan, Q.; Xiao, W. STM: Spectrogram Transformer Model for Underwater Acoustic Target Recognition. J. Mar. Sci. Eng. 2022, 10, 1428. [Google Scholar] [CrossRef]
- Wang, X.; Meng, J.; Liu, Y.; Zhan, G.; Tian, Z. Self-supervised acoustic representation learning via acoustic-embedding memory unit modified space autoencoder for underwater target recognition. J. Acoust. Soc. Am. 2022, 152, 2905–2915. [Google Scholar] [CrossRef]
- Xu, K.; Xu, Q.; You, K.; Zhu, B.; Feng, M.; Feng, D.; Liu, B. Self-supervised learning–based underwater acoustical signal classification via mask modeling. J. Acoust. Soc. Am. 2023, 154, 5–15. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Xie, L.; Wang, Y.; Zou, J.; Xiong, J.; Ying, Z.; Vasilakos, A.V. Privacy and security issues in deep learning: A survey. IEEE Access 2020, 9, 4566–4593. [Google Scholar] [CrossRef]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. arXiv 2017, arXiv:1706.06083. [Google Scholar]
- Gong, Y.; Poellabauer, C. Crafting adversarial examples for speech paralinguistics applications. arXiv 2017, arXiv:1711.03280. [Google Scholar]
- Kong, Z.; Xue, J.; Wang, Y.; Huang, L.; Niu, Z.; Li, F. A survey on adversarial attack in the age of artificial intelligence. Wirel. Commun. Mob. Comput. 2021, 2021, 4907754. [Google Scholar] [CrossRef]
- Kreuk, F.; Adi, Y.; Cisse, M.; Keshet, J. Fooling end-to-end speaker verification with adversarial examples. In Proceedings of the 2018 IEEE international conference on acoustics, speech and signal processing (ICASSP), IEEE, Calgary, AB, Canada, 15–20 April 2018; pp. 1962–1966. [Google Scholar]
- Subramanian, V.; Benetos, E.; Xu, N.; McDonald, S.; Sandler, M. Adversarial Attacks in Sound Event Classification. arXiv 2019, arXiv:1907.02477. [Google Scholar]
- Joshi, S.; Villalba, J.; Żelasko, P.; Moro-Velázquez, L.; Dehak, N. Study of pre-processing defenses against adversarial attacks on state-of-the-art speaker recognition systems. IEEE Trans. Inf. Forensics Secur. 2021, 16, 4811–4826. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. arXiv 2016, arXiv:1602.04938. [Google Scholar]
- Lauritsen, S.M.; Kristensen, M.; Olsen, M.V.; Larsen, M.S.; Lauritsen, K.M.; Jørgensen, M.J.; Lange, J.; Thiesson, B. Explainable artificial intelligence model to predict acute critical illness from electronic health records. Nat. Commun. 2020, 11, 3852. [Google Scholar] [CrossRef]
- Jiménez-Luna, J.; Grisoni, F.; Schneider, G. Drug discovery with explainable artificial intelligence. Nat. Mach. Intell. 2020, 2, 573–584. [Google Scholar] [CrossRef]
- Jiang, J.; Wu, Z.; Lu, J.; Huang, M.; Xiao, Z. Interpretable features for underwater acoustic target recognition. Measurement 2021, 173, 108586. [Google Scholar] [CrossRef]
- Xiao, X.; Wang, W.; Ren, Q.; Gerstoft, P.; Ma, L. Underwater acoustic target recognition using attention-based deep neural network. JASA Express Lett. 2021, 1, 106001. [Google Scholar] [CrossRef]
- Song, L.; Qian, X.; Li, H.; Chen, Y. Pipelayer: A pipelined reram-based accelerator for deep learning. In Proceedings of the 2017 IEEE International Symposium on High Performance Computer Architecture (HPCA), IEEE, Austin, TX, USA, 4–8 February 2017; pp. 541–552. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; 2017. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Santos-Domínguez, D.; Torres-Guijarro, S.; Cardenal-López, A.; Pena-Gimenez, A. ShipsEar: An underwater vessel noise database. Appl. Acoust. 2016, 113, 64–69. [Google Scholar] [CrossRef]
- Irfan, M.; Jiangbin, Z.; Ali, S.; Iqbal, M.; Masood, Z.; Hamid, U. DeepShip: An underwater acoustic benchmark dataset and a separable convolution based autoencoder for classification. Expert Syst. Appl. 2021, 183, 115270. [Google Scholar] [CrossRef]
- Jiang, J.; Shi, T.; Huang, M.; Xiao, Z. Multi-scale spectral feature extraction for underwater acoustic target recognition. Measurement 2020, 166, 108227. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q. Densely Connected Convolutional Networks. arXiv 2016, arXiv:1608.06993. [Google Scholar]
- Gong, Y.; Chung, Y.; Glass, J.R. AST: Audio Spectrogram Transformer. arXiv 2021, arXiv:2104.01778. [Google Scholar]
- Shao, R.; Shi, Z.; Yi, J.; Chen, P.Y.; Hsieh, C.J. On the adversarial robustness of visual transformers. arXiv 2021, arXiv:2103.15670. [Google Scholar]




| Class | Ship Types | Training Sample | Testing Sample |
|---|---|---|---|
| A | Fish boats, trawlers, mussel boats, tugboats, dredger | 182 | 83 |
| B | Motorboat, pilot boat, sailboat | 196 | 79 |
| C | Passengers | 210 | 90 |
| D | Ocean liner, RORO | 215 | 85 |
| E | Background noise | 204 | 96 |
| Class | Ship Types | Training Sample | Testing Sample |
|---|---|---|---|
| A | Cargo | 1766 | 734 |
| B | Passengers | 1773 | 727 |
| C | Tanker | 1710 | 790 |
| D | Tug | 1751 | 749 |
| Attack Methods | ResNet | DenseNet | STM | UATRT | |
|---|---|---|---|---|---|
| FGSM | 0.01 | 22.60 (84.5%) | 23.37 (67.9%) | 24.29 (31.6%) | 21.85 (15.9%) |
| 0.02 | 20.50 (62.4%) | 17.88 (36.3%) | 21.24 (24.9%) | 18.81 (0.5%) | |
| 0.03 | 18.86 (38.3%) | 16.71 (20.3%) | 18.69 (22.4%) | 19.08 (0%) | |
| 0.04 | 16.92 (24.7%) | 16.61 (12.7%) | 18.04 (22.4%) | 16.31 (0%) | |
| 0.05 | 16.68 (18.0%) | 15.63 (9.0%) | 17.00 (20.8%) | 15.67 (0%) | |
| 0.06 | 14.97 (13.2%) | 15.03 (5.5%) | 15.87 (20.1%) | 14.85 (0%) | |
| PGD | 0.01 | 23.88 (83.8%) | 21.84 (53.1%) | 24.13 (23.3%) | 22.64 (8.1%) |
| 0.02 | 20.99 (53.6%) | 21.19 (12.0%) | 22.31 (21.2%) | 20.43 (0%) | |
| 0.03 | 19.06 (25.4%) | 18.55 (5.1%) | 21.04 (19.9%) | 18.24 (0%) | |
| 0.04 | 18.91 (12.2%) | 18.32 (3.5%) | 20.23 (19.9%) | 18.33 (0%) | |
| 0.05 | 18.55 (8.8%) | 16.91 (3.0%) | 19.18 (17.8%) | 16.37 (0%) | |
| 0.06 | 16.25 (6.9%) | 16.88 (2.8%) | 19.4 (18.7%) | 17.05 (0%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, S.; Zhu, X.; Ma, S.; Lan, Q. Adversarial Attacks in Underwater Acoustic Target Recognition with Deep Learning Models. Remote Sens. 2023, 15, 5386. https://doi.org/10.3390/rs15225386
Feng S, Zhu X, Ma S, Lan Q. Adversarial Attacks in Underwater Acoustic Target Recognition with Deep Learning Models. Remote Sensing. 2023; 15(22):5386. https://doi.org/10.3390/rs15225386
Chicago/Turabian StyleFeng, Sheng, Xiaoqian Zhu, Shuqing Ma, and Qiang Lan. 2023. "Adversarial Attacks in Underwater Acoustic Target Recognition with Deep Learning Models" Remote Sensing 15, no. 22: 5386. https://doi.org/10.3390/rs15225386
APA StyleFeng, S., Zhu, X., Ma, S., & Lan, Q. (2023). Adversarial Attacks in Underwater Acoustic Target Recognition with Deep Learning Models. Remote Sensing, 15(22), 5386. https://doi.org/10.3390/rs15225386