An Adaptive Learning Approach for Tropical Cyclone Intensity Correction
Abstract
:1. Introduction
2. Methodology
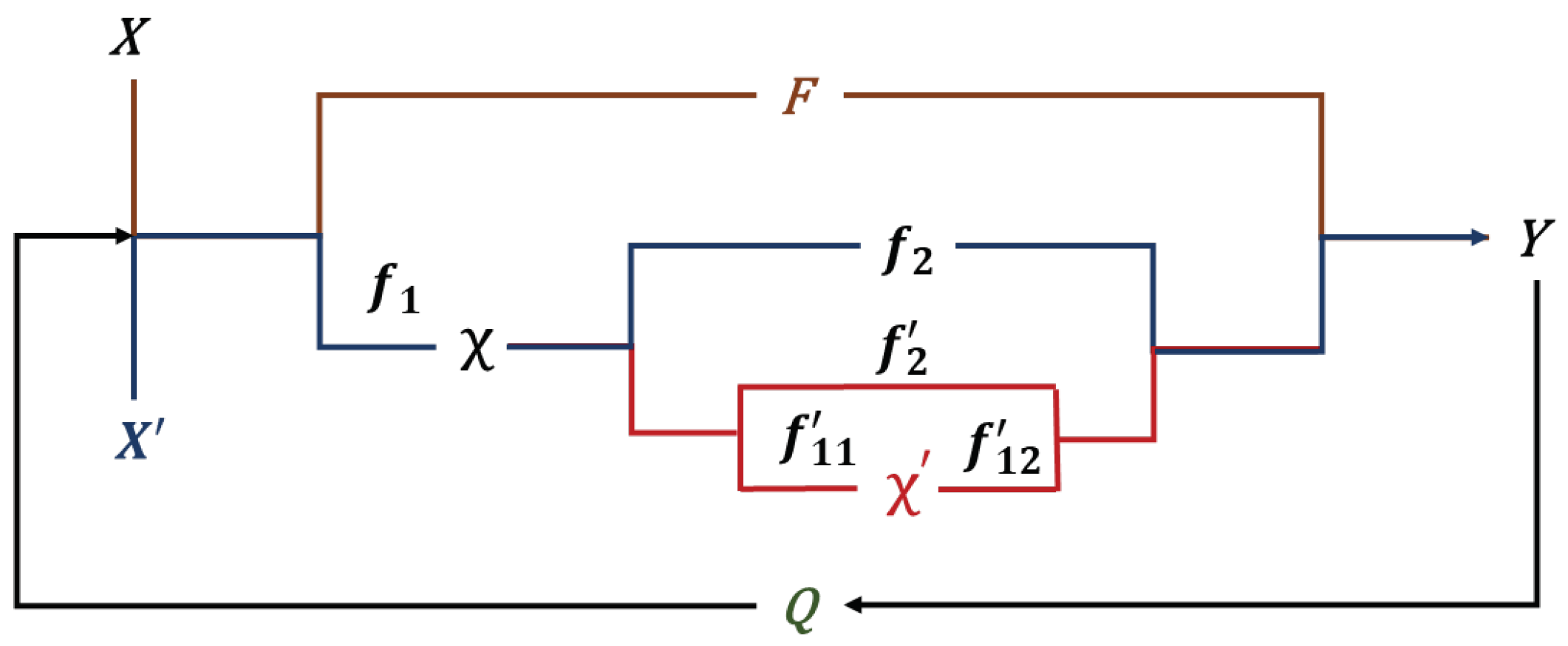
2.1. Our Approach
2.2. Basic Descriptions
2.2.1. Data
2.2.2. Deep Neural Networks
2.2.3. Transfer Learning
2.3. Experimental Setting
2.3.1. Dataset
- Data are post-reanalysed by agencies, and it means that ‘TRACK_TYPE’ is flagged as the ‘main’;
- Only tropical cyclones (‘NATURE’ is marked as ‘TS’) are analysed, and ‘USA_SSHS’ (Saffir-Simpson Hurricane Scale) is larger than 0. This means that the wind speed provided by the US agencies is ≥64 kts;
- Records from 2004 to 2022, only in the North Atlantic, and they are provided by US agencies.
- Atmospheric variables: u (u-component of wind), v (v-component of wind), t (temperature), and r (relative humidity);
- Pressure levels: 850 hPa/500 hPa/200 hPa;
- Surface variables: (10 m u-component of wind), (10 m v-component of wind);
- Region size: , and the spatial resolution is .
2.3.2. Objective Function
2.3.3. Evaluation Metrics
3. Results
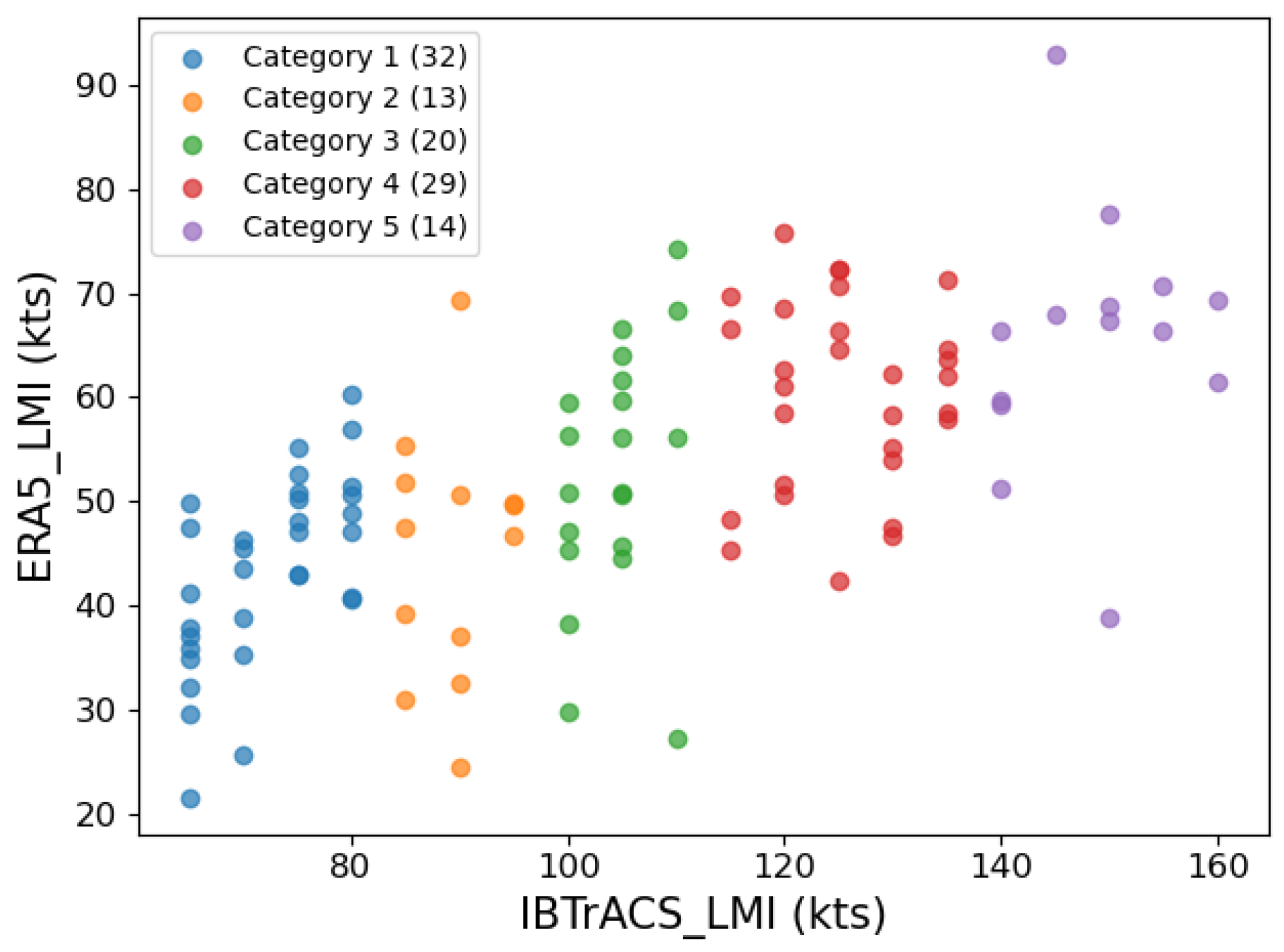
3.1. Data Analysis
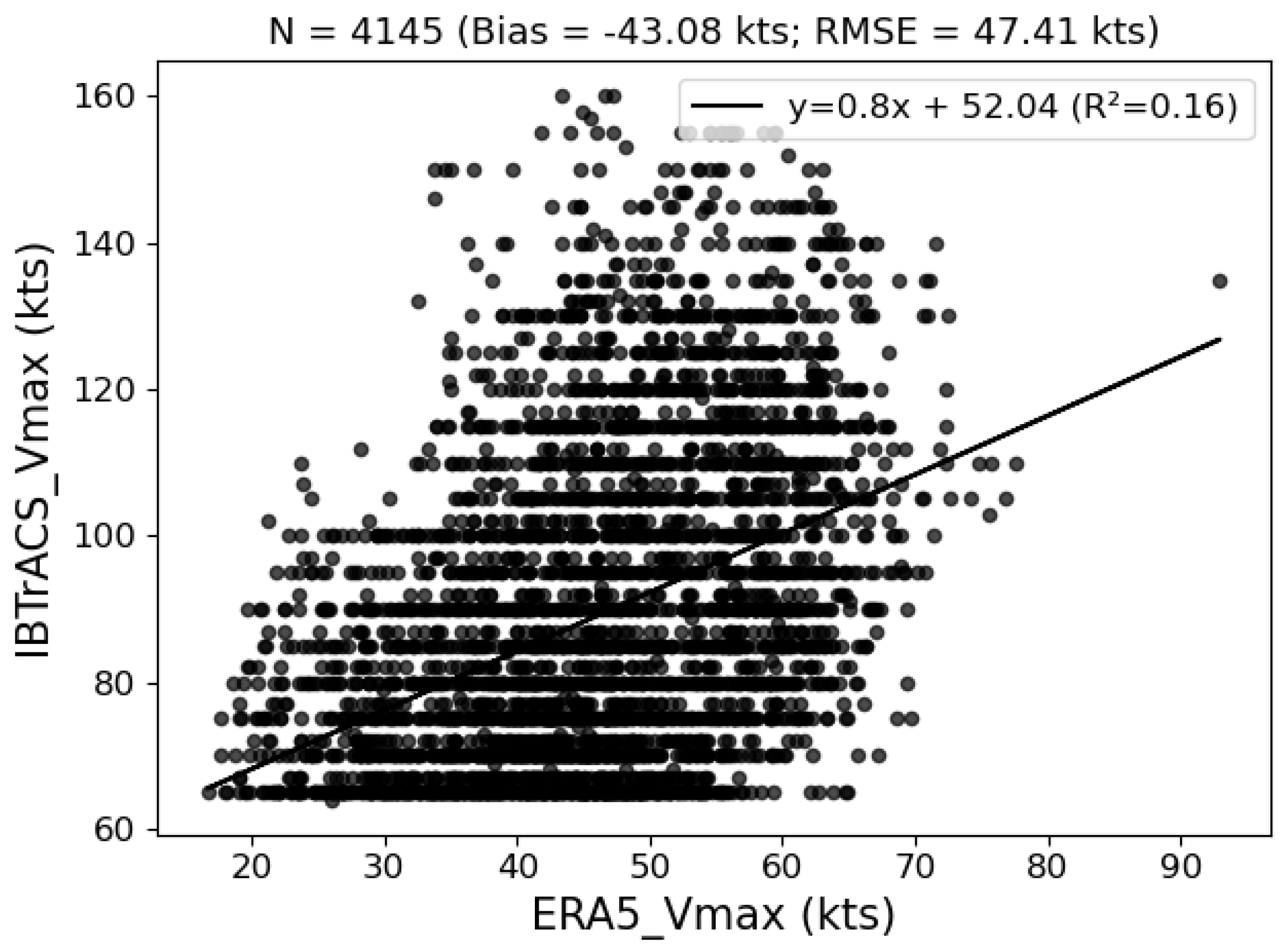
3.1.1. Original Information
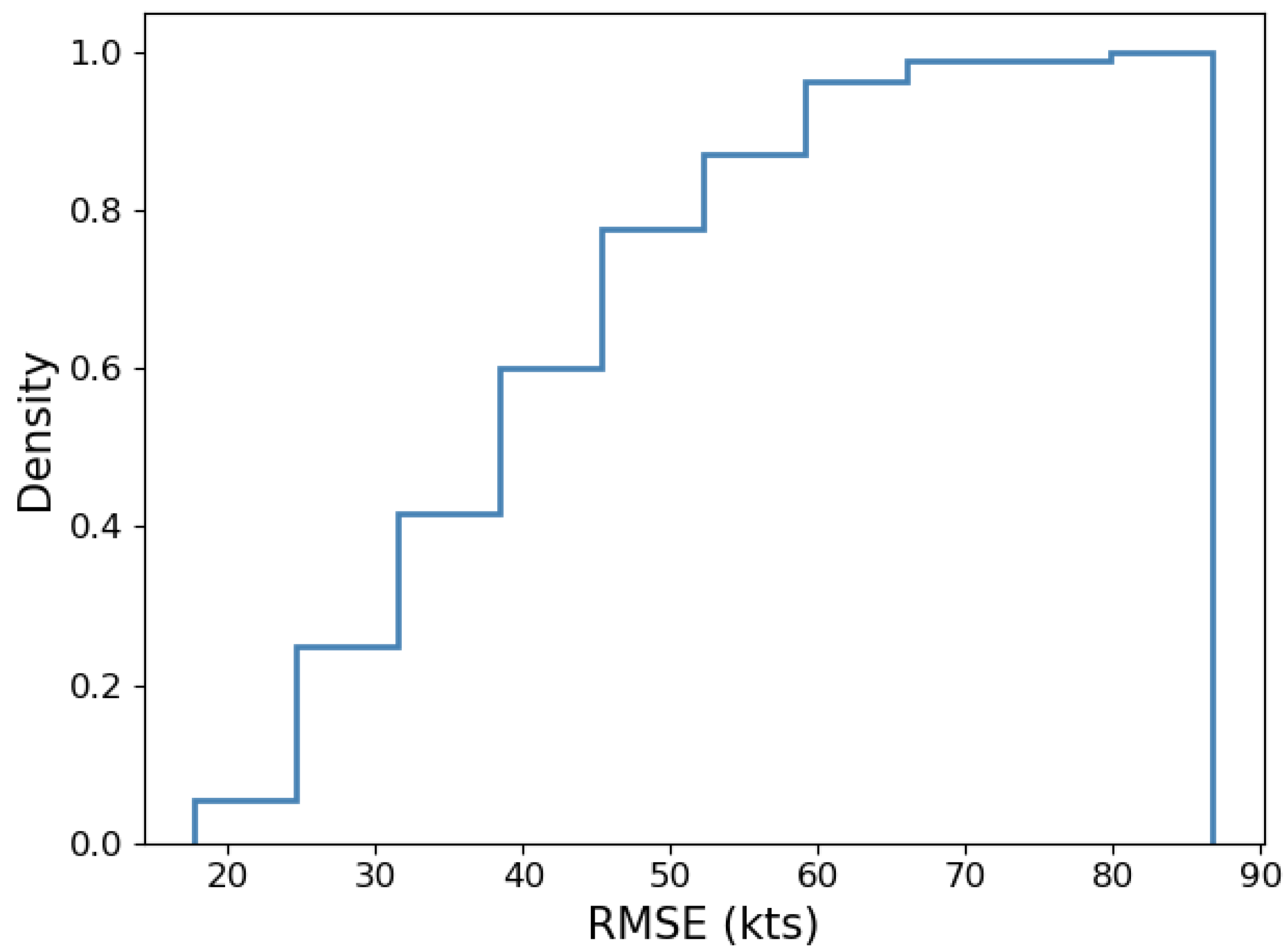
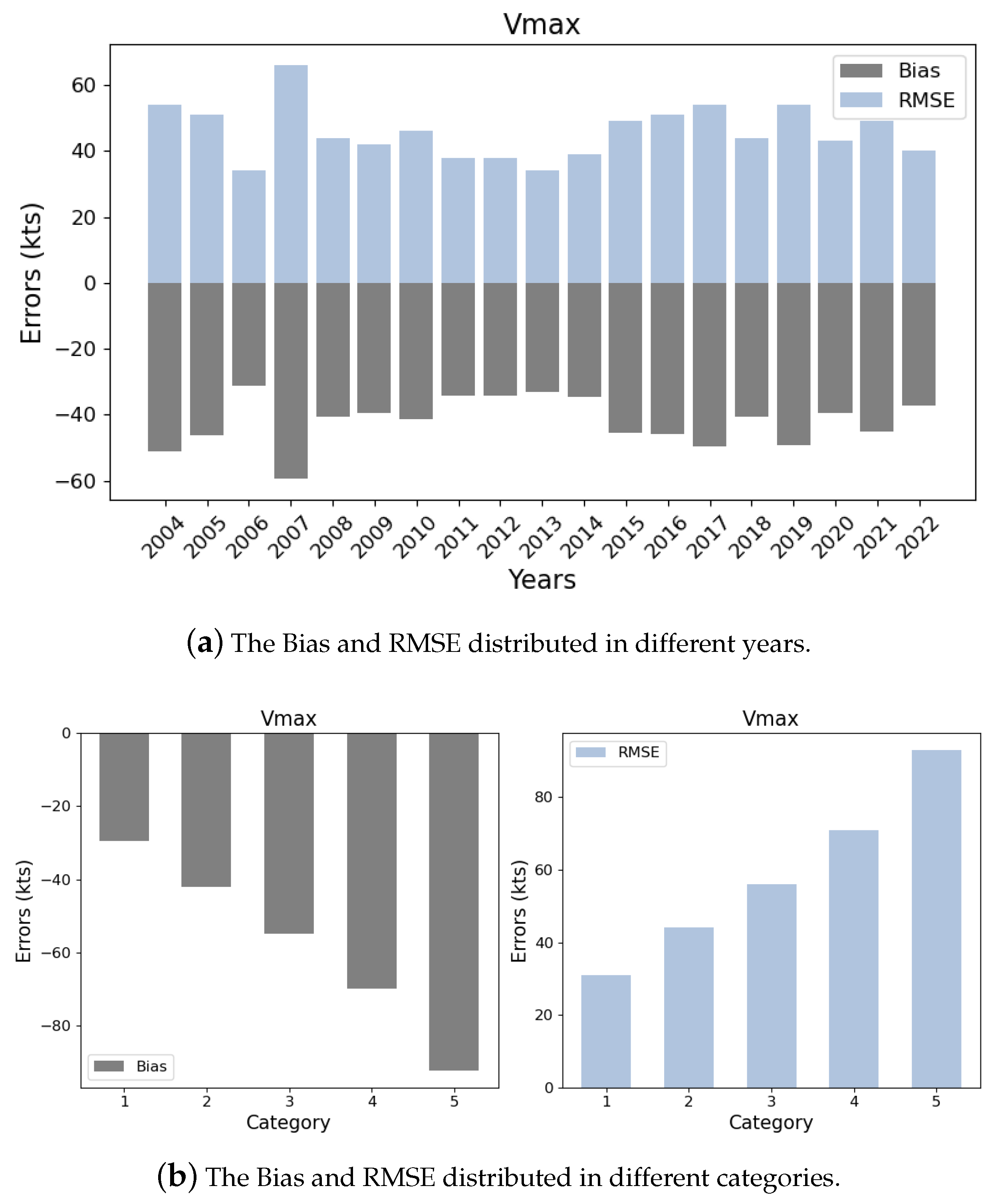
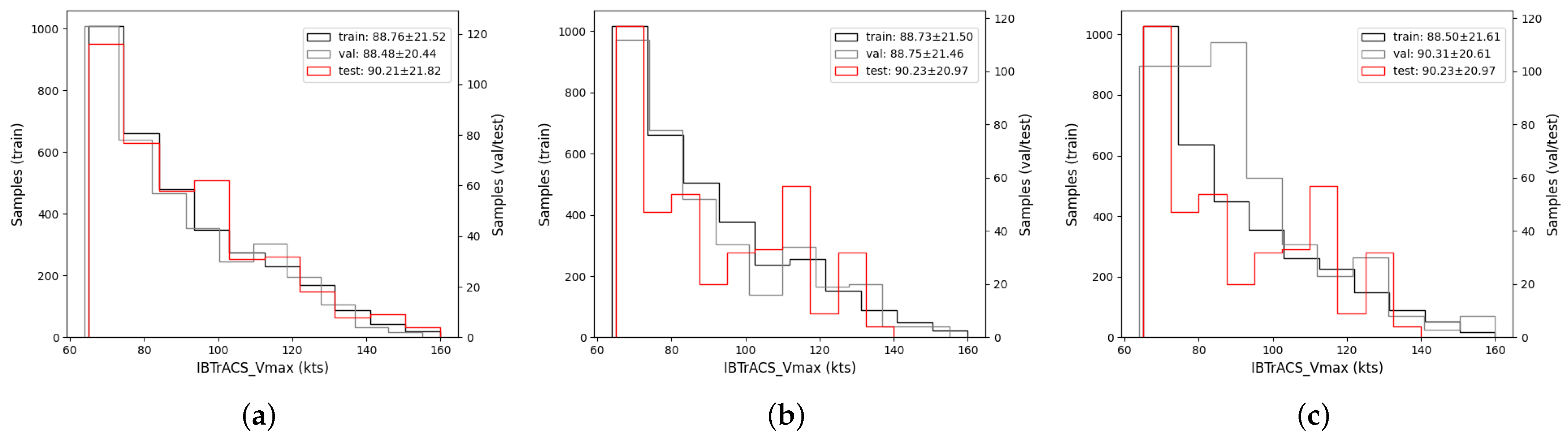
3.1.2. Error Analysis
3.1.3. Storms’ Correspondence
3.2. Our Adaptive Approach
3.2.1. Baseline
3.2.2. TC Knowledge for Optimising the Inputs
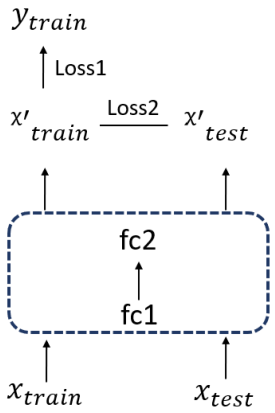
3.2.3. Feature Learning for Improving the Generalisability
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Emanuel, K. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 2005, 436, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Peduzzi, P.; Chatenoux, B.; Dao, H.; De Bono, A.; Herold, C.; Kossin, J.; Mouton, F.; Nordbeck, O. Global trends in tropical cyclone risk. Nat. Clim. Chang. 2012, 2, 289–294. [Google Scholar] [CrossRef]
- Wang, S.; Toumi, R. Recent migration of tropical cyclones toward coasts. Science 2021, 371, 514–517. [Google Scholar] [CrossRef]
- Emanuel, K.; DesAutels, C.; Holloway, C.; Korty, R. Environmental control of tropical cyclone intensity. J. Atmos. Sci. 2004, 61, 843–858. [Google Scholar] [CrossRef]
- Wang, Y.q.; Wu, C.C. Current understanding of tropical cyclone structure and intensity changes—A review. Meteorol. Atmos. Phys. 2004, 87, 257–278. [Google Scholar] [CrossRef]
- DeMaria, M.; Sampson, C.R.; Knaff, J.A.; Musgrave, K.D. Is tropical cyclone intensity guidance improving? Bull. Am. Meteorol. Soc. 2014, 95, 387–398. [Google Scholar] [CrossRef]
- Emanuel, K. 100 years of progress in tropical cyclone research. Meteorol. Monogr. 2018, 59, 15.1–15.68. [Google Scholar] [CrossRef]
- Knapp, K.R.; Kruk, M.C. Quantifying interagency differences in tropical cyclone best-track wind speed estimates. Mon. Weather Rev. 2010, 138, 1459–1473. [Google Scholar] [CrossRef]
- Levinson, D.H.; Diamond, H.J.; Knapp, K.R.; Kruk, M.C.; Gibney, E.J. Toward a homogenous global tropical cyclone best-track dataset. Bull. Am. Meteorol. Soc. 2010, 91, 377–380. [Google Scholar]
- Kossin, J.P.; Olander, T.L.; Knapp, K.R. Trend analysis with a new global record of tropical cyclone intensity. J. Clim. 2013, 26, 9960–9976. [Google Scholar] [CrossRef]
- Emanuel, K.; Caroff, P.; Delgado, S.; Guishard, M.; Hennon, C.; Knaff, J.; Knapp, K.R.; Kossin, J.; Schreck, C.; Velden, C.; et al. On the desirability and feasibility of a global reanalysis of tropical cyclones. Bull. Am. Meteorol. Soc. 2018, 99, 427–429. [Google Scholar] [CrossRef]
- Dvorak, V.F. Tropical cyclone intensity analysis and forecasting from satellite imagery. Mon. Weather Rev. 1975, 103, 420–430. [Google Scholar] [CrossRef]
- Velden, C.; Harper, B.; Wells, F.; Beven, J.L.; Zehr, R.; Olander, T.; Mayfield, M.; Guard, C.C.; Lander, M.; Edson, R.; et al. The Dvorak tropical cyclone intensity estimation technique: A satellite-based method that has endured for over 30 years. Bull. Am. Meteorol. Soc. 2006, 87, 1195–1210. [Google Scholar] [CrossRef]
- Knaff, J.A.; Brown, D.P.; Courtney, J.; Gallina, G.M.; Beven, J.L. An evaluation of Dvorak technique–based tropical cyclone intensity estimates. Weather Forecast. 2010, 25, 1362–1379. [Google Scholar] [CrossRef]
- DeMaria, M.; Kaplan, J. An updated statistical hurricane intensity prediction scheme (SHIPS) for the Atlantic and eastern North Pacific basins. Weather Forecast. 1999, 14, 326–337. [Google Scholar] [CrossRef]
- Knaff, J.A.; DeMaria, M.; Sampson, C.R.; Gross, J.M. Statistical, 5-day tropical cyclone intensity forecasts derived from climatology and persistence. Weather Forecast. 2003, 18, 80–92. [Google Scholar] [CrossRef]
- DeMaria, M.; Mainelli, M.; Shay, L.K.; Knaff, J.A.; Kaplan, J. Further improvements to the statistical hurricane intensity prediction scheme (SHIPS). Weather Forecast. 2005, 20, 531–543. [Google Scholar] [CrossRef]
- Lee, C.Y.; Tippett, M.K.; Camargo, S.J.; Sobel, A.H. Probabilistic multiple linear regression modeling for tropical cyclone intensity. Mon. Weather Rev. 2015, 143, 933–954. [Google Scholar] [CrossRef]
- Cangialosi, J.P.; Blake, E.; DeMaria, M.; Penny, A.; Latto, A.; Rappaport, E.; Tallapragada, V. Recent progress in tropical cyclone intensity forecasting at the National Hurricane Center. Weather Forecast. 2020, 35, 1913–1922. [Google Scholar] [CrossRef]
- DeMaria, M.; Franklin, J.L.; Zelinsky, R.; Zelinsky, D.A.; Onderlinde, M.J.; Knaff, J.A.; Stevenson, S.N.; Kaplan, J.; Musgrave, K.D.; Chirokova, G.; et al. The national hurricane center tropical cyclone model guidance suite. Weather Forecast. 2022, 37, 2141–2159. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, W.; Wang, X. Machine learning in tropical cyclone forecast modeling: A review. Atmosphere 2020, 11, 676. [Google Scholar] [CrossRef]
- Pradhan, R.; Aygun, R.S.; Maskey, M.; Ramachandran, R.; Cecil, D.J. Tropical cyclone intensity estimation using a deep convolutional neural network. IEEE Trans. Image Process. 2017, 27, 692–702. [Google Scholar] [CrossRef] [PubMed]
- Combinido, J.S.; Mendoza, J.R.; Aborot, J. A convolutional neural network approach for estimating tropical cyclone intensity using satellite-based infrared images. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 1474–1480. [Google Scholar]
- Chen, B.F.; Chen, B.; Lin, H.T.; Elsberry, R.L. Estimating tropical cyclone intensity by satellite imagery utilizing convolutional neural networks. Weather Forecast. 2019, 34, 447–465. [Google Scholar] [CrossRef]
- Zhuo, J.Y.; Tan, Z.M. Physics-augmented deep learning to improve tropical cyclone intensity and size estimation from satellite imagery. Mon. Weather Rev. 2021, 149, 2097–2113. [Google Scholar] [CrossRef]
- Lee, Y.J.; Hall, D.; Liu, Q.; Liao, W.W.; Huang, M.C. Interpretable tropical cyclone intensity estimation using Dvorak-inspired machine learning techniques. Eng. Appl. Artif. Intell. 2021, 101, 104233. [Google Scholar] [CrossRef]
- Xu, W.; Balaguru, K.; August, A.; Lalo, N.; Hodas, N.; DeMaria, M.; Judi, D. Deep learning experiments for tropical cyclone intensity forecasts. Weather Forecast. 2021, 36, 1453–1470. [Google Scholar]
- Chen, R.; Wang, X.; Zhang, W.; Zhu, X.; Li, A.; Yang, C. A hybrid CNN-LSTM model for typhoon formation forecasting. GeoInformatica 2019, 23, 375–396. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, X.; Shi, L.; Wang, B.; Du, Z.; Zhang, F.; Liu, R. A neural network framework for fine-grained tropical cyclone intensity prediction. Knowl.-Based Syst. 2022, 241, 108195. [Google Scholar] [CrossRef]
- Boussioux, L.; Zeng, C.; Guénais, T.; Bertsimas, D. Hurricane forecasting: A novel multimodal machine learning framework. Weather Forecast. 2022, 37, 817–831. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Zhou, Z.H. Machine Learning; Springer Nature: Singapore, 2021. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Huh, M.; Agrawal, P.; Efros, A.A. What makes ImageNet good for transfer learning? arXiv 2016, arXiv:1608.08614. [Google Scholar]
- Bengio, Y. Deep learning of representations for unsupervised and transfer learning. In Proceedings of the ICML Workshop on Unsupervised and Transfer Learning, Bellevue, DC, USA, 2 July 2011; pp. 17–36. [Google Scholar]
- Pang, S.; Xie, P.; Xu, D.; Meng, F.; Tao, X.; Li, B.; Li, Y.; Song, T. NDFTC: A new detection framework of tropical cyclones from meteorological satellite images with deep transfer learning. Remote Sens. 2021, 13, 1860. [Google Scholar] [CrossRef]
- Deo, R.V.; Chandra, R.; Sharma, A. Stacked transfer learning for tropical cyclone intensity prediction. arXiv 2017, arXiv:1708.06539. [Google Scholar]
- Smith, M.; Toumi, R. Using video recognition to identify tropical cyclone positions. Geophys. Res. Lett. 2021, 48, e2020GL091912. [Google Scholar]
- Zhuo, J.Y.; Tan, Z.M. A Deep-learning Reconstruction of Tropical Cyclone Size Metrics 1981–2017: Examining Trends. J. Clim. 2023, 36, 5103–5123. [Google Scholar] [CrossRef]
- Fu, D.; Chang, P.; Liu, X. Using convolutional neural network to emulate seasonal tropical cyclone activity. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003596. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Bian, G.F.; Nie, G.Z.; Qiu, X. How well is outer tropical cyclone size represented in the ERA5 reanalysis dataset? Atmos. Res. 2021, 249, 105339. [Google Scholar] [CrossRef]
- Slocum, C.J.; Razin, M.N.; Knaff, J.A.; Stow, J.P. Does ERA5 mark a new era for resolving the tropical cyclone environment? J. Clim. 2022, 35, 7147–7164. [Google Scholar] [CrossRef]
- Han, Z.; Yue, C.; Liu, C.; Gu, W.; Tang, Y.; Li, Y. Evaluation on the applicability of ERA5 reanalysis dataset to tropical cyclones affecting Shanghai. Front. Earth Sci. 2022, 16, 1025–1039. [Google Scholar] [CrossRef]
- Gardoll, S.; Boucher, O. Classification of tropical cyclone containing images using a convolutional neural network: Performance and sensitivity to the learning dataset. Geosci. Model Dev. 2022, 15, 7051–7073. [Google Scholar] [CrossRef]
- Bourdin, S.; Fromang, S.; Dulac, W.; Cattiaux, J.; Chauvin, F. Intercomparison of four algorithms for detecting tropical cyclones using ERA5. Geosci. Model Dev. 2022, 15, 6759–6786. [Google Scholar] [CrossRef]
- Accarino, G.; Donno, D.; Immorlano, F.; Elia, D.; Aloisio, G. An Ensemble Machine Learning Approach for Tropical Cyclone Detection Using ERA5 Reanalysis Data. arXiv 2023, arXiv:2306.07291. [Google Scholar]
- Ito, K. Errors in tropical cyclone intensity forecast by RSMC Tokyo and statistical correction using environmental parameters. SOLA 2016, 12, 247–252. [Google Scholar] [CrossRef]
- Chan, M.H.K.; Wong, W.K.; Au-Yeung, K.C. Machine learning in calibrating tropical cyclone intensity forecast of ECMWF EPS. Meteorol. Appl. 2021, 28, e2041. [Google Scholar] [CrossRef]
- Faranda, D.; Messori, G.; Bourdin, S.; Vrac, M.; Thao, S.; Riboldi, J.; Fromang, S.; Yiou, P. Correcting biases in tropical cyclone intensities in low-resolution datasets using dynamical systems metrics. Clim. Dyn. 2023, 61, 4393–4409. [Google Scholar] [CrossRef]
- Knapp, K.R.; Diamond, H.J.; Kossin, J.P.; Kruk, M.C.; Schreck, C.J., III. International Best Track Archive for Climate Stewardship (IBTrACS) Project, Version 4; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2018; Volume 10. [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Cione, J.J.; Kalina, E.A.; Zhang, J.A.; Uhlhorn, E.W. Observations of air–sea interaction and intensity change in hurricanes. Mon. Weather Rev. 2013, 141, 2368–2382. [Google Scholar] [CrossRef]
- Ghifary, M.; Kleijn, W.B.; Zhang, M. Domain adaptive neural networks for object recognition. In Proceedings of the PRICAI 2014: Trends in Artificial Intelligence: 13th Pacific Rim International Conference on Artificial Intelligence, Gold Coast, Australia, 1–5 December 2014; Proceedings 13. Springer: Berlin/Heidelberg, Germany, 2014; pp. 898–904. [Google Scholar]
- Tzeng, E.; Hoffman, J.; Zhang, N.; Saenko, K.; Darrell, T. Deep domain confusion: Maximizing for domain invariance. arXiv 2014, arXiv:1412.3474. [Google Scholar]


| Variable name (units) | Maximum Sustained Wind Speed (kts) Storm Center (degrees lat/lon) Other variables |
| Temporal resolution | Interpolated to 3 hourly (Most data reported at 6 hourly) |
| Coverage | 70°N to 70°S and 180°W to 180°E 1841—present (Not all storms captured) |
| Data Type | Gridded |
|---|---|
| Horizontal coverage | Global |
| Horizontal resolution | 0.25 × 0.25 |
| Vertical coverage | 1000 hPa to 1 hPa |
| Vertical resolution | 37 pressure levels |
| Temporal coverage | 1940 to present |
| Temporal resolution | Hourly |
| TC Numbers | Samples | |
|---|---|---|
| Category 1 (64 ≤ < 83) | 32 | 2061 |
| Category 2 (83 ≤ W < 96) | 13 | 774 |
| Category 3 (96 ≤ W < 113) | 20 | 626 |
| Category 4 (113 ≤ W < 137) | 29 | 562 |
| Category 5 (W ≥ 137) | 14 | 122 |
| Total | 108 | 4145 |
| 10% | 20% | 30% | 40% | 50% | |
|---|---|---|---|---|---|
| Category 1 | 0.00 | 0.33 | 0.60 | 0.77 | 0.75 |
| Category 2 | 0.00 | 0.00 | 0.25 | 0.40 | 0.50 |
| Category 3 | 0.50 | 0.50 | 0.33 | 0.50 | 0.70 |
| Category 4 | 0.00 | 0.17 | 0.11 | 0.25 | 0.43 |
| Category 5 | 0.00 | 0.33 | 0.50 | 0.33 | 0.57 |
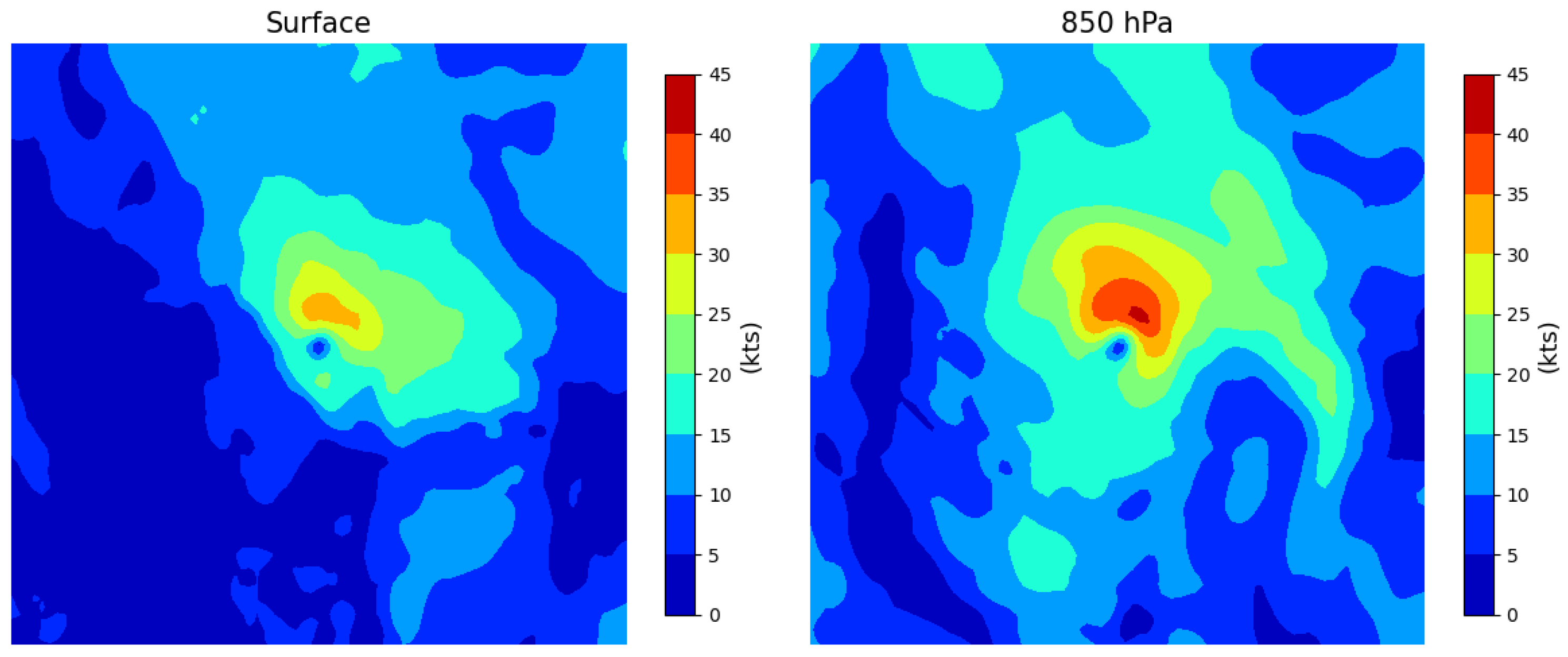
| Data | Method | Testing Dataset (10%) | Testing Dataset (2021–2022) | ||
|---|---|---|---|---|---|
| Bias (kts) | RMSE (kts) | Bias (kts) | RMSE (kts) | ||
| Surface | Point to Point | −66.65 | 69.82 | −65.16 | 67.98 |
| Linear model | −1.48 | 20.86 | 1.08 | 19.01 | |
| 850 hPa | Point to Point | −52.48 | 56.7 | −49.72 | 53.6 |
| Linear model | −1.51 | 21.04 | 0.53 | 19.74 | |
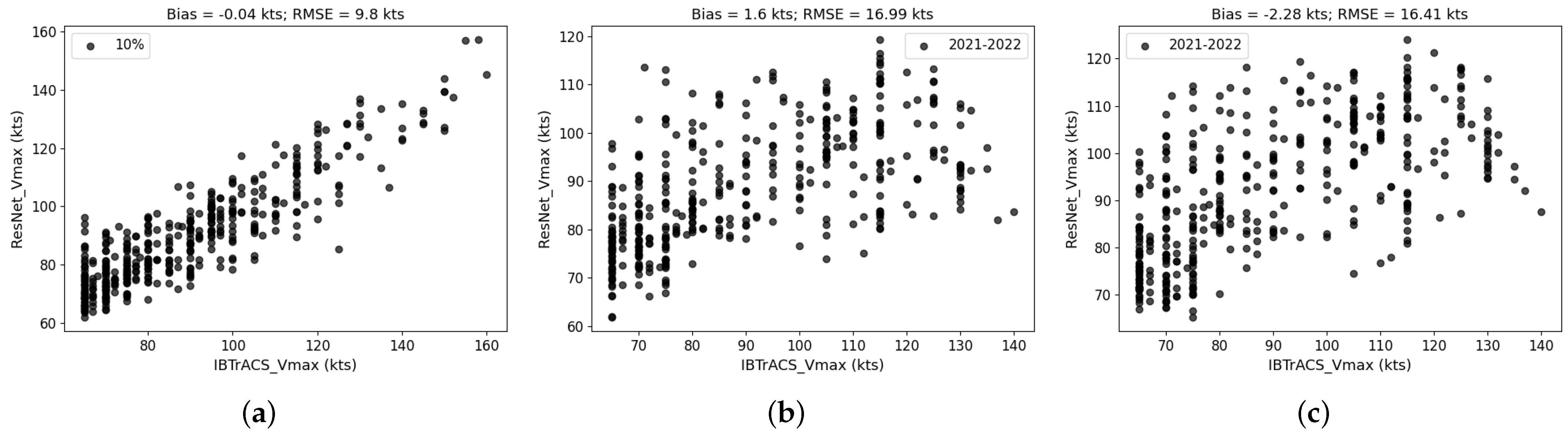
| Data | Testing Dataset (10%) | Testing Dataset (2021–2022) | ||||
|---|---|---|---|---|---|---|
| Validation (10%) | Validation (10% in 2004–2020) | Validation (2019–2020) | ||||
| Bias (kts) | RMSE (kts) | Bias (kts) | RMSE (kts) | Bias (kts) | RMSE (kts) | |
| Surface | 0.70 | 11.03 | −0.64 | 16.06 | −1.99 | 16.67 |
| 850 hPa | −0.04 | 9.8 | 1.60 | 16.99 | −2.28 | 16.41 |
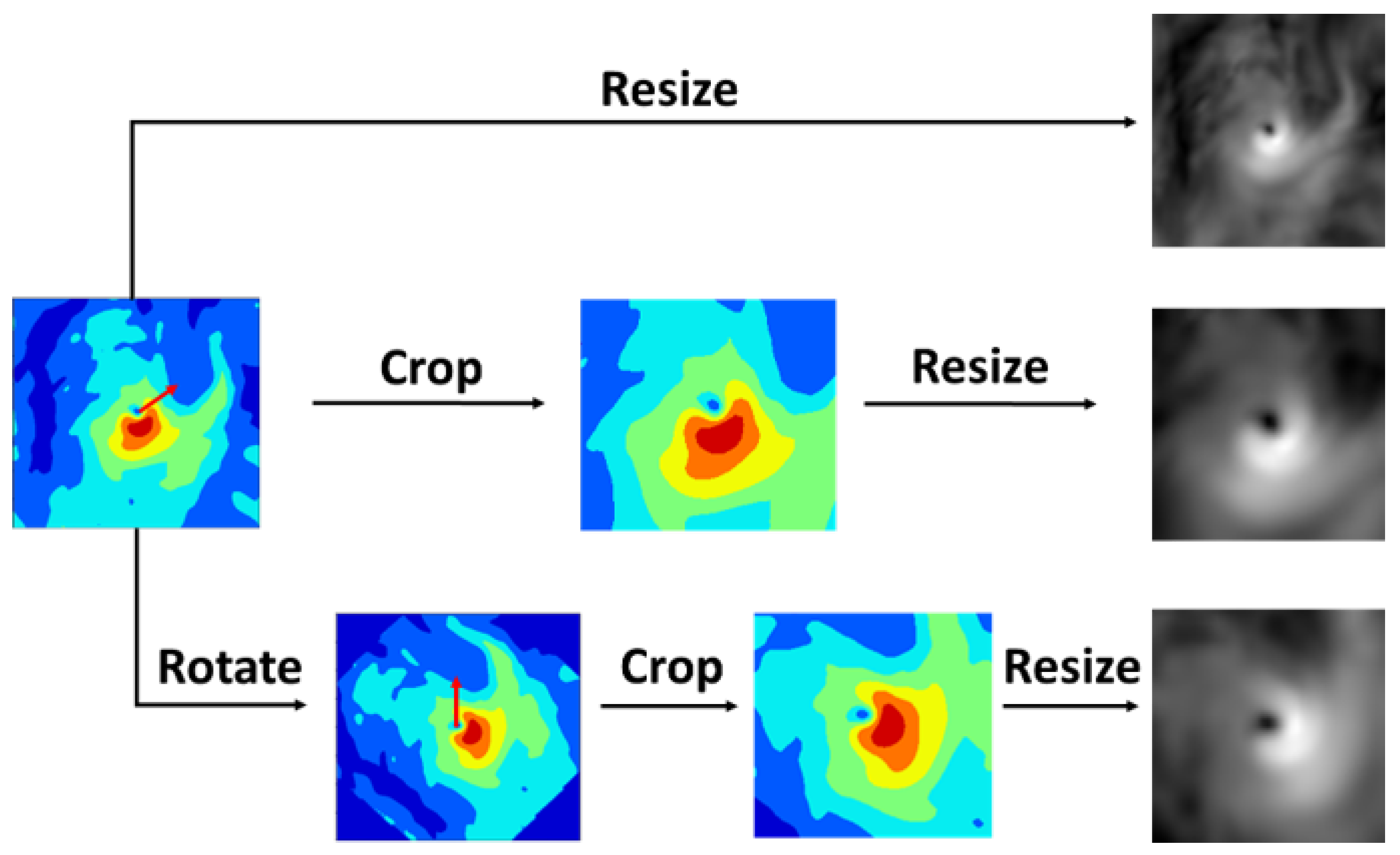
| Data Augmentation | Inputs’ Shape | Bias (kts) | RMSE (kts) |
|---|---|---|---|
| Original | (None, 81, 81, 1) | 0.88 | 17.46 |
| Crop + Resize | (None, 224, 224, 1) | −1.54 | 15.21 |
| Rotate + Crop + Resize | (None, 224, 224, 1) | −1.56 | 16.08 |
| Variables | Levels | Input Shape | Bias (kts) | RMSE (kts) |
|---|---|---|---|---|
| Wind | 850 hPa, 200 hPa | (224, 224, 2) | −0.66 | 16.19 |
| 850 hPa, 500 hPa | (224, 224, 2) | −1.11 | 16.60 | |
| 850 hPa, 500 hPa, 200 hPa | (224, 224, 3) | −1.36 | 15.47 | |
| 850 hPa | (224, 224, 2) | 0.54 | 18.00 | |
| Wind, | 850 hPa, 200 hPa | (224, 224, 4) | −0.52 | 16.45 |
| 850 hPa, 500 hPa | (224, 224, 4) | 2.32 | 17.03 | |
| 850 hPa, 500 hPa, 200 hPa | (224, 224, 6) | 0.82 | 14.90 |
| Fold | Sample Size (Training Dataset) | Bias (kts) | RMSE (kts) |
|---|---|---|---|
| 0 | 3258 | 0.82 | 14.90 |
| 1 | 6516 | −2.43 | 15.47 |
| 2 | 9774 | −1.07 | 14.76 |
| 3 | 13,032 | −0.77 | 15.16 |
| 4 | 16,290 | −0.26 | 15.14 |
| Training Dataset () | Validation Dataset () | Testing Dataset () | |
|---|---|---|---|
| D1 | (, ) * | (, ) | (, ) |
| D2 | 90% of (, ) | 10% of (, ) | (, ) |
| D3 | 90% of ((, ) + (, )) | 10% of ((, ) + (, )) | (, ) |
| Data | Methods | Setting | Bias (kts) | RMSE (kts) |
|---|---|---|---|---|
| D1 | ML | LR | −1.15 | 14.83 |
| SVR | −1.53 | 14.76 | ||
| GBR | −1.30 | 14.92 | ||
| MLP | 1 (1) | −1.09 | 14.89 | |
| 3 (1024/512/1) | 1.24 | 15.12 | ||
| 5 (1024/4096/1024/512/1) | −0.39 | 15.18 | ||
| D2 | ML | LR | 9.51 | 52.31 |
| SVR | −0.06 | 15.71 | ||
| GBR | 2.24 | 15.88 | ||
| MLP | 1 (1) | 1.63 | 15.26 | |
| 3 (1024/512/1) | −1.09 | 14.89 | ||
| 5 (1024/4096/1024/512/1) | 0.69 | 14.76 | ||
| D3 | ML | LR | −0.52 | 14.82 |
| SVR | −1.46 | 14.73 | ||
| GBR | −0.63 | 14.72 | ||
| MLP | 1 (1) | 1.23 | 11.74 | |
| 3 (1024/512/1) | 0.27 | 11.55 | ||
| 5 (1024/4096/1024/512/1) | 0.61 | 11.51 | ||
| DA | 1 | −2.45 | 5.99 | |
| 100 | −2.43 | 5.99 | ||
| 1000 | −2.35 | 10.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Toumi, R.; Shi, X.; Wang, X.; Duan, Y.; Zhang, W. An Adaptive Learning Approach for Tropical Cyclone Intensity Correction. Remote Sens. 2023, 15, 5341. https://doi.org/10.3390/rs15225341
Chen R, Toumi R, Shi X, Wang X, Duan Y, Zhang W. An Adaptive Learning Approach for Tropical Cyclone Intensity Correction. Remote Sensing. 2023; 15(22):5341. https://doi.org/10.3390/rs15225341
Chicago/Turabian StyleChen, Rui, Ralf Toumi, Xinjie Shi, Xiang Wang, Yao Duan, and Weimin Zhang. 2023. "An Adaptive Learning Approach for Tropical Cyclone Intensity Correction" Remote Sensing 15, no. 22: 5341. https://doi.org/10.3390/rs15225341
APA StyleChen, R., Toumi, R., Shi, X., Wang, X., Duan, Y., & Zhang, W. (2023). An Adaptive Learning Approach for Tropical Cyclone Intensity Correction. Remote Sensing, 15(22), 5341. https://doi.org/10.3390/rs15225341





