Abstract
Rapid and accurate measurement of the soil organic carbon (SOC) content is a pre-condition for sustainable grain production and land development, and contributes to carbon neutrality in the agricultural industry. To provide technical support for the development and utilization of land resources, the SOC content can be estimated using Vis-NIR diffuse reflectance spectroscopy. However, the spectral redundancy and co-linearity issues of Vis-NIR spectra pose extreme challenges for spectral analysis and model construction. This study compared the effects of different pre-processing methods and feature variable algorithms on the estimation of the SOC content. To this end, in situ hyperspectral data and soil samples were collected from the lakeside oasis of Bosten Lake in Xinjiang, China. The results showed that the combination of continuous wavelet transform (CWT)-random frog could rapidly estimate the SOC content with excellent estimation accuracy (R2 of 0.65–0.86). The feature variable selection algorithm effectively improved the estimation accuracy (average improvement of (0.30–0.48); based on their ability to improve model estimation on average, the algorithms can be ranked as follows: particle swarm optimization (PSO) > ant colony optimization (ACO) > random frog > Boruta > simulated annealing (SA) > successive projections algorithm (SPA). The CWT-XGBoost model based on random frog showed the best results, with R2 = 0.86, RMSE = 2.44, and RPD = 2.78. The feature bands accounted for only 0.57% of the Vis-NIR bands, and the most important sensitive bands were distributed at 755–1195 nm, 1602 nm, 1673 nm, and 2213 nm. These findings are of significance for the extraction of precise information on lakeside oases in arid areas, which would aid in achieving human–land sustainability.
1. Introduction
Oases are non-zonal landscapes formed under dry climatic conditions with a desert substrate, lakes, and oasis land as main patches, supporting high agricultural productivity. Physicochemical processes in lakeside oasis soil environments are controlled by soil organic carbon (SOC), which is also a key determinant of soil fertility and agricultural potential [1,2]. Therefore, the rapid monitoring of the SOC content could provide a scientific basis for the rational development of land resources and precision agriculture. High-precision data on the SOC content could provide theoretical support to local governments for the implementation of relevant farmland policies [3]. However, the traditional chemical analysis method and the indoor Vis-NIR spectroscopy method for determining the SOC content are time-consuming, laborious, and expensive, and they are not suitable for large-scale estimations [4]. Recently, hyperspectral technology has been widely used to extract soil information, and Vis-NIR-IR hyperspectral technology has emerged as a rapid, accurate, economical, and non-destructive soil analysis method [5]. Using this technique, the soil organic carbon content can be accurately estimated based on the spectral reflectance of only a small number of soil samples. It could effectively replace the traditional method [6]. In particular, in situ spectra are more effective and simpler than traditional laboratory methods and could improve estimation accuracy [7].
Drying and grinding soils greatly increases the accuracy and determination of soil properties [8]. However, the accuracy of related estimation models is limited by the instability factor of outdoor environments and the redundancy of spectral data. Therefore, spectral pre-processing and feature variable selection are prerequisites for the accurate estimation of the SOC content. Traditional methods for reducing the interference of spectral information include Savitzky–Golay smoothing, continuum removal, normalization, and spectral logarithm [9]. However, no single pre-processing method (or combination) is currently applicable to different geographic soil landscapes. Many scholars have attempted to use standard normal variate (SNV) and multiplicative scatter correction (MSC) to solve spectral errors associated with scattering and the spectral differences arising from different scattering levels [10,11]. Continuous wavelet transformation (CWT) has an excellent capability for time–frequency analysis, and it has potential as an effective method for enhancing the spectral response, characterizing local features of the spectral signal, and more effectively extracting information of small spectral features in soil [12]. It has also been proven to be effective as a pre-processing method [2,13]. The accuracy of SOC content estimation is affected by various factors, such as outdoor temperature, vegetation cover, soil surface roughness, wind, and the redundancy of the full-band spectra. Therefore, current research is focusing on solutions toward reducing the interference of irrelevant variables and improving the accuracy of SOC content estimation using in situ Vis-NIR spectroscopy [14]. Model accuracy can be improved and model complexity can be reduced by using a reasonable feature variable algorithm to select feature bands [15]. Previous studies have reported good results using in situ spectroscopy combined with particle swarm optimization (PSO), ant colony optimization (ACO), and simulated annealing (SA) for estimating the soil organic matter content in the desert areas of southern Xinjiang [16]. The successive projections algorithm (SPA) and Boruta algorithm eliminate a certain amount of redundancy in spectral information and effectively preserve the integrity of the spectral data and the physical meaning of the original bands [17]. The random frog algorithm, which has been shown to be a better variable selection algorithm, simulates a smoothly distributed Markov chain in the feature space and calculates the probability of each variable being selected to perform the selection of important variables [18]. However, the results of these methods show certain differences, which may affect the final estimation accuracy. Therefore, a comprehensive assessment is required.
The ability to accurately estimate the SOC content depends on the modeling strategies constructed. Partial least squares regression (PLSR) is a conventional linear model that can reduce the collinearity problem caused by spectral overlap and thus improve the accuracy and robustness of the estimation model [19]. However, problems such as autocorrelation and the multicollinearity of the samples are ignored when constructing the model using the linear model. Meanwhile, the complexity and uncertainty of soil spectral reflectance and possible noise reduce the fit and reliability of the estimation model for SOC content estimation. Previous studies have shown that the feature variables are not simply linearly related to soil organic matter [16]. Therefore, various nonlinear models have been widely used for the estimation of SOC contents, including extreme gradient boosting machine (XGBoost), back propagation neural network (BPNN), and random forest (RF) [2,19]. This study mainly focused on the ability of (in situ) hyperspectral imaging systems to estimate the SOC content in a lakeside oasis in the dry zone of Xinjiang. The research objectives are as follows: (1) Assessment of the effects of different pre-processing methods and feature variable algorithms combined with in situ soil hyperspectral data on the accuracy of SOC content estimation in lakeside oases in arid regions. (2) Constructing optimal modeling strategies. (3) Exploring the sensitive bands of the SOC of the lakeside oasis. The findings provide technical support for monitoring soil fertility in lakeside oases.
2. Materials and Methods
2.1. Study Area
The study area is located in Bohu County in Xinjiang, northwestern China (Geographical coordinates: 41°45′–42°10′N, 86°15′–86°55′E). It has a total area of 1360 km2 (Figure 1) and a continental desert climate. The average monthly temperatures in summer and winter are 22.80 °C and 9.00 °C, respectively, and the average annual temperature ranges from 8.00 to 8.60 °C. The frost-free period is 176–200 d, the average annual precipitation is 83.55 mm, and the annual evaporation is 1880–2785.80 mm. The main soil types are fluvo-aquic soils, meadow soils, and bog soils. The land use types in the study area are mainly cropland and unused land.
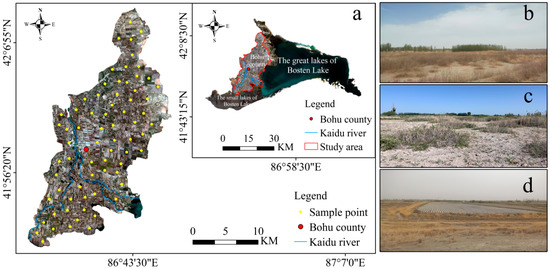
Figure 1.
Map of the study area and the spatial distribution of the sampling points (a); typical landscape of the study area (b–d).
2.2. Soil Sampling and Laboratory SOC Measurement
According to previous studies, 33% of the SOC content is distributed within the soil depth of 1 m, with the topsoil (0–20 cm) playing an important role in plant growth by determining soil fertility [20]. A total of 70 sampling points (0–20 cm) were selected for this study on 22–25 April 2023 based on the typical landscape characteristics of the study area. The latitude and longitude of the soil sampling points were recorded using a portable GPS device (Garmin GPS 72, accuracy < 10 m). The samples were then transferred to the Xinjiang Laboratory of Lake Environment and Resources in Arid Zone. Impurities (plant roots and rock fragments) were removed from the collected soil samples, and then the samples were air-dried, ground, and filtered through a 0.14 mm sieve. The SOC content was determined using the potassium dichromate–external heating method.
2.3. In Situ Spectral Measurement and Pre-Processing
The soil hyperspectral data were obtained using an ASD FieldSpec3 geophysical spectrometer (Analytical Spectral Devices, Inc., Boulder, CO, USA), which has a spectral range of 350–2500 nm. The equipment was warmed up for 30 min, the white reference panel was calibrated (25 cm × 25 cm, 99% reflectance) before measuring the spectral data, and the white reference panel was performed at intervals of 10 samples during the measurement. The spectral data were required to be collected on a clear and windless day with less than 5% cloud cover, less than 45° solar zenith angle, stable solar illumination, and the sun as the only light source during the measurement period. The collection time ranged from 11:00 to 14:00 Beijing time. Spectral bands located at the edges (350–399 nm and 2451–2500 nm) were excluded because they included severe noise. The spectral bands near 1400 nm and 1900 nm are affected by water vapor due to outdoor environmental factors [16]. In this study, the 1360–1570 nm and 1831–1930 nm wavelength ranges were affected by atmospheric water vapor absorption, which were thus excluded. The soil samples were filtered using a 0.14 mm sieve prior to spectral measurements. The spectral measurements were taken at a vertical distance of 15 cm from the ground (with a ground field of view at 25°), in which 10 measurements were taken at each sampling point, and then averaged as in situ spectral reflectance. The raw spectral data were exported in ASCII format. The acquired in situ spectral data were sequentially subjected to standard normal variation to reduce scattering-related errors, multiple scattering correction to eliminate multiplicative interferences, and CWT to enhance the spectral response. Figure 2 depicts the in situ hyperspectral data collection and pre-processing workflow.
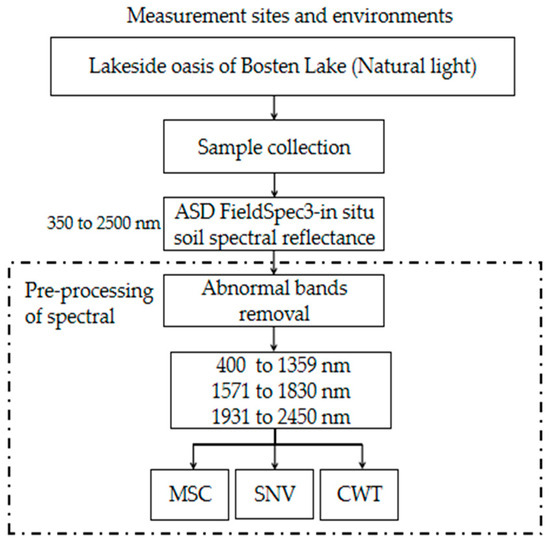
Figure 2.
Workflow of the in situ soil spectral reflectance data collection and pre-processin.
2.4. Feature Variable Selection Algorithms
For the feature variable selection algorithm, the interaction between spectral variables was considered, which could effectively eliminate unrelated variables, thus improving the estimation accuracy and robustness of the model [21].
The successive projections algorithm (SPA) is a forward selection method that has widely been used for feature band selection in Vis-NIR. It can effectively reduce information overlaps and minimize the covariance between variables [22]. At the same time, it significantly reduces the number of modeling variables and effectively improves modeling efficiency [23].
Proposed by Kennedy and Eberhart in 1995, particle swarm optimization (PSO) was inspired by the basic idea of modeling and simulating the behavior of bird populations. Its core idea is to use the sharing of information by individuals in a group to induce the evolution of the motion of the whole group, from disorder to order in the problem solution space, so as to obtain the optimal solution of the problem [24].
The simulated annealing (SA) was proposed by Metropolis et al. [25] in 1953 as a stochastic optimization algorithm based on the Monte–Carlo iterative solution strategy, which starts from a high initial temperature and decreases with the temperature parameter, combining the probabilistic jump property to randomly find the global optimal solution of the objective function in the solution space.
Ant colony optimization (ACO) was proposed by M. Dorigo in 1991 as an optimization algorithm that simulates the foraging behavior of ants. In nature, during the foraging process of ants, the colony is always able to follow and find an optimal path between the nest and the food source [16].
The Boruta algorithm is a feature selection method based on two core ideas: shadow features and binomial distribution, and the algorithm automatically performs feature selection on a dataset by making a copy of the original feature and randomly breaking it by rows, creating shadow features. Starting from X, for each real feature R, the order is randomly disrupted and the disrupted original features are called shadow features. At this point, the shadow data j matrix is appended to the original data frame to obtain a new data j matrix with twice the number of columns of X. In Boruta, the original features do not compete with each other. Instead, the original features compete with the shuffled features (shadow features) [26].
Random frog is a novel feature variable algorithm proposed by Eusuff et al. [27] for solving combinatorial optimization problems. It enables model construction using only a small number of variable iterations, which is very effective for variable selection involving high-dimensional data. The algorithm aims to optimize the prediction accuracy of the calibration model; taking the probability of each wavelength being selected in the cyclic calculation as a benchmark, through cyclic iteration, the 10 feature wavelengths with the highest probability are selected to build the prediction model [28].
2.5. Model Strategies
PLSR is widely used for quantitative analysis in Vis-NIR bands and has become a common method for building linear quantitative correction models in spectral analysis. It is a method combining principal component analysis, typical correlation analysis, and multiple linear regression analysis that can facilitate regression modeling, data structure simplification, and correlation analysis between two sets of variables [29]. PLSR finds the best function match for the data by minimizing the sum of the squares of the errors, using least squares to easily find unknown data and minimize the sum of the squares of the errors between these found data and the actual data. In hyperspectral modeling, PLSR analysis can facilitate the quantitative prediction of SOC [30,31].
Random forest (RF) is a bagging principle method based on classification and regression tree analysis and classification. It is advantageous in that the regression process can be used to assess the importance of each feature through unbiased estimation, and it offers higher efficiency than the traditional linear model while handling complex nonlinear relationships [32,33].
BPNN is a multilayer feed-forward neural network trained according to the error back-propagation algorithm, with excellent nonlinear simulation capability and flexible network structure, consisting of the input layer (spectral data: full bands and featured bands), implicit layer (also known as the intermediate layer), and output layer (SOC content), and it is the most widely used neural network [34,35].
XGBoost is a boosting integration algorithm for solving classification or regression problems. Its core idea is to use the residuals obtained from the training of the previous weak classifier as a reference, and then optimize the next new weak classifier. This manner of fitting residuals could effectively reduce the loss of training samples, optimize the complexity of the model, and essentially improve the accuracy and robustness of the model [36,37]. While the traditional GBDT uses only first-order derivative information (negative gradient) in optimization, XGBoost performs a second-order Taylor expansion of the cost function using both first- and second-order derivatives. Figure 3 shows the specific flow chart.
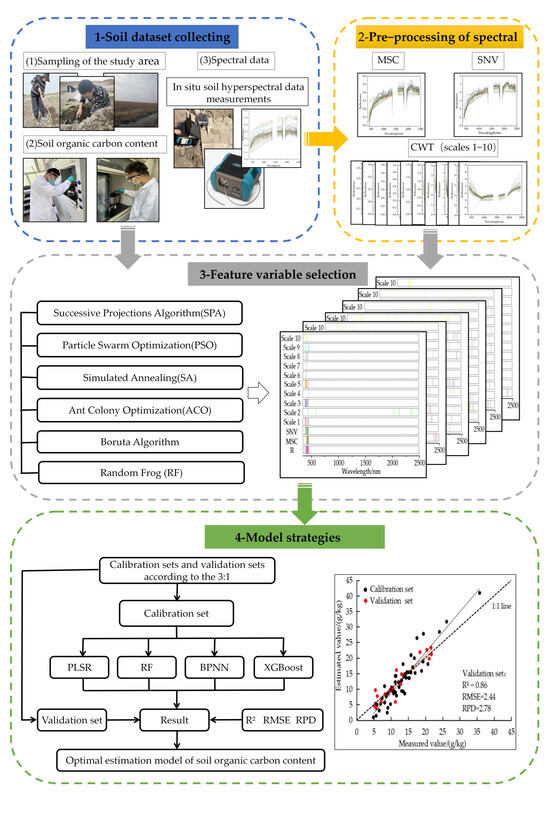
Figure 3.
Construction process of the soil organic carbon content model for the study area.
2.6. Model Accuracy Evaluation
The coefficient of determination (R2), root mean square error (RMSE), and relative analysis error (RPD) were used to assess model robustness and stability. The closer R2 is to 1, the smaller the RMSE; RPD < 1.40 indicates that the model has a poor ability to estimate accuracy, 1.4 < RPD < 2 indicates that the model has an average ability to estimate accuracy, and RPD > 2 indicates that the model has an excellent ability to estimate accuracy [38,39,40]. The specific calculation formulae are as follows:
where SOCi is the measured soil organic carbon content, SOCPi is the predicted value based on the SOC content prediction model, SOCi,mean is the mean of the measured soil organic content, and SD is the standard deviation based on the predicted value of the SOC content.
3. Results and Analysis
3.1. Descriptive Statistics of Soil Organic Carbon Content
The soil samples were divided into calibration sets and validation sets according to 3:1 using the SPXY method. Descriptive statistics of the total set, calibration set, and validation set of the SOC content are shown in Table 1. The mean value of the calibration set (1.40–40.92 g/kg) and the mean value of the validation set (0.91–23.29 g/kg) for SOC content were 13.02 g/kg and 11.93 g/kg, with standard deviations of 7.59 g/kg and 7.35 g/kg, respectively, and coefficients of variation (CV) of 58.33% and 61.67%, respectively. The mean value of the total set of SOC content was 12.76 g/kg, with standard deviation of 7.50 g/kg and CV of variation of 58.80%. CV indicates the degree of dispersion; CV ≥ 100% indicates strong variability; 10% ≤ CV ≤ 100% indicates moderate variability; and CV ≤ 10% indicates weak variability. The total set of samples was between the calibration and validation sets, and the data discretization was not strong. The standard deviation and the mean value were close to indicating that the calibration set and the validation set had similar statistical distributions compared with the total set; therefore, the sample division was reasonable.

Table 1.
Descriptive statistics of soil organic carbon content in the study area. Max: Maximum SOC content; Min: Minimum SOC content; SD: Standard deviation; CV: Coefficient of variation.
3.2. Feature Variable Selected Using SPA, PSO, SA, ACO, Boruta and Random Frog Algorithms
The typical feature bands could reduce the influence of irrelevant variables and thus improve the accuracy and robustness of the estimation model. We used Vis-NIR in situ spectra from 400 to 2450 nm as the full bands and selected the feature bands from the full bands using the SPA, PSO, SA, ACO, Boruta, and random frog algorithms. However, the six feature variable selection algorithms selected different number of feature bands: 1–21, 8–38, 13–28, 11–32, 4–21, and 10 for SPA, PSO, SA, ACO, Boruta, and random frog, respectively. Among them, the lowest number of bands was selected by the Boruta algorithm, followed by SPA, random frog, PSO, ACO, and SA. The feature bands selected by the algorithms were distributed in the visible and near-infrared bands, as follows: Boruta Vis (404 nm, 459–599 nm, and 724–760 nm) and NIR (1686 nm, 1714 nm, and 1963–2420 nm); SPA Vis (400–469 nm and 607 nm) and NIR (2041 nm, 2143 nm, 2358 nm, and 2392 nm); PSO Vis (400–469 nm and 607 nm) and NIR (2041 nm, 2143 nm, 2358 nm, and 2392 nm); SA Vis (402–756 nm) and NIR (768–1359 nm, 1581–1821 nm, and 1945–2414 nm); ACO Vis (421–745 nm) and NIR (761–1358 nm, 1572–1830 nm, and 1931–2448 nm); and random frog Vis (425 nm, 460 nm, and 618–755 nm) and NIR (788–1195 nm, 1317 nm, 1573–1827 nm, 1934 to 2169 nm, and 2346 nm). The distributions of feature band positions selected by the six feature variable algorithms are shown in Figure 4. Feature bands at the water vapor of 1360–1570 nm and 1831–1930 nm were excluded because they were affected by water vapor. Specifically, more than 97% of the bands were rejected, indicating that the feature variable algorithms could reduce the redundancy of the spectral data.
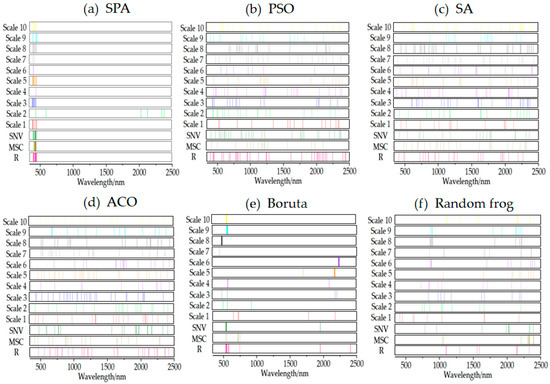
Figure 4.
Distribution of SOC content feature bands selected by SPA, PSO, SA, ACO, Boruta, and random frog.
3.3. Model Validation
To improve the estimation model accuracy, we used the full bands and the feature bands selected by the algorithms as independent variables and the measured SOC content as dependent variables to construct the PLSR, RF, BPNN, and XGBoost estimation models for SOC content. Table 2 shows the comparison results of the SOC content estimation models constructed separately for the full-band spectral data and the feature bands. Among the full-band estimation models, the pre-processing of MSC, SNV, and CWT could improve the estimation accuracy of the SOC content. In particular, CWT–random frog–XGBoost presented the most prominent improvement, with estimation accuracies of R2 = 0.86, RMSE = 2.44, and RPD = 2.78; its feature bands accounted for only 0.57% of the Vis-NIR bands. From the viewpoint of using feature variable selection, the feature-band models showed higher estimation than the full-band model. The models based on SPA, PSO, SA, ACO, Boruta, and random frog showed average improvements of 0.30, 0.48, 0.38, 0.45 0.42, and 0.43, respectively. In terms of improving estimation accuracy, the algorithms could be ranked as follows: PSO > ACO > random frog > Boruta > SA > SPA. The most important sensitive bands for the random frog algorithm were distributed at 755–1195 nm, 1602 nm, 1673 nm, and 2213 nm, indicating that the algorithm could effectively eliminate the redundancy of spectral information and improve the model accuracy.

Table 2.
Comparison of PLSR, RF, BPNN, and XGBoost models constructed based on in situ full spectral bands and feature bands.
In terms of their estimation ability, the four estimation models could be ranked as follows: XGBoost > BPNN > RF > PLSR. In particular CWT–XGBoost, combined with the six feature variable algorithms provided excellent results, with its RPD ranging from 2.14 to 2.78.
In order to further validate the accuracy of the estimation model, scatter plots were generated for the measured and predicted values of the optimal estimation results of PLSR, RF, BPNN, and XGBoost (Figure 5). The measured and predicted values of the CWT–random frog–XGBoost model appeared to be close to the 1:1 line.
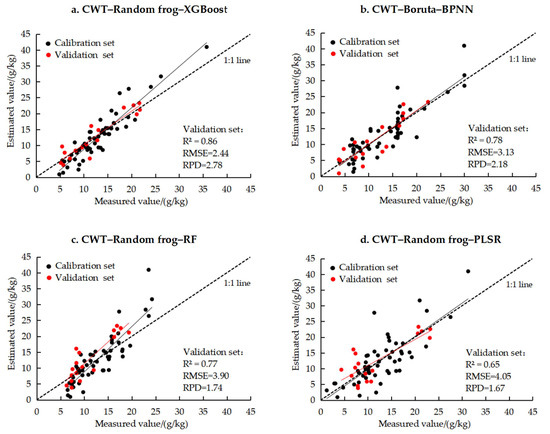
Figure 5.
Scatterplot of the optimal estimation results based on PLSR, RF, BPNN, and XGBoost.
4. Discussion
4.1. Effects of Different Spectral Pre−Processing and Feature Variable Algorithms on Estimation Accuracy
The accuracy of estimation models can be improved by combining effective spectral pre-processin methods with spectral data [41]. However, not all combinations of pre-processin methods are effective for datasets from different regions. Therefore, the selection of a reasonable spectral pre-processin method for the analysis of soil characteristics using Vis-NIR bands is extremely important. In this study, the models using CWT pre-processin were found to have the highest accuracy. Compared with the full-band models, the feature-band models showed an accuracy improvement of 0.75. This is consistent with the results of previous studies on the hyperspectral estimation of SOC contents [42]. This may be attributable to CWT effectively capturing the weak signals of spectral information and improving the response between spectral information and the SOC content. SNV and MSC, as common methods for pre-processin spectral data, can effectively eliminate the spectral differences caused by different scattering levels, thus enhancing the correlation between spectra and data [43,44]. However, most of the estimation results from the PLSR model constructed after MSC and SNV pre-processin were not meaningful, which is inconsistent with the findings of previous studies [8]. This may be due to the decrease in spectral reflectance caused by environmental factors (mainly soil moisture) during spectral measurements in the field, thus affecting the estimation results. The effect of soil moisture on estimation accuracy will be further researched in future work. Previous studies on the SOC content showed that different pre–processing methods affected the accuracy of their estimation [9].
Feature bands are key to improving the accuracy of the model. However, the differences in feature bands may affect the accuracy of SOC content estimation. Such differences may be caused by the electron leap of metal ions in the visible bands, the electron leap of organic matter and clay minerals in the near-infrared bands, and soil stretching and bending vibrations [45]. Bai et al. argued that the use of feature variable algorithms reduced irrelevant variables by more than 90% and significantly reduced the amount of model inputs [46]. In this study, the feature variable algorithm rejected more than 97% of irrelevant variables. The comparison of the accuracies of the full-band and feature-band models showed that the feature-band models achieved higher accuracy, indicating that the feature variable algorithm could effectively reduce the redundancy of the spectral data and improve the estimation accuracy of the model. In this study, the algorithms for improving model estimation could be ranked as follows: PSO > ACO > random frog > Boruta > SA > SPA (Figure 6). Yang et al. showed that a model constructed based on the PSO algorithm improved the accuracy better than the ACO and SA algorithms [16]. Although the ACO algorithm had the highest number of feature bands, the average improvement capability (an improvement of 0.45) was lower than that of the PSO algorithm (an improvement of 0.48), which may be due to the interference of redundant information in the feature bands selected by the ACO algorithm. In contrast, Wang et al. concluded that the accuracy improvement of SA was superior to that of PSO, which may be attributable to the fact that the initial temperature level affected the rate of convergence; therefore a reasonable selection of initial parameters is needed [47]. The feature bands based on the SPA algorithm were mainly distributed in the 400 to 607 nm range. This region proved to be an important band for the spectral response [48]. Compared with other algorithms, the Boruta and SPA algorithms effectively reduced spectral redundancy, but their ability to improve model accuracy was not prominent [49]. The reason may be because the excessive exclusion of feature variables was correlated with SOC. In this study, although the CWT-2-random frog-XGBoost presented the highest accuracy, with R2 = 0.86, RMSE = 2.44, and RPD = 2.78, the average improvement ability (improvement of 0.43) was not as high as those of the PSO and ACO algorithms (improvements of 0.48 and 0.45).
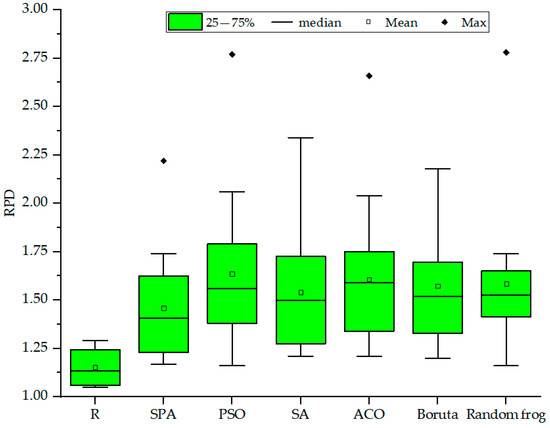
Figure 6.
Model estimation accuracy based on different feature variable algorithms.
4.2. Effects of Modeling Strategies on Estimation Accuracy
From the viewpoint of modeling strategies, nonlinear models showed better results than the linear model. As a conventional linear model, PLSR could effectively estimate the SOC content, but it could not explain the nonlinearity problem between SOC and the spectral response variables [50]. Therefore, the PLSR model provided the poorest results in this study. Among the three nonlinear machine learning models, XGBoost had a better anti-fitting function considering the complexity of the model, which improved the generalizability of the model. BPNN has a strong nonlinear mapping ability, which is attributable to its self-learning, self-organization, and self-adaptation ability, which could effectively make up for the deficiency of the linear model [47]. Compared with the first two models, RF is only a tree model. In this study, the CWT-2–random frog-XGBoost model showed the highest estimation capability, with R2 = 0.86, RMSE = 2.44, and RPD = 2.78. This may be attributable to CWT-2 being capable of decomposing feature information more effectively. Xie et al. further confirmed that the XGBoost model presented the best results in estimating the SOC content [51]. Nevertheless, the BPNN and RF methods can be combined with other methods to construct the SOC content. In this study, we found that the combination of CWT–Boruta–BPNN showed R2 = 0.78, RMSE = 3.13, and RPD = 2.18, and the combination of CWT–random frog–RF had R2 = 0.77, RMSE = 3.90, and RPD = 1.74. These methods proved to be effective in estimating the SOC content using hyperspectral data [14,52]. However, due to the spatial heterogeneity in the SOC content during in situ spectroscopy, regional differences may occur in high-precision models [53]. The applicability of CWT–random frog–XGBoost as a prerequisite for improving the SOC content to other lakeside oases needs to be further explored. The combination of the CWT–random frog–XGBoost methods is effective for high-precision estimation of the SOC content in lakeside oases. In future studies, attempts will be made to explore the combination of machine learning models with other methods based on the current study. Furthermore, the resulting models will be applied to the estimation of the SOC content of lakeside oases in arid zones using in situ spectral data in order to achieve higher accuracy.
4.3. Uncertainty Analysis and Perspectives
The estimation of the SOC content using in situ spectral data is affected by numerous factors, such as soil moisture, vegetation cover, soil surface roughness, and atmospheric water vapor [54]. In particular, soil moisture is a key factor affecting the accuracy of model estimation, and many scholars have conducted relevant studies on this problem [55,56]. With increasing soil water content, in situ spectral reflectance shows a nonlinear decrease. Studies have shown that Vis-NIR techniques achieve higher accuracy in predicting the SOC content when dry soil is involved [57]. The study area is located in Xinjiang, northwestern China, which receives little rainfall, long sunshine hours, and has relatively dry soils. To avoid the influence of soil moisture on in situ spectral data and ensure prediction accuracy, the relatively dry springtime was selected as the sampling time. Vegetation cover also affects the prediction accuracy of in situ spectra, and to avoid its influence, an area without vegetation cover was selected in this study. Moreover, the roughness of the soil surface leads to a decrease in spectral reflectance, which affects the estimation accuracy [58,59]. Therefore, a relatively flat area of the soil surface was selected. In addition, in situ spectral reflectance and model accuracy are influenced by atmospheric water vapor. Previous studies have showed that there are significant water vapor absorption bands near 1400 nm and 1900 nm [60,61,62]. In this study, in situ spectral measurements revealed significant absorption bands in the 1360–1570 nm and 1831–1930 nm regions, and spectral reflectance in these band ranges was more than 1. The bands affected by water vapor were not selected as sensitive bands. Therefore, the SPA, PSO, SA, ACO, Boruta, and random frog algorithms could effectively reject irrelevant variables, reduce spectral redundancy, and thus improve estimation accuracy.
As soil characteristics are highly variable and complex, multiple factors are involved in SOC content estimation [63]. Therefore, research on different land-use types needs to be further explored.
5. Conclusions
In this study, the effects of spectral pre–processing and feature variable selection algorithms combined with in situ hyperspectral data on the accuracy of SOC content estimation in a lakeside oasis in an arid zone were analyzed. The results show that CWT is one of the most effective spectral pre–processing methods. The application of feature variable algorithms clearly improved the estimation accuracy of the SOC content. Specifically, the SPA, PSO, SA, ACO, Boruta, and random frog algorithms could eliminate more than 97% of irrelevant variables. Compared with the in situ full-band models, the six feature variable algorithms all reduced the redundancy of in situ spectral data and thus improved the estimation accuracy of the model. The average improvements afforded by SPA, PSO, SA, ACO, Boruta, and random frog were 0.30, 0.48, 0.38, 0.45, 0.42, and 0.43, respectively. On average, the algorithms for improving model estimation could be ranked as follows: PSO > ACO > random frog > Boruta > SA > SPA. Overall, the random frog-based estimation model (CWT–random frog–XGBoost) showed the highest performance, with R2 = 0.86, RMSE = 2.44, and RPD = 2.78. The feature bands of this model accounted for only 0.57% of the Vis-NIR bands. This study provides technical support for the estimation of SOC content in lakeside oases using in situ spectral methods.
Author Contributions
Conceptualization, J.Y. and X.L.; methodology, J.Y. and X.L.; funding, X.L.; validation, J.Y. and X.L.; formal analysis, J.Y. and X.L.; investigation, J.Y. and X.L.; resources, J.Y. and X.L.; data curation, J.Y. and X.L.; writing—original draft preparation, J.Y., X.L. and X.M.; writing—review and editing, J.Y., X.L. and X.M; supervision, J.Y. and X.L.; project administration, J.Y. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was sponsored by the Natural Science Foundation of the Xinjiang Uygur Autonomous Region (Grant No. 2022D01A214) and National Science Foundation of China (Grant No. 32160271).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, T.; Geng, Y.; Ji, C.; Xu, X.; Wang, H.; Pan, J.; Bumberger, J.; Haase, D.; Lausch, A. Prediction of soil organic carbon and the CN ratio on a national scale using machine learning and satellite data: A comparison between Sentinel-2, Sentinel-3 andLandsat-8 images. Sci. Total Environ. 2021, 755, 142661. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Wang, X.; Baishan, K.; An, B. Hyperspectral Estimation of Soil Organic Carbon Content Based on Continuous Wavelet Transform and Successive Projection Algorithm in Arid Area of Xinjiang, China. Sustainability 2023, 15, 2587. [Google Scholar] [CrossRef]
- Guo, L.; Sun, X.; Fu, P.; Shi, T.; Dang, L.; Chen, Y.; Linderman, M.; Zhang, G.; Zhang, Y.; Jiang, Q.; et al. Mapping soil organic carbon stock by hyperspectral and time-series multispectral remote sensing images in low-relief agricultural areas. Geoderma 2021, 398, 115118. [Google Scholar] [CrossRef]
- Kuang, B.; Mouazen, A.M. Influence of the number of samples on prediction error of visible and near infrared spectroscopy of selected soil properties at the farm scale. Eur. J. Soil Sci. 2012, 63, 421–429. [Google Scholar] [CrossRef]
- Qi, H.; Paz-Kagan, T.; Karnieli, A.; Jin, X.; Li, S. Evaluating calibration methods for predicting soil available nutrients using hyperspectral VNIR data. Soil Till. Res. 2018, 175, 267–275. [Google Scholar] [CrossRef]
- Demattȇ, J.A.M.; Andre, C.D.; Luis, G.B.; Veridiana, M.S.; Arnaldo, B.S. Soil analytical quality control by traditional and spectroscopy techniques: Constructing the future of a hybrid laboratory for low environmental impact. Geoderma 2019, 337, 111–121. [Google Scholar] [CrossRef]
- Biney, J.K.M.; Blöcher, J.R.; Bell, S.M.; Borůvka, M.; Vašát, R. Can in situ spectral measurements under disturbance-reduced environmental conditions help improve soil organic carbon estimation? Sci. Total Environ. 2022, 838, 156304. [Google Scholar] [CrossRef]
- James, K.M.B.; Luboš, B.; Prince, C.A.; Karel, N.; Aleš, K. Comparison of field and laboratory wet soil spectra in the Vis-NIR range for soil organic carbon prediction in the absence of laboratory dry measurements. Remote Sens. 2020, 12, 3082. [Google Scholar]
- Ismayilov, A.; Feyziyev, F.; Elton, M.; Maharram, B. Soil Organic Carbon Prediction by Vis-NIR Spectroscopy: Case Study the Kur-Aras Plain, Azerbaijan. Commun. Soil Sci. Plant Anal. 2020, 51, 726–734. [Google Scholar]
- Shi, T.; Chen, Y.; Liu, Y.; Wu, G. Visible and near-infrared reflectance spectroscopy-An alternative formonitoring soil contamination by heavy metals. J. Hazard. Mater. 2014, 265, 166–176. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Borivka, L.; Saberioon, M.M.; Kozak, J.; Vasat, R.; Nemecek, K. Comparing different datapreprocessing methods for monitoring soil heavy metals based on soil spectral features. Soil Water Res. 2015, 10, 218–227. [Google Scholar] [CrossRef]
- Zhang, S.; Shen, Q.; Nie, C.; Huang, Y.; Wang, J.; Hu, Q.; Ding, X.; Zhou, Y.; Chen, Y. Hyperspectral inversion of heavy metal content in reclaimed soil from a mining wasteland based on different spectral transformation and modeling methods. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 211, 393–400. [Google Scholar] [CrossRef] [PubMed]
- Gu, X.; Wang, Y.; Sun, Q.; Yang, G.; Zhang, C. Hyperspectral inversion of soil organic matter content in cultivated land based on wavelet transform. Comput. Electron. Agric. 2019, 167, 105053. [Google Scholar] [CrossRef]
- Nocita, M.; Kooistra, L.; Bachmann, M.; Müller, A.; Powell, M.; Weel, S. Predictions of soil surface and topsoil organic carbon content through the use of laboratory and field spectroscopy in the Albany Thicket Biome of Eastern Cape Province of South Africa. Geoderma 2011, 167, 295–302. [Google Scholar] [CrossRef]
- Hong, Y.; Guo, L.; Chen, S.; Linderman, M.; Mouazen, A.M.; Yu, L.; Chen, Y.; Liu, Y.; Liu, Y.; Cheng, H.; et al. Exploring the potential of airborne hyperspectral image for estimating opsoil organic carbon: Effects of fractional-order derivative and optimal band com-bination algorithm. Geoderma 2020, 365, 114228. [Google Scholar] [CrossRef]
- Yang, P.; Hu, J.; Hu, B.; Luo, D.; Peng, J. Estimating Soil Organic Matter Content in Desert Areas Using In Situ Hyperspectral Data and Feature Variable Selection Algorithms in Southern Xinjiang, China. Remote Sens. 2022, 14, 5221. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, B.; Su, Y.; Zhang, D.; Wang, Y.; Bian, Y.; Suo, L.; Guo, X.; Bai, H. Retrieving zinc concentrations in topsoil with reflectance spectroscopy at Opencast Coal Mine sites. Sci. Rep. 2021, 11, 19909. [Google Scholar] [CrossRef]
- Chen, X.; Li, F.; Chang, Q. Combination of Continuous Wavelet Transform and Successive Projection Algorithm for the Estimation of Winter Wheat Plant Nitrogen Concentration. Remote Sens. 2023, 15, 997. [Google Scholar] [CrossRef]
- Yang, C.; Feng, M.; Song, L.; Wang, C.; Yang, W.; Xie, Y.; Ji, B.; Xiao, L.; Zhang, M.; Song, X.; et al. Study on hyperspectral estimation model of soil organic carbon content in the wheat field under different water treatments. Sci. Rep. 2021, 11, 18582. [Google Scholar] [CrossRef]
- Jobaggy, E.G.; Jackson, R.B. The vertical distribution of soil organic carbon and its relation to climate and vegetation. Ecol. Appl. 2000, 10, 423–436. [Google Scholar] [CrossRef]
- Jin, X.; Du, J.; Liu, H.; Wang, Z.; Song, K. Remote estimation of soil organic matter content in the Sanjiang Plain, Northest China: The optimal band algorithm versus the GRA-ANN model. Agric. For. Meteorol. 2016, 218–219, 250–260. [Google Scholar] [CrossRef]
- Galvao, R.K.; Araujo, M.C.; Fragoso, W.D.; Silva, E.C.; Jose, G.E.; Soares, S.F.; Paiva, H.M. A variable elimination method to improve the parsimony of MLR models using the successive projections algorithm. Chemom. Intell. Lab. Syst. 2008, 92, 83–91. [Google Scholar] [CrossRef]
- Araújo, M.C.U.; Saldanha, T.C.B.; Galvão, R.k.h.; Yoneyama, T.; Chame, H.c.; Visani, V. The successive projections algorithm for variable selection in spectroscopic multicomponent analysis. Chemom. Intell. Lab. Syst. 2001, 57, 65–73. [Google Scholar] [CrossRef]
- Chatterjeea, A.; Siarry, P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization. Comput. Oper. Res. 2006, 33, 859–871. [Google Scholar] [CrossRef]
- Ong, P.; Tung, I.; Chiu, C.; Tsai, I.; Shi, H.; Chen, S.; Chuang, Y. Determination of aflatoxin B1 level in rice (Oryza sativa L.) through near-infrared spectroscopy and an improved simulated annealing variable selection method. Food Control 2022, 136, 108886. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, Y.; Peng, Y.; Zhao, L.; Wang, G.; Hu, Y. Estimation of Soil Heavy Metal Content Using Hyperspectral Data. Remote Sens. 2019, 11, 1464. [Google Scholar] [CrossRef]
- Zhang, C.; Ye, H.; Liu, F.; He, Y.; Kong, W.; Sheng, K. Determination and Visualization of pH Values in Anaerobic Digestion of Water Hyacinth and Rice Straw Mixtures Using Hyperspectral Imaging with Wavelet Transform Denoising and Variable Selection. Sensors 2016, 16, 244. [Google Scholar] [CrossRef]
- Hu, M.; Dong, Q.; Liu, B.; Umezuruike, L.O.; Chen, L. Estimating blueberry mechanical properties based on random frog selected hyperspectral data. Postharvest Biol. Technol. 2015, 106, 1–10. [Google Scholar] [CrossRef]
- Anronios, M.; Xanthoula-Eirini, P.; Dimitrios, M.; Thomas, A.; Rebecca, W.; Georgios, T.; Jens, W.; Ralf, B.; Abdul, M. Mouazen Machine learning based prediction of soil total nitrogen, organic carbon and moisture content by using VIS-NIR spectroscopy. Biosyst. Eng. 2016, 152, 104–116. [Google Scholar]
- Meng, X.; Bao, Y.; Wang, Y.; Zhang, X.; Liu, H. An advanced soil organic carbon content prediction model via fused temporal-spatial-spectral (TSS) information based on machine learning and deep learning algorithms. Remote Sens. Environ. 2022, 280, 113166. [Google Scholar] [CrossRef]
- Wang, S.; Guan, K.; Zhang, C.; Lee, D.; Margenot, A.J.; Ge, Y.; Peng, J.; Zhou, W.; Zhou, Q.; Huang, Y. Using soil library hyperspectral reflectance and machine learning to predict soil organic carbon: Assessing potential of airborne and spaceborne optical soil sensing. Remote Sens. Environ. 2022, 271, 112914. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Chen, Y.; Marc, L.; Abdul, M.M.; Liu, Y.; Guo, L.; Yu, L.; Chen, H.; Liu, Y. Comparing laboratory and airborne hyperspectral data for the estimation andmapping of topsoil organic carbon: Feature selection coupled with random forest. Soil Till. Res. 2020, 199, 104589. [Google Scholar] [CrossRef]
- Liu, S.; Chen, J.; Guo, L.; Wang, J.; Zhou, Z.; Luo, J.; Yang, R. Prediction of soil organic carbon in soil profiles based on visible-near-infrared hyperspectral imaging spectroscopy. Soil Till. Res. 2023, 232, 105736. [Google Scholar] [CrossRef]
- Meng, X.; Bao, Y.; Liu, J.; Liu, H.; Zhang, X.; Zhang, Y.; Wang, P.; Tang, H.; Kong, F. Regional soil organic carbon prediction model based on a discrete wavelet analysis of hyperspectral satellite data. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102111. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, T.; Yang, Z.; Bo, H.; Lin, Y.; Yang, Q.; Liu, X.; Zhang, Q.; Zhuo, X.; Wu, T. Zinc concentration prediction in rice grain using back-propagation neural network based on soil properties and safe utilization of paddy soil: A large-scale field study in Guangxi, China. Sci. Total Environ. 2021, 798, 149270. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.T.; Pham, T.D.; Nguyen, C.T.; Delfos, J.; Archibald, R.; Dang, K.B.; Hoang, N.B.; Guo, W.; Ngo, H.H. A novel intelligence approach based active and ensemble learning for agricultural soil organic carbon prediction using multispectral and SAR data fusion. Sci. Total Environ. 2022, 804, 150187. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, J.; Jiang, X.; Zhen, J.; Miao, J.; Wang, J.; Wu, G. Reflectance spectroscopy for assessing heavy metal pollution indices in mangrove sediments using XGBoost method and physicochemical properties. Catena 2022, 211, 105967. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Liu, Y.; Zhang, Y.; Yu, L.; Chen, Y.; Liu, Y.; Chen, H.; Liu, Y. Combination of fractional order derivative and memory-based learning algorithm to improve the estimation accuracy of soil organic matter by visible and near-infrared spectroscopy. Catena 2019, 174, 104–116. [Google Scholar] [CrossRef]
- Wang, L.; Wang, R.; Lu, C.; Wang, J.; Huang, W. Rapid determination of moisture content in compound fertilizer using visible and near infrared spectroscopy combined with chemometrics. Infrared Phys. Technol. 2019, 102, 103045. [Google Scholar] [CrossRef]
- Fu, C.; Gan, S.; Xiong, H.; Tian, A. A new method to estimate soil organic matter using the combination model basedon short memory fractional order derivativeand machine learning model. Infrared Phys. Technol. 2019, 134, 104922. [Google Scholar] [CrossRef]
- Rossel, R.V.; Behrens, T.; Ben-Dor, E.; Brown, D.J.; Demattê, J.A.M.; Shepherd, K.D.; Shi, Z.; Stenberg, B.; Stevens, A.; Adamchuk, V.; et al. A global spectral library to characterize the world’s soil. Earth-Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef]
- Yang, H.; Qian, Y.; Yang, F.; Li, J.; Ju, W. Using wavelet transform of hyperspectral reflectance data for extracting spectral features of soil organic carbon and nitrogen. Soil Sci. 2012, 177, 674–681. [Google Scholar] [CrossRef]
- Rinnan, A.; Frans, B.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. Trac-Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, J.; Zhu, C.; Wang, J. Combination of efficient signal pre-processing and optimal band combination algorithm to predict soil organic matter through visible and near-infrared spectra. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 240, 118553. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, J.; Wang, J.; Ge, X. Prediction of soil organic matter in northwestern China using fractional order derivative spectroscopy and modified normalized difference indices. Catena 2020, 185, 104257. [Google Scholar] [CrossRef]
- Bai, Z.; Xie, M.; Hu, B.; Luo, D.; Wan, C.; Peng, J.; Shi, Z. Estimation of Soil Organic Carbon Using Vis-NIR Spectral Data and Spectral Feature Bands Selection in Southern Xinjiang, China. Sensors 2022, 22, 6124. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, M.; Hu, B.; Jiang, Q.; Shi, Z.; He, Y.; Peng, J. Desert Soil Salinity Inversion Models Based on Field In Situ Spectroscopy in Southern Xinjiang, China. Remote Sens. 2022, 14, 4962. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, J.; Ji, J.; Gong, P.; Liao, Q.; Tian, Q.; Ma, H. A mechanism study of reflectance spectroscopy for investigating heavy metals in soils. Soil Sci. Soc. Am. J. 2007, 71, 918–926. [Google Scholar] [CrossRef]
- Fei, S.; Li, L.; Han, Z.; Chen, Z.; Xiao, Y. Combining novel feature selection strategy and hyperspectral vegetation indices to predict crop yield. Plant Methods 2022, 18, 119. [Google Scholar] [CrossRef]
- Xu, M.; Chu, X.; Fu, Y.; Wang, C.; Wu, S. Improving the accuracy of soil organic carbon content prediction based on visible and near-infrared spectroscopy and machine learning. Environ. Earth Sci. 2021, 80, 326. [Google Scholar] [CrossRef]
- Xie, B.; Ding, J.; Ge, X.; Li, X.; Han, L.; Wang, Z. Estimation of Soil Organic Carbon Content in the Ebinur Lake Wetland, Xinjiang, China, Based on Multisource Remote Sensing Data and Ensemble Learning Algorithms. Sensors 2022, 22, 2685. [Google Scholar] [CrossRef]
- Seema; Ghosh, A.K.; Das, B.S.; Reddy, N. Application of VIS-NIR spectroscopy for estimation of soil organic carbon using different spectral preprocessing techniques and multivariate methods in the middle Indo-Gangetic plains of India. Geoderma Reg. 2020, 23, e00349. [Google Scholar] [CrossRef]
- Liu, S.; Shen, H.; Chen, S.; Zhao, X.; Biswas, A.; Jia, X. Estimating frog soil organic carbon content using vis-NIR spectroscopy: Implications for large-scale soil carbon spectroscopic assessment. Geoderma 2019, 348, 37–44. [Google Scholar] [CrossRef]
- Stevens, A.; van Wesemael, B.; Bartholomeus, H.; Rosillon, D.; Tychon, B.; Ben-Dor, E. Laboratory, field and airborne spectroscopy for monitoring organic carbon content in agricultural soils. Geoderma 2008, 144, 395–404. [Google Scholar] [CrossRef]
- Bogrekci, I.; Lee, W. Effects of soil moisture content on absorbance spectra of sandy soils in sensing phosphorus concentrations using UV-Vis-NIR spectroscopy. Trans. ASABE 2006, 49, 1175–1180. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Karoui, R.; De, B.J.; Ramon, H. Characterization of soil water content using measured visible and near infrared spectra. Soil Sci. Soc. Am. J. 2006, 70, 1295–1302. [Google Scholar] [CrossRef]
- Tekin, Y.; Tumsavas, Z.; Mouazen, A.M. Effect of moisture content on prediction of organic carbon and pH using visible and near-infrared spectroscopy. Soil Sci. Soc. Am. J. 2012, 76, 188–198. [Google Scholar] [CrossRef]
- Wu, C.Y.; Jacobson, A.R.; Laba, M.; Baveye, P.C. Accounting for surface roughness effects in the near-infrared reflectance sensing of soils. Geoderma 2009, 152, 171–180. [Google Scholar] [CrossRef]
- Wang, Z.; Coburn, C.A.; Ren, X.; Teillet, M. Effect of soil surface roughness and scene components on soil surface bidirectional reflectance factor. Can. J. Soil Sci. 2012, 92, 297–313. [Google Scholar] [CrossRef]
- Summers, D.; Lewis, M.; Ostendorsf, B.; Chittleborough, D. Visible near-infrared reflectance spectroscopy as apredictive indicator of soil properties. Ecol. Indic. 2011, 11, 123–131. [Google Scholar] [CrossRef]
- Hong, Y.; Shen, R.; Chen, H.; Chen, S.; Chen, Y.; Guo, L.; He, J.; Liu, Y.; Yu, L.; Yi, L. Cadmium concentration estimation in peri-urban agricultural soils: Using reflectance spectroscopy, soil auxiliary information, or a combination of both? Geoderma 2019, 354, 113875. [Google Scholar] [CrossRef]
- Dharumarajan, S.; Gomez, C.; Lalitha, M.; Kalaiselvi, B.; Hegde, R. Soil order knowledge as a driver in soil properties estimation from Vis-NIR spectral data—Case study from northern Karnataka (India). Geoderma Reg. 2023, 32, e00596. [Google Scholar] [CrossRef]
- Horta, A.; Malone, B.; Stockmann, U.; Minasny, B.; Bishop, T.F.A.; McBratney, A.B.; Pallasser, R.; Pozza, L. Potential of integrated field spectroscopy and spatial analysis for enhanced assessment of soil contamination: A prospective review. Geoderma 2015, 241–242, 180–209. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).