Fine Resolution Mapping of Soil Organic Carbon in Croplands with Feature Selection and Machine Learning in Northeast Plain China
Abstract
:1. Introduction
2. Materials and Methods
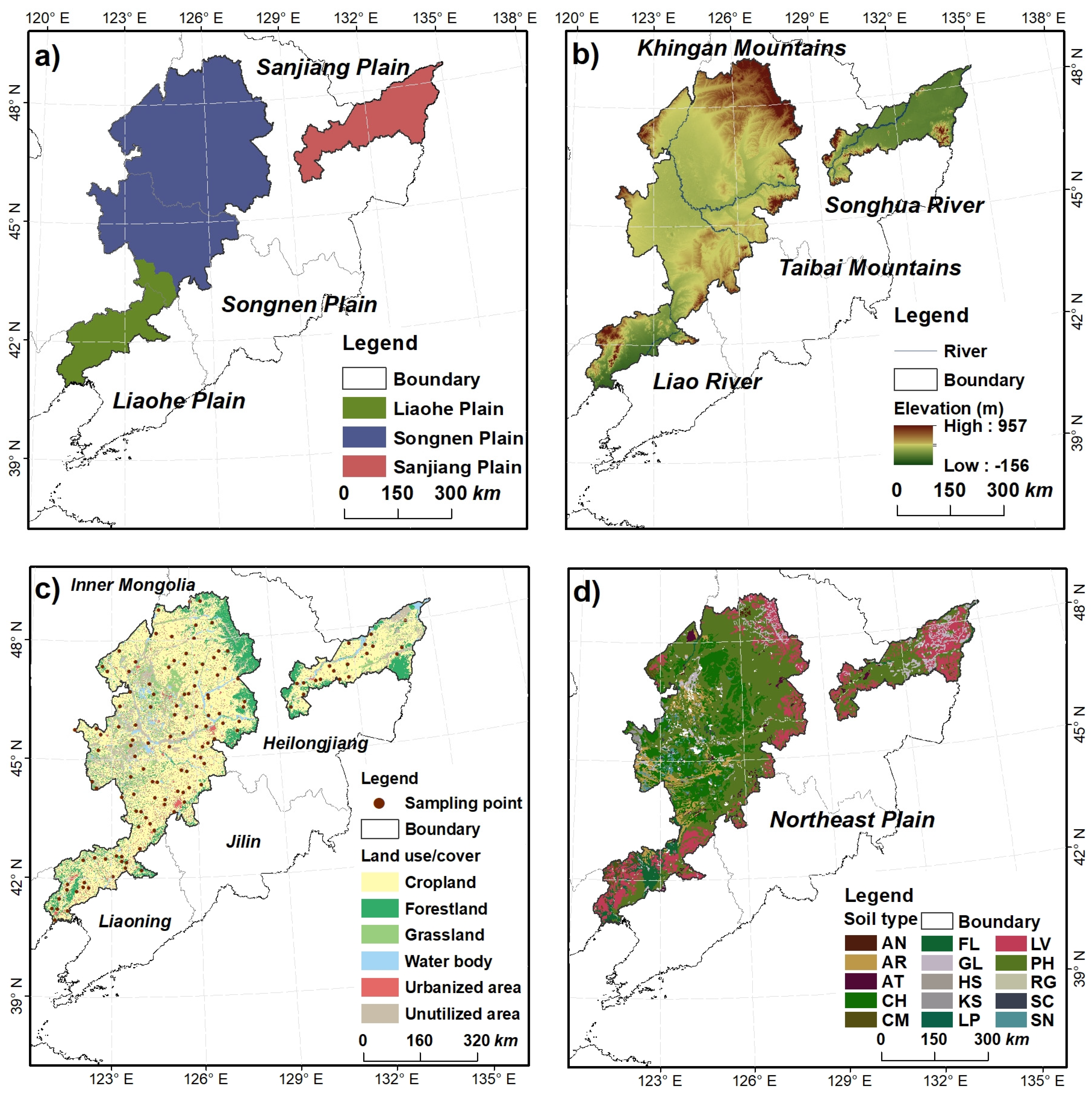
2.1. Study Area
2.2. Soil Sampling and Laboratory Analysis
2.3. Environmental Covariates
2.3.1. Soil and Parent Covariates
2.3.2. Climate Covariates
2.3.3. Organism Covariates
2.3.4. Relief Covariates
2.3.5. Position Covariates
2.3.6. Covariate Harmonization
2.4. Modeling Methodology
2.4.1. Feature Selection
- (1)
- Extend the variable database by adding >5 shadow attributes for each variable.
- (2)
- Shuffle all attributes to remove the correlations.
- (3)
- Perform RF on the extended database and calculate the Z scores of each attribute. The Z score for each variable were calculated based on the variable importance of each classification and regression tree (CART) with the following equations:
- (4)
- Find the maximum Z score (MZSA) and select attributes with a Z score better than MZSA.
- (5)
- Run the two-side test in undermined importance attributes with MZSA.
- (6)
- Remove unimportant attributes where the Z score is significantly lower than MZSA.
- (7)
- Retain important attributes where the Z score is significantly higher than MZSA.
- (8)
- Define important original variables as the selected database.
- (9)
- Repeat these procedures until attachment of assigned criteria.
2.4.2. Model Fitness
2.4.3. Model Performance
2.4.4. Model Environment
3. Results
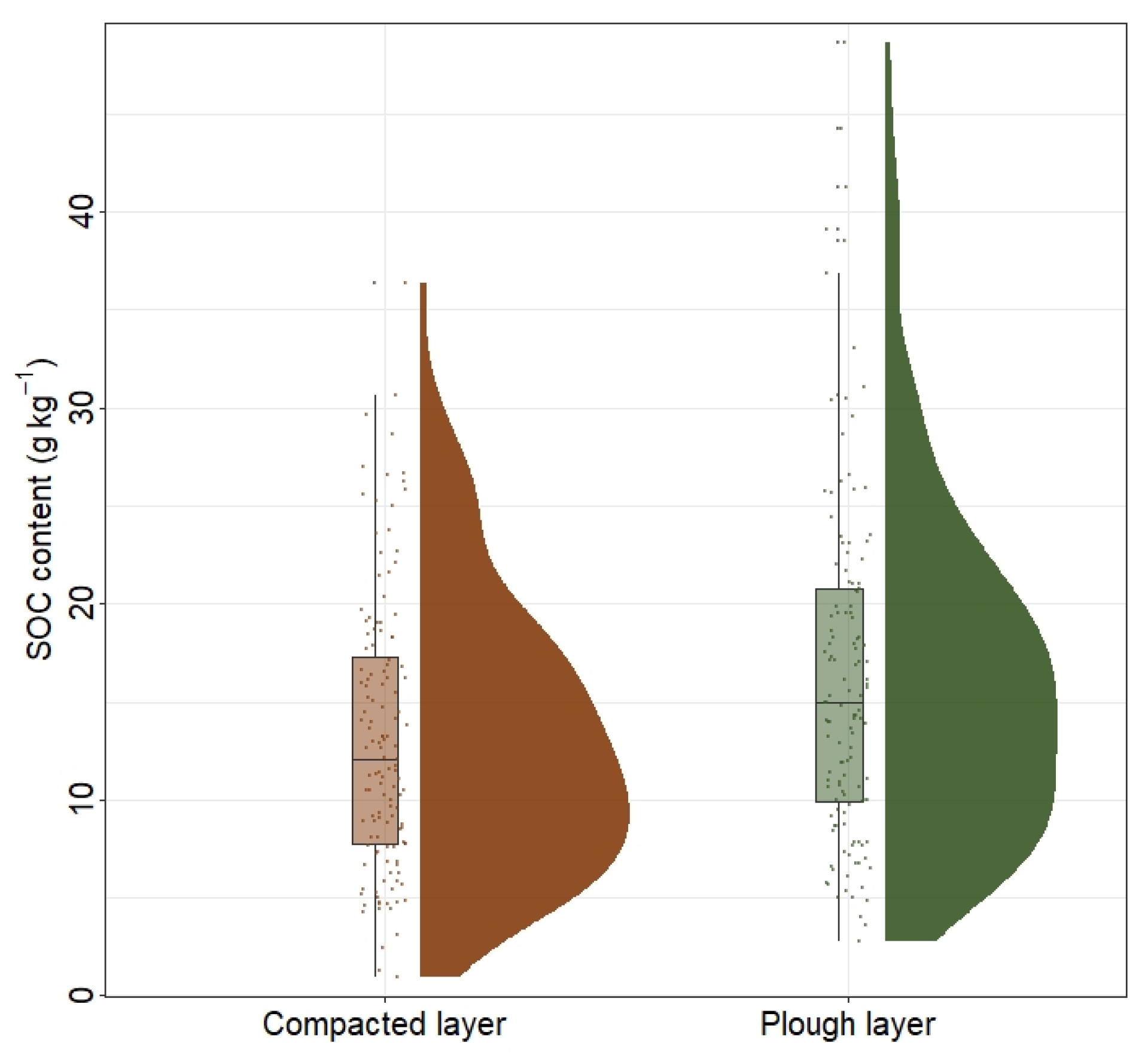
3.1. Descriptive Statistics for Soil Samples
3.2. Model Accuracy and Uncertainty
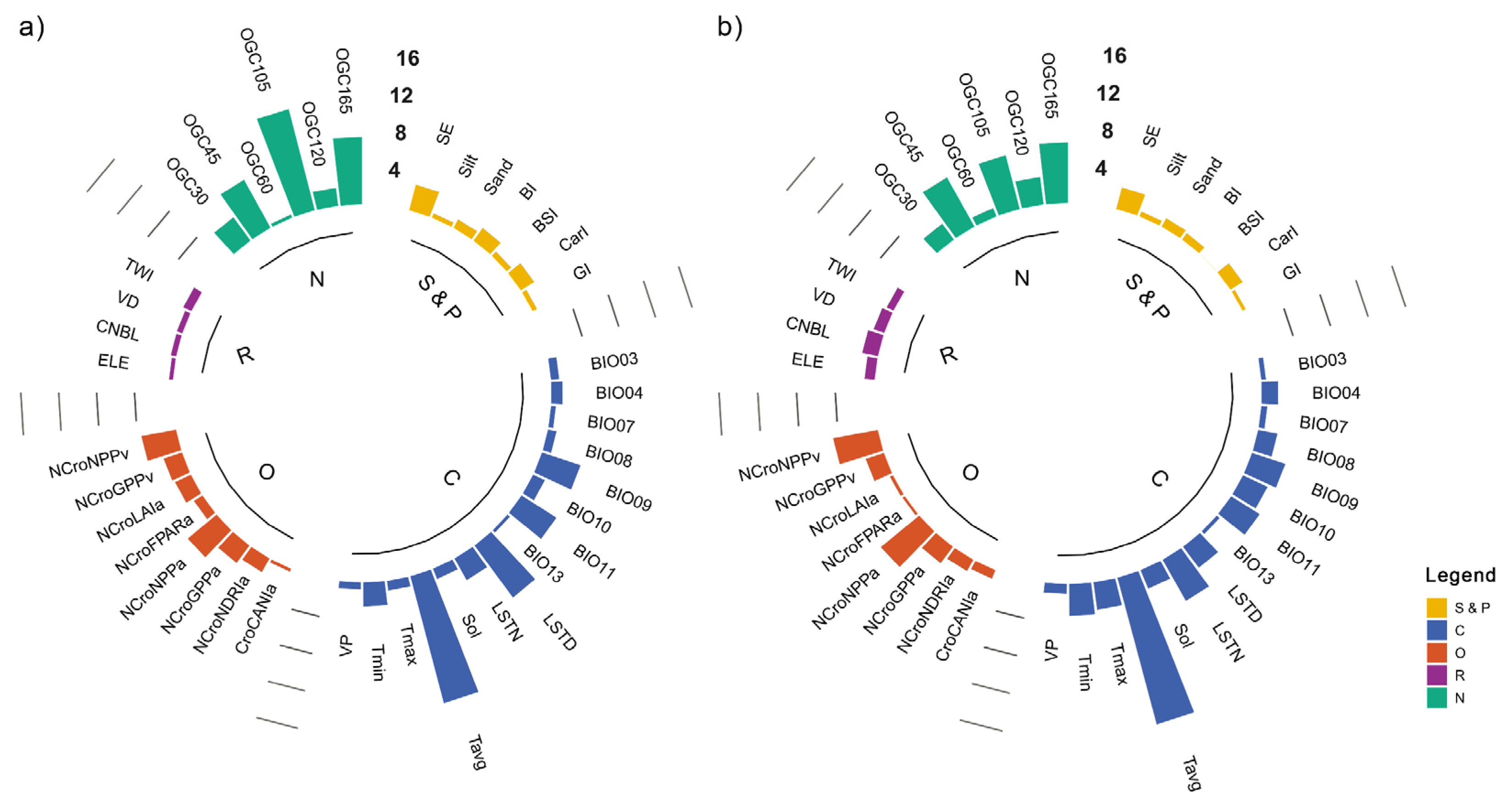
3.3. Importance of Environmental Covariates
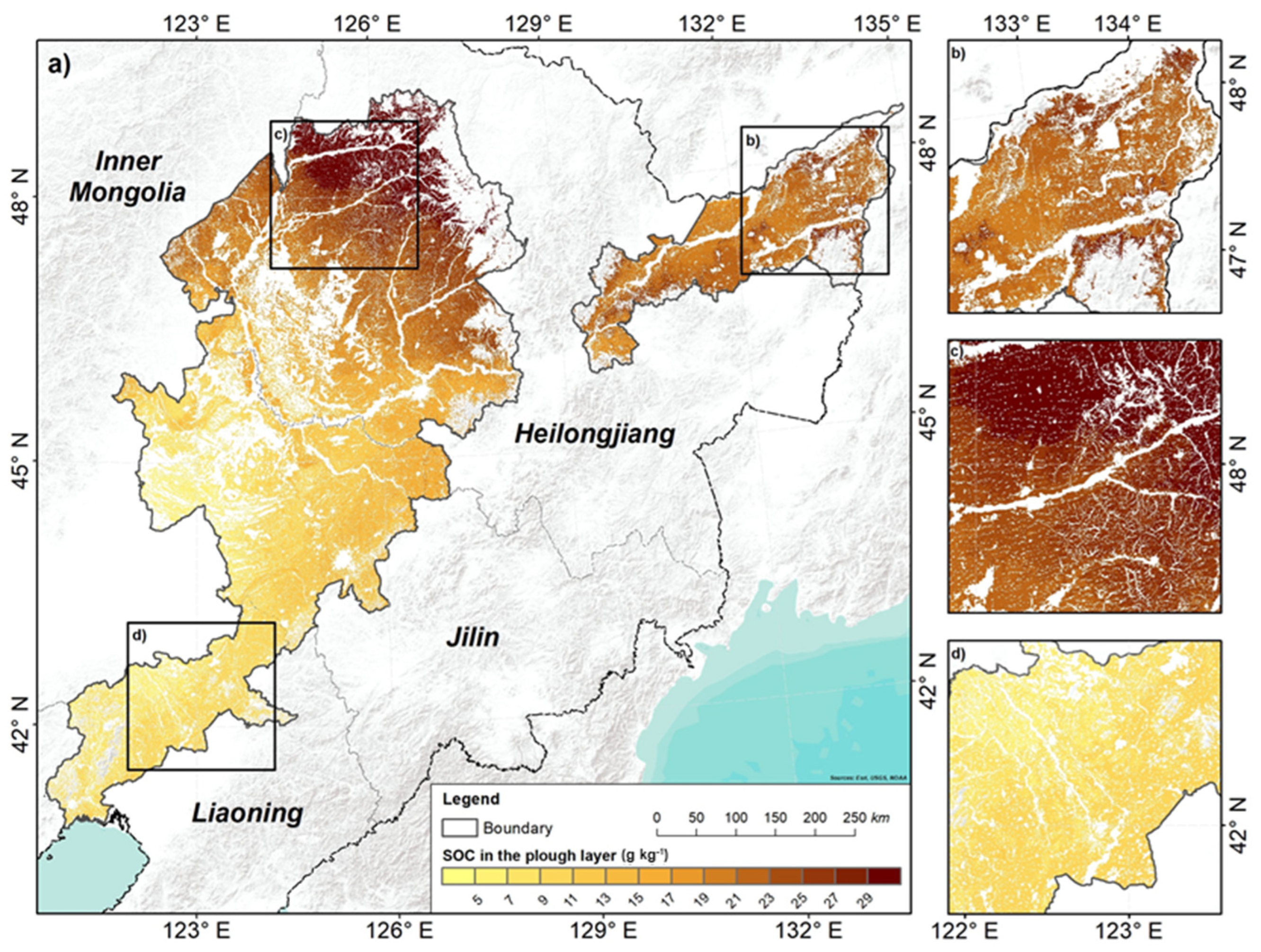
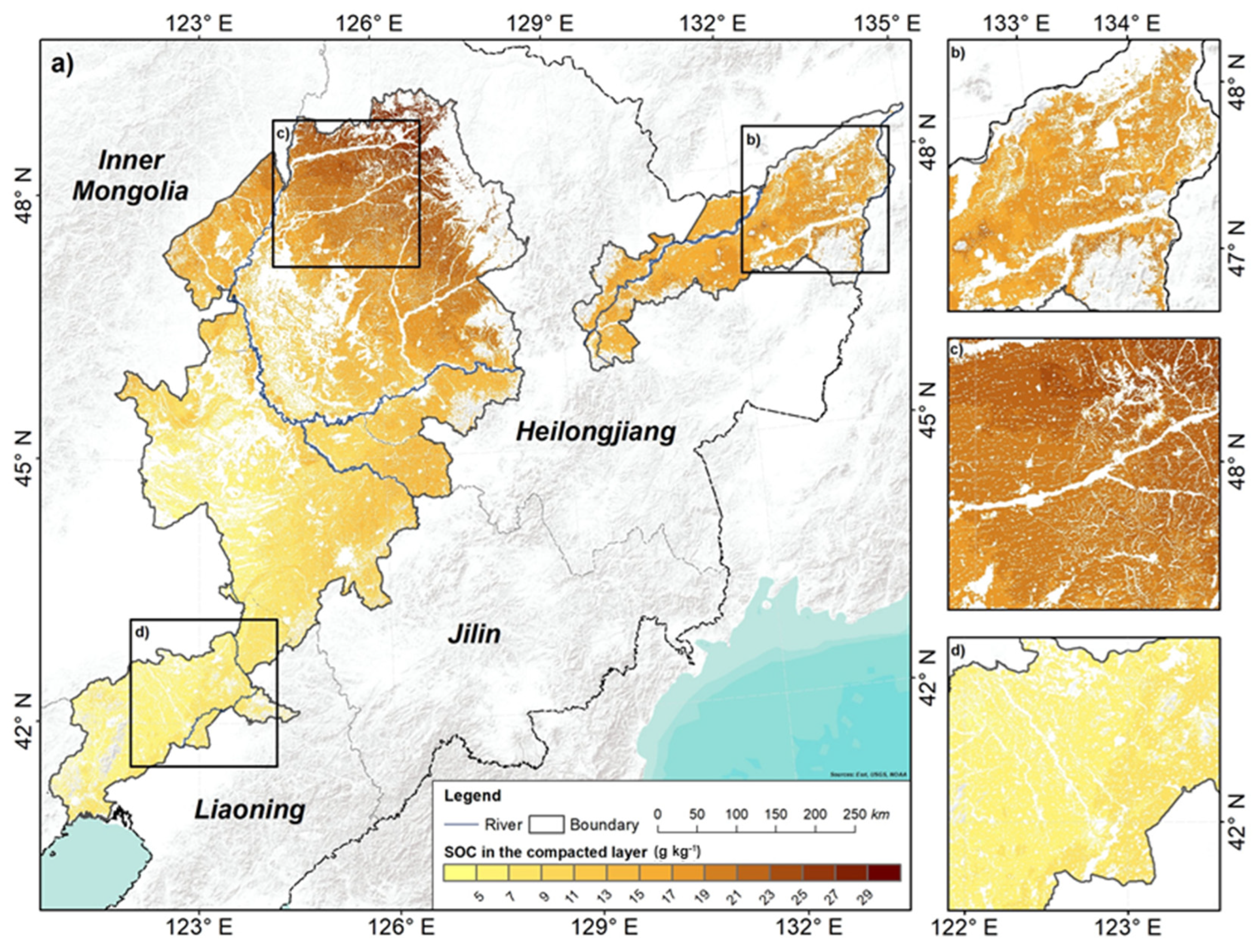
3.4. Spatial Distribution Pattern of SOC
4. Discussion
4.1. Feature Selection
4.2. Model Accuracy
4.3. Uncertainty Assessments
4.4. Spatial Distribution Pattern of SOC and Controlling Factors
4.5. Perspectives and Limitation
5. Conclusions
- (1)
- Boruta was a compelling feature selection method to eliminate redundant variables and develop the optimal QRF model.
- (2)
- SOC overall increased from the southern to the northern areas, with an average of 17.34 g kg−1 in the plough layer and 13.92 g kg−1 in the compacted layer. At the vertical scale, SOC decreased, with depths getting deeper. The average decreasing SOC is 3.41 g kg−1, and the northern area decreased more than the southern area.
- (3)
- Climate (i.e., average temperature, daytime and nighttime land surface temperature, and mean temperature of driest quarter) was the dominant controlling factor, followed by position (i.e., oblique geographic coordinate at 105°), and organism (i.e., the average and variance of net primary productivity in the non-crop period).
- (4)
- The average uncertainty values were 1.04 in the plough layer and 1.07 in the compacted layer. The high uncertainty appeared in the areas with relatively scattered fields, high altitudes, and complex landforms.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wiesmeier, M.; Urbanski, L.; Hobley, E.; Lang, B.; von Lutzow, M.; Marin-Spiotta, E.; van Wesemael, B.; Rabot, E.; Liess, M.; Garcia-Franco, N.; et al. Soil organic carbon storage as a key function of soils-A review of drivers and indicators at various scales. Geoderma 2019, 333, 149–162. [Google Scholar] [CrossRef]
- Zomer, R.J.; Bossio, D.A.; Sommer, R.; Verchot, L.V. Global Sequestration Potential of Increased Organic Carbon in Cropland Soils. Sci. Rep. 2017, 7, 15554. [Google Scholar] [CrossRef] [PubMed]
- Robinson, D.A.; Emmett, B.A.; Reynolds, B.; Rowe, E.C.; Spurgeon, D.; Keith, A.M.; Lebron, I.; Hockley, N.; Hester, R.; Harrison, R. Soil natural capital and ecosystem service delivery in a world of global soil change. Soils Food Secur. 2012, 35, 41. [Google Scholar]
- Xue, J.; Zhang, X.L.; Chen, S.C.; Hu, B.F.; Wang, N.; Shi, Z. Quantifying the agreement and accuracy characteristics of four satellite-based LULC products for cropland classification in China. J. Integr. Agric. 2023. [Google Scholar] [CrossRef]
- Zhuo, Z.Q.; Xing, A.; Cao, M.; Li, Y.; Zhao, Y.Z.; Guo, X.L.; Huang, Y.F. Identifying the position of the compacted layer by measuring soil penetration resistance in a dryland farming region in Northeast China. Soil Use Manag. 2020, 36, 494–506. [Google Scholar] [CrossRef]
- Colombi, T.; Braun, S.; Keller, T.; Walter, A. Artificial macropores attract crop roots and enhance plant productivity on compacted soils. Sci. Total Environ. 2017, 574, 1283–1293. [Google Scholar] [CrossRef]
- Chen, S.; Arrouays, D.; Mulder, V.L.; Poggio, L.; Minasny, B.; Roudier, P.; Libohova, Z.; Lagacherie, P.; Shi, Z.; Hannam, J.J.G. Digital mapping of GlobalSoilMap soil properties at a broad scale: A review. Geoderma 2022, 409, 115567. [Google Scholar] [CrossRef]
- Arrouays, D.; Poggio, L.; Guerrero, O.A.S.; Mulder, V.L. Digital soil mapping and GlobalSoilMap. Main advances and ways forward. Geoderma Reg. 2020, 21, e00265. [Google Scholar] [CrossRef]
- Tziolas, N.; Tsakiridis, N.; Chabrillat, S.; Demattê, J.A.; Ben-Dor, E.; Gholizadeh, A.; Zalidis, G.; Van Wesemael, B. Earth observation data-driven cropland soil monitoring: A review. Remote Sens. 2021, 13, 4439. [Google Scholar] [CrossRef]
- Poggio, L.; de Sousa, L.M.; Batjes, N.H.; Heuvelink, G.B.M.; Kempen, B.; Ribeiro, E.; Rossiter, D. SoilGrids 2.0: Producing soil information for the globe with quantified spatial uncertainty. Soil 2021, 7, 217–240. [Google Scholar] [CrossRef]
- Safanelli, J.L.; Dematte, J.A.M.; Chabrillat, S.; Poppiel, R.R.; Rizzo, R.; Dotto, A.C.; Silvero, N.E.Q.; Mendes, W.D.; Bonfatti, B.R.; Ruiz, L.F.C.; et al. Leveraging the application of Earth observation data for mapping cropland soils in Brazil. Geoderma 2021, 396, 115042. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, S.; Yang, Y.; Zhao, R.; Shi, Z.; Viscarra Rossel, R.A. National digital soil map of organic matter in topsoil and its associated uncertainty in 1980’s China. Geoderma 2019, 335, 47–56. [Google Scholar] [CrossRef]
- Chen, S.; Liang, Z.; Webster, R.; Zhang, G.; Zhou, Y.; Teng, H.; Hu, B.; Arrouays, D.; Shi, Z. A high-resolution map of soil pH in China made by hybrid modelling of sparse soil data and environmental covariates and its implications for pollution. Sci. Total Environ. 2019, 655, 273–283. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Xue, J.; Chen, S.C.; Zhou, Y.; Liang, Z.Z.; Wang, N.; Shi, Z. Fine-Resolution Mapping of Soil Total Nitrogen across China Based on Weighted Model Averaging. Remote Sens. 2020, 12, 85. [Google Scholar] [CrossRef]
- Keskin, H.; Grunwald, S.; Harris, W.G. Digital mapping of soil carbon fractions with machine learning. Geoderma 2019, 339, 40–58. [Google Scholar] [CrossRef]
- Ye, Y.; Fang, X.Q.; Ren, Y.Y.; Zhang, X.Z.; Chen, L. Cropland cover change in Northeast China during the past 300 years. Sci. China Ser. D 2009, 52, 1172–1182. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xue, J.; Chen, S.C.; Wang, N.; Shi, Z.; Huang, Y.F.; Zhuo, Z.Q. Digital Mapping of Soil Organic Carbon with Machine Learning in Dryland of Northeast and North Plain China. Remote Sens. 2022, 14, 2504. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, M.Y.; Adhikari, K.; Zhuang, Q.L.; Bian, Z.X.; Wang, Y.; Jin, X.X. Anthropogenic controls over soil organic carbon distribution from the cultivated lands in Northeast China. Catena 2022, 210, 105897. [Google Scholar] [CrossRef]
- Zhou, Y.; Hartemink, A.E.; Shi, Z.; Liang, Z.; Lu, Y. Land use and climate change effects on soil organic carbon in North and Northeast China. Sci. Total Environ. 2019, 647, 1230–1238. [Google Scholar] [CrossRef]
- Guo, L.; Sun, X.R.; Fu, P.; Shi, T.Z.; Dang, L.N.; Chen, Y.Y.; Linderman, M.; Zhang, G.L.; Zhang, Y.; Jiang, Q.H.; et al. Mapping soil organic carbon stock by hyperspectral and time-series multispectral remote sensing images in low-relief agricultural areas. Geoderma 2021, 398, 115118. [Google Scholar] [CrossRef]
- Nachtergaele, F.; Velthuizen, H.; Verelst, L.; Wiberg, D.J.F. Food and Agriculture Organization of the United Nations, Rome Harmonized World Soil Database (HWSD); Food and Agriculture Organization of the United Nations: Rome, Italy, 2009. [Google Scholar]
- Kendall, M.G. Rank Correlation Methods; American Psychological Association: Worcester, MA, USA, 1948. [Google Scholar]
- Bao, S. Soil Agro-Chemistrical Analysis; China Agriculture Press: Beijing, China, 2000; Volume 2030, pp. 30–107. [Google Scholar]
- McBratney, A.B.; Santos, M.L.M.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The next Landsat satellite: The Landsat Data Continuity Mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar] [CrossRef]
- Foga, S.; Scaramuzza, P.L.; Guo, S.; Zhu, Z.; Dilley, R.D.; Beckmann, T.; Schmidt, G.L.; Dwyer, J.L.; Hughes, M.J.; Laue, B. Cloud detection algorithm comparison and validation for operational Landsat data products. Remote Sens. Environ. 2017, 194, 379–390. [Google Scholar] [CrossRef]
- Teng, H.F.; Hu, J.; Zhou, Y.; Zhou, L.Q.; Shi, Z. Modelling and mapping soil erosion potential in China. J. Integr. Agr. 2019, 18, 251–264. [Google Scholar] [CrossRef]
- Hengl, T.; Mendes de Jesus, J.; Heuvelink, G.B.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotic, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Wan, Z.; Hook, S.; Hulley, G. MOD11A1 MODIS/Terra Land Surface Temperature/Emissivity Daily L3 Global 1km SIN Grid V006 [Data set]. NASA EOSDIS Land Processes DAAC. 2015. Available online: https://lpdaac.usgs.gov/products/mod11a1v006/ (accessed on 26 November 2022).
- Myneni, R.; Knyazikhin, Y.; Park, T. MODIS/Terra+Aqua Leaf Area Index/FPAR 4-Day L4 Global 500m SIN Grid V061 [Data Set]; Land Processes Distributed Active Archive Center: Sioux Falls, SD, USA, 2021. [CrossRef]
- Running, S.; Mu, Q.; Zhao, M. MOD17A2H MODIS/Terra Gross Primary Productivity 8-Day L4 Global 500m SIN Grid V006 [Data Set]; Land Processes Distributed Active Archive Center: Sioux Falls, SD, USA, 2015. [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-filled SRTM for the globe Version 4, available from the CGIAR-CSI SRTM 90m Database. 2008. Available online: https://srtm.csi.cgiar.org (accessed on 9 November 2018).
- Møller, A.B.; Beucher, A.M.; Pouladi, N.; Greve, M.H. Oblique geographic coordinates as covariates for digital soil mapping. Soil 2020, 6, 269–289. [Google Scholar] [CrossRef]
- Schad, P.; Dondeyne, S.; Lal, R. World Reference Base for Soil Resources 2014, Update 2015: International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; Fao: Rome, Italy, 2015. [Google Scholar]
- Hartmann, J.; Moosdorf, N. The new global lithological map database GLiM: A representation of rock properties at the Earth surface. Geochem. Geophys. Geosystems 2012, 13. [Google Scholar] [CrossRef]
- Zhuo, Z.Q.; Chen, Q.Q.; Zhang, X.L.; Chen, S.C.; Gou, Y.X.; Sun, Z.X.; Huang, Y.F.; Shi, Z. Soil organic carbon storage, distribution, and influencing factors at different depths in the dryland farming regions of Northeast and North China. Catena 2022, 210, 105934. [Google Scholar] [CrossRef]
- Running, S.; Mu, Q.; Zhao, M. MOD16A2 MODIS/Terra Net Evapotranspiration 8-Day L4 Global 500m SIN Grid V006 [Data set], NASA EOSDIS Land Processes DAAC. 2017. Available online: https://lpdaac.usgs.gov/products/mod16a2v006/ (accessed on 9 January 2020).
- Mladenova, I.E.; Bolten, J.D.; Crow, W.T.; Sazib, N.; Cosh, M.H.; Tucker, C.J.; Reynolds, C. Evaluating the Operational Application of SMAP for Global Agricultural Drought Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3387–3397. [Google Scholar] [CrossRef]
- Riggs, G.A.; Hall, D.K.; Salomonson, V.V. A snow index for the Landsat thematic mapper and moderate resolution imaging spectroradiometer. In Proceedings of the IGARSS’94-1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; pp. 1942–1944. [Google Scholar]
- Zhang, M.; Wu, B.F.; Zeng, H.W.; He, G.J.; Liu, C.; Tao, S.Q.; Zhang, Q.; Nabil, M.; Tian, F.Y.; Bofana, J.; et al. GCI30: A global dataset of 30 m cropping intensity using multisource remote sensing imagery. Earth Syst. Sci. Data 2021, 13, 4799–4817. [Google Scholar] [CrossRef]
- You, N.; Dong, J.; Huang, J.; Du, G.; Zhang, G.; He, Y.; Yang, T.; Di, Y.; Xiao, X. The 10-m crop type maps in Northeast China during 2017-2019. Sci. Data 2021, 8, 41. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wichmann, V.; Böhner, J. System for automated geoscientific analyses (SAGA) v. 2.1. 4. Geoscientific Model Development 2015, 8(7), 1991–2007. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Stoppiglia, H.; Dreyfus, G.; Dubois, R.; Oussar, Y.J. Ranking a random feature for variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1399–1414. [Google Scholar]
- Amiri, M.; Pourghasemi, H.R.; Ghanbarian, G.A.; Afzali, S.F. Assessment of the importance of gully erosion effective factors using Boruta algorithm and its spatial modeling and mapping using three machine learning algorithms. Geoderma 2019, 340, 55–69. [Google Scholar] [CrossRef]
- Meinshausen, N.; Ridgeway, G. Quantile regression forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Lalitha, M.; Dharumarajan, S.; Suputhra, A.; Kalaiselvi, B.; Hegde, R.; Reddy, R.S.; Shiva Prasad, C.R.; Harindranath, C.S.; Dwivedi, B.S. Spatial prediction of soil depth using environmental covariates by quantile regression forest model. Environ. Monit. Assess. 2021, 193, 660. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed]
- Matthew, W. Bias of the Random Forest out-of-bag (OOB) error for certain input parameters. Open J. Stat. 2011, 1, 8072. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2013. [Google Scholar]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Bivand, R.; Keitt, T.; Rowlingson, B.; Pebesma, E.; Sumner, M.; Hijmans, R.; Rouault, E.; Bivand, M.R. Package ‘rgdal’. Bindings for the Geospatial Data Abstraction Library. 2015. Available online: https://cran.r-project.org/web/packages/rgdal/index.html (accessed on 13 February 2022).
- Pebesma, E.; Bivand, R.S. S classes and methods for spatial data: The sp package. R News 2005, 5, 9–13. [Google Scholar]
- Hijmans, R.J.; Van Etten, J.; Cheng, J.; Mattiuzzi, M.; Sumner, M.; Greenberg, J.A.; Lamigueiro, O.P.; Bevan, A.; Racine, E.B.; Shortridge, A. Package ‘raster’. R Package 2015, 734, 473. [Google Scholar]
- Wickham, H.; Wickham, M.H. Package ‘plyr’. Available online: https://cran.r-project.org/web/packages/plyr/index.html (accessed on 14 August 2021).
- Sarkar, D. Lattice: Multivariate Data Visualization With R; Springer: New York, NY, USA, 2008. [Google Scholar]
- Wickham, H. ggplot2. Wiley Interdiscip Rev. Comput. Stat. 2011, 3, 180–185. [Google Scholar] [CrossRef]
- Wilding, L. Spatial variability: Its documentation, accomodation and implication to soil surveys. In Proceedings of the Soil Spatial Variability, Las Vegas, NV, USA, 30 November–1 December 1984; pp. 166–194. [Google Scholar]
- Marsaglia, G.; Tsang, W.W.; Wang, J. Evaluating Kolmogorov’s Distribution. J. Stat. Softw. 2003, 8, 1–4. [Google Scholar] [CrossRef]
- Xiong, X.; Grunwald, S.; Myers, D.B.; Kim, J.; Harris, W.G.; Comerford, N.B. Holistic environmental soil-landscape modeling of soil organic carbon. Environ. Model. Softw. 2014, 57, 202–215. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, G.L.; Song, X.D.; Li, D.C.; Zhao, Y.G.; Yang, J.L.; Wu, H.Y.; Yang, F. High-resolution and three-dimensional mapping of soil texture of China. Geoderma 2020, 361, 114061. [Google Scholar] [CrossRef]
- Guo, B.; Lu, M.; Fan, Y.; Wu, H.; Yang, Y.; Wang, C. A novel remote sensing monitoring index of salinization based on three-dimensional feature space model and its application in the Yellow River Delta of China. Geomat. Nat. Hazards Risk 2023, 14, 95–116. [Google Scholar] [CrossRef]
- Rial, M.; Martinez Cortizas, A.; Rodriguez-Lado, L. Understanding the spatial distribution of factors controlling topsoil organic carbon content in European soils. Sci. Total Environ. 2017, 609, 1411–1422. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.; Liu, Y.; Fan, J.; Lu, M.; Zang, W.; Liu, C.; Wang, B.; Huang, X.; Lai, J.; Wu, H. The salinization process and its response to the combined processes of climate change–human activity in the Yellow River Delta between 1984 and 2022. Catena 2023, 231, 107301. [Google Scholar]
- Lamichhane, S.; Kumar, L.; Wilson, B. Digital soil mapping algorithms and covariates for soil organic carbon mapping and their implications: A review. Geoderma 2019, 352, 395–413. [Google Scholar] [CrossRef]
- Yu, Y.; Guo, B.; Wang, C.; Zang, W.; Huang, X.; Wu, Z.; Xu, M.; Zhou, K.; Li, J.; Yang, Y. Carbon storage simulation and analysis in Beijing-Tianjin-Hebei region based on CA-plus model under dual-carbon background. Geomat. Nat. Hazards Risk 2023, 14, 2173661. [Google Scholar] [CrossRef]
- Xiao, Y.; Xue, J.; Zhang, X.; Wang, N.; Hong, Y.; Jiang, Y.; Zhou, Y.; Teng, H.; Hu, B.; Lugato, E. Improving pedotransfer functions for predicting soil mineral associated organic carbon by ensemble machine learning. Geoderma 2022, 428, 116208. [Google Scholar] [CrossRef]
- Chen, S.C.; Richer-de-Forges, A.C.; Mulder, V.L.; Martelet, G.; Loiseau, T.; Lehmann, S.; Arrouays, D. Digital mapping of the soil thickness of loess deposits over a calcareous bedrock in central France. Catena 2021, 198, 105062. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, S.; Xue, J.; Wang, N.; Xiao, Y.; Chen, Q.; Hong, Y.; Zhou, Y.; Teng, H.; Hu, B.; et al. Improving model parsimony and accuracy by modified greedy feature selection in digital soil mapping. Geoderma 2023, 432, 116383. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xue, J.; Xiao, Y.; Shi, Z.; Chen, S.C. Towards Optimal Variable Selection Methods for Soil Property Prediction Using a Regional Soil Vis-NIR Spectral Library. Remote Sens. 2023, 15, 465. [Google Scholar] [CrossRef]

| Variable | Abbreviation | Scale | Covariate a) | Type b) | Period | Reference |
|---|---|---|---|---|---|---|
| Soil erosion | SE | 1000 m | S&P | Q | 2002–2016 | [27] |
| Silt content | Silt | 250 m | S&P | Q | 1960–2020 | [10,28] |
| Sand content | Sand | 250 m | S&P | Q | 1960–2020 | [10,28] |
| Brightness index | BI | 30 m | S&P | Q | 2015–2017 | [25] |
| Bare soil index | BSI | 30 m | S&P | Q | 2015–2017 | [25] |
| Carbonate index | CarI | 30 m | S&P | Q | 2015–2017 | [25] |
| Gypsum index | GI | 30 m | S&P | Q | 2015–2017 | [25] |
| Isothermality | BIO03 | 1000 m | C | Q | 1970–2000 | [29] |
| Temperature seasonality | BIO04 | 1000 m | C | Q | 1970–2000 | [29] |
| Temperature annual range | BIO07 | 1000 m | C | Q | 1970–2000 | [29] |
| Mean temperature of wettest quarter | BIO08 | 1000 m | C | Q | 1970–2000 | [29] |
| Mean temperature of driest quarter | BIO09 | 1000 m | C | Q | 1970–2000 | [29] |
| Mean temperature of warmest quarter | BIO10 | 1000 m | C | Q | 1970–2000 | [29] |
| Mean temperature of coldest quarter | BIO11 | 1000 m | C | Q | 1970–2000 | [29] |
| Precipitation of wettest month | BIO13 | 1000 m | C | Q | 1970–2000 | [29] |
| Daytime land surface temperature | LSTD | 1000 m | C | Q | 2002–2017 | [30] |
| Nighttime land surface temperature | LSTN | 1000 m | C | Q | 2002–2017 | [30] |
| Solar radiation | Sol | 1000 m | C | Q | 1970–2000 | [29] |
| Average temperature | Tavg | 1000 m | C | Q | 1970–2000 | [29] |
| Maximum temperature | Tmax | 1000 m | C | Q | 1970–2000 | [29] |
| Minimum temperature | Tmin | 1000 m | C | Q | 1970–2000 | [29] |
| Vapor pressure | VP | 1000 m | C | Q | 1970–2000 | [29] |
| The average of CANI in the crop period | CroCANIa | 30 m | O | Q | 2015–2017 | [25] |
| The average of NDRI in the non-crop period | NCroNDRIa | 30 m | O | Q | 2015–2017 | [25] |
| The average of GPP in the non-crop period | NCroGPPa | 500 m | O | Q | 2015–2017 | [31] |
| The average of NPP in the non-crop period | NCroNPPa | 500 m | O | Q | 2015–2017 | [31] |
| The average of FPAR in the non-crop period | NCroFPARa | 500 m | O | Q | 2015–2017 | [32] |
| The average of LAI in the non-crop period | NCroLAIa | 500 m | O | Q | 2015–2017 | [32] |
| The variance of GPP in the non-crop period | NCroGPPv | 500 m | O | Q | 2015–2017 | [31] |
| The variance of NPP in the non-crop period | NCroNPPv | 500 m | O | Q | 2015–2017 | [31] |
| Elevation | ELE | 90 m | R | Q | 2000 | [33] |
| Channel network base level | CNBL | 90 m | R | Q | 2000 | [33] |
| Valley depth | VD | 90 m | R | Q | 2000 | [33] |
| Terrain wetness index | TWI | 90 m | R | Q | 2000 | [33] |
| Oblique geographic coordinate at 30° | OGC30 | 30 m | N | Q | / | [34] |
| Oblique geographic coordinate at 45° | OGC45 | 30 m | N | Q | / | [34] |
| Oblique geographic coordinate at 60° | OGC60 | 30 m | N | Q | / | [34] |
| Oblique geographic coordinate at 105° | OGC105 | 30 m | N | Q | / | [34] |
| Oblique geographic coordinate at 120° | OGC120 | 30 m | N | Q | / | [34] |
| Oblique geographic coordinate at 165° | OGC165 | 30 m | N | Q | / | [34] |
| Layer | Min | 1st Qu | Median | Average | 3rd Qu | Max | SD | %CV | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|
| SOC PL | 2.78 | 9.95 | 14.93 | 16.33 | 20.76 | 48.65 | 8.80 | 53.88 | 1.12 | 4.56 |
| SOC CL | 0.96 | 7.75 | 12.09 | 13.21 | 17.41 | 36.40 | 6.99 | 52.91 | 0.72 | 3.19 |
| Depth | OOB | CV | Uncertainty | |||
|---|---|---|---|---|---|---|
| R2 | RMSE (g kg−1) | R2 | RMSE (g kg−1) | U | PICP | |
| PL | 0.61 | 5.45 | 0.68 | 5.10 | 1.05 | 0.88 |
| CL | 0.54 | 4.75 | 0.58 | 4.64 | 1.09 | 0.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xue, J.; Chen, S.; Wang, N.; Xie, T.; Xiao, Y.; Chen, X.; Shi, Z.; Huang, Y.; Zhuo, Z. Fine Resolution Mapping of Soil Organic Carbon in Croplands with Feature Selection and Machine Learning in Northeast Plain China. Remote Sens. 2023, 15, 5033. https://doi.org/10.3390/rs15205033
Zhang X, Xue J, Chen S, Wang N, Xie T, Xiao Y, Chen X, Shi Z, Huang Y, Zhuo Z. Fine Resolution Mapping of Soil Organic Carbon in Croplands with Feature Selection and Machine Learning in Northeast Plain China. Remote Sensing. 2023; 15(20):5033. https://doi.org/10.3390/rs15205033
Chicago/Turabian StyleZhang, Xianglin, Jie Xue, Songchao Chen, Nan Wang, Tieli Xie, Yi Xiao, Xueyao Chen, Zhou Shi, Yuanfang Huang, and Zhiqing Zhuo. 2023. "Fine Resolution Mapping of Soil Organic Carbon in Croplands with Feature Selection and Machine Learning in Northeast Plain China" Remote Sensing 15, no. 20: 5033. https://doi.org/10.3390/rs15205033
APA StyleZhang, X., Xue, J., Chen, S., Wang, N., Xie, T., Xiao, Y., Chen, X., Shi, Z., Huang, Y., & Zhuo, Z. (2023). Fine Resolution Mapping of Soil Organic Carbon in Croplands with Feature Selection and Machine Learning in Northeast Plain China. Remote Sensing, 15(20), 5033. https://doi.org/10.3390/rs15205033








