Abstract
Image super-resolution (SR) techniques can improve the spatial resolution of remote sensing images to provide more feature details and information, which is important for a wide range of remote sensing applications, including land use/cover classification (LUCC). Convolutional neural networks (CNNs) have achieved impressive results in the field of image SR, but the inherent localization of convolution limits the performance of CNN-based SR models. Therefore, we propose a new method, namely, the dilated Transformer generative adversarial network (DTGAN) for the SR of multispectral remote sensing images. DTGAN combines the local focus of CNNs with the global perspective of Transformers to better capture both local and global features in remote sensing images. We introduce dilated convolutions into the self-attention computation of Transformers to control the network’s focus on different scales of image features. This enhancement improves the network’s ability to reconstruct details at various scales in the images. SR imagery provides richer surface information and reduces ambiguity for the LUCC task, thereby enhancing the accuracy of LUCC. Our work comprises two main stages: remote sensing image SR and LUCC. In the SR stage, we conducted comprehensive experiments on Landsat-8 (L8) and Sentinel-2 (S2) remote sensing datasets. The results indicate that DTGAN generates super-resolution (SR) images with minimal computation. Additionally, it outperforms other methods in terms of the spectral angle mapper (SAM) and learned perceptual image patch similarity (LPIPS) metrics, as well as visual quality. In the LUCC stage, DTGAN was used to generate SR images of areas outside the training samples, and then the SR imagery was used in the LUCC task. The results indicated a significant improvement in the accuracy of LUCC based on SR imagery compared to low-resolution (LR) LUCC maps. Specifically, there were enhancements of 0.130 in precision, 0.178 in recall, and 0.157 in the F1-score.
1. Introduction
Long time series and high-spatial-resolution remote sensing images play a crucial role in high-precision LUCC [1]. However, due to the limitation of hardware technology and cost, publicly available remote sensing data with high spatial resolution usually do not have long time series. For example, the Sentinel-2 satellite has a spatial resolution of up to 10 m, but its temporal coverage starts from 2015, and even expensive commercial satellite data are usually available from 2000 onwards. In contrast, remote sensing data with long time series usually do not have high spatial resolution. For example, Landsat series satellites have been providing valuable data since 1972. These data are frequently utilized for time series land use analysis. However, their spatial resolution is limited to 30 m, which restricts their application in long-term series and high-precision LUCC analysis. Therefore, it is crucial to improve the spatial resolution of long time series and low-spatial-resolution remote sensing images by means of algorithm development. Traditional SR methods for remote sensing images mainly include interpolation [2], Pansharp [3], sparse representation-based [4], and convex set projection [5]. The interpolation method has the advantage of simplicity and speed, but the interpolation results are usually blurred. The Pansharp method requires the sensor to have a high spatial resolution of the panchromatic bands, and can then improve the spatial resolution of other bands by data fusion. Methods based on sparse representation and convex set projection have high computational complexity and have difficulty recovering high-frequency details of the image. Convex set projection, in particular, demands a substantial amount of prior knowledge [6]. In recent years, deep learning techniques have been rapidly developed and have achieved impressive results in various computer vision (CV) tasks, including image super-resolution. Using deep learning techniques, LR data can be processed with super-resolution to improve the spatial resolution, which provides an opportunity to obtain higher-quality LUCC maps [7].
1.1. Deep Learning for Image Super-Resolution
The super-resolution convolutional neural network (SRCNN) [8] was the first convolutional neural network used for image super-resolution. SRCNN uses a stack of three convolutional layers to directly learn the mapping relationship between LR and HR end-to-end. Deep residual learning [9] was proposed to shift the structure of deep learning networks towards greater depth. The very deep super-resolution network (VDSR) [10] improves the super-resolution performance of the network by using residual concatenation and stacking very deep convolutional layers. SRCNN and VDSR up-sample the image when it is fed into the network, which results in slower training and high computational resource usage. The fast super-resolution convolutional neural network (FSRCNN) [11] and the enhanced deep super-resolution network (EDSR) [12] up-sample the feature maps in the last part of the network and achieved better super-resolution results in terms of the peak signal-to-noise ratio (PSNR) metric. Subsequently, the residual channel attention network (RCAN) [13] achieved better performance than deep convolutional networks such as VDSR and EDSR. This improvement was achieved by integrating the attention mechanism into the super-resolution network. This breakthrough showcased the mechanism’s ability to reconstruct intricate texture details within the image. Consequently, the attention mechanism has become a widespread inclusion in various super-resolution networks. The multispectral remote sensing images super-resolution convolutional neural network (msiSRCNN) [14] verified the feasibility of applying a convolutional neural network to the super-resolution of multispectral remote sensing images by fine-tuning SRCNN, and achieved better results than the traditional methods. The convolutional neural network became the mainstream method for the super-resolution of remote sensing images. Remote sensing images are distinct from ordinary optical images due to their diverse feature types and varying scales among these features. Aiming to address these problems, researchers have proposed many new structures [15,16,17,18,19], which are used to enhance the feature-learning capability of super-resolution networks for remote sensing images. Although CNN-based methods have achieved significant results in remote sensing image super-resolution tasks, the inherent localization of CNNs makes it difficult to model the global pixel dependencies of remote sensing images, which limits the further improvement of CNN performance in super-resolution tasks.
The Transformer [20] has quickly become the dominant approach in the field of natural language processing (NLP) with its powerful global modeling capabilities. The emergence of Vision Transformer (VIT) [21] introduced Transformer to the CV domain, achieving performance beyond CNNs on large datasets. Currently, there have been many works combining CNNs with Transformers for image super-resolution [22,23,24,25,26,27]. These methods use a CNN as a shallow feature extractor and Transformer for deep feature extraction, combining the local feature extraction capability of the CNN and the global modeling capability of Transformer to further improve the quality of SR images. Although Transformer can effectively compensate for the localization of CNN, in addition to the local–global learning capability, multi-scale feature learning is equally important for the super-resolution task of remote sensing images [17,18,27]. Unfortunately, Transformer does not have the ability of multi-scale feature learning. Numerous researchers have explored the integration of multi-scale information into the Transformer model [28,29,30,31]. However, these methods generally result in an increase in the number of network parameters, thereby further impeding the training process of the already large Transformer model. In addition to that, there are ways [29,32] to realize Transformer’s multiscale hierarchical representation of images by gradual down-sampling, but this is not applicable to the image super-resolution task. Although the CNN and Transformer-based methods are better than the traditional super-resolution methods and result in higher peak PSNR values, they are more ambiguous in visual perception.
Generative adversarial networks (GAN) [33] have powerful image-generation capabilities in image generation [34], style migration [35], and image super-resolution [36,37,38]. The GAN consists of two sub-networks, the generator and the discriminator, which are trained against each other in a ”zero-sum game”. The generator’s goal is to generate realistic images to deceive the discriminator, while the discriminator’s goal is to determine the authenticity of the input images. The generator updates the gradient based on the feedback from the discriminator. Adversarial training allows the GAN to generate images that are visually superior to the CNN. Super-resolution GAN (SRGAN) [36] uses the GAN network for the image super-resolution task and the pretrained VGG19 [39] network is used as a feature extractor to compute the perceptual loss to optimize the perceptual quality of the SR images. The enhanced super-resolution GAN (ESRGAN) [37] is an improvement of SRGAN; ESRGAN uses dense residual blocks to enhance the feature-learning capability of the network and removes the BatchNorm layer [40] from SRGAN. ESRGAN is still one of the most advanced image super-resolution methods. For the task of remote sensing image super-resolution, researchers have made many improvements to the GAN network, including the introduction of the attention mechanism [41,42], processing after super-resolution [43], and improvements to the discriminator [44], etc. GAN-based methods have more powerful image-generation capabilities than CNN-based methods, which generate SR images with more details. Therefore, we choose to train our model using the GAN framework.
1.2. Deep Learning for Land Use/Cover Classification
Land use/cover classification can extract information of natural land types as well as artificially utilized land types from remote sensing images, which is important in the fields of ecological protection, urban planning, and precision agriculture. The traditional LUCC methods [45,46,47] often rely on artificially designed features, such as spectral indices [48], and the spatial correlation of pixels is ignored. In contrast to traditional classification methods, deep-learning-based approaches eliminate the dependence on artificial features. They effectively capture both the spatial and spectral features inherent in remote sensing images [49], leading to superior classification accuracy and enhanced robustness. Fully convolutional neural networks (FCN) [50] represent an enlightening approach for the semantic segmentation task based on deep learning, which can realize the classification of images at pixel level. U-net [51] is a new approach for semantic segmentation, which was initially proposed for biomedical image segmentation, but has been widely used for image segmentation in various fields, including remote sensing, due to its superior performance. The Deeplab [52,53,54,55] family of models are another classic set of approaches for image segmentation tasks as well as U-net networks. In contrast to the stepwise down-sampling structure of U-net, Deeplab employs dilated convolutions [56] to facilitate multi-scale feature learning, thereby enhancing the segmentation accuracy. At present, in the remote sensing image LUCC task, the Transformer-based classification method is one of the hotspots in research. The self-attention mechanism of Transformer means that it can model the spectral features well. Many researchers have opted to integrate CNNs and Transformer by utilizing a CNN for extracting the spatial features and employing Transformer to capture the spectral features. These methods incorporating both spatial and spectral features have achieved better accuracy in the LUCC task [57,58,59,60]. The morphFormer, proposed by Roy et al. [61], integrates the learnable spectral morphological convolution operation and a self-attention mechanism. This combination enhances the interaction between the spectral features and improves the representation of the structure and shape information in tokens. When compared to traditional CNNs and other Transformer LUCC models, morphFormer achieves higher classification accuracy in experiments. Thus, it stands as one of the most advanced LUCC methods available at present. In this study, this method was directly employed for the SR data in the second stage, specifically for the LUCC task.
The objective of this study is to enhance the spatial resolution of remote sensing images using deep learning techniques. This enhancement aims to provide richer and more accurate surface information for LUCC tasks, thereby further improving the precision of LUCC. This study is mainly divided into two stages: remote sensing image SR and LUCC. In the SR stage, we propose a new model named the dilated Transformer GAN (DTGAN) for real remote sensing image super-resolution. The generator of this model combines CNN and Transformer, using a CNN as a shallow feature extractor and Transformer for deep feature extraction. At the same time, we seek to solve the problems of Transformer’s inability to learn multi-scale features and its slow computation and large resource consumption. This research is influenced by [32,62,63,64], with regard to the attention mechanism called dilated window multi-head self-attention (DW-MHSA), which can introduce multi-scale information into the Transformer and improve the computation efficiency of the self-attention without increasing the network parameters. The discriminator of DTGAN uses PatchGAN [38]. In the LUCC stage, we directly adopt morphFormer [61] in the LUCC of SR to verify the availability of the SR data.
2. Method for Remote Sensing Image Super-Resolution
2.1. The Overall Structure of the Generator
The generator structure of DTGAN is shown in Figure 1. Given a low-resolution input image , it is first mapped from the real image to the feature space by a convolutional layer:
where the number of input channels of Conv is 4, the number of output channels is 64, the convolution kernel size is 3, and the padding width is 1. represents the initial shallow features.
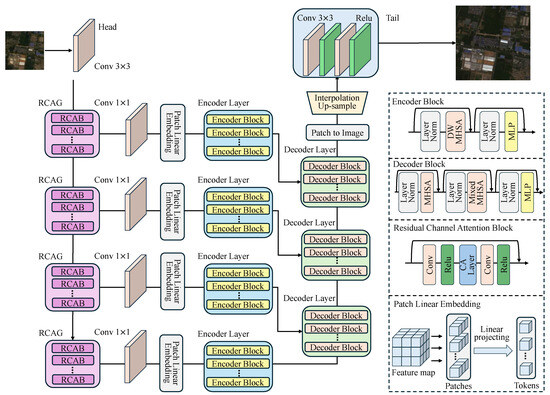
Figure 1.
The architecture of the generator of the proposed DTGAN.
As shown in Figure 1, the residual channel attention group (RCAG) in RCAN [13] is used as the base CNN backbone network to extract the shallow features. RCAG contains n residual channel attention blocks (RCAB). Each RCAB consists of two Conv&Relu layers, with the channel attention (CA) layer positioned between them. Moreover, the CA layer incorporates residual connections between the inputs and outputs. The structure of the CA layer is shown in Figure 2.

Figure 2.
The architecture of the channel attention layer.
For the CA layer, if the input feature map is , the CA process can be represented as follows:
where AvgPool and MaxPool represent the global average pooling and maximum pooling operations, respectively, applied to in the spatial dimensions. Subsequently, the global average and maximum information are fused through a Conv&Relu layer to obtain the merged result. The SoftMax function maps the fused information to the range [0,1], representing the importance of each channel. Element-wise multiplication of this attention with results in . The process of through the RCAG backbone network can be expressed as:
where represents the nth RCAG. In this study, we used four RCAGs as the CNN backbone network for feature extraction and each RCAG contains five RCABs.
Prior to feeding the features into the enhanced encoder layer with multiscale hierarchical feature enhancement, a convolutional layer is employed to reduce the dimensionality of the feature maps. This step aims to minimize the redundant features and to improve the computational efficiency. Then the feature map is divided into feature patches to obtain tokens by patch linear embedding. This embedding method is achieved using a convolutional layer with a convolutional kernel of the same size as the patch.
where represents the feature map output from the RCAG backbone network, with , represents the corresponding feature maps after dimensionality reduction, and represents a convolutional layer with a convolutional kernel size of . Then a convolutional layer with kernel size and stride equal to P is used to divide the feature map into patches and embed them into tokens.
Subsequently, enter the Transformer-based encoder layer feature enhancement module. The encoder layer has different dilated rates to learn the multi-scale representation of the features when calculating the DW-MHSA. These multi-scale features are fused in the decoder layer. The query matrix of the last decoder layer comes from the output of the last encoder layer, while the query matrix of the remaining decoder layers comes from the output of the previous decoder layer. The key and value matrices of all the decoder layers come from the output of the multi-scale encoder layer. The decoder layer fuses the multi-scale features by mixed multi-head attention (mixed-MHSA). Figure 3 shows the detailed information flow of the last encoder layer and decoder layer. The hierarchical multiscale feature fusion enhancement module can be represented as:
where De.ly. and En.ly. denote the decoder layer and the encoder layer, and represents the output feature of the ith decoder layer. The output feature from the decoder layer undergoes a depth-to-space transformation, reconstructing patches into feature maps. Subsequently, bicubic interpolation is applied to up-sample the feature maps by a specified factor. Finally, the up-sampled feature maps pass through two stacked Conv-Relu layers to obtain the ultimate output. This process can be expressed as:
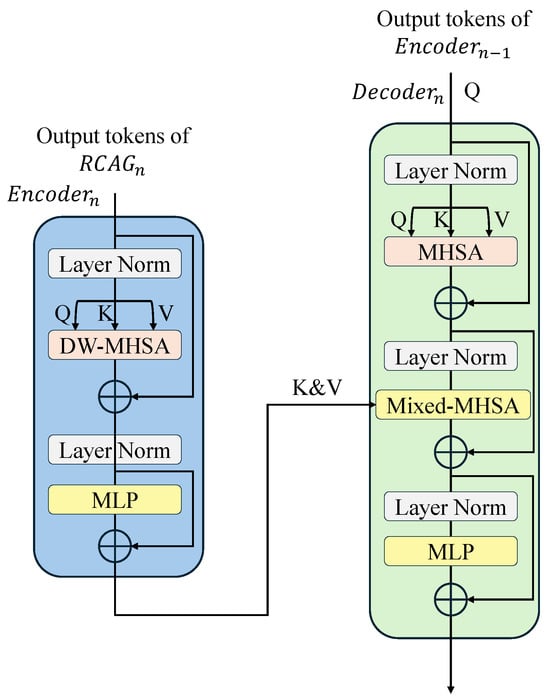
Figure 3.
Illustration of how the decoder fuses the multi-scale features.
2.2. Multi-Scale Feature Fusion and Enhance Module
2.2.1. Dilated Window Multi-Head Self-Attention
As shown in Figure 4c, in the computation of self-attention, the input features are first mapped into Query(Q), Key(K), and Value(V) matrices through three linear layers. In the scaled dot-product attention mechanism of the Transformer, the calculation of the pixel value at position in the output feature map is performed as follows:
where H and W denote the height and width of the feature map, respectively. denotes the scaling factor, and the default value of d is equal to the hidden dimension of the K and the V matrix. The scaled dot-product attention calculates the attention score for each pixel by considering its relationship with all the other pixels. This operation becomes computationally expensive when the input feature map is large. To address this issue and introduce multi-scale information into the Transformer for enhancing the model’s capability of reconstructing SR images, we propose a multi-scale attention mechanism based on dilated convolution. This idea is inspired by studies such as [32,62,63,64]
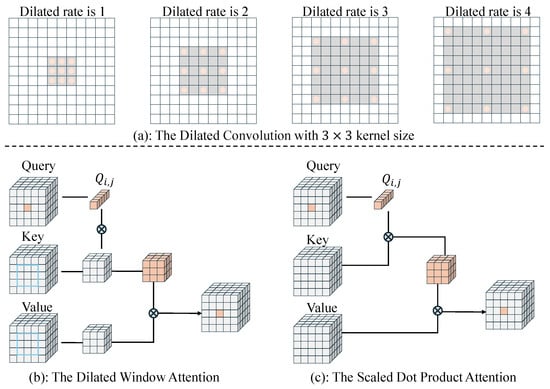
Figure 4.
Comparison diagram between dilated window self-attention (DWSA) proposed in this study and scaled dot-product attention in VIT.
As shown in Figure 4a, dilated convolution expands the receptive field and captures multi-scale information by utilizing different dilated rates. As shown in Figure 4b, we introduce this idea into Transformer and propose a new attention mechanism called dilated window self-attention (DWSA). DWSA uses window attention to replace global attention, which helps to improve the network computation speed, reduce resource overhead, and ensure the high-fidelity reconstruction of the remote sensing images. For any query pixel in the Q matrix, its attention is computed using a window centered at on the K and V matrix. The set of positions of the pixel points within the window can be expressed as:
where r denotes the dilated rate and w denotes the size of the window. For pixels at the edges of the feature map, we use mirrored edge filling to ensure that the feature map size does not change. The DWSA can be expressed as:
where and denote the window with a dilated ratio r on the K and V matrices, respectively.
Considering an input feature map and a window size of for dilated convolutions, the computational complexity for DW-MHSA and MHSA can be defined as follows:
This is analogous to the windowed attention computation in the Swin Transformer [32]. However, it eliminates the need for intricate window-shifting operations to facilitate communication between different windows. Moreover, it enables the control of window size through the dilation rate r, thereby enabling the learning of multiscale information.
2.2.2. Transformer Encoder Layer
In this study, we set the number of Transformer encoder layers to 4, as shown in Figure 1. Each encoder layer has different dilation rates to extract the multiscale features and the number of encoder blocks is set to 1. The detailed structure of the encoder block is illustrated in Figure 3. In contrast to the approach proposed in [20], we replaced MHSA with DW-MHSA. Furthermore, we positioned a layer norm [65] before the attention and multi-layer perceptron (MLP) sub-layers within the encoder block. For the ith encoder layer, with input , where , the encoder layer can be represented as:
where j denotes the number of blocks in the encoder layer, and represents the output feature of the jth encoder block.
2.2.3. Transformer Decoder Layer
In our approach, we utilized decoder layers to fuse the multiscale features obtained from the encoder layers. Similarly, each decoder layer comprises several decoder blocks. Within the decoder block, we employed MHSA to extract the deep features at a global scale. Unlike the encoder block, the decoder block incorporates a hybrid attention module in addition to the MHSA module and MLP sub-network. As depicted in Figure 3, this module takes the multiscale features from the output of the encoder layer as the K, V matrices for computing attention, while the Q matrix is derived from the output of the previous decoder layer. In our work, the encoder layer produces features of different scales, which are gradually fused within the decoder layer through the mixed-MHSA module. Let denote the output of the encoder layer . The process of the decoder layer can be represented as:
where denotes the output feature of the jth decoder block in the decoder layer.
2.3. The Overall Structure of the Discriminator
As illustrated in Figure 5, the traditional VGG-style discriminator was replaced with a PatchGAN discriminator using the U-Net structure, similar to [38]. This U-Net PatchGAN demonstrates superior discriminative ability for complex remote sensing images. It provides precise gradient feedback for local textures instead of distinguishing the global style of the generated image. The U-Net discriminator yields relative authenticity values for each pixel, offering detailed per-pixel feedback to the generator. However, the introduction of the U-Net structure also increased the instability of GAN training. To address this, spectral normalization regularization [66] was employed to stabilize the training process. Additionally, spectral normalization helps mitigate excessive sharpness and artifacts introduced by GAN training. The down-sampling in PatchGAN is achieved through convolution with a stride of 2, and up-sampling is implemented using bicubic interpolation.
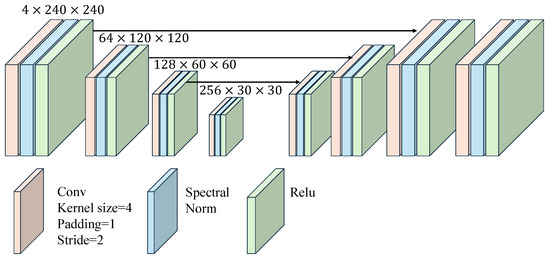
Figure 5.
The architecture of the discriminator of the proposed DTGAN.
3. Dataset and Experimental Setup
3.1. Dataset
For the first stage of the remote sensing image super-resolution task, our study utilized Landsat-8 Collection 2 Tier 1 and Sentinel-2 data as the experimental datasets. Both L8 and S2 provide multiple spectral bands, including visible and infrared bands, enhancing the accuracy of the LUCC task in the second stage. The focus of the first stage was on the remote sensing image SR, where we utilized a total of five L8 images and seven S2 images. The data used in the SR stage covered the northern regions of Henan Province and the western regions of Shandong Province. This area experiences a warm temperate monsoon climate with concurrent rain and heat. The earliest image was captured on 29 April 2023, during spring, and the most recent image was captured on 23 June 2023, during summer. The primary land types in this region include cultivated land and certain areas of the Taihang Mountains. The predominant vegetation consists of crops, coniferous forests, deciduous broadleaf forests, urban vegetation, and small wetlands and grasslands. In the second stage LUCC tasks, we utilized two images each from L8 and S2, captured on 1 May 2023, and 14 May 2023, respectively. These images were stitched and cropped to obtain remote sensing images of the Yongcheng City area. All the data used had cloud coverage controlled at 10% or below. Figure 6 displays the geographical locations of the selected data for the SR stage. To differentiate between Landsat-8 and Sentinel-2 data, L8 data is represented in true colors, while S2 data is displayed in false colors.
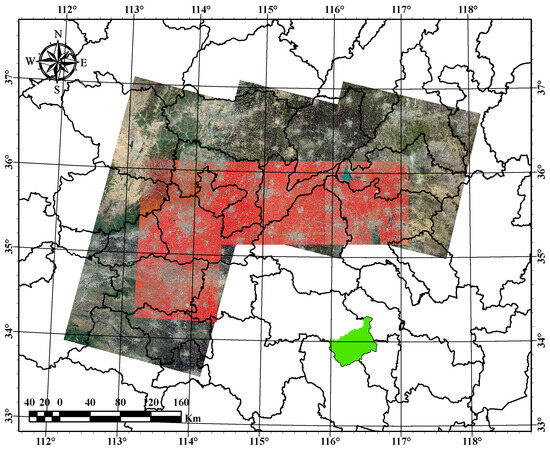
Figure 6.
Geographic location of remote sensing images for the SR stage. The green area indicates the location of Yongcheng City in the second stage of the LUCC task.
In the experiments, the 10 m resolution red (R), green (G), blue (B), and near-infrared (NIR) bands of the S2 data were used as the high-resolution target data. Corresponding bands with 30 m resolution from the L8 imagery were used as the LR input data. The acquired data were preprocessed with coordinate system alignment and atmospheric correction. The matched regions were then cropped into training samples. The L8 low-resolution samples were cropped into patches of size pixels with a stride of 70 pixels, while the corresponding high-resolution S2 samples were pixels with a cropping stride of 210 pixels. After manual screening to exclude data with noise, cloud cover, and other disturbances, a total of 12,800 patches were obtained. These patches were divided into training, validation, and test sets in a ratio of 8:1:1. Figure 7 illustrates some sample training images.

Figure 7.
The paired image patch used for training the SR model.
For the second stage of the LUCC task, we selected Yongcheng City in Shangqiu, China, as our study area. The image acquisition and preprocessing methods were consistent with the first stage. The processed images were stitched and cropped to obtain L8 and S2 images within the Yongcheng City area. The pre-trained DTGAN from the first stage was employed to generate SR images for the L8 imagery, as illustrated in Figure 8. The samples used for classification were the SR images of Yongcheng City. The land use/cover types in the Yongcheng City area were classified into five classes: barren land, building land, vegetation land, water, and mulching film.
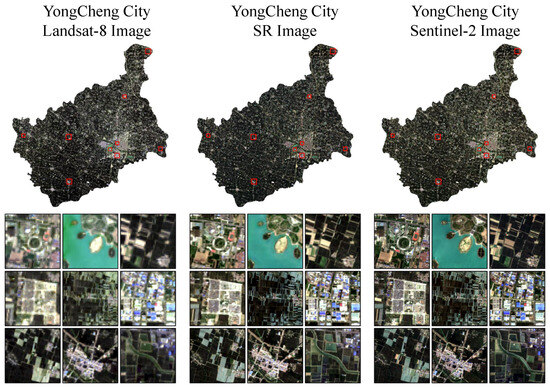
Figure 8.
SR image of Yongcheng City.
3.2. Experimental Setup
This study employed the PyTorch framework [67,68] and was trained on an NVIDIA GeForce RTX 3090 graphics card. For the remote sensing image super-resolution task, a fixed global random seed of 0 was set during training. The Adam optimizer [69] was employed with an initial learning rate of , a learning rate decay factor of , decay epochs every 150 rounds, and a total of 500 epochs. The batch size was set to 64. Data augmentation techniques were employed during data loading, including random rotations of , , and , as well as horizontal and vertical flips. The detailed configuration of the generator used in training is provided in Table 1.

Table 1.
The generator details of DTGAN.
In the table, En.Ly. and De.Ly. represent the number of encoder layers and decoder layers, as shown in Figure 1. En.Ly. Depth and De.Ly. Depth indicate the number of encoder blocks and decoder blocks within a single encoder layer and decoder layer, respectively.
The pixel loss, perceptual loss, and spectral angle mapping (SAM) loss were utilized to train the generator, while the RaGAN loss [70] was employed to train the entire GAN network. We used the loss to denote the pixel loss. Given the training dataset , the loss can be expressed as:
where represents the generator with parameters w, represents the super-resolution image , and N denotes the total number of images used for training.
The perceptual loss utilizes a pretrained model as a feature extraction network to compare the feature representations of the generated images and the real images, thereby measuring their similarity. The perceptual loss aims to assess the image quality from a perceptual perspective by optimizing high-level semantic features to generate more visually realistic images. In the context of remote sensing image SR, we employed a ConvNet [71] model pretrained on the BigEarthNet [72,73] as our feature extraction network. The perceptual loss can be defined as:
where represents the pretrained neural network with parameters .
The Landsat-8 and Sentinel-2 images exhibit distinct spectral differences. To constrain the spectral changes during network training, we employed the SAM loss to optimize the spectral information of the SR images. SAM measures spectral similarity by calculating the angles between spectra. The SAM loss can be defined as:
where represents the transpose of , and denotes a small value used to prevent division by zero.
In contrast to the standard GAN network, which directly determines whether the input is real or fake, RaGAN evaluates the probability that the input data is more authentic than the real data. The optimization objective of RaGAN is to minimize the relative discrimination score of the generator and to maximize that of the discriminator. This enables the generator to better capture the overall data distribution, resulting in the generation of more realistic and diverse samples. The RaGAN loss can be expressed as:
where and represent the distributions of the HR and SR data, respectively, and denotes the discriminator with parameters . Hence, the total loss of the network can be expressed as:
where represents the weight coefficients for different loss functions. In our experiment, the different values of are [1.0, 0.2, 0.05, 0.5].
For the LUCC task, we employed morphFormer [61] as the classifier. We partitioned a window around each pixel as the input for the network, and the output was the category of the central pixel. The model utilized the Adam optimizer [69], with an initial learning rate set to and a batch size of 256. The model was trained for a total of 50 batches.
3.3. Metrics
For the remote sensing SR task, we employed several quality evaluation metrics for the SR images, including the peak signal-to-noise ratio (PSNR), the structural similarity index measure (SSIM) [74], the spectral angle mapper (SAM), and the learned perceptual image patch similarity (LPIPS) [75].
PSNR is one of the most commonly used metrics for image quality evaluation. It measures the relationship between the maximum signal value and the noise in the image, and its unit is decibels (dB). Higher PSNR values indicate better image quality. The expression for PSNR is:
where MSE represents the mean squared error between the SR image and the ground truth image.
SSIM measures the similarity between two images in terms of brightness, contrast, and structural information, with values ranging from 0 to 1. A value closer to 1 indicates a higher similarity between the two images. SSIM can be expressed as:
where and represent the mean and variance of the image, respectively. , are constants, L represents the dynamic range of the image pixel values, and and are usually set to and , respectively.
SAM measures the spectral similarity between a multispectral image and a reference image by calculating the angles between their spectra. A smaller angle indicates higher similarity, while a larger angle indicates lower similarity. SAM can be expressed as:
where represents the transpose of .
LPIPS calculates the distance between the image activation maps using a pretrained network to measure the perceptual similarity between the images. A lower LPIPS score indicates a higher perceptual similarity between the images. LPIPS can be expressed as:
For the LUCC task, we utilized precision, recall, and the F1-score to measure the accuracy of the classification results.
4. Experimental Results and Discussion
4.1. Experimental Comparison of the SR Model
To validate the effectiveness of our proposed DTGAN, we conducted comparisons with traditional interpolation methods as well as several state-of-the-art deep-learning-based image super-resolution techniques. The interpolation method employed bicubic interpolation. The deep learning methods included VDSR [10], DCMNet [76], LGCNet [15], RCAN [13], SwinIR [25], SRFormer [77], TransENet [22], and SRGAN [36]. Among these, VDSR [10], DCMNet [76], LGCNet [15], and RCAN [13] are CNN-based methods, while SwinIR [25], SRFormer [77], and TransENet [22] leverage the Transformer architecture for image super-resolution. SRGAN [36] is an advanced algorithm based on the GAN framework.
In Table 2, the performance of different methods on the test dataset is displayed. The cells highlighted in red indicate the best accuracy, while the ones in blue represent the second-best accuracy. When compared to methods based on CNN and Transformer, GAN-based methods exhibit lower PSNR and SSIM scores but perform better in terms of the LPIPS perceptual metric. This suggests that images generated by GAN-based methods are more perceptually aligned with human vision. DTGAN achieved the best accuracy in the SAM and LPIPS metrics, indicating that our method’s images are closer to real images both in terms of their spectral and perceptual quality. Additionally, we compared the parameter count and computational complexity of different models. The parameter count signifies the model size, while the computational complexity indicates the model’s inference speed, with lower complexity leading to faster inference. For SRGAN and DTGAN, we only considered the parameter count and the computational complexity of the generator. Among the compared methods, LGCNet and VDSR have the fewest and second-fewest parameters, while DTGAN has the lowest computational complexity. DTGAN ranks fourth in terms of parameter count, but still outperforms several Transformer-based methods.

Table 2.
Metrics of methods on test data.
Figure 9 illustrates the visual results of the SR images produced by different methods, along with a comparison of the absolute errors with real images. From Figure 9, it can be observed that compared to GAN-based methods, the CNN and Transformer-based methods have higher PSNR and SSIM values but lower perceptual quality, appearing visually smoother and lacking detailed information. Hence, they exhibit larger absolute errors when compared with real images. The super-resolution results of SRGAN and DTGAN are visually similar, with smaller absolute errors when compared to HR images. However, DTGAN outperforms SRGAN in some texture details.

Figure 9.
Visual comparison of SR results from different methods. On the left are RGB true-color images representing SR results obtained using different methods. On the right are the absolute error values between the SR images and the HR images. The image reflectance values range from [0–1]. (a) Sample 1. (b) Sample 2. (c) Sample 3.
The spectral information of remote sensing images plays a crucial role in the accuracy of the LUCC task. We calculated the MSE between the SR images generated by different methods and the corresponding HR images for different bands on the test dataset. The results are illustrated in Figure 10. DTGAN achieved the smallest MSE in the blue and red bands, while SRGAN had the smallest MSE in the green and near-infrared bands. DTGAN exhibited the smallest total band MSE.
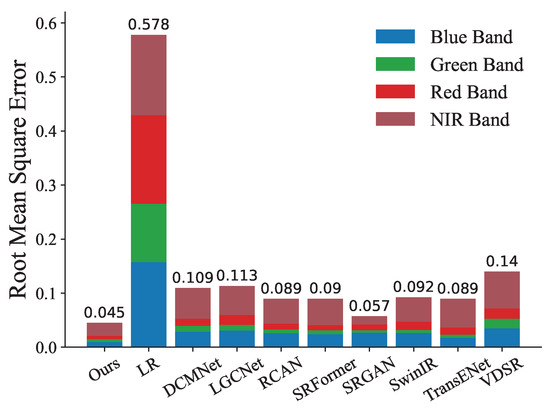
Figure 10.
Root mean square errors of bands on test data for different methods, where the number at the top of the bar represents the total RMSE across the four spectral bands. During RMSE calculation, the image values are normalized within the range [0–1].
Due to differences in the radiometric values, the L8 and S2 images exhibit variations in the grayscale distribution. The histograms reflect the distribution of the grayscale values in the images. We calculated and compared the grayscale histograms of the LR, SR, and HR data for different bands in the Yongcheng City to assess our method’s capability to learn the grayscale distribution of the HR images. The results in Figure 11 demonstrate that, compared to the LR images, the grayscale distribution of the SR images is much closer to that of the HR images. In the blue and green bands, the grayscale distribution of the SR images is almost identical to that of the HR images. However, in the red and near-infrared (NIR) bands, the overall grayscale distribution of the SR images closely resembles that of the HR images, although there are significant differences in the peak values. We posit that this outcome arises from the wavelength disparities in the L8 and S2 imagery across these four spectral bands, coupled with the growth stages of the predominant winter wheat crops within the study area. Overall, DTGAN effectively learns the mapping relationship between the LR and HR image grayscale distributions, generating SR images that are visually, spectrally, and in terms of grayscale distribution, closer to the HR images.
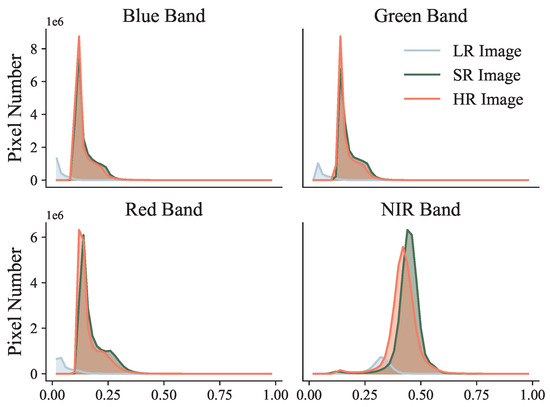
Figure 11.
Histograms of gray levels for different bands in Yongcheng City SR imagery by DTGAN.
4.2. Ablation Experimental of the SR Model
In this study, we conducted a series of ablation experiments to explore the impact of various components of the network on the reconstruction results of the SR images. Table 3 presents the initial generator configuration used in the ablation experiments.

Table 3.
The initial setup of the ablation experiment.
The ablation about patch size: Prior to feeding the shallow features extracted by the RCAG module into the encoder layer, the feature maps need to be divided into patches of size . Table 4 demonstrates the influence of different patch sizes on the network performance in the SR task. When , the network achieved the best results in terms of the PSNR, SSIM, and SAM metrics, while the perceptual metric LPIPS reached its optimum value at . The process of partitioning the image into patches can be approximated as a down-sampling process. Larger patches imply a larger receptive field, aiding the model in capturing contextual information better. However, larger patches also mean more loss of local information. Smaller patches help the network handle local detailed features better but lead to the loss of global information, hindering the network in reconstructing the global structure of the SR images. The optimal value of P varies for different tasks and image resolutions. In our experiments, we ultimately set the value of P to 4.

Table 4.
The result of the ablation for the patch size.
The ablation about P.E.: Positional encoding is utilized for the network to learn the position information of the patches. Table 5 presents the results of ablation experiments on positional encoding. When both the encoder layer and decoder layer have positional encoding, the model achieves the best PSNR, SSIM, and SAM metrics, but obtains the lowest LPIPS value. This suggests that positional encoding is crucial for the SR task, improving the performance of the SR images according to traditional image evaluation metrics, but potentially reducing the perceptual quality of the SR images. Based on our experiments, we ultimately decided to retain positional encoding in both the encoder layer and the decoder layer.

Table 5.
The result of the ablation for the position encoding.
The ablation about DW-MHSA: The extraction and fusion of the multiscale features represent the core of the proposed method. Table 6 illustrates the impact of different scale attention mechanisms on the network performance. The numbers in the table represent the dilation rates used in calculating DW-MHSA in the corresponding encoder layer, and False indicates the use of MHSA. DW-MHSA calculates the local attention, focusing on the multiscale local details by adjusting the dilation rate r, but lacks the ability to capture the global contextual information. Therefore, when all the encoder layers use DW-MHSA, the network performance does not reach its optimum due to the absence of global information. Similarly, when all the encoder layers use MHSA, the network fails to achieve optimal performance due to the lack of multiscale local information. When the attention configuration is set to , the model achieves the best performance across all the metrics. At this configuration, the encoder layers strike a balance between learning global information and multiscale local information.

Table 6.
The result of the ablation for the dilated rate of DW-MHSA in encoder.
The ablation about depths of En.Ly. and De.Ly.: The number of blocks in the encoder layer and the decoder layer affects the final quality of the generated SR images. A series of ablation experiments were conducted to investigate the depths of En.Ly. and De.Ly., and the results are shown in Table 7. It can be observed that when the depth of the encoder layers is set to 1 and the depth of the decoder layers is set to 4, the model achieves the best accuracy in terms of PSNR, SAM, and LPIPS. This indicates that as the decoder layers become deeper, the model’s performance initially improves and then reaches a certain degree of overfitting.

Table 7.
The result of the ablation for the encoder layer and the decoder layer depths.
4.3. Evaluation of SR Images for LUCC
The proposed DTGAN in this study achieved the best overall performance in the SR task. We applied it to the L8 image SR in the Yongcheng City area, and the resulting SR images are shown in Figure 8. We used the method proposed in [61] for the second-stage experiments. Land use classification was performed on the original LR, SR, and HR images. The macro average classification accuracy for images of different resolution is shown in Table 8. It can be observed that compared to the LR classification map, the SR classification map achieved better performance in the various metrics.

Table 8.
The macro average score of the classification map for different spatial resolution.
Figure 12 and Figure 13 display the confusion matrix and the class accuracy of the classification results, respectively. It can be observed that for the vegetation category, the classification results at different spatial resolutions are very similar, as Yongcheng City has large areas of plain farmland. Vegetation has simple spatial characteristics and distinct spectral features compared to other land covers, making the classification results less dependent on spatial information. For land covers, such as bare land and building areas, with similar spectral but complex spatial features, higher spatial resolution provides richer spatial information, which helps improve the accuracy of classification.

Figure 12.
Confusion matrix for image classification results of different spatial resolution.
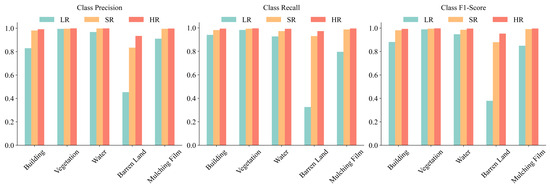
Figure 13.
Scores for each class of image with different spatial resolutions.
Figure 14 provides a visual comparison of the classification results at various spatial resolutions. It can be observed that the LR classification map exhibits poor differentiation for buildings and bare land, with the finer linear roads being nearly indistinguishable in the LR image. For the regular rectangular-shaped pondwater bodies and mulching film land, the SR classification map has clearer edges due to the increased spatial resolution. However, it can be seen that the finer water bodies are also not well-classified in the SR map. This indicates that the SR images can furnish more detailed spatial information, thereby enhancing the accuracy of the LUCC. However, they are unable to retrieve all the information available in the LR images. As shown in Table 8 and Figure 13, compared to the LR classification map, the SR classification results show improvements in both overall accuracy and class accuracy. This enhancement is particularly notable for land categories, such as barren land and buildings, which possess similar spectral characteristics. The higher spatial resolution provided by the SR imaging captures more spatial details, aiding in the differentiation of land features with similar spectral properties but distinct spatial characteristics.
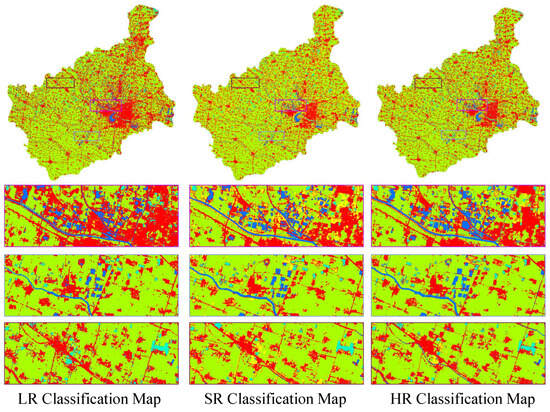
Figure 14.
Classification map of different spatial resolution images with morphFormer [61].
5. Discussion
In this study, we constructed a GAN based on a CNN and the Transformer architecture for Landsat-8 multispectral image super-resolution in real-world scenarios. The results indicate that our method outperforms other techniques in visual quality, as demonstrated by metrics such as LPIPS and SAM. The generated super-resolution data contribute significantly to enhancing the accuracy of the LUCC tasks. Compared to CNN, the GAN networks possess a more realistic image-generation capability. The GAN networks are designed to learn the distribution of real data, enabling them to generate high-resolution images that closely resemble real data. Moreover, the adversarial training approach of the GAN networks aids in recovering the edge and detail information from low-resolution images, resulting in SR images that perceptually resemble real HR images. On the other hand, the CNN-based super-resolution images typically exhibit higher PSNR values but may lack detailed features and sharp boundaries, providing a smoother effect on the fine details and the object edges. For remote sensing imagery, improved visual perception and the recovery of more detailed object boundaries are crucial. Enhanced visual perception leads to better visual interpretation and understanding of the surface information, aiding in a more intuitive analysis. Additionally, recovering more object boundaries and fine details provides richer surface information for various remote sensing applications, including LUCC, resulting in more refined land cover classification maps.
6. Conclusions
This study proposed a generative adversarial network that combines convolutional neural networks with Transformers to improve the spatial resolution of multispectral remote sensing images and to enhance the accuracy of LUCC maps. The research was conducted in two stages: image SR and LUCC. In the SR stage, we introduced Transformers into the generator to compensate for the local nature of CNNs and to enhance the model’s ability to learn local and global features. Additionally, we incorporated multi-scale information and dilated convolutions to improve the computational efficiency. In the LUCC stage, a pretrained model was used to generate HR images from L8 data. We demonstrated that using these SR images significantly improves the accuracy of LUCC maps. This study presents a novel approach for remote sensing image super-resolution, showing promising practical applications.
Author Contributions
Methodology, X.Z. Validation, B.L.; Data curation, Z.Z.; Writing—original draft, X.Z.; Writing—review&editing, C.W., W.Y. and G.W.; Visualization, X.L.; Funding acquisition, C.W. and W.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Chunhui Program Cooperative Research Project of the Chinese Ministry of Education (HZKY20220279), the Henan Provincial Science and Technology Research Project (232102211019, 222102210131), the Key Research Project Fund of the Institution of Higher Education in Henan Province (23A520029), and the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant (No. 20K12146).
Data Availability Statement
The data used in this paper and the code for the proposed method can be found at https://github.com/zxyl1003/dtgan.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SR | Super-resolution |
| LR | Low-resolution |
| HR | High-resolution |
| LUCC | Land use/cover classification |
| CNN | Convolutional neural networks |
| GAN | Generative adversarial network |
| DTGAN | Dilated transformer generative adversarial network |
| SRCNN | Super-resolution convolutional neural network |
| VDSR | Very deep super-resolution network |
| FSRCNN | Fast super-resolution convolutional neural network |
| EDSR | Enhanced deep super-resolution network |
| RCAN | Residual channel attention network |
| msiSRCNN | Multispectral remote sensing images super-resolution convolutional neural network |
| NLP | Natural language processing |
| VIT | Vision Transformer |
| SRGAN | Super-resolution generative adversarial network |
| ESRGAN | Enhanced super-resolution generative adversarial network |
| FCN | Fully convolutional neural networks |
| RCAG | Residual channel attention group |
| RCAB | Residual channel attention block |
| CA | Channel attention |
| L8 | Landsat-8 |
| S2 | Sentinel-2 |
| MHSA | Multi-head self-attention |
| DWSA | Dilated window self-attention |
| DW-MHSA | Dilated window multi-head self-attention |
| Mixed-MHSA | Mixed multi-head attention |
| NIR | Near-infrared |
| PSNR | Peak signal-to-noise ratio |
| SSIM | Structural similarity index measure |
| SAM | Spectral angle mapper |
| LPIPS | Learned perceptual image patch similarity |
References
- Vuolo, F.; Neuwirth, M.; Immitzer, M.; Atzberger, C.; Ng, W.T. How much does multi-temporal Sentinel-2 data improve crop type classification? Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 122–130. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X. An edge-guided image interpolation algorithm via directional filtering and data fusion. IEEE Trans. Image Process. 2006, 15, 2226–2238. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A Critical Comparison Among Pansharpening Algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image Super-Resolution Via Sparse Representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Lei, J.; Zhang, S.; Luo, L.; Xiao, J.; Wang, H. Super-resolution enhancement of UAV images based on fractional calculus and POCS. Geo-Spat. Inf. Sci. 2018, 21, 56–66. [Google Scholar] [CrossRef]
- Anna, H.; Rui, L.; Liang, W.; Jin, Z.; Yongyang, X.; Siqiong, C. Super-resolution reconstruction method for remote sensing images considering global features and texture features. Acta Geod. Cartogr. Sin. 2023, 52, 648. [Google Scholar] [CrossRef]
- Zhu, Y.; Geiß, C.; So, E. Image super-resolution with dense-sampling residual channel-spatial attention networks for multi-temporal remote sensing image classification. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102543. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. In Proceedings of the Computer Vision—ECCV 2014, Zurich, Switzerland, 6–12 September 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; pp. 184–199. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. arXiv 2016, arXiv:1511.04587. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the Super-Resolution Convolutional Neural Network. arXiv 2016, arXiv:1608.00367. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. arXiv 2017, arXiv:1707.02921. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; pp. 294–310. [Google Scholar]
- Liebel, L.; Körner, M. Single-Image Super Resolution for Multispectral Remote Sensing Data Using Convolutional Neural Networks. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41B3, 883–890. [Google Scholar] [CrossRef]
- Lei, S.; Shi, Z.; Zou, Z. Super-Resolution for Remote Sensing Images via Local–Global Combined Network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1243–1247. [Google Scholar] [CrossRef]
- Zhang, D.; Shao, J.; Li, X.; Shen, H.T. Remote Sensing Image Super-Resolution via Mixed High-Order Attention Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5183–5196. [Google Scholar] [CrossRef]
- Lei, S.; Shi, Z. Hybrid-Scale Self-Similarity Exploitation for Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Dong, X.; Wang, L.; Sun, X.; Jia, X.; Gao, L.; Zhang, B. Remote Sensing Image Super-Resolution Using Second-Order Multi-Scale Networks. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3473–3485. [Google Scholar] [CrossRef]
- Huang, B.; He, B.; Wu, L.; Guo, Z. Deep Residual Dual-Attention Network for Super-Resolution Reconstruction of Remote Sensing Images. Remote Sens. 2021, 13, 2784. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2023, arXiv:1706.03762. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Lei, S.; Shi, Z.; Mo, W. Transformer-Based Multistage Enhancement for Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5615611. [Google Scholar] [CrossRef]
- Conde, M.V.; Choi, U.J.; Burchi, M.; Timofte, R. Swin2SR: SwinV2 Transformer for Compressed Image Super-Resolution and Restoration. In Proceedings of the Computer Vision—ECCV 2022 Workshops, Tel Aviv, Israel, 23–27 October 2022; Karlinsky, L., Michaeli, T., Nishino, K., Eds.; pp. 669–687. [Google Scholar]
- Lu, Z.; Li, J.; Liu, H.; Huang, C.; Zhang, L.; Zeng, T. Transformer for Single Image Super-Resolution. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–20 June 2022; pp. 456–465. [Google Scholar] [CrossRef]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Gool, L.V.; Timofte, R. SwinIR: Image Restoration Using Swin Transformer. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Montreal, BC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, J.; Shi, J.; Weng, S. Efficient Mixed Transformer for Single Image Super-Resolution. arXiv 2023, arXiv:2305.11403. [Google Scholar]
- Shang, J.; Gao, M.; Li, Q.; Pan, J.; Zou, G.; Jeon, G. Hybrid-Scale Hierarchical Transformer for Remote Sensing Image Super-Resolution. Remote Sens. 2023, 15, 3442. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, J.; Willette, J.; Hwang, S.J. MPViT: Multi-Path Vision Transformer for Dense Prediction. arXiv 2021, arXiv:2112.11010. [Google Scholar]
- Wang, W.; Yao, L.; Chen, L.; Lin, B.; Cai, D.; He, X.; Liu, W. CrossFormer: A Versatile Vision Transformer Hinging on Cross-scale Attention. arXiv 2021, arXiv:2108.00154. [Google Scholar]
- Fan, H.; Xiong, B.; Mangalam, K.; Li, Y.; Yan, Z.; Malik, J.; Feichtenhofer, C. Multiscale Vision Transformers. arXiv 2021, arXiv:2104.11227. [Google Scholar]
- Ren, S.; Zhou, D.; He, S.; Feng, J.; Wang, X. Shunted Self-Attention via Multi-Scale Token Aggregation. arXiv 2022, arXiv:2111.15193. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. arXiv 2021, arXiv:2103.14030. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014, arXiv:1406.2661. [Google Scholar] [CrossRef]
- Yu, Y.; Gong, Z.; Zhong, P.; Shan, J. Unsupervised Representation Learning with Deep Convolutional Neural Network for Remote Sensing Images. In Proceedings of the Image and Graphics, Shanghai, China, 13–15 September 2017; pp. 97–108. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. arXiv 2017, arXiv:1609.04802. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Loy, C.C.; Qiao, Y.; Tang, X. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. arXiv 2018, arXiv:1809.00219. [Google Scholar]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-ESRGAN: Training Real-World Blind Super-Resolution with Pure Synthetic Data. arXiv 2021, arXiv:2107.10833. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Jia, S.; Wang, Z.; Li, Q.; Jia, X.; Xu, M. Multiattention Generative Adversarial Network for Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5624715. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Yang, W.; Li, X.; Lu, B.; Wang, J. MSAGAN: A New Super-Resolution Algorithm for Multispectral Remote Sensing Image Based on a Multiscale Attention GAN Network. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5001205. [Google Scholar] [CrossRef]
- Jiang, K.; Wang, Z.; Yi, P.; Wang, G.; Lu, T.; Jiang, J. Edge-Enhanced GAN for Remote Sensing Image Superresolution. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5799–5812. [Google Scholar] [CrossRef]
- Lei, S.; Shi, Z.; Zou, Z. Coupled Adversarial Training for Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3633–3643. [Google Scholar] [CrossRef]
- Cariou, C.; Chehdi, K. A new k-nearest neighbor density-based clustering method and its application to hyperspectral images. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 6161–6164. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral–Spatial Hyperspectral Image Segmentation Using Subspace Multinomial Logistic Regression and Markov Random Fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 809–823. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Kulkarni, K.; Vijaya, P.A. NDBI Based Prediction of Land Use Land Cover Change. J. Indian Soc. Remote Sens. 2021, 49, 2523–2537. [Google Scholar] [CrossRef]
- Huang, B.; Zhao, B.; Song, Y. Urban land-use mapping using a deep convolutional neural network with high spatial resolution multispectral remote sensing imagery. Remote Sens. Environ. 2018, 214, 73–86. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. arXiv 2015, arXiv:1411.4038. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Semantic Image Segmentation with Deep Convolutional Nets and Fully Connected CRFs. arXiv 2016, arXiv:1412.7062. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking Atrous Convolution for Semantic Image Segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. arXiv 2018, arXiv:1802.02611. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Mei, S.; Song, C.; Ma, M.; Xu, F. Hyperspectral Image Classification Using Group-Aware Hierarchical Transformer. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5539014. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–Spatial Feature Tokenization Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5522214. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking Hyperspectral Image Classification With Transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5518615. [Google Scholar] [CrossRef]
- Huang, X.; Dong, M.; Li, J.; Guo, X. A 3-D-Swin Transformer-Based Hierarchical Contrastive Learning Method for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5411415. [Google Scholar] [CrossRef]
- Roy, S.K.; Deria, A.; Shah, C.; Haut, J.M.; Du, Q.; Plaza, A. Spectral–Spatial Morphological Attention Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5503615. [Google Scholar] [CrossRef]
- Beltagy, I.; Peters, M.E.; Cohan, A. Longformer: The Long-Document Transformer. arXiv 2020, arXiv:2004.05150. [Google Scholar]
- Hassani, A.; Walton, S.; Li, J.; Li, S.; Shi, H. Neighborhood Attention Transformer. arXiv 2023, arXiv:2204.07143. [Google Scholar]
- Hassani, A.; Shi, H. Dilated Neighborhood Attention Transformer. arXiv 2023, arXiv:2209.15001. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Miyato, T.; Kataoka, T.; Koyama, M.; Yoshida, Y. Spectral Normalization for Generative Adversarial Networks. arXiv 2018, arXiv:1802.05957. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Rogozhnikov, A. Einops: Clear and Reliable Tensor Manipulations with Einstein-like Notation. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Jolicoeur-Martineau, A. The relativistic discriminator: A key element missing from standard GAN. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A ConvNet for the 2020s. arXiv 2022, arXiv:2201.03545. [Google Scholar]
- Sumbul, G.; Charfuelan, M.; Demir, B.; Markl, V. Bigearthnet: A Large-Scale Benchmark Archive for Remote Sensing Image Understanding. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5901–5904. [Google Scholar] [CrossRef]
- Sumbul, G.; de Wall, A.; Kreuziger, T.; Marcelino, F.; Costa, H.; Benevides, P.; Caetano, M.; Demir, B.; Markl, V. BigEarthNet-MM: A Large-Scale, Multimodal, Multilabel Benchmark Archive for Remote Sensing Image Classification and Retrieval [Software and Data Sets]. IEEE Geosci. Remote Sens. Mag. 2021, 9, 174–180. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. arXiv 2018, arXiv:1801.03924. [Google Scholar]
- Haut, J.M.; Paoletti, M.E.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.; Li, J. Remote Sensing Single-Image Superresolution Based on a Deep Compendium Model. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1432–1436. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Z.; Guo, C.L.; Bai, S.; Cheng, M.M.; Hou, Q. SRFormer: Permuted Self-Attention for Single Image Super-Resolution. arXiv 2023, arXiv:2303.09735. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).