Rainfall Erosivity Mapping for Tibetan Plateau Using High-Resolution Temporal and Spatial Precipitation Datasets for the Third Pole
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Daily Precipitation Data
2.3. RE Calculation and Accuracy Evaluation
2.4. Trend Analysis
3. Results
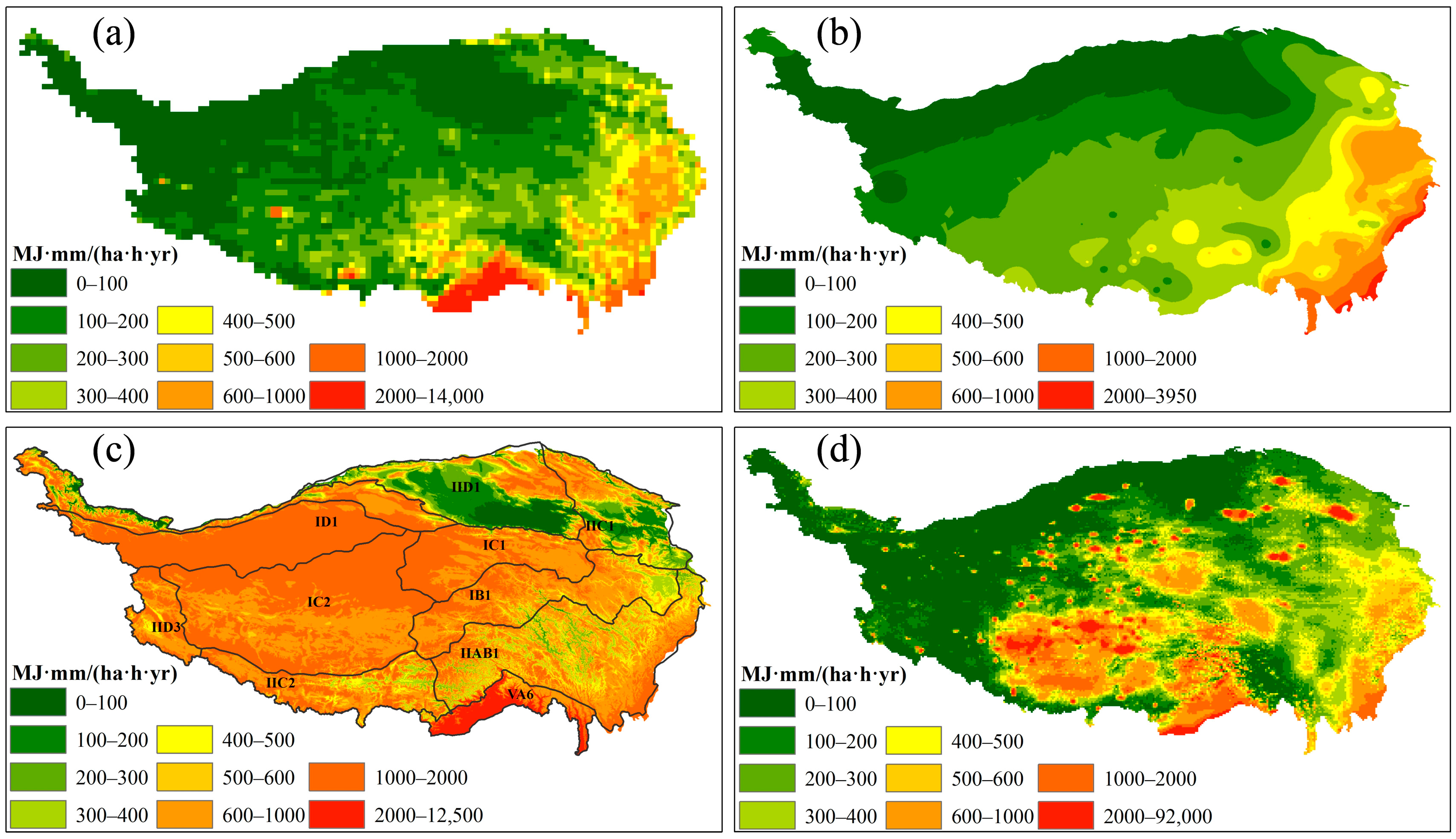
3.1. Spatial Distribution of Average Annual RE for Different Data Sources
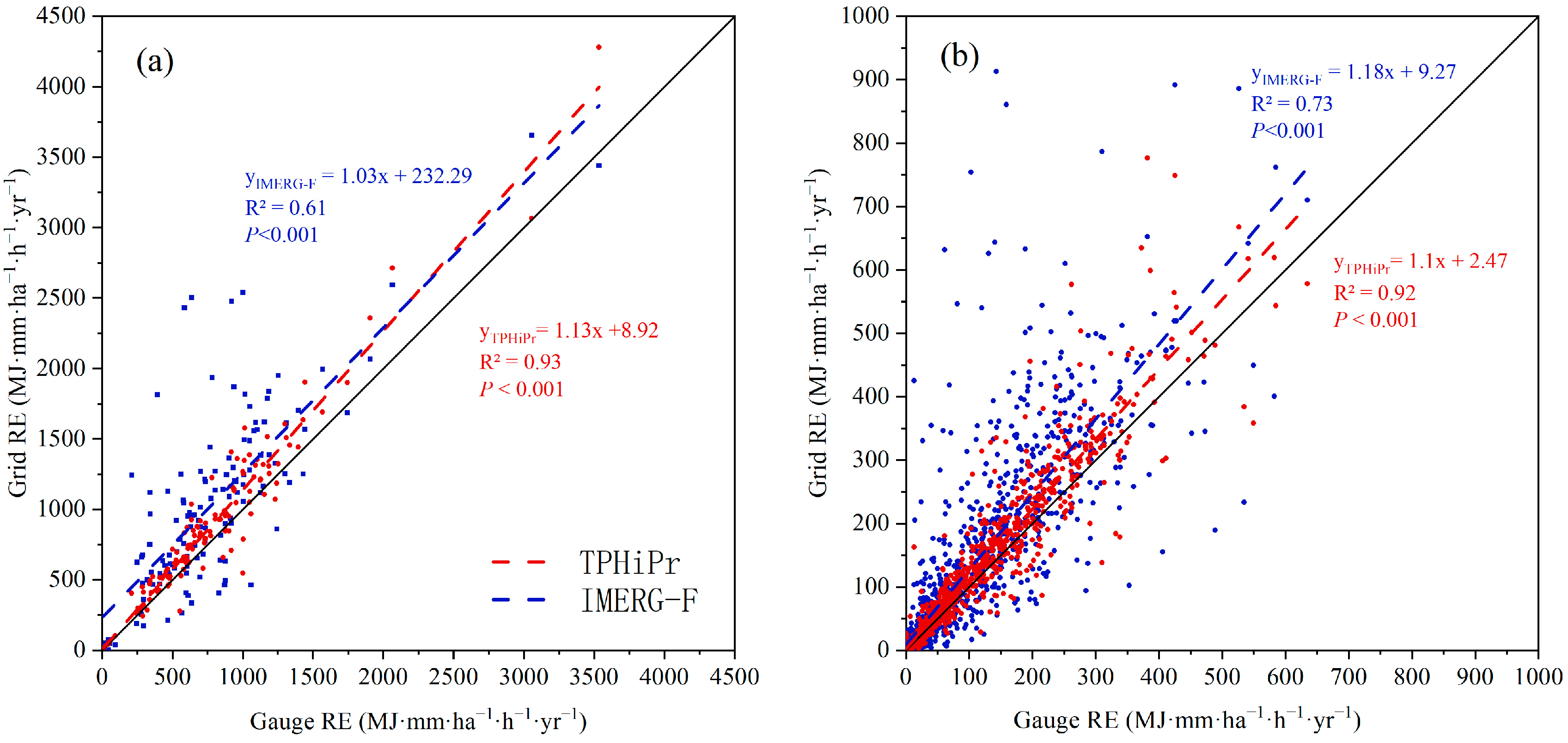
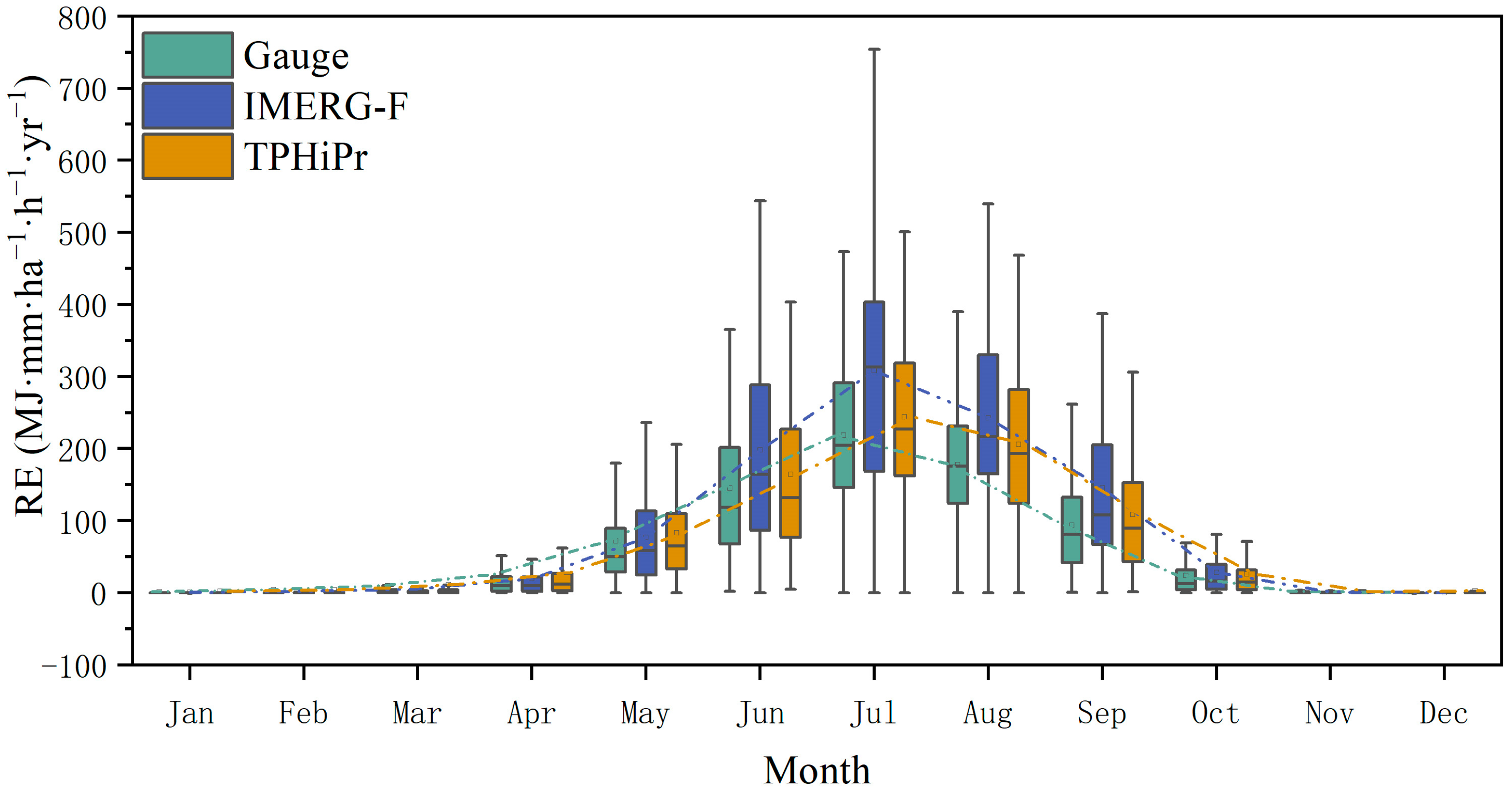
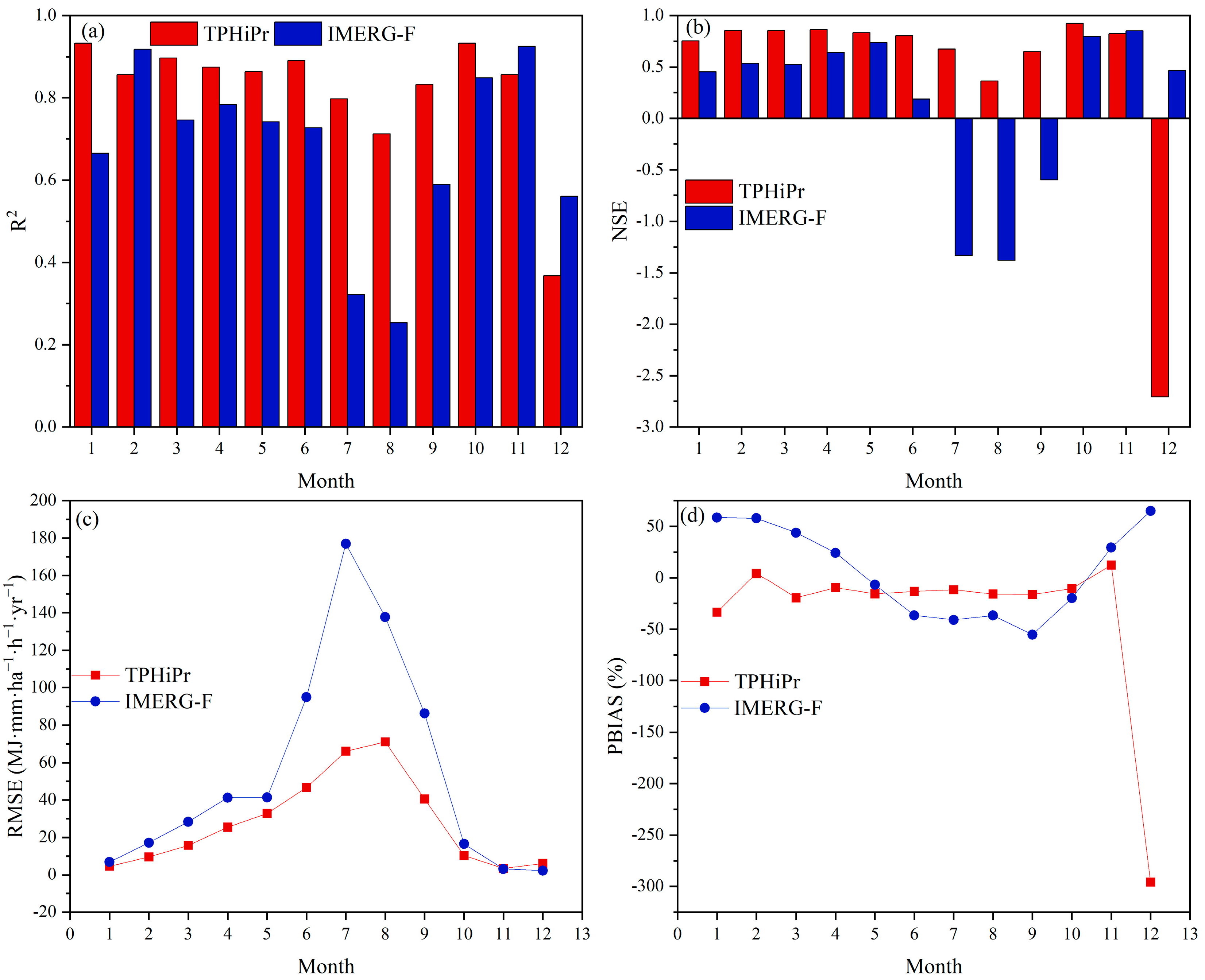
3.2. Evaluation of RE Accuracy at Station Scale
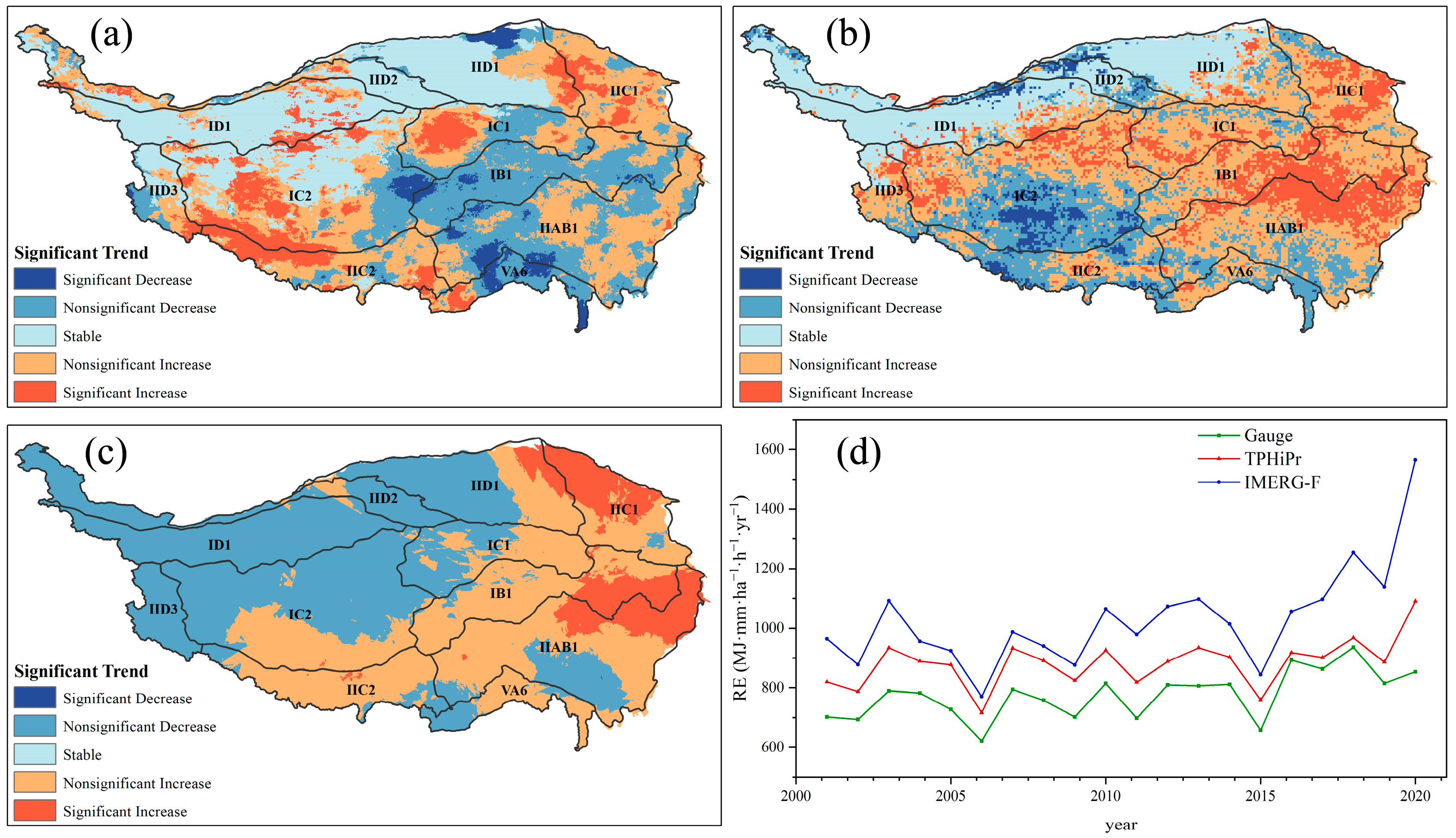
3.3. Comparison of RE Trends on the TP
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smith, P.; House, J.I.; Bustamante, M.; Kuikman, P.; Pugh, T.A.M. Global change pressures on soils from land use and management. Glob. Chang. Biol. 2016, 22, 1008–1028. [Google Scholar] [CrossRef] [PubMed]
- Wuepper, D.; Borrelli, P.; Finger, R. Countries and the global rate of soil erosion. Nat. Sustain. 2020, 3, 51–55. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K.; Klik, A.; Rousseva, S.; Tadić, M.P.; Michaelides, S.; Hrabalíková, M.; Olsen, P.; et al. Rainfall erosivity in Europe. Sci. Total Environ. 2015, 511, 801–814. [Google Scholar] [CrossRef]
- Nearing, M.A.; Yin, S.-q.; Borrelli, P.; Polyakov, V.O. Rainfall erosivity: An historical review. Catena 2017, 157, 357–362. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Rainfall energy and its relationship to soil loss. Eos Trans. Am. Geophys. Union 1958, 39, 285–291. [Google Scholar]
- Renard, K.G. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); United States Government Printing: Washington, DC, USA, 1997.
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; Department of Agriculture, Science and Education Administration: Washington, DC, USA, 1978. [Google Scholar]
- Margiorou, S.; Kastridis, A.; Sapountzis, M. Pre/Post-Fire Soil Erosion and Evaluation of Check-Dams Effectiveness in Mediterranean Suburban Catchments Based on Field Measurements and Modeling. Land 2022, 11, 1705. [Google Scholar] [CrossRef]
- Phinzi, K.; Ngetar, N.S. The assessment of water-borne erosion at catchment level using GIS-based RUSLE and remote sensing: A review. Int. Soil Water Conserv. Res. 2019, 7, 27–46. [Google Scholar] [CrossRef]
- Xie, Y.; Yin, S.-q.; Liu, B.-y.; Nearing, M.A.; Zhao, Y. Models for estimating daily rainfall erosivity in China. J. Hydrol. 2016, 535, 547–558. [Google Scholar] [CrossRef]
- Angulo-Martínez, M.; Beguería, S. Estimating rainfall erosivity from daily precipitation records: A comparison among methods using data from the Ebro Basin (NE Spain). J. Hydrol. 2009, 379, 111–121. [Google Scholar] [CrossRef]
- Chen, Y.; Ding, M.; Zhang, G.; Duan, X.; Wang, C. The possible role of fused precipitation data in detection of the spatiotemporal pattern of rainfall erosivity over the Tibetan Plateau, China. Catena 2023, 228, 107114. [Google Scholar] [CrossRef]
- Liu, B.; Xie, Y.; Li, Z.; Liang, Y.; Guo, Q. The assessment of soil loss by water erosion in China. Int. Soil Water Conserv. Res. 2020, 8, 430–439. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Lin, Y. Suitability of TRMM Products with Different Temporal Resolution (3-Hourly, Daily, and Monthly) for Rainfall Erosivity Estimation. Remote Sens. 2020, 12, 3924. [Google Scholar] [CrossRef]
- Gu, Z.; Feng, D.; Duan, X.; Gong, K.; Li, Y.; Yue, T. Spatial and Temporal Patterns of Rainfall Erosivity in the Tibetan Plateau. Water 2020, 12, 200. [Google Scholar] [CrossRef]
- Yin, S.; Xie, Y.; Liu, B.; Nearing, M.A. Rainfall erosivity estimation based on rainfall data collected over a range of temporal resolutions. Hydrol. Earth Syst. Sci. 2015, 19, 4113–4126. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Yu, B.; Klik, A.; Jae Lim, K.; Yang, J.E.; Ni, J.; Miao, C.; Chattopadhyay, N. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep. 2017, 7, 4175. [Google Scholar] [CrossRef] [PubMed]
- Yue, T.; Yin, S.; Xie, Y.; Yu, B.; Liu, B. Rainfall erosivity mapping over mainland China based on high-density hourly rainfall records. Earth Syst. Sci. Data 2022, 14, 665–682. [Google Scholar] [CrossRef]
- Teng, H.F.; Liang, Z.Z.; Chen, S.C.; Liu, Y.; Rossel, R.A.V.; Chappell, A.; Yu, W.; Shi, Z. Current and future assessments of soil erosion by water on the Tibetan Plateau based on RUSLE and CMIP5 climate models. Sci. Total Environ. 2018, 635, 673–686. [Google Scholar] [CrossRef]
- Das, S.; Jain, M.K.; Gupta, V. A step towards mapping rainfall erosivity for India using high-resolution GPM satellite rainfall products. Catena 2022, 212, 106067. [Google Scholar] [CrossRef]
- Delgado, D.; Sadaoui, M.; Ludwig, W.; Méndez, W. Spatio-temporal assessment of rainfall erosivity in Ecuador based on RUSLE using satellite-based high frequency GPM-IMERG precipitation data. Catena 2022, 219, 106597. [Google Scholar] [CrossRef]
- Bezak, N.; Borrelli, P.; Panagos, P. Exploring the possible role of satellite-based rainfall data in estimating inter- and intra-annual global rainfall erosivity. Hydrol. Earth Syst. Sci. 2022, 26, 1907–1924. [Google Scholar] [CrossRef]
- Teng, H.; Ma, Z.; Chappell, A.; Shi, Z.; Liang, Z.; Yu, W. Improving Rainfall Erosivity Estimates Using Merged TRMM and Gauge Data. Remote Sens. 2017, 9, 1134. [Google Scholar] [CrossRef]
- Tang, L.; Tian, Y.; Yan, F.; Habib, E. An improved procedure for the validation of satellite-based precipitation estimates. Atmos. Res. 2015, 163, 61–73. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, C.; Xie, Y.; Liu, B.; Yin, S.; Liu, Y.; Hao, Y. Increasing trends in rainfall-runoff erosivity in the Source Region of the Three Rivers, 1961–2012. Sci. Total Environ. 2017, 592, 639–648. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhang, F.; Fu, S.H.; Shi, X.N.; Chen, Y.; Jagirani, M.D.; Zeng, C. Assessment of soil erosion risk and its response to climate change in the mid-Yarlung Tsangpo River region. Environ. Sci. Pollut. Res. 2020, 27, 607–621. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Duan, X.; Ding, M.; Qi, W.; Wei, T.; Li, J.; Xie, Y. New gridded dataset of rainfall erosivity (1950–2020) on the Tibetan Plateau. Earth Syst. Sci. Data 2022, 14, 2681–2695. [Google Scholar] [CrossRef]
- Chen, Y. Rainfall erosivity estimation over the Tibetan plateau based on high spatial-temporal resolution rainfall records. Int. Soil Water Conserv. Res. 2022, 10, 422–432. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.-H. NASA global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). Algorithm Theor. Basis Doc. (ATBD) Version 2015, 4, 30. [Google Scholar]
- Xu, R.; Tian, F.Q.; Yang, L.; Hu, H.C.; Lu, H.; Hou, A.Z. Ground validation of GPM IMERG and TRMM 3B42V7 rainfall products over southern Tibetan Plateau based on a high-density rain gauge network. J. Geophys. Res.-Atmos. 2017, 122, 910–924. [Google Scholar] [CrossRef]
- Lu, D.; Yong, B. Evaluation and Hydrological Utility of the Latest GPM IMERG V5 and GSMaP V7 Precipitation Products over the Tibetan Plateau. Remote Sens. 2018, 10, 2022. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, M.; Wang, Z.; Gao, P.; Lai, C. Applicability of two satellite-based precipitation products for assessing rainfall erosivity in China. Sci. Total Environ. 2021, 757, 143975. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Yang, K.; Qi, Y.; Zhou, X.; He, J.; Lu, H.; Li, X.; Chen, Y.; Li, X.; Zhou, B. TPHiPr: A long-term (1979–2020) high-accuracy precipitation dataset (1∕30°, daily) for the Third Pole region based on high-resolution atmospheric modeling and dense observations. Earth Syst. Sci. Data 2023, 15, 621–638. [Google Scholar] [CrossRef]
- Li, G.; Yu, Z.; Wang, W.; Ju, Q.; Chen, X. Analysis of the spatial Distribution of precipitation and topography with GPM data in the Tibetan Plateau. Atmos. Res. 2021, 247, 105259. [Google Scholar] [CrossRef]
- Zheng, D.; Zhao, D.S. Characteristics of natural environment of the Tibetan Plateau. Sci. Technol. Rev 2017, 35, 13–22. [Google Scholar]
- Yang, K.; Jiang, Y. A Long-Term (1979–2020) High-Resolution (1/30°) Precipitation Dataset for the Third Polar Region (TPHiPr); N.T.P.D. Center, Ed.; National Tibetan Plateau Data Center: Beijing, China, 2022. [Google Scholar]
- GES DISC. Available online: https://disc.gsfc.nasa.gov/ (accessed on 11 July 2021).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Kastridis, A.; Theodosiou, G.; Fotiadis, G. Investigation of Flood Management and Mitigation Measures in Ungauged NATURA Protected Watersheds. Hydrology 2021, 8, 170. [Google Scholar] [CrossRef]
- Moriasi, N.D.; Arnold, G.J.; Van Liew, W.M.; Bingner, L.R.; Harmel, D.R.; Veith, L.T. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Arnold, J.; Demissie, M. Hydrological modeling of the Iroquois river watershed using HSPF and SWAT 1. JAWRA J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Wang, Y.; Kong, Y.; Chen, H.; Zhao, L. Improving daily precipitation estimates for the Qinghai-Tibetan plateau based on environmental similarity. Int. J. Climatol. 2020, 40, 5368–5388. [Google Scholar] [CrossRef]
- Ma, Z.; Xu, Y.; Peng, J.; Chen, Q.; Wan, D.; He, K.; Shi, Z.; Li, H. Spatial and temporal precipitation patterns characterized by TRMM TMPA over the Qinghai-Tibetan plateau and surroundings. Int. J. Remote Sens. 2018, 39, 3891–3907. [Google Scholar] [CrossRef]
- Li, G.; Chen, H.; Xu, M.; Zhao, C.; Zhong, L.; Li, R.; Fu, Y.; Gao, Y. Impacts of Topographic Complexity on Modeling Moisture Transport and Precipitation over the Tibetan Plateau in Summer. Adv. Atmos. Sci. 2022, 39, 1151–1166. [Google Scholar] [CrossRef]
- Lin, C.; Chen, D.; Yang, K.; Ou, T. Impact of model resolution on simulating the water vapor transport through the central Himalayas: Implication for models’ wet bias over the Tibetan Plateau. Clim. Dyn. 2018, 51, 3195–3207. [Google Scholar] [CrossRef]
- Xu, K.; Zhong, L.; Ma, Y.; Zou, M.; Huang, Z. A study on the water vapor transport trend and water vapor source of the Tibetan Plateau. Theor. Appl. Climatol. 2020, 140, 1031–1042. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, K.; Zhou, X.; Wang, B.; Chen, D.; Lu, H.; Lin, C.; Zhang, F. The Formation of a Dry-Belt in the North Side of Central Himalaya Mountains. Geophys. Res. Lett. 2019, 46, 2993–3000. [Google Scholar] [CrossRef]

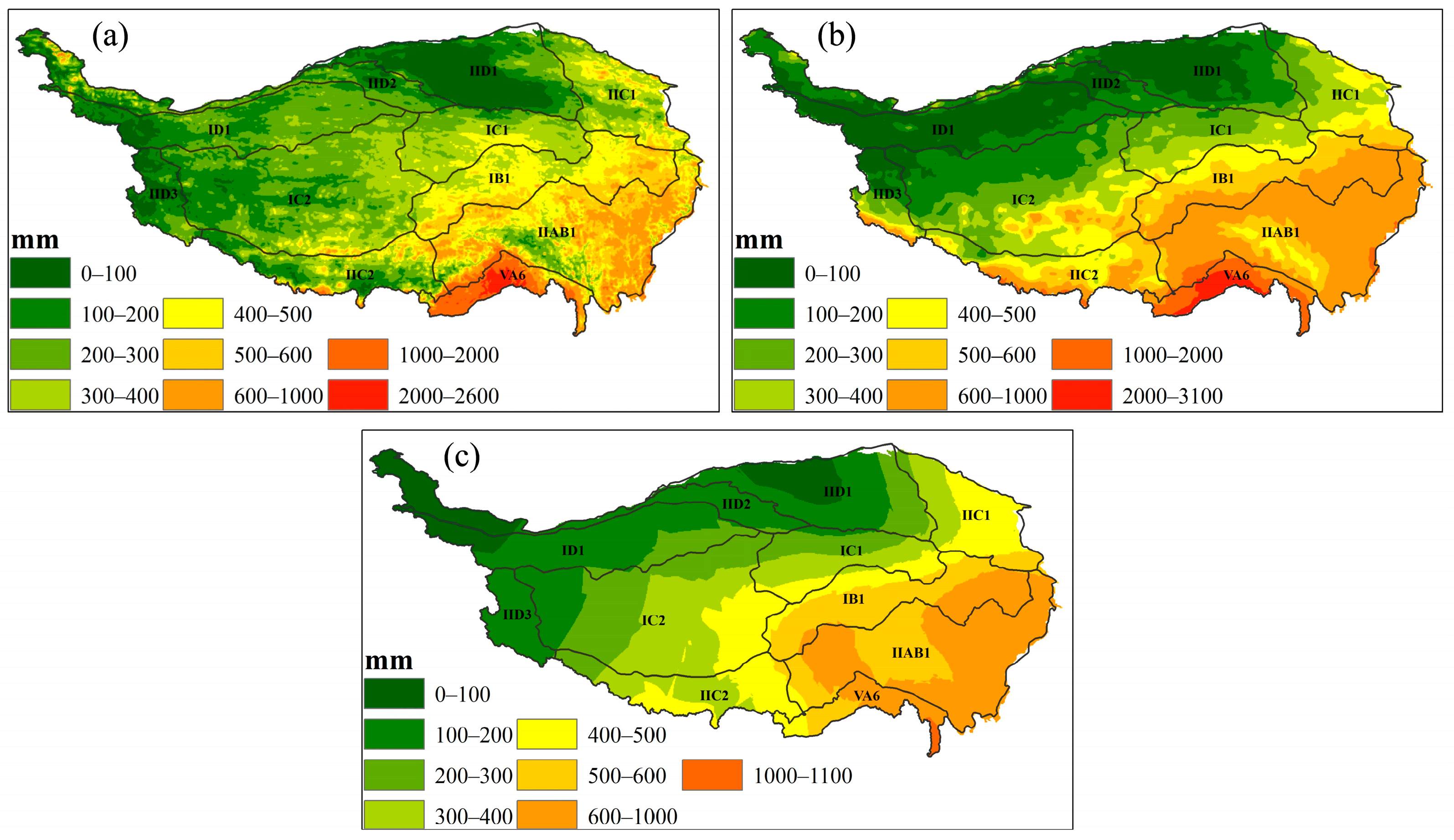
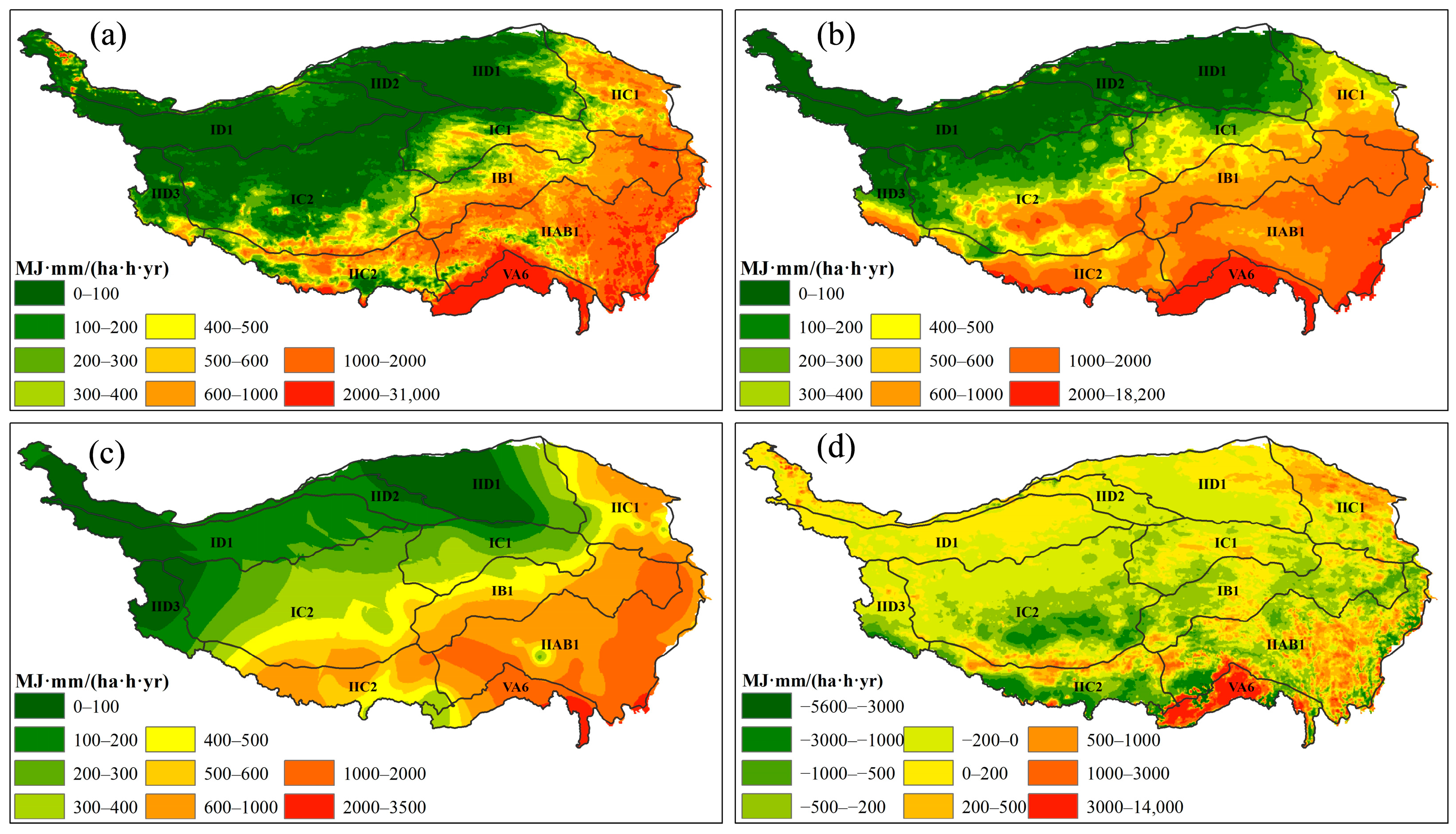
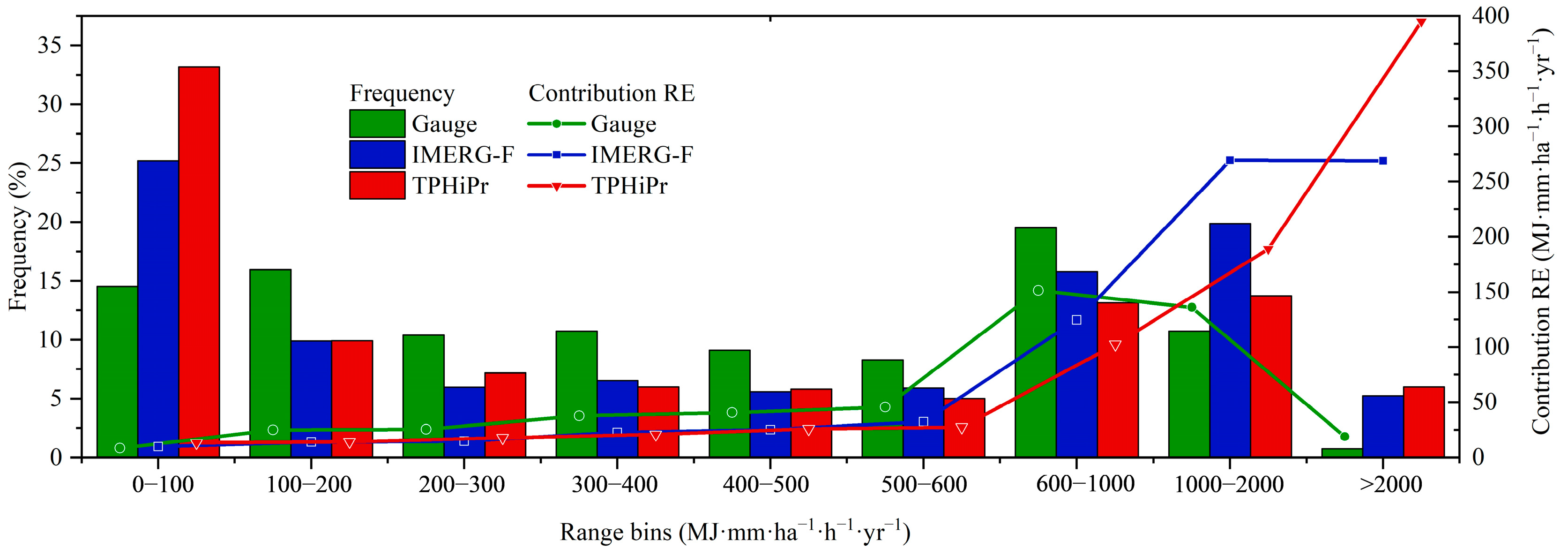

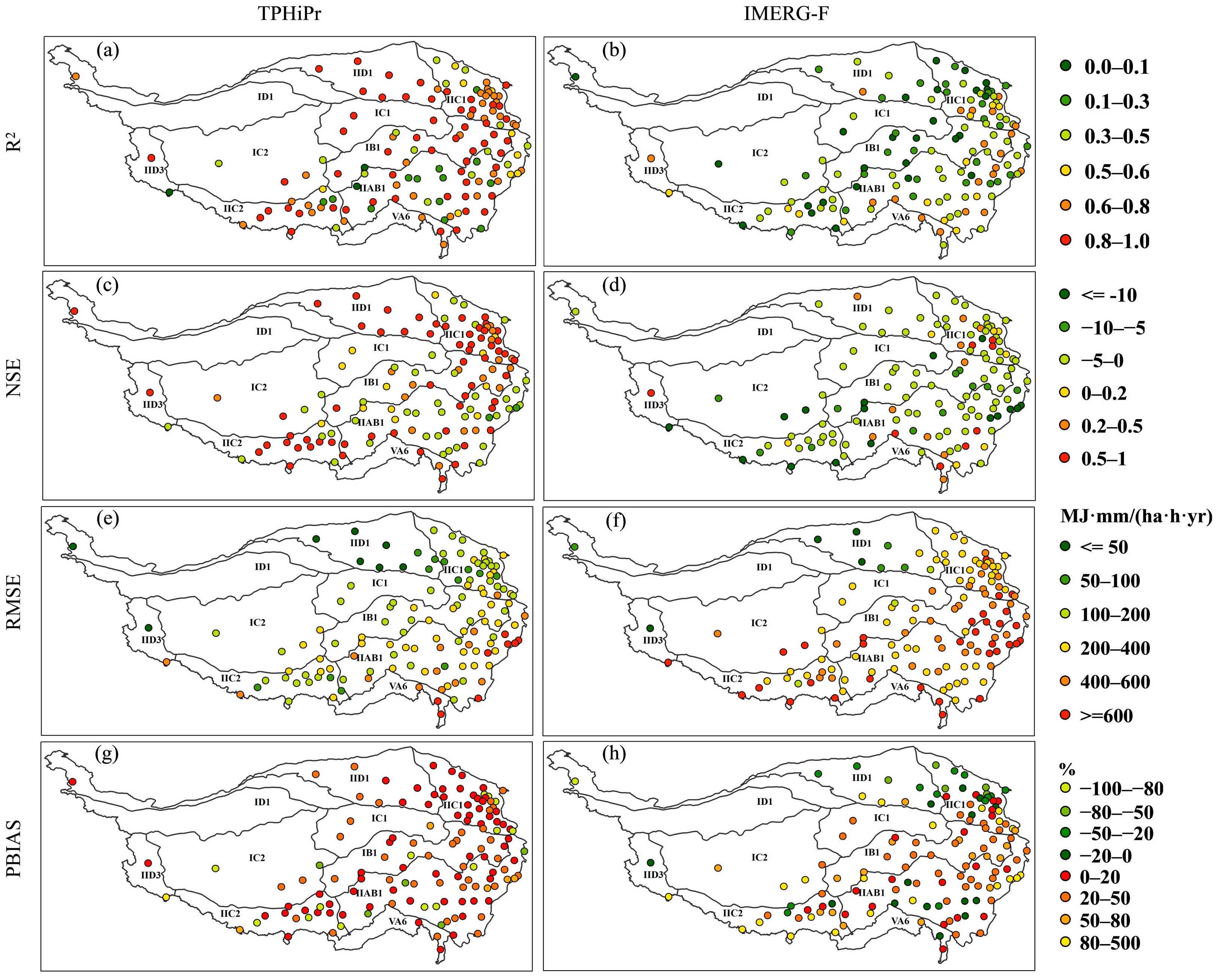
| Zone | Annual Precipitation (mm) | Average Temperature of Warmest Month (°C) | Area (Million km2) | No. Stations (Stations) | Station Density (Unit/10,000 km2) |
|---|---|---|---|---|---|
| Broad-leaved evergreen forest zone on the southern flank of the Himalayas (VA6) | 1000–4000 | 18–25 | 0.087 | 3 | 0.34 |
| Eastern Qinghai–Qilian montane basin coniferous forest steppe zone (IIC1) | 300–600 | 12–18 | 0.171 | 32 | 1.87 |
| Eastern Sichuan and Tibet montane coniferous forest (IIAB1) | 500–1000 | 6–18 | 0.424 | 45 | 1.06 |
| Golog-Nagqu plateau high–cold shrub–meadow zone (IB1) | 400–700 | 6–12 | 0.255 | 16 | 0.63 |
| Qiangtang Plateau internally flowing rivers zone (IC1) | 200–400 | 6–10 | 0.186 | 3 | 0.16 |
| Qiangtang Plateau lake basin high–cold steppe zone (IC2) | 100–300 | 6–10 | 0.52 | 4 | 0.08 |
| Qaidam basin desert zone (IID1) | 10–200 | 10–18 | 0.257 | 9 | 0.35 |
| Southern Tibet montane valley shrub–steppe zone (IIC2) | 200–300 | 10–16 | 0.177 | 16 | 0.90 |
| Northern flank of Kunlun Mountains desert zone (IID2) | 70–150 | 12–20 | 0.158 | 1 | 0.06 |
| Kunlun montane plateau high–cold desert zone (ID1) | <100 | 3–7 | 0.266 | 0 | 0 |
| Ali Mountains desert zone (IID3) | 50–200 | 10–14 | 0.079 | 2 | 0.25 |
| Zone | Gauge | IMERG-F | TPHiPr | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Min | Max | Mean | Min | Max | Mean | |
| TP | 8 | 3534 | 775 | 4 | 3655 | 1028 | 10 | 4280 | 883 |
| VA6 | 1186 | 3534 | 2591 | 1837 | 3655 | 2977 | 1307 | 4280 | 2884 |
| IIAB1 | 249 | 2065 | 1035 | 602 | 2593 | 1398 | 277 | 2713 | 1182 |
| IB1 | 351 | 1254 | 744 | 470 | 1950 | 1068 | 410 | 1517 | 892 |
| IIC2 | 320 | 1125 | 643 | 500 | 2477 | 1025 | 286 | 1407 | 715 |
| IIC1 | 255 | 1154 | 658 | 213 | 1622 | 700 | 295 | 1154 | 736 |
| IC2 | 288 | 553 | 413 | 478 | 1129 | 841 | 243 | 576 | 398 |
| IC1 | 288 | 361 | 314 | 360 | 677 | 501 | 412 | 522 | 462 |
| IID1 | 8 | 294 | 112 | 5 | 256 | 93 | 10 | 326 | 125 |
| IID2 | 42 | 42 | 42 | 4 | 4 | 4 | 43 | 43 | 43 |
| IID3 | 53 | 211 | 132 | 50 | 1245 | 647 | 58 | 404 | 231 |
| ID1 | / | / | / | / | / | / | / | / | / |
| Dataset | Time | R2 | NSE | RMSE (MJ·mm·ha−1·h−1·yr−1) | SD (MJ·mm·ha−1·h−1·yr−1) | RMSE/SD | PBIAS (%) |
|---|---|---|---|---|---|---|---|
| Gauge | Year | / | / | / | 499.27 | / | / |
| TPHiPr | 0.93 | 0.85 | 195.84 | / | 0.39 | 14.03 | |
| IMERG-F | 0.61 | 0.07 | 481.19 | / | 0.96 | 32.77 | |
| Gauge | Month | / | / | / | 90.09 | / | / |
| TPHiPr | 0.92 | 0.87 | 35.89 | / | 0.40 | 14.03 | |
| IMERG-F | 0.73 | 0.39 | 77.22 | / | 0.86 | 32.77 |
| Significance Trend | Gauge (%) | IMERG-F (%) | TPHiPr (%) |
|---|---|---|---|
| Significant Decrease | 0.00 | 4.00 | 0.32 |
| Nonsignificant Decrease | 49.24 | 22.16 | 16.21 |
| Stable | 0.00 | 17.30 | 17.36 |
| Nonsignificant Increase | 40.03 | 40.15 | 45.37 |
| Significant Increase | 10.73 | 16.39 | 20.74 |
| Study Area | Precipitation Data Source | No. Station | Time Resolution | Spatial Resolution | Calculation Method | Spatial Method | Max. RE | Avg. RE | Reference |
|---|---|---|---|---|---|---|---|---|---|
| TP | Weather stations, ERA5 | 1787 | 1 min, hour | 0.25° | Standard | Proportional IDW interpolation correction | 13,947 | 290 | Chen et al. [27] |
| China | Weather stations | 2381 | Hourly | 1 km | Standard | Universal kriging | 3906 | 288 | Yue et al. [18] |
| Global | Precipitation stations | 3540 | Hourly and sub-hourly | 30 arc seconds | Standard | Gaussian process regression | 12,347 | 980 | Panagos et al. [17] |
| Global | CMORPH | 30 min | 8 km | Standard | Generic correction linear | 91,746 | 440 | Bezak et al. [22] | |
| TP | Weather stations | 131 | Daily | 1/30° | Experience | Ordinary kriging | 3521 | 490 | This study |
| TP | TPHiPr | Daily | 1/30° | Experience | 30,685 | 806 | This study | ||
| TP | IMERG-F | Daily | 0.1° | Experience | 18,203 | 787 | This study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, B.; Xie, Y.; Liu, B.; Liu, B. Rainfall Erosivity Mapping for Tibetan Plateau Using High-Resolution Temporal and Spatial Precipitation Datasets for the Third Pole. Remote Sens. 2023, 15, 5267. https://doi.org/10.3390/rs15225267
Yin B, Xie Y, Liu B, Liu B. Rainfall Erosivity Mapping for Tibetan Plateau Using High-Resolution Temporal and Spatial Precipitation Datasets for the Third Pole. Remote Sensing. 2023; 15(22):5267. https://doi.org/10.3390/rs15225267
Chicago/Turabian StyleYin, Bing, Yun Xie, Bing Liu, and Baoyuan Liu. 2023. "Rainfall Erosivity Mapping for Tibetan Plateau Using High-Resolution Temporal and Spatial Precipitation Datasets for the Third Pole" Remote Sensing 15, no. 22: 5267. https://doi.org/10.3390/rs15225267
APA StyleYin, B., Xie, Y., Liu, B., & Liu, B. (2023). Rainfall Erosivity Mapping for Tibetan Plateau Using High-Resolution Temporal and Spatial Precipitation Datasets for the Third Pole. Remote Sensing, 15(22), 5267. https://doi.org/10.3390/rs15225267





