Abstract
Realization and enhancement of detection techniques for multiple-input–multiple-output (MIMO) radar systems require polyphase code sequences with excellent orthogonality characteristics. Therefore, orthogonal waveform design is the key to realizing MIMO radar. Conventional orthogonal waveform design methods fail to ensure acceptable orthogonal characteristics by individually optimizing the autocorrelation sidelobe peak level and the cross-correlation sidelobe peak level. In this basis, the multi-objective Archimedes optimization algorithm (MOIAOA) is proposed for orthogonal waveform optimization while simultaneously minimizing the total autocorrelation sidelobe peak energy and total cross-correlation peak energy. A novel optimal individual selection method is proposed to select those individuals that best match the weight vectors and lead the evolution of these individuals to their respective neighborhoods. Then, new exploration and development phases are introduced to improve the algorithm’s ability to increase its convergence speed and accuracy. Subsequently, novel incentive functions are formulated based on distinct evolutionary phases, followed by the introduction of a novel environmental selection method aimed at comprehensively enhancing the algorithm’s convergence and distribution. Finally, a weight updating method based on the shape of the frontier surface is proposed to dynamically correct the shape of the overall frontier, further enhancing the overall distribution. The results of experiments on the orthogonal waveform design show that the multi-objective improved Archimedes optimization algorithm (MOIAOA) achieves superior orthogonality, yielding lower total autocorrelation sidelobe peak energy and total cross-correlation peak energy than three established methods.
1. Introduction
MIMO radar is an effective detection technique with good applications [1]. The application of MIMO technology and space–time coding to radar systems can provide excellent performance in target parameter estimation, detection and identification, and tracking [2,3,4]. It has already received attention from experts and scholars in the radar community. For example, De et al. considered the problem of implementing MIMO radar with diversity using space–time coding (STC) and performed a comprehensive performance evaluation to determine the best achievable performance for MIMO radar systems [5]. Jajamovich et al. elucidated the optimal firing strategy of a radar when detecting a target at an unknown location [6]. Deng et al. developed an innovative approach for waveform design that enables MIMO radars to satisfy the space-domain transmission beamforming limitations and the time-domain waveform orthogonality criteria [7]. Naghibi et al. investigated waveform design for target detection and classification in MIMO radar systems under two different scenarios [8]. Zhang et al. investigated the multi-parameter estimation of a dual-base EMVS-MIMO radar in the presence of coherent targets [9]. Wang et al. proposed a method that combines time-domain binomial design and frequency-domain binomial design through a pointwise minimum processor (PMP). Their results showed that this new method has an improved Doppler paravalvular suppression effect [10]. Zhu et al. combined the Golay complementary waveform radar echo with a proposed point-by-point threshold processor (PTP), and introduced an improved filtering process for the delay-Doppler map of the PTP. Their simulations verified that this method results in a delay-Doppler map virtually free of range sidelobes [11]. Compared with conventional phased array radar (PAR), MIMO radar is capable of independently emitting distinct waveforms from each transmitting antenna. The signals transmitted by each transmitting antenna should be orthogonal to one another in order to ensure independent and uninterrupted reception of scattered echoes from the target, as well as to achieve higher gain pointing, measurement accuracy, resolution, anti-jamming capability, and target recognition ability. However, achieving completely orthogonal signals is infeasible in practice. Therefore, the waveforms emitted by each antenna of the MIMO radar should be optimized and designed to approximate orthogonality. This process is known as orthogonal waveform optimization design, and is a key element of MIMO radar.
In the design of orthogonal waveform optimization, it is usually necessary to ensure that the waveform has good autocorrelation performance and cross-correlation performance, among others. This amounts to a very complex nonlinear multivariate optimization problem. Various methods have been proposed for orthogonal waveform optimization design. For instance, He et al. proposed computationally efficient round-robin algorithms for MIMO radar waveform synthesis that can be applied to design single-mode MIMO sequences [12]. Song et al. proposed a fast Fourier transform-based algorithm for designing sets of sequences with good correlation [13]. Li et al. introduced a novel, rapid, and efficient algorithm that can be applied to design single or multiple single-module waveforms with favorable autocorrelation, cross-correlation, or weighted correlation properties [14]. Wang et al. introduced a MIMO radar waveform design approach allowing for the design of spatial signals with low sidelobe level, low spatial cross-correlation level, and low time-varying characteristics, and demonstrated the efficacy of their proposed algorithm through a practical example [15]; this analysis showed that the convergence speed and convergence accuracy of these algorithms struggle to meet practical requirements. The problem of multi-objective optimization is usually characterized as a simple single-objective optimization problem relying on weighting or other methods. Although the optimization objectives are simple, they struggle to effectively choose between the weights of each objective, which is not conducive to the overall consideration.
Meta-heuristic algorithms have been applied to waveform design as well. Khan et al. employed an enhanced Fletcher–Reeves algorithm. The orthogonal waveform was designed with the autocorrelation sidelobe and the fourth power sum of the cross-correlation as the cost function [16]. Deng et al. introduced an enhanced statistical simulated annealing algorithm to minimize a single energy-based objective function for numerical optimization of orthogonal multiplexed code sets, achieving a relatively low autocorrelation sidelobe [17]. Lellouch et al. utilized a Genetic Algorithm (GA)-based waveform design framework to enhance the radar pulse characteristics, employing various metrics as optimization functions in both the frequency and time domains with the aim of discovering the optimal polyphase code set [18]. Zhang et al. proposed an optimal design method for MIMO radar orthogonal waveforms based on the ion motion algorithm, with the objective of minimizing both the weighted autocorrelation sidelobe and the cross-correlation sidelobe [19]. Ren et al. designed a modal algorithm based on greedy code searching (MA-GCS) for the design of orthogonal polyphase codes; their experiments showed that the code set designed by this algorithm has better autocorrelation and cross-correlation properties than other methods [20]. Liu et al. proposed integrating a statistical genetic algorithm (GA) with a conventional iterative code selection method; their experimental results indicated the effectiveness of this algorithm for designing MIMO radar multiple-phase signals [21]. Zeng et al. proposed a multi-objective microparticle swarm optimization algorithm to solve the design of polyphase coded signals. Their MO-MicPSO algorithm showed better optimization efficiency and less time consumption compared with particle swarm optimization or genetic algorithms [22]. Li et al. proposed an adaptive simulated annealing genetic hybrid algorithm to improve the orthogonality of the signals and Doppler tolerance of a MIMO radar system for the design of orthogonal polyphase codes. Their experimental results showed that this method is capable of obtaining polyphase codes with lower autocorrelation sidelobe peak and better Doppler tolerance [23]. Stringer et al. used three multi-objective evolutionary algorithms (MOEAs) applied to the issue of designing radar phase coding waveforms; their experimental results showed that NSGA-II-generated phase codes exhibit superior autocorrelation characteristics compared to those generated by SPEA2 or MOEA/D [24].
Waveform design based on meta-heuristic algorithms can achieve improved results due to its own intelligent properties. However, related studies have generally considered the minimization of the autocorrelation sidelobe value, the cross-correlation sidelobe value, the total autocorrelation sidelobe peak energy, or the total cross-correlation peak energy. While a few have selected the weighted sum of two or three of these as the objectives, very few orthogonal waveform design models can optimize more than one objective at the same time. In [22], multiple metrics describing autocorrelation and cross-correlation characteristics were simultaneously selected to construct a multi-objective orthogonal waveform optimization model. However, there is a high degree of redundancy between several of these objective functions; thus, as the number of objectives increases, the solution performance of multi-objective algorithms declines significantly. This situation leads to the codeword signal set ultimately not achieving a very high level of orthogonality. The total autocorrelation parametric peak energy and the total cross-correlation peak energy are the two most important factors affecting the optimal design of orthogonal waveforms. Therefore, in this paper we present a multi-objective MIMO radar quadrature waveform design model that simultaneously minimizes both objectives. Moreover, a new multi-objective Archimedes optimization algorithm is proposed for MIMO radar quadrature waveform design. The main innovations of this paper are as follows:
- A new optimal individual selection method is proposed to select the individuals that best match the weight vectors and lead the evolution of the individuals in their respective neighborhoods.
- New exploration and development phases are proposed to ensure that the algorithm has sufficient development capability for individuals, improving the convergence speed and convergence accuracy of the algorithm.
- A new environment selection method is proposed that evaluates different incentive functions according to whether or not they are boundary weight vectors, resulting in a better distributed algorithm;
- A weight updating method based on the shape of the frontier surface is proposed to dynamically correct the shape of the overall frontier according to the current concavity and convexity of the frontier surface and the gap in the function values between different objectives.
The experimental results of the proposed orthogonal waveform design show that MOIAOA obtains lower total autocorrelation sidelobe peak energy and total cross-correlation peak energy than three established methods while achieving better orthogonality.
2. MIMO Radar Quadrature Phase-Encoded Waveform Design
Assuming that the MIMO radar system has L transmitting antennas, each of which transmits a signal in an orthogonal polyphase code set each having length N, the signal can be expressed as a polyphase sequence
where denotes the pulse in the signal , a randomly selected one from the set . M is the number of phases selected for the pulse.
The set of L-row N-column codeword signals consisting of can be expressed as follows:
This codeword signals set contains the polyphase sequences, and its corresponding autocorrelation function and cross-correlation function are shown in Equations (1) and (2), respectively [17]:
where denotes the nonperiodic autocorrelation function; k denotes the discrete time; p denotes the pth signal; and indicates sub-pulse’s phase in signal p.
where indicates the nonperiodic cross correlation function, k denotes the discrete time, p and q denote the and signals, respectively, indicates the phase of the sub-pulse in signal p, and indicates the phase of the sub-pulse in signal q.
In general, waveforms with good orthogonality characteristics are more effective in matching the radar to the detection environment, which can significantly enhance MIMO radar systems’ ability to detect target signals; therefore, it is often desirable to ensure orthogonality in the design of polyphase sequences. However, because perfect orthogonal signals are not found in reality, it is important to ensure that either the autocorrelation sidelobe peak energy or the cross-correlation peak energy is minimized in the orthogonal design of polyphase sequences. In order to better achieve the orthogonality of polyphase sequences, in this paper we take the simultaneous minimization of the total autocorrelation sidelobe peak energy and total cross-correlation peak energy as the objective function, as shown in Equation (3).
3. MIMO Radar Orthogonal Waveform Optimization Method Based on Multi-Objective Archimedes Optimization Algorithm
As shown in Equation (3), the total autocorrelation sidelobe peak energy and the total cross-correlation peak energy should be minimized at the same time in the design of orthogonal waveforms for polyphase sequences. As a mathematical concept, this belongs to the class of multi-objective optimization problems. In this section, the newly proposed Archimedes optimization algorithm is considered the core evolution strategy to achieve better design results and the multi-objective evolutionary algorithm based on decomposition (MOEA/D) is used as the basic framework to propose the MOIAOA. Finally, a MIMO radar waveform optimization design method based on MOIAOA is established.
3.1. Archimedes Optimization Algorithm
The Archimedes principle of physics states that when an object is immersed in a stationary fluid, it experiences buoyancy, the direction of which is vertically upward and the size of which is equal to the weight of the fluid displaced by the object. Inspired by the above law, Fatma A. Hashim et al. proposed an Archimedes optimization algorithm [25]; its pseudo-code is shown in Algorithm 1.
| Algorithm 1: AOA |
| Input:population size , maximum number of iterations , Dimensionalities of optimizing problem , fixed constants , , , Output: The optimal solution and its fitness value
|
3.2. Multi-Objective Archimedes Optimization Algorithm
To further enhance the convergence and distribution of the multi-objective algorithm, in this section we use the Archimedes optimization algorithm as the main evolution algorithm, and the MOEA/D algorithm [26] as the basic framework to introduce the Multi-Objective Improved Archimedes Optimization Algorithm (MOIAOA). The pseudo-code is presented in Algorithm 2.
| Algorithm 2: MOIAOA |
|
3.2.1. A New Optimal Individual Selection Method
As shown in Algorithm 2, MOIAOA uses a decomposition mechanism for multi-objective processing. The multi-objective technique based on decomposition relies on weight vectors to break down a multi-objective problem into a series of individual single-objective subproblems associated with the weight vectors. The difference with single-objective optimization, which has only one optimal solution, is that each single-objective subproblem in the decomposition mechanism corresponds to an optimal value. Evidently, under the pull of the optimal position of each single-objective subproblem, the evolutionary direction and evolutionary information that correspond each individual are relatively biased. If we adopt the AOA method that relies solely on a globally optimal individual to drive the evolution of other individuals, then it is only possible to drive each individual closer to the optimal individual, and we cannot rapidly obtain the optimal solution of each single-objective subproblem. In general, non-dominated fronts do not mutate, the optimal solutions of subproblems associated with neighboring weights exhibit greater similarity, and the evolutionary directions of individuals in the corresponding weight vector neighborhoods align more closely. Therefore, in MOIAOA, instead of selecting an optimal individual to guide the evolution of other individuals as in AOA, each single-objective subproblem selects the optimal individual within the neighborhood of the corresponding weight.
The performance of individuals on single-objective subproblems primarily relies on Chebyshev aggregation function values and PBI values [26]. However, the Chebyshev aggregation function ignores the requirement of distribution in the overall evolution process and favors the pursuit of convergence. On the other hand, the PBI estimation method utilizes the projection distance to evaluate the convergence and the vertical distance to evaluate the distribution; in addition, it balances them with the value of ; however, is often a fixed value and cannot correspond to the performance of an individual on the corresponding sub-problem in real time. As a result, the requirements of the algorithms cannot be effectively balanced for convergence and distribution in the different evolution stages.
In summary, the computation of a combined incentive value is introduced to enhance the equilibrium between algorithmic convergence and distribution, as depicted in Equation (11). This value is derived from the Chebyshev aggregation function, vertical distance, and projection distance. Subsequently, the individual with the lowest combined incentive value is selected from the neighborhoods corresponding to each weight, then this individual is considered the optimal option within the spectrum of neighborhoods associated with that weight.
Here, j represents an individual within the neighborhood BBi corresponding to the current weight , the number of individuals within BBi is indicated in Equation (12), represents the min–max linear normalization operation, the calculation of is demonstrated in Equation (13), and , , and respectively represent the projection distance, aggregation function value, and vertical distance of individual j with respect to the current weight ; the specific calculation methods are shown in Equations (14)–(16). Finally, and represent penalty factors that are respectively detailed in Equations (17) and (18).
Here, represents rounding up and is the minimum neighborhood size, the value of which is generally 3 to achieve better results
Here, M indicates the number of objectives and indicates the ideal point consisting of the optimal values on each objective.
Here, , , , and are artificially set constants, typically set to 0.45, 1, 0.2, and 0.3, respectively, although these values can also be adjusted.
In summary, the proposed method, which relies on the combined incentive values of individuals to determine the optimal individual corresponding to each subproblem, offers the following advantages. First, Equation (12) changes the traditional form of the constant neighborhood size to make it change adaptively following the number of iterations. In the early phase of algorithmic evolution, a significant discrepancy arises in the extent of evolution among individuals, many of whom are far from the optimal frontier. A larger number of neighboring individuals provide considerable options, thereby rapidly shortening the evolutionary gap between them and other subproblems by taking advantage of the evolutionary information of better individuals in the neighboring subproblems. As a result, the speed of convergence to the optimal frontier is accelerated. In the later phase of the algorithm, all individuals approach the optimal frontier, reducing the number of individuals in the neighborhood. Thus, the optimal individual can be more accurately selected, precisely guiding the evolution of this neighborhood. This condition is conducive to the formation of excellent distributivity, and can effectively save computational resources as well. Second, in Equation (11), the composite incentive value of the individual is primarily affected by the normalized Chebyshev function when TF is less than 0.55, signifying the early phase of algorithmic evolution. The influence of the projection distance is larger than that of the vertical distance, and the parameter increases gradually with the number of iterations, increasing the influence of the vertical distance to an extent. However, it is inferior to the influence of the vertical distance. This method is conducive to ensuring the convergence of the algorithm and avoiding the disadvantage of an abundant individuals, which can result in poor distribution. The composite incentive value of the individual is primarily affected by the normalized Chebyshev function when the TF is more than 0.55, signifying the later phase of algorithmic evolution. The influence of the vertical distance is larger than that of the projection distance, and the parameter increases gradually with the number of iterations, reducing the influence of projection distance to a certain extent. Evidently, when the late evolutionary stage is already closer to the theoretically optimal nondominated frontier, a uniform distribution of nondominated solutions is achieved while ensuring that the frontier surface does not recede.
3.2.2. New Exploration Phase
As shown in Equation (6), each individual in the exploration strategy proposed by the AOA algorithm has an opportunity to learn from any individual within the population. In this way, the diversity of the population is maintained and global search is realized. However, the local search capability is insufficient, decreasing the convergence speed of the algorithm. Thus, the novel exploration strategy shown in Algorithm 3 is proposed to further balance the global and local search capabilities of the algorithm. The algorithm shown below involves an oppositional search mechanism, a simulated binary cross search mechanism, and a mutation search mechanism.
| Algorithm 3: New exploration phase framework |
|
Oppositional Search Mechanism
This section describes the oppositional search mechanism, as shown in Equation (19):
where denotes the opposing individuals of individual obtained according to Equation (20), is an individual selected randomly from its neighboring population , is a randomly selected individual different from obtained from the population, C1 and are the original definitions in the AOA algorithm, which represent the learning factor and the acceleration of , respectively, and F denotes the updating direction of each dimension, which is calculated according to Equation (21).
Here, and denote the upper and lower bounds of , respectively. The opposing individual of individual only performs the transformation shown in Equation (20) on the SD randomly selected dimensions of . In general, .
Simulated Binary Cross Search Mechanism
This section employs a simulated binary search mechanism similar to the one used [27], shown in Equation (22). To further improve population diversity, the parameter in [27] is improved in this section to further improve population diversity, as shown in Equation (23).
Here, , are two distinct individuals randomly selected from and F determines the update direction of each dimension, which is calculated according to Equation (21).
Here, denotes the generation of a random number with mean 1 and variance , while is the original value obtained from [27] as shown in Equation (24):
where mu = rand(1,Dim) denotes a vector of length Dim and magnitude between 0 and 1.
Mutation Search Mechanism
This section proposes a mutation search mechanism, shown in Equation (25), where each dimension of an individual is mutated with a probability of 1/Dim:
where denotes the polynomial variance factor [27], which is calculated as shown in Equation (26) and and represent the factors regulating the polynomial, Gaussian, and Cauchy variances, and are calculated according to Equations (27) and (28), respectively:
where u is a random number between [0,1] and denote artificial set numbers, which are generally set to 0.5.
In summary, the new exploration strategy proposed in this section has the following advantages. First, a comparison between Equations (23) and (24) indicates that the improved adds a normal random distribution to the original random exponential, which increases the range of perturbations of the difference vector in Equation (22). However, because the individuals and in Equation (22) are in a neighborhood and the evolutionary information gap between them is small, the improved can further expand the population diversity without destroying the evolutionary direction, satisfying the algorithm’s requirements for population diversity and convergence speed. Second, Equation (25) integrates polynomial mutation, Gaussian mutation, and Cauchy mutation. The proposed mutation approach provides more ways of generating individuals than a variant approach that simply applies one strategy, further increasing the ability of the algorithm to jump out of local optima. Throughout the early evolution phase, the algorithm focuses on finding as many good individuals as possible in a wider and larger search space; thus, larger mutation perturbations are required. However, and are set such that the algorithm’s mutation power in the early stage originates mainly from polynomial and Cauchy mutations. Polynomial mutations serve to prevent excessive individual deviations due to the large perturbation range of the Cauchy mutations, whereas the Cauchy mutations serve to enable a globally robust search of the solution space. As t increases, the algorithm enters a late evolution phase in which it focuses on fine search in the vicinity of excellent individuals, as it is at this point that excellent individuals can be obtained. At the same time, the adjustment factors and gradually increase and decrease, respectively; therefore, the fine mutation of the algorithm in the subsequent phase is mainly due to polynomial and Gaussian mutations, and the effect of Cauchy mutation gradually becomes negligible. The algorithm uses polynomial mutation to ensure that the evolutionary information of the original individual is not destroyed, while Gaussian mutation is used for fine search of the neighboring range. Third, the new exploration strategy incorporates an oppositional search mechanism, a simulated binary cross-search mechanism, and a mutation search mechanism. Among these, the oppositional search mechanism utilizes the ability of oppositional learning to produce individuals with greater randomness and broadness, thereby expanding the search solution space of individuals and greatly improving the global search capability. The simulated binary cross-search mechanism operates on two different individuals in the neighborhood, fully using the good genes carried by the neighboring individuals and improving the algorithm’s local search capability to a certain extent. The mutation search mechanism, on the contrary, allows the individual dimensions to mutate with relatively low probability, further increasing population diversity without significantly disrupting the evolutionary direction of the population. In addition, the probability of conducting the oppositional search is the highest, and is significantly higher than that of the simulated binary cross search and mutation search. This new exploration strategy is able to consider the local search on the basis of a better realization of the global search. Consequently, the possibility of the algorithm converging to the optimal frontier is greatly improved; in addition, the convergence speed of the algorithm is improved to a certain extent.
3.2.3. New Development Phase
The AOA algorithm enters the development phase during the later evolution stage. According to Equation (9), all individuals utilize the optimal individual as a reference vector and learn from the difference vector between the optimal individual and the current individual. This approach helps speeds up the evolution of the algorithm to the theoretical optimum. However, unlike single-objective optimization, in decomposition-based multi-objective optimization the subproblem corresponding to each weight vector is most likely associated with only one individual. Thus, the optimal individual is most likely the individual itself. Furthermore, directly following the evolutionary strategy of the original development phase for solving the multi-objective problem is impossible. Therefore, a new development strategy, shown in Algorithm 4, is proposed to address numerous multi-objective problems. The specific mechanisms of search mode 1 and search mode 2 are detailed below.
| Algorithm 4: New development phase framework |
|
Search Mode 1
Search mode 1 is shown in Equation (29):
where denotes an individual selected randomly from an intimate population with a probability of 0.8 or from a neighboring population with a probability of 0.2. The intimate population is the part of the neighboring population that is closest to the individuals and contains the number of individuals, as shown in Equation (30); the basis vectors are determined by Equation (31) in accordance with the probability.
Here, denotes the optimal individual corresponding to the current weight vector . When rand > 0.6, if , then should be operated against according to Equation (20); at this time, .
Search Mode 2
Search mode 2 is shown in Equation (32):
where and denote one different individual randomly selected from the neighboring population and intimate population , respectively.
In summary, the new development mechanism proposed in this section has the following advantages. First, the new development mechanism in this section only adapts the oppositional search mechanism in the exploration search in Section 3.2 to a new search mechanism that combines search modes 1 and 2. In a binary search strategy, one individual is obtained from the intimate population and the others remain unchanged; the population is already relatively close to the optimal frontier, following the early exploration phase. The development phase no longer uses the adversarial search mechanism of the exploration phase, which focuses on global search; instead, it uses search modes 1 and 2, which focus on exploring the vicinity of or the neighborhood of the optimal individual corresponding to each subproblem. The binary and mutation searches ensure the diversity of the population, thereby improving the algorithm’s power to converge while providing more candidate space for search modes 1 and 2. Evidently, the new development mechanism can greatly enhance the exploration of the algorithm near the optimal frontier as well as the speed of convergence to the optimal frontier. Second, search modes 1 and 2 are applied in the early and late development phases, respectively. A comparison between search modes 1 and 2 indicates that the difference between them is mainly reflected in the selection of the basis vectors and difference vectors. In selecting the basis vectors, the original approach of using the optimal individuals in AOA is retained in search mode 1, whereas the use of individuals and the centers of the individuals and the optimal individuals as basis vectors is introduced. Search mode 1 enhances the direct search in the vicinity of the optimal individual and further improves the speed of exploring out the optimal frontier. Conversely, in search mode 2 the base vector is selected as either the individual itself or the midpoint between the optimal individual and its oppositional counterpart. This preference amplifies the search within its immediate vicinity. Evidently, the shift from search mode 1 to search mode 2 aligns with the algorithm’s evolving behavior, as the obtained front surface gradually approaches the optimal front. This transition facilitates swift convergence toward the optimal front in proximity to the optimal front itself. Subsequently, the algorithm progressively refines the fine search towards the theoretical optimal frontier. When selecting difference vectors, in search mode 1, individuals communicate primarily with themselves; the selection process favors individuals from the intimate population with high probability and individuals from the neighboring population are selected randomly with low probability. A large number of full exchanges between individuals and intimate individuals plays a role in guiding them closer to the current optimal frontier, considering that individuals within intimate populations typically possess superior evolutionary insights. Furthermore, limited interaction and learning with individuals from neighboring populations extends the scope of search, contributing to an increased exploration range. This approach aids in generating new evolutionary traits, thereby mitigating instances of evolutionary stagnation to a certain extent. The optimal frontier obtained for the period corresponding to search mode 2 has been largely formed; at this point, two individuals are randomly selected directly from the intimate population to communicate with each other. Communication and learning between them makes for a finer search in their own neighborhood, considering that the evolutionary information between an individual and the individuals in its intimate neighborhood is already similar. This condition better facilitates the achievement of a balanced distribution.
3.2.4. A New Approach to Environmental Selection
Numerous experiments and sources in the literature confirm that in terms of convergence the performance of MOEA/D is generally good. However, there is room for improvement in terms of its distributivity, especially in the boundary part of the frontier surface. The algorithm should focus on improving convergence, considering that the frontier obtained by the multi-objective algorithm in the early phase of evolution is generally far away from the theoretical frontier. In the subsequent stage of evolution, it is relatively close to the theoretical frontier, and the algorithm should focus on pursuing distributivity. Accordingly, this section describes improvements to the environment selection method of the MOEA/D mechanism [26]. The new environment selection approach is proposed according to the different requirements of the various evolutionary phases, as follows.
An environmental selection approach is applied to the early evolutionary phase.
In addition to the Chebyshev aggregation function value, which can reflect the convergence effect of the individual, the projection distance from the individual to the weight vector can allow us to directly consider the convergence of the current frontier. Moreover, a smaller projection distance indicates that the current individual is closer to the theoretical frontier. In this view, to further improve the convergence speed of the algorithm in the early phase of evolution, when TF < 0.5, the projection distance is added to the Chebyshev aggregation function, as shown in Equation (33):
where a is an artificial setting of the constant; generally, 10 can achieve better results, though this setting can be modified according to the specific problem at hand.
An environmental selection approach is applied to the subsequent evolutionary phase.
An intensive study revealed the following main reasons for the poor distributivity of the MOEA/D mechanism. The iterative individuals to which the weight vectors belong are selected through a comparison of the Chebyshev aggregation function values among individuals within the neighborhood. Multiple neighboring weight vectors can select the same individual within the neighborhood for the next generation of evolution. This condition inevitably leads to the number of intersections between the weight vector and the theoretical frontier being less than the number of weight vectors. This finding leads to discontinuities at certain locations, resulting in poor distributivity. However, individuals are associated with weight vectors by angle, and the associated individuals of neighboring weight vectors are different from each other compared with individuals of neighboring domains. If the weight vectors are used to select individuals from among their own associated individuals to participate in the next evolution, then the probability of neighboring weight vectors selecting the same individual must be much lower than the MOEA/D mechanism. Using the weight vector can enhance distributivity more effectively than the MOEA/D decomposition mechanism by selecting suitable individuals from among the associated individuals. However, a large number of experiments have confirmed that boundary weight vectors generally exhibit worse distributivity than non-boundary weight vectors that simply use the Chebyshev aggregation function to select superior individuals from among the associated individuals. A more comprehensive analysis uncovers that this phenomenon stems from the proximity of boundary weights to 0 along at least one dimension. For the optimal individual associated with such a weight vector, the corresponding fitness value is also inevitably close to 0 in the dimension where the weight vector approaches 0. As a result, computation of the TCH value according to Equation (14) inevitably yields an exceedingly large result. The best individual that most closely matches the boundary weights cannot be selected due to the nonnadaptability of the boundary individual during TCH computation. This condition results in extremely poor distributivity in the vicinity of the boundary weight vectors.
In summary, in order to effectively improve the distributivity, different environment selection mechanisms should be adopted for boundary weight vectors and non-boundary weight vectors. In the later evolutionary phase, when TF ⩾ 0.5, a new environment selection method based on boundary separation is proposed with the following steps.
Step 1: The old and new populations are merged, the cosine angle of each individual with each weight vector is calculated, each individual is associated with the weight vector with the smallest angle, and the weight vectors of the associated individuals and the unassociated individuals are identified.
Step 2: For the weight vector with associated individuals, the corresponding set of associated individuals, which is , is determined. Whether the weight vector is a boundary weight according to Equation (34) is identified. If it is a boundary weight with all its associated individuals, then their incentive values are calculated according to Equation (35); otherwise, Equation (36) is used. Then, the individual with the smallest incentive value is selected from among the individuals associated with each weight vector to belong to the weight vector that participates in the next evolution.
Here, denotes the number of dimensions less than in each dimension of the weight vector and M represents the number of objectives. If Equation (34) is satisfied, then it is considered a boundary weight.
Here, c is an artificially set constant and denotes the angle value between the weight vector and its corresponding associated individual.
Here, b is an artificially set constant.
Step 3: For the weight vectors without associated individuals, the incentive values of all individuals are calculated according to Equation (35) and the individual with the smallest incentive value is selected to participate in the next evolution.
In summary, the environment selection method based on boundary separation applied to subsequent evolution phases possesses the following advantages. First, for the non-boundary weight vectors, the original Chebyshev aggregation function, which is part of the decomposition mechanism, continues to be retained in the computation of the excitation function, as shown in Equation (36). This condition ensures the convergence of the algorithm and avoids the backwardness of the acquired frontier due to the pursuit of distributivity. On this basis, the vertical distance reflecting the strengths and weaknesses of individual distributivity is added and the influence of distributivity on individual assessment increases with the number of iterations. This finding is conducive to the realization of uniform distribution. Second, as shown in Equation (35), the incentive function contains the angle, vertical distance, and projection distance, avoiding the drawback of the boundary weight vector being unable to consider distributivity due to the calculation of the Chebyshev aggregation function. The vertical distance and angle are the most intuitive data reflecting the distributivity of the algorithm. Thus, as the number of iterations increases, the influence of the vertical distance and angle on the excitation function is gradually added. This condition is conducive to the realization of a uniform distribution. In addition, if the projection distance differs from the angle and vertical distance, the algorithm approaches the PF surface anyway. At the same time, the effect of using the projection distance is remarkable in that no loss of convergence occurs due to taking these measures to maintain distributivity.
3.2.5. Weight Update Method Based on the Shape of the Frontier Surface
Currently, multi-objective algorithms based on decomposition commonly use the two-layer generation scheme proposed in NSGAIII to generate the weight vectors [27]. If the theoretical front is in the form of a hyperplane, then this approach ensures that the weight vectors are evenly distributed on it. However, when the frontier surface shows a convex shape, the distribution state of the weight vectors is more dispersed in the convex region. Meanwhile, the distribution state of the weight vectors becomes concentrated when the frontier surface shows a concave shape. The best practical optimal frontier obtained by multi-objective methods based on decomposition is the intersection of the theoretical frontier and the weight vectors. Thus, when the front surface is a non-hyperplane, the solution set distribution of the multi-objective methods based on decomposition is not uniform.
As shown in Figure 1, the normalized fitness value of each dimension of the point on the hyperplane is equal to 1, using the hyperplane where the black point is located as a criterion. For points within the convex region, where the red dot is located, the normalized fitness values across various dimensions exhibit a pattern where values are larger as they move closer to the central region and conversely smaller as they approach the boundary areas. These values fall within the range of 1 to 2. For points within the concave region, where the blue dot is located, the normalized fitness values across various dimensions exhibit a pattern where values are smaller as they move closer to the central region and conversely larger as they approach the boundary areas. These values fall within the range of 0 to 1. Therefore, the concave–convex character of the frontier surface can be discriminated using the individual’s normalized fitness value versus 1. Considerable experimental studies have found that, for , the weight vector forms a uniformly distributed convex weight vector when a < 1. Conversely, when a > 1, form a uniformly distributed concave weight vector. When generating uniformly distributed concave–convex weight vectors, if the current surface exhibits a convex shape then the dispersion of weight vectors within the convex region is mitigated. Similarly, if the current surface takes on a concave shape, then the concentration of weight vector distribution within the concave region is improved.

Figure 1.
Different types of nondominated frontier surfaces.
On this basis, the following strategy for adjusting the weight vector using the shape of the frontier surface is introduced:
where a is an artificially set constant, which is usually set to 0.05 for convex fronts and −0.4 for concave fronts, denotes the scale size of the ith individual, and denotes the normalized ratio between the dimensions of each individual in the currently obtained frontier, which is calculated according to Equation (38):
where represents the ideal fitness value for all individuals. The fitness values in Equation (37) are not used; rather, the normalized fitness values are used in order to avoid bias due to the large differences between the values of each objective function. This bias can lead to an overall front surface that leans toward the side with relatively small objective function values, subsequently impacting the shape of the front surface. Consequently, a front surface with a hyperplane-like shape cannot be achieved, which impacts the overall distribution.
In summary, this section presents a weight update method based on the shape of frontier surface, which is outlined in Algorithm 5.
| Algorithm 5: Weight update method based on the shape of the frontier surface |
|
3.2.6. Algorithm Complexity Analysis
In this analysis, the population size is N, the maximum number of iterations is T, the problem dimension is D, and the number of neighbors is NI. The MOIAOA algorithm mainly consists of the new exploration phase, the new development phase, and the new approach to environmental selection. The worst time complexity of each phase of the MOIAOA algorithm in a single run is analyzed as follows: in the new exploration phase, at most N times (19) or N × D times (22) or (25) needs to be computed; thus, the worst time complexity of this phase is O (N × D). In the new development phase, at most N times (29) or N × D times (22) or (25) needs to be computed; thus, the worst time complexity of this phase is O (N × D). In the new approach to environmental selection phase, at most N × NI times (33) needs to be computed; thus, the worst time complexity of this phase is O (N × NI).
Therefore, the worst time complexity required for a single run of MOIAIA is O (N × D) + O (N × D) + O (N × NI) = O (N × (2D + NI)).
3.3. MIMO Radar Quadrature Waveform Optimization Based on the MOIAOA Algorithm
The MOIAOA algorithm proposed in Section 3.2 was used as the main optimization method to optimize the mathematical model of the MIMO radar quadrature waveform design optimization shown in Equation (3). A MIMO radar quadrature waveform design optimization algorithm based on MOIAOA was formed; its operation steps are specified as follows.
Step 1: Initialization
Initialization includes parameter initialization and population initialization, as follows.
Step 1.1: Parameter Initialization
Initialize the following parameters: the number of signals in the signal set is L, the length of the signals is N, the number of selectable pulse phases is M, the number of populations is set to , and the maximum number of iterations is .
Step 1.2: Population Initialization
In order to satisfy the criteria of polyphase sequence coding, each individual in the population is expanded into an L × N matrix with M-binary encoding. Then, the elements of each individual are randomly selected from while corresponding to the polyphase code phase .
Step 2: Single Evolution of the MOIAOA Algorithm
Step 2.1: The fitness value corresponding to Equation (3) is alculated separately for each individual
Step 2.2: The migration operator is calculated; if TF < 0.5, then each individual is individually updated according to the new exploration phase from Section 3.2.2 to produce a new population (newpop). Otherwise, each individual is individually updated according to the new exploitation phase from Section 3.2.3 to produce a new population.
Step 2.3: The environmental selection framework outlined in Section 3.2.4 is executed to choose the next generation of evolved individuals, denoted as X.
Step 2.4: The weight update strategy from Section 3.2.5 is performed.
Step 2.5: The individual attributes are updated according to Equation (10).
Step 2.6: The optimal individual evaluation method from Section 3.2.1 is performed to identify the optimal individual corresponding to each weight in the iteration thus far along with its corresponding , , and .
Step 3: Determine Whether Further Iterations are Needed
If the maximum number of iterations has been reached, the Pareto optimal frontier is output; otherwise, the process returns to Step 2 and evolution continues.
4. Experimental Results and Analysis
In order to thoroughly validate the performance of the MOIAOA algorithm, in this section we describe our experiments in terms of the following two aspects. First, the MOIAOA algorithm is compared with three high-performance multi-objective evolutionary algorithms: the MOEA/D algorithm based on differential evolution (MOEA/D-DE) [28]; a novel multi-objective particle swarm algorithm based on decomposition (MPSO-D) [29]; and a vector angle-based evolutionary algorithm for unconstrained multi-objective optimization [30]. Our comparative experiments were conducted on a multi-objective test dataset. Second, the MOIAOA algorithm is compared with orthogonal waveform optimization methods constructed using the three algorithms mentioned above. These comparative experiments were conducted on orthogonal waveform design. All simulations were conducted on a computer with an i5-8265U CPU running the Windows 10 operating system. MATLAB R2021a was used for programming and running the experiments.
For the sake of fairness in conducting the comparative experiments on the multi-objective test dataset, all algorithms had a maximum of 1000 iterations, and the initial population sizes were as indicated in Table 1. The neighborhood size for MOIAOA was calculated as , while for the other algorithms the neighborhood size was calculated as . In the orthogonal waveform design comparative experiments, all algorithms had a maximum of 500 iterations and an initial population size of 50, and the calculation of the neighborhood size followed the same method as described for the previous experiments. The parameters for each algorithm were set to be the same as described in the original references, as shown in Table 2.

Table 1.
Settings for population size.

Table 2.
Parameter settings for each algorithm.
4.1. Testing and Analysis of Multi-Objective Experiments
In this section, the most commonly used performance evaluation functions, HV and IGD, were selected to evaluate the performance of the algorithms. To prevent the adverse effects on algorithm evaluation of serendipity associated with a single algorithm run, each algorithm was independently executed 30 times for each test problem. The results of HV and IGD for each algorithm on the WFG test dataset [31] with different numbers of objectives (M = 3, 5, 8, 10, and 15) are summarized in Table 3 and Table 4, respectively. In the tables, the values outside and inside the parentheses represent the mean and standard deviations, respectively, of HV and IGD obtained from 30 experiments. The bolded values indicate that the corresponding algorithm achieved the best performance on the test functions with that number of objectives.

Table 3.
The HV results for each algorithm on the WFG test functions.

Table 4.
The IGD results for each algorithm on the WFG test functions.
From Table 3 and Table 4, it can be seen that although the MOIAOA algorithm exhibits slightly lower performance in terms of the HV metric compared to the MOEA/D-DE algorithm on the WFG3 test function with 10 and 15 objectives, in terms of the IGD metric the MOIAOA algorithm exhibits significant advantages over the other three comparison algorithms on the WFG3-9 test functions with 3, 5, 8, and 10 objectives. However, it performs slightly worse than the VaEa algorithm on the WFG1 and WFG2 test functions with 15 objectives. Although MOIAOA did not significantly outperform the comparison algorithms for certain target numbers of test functions, it significantly outperformed the comparison algorithms on most of the objectives of the test function.
4.2. Testing and Analysis of Orthogonal Waveform Design Experiments
Figure 2 shows the results of the closest average effect obtained by each multi-objective algorithm in 30 independent runs when the number of signals L is 4, the length of signals N is 36, and the number of optional phases M is 4. As can be seen from Figure 2, the Pareto frontiers obtained by our proposed algorithm are significantly better than those obtained by the comparison algorithms in terms of both convergence and distribution, and the results in terms of VaEa are slightly better than those of MOEA/D-DE and MPSOD. In other words, under the same autocorrelation side flap peak energy, the total cross-correlation peak energy value obtained by our proposed MIMO radar orthogonal waveform optimization method based on the MOIAOA algorithm is clearly lower than those of the other three methods. Meanwhile, under the same crosscorrelation peak energy, the autocorrelation sidelobe peak energy value obtained by our proposed MIMO radar orthogonal waveform optimization method based on the MOIAOA algorithm is clearly lower than those of the other three methods.
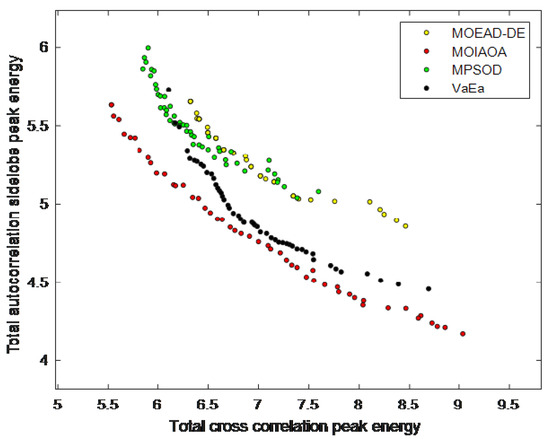
Figure 2.
Non-dominated frontiers obtained from four multi-objective algorithms.
Considering that the VaEa results are slightly better than those of MOEA/D-DE and MPSOD, only MOIAOA and VaEa are compared below. The autocorrelation and cross-correlation outcomes of the optimal four-phase code attained using the two algorithms for L = 4 and N = 36 are depicted in Figure 3 and Figure 4, respectively. As can be seen in Figure 3 and Figure 4, the MOIAOA algorithm achieves lower autocorrelation sidelobe values than the VaEa algorithm, with comparable values for the cross-correlation sidelobe.
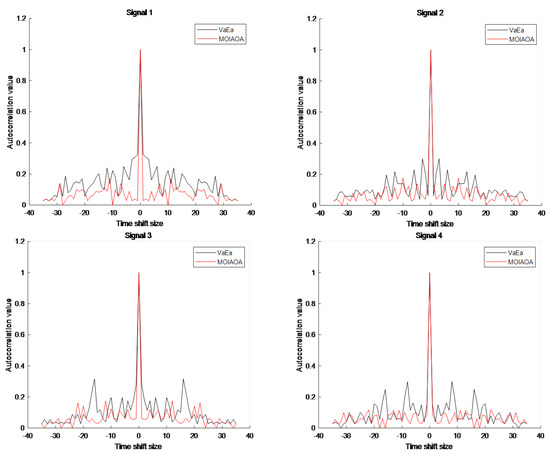
Figure 3.
Comparison of autocorrelation results for MOIAOA and VaEa when L = 4 and N = 36.

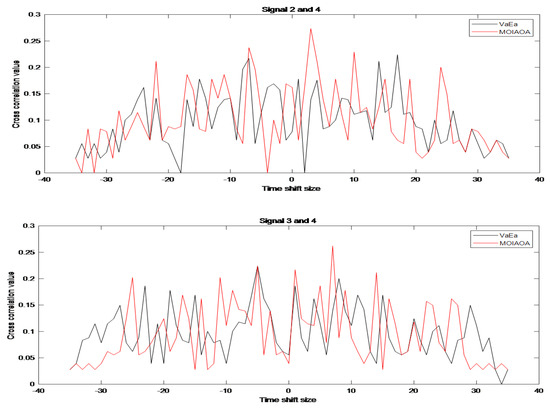
Figure 4.
Comparison of cross-correlation results for MOIAOA and VaEa when L = 4 and N = 36.
In order to further demonstrate the performance of MOIAOA, we experimented with sets of signals of different scale sizes. Figure 5 shows the autocorrelation and cross-correlation curves of the optimal four-phase code obtained by MOIAOA when L = 3 and N = 128. From Figure 5, it is clear that the optimized signal set obtained using the introduced multi-objective optimization algorithm performs well in terms of both the autocorrelation and cross-correlation aspects.
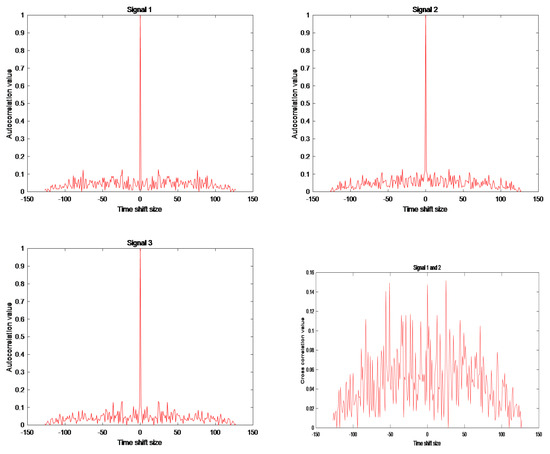
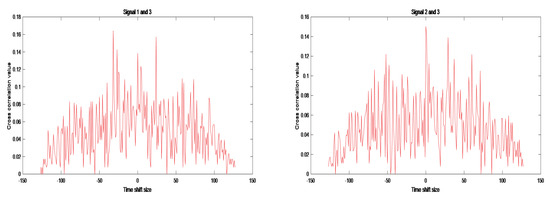
Figure 5.
Autocorrelation and cross-correlation results for MOIAOA when L = 3 and N = 128.
5. Conclusions
In this paper, we have proposed an improved MOIAOA for orthogonal waveform design optimization to obtain orthogonal polyphase codes. First, a novel optimal individual selection method is proposed to select individuals that best match the weight vectors and lead to the evolution of the individuals in their respective neighborhoods. Then, a new exploration phase and development phase are proposed to enable the algorithm to have sufficient development capability for individuals and to improve the convergence speed and accuracy of the algorithm. Subsequently, a novel environment selection method is proposed to evaluate different incentive functions according to whether or not they are boundary weight vectors in order to ultimately obtain a well-distributed algorithm. Finally, a weight update method based on the shape of frontier surface is proposed to dynamically correct the shape of the overall frontier according to the current concavity and convexity of the frontier surface and the gap of the function values between different objectives. To showcase the competitiveness of the proposed algorithm, we conducted a thorough experimental comparison with three state-of-the-art algorithms: MOEA/D-DE, MPSO-D, and VaEa. Drawing upon comprehensive data analysis, the waveforms engineered by MOIAOA possess heightened ability to capture the frontier facets of the multi-objective optimization problem addressed in this study in comparison to those fashioned by the state-of-the-art algorithms. In addition, the waveforms constructed by MOIAOA exhibit excellent autocorrelation and cross-correlation properties.
Author Contributions
Y.W. was responsible for data processing and interpretation, supervised the work, and revised the manuscript; M.C. designed the work and wrote the manuscript; Y.W. and M.C. were involved in discussion and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Project of Scientific and Technological Innovation Development of Jilin, China under Grant 20210103090.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wen, F.; Ren, D.; Zhang, X. Fast Localizing for Anonymous UAVs Oriented Toward Polarized Massive MIMO Systems. IEEE Internet Things J. 2023, 1. [Google Scholar] [CrossRef]
- Zhang, Z.; Wen, F.; Shi, J. 2D-DOA estimation for coherent signals via a polarized uniform rectangular array. IEEE Signal Process. Lett. 2023, 30, 893–897. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Y.; Wen, F.; He, J.; Truong, K.T. EMVS-MIMO radar with sparse Rx geometry: Tensor modeling and 2D direction finding. IEEE Trans. Aerosp. Electron. Syst. 2023, 1–14. [Google Scholar] [CrossRef]
- Wen, F.; Gui, G.; Gacanin, H. Compressive sampling framework for 2D-DOA and polarization estimation in mmWave polarized massive MIMO systems. IEEE Trans. Wirel. Commun. 2023, 22, 3071–3083. [Google Scholar] [CrossRef]
- De Maio, A.; Lops, M. Design principles of MIMO radar detectors. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 886–898. [Google Scholar] [CrossRef]
- Jajamovich, G.H.; Lops, M.; Wang, X.D. Space-time coding for MIMO radar detection and ranging. IEEE Trans. Signal Process 2010, 58, 6195–6206. [Google Scholar] [CrossRef]
- Deng, H.; Geng, Z.; Himed, B. MIMO radar waveform design for transmit beamforming and orthogonality. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1421–1433. [Google Scholar] [CrossRef]
- Naghibi, T.; Namvar, M.; Behnia, F. Optimal and robust waveform design for MIMO radars in the presence of clutter. Signal Process. 2010, 90, 1103–1117. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Wen, F.N.; Shi, J.P. PARAFAC estimators for coherent targets in EMVS-MIMO radar with arbitrary geometry. Remote Sens. 2022, 14, 2905. [Google Scholar] [CrossRef]
- Wang, J.H.; Fan, P.Z.; Yang, Y.; Guan, Y.L. Range/Doppler Sidelobe Suppression in Moving Target Detection Based on Time-Frequency Binomial Design. In Proceedings of the 2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Istanbul, Turkey, 8–11 September 2019; pp. 1–5. [Google Scholar]
- Zhu, J.H.; Song, Y.P.; Jiang, N.; Xie, Z.; Fan, C.Y.; Huang, X.T. Enhanced Doppler Resolution and Sidelobe Suppression Performance for Golay Complementary Waveforms. Remote Sens. 2023, 15, 2452. [Google Scholar] [CrossRef]
- He, H.; Stoica, P.; Li, J. Designing unimodular sequence sets with good correlations—Including an application to MIMO radar. IEEE Trans. Signal Process. 2009, 57, 4391–4405. [Google Scholar] [CrossRef]
- Song, J.; Babu, P.; Palomar, D.P. Sequence set design with good correlation properties via majorization-minimization. IEEE Trans. Signal Process. 2016, 64, 2866–2879. [Google Scholar] [CrossRef]
- Li, Y.; Vorobyov, S.A. Fast algorithms for designing unimodular waveform(s) with good correlation properties. IEEE Trans. Signal Process. 2018, 66, 1197–1212. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H.; Yan, J.; Hu, L.; Bao, Z. Waveform design with low sidelobe and low correlation properties for MIMO radar. In Proceedings of the 2011 IEEE CIE International Conference on Radar, Chengdu, China, 24–27 October 2011; pp. 564–567. [Google Scholar]
- Khan, H.A.; Zhang, Y.; Ji, C.; Stevens, C.J.; Edwards, D.J.; O’Brien, D. Optimizing polyphase sequences for orthogonal netted radar. IEEE Signal Process. Lett. 2006, 13, 589–592. [Google Scholar] [CrossRef]
- Deng, H. Polyphase code design for orthogonal netted radar systems. IEEE Trans. Signal Process. 2004, 52, 3126–3135. [Google Scholar] [CrossRef]
- Lellouch, G.; Mishra, A.K.; Inggs, M. Design of OFDM radar pulses using genetic algorithm based techniques. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1953–1966. [Google Scholar] [CrossRef]
- Zhang, L.; Wen, F.Q. A novel MIMO radar orthogonal waveform design algorithm based on intelligent ions motion. Remote Sens. 2021, 13, 1968. [Google Scholar] [CrossRef]
- Ren, W.; Zhang, H.; Liu, Q.; Yang, Y. Greedy Code Search Based Memetic Algorithm for the Design of Orthogonal Polyphase Code Sets. IEEE Access 2019, 7, 13561–13576. [Google Scholar] [CrossRef]
- Liu, B.; He, Z.S.; Zeng, J.K.; Liu, B.Y. Polyphase orthogonal code design for MIMO radar systems. Proc. Int. Conf. Radar. 2006, 1–4. [Google Scholar]
- Zeng, X.; Zhang, Y.; Guo, Y. Polyphase coded signal design for MIMO radar using MO-MicPSO. J. Syst. Eng. Electron. 2011, 22, 381–386. [Google Scholar] [CrossRef]
- Li, Y.R.; Hu, H.Y. Orthogonal poly-phase code design based on adaptive mix algorithm in MIMO radar. In Proceedings of the 2015 International Conference on Automation, Mechanical Control and Computational Engineering, Changsha, China, 24–25 October 2015; Atlantis Press: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Stringer, J.; Lamont, G.; Akers, G. Radar phase-coded waveform design using MOEAs. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Hashim, F.A.; Hussain, K.; Houssein, E.H. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 2021, 51, 1531–1551. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multi-objective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2018, 66, 577–601. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q.F. Multi-objective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]
- Dai, C.; Wang, Y.P.; Ye, M. A new multi-objective particle swarm optimization algorithm based on decomposition. Inf. Sci. 2015, 325, 541–557. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhou, Y.; Li, M.; Chen, Z. A vector angle-based evolutionary algorithm for unconstrained many-objective optimization. IEEE Trans. Evol. Comput. 2017, 21, 131–152. [Google Scholar] [CrossRef]
- Huband, S.; Hingston, P.; Barone, L. A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans. Evol. Comput. 2006, 10, 477–506. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).