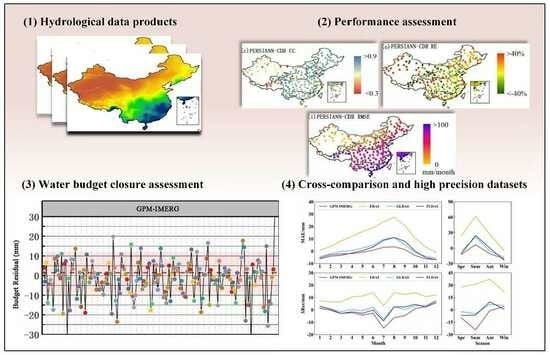
Assessing the Water Budget Closure Accuracy of Satellite/Reanalysis-Based Hydrological Data Products over Mainland China
Abstract
:1. Introduction
2. Study Area, Datasets, and Methodology
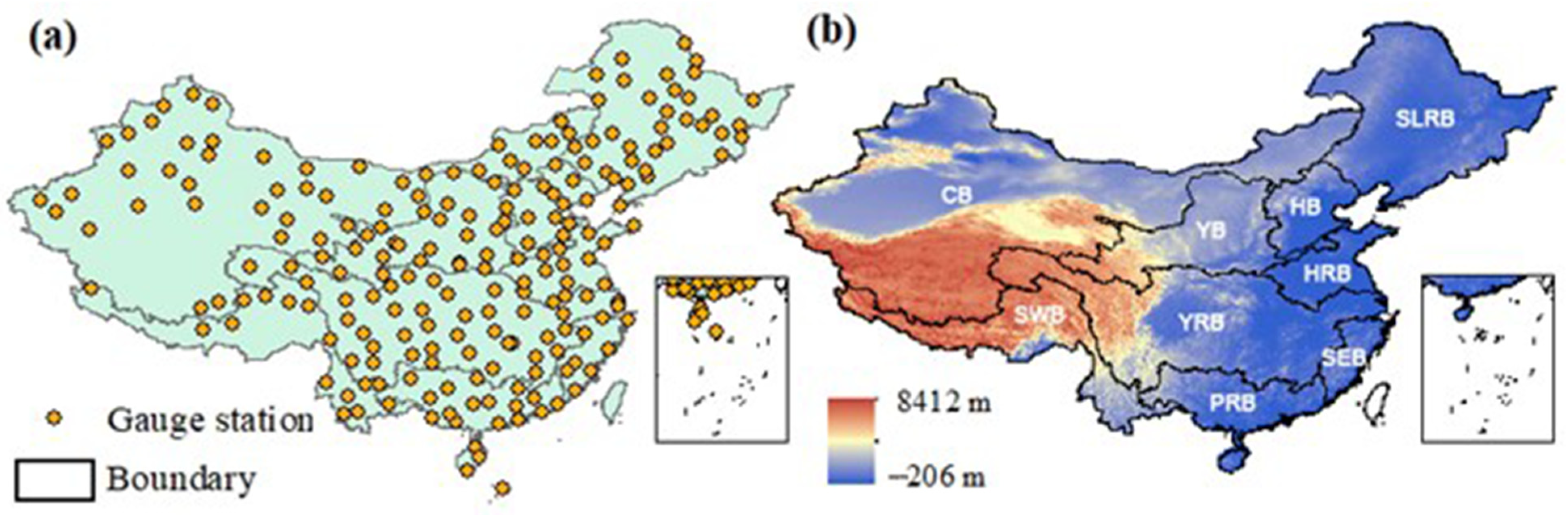
2.1. Study Area
2.2. Datasets
2.2.1. Rain Gauge Observations
2.2.2. SRP Products
2.2.3. Datasets of Additional Budget Components
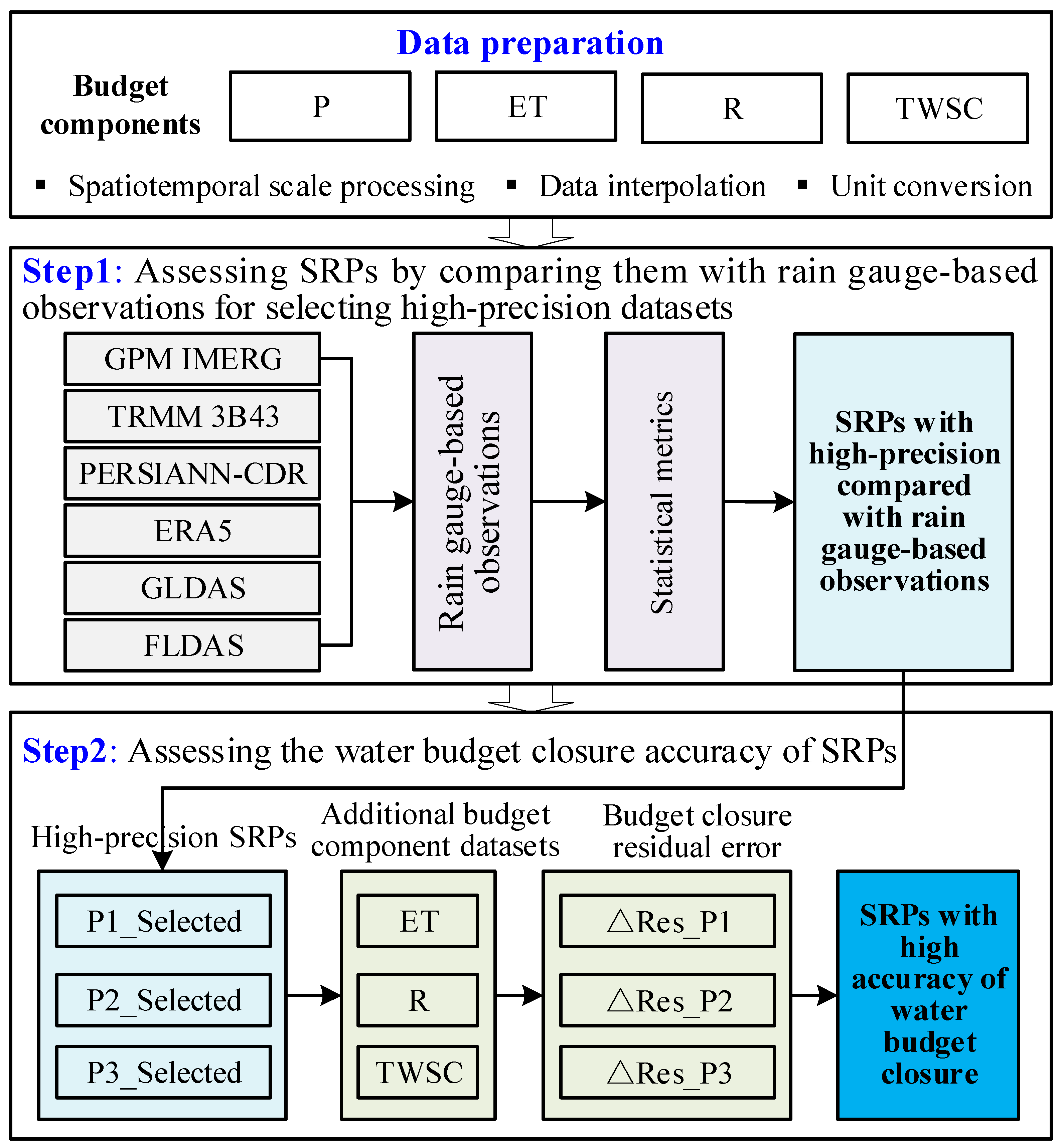
2.3. Methodology
2.3.1. Data Preparation and Statistical Metrics
2.3.2. Water Budget Closure Assessment
3. Results
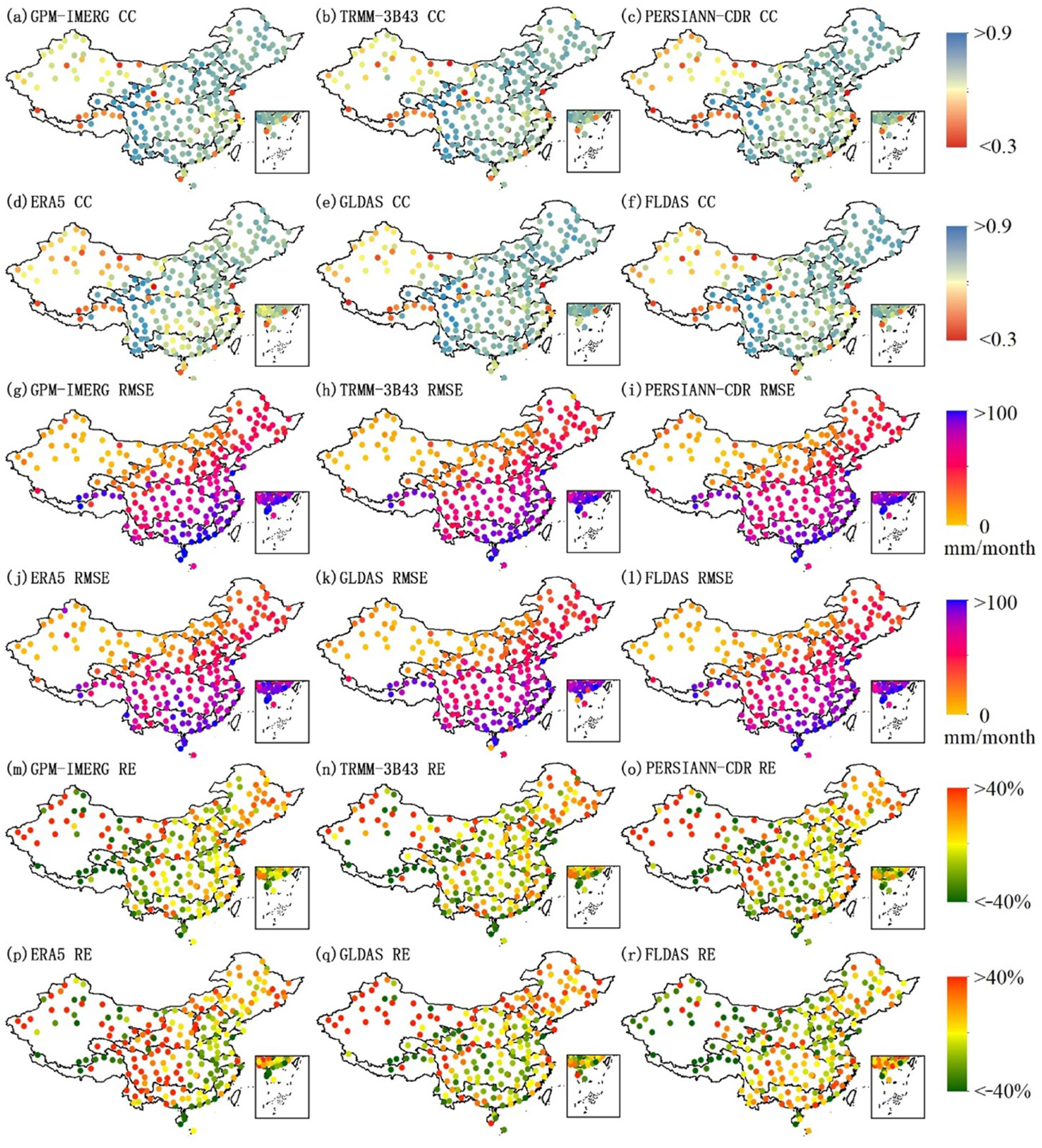
3.1. Assessment of SRP Products Using Statistic Metrics
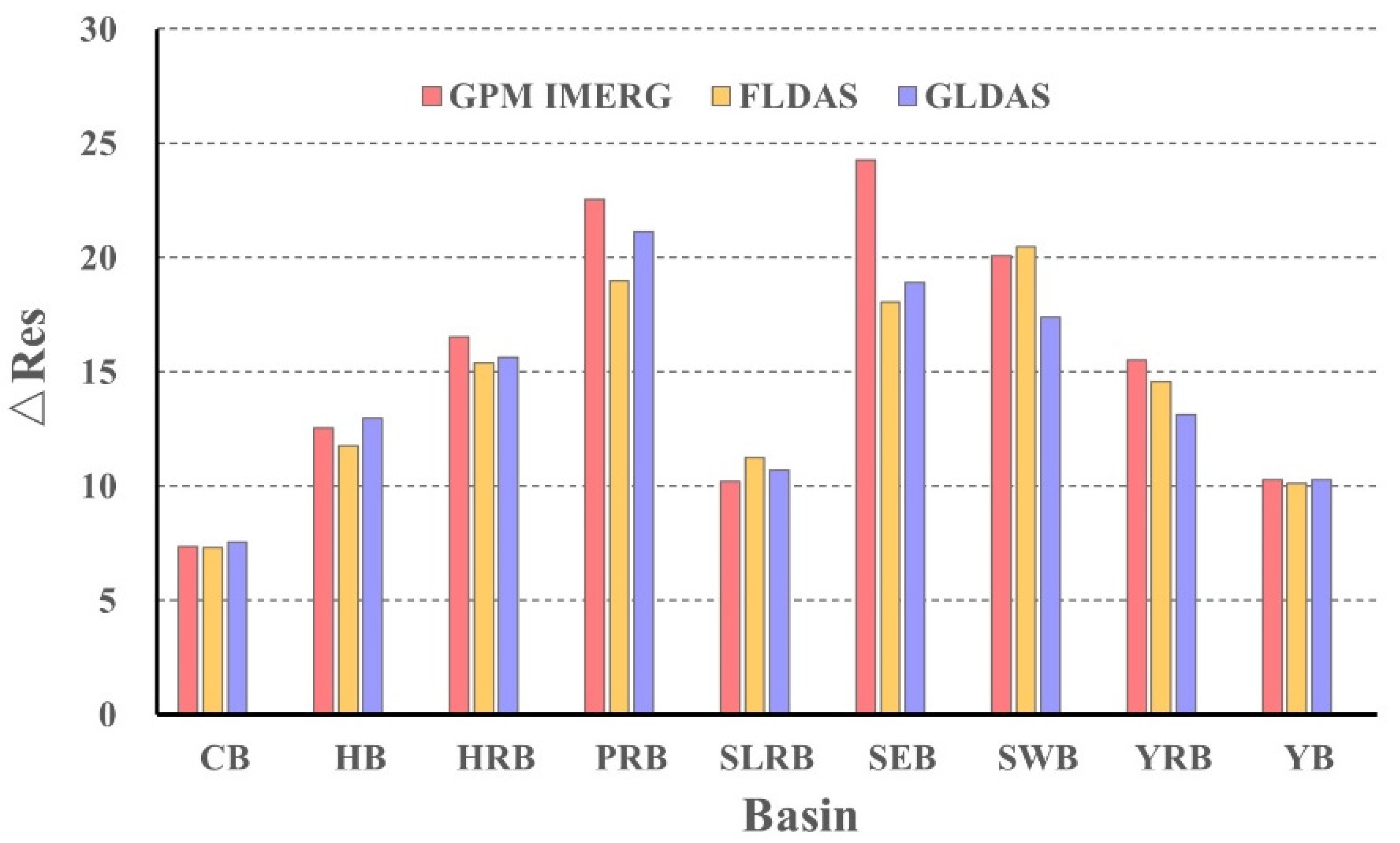
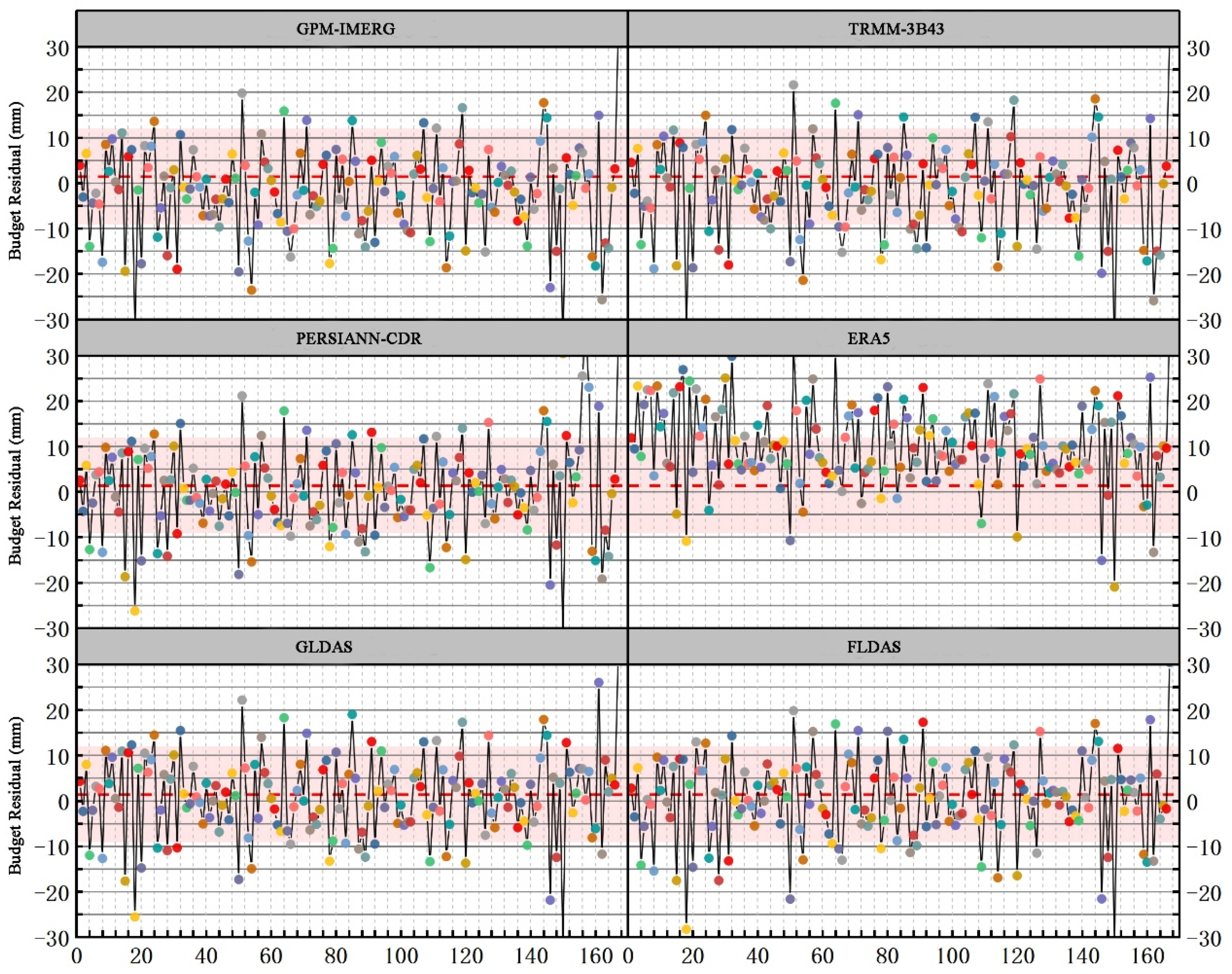
3.2. Water Budget Closure Assessment of SRP Products Relative to Additional Budget Component Products
3.3. Monthly and Seasonal Variations of the ΔRes
4. Discussion
5. Conclusions
- (1)
- The ΔRes for reanalysis products of budget components is smaller than that of satellite products, although the accuracy of the latter is higher than the former when compared with ground-based observations. Combinations based on GLDAS and FLDAS showed a smaller ΔRes than GPM IMERG and TRMM 3B43. However, when compared with rain gauge-based observations, the accuracy of GPM IMERG and TRMM 3B43 is higher than GLDAS and FLDAS.
- (2)
- In contrast to the results of statistical metrics, which showed an increasing accuracy of SRP products, the ΔRes for all combinations did not show a significant decreasing trend in mainland China. This implies that there was a lack of attention on water budget closure in the production of budget component products in previous studies, although it is critical for more accurate hydrological research and has attracted widespread attention recently.
- (3)
- The main error sources affecting the SRP assessment include the inconsistent spatial and temporal resolution of budget component datasets, the quality of rain gauge-based observations, the selection of statistical metrics, and the error in datasets of additional budget components. Methods that reduce uncertainties of budget components should be integrated with existing water budget closure assessment methods for reducing the uncertainties during water budget closure assessment.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Forman, B.A.; Vivoni, E.R.; Margulis, S.A. Evaluation of ensemble-based distributed hydrologic model response with disaggregated precipitation products. Water Resour. Res. 2008, 44, 12. [Google Scholar] [CrossRef]
- Bonan, D.B.; Siler, N.; Roe, G.H.; Armour, K.C. Energetic constraints on the pattern of changes to the hydrological cycle under global warming. J. Clim. 2023, 36, 3499–3522. [Google Scholar] [CrossRef]
- Levizzani, V.; Cattani, E. Satellite remote sensing of precipitation and the terrestrial water cycle in a changing climate. Remote Sens. 2019, 11, 2301. [Google Scholar] [CrossRef]
- Hong, Y.; Tang, G.; Ma, Y.; Huang, Q.; Han, Z.; Zeng, Z.; Yang, Y.; Wang, C.; Guo, X. Remote sensing precipitation: Sensors, retrievals, validations, and applications. In Observation and Measurement of Ecohydrological Processes; Springer: Berlin/Heidelberg, Germany, 2019; pp. 107–128. [Google Scholar]
- Kim, J.; Han, H. Evaluation of the CMORPH high-resolution precipitation product for hydrological applications over South Korea. Atmos. Res. 2021, 258, 105650. [Google Scholar] [CrossRef]
- Luo, Z.; Gao, Z.; Wang, L.; Wang, S.; Wang, L. A method for balancing the terrestrial water budget and improving the estimation of individual budget components. Agric. For. Meteorol. 2023, 341, 109667. [Google Scholar] [CrossRef]
- Luo, Z.; Li, H.; Zhang, S.; Wang, L.; Wang, S.; Wang, L. A Novel Two-Step Method for Enforcing Water Budget Closure and an Intercomparison of Budget Closure Correction Methods Based on Satellite Hydrological Products. Water Resour. Res. 2023, 59, e2022WR032176. [Google Scholar] [CrossRef]
- Ombadi, M.; Nguyen, P.; Sorooshian, S.; Hsu, K.-l. Developing Intensity-Duration-Frequency (IDF) Curves from Satellite-Based Precipitation: Methodology and Evaluation. Water Resour. Res. 2018, 54, 7752–7766. [Google Scholar] [CrossRef]
- Sheffield, J.; Ferguson, C.R.; Troy, T.J.; Wood, E.F.; McCabe, M.F. Closing the terrestrial water budget from satellite remote sensing. Geophys. Res. Lett. 2009, 36, 07403. [Google Scholar] [CrossRef]
- Amjad, M.; Yilmaz, M.T.; Yucel, I.; Yilmaz, K.K. Performance evaluation of satellite-and model-based precipitation products over varying climate and complex topography. J. Hydrol. 2020, 584, 124707. [Google Scholar] [CrossRef]
- Moges, D.M.; Kmoch, A.; Uuemaa, E. Application of satellite and reanalysis precipitation products for hydrological modeling in the data-scarce Porijõgi catchment, Estonia. J. Hydrol. Reg. Stud. 2022, 41, 101070. [Google Scholar] [CrossRef]
- Luo, Z.; Shao, Q.; Wan, W.; Li, H.; Chen, X.; Zhu, S.; Ding, X. A new method for assessing satellite-based hydrological data products using water budget closure. J. Hydrol. 2021, 594, 125927. [Google Scholar] [CrossRef]
- Pan, M.; Wood, E.F. Data assimilation for estimating the terrestrial water budget using a constrained ensemble kalman filter. J. Hydrometeorol. 2006, 7, 534–547. [Google Scholar] [CrossRef]
- Dagan, G.; Stier, P.; Watson-Parris, D. Analysis of the atmospheric water budget for elucidating the spatial scale of precipitation changes under climate change. Geophys. Res. Lett. 2019, 46, 10504–10511. [Google Scholar] [CrossRef]
- Lv, M.; Ma, Z.; Yuan, X.; Lv, M.; Li, M.; Zheng, Z. Water budget closure based on GRACE measurements and reconstructed evapotranspiration using GLDAS and water use data for two large densely-populated mid-latitude basins. J. Hydrol. 2017, 547, 585–599. [Google Scholar] [CrossRef]
- Wang, S.; Huang, J.; Li, J.; Rivera, A.; McKenney, D.W.; Sheffield, J. Assessment of water budget for sixteen large drainage basins in Canada. J. Hydrol. 2014, 512, 1–15. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef]
- Soltani, S.S.; Ataie-Ashtiani, B.; Danesh-Yazdi, M.; Simmons, C.T. A probabilistic framework for water budget estimation in low runoff regions: A case study of the central Basin of Iran. J. Hydrol. 2020, 586, 124898. [Google Scholar] [CrossRef]
- Rodell, M.; Reager, J.T. Water cycle science enabled by the GRACE and GRACE-FO satellite missions. Nat. Water 2023, 1, 47–59. [Google Scholar] [CrossRef]
- Hobeichi, S.; Abramowitz, G.; Evans, J. Conserving Land–Atmosphere Synthesis Suite (CLASS). J. Clim. 2020, 33, 1821–1844. [Google Scholar] [CrossRef]
- Lehmann, F.; Vishwakarma, B.D.; Bamber, J. How well are we able to close the water budget at the global scale? Hydrol. Earth Syst. Sci. 2022, 26, 35–54. [Google Scholar] [CrossRef]
- Abhishek Kinouchi, T.; Abolafia-Rosenzweig, R.; Ito, M. Water budget closure in the Upper Chao Phraya River basin, Thailand using multisource data. Remote Sens. 2021, 14, 173. [Google Scholar] [CrossRef]
- Gao, H.; Tang, Q.; Ferguson, C.R.; Wood, E.F.; Lettenmaier, D.P. Estimating the water budget of major US river basins via remote sensing. Int. J. Remote Sens. 2010, 31, 3955–3978. [Google Scholar] [CrossRef]
- Abolafia-Rosenzweig, R.; Pan, M.; Zeng, J.L.; Livneh, B. Remotely sensed ensembles of the terrestrial water budget over major global river basins: An assessment of three closure techniques. Remote Sens. Environ. 2021, 252, 112191. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Pan, M.; Troy, T.J.; Vinukollu, R.K.; Sheffield, J.; Wood, E.F. Reconciling the global terrestrial water budget using satellite remote sensing. Remote Sens. Environ. 2011, 115, 1850–1865. [Google Scholar] [CrossRef]
- Hamed, M.M.; Nashwan, M.S.; Shahid, S. Performance evaluation of reanalysis precipitation products in Egypt using fuzzy entropy time series similarity analysis. Int. J. Climatol. 2021, 41, 5431–5446. [Google Scholar] [CrossRef]
- Chen, H.; Yong, B.; Shen, Y.; Liu, J.; Hong, Y.; Zhang, J. Comparison analysis of six purely satellite-derived global precipitation estimates. J. Hydrol. 2020, 581, 124376. [Google Scholar] [CrossRef]
- Zhou, Z.; Guo, B.; Xing, W.; Zhou, J.; Xu, F.; Xu, Y. Comprehensive evaluation of latest GPM era IMERG and GSMaP precipitation products over mainland China. Atmos. Res. 2020, 246, 105132. [Google Scholar] [CrossRef]
- Pan, M.; Li, H.; Wood, E. Assessing the skill of satellite-based precipitation estimates in hydrologic applications. Water Resour. Res. 2010, 46, 9. [Google Scholar] [CrossRef]
- Bouizrou, I.; Bouadila, A.; Aqnouy, M.; Gourfi, A. Assessment of remotely sensed precipitation products for climatic and hydrological studies in arid to semi-arid data-scarce region, central-western Morocco. Remote Sens. Appl. Soc. Environ. 2023, 30, 100976. [Google Scholar] [CrossRef]
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. GPM IMERG Final Precipitation L3 Half Hourly 0.1 Degree x 0.1 Degree V06; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2019. [Google Scholar]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM Multi-Satellite Precipitation Analysis (TMPA). In Satellite Rainfall Applications for Surface Hydrology; Gebremichael, M., Hossain, F., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service (C3S). ERA5: Fifth Generation of ECMWF Atmospheric Reanalysis of the Global Climate; Copernicus Climate Change Service Climate Data Store (CDS): Frankfurt, Germany, 2017. [Google Scholar]
- Rodell, M.; Houser, P.R.; Jambor UE, A.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- McNally, A.; Arsenault, K.; Kumar, S.; Shukla, S.; Peterson, P.; Wang, S.; Funk, C.; Peters-Lidard, C.D.; Verdin, J.P. A land data assimilation system for sub-Saharan Africa food and water security applications. Sci. Data 2017, 4, 170012. [Google Scholar] [CrossRef] [PubMed]
- Mehrnegar, N.; Schumacher, M.; Jagdhuber, T.; Forootan, E. Making the Best Use of GRACE, GRACE-FO and SMAP Data through a Constrained Bayesian Data-Model Integration. Water Resour. Res. 2023, 59, e2023WR034544. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M.; Zaitchik, B.F.; Reichle, R.H.; Koster, R.D.; van Dam, T.M. Assimilation of GRACE ter-restrial water storage into a land surface model: Evaluation and potential value for drought monitoring in western and central Europe. J. Hydrol. 2012, 446, 103–115. [Google Scholar] [CrossRef]
- Schulze, K.; Kusche, J.; Gerdener, H.; Engels, O.; Döll, P.; Müller Schmied, H.; Sebastian, A.; Shadkam, S. Joint assimilation of GRACE Total Water Storage Anomalies and In-Situ Streamflow Data into a Global Hydrological Model. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–27 May 2022; p. p. EGU22–5321. [Google Scholar]
- Sun, A.Y.; Scanlon, B.R.; Save, H.; Rateb, A. Reconstruction of GRACE Total Water Storage Through Automated Machine Learning. Water Resour. Res. 2021, 57, e2020WR028666. [Google Scholar] [CrossRef]
- Munier, S.; Aires, F.; Schlaffer, S.; Prigent, C.; Papa, F.; Maisongrande, P.; Pan, M. Combining data sets of satellite-retrieved products for basin-scale water balance study: 2. Evaluation on the Mississippi Basin and closure correction model. J. Geophys. Res.-Atmos. 2014, 119, 12100–12116. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, M.; Sheffield, J.; Siemann, A.L.; Fisher, C.K.; Liang, M.; Beck, H.E.; Wanders, N.; MacCracken, R.F.; Houser, P.R. A Climate Data Record (CDR) for the global terrestrial water budget: 1984–2010. Hydrol. Earth Syst. Sci. 2018, 22, 241–263. [Google Scholar] [CrossRef]
- Pradhan, A.; Indu, J. Assessment of SM2RAIN derived and IMERG based precipitation products for hydrological simulation. J. Hydrol. 2021, 603, 127191. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Z.; Yan, S.; Peng, J. Do ERA5 and ERA5-land precipitation estimates outperform satellite-based precipitation products? A comprehensive comparison between state-of-the-art model-based and satellite-based precipitation products over mainland China. J. Hydrol. 2022, 605, 127353. [Google Scholar] [CrossRef]
- Chen, S.; Xiong, L.; Ma, Q.; Kim, J.-S.; Chen, J.; Xu, C.-Y. Improving daily spatial precipitation estimates by merging gauge observation with multiple satellite-based precipitation products based on the geographically weighted ridge regression method. J. Hydrol. 2020, 589, 125156. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Xie, X.; Cheng, J.; Jia, K.; Li, Y.; Liu, R. Estimation of the terrestrial water budget over northern China by merging multiple datasets. J. Hydrol. 2014, 519, 50–68. [Google Scholar] [CrossRef]
- Wei, L.; Jiang, S.; Ren, L.; Wang, M.; Zhang, L.; Liu, Y.; Yuan, F.; Yang, X. Evaluation of seventeen satellite-, reanalysis-, and gauge-based precipitation products for drought monitoring across mainland China. Atmos. Res. 2021, 263, 105813. [Google Scholar] [CrossRef]
- Chaudhary, S.; Dhanya, C.T. An improved error decomposition scheme for satellite-based precipitation products. J. Hydrol. 2021, 598, 126434. [Google Scholar] [CrossRef]
- Pradhan, R.K.; Markonis, Y.; Vargas Godoy, M.R.; Villalba-Pradas, A.; Andreadis, K.M.; Nikolopoulos, E.I.; Papalexiou, S.M.; Rahim, A.; Tapiador, F.J.; Hanel, M. Review of GPM IMERG performance: A global perspective. Remote Sens. Environ. 2022, 268, 112754. [Google Scholar] [CrossRef]
- Liu, Z.; Di, Z.; Qin, P.; Zhang, S.; Ma, Q. Evaluation of Six Satellite Precipitation Products over the Chinese Mainland. Remote Sens. 2022, 14, 6277. [Google Scholar] [CrossRef]
- Fang, J.; Yang, W.; Luan, Y.; Du, J.; Lin, A.; Zhao, L. Evaluation of the TRMM 3B42 and GPM IMERG products for extreme precipitation analysis over China. Atmos. Res. 2019, 223, 24–38. [Google Scholar] [CrossRef]
- He, Q.; Yang, J.; Chen, H.; Liu, J.; Ji, Q.; Wang, Y.; Tang, F. Evaluation of extreme precipitation based on three long-term gridded products over the Qinghai-Tibet Plateau. Remote Sens. 2021, 13, 3010. [Google Scholar] [CrossRef]
- Jiang, S.H.; Wei, L.Y.; Ren, L.L.; Zhang, L.Q.; Wang, M.H.; Cui, H. Evaluation of IMERG, TMPA, ERA5, and CPC precipitation products over mainland China: Spatiotemporal patterns and extremes. Water Sci. Eng. 2023, 16, 45–56. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Integrated multi-satellite retrievals for the global precipitation measurement (GPM) mission (IMERG). Satell. Precip. Meas. 2020, 1, 343–353. [Google Scholar]
- Mega, T.; Ushio, T.; Takahiro, M.; Kubota, T.; Kachi, M.; Oki, R. Gauge-adjusted global satellite mapping of precipitation. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1928–1935. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Kurkute, S.; Li, Z.; Li, Y.; Huo, F. Assessment and projection of the water budget over western Canada using convection-permitting weather research and forecasting simulations. Hydrol. Earth Syst. Sci. 2020, 24, 3677–3697. [Google Scholar] [CrossRef]
- Nundy, S.; Kakar, A.; Bhutta, Z.A. How to calculate an adequate sample size? How to Practice Academic Medicine and Publish from Developing Countries? A Pract. Guide 2022, 81–93. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S.; Dewan, A.; Ismail, T.; Alias, N. Performance of five high resolution satellite-based precipitation products in arid region of Egypt: An evaluation. Atmos. Res. 2020, 236, 104809. [Google Scholar] [CrossRef]
- Derin, Y.; Yilmaz, K.K. Evaluation of Multiple Satellite-Based Precipitation Products over Complex Topography. J. Hydrometeorol. 2014, 15, 1498–1516. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Q.; Xu, C.-Y. Assessing the performance of satellite-based precipitation products and its dependence on topography over Poyang Lake basin. Theor. Appl. Climatol. 2014, 115, 713–729. [Google Scholar] [CrossRef]
- Oliveira, P.T.S.; Nearing, M.A.; Moran, M.S.; Goodrich, D.C.; Wendland, E.; Gupta, H.V. Trends in water balance components across the Brazilian Cerrado. Water Resour. Res. 2014, 50, 7100–7114. [Google Scholar] [CrossRef]
- Wang, Q.; Xia, J.; She, D.; Zhang, X.; Liu, J.; Zhang, Y. Assessment of four latest long-term satellite-based precipitation products in capturing the extreme precipitation and streamflow across a humid region of southern China. Atmos. Res. 2021, 257, 105554. [Google Scholar] [CrossRef]
- Lei, H.; Li, H.; Zhao, H.; Ao, T.; Li, X. Comprehensive evaluation of satellite and reanalysis precipitation products over the eastern Tibetan plateau characterized by a high diversity of topographies. Atmos. Res. 2021, 259, 105661. [Google Scholar] [CrossRef]
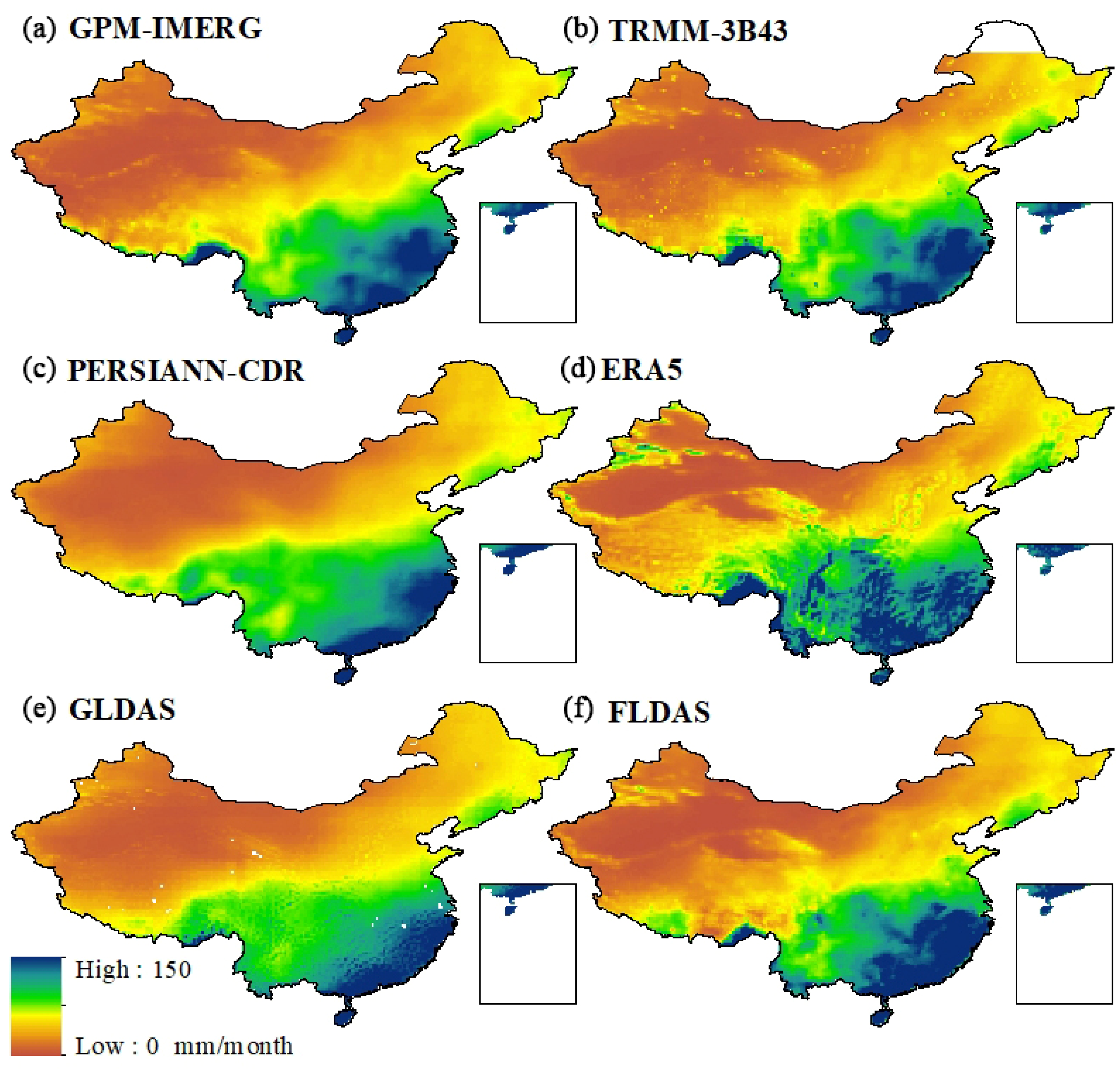


| Precipitation Product | Resolution | Period | Provider | Reference |
|---|---|---|---|---|
| Monthly Global Precipitation Measurement (GPM) v6 (GPM IMERG) | 0.1 degree 3 h | 2000-present | NASA GES DISC at NASA Goddard Space Flight Center, Maryland, United States | Huffman et al. 2019 [31] |
| TRMM (TMPA/3B43) Rainfall Estimate L3 (TRMM 3B43) | 0.25 degree 1 month | 1998–2019 | NASA GES DISC at NASA Goddard Space Flight Center, Maryland, United States | Huffman et al 2010 [32] |
| NOAA Climate Data Record (CDR) of Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks (PERSIANN-CDR), Version 1 Revision 1 (PERSIANN-CDR) | 0.25 degree 1 day | 1983-present | NOAA NCDC, North Carolina, United States | Sorooshian et al. 2014 [33] |
| The fifth generation ECMWF atmospheric reanalysis of the global climate (ERA5) | 0.25 degree 1 month | 1979-present | ECMWF/Copernicus Climate Change Service, Reading, United Kingdom | Copernicus Climate Change Service, 2017 [34] |
| GLDAS Noah Land Surface Model L4 (GLDAS) | 0.25 degree 3 h | 2000-present | NASA GES DISC at NASA Goddard Space Flight Center, Maryland, United States | Rodell et al. 2004 [35] |
| FLDAS Noah Land Surface Model L4 (FLDAS) | 0.10 degree 1 month | 1982-present | NASA GES DISC at NASA Goddard Space Flight Center, Maryland, United States | McNally et al. 2017 [36] |
| Month | GPM-IMERG | TRMM-3B43 | PERSIANN-CDR | ERA5 | GLDAS | FLDAS |
|---|---|---|---|---|---|---|
| 1 | 2.64 | 3.44 | 3.22 | 7.51 | 3.35 | 1.33 |
| 2 | 0.6 | 1.65 | 1.95 | 6.57 | 1.07 | −0.2 |
| 3 | −2.79 | −1.29 | −1.46 | 6.42 | −1.42 | −2.86 |
| 4 | −2.26 | −0.81 | −0.91 | 10.49 | 0.32 | −1.56 |
| 5 | −4.25 | −3.27 | −2.11 | 11.29 | −0.65 | −2.71 |
| 6 | −2.58 | −2.17 | 0.88 | 13.95 | 2.2 | −0.1 |
| 7 | −14.69 | −14.64 | −8.18 | 3.26 | −7.6 | −8.89 |
| 8 | −6.25 | −6.76 | 1.54 | 14.01 | 2.54 | 2.44 |
| 9 | −4.72 | −5.23 | −1.08 | 12.49 | 0.36 | 2.46 |
| 10 | 1.07 | 1.72 | 2.57 | 13.91 | 3.45 | 4.5 |
| 11 | 2.54 | 3.81 | 3.12 | 10.79 | 3.61 | 2.43 |
| 12 | 7.44 | 8.47 | 6.79 | 12.17 | 7.52 | 5.9 |
| Spring | −9.52 | −5.42 | −4.89 | 27.72 | −1.99 | −6.85 |
| Summer | −24.23 | −23.06 | −6.99 | 31.27 | −4.76 | −6.26 |
| Autumn | −0.92 | 0.64 | 4.03 | 37.28 | 6.85 | 9.89 |
| Winter | 4.08 | 6.83 | −0.53 | 22.23 | 5.35 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z.; Yu, H.; Liu, H.; Chen, J. Assessing the Water Budget Closure Accuracy of Satellite/Reanalysis-Based Hydrological Data Products over Mainland China. Remote Sens. 2023, 15, 5230. https://doi.org/10.3390/rs15215230
Luo Z, Yu H, Liu H, Chen J. Assessing the Water Budget Closure Accuracy of Satellite/Reanalysis-Based Hydrological Data Products over Mainland China. Remote Sensing. 2023; 15(21):5230. https://doi.org/10.3390/rs15215230
Chicago/Turabian StyleLuo, Zengliang, Han Yu, Huan Liu, and Jie Chen. 2023. "Assessing the Water Budget Closure Accuracy of Satellite/Reanalysis-Based Hydrological Data Products over Mainland China" Remote Sensing 15, no. 21: 5230. https://doi.org/10.3390/rs15215230
APA StyleLuo, Z., Yu, H., Liu, H., & Chen, J. (2023). Assessing the Water Budget Closure Accuracy of Satellite/Reanalysis-Based Hydrological Data Products over Mainland China. Remote Sensing, 15(21), 5230. https://doi.org/10.3390/rs15215230