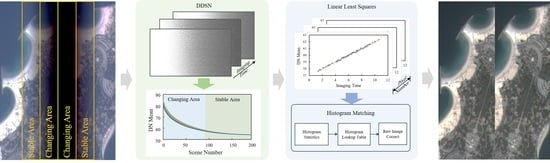
A General Relative Radiometric Correction Method for Vignetting Noise Drift
Abstract
:1. Introduction
- A general relative radiometric correction method for vignetting is proposed, including a vignetting stability analysis method, data on the deep sea during nighttime (DDSN), a noise drift model for vignetting, and histogram matching, which can effectively improve the relative radiometric correction effect;
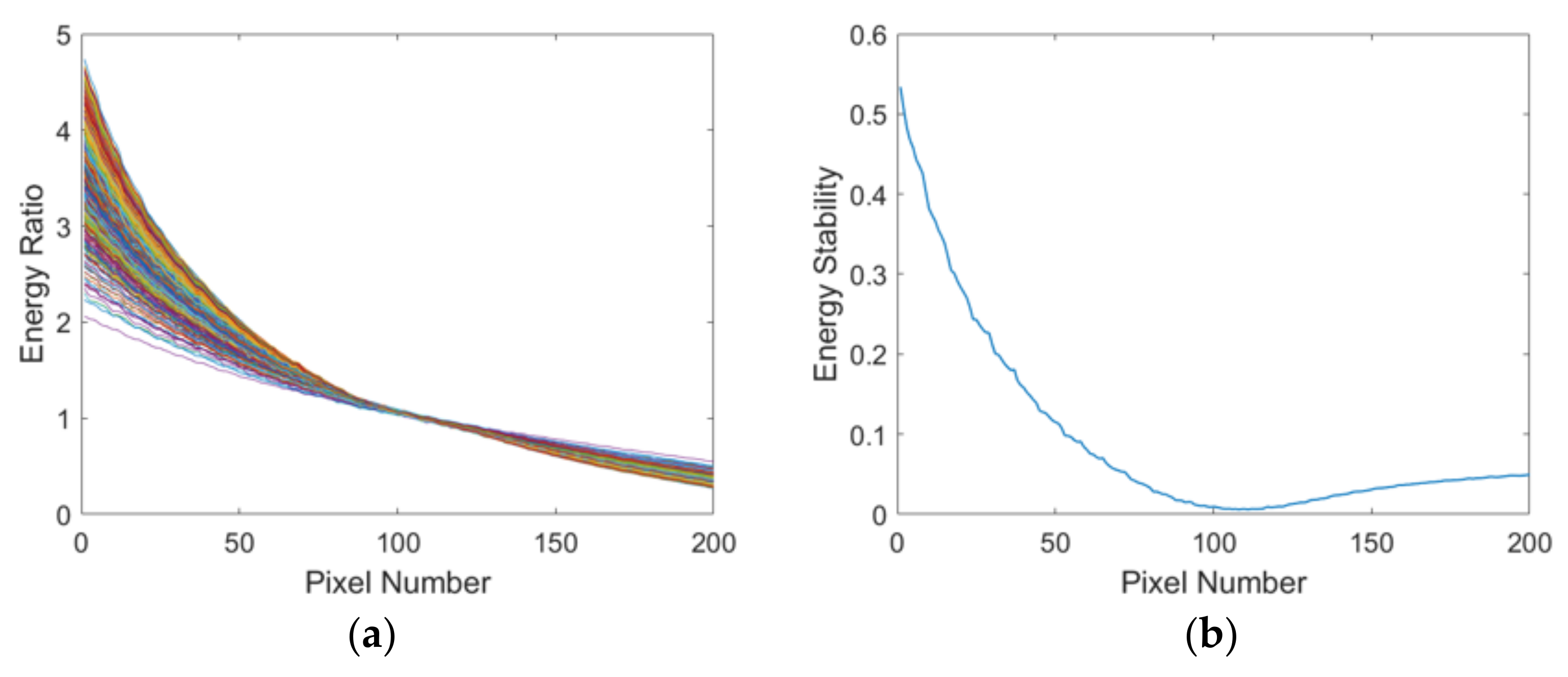
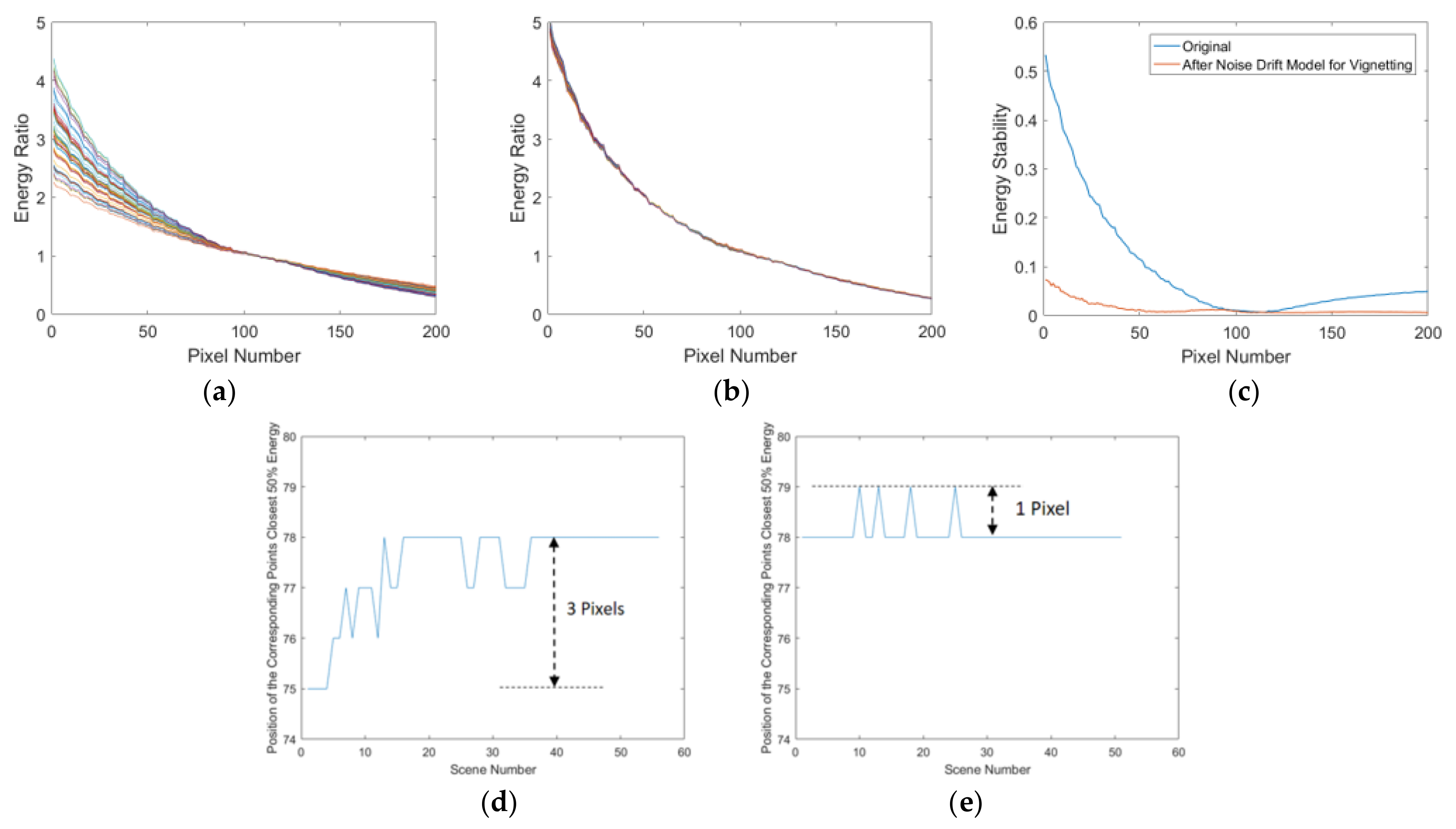
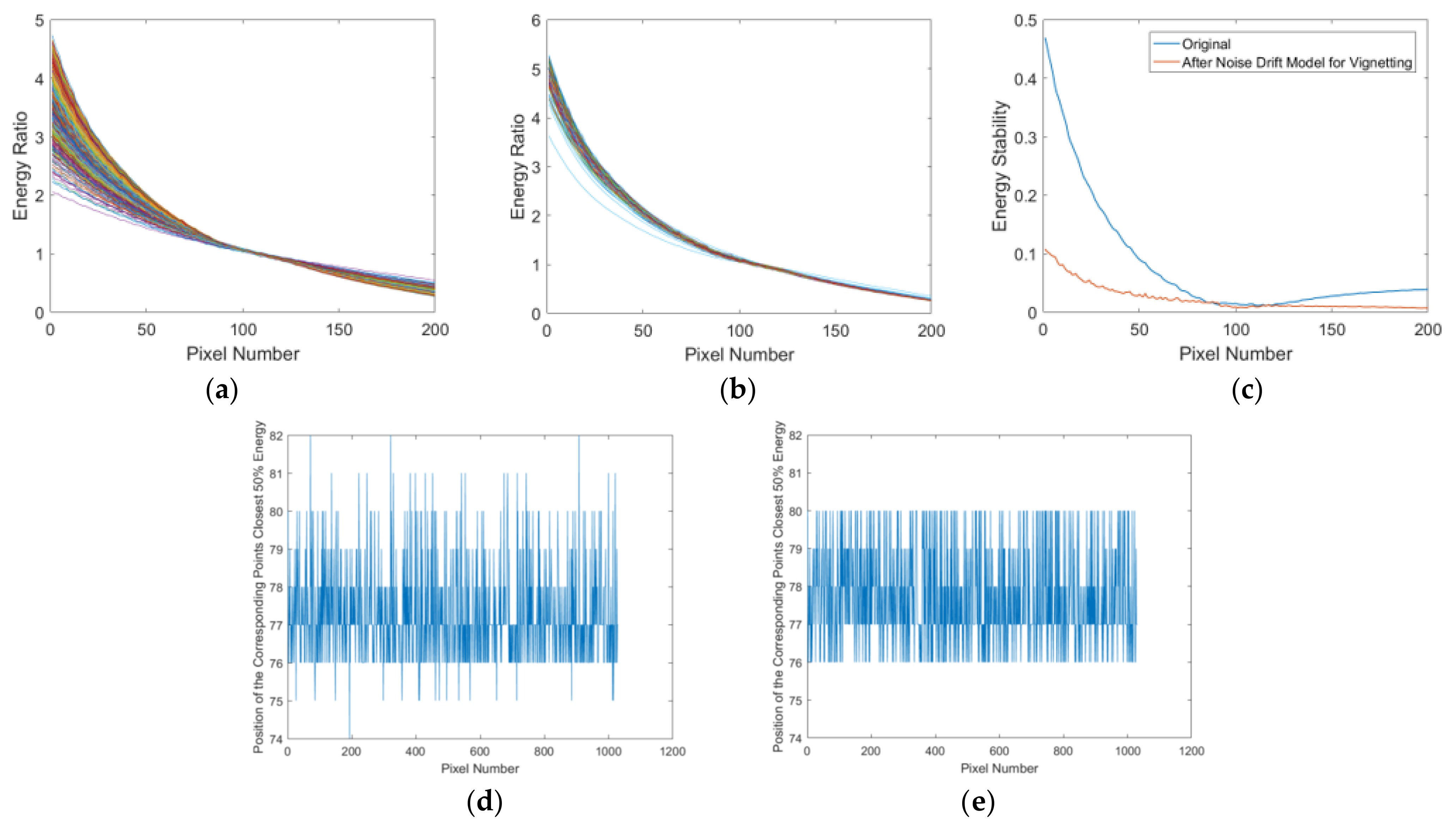
- A vignetting stability analysis method is proposed by calculating the variation in response differences of corresponding points to explore the stability and effect of vignetting noise;
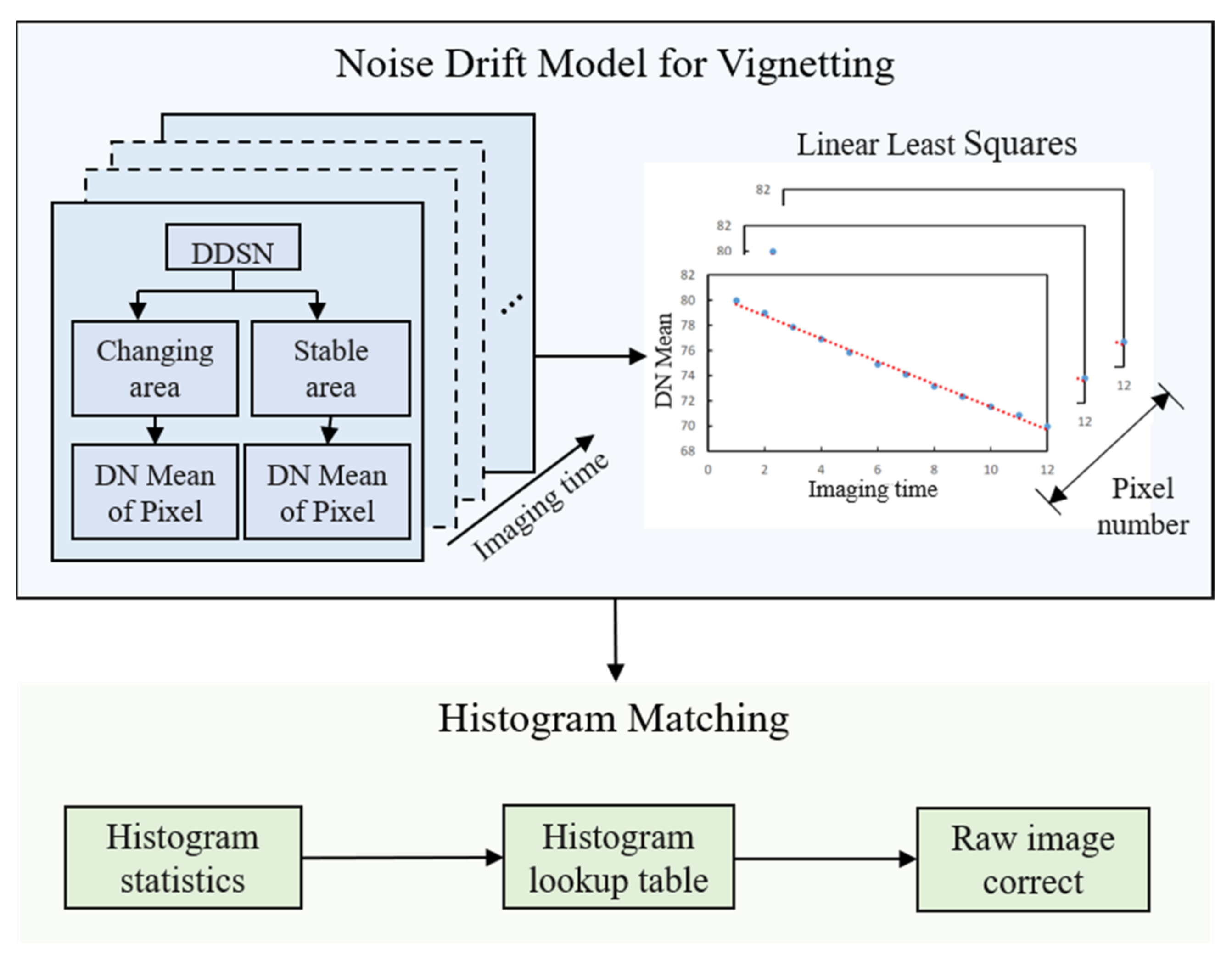
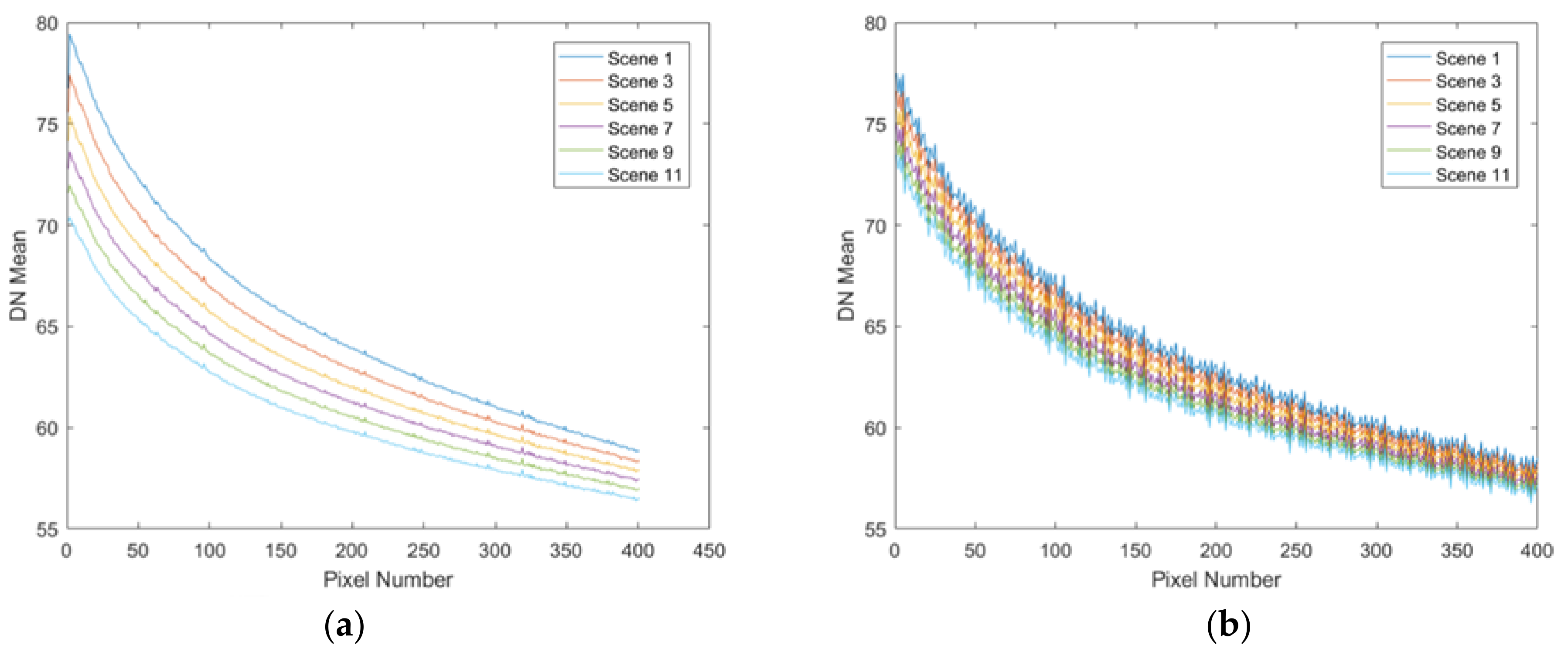
- The noise drift model for vignetting is built using the DDSN of Jilin-1 GF03D satellites. The imaging time and the mean of each pixel of vignetting are used to calculate the coefficient of the model. The coefficient is used to eliminate the noise and noise drift, and the experiments show that the average response stability increased by 37.64% using the method;
- Histogram matching is used to correct the image after the noise drift model for vignetting;
- The results of the comparison of 56,843 images from the Jilin-1 GF03D satellites show that the average improvement rate of color aberration metrics (CAMs) of images after correction in this paper is 15.97%, which is significantly better than the existing method and verifies the generality of the proposed method.
2. Methods
- Analyze the stability of the energy and the noise effect of vignetting using the vignetting stability analysis method;
- Obtain the noise of vignetting by the DDSN of Jilin-1 GF03D satellites;
- Build a noise drift model for vignetting based on the DDSN;
- Histogram matching is used to complete a relative radiometric correction method after the noise drift model correction.
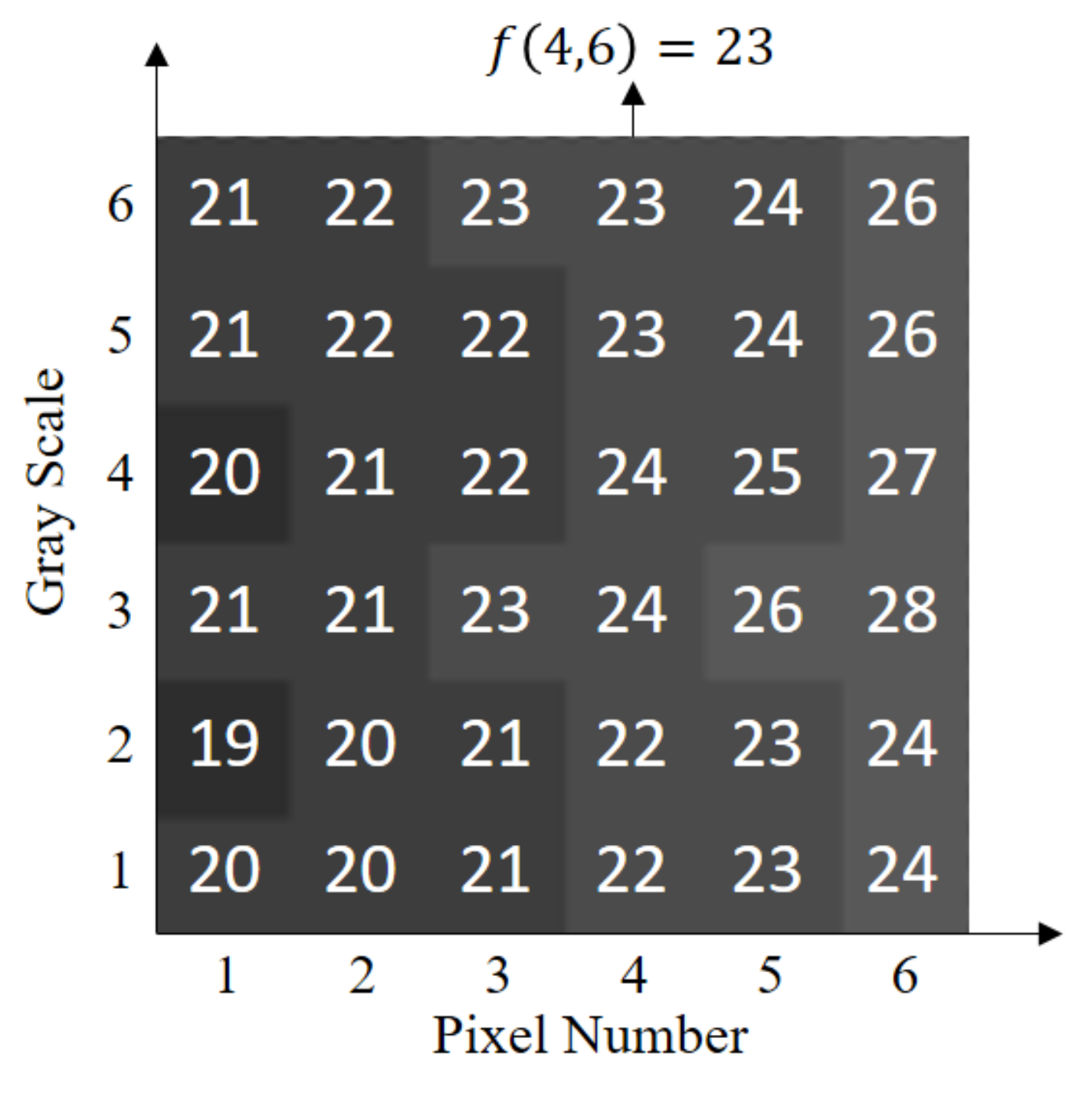
2.1. The Vignetting Stability Analysis Method
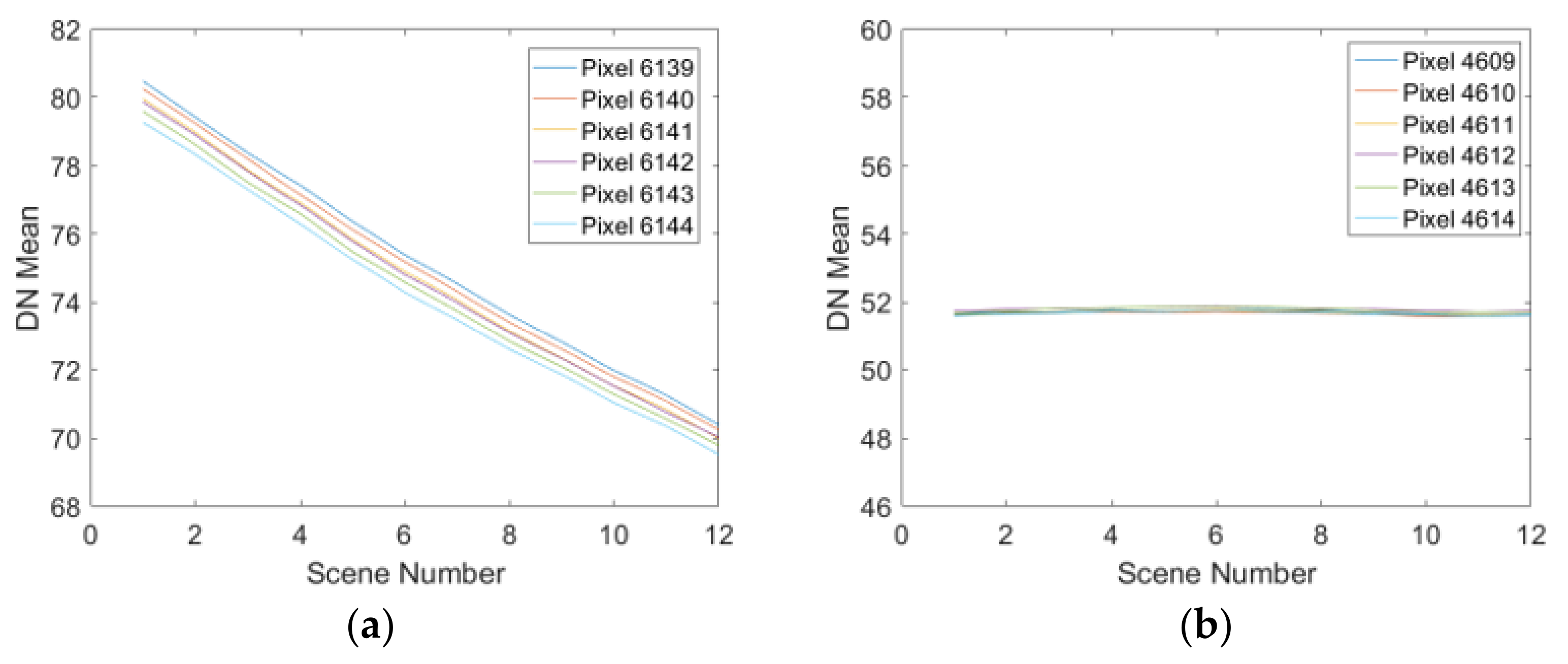
2.2. Data on the Deep Sea during Nighttime (DDSN)
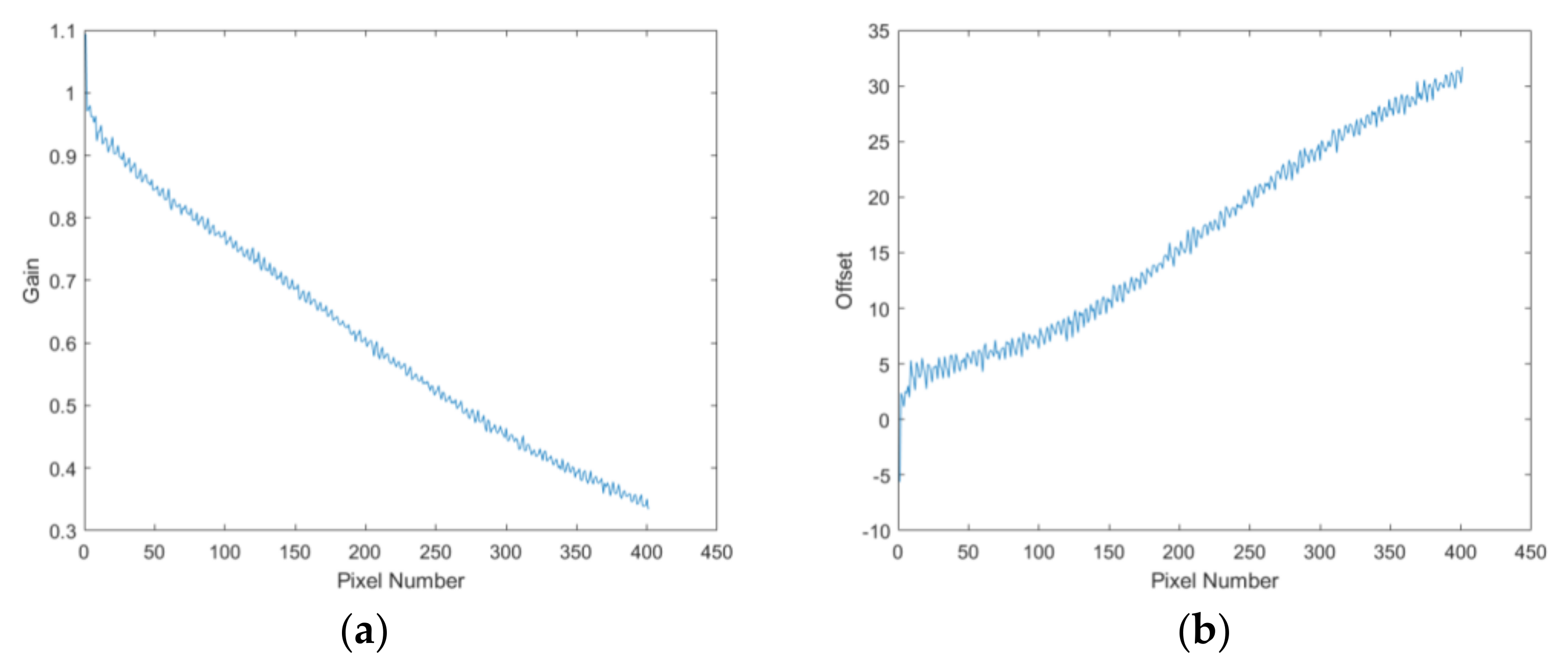
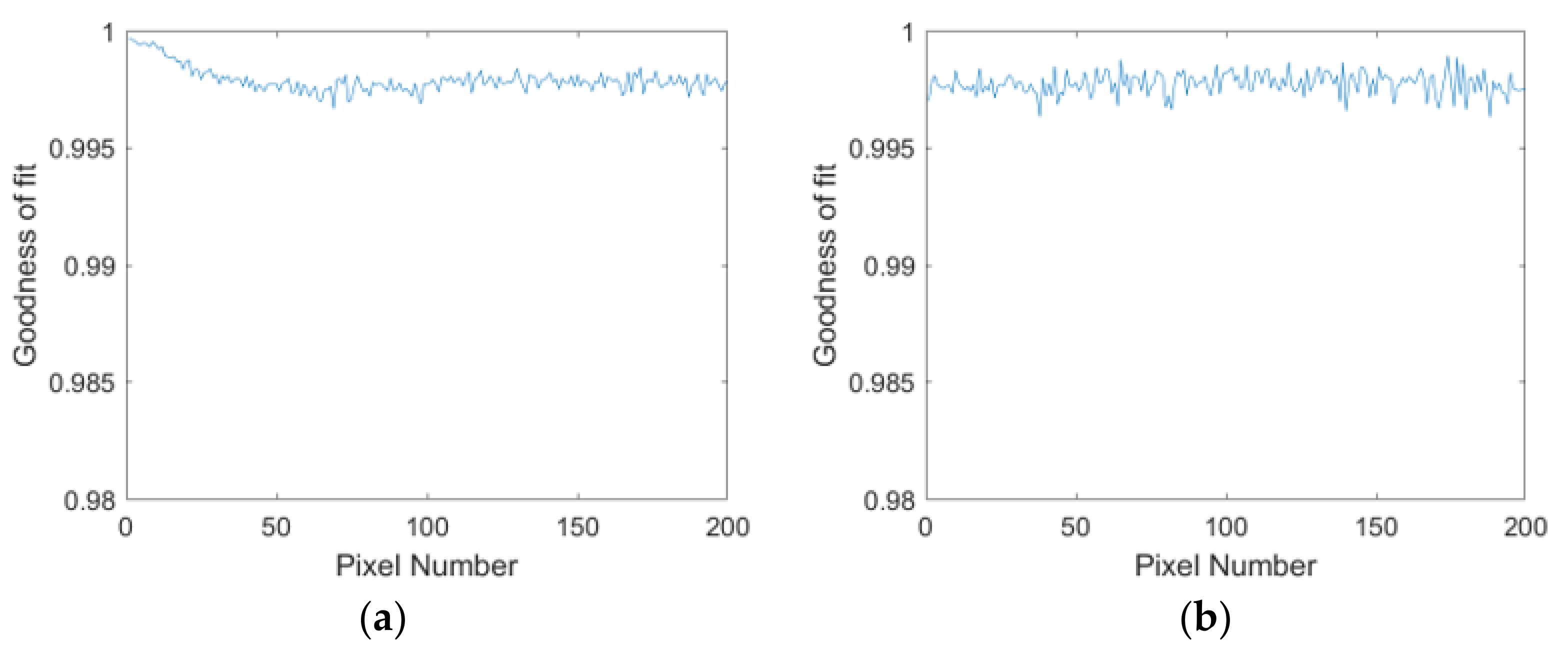
2.3. The Noise Drift Model for Vignetting
2.4. The Relative Radiometric Correction Method
2.5. Accuracy Assessment Index
2.5.1. Root-Mean-Square Deviation of the Mean Line (RA)
2.5.2. Streaking Metrics (SMs)
2.5.3. Root-Mean-Square of Vignetting and Non-Vignetting (RSVN)
2.5.4. Color Aberration Metrics (CAMs)
3. Results
Experiment Setup
4. Discussion
4.1. Evaluation of the Stability of Vignetting
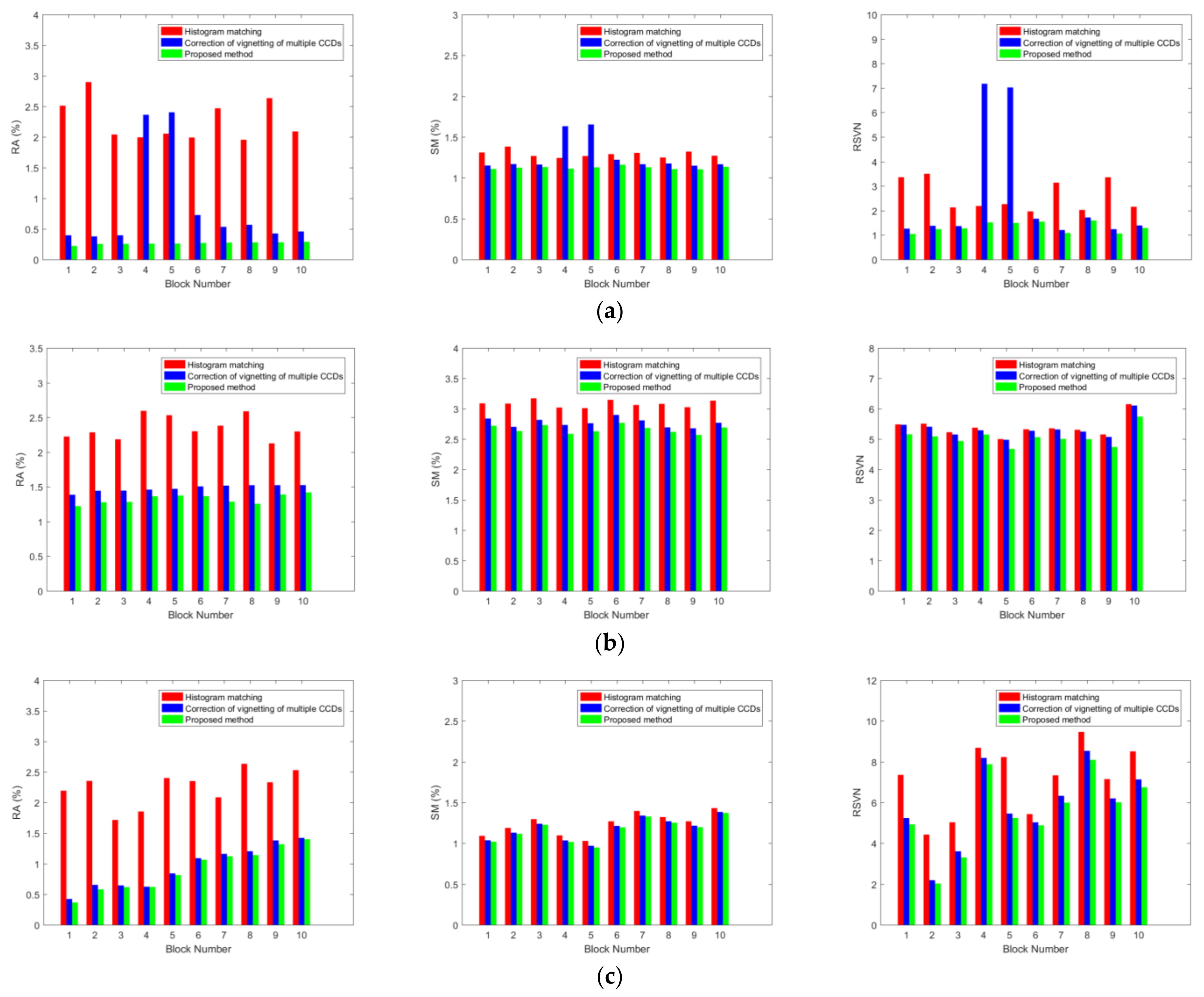
4.2. Evaluation of Relative Radiometric Correction
4.3. Evaluation of Generality
5. Conclusions
- (1)
- A total of 1031 imaging tasks and 15,927 images of the JL1GF03D28 satellite were used to verify the effectiveness of the noise drift model for vignetting. The response stability was improved by 37.64% in the experiments. Moreover, the maximum deviation of the positions of the corresponding points closest to 50% energy was optimized from eight pixels to four pixels.
- (2)
- Three types of object features were used to verify the effect of the proposed method. The RA values of water, vegetation, and desert were 0.27%, 1.32%, and 0.90%, respectively, the streaking metric values were all less than 3%, and the RSVN values obtained using the proposed method were 1.31, 5.01, and 5.51, which were significantly lower than the existing methods.
- (3)
- A total of 56,843 images from 16 Jilin-1 GF03D satellites were used to verify the generality of the proposed method. The CAM results of the experiments show that the average rate is about 93.17%, and the average increasing rate is 15.97%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peng, X.; Zhong, R.; Li, Z.; Li, Q. Optical Remote Sensing Image Change Detection Based on Attention Mechanism and Image Difference. IEEE Trans. Geosci. Remote Sens. 2020, 59, 7296–7307. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, H.; Li, Y.; Ma, M.; Liu, Q.; Lin, J. Analysis of the influence of vibrations on the imaging quality of an integrated TDICCD aerial camera. Opt. Express 2021, 29, 18108–18121. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Ye, G.; Zhu, Y.; Song, X.; Hu, F.; Zhang, C.; Wang, M. Jitter Detection and Image Restoration Based on Continue Dynamic Shooting Model for High-Resolution TDI CCD Satellite Images. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4915–4933. [Google Scholar] [CrossRef]
- Saeed, N.; Guo, S.; Park, K.H.; Al-Naffouri, T.Y.; Alouini, M.S. Optical camera communications: Survey, use cases, challenges, and future trends. Phys. Commun. 2019, 37, 100900. [Google Scholar]
- Li, Z.; Hou, W.; Hong, J.; Zheng, F.; Luo, D.; Wang, J.; Gu, X.; Qiao, Y. Directional Polarimetric Camera (DPC): Monitoring aerosol spectral optical properties over land from satellite observation. J. Quant. Spectrosc. Radiat. Transf. 2018, 218, 21–37. [Google Scholar] [CrossRef]
- Jiao, N.; Wang, F.; Chen, B.; Zhu, J.; You, H. Pre-Processing of Inner CCD Image Stitching of the SDGSAT-1 Satellite. Appl. Sci. 2022, 12, 9693. [Google Scholar]
- Alvarez-Vanhard, E.; Corpetti, T.; Houet, T. UAV & satellite synergies for optical remote sensing applications: A literature review. Sci. Remote Sens. 2021, 3, 100019. [Google Scholar]
- Sheffield, J.; Wood, E.F.; Pan, M.; Beck, H.; Coccia, G.; Serrat-Capdevila, A.; Verbist, K. Satellite Remote Sensing for Water Resources Management: Potential for Supporting Sustainable Development in Data-Poor Regions. Water Resour. Res. 2018, 54, 9724–9758. [Google Scholar]
- Liu, H.; Wang, P.; Liu, C.; Zhu, H.; Xu, S. Application and research of the accuracy calibration and detection instrument for installation of dual imaging module for aerial camera. In Proceedings of the 2017 IEEE 2nd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 December 2017. [Google Scholar]
- Shi, Y.; Wang, S.; Zhou, S.; Kamruzzaman, M.M. Study on Modeling Method of Forest Tree Image Recognition Based on CCD and Theodolite. IEEE Access 2020, 8, 159067–159076. [Google Scholar] [CrossRef]
- Qiu, M.; Ma, W. Optical butting of linear infrared detector array for pushbroom imager. In Proceedings of the Second International Conference on Photonics and Optical Engineering, Xi’an, China, 28 February 2017; Volume 10256. [Google Scholar]
- Honkavaara, E.; Khoramshahi, E. Radiometric Correction of Close-Range Spectral Image Blocks Captured Using an Unmanned Aerial Vehicle with a Radiometric Block Adjustment. Remote Sens. 2018, 10, 256. [Google Scholar] [CrossRef]
- Liu, Y.; Long, T.; Jiao, W.; He, G.; Chen, B.; Huang, P. Vignetting and Chromatic Aberration Correction for Multiple Spaceborne CCDS. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 12–16 July 2021. [Google Scholar]
- Goossens, T.; Geelen, B.; Lambrechts, A.; Van Hoof, C. A vignetting advantage for thin-film filter arrays in hyperspectral cameras. arXiv 2020, arXiv:2003.11983. [Google Scholar]
- Cui, H.; Zhang, L.; Li, W.; Yuan, Z.; Wu, M.; Wang, C.; Ma, J.; Li, Y. A new calibration system for low-cost Sensor Network in air pollution monitoring. Atmos. Pollut. Res. 2021, 12, 101049. [Google Scholar] [CrossRef]
- Zhang, G.; Li, L.; Jiang, Y.; Shen, X.; Li, D. On-Orbit Relative Radiometric Calibration of the Night-Time Sensor of the LuoJia1-01 Satellite. Sensors 2018, 18, 4225. [Google Scholar] [CrossRef] [PubMed]
- Moghimi, A.; Sarmadian, A.; Mohammadzadeh, A.; Celik, T.; Amani, M.; Kusetogullari, H. Distortion robust relative radiometric normalization of multitemporal and multisensor remote sensing images using image features. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–20. [Google Scholar] [CrossRef]
- Li, J.; Zhao, J.K.; Chang, M.; Hu, X.R.; Li, J. Radiometric calibration of photographic camera with a composite plane array CCD in laboratory. Guangxue Jingmi Gongcheng/Opt. Precis. Eng. 2017, 25, 73–83. [Google Scholar]
- Duan, Y.; Chen, W.; Wang, M.; Yan, L. A Relative Radiometric Correction Method for Airborne Image Using Outdoor Calibration and Image Statistics. IEEE Trans. Geosci. Remote Sens. 2013, 52, 5164–5174. [Google Scholar] [CrossRef]
- Helder, D.L.; Basnet, B.; Morstad, D.L. Optimized identification of worldwide radiometric pseudo-invariant calibration sites. Can. J. Remote Sens. 2010, 36, 527–539. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, Q.; Wang, W.; Wu, Y.; Zheng, H.; Yao, X.; Zhu, Y.; Cao, W.; Cheng, T. MACA: A Relative Radiometric Correction Method for Multiflight Unmanned Aerial Vehicle Images Based on Concurrent Satellite Imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar]
- Li, Y.; Zhang, B.; He, H. Relative radiometric correction of imagery based on the side-slither method. In Proceedings of the 2017 2nd International Conference on Multimedia and Image Processing (ICMIP), Wuhan, China, 17–19 March 2017. [Google Scholar]
- Chen, C.; Pan, J.; Wang, M.; Zhu, Y. Side-Slither Data-Based Vignetting Correction of High-Resolution Spaceborne Camera with Optical Focal Plane Assembly. Sensors 2018, 18, 3402. [Google Scholar]
- Cheng, X.-Y.; Zhuang, X.-Q.; Zhang, D.; Yao, Y.; Hou, J.; He, D.-G.; Jia, J.-X.; Wang, Y.-M. A relative radiometric correction method for airborne SWIR hyperspectral image using the side-slither technique. Opt. Quantum Electron. 2019, 51, 105. [Google Scholar] [CrossRef]
- Tan, K.C.; Lim, H.S.; MatJafri, M.Z.; Abdullah, K. A comparison of radiometric correction techniques in the evaluation of the relationship between LST and NDVI in Landsat imagery. Environ. Monit. Assess. 2012, 184, 3813–3829. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Long, T.; Jiao, W.; Du, Y.; He, G.; Chen, B.; Huang, P. Automatic segment-wise restoration for wide irregular stripe noise in SDGSAT-1 multispectral data using side-slither data. Egypt. J. Remote Sens. Space Sci. 2023, 26, 747–757. [Google Scholar] [CrossRef]
- Cao, B.; Du, Y.; Liu, Q.; Liu, Q. The improved histogram matching algorithm based on sliding windows. In Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, China, 24–26 June 2011. [Google Scholar]
- Shapira, D.; Avidan, S.; Hel-Or, Y. Multiple histogram matching. In Proceedings of the 2013 IEEE International Conference on Image Processing, Melbourne, Australia, 15–18 September 2013. [Google Scholar]
- Wu, Y.; Yang, P. Chebyshev polynomials, moment matching, and optimal estimation of the unseen. Ann. Stat. 2019, 47, 857–883. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Chen, F.; Zhao, K.; Zeng, D. Adaptive material matching for hyperspectral imagery destriping. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–20. [Google Scholar]
- Liu, Y.; Long, T.; Jiao, W.; He, G.; Chen, B.; Huang, P. A General Relative Radiometric Correction Method for Vignetting and Chromatic Aberration of Multiple CCDs: Take the Chinese Series of Gaofen Satellite Level-0 Images for Example. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–25. [Google Scholar] [CrossRef]
- Li, L.; Li, Z.; Wang, Z.; Jiang, Y.; Shen, X.; Wu, J. On-Orbit Relative Radiometric Calibration of the Bayer Pattern Push-Broom Sensor for Zhuhai-1 Video Satellites. Remote Sens. 2023, 15, 377. [Google Scholar] [CrossRef]










| Band | Integral Level | Gain | Scenes |
|---|---|---|---|
| PAN | 64 | 2 | 12 |
| MSS1 | 16 | 2 | |
| MSS2 | 12 | 2 | |
| MSS3 | 8 | 3 | |
| MSS4 | 8 | 4 |
| Satellite | Imaging Time | Longitude | Latitude | Scene | Minimum Goodness of Fit |
|---|---|---|---|---|---|
| JL1GF03D01 | 2023-01-17 | −17.9957 | 10.3161 | 13 | 0.9984 |
| JL1GF03D03 | 2023-01-17 | 49.1638 | 29.1192 | 12 | 0.9962 |
| JL1GF03D05 | 2023-01-13 | 96.9982 | 15.8312 | 12 | 0.9975 |
| JL1GF03D07 | 2023-01-17 | 50.2294 | 28.0700 | 13 | 0.9972 |
| JL1GF03D11 | 2022-11-28 | 40.122 | 17.9956 | 13 | 0.9971 |
| JL1GF03D12 | 2022-11-17 | 5.9106 | 42.3907 | 13 | 0.9976 |
| JL1GF03D13 | 2022-12-30 | 34.8815 | 26.7517 | 12 | 0.9915 |
| JL1GF03D14 | 2023-01-13 | 35.6616 | 43.8903 | 12 | 0.9870 |
| JL1GF03D15 | 2023-01-13 | 40.1879 | 42.0227 | 12 | 0.9972 |
| JL1GF03D16 | 2023-01-13 | 11.6455 | −27.7515 | 12 | 0.9887 |
| JL1GF03D17 | 2023-01-13 | 34.8815 | 26.7517 | 12 | 0.9953 |
| JL1GF03D18 | 2023-01-14 | 7.1630 | 42.6434 | 13 | 0.9968 |
| JL1GF03D27 | 2022-12-30 | 50.2294 | 28.0700 | 13 | 0.9922 |
| JL1GF03D28 | 2022-12-30 | 36.8701 | 43.9123 | 13 | 0.9978 |
| JL1GF03D29 | 2023-01-17 | 35.8593 | 25.3234 | 13 | 0.9971 |
| JL1GF03D30 | 2023-01-17 | 36.8701 | 43.9123 | 13 | 0.9510 |
| Object Features | Block | Methods | RA (%) | SM (%) | RSVN |
|---|---|---|---|---|---|
| Water | 10 | Histogram matching | 2.2636 | 1.2905 | 2.6082 |
| Correction of the vignetting of multiple CCDs | 0.8645 | 1.2643 | 2.5420 | ||
| Proposed method | 0.2652 | 1.1254 | 1.3147 | ||
| Vegetation | 10 | Histogram matching | 2.3512 | 3.0824 | 5.3877 |
| Correction of the vignetting of multiple CCDs | 1.4788 | 2.7696 | 5.3306 | ||
| Proposed method | 1.3231 | 2.6626 | 5.0059 | ||
| Desert | 10 | Histogram matching | 2.2443 | 1.2386 | 7.1620 |
| Correction of the vignetting of multiple CCDs | 0.9444 | 1.1832 | 5.7892 | ||
| Proposed method | 0.9044 | 1.1671 | 5.5105 |
| Object Feature | Target Number | Mean of Raw (CAM) | Mean of Histogram Matching (CAM) | Mean of Proposed Method (CAM) |
|---|---|---|---|---|
| Mountain | 3 | 118 | 504 | 1038 |
| Water | 7 | 77 | 353 | 901 |
| Desert | 2 | 55 | 486 | 820 |
| Cloud | 2 | 55 | 208 | 789 |
| Farmland | 5 | 64 | 451 | 917 |
| Bare Soil | 4 | 60 | 291 | 968 |
| City | 2 | 69 | 365 | 912 |
| Vegetation | 4 | 66 | 399 | 996 |
| Snow | 1 | 51 | 513 | 883 |
| Satellite | Scene Number | Histogram Matching (%) (CAM 600) | Proposed Method (%) (CAM 600) | Improvement Ratio (%) |
|---|---|---|---|---|
| JL1GF03D01 | 3331 | 75.36 | 91.10 | 15.74 |
| JL1GF03D03 | 5686 | 74.30 | 93.42 | 19.12 |
| JL1GF03D05 | 3058 | 78.67 | 92.42 | 13.75 |
| JL1GF03D07 | 4529 | 78.12 | 90.78 | 12.66 |
| JL1GF03D11 | 732 | 73.58 | 90.75 | 17.18 |
| JL1GF03D12 | 5729 | 75.31 | 88.62 | 13.31 |
| JL1GF03D13 | 826 | 81.59 | 96.80 | 15.21 |
| JL1GF03D14 | 3516 | 76.43 | 93.25 | 16.82 |
| JL1GF03D15 | 3536 | 81.83 | 98.03 | 16.20 |
| JL1GF03D16 | 2477 | 81.14 | 93.09 | 11.96 |
| JL1GF03D17 | 3459 | 73.42 | 91.62 | 18.20 |
| JL1GF03D18 | 3109 | 81.39 | 97.55 | 16.16 |
| JL1GF03D27 | 2959 | 74.16 | 88.52 | 14.36 |
| JL1GF03D28 | 3536 | 77.18 | 92.78 | 15.61 |
| JL1GF03D29 | 6607 | 78.20 | 97.87 | 19.67 |
| JL1GF03D30 | 3753 | 74.62 | 94.13 | 19.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, L.; Yu, S.; Zhong, X.; Chen, M.; Wang, D.; Cao, J.; Cai, X. A General Relative Radiometric Correction Method for Vignetting Noise Drift. Remote Sens. 2023, 15, 5129. https://doi.org/10.3390/rs15215129
Fan L, Yu S, Zhong X, Chen M, Wang D, Cao J, Cai X. A General Relative Radiometric Correction Method for Vignetting Noise Drift. Remote Sensing. 2023; 15(21):5129. https://doi.org/10.3390/rs15215129
Chicago/Turabian StyleFan, Liming, Shuhai Yu, Xing Zhong, Maosheng Chen, Dong Wang, Jinyan Cao, and Xiyan Cai. 2023. "A General Relative Radiometric Correction Method for Vignetting Noise Drift" Remote Sensing 15, no. 21: 5129. https://doi.org/10.3390/rs15215129
APA StyleFan, L., Yu, S., Zhong, X., Chen, M., Wang, D., Cao, J., & Cai, X. (2023). A General Relative Radiometric Correction Method for Vignetting Noise Drift. Remote Sensing, 15(21), 5129. https://doi.org/10.3390/rs15215129