Figure 1.
The flowchart of 2OC. M represents the transformation matrix between images, and GCP is the abbreviation for generalized control points.
Figure 1.
The flowchart of 2OC. M represents the transformation matrix between images, and GCP is the abbreviation for generalized control points.
Figure 2.
Schematic of film and PG reference data in KH-4B missions. All dimensions are in meters unless otherwise stated.
Figure 2.
Schematic of film and PG reference data in KH-4B missions. All dimensions are in meters unless otherwise stated.
Figure 3.
The imaging of KH-4B images. (a) The imaging process; (b) the imaging geometric relationship.
Figure 3.
The imaging of KH-4B images. (a) The imaging process; (b) the imaging geometric relationship.
Figure 4.
The Estimation process of primary orientation with , . (a) computes weighted norm sums for pixels in each sector, while (b) identifies the sector with the highest norm value and assigns its central axis orientation as the primary orientation.
Figure 4.
The Estimation process of primary orientation with , . (a) computes weighted norm sums for pixels in each sector, while (b) identifies the sector with the highest norm value and assigns its central axis orientation as the primary orientation.
Figure 5.
The pipeline of feature description. (a) shows sampling point distribution and numbering; (b) illustrates the construction of the sampling vector for point (3,1); (c) demonstrates feature vector construction by concatenating sampling vectors.
Figure 5.
The pipeline of feature description. (a) shows sampling point distribution and numbering; (b) illustrates the construction of the sampling vector for point (3,1); (c) demonstrates feature vector construction by concatenating sampling vectors.
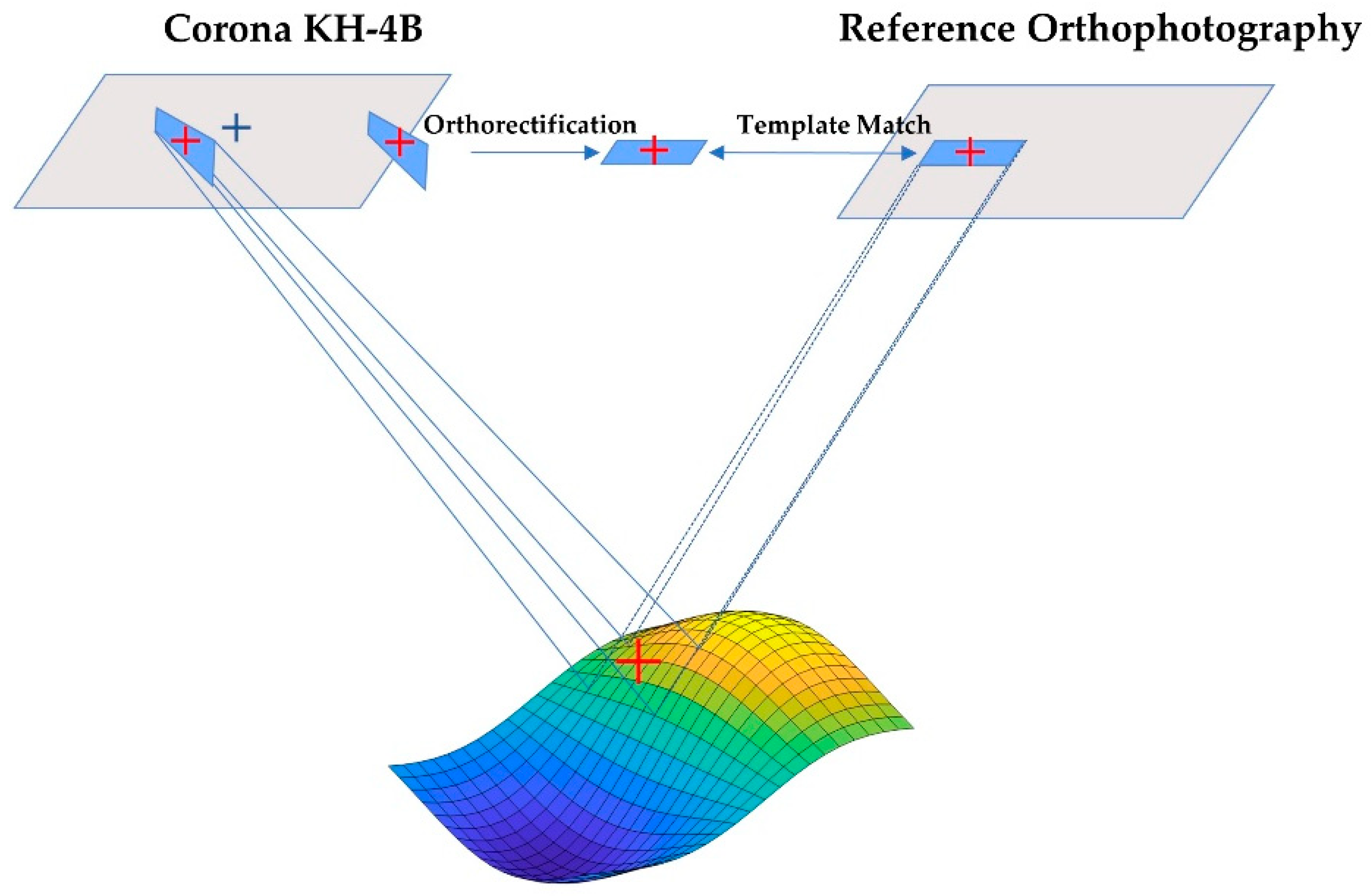
Figure 6.
Model-guided image matching. First, translate the reference image’s feature points to the panoramic image. Then, reapply the template matching between the orthorectified local KH image block and the reference image. Finally, utilize these matching results as generalized control points.
Figure 6.
Model-guided image matching. First, translate the reference image’s feature points to the panoramic image. Then, reapply the template matching between the orthorectified local KH image block and the reference image. Finally, utilize these matching results as generalized control points.
Figure 7.
The matches, namely the generalized control points, between the DS1101-1069DF090b image (c) and the reference Google orthophoto image (d), and the green dots indicate the control points, and the red numbers indicate the point numbers. (a,b,e,f) are the corresponding zoomed-in areas in (c,d).
Figure 7.
The matches, namely the generalized control points, between the DS1101-1069DF090b image (c) and the reference Google orthophoto image (d), and the green dots indicate the control points, and the red numbers indicate the point numbers. (a,b,e,f) are the corresponding zoomed-in areas in (c,d).
Figure 8.
The orientation accuracy in various areas. The red font in the yellow square represents the orientation mean square error of each panoramic image. (a) The orthophoto of Russia; (b) The orthophoto of Gansu, China; (c) The orthophoto of Beijing, China; (d) The orthophoto of Vermont, USA; (e) The partial map of Russia; (f) The partial map of USA; (g) The world map; (h) The China Map; (i) The orthophoto of Chongqing, China; (j) The orthophoto of Arizona, USA; (k) The Burkina Faso map; (l) The Ethiopia map; (m) The orthophoto of Burkina Faso; (n) The orthophoto of Ethiopia; (o) The orthophoto of the Qinghai–Tibet Plateau.
Figure 8.
The orientation accuracy in various areas. The red font in the yellow square represents the orientation mean square error of each panoramic image. (a) The orthophoto of Russia; (b) The orthophoto of Gansu, China; (c) The orthophoto of Beijing, China; (d) The orthophoto of Vermont, USA; (e) The partial map of Russia; (f) The partial map of USA; (g) The world map; (h) The China Map; (i) The orthophoto of Chongqing, China; (j) The orthophoto of Arizona, USA; (k) The Burkina Faso map; (l) The Ethiopia map; (m) The orthophoto of Burkina Faso; (n) The orthophoto of Ethiopia; (o) The orthophoto of the Qinghai–Tibet Plateau.
Figure 9.
The registration checkboard of the KH-4B orthophoto and reference image with complex image contents, where the image with a red dot is the KH-4B Orthophoto. (a–c) are located at the Qinghai–Tibet Plateau, and Beijing, China, with large NID; (d,e) are located in America and Beijing with land cover change; (f,h) are both located in Burkina Faso with noises; (g) is located in Gansu province, China with few textures; (i) is located in Ethiopia with large cloud coverage; (j) is located in Chongqing, China with repetitive textures.
Figure 9.
The registration checkboard of the KH-4B orthophoto and reference image with complex image contents, where the image with a red dot is the KH-4B Orthophoto. (a–c) are located at the Qinghai–Tibet Plateau, and Beijing, China, with large NID; (d,e) are located in America and Beijing with land cover change; (f,h) are both located in Burkina Faso with noises; (g) is located in Gansu province, China with few textures; (i) is located in Ethiopia with large cloud coverage; (j) is located in Chongqing, China with repetitive textures.
Figure 10.
The registration results of the KH-4B image, DS1101-1069DF092c, and the reference image. (a–c) show the zoomed-in registration results of unchanged mountains; (d) shows the zoomed-in registration result of changed rivers. (e) The registration checkboard of the KH-4B orthophoto and reference image. (f) shows the zoomed-in registration result of the changed mountains area. (g,h) show the zoomed-in registration results of the changed plain area, where rivers have transformed into farmland and roads have undergone alterations. (i) shows the zoomed-in registration result of partially unchanged mountainous regions where rivers have experienced minor changes.
Figure 10.
The registration results of the KH-4B image, DS1101-1069DF092c, and the reference image. (a–c) show the zoomed-in registration results of unchanged mountains; (d) shows the zoomed-in registration result of changed rivers. (e) The registration checkboard of the KH-4B orthophoto and reference image. (f) shows the zoomed-in registration result of the changed mountains area. (g,h) show the zoomed-in registration results of the changed plain area, where rivers have transformed into farmland and roads have undergone alterations. (i) shows the zoomed-in registration result of partially unchanged mountainous regions where rivers have experienced minor changes.
Figure 11.
The orthophoto of DS1101-1069DF089, along with 42 checkpoints marked with red-cross dots.
Figure 11.
The orthophoto of DS1101-1069DF089, along with 42 checkpoints marked with red-cross dots.
Figure 12.
The PG stripe curves of the four sub-images, a, b, c, d, of DS1101-1069DF089.
Figure 12.
The PG stripe curves of the four sub-images, a, b, c, d, of DS1101-1069DF089.
Figure 13.
The PG stripe curves of the four sub-images, a, b, c, d, of DS1101-1069DF090.
Figure 13.
The PG stripe curves of the four sub-images, a, b, c, d, of DS1101-1069DF090.
Figure 14.
The PG stripe curves of sub-images, a, b, c, d, of DS1105-1071DF141.
Figure 14.
The PG stripe curves of sub-images, a, b, c, d, of DS1105-1071DF141.
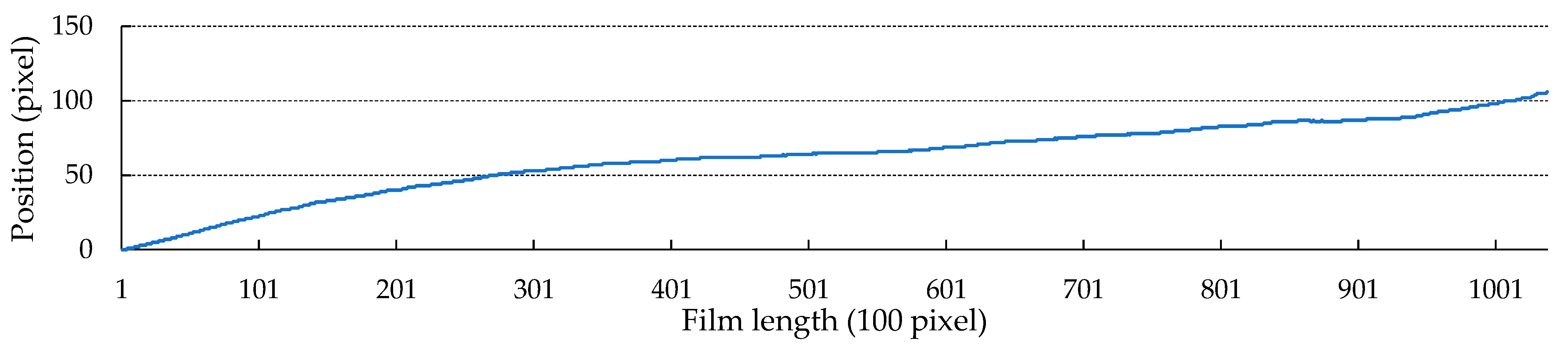
Figure 15.
The PG stripe curve of the stitched panoramic image DS1105-1071DF141.
Figure 15.
The PG stripe curve of the stitched panoramic image DS1105-1071DF141.
Figure 16.
The NCM curve of NIFT under various rotational distortions.
Figure 16.
The NCM curve of NIFT under various rotational distortions.
Table 1.
The details of the KH-4B images and the reference images used in the experiments.
Table 1.
The details of the KH-4B images and the reference images used in the experiments.
| KH-4B Scenes | Reference Image | Distortion |
|---|
| Region | Terrain |
|---|
| USA, Russia, Ethiopia, Burkina Faso, and China’s Beijing, Chongqing, Gansu, and the Qinghai–Tibet plateau | Loess plateau, glacier, plain, hill, high mountain | Google Earth, Bing, and ArcGIS | Temporal disparities (50-year), scale variations (1:5), rotational disparities (0–360 degrees), radiometric differences, and local land cover alterations |
Table 2.
The detailed information of KH images.
Table 2.
The detailed information of KH images.
| Mission Designators | Film Size | Micron Size | File Size |
|---|
| KH-1; KH-2; KH-3 | 70 × 745 mm | 12 Micron (1800 dpi) | 80 MB (4 files) |
| KH-4; KH-4A; KH-4B | 7 Micron (3600 dpi) | 319 MB (4 files) |
Table 3.
The relationship between the layers order of MR and primary orientation.
Table 3.
The relationship between the layers order of MR and primary orientation.
| Primary Orientation | The Order of Layers of MR |
|---|
| 350–15°, 170–195° | {0°, 30°, 60°, 90°, 120°, 150°} |
| 20–45°, 200–225° | {30°, 60°, 90°, 120°, 150°, 0°} |
| 50–75°, 230–255° | {60°, 90°, 120°, 150°, 0°, 30°} |
| 80–105°, 260–285° | {90°, 120°, 150°, 0°, 30°, 60°} |
| 110–135°, 290–315° | {120°, 150°, 0°, 30°, 60°, 90°} |
| 140–165°, 320–345° | {150°, 0°, 30°, 60°, 90°, 120°} |
Table 4.
The details of multi-region Corona images and reference images.
Table 4.
The details of multi-region Corona images and reference images.
| KH-4A/B Image | Reference Image | Distortion |
|---|
| Region | Serial Number | Geomorphic Type | Resolution | Source | Resolution |
|---|
| United States | Vermont state | DS11161030DF009-10 | Forest, Grassland, Lakes | ~1.8 | Google Earth | 2.3 | Land cover change, Radiometric distortion, Low/Repetitive texture, Image noise, Scale distortion, Rotation distortion, Panoramic geometry, Cloud occlusion |
| Arizona state | DS11162161DA012-14 | Plateau, Basin, Plain | ~1.8 | Google Earth | 4.2 |
| Russia | Khanty-Mansi | DS11102201DA033-34 | Plain, Lakes | ~1.8 | Bing | 4.2 |
| China | Beijing | DS11011069DF089-94 | Plain, Mountains | ~1.8 | Google Earth | 4.2 |
| Chongqing | DS11142119DF045-49 | Hills, Mountains | ~1.8 | Google Earth | 2.3 |
| Gansu | DS11162297DA009-10 | Loess Plateau | ~1.8 | Google Earth | 4.2 |
| Qinghai–Tibet Plateau | DS11122265DA091-92 | Glacier, Plateau | ~1.8 | Google Earth | 4.2 |
| Ethiopia | South West Shewa | DS11022203DA071-73 | Plateau | ~1.8 | ArcGIS | 4.2 |
| Burkina Faso | Centre-sub | DS10451058DF045 | Plateau | ~2.75 | ArcGIS | 4.2 |
Table 5.
The RMSE of orientation.
Table 5.
The RMSE of orientation.
| KH-4B Scenes | RMSE (Pixels) |
|---|
| First Stage | Second Stage |
|---|
| DS1101-1069DF089 | a | 3.50 | 1.9 |
| b | 2.1 | 1.2 |
| c | 2.1 | 1.19 |
| d | 2.3 | 1.3 |
| DS1101-1069DF090 | a | 2.88 | 1.9 |
| b | 2 | 1.2 |
| c | 1.9 | 1.3 |
| d | 2.4 | 1.4 |
Table 6.
The 14 parameters of the four sub-images of DS1101-1069DF090.
Table 6.
The 14 parameters of the four sub-images of DS1101-1069DF090.
| Parameter | a | b | c | d |
|---|
| 4,564,318.00 | 4,564,053.000 | 4,564,089.500 | 4,563,850 |
| 473.785004 | 1010.521729 | 552.231567 | 1008.983704 |
| 384,394.15625 | 386,881.375000 | 387,326.562500 | 391,244.68750 |
| −796.56854 | −1383.837524 | −1283.782349 | −909.642029 |
| 169,839.609375 | 170,634.375000 | 170,839.453125 | 169,477.796875 |
| −812.061096 | −605.189026 | −630.709961 | −196.461411 |
| −11.1166419 | −13.7147451 | −16.6276366 | −19.6613908 |
| 0.07700553 | 0.0135791 | −0.02675713 | −0.2566851 |
| 28.2159374 | 13.3082628 | −4.44374614 | −23.0435035 |
| 0.19194086 | 0.35964561 | 0.37299553 | −0.37213609 |
| −11.274399 | −9.7904165 | −9.5870738 | −10.9570732 |
| −0.27398842 | 0.06073353 | 0.15630289 | 0.08623015 |
| P | −0.014932 | 0.017280 | 0.006359 | −0.001736 |
| 0.6025 | 0.6028 | 0.609602 | 0.6029 |
Table 7.
The detailed mosaic error of DS1101-1069DF089 and DS1101-1069DF090.
Table 7.
The detailed mosaic error of DS1101-1069DF089 and DS1101-1069DF090.
| Corona Scenes | Evaluation Metrics | X (Pixel) | Y (Pixel) |
|---|
| DS1101-1069DF089 | a-b | SD | 1.2762 | 1.3553 |
| Max | 3.7658 | 4.3370 |
| Mean | 0.9806 | 1.1052 |
| b-c | SD | 0.5611 | 0.7644 |
| Max | 1.4606 | 1.7897 |
| Mean | 0.4570 | 0.6427 |
| c-d | SD | 0.8033 | 0.8411 |
| Max | 2.8138 | 1.9079 |
| Mean | 0.6324 | 0.6927 |
| DS1101-1069DF090 | a-b | SD | 0.4865 | 0.5811 |
| Max | 1.5006 | 1.5650 |
| Mean | 0.3814 | 0.4690 |
| b-c | SD | 0.4614 | 0.8178 |
| Max | 1.5528 | 1.9974 |
| Mean | 0.3712 | 0.6845 |
| c-d | SD | 0.8547 | 0.5226 |
| Max | 2.4385 | 1.7930 |
| Mean | 0.6790 | 0.4120 |
Table 8.
The orientation accuracy for the four sub-images of DS1101-1069DF089 with/without film deformation adjustment based on PG stripe.
Table 8.
The orientation accuracy for the four sub-images of DS1101-1069DF089 with/without film deformation adjustment based on PG stripe.
| KH-4B Scenes | Without PG | With PG |
|---|
| DS1101-1069DF089 | a | 2.1 | 1.9 |
| b | 1.34 | 1.2 |
| c | 1.29 | 1.19 |
| d | 1.4 | 1.3 |
| DS1101-1069DF090 | a | 2.2 | 1.9 |
| b | 1.3 | 1.2 |
| c | 1.4 | 1.3 |
| d | 1.5 | 1.4 |
Table 9.
The details of the dataset used in feature matching.
Table 9.
The details of the dataset used in feature matching.
| Size (Pixel) | Resolution (m) | Number | Difference |
|---|
| 500 × 200~1400 × 600 | 64~128 | 30 | Radiometric distortion, land cover change, scale/rotation. |
Table 10.
The compared matching results.
Table 10.
The compared matching results.
| NCM | SR |
|---|
| SIFT | LNIFT | RIFT | NIFT | SIFT | LNIFT | RIFT | NIFT |
|---|
| 20 | 108 | 109 | 373 | 6.6 | 3.3 | 53.3 | 100 |
Table 11.
The RMSE of orientation for DS101-1069DF90 of three methods. a, b, c, and d represent the sub-image of DS101-1069DF90.
Table 11.
The RMSE of orientation for DS101-1069DF90 of three methods. a, b, c, and d represent the sub-image of DS101-1069DF90.
| Method | The RMSE (Pixels) |
|---|
| a | b | c | d |
|---|
| 2.6 | 1.3 | 4.2 | - |
| 2.5 | 1.3 | 3.1 | - |
| 1.9 | 1.2 | 1.3 | 1.4 |